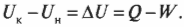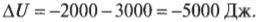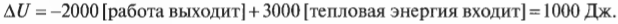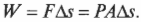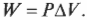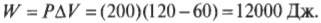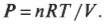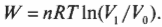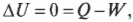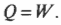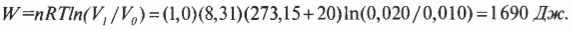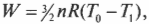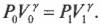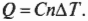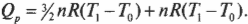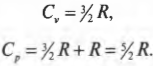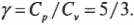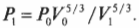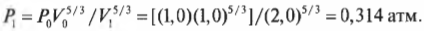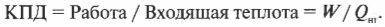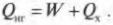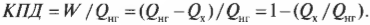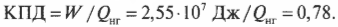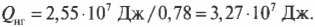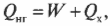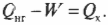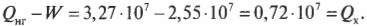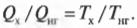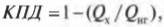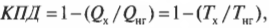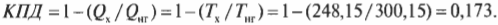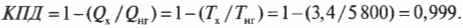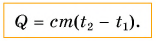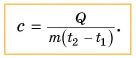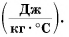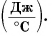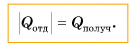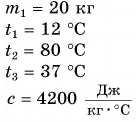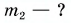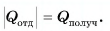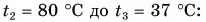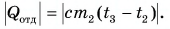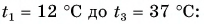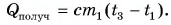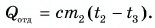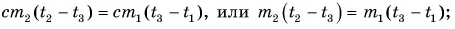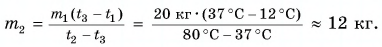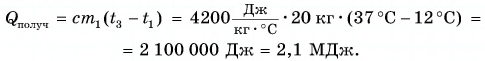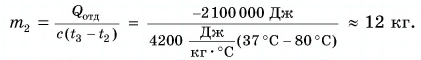Как найти кол-во теплоты, выделяемое при неупругом столкновении двух тел? Известны обе массы и обе скорости
Наталия Дмитриева
Ученик
(98),
закрыт
8 лет назад
ВиталийГорностаев
Мастер
(2365)
10 лет назад
Обозначим скорости тел до столкновения V1 V2
Общая скорость после столкновения U
Закон сохранения импульса m1*V1+m2*V2=U*(m1+m2)
Отсюда U=(m1*V1+m2*V2)/(m1+m2)
Кинетическая энергия до столкновения Ek1=m1*(V1)^2+m2*(V2)^2
Кинетическая энергия после столкновения Ek2=(m1+m2)*(U)^2
Количество теплоты Q=Ek2-Ek1
В этой главе…
- Достигаем теплового равновесия
- Сохраняем тепловую энергию при различных условиях
- Повышаем эффективность тепловых двигателей
- Падаем почти до абсолютного нуля
Каждому, кому когда-либо приходилось работать летом на открытом воздухе, хорошо известны понятия “тепло” и “работа”, связь между которыми изучает термодинамика. В данной главе, наконец-то, встречаются эти два незабвенных понятия, о которых подробно рассказывается в главе 8 (о работе) и в главе 13 (о тепле, теплоте и тепловой энергии). В термодинамике имеется три закона, а точнее начала, которые также важны для термодинамики, как и законы Ньютона для механики. Кроме того, уж в одном отношении они даже превосходят законы Ньютона, а именно в том, что в термодинамике имеется еще и нулевой закон, который чаще называют нулевым началом термодинамики. В этой главе рассказывается о термодинамическом равновесии (нулевое начало), сохранении энергии (первое начало), о тепловых потоках (второе начало) и недостижимости абсолютного нуля (третье начало). Итак, самое время обратиться к термодинамике.
Содержание
- Стремимся к тепловому равновесию: нулевое начало термодинамики
- Сохраняем энергию: первое начало термодинамики
- Применяем закон сохранения энергии
- Изучаем изобарические, изохорические, изотермические и адиабатические процессы
- Постоянное давление: изобарический процесс
- Постоянный объем: изохорический процесс
- Постоянная температура: изотермический процесс
- Постоянная энергия: адиабатический процесс
- Вычисляем удельную теплоемкость
- Передаем тепловую энергию: второе начало термодинамики
- Заставим тепловую энергию работать: тепловые двигатели
- Оцениваем эффективность работы: КПД теплового двигателя
- Как сказал Карно: нельзя все тепло превратить в работу
- Построение двигателя Карно
- Используем формулу Карно
- Охлаждаемся: третье (и абсолютно последнее) начало термодинамики
Стремимся к тепловому равновесию: нулевое начало термодинамики
Основные законы термодинамики начинаются с нулевого начала. Возможно, эта нумерация покажется странной, ведь мало какой набор вещей из повседневной жизни начинается подобным образом (“Будь осторожен на нулевой ступеньке…”), но, знаете ли, физикам нравятся их традиции. Так вот, нулевое начало термодинамики гласит, что два тела находятся в тепловом равновесии, если они могут передавать друг другу теплоту, но не делают этого. (В русскоязычной научной литературе нулевое начало термодинамики называют также общим началом термодинамики. — Примеч. ред.)
Например, если у вас и у воды в плавательном бассейне, в котором вы находитесь, одна и та же температура, то никакое тепло от вас к воде или от воды к вам не передается (хотя такая передача возможна). Ваше тело и бассейн находятся в тепловом равновесии. Однако, если вы прыгнете в бассейн зимой, проломив при этом его ледяную корку, то первое время вряд ли будете в тепловом равновесии с его водой. Впрочем, вы и не захотите этого. (Не пытайтесь проделать этот физический опыт дома!)
Чтобы обнаружить тепловое равновесие (особенно в замерзших бассейнах, куда вы собираетесь прыгнуть), надо использовать термометр. Измерьте с его помощью температуру воды в бассейне, а затем — свою температуру. Если обе температуры совпадают (другими словами, наблюдается тепловое равновесие: ваше — с термометром, а термометра — с водой в бассейне), то в таком случае вы находитесь в тепловом равновесии с водой бассейна.
Использование термометра показывает: два тела, находящиеся в тепловом равновесии с третьим, также находятся в тепловом равновесии друг с другом; вот вам еще одна формулировка нулевого начала.
Кроме всего прочего, нулевое начало содержит идею, что температура — это индикатор теплового равновесия. То, что два тела, упомянутые в нулевом законе, находятся в тепловом равновесии с третьим, дает все нужное дая задания температурной шкалы, например шкалы Кельвина. Ну а с физической точки зрения нулевой закон устанавливает точку отсчета, утверждая, что между двумя телами, имеющими одинаковую температуру, тепловой поток в целом отсутствует.
Сохраняем энергию: первое начало термодинамики
Первое начало термодинамики — это, попросту говоря, закон сохранения энергии. Он утверждает, что энергия никуда не исчезает. Когда системой поглощается или высвобождается тепловая энергия ( Q ), а сама система выполняет над окружающими телами работу ( W ) (или, наоборот, окружающие тела выполняют работу над ней), то внутренняя энергия системы, имевшая начальное значение ( U_н ), становится равной ( U_к ) следующим образом:
В главе 8 немало говорится о сохранении механической энергии. Там показано, что общая механическая энергия (сумма потенциальной и кинетической энергии) сохраняется. Чтобы утверждать такое, надо было работать с системами, где энергия не тратится на нагревание, — например, когда отсутствует трение. Теперь все изменилось. Тепловая энергия, наконец-то, учитывается нами (как вы, вероятно, поняли из рассуждений), и теперь общую энергию системы можно рассматривать с учетом передачи тепловой энергии, проделанной работы и внутренней энергии системы.
На основании комбинации этих трех величин (тепловой энергии, работы и внутренней энергии) определяется общая энергия системы, которая в целом сохраняется. Если передать системе количество тепловой энергии, равное ( Q ), то при отсутствии работы ее количество внутренней энергии, обозначаемое как ( U ), изменится на ( Q ). Система может терять энергию, выполняя работу над окружающими телами, например, когда машина поднимает груз, висящий на конце каната. Так вот, когда система выполняет работу над окружающими телами и никакой тепловой энергии не тратит, ее внутренняя энергия ( U ) изменится на ( W ). Иначе говоря, если учитывать тепловую энергию, то с учетом всех этих трех величин (тепловой энергии, работы и внутренней энергии) общая энергия системы сохраняется.
Польза первого начала термодинамики состоит в том, что оно связывает все три основные величины: тепловую энергию, работу и внутреннюю энергию. Зная две из них, всегда можно определить третью.
Применяем закон сохранения энергии
Величина передаваемой тепловой энергии ( Q ) является положительной или отрицательной, когда система, соответственно, поглощает или высвобождает тепловую энергию. Величина работы ( W ) является положительной или отрицательной, когда работа, соответственно, выполняется системой над окружающими телами или окружающими телами над системой.
Новички часто путаются, пытаясь определить, являются ли значения каждой из величин положительными или отрицательными. Чтобы не запутаться, при работе с первым началом термодинамики рекомендуется исходить из общей идеи сохранения энергии. Допустим, что мотор выполняет над окружающими телами работу в 2000 Дж, высвобождая при этом 3000 Дж тепловой энергии. Насколько меняется его внутренняя энергия? В данном случае известно, что мотор выполняет над окружающими телами работу в 2000 Дж, поэтому ясно, что его внутренняя энергия уменьшается на 2000 Дж. Кроме того, выполняя работу, он еще высвобождает 3000 Дж тепловой энергии, так что внутренняя энергия мотора уменьшается еще на 3000 Дж.
Значения работы и передаваемой тепловой энергии следует считать отрицательными. Тогда в предыдущем примере получим такое изменение внутренней энергии:
Внутренняя энергия системы уменьшается на 5000 Дж, что определенно имеет смысл, ведь система выполняет над окружающими телами работу в 2000 Дж и высвобождает 3000 Дж тепловой энергии. С другой стороны, а что если система, выполняя над окружающими телами работу в 2000 Дж, поглощает 3000 Дж их тепловой энергии? В таком случае получилось бы 2000 Дж входящей и 3000 Дж исходящей энергии. Теперь понятно, какими должны быть знаки:
В данном случае общее изменение внутренней энергии системы равно +1000 Дж. Отрицательное значение работа принимает, когда она выполняется над системой окружающими телами. Например, система поглощает 3000 Дж, в то время как окружающие тела выполняют над ней работу в 4000 Дж. Это значит, что внутренняя энергия системы увеличивается на 3000 Дж + 4000 Дж = 7000 Дж. А если нужно все просчитать, то воспользуйтесь следующей формулой:
а затем обратите внимание, что поскольку окружающие тела выполняют работу над системой, значение ( W ) считается отрицательным. Таким образом, получаем:
Изучаем изобарические, изохорические, изотермические и адиабатические процессы
В этой главе рассматриваются процессы, при анализе которых приходится работать с такими параметрами, как объем, давление, температура и энергия. Причем полученные результаты очень сильно зависят от того, как эти величины меняются. Например, если газ выполняет работу, сохраняя свой объем постоянным, то этот процесс будет отличаться от того, при котором остается постоянным не объем, а давление газа.
В термодинамике обычно рассматривают четыре стандартных режима, которые отличаются постоянством одного из вышеперечисленных параметров (давление, объем, температура и энергия).
Обратите внимание, что изменения в процессах, описанных в последующих разделах, называются квазистатическими, т.е. эти изменения проходят достаточно медленно, позволяя давлению и температуре оставаться одинаковыми в любом месте системы.
Постоянное давление: изобарический процесс
Процесс, в котором давление остается постоянным, называется изобарическим (“барический” означает “относящийся к давлению”). На рис. 15.1 показан цилиндр с поршнем, поднимаемым некоторым количеством газа, когда этот газ нагревается. Объем газа меняется, но утяжеленный поршень сохраняет давление постоянным.
Какую работу выполняет система при расширении газа? Работа равна произведению ( F ) на ( s ), означающих, соответственно, силу и перемещение. Кроме того, сила равна произведению ( P ) на ( A ), означающих, соответственно, давление и площадь. Это значит, что:
Но произведение площади ( A ) и перемещения ( s ) равно изменению объема ( Delta!V ). Таким образом:
Изобарический процесс можно показать в виде графика (как на рис. 15.2), на котором видно, что объем меняется, в то время как давление остается постоянным. Так как ( W=PDelta!V ), то работа — это площадь, ограниченная графиком.
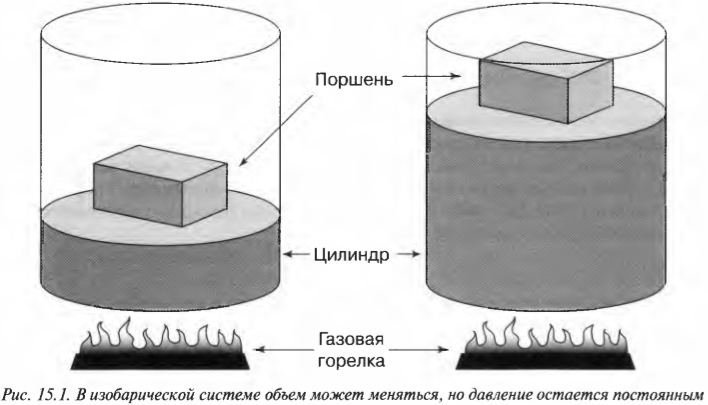
Допустим, имеется 60 м3 идеального газа под давлением в 200 Па (см. главу 2), который нагревается до тех пор, пока он не расширится до объема в 120 м3 (( PV= nRT ), где ( n ), ( R ) и ( Т ) означают, соответственно, количество молей, универсальную газовую постоянную (8,31) и температуру; см. главу 14). Какую работу выполняет газ? Все, что вам нужно, — это подставить в формулу численные значения:
Расширяясь при постоянном давлении, газ выполняет работу в 12000 Дж.
Постоянный объем: изохорический процесс
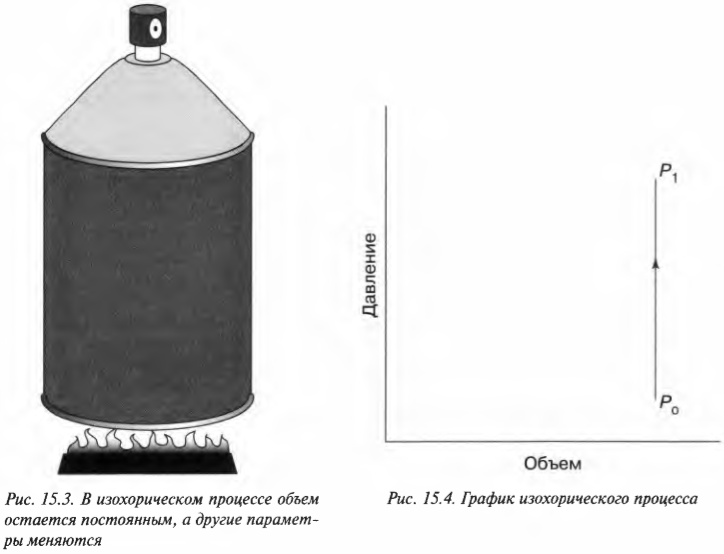
А что если давление в системе не постоянно? В конце концов, не так уж и часто попадаются устройства с утяжеленным поршнем, как на рис. 15.1. Чаще всего приходится иметь дело с простым замкнутым сосудом, как на рис. 15.3, где показан баллончик с дезодорантом, кем-то неосторожно брошенный в огонь. В этом случае объем остается постоянным, а такой процесс называется изохорическим. По мере того как газ внутри баллончика нагревается, его давление возрастает, но объем остается постоянным (если, конечно, баллончик не взорвется).
Какая работа выполняется с баллончиком распылителя? Посмотрите на график (рис. 15.4). В данном случае объем постоянный, поэтому ( Fs ) (произведение силы и перемещения) равно нулю. Никакая работа не выполняется — площадь под графиком равна нулю.
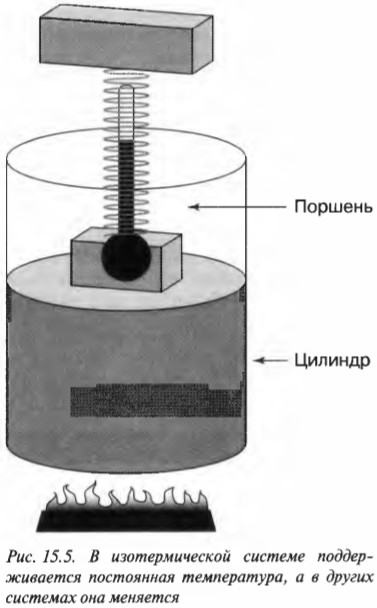
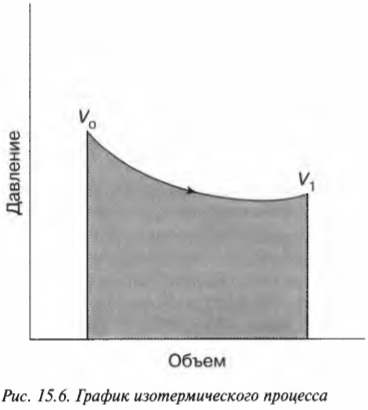
Постоянная температура: изотермический процесс
В изотермическом процессе температура остается постоянной, в то время как другие величины меняются. Посмотрите, какой замечательный аппарат показан на рис. 15.5. Этот аппарат специально предназначен для того, чтобы сохранять температуру газа постоянной, причем даже при подъеме поршня. При добавлении к системе (или отводе от системы) тепловой энергии поршень медленно поднимается (или медленно опускается) таким образом, чтобы произведение давления и объема сохранялось постоянным. Так как ( PV= nRT ) (см. главу 14), то температура также остается постоянной.
Какая работа выполняется при изменении объема? Поскольку ( PV= nRT ), то получается такое отношение между ( P ) и ( V ):
Эту формулу иллюстрирует график, показанный на рис. 15.6.
Выполненную работу “показывает” область, лежащая под графиком. Но какова же площадь этой области? Выполненная работа определяется следующей формулой, где ( ln ) — натуральный логарифм, ( R ) — газовая постоянная (8,31), ( V_1 ) и ( V_0 ) означают, соответственно, конечный и начальный объем:
Так как при изотермическом процессе температура остается постоянной, а внутренняя энергия идеального газа равна ( (3/2)nRT ) (см. главу 14), то эта энергия не меняется. Таким образом:
другими словами:
Итак, что произойдет, если цилиндр, показанный на рис. 15.5, погрузить в горячую ванну? В аппарат должна перейти тепловая энергия ( Q ), а поскольку температура газа остается постоянной, вся эта тепловая энергия должна превратиться в работу, выполненную системой. Скажем, к примеру, у вас имеется моль гелия при температуре 20°С, и, забавы ради, вы решили увеличить его объем с ( V_0 ) = 0,010 м3 до ( V_1 ) = 0,020 м3. Какую работу выполнит газ при расширении? Все, что вам нужно, — это подставить в формулу численные значения:
Работа, выполняемая газом, равна 1690 Дж. Изменение его внутренней энергии равно 0 Дж, как всегда при изотермическом процессе. А так как ( Q=W ), то добавляемая к газу тепловая энергия также равна 1690 Дж.
Постоянная энергия: адиабатический процесс
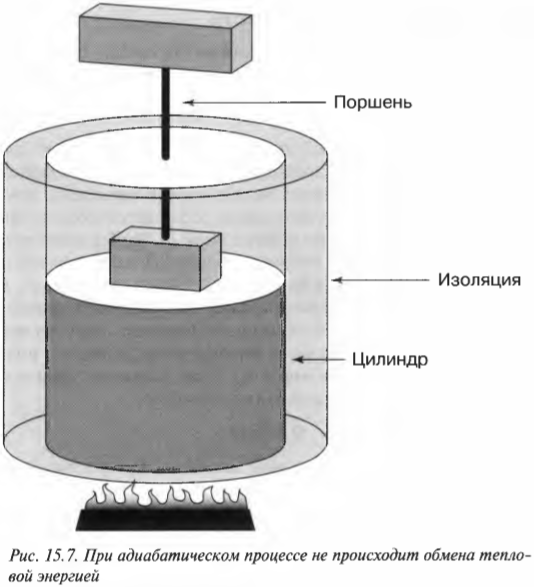
При адиабатическом процессе общая тепловая энергия системы остается постоянной. Посмотрите на рис. 15.7, где показан цилиндр, окруженный изоляционным материалом. Тепловая энергия из системы никуда не уходит, поэтому если происходит изменение, то оно является адиабатическим.
Вычисляя работу, выполняемую при адиабатическом процессе, вы можете сказать, что ( Q ) = 0, таким образом:
Так как внутренняя энергия ( U ) идеального газа равна ( (3/2)nRT ) (см. главу 14), то выполняется работа:
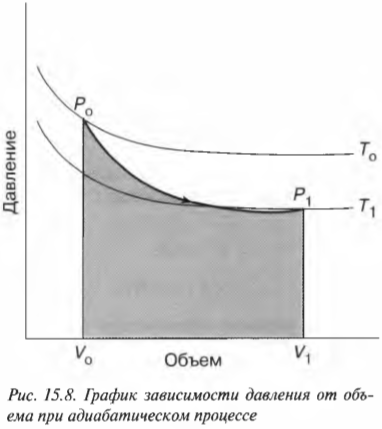
где ( T_0 ) и ( T_1 ) означают, соответственно, начальную и конечную температуру. Таким образом, если газ выполняет работу, то это происходит благодаря изменению температуры — при падении температуры газ выполняет работу над окружающими телами. На рис. 15.8 показан график зависимости давления от объема при адиабатическом процессе. Адиабатическая кривая, показанная на этом рисунке, так называемая адиабата, отличается от изотермических кривых, так называемых изотерм. Работа, выполненная, когда общая тепловая энергия системы постоянна, — это область под адиабатой (см. рис. 15.8).
Вычисляем удельную теплоемкость
Начальные значения давления и объема можно так связать с их конечными значениями по следующей формуле:
Что такое ( gamma )? Это отношение ( C_p/C_v ) двух удельных теплоемкостей идеального газа: в числителе — теплоемкость при постоянном давлении ( C_p ), а в знаменателе — теплоемкость при постоянном объеме ( C_v ). Удельной теплоемкостью называется отношение тепловой энергии, полученной телом единичной массы, к соответствующему приращению его температуры; подробнее об этом можно узнать в главе 13. Чтобы вычислить удельную теплоемкость, надо найти количество тепловой энергии ( Q ), необходимой для изменения температуры тела единичной массы на величину ( Delta T ), т.е. ( c=Q/mDelta T ), где ( c ), ( m ) и ( Delta T ) означают, соответственно, удельную теплоемкость, массу и изменение температуры. Впрочем, сейчас удобнее использовать молярную удельную теплоемкость, которая определяется как и удельная, но только рассчитывается не на единицу массу, а на один моль. Она обозначается символом ( C ) и измеряется в Дж/(моль·К). Итак, молярная удельная теплоемкость используется вместе с количеством молей ( n ), а не массой ( m ):
Как найти ( C )? Надо вычислить две разные величины: ( C_mathrm{p} ) (при постоянном давлении) и ( C_mathrm{v} ) (при постоянном объеме). Согласно первому началу термодинамики (см. предыдущий раздел этой главы), ( Q=Delta U+W ). Поэтому достаточно только выразить ( Delta U ) через ( T ). Выполняемая работа ( W ) равна ( PDelta!V ), тогда при постоянном объеме ( W ) = 0. А изменение внутренней энергии идеального газа равно ( (3/2)nRDelta T ) (см. главу 14), поэтому ( Q ) при постоянном объеме выражается следующей формулой:
При постоянном давлении работа ( W ) равна ( PDelta!V ). А поскольку ( PV= nRT ), то ( W=P(V_1-V_0)=nR(T_1-T_0) ). Поэтому ( Q ) при постоянном давлении выражается следующей формулой:
Каким образом можно получить из всего этого значения молярных удельных теплоемкостей? Как уже нам известно, ( Q=CnDelta T ), поэтому ( C=Q/nDelta T ). Деля предыдущие две формулы на ( nDelta T ), получаем:
Теперь вы имеете молярные удельные теплоемкости идеального газа. Нужное вам отношение ( gamma ) равно отношению этих двух формул:
Связать давление и объем в любых двух точках адиабаты (см. предыдущий раздел об адиабатическом процессе) можно таким образом:
Например, если сначала 1 л газа находился под давлением 1 атм, а после адиабатического изменения (когда обмена тепловой энергией нет), объем газа стал 2 л, то каким должно быть новое давление ( P_1 )? Путем простой алгебраической операции деления на ( V_1^{5/3} ) оставляем в левой части равенства только ( P_1 ) и получаем:
Подставив в эту формулу численные значения, получим:
Итак, новое давление должно быть равно 0,314 атмосферы.
Передаем тепловую энергию: второе начало термодинамики
Формально говоря, второе начало термодинамики гласит, что тепловая энергия естественно переходит из тела с более высокой температурой в тело с более низкой температурой, но не в обратном направлении.
Это начало, конечно же, появилось в результате простых наблюдений: приходилось ли вам когда-либо видеть, чтобы тело само становилось холоднее окружающих его тел, если только другое тело не проделало над ним определенной работы? Путем определенной работы можно заставить теплоту переходить из тела, когда естественно ожидать перехода тепловой энергии в тело (вспомните холодильники или кондиционеры), но такое явление само по себе не происходит.
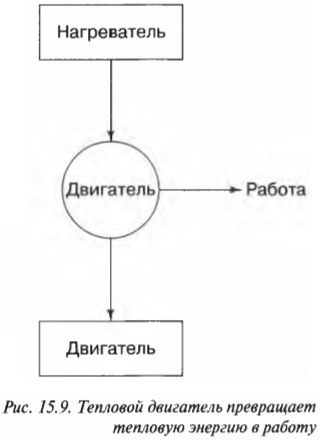
Заставим тепловую энергию работать: тепловые двигатели
Имеется много способов заставить тепловую энергию работать. Возможно, у вас имеется, например, паровая машина с котлом и поршнями или атомный реактор, производящий перегретый пар, который может вращать турбину. Двигатели, выполняющие работу благодаря источнику тепловой энергии, называются тепловыми. Как они это делают, можно увидеть на рис. 15.9. Тепловая энергия идет от нагревателя к двигателю, который выполняет работу, а неизрасходованная тепловая энергия отправляется в холодильник. Им может быть, например, окружающий воздух или наполненный водой радиатор. Если температура холодильника меньше температуры нагревателя, то тепловой двигатель может работать — хотя бы теоретически.
Оцениваем эффективность работы: КПД теплового двигателя
Тепловая энергия, подаваемая нагревателем, обозначается как ( Q_{нг} ), а отправляемая в холодильник (см. предыдущий раздел) — как ( Q_{mathrm{x}} ). Путем некоторых вычислений можно найти коэффициент полезного действия (КПД) теплового двигателя. Он равен отношению работы ( W ), выполняемой двигателем, к входящей тепловой энергии — иными словами, это та доля входящей тепловой энергии, которую двигатель превращает в работу:
Когда вся входящая тепловая энергия превращается в работу, КПД равен 1. Если никакая входящая тепловая энергия не превращается в работу, КПД равен 0. Часто КПД выражается в виде процентов, поэтому только что названные значения можно представить как 100% и 0%. Поскольку общая энергия сохраняется, то тепловая энергия, входящая в двигатель, должна быть равна сумме выполняемой работы и тепловой энергии, отправляемой в холодильник, то есть:
Это значит, что для записи КПД достаточно использовать ( Q_{нг} ) и ( Q_{mathrm{x}} ):
Допустим, что имеется тепловой двигатель с КПД, равным 78%. Этот двигатель производит работу величиной 2,55·107 Дж. Сколько тепловой энергии он использует, а сколько выбрасывает? Известно, что ( W ) = 2,55·107 Дж и
Это значит, что:
Количество входящей тепловой энергии равно 3,27·107 Дж. А сколько тепловой энергии ( Q_{mathrm{x}} ) остается неизрасходованной и отправляется в холодильник? Как известно:
поэтому:
Подставив в эту формулу численные значения, получим:
Количество тепловой энергии, отправляемое в холодильник, равно 0,72·107 Дж.
Как сказал Карно: нельзя все тепло превратить в работу
Зная работу и КПД теплового двигателя, можно вычислить количество входящей и исходящей тепловой энергии (тут нам, конечно, поможет закон сохранения энергии, связывающий друг с другом работу, входящую и исходящую тепловую энергию; см. главу 8). А как насчет создания тепловых двигателей со 100%-ным КПД? С точки зрения производительности было бы прекрасно превращать в работу всю тепловую энергию, какая поступает в тепловой двигатель, но это невозможно. Кроме того, в реально работающих тепловых двигателях неизбежны определенные потери, например, из-за трения поршней в паровом двигателе. В XIX веке эту проблему изучал один инженер, которого звали Сади Карно, и он пришел к выводу: в сущности, лучшее, что можно сделать, — это попытаться изобрести двигатель, не имеющий таких потерь.
А если в двигателе нет потерь, то система будет возвращаться в то же состояние, что и перед началом процесса. Такой процесс называется обратимым. Например, если тепловой двигатель тратит энергию на преодоление трения, то обратимым процесс назвать нельзя, так как он не заканчивается в том же состоянии, в каком был сначала. При каких условиях работы тепловой двигатель будет иметь самый высокий КПД? Когда работа двигателя обратима (т.е. в системе нет потерь). Сегодня физики называют это принципом Карно. Итак, принцип Карно гласит, что ни у одного необратимого двигателя не будет такого же высокого КПД, как у обратимого, а все обратимые двигатели, работающие в промежутке между одинаковыми максимальными и одинаковыми минимальными температурами, имеют один и тот же КПД.
Построение двигателя Карно
Карно предложил свою идею двигателя — двигателя Карно. Этот двигатель должен работать обратимо, что не может быть ни в одном реально работающем двигателе, поэтому он представляет собой нечто идеальное. В двигателе Карно тепловая энергия идет от нагревателя, имеющего постоянную температуру ( T_{нг} ). А отработанная тепловая энергия уходит в холодильник, имеющий постоянную температуру ( T_{х} ). Поскольку температуры нагревателя и холодильника никогда не меняются, то можно сказать, что отношение подаваемой и отводимой тепловой энергии равно отношению их температур (в кельвинах):
А так как КПД теплового двигателя вычисляется по следующей формуле:
то получается такая формула для вычисления КПД двигателя Карно:
где температура выражается в кельвинах.
В этой формуле показан максимально возможный КПД теплового двигателя. И лучшего результата достичь нельзя. А как гласит третье начало термодинамики (в последнем разделе этой главы), абсолютного нуля достичь нельзя, т.е. ( T_{х} ) никогда не будет равна нулю, следовательно, невозможно получить тепловой двигатель со 100%-ным КПД.
Используем формулу Карно
Формулу максимально возможного КПД (см. предыдущий раздел) использовать довольно легко. Предположим, сделано потрясающее новое изобретение: машина Карно, в которой самолет совершает работу, причем земная поверхность играет роль нагревателя (с температурой примерно 27°С), а воздух на высоте 10000 м — роль холодильника (с температурой примерно -27°С). Какой максимальный КПД такой машины? Преобразуем значения температуры в кельвины и подставив их в формулу машины Карно:
Итак, КПД такой машины Карно равен всего 17,3%. Результат, скажем, не очень. А теперь представим, что в качестве нагревателя используется поверхность Солнца (примерно 5800 К), а в качестве холодильника — межзвездное пространство (примерно 3,4 К), совсем как в научно-фантастических рассказах. Тогда совсем другое дело:
Итак, в таких научно-фантастических условиях для машины Карно можно получить КПД, равный 99,9% и близкий к теоретически максимальному значению.
Охлаждаемся: третье (и абсолютно последнее) начало термодинамики
Третье начало термодинамики достаточно просто формулируется: нельзя достичь абсолютного нуля с помощью любого процесса, состоящего из конечного числа этапов, к нему можно лишь бесконечно приближаться. Иначе говоря, никогда нельзя достичь абсолютного нуля. Каждое действие по понижению температуры физического тела до абсолютного нуля может немного приблизить к цели, но достигнуть ее нельзя, если не выполнить бесконечного числа действий, что невозможно.
Странные явления вблизи абсолютного нуля
Хотя до абсолютного нуля нельзя добраться с помощью какого-либо известного конечного процесса, но к нему можно приблизиться. Причем, имея очень дорогое оборудование, вблизи абсолютного нуля можно столкнуться с множеством странных физических явлений и фактов. Один мой приятель изучает поведение жидкого гелия при очень низких температурах. Например, гелий становится таким эксцентричным, что может самостоятельно выбраться из любого сосуда, в котором он находится. За открытие и исследования этого явления сверхтекучести гелия и некоторые другие наблюдения кое-кто получил Нобелевскую премию. Везет же людям!
(Сверхтекучесть жидкого гелия-4 была открыта в 1938 году П. Л. Капицей, за что он был удостоен Нобелевской премии по физике за 1978 год. Теория сверхтекучего гелия-Н была разработана Л. Д. Ландау, за что он был удостоен Нобелевской премии по физике за 1962 год. — Примеч. ред.)
Глава 15. Тепловая энергия и работа: начала термодинамики
3.1 (62.86%) 7 votes
Содержание:
- Определение и формула количества теплоты
- Формула расчета теплоты при изменении температуры
- Формула количества теплоты при фазовых переходах
- Единицы измерения количества теплоты
- Примеры решения задач
Определение и формула количества теплоты
Внутреннюю энергию термодинамической системы можно изменить двумя способами:
- совершая над системой работу,
- при помощи теплового взаимодействия.
Передача тепла телу не связана с совершением над телом макроскопической работы. В данном случае изменение внутренней энергии вызвано тем,
что отдельные молекулы тела с большей температурой совершают работу над некоторыми молекулами тела, которое имеет меньшую температуру. В этом
случае тепловое взаимодействие реализуется за счет теплопроводности. Передача энергии также возможна при помощи излучения. Система
микроскопических процессов (относящихся не ко всему телу, а к отдельным молекулам) называется теплопередачей. Количество энергии,
которое передается от одного тела к другому в результате теплопередачи, определяется количеством теплоты, которое предано от одного тела другому.
Определение
Теплотой называют энергию, которая получается (или отдается) телом в процессе теплообмена с окружающими телами (средой).
Обозначается теплота, обычно буквой Q.
Это одна из основных величин в термодинамике. Теплота включена в математические выражения первого и второго начал термодинамики.
Говорят, что теплота – это энергия в форме молекулярного движения.
Теплота может сообщаться системе (телу), а может забираться от нее. Считают, что если тепло сообщается системе, то оно положительно.
Формула расчета теплоты при изменении температуры
Элементарное количество теплоты обозначим как $delta Q$. Обратим внимание,
что элемент тепла, которое получает (отдает) система при малом изменении ее состояния не является полным дифференциалом.
Причина этого состоит в том, что теплота является функцией процесса изменения состояния системы.
Элементарное количество тепла, которое сообщается системе, и температура при этом меняется от Tдо T+dT, равно:
$$delta Q=C d T(1)$$
где C – теплоемкость тела. Если рассматриваемое тело однородно, то формулу (1) для количества теплоты можно представить как:
$$delta Q=c m d T=nu c_{mu} d T(2)$$
где $c=frac{C}{m}$ – удельная теплоемкость тела, m – масса тела,
$c_{mu}=c cdot mu$ – молярная теплоемкость,
$mu$ – молярная масса вещества,
$nu=frac{m}{mu}$ – число молей вещества.
Если тело однородно, а теплоемкость считают независимой от температуры, то количество теплоты
($Delta Q$), которое получает тело при увеличении его температуры на величину
$Delta t = t_2 – t_1$ можно вычислить как:
$$Delta Q=c m Delta t(3)$$
где t2, t1 температуры тела до нагрева и после. Обратите внимание, что температуры при нахождении разности
($Delta t$) в расчетах можно подставлять как в градусах Цельсия, так и в кельвинах.
Формула количества теплоты при фазовых переходах
Переход от одной фазы вещества в другую сопровождается поглощением или выделением некоторого количества теплоты,
которая носит название теплоты фазового перехода.
Так, для перевода элемента вещества из состояния твердого тела в жидкость ему следует сообщить количество теплоты
($delta Q$) равное:
$$delta Q=lambda d m$$
где $lambda$ – удельная теплота плавления, dm – элемент массы тела.
При этом следует учесть, что тело должно иметь температуру, равную температуре плавления рассматриваемого вещества.
При кристаллизации происходит выделение тепла равного (4).
Количество теплоты (теплота испарения), которое необходимо для перевода жидкости в пар можно найти как:
$$delta Q=r d m$$
где r – удельная теплота испарения. При конденсации пара теплота выделяется. Теплота испарения равна теплоте конденсации одинаковых масс вещества.
Единицы измерения количества теплоты
Основной единицей измерения количества теплоты в системе СИ является: [Q]=Дж
Внесистемная единица теплоты, которая часто встречается в технических расчетах. [Q]=кал (калория). 1 кал=4,1868 Дж.
Примеры решения задач
Пример
Задание. Какие объемы воды следует смешать, чтобы получить 200 л воды при температуре t=40С, если температура
одной массы воды t1=10С, второй массы воды t2=60С?
Решение. Запишем уравнение теплового баланса в виде:
$$Q=Q_{1}+Q_{2}(1.1)$$
где Q=cmt – количество теплоты приготовленной после смешивания воды; Q1=cm1t1 –
количество теплоты части воды температурой t1 и массой m1;
Q2=cm2t2– количество теплоты части воды температурой t2 и массой m2.
Из уравнения (1.1) следует:
$$
begin{array}{l}
mathrm{cmt}=mathrm{cm}_{1} t_{1}+mathrm{~cm}_{2} t_{2} rightarrow mathrm{mt}=mathrm{m}_{1} t_{1}+mathrm{~m}_{2} t_{2} rightarrow \
rightarrow rho mathrm{Vt}=rho V_{1} t_{1}+rho mathrm{V}_{2} t_{2} rightarrow mathrm{Vt}=V_{1} t_{1}+V_{2} t_{2}(1.2)
end{array}
$$
При объединении холодной (V1) и горячей (V2) частей воды в единый объем (V) можно принять то, что:
$$$
V=V_{1}+V_{2}(1.3)
$$$
Так, мы получаем систему уравнений:
$$
left{begin{array}{c}
V t=V_{1} t_{1}+V_{2} t_{2} \
V=V_{1}+V_{2}
end{array}right.
$$
Решив ее получим:
$$
begin{array}{l}
V_{1}=frac{left(t_{2}-tright)}{t_{2}-t_{1}} V \
V_{2}=frac{left(t-t_{1}right)}{t_{2}-t_{1}} V
end{array}
$$
Проведем вычисления (это можно сделать, не переходя в систему СИ):
$$
begin{array}{l}
V_{1}=frac{(60-40)}{60-10} 200=80 text { (л) } \
V_{2}=frac{(40-10)}{60-10} 200=120 text { (л) }
end{array}
$$
Ответ. V1=80 л, V2=120 л.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
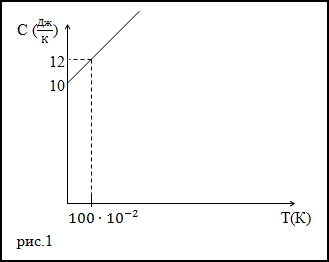
Задание. Теплоемкость тела изменяется по линейному закону (рис.1) в зависимости от абсолютной температуры в
рассматриваемом интервале $T_{1} leq T leq T_{2}$ .
Какое количество теплоты получает тело, если T1=300 К, T2=400 К.
Решение. Исследуя график функции теплоемкости (C(T)) (рис.1) запишем его аналитическое выражение, оно получится:
$C(T)=10+2 cdot 10^{-2} T$ (Дж/К)
Основой для решения задачи послужит формула для количества теплоты в виде:
$$delta Q=C d T(2.2)$$
Подставим полученное выражение для теплоемкости (2.1) в формулу (2.2) поведем интегрирование в заданном интервале температур:
$$
begin{array}{c}
Delta Q=int_{300}^{400}left(10+2 cdot 10^{-2} Tright) d T=left.left(10 cdot T+10^{-2} T^{2}right)right|_{300} ^{400}= \
=left(10 cdot 400+10^{-2} cdot(400)^{2}right)-left(10 cdot 300+10^{-2} cdot(300)^{2}right)=1700left(mathrm{~A}^{*}right)
end{array}
$$
Ответ. $Delta Q$=1700 Дж
Читать дальше: Формула напряженности магнитного поля.
Расчет количества теплоты при нагревании и охлаждении:
Вы уже знаете, что изменить внутреннюю энергию тела можно передачей ему количества теплоты. Как связано изменение внутренней энергии тела, т. е. количество теплоты, с характеристиками самого тела?
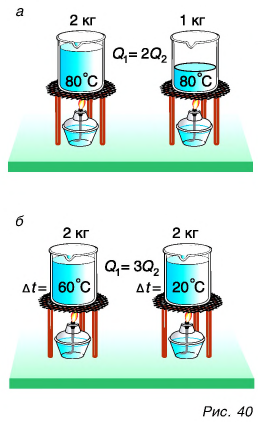
Внутренняя энергия тела есть суммарная энергия всех его частиц. Значит, если массу данного тела увеличить в два или три раза, то и количество теплоты, необходимое для его нагревания на одно и то же число градусов, увеличится в два или три раза. Например, на нагревание двух килограммов воды от 20 °C до 80 °C потребуется в два раза больше теплоты, чем на нагревание одного килограмма воды (рис. 40, а).
Очевидно также, что для нагревания воды на
Из этих рассуждений следует подтвержденный опытами вывод. Количество теплоты, необходимое для нагревания тела, прямо пропорционально его массе и изменению температуры.
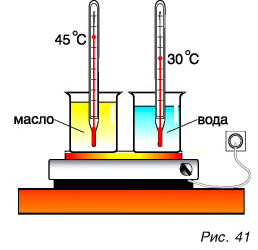
А зависит ли количество теплоты, идущее на нагревание, от рода вещества, которое нагревается?
Для ответа на этот вопрос проведем опыт. В два одинаковых стакана нальем по 150 г подсолнечного масла и воды. Поместим в них термометры и поставим на нагреватель (рис. 41).
Получив за одинаковое время от нагревателя равное с водой количество теплоты, масло нагрелось больше, чем вода. Значит, для изменения температуры масла на одну и ту же величину требуется меньше теплоты, чем для изменения температуры такой же массы воды.
Поэтому для всех веществ вводят специальную величину — удельную теплоемкость вещества. Эту величину обозначают буквой с (от лат. capacite — емкость, вместимость). Теперь мы можем записать строгую формулу для количества теплоты, необходимого для нагревания:
Выразим из этой формулы с:
Удельная теплоемкость есть физическая величина, численно равная количеству теплоты, которое необходимо передать 1 кг данного вещества, чтобы изменить его температуру на 1 °C. Удельная теплоемкость измеряется в джоулях на килограмм-градус Цельсия
Для любознательных:
Часто формулу 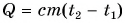
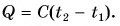
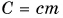
В таблице 1 представлены значения удельной теплоемкости различных веществ (в различных состояниях). Как следует из этой таблицы, среди жидкостей максимальное значение удельной теплоемкости имеет вода: для нагревания 1 кг воды на 1 °C требуется 4200 Дж теплоты — это почти в 2,5 раза больше, чем для нагревания 1 кг подсолнечного масла, и в 35 раз больше, чем для нагревания 1 кг ртути.
Формула 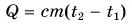
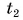
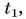
В заключение заметим, что при теплообмене двух или нескольких тел абсолютное значение количества теплоты, которое отдано более нагретым телом (телами), равно количеству теплоты, которое получено более холодным телом (телами):
Это равенство называется уравнением теплового баланса и выражает, по сути, закон сохранения энергии. Оно справедливо при отсутствии потерь теплоты.
Таблица 1. Удельная теплоемкость некоторых веществ
Главные выводы:
- Количество теплоты, необходимое для нагревания тела (выделившееся при охлаждении), прямо пропорционально его массе, изменению температуры тела и зависит от вещества тела.
- Удельная теплоемкость вещества численно равна количеству теплоты, которое надо передать 1 кг данного вещества, чтобы изменить его температуру на 1 °C.
- При теплообмене количество теплоты, отданное более горячим телом, равно по модулю количеству теплоты, полученному более холодным телом, если нет потерь теплоты.
- Заказать решение задач по физике
Пример решения задачи:
Для купания ребенка в ванночку влили холодную воду массой 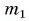
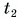
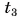
Дано:
Решение
По закону сохранения энергии
Отдавала теплоту горячая вода, изменяя свою температуру от
Холодная вода получила эту теплоту и нагрелась от
Так как нас интересует только модуль 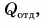
Тогда
При решении мы пренебрегали потерями теплоты на нагревание ванночки, окружающего воздуха и т. д.
Возможен и другой вариант решения.
Рассчитаем сначала количество теплоты, которое было получено холодной водой:
Полагая, что эта теплота отдана горячей водой, запишем: 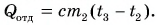
Ответ:
- Удельная теплота сгорания топлива
- Плавление и кристаллизация в физике
- Испарение жидкостей в физике
- Поверхностное натяжение жидкости
- Излучение тепла в физике
- Виды излучений в физике
- Инфракрасные излучения
- Количество теплоты в физике
О тепловой энергии простым языком!
Опубликовано 13 Окт 2013
Рубрика: Теплотехника | 117 комментариев

…энергию вакуума и еще существующую только в теории – темную энергию. В этой статье, первой в рубрике «Теплотехника», я попытаюсь на простом и доступном языке, используя практический пример, рассказать о важнейшем виде энергии в жизни людей — о тепловой энергии и о рождающей ее во времени тепловой мощности.
Несколько слов для понимания места теплотехники, как раздела науки о получении, передаче и применении тепловой энергии. Современная теплотехника выделилась из общей термодинамики, которая в свою очередь является одним из разделов физики. Термодинамика – это дословно «теплый» плюс «силовой». Таким образом, термодинамика – это наука об «изменении температуры» системы.
Воздействие на систему извне, при котором изменяется ее внутренняя энергия, может являться результатом теплообмена. Тепловая энергия, которая приобретается или теряется системой в результате такого взаимодействия с окружающей средой, называется количеством теплоты и измеряется в системе СИ в Джоулях.
Если вы не инженер-теплотехник, и ежедневно не занимаетесь теплотехническими вопросами, то вам, столкнувшись с ними, иногда без опыта бывает очень трудно быстро в них разобраться. Трудно без наличия опыта представить даже размерность искомых значений количества теплоты и тепловой мощности. Сколько Джоулей энергии необходимо чтобы нагреть 1000 метров кубических воздуха от температуры -37˚С до +18˚С?.. Какая нужна мощность источника тепла, чтобы сделать это за 1 час?.. На эти не самые сложные вопросы способны сегодня ответить «сходу» далеко не все инженеры. Иногда специалисты даже помнят формулы, но применить их на практике могут лишь единицы!
Прочитав до конца эту статью, вы сможете легко решать реальные производственные и бытовые задачи, связанные с нагревом и охлаждением различных материалов. Понимание физической сути процессов теплопередачи и знание простых основных формул – это главные блоки в фундаменте знаний по теплотехнике!
Количество теплоты при различных физических процессах.
Большинство известных веществ могут при разных температуре и давлении находиться в твердом, жидком, газообразном или плазменном состояниях. Переход из одного агрегатного состояния в другое происходит при постоянной температуре (при условии, что не меняются давление и другие параметры окружающей среды) и сопровождается поглощением или выделением тепловой энергии. Не смотря на то, что во Вселенной 99% вещества находится в состоянии плазмы, мы в этой статье не будем рассматривать это агрегатное состояние.
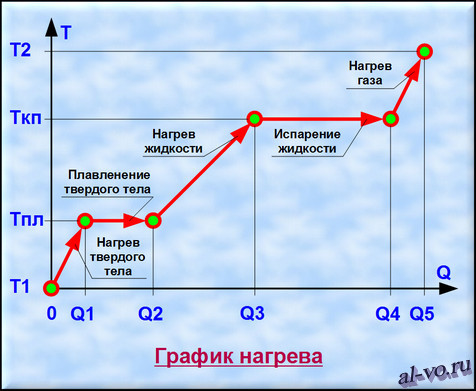
Рассмотрим график, представленный на рисунке. На нем изображена зависимость температуры вещества Т от количества теплоты Q, подведенного к некой закрытой системе, содержащей определенную массу какого-то конкретного вещества.
1. Твердое тело, имеющее температуру T1, нагреваем до температуры Tпл, затрачивая на этот процесс количество теплоты равное Q1.
2. Далее начинается процесс плавления, который происходит при постоянной температуре Тпл (температуре плавления). Для расплавления всей массы твердого тела необходимо затратить тепловой энергии в количестве Q2— Q1.
3. Далее жидкость, получившаяся в результате плавления твердого тела, нагреваем до температуры кипения (газообразования) Ткп, затрачивая на это количество теплоты равное Q3–Q2.
4. Теперь при неизменной температуре кипения Ткп жидкость кипит и испаряется, превращаясь в газ. Для перехода всей массы жидкости в газ необходимо затратить тепловую энергию в количестве Q4–Q3.
5. На последнем этапе происходит нагрев газа от температуры Ткп до некоторой температуры Т2. При этом затраты количества теплоты составят Q5–Q4. (Если нагреем газ до температуры ионизации, то газ превратится в плазму.)
Таким образом, нагревая исходное твердое тело от температуры Т1 до температуры Т2 мы затратили тепловую энергию в количестве Q5, переводя вещество через три агрегатных состояния.
Двигаясь в обратном направлении, мы отведем от вещества то же количество тепла Q5, пройдя этапы конденсации, кристаллизации и остывания от температуры Т2 до температуры Т1. Разумеется, мы рассматриваем замкнутую систему без потерь энергии во внешнюю среду.
Заметим, что возможен переход из твердого состояния в газообразное состояние, минуя жидкую фазу. Такой процесс именуется возгонкой, а обратный ему процесс – десублимацией.
Итак, уяснили, что процессы переходов между агрегатными состояниями вещества характеризуются потреблением энергии при неизменной температуре. При нагреве вещества, находящегося в одном неизменном агрегатном состоянии, повышается температура и также расходуется тепловая энергия.
Главные формулы теплопередачи.
Формулы очень просты.
Количество теплоты Q в Дж рассчитывается по формулам:
1. Со стороны потребления тепла, то есть со стороны нагрузки:
1.1. При нагревании (охлаждении):
Q=m*c*(Т2–Т1)
Здесь и далее:
m – масса вещества в кг
с – удельная теплоемкость вещества в Дж/(кг*К)
1.2. При плавлении (замерзании):
Q=m*λ
λ – удельная теплота плавления и кристаллизации вещества в Дж/кг
1.3. При кипении, испарении (конденсации):
Q=m*r
r – удельная теплота газообразования и конденсации вещества в Дж/кг
2. Со стороны производства тепла, то есть со стороны источника:
2.1. При сгорании топлива:
Q=m*q
q – удельная теплота сгорания топлива в Дж/кг
2.2. При превращении электроэнергии в тепловую энергию (закон Джоуля — Ленца):
Q=t*I*U=t*R*I^2=(t/R)*U^2
t – время в с
I – действующее значение тока в А
U – действующее значение напряжения в В
R – сопротивление нагрузки в Ом
Делаем вывод – количество теплоты прямо пропорционально массе вещества при всех фазовых превращениях и при нагреве дополнительно прямо пропорционально разности температур. Коэффициенты пропорциональности (c, λ, r, q) для каждого вещества имеют свои значения и определены опытным путем (берутся из справочников).
Тепловая мощность N в Вт – это количество теплоты переданное системе за определенное время:
N=Q/t
Чем быстрее мы хотим нагреть тело до определенной температуры, тем большей мощности должен быть источник тепловой энергии – все логично.
В жизни бывает часто необходимо сделать быстрый оценочный расчет, чтобы понять – имеет ли смысл продолжать изучение темы, делая проект и развернутые точные трудоемкие расчеты. Сделав за несколько минут расчет даже с точностью ±30%, можно принять важное управленческое решение, которое будет в 100 раз более дешевым и в 1000 раз более оперативным и в итоге в 100000 раз более эффективным, чем выполнение точного расчета в течение недели, а то и месяца, группой дорогостоящих специалистов…
Условия задачи:
В помещение цеха подготовки металлопроката размерами 24м х 15м х 7м завозим со склада на улице металлопрокат в количестве 3т. На металлопрокате есть лед общей массой 20кг. На улице -37˚С. Какое количество теплоты необходимо, чтобы нагреть металл до +18˚С; нагреть лед, растопить его и нагреть воду до +18˚С; нагреть весь объем воздуха в помещении, если предположить, что до этого отопление было полностью отключено? Какую мощность должна иметь система отопления, если все вышесказанное необходимо выполнить за 1час? (Очень жесткие и почти не реальные условия – особенно касающиеся воздуха!)
Расчет выполним в программе MS Excel или в программе OOo Calc.
С цветовым форматированием ячеек и шрифтов ознакомьтесь на странице «О блоге».
Исходные данные:
1. Названия веществ пишем:
в ячейку D3: Сталь
в ячейку E3: Лед
в ячейку F3: Лед/вода
в ячейку G3: Вода
в ячейку G3: Воздух
2. Названия процессов заносим:
в ячейки D4, E4, G4, G4: нагрев
в ячейку F4: таяние
3. Удельную теплоемкость веществ c в Дж/(кг*К) пишем для стали, льда, воды и воздуха соответственно
в ячейку D5: 460
в ячейку E5: 2110
в ячейку G5: 4190
в ячейку H5: 1005
4. Удельную теплоту плавления льда λ в Дж/кг вписываем
в ячейку F6: 330000
5. Массу веществ m в кг вписываем соответственно для стали и льда
в ячейку D7: 3000
в ячейку E7: 20
Так как при превращении льда в воду масса не изменяется, то
в ячейках F7 и G7: =E7=20
Массу воздуха находим произведением объема помещения на удельный вес
в ячейке H7: =24*15*7*1,23=3100
6. Время процессов t в мин пишем только один раз для стали
в ячейку D8: 60
Значения времени для нагрева льда, его плавления и нагрева получившейся воды рассчитываются из условия, что все эти три процесса должны уложиться в сумме за такое же время, какое отведено на нагрев металла. Считываем соответственно
в ячейке E8: =E12/(($E$12+$F$12+$G$12)/D8)=9,7
в ячейке F8: =F12/(($E$12+$F$12+$G$12)/D8)=41,0
в ячейке G8: =G12/(($E$12+$F$12+$G$12)/D8)=9,4
Воздух также должен прогреться за это же самое отведенное время, читаем
в ячейке H8: =D8=60,0
7. Начальную температуру всех веществ T1 в ˚C заносим
в ячейку D9: -37
в ячейку E9: -37
в ячейку F9: 0
в ячейку G9: 0
в ячейку H9: -37
8. Конечную температуру всех веществ T2 в ˚C заносим
в ячейку D10: 18
в ячейку E10: 0
в ячейку F10: 0
в ячейку G10: 18
в ячейку H10: 18
Думаю, вопросов по п.7 и п.8 быть недолжно.
Результаты расчетов:
9. Количество теплоты Q в КДж, необходимое для каждого из процессов рассчитываем
для нагрева стали в ячейке D12: =D7*D5*(D10-D9)/1000=75900
для нагрева льда в ячейке E12: =E7*E5*(E10-E9)/1000= 1561
для плавления льда в ячейке F12: =F7*F6/1000= 6600
для нагрева воды в ячейке G12: =G7*G5*(G10-G9)/1000= 1508
для нагрева воздуха в ячейке H12: =H7*H5*(H10-H9)/1000= 171330
Общее количество необходимой для всех процессов тепловой энергии считываем
в объединенной ячейке D13E13F13G13H13: =СУММ(D12:H12) = 256900
В ячейках D14, E14, F14, G14, H14, и объединенной ячейке D15E15F15G15H15 количество теплоты приведено в дугой единице измерения – в ГКал (в гигакалориях).
10. Тепловая мощность N в КВт, необходимая для каждого из процессов рассчитывается
для нагрева стали в ячейке D16: =D12/(D8*60)=21,083
для нагрева льда в ячейке E16: =E12/(E8*60)= 2,686
для плавления льда в ячейке F16: =F12/(F8*60)= 2,686
для нагрева воды в ячейке G16: =G12/(G8*60)= 2,686
для нагрева воздуха в ячейке H16: =H12/(H8*60)= 47,592
Суммарная тепловая мощность необходимая для выполнения всех процессов за время t рассчитывается
в объединенной ячейке D17E17F17G17H17: =D13/(D8*60) = 71,361
В ячейках D18, E18, F18, G18, H18, и объединенной ячейке D19E19F19G19H19 тепловая мощность приведена в дугой единице измерения – в Гкал/час.
На этом расчет в Excel завершен.
Выводы:
Обратите внимание, что для нагрева воздуха необходимо более чем в два раза больше затратить энергии, чем для нагрева такой же массы стали.
При нагреве воды затраты энергии в два раза больше, чем при нагреве льда. Процесс плавления многократно больше потребляет энергии, чем процесс нагрева (при небольшой разности температур).
Нагрев воды в десять раз затрачивает больше тепловой энергии, чем нагрев стали и в четыре раза больше, чем нагрев воздуха.
Мы вспомнили понятия «количество теплоты» и «тепловая мощность», рассмотрели фундаментальные формулы теплопередачи, разобрали практический пример. Надеюсь, что мой язык был прост и понятен.
Ссылка на скачивание файла: raschet-teplovoy-moshchnosti (xls 19,5KB).
Другие статьи автора блога
На главную