Как найти энергию заряженного конденсатора задачи

Энергия конденсатора .

Конденсатор это устройство, способное накапливать электрический заряд.

Энергия заряженного конденсатора:

(W=dfrac{q^2}{2C} )

(q ) – заряд конденсатора

(C )- емкость конденсатора

---

Заряд, емкость и напряжение на конденсаторе связаны следующим соотношением:

( q=CU )

Подставим в его в числитель дроби:

(W=dfrac{q^2}{2C} = dfrac{C^2U^2}{2C}=dfrac{CU^2}{2} )

Значит энергию конденсатора можно вычислить по формуле:

( W= dfrac{CU^2}{2} )

---

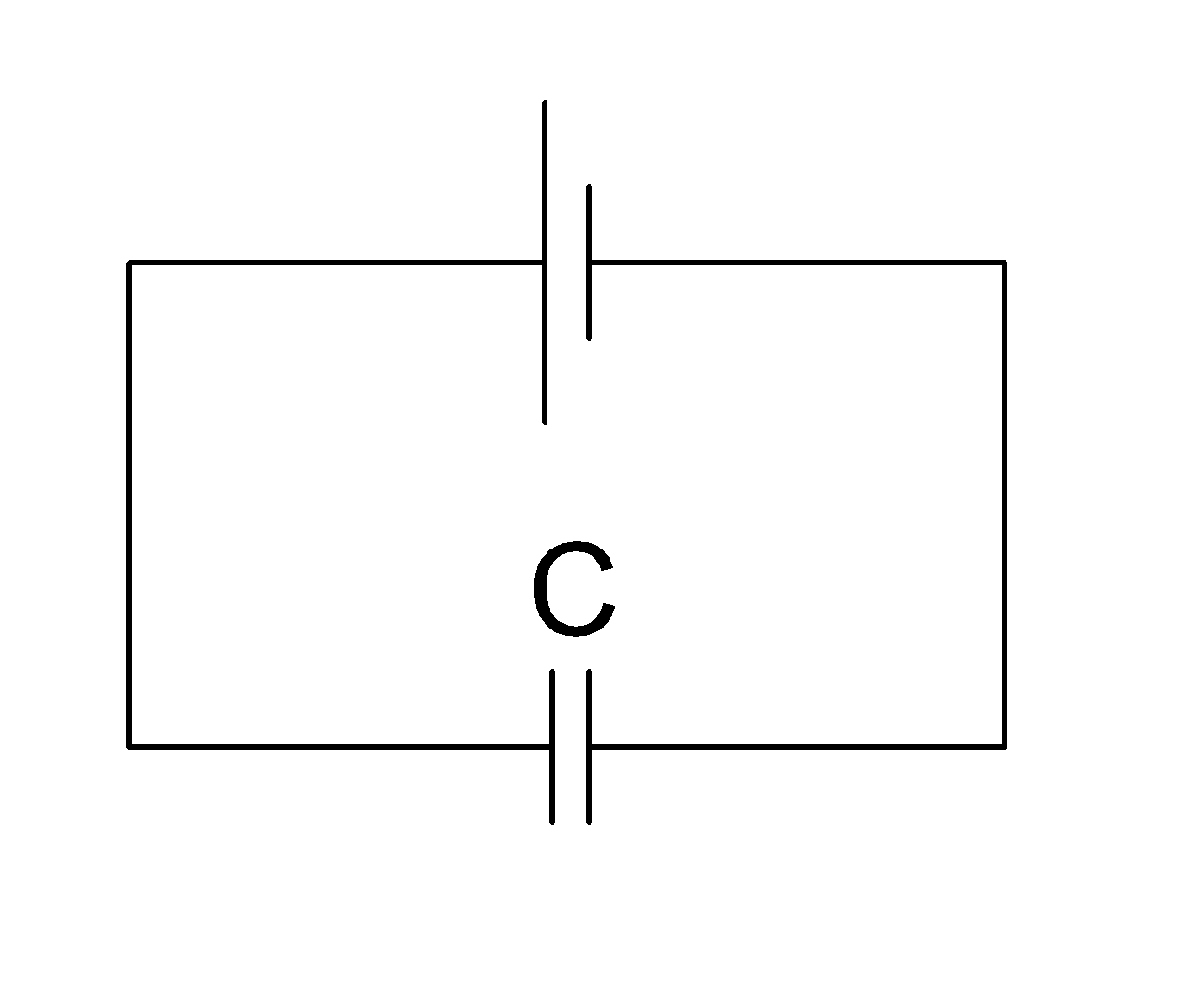
На этой схеме конденсатор подключен к источнику питания(батарейке):

---

Задача 1.

Найти энергию

конденсатора, если его заряд (q=0,01 Кл ), а

емкость (C=0,0001 Ф . )

Показать ответ
Показать решение
Видеорешение

---

Задача 2.

Какова энергия конденсатора емкостью ( C=0,4 мкФ ), если его заряд ( q=800 мкКл . )

Показать ответ
Показать решение
Видеорешение

---

Задача 3.

Какова энергия конденсатора емкостью ( C=0,5 нФ ), если его заряд ( q=2 мкКл . )

Показать ответ
Показать решение
Видеорешение

---

Задача 4.

Энергия конденсатора емкостью ( C=64 мкФ ), равна 0,5 Джоуля.

Найдите заряд этого конденсатора .

Показать ответ
Показать решение
Видеорешение

---

Задача 5.

Энергия конденсатора емкостью ( C=500 пкФ ), равна 10 микроджоулей.

Найдите заряд этого конденсатора .

Дать ответ в микрокулонах.

Показать ответ
Показать решение
Видеорешение

---

Задача 6.

Энергия заряженного конденсатора (E=10^{-9} Дж ), а его емкость ( C=98 нФ . )

Найдите заряд этого конденсатора .

Дать ответ в нанокулонах.

Показать ответ
Показать решение
Видеорешение

---

Задача 7.

Напряжение на контактах конденсатора составляет 250 Вольт.

Какова энергия этого конденсатора, если его емкость (C=80 мкФ ? )

Показать ответ
Показать решение
Видеорешение

---

Задача 8.

Конденсатор, емкостью (C=5 мкФ ), подключен к источнику тока с напряжением (U= 12 В . )

Найдите энергию этого конденсатора .

Дать ответ в микроджоулях.

Показать ответ
Показать решение
Видеорешение

---

Конденсатор – деталька, без которой не обойдется работа ни одного электронного прибора. Но прежде чем разбираться с основами электроники, нужно научиться решать физические задачи на конденсатор и электроемкость. Именно этим мы и займемся в сегодняшней статье, посвященной подробному разбору решений задач.

Подписывайтесь на наш телеграм: теперь помимо полезных и интересных материалов там можно найти скидки и акции на любые работы.

Задачи на конденсаторы и электроемкость с решением

Если вы не знаете, как решать задачи с конденсаторами, сначала посмотрите теорию и вспомните про памятку по решению задач по физике и полезные формулы.

Задача №1 на электроемкость батареи конденсаторов

Условие

Плоский конденсатор емкостью 16 мкФ разрезают на 4 равные части вдоль плоскостей, перпендикулярных обкладкам. Полученные конденсаторы соединяют последовательно. Чему равна емкость батaреи конденсаторов?

Решение

Из условия следует, что площадь получившихся конденсаторов в 4 раза меньше, чем у исходного. Зная это, можно найти емкость каждого полученного конденсатора:

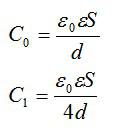
Соединяя 4 таких конденсатора последовательно, получаем:

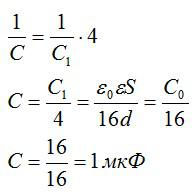
Ответ: 1 мкФ.

Задача №2 на энергию плоского конденсатора

Условие

Плоский конденсатор заполнили диэлектриком с диэлектрической проницаемостью, равной 2. Энергия конденсатора без диэлектрика равна 20 мкДж. Чему равна энергия конденсатора после заполнения диэлектриком? Считать, что источник питания отключен от конденсатора.

Решение

Энергия конденсатора до заполнения диэлектриком равна:

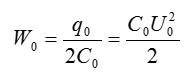
После заполнения емкость конденсатора изменится:

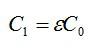
Энергия конденсатора после заполнения:

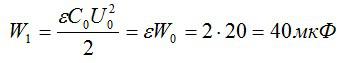
Ответ: 40 мкФ.

Задача №3 на последовательное и параллельное соединение конденсаторов

Условие

На рисунке изображена батарея конденсаторов. Каждый конденсатор имеет емкость 1 мкФ. Найдите емкость батареи.

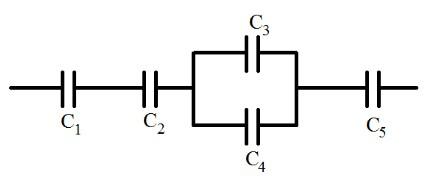
Решение

Как видим, часть конденсаторов соединена параллельно, а часть последовательно. Это типичный пример смешанного соединения конденсаторов. Алгоритм решения задач при смешанном соединении конденсаторов сводится к тому, чтобы упростить схему и свести все только к параллельному или последовательному соединению.

Конденсаторы 3 и 4 соединены параллельно. Складывая их емкость, получаем в итоге последовательное соединение четырех конденсаторов: 1, 2, 5 и 3-4. Для параллельного соединения:

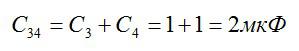
Для последовательного соединения:

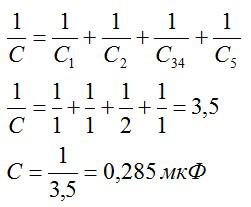
Ответ: 0,285 мкФ.

Задача №4 на пролет частицы в конденсаторе

Заряд конденсатора равен 0,3 нКл, а емкость – 10 пФ. Какую скорость приобретет электрон, пролетая в конденсаторе от одной пластины к другой. Начальная скорость электрона равна нулю. 

Решение

По закону сохранения энергии, разность кинетических энергий электрона в начале и в конце пути будет равна работе поля по его перемещению. По условию, начальная кинетическая энергия электрона равна 0. Запишем:

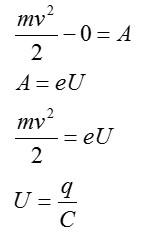
С учетом этого, получим:

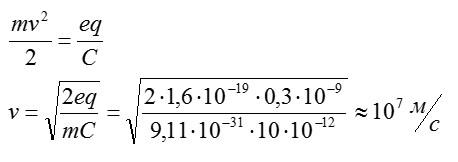
Ответ: 10^7 м/с.

Задача №5 на вычисление энергии электрического поля конденсатора

Условие

Конденсатор подключен к источнику постоянного напряжения U=1 кВ. Емкость конденсатора равна 5 пФ. Как изменяться заряд на обкладках конденсатора и его энергия, если расстояние между обкладками уменьшить в три раза.

Решение

Заряд конденсатора равен:

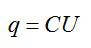
Изменение заряда будет равно:

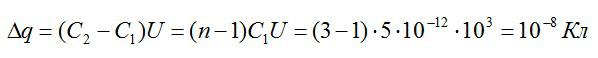
Изменение энергии:

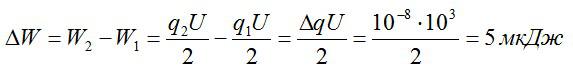
Ответ: 5 мкДж.

Вопросы на тему «Конденсатор и электроемкость»

Вопрос 1. Что такое конденсатор?

Ответ. Конденсатор – устройство, имеющее два полюса и предназначенное для накопления электрического заряда.

Простейший тип конденсатора – плоский воздушный конденсатор. Он состоит из двух пластин (обкладок), имеющих разные заряды и разделенных воздухом. В зависимости от диэлектрика, разделяющего обкладки, разделяют:

• воздушные конденсаторы;
• бумажные конденсаторы;
• слюдяные и другие конденсаторы.

Основная роль конденсатора в электронных приборах – накапливать заряд, а потом передавать его дальше в цепь.

Вопрос 2. Что такое электроемкость?

Ответ. Электроемкость – скалярная физическая величина, характеризующая способность накапливать электрический заряд. В системе СИ измеряется в Фарадах.

Вопрос 3. Какие есть способы соединения конденсаторов?

Ответ. Конденсаторы можно соединить последовательно и параллельно.

При параллельном соединении емкость цепи равна сумме емкостей отдельных конденсаторов.

При последовательном соединении величина, обратная общей емкости, равна сумме обратных емкостей каждого конденсатора.

Вопрос 4. Что такое колебательный контур?

Ответ. Это простейшая электрическая цепь, состоящая из конденсатора, катушки индуктивности и источника тока. В колебательном контуре происходят свободные электромагнитные колебания: энергия конденсатора переходит в энергию катушки, и наоборот. 

Вопрос 5. Что происходит при отключении источника питания, к которому подключен конденсатор в цепи?

Ответ. В этот момент конденсатор начинает разряжаться,  отдавая накопленный заряд другим элементам цепи.

Мы не понасылшке знаем, что от сложных задач на конденсаторы мозги буквально плавятся. Если ваш мозг устал от постоянного решения задач по физике и других заданий, обращайтесь в профессиональный образовательный сервис за консультацией и поддержкой в любое время. У нас есть решение для ваших проблем с учебой!

Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»

Подробности

Обновлено 13.08.2018 18:26

Просмотров: 1351

«Физика – 10 класс»

«Электроёмкость» — последняя тема раздела «Электростатика». При решении задач на эту тему могут потребоваться все сведения, полученные при изучении электростатики: закон сохранения электрического заряда, понятия напряжённости поля и потенциала, сведения о поведении проводников в электростатическом поле, о напряжённости поля в диэлектриках, о законе сохранения энергии применительно к электростатическим явлениям. Основной формулой при решении задач на электроёмкость является формула (14.22).

Задача 1.

Электроёмкость конденсатора, подключённого к источнику постоянного напряжения U = 1000 В, равна C₁ = 5 пФ. Расстояние между его обкладками уменьшили в n = 3 раза. Определите изменение заряда на обкладках конденсатора и энергии электрического поля.

Р е ш е н и е.

Согласно формуле (14.22) заряд конденсатора q = CU. Отсюда изменение заряда Δq — (С₂ – C)U = (nC₁ – C₁)U = (п — 1)С₁U = 10^-8 Кл.

Изменение энергии электрического поля

Задача 2.

Заряд конденсатора q = 3 • 10^-8 Кл. Ёмкость конденсатора С = 10 пФ. Определите скорость, которую приобретает электрон, пролетая в конденсаторе путь от одной пластины к другой. Начальная скорость электрона равна нулю. Удельный заряд электрона

Р е ш е н и е.

Начальная кинетическая энергия электрона равна нулю, а конечная равна Применим закон сохранения энергии где А — работа электрического поля конденсатора:

Следовательно,

Окончательно

Задача 3.

Четыре конденсатора ёмкостями С₁ = С₂ = = 1 мкФ, С₃ = 3 мкФ, С₄ = 2 мкФ соединены, как показано на рисунке 14.46. К точкам А и В подводится напряжение U = 140 В. Определите заряд q1 и напряжение U1, на каждом из конденсаторов.

Р е ш е н и е.

Для определения заряда и напряжения прежде всего найдём ёмкость батареи конденсаторов. Эквивалентная ёмкость второго и третьего конденсаторов С_2,3 = С₂ + С₃, а эквивалентную ёмкость всей батареи конденсаторов, представляющей собой три последовательно соединённых конденсатора ёмкостями С₁, С_2,3, С₄, найдём из соотношения

1/Cэкв = 1 /С₁ + 1/С_2,3 + 1 /С₄, Сэкв = (4/7) • 10^-6 Ф.

Заряды на этих конденсаторах одинаковы:

q₁ = q_2,3 = q₄ = Сэкв = 8 • 10^-5 Кл.

Следовательно, заряд первого конденсатора q₁ = 8 • 10^-5 Кл, а разность потенциалов между его обкладками, или напряжение, U₁ = q₁/С₁ = 80 В.

Для четвёртого конденсатора аналогично имеем q₄ = 8 • 10^-5 Кл, U₄ = q₄/C₄ = 40 В.

Найдём напряжение на втором и третьем конденсаторах: U₂ = U₃ = q_2,3/C_2,3 = 20 В.

Таким образом, на втором конденсаторе заряд q₂ = C₂U₂ = 2 • 10-5 Кл, а на третьем конденсаторе q₃ = C₃U₃ = 6 • 10^-5 Кл. Отметим, что q_2,3 = q₂ + g₃.

Задача 4.

Определите эквивалентную электрическую ёмкость в цепи, изображённой на рисунке (14.47 а), если ёмкости конденсаторов известны.

Р е ш е н и е.

Часто при решении задач, в которых требуется определить эквивалентную электрическую ёмкость, соединение конденсаторов не очевидно. В этом случае если удаётся определить точки цепи, в которых потенциалы равны, то можно соединить эти точки или исключить конденсаторы, присоединённые к этим точкам, так как они не могут накапливать заряд (Δφ = 0) и, следовательно, не играют роли при распределении зарядов.

В приведённой на рисунке (14.47, а) схеме нет очевидного параллельного или последовательного соединения конденсаторов, так как в общем случае φ_A ≠ φ_B в и к конденсаторам С1 и С2 приложены разные напряжения. Однако заметим, что в силу симметрии и равенства ёмкостей соответствующих конденсаторов потенциалы точек А и В равны. Следовательно, можно, например, соединить точки А и В. Схема преобразуется к виду, изображённому на рисунке (14.47, б). Тогда конденсаторы С1, так же как и конденсаторы С2, будут соединены параллельно и С_экв определим по формуле 1/С_экв = 1/2С₁ + 1/2С₂, откуда

Можно также просто не учитывать присутствие в схеме конденсатора СЗ, так как заряд на нём равен нулю. Тогда схема преобразуется к виду, изображённому на рисунке (14.47, в). Конденсаторы С1 и С2 соединены последовательно, следовательно,

Эквивалентные конденсаторы с С’_экв соединены параллельно, так что окончательно получим такое же выражение для эквивалентной ёмкости:

Задача 5.

Энергия плоского воздушного конденсатора W₁ = 2 • 10^-7 Дж. Определите энергию конденсатора после заполнения его диэлектриком с диэлектрической проницаемостью ε = 2, если:

1) конденсатор отключён от источника питания;

2) конденсатор подключён к источнику питания.

Р е ш е н и е.

1) Так как конденсатор отключён от источника питания, то его заряд q₀ остаётся постоянным. Энергия конденсатора до заполнения его диэлектриком после заполнения где С₂ = εС₁.

Тогда

Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Электростатика – Физика, учебник для 10 класса – Класс!ная физика

Что такое электродинамика —
Электрический заряд и элементарные частицы. Закон сохранения заряд —
Закон Кулона. Единица электрического заряда —
Примеры решения задач по теме «Закон Кулона» —
Близкодействие и действие на расстоянии —
Электрическое поле —
Напряжённость электрического поля. Силовые линии —
Поле точечного заряда и заряженного шара. Принцип суперпозиции полей —
Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» —
Проводники в электростатическом поле —
Диэлектрики в электростатическом поле —
Потенциальная энергия заряженного тела в однородном электростатическом поле —
Потенциал электростатического поля и разность потенциалов —
Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности —
Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» —
Электроёмкость. Единицы электроёмкости. Конденсатор —
Энергия заряженного конденсатора. Применение конденсаторов —
Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»

Главная
→
Примеры решения задач ТОЭ
→
Расчет электрической цепи постоянного тока с конденсаторами

Расчет электрической цепи постоянного тока с конденсаторами

Расчет электрической цепи постоянного тока с конденсаторами

Основные положения и соотношения

1. Общее выражение емкости конденсатора

C= Q U .

2. Емкость плоского конденсатора

C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d ,

здесь

S — поверхность каждой пластины конденсатора;

d — расстояние между ними;

ε_a = ε_r·ε₀ — абсолютная диэлектрическая проницаемость среды;

ε_r — диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);

ε 0 = 1 4π⋅ с 2 ⋅ 10 −7 ≈8,85418782⋅ 10 −12    Ф м  – электрическая постоянная.

3. При параллельном соединении конденсаторов С₁, С₂, …, С_n эквивалентная емкость равна

C= C 1 + C 2 +…+ C n = ∑ k=1 n C k .

4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:

C= C 1 ⋅ C 2 C 1 + C 2 ,

а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:

U 1 =U⋅ C 2 C 1 + C 2 ;    U 2 =U⋅ C 1 C 1 + C 2 .

5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)

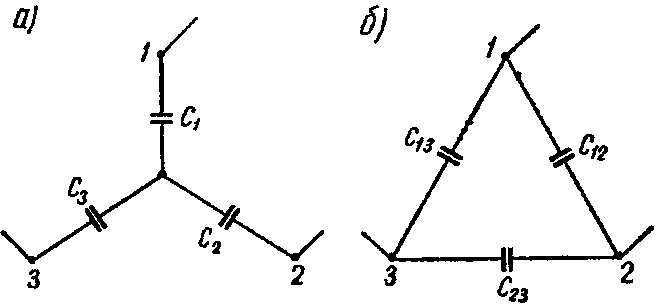
Рис. 0

осуществляется по формулам:

Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ;   C 13 = C 1 ⋅ C 3 ΣC ;   C 23 = C 2 ⋅ C 3 ΣC , где          ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .

6. Энергия электростатического поля конденсатора:

W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .

7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:

1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:

ΣQ=Σ Q ′ .

2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:

∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k .

Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.

Решение задач на расчет электрической цепи постоянного тока с конденсаторами

Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).

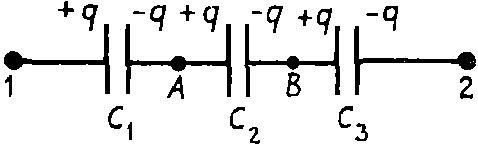
Рис. 1

Решение

На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U₁₂, то на левую пластину конденсатора С₁ перейдет заряд +q, на правую пластину конденсатора С₃ заряд –q.

Вследствие электризации через влияние правая пластина конденсатора С₁ будет иметь заряд –q, а так как пластины конденсаторов С₁ и С₂ соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C₂ будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.

Найти эквивалентную емкость — это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.

Разность потенциалов U₁₂ = φ₁ — φ₂ складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов

U 12 = φ 1 − φ 2 =( φ 1 − φ A )+( φ A − φ B )+( φ B − φ 2 )= U 1A + U AB + U B2 .

Воспользовавшись формулой напряжения на конденсаторе

U= q C ,

запишем

q C = q C 1 + q C 2 + q C 3 .

Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов

1 C = 1 C 1 + 1 C 2 + 1 C 3 .

В общем случае эквивалентная емкость при последовательном соединении конденсаторов

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.

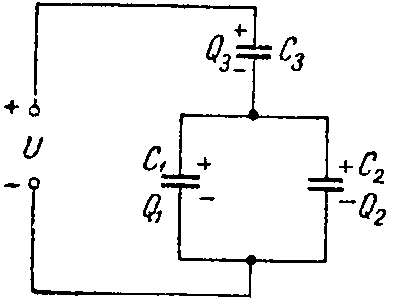
Рис. 2

Емкости конденсаторов: C₁ =50 мкФ; C₂ =150 мкФ; C₃ =300 мкФ.

Решение

Эквивалентная емкость конденсаторов C₁ и C₂, соединенных параллельно

C₁₂ = C₁ + C₂ = 200 мкФ,

эквивалентная емкость всей цепи равна

C= C 12 ⋅ C 3 C 12 + C 3 = 200⋅300 500 =120  мкФ.

Заряд на эквивалентной емкости

Q = C·U = 120·10^–6·240 = 288·10^–4 Кл.

Той же величине равен заряд Q₃ на конденсаторе C₃, т.е. Q₃ = Q = 288·10^–4 Кл; напряжение на этом конденсаторе

U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96  В.

Напряжение на конденсаторах C₁ и C₂ равно

U₁ = U₂ = U — U₃ = 240 — 96 = 144 В.

их заряды имеют следующие значения

Q₁ = C₁·U₁ = 50·10^–6·144 = 72·10^–4 Кл;

Q₂ = C₂·U₂ = 150·10^–6·144 = 216·10^–4 Кл.

Энергии электростатического поля конденсаторов равны

W 1 = Q 1 ⋅ U 1 2 = 72⋅ 10 −4 ⋅144 2 ≈0,52  Дж; W 2 = Q 2 ⋅ U 2 2 = 216⋅ 10 −4 ⋅144 2 ≈1,56  Дж; W 3 = Q 3 ⋅ U 3 2 = 288⋅ 10 −4 ⋅96 2 ≈1,38  Дж.

Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см², имеет диэлектрик, состоящий из слюды (ε_r1 = 6) толщиною d₁ = 0,3 мм и стекла (ε_r2 = 7) толщиною d₂ =0,4 мм.

Пробивные напряженности слюды и стекла соответственно равны E₁ = 77 кВ/мм, E₂ = 36 кВ/мм.

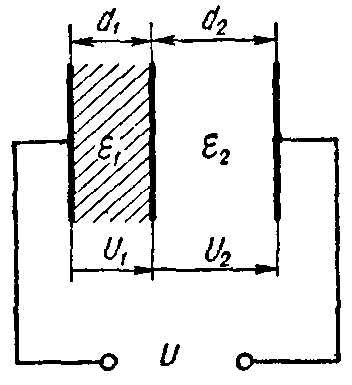
Рис. 3

Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.

Решение

Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов

C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .

Подставляя сюда числовые значения, предварительно заменив ε_a1 = ε_r1·ε₀ и ε_a2 = ε_r2·ε₀, получим

C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12   Ф.

Обозначим общее напряжение, подключаемое к слоистому конденсатору, через U_пр, при этом заряд конденсатора будет равен

Q = C·U_пр.

Напряжения на каждом слое будут равны

U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .

Напряженности электростатического поля в каждом слое

E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .

Здесь U’_np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U”_np — общее напряжение, при котором происходит пробой второго слоя.

Из последнего выражения находим

U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5  кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0  кВ.

Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное

27,0 кВ / 2 = 13,5 кВ.

Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d₁ = 1 см друг от друга. Площадь обкладок S = 50 см². Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.

Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d₂ = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.

Решение

Энергия заряженного плоского конденсатора равна

W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,

где С₁ — емкость до раздвижения обкладок.

Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения

Q = C₂·U₂,

где C₂ — емкость конденсатора после раздвижения обкладок, следует, что, так как C₂ = ε₀·S/d₂ стало меньше в 10 раз (d₂ увеличилось в 10 раз), то напряжение на конденсаторе U₂ увеличилось в 10 раз, т. е. U₂ = 10U.

Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d₂ будет больше первоначальной

W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .

Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.

Таким образом, надо совершить работу, равную

W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7   Дж.

Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.

Даны: C₁ = 30 мкФ; C₂ = 20 мкФ; r₁ = 100 Ом. r₂ = 400 Ом. r₃ = 600 Ом, U = 20 В.

Решение

Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям

U 1 = C 2 C 1 + C 2 ⋅U= 20⋅ 10 −6 30⋅ 10 −6 +20⋅ 10 −6 ⋅20=8  В; U 2 =U− U 1 =20−8=12  В.

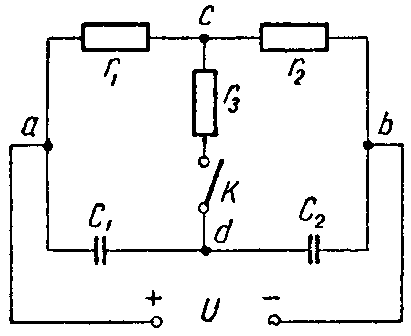
Рис. 4

Ключ К замкнут. Через сопротивления r₁ и r₂ протекает ток

I= U r 1 + r 2 = 20 500 =0,04  А,

а через сопротивление r₃ ток не протекает.

Поэтому точки c и d равнопотенциальны (φ_c = φ_d). Следовательно, напряжение между точками a и c (U_ac = φ_a — φ_c) равно напряжению между точками a и d (U_ad = φ_a — φ_d).

Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r₁

U_C1 = I·r₁ = 0,04·100 = 4 В.

Аналогично напряжение на втором конденсаторе равно

U_C2 = I·r₂ = 0,04·400 = 16 В.

Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C₁ = 5 мкФ; C₂ = 120 мкФ. Конденсатор C₂ предварительно не был заряжен.

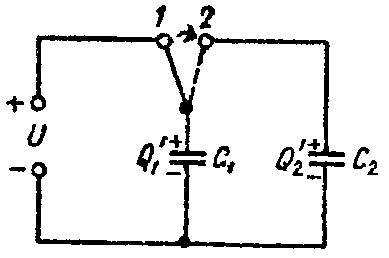
Рис. 5

Решение

Когда рубильник находится в положении 1, то конденсатор C₁ заряжен до напряжения U и его заряд равен

Q = C₁·U = 5·10^–6·25 = 125·10^–6 Кл.

После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C₁ и C₂ (рис. 5). Обозначим эти заряды через Q’₁ и Q’₂.

На основании закона сохранения электричества имеем

Q = Q’₁ + Q’₂ = 125 10^–6 Кл. (1)

По второму закону Кирхгофа имеем

0= U C1 − U C2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,

или

Q ′ 1 5⋅ 10 −6 − Q ′ 2 120⋅ 10 −6 =0.   (2)

Решая уравнения (1) и (2), найдем

Q’₁ = 5 10^–6 Кл; Q’₂ = 120 10^–6 Кл.

Доставка свежих и аппетитных японских суши в Новороссийске – ям ям..

Напряжение на зажимах конденсаторов станет равным

U C1 = Q ′ 1 C 1 = U C2 = Q ′ 2 C 2 = 5⋅ 10 −6 5⋅ 10 −6 =1  В.

Энергия обоих конденсаторов будет равна

W= C 1 ⋅ U C1 2 2 + C 2 ⋅ U C2 2 2 =62,5⋅ 10 −6   Дж.

Подсчитаем энергию, которая была запасена в конденсаторе С₁, при его подключении к источнику электрической энергии

W нач = C 1 ⋅U 2 = 5⋅ 10 −6 ⋅ 25 2 2 =1562,5⋅ 10 −6   Дж.

Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10^–6 — 62,5·10^–6 = 1500·10^–6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C₁ в конденсатор C₂ после перевода рубильника в положение 2.

Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.

Емкости конденсаторов равны: C₁ = 10 мкФ; C₂ = 30 мкФ; C₃ = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.

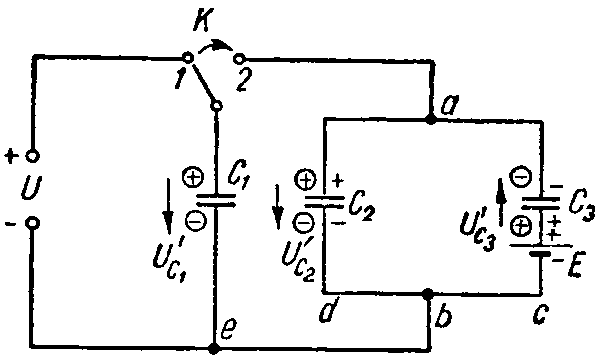
Рис. 6

Решение

Рубильник находится в положении 1. Заряд конденсатора C₁ равен

Q₁ = C₁·U = 10·10^–6·30 = 0,3·10^–3 Кл.

В указанном положении рубильника конденсаторы C₂ и C₃ соединены последовательно друг с другом, поэтому их заряды равны: Q₂ = Q₃. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем

E= U C2 + U C3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,

откуда

Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅E= 30⋅ 10 −6 ⋅60⋅ 10 −6 90⋅ 10 −6 ⋅50=1⋅ 10 −3   Кл.

При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’₁, Q’₂ и Q’₃. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.

Для узла a

Q’₁ + Q’₂ — Q’₃ = Q₁ + Q₂ — Q₃. (1)

Для контура 2ebda2

0= U ′ C1 − U ′ C2 = Q ′ 1 C 1 − Q ′ 2 C 1 .

Для контура bcadb

E= U ′ C2 − U ′ C3 = Q ′ 2 C 2 + Q ′ 3 C 3 .

Уравнения (1) — (3), после подстановки числовых значений величин, примут вид

Q’₁ + Q’₂ — Q’₃ = 0,3·10^–3; (4)

3Q’₁ — Q’₂ = 0; (5)

2Q’₂ + Q’₃ = 3·10^–3. (6)

Решая совместно уравнения (4) — (6), получим

Q’₁ = 0,33·10^–3 Кл; Q’₂ = 0,99·10^–3 Кл; Q’₃ = 1,02·10^–3 Кл.

Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.

Напряжения на конденсаторах после перевода рубильника будут равны

U C1 = Q ′ 1 C 1 = 0,33⋅ 10 −3 10⋅ 10 6 =33  В; U C2 = Q ′ 2 C 2 = 0,99⋅ 10 −3 30⋅ 10 6 =33  В; U C3 = Q ′ 3 C 3 = 1,02⋅ 10 −3 60⋅ 10 6 =17  В.

Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C₁ = 5 мкФ; C₂ = 4 мкФ; C₃ = 3 мкФ; э. д. с. источников E₁ = 20 В и E₂ = 5 В.

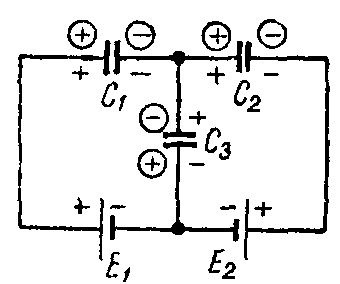
Рис. 7

Решение

Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках

− Q 1 + Q 2 − Q 3 =0; E 1 = U C1 − U C3 = Q 1 C 1 − Q 3 C 3 ; E 2 =− U C2 − U C3 =− Q 2 C 2 − Q 3 C 3 .

Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q₁ = 50 мкКл; Q₂ = 20 мкКл; Q₃ = –30 мкКл.

Таким образом, истинная полярность зарядов на обкладках конденсаторов C₁ и C₂ соответствует выбранной, а у конденсатора C₃ — противоположна выбранной.

Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C₁ = 2 мкФ; C₂ = 3 мкФ; C₃ = 5 мкФ; C₄ = 1 мкФ; C₅ = 2,4 мкФ.

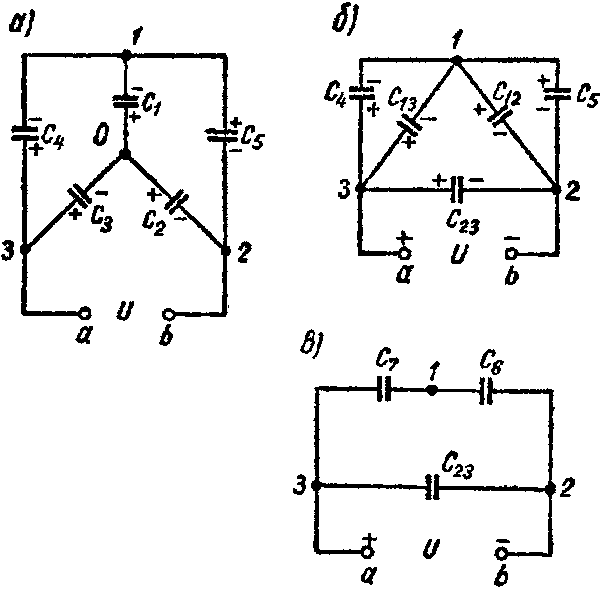
Рис. 8

Индивидуалка Дана (34 лет) т.8 926 650-82-63 Москва, метро Сокол.

Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.

Решение

1-й способ. Звезду емкостей C₁, C₂ и C₃ (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)

C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 =0,6  мкФ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 =1,0  мкФ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 =1,5  мкФ.

Емкости C₁₂ и C₅ оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость

C₆ = C₁₂ + C₅ = 3 мкФ.

Аналогично

C₇ = C₁₃ + C₄ = 2 мкФ.

Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется

C ab = C 23 + C 6 ⋅ C 7 C 6 + C 7 =2,7  мкФ.

Вычислим напряжение на каждом из конденсаторов.

На конденсаторе C₇ напряжение равно

U 7 = C 6 C 6 + C 7 ⋅U=6  В.

Таково же напряжение и на конденсаторах C₄ и C₁₃

U₄ = U₃₁ = 6 В.

Напряжение на конденсаторе C₆ равно

U₆ = U — U₇ = 4 В;

U₅ = U₁₂ = 4 В.

Вычислим заряды

Q₄ = C₄·U₄ = 6·10^–6 Кл;

Q₅ = C₅·U₅ = 9,6·10^–6 Кл;

Q₁₂ = C₁₂·U₁₂ = 6·10^–6 Кл;

Q₁₃ = C₁₃·U₃₁ = 2,4·10^–6 Кл.

По закону сохранения электричества для узла 1 схем 8, а и б имеем

–Q₄ — Q₁ + Q₅ = –Q₄ — Q₁₃ + Q₁₂ + Q₅,

отсюда

Q₁ = Q₁₃ — Q₁₂ = 3,6·10^–6 Кл,

а напряжение на конденсаторе, емкостью C₁ составляет

U 1 = Q 1 C 1 =1,8  В.

Далее находим напряжения и заряды на остальных конденсаторах

U₃₁ = U₁ + U₃,

отсюда

U₃ = U₃₁ — U₁ = 4,2 В;

Q₃ = C₃·U₃ = 21·10^–6 Кл,

также

U₁₂ = U₂ — U₁ = 4,2 В,

откуда

U₂ = U₁₂ + U₁ = 5,8 В;

Q₂ = C₂·U₂ = 17,4·10^–6 Кл.

Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.

2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)

для узла 1

Q₅ — Q₁ — Q₄ = 0; (1)

для узла О

Q₁ + Q₂ — Q₃ = 0; (2)

для контура О13О

Q 1 C 1 − Q 4 C 4 + Q 3 C 3 =0;  (3)

для контура О12О

Q 1 C 1 + Q 5 C 5 − Q 2 C 2 =0;  (4)

для контура a3О2b

Q 3 C 3 + Q 2 C 2 =U.  (5)

Система уравнений (1) — (5) — содержит пять неизвестных: Q₁, Q₂, Q₃, Q₄ и Q₅. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы С_ab можно найти из отношения

C ab = Q U ,

где Q = Q₃ + Q₄, или Q = Q₂ + Q₅.

Задача 9. В схеме рис. 9 найти распределение зарядов, если E₁ = 20 В; E₂ = 7 В; C₁ = 7 мкФ; C₂ = 1 мкФ; C₃ = 3 мкФ; C₄ = 4 мкФ; C₅ = C₆ = 5 мкФ.

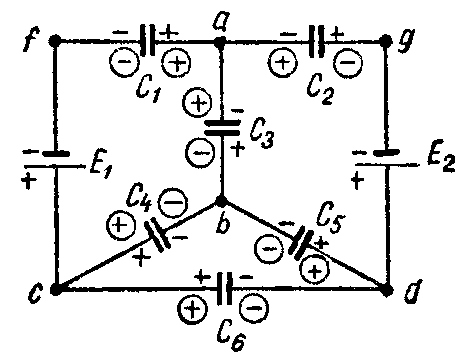
Рис. 9

Решение

При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:

для узла а

Q₁ + Q₂ + Q₃ = 0;

для узла b

–Q₃ — Q₄ — Q₅ = 0;

для узла c

–Q₁ + Q₄ + Q₆ = 0;

для контура afcba

E 1 = U C1 + U C4 − U C3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;

ля контура gdbag

E 2 = U C5 − U C3 + U C2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;

для контура cbdc

0= U C4 − U C5 − U C6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .

Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды

Q₁ = 35 мкКл; Q₂ = –5 мкКл; Q₃ = –30 мкКл;

Q₄ = 20 мкКл; Q₅ = 10 мкКл; Q₆ = 15 мкКл.

Таким образом, истинные знаки зарядов Q₁, Q₄, Q₅ и Q₆ соответствуют выбранным, а знаки Q₂ и Q₃ противоположны выбранным.

Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.

Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C₁ = 6 мкФ; C₂ = 2 мкФ; C₃ = 3 мкФ; r₁ = 500 Ом; r₂ = 400 Ом; U = 45 В.

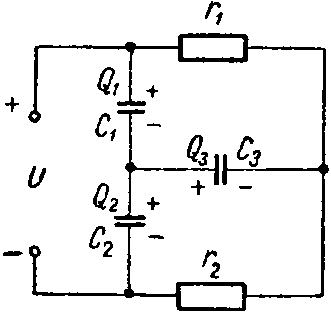
Рис. 10

Решение

Через сопротивления протекает ток

I= U r 1 + r 2 =0,05  А.

Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:

− Q 1 + Q 2 + Q 3 =0; U= U C1 + U C2 = Q 1 C 1 + Q 2 C 2 ; I⋅ r 1 = U C1 + U C3 = Q 1 C 1 + Q 3 C 3 ,

или

Q 1 = Q 2 + Q 3 ; 45= Q 1 6⋅ 10 −6 + Q 2 2⋅ 10 −6 ; 25= Q 1 6⋅ 10 −6 + Q 3 3⋅ 10 −6 .

Решив эту систему уравнений, найдем, что

Q₁ = 90 мкКл; Q₂ = 60 мкКл; Q₃ = 30 мкКл.

---

последовательное соединение конденсаторов,
параллельное соединение конденсаторов,
Расчет цепи конденсаторов,
Конденсатор в цепи постоянного тока,
Цепи с конденсаторами

Комментарии

«То,
что мы знаем, – ограничено,

а
то, чего мы не знаем, – бесконечно»

Пьер-Симон
Лаплас

Данная
тема посвящена решению задач на конденсаторы.

Задача
1.
Найдите электроёмкость конденсатора, который при зарядке до напряжения 1,5 кВ,
получает заряд, равный 60 мкКл.

ДАНО:	СИ	РЕШЕНИЕ Запишем формулу, по которой рассчитывается электроёмкость Тогда получаем, что при условиях задача она равна

Ответ:
40 нФ.

Задача
2.
На первый конденсатор подаётся напряжение 100 В, а на второй — 250 В. При
этом, конденсаторы накапливают одинаковые заряды. Сравните электроёмкости этих
конденсаторов.

ДАНО:	РЕШЕНИЕ Запишем формулу для вычисления электроёмкости Тогда электроёмкости первого и второго конденсаторов равны Т.к. заряды равны, то отношение электроёмкостей обратно пропорционально отношению напряжений

Ответ:
электроёмкость первого конденсатора в  2,5 раза больше, чем электроёмкость
второго конденсатора.

Задача
3.
Плоский конденсатор, в котором в качестве диэлектрика используется бумага,
имеет электроёмкость 20 нФ. Расстояние между пластинами конденсатора равно 0,4
мм. Если при напряжении 500 В, конденсатор обладает потенциальной энергией 12
мкДж, то какова площадь одной пластины этого конденсатора?

ДАНО:	СИ	РЕШЕНИЕ Запишем формулу для определения электроёмкости плоского конденсатора Потенциальная энергия заряженного конденсатора равна Подставляя первую формулу во вторую получим

Ответ:
17
см².

Задача
4.
На пластинах плоского бумажного конденсатора равномерно распределен заряд с
поверхностной плотностью 600 нКл/м². Расстояние между
пластинами равно 0,5 мм. Как изменится напряжение между его обкладками при
увеличении расстояния между пластинами до 2 мм?

ДАНО:	СИ	РЕШЕНИЕ Запишем формулу для расчета электроёмкости плоского конденсатора Электроёмкость в общем виде может быть выражена по формуле Поверхностная плотность заряда определяется по выражению Приравняем первые две формулы Исходя из формулы для определения поверхностной плотности, величина заряда равна Тогда

Ответ:
напряжение увеличится на 40,7 В.

Задача
5.
При увеличении напряжения, поданного на конденсатор с ёмкостью 6 мкФ, в 3
раза, энергия поля возросла на 0,2 Дж. Найдите заряд на конденсаторе до
увеличения напряжения.

ДАНО:	СИ	РЕШЕНИЕ Запишем формулу, по которой вычисляется потенциальная энергия заряженного конденсатора Запишем общую формулу для определения электроёмкости конденсатора Запишем теперь выражения для начальной и конечной энергии конденсатора Разность этих энергий равна В условии задачи сказано, что С учетом последнего равенства получаем Из общего определения электроёмкости Тогда

Ответ:
2,2 мКл.