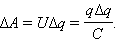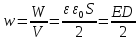Энергия заряженного конденсатора. Калькулятор онлайн для любых конденсаторов.
Онлайн калькулятор вычисления энергии электростатического поля заряженного конденсатора, позволит найти энергию заряженного конденсатора через напряжение, емкость и электрический заряд на одной из обкладок. Калькулятор произведет вычисление и даст подробное решение. Единицы измерения, могут включать любые приставки Си. Калькулятор автоматически переведет одни единицы в другие.
Калькулятор вычислит:
Энергию заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и емкость.
Энергию заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и электрический заряд на одной из обкладок
Энергию заряженного конденсатора через электрический заряд на одной из обкладок и емкость
Так же для вычисления энергии электростатического поля плоского, цилиндрического и сферического конденсаторов, можно воспользоваться
калькулятором вычисления энергии заряженного конденсатора для плоского, цилиндрического и сферического конденсаторов.
Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и емкость
Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и емкость определяется формулой, где
C – емкость конденсатора
U – напряжение (разность потенциалов), до которого заряжен конденсатор
Единицей измерения энергии является – Джоуль (Дж, J).
Электроемкость C =
Напряжение U =
Единица измерения энергии W
Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и электрический заряд на одной из обкладок
Энергия заряженного конденсатора через напряжение (разность потенциалов), до которого заряжен конденсатор и электрический заряд на одной из обкладок определяется формулой, где
q – электрический заряд на одной из обкладок
U – напряжение (разность потенциалов), до которого заряжен конденсатор
Единицей измерения энергии является – Джоуль (Дж, J).
Заряд q =
Напряжение U =
Единица измерения энергии W
Энергия заряженного конденсатора через электрический заряд на одной из обкладок и емкость
Энергия заряженного конденсатора через электрический заряд на одной из обкладок и емкость определяется формулой, где
q – электрический заряд на одной из обкладок
C – емкость конденсатора
Единицей измерения энергии является – Джоуль (Дж, J).
Заряд q =
Электроемкость C =
Единица измерения энергии W
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Любой конденсатор — система, которая может запасать энергию в виде заряда, сохранённого на обкладках конденсатора. Попробуем просчитать энергию плоского конденсатора.
Для зарядки конденсатора нужно совершить работу. Эту работу за нас совершает электрическое поле. Энергия заряженного конденсатора в идеальном случае численно равна работе электростатического поля:
(1)
Напряжённость поля внутри конденсатора можем выразить в виде:
(2)
- где
Однако при зарядке конденсатора заряд необходимо загнать только на одну пластину, таким образом, напряжённость нужно брать только от одной пластины:
(3)
Подставим (3) в (1):
(4)
Вспомним электроёмкость плоского конденсатора:
(5)
Откуда:
(6)
Подставим (6) в (4):
(7)
Соотношение (7) можно адаптировать под условия задачи, используя определение электроёмкости:
(8)
Тогда подставим (8) в (7):
(9)
Или, выделив из (8) и подставив в (7), получим:
(10)
Тогда, совместив все формы записи энергии:
(11)
Вывод: Для задачи с энергией конденсатора достаточно выбрать форму записи энергии (11), исходя из условий задачи.
Энергия
заряженного конденсатораравна
работе внешних сил, которую необходимо
затратить, чтобы зарядить конденсатор.
Процесс
зарядки конденсатора можно представить
как последовательный перенос достаточно
малых порций заряда Δq > 0 с одной
обкладки на другую. При этом одна
обкладка постепенно заряжается
положительным зарядом, а другая –
отрицательным. Поскольку каждая порция
переносится в условиях, когда на
обкладках уже имеется некоторый заряд
q, а между ними существует некоторая
разность потенциалов
,
при переносе каждой порции Δq внешние
силы должны совершить работу
(С – емкость)
Энергия We
конденсатора емкости C, заряженного
зарядом Q, может быть найдена путем
интегрирования этого выражения в
пределах от 0 до Q:
Энергия
заряженного плоского конденсатора Eк
равна работе A, которая была затрачена
при его зарядке, или совершается при
его разрядке.
=Eк
Поскольку
напряжение на конденсаторе может быть
рассчитано из соотношения:
U=E*d,
где E- напряженность поля между обкладками
конденсатора,d- расстояние
между пластинами конденсатора, то
энергия заряженного конденсатора
равна:
где V- объем пространства между обкладками
конденсатора.
Энергия
заряженного конденсатора сосредоточена
в его электрическом поле.
Объемная
плотность энергии
электростатического поля (энергия
единицы объема)
18. Электрический ток. Сила и плотность тока.
Ток —
направленное движение электрически
заряженных частиц. Величина тока
измеряется так называемой силой тока,
которая в системе СИ измеряется в
амперах.
Токбывает постоянный и переменный.
Постоянный ток — это ток, имеющий
постоянную величину. Переменный ток
периодически изменяет направление
своего движения по синусоиде с
определенной частотой, измеряемой в
герцах (Гц). Переменный ток высокой
частоты вытесняется на поверхность
проводника
Материал,
в котором течёт ток, называется
проводником
Сила тока
в проводнике — скалярная величина,
численно равная заряду, протекающему
в единицу времени через сечение
проводника. Обозначается буквой :I
I=q/t
Плотность
тока — векторная величина, имеющая
смысл силы тока, протекающего через
единицу площади. Например, при равномерном
распределении плотности jтока по сечениюSпроводника
|j|=I/S
19.Сторонние силы. Электродвижущая сила и напряжение.
Сторонние
силы –силы неэлектрической
природы, вызывающие перемещение
электрических зарядов внутри источника
постоянного тока.
Сторонними
считаются все силы отличные от кулоновских
сил.
Электродвижущая
сила
(эдс), физическая
величина, характеризующая действие
сторонних (непотенциальных) сил в
источниках постоянного или переменного
тока; в замкнутом проводящем контуре
равна работе этих сил по перемещению
единичного положительного заряда вдоль
контура.
ЭДС можно
выразить через напряжённость
электрического поля сторонних сил
(Eex). В замкнутом контуре (L) тогда ЭДС
будет равна:
где dl — элемент длины контура.
Напряжение
(разность потенциалов) между точками
A и B — это отношение работы электрического
поля при переносе пробного электрического
заряда из точки A в точку B к величине
пробного заряда.
Ф1-Ф2=U12
При этом
считается, что перенос пробного заряда
не изменяет распределения зарядов на
источниках поля.
Альтернативное
определение (для электростатического
поля) —
(интеграл от
проекции поля на траекторию между
точками AиBвдоль любой траектории, идущей изAвB)
Единицей
измерения напряжения в системе СИ
является Вольт.
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое конденсатор
Конструкция простейшего устройства этой категории состоит их двух проводящих пластин с диэлектриком в промежутке. Подключением такого устройства к источнику постоянного тока накапливают на рабочих элементах положительные и отрицательные заряды. После разрыва цепи питания энергетический потенциал сохраняется.
Характеристики конденсатора
Основной характеристикой данного элемента является емкость, или С. Она определяет способность устройства собирать электрический заряд, зависит от геометрической конфигурации крышек и от электрической проницаемости диэлектрика между крышками.
Важно! Емкость зависит от типа используемого диэлектрика, а также от геометрических размеров элемента.
Для того, чтобы описать принцип работы устройства формулой, необходимо понять, что это постоянная пропорциональность в уравнении, представляющая собой взаимную зависимость накопленного заряда q от площади пластинок и от разности потенциалов V между ними.
Мощность выражается в единицах, называемых фарадами F. Но на практике используются и более мелкие единицы, такие как микрофарады и пикофарады.

Внешний вид устройств
Таким образом, если напряжение U приложено к конденсатору, электрический заряд накапливается на крышках детали. Значение накопленного заряда на каждой пластинке одинаково, они отличаются только знаком. Этот процесс накопления электрического показателя на называется зарядкой.
Другим параметром детали является номинальное напряжение, а именно, его максимальное значение, которое может подаваться на конденсатор. При подключении более высокого напряжения возникает пробой диэлектрика. Это приводит к короткому замыканию элемента. Каким будет номинальное значение напряжения, зависит от типа диэлектрика и его толщины.
Важно! Чем толще диэлектрик, тем выше номинальное напряжение, которое он выдерживает.
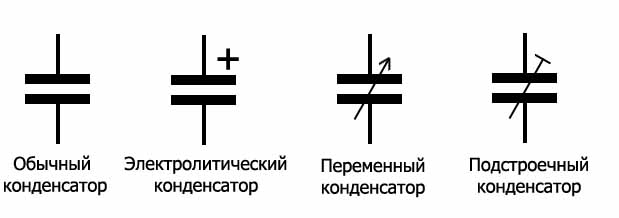
Условные обозначения
Ещё одним параметром является ток утечки -значение проводящего показателя, возникающее при подаче постоянного напряжения на концы элемента.
Виды конденсаторов
Энергия конденсатора
У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.
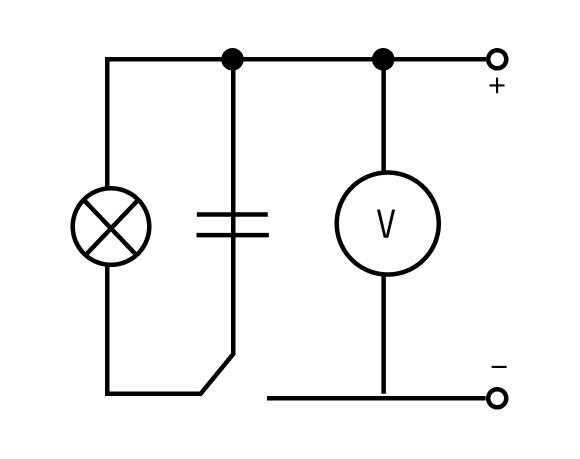
Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.
Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.
Wp = qEd
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
E — напряженность электрического поля [В/м]
d — расстояние от заряда [м]
В случае с конденсатором d будет представлять собой расстояние между пластинами.
Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.
Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.
В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.
Тогда энергия конденсатора равна:
Wp = qEd/2
Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:
U = Ed
Поэтому:
Wp = qU/2
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.
Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:
Wp = qU/2
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
U — напряжение на конденсаторе [В]
Wp = q2/2C
Wp — энергия электростатического поля [Дж]
q — электрический заряд [Кл]
C — электроемкость конденсатора [Ф]
Wp = CU2/2
Wp — энергия электростатического поля [Дж]
C — электроемкость конденсатора [Ф]
U — напряжение на конденсаторе [В]
Эти формулы справедливы для любого конденсатора.
Определение энергии конденсатора
Электроемкость плоского конденсатора
Чтобы выяснить, от чего будут зависеть накопительные характеристики, можно применить две методики. Первая – это определение работы, которая выполняется для распределения зарядов на обкладках. Подразумевается, что для этого понадобится затратить определенную энергию. Во втором варианте пользуются притяжением разноименных зарядов. Для перемещения пластин до прямого контакта нужно выполнить соответствующую работу.
Энергия заряженного конденсатора
Существует еще одна эквивалентная запись заряженного конденсатора при использовании соотношения Q=CU:
We=Q22C=CU22=QU2.
Электрическая энергия We рассматривается как потенциальная. Формулы для We аналогичны формулам потенциальной энергии Ep деформированной пружины, а именно:
Ep=kx22=F22k=Fx2, где k является жесткостью пружины, х – деформацией, F=kx – внешней силой.
Современные представления электрической энергии говорят о том, что она сосредоточена между пластинами конденсатора. В связи с этим и получила название энергии электрического поля. Это объяснимо с помощью иллюстрирования заряженного плоского конденсатора.
Плоский конденсатор.
Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:
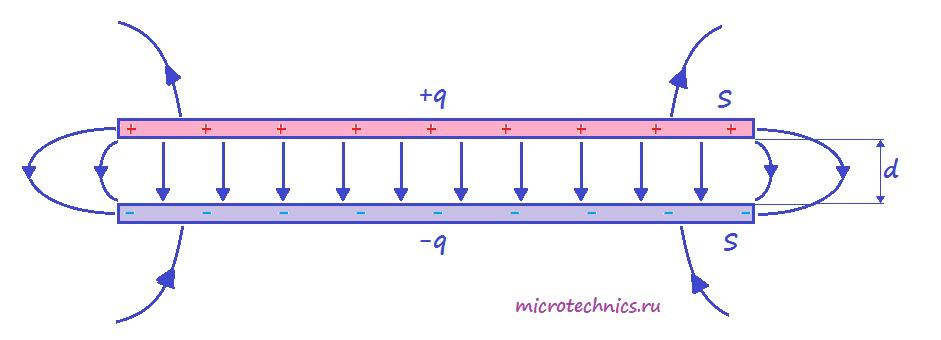
Такое устройство называется плоским конденсатором, а пластины — обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).
А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.
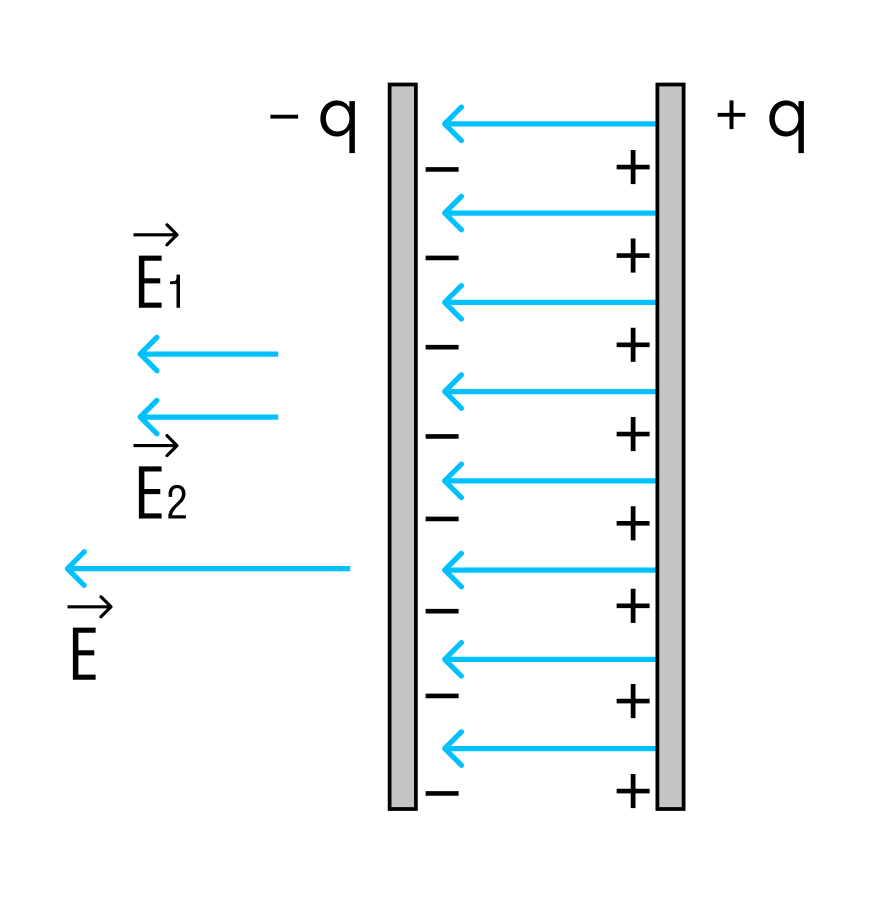
Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:
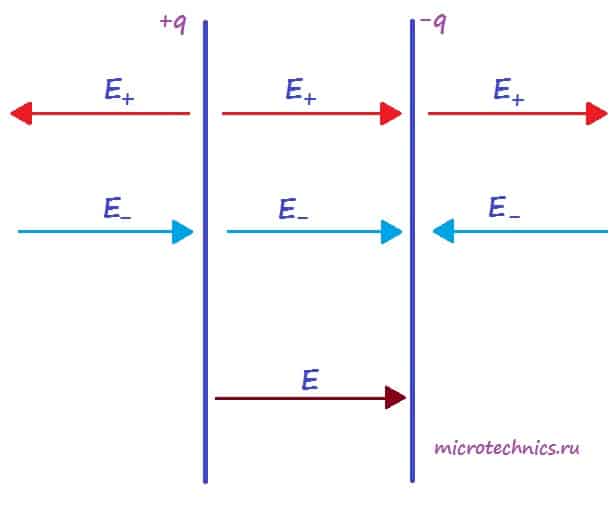
Каждая из обкладок конденсатора в отдельности создает электрическое поле:
- положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
- отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}
Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:
E = frac{sigma}{2varepsilon_0thinspacevarepsilon}
Здесь sigma— это поверхностная плотность заряда: sigma = frac{q}{S}, а varepsilon — диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:
E_+ = E_- = frac{q}{2varepsilon_0thinspacevarepsilon S}
Но направления векторов разные — внутри конденсатора вектора направлены в одну сторону, а вне — в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:
E = E_+ + E_- = frac{q}{2varepsilon_0thinspacevarepsilon S} + frac{q}{2varepsilon_0thinspacevarepsilon S} = frac{q}{varepsilon_0thinspacevarepsilon S}
А какая же будет величина напряженности вне конденсатора? А все просто — слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0
Процессы зарядки и разрядки конденсаторов.
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:
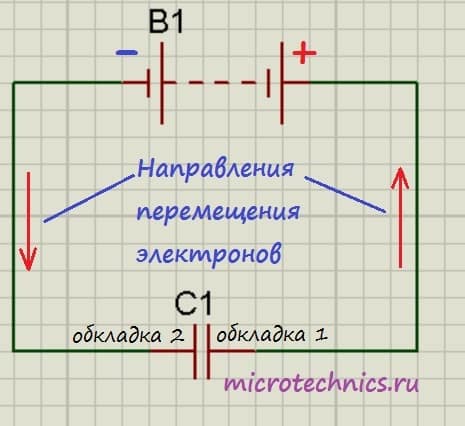
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?
Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.
При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.
Из истории
Первым конденсатором считается лейденская банка. Её разработали независимо сразу двое учёных:
- Эвальд Георг фон Клейст (11 октября 1745 года).
- Питер ван Мушенбрук (1745 – 1746 годы).
Двумя десятилетиями позже на свет появился электрофорус (1762 год), рассматриваемый как первый плоский конденсатор. Тогда не существовало терминов, вопросы накопления заряда мало интересовали. Учёные пока что развлекались получением статического заряда. К примеру, ван Мушенбрук испытывал лейденскую банку на слишком смелых студентах, когда сам оказался однажды полупарализован электрическим зарядом.
Наука не шла вперёд, хотя светила, включая Бенджамина Франклина, вовсю толкали паровоз. Современный этап развития физики начался с Алессандро Вольта. Учёный оказался привлечён конструкцией электрофоруса и заинтригован. Натёртая резина могла сколь угодно долго заряжать металлическую пластину. В то время предполагалось, что электричество переносится флюидами атмосферы, и Вольта считал аналогично. Узрев, что электрофорус способен запасать заряд, учёный решил посчитать и количество.
Концепция Вольты
Как свидетельствуют записки учёного, уже в 1778 году он получил представление о разнице потенциалов, которые называл tension – напряжение. С 1775 года Вольта придерживается концепции электрической ёмкости – capacita, выдвинутой его учителем Беккарией. Вольта уже знает, что электрофорус способен накопить заряд, называет прибор конденсатором, и решает подтвердить теорию практикой. Иначе – найти взаимосвязь напряжения, ёмкости и объёмом (quantita) заряда.
Вольта начал с лейденской банки. Он заряжал её от статического генератора и пробовал определить энергию конденсатора тремя путями:
- Наблюдал получаемую искру электрической дуги от различной конструкции лейденских банок, заряженных одинаковым напряжением.
- Измерял количество произведённой электростатическими генераторами трения работу, пока показания электрометра не росли до определённого уровня.
- Разряжал лейденские банки на открытом воздухе и пытался сравнить производимый ими электрический шок по истечении времени.
Все перечисленное привело исследователя к странным выводам, что высокие лейденские банки более вместительные (при одинаковых площадях обкладок и прочих равных условиях). Вероятно, это связано со скоростью разряда их дуги на воздухе вследствие различий в кривизне поверхностей. Силу разряда Вольта увязывал с электрическим током: чем быстрее течёт флюид, тем более жаркий (по ощущениям) эффект. В результате, Вольта счёл, что разница потенциалов единственная определяет процесс возникновения удара. Он решил, что напряжение допустимо измерить двумя путями:
- Через количество оборотов генератора статического заряда.
- Сравнивая силу электрического удара при разряде лейденской банки.
Вольта нашёл, что заряжая пустую лейденскую банку от полной, шок получается вдвое слабее. Постепенно (1782 год) Вольта пришёл к выводу, что вышеуказанные величины соотносятся между собой: tension x capacity ~ load, в современном мире выглядит как U C = q или C = q / U.
Вольта заключил, что ёмкость больше там, где при меньшем напряжении вмещается больше заряда. Последовало заключение, что количество накопленного флюида прямо пропорционально площади обкладок плоского конденсатора. Что согласуется с современными формулами. Вольта обобщил знания на случай произвольного проводника (экспериментировал со стержнями лейденских банок). Изменяя расстояние между обкладками, установил:
С ~ S / d.
Что фактически стало выражением ёмкости плоского конденсатора. Вольта объяснил зависимость наличием некоего сопротивления (resistance) между обкладками, подразумевая воздух. Изменяя дистанцию, удаётся варьировать этот параметр в обе стороны. Это слегка не согласуется с современными концепциями, но Вольта помог Георгу Ому 40 лет спустя вывести зависимость между током и напряжением.
Фактически измерения проделывались на основе работы поля, проявлявшейся лишь вследствие заряда конденсатора. Очевидно, что указанная величина равна энергии – одной из первых физических характеристики, использованных для вывода аналитических выражений.
Единицы измерения
Энергию и работу принято измерять в джоулях, электрическое напряжение и потенциал – в вольтах.
Вольтом называется разница потенциалов, при перемещении единичного положительного заряда между которыми совершается работа в 1 джоуль.
Мера энергии заряженного конденсатора
При расчёте фильтров цепей питания и прочих электрических фильтров встаёт задача определения номиналов. Кажется, достаточно взять формулу частоты резонансного контура, но простота обманчива. Легко убедиться, что одинаковому ответу соответствует множество значений. Которое выбрать?
Чем больше мощность источника, питания прибора, тем большая энергия здесь проходит в единицу времени. Для конденсатора она зависит от квадрата напряжения и ёмкости, для дросселя – от величины электрического тока и индуктивности. Узнав период единственного колебания, эту цифру легко привязать к мощности, как выполняемой работе в единицу времени.
В результате инженер сумеет сказать приблизительно, какого размера ёмкость требуется в конкретном случае. Расчёт ведётся изначально по энергии заряженного конденсатора.
Аналогичное происходит в любой цепи. Конденсаторы служат для фильтрации и гальванической развязки, обязаны легко пропускать нужную частоту и оставаться ёмкими, чтобы не стать бутылочным горлышком в системе.
Калькулятор расчета запасаемой энергии в конденсаторе
| Напряжение (V): | В |
| Емкость (C): | мкФ |
| Сопротивление (R): | Ом |
| T (RC): | секунд |
| E: | Джоулей |
Величина энергии
Как будет вычисляться накопленный энергетический потенциал, разобраться можно с помощью показанного на снимке блока фотовспышки. Следует напомнить о том, что для увеличения емкости применяют параллельное соединение (Cобщ = C1 + C2 +…+ Cn). При последовательном варианте пропорциональная зависимость обратная (1/Cобщ = 1/C1 + 1/C2 +…+ 1/Cn).
Расчет:
- 2 емкости по 400 мкФ (Cобщ = C1 + C2 = 400 + 400 = 800 мкФ);
- источник питания будет заряжать элемент напряжением 300 В;
- энергия конденсатора W = ½ *C * U2 = ½ * 800 * 10-6 * 300 = 0,12 джоуля.
Использование конденсаторов
Подученное соотношение величин характерно для всех типов конденсаторов. Его используют для того, чтобы определить накопленную энергию при подключении к источнику питания. Измерить напряжение на выводах можно с помощью мультиметра. Кроме емкости, на корпусе конденсатора указывают другие важные параметры:
- рабочий ток;
- номинальное напряжение;
- диэлектрический материал;
- тип элемента.
К сведению. На миниатюрных деталях места для размещения всех данных недостаточно. Применяют систему сокращенных кодировок. Необходимые сведения уточняют в сопроводительной документации либо на официальном сайте производителя.
В следующем перечне приведены примеры электротехнических схем и устройств, которые создают с применением конденсаторов:
- частотный (сглаживающий) фильтр;
- колебательный контур;
- накопитель энергии для формирования мощного импульса (лазер, фотовспышка);
- ограничитель силы тока (компенсатор подключаемой реактивной нагрузки);
- измерение перемещений (изменение емкости при сближении/ отдалении обкладок).
Для автоматизированного расчета типовой схемы можно использовать специализированный калькулятор онлайн. Следующий пример демонстрирует расчет корректного подключения электродвигателя:
- соединение обмоток – треугольник;
- мощность потребления – 1 200 Вт;
- напряжения сети – 220 В;
- cos ϕ – 0,9;
- КПД – 85%;
- емкость рабочего (пускового) конденсатора – 52 (130) мкФ.
Как рассчитать емкость конденсатора
Расчеты, производимые с помощью онлайн калькулятора, позволяют вычислить емкость конденсатора в течение нескольких секунд. Кроме этого параметра, можно определить показатели заряда, мощности, тока, энергии и прочих качеств конденсатора, необходимых в конкретном устройстве.
Наиболее часто встречаются электролитические конденсаторы, применяемые в схеме асинхронного электродвигателя. Конструкции этих устройств могут быть полярными или неполярными. В первом случае отмечается более высокая емкость, поэтому перед подключением конденсатора к двигателю, необходимо в обязательном порядке выполнить расчеты. С помощью проводимых вычислений устанавливается необходимая емкость, соответствующая конкретному двигателю.
Особое значение придается дополнительным расчетам при эксплуатации трехфазных электродвигателей. В обычном режиме конденсатор функционирует нормально, однако при включении в однофазную сеть, его емкость заметно снижается. Это приводит к увеличению частоты вращения вала. Предварительные расчеты и правильное подключение позволяют избежать подобных ситуаций.

При запуске асинхронного двигателя, работающего от напряжения 220 вольт, требуется конденсатор с высокой емкостью. В связи с этим, невозможно обойтись без проведения расчетов с помощью онлайн калькулятора. Проведение расчетов полностью зависит от способа соединения обмоток электродвигателя. Данное соединение может быть выполнено двумя способами – звездой и треугольником. В первом случае применяется формула Ср=2800хI/U, а для второго случая используется немного измененная формула Ср=4800хI/U.
Следует учитывать, что в цепочке соединенных конденсаторов емкость пускового устройства должна быть примерно в три раза выше, чем в рабочем приборе. Для расчета применяется формула Сп=2.5хСр, в которой Сп и Ср являются соответственно пусковым и рабочим конденсатором.
Следующая
РазноеЧто такое активная мощность?
Исходя из опытов, заряженный конденсатор имеет запас энергии.
Энергия заряженного конденсатора равняется работе внешних сил, которая необходима для его зарядки.
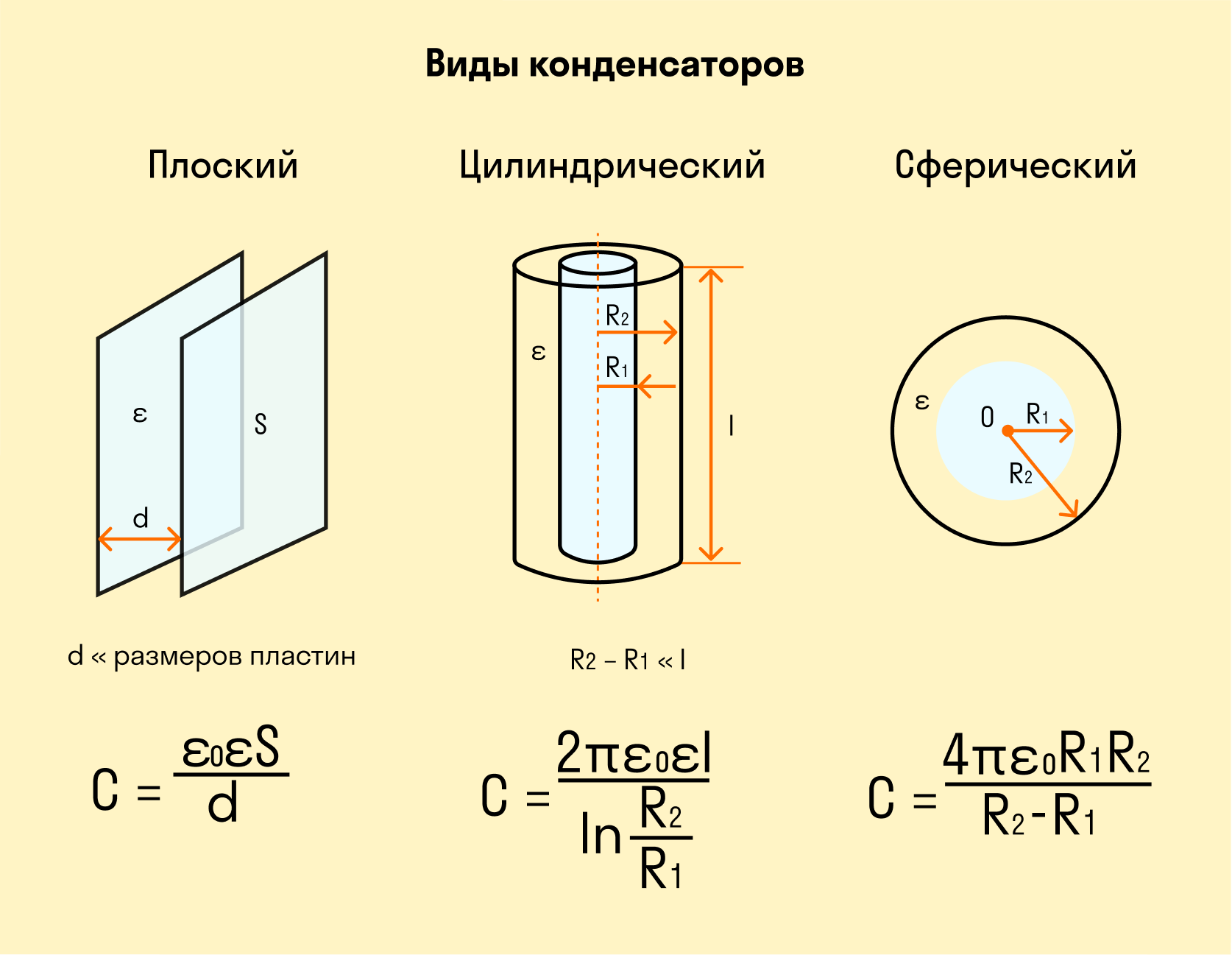
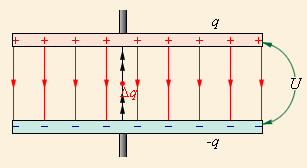
Его заряжение представляется как последовательный перенос малых порций заряда ∆q>0 с одной обкладки на другую, как изображено на рисунке 1.7.1 Одна из них заряжается положительным зарядом, другая – отрицательным. Процесс производится при уже имеющемся некотором заряде q, тогда как между обкладками существует разность потенциалов U=qC, а при переносе ∆q внешние силы совершают работу ∆A=U∆q=q∆qC.
Нахождение энергии We конденсатора с емкостью С и с зарядом Q производится с помощью интегрирования в переделах от 0 до Q. Формула примет вид:
We=A=Q22C.
Рисунок 1.7.1. Процесс зарядки конденсатора.
Энергия заряженного конденсатора
Существует еще одна эквивалентная запись заряженного конденсатора при использовании соотношения Q=CU:
We=Q22C=CU22=QU2.
Электрическая энергия We рассматривается как потенциальная. Формулы для We аналогичны формулам потенциальной энергии Ep деформированной пружины, а именно:
Ep=kx22=F22k=Fx2, где k является жесткостью пружины, х – деформацией, F=kx – внешней силой.
Современные представления электрической энергии говорят о том, что она сосредоточена между пластинами конденсатора. В связи с этим и получила название энергии электрического поля. Это объяснимо с помощью иллюстрирования заряженного плоского конденсатора.
Объемная плотность электрической энергии
Напряженность однородного поля плоского конденсатора равняется E=Ud, его емкость – C=ε0εSd.
Отсюда следует, что We=C·U22=ε0·ε·S·E2·d22d=ε0·ε·E22V, где V=Sd обозначает объем пространства между обкладками с наличием электрического поля. Данное соотношение приводит к формуле следующей физической величины.
Физическая величина We=ε0·ε·E22 – это электрическая энергия на единицу объема пространства, в котором создается электрическое поле. Ее называют объемной плотностью данной электрической энергии.
Энергия поля конденсатора, создаваемая любыми распределениями электрических зарядов в пространстве, находится путем интегрирования We по всему объему, в котором было создано электрическое поле.