Как найти энтальпию образования формула - Сайт, где вы сможете решить свои вопросы

Для расчетов
тепловых эффектов используют величину,
называемую энтальпией.

Энтальпией
(теплотой) образования химического
соединения ∆ H_Tназывается изменение энтальпии
в процессе получения 1 моля этого
соединения из простых веществ (элементов)
при постоянном давлении.

Так, например,
энтальпией образования этилового спирта
C₂H₅OHназывается изменение энтальпии при
реакции углерода, кислорода и водорода
при постоянном давлении

2C
+ 3H₂+ 1/2
O₂→ CH₃
– CH₂ – OH

И наоборот, реакции

CH₂= CH₂+H₂O→CH₃
– CH₂
– OH

CH₃
– CHO+H₂→CH₃
– CH₂
– OH

не являются
реакциями ”образования” спирта, хотя
и приводят к синтезу этилового спирта.

Важным термодинамическим
представлением является понятие о
стандартном состоянии вещества, под
которым понимается его реальное состояние
при 298 Ки атмосферном давлении (илиp = 101 кПа).

Стандартной
энтальпией (теплотой) образования
химического соединения
называется изменение энтальпии в
процессе образования 1 моля этого
соединения, находящегося в стандартном
состоянии, из простых веществ, также
находящихся в стандартных состояниях
и термодинамически устойчивых при
данной температуре фазах и модификациях.

Стандартные
энтальпии образования простых веществ
принимают равными нулю, если их агрегатные
состояния и модификации устойчивы при
стандартных условиях.

Стандартная
энтальпия образования соединения –
мера его термодинамической устойчивости,
прочности, количественное выражение
энергетических свойств соединения.
Если стандартная энтальпия образования
отрицательна, то соединение более
устойчиво, чем элементы, из которых оно
состоит, или наоборот, если она
положительна, то соединение менее
устойчиво. Из различных молекул более
устойчивы те, энтальпии, образования
которых меньше.

Например, этан (∆
H₂₉₈= –
24,82 ккал/моль)более устойчив, чем
этилен

Термохимические
расчеты.Значения энтальпий
образования позволяет определить
изменения энтальпии, сопровождающие
реакции, не прибегая к прямым измерениям.

В основе большинства
термохимических расчетов лежит следствие
из закона Гесса:

Тепловой эффект
химической реакции равен сумме теплот
(энтальпий) образования продуктов
реакции за вычетом суммы теплот
(энтальпий) образования исходных веществ.

Так, для уравнения
вида

aA
+ bB +…= dD
+ eE +…

Тепловой эффект
∆ Hопределяется
равенством

При этом следует
иметь в виду, что при алгебраическом
суммировании следует учитывать
стехиометрические коэффициенты в
уравнении реакции (а, в, d,
e).

Приведенное
уравнение позволяет определять как
тепловой эффект реакции по известным
энтальпиям образования веществ,
участвующих в реакции, так и одну из
энтальпий образования, если известны
тепловой эффект реакции и все остальные
энтальпии образования.

В настоящее время
энтальпии образования известны примерно
для четырех тысяч веществ, и это позволяет
расчётным путем установить тепловые
эффекты самых разнообразных реакций.

Пример 1. Расчет
теплового эффекта реакции по стандартным
энтальпиям образования веществ.

Al₂O₃(к)
+3SO₃(г)
= Al₂(SO₄)₃
(к)

=-1675
кДж/моль;
=-395,
2 кДж/моль

=-3434
кДж/моль

Тепловой эффект
реакции
определяется по уравнению:

После подстановки
значений стандартных энтальпий

-3434-(-1675-3.395,
2)=-599 кДж/моль

Видно, что
<
0, т.е. это реакция экзотермическая.

Пример 2. Расчет
энтальпии образования химического
соединения по известному тепловому
эффекту реакции.

Определить
в реакции:

CH₄
(г) + 2 H₂O
(г) = CO₂
(г) + 4 H₂
(г)

=-241,82
кДж/моль;
=-393,51
кДж/моль;
=
+164,98 кДж

Стандартный
тепловой эффект реакции равен:

,
откуда

После подстановки
стандартных энтальпий образования
веществ:

(-1
моль∙ 393,51 кДж/моль + 2 моль ∙ – 241,82
кДж/моль – 164,98 кДж) / 1 моль = – 74,85 кДж/моль

Видно, что реакция
образования метана является экзотермической.

Пример 3. Расчет
теплового эффекта реакции, который
экспериментально определить невозможно.

Реакция 1) C
+ O₂ = CO₂,

= -396 кДж/моль

может быть также
осуществлена в две стадии

2)
C + 1/2 O₂
= CO,

= -110, 5 кДж/моль

3)
CO + 1/2 O₂= CO₂

Тепловой эффект
реакции 2) можно провести экспериментально
и определить
=-110, 5 кДж/моль.

А вот тепловой
эффект реакции 3) экспериментально
осуществить и определить невозможно,
поэтому
реакции
3) получают расчетным путем, используя
закон Гесса

– 396 – (-110, 5) = – 285,5
кДж/моль

С помощью
термохимических расчетов можно определить
энергию химических связей, энергии
кристаллических решеток, теплоты
растворения и гидратации, тепловые
эффекты фазовых превращений и т.д.

Энтальпия есть
возрастающая функция температуры,
непрерывная во всей области изменения
последней, когда существует данная
фаза. Для расчета теплового эффекта при
температурах, более высоких, чем
стандартные, используют уравнение
Кирхгофа:

где
– стандартный тепловой эффект реакции
приT = 298 К;

–
стандартный тепловой эффект реакции
при T.

разность молярных
изобарных теплоемкостей всех продуктов
реакции и молярных изобарных теплоемкостей
всех исходных веществ, т.е.

Расчеты по уравнению
Кирхгофа показывают, что в том интервале
температур, который может иметь
практическое значение, изменение
величины теплового эффекта реакции
невелико.

Так, например,
тепловой эффект процесса 1/2 N₂+ 1/2 O₂
= NO (г)при
повышении температуры от298до4000Кизменяется всего лишь на2,0
кДж/моль. Еще меньше влияние давления
на тепловой эффект реакции. Так, для
реакции синтеза аммиака из азота и
водорода различие между величинами
приp = 101 кПаиp
= 50 МПане превышает5 %.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Загрузить PDF

Во время химических реакций происходит поглощение или выделение тепла в окружающую среду. Такой теплообмен между химической реакцией и окружающей средой называется энтальпией, или H. Однако измерить энтальпию напрямую невозможно, поэтому принято рассчитывать изменение температуры окружающей среды (обозначаемое ∆H). ∆H показывает, что в ходе химической реакции происходит выделение тепла в окружающую среду (экзотермическая реакция) или поглощение тепла (эндотермическая реакция). Рассчитывается энтальпия так: ∆H = m x s x ∆T, где m — масса реагентов, s — теплоемкость продукта реакции, ∆T — изменение температуры в результате реакции.

1
Определите реагенты и продукты реакции. Любая химическая реакция имеет реагенты и продукты реакции. Продукт реакции создается в результате взаимодействия реагентов. Другими словами реагенты — это ингредиенты в рецепте, а продукт реакции — это готовое блюдо. Чтобы найти ∆H реакции, необходимо знать реагенты и продукты реакции.
- Например, необходимо найти энтальпию реакции образования воды из водорода и кислорода: 2H₂ (водород) + O₂ (кислород) → 2H₂O (вода). В этой реакции H₂ и O₂ – реагенты, а H₂O — продукт реакции.
2
Определите общую массу реагентов. Далее необходимо подсчитать массу реагентов. Если вы не можете взвесить их, то подсчитайте молекулярную массу, чтобы найти фактическую. Молекулярная масса — это постоянная, которую можно найти в периодической таблице Менделеева или в других таблицах молекул и соединений. Умножьте массу каждого реагента на число молей.
- В нашем примере реагенты водород и кислород имеют молекулярные массы 2 г и 32 г соответственно. Поскольку мы используем 2 моль водорода (коэффициент в химической реакции перед водородом H₂) и 1 моль кислорода (отсутствие коэффициента перед O₂ обозначает 1 моль), то общая масса реагентов рассчитывается следующим образом:
  2 × (2 г) + 1 × (32 г) = 4 г + 32 г = 36 г
3
Определите теплоемкость продукта. Далее определите теплоемкость продукта реакции. Каждая молекула имеет определенную величину теплоемкости, которая является постоянной. Найдите эту постоянную в таблицах учебника по химии. Существует несколько единиц измерения теплоемкости; в наших расчетах мы будем использовать Дж/г°C.
- Обратите внимание на то, что при наличии нескольких продуктов реакции вам потребуется рассчитать теплоемкость каждого, а затем сложить их, чтоб получить энтальпию всей реакции.
- В нашем примере, продукт реакции — вода, которая имеет теплоемкость 4,2 Дж/г°C.
4
Найдите изменение температуры. Теперь мы найдем ∆T — разницу температур до и после реакции. Из начальной температуры (T1) вычтите конечную температуру (T2). Чаще всего в задачах по химии используется шкала Кельвина (К) (хотя по шкале Цельсия (°С) получится тот же результат).
- В нашем примере давайте предположим, что начальная температура реакции была 185 K, а после реакции стала 95 K, значит, ∆T вычисляется так:
  ∆T = T2 – T1 = 95 K – 185 K = -90 K
5
Найдите энтальпию по формуле ∆H = m x s x ∆T. Если известна m — масса реагентов, s — теплоемкость продукта реакции и ∆T — изменение температуры, то можно подсчитать энтальпию реакции. Подставьте значения в формулу ∆H = m x s x ∆T и получите энтальпию. Результат вычисляется в Джоулях (Дж).
- В нашем примере энтальпия вычисляется так:
  ∆H = (36 г) × (4,2 ДжK – 1 г – 1) × (-90 K) = -13608 Дж
6
Определите, выделяется или поглощается энергия в ходе рассматриваемой реакции. Одна из самых распространенных причин, по которой требуется вычислить ∆H на практике, — узнать, будет ли реакция экзотермической (выделение тепла и снижение собственной энергии) или эндотермической (поглощение тепла из окружающей среды и повышение собственной энергии). Если значение ∆H положительное, значит, реакция эндотермическая. Если отрицательное, значит, реакция экзотермическая. Чем больше абсолютное значение ∆H, тем больше энергии выделяется или поглощается. Будьте осторожны, если собираетесь проводить практический опыт: во время реакций с высоким значением энтальпии может произойти большое высвобождение энергии, и если оно протекает быстро, то может привести ко взрыву.
- В нашем примере конечный результат получился равным -13608 Дж. Перед значением энтальпии отрицательный знак, а это означает, что реакция экзотермическая. Горячие газы (в виде пара) H₂ и O₂ должны выделить некоторое количество тепла, чтобы образовать молекулу воды, то есть реакция образования H₂O является экзотермической.
Реклама

1
Подсчитайте энергию связей для оценки энтальпии. Почти все химические реакции приводят к разрыву одних связей и образованию других. Энергия в результате реакции не возникает ниоткуда и не разрушается: это та энергия, которая требуется для разрыва или образования этих связей. Поэтому изменение энтальпии всей реакции можно довольно точно оценить путем суммирования энергии этих связей.
- Например, рассмотрим реакцию: H₂ + F₂ → 2HF. В этом случае, энергия для разрыва связи в молекуле H₂ составляет 436 кДж/моль, а энергия для разрыва F₂ составляет 158 кДж/моль.^[1] Наконец, энергия необходимая для образования связи в молекуле HF из H и F = -568 кДж/моль.^[2] Умножаем последнее значение на 2, так как в ходе реакции получаем 2 моль HF: 2 × -568 = -1136 кДж/моль. Складываем значения:
  436 + 158 + (-1136) = -542 кДж/моль.
2
Используйте энтальпию образования для оценки энтальпии. Энтальпия образования позволяет рассчитать ∆H через вычисление реакций образования реагентов и продуктов. Если известна энтальпия образования продуктов реакции и реагентов, то вы можете оценить энтальпию в целом путем сложения, как и в случае энергии, рассмотренном выше.
- Например, рассмотрим следующую реакцию: C₂H₅OH + 3O₂ → 2CO₂ + 3H₂O. Мы знаем, что энтальпия образования рассчитывается:^[3]
  C₂H₅OH → 2C + 3H₂ + 0,5O₂ = 228 кДж/моль
  2C + 2O₂ → 2CO₂ = -394 × 2 = -788 кДж/моль
  3H₂ + 1.5 O₂ → 3H₂O = -286 × 3 = -858 кДж/моль
  Теперь необходимо сложить значения образованных веществ, полученные выше, для определения энтальпии реакции: C₂H₅OH + 3O₂ → 2CO₂ + 3H₂O,
  228 + -788 + -858 = -1418 кДж/моль.
3
Не забывайте о знаках перед значениями энтальпии. При вычислении энтальпии образования формулу для определения энтальпии реакции продукта вы переворачиваете, и знак энтальпии должен поменяться. Другими словами, если вы переворачиваете формулу, то знак энтальпии должен смениться на противоположный.
- В примере обратите внимание на то, что реакция образования для продукта C₂H₅OH записана наоборот. C₂H₅OH → 2C + 3H₂ + 0,5O₂ то есть C₂H₅OH распадается, а не синтезируется. Поэтому знак перед энтальпией в такой реакции положительный, 228 кДж/моль, хотя энтальпия образования C₂H₅OH составляет -228 кДж/моль.
Реклама

1
Возьмите чистую емкость и налейте туда воды. Увидеть принципы энтальпии в действии нетрудно — достаточно провести простой опыт. Необходимо, чтобы на результат эксперимента не повлияли посторонние загрязнители, так что емкость нужно вымыть и простерилизовать. Ученые для измерения энтальпии используют специальный закрытые контейнеры — калориметры, но вам вполне подойдет стеклянный стакан или колба. Заполните емкость чистой водопроводной водой комнатной температуры. Желательно проводить эксперимент в прохладном помещении.
- Для эксперимента желательно использовать небольшую емкость. Мы будем рассматривать энтальпию реакции воды с «Алка-Зельтцер», поэтому, чем меньше воды используется, тем более очевидным будет изменение температуры.
2
Поместите термометр в емкость. Возьмите термометр и опустите его в емкость с водой так, чтобы граница прочтения температуры была ниже уровня воды. Снимите показания термометра — это будет начальная температура, T1.
- Предположим, что температуры воды 10 °C. Мы будем использовать это значение для демонстрации принципов энтальпии.
3

Добавьте в емкость одну таблетку «Алка-Зельтцер». Готовы начать опыт? Бросьте в воду одну таблетку «Алка-Зельтцер». Она сразу начнет пузыриться и шипеть. Это происходит из-за реакции между бикарбонатом (HCO₃^–) и лимонной кислотой (H⁺). В результате образуются вода и углекислый газ по формуле: 3HCO₃⁻ + 3H⁺ → 3H₂O + 3CO₂.
4
Измерьте конечную температуру. Наблюдайте за ходом реакции: таблетка «Алка-Зельтцер» будет постепенно растворяться. Когда она растворится полностью, измерьте температуру еще раз. Вода должна стать немного холоднее. Если температура воды напротив стала выше начальной, значит, эксперименту помешали какие-то внешние факторы (например, слишком теплое помещение, где проводился эксперимент).
- Предположим, что температура составляет теперь 8 °C.
5
Подсчитаем энтальпию реакции. Когда таблетка «Алка-Зельтцер» вступает в реакцию с водой, образуются вода и углекислый газ (те самые шипучие пузырьки) и происходит снижение температуры (это тот результат, который должен получиться, если опыт прошел успешно). Можно сделать вывод, что данная химическая реакция является эндотермической, то есть она сопровождается поглощением энергии из окружающей среды — в данном случае из воды. В результате температура воды снижается.
- В нашем эксперименте температура воды снизилась на два градуса. Это согласуется с теорией: реакция растворения «Алка-Зельтцер» в воде эндотермическая и сопровождается небольшим поглощением энергии.
Реклама

Советы

В подсчетах используется шкала Кельвина (K) — это температурная шкала, аналогическая шкале Цельсия, и часто применяемая в химии и физике. Чтобы перевести значение градусов Цельсия в кельвины, необходимо добавить или вычесть 273 градуса: K = °C + 273.

Об этой статье

Эту страницу просматривали 115 669 раз.

Была ли эта статья полезной?

Источник

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Тепловой эффект процесса

Термохимические уравнения

Закон Гесса

Следствия из закона Гесса

Стандартные термодинамические величины

Стандартные энтальпии образования и сгорания

Примеры решения задач

Задачи для самостоятельного решения

Тепловой эффект процесса

Количество выделенной (или поглощенной) теплоты Q в данном процессе называют тепловым эффектом процесса. Экзотермической является реакция, протекающая с выделением теплоты, а эндотермической – с поглощением теплоты из окружающей среды.

Для лабораторных и промышленных процессов наиболее типичен изобарный режим (Р=const). Поэтому обычно рассматривают тепловой эффект при Р,Т = const, т.е. изменение энтальпии процесса ΔН.

Следует отметить, что абсолютные значения энтальпии Н определить не представляется возможным, так как не известна абсолютная величина внутренней энергии.

Для экзотермической реакции (Q > 0) ΔН < 0, а в эндотермическом процессе (Q < 0) ΔН > 0.

Термохимические уравнения

Химические уравнения, в которых дополнительно указывается величина изменения энтальпии реакции, а также агрегатное состояние веществ и температура, называются термохимическими уравнениями.

В термохимических уравнениях отмечают фазовое состояние и аллотропные модификации реагентов и образующихся веществ: г – газообразное, ж – жидкое, к – кристаллическое; S_(ромб), S_{(монокл)}, С_{(графит)}, С_(алмаз) и т.д.

Важно подчеркнуть, что с термохимическими уравнениями можно проводить алгебраические операции сложения, вычитания, деления, умножения.

Закон Гесса

Изменение энтальпии (внутренней энергии) химической реакции зависит от вида, состояния и количества исходных веществ и продуктов реакции, но не зависит от пути процесса.

Следствия из закона Гесса

Изменение энтальпии реакции равно сумме энтальпий образования продуктов реакции за вычетом суммы энтальпий образования исходных веществ (суммирование проводится с учетом стехиометрических коэффициентов).
Изменение энтальпии реакции равно сумме энтальпий сгорания исходных веществ за вычетом суммы энтальпий сгорания продуктов реакции (суммирование проводится с учетом стехиометрических коэффициентов).

Стандартные термодинамические величины

Стандартные термодинамические величины – это такие величины, которые относятся к процессам, все ингредиенты которых находятся в стандартных состояниях.

Стандартным состоянием вещества, находящегося в конденсированной фазе (кристаллической или жидкой), является реальное состояние вещества, находящегося при данной температуре и давлении 1 атм.

Следует подчеркнуть, что стандартное состояние может иметь место при любой температуре.

Обычно тепловой эффект (изменение энтальпии) реакции приводится для температуры 25^оС (298,15 К) и давления 101,325 кПа (1 атм), т.е. указывается стандартная энтальпия ΔН^о₂₉₈.

Стандартные энтальпии образования и сгорания

Стандартная энтальпия образования ΔН^о_f,298 (или ΔН^о_обр,298) – это изменение энтальпии в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии, причем простые вещества присутствуют в наиболее термодинамически устойчивых состояниях при данной температуре.

Например, ΔН^o_f,298(Н₂О(ж)) = — 285,83 кДж/моль соответствует изменению энтальпии в процессе

Н_2(г) + ½O_2(г) = Н₂О_(ж)

при Т = 298,15 К и Р = 1 атм.

Стандартная энтальпия образования простых веществ равна нулю по определению (для наиболее устойчивых их модификаций при данной температуре).

Стандартной энтальпией сгорания ΔН^o_сгор,298 называют энтальпию сгорания вещества (обычно 1 моль), находящегося в стандартном состоянии с образованием СО_2(г), Н₂О_(ж) и других веществ, состав которых должен быть специально указан. Все продукты сгорания также должны находиться в стандартном состоянии.

Примеры решения задач

Задача 1. Используя справочные термодинамические данные вычислить ΔН^o₂₉₈ реакции:

2H₂S(г) + 3O₂(г) = 2SO₂(г) + 2H₂O(ж); ΔН^oх.р.,₂₉₈ = ?

Решение. Решим задачу, используя оба следствия из закона Гесса. Ниже для исходных веществ и продуктов реакции приведены значения энтальпий образования и сгорания в кДж/моль (энтальпия сгорания сероводорода до SO_2(г) и H₂O_(ж)):

Вещество	H₂S(г)	O₂(г)	SO₂(г)	H₂O(ж)
ΔН^o_f,298	-20,60	0	-296,90	-285,83
ΔН^o_сгор,298	-562,10	0	0	0

Cогласно первому следствию закона Гесса энтальпия этой реакции ΔН^о_х.р. равна:

ΔН^о_х.р.,298 = 2ΔН^о_f,298(SO_2(г)) + 2ΔН^о_f,298(H₂O_(ж)) — 2ΔН^о_f,298(H₂S_(г)) — 3ΔН^о_f,298(O_2(г)) = 2(- 296,90) + 2(- 285,83) — 2(- 20,60) = — 1124,21 кДж.

В соответствии со вторым следствием закона Гесса получаем:

ΔН^о_х.р.,298 = 2ΔН^о_сгор,298(H₂S(г)) = 2(-562,10) = — 1124,20 кДж.

Задача 2. Вычислите ΔН^о₂₉₈ реакции N₂(г) + 3H₂(г) = 2NH₃(г), используя следующие данные:

4NH_3(г) + 3O_2(г) = 2N_2(г) + 6H₂O_(ж); ΔН^о₁ = -1531,22 кДж;

2H₂O_(ж) = O_2(г) + 2H_2(г); ΔН^о₂= 571,66 кДж.

Определите стандартную энтальпию образования NH₃(г).

Решение. Поскольку с термохимическими уравнениями можно производить все алгебраические действия, то искомое уравнение получится, если:

- - разделить на два тепловой эффект первого уравнения и изменить его знак на противоположный, т.е:

N_2(г) + 3H₂O_(ж) = 2NH_3(г) + 3/2O_2(г); ΔН^о = 765,61 кДж;

- - умножить на 3/2 второе уравнение и соответствующую ему величину δН^o , изменив ее знак на противоположный:

3/2O_2(г) + 3H_2(г) = 3H₂O_(ж); ΔН^о = -857,49 кДж;

- - сложить полученные первое и второе уравнения.

Таким образом, тепловой эффект реакции N_2(г) + 3H_2(г) = 2NH_3(г) равен:

Δ Н^о₂₉₈ = (- ΔН^о₁/2) + (- 3/2·ΔН^о₂) = 765,61 + (- 857,49) = — 91,88 кДж.

Поскольку в рассматриваемой реакции образуется 2 моль NH_3(г), то

ΔН^о_f,298(NH_3(г)) = — 91,88/2 = — 45,94 кДж/моль.

Задача 3. Определите энтальпию процесса

CuSO_4(к) + 5H₂O_(ж) = CuSO₄·5H₂O_(к)

если при 298,15 К энтальпия растворения CuSO_4(к) в n моль Н₂О с образованием раствора CuSO₄(р-р, nH₂O) равна –40, а энтальпия растворения CuSO₄·5H₂O_(к) с образованием раствора той же концентрации равна +10,5 кДж/моль.

Решение. Составляем цикл Гесса:

ΔН^о₁ = ΔН^о₂+ ΔН^о_х (по закону Гесса). Отсюда получаем:

ΔН^о_х = ΔН^о₁ – ΔН^о₂ = – 40,0 – 10,5 = -50,5 кДж.

Другой вариант решения.

CuSO_4(к) + (n H₂O) = CuSO₄(р-р, n H₂O); ΔН^о₁ = – 40,0 кДж; (1)

CuSO_4(к) + 5H₂O(ж) = CuSO₄·5H₂O(к); ΔН^о_х = Н^о₂; (2)

CuSO₄·5H₂O_(к)+ (n – 5)H₂O = CuSO₄(р-р, nH₂O); ΔН^о₃ = 10,5 кДж. (3)

По закону Гесса: ΔН^о₁ = ΔН^о_х+ ΔН^о₃, т.е. при сложении уравнений (2) и (3) получим уравнение (1).

Задача 4. Вычислите энтальпию образования химической связи С= С в молекуле этилена, если его стандартная энтальпия образования равна 52,3 кДж/моль, энтальпия возгонки графита составляет 716,7 кДж/моль, энтальпия атомизации водорода равна +436,0 кДж/моль, энтальпия образования связи С–Н равна –414,0 кДж/моль.

Решение. Составляем цикл Гесса:

ΔН^о_f,298(С₂Н_4(г)) = 2ΔН^о_возг(С_{(графит)}) + 2ΔН^о_атом(H_2(г)) + ΔН^о_(С= С) + 4ΔН^о_(С–Н).

ΔН^о_(С = С) = 52,3 — 2·716,7 — 2·436,0 + 4·414,0 = — 597,1 кДж/моль.

Задачи для самостоятельного решения

1. Составьте уравнение реакции, для которой ΔН^о соответствует стандартной энтальпии образования ВaCl₂·2H₂O_(к).

2. Определить ΔН^о₂₉₈ реакции:

CH₃CНO_(ж) + H_2(г) = CH₃CH₂OH_(ж),

если ΔН^о_сгор,298(CH₃CНO_(ж)) = — 1193,07 кДж/моль; ΔН^о_сгор,298(CH₃CH₂OH_(ж)) = — 1370,68 кДж/моль; ΔН^о_f,298(Н₂О_(ж)) = — 285,83 кДж/моль.

10.3. Энтальпии растворения BaCl_2(к) и BaCl₂·2H₂O_(к) с образованием раствора хлорида бария (с мольным отношением BaCl₂: H₂O = 1: 500) соответственно равны –11,18 и 18,74 кДж/моль.
Определить величину ΔН^о присоединения воды к BaCl_2(к) с образованием BaCl₂·2H₂O_(к).

10.4. Рассчитать энтальпию связи в молекуле NO на основании следующих термохимических уравнений:

N_2(г) + O_2(г) = 2NO_(г); ΔН^о₂₉₈ = +182,52 кДж;

2O_(г) = O_2(г); ΔН^о₂₉₈ = — 498,34 кДж;

N_2(г) = 2N_(г); ΔН^о₂₉₈ = +945,42 кДж.

10.5. Вычислить ΔН^о₂₉₈ реакции 2C(г) + 2H₂(г) = C₂H₄(г), используя следующие термохимические уравнения:

С_{(графит)} = С_(г); ΔН^о₂₉₈ = +716,67 кДж;
С₂H_4(г) + 3O_2(г) = 2CO_2(г) + 2H₂O_(г); ΔН^о₂₉₈ = — 1322,94 кДж;
C_{(графит)} + O_2(г) = CO_2(г); ΔН^о₂₉₈ = — 393,51 кДж;

H_2(г) + 1/2O_2(г) = H₂O_(г); ΔН^о₂₉₈ = — 241,81 кДж.

10.6. Определите стандартную энтальпию реакции взаимодействия метана с оксидом углерода (IV), если стандартные энтальпии образования метана, оксида углерода (IV) и оксида углерода (II) при 298 К равны соответственно: -75; -393 и -111 кДж/моль.

7. Определите стандартную энтальпию образования С₂Н₅ОН_(ж), если стандартные энтальпии сгорания углерода, водорода и этанола при 298 К равны соответственно: -393; -286 и -1366 кДж/моль.

8. Вычислите энтальпию химической реакции 4KClO_3(к)=KCl_(к)+3KClO_4(к) по следующим данным:

2KClO_3(к)=2KCl_(к)+3O_2(г); ΔН^о₂₉₈ = — 95 кДж;
4KClO_4(к)=KCl_(к)+2O_2(г); ΔН^о₂₉₈ = 9 кДж/моль.

9. Вычислите среднюю энтальпию связи P-Cl в молекуле PCl₅, используя следующие термохимические уравнения:

P_{(к, бел.)}+5/2Cl_2(г)=PCl_5(г); ΔН^о₁ = — 374,8 кДж;
P_{(к, бел.)}=P_(г); ΔН^о₂ = — 17,4 кДж;
Cl_2(г)=2Cl_(г); ΔН^о₃ = 242,6 кДж.

10. Вычислите среднюю энтальпию связи N-H в молекуле NH₃, используя следующие термохимические уравнения:

1/2N_2(г)+3/2H_2(г)=NH_3(г); ΔН^о₁ = — 46,2 кДж;
N_2(г)=2N_(г); ΔН^о₂ = 945,4 кДж;
H_2(г)=2H_(г); ΔН^о₃ = 436,0 кДж.

Источник

Энтальпия

Размерность	$L^{2}MT^{{-2}}$
Единицы измерения
СИ	Дж
СГС	эрг
Примечания
Внесистемные единицы: калория, британская тепловая единица

Энтальпи́я (от др.-греч. ενθαλπω — «нагреваю», также теплова́я фу́нкция^[1]^[2], теплова́я фу́нкция Гиббса^[3], теплосодержа́ние^[1]^[3] и изобарно-изоэнтропийный потенциал^[4]) — функция состояния термодинамической системы, определяемая как сумма внутренней энергии и произведения давления на объём ^[1]^[5]^[6]^{[K 1]}:

{displaystyle Hequiv U+PV.qquad qquad qquad qquad }

(Определение энтальпии)

Из уравнения для дифференциала внутренней энергии^[9]^[10]:

{displaystyle mathrm {d} U=Tmathrm {d} S-Pmathrm {d} V,qquad }

(Дифференциал внутренней энергии)

где — термодинамическая температура, а — энтропия, следует выражение для дифференциала энтальпии^[3]^[11]^{[K 2]}:

{displaystyle mathrm {d} H=Tmathrm {d} S+Vmathrm {d} P,qquad qquad qquad }

(Дифференциал энтальпии)

которое является полным дифференциалом функции ^{[K 3]}. Она представляет собой термодинамический потенциал^[⇨] относительно естественных независимых переменных — энтропии, давления и, возможно, числа частиц^[⇨] и других переменных состояния ^[⇨].

Понятие энтальпии существенно дополняет математический аппарат термодинамики^[⇨] и гидродинамики^[⇨].
Важно, что в изобарном процессе при постоянном изменение энтальпии

${displaystyle H_{2}-H_{1}=U_{2}-U_{1}+Pleft(V_{2}-V_{1}right)=Q,}$

равное сумме изменения внутренней энергии ${displaystyle U_{2}-U_{1}}$ и совершённой системой работы ${displaystyle Pleft(V_{2}-V_{1}right)}$ , в силу первого начала термодинамики равно количеству теплоты , сообщенной системе. Это свойство энтальпии позволяет использовать её для вычисления тепловыделения при различных изобарных процессах, например, химических^[⇨].

Отношение малого количества теплоты, переданного системе в изобарном процессе, к изменению температуры является теплоёмкостью при постоянном давлении^{[K 4]}^[20]:

${displaystyle C_{P}equiv Tleft({frac {partial S}{partial T}}right)_{P}=left({frac {partial H}{partial T}}right)_{P}.}$

Это экспериментально измеримая величина, и из её измерений находят температурную зависимость энтальпии^[⇨].

Энтальпия — экстенсивная величина: для составной системы она равна сумме энтальпий её независимых частей. Как и внутренняя энергия, энтальпия определяется с точностью до произвольного постоянного слагаемого.

Первое упоминание об использовании термина «энтальпия» в его современном значении^[21]

История вопроса[править | править код]

Понятие энтальпии было введено и развито Дж. В. Гиббсом^[22]^[23]^[24] в 1875 году в классической работе «О равновесии гетерогенных веществ». Для обозначения этого понятия Гиббс использовал термин «тепловая функция при постоянном давлении»^[25]^[26].

Автором термина «энтальпия» в его современном значении считают Х. Камерлинг-Оннеса. Впервые о его авторстве упоминает работа 1909 года^[27]^[28] в связи с обсуждением сохранения энтальпии в эффекте Джоуля — Томсона^[⇨], хотя в печатных публикациях самого Камерлинг-Оннеса это слово не встречается^[29]. Что же касается буквенного обозначения , до 1920-х годов оно использовалось для количества теплоты вообще. Определение физической величины строго как энтальпии или «теплосодержания при постоянном давлении» было официально предложено Альфредом У. Портером в 1922 году^[23].

Энтальпия как термодинамический потенциал[править | править код]

Поскольку внутренняя энергия является термодинамическим потенциалом относительно энтропии и объёма^[30],
определение энтальпии можно рассматривать как преобразование Лежандра для перехода от потенциала относительно переменных к таковому относительно переменных Как и для любого термодинамического потенциала, естественные независимые переменные совокупно с производными энтальпии по этим переменным позволяют выразить любой термодинамический параметр системы, поэтому задание термодинамического потенциала является самым общим способом задания уравнения состояния^[31].

Из выражения для дифференциала энтальпии получаются ещё два уравнения состояния, непосредственно выражающие температуру и объём через энтальпию и давление^[32]:

${displaystyle T(S,P)=left({frac {partial H}{partial S}}right)_{P},qquad V(S,P)=left({frac {partial H}{partial P}}right)_{S}.}$

Если известна энтальпия, другие термодинамические потенциалы — внутренняя энергия , свободная энергия Гельмгольца и энергия Гиббса — могут быть получены с помощью преобразования Лежандра:

${displaystyle G=H-TS=H-Sleft({frac {partial H}{partial S}}right)_{P},qquad U=H-PV=H-Pleft({frac {partial H}{partial P}}right)_{S},}$

${displaystyle F=H-TS-PV=H-Sleft({frac {partial H}{partial S}}right)_{P}-Pleft({frac {partial H}{partial P}}right)_{S}.}$

Из равных друг другу смешанных производных энтальпии выводятся две термодинамические производные, связанные третьим соотношением Максвелла^[33]:

${displaystyle left({frac {partial T}{partial P}}right)_{S}={frac {partial }{partial P}}left({frac {partial H}{partial S}}right)_{P}={frac {partial }{partial S}}left({frac {partial H}{partial P}}right)_{S}=left({frac {partial V}{partial S}}right)_{P}.}$

Через вторые производные энтальпии выражаются ещё две термодинамические производные:

${displaystyle left({frac {partial ^{2}H}{partial S^{2}}}right)_{P}=left({frac {partial T}{partial S}}right)_{P},qquad left({frac {partial ^{2}H}{partial P^{2}}}right)_{S}=left({frac {partial V}{partial P}}right)_{S}.}$

Первая из этих производных характеризует теплоёмкость при постоянном давлении ${displaystyle left({frac {partial T}{partial S}}right)_{P}={frac {T}{C_{P}}},}$ вторая — адиабатическую сжимаемость.
Метод якобианов позволяет получить тождества, аналогичные соотношениям Бриджмена, для выражения любых термодинамических производных через приведённые производные энтальпии.

Зависимость энтальпии от числа частиц[править | править код]

Для состоящей из одинаковых частиц открытой системы число частиц может быть переменным^{[K 5]}. В этом случае выражения для дифференциалов внутренней энергии и энтальпии обобщаются следующим образом^[35]^[36]:

${displaystyle mathrm {d} U=Tmathrm {d} S-Pmathrm {d} V+mu _{N}mathrm {d} N,qquad mathrm {d} H=Tmathrm {d} S+Vmathrm {d} P+mu _{N}mathrm {d} N,}$

где ${displaystyle mu _{N}=left({frac {partial U}{partial N}}right)_{S,V}=left({frac {partial H}{partial N}}right)_{S,P}}$ — химический потенциал, который равен энергии Гиббса ^[37], приходящейся на одну частицу^[38]: ${displaystyle mu _{N}=(H-TS)/N}$ . Если частицы не рождаются и не уничтожаются в рассматриваемом процессе, можно характеризовать их количество, например, (переменной) массой тела и химический потенциал также относить к единице массы. В этом случае вклад от изменения массы вещества в дифференциалы энергии и энтальпии описывается членом , где модифицированный химический потенциал равен удельной (отнесенной к единице массы) энергии Гиббса: ${displaystyle {mu }={frac {H-TS}{m}}}$ .

Схема контрольного объёма. За малый интервал времени изменение массы равно ${displaystyle mathrm {d} m=left({dot {m}}_{rm {in}}-{dot {m}}_{rm {out}}right)dt.}$

В англоязычной литературе, особенно технической, понятие открытой системы обычно отождествляют с понятием «контрольного объёма» (англ. control volume)^[39], который ограничен воображаемой неподвижной контрольной^[40] поверхностью, проницаемой для вещества, но оставляющей неизменной заключённый в ней объём. В то же время закрытую систему называют «контрольной массой» (англ. control mass). Последнее название подчеркивает постоянство массы (), вследствие которого справедливо приведённое выше соотношение для дифференциала внутренней энергии и термодинамическое состояние системы характеризуется только двумя параметрами, например, и . С другой стороны, при постоянстве контрольного объёма () заключённая в нём внутренняя энергия тоже характеризуется только двумя параметрами, например, энтропией и переменной массой , причём в практически важное выражение для дифференциала внутренней энергии контрольного объёма входит (удельная) энтальпия^[41]:

${displaystyle mathrm {d} U=Tmathrm {d} S+{mu }mathrm {d} m=Tmathrm {d} S+{frac {H-TS}{m}}mathrm {d} m=mTmathrm {d} left({frac {S}{m}}right)+{frac {H}{m}}mathrm {d} m.qquad (}$

Энергия контрольного объёма)

Если в системе присутствуют несколько различных веществ характеризующихся массами $m_{j}$ и химическими потенциалами $mu _{j}$ , выражение для дифференциала энтальпии обобщается следующим образом^[42]^[43]:

${displaystyle mathrm {d} H=Tmathrm {d} S+Vmathrm {d} P+sum _{j}mu _{j}mathrm {d} m_{j}.}$

Удельная энтальпия[править | править код]

Удельная энтальпия
${displaystyle h= {frac {H}{m}}}$
Размерность	${displaystyle L^{2}T^{-2}}$
Единицы измерения
СИ	Дж/кг
СГС	эрг/г
Примечания
Внесистемные единицы: кал/г, кал/кг

Молярная (мольная) энтальпия
${displaystyle H_{m}= {frac {H}{n}}=hM_{r}M_{u}}$
Размерность	$L^{2}MT^{{-2}}$
Единицы измерения
СИ	Дж/моль ( ${displaystyle M_{u}=10^{-3},}$ кг/моль)
СГС	эрг/моль ( ${displaystyle M_{u}=,}$ 1 г/моль)
Примечания
Внесистемная единица: кал/моль

Плотность энтальпии
${displaystyle hrho = {frac {H}{V}}}$
Размерность	${displaystyle L^{-1}MT^{-2}}$
Единицы измерения
СИ	Дж/м³
СГС	эрг/см³

Вместо экстенсивной величины энтальпии часто используют её отношение ${displaystyle h={frac {H}{m}}}$ её величины к массе тела , называемое удельной энтальпией. Продолжая обозначать экстенсивные величины заглавными буквами, соответствующие им удельные величины будем обозначать строчными, за исключением удельного объёма, вместо которого введём обратную к этой величине плотность:

${displaystyle s={frac {S}{m}},qquad {frac {1}{rho }}={frac {V}{m}},qquad u={frac {U}{m}},qquad h={frac {H}{m}}=u+{frac {P}{rho }}.}$

Соотношение для полного дифференциала удельной энтальпии можно получить, разделив уравнение для дифференциала энтальпии на :

${displaystyle mathrm {d} h=Tmathrm {d} s+{frac {1}{rho }}mathrm {d} P.qquad }$

(Дифференциал удельной энтальпии)

Удельную энтальпию можно представлять графически в виде -диаграммы Молье. На диаграмме кривые (изобары) для различных значений давления задают функцию ^[44]. Большой практический интерес представляет диаграмма Молье для воды/водяного пара^[45], схематически изображённая на рисунке: синие линии — изобары, зелёные — изотермы. Область ниже красной кривой соответствует двухфазной среде пара и воды. В этой области красные линии соответствуют различным значениям величины — массовой доли водяного пара — и пересекаются в критической точке K, а изобары совпадают с изотермами и являются прямыми линиями.

Вводят также молярную (мольную) энтальпию ${displaystyle H_{m}={frac {H}{n}}}$ , отнесённую не к массе, а к количеству вещества в теле в молях n, что удобно для приложений к химии. Молярные величины обозначают нижним индексом m. Альтернативное определение через удельную энтальпию: ${displaystyle H_{m}=hM_{r}M_{u}}$ , где M_r — относительная молекулярная масса, а ${displaystyle M_{u}=10^{-3},}$ кг/моль =1 г/моль — коэффициент для перевода относительной молекулярной массы в молярную^[46].

Плотности внутренней энергии и энтальпии (на единицу объёма) вводят как отношение этих величин к объёму. Отдельные обозначения для этих величин здесь не вводятся, их можно выразить через удельные величины и массовую плотность:

${displaystyle {frac {U}{V}}={frac {m}{V}}u=rho u,qquad {frac {H}{V}}={frac {m}{V}}h=rho h.}$

Деление уравнения для дифференциала энергии контрольного объёма на величину контрольного объёма даёт соотношение^[47]:

{displaystyle mathrm {d} left(rho uright)=rho Tmathrm {d} s+hmathrm {d} rho .qquad }

(Дифференциал плотности энергии)

Плотность энергии и энтальпии идеального газа[править | править код]

Для идеального газа с постоянной теплоёмкостью плотность внутренней энергии и энтальпии простым образом выражается через давление^[48]:

${displaystyle {frac {U}{V}}={frac {1}{gamma -1}}P,qquad qquad {frac {H}{V}}={frac {gamma }{gamma -1}}P,}$

где gamma — показатель адиабаты, равный для одноатомного газа, для фотонного газа (излучения чёрного тела)^[49].

Энтальпия сложных термодинамических систем[править | править код]

Для термодинамических систем сложного типа, в которых термодинамическая работа^[50] не сводится к работе внешних сил давления , первое начало термодинамики, а значит и выражение для дифференциала внутренней энергии, включают вклад от термодинамической работы в виде^[35]^[51]:

${displaystyle mathrm {d} U=Tmathrm {d} S+sum _{i}{X_{i}mathrm {d} x_{i}}=Tmathrm {d} S-Pmathrm {d} V+sum _{ineq 1}{X_{i}mathrm {d} x_{i}}.}$

где $X_{i}$ — -я обобщённая сила и $x_{i}$ — сопряжённая с ней -я обобщённая координата, во втором равенстве из общего перечня переменных выделена обобщённая сила ${displaystyle X_{1}=-P}$ и обобщённая координата ${displaystyle x_{1}=V}$ . Для этого случая определение обобщённой энтальпии ${displaystyle H^{*}=U+PV-sum _{ineq 1}X_{i}x_{i}}$ ^[52] даёт^[53]:

${displaystyle mathrm {d} H^{*}=Tmathrm {d} S+Vmathrm {d} P-sum _{ineq 1}x_{i}mathrm {d} X_{i}.}$

Обобщенная энтальпии сохраняет смысл эквивалента теплоты для изобарного процесса^[54]^[55], если не только давление, но и все остальные обобщённые силы поддерживаются постоянными: ${displaystyle mathrm {d} X_{i}equiv 0}$ .

Энтальпия образования[править | править код]

Для приложений к химии в общем случае открытых систем для полного дифференциала энтальпии получаем:

{displaystyle mathrm {d} H=mathrm {d} U+mathrm {d} (PV)=mathrm {d} U+Vmathrm {d} P+Pmathrm {d} V.qquad qquad (***)}

Выражение для заимствуем из дифференциальной версии фундаментального уравнения Гиббса для внутренней энергии открытой термодинамической системы^[56]^[57]:

${displaystyle mathrm {d} U=Tmathrm {d} S+sum _{j}mu _{j}mathrm {d} m_{j},}$

где $m_{j}$ — масса -го независимого компонента^{[K 6]}, $mu _{j}$ — химический потенциал этого компонента. Запишем уравнение Гиббса в следующем виде:

${displaystyle mathrm {d} U=Tmathrm {d} S-Pmathrm {d} V+sum _{j}mu _{j}mathrm {d} m_{j}.}$

Подставив это выражение в соотношение (***), получаем дифференциальную версию фундаментального уравнения Гиббса для энтальпии:

${displaystyle mathrm {d} H=Tmathrm {d} S+Vmathrm {d} P+sum _{j}mu _{j}mathrm {d} m_{j}.}$

Все химические реакции сопровождаются выделением (экзотермические) или поглощением (эндотермические) тепла. Одно из приложений энтальпии основано на том, что множество химических процессов в реальных или лабораторных условиях реализуются именно при постоянном (атмосферном) давлении. Поэтому мерой теплового эффекта реакции служит изменение энтальпии ΔН в ходе химической реакции, в результате которой исходные вещества исчезают и образуются продукты реакции. В случае экзотермических реакций система теряет тепло и ΔН — величина отрицательная. В случае эндотермических реакций система поглощает тепло и ΔН — величина положительная. В частности, энтальпия образования — это количество теплоты, которое поглощается (если энтальпия образования положительна) или выделяется (если энтальпия образования отрицательна) при образовании сложного вещества из простых веществ.

Значение энтальпии образования и другие термодинамические свойства веществ приведены в справочниках^[58]^[59].

Зависимость энтальпии от температуры[править | править код]

Во многих приложениях (но только не в качестве термодинамического потенциала!) энтальпию системы удобно представлять в виде функции от давления и температуры . Чтобы получить выражение для дифференциала энтальпии в переменных дифференциал энтропии выражается через :

${displaystyle mathrm {d} S=left({frac {partial S}{partial T}}right)_{P}mathrm {d} T+left({frac {partial S}{partial P}}right)_{T}mathrm {d} P.}$

Температурная производная энтропии выражается через (измеримую) теплоёмкость при постоянном давлении ${displaystyle C_{P}equiv left({frac {partial H}{partial T}}right)_{P}=Tleft({frac {partial S}{partial T}}right)_{P}}$ . Производная энтропии по давлению выражаются с помощью четвёртого соотношения Максвелла (G2) ${displaystyle left({frac {partial S}{partial P}}right)_{T}=-left({frac {partial V}{partial T}}right)_{P},}$ что даёт ${displaystyle mathrm {d} S={frac {C_{P}}{T}}mathrm {d} T-left({frac {partial V}{partial T}}right)_{P}mathrm {d} Pquad }$ и:

${displaystyle quad mathrm {d} H=C_{P}mathrm {d} T+left[V-Tleft({frac {partial V}{partial T}}right)_{P}right]mathrm {d} P.}$

Для идеального газа в силу закона Гей-Люссака ${displaystyle left({frac {partial V}{partial T}}right)_{P}={rm {const}}={frac {V}{T}},}$ так что выражение в квадратных скобках равно нулю, и энтальпия идеального газа зависит только от температуры. Если к тому же идеальный газ имеет постоянную темплоёмкость, его энтальпия линейно зависит от температуры^[60]:

${displaystyle H=C_{P}T+Nvarepsilon _{0},qquad h=c_{P}T+{frac {varepsilon _{0}}{M}},qquad qquad }$

(Энтальпия идеального газа)

где $varepsilon _{0}$ — внутренняя энергия молекулы при нулевой температуре^{[K 7]}, — масса молекулы. Удельная энтальпии выражена через удельную теплоёмкость ${displaystyle c_{P},}$ отнесённую к единице массы.

Для реальных систем изменение энтальпии при изменении температуры в изобарическом процессе практически удобно рассчитывать, если известна теплоёмкость при постоянном давлении ${displaystyle C_{P}(T)}$ (например, в виде ряда ${displaystyle C_{P}(T)=sum _{i=0}^{n}a_{i}T^{i}}$ по степеням с эмпирическими коэффициентами^[61]^[62]):

${displaystyle H(T_{2},P)-H(T_{1},P)=int limits _{T_{1}}^{T_{2}}{C_{P}(T)mathrm {d} T}=sum _{i=0}^{n}{{frac {a_{i}}{i+1}}left(T_{2}^{i+1}-T_{1}^{i+1}right)}.}$

Поскольку разности энтальпий продуктов химической реакции и исходных веществ определяет тепловой эффект химической реакции^[⇨], разность теплоёмкостей продуктов реакции и исходных веществ определяет зависимость теплового эффекта реакции от температуры (термохимический закон Кирхгофа).

Сохранение энтальпии в эффекте Джоуля — Томсона[править | править код]

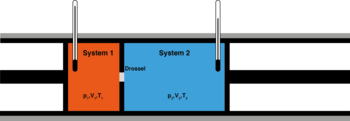
Рис. 2 — Сохранение энтальпии в эффекте Джоуля — Томсона. Изменение энергии газа в ходе этого процесса равно работе: ${displaystyle U_{2}-U_{1}=P_{1}V_{1}-P_{2}V_{2} }$ . Из определения энтальпии () следует, что ${displaystyle H_{1}=H_{2}}$

Сохранение энтальпии в процессе Джоуля — Томсона привлекается для количественного описания эффекта. Схема процесса представлена на рисунке 2. Левый поршень, вытесняя газ под давлением ${displaystyle P_{1}>P_{2}}$ из объёма $V_{1}$ , совершает над ним работу ${displaystyle P_{1}V_{1}}$ . Пройдя через дроссель и расширяясь в объём $V_{2}$ , газ совершает работу ${displaystyle P_{2}V_{2}}$ над правым поршнем. Суммарная работа ${displaystyle P_{1}V_{1}-P_{2}V_{2}}$ , совершенная над газом, равна изменению его внутренней энергии ${displaystyle U_{2}-U_{1}=P_{1}V_{1}-P_{2}V_{2}}$ , так что энтальпия сохраняется: ${displaystyle H_{1}=H_{2}}$ ^[63]^[64]

Из уравнения для дифференциала энтальпии выводится выражение для коэффициента Джоуля — Томсона ${displaystyle mu _{mathrm {JT} }}$ , который связывает малые изменения температуры и давления в этом процессе. Приравнивание нулю дифференциала (сохраняющейся) энтальпии в переменных даёт^[65]^[66] ${displaystyle C_{P}mathrm {d} T+left[V-Tleft({frac {partial V}{partial T}}right)_{P}right]mathrm {d} P=0}$ и

${displaystyle mu _{mathrm {JT} }={frac {mathrm {d} T}{mathrm {d} P}}={frac {Tleft({frac {partial V}{partial T}}right)_{P}-V}{C_{P}}},}$

а выражение для дифференциала энтальпии в переменных даёт связь между изменениями давления и энтропии:

${displaystyle {frac {mathrm {d} S}{mathrm {d} P}}=-{frac {V}{T}}<0.}$

В процессе Джоуля — Томсона давление всегда убывает, следовательно, энтропия возрастает.

Полная энергия и полная энтальпия[править | править код]

Полная энтальпия (удельная) (энтальпия торможения)
${displaystyle {bar {h}}=h+{frac {1}{2}}{vec {v}}^{2}}$
Размерность	${displaystyle L^{2}T^{-2}}$
Единицы измерения
СИ	Дж/кг
СГС	эрг/г
Примечания
Зависит от выбора системы отсчёта

Для движущихся тел помимо внутренней энергии, включающей кинетическую энергию теплового движения составляющих тело частиц (измеренную в системе координат, в которой тело как целое покоится), вводят также его полную энергию в системе координат, относительно которой тело движется со скоростью vec{v} . Обычно полная энергия тела есть просто сумма его внутренней и кинетической энергий ${displaystyle E=U+{frac {1}{2}}m{vec {v}}^{2}.}$ Более общий и строгий подход^[⇨] определяет не полную энергию, а её дифференциал^[67]:

{displaystyle mathrm {d} E=Tmathrm {d} S-Pmathrm {d} V+{vec {v}}cdot mathrm {d} {vec {g}},qquad }

(Дифференциал полной энергии)

где – импульс тела и точка между векторами означает их скалярное произведение. В полную энтальпию также включается кинетическая энергия. Имеющие большое значение для физики сплошных сред удельная полная энергия и удельная полная энтальпия (обычно называемая просто «полная энтальпия» или, особенно в технических науках, «энтальпия торможения»^[⇨]) даются формулами:

${displaystyle e=u+{frac {1}{2}}{vec {v}}^{2},qquad {bar {h}}=h+{frac {1}{2}}{vec {v}}^{2}=u+{frac {P}{rho }}+{frac {1}{2}}{vec {v}}^{2}}$

Обобщение дифференциала плотности энергии для полной энергии принимает вид^[47]:

{displaystyle mathrm {d} left(rho eright)=rho Tmathrm {d} s+{bar {h}}mathrm {d} rho +rho {vec {v}}cdot mathrm {d} {vec {v}}.qquad }

(Дифференциал плотности полной энергии)

Релятивистская энтальпия[править | править код]

Полная энтальпия (инвариантная релятивистская)
${displaystyle {bar {H}}_{0}=E_{0}+P_{0}V_{0}}$
Размерность	$L^{2}MT^{{-2}}$
Единицы измерения
СИ	Дж
СГС	эрг
Примечания
Лоренц-инвариант

Полная энтальпия (релятивистская)
${displaystyle {bar {H}}={frac {{bar {H}}_{0}}{sqrt {1-{vec {v}}^{2}/c^{2}}}}}$
Размерность	$L^{2}MT^{{-2}}$
Единицы измерения
СИ	Дж
СГС	эрг
Примечания
Образует 4-вектор вместе с импульсом ${displaystyle {vec {g}}={vec {v}}{bar {H}}/c^{2}}$

Если скорость тела vec{v} сравнима по величине со скоростью света , термодинамика строится с учётом специальной теории относительности)^[67]. При этом используется инвариантная энтальпия ${displaystyle {bar {H}}_{0}=E_{0}+P_{0}V_{0}}$ , которая представляет собой полную энтальпию, определённую в движущейся вместе с телом системе отсчета; все величины в этой системе отсчёта обозначаем нижним индексом «0».

Релятивистская полная энергия $E_{0}$ , включает энергию покоя всех частиц тела и учитывает релятивистскую зависимость их энергии от импульса , а именно: 1) энергия и импульс образуют 4-вектор, 2) величина ${displaystyle {sqrt {{cal {E}}^{2}-c^{2}{vec {p}}^{2}}}}$ является Лоренц-инвариантом и 3) величина ${displaystyle c^{2}{vec {p}}/{cal {E}}}$ являются скоростью частицы.
В неподвижной системе отсчета энтальпия и импульс движущегося тела^[68]^[67]

${displaystyle {bar {H}}={frac {{bar {H}}_{0}}{sqrt {1-{vec {v}}^{2}/c^{2}}}},qquad {vec {g}}={frac {{vec {v}}{bar {H}}_{0}/c^{2}}{sqrt {1-{vec {v}}^{2}/c^{2}}}}={vec {v}}{bar {H}}/c^{2}}$

образуют 4-вектор, а инвариантная энтальпии в движущейся с телом системы отсчёта даётся инвариантной функцией этого 4-вектора:

${displaystyle {bar {H}}_{0}={sqrt {{bar {H}}^{2}-c^{2}{vec {g}}^{2}}}.}$

Именно полная энтальпия (а не энергия) релятивистского тела оказывается аналогом энергии релятивистской частицы. Давление $P=P_{0}$ лоренц-инвариантно, а преобразование объёма :

${displaystyle {frac {V}{sqrt {1-{vec {v}}^{2}/c^{2}}}}=V_{0}}$

является следствием Лоренцева сокращения. Уравнение релятивистской термодинамики даётся выражением^[68]:

${displaystyle mathrm {d} {bar {H}}_{0}=T_{0}mathrm {d} S_{0}+{frac {V}{sqrt {1-{vec {v}}^{2}/c^{2}}}}mathrm {d} P_{0}}$

Оно позволяет решить любой вопрос термодинамики движущихся систем, если известна функция ${displaystyle {bar {H}}_{0}(S_{0},P_{0})}$ ^[68]. В частности, из выражения для Дифференциала полной энергии можно получить выражение для малого количества теплоты^[67]: ${displaystyle Q={sqrt {1-{frac {{vec {v}}^{2}}{c^{2}}}}}T_{0}mathrm {d} S_{0}.}$

Энтальпия в гидродинамике[править | править код]

Механика сплошных сред

Сплошная среда
Классическая механика Закон сохранения массы · Закон сохранения импульса
Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоупругость
Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение
Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнение Громеки — Лэмба · Уравнение Бернулли · Уравнения Навье — Стокса · Уравнение вихря · Уравнение диффузии · Закон Гука
См. также: Портал:Физика

Энтальпия играет большую роль в гидродинамике, науке о движениях жидкостей и газов (в гидродинамике газы тоже называют жидкостями). Течения идеальной жидкости (то есть без вязкости и теплопроводности) описываются следующими уравнениями в частных производных^[69]:

${displaystyle {frac {partial rho }{partial t}}+mathrm {div} left(rho {vec {v}}right)=0,qquad qquad qquad }$

(Уравнение непрерывности)

${displaystyle {frac {partial {vec {v}}}{partial t}}+({vec {v}}cdot nabla ){vec {v}}=-{frac {1}{rho }}nabla P-nabla varphi ,qquad qquad }$

(Уравнение Эйлера)

где — плотность; — скорость; — давление; — время; ${displaystyle nabla =left({frac {partial }{partial x}},{frac {partial }{partial y}},{frac {partial }{partial z}}right)}$ — векторный оператор частного дифференцирования по координатам x,y,z ; точка между векторами в круглых скобках означает их скалярное произведение, а — ускорение силы тяжести, выраженное через гравитационный потенциал Уравнение для Дифференциала удельной энтальпии даёт: ${displaystyle nabla h={frac {1}{rho }}nabla P+Tnabla s,}$ что позволяет выразить уравнение Эйлера через энтальпию:

${displaystyle {frac {partial {vec {v}}}{partial t}}+({vec {v}}cdot nabla ){vec {v}}=Tnabla s-nabla (h+varphi ).qquad qquad }$

(Уравнение Эйлера, выраженное через энтальпию)

Такое представление обладает значительными преимуществами, поскольку в силу «адабатичности» течения идеальной жидкости, задаваемого уравнением сохранения энтропии:

${displaystyle {frac {partial s}{partial t}}+({vec {v}}cdot nabla )s=0,}$

член в уравнении Эйлера, связанный с градиентом энтропии, во многих случаях не даёт вклада в рассчитываемые эффекты.

Поток энергии[править | править код]

Выражение для дифференциала плотности полной энергии позволяет получить скорость изменения последней^[47]:

${displaystyle {frac {partial }{partial t}}left(rho eright)=rho T{frac {partial s}{partial t}}+{bar {h}}{frac {partial rho }{partial t}}+rho {vec {v}}cdot {frac {partial {vec {v}}}{partial t}}.}$

Интеграл Бернулли[править | править код]

Из приведённых здесь термодинамических соотношений для энтальпии следует простой вывод интеграла Бернулли и в наиболее общей его форме. Закон утверждает, что вдоль линии тока для стационарного течения идеальной жидкости^[70] сохраняется следующая величина:

{displaystyle {bar {h}}+varphi =mathrm {const} ,}

где varphi — гравитационный потенциал (равный для однородной силы тяжести, — ускорение свободного падения, — вертикальная координата).

Вывод закона Бернулли из уравнения Эйлера и термодинамических соотношений

1. В уравнении Эйлера для стационарного ( ${frac {partial {vec v}}{partial t}}=0$ ) движения идеальной жидкости в поле силы тяжести^[69] ускорение силы тяжести можно выразить через гравитационный потенциал (для однородного поля ).

2. Скалярное произведение этого уравнения на единичный вектор ${displaystyle {vec {l}}={frac {vec {v}}{v}},}$ касательный к линии тока даёт:

${displaystyle {frac {partial }{partial l}}left({frac {v^{2}}{2}}+varphi right)=-{frac {1}{rho }}{frac {partial p}{partial l}},}$

так как произведение градиента на единичный вектор даёт производную по направлению ${displaystyle {frac {partial }{partial l}}.}$

3. Выражение для Дифференциала удельной энтальпии даёт:

${displaystyle {frac {partial h}{partial l}}={frac {1}{rho }}{frac {partial p}{partial l}}+T{frac {partial s}{partial l}},qquad }$

так что ${displaystyle {frac {partial }{partial l}}left({frac {v^{2}}{2}}+h+varphi right)=T{frac {partial s}{partial l}}.}$

В стационарном течении идеальной жидкости все частицы, движущиеся вдоль данной линии тока, имеют одинаковую энтропию^[71] ( ${displaystyle {tfrac {partial s}{partial l}}=0}$ ), поэтому вдоль линии тока:

{displaystyle {bar {h}}+varphi =operatorname {const} }

См. также[править | править код]

Тепловой эффект химической реакции
Удельная теплота плавления

Комментарии[править | править код]

↑ В России определение энтальпии как суммы закреплено действующими стандартами^[7]^[8].
↑ Это соотношение носит название дифференциальной формы фундаментального уравнения Гиббса для энтальпии закрытой термодеформационной системы^[12]^[13]^[14].
↑ Энтальпию, заданную в виде функции её естественных независимых переменных, называют интегральной формой фундаментального уравнения Гиббса^[15]^[16]^[17] для энтальпии закрытой термодеформационной системы^[12]^[18]^[19].
↑ В термодинамике при написании частных производных внизу справа указывают переменные, который при вычислении производной считают постоянным. Причина в том, что в термодинамике для одной и той же функции используют различные наборы независимых переменных, которые, во избежание неопределённости, приходится перечислять.
↑ Число частиц в закрытой системе тоже может быть переменным, например числе фотонов равновесного излучения в полости с абсолютно чёрными стенками^[34].
↑ Использование масс независимых компонентов, а не масс составляющих систему веществ, позволяет учитывать химические превращения в системе без явного рассмотрения протекающих в ней химических реакций (см. статью Химическая термодинамика).
↑ Энергия $varepsilon _{0}$ включает в себя энергию химической связи и вносит значительный вклад в энтальпию образования^[⇨] газообразных сложных веществ

Примечания[править | править код]

↑ ¹ ² ³ Энтальпия // Большая российская энциклопедия. Том 35. Москва, 2017, стр. 396.
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, §14. Тепловая функция.
↑ ¹ ² ³ Зубарев Д. Н., Энтальпия, 1992.
↑ Горшков В. И., Кузнецов И. А., Основы физической химии, 2009, с. 111.
↑ Enthalpy, H // IUPAC Gold Book.
↑ Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин, 1984, с. 13.
↑ §113-04-21. Энтальпия (Н)//ГОСТ IEC 60050-113-2015 (2015). Дата обращения: 1 декабря 2018.
↑ §54. Энтальпия(теплосодержание)//ГОСТ Р 57700.4-2017 (2017). Дата обращения: 1 декабря 2018.
↑ Зубарев Д. Н., Термодинамика, 1992.
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (12.3).
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (16.3).
↑ ¹ ² Белов Г. В., Термодинамика, ч. 1, 2017, с. 155.
↑ Степановских Е. И. и др., Химическая термодинамика в вопросах и ответах, 2014, с. 37.
↑ Мечковский Л. А., Блохин А. В., Химическая термодинамика, ч. 1, 2012, с. 124.
↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 312.
↑ Воронин Г. Ф., Основы термодинамики, 1987, с. 76.
↑ Мюнстер А., Химическая термодинамика, 2002, с. 90—91.
↑ Белов Г. В., Термодинамика, ч. 2, 2016, с. 23.
↑ Зарубин Д. П., Физическая химия, 2017, с. 45.
↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, с. 67.
↑ Dalton, 1909.
↑ Гиббс Дж. В., Термодинамические работы, 1950, Примечание 3, с. 448.
↑ ¹ ² Howard, 2002, с. 697.
↑ Ахметов Б. В. и др. Физическая и коллоидная химия, 1986, с. 64.
↑ Гиббс Дж. В., Термодинамика. Статистическая механика, 1982, с. 96, 510.
↑ Henderson, Douglas; Eyring, Henry; Jost, Wilhelm. Physical Chemistry: An Advanced Treatise (неопр.). — Academic Press, 1967. — С. 29.
↑ Dalton, 1909, с. 863.
↑ Laidler (англ.) (рус.; Keith. The World of Physical Chemistry (англ.). — Oxford University Press, 1995. — P. 110.
↑ Van Ness, 2003, с. 486.
↑ Зубарев Д. Н., Потенциал термодинамический, 1994, с. 89.
↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, §45. Термодинамические функции.
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (14.4).
↑ Беляев Н. М., Термодинамика, 1987, с. 126.
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, §63. Чёрное излучение.
↑ ¹ ² Зубарев Д. Н., Термодинамика, 1992.
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнения (24.5–7).
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (15.7).
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (24.11).
↑ Automotive Encyclopedia, 2015, §1.1.2.2. Open dynamic system, с. 27.
↑ Белов Г. В., Термодинамика, ч. 1, 2017, с. 11.
↑ Automotive Encyclopedia, 2015, Уравнение (15), с. 28.
↑ Мюнстер А., Химическая термодинамика, 2002, с. 103.
↑ Кубо Р., Термодинамика, 1970, с. 24—25.
↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 446.
↑ Поль Р. В., Механика, акустика и учение о теплоте, 2013, с. 449–451.
↑ Quantities, Units and Symbols in Physical Chemistry (англ.). IUPAC (2015). Дата обращения: 7 декабря 2018. Архивировано из оригинала 11 февраля 2014 года.
↑ ¹ ² ³ Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2015, §6. Поток энергии.
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнения (42.5), (43.2) и (43.4).
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, §63.
↑ Зубарев Д. Н., Работа в термодинамике, 1994.
↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, §12.
↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (45.21).
↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (45.25).
↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 121.
↑ Базаров И. П., Термодинамика, 2010, с. 113.
↑ Артемов А. В., Физическая химия, 2013, с. 23.
↑ Ипполитов Е. Г. и др., Физическая химия, 2005, с. 35.
↑ Search for Species Data by Chemical Formula (англ.). Дата обращения: 3 декабря 2018.
↑ Термодинамические свойства. Дата обращения: 3 декабря 2018.
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (43.4).
↑ Пригожин И., Дефэй Р., Химическая термодинамика, 2009, с. 51.
↑ Алабовский А. Н., Недужий И. А., Техническая термодинамика и теплопередача, 1990, с. 25—26.
↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (19.3).
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (18.1).
↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, Уравнение (46.1).
↑ Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1, 2002, Уравнение (18.2).
↑ ¹ ² ³ ⁴ Зубарев Д. Н., Релятивистская термодинамика, 1994.
↑ ¹ ² ³ Каллен Г., Горвиц Дж., Релятивистская термодинамика, 1972.
↑ ¹ ² Ландау Л. Д., Лифшиц Е. М. Гидродинамика, 2015, Уравнение (2.4).
↑ Вишневецкий С. Л., Бернулли уравнение, 1988, с. 187.
↑ Седов Л. И. Механика сплошной среды, 1970, Глава VII. §2. Функция давления.

Литература[править | править код]

Алабовский А. Н., Недужий И. А. Техническая термодинамика и теплопередача. — 3-е изд., пераб. и доп. — Киев: Выща школа, 1990. — 256 с. — ISBN 5-11-001997-5.
Ансельм А. И. Основы статистической физики и термодинамики. — 2-е изд., стереотип. — СПб.: Лань, 2007. — 427 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-0756-9.
Артемов А. В. Физическая химия. — М.: Академия, 2013. — 288 с. — (Бакалавриат). — ISBN 978-5-7695-9550-9.
Ахметов Б. В., Новиченко Ю. П., Чапурин В. И. Физическая и коллоидная химия. — Л.: Химия, 1986. — 320 с.
Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
Белов Г. В. Термодинамика. Часть 1. — 2-е изд., испр. и доп. — М.: Юрайт, 2017. — 265 с. — (Бакалавр. Академический курс). — ISBN 978-5-534-02731-0.
Белов Г. В. Термодинамика. Часть 2. — М.: Юрайт, 2016. — 249 с. — (Бакалавриат). — ISBN 978-5-9916-7252-8.
Беляев Н. М. Термодинамика. — Киев: Вища школа, 1987. — 344 с.
Болгарский А. В., Мухачев Г. А., Щукин В. К. Термодинамика и теплопередача. — 2-е изд., перераб. и доп. — М.: Высшая школа, 1975. — 496 с.
Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М.: Инфра-М, 2017. — 868 с. — (Высшее образование: Бакалавриат). — ISBN 978-5-16-104227-4.
Буданов В. В., Максимов А. И. Химическая термодинамика / Под ред. О. И. Койфмана. — 3-е изд., стер. — СПб.: Лань, 2017. — 320 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-2271-5.
Вишневецкий С. Л. Бернулли уравнение // Физическая энциклопедия. — Большая Российская энциклопедия, 1988. — Т. 5: Стробоскопические приборы — Яркость. — С. 187.
Воронин Г. Ф. Основы термодинамики. — М.: Изд-во Моск. ун-та, 1987. — 192 с.
Гамбург Ю. Д. Химическая термодинамика. — М.: Лаборатория знаний, 2016. — 237 с. — (Учебник для высшей школы). — ISBN 978-5-906828-74-3.
Герасимов Я. И., Древинг В. П., Еремин Е. Н. и др. Курс физической химии / Под общ. ред. Я. И. Герасимова. — 2-е изд., испр. — М.: Химия, 1970. — Т. 1. — 592 с.
Гиббс Дж. В. Термодинамические работы / Пер. с англ. под ред. проф. В. К. Семенченко. — М. — Л.: Гостехиздат, 1950. — 492 с. — (Классики естествознания).
Гиббс Дж. В. Термодинамика. Статистическая механика / Отв. ред. Д. Н. Зубарев. — М.: Наука, 1982. — 584 с. — (Классики науки).
Горшков В. И., Кузнецов И. А. Основы физической химии. — 3-е изд. — М.: Бином. Лаборатория знаний, 2009. — 408 с. — ISBN 978-5-94774-375-3.
Еремин В. В., Каргов С. И., Успенская И. А. и др. Основы физической химии. Теория и задачи. — М.: Экзамен, 2005. — 481 с. — (Классический университетский учебник). — ISBN 5-472-00834-4.
Зарубин Д. П. Физическая химия. — М.: Инфра-М, 2017. — 474 с.
Зубарев, Д. Н. Потенциал термодинамический // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 89—91. — 704 с. — ISBN 5-85270-087-8.
Зубарев, Д. Н. Работа в термодинамике // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 193. — 704 с. — ISBN 5-85270-087-8.
Зубарев, Д. Н. Релятивистская термодинамика // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга-Робертсона эффект — Стримеры. — С. 333—334. — 704 с. — ISBN 5-85270-087-8.
Зубарев Д. Н. Термодинамика // Физическая энциклопедия / Ред.А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 83—87.
Зубарев Д. Н. Энтальпия // Физическая энциклопедия / Ред. А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 616.
Ипполитов Е. Г., Артемов А. В., Батраков В.В. Физическая химия / Под ред. Е. Г. Ипполитова. — М.: Академия, 2005. — 448 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-1456-6.
Каллен Г., Горвиц Дж. Релятивистская термодинамика // Успехи Физических Наук : журнал. — 1972. — Т. 107, вып. 7. — С. 489—502. — doi:10.3367/UFNr.0107.197207g.0489.
Колесников И. М., Винокуров В. А. Термодинамика физико-химических процессов. — 2-е, перераб. и доп. — М.: Нефть и газ, 2005. — 480 с. — ISBN 5-7246-0351-9.
Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
Ландау Л. Д., Лифшиц Е. М. Гидродинамика. — Издание 6-е, исправленное. — М.: Физматлит, 2015. — 728 с. — («Теоретическая физика», том VI). — ISBN 978-5-9221-1625-1.
Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — Издание 5-е. — М.: Физматлит, 2002. — 616 с. — («Теоретическая физика», том V). — ISBN 5-9221-0054-8.
Мечковский Л. А., Блохин А. В. Химическая термодинамика. В двух частях. Часть 1. Феноменологическая термодинамика. Основные понятия, фазовые равновесия. — Минск: Издательство БГУ, 2012. — 141 с. — ISBN 978-985-518-635-0.
Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — 2-е изд., стереотип. — М.: УРСС, 2002. — 296 с. — ISBN 5-354-00217-6.
Новиков И. И. Термодинамика. — 2-е изд., испр. — СПб.: Лань, 2009. — 592 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-0987-7.
Поль Р. В. Механика, акустика и учение о теплоте. — Рипол Классик, 2013. — 490 с. — ISBN 5458431251, 9785458431255.
Пригожин И., Дефэй Р. Химическая термодинамика / Пер. с англ. под ред. В. А. Михайлова. — 2-е изд.. — М.: Бином. Лаборатория знаний, 2009. — 533 с. — (Классика и современность. Естествознание). — ISBN 978-5-9963-0201-7.
Савельев И. В. Курс общей физики. — М.: КноРус, 2012. — Т. 1. Механика. Молекулярная физика и термодинамика. — 528 с. — ISBN 9785406025888.
Свиридов В. В., Свиридов А. В. Физическая химия. — СПб.: Лань, 2016. — 597 с. — ISBN 978-5-8114-2262-3.
Седов Л. И. Механика сплошной среды. — М.: Наука, 1970. — Т. 2. — 568 с.
Сивухин Д. В. Общий курс физики. — Издание 5-е, исправленное. — М.: Физматлит, 2005. — Т. II. Термодинамика и молекулярная физика. — 544 с. — ISBN 5-9221-0601-5.
Степановских Е. И., Брусницына Л. А., Маскаева Л. Н. Химическая термодинамика в вопросах и ответах. — Екатеринбург: Уральский издательско-полиграфический центр, 2014. — 221 с. — ISBN 978-5-4430-0061-9.
Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.
Хаазе Р. Термодинамика необратимых процессов / Пер. с нем. под ред. А. В. Лыкова. — М.: Мир, 1967. — 544 с.
Хачкурузов Г. А. Основы общей и химической термодинамики. — М.: Высшая школа, 1979. — 268 с.
Dalton J. P. Researches on the Joule-Kelvin effect, especially at low temperatures. I. Calculations for hydrogen // KNAW Proceedings. — 1909. — Т. 11. — С. 863—873.
Howard Irmgard K. H Is for Enthalpy, Thanks to Heike Kamerlingh Onnes and Alfred W. Porter (англ.) // Journal of Chemical Education : журнал. — 2002. — Vol. 79, iss. 6. — P. 697—698. — ISSN 0021-9584. — doi:10.1021/ed079p697.
Van Ness Hendrick C. H Is for Enthalpy (англ.) // Journal of Chemical Education : журнал. — 2003. — Vol. 80, iss. 5. — P. 486. — ISSN 0021-9584. — doi:10.1021/ed080p486.1.
Part 1 : Engines — Fundamentals // Encyclopedia of Automitive Engineering / Editors-in-Chief : David Crolla, David E. Foster, Toshio Kobayashi, Nicolas Vaughan. — John Wiley & Sons, 2015. — Т. 1. — 607 с. — ISBN 978-0-470-97402-5.

Источник

From Wikipedia, the free encyclopedia

In chemistry and thermodynamics, the standard enthalpy of formation or standard heat of formation of a compound is the change of enthalpy during the formation of 1 mole of the substance from its constituent elements in their reference state, with all substances in their standard states. The standard pressure value p^⦵ = 10⁵ Pa (= 100 kPa = 1 bar) is recommended by IUPAC, although prior to 1982 the value 1.00 atm (101.325 kPa) was used.^[1] There is no standard temperature. Its symbol is Δ_fH^⦵. The superscript Plimsoll on this symbol indicates that the process has occurred under standard conditions at the specified temperature (usually 25 °C or 298.15 K). Standard states are as follows:

For a gas: the hypothetical state the gas would assume if it obeyed the ideal gas equation at a pressure of 1 bar
For a gaseous or solid solute present in a diluted ideal solution: the hypothetical state of concentration of the solute of exactly one mole per liter (1 M) at a pressure of 1 bar extrapolated from infinite dilution
For a pure substance or a solvent in a condensed state (a liquid or a solid): the standard state is the pure liquid or solid under a pressure of 1 bar

For elements that have multiple allotropes, the reference state usually is chosen to be the form in which the element is most stable under 1 bar of pressure. One exception is phosphorus, for which the most stable form at 1 bar is black phosphorus, but white phosphorus is chosen as the standard reference state for zero enthalpy of formation.^[2]

For example, the standard enthalpy of formation of carbon dioxide would be the enthalpy of the following reaction under the above conditions:

{displaystyle {ce {C(s, graphite) + O2(g) -> CO2(g)}}}

All elements are written in their standard states, and one mole of product is formed. This is true for all enthalpies of formation.

The standard enthalpy of formation is measured in units of energy per amount of substance, usually stated in kilojoule per mole (kJ mol⁻¹), but also in kilocalorie per mole, joule per mole or kilocalorie per gram (any combination of these units conforming to the energy per mass or amount guideline).

All elements in their reference states (oxygen gas, solid carbon in the form of graphite, etc.) have a standard enthalpy of formation of zero, as there is no change involved in their formation.

The formation reaction is a constant pressure and constant temperature process. Since the pressure of the standard formation reaction is fixed at 1 bar, the standard formation enthalpy or reaction heat is a function of temperature. For tabulation purposes, standard formation enthalpies are all given at a single temperature: 298 K, represented by the symbol Δ_fH^⦵
_{298 K}.

Hess’s law[edit]

For many substances, the formation reaction may be considered as the sum of a number of simpler reactions, either real or fictitious. The enthalpy of reaction can then be analyzed by applying Hess’s Law, which states that the sum of the enthalpy changes for a number of individual reaction steps equals the enthalpy change of the overall reaction. This is true because enthalpy is a state function, whose value for an overall process depends only on the initial and final states and not on any intermediate states. Examples are given in the following sections.

Ionic compounds: Born–Haber cycle[edit]

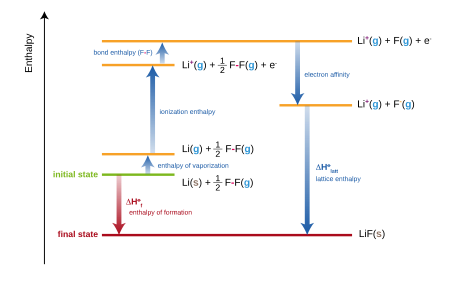
Standard enthalpy change of formation in Born–Haber diagram for lithium fluoride. ΔH_latt corresponds to U_L in the text. The downward arrow “electron affinity” shows the negative quantity –EA_F, since EA_F is usually defined as positive.

For ionic compounds, the standard enthalpy of formation is equivalent to the sum of several terms included in the Born–Haber cycle. For example, the formation of lithium fluoride,

{displaystyle {ce {Li(s) + 1/2F2(g) -> LiF(s)}}}

may be considered as the sum of several steps, each with its own enthalpy (or energy, approximately):

H_sub, the standard enthalpy of atomization (or sublimation) of solid lithium.
IE_Li, the first ionization energy of gaseous lithium.
B(F–F), the standard enthalpy of atomization (or bond energy) of fluorine gas.
EA_F, the electron affinity of a fluorine atom.
U_L, the lattice energy of lithium fluoride.

The sum of all these enthalpies will give the standard enthalpy of formation (ΔH_f) of lithium fluoride:

${displaystyle Delta H_{text{f}}=Delta H_{text{sub}}+{text{IE}}_{text{Li}}+{frac {1}{2}}{text{B(F–F)}}-{text{EA}}_{text{F}}+{text{U}}_{text{L}}.}$

In practice, the enthalpy of formation of lithium fluoride can be determined experimentally, but the lattice energy cannot be measured directly. The equation is therefore rearranged in order to evaluate the lattice energy:^[3]

${displaystyle -U_{text{L}}=Delta H_{text{sub}}+{text{IE}}_{text{Li}}+{frac {1}{2}}{text{B(F–F)}}-{text{EA}}_{text{F}}-Delta H_{text{f}}.}$

Organic compounds[edit]

The formation reactions for most organic compounds are hypothetical. For instance, carbon and hydrogen won’t directly react to form methane (CH₄), so that the standard enthalpy of formation cannot be measured directly. However the standard enthalpy of combustion is readily measurable using bomb calorimetry. The standard enthalpy of formation is then determined using Hess’s law. The combustion of methane:

{displaystyle {ce {CH4 + 2 O2 -> CO2 + 2 H2O}}}

is equivalent to the sum of the hypothetical decomposition into elements followed by the combustion of the elements to form carbon dioxide (CO₂) and water (H₂O):

Applying Hess’s law,

${displaystyle Delta _{text{comb}}H^{ominus }({text{CH}}_{4})=[Delta _{text{f}}H^{ominus }({text{CO}}_{2})+2Delta _{text{f}}H^{ominus }({text{H}}_{2}{text{O}})]-Delta _{text{f}}H^{ominus }({text{CH}}_{4}).}$

Solving for the standard of enthalpy of formation,

${displaystyle Delta _{text{f}}H^{ominus }({text{CH}}_{4})=[Delta _{text{f}}H^{ominus }({text{CO}}_{2})+2Delta _{text{f}}H^{ominus }({text{H}}_{2}{text{O}})]-Delta _{text{comb}}H^{ominus }({text{CH}}_{4}).}$

The value of ${displaystyle Delta _{text{f}}H^{ominus }({text{CH}}_{4})}$ is determined to be −74.8 kJ/mol. The negative sign shows that the reaction, if it were to proceed, would be exothermic; that is, methane is enthalpically more stable than hydrogen gas and carbon.

It is possible to predict heats of formation for simple unstrained organic compounds with the heat of formation group additivity method.

Use in calculation for other reactions[edit]

The standard enthalpy change of any reaction can be calculated from the standard enthalpies of formation of reactants and products using Hess’s law. A given reaction is considered as the decomposition of all reactants into elements in their standard states, followed by the formation of all products. The heat of reaction is then minus the sum of the standard enthalpies of formation of the reactants (each being multiplied by its respective stoichiometric coefficient, ν) plus the sum of the standard enthalpies of formation of the products (each also multiplied by its respective stoichiometric coefficient), as shown in the equation below:^[4]

${displaystyle Delta _{text{r}}H^{ominus }=sum nu Delta _{text{f}}H^{ominus }({text{products}})-sum nu Delta _{text{f}}H^{ominus }({text{reactants}}).}$

If the standard enthalpy of the products is less than the standard enthalpy of the reactants, the standard enthalpy of reaction is negative. This implies that the reaction is exothermic. The converse is also true; the standard enthalpy of reaction is positive for an endothermic reaction. This calculation has a tacit assumption of ideal solution between reactants and products where the enthalpy of mixing is zero.

For example, for the combustion of methane, :

${displaystyle Delta _{text{r}}H^{ominus }=[Delta _{text{f}}H^{ominus }({text{CO}}_{2})+2Delta _{text{f}}H^{ominus }({text{H}}_{2}{text{O}})]-Delta _{text{f}}H^{ominus }({text{CH}}_{4})+2Delta _{text{f}}H^{ominus }({text{O}}_{2})].}$

However is an element in its standard state, so that ${displaystyle Delta _{text{f}}H^{ominus }({text{O}}_{2})=0}$ , and the heat of reaction is simplified to

${displaystyle Delta _{text{r}}H^{ominus }=[Delta _{text{f}}H^{ominus }({text{CO}}_{2})+2Delta _{text{f}}H^{ominus }({text{H}}_{2}{text{O}})]-Delta _{text{f}}H^{ominus }({text{CH}}_{4}),}$

which is the equation in the previous section for the enthalpy of combustion ${displaystyle Delta _{text{comb}}H^{ominus }}$ .

Key concepts for enthalpy calculations[edit]

When a reaction is reversed, the magnitude of ΔH stays the same, but the sign changes.
When the balanced equation for a reaction is multiplied by an integer, the corresponding value of ΔH must be multiplied by that integer as well.
The change in enthalpy for a reaction can be calculated from the enthalpies of formation of the reactants and the products
Elements in their standard states make no contribution to the enthalpy calculations for the reaction, since the enthalpy of an element in its standard state is zero. Allotropes of an element other than the standard state generally have non-zero standard enthalpies of formation.

Examples: standard enthalpies of formation at 25 °C[edit]

Thermochemical properties of selected substances at 298.15 K and 1 atm

Inorganic substances[edit]

Species	Phase	Chemical formula	Δ_fH^⦵ /(kJ/mol)
Aluminium	Solid	Al	0
Aluminium chloride	Solid	AlCl₃	−705.63
Aluminium oxide	Solid	Al₂O₃	−1675.5
Aluminium hydroxide	Solid	Al(OH)₃	−1277
Aluminium sulphate	Solid	Al₂(SO₄)₃	−3440
Barium chloride	Solid	BaCl₂	−858.6
Barium carbonate	Solid	BaCO₃	−1216
Barium hydroxide	Solid	Ba(OH)₂	−944.7
Barium oxide	Solid	BaO	−548.1
Barium sulfate	Solid	BaSO₄	−1473.3
Beryllium	Solid	Be	0
Beryllium hydroxide	Solid	Be(OH)₂	−903
Beryllium oxide	Solid	BeO	−609.4
Boron trichloride	Solid	BCl₃	−402.96
Bromine	Liquid	Br₂	0
Bromide ion	Aqueous	Br⁻	−121
Bromine	Gas	Br	111.884
Bromine	Gas	Br₂	30.91
Bromine trifluoride	Gas	BrF₃	−255.60
Hydrogen bromide	Gas	HBr	−36.29
Cadmium	Solid	Cd	0
Cadmium oxide	Solid	CdO	−258
Cadmium hydroxide	Solid	Cd(OH)₂	−561
Cadmium sulfide	Solid	CdS	−162
Cadmium sulfate	Solid	CdSO₄	−935
Caesium	Solid	Cs	0
Caesium	Gas	Cs	76.50
Caesium	Liquid	Cs	2.09
Caesium(I) ion	Gas	Cs⁺	457.964
Caesium chloride	Solid	CsCl	−443.04
Calcium	Solid	Ca	0
Calcium	Gas	Ca	178.2
Calcium(II) ion	Gas	Ca²⁺	1925.90
Calcium(II) ion	Aqueous	Ca²⁺	−542.7
Calcium carbide	Solid	CaC₂	−59.8
Calcium carbonate (Calcite)	Solid	CaCO₃	−1206.9
Calcium chloride	Solid	CaCl₂	−795.8
Calcium chloride	Aqueous	CaCl₂	−877.3
Calcium phosphate	Solid	Ca₃(PO₄)₂	−4132
Calcium fluoride	Solid	CaF₂	−1219.6
Calcium hydride	Solid	CaH₂	−186.2
Calcium hydroxide	Solid	Ca(OH)₂	−986.09
Calcium hydroxide	Aqueous	Ca(OH)₂	−1002.82
Calcium oxide	Solid	CaO	−635.09
Calcium sulfate	Solid	CaSO₄	−1434.52
Calcium sulfide	Solid	CaS	−482.4
Wollastonite	Solid	CaSiO₃	−1630
Carbon (Graphite)	Solid	C	0
Carbon (Diamond)	Solid	C	1.9
Carbon	Gas	C	716.67
Carbon dioxide	Gas	CO₂	−393.509
Carbon disulfide	Liquid	CS₂	89.41
Carbon disulfide	Gas	CS₂	116.7
Carbon monoxide	Gas	CO	−110.525
Carbonyl chloride (Phosgene)	Gas	COCl₂	−218.8
Carbon dioxide (un–ionized)	Aqueous	CO₂(aq)	−419.26
Bicarbonate ion	Aqueous	HCO₃^–	−689.93
Carbonate ion	Aqueous	CO₃^2–	−675.23
Monatomic chlorine	Gas	Cl	121.7
Chloride ion	Aqueous	Cl⁻	−167.2
Chlorine	Gas	Cl₂	0
Chromium	Solid	Cr	0
Copper	Solid	Cu	0
Copper(II) oxide	Solid	CuO	−155.2
Copper(II) sulfate	Aqueous	CuSO₄	−769.98
Fluorine	Gas	F₂	0
Monatomic hydrogen	Gas	H	218
Hydrogen	Gas	H₂	0
Water	Gas	H₂O	−241.818
Water	Liquid	H₂O	−285.8
Hydrogen ion	Aqueous	H⁺	0
Hydroxide ion	Aqueous	OH⁻	−230
Hydrogen peroxide	Liquid	H₂O₂	−187.8
Phosphoric acid	Liquid	H₃PO₄	−1288
Hydrogen cyanide	Gas	HCN	130.5
Hydrogen bromide	Liquid	HBr	−36.3
Hydrogen chloride	Gas	HCl	−92.30
Hydrogen chloride	Aqueous	HCl	−167.2
Hydrogen fluoride	Gas	HF	−273.3
Hydrogen iodide	Gas	HI	26.5
Iodine	Solid	I₂	0
Iodine	Gas	I₂	62.438
Iodine	Aqueous	I₂	23
Iodide ion	Aqueous	I⁻	−55
Iron	Solid	Fe	0
Iron carbide (Cementite)	Solid	Fe₃C	5.4
Iron(II) carbonate (Siderite)	Solid	FeCO₃	−750.6
Iron(III) chloride	Solid	FeCl₃	−399.4
Iron(II) oxide (Wüstite)	Solid	FeO	−272
Iron(II,III) oxide (Magnetite)	Solid	Fe₃O₄	−1118.4
Iron(III) oxide (Hematite)	Solid	Fe₂O₃	−824.2
Iron(II) sulfate	Solid	FeSO₄	−929
Iron(III) sulfate	Solid	Fe₂(SO₄)₃	−2583
Iron(II) sulfide	Solid	FeS	−102
Pyrite	Solid	FeS₂	−178
Lead	Solid	Pb	0
Lead dioxide	Solid	PbO₂	−277
Lead sulfide	Solid	PbS	−100
Lead sulfate	Solid	PbSO₄	−920
Lead(II) nitrate	Solid	Pb(NO₃)₂	−452
Lead(II) sulfate	Solid	PbSO₄	−920
Lithium fluoride	Solid	LiF	−616.93
Magnesium	Solid	Mg	0
Magnesium ion	Aqueous	Mg²⁺	−466.85
Magnesium carbonate	Solid	MgCO₃	−1095.797
Magnesium chloride	Solid	MgCl₂	−641.8
Magnesium hydroxide	Solid	Mg(OH)₂	−924.54
Magnesium hydroxide	Aqueous	Mg(OH)₂	−926.8
Magnesium oxide	Solid	MgO	−601.6
Magnesium sulfate	Solid	MgSO₄	−1278.2
Manganese	Solid	Mn	0
Manganese(II) oxide	Solid	MnO	−384.9
Manganese(IV) oxide	Solid	MnO₂	−519.7
Manganese(III) oxide	Solid	Mn₂O₃	−971
Manganese(II,III) oxide	Solid	Mn₃O₄	−1387
Permanganate	Aqueous	MnO⁻ ₄	−543
Mercury(II) oxide (red)	Solid	HgO	−90.83
Mercury sulfide (red, cinnabar)	Solid	HgS	−58.2
Nitrogen	Gas	N₂	0
Ammonia (ammonium hydroxide)	Aqueous	NH₃ (NH₄OH)	−80.8
Ammonia	Gas	NH₃	−46.1
Ammonium nitrate	Solid	NH₄NO₃	−365.6
Ammonium chloride	Solid	NH₄Cl	−314.55
Nitrogen dioxide	Gas	NO₂	33.2
Hydrazine	Gas	N₂H₄	95.4
Hydrazine	Liquid	N₂H₄	50.6
Nitrous oxide	Gas	N₂O	82.05
Nitric oxide	Gas	NO	90.29
Dinitrogen tetroxide	Gas	N₂O₄	9.16
Dinitrogen pentoxide	Solid	N₂O₅	−43.1
Dinitrogen pentoxide	Gas	N₂O₅	11.3
Nitric acid	Aqueous	HNO₃	−207
Monatomic oxygen	Gas	O	249
Oxygen	Gas	O₂	0
Ozone	Gas	O₃	143
White phosphorus	Solid	P₄	0
Red phosphorus	Solid	P	−17.4^[5]
Black phosphorus	Solid	P	−39.3^[5]
Phosphorus trichloride	Liquid	PCl₃	−319.7
Phosphorus trichloride	Gas	PCl₃	−278
Phosphorus pentachloride	Solid	PCl₅	−440
Phosphorus pentachloride	Gas	PCl₅	−321
Phosphorus pentoxide	Solid	P₂O₅	−1505.5^[6]
Potassium bromide	Solid	KBr	−392.2
Potassium carbonate	Solid	K₂CO₃	−1150
Potassium chlorate	Solid	KClO₃	−391.4
Potassium chloride	Solid	KCl	−436.68
Potassium fluoride	Solid	KF	−562.6
Potassium oxide	Solid	K₂O	−363
Potassium nitrate	Solid	KNO₃	−494.5
Potassium perchlorate	Solid	KClO₄	−430.12
Silicon	Gas	Si	368.2
Silicon carbide	Solid	SiC	−74.4,^[7] −71.5^[8]
Silicon tetrachloride	Liquid	SiCl₄	−640.1
Silica (Quartz)	Solid	SiO₂	−910.86
Silver bromide	Solid	AgBr	−99.5
Silver chloride	Solid	AgCl	−127.01
Silver iodide	Solid	AgI	−62.4
Silver oxide	Solid	Ag₂O	−31.1
Silver sulfide	Solid	Ag₂S	−31.8
Sodium	Solid	Na	0
Sodium	Gas	Na	107.5
Sodium bicarbonate	Solid	NaHCO₃	−950.8
Sodium carbonate	Solid	Na₂CO₃	−1130.77
Sodium chloride	Aqueous	NaCl	−407.27
Sodium chloride	Solid	NaCl	−411.12
Sodium chloride	Liquid	NaCl	−385.92
Sodium chloride	Gas	NaCl	−181.42
Sodium chlorate	Solid	NaClO₃	−365.4
Sodium fluoride	Solid	NaF	−569.0
Sodium hydroxide	Aqueous	NaOH	−469.15
Sodium hydroxide	Solid	NaOH	−425.93
Sodium hypochlorite	Solid	NaOCl	−347.1
Sodium nitrate	Aqueous	NaNO₃	−446.2
Sodium nitrate	Solid	NaNO₃	−424.8
Sodium oxide	Solid	Na₂O	−414.2
Sulfur (monoclinic)	Solid	S₈	0.3
Sulfur (rhombic)	Solid	S₈	0
Hydrogen sulfide	Gas	H₂S	−20.63
Sulfur dioxide	Gas	SO₂	−296.84
Sulfur trioxide	Gas	SO₃	−395.7
Sulfuric acid	Liquid	H₂SO₄	−814
Titanium	Gas	Ti	468
Titanium tetrachloride	Gas	TiCl₄	−763.2
Titanium tetrachloride	Liquid	TiCl₄	−804.2
Titanium dioxide	Solid	TiO₂	−944.7
Zinc	Gas	Zn	130.7
Zinc chloride	Solid	ZnCl₂	−415.1
Zinc oxide	Solid	ZnO	−348.0
Zinc sulfate	Solid	ZnSO₄	−980.14

Aliphatic hydrocarbons[edit]

Formula	Name	Δ_fH^⦵ /(kcal/mol)	Δ_fH^⦵ /(kJ/mol)
Straight-chain
CH₄	Methane	−17.9	−74.9
C₂H₆	Ethane	−20.0	−83.7
C₂H₄	Ethylene	12.5	52.5
C₂H₂	Acetylene	54.2	226.8
C₃H₈	Propane	−25.0	−104.6
C₄H₁₀	n-Butane	−30.0	−125.5
C₅H₁₂	n-Pentane	−35.1	−146.9
C₆H₁₄	n-Hexane	−40.0	−167.4
C₇H₁₆	n-Heptane	−44.9	−187.9
C₈H₁₈	n-Octane	−49.8	−208.4
C₉H₂₀	n-Nonane	−54.8	−229.3
C₁₀H₂₂	n-Decane	−59.6	−249.4
C₄ Alkane branched isomers
C₄H₁₀	Isobutane (methylpropane)	−32.1	−134.3
C₅ Alkane branched isomers
C₅H₁₂	Neopentane (dimethylpropane)	−40.1	−167.8
C₅H₁₂	Isopentane (methylbutane)	−36.9	−154.4
C₆ Alkane branched isomers
C₆H₁₄	2,2-Dimethylbutane	−44.5	−186.2
C₆H₁₄	2,3-Dimethylbutane	−42.5	−177.8
C₆H₁₄	2-Methylpentane (isohexane)	−41.8	−174.9
C₆H₁₄	3-Methylpentane	−41.1	−172.0
C₇ Alkane branched isomers
C₇H₁₆	2,2-Dimethylpentane	−49.2	−205.9
C₇H₁₆	2,2,3-Trimethylbutane	−49.0	−205.0
C₇H₁₆	3,3-Dimethylpentane	−48.1	−201.3
C₇H₁₆	2,3-Dimethylpentane	−47.3	−197.9
C₇H₁₆	2,4-Dimethylpentane	−48.2	−201.7
C₇H₁₆	2-Methylhexane	−46.5	−194.6
C₇H₁₆	3-Methylhexane	−45.7	−191.2
C₇H₁₆	3-Ethylpentane	−45.3	−189.5
C₈ Alkane branched isomers
C₈H₁₈	2,3-Dimethylhexane	−55.1	−230.5
C₈H₁₈	2,2,3,3-Tetramethylbutane	−53.9	−225.5
C₈H₁₈	2,2-Dimethylhexane	−53.7	−224.7
C₈H₁₈	2,2,4-Trimethylpentane (isooctane)	−53.5	−223.8
C₈H₁₈	2,5-Dimethylhexane	−53.2	−222.6
C₈H₁₈	2,2,3-Trimethylpentane	−52.6	−220.1
C₈H₁₈	3,3-Dimethylhexane	−52.6	−220.1
C₈H₁₈	2,4-Dimethylhexane	−52.4	−219.2
C₈H₁₈	2,3,4-Trimethylpentane	−51.9	−217.1
C₈H₁₈	2,3,3-Trimethylpentane	−51.7	−216.3
C₈H₁₈	2-Methylheptane	−51.5	−215.5
C₈H₁₈	3-Ethyl-3-Methylpentane	−51.4	−215.1
C₈H₁₈	3,4-Dimethylhexane	−50.9	−213.0
C₈H₁₈	3-Ethyl-2-Methylpentane	−50.4	−210.9
C₈H₁₈	3-Methylheptane	−60.3	−252.5
C₈H₁₈	4-Methylheptane	?	?
C₈H₁₈	3-Ethylhexane	?	?
C₉ Alkane branched isomers (selected)
C₉H₂₀	2,2,4,4-Tetramethylpentane	−57.8	−241.8
C₉H₂₀	2,2,3,3-Tetramethylpentane	−56.7	−237.2
C₉H₂₀	2,2,3,4-Tetramethylpentane	−56.6	−236.8
C₉H₂₀	2,3,3,4-Tetramethylpentane	−56.4	−236.0
C₉H₂₀	3,3-Diethylpentane	−55.7	−233.0

Other organic compounds[edit]

Species	Phase	Chemical formula	Δ_fH^⦵ /(kJ/mol)
Acetone	Liquid	C₃H₆O	−248.4
Benzene	Liquid	C₆H₆	48.95
Benzoic acid	Solid	C₇H₆O₂	−385.2
Carbon tetrachloride	Liquid	CCl₄	−135.4
Carbon tetrachloride	Gas	CCl₄	−95.98
Ethanol	Liquid	C₂H₅OH	−277.0
Ethanol	Gas	C₂H₅OH	−235.3
Glucose	Solid	C₆H₁₂O₆	−1271
Isopropanol	Gas	C₃H₇OH	−318.1
Methanol (methyl alcohol)	Liquid	CH₃OH	−238.4
Methanol (methyl alcohol)	Gas	CH₃OH	−201.0
Methyl linoleate (Biodiesel)	Gas	C₁₉H₃₄O₂	−356.3
Sucrose	Solid	C₁₂H₂₂O₁₁	−2226.1
Trichloromethane (Chloroform)	Liquid	CHCl₃	−134.47
Trichloromethane (Chloroform)	Gas	CHCl₃	−103.18
Vinyl chloride	Solid	C₂H₃Cl	−94.12

References[edit]

^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”) (1997). Online corrected version: (2006–) “standard pressure”. doi:10.1351/goldbook.S05921
^ Oxtoby, David W; Pat Gillis, H; Campion, Alan (2011). Principles of Modern Chemistry. p. 547. ISBN 978-0-8400-4931-5.
^ Moore, Stanitski, and Jurs. Chemistry: The Molecular Science. 3rd edition. 2008. ISBN 0-495-10521-X. pages 320–321.
^ “Enthalpies of Reaction”. www.science.uwaterloo.ca. Archived from the original on 25 October 2017. Retrieved 2 May 2018.
^ ^a ^b Housecroft, C. E.; Sharpe, A. G. (2004). Inorganic Chemistry (2nd ed.). Prentice Hall. p. 392. ISBN 978-0-13-039913-7.
^ Green, D.W., ed. (2007). Perry’s Chemical Engineers’ Handbook (8th ed.). Mcgraw-Hill. p. 2–191. ISBN 9780071422949.
^ Kleykamp, H. (1998). “Gibbs Energy of Formation of SiC: A contribution to the Thermodynamic Stability of the Modifications”. Berichte der Bunsengesellschaft für physikalische Chemie. 102 (9): 1231–1234. doi:10.1002/bbpc.19981020928.
^ “Silicon Carbide, Alpha (SiC)”. March 1967. Retrieved 5 February 2019.

Zumdahl, Steven (2009). Chemical Principles (6th ed.). Boston. New York: Houghton Mifflin. pp. 384–387. ISBN 978-0-547-19626-8.

External links[edit]

NIST Chemistry WebBook

Источник

Советы

Об этой статье

Была ли эта статья полезной?

Тепловой эффект процесса

Термохимические уравнения

Закон Гесса

Следствия из закона Гесса

Стандартные термодинамические величины

Стандартные энтальпии образования и сгорания

Примеры решения задач

Задачи для самостоятельного решения

История вопроса[править | править код]

Энтальпия как термодинамический потенциал[править | править код]

Зависимость энтальпии от числа частиц[править | править код]

Удельная энтальпия[править | править код]

Плотность энергии и энтальпии идеального газа[править | править код]

Энтальпия сложных термодинамических систем[править | править код]

Энтальпия образования[править | править код]

Зависимость энтальпии от температуры[править | править код]

Сохранение энтальпии в эффекте Джоуля — Томсона[править | править код]

Полная энергия и полная энтальпия[править | править код]

Релятивистская энтальпия[править | править код]

Энтальпия в гидродинамике[править | править код]

Поток энергии[править | править код]

Интеграл Бернулли[править | править код]

См. также[править | править код]

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

Hess’s law[edit]

Ionic compounds: Born–Haber cycle[edit]

Organic compounds[edit]

Use in calculation for other reactions[edit]

Key concepts for enthalpy calculations[edit]

Examples: standard enthalpies of formation at 25 °C[edit]

Inorganic substances[edit]

Aliphatic hydrocarbons[edit]

Other organic compounds[edit]

See also[edit]

References[edit]

External links[edit]

Вам также может понравиться

Как исправить лордоз поясницы у взрослого упражнения

Как составить текст на ноутбуке

Как могут найти потерянный смартфон

Добавить комментарий Отменить ответ