Как найти энтальпию по графику

Размер: 3070х3995 пикселей

Форматы: .PDF, .JPG

Диаграмма цветная — степени сухости, температура, давление и объем выделены разными цветами, что делает работу с диаграммой очень удобной.

Большой размер позволит распечатать диаграмму на формате А3 и больше.

is-диаграмма применяется для практических расчетов процессов водяного пара. На ней теплота и энтальпия измеряются линейными отрезками.

is-диаграмма обладает рядом важных свойств: по ней можно быстро определить параметры пара и разность энтальпий в виде отрезков, наглядно изобразить адиабатный процесс, и решать другие задачи.

Так же вы можете использовать очень удобную и наглядную программу.

Описание is-диаграммы

На is-диаграмме изображены термодинамические процессы:

• Изобарный процесс (p = const) — фиолетовые линии (изобары),
• Изотермический процесс (t = const) — зеленые линии (изотермы),
• Изохорный процесс (v = const) — красные линии (изохоры).

Степень сухости и паросодержание (х) — розовые линии. Жирная розовая линия — степень сухости х=1. Все что ниже этой линии — зона влажного пара.

Подробнее о термодинамических процессах читайте в статье «Основные термодинамические процессы»

Ось «Х» — энтропия, ось «Y» — энтальпия.

Семейство изобар в области насыщения представляет собой пучок расходящихся прямых, начинающихся на нижней и оканчивающихся на верхней пограничной кривой. Чем больше давление, тем выше лежит соответствующая изобара. Переход изобар из области влажного насыщенного в область перегретого пара происходит без перелома на верхней пограничной кривой.

В i, s-диаграмме водяного пара наносятся также линии постоянного паросодержания (x = const) и линии постоянного удельного объема (v = const). Изохоры идут несколько круче, чем изобары.

Состояние перегретого пара обычно определяется в технике давлением p и температурой t. Точка, изображающая это состояние, находится на пересечении соответствующей изобары и изотермы. Состояние влажного насыщенного пара определяется давлением p и паросодержанием x.

Точка, изображающее это состояние, определяется пересечением изобары и линии x = const.

Как пользоваться is-диаграммой

Для описания воспользуемся небольшой задачей. Возьмем с потолка условие.

Пусть начальные параметры пара будут: давление пара р = 120 бар, температура пара t = 550°С. Пар адиабатно расширяется в турбине до температуры, например, 400 °С.

Для примера этого будет достаточно.

Адиабатный процесс на is-диаграмме — это вертикальная линия (горизонтальная линия — дросселирование). Это для справки.

Итак, начальное давление и температура у нас есть. Найдем эту точку на is-диаграмме:

Нам нужна изобара, соответствующая давлению 120 бар и изотерма, соответствующая температуре 550 °С. На их пересечении и будет точка, соответствующая начальным параметрам пара в нашей задаче.

Найдя эту точку, мы уже можем определить в ней энтальпию и энтропию. Опустив на оси проекции найденной точки, узнаем значения энтальпии (ось «Y») и энтропии (ось «Х»).

i = ~3480 кДж/кг, S = 6,65 кДж/(кг•К)

Далее нам нужно узнать параметры пара после адиабатного расширения. Мы знаем, что по поставленным нами условиям, пар расширился и его температура в точке 2 = 400 °С. Я уже упоминал, что на is-диаграмме адиабатный процесс изображается в виде вертикальной линии. Проведем эту линию из точки 1 (начальные параметры) до пересечения с изотермой 400 °С.

Получена точка 2. Через эту точку проходит изобара. Она соответствует давлению 50 бар. Энтропия у нас не изменилась, так как процесс адиабатный, а вот энтальпия стала равна i = 3200 кДж/кг. 

Вот и все. Дальше остаются только расчеты: определение изменения внутренней энергии (Δu), работы (l, l’) и т. д. Все это считается по формулам (формулы можете найти в статье «Основные термодинамические процессы»), а значения и график процесса расширения пара у вас уже есть.

Одной из энергетических
характеристик термодинамической системы
является тепловая функцияили
энтальпия. Выражение для энтальпии
можно получить из первого закона
термодинамики

dQ
= dU + pdV (4.1)

Так как d(pV) = pdV + Vdp,
то pdV = d(pV) – Vdp. Подставляя это значение
pdV в уравнение (4.1) , получим

dQ =
dU + d(pV) – Vdp = d(U + pV) – Vdp (4.2)

Сумма (U + pV) = Iи является энальпией.
С учетом выражения для энтальпии
уравнение (4.2) можно записать в следующем
виде

dQ = dI – Vdp (4.3)

свойства энтальпии:

– энтальпия системы
является однозначной функцией состояния
системы;

– дифференциал dI
является полным дифференциалом;

– энтальпия является
аддитивной величиной ;

энтальпия тела
определяется в термодинамике с точностью
до некоторой постоянной слагающей. Для
изохорного процесса (C = Cv и dV = 0) на
основании уравнения
(4.1)
имеем dU = C_vdT
(4.4)

Аналогично из уравнения
(4.3) для изобарного процесса получаем

dI = C_pdT (4.5)

Первый закон термодинамики
справедлив для веществ с любыми
свойствами, поэтому по уравнению (4.4) в
изохорном процессе, а по уравнению (4.5)
в изобарном процессе соответственно
dU и dI можно рассчитывать для веществ с
любыми свойствами.

Формулы для
расчета изменения энтропии идеального
газа

1. dQ = dU + pdV или TdS = CvdT
+ pdV (4.6)

Из последнего уравнения
следует

dS = C_v (4.6а)

После интегрирования
уравнения (4.6а) получим

S₂– S₁=
(4.7)

2. dQ = dI – Vdp или TdS = C_pdT
– Vdp
(4.8)

Из формулы (4.8) следует

dS
= C_p (4.9)

Из формулы (4.9) следует

S₂– S₁ = (4.10)

Графический метод в термодинамике

Равновесное состояние системы можно
отобразить графически в различных
системах координат:p – V – T;T – S – Vи др. На рис. 4.1 в координатахp – V – Tзаданное равновесное
состояние отображено точкойА.
Под влиянием внешнего воздействия газ будет
изменять свое
состояние, в результате чего
координаты точки будут изменяться.
Соединив множество точек, характеризующих
различные состояния, получим некоторую
термодинамическую поверхность.
Уравнением термодинамической
поверхности является уравнение состояния.
Если в термодинамическом процессе
изменяются все три параметра газа ( p
,
V
,
T
), то этот процесс изобразится
вp – V – Tкоординатах пространственной
кривой, расположенной на термодинамической
поверхности.

Диаграмма p – Vпримечательна тем, что в этих координатах
площадь под кривой, характеризующей
процесс, определяет работу, совершаемую
газа при расширении, или работу,
затраченную на сжатие. Действительно,
площадка под элементарным процессом
(рис. 4.2) есть работа A = pdV. Полная работа
в процессе1-2будет равна

A = (4.11)

Рис.
4.2 Рис.
4.3

Процесс можно
рассматривать и в координатах T – S – V.
Проекция пространственной кривой на
плоскость T – S даст плоскую кривую.
Представление процесса в координатах
T – S дает возможность определить
количество теплоты, подведенное к
системе (dS >0) из
внешней среды, или отведенное от нее в
окружающую среду (dS<0). Площадь под элементарным процессом
равна TdS, т.е. количеству теплоты dQ,
рис. 4.3.

Полное
количество теплоты в процессе 1-2 может
быть представлено следующим выражением
Q =
.

T
– S
диаграмма для идеального газа

Из
формулы (4.7) следует, что в изохорном
процессе

(DS)_v
=
(4.12)

Для
изобарного процесса из формулы (4.10)
имеем

(DS)_p
= (C_p)
(4.13)

Из уравнений (4.12) и (4.13)
видно , что в T – S координатах изохоры и
изобары представляют собой логарифмические
линии. Тангенс угла наклона касательной
к изохоре и изобаре получим соответственно
из соотношений (4.6) и (4.8):
tga_v
= (¶T/¶S)_v= T/C_v ;
tga_p = (¶T/¶S)_p= T/C_p. Отсюда следует, что с ростом
температуры тангенсы углов наклона
касательной и изохоре tga_v
и
к изобаре tga_pувеличиваются. Поэтому кривые обращены
выпуклостью вниз. Так как C_p >C_v, то tga_v >tga_p , рис. 4.4. Для
того, чтобы определит расстояние по
горизонтали между двумя соседними
изохорами и соседними изобарами
воспользуемся формулами (4.7) и (4.10), из
которых следует, что при постоянной
температуреDS)_T= R ln V₁/V₂и (DS)_T= – R ln p₂/p₁.

Следовательно, изохоры
больших объёмов располагаются правее
от основной изохоры, а меньших объёмов
– левее. Следовательно область низких
давлений располагается правее от
основной изобары, а область высоких
давлений – левее.

Расстояние между
основной изохорой и изохорами двойного,
тройного и больших объёмов равны R ln2,
R ln3
и так далее. Расстояние между изобарами:
-R ln2, R ln3 и так далее.

Процессы при постоянной температуре
(изотермические) изображаются
горизонтальными линиями (рис. 4.5). В
изотермических процессах с идеальным
газомDU = 0, поэтому
теплота подведенная к газу расходуется
только на работу расширения. Следовательно
процесс А – В (DS>0) – изотермическое расширение, а процесс
А – С – изотермическое сжатие. Процессы
, протекающие без теплообмена с окружающей
средой (Q = 0;DS = 0),
называются адиабатными и изображаются
вертикальными линиями. В этих процессах
в соответствии с первым законом
термодинамики, работа совершается за
счет внутренней энергии (dQ = – dU). Уменьшение
внутренней энергии влечет за собой
снижение температуры. Следовательно
процесс 1-2 – адиабатное расширение, а
процесс 1-3 – адиабатное сжатие. При
адиабатном сжатии работа, затраченная
на сжатие преобразуется во внутреннюю
энергию газа, следствием чего является
повышение температуры газа. Все выше
рассмотренные процессы относятся к
равновесным.

При неравновесном
адиабатном расширении (1-4) или сжатии
(1-5) вследствие выделения теплоты трения
энтропия увеличивается. При этом, в
процессе неравновесного адиабатного
расширения газ совершает меньшую работу,
чем в равновесном, так как часть энергии
газа расходуется на преодоление
сопротивления трения. При неравновесном
сжатии работа затрачивается большая,
по сравнению с равновесным процессом.

Действительно, в
процессе расширения:

A_1-2 = -DU_1-2= –и A_1-4= -DU_1-4= –

Откуда следует, что
А_1-2>А_1-4

При сжатии:

A_1-3=-DU_1-3=и A_1-5= -DU_1-
5 = –

Откуда следует, что
А_1-3<А_1-5.

I
– S
диаграмма для идеального газа

В I-S координатах так же как и
в T-S изохоры и изобары изображаются
логарифмическими линиями. Из соотношения
(4.12) следует, что тангенс угла наклона
касательной к изобаре в I-S координатах
(tga)_p= (¶I/¶S)_p= T. Следовательно, с ростом температуры
значение (tga)_p увеличивается т. е. изобары обращены
выпуклостью вниз, как и в T-S координатах.
Изотермы в правой части диаграммы
представляют собой прямые горизонтальные
линии, которые изгибаются в левой части
диаграммы (рис. 4.6) . Такой ход изотерм
объясняется тем, что при низких давлениях
(правая часть диаграммы) газ ведет себя
как идеальный газ, для которого энтальпия
является функцией только температуры,
область высоких давлений (левая часть
диаграммы) – область реального газа, при
котором энтальпия зависит не только от
температуры , но и от давления.

Анализ
составляющих уравнения первого закона
термодинамики

dQ = dU + pdV = dU + dA

Внутренняя энергия
является функцией состояния, поэтому
изменение её не зависит от пути, по
которому рабочее тело перешло из одного
состояния в другое, рис. 4.7.

DU_1-a-2=DU_1-b-2=DU_1-c-2

следовательно,
dU есть полный дифференциал функции U,
значение которой однозначно определяется
заданием всех координат состояния
U=U(x₁,x₂,…., x_m).Для термодеформационной системы =
U(S,V). Как видно из рис. 4.7 работа, т. е. А,
в указанных процессах (площадь под
кривой, описывающей процесс) различная.
Аналогично и количество теплоты Q в T-S
координатах будет отличаться друг от
друга в зависимости от вида процесса.
Следовательно, dQ и dA в уравнении первого
закона термодинамики не являются полными
дифференциалами, а представляют собой
элементарные количества теплоты и
работы.

Глава
5.
Разомкнутые термодинамические процессы.
Круговые процессы (циклы). Особенности
тепловых и холодильных машин. термический
коэффициент полезного действия цикла
тепловой и холодильной машин. Цикл и
теорема Карно.

Очевидно, что изменение
состояния системы возможно только в
результате её взаимодействия с окружающей
средой. Закон изменения состояния
зависит от характера внешних воздействий,
т. е. от того в каких формах происходит
обмен энергией системы с окружающей
средой и в каких соотношениях между
собой находятся значения количеств
взаимодействий. Для термодеформационного
взаимодействия системы, варьируя
количеством теплоты и работы, можно
осуществить любой закон изменения
состояния газа.

Например, на рис.5.1 в T-S координатах
изображены три процесса, в каждом из
которых теплота подводится (dS>0). При этом температура в процессе 1-2
повышается, а в процессе 1-4 понижается.
Это является следствием того, что в
процессе 1-2 количество подведенной
теплоты больше совершенной газом работы
(Q>А), поэтому
часть теплоты затрачивается на повышение
внутренней энергии газа, в результате
чего его температура повышается.
В процессе 1-4 Q<A , следовательно часть работы совершается
за счет внутренней энергии газа, и
температура последнего понижается.
В процессе 1-3 для идеального
газа dU = 0 , поэтому Q = A.Процесс изменения
состояния газа при заданном в нем
соотношении между Q и A называется
политропным процессом.
Множество процессов с различными
значениями соотношения Q/A можно обобщить
одним уравнением – уравнением политропного
процесса или кратко – уравнением политропы

(5.1)

Здесь n – показатель
политропы, значение которого остается
неизменным в данном процессе.

Вывод уравнения
политропы, как и других термодинамических
соотношений, основан на первом законе
термодинамики.

dQ = dU + dA или CdT =
C_vdT + pdV.
Вынося за скобки dT, получим

(С – С_v)
dT – pdV = 0 (5.2)

Дифференцируя уравнение
состояния идеального газа pV = RT, получим

dT = (pdV + Vdp) / R. Подставим
это значение dT в уравнение (5.2)

(5.3)

Так как R = C_p
– C_v,
то подставив это значение в уравнение
(5.3), получим

(5.4)

Обозначим
, и поделив (5.4) на произведение pV, получим

. После интегрирования полученного
соотношения находим окончательный
результатили(5.5)

Из уравнения (5.5) следует
, что для :

– изобарного
процесса (p = Const) n = 0

– изотермического
процесса (T = Const) n = 1,0.

В адиабатном процессе
– Q = 0, следовательно, С = 0 и показатель
политропы
– показатель адиабаты , значение которого
для двухатомных газов при относительно
невысоких температурах равно 1,4 , а для
трехатомных газов

k = 1,3. k =

C увеличением температуры
теплоёмкость газов увеличивается,
поэтому значение
k уменьшается, однако очень
незначительно.

Извлечением корня n– ой степени (см. уравнение (5.5)) получим

.
Следовательно , в изохорном процессе
(V = Const ) величина n =¥. На рис. 5.2 и 5.3 рассматриваемые процессы
представлены в p-V и T-S координатах.

Соотношения
между параметрами в политропном процессе

На
основании закона Бойля-Мариотта для
политропного процесса можем записать
. Откуда(5.6)

Из
уравнения состояния идеального газа
получим
.

Подставляя
это значение
в уравнение (5.6) , получим

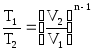(5.7)

После несложных
преобразований из уравнений (5.6) и (5.7)
определяем

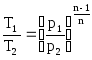(5.8)

Работа
в политропном процессе

Для
получения уравнения, характеризующего
работу в политропном процессе,
воспользуемся выражениями для полной
работы процесса A=и уравнением политропы.Из последнего выражения выразим текущее
значение давления.
Подставив это выражение для давления
в формулу для работы ,получим

Если ввести ещё одну
характеристику политропного
процессаa=DU/Q,
то, не производя расчета, только на
основании значения показателя политропы
n можно определить в каком соотношении
находятся между собой Q,aиDU.

Используя выражение
для n ()
, произведя несложные преобразования,
получим.
Откуда, где k = C_p / C_{v .} Тогдаa=DU / Q =

Пример: рассчитать
доли затрат подведенной к системе
теплоты на изменение внутренней энергии
и на совершение работы для показателя
политропы n = 0,8 и двухатомного газа ( k
= 1,4). Величина коэффициента aa= -0,2 / -0,6 = 1/3. Таким
образом,DU = 1/3 Q , а А
= 2/3 Q, т. е. 1/3 подведенной теплоты
затрачивается на изменение внутренней
энергии , а 2/3 – на совершение работы.

Круговые
термодинамические процессы (циклы)

Тепловой двигатель, в котором теплота
сколь угодно долго превращалась бы в
работу, не может работать по разомкнутому
процессу. Действительно, теплота должна
подводиться от какого-то источника с
заданной температурой Т_ист
.Если процесс расширения осуществляется
при p = Const , то температура рабочего тела
будет возрастать до тех пор, пока её
величина не станет равной температуре
источника. Если в цилиндре двигателя
газ расширяется при постоянной
температуре, то давление в нем будет
уменьшаться. И как только оно станет
равным давлению в окружающей среде –
двигатель остановится. В связи с этим
рабочее тело (например,
газ)в тепловом двигателе
осуществляет круговой процесс (цикл) ,
возвращаясь каждый раз в исходное
состояние рис. 5.4. При подводе к газу (от
источника) теплоты в количестве Q_под
происходит процесс расширения по
политропе 1-а-2 и газ производит работу
А_расш, равную площади
1-а-2-с-d-1 . При этом энтропия рабочего
тела возрастает. В обратном процессе
2-в-1 восстанавливаются прежние значения
координат состояния – S и V (соответственно
восстанавливаются значения потенциалов
Т и р). При сжатии газа до первоначального
объема от него отводится теплота в
количестве Q_отв, а
энтропия уменьшается до начального
значения. Работа , затраченная на сжатие
газа А_сж, в
p-V координатах определяется
площадью
2-в-1-d-c-2. Таким образом, полезная
работа за цикл А_полравна разности работ расширения и сжатия
и изобразится площадью, заключенной
внутри цикла

А_пол= А_расш– А_сж
(5.10)

Цикл тепловой машины в T-S координатах
представлен на рис.5.5. Здесь Q_под
определяется
площадью 1-а-2-в-с-d-1, Q_отв
– площадью
2-в-1-d-c-2. Количество теплоты,
преобразованной в работу, изобразится
площадью, заключенной внутри цикла.

Аналогичные результаты
можно получить , используя первый закон
термодинамики для процессов расширения
(Q_под
=DU_1-a-2
+ A_расш)
и сжатия (- Q_отв=DU_2-b-1– A_сж
). При отводе теплоты и сжатии газа
теплота и работа отрицательные (поставлен
знак минус). Суммируя эти уравнения и
учитывая, что внутренняя энергия, как
функция состояния, не изменяется в
цикле,
(DU_1-а-2=DU_2-b-1)
запишем

Q_под– Q_отв=
А_расш–
А_сж=
А_под
(5.11)

Эффективность работы
теплового двигателя оценивается
термическим коэффициентом полезного
действия

(5.12)

В уравнение (5.12) значение
Q_отвподставляется по абсолютной величине,
так как знак (минус) при Q_отвбыл учтен ранее.

Особенности циклов тепловых машин

1. Линия расширения
лежит выше линии сжатия.

1. Теплота
   подводится при высокой температуре, а
   отводится при более низкой температуре.
   Таким образом, в тепловом двигателе
   происходит перенос теплоты с верхнего
   температурного уровня на нижний
   температурный уровень.

Все процессы в цикле
равновесные. Для того, чтобы подвести
или отвести от рабочего тела теплоту
равновесным образом при переменной его
температуре необходимо иметь бесконечно
большое количество источников теплоты
и холодильников, еак как в каждый данный
момент разность температур источника
и рабочего тела, а также рабочего тела
и холодильника должна быть бесконечно
малой.

Цикл Карно

Цикл, дающий
максимальное значение термического
к.п.д. (при определенных температурах
нагревателя и охладителя), предложенный
французским ученым-инженером Сади
Карно, носит название цикла Карно.

Цикл Карно, состоящий из двух
изотермических и двух адиабатных
процессов и изображенный в различных
координатах, представлен на рис. 5.6 (в
координатах p-V – рис 5.6,а , в координатах
T-S – на рис. 5.6,б). Процессы считаются
равновесными, поэтому подвод теплоты
к рабочему телу в изотермическом процессе
1-2 осуществляется от теплового источника,
температура которого выше температуры
рабочего тела на бесконечно малую
величину (Т_ист= T₁+ dT). Понижение температуры рабочего
тела от Т₁до Т₂осуществляется
в процессе 2-3 при равновесном адиабатном
расширении газа. Для уменьшения энтропии
рабочего тела до первоначального
значения от него в процессе 3-4 отводится
теплота в холодильник, температура
которого на бесконечно малую величину
меньше температуры рабочего тела Т₂.
Цикл замыкается адиабатным сжатием в
процессе 4-1.

Термический
к.п.д. цикла Карно в соответствии с
уравнением (5.12) определяется

следующим
образом:

Так
как DS_1-2
= êDS_3-4
ê,
то
(5.13)

Теорема
Карно

Теорема формулируется
следующим образом. Термический КПД
цикла Карно не зависит от физических
свойств рабочего тела и имеет максимальное
значение из всех возможных циклов в
заданном интервале температур. Первая
часть теоремы не требует доказательства,
так как в выражение для

не входят физические константы
рабочего тела. Значениезависит только от разности температур,
при которых подводится и отводится
теплота в цикле. На рис 5.7 изображен
цикл Карно 1-2-3-4 и вписанный в него
произвольный цикл АBCD .

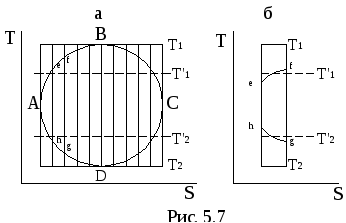
Для доказательства второй части
теоремы Карно разобьем диаграмму цикла
множеством адиабат и рассмотрим
какой-либо из полученных элементарных
циклов, например, efgh. В более крупном
масштабе последний изображен на рис.5.7б.
Этот цикл состоит из двух адиабат и двух
политроп ef и gf. При бесконечно большом
числе элементарных циклов изменение
температуры в политропных процессах
ef и gh будет бесконечно малым, поэтому
указанные политропы можно будет заменить
изотермами с температурамии. Тогда термический КПД цикла efgh можно
рассчитать по формуле (5.13)

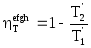, а

Так как
>, а Т₂ <, то<. Аналогичный вывод можно сделать по
отношению к каждому из элементарных
циклов. Поэтому данный вывод справедлив
и для цикла ABCD , т.е.<.

Полученный результат
объясняется тем, что термический КПД
любого цикла зависит не от максимальной
разности температур, достигаемой в
цикле, а зависит от средне интегральных
температур, при которых подводится и
отводится теплота в цикле. В цикле АBCD
теплота подводится от точки А до точки
С при средне интегральной температуре

, а отводится – при средне интегральной
температуре
. Следовательно, эффективная разность
температур в цикле АВСD меньше разности
температур в цикле Карно, поэтому<.

Несмотря на то, что в
цикле Карно теплота наиболее эффективно
преобразуется в работу, этот цикл в
реальных тепловых двигателях не
применяется по следующим причинам:

1. Если цикл Карно в p-V координатах
изобразить в масштабе, то то окажется,
что полезная работа за цикл будет очень
незначительной (рис. 5.8). Для того чтобы
от машины получить большую мощность,
она должна совершать большое число
циклов в единицу времени, т. е. должна
быть быстроходной. У быстроходной
машины будет низкий механический КПД
и выигрыш в термическом КПД не компенсирует
проигрыш в механическом КПД.

2. В цилиндре двигателя,
работающего по циклу Карно, будут
развиваться очень высокие давления.
Рассмотрим это на примере двигателя
внутреннего сгорания, работающего по
адиабатическому процессу:

или

В двигателях внутреннего
сгорания подводится при температуре
сгорания топлива Т₁ @1800 К, а отводится в атмосферу при Т₄@300 К и давлении р₁= = 0,1 МПа. Приняв величину k = 1,35 , получим
значение р₄= 120 Мпа.

Несмотря на указанные
причины цикл Карно имеет большое
значение, так как служит эталоном при
проектировании реальных двигателей.

Некоторые
общие сведения о циклах холодильных
машин

Цикл холодильной
машины в p-V и T-S координатах изображен
на рис. 5.9 и 5.10.

В холодильной машине
теплота подводится к рабочему телу
(хладагенту) от охлаждаемого тела,
например, от охлаждаемых продуктов,
находящихся в холодильной камере. в
которой поддерживается минусовая
температура. Теплота от рабочего тела
отводится при более высокой температуре.
Перенос теплоты от нижнего температурного
уровня на верхний в холодильной машине
оказывается возможным благодаря работе,
затрачиваемой на проведение цикла.
Эффективность работы холодильной машины
оценивается значением холодильного
коэффициента

e=Q_под/ A_затр ,

представляющий собой
отношение хладопроизводительности
машины хладопроизводительность машины
(Q_под) к затраченной работе.

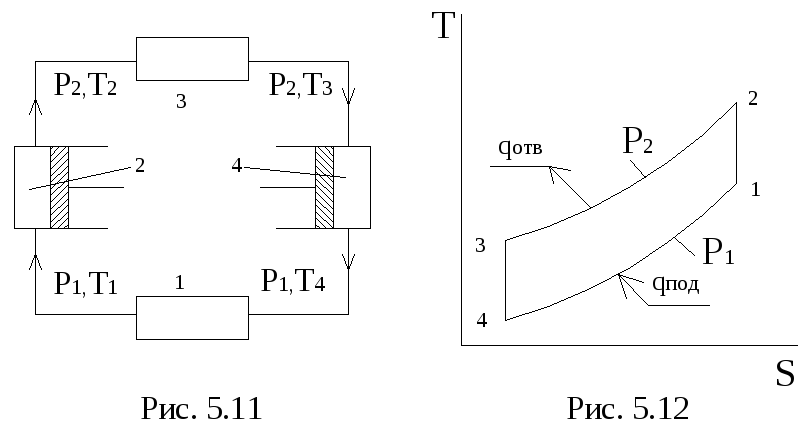
Для примера на рис 5.11 и 5.12 приведены
принципиальная схема и цикл
воздушно-комперессионной холодильной
машины. И теплообменника охлаждаемой
камеры 1 воздух засасывается компрессором,
в котором адиабатически сжимается, в
результате чего температура его
повышается с Т₁ до Т₂. В
холодильнике 3 воздух при давлении р₂охлаждается до температуры Т₃.
Из холодильника воздух направляется в
расширительную машину (детандер) 4, в
которой при адиабатическом расширении
его температура понижается до Т₄ .
В холодильной камере воздух отбирает
теплоту от охлаждаемых продуктов и
нагревается до температуры Т₁

После прочтения данной статьи, рекомендую прочитать статью про энтальпию, скрытую холодопроизводительность и определение количества конденсата, образующегося в системах кондиционирования и осушения: http://mrcynognathus.livejournal.com/7758.html

Доброго времени суток уважаемые начинающие коллеги!

В самом начале своего профессионального пути я наткнулся на данную диаграмму. При первом взгляде она может показаться страшноватой, но если разобраться в главных принципах, по которым она работает, то можно её и полюбить :D. В быту она называется и-д диаграмма.

(для увеличения рисунка необходимо щелкнуть и потом еще раз щелкнуть по нему)

Я уберу все то лишнее, что не будет мне нужным для моего объяснения и представлю и-д диаграмму в таком виде:

(для увеличения рисунка необходимо щелкнуть и потом еще раз щелкнуть по нему)

Все равно еще не совсем понятно, что это такое. Разберем её на 4 элемента:

Первый элемент – влагосодержание (D или d). Но прежде чем я начну разговор об влажности воздуха в целом, я бы хотел кое о чем с вами договориться.

Давайте договоримся “на берегу” сразу об одном понятии. Избавимся от одного прочно засевшего в нас (по крайней мере, в меня) стереотипа о том, что такое пар. С самого детства мне показывали на кипящую кастрюлю или чайник и говорили, тыкая пальцем на валящий из сосуда “дым”: “ Смотри! Вот это пар”. Но как многие, дружащие с физикой люди, мы должны понимать, что “Водяной пар — газообразное состояние воды. Не имеет цвета, вкуса и запаха”. Это всего лишь, молекулы H2O в газообразном состоянии, которых не видно. А то что мы видим, валящее из чайника – это смесь воды в газообразном состоянии(пар) и “капелек воды в пограничном состоянии между жидкостью и газом”, вернее видим мы последнее (так же, с оговорками, можно назвать то что мы видим – туманом). В итоге мы получаем, что в данный момент, вокруг каждого из нас находится сухой воздух (смесь кислорода, азота…) и пар (H2O).

Так вот, влагосодержание говорит нам о том, сколько этого пара присутствует в воздухе. На большинстве и-д диаграмм данная величина измеряется в [г/кг], т.е. сколько грамм пара(H2O в газообразном состоянии) находится в одном килограмме воздуха (1 кубический метр воздуха в вашей квартире весит около 1,2 килограмма). В вашей квартире для комфортных условий в 1 килограмме воздуха должно быть 7-8 грамм пара.

На и-д диаграмме влагосодержание изображается вертикальными линиями, а информация о градации расположена в нижней части диаграммы:

(для увеличения рисунка необходимо щелкнуть и потом еще раз щелкнуть по нему)

(для увеличения рисунка необходимо щелкнуть и потом еще раз щелкнуть по нему)

Третий элемент ИД-диаграммы – относительная влажность (φ). Относительная влажность, это как раз та влажность, о которой мы слышим из телевизоров и радио, когда слушаем прогноз погоды. Измеряется она в процентах [%].

Возникает резонный вопрос: “Чем отличается относительная влажность от влагосодержания?” На данный вопрос я отвечу поэтапно:

Первый этап:

Воздух способен вмещать в себя определенное количество пара. У воздуха есть определенная  “паровая грузоподъемность”. Например, в вашей комнате килограмм воздуха может “взять на свой борт” не больше 15 грамм пара.

Предположим, что в вашей комнате комфортно, и в каждом килограмме воздуха, находящегося в вашей комнате, имеется по 8 грамм пара, а вместить каждый килограмм воздуха в себя может по 15 грамм пара. В итоге мы получаем, что в воздухе находится 53,3% пара от максимально возможного, т.е. относительная влажность воздуха – 53,3%.

Второй этап:

Вместимость воздуха различна при разных температурах. Чем выше температура воздуха, тем больше пара он может в себя вместить, чем ниже температура, тем меньше вместимость.

Предположим, что мы нагрели воздух в вашей комнате обычным нагревателем с +20 градусов до +30 градусов, но при этом количество пара в каждом килограмме воздуха осталось прежним – по 8 грамм. При +30 градусах воздух может “взять себе на борт” до 27 грамм пара, в итоге в нашем нагретом воздухе – 29,6% пара от максимально возможного, т.е. относительная влажность воздуха – 29,6%.

Тоже самое и с охлаждением. Если мы охладим воздух до +11 градусов, то мы получим “грузоподъемность” равную 8,2 грамм пара на килограмм воздуха и относительную влажность равную 97,6%.

Заметим, что влаги в воздухе было одинаковое количество – 8 грамм, а относительная влажность прыгала от 29,6% до 97,6%. Происходило это из-за скачков температуры.

Когда вы зимой слышите о погоде по радио, где говорят, что на улице минус 20 градусов и влажность 80%, то это значит, что в воздухе около 0,3 граммов пара. Попадая к вам в квартиру этот воздух нагревается до +20 и относительная влажность такого воздуха становится равна 2%, а это очень сухой воздух (на самом деле в квартире зимой влажность держится на уровне 10-30% благодаря выделениям влаги из сан-узлов, из кухни и от людей, но что тоже ниже параметров комфорта).

Третий этап:

Что произойдет, если мы опустим температуру до такого уровня, когда “грузоподъемность” воздуха будет ниже, чем количество пара в воздухе? Например, до +5 градусов, где вместимость воздуха равна 5,5 грамм/килограмм. Та часть газообразного H2O, которая не умещается в “кузов” (у нас это 2,5 грамм), начнет превращаться в жидкость, т.е. в воду. В быту особенно хорошо виден этот процесс, когда запотевают окна в связи с тем, что температура стекол ниже, чем средняя температура в комнате, на столько что влаге становится мало места в воздухе и пар, превращаясь в жидкость, оседает на стеклах.

На и-д диаграмме относительная влажность изображается изогнутыми линиями, а информация о градации расположена на самих линиях:

(для увеличения рисунка необходимо щелкнуть и потом еще раз щелкнуть по нему)

(для увеличения рисунка необходимо щелкнуть и потом еще раз щелкнуть по нему)

Дальше все просто! Пользоваться диаграммой легко! Возьмем, например, вашу комфортную комнату, в которой температура +20°С, и относительная влажность 50%. Находим пересечение этих двух линий (температуры и влажности) и смотрим сколько грамм пара в нашем воздухе.

Нагреваем воздух до +30°С – линия идет вверх, т.к. влаги в воздухе остается столько же, а увеличивается только температура, ставим точку, смотрим какая получается относительная влажность – получилось 27,5%.

Подпишись на мой

YouTube-канал FAN-tastiK – канал о проектировании Вентиляции, Кондиционирования и Отопления

Охлаждаем воздух до 5 градусов – опять же ведем вертикальную линию вниз, и в районе +9,5°С натыкаемся на линию 100% относительной влажности. Эта точка называется “точка росы” и в этой точке(теоретически, т.к. практически выпадение начинается чуть раньше) начинается выпадение конденсата. Ниже по вертикальной прямой(как раньше) мы не можем двигаться, т.к. в этой точке “грузоподъемность” воздуха при температуре +9,5°С максимальная. Но нам необходимо охладить воздух до +5°С поэтому мы продолжаем движение вдоль линии относительной влажности (изображено на рисунке ниже), пока не достигнем наклонной прямой линии +5°С. В итоге наша окончательная точка оказалась на пересечении линий температуры +5°С и линии относительной влажности 100%. Посмотрим сколько пара осталось в нашем воздухе – 5,4 грамма в одном килограмме воздуха. А остальные 2,6 грамма выделились. Наш воздух осушился.

(для увеличения рисунка необходимо щелкнуть и потом еще раз щелкнуть по нему)

Другие процессы, которые можно выполнять с воздухом с помощью различных приборов (осушение, охлаждение, увлажнение, нагрев…) можно найти в учебниках.

Помимо точки росы – еще одной важной точкой является “температура мокрого термометра”. Данная температура активно используется в расчете градирен. Грубо говоря, это та точка, до которой может упасть температура предмета, если мы этот предмет обернем в мокрую тряпку и интенсивно начнем на него “дуть”, например, с помощью вентилятора. По этому принципу работает система терморегуляции человека.

Как найти эту точку? Для этих целей нам понадобятся линии энтальпии. Снова возьмем нашу комфортную комнату, найдем точку пересечения линии температуры +20°С, и относительной влажности 50%. Из этой точки необходимо прочертить линию, параллельную линиям энтальпии до линии влажности 100%(как на рисунке ниже). Точка пересечения линии энтальпии и линии относительной влажности и будет являться точкой мокрого термометра. В нашем случае из этой точки мы можем узнать, что в нашей комнате, таким образом, мы можем охладить предмет до температуры +14°С.

(для увеличения рисунка необходимо щелкнуть и потом еще раз щелкнуть по нему)

Луч процесса(угловой коэффициент, тепловлажностное отношение, ε) строится для того чтобы определить изменение воздуха от одновременного выделения неким источником(-ами) тепла и влаги. Обычно этим источником является человек. Очевидная вещь, но понимание процессов и-д диаграммы поможет обнаружить возможную арифметическую ошибку, если таковая случилась. Например, если вы наносите луч на диаграмму и при обычных условиях и наличии людей у вас уменьшается влагосодержание или температура, то здесь стоит задуматься и проверить расчеты.

В данной статье многое упрощено для лучшего понимания диаграммы на начальной стадии её изучения. Более точную, более подробную и более научную информацию необходимо искать в учебной литературе.

P.S. В некоторых источниках I–d(i–d) диаграмму именуют J–d(j–d) диаграммой, h-d диаграммой, диаграммой Молье и диаграммой Рамзина.

P.P.S Так же, в моем журнале есть еще одна моя статья, посвященная энтальпии, скрытой холодопроизводительности и определению количества конденсата, образующегося в системах кондиционирования и осушения:

http://mrcynognathus.livejournal.com/7758.html

    Для определения с помощью графиков удельной энтальпии двухфазных потоков рекомендуется следующий порядок расчета. [c.39]

    Энтальпию парообразования смесей углеводородов можио определить с помощью графика, представленного на рис. 60, а. С повышением давления энтальпия фазового перехода уменьшается. Величина поправки энтальпии на давление, которая вычитается из значения определенного с помощью [c.110]

    Определить энтальпию многокомпонентных смесей углеводородов гораздо сложнее, чем индивидуальных, так как состав смесей очень разнообразен. На рис. 63, 64 представлены удобные для пользования соотношения для смесей легких углеводородных жидкостей и их паров, с помощью которых можно легко определить их удельную энтальпию. Так как свойства жидкости практически не зависят от давления, то для определения удельной энтальпии смесей жидких углеводородов достаточно кривых, представленных на рис. 63. На рис. 64 представлены графики, относящиеся к парам легких углеводородных жидкостей при давлениях 3,5—140,6 кгс/см . Удельная энтальпия при промежуточных давлениях может быть определена методом интерполяции. Для определения с помощью этих графиков удельной энтальпии двухфазных потоков рекомендуется следующая методика  [c.110]

    Первый этап. Способ определения /д] по (28) можно объяснить с помощью графика зависимости и hg от (рис, 3). На горизонтальной оси также отложены значения температуры воды, которые встречаются в исходных данных чаще, чем энтальпия. Значения, и отмеченные на [c.123]

    Обязательной частью любого процесса переработки природных газов является контроль массо- и энергообмена, происходящих в системе. Поэтому проеК тирование этих процессов включает в себя оценку изменений энтальпии Я, энтропии 5 и внутренней энергии 11 системы. Так как величина этих термодинамических характеристик определяется только начальным и конечным состоянием системы и не зависит от пути изменения его, то при расчетах в основном приходится иметь дело с изменениями этих характеристик, а не с их абсолютными значениями. В большинстве источников приводятся значения и, 8 ж Н, отнесенные к определенным, так называемым начальным условиям. Начальными условиями является такое сочетание давления, температуры и фазового состояния, при котором Н = О ж 8 = О для насыщенной жидкой фазы. Например, в большинстве справочных данных по водяному пару начальными условиями являются температура — 0° С, давление — 1 кгс/см , фазовое состояние — насыщенная жидкость. Изменения энтальпии АН и энтропии Аб” можно определить с помощью табличных данных графиков зависимости Н п 8 от. р, V п Т обобщенных соотношений для газов расчетов, основанных на рУГ-данных, и уравнении состояния. Типичные табличные данные представлены в приложении. [c.103]

    Пересчет энтальпий с одной приведенной влажности на другую производится с помощью вспомогательных графиков к I, -диаграммам (для определения коэффициентов 5в и Эг) либо по следующим формулам  [c.69]

    При расчетах тепловых параметров постоянно приходится пользоваться энтальпией водяного пара. В Приложениях 24—27 даны таблицы и график, при помощи которых определяют энтальпию насыщенного и перегретого водяного пара. Следует напомнить, что при данной температуре насыщенный водяной пар всегда имеет определенное давление. Зная один из этих параметров (давление или температуру), можно по таблицам найти тепловые свойства воды и водяного пара, находящихся в равновесии, т. е. в состоянии насыщения. Перегретый водяной пар при одинаковом давлении с насыщенным имеет более высокую температуру. Для его характеристики необходимо знать оба параметра (давление и температуру). [c.30]

    Интегрирование можно произвести графически с помощью значений определенных по графику. Эдмистер дал обширную таблицу приведенных термодинамических функций , по которым можно определить летучесть, теплоемкость, энтальпию и энтропию любого углеводорода, для которого известны критические давление и температура. [c.300]

    Рассмотрим вначале порядок последовательного определения составов фаз в отгонной колонне графическим методом по тепловой диаграмме. Пусть выбран определенный расход тепла BIR в кипятильнике, больший минимального. По известному BIR и по энтальпии остатка, которая непосредственно снимается с тепловой диаграммы для состава х , можно при помощи (IV.7) рассчитать Oj и нанести на график полюс б ). Если при помощи равно- [c.147]

    Пусть выбран определенный съем тепла (НО в парциальном конденсаторе, больший мпнимального. По известному сИО и по энтальпии Q дпстиллята можно при помош.и (IV.37) рассчитать и нанести на график полюс 82 (г/ , Если при помощи равновесных данных из точки В (у , Q ), расположенной на линии энтальпий насыщенного пара, провести конодудо пересечения [c.163]

    Если при определении р иг воспользоваться ЭМР, то можно получить более точные результаты, чем при использовании традиционных псевдокритических значений. NGPA располагает этими данными как в виде графиков, так и в виде алгоритмов для расчетов на ЭВМ. Методика использования этих данных приведена в работе [45]. Она основана на применении принципа соответственных состояний. В этой методике используется энтропия и энтальпия индивидуальных компонентов для расчета энтропии и энтальпии смесей с помощью закона Кея и коэффициента ацентричности Питцера. Методика применима как к паровой, так и к жидкой фазе. [c.122]

    Сказанное относится к формулам пересчета и вспомогательным графикам в части определений и (а=1). При пересчетах приведенной энтальпии продуктов сгорания непосредственно по (4-17) и (4-18) либо с помощью вспомогательных графиков в случаях, когда а>-1, возникает дополнительная небольшая погрешность, так как (4-18) для удобства номографирования упрощена. Она основана на допущении, что относительный прирост энтальпии / г при увеличении приведенной влажности топлива от. нуля до составляет  [c.70]

    Плавление — это фазовый переход первого рода, сопровождающийся скачкообразным изменением основных термодинамических характеристик полимера — удельного объема V и энтальпии Н. Как следует из соотношения (2.1), и зависят от степени кристалличности образца X. Для образца со 100 %-ной кристалличностью они определяются конформационными характеристиками макромолекулы и силами межцепного взаимодействия и рассчитываются с помощью соотношения (2.1) по измеренным значениям и ДЯ и значению X, определенному для этого же образца независимым способом. Этим методом было получено большинство значений Ду и АНт, приведенных в табл. 2.4. Значения АНщ можно определить и другими способами. Например, по зависимости температуры плавления полимера от содержания низкомолекулярного разбавителя, описываемой уравнением Флори [58] 1/Тт — 1/Г . р = (Я АНт) У Ур) (фр — Ххф ), где Тт и Т — температуры плавления смеси полимер — разбавитель и исходного полимера соответственно. Для этого строят график зависимости 11Тт—11Т о)/Фс от фр и из отрезка, отсекаемого полученной прямой на оси ординат, который равен (Я/АНт) У1Ур)< определяют АНт- [c.173]

    Пусть выбран определенный съем тепла d/D в парциальном конденсаторе, больший минимального. По известному d/D и по энтальпии дистил.лята можно нри помощи (IV.37) рассчитать 9 и нанести на график полюс Si (г/ , 62). Если при помощи равновесных данных нз точки D (г/ , Qj), расположенной на линии энтальпий насыщенного пара, провести коноду до пересечения [c.163]

---