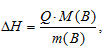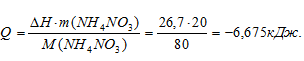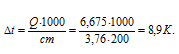Как найти энтальпию растворения

Макеты страниц

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Тепловой эффект процесса

Термохимические уравнения

Закон Гесса

Следствия из закона Гесса

Стандартные термодинамические величины

Стандартные энтальпии образования и сгорания

Примеры решения задач

Задачи для самостоятельного решения

Тепловой эффект процесса

Количество выделенной (или поглощенной) теплоты Q в данном процессе называют тепловым эффектом процесса. Экзотермической является реакция, протекающая с выделением теплоты, а эндотермической – с поглощением теплоты из окружающей среды.

Для лабораторных и промышленных процессов наиболее типичен изобарный режим (Р=const). Поэтому обычно рассматривают тепловой эффект при Р,Т = const, т.е. изменение энтальпии процесса ΔН.

Следует отметить, что абсолютные значения энтальпии Н определить не представляется возможным, так как не известна абсолютная величина внутренней энергии.

Для экзотермической реакции (Q > 0) ΔН < 0, а в эндотермическом процессе (Q < 0) ΔН > 0.

Термохимические уравнения

Химические уравнения, в которых дополнительно указывается величина изменения энтальпии реакции, а также агрегатное состояние веществ и температура, называются термохимическими уравнениями.

В термохимических уравнениях отмечают фазовое состояние и аллотропные модификации реагентов и образующихся веществ: г – газообразное, ж – жидкое, к – кристаллическое; S_(ромб), S_{(монокл)}, С_{(графит)}, С_(алмаз) и т.д.

Важно подчеркнуть, что с термохимическими уравнениями можно проводить алгебраические операции сложения, вычитания, деления, умножения.

Закон Гесса

Изменение энтальпии (внутренней энергии) химической реакции зависит от вида, состояния и количества исходных веществ и продуктов реакции, но не зависит от пути процесса.

Следствия из закона Гесса

1. Изменение энтальпии реакции равно сумме энтальпий образования продуктов реакции за вычетом суммы энтальпий образования исходных веществ (суммирование проводится с учетом стехиометрических коэффициентов).
2. Изменение энтальпии реакции равно сумме энтальпий сгорания исходных веществ за вычетом суммы энтальпий сгорания продуктов реакции (суммирование проводится с учетом стехиометрических коэффициентов).

Стандартные термодинамические величины

Стандартные термодинамические величины – это такие величины, которые относятся к процессам, все ингредиенты которых находятся в стандартных состояниях.

Стандартным состоянием вещества, находящегося в конденсированной фазе (кристаллической или жидкой), является реальное состояние вещества, находящегося при данной температуре и давлении 1 атм.

Следует подчеркнуть, что стандартное состояние может иметь место при любой температуре.

Обычно тепловой эффект (изменение энтальпии) реакции приводится для температуры 25^оС (298,15 К) и давления 101,325 кПа (1 атм), т.е. указывается стандартная энтальпия ΔН^о₂₉₈.

Стандартные энтальпии образования и сгорания

Стандартная энтальпия образования ΔН^о_f,298 (или ΔН^о_обр,298) – это изменение энтальпии в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии, причем простые вещества присутствуют в наиболее термодинамически устойчивых состояниях при данной температуре.

Например, ΔН^o_f,298(Н₂О(ж)) = — 285,83 кДж/моль соответствует изменению энтальпии в процессе

Н_2(г) + ½O_2(г) = Н₂О_(ж)

при Т = 298,15 К и Р = 1 атм.

Стандартная энтальпия образования простых веществ равна нулю по определению (для наиболее устойчивых их модификаций при данной температуре).

Стандартной энтальпией сгорания ΔН^o_сгор,298 называют энтальпию сгорания вещества (обычно 1 моль), находящегося в стандартном состоянии с образованием СО_2(г), Н₂О_(ж) и других веществ, состав которых должен быть специально указан. Все продукты сгорания также должны находиться в стандартном состоянии.

Примеры решения задач

Задача 1. Используя справочные термодинамические данные вычислить ΔН^o₂₉₈ реакции:

2H₂S(г) + 3O₂(г) = 2SO₂(г) + 2H₂O(ж); ΔН^oх.р.,₂₉₈ = ?

Решение. Решим задачу, используя оба следствия из закона Гесса. Ниже для исходных веществ и продуктов реакции приведены значения энтальпий образования и сгорания в кДж/моль (энтальпия сгорания сероводорода до SO_2(г) и H₂O_(ж)):

Вещество	H2S(г)	O2(г)	SO2(г)	H2O(ж)
ΔНof,298	-20,60	0	-296,90	-285,83
ΔНoсгор,298	-562,10	0	0	0

Cогласно первому следствию закона Гесса энтальпия этой реакции ΔН^о_х.р. равна:

ΔН^о_х.р.,298 = 2ΔН^о_f,298(SO_2(г)) + 2ΔН^о_f,298(H₂O_(ж)) — 2ΔН^о_f,298(H₂S_(г)) — 3ΔН^о_f,298(O_2(г)) = 2(- 296,90) + 2(- 285,83) — 2(- 20,60) = — 1124,21 кДж.

В соответствии со вторым следствием закона Гесса получаем:

ΔН^о_х.р.,298 = 2ΔН^о_сгор,298(H₂S(г)) = 2(-562,10) = — 1124,20 кДж.

Задача 2. Вычислите ΔН^о₂₉₈ реакции N₂(г) + 3H₂(г) = 2NH₃(г), используя следующие данные:

4NH_3(г) + 3O_2(г) = 2N_2(г) + 6H₂O_(ж); ΔН^о₁ = -1531,22 кДж;

2H₂O_(ж) = O_2(г) + 2H_2(г); ΔН^о₂= 571,66 кДж.

Определите стандартную энтальпию образования NH₃(г).

Решение. Поскольку с термохимическими уравнениями можно производить все алгебраические действия, то искомое уравнение получится, если:

• • • разделить на два тепловой эффект первого уравнения и изменить его знак на противоположный, т.е:

N_2(г) + 3H₂O_(ж) = 2NH_3(г) + 3/2O_2(г); ΔН^о = 765,61 кДж;

• • • умножить на 3/2 второе уравнение и соответствующую ему величину  δН^o , изменив ее знак на противоположный:

3/2O_2(г) + 3H_2(г) = 3H₂O_(ж); ΔН^о = -857,49 кДж;

• • • сложить полученные первое и второе уравнения.

Таким образом, тепловой эффект реакции N_2(г) + 3H_2(г) = 2NH_3(г) равен:

Δ Н^о₂₉₈ = (- ΔН^о₁/2) + (- 3/2·ΔН^о₂) = 765,61 + (- 857,49) = — 91,88 кДж.

Поскольку в рассматриваемой реакции образуется 2 моль NH_3(г), то

ΔН^о_f,298(NH_3(г)) = — 91,88/2 = — 45,94 кДж/моль.

Задача 3. Определите энтальпию процесса

CuSO_4(к) + 5H₂O_(ж) = CuSO₄·5H₂O_(к)

если при 298,15 К энтальпия растворения CuSO_4(к) в n моль Н₂О с образованием раствора CuSO₄(р-р, nH₂O) равна –40, а энтальпия растворения CuSO₄·5H₂O_(к) с образованием раствора той же концентрации равна +10,5 кДж/моль.

Решение. Составляем цикл Гесса:

ΔН^о₁ = ΔН^о₂ + ΔН^о_х (по закону Гесса). Отсюда получаем:

ΔН^о_х = ΔН^о₁ – ΔН^о₂ = – 40,0 – 10,5 = -50,5 кДж.

Другой вариант решения.

CuSO_4(к) + (n H₂O) = CuSO₄(р-р, n H₂O); ΔН^о₁ = – 40,0 кДж; (1)

CuSO_4(к) + 5H₂O(ж) = CuSO₄·5H₂O(к); ΔН^о_х = Н^о₂; (2)

CuSO₄·5H₂O_(к) + (n – 5)H₂O = CuSO₄(р-р, nH₂O); ΔН^о₃ = 10,5 кДж. (3)

По закону Гесса:  ΔН^о₁ =  ΔН^о_х+  ΔН^о₃, т.е. при сложении уравнений (2) и (3) получим уравнение (1).

Задача 4. Вычислите энтальпию образования химической связи С= С в молекуле этилена, если его стандартная энтальпия образования равна 52,3 кДж/моль, энтальпия возгонки графита составляет 716,7 кДж/моль, энтальпия атомизации водорода равна +436,0 кДж/моль, энтальпия образования связи С–Н равна –414,0 кДж/моль.

Решение. Составляем цикл Гесса:

ΔН^о_f,298(С₂Н_4(г)) = 2ΔН^о_возг(С_{(графит)}) + 2ΔН^о_атом (H_2(г)) + ΔН^о_(С= С) + 4ΔН^о_(С–Н).

ΔН^о_(С = С) = 52,3 — 2·716,7 — 2·436,0 + 4·414,0 = — 597,1 кДж/моль.

Задачи для самостоятельного решения

1. Составьте уравнение реакции, для которой ΔН^о соответствует стандартной энтальпии образования ВaCl₂·2H₂O_(к).

2. Определить ΔН^о₂₉₈ реакции:

CH₃CНO_(ж) + H_2(г) = CH₃CH₂OH_(ж),

если ΔН^о_сгор,298(CH₃CНO_(ж)) = — 1193,07 кДж/моль; ΔН^о_сгор,298(CH₃CH₂OH_(ж)) = — 1370,68 кДж/моль; ΔН^о_f,298(Н₂О_(ж)) = — 285,83 кДж/моль.

10.3. Энтальпии растворения BaCl_2(к) и BaCl₂·2H₂O_(к) с образованием раствора хлорида бария (с мольным отношением BaCl₂: H₂O = 1: 500) соответственно равны –11,18 и 18,74 кДж/моль.
Определить величину ΔН^о присоединения воды к BaCl_2(к) с образованием BaCl₂·2H₂O_(к).

10.4. Рассчитать энтальпию связи в молекуле NO на основании следующих термохимических уравнений:

N_2(г) + O_2(г) = 2NO_(г); ΔН^о₂₉₈ = +182,52 кДж;

2O_(г) = O_2(г); ΔН^о₂₉₈ = — 498,34 кДж;

N_2(г) = 2N_(г); ΔН^о₂₉₈ = +945,42 кДж.

10.5. Вычислить ΔН^о₂₉₈ реакции 2C(г) + 2H₂(г) = C₂H₄(г), используя следующие термохимические уравнения:

С_{(графит)} = С_(г) ; ΔН^о₂₉₈ = +716,67 кДж;
С₂H_4(г) + 3O_2(г) = 2CO_2(г) + 2H₂O_(г); ΔН^о₂₉₈ = — 1322,94 кДж;
C_{(графит)} + O_2(г) = CO_2(г); ΔН^о₂₉₈ = — 393,51 кДж;

H_2(г) + 1/2O_2(г) = H₂O_(г); ΔН^о₂₉₈ = — 241,81 кДж.

10.6. Определите стандартную энтальпию реакции взаимодействия метана с оксидом углерода (IV), если стандартные энтальпии образования метана, оксида углерода (IV) и оксида углерода (II) при 298 К равны соответственно: -75; -393 и -111 кДж/моль.

7. Определите стандартную энтальпию образования С₂Н₅ОН_(ж), если стандартные энтальпии сгорания углерода, водорода и этанола при 298 К равны соответственно: -393; -286 и -1366 кДж/моль.

8. Вычислите энтальпию химической реакции 4KClO_3(к)=KCl_(к)+3KClO_4(к) по следующим данным:

2KClO_3(к)=2KCl_(к)+3O_2(г); ΔН^о₂₉₈ = — 95 кДж;
4KClO_4(к)=KCl_(к)+2O_2(г); ΔН^о₂₉₈ = 9 кДж/моль.

9. Вычислите среднюю энтальпию связи P-Cl в молекуле PCl₅, используя следующие термохимические уравнения:

P_{(к, бел.)}+5/2Cl_2(г)=PCl_5(г); ΔН^о₁ = — 374,8 кДж;
P_{(к, бел.)}=P_(г); ΔН^о₂ = — 17,4 кДж;
Cl_2(г)=2Cl_(г); ΔН^о₃ = 242,6 кДж.

10. Вычислите среднюю энтальпию связи N-H в молекуле NH₃, используя следующие термохимические уравнения:

1/2N_2(г)+3/2H_2(г)=NH_3(г); ΔН^о₁ = — 46,2 кДж;
N_2(г)=2N_(г); ΔН^о₂ = 945,4 кДж;
H_2(г)=2H_(г); ΔН^о₃ = 436,0 кДж.

Тепловой эффект химической реакции — изменение внутренней энергии или энтальпии системы вследствие протекания химической реакции и превращения исходных веществ (реактантов) в продукты реакции в количествах, соответствующих уравнению химической реакции (стехиометрии реакции^[1]) при следующих условиях:

• единственно возможной работой при этом является работа против внешнего давления,
• как исходные вещества, так и продукты реакции имеют одинаковую температуру^[2][3].

Теплота термохимического процесса и тепловой эффект химической реакции[править | править код]

Поясним приведённое выше определение теплового эффекта химической реакции^{[K 1]}. Для этого запишем фундаментальные уравнения Гиббса для внутренней энергии и энтальпии простой^[10] открытой однородной термодинамической системы^[11][12]:

(Фундаментальное уравнение Гиббса для внутренней энергии)

(Фундаментальное уравнение Гиббса для энтальпии)

Здесь  — абсолютная температура,  — энтропия,  — давление,  — объём,  — количество (или масса) -го составляющего систему вещества,  — химический потенциал этого вещества (см. Энтропия открытой системы).

Для бесконечно малого^[13] квазистатического изохорного процесса ()

(Изменение внутренней энергии в бесконечно малом квазистатическом изохорном процессе)

для бесконечно малого квазистатического изобарного процесса ()

(Изменение энтальпии в бесконечно малом квазистатическом изобарном процессе)

Важно понимать, что представление о теплоте химической реакции при сохранении исторически сложившегося названия (восходящего ко временам, когда любое изменение температуры связывали с поглощением или выделением теплоты) уже не имеет прямого отношения к общефизическому понятию количества теплоты. Действительно, при химической реакции в изолированной системе (например, инициируемом электрической искрой взрыве гремучего газа в герметически закрытом термосе) может иметь место изменение температуры (за счёт выделения теплоты), но не происходит обмена с окружающей средой(так как попросту это термос — изолированная система), ни изменения внутренней энергии системы. Наконец, традиционная трактовка теплоты, основанная на представлении об адиабатической изоляции системы от окружающей среды^[14] (см. Неоднозначность понятий «теплота» и «работа») к открытым системам не применима, и для них теплоту бесконечно малого квазистатического процесса полагают равной^[15][16]

(Дефиниция теплоты для любого бесконечно малого квазистатического процесса)

Таким образом, теплота бесконечно малого квазистатического изохорного процесса равна

(Теплота бесконечно малого квазистатического изохорного процесса)

а теплота бесконечно малого квазистатического изобарного процесса равна

(Теплота бесконечно малого квазистатического изобарного процесса)

Для закрытых систем изменение энергии системы за счёт изменения масс составляющих систему веществ (химическую работу^{[17][18][19][20][21]}, работу перераспределения масс составляющих систему веществ^[22]) учитывать не требуется^[23][24], и выражения для теплот ещё более упрощаются:

(Теплота бесконечно малого квазистатического изохорного процесса в простой закрытой системе)

(Теплота бесконечно малого квазистатического изобарного процесса в простой закрытой системе)

Из сказанного ясно, почему в дефиниции теплового эффекта химической реакции фигурируют внутренняя энергия, энтальпия и запрет на любые виды работ в системе, кроме работы расширения/сжатия. Уточним, что в понятии «химическая работа» термин «работа» не имеет отношения к понятию «термодинамическая работа» и использован просто как синоним словосочетания «изменение энергии». Наконец, подчеркнём, что когда речь идёт о тепловом эффекте химической реакции, то, как и во многих других случаях, касающихся термохимии, подразумевается, что речь идёт о закрытой системе и полномасштабное применение мощного, но громоздкого математического аппарата термодинамики систем переменного состава не требуется^[23][24][25].

Энергетический эффект химической реакции всегда рассматривают применительно к конкретному термохимическому уравнению, которое может не иметь отношения к реальному химическому процессу. Термохимическое уравнение лишь показывает, какие наборы начальных и конечных индивидуальных веществ, находящихся в определённых состояниях и количественных соотношениях, исчезают и образуются. В начальном состоянии должны присутствовать только исходные вещества (реактанты), а в конечном — только продукты химической реакции. Единственным условием при записи термохимического уравнения является соблюдение материального и зарядового баланса. Вещества в растворённом или адсорбированном состоянии тоже считаются индивидуальными соединениями; если растворитель или адсорбент не участвует непосредственно в химической реакции и не реагирует с растворённым веществом, то он рассматривается просто как фактор, влияющий на термодинамические свойства рассматриваемого вещества. Наконец, в термохимическом уравнении могут фигурировать частицы, не способные к самостоятельному существованию (электроны, протоны, ионы, радикалы, атомарные простые вещества)^[26].

Энергетический эффект реального процесса с химической реакцией зависит от условий проведения процесса и не может служить стандартной характеристикой конкретной химической реакции^[3]. Химическая же термодинамика нуждается в показателе, связанном с энергетикой химической реакции, но не зависящем от условий её проведения. Покажем, как может быть получен интересующий нас показатель. Для этого рассмотрим следующий мысленный эксперимент. Возьмем чистые индивидуальные исходные вещества в мольных количествах, соответствующих стехиометрическим коэффициентам интересующего нас термохимического уравнения, и находящиеся при определённых температуре и давлении. Если привести эти вещества в контакт, то энтальпия образовавшейся неравновесной системы в начальный момент времени будет равна сумме энтальпий исходных веществ. Теперь рассмотрим конечное состояние изучаемой системы в предположении, что реактанты прореагировали полностью^[27] и продукты реакции находятся при той же температуре и том же давлении, что и реактанты. Энтальпия системы (в общем случае неравновесной) из продуктов химической реакции будет равна сумме энтальпий этих веществ. Поскольку энтальпия — функция состояния, то разность энтальпий системы в конце и начале рассмотренного мысленного эксперимента не зависит от условий проведения химической реакции. Эту разность энтальпий и называют изобарным тепловым эффектом (термохимической теплотой) химической реакции, соответствующей определённому термохимическому уравнению^[28][29]. Важно, что реальная осуществимость рассмотренного мысленного эксперимента, гипотетические условия его проведения и неравновесность исходного и конечного состояний термохимической системы не сказываются на дефиниции теплового эффекта химической реакции.

Часто тепловой эффект химической реакции относят к 1 молю одного из продуктов реакции^[30].

Резюмируем сказанное: теплота процесса, связанного с фактическим протеканием химической реакции, и энергетический эффект химической реакции отнюдь не одно и то же, а дефиниция теплового эффекта химической реакции вообще не предполагает действительного осуществления реакции, соответствующей рассматриваемому термохимическому уравнению^[31].

И внутренняя энергия, и энтальпия представляют собой функции состояния, поэтому тепловой эффект химической реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, то есть от числа и характера промежуточных стадий (закон Гесса)^{[32][33][34][35]}.

Тепловой эффект химической реакции, протекающей при постоянном давлении, и равный изменению энтальпии системы в процессе, соответствующем термохимическому уравнению, называется изобарным тепловым эффектом или энтальпией химической реакции. Тепловой эффект химической реакции, протекающей при постоянном объёме, и равный изменению внутренней энергии системы в процессе, соответствующем термохимическому уравнению, называют изохорным тепловым эффектом^[2].

Для отдельных типов химических реакций вместо общего термина «тепловой эффект химической реакции» используют специальные (сокращённые) термины: теплота образования, теплота сгорания и т. п.^[1]

Дефиниции тепловых эффектов должны быть дополнены указанием на начальные точки отсчёта значений энергии и энтальпии. Для сравнения тепловых эффектов и упрощения термодинамических расчётов все величины тепловых эффектов реакций относят к стандартным условиям (все вещества находятся в стандартных состояниях)^[1]. Если реакцию — реально или гипотетически — проводят при стандартных условиях (T = 298,15 К = 25 °С и P = 1 бар = 100 кПа)^[36], то тепловой эффект называют стандартным тепловым эффектом реакции или стандартной энтальпией реакции ΔHo
r.

Химические реакции, сопровождающиеся повышением температуры, называют экзотермическими, понижением температуры — эндотермическими. В термодинамической системе знаков тепловой эффект экзотермической реакции ( или ) считают отрицательным, эндотермической ( или ) — положительным. В устаревшей и не рекомендуемой к употреблению термохимической системе знаков положительным, наоборот, считается тепловой эффект экзотермической реакции, а отрицательным — эндотермической^[37].

Тепловые эффекты химических реакций важны для теоретической химии и необходимы при расчётах равновесных составов смесей, выхода продуктов реакций, удельной тяги топлив реактивных двигателей и для решения многих других прикладных задач^[1].

Изучение тепловых эффектов химических реакций составляет важнейшую задачу термохимии^[3]. Для расчёта стандартных тепловых эффектов химических реакций используют таблицы стандартных теплот образования или сгорания^[37].

Стандартная энтальпия образования (стандартная теплота образования)[править | править код]

Под стандартной теплотой образования понимают тепловой эффект реакции образования одного моля вещества из простых веществ, его составляющих, находящихся в устойчивых стандартных состояниях.

Например, стандартная энтальпия образования 1 моля метана из углерода и водорода равна тепловому эффекту реакции:

С(тв) + 2H₂(г) = CH₄(г) + 74,9 кДж/моль.

Стандартная энтальпия образования обозначается ΔHo
f. Здесь индекс f означает formation (образование), а знак «O» в верхнем индексе указывает, что величина относится к стандартному состоянию вещества: один моль индивидуального химического соединения, взятого в чистом виде при стандартных условиях в том агрегатном состоянии, которое устойчиво в этих условиях (если нет специальной оговорки)^[38]. Иногда для обозначения стандартного состояния используют перечёркнутый символ «O» в верхнем индексе; согласно рекомендациям ИЮПАК по использованию обозначений в физической химии^[39], перечёркнутый и неперечёркнутый символ «O», используемые для обозначения стандартного состояния, одинаково приемлемы. В литературе часто встречается другое обозначение стандартной энтальпии — ΔHo
298,15, где знак «O» указывает на равенство давления одной атмосфере^[40] (или, несколько более точно, на стандартные условия^[41]), а 298,15 — температура. Иногда индекс «O» используют для величин, относящихся к чистому веществу, оговаривая, что обозначать им стандартные термодинамические величины можно только тогда, когда в качестве стандартного состояния выбрано именно чистое вещество^[42]. Стандартным также может быть принято, например, состояние вещества в предельно разбавленном растворе.

Энтальпия образования простых веществ принимается равной нулю, причем нулевое значение энтальпии образования относится к агрегатному состоянию, устойчивому при T = 298,15 K. Например, для иода в кристаллическом состоянии ΔH^o(I₂, тв) = 0 кДж/моль, а для жидкого иода ΔH^o(I₂, ж) = 22 кДж/моль. Энтальпии образования простых веществ при стандартных условиях являются их основными энергетическими характеристиками.

Тепловой эффект любой реакции находится как разность между суммой теплот образования всех продуктов и суммой теплот образования всех реагентов в данной реакции (следствие закона Гесса):

ΔH^o_{реакции} = ΣΔHo
f (продукты) — ΣΔHo
f (реагенты).

Термохимические эффекты можно включать в химические реакции. Химические уравнения в которых указано количество выделившейся или поглощенной теплоты, называются термохимическими уравнениями. Реакции, сопровождающиеся выделением тепла в окружающую среду имеют отрицательный тепловой эффект и называются экзотермическими. Реакции, сопровождающиеся поглощением тепла имеют положительный тепловой эффект и называются эндотермическими. Тепловой эффект обычно относится к одному молю прореагировавшего исходного вещества, стехиометрический коэффициент которого максимален.

Температурная зависимость теплового эффекта (энтальпии) реакции[править | править код]

Чтобы рассчитать температурную зависимость энтальпии реакции, необходимо знать мольные теплоемкости веществ, участвующих в реакции. Изменение энтальпии реакции при увеличении температуры от Т₁ до Т₂ рассчитывают по закону Кирхгофа (предполагается, что в данном интервале температур мольные теплоемкости не зависят от температуры и нет фазовых превращений):

Если в данном интервале температур происходят фазовые превращения, то при расчёте необходимо учесть теплоты соответствующих превращений, а также изменение температурной зависимости теплоемкости веществ, претерпевших такие превращения:

где ΔC_p(T₁, T_φ) — изменение теплоемкости в интервале температур от Т₁ до температуры фазового перехода;  — тепловой эффект фазового перехода; ΔC_p(T_φ, T₂) — изменение теплоемкости в интервале температур от температуры фазового перехода до конечной температуры, и T_φ — температура фазового перехода.

Стандартная энтальпия сгорания[править | править код]

Стандартная энтальпия сгорания — ΔHо
гор., тепловой эффект реакции сгорания одного моля вещества в кислороде до образования оксидов в высшей степени окисления. Теплота сгорания негорючих веществ принимается равной нулю.

Стандартная энтальпия растворения[править | править код]

Стандартная энтальпия растворения — ΔHо
раств., тепловой эффект процесса растворения 1 моля вещества в бесконечно большом количестве растворителя. Складывается из теплоты разрушения кристаллической решётки и теплоты гидратации (или теплоты сольватации для неводных растворов), выделяющейся в результате взаимодействия молекул растворителя с молекулами или ионами растворяемого вещества с образованием соединений переменного состава — гидратов (сольватов). Разрушение кристаллической решетки, как правило, эндотермический процесс — ΔH_реш. > 0, а гидратация ионов — экзотермический, ΔH_гидр. < 0. В зависимости от соотношения значений ΔH_реш. и ΔH_гидр. энтальпия растворения может иметь как положительное, так и отрицательное значение. Так растворение кристаллического гидроксида калия сопровождается выделением тепла:

ΔHо
раств.KOH = ΔHо
реш. + ΔHо
гидр.К⁺ + ΔHо
гидр.OH⁻ = −59 кДж/моль.

Под энтальпией гидратации ΔH_гидр. понимается теплота, которая выделяется при переходе 1 моля ионов из вакуума в раствор.

Стандартная энтальпия нейтрализации[править | править код]

Стандартная энтальпия нейтрализации ΔHо
нейтр. — энтальпия реакции взаимодействия сильных кислот и оснований с образованием 1 моля воды при стандартных условиях:

HCl + NaOH = NaCl + H₂O

H⁺ + OH⁻ = H₂O, ΔHо
нейтр. = −55,9 кДж/моль

Стандартная энтальпия нейтрализации для концентрированных растворов сильных электролитов зависит от концентрации ионов, вследствие изменения значения ΔHо
гидратации ионов при разбавлении.

См. также[править | править код]

• Термохимия
• Химическая термодинамика

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

• Callen H. B. Thermodynamics and an Introduction to Thermostatistics. — 2nd ed. — N. Y. e. a.: John Wiley, 1985. — XVI + 493 p. — ISBN 0471862568, 9780471862567.
• Lebon G., Jou D., Casas-Vázquez J. Understanding Non-equilibrium Thermodynamics: Foundations, Applications, Frontiers. — Berlin — Heidelberg: Springer, 2008. — XIII + 325 p. — ISBN 978-3-540-74251-7, 978-3-540-74252-4. — doi:10.1007/978-3-540-74252-4.
• Александров Н. Е., Богданов А. И., Костин К. И. и др. Основы теории тепловых процессов и машин. Часть II / Под ред. Н. И. Прокопенко. — 5-е изд. (электронное). — М.: Бином. Лаборатория знаний, 2015. — 572 с. — ISBN 978-5-9963-2613-6. (недоступная ссылка)
• Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
• Большая Советская Энциклопедия / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: Советская Энциклопедия, 1976. — Т. 25: Струнино — Тихорецк. — 600 с. Архивная копия от 5 августа 2017 на Wayback Machine
• Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М.: Инфра-М, 2017. — 868 с. — ISBN 978-5-16-104227-4.
• Бурдаков В. П., Дзюбенко Б. В., Меснянкин С. Ю., Михайлова Т. В. Термодинамика. Часть 2. Специальный курс. — М.: Дрофа, 2009. — 362 с. — (Высшее образование. Современный учебник). — ISBN 978-5-358-06140-8.
• Жариков В. А. Основы физической геохимии. — М.: Наука; Изд-во МГУ, 2005. — 656 с. — (Классический университетский учебник). — ISBN 5-211-04849-0, 5-02-035302-7.
• Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с.
• Карякин Н. В. Основы химической термодинамики. — М.: Академия, 2003. — 463 с. — (Высшее профессиональное образование). — ISBN 5-7695-1596-1. (недоступная ссылка)
• Кнорре Д. Г., Крылова Л. Ф., Музыкантов В. С. Физическая химия. — 2. — М.: Высшая школа, 1990. — 416 с. — ISBN 5-06-000655-7.
• Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
• Ляшков В. И. Теоретические основы теплотехники. — М.: Курс; Инфра-М, 2015. — 328 с. — ISBN 978-5-905554-85-8, 978-5-16-0І0639-7.
• Морачевский А. Г., Кохацкая М. С. Прикладная химическая термодинамика. — СПб.: Изд-во Политехн. ун-та, 2008. — 254 с. — ISBN 978-5-7422-2006-0.
• Морачевский А. Г., Фирсова Е. Г. Физическая химия. Термодинамика химических реакций. — 2-е изд., испр. — СПб.: Лань, 2015. — 101 с. — (Учебники

для вузов. Специальная литература). — ISBN 978-5-8114-1858-9. (недоступная ссылка)

• Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — М.: Мир, 1971. — 296 с.
• Нараев В. Н. Физическая химия. Часть 1. Химическая термодинамика. Фазовые равновесия и учение о растворах. Электрохимия. — СПб.: Санкт-Петербургский государственный технологический институт (Технический университет), 2007. — 262 с. (недоступная ссылка)
• Никольский Б. П., Смирнова Н. А., Панов М. Ю. и др. Физическая химия. Теоретическое и практическое руководство / Под ред. Б. П. Никольского. — 2-е изд., перераб. и доп. — Л.: Химия, 1987. — 880 с. — (Для высшей школы).
• Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М.: Наука, 1971. — 376 с.
• Степановских Е. И., Брусницына Л. А., Маскаева Л. Н. Химическая термодинамика в вопросах и ответах. — Екатеринбург: УИПЦ, 2014. — 221 с. — ISBN 978-5-4430-0061-9.
• Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
• Тамм М. Е., Третьяков Ю. Д. Неорганическая химия. Том 1. Физико-химические основы неорганической химии / Под. ред. акад. Ю. Д. Третьякова. — М.: Академия, 2004. — 240 с. — (Высшее профессиональное образование). — ISBN 5-7695-1446-9.
• Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.
• Химическая энциклопедия / Гл. ред. Н. С. Зефиров. — М.: Большая Российская энциклопедия, 1995. — Т. 4: Пол — Три. — 640 с. — ISBN 5-85270-092-4.
• Химический энциклопедический словарь / Гл. ред. И. Л. Кнунянц. — М.: Советская энциклопедия, 1983. — 792 с.
• Шмидт Э. Введение в техническую термодинамику / Пер. с нем. — М.—Л.: Энергия, 1965. — 392 с.
• Эткинс П. Физическая химия. — М.: Мир, 1980.

Определение энтальпии растворения вещества, используя удельную теплоемкость раствора

Задача 458. 
При растворении 10 г NаОН в 250 г воды температура повысилась на 9,70 °С. Определить энтальпию растворения NаОН, принимая удельную теплоемкость раствора равной 4,18 дж/(г ^. К).
Решение:
М(NaOH) = 40г/моль. При растворении 10 г NаОН в 250 г воды температура повысилась на 9,70 °С, при этом образуется довольно разбавленный раствор. Общая масса раствора (m) равна 260 г (250 + 10 = 260). По повышению температуры 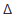t) находим количество выделенной теплоты по формуле:

   Q = cm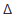t,

где
c – удельная теплоёмкость вещества, m – масса раствора, 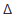t – повышение температуры.

Тогда

Q = 4,18 ^. 260 ^. 9,70 = 10541,96 Дж или 10,542 кДж.

Изменение энтальпии 10 г щёлочи составляет 10,542 кДж, а мольная масса NaOH –  40 г/моль. Отсюда энтальпия растворения NaOH находим из пропорции: 

10 : (-10,542) = 40 : х; х = [40 ^. (-10,542)]/10 = – 42,2 кДж/моль.

Ответ: – 42 кДж/моль.

---

Задача 459.
При растворении одного моля   в 800 г воды температура повысилась на 22,4 К. Определить энтальпию растворения  H₂SO₄, принимая удельную теплоемкость раствора равной 3,76 Дж/(г ^. К).
Решение:
Мольная масса   равна 98г/моль. При растворении одного моля кислоты образуется довольно разбавленный раствор, удельная теплоёмкость (с) которого равна 3,76 Дж/(г . К). Общая масса раствора (m)равна 898 г (800 + 98 = 898). По повышению (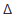t) рассчитаем количество выделенной теплоты по формуле:

Q = cm(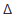t),

где
c – удельная теплоёмкость вещества, m – масса раствора, 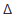t – повышение температуры.

Тогда

Q = 3,76 ^. 898 ^. 22,4 = 75,6 кДж/моль.

Количество выделенной или поглощенной теплоты при растворении 1 моля вещества численно равно энтальпии растворения, причём при выделении теплоты энтальпия принимает отрицательное значение. Тогда энтальпия растворения H₂SO₄  равна 75,6 кДж/моль.

Ответ: 75,6 кДж/моль.

---

Задача 460.
Энтальпия растворения NH₄NO₃ в воде равна 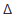H  = 26,7 кДж/моль. На сколько градусов понизится температура при растворении 20 г NH₄NO₃  в 180 г Н₂О, если удельную теплоемкость получающегося раствора принять равной 3,76 Дж/(г ^. К)?
Решение:
M(NH₄NO₃) = 80 г/моль.
Энтальпией растворения вещества называют изменение энтальпии при растворении 1 моля этого вещества в данном растворителе. Энтальпия вещества рассчитывается по формуле:

где
Q – количество поглощенной или выделившейся теплоты при растворении вещества, m(B) – масса растворённого вещества, M_Э(В) – мольная масса растворённого вещества.

Рассчитаем количество поглощённой теплоты

Понижение температуры находим по формуле:

Q = c m 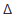t,

где
c – удельная теплоёмкость вещества, m – масса раствора, 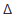t – повышение температуры.

Тогда

Следовательно, понижение температуры раствора NH₄NO₃ составляет 8,9 К.

Ответ: 8,9 К.

---

8.1. Определение энтальпии реакции нейтрализации

Реакции
между растворами сильных кислот и
сильных оснований, например:

NaOH + HCl→
NaCl+H₂O,

KOH + ½
H₂SO₄→½
K₂SO₄
+ H₂O,

выражаются общим
для них термохимическим уравнением

H⁺
+ OH^–→
H₂O;
_.∆H=
– 56,9 кДж/моль.

Теплота
реакций нейтрализации слабых электролитов
меньше 56,9Дж/моль. Значение теплоты
реакции нейтрализации в этих случаях
не является постоянным, т.к. оно зависит
от
природы
слабой кислоты и слабого основания. Это
объясняется
тем,
что экзотермическому процессу образования
воды из ионов H⁺
и OH^–
в
случае взаимодействия слабых электролитов
предшествует эндотермический процесс
диссоциации электролитов (кислот и
оснований). Чем
меньше
количество
тепла, выделяющееся в результате реакции
нейтрализации слабого электролита, тем
больше энергии поглощается при его
диссоциации, тем слабее электролит.
Таким образом,
силу электролита можно
сопоставить,
сравнивая величину

∆H_{нейтр.
сл.эл–та}
– (–56,9) = _.∆H_{дисс.
сл.эл–та}

Чем больше эта
величина, тем слабее электролит.

Выполнение работы

1. Получить у
лаборанта растворы необходимых веществ:

а) NaOH
и HCl;

б) NH₄OH
и HCl;

в) NaOH
и CH₃COOH;

г) NH₄OH
и CH₃COOH;

д) KOH
и HNO_3.

2.
Налить во внутренний стакан калориметра
40 мл раствора электролита с меньшей
концентрацией (0,3–0,5 – молярный раствор).
Измерить начальную температуру раствора
(при работающей мешалке).

3.
Быстро влить через воронку 10 мл электролита
с большей концентрацией (1–2 –молярный
раствор). Произвести измерение по
методике, описанной в общих указаниях
(гл. 7).

4.
Рассчитать тепловые эффекты по формуле
(10) и энтальпии реакции нейтрализации
по формуле (11):

,
где n
–
число молей электролита, взятого в
недостатке.

5.
Оформить результаты работы и расчетов
в виде следующей таблицы:

Система	V, мл	СМ, моль/л		∆t, оС	Q, кДж	∆H, кДж/моль
Кислота
Основание

6.
Сделать вывод по результатам работы.

7.
Составить молекулярные и сокращенные
уравнения реакций взаимодействия
указанных электролитов.

8.2. Определение энтальпии реакции присоединения кристаллизационной воды к безводной соли (энтальпия гидратации)

Энтальпию
реакции присоединения кристаллизационной
воды к безводной соли можно определить,
зная изменение энтальпии при растворении
безводной соли
и
изменение энтальпии при растворении
кристаллогидрата этой соли.

В
термохимии под энтальпией
растворения
понимают изменение энтальпии процесса
растворения 1 моля вещества в большом
количестве растворителя, т.е. в таком
его количестве, когда дальнейшее
разбавление раствора не влияет на
величину энтальпии растворения (это
так называемая дифференциальная
энтальпия растворения). Энтальпия
растворения веществ состоит в основном
из двух слагаемых: энтальпии процесса
перехода твердого или газообразного
вещества
в то состояние, в котором оно существует
в растворе ∆H_р,
и энтальпии процесса взаимодействия
вещества с растворителем (энтальпия
сольватации)
∆H_с.
В
зависимости от величины и знака этих
двух слагаемых процесс растворения
может быть эндотермическим или
экзотермическим.

Для
газов ∆H_р
< 0 и величина ∆H_р
представляет собой энтальпию конденсации
при изменении объема газа до объема
жидкого раствора.

У
твердых веществ ∆H_р
> 0, т.к. при их растворении затрачивается
энергия на разрушение кристаллической
решетки.

Таким
образом, процесс растворения соли может
быть представлен в виде двух этапов:
разрушение кристаллической решетки
соли с образованием раствора ее и
взаимодействия частиц соли с растворителем.
Процесс же
растворения
кристаллогидрата соли состоит только
из разрушения кристаллической решетки,
т.к. взаимодействия частиц кристаллогидрата
с растворителем, можно считать, не
происходит (молекулы соли уже связаны
с молекулами растворителя).

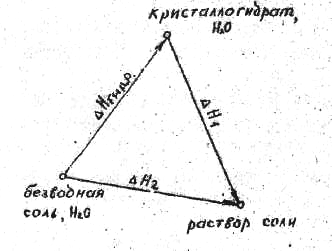
Следовательно,
энтальпия растворения безводной соли
и ее кристаллогидрата отличается на
величину энтальпии гидратации ∆H_гидр.

По закону Гесса:

∆H_гидр.
+ ∆H₁
= ∆H₂,
(12)

где
∆H_гидр
– изменение энтальпии в процессе
образования кристаллогидрата, энтальпия
гидратации или сольватации.

∆H₁
– изменение энтальпии при растворении
кристаллогидрата, энтальпия растворения
кристаллогидрата;

∆H₂
– изменение энтальпии при образовании
раствора соли, энтальпия растворения
соли.

Из
уравнения (12) следует, что

∆H_гидр.
= ∆H₂
– ∆H₁,
(13)

где
∆H₁;
∆H₂

–
величины,
определяемые на основании экспериментальных
данных.

Определив
значения ∆H₁
и ∆H₂,
рассчитайте значение ∆H_гидр.
по уравнению (13) и, сравнивая полученную
величину с табличными значениями
энтальпий гидратации различных солей,
установите, какая соль была выдана для
исследования.

Формула кристаллогидрата	∆Hгидр., кДж/моль (∆Hс)
Na2CO3∙10H2O	–91
ZnSO4∙7H2O	–95
Na2SO4∙10H2O	–82
Na2HPO4∙12H2O	–111
SrCl2∙6H2O	–73

Найдя
отклонение подученной опытной величины
∆H_гидр.
от ее табличного значения, рассчитайте
относительную ошибку в определении
этой величины:

Выполнение работы

1. Получить у
лаборанта навески безводной соли и ее
кристаллогидрата с указанием числа
молей и массы того и другого вещества
(около 7 г, взвешенного с точностью до
0,01 г).

2. Налить во
внутренний стакан калориметра мерным
цилиндром 200 мл дистиллированной воды.
Отметить начальную температуру (при
работающей мешалке).

3.
Быстро всыпать безводную соль в
калориметрический стакан, измерение
температуры осуществлять по методике,
описанной в общих указаниях (гл. 7).
Повторить аналогичный эксперимент c
кристаллогидратом этой соли.

4.
Рассчитать тепловые эффекты по формуле
(10) и энтальпии процессов растворения
соли и ее кристаллогидрата по формуле
(11).

5. Рассчитать
энтальпию гидратации соли и относительную
ошибку этой величины.

6.
Оформить результаты работы и расчетов
в виде следующей таблицы.

Число молей n	Масса вещества m	m + m(н2о), г	∆t, ◦C	Q, кДж/моль	∆H, кДж/моль	∆Hгидр и δ(Hгидр)
Безводная соль
Кристаллогидрат

8.3. Определение
энтальпии гидролиза карбонатов щелочных
металлов

Процесс гидролиза
растворимых карбонатов представляется
в виде следующего уравнения:

CO₃^2–
+ H₂O
↔ HCO₃^–
+ OH^–.

Изменение
энтальпии этого процесса ∆Н_{гидролиза}
связано с некоторыми трудностями,
обусловленными в основном небольшой
степенью гидролиза карбонатов, тогда
как определение энтальпии обратного
процесса – нейтрализации кислой соли
– легко осуществимо.

Определив
тепловой эффект этого процесса, Q
можно рассчитать искомую величину
∆Н_{гидролиза}:

(14)

где ;n
–
число молей соли, взятой для

нейтрализации

;
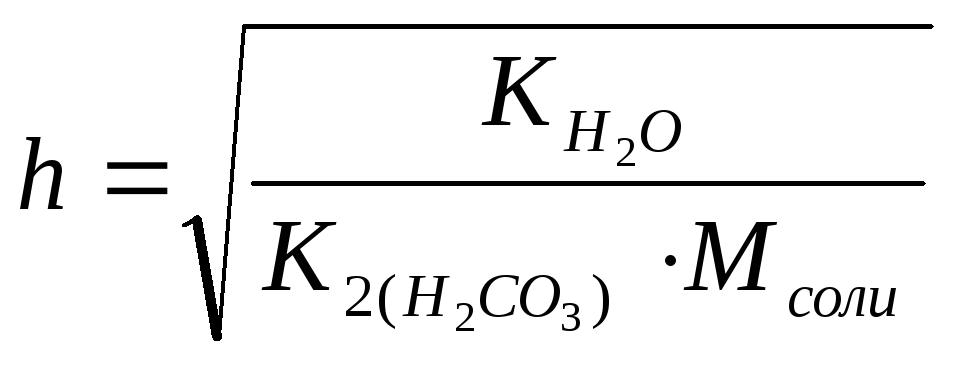
h
– степень гидролиза;

;
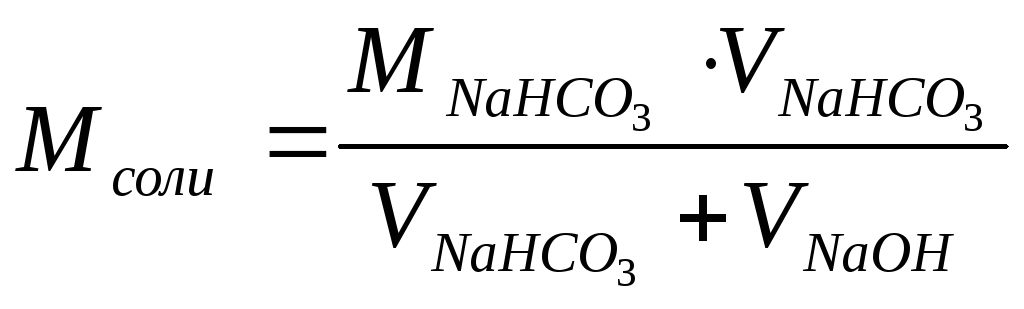
K₂

=4.7∙10^-11–
константа диссоциации угольной кислоты
по второй ступени;

M–
молярная концентрация исходного раствора
кислой соли, моль/л;

VиV_NaOH
– объемы растворов кислой соли и щёлочи
соответственно, вятые для исследования,
мл.

Выполнение работы

1. Влить
во внутренний стакан калориметра 150 мл
0,5-молярного раствора NаНСO₃
и
отметить начальную температуру (при
работающей мешалке).

2. Через
воронку быстро влить туда же 150 мл
0,5-молярного раствора NaOH.
Произвести измерение изменения
температуры по методике, описанной в
общих указаниях (гл. 7). (Вести отсчет
времени от начала вливания раствора
щелочи).

3. Записать результаты
наблюдений в таблицу и произвести
расчеты искомой величины.

V,мл	VNaOH,мл	Мсоли , моль/л	h	∆t, оС	Q, кДж	n	∆Нгидролиза, кДж/моль

4. Какой знак имеет
энтальпия процесса гидролиза? Дайте
объяснение.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #