Как найти энтальпию сгорания по энтальпии образования

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Тепловой эффект процесса

Термохимические уравнения

Закон Гесса

Следствия из закона Гесса

Стандартные термодинамические величины

Стандартные энтальпии образования и сгорания

Примеры решения задач

Задачи для самостоятельного решения

Тепловой эффект процесса

Количество выделенной (или поглощенной) теплоты Q в данном процессе называют тепловым эффектом процесса. Экзотермической является реакция, протекающая с выделением теплоты, а эндотермической – с поглощением теплоты из окружающей среды.

Для лабораторных и промышленных процессов наиболее типичен изобарный режим (Р=const). Поэтому обычно рассматривают тепловой эффект при Р,Т = const, т.е. изменение энтальпии процесса ΔН.

Следует отметить, что абсолютные значения энтальпии Н определить не представляется возможным, так как не известна абсолютная величина внутренней энергии.

Для экзотермической реакции (Q > 0) ΔН < 0, а в эндотермическом процессе (Q < 0) ΔН > 0.

Термохимические уравнения

Химические уравнения, в которых дополнительно указывается величина изменения энтальпии реакции, а также агрегатное состояние веществ и температура, называются термохимическими уравнениями.

В термохимических уравнениях отмечают фазовое состояние и аллотропные модификации реагентов и образующихся веществ: г – газообразное, ж – жидкое, к – кристаллическое; S_(ромб), S_{(монокл)}, С_{(графит)}, С_(алмаз) и т.д.

Важно подчеркнуть, что с термохимическими уравнениями можно проводить алгебраические операции сложения, вычитания, деления, умножения.

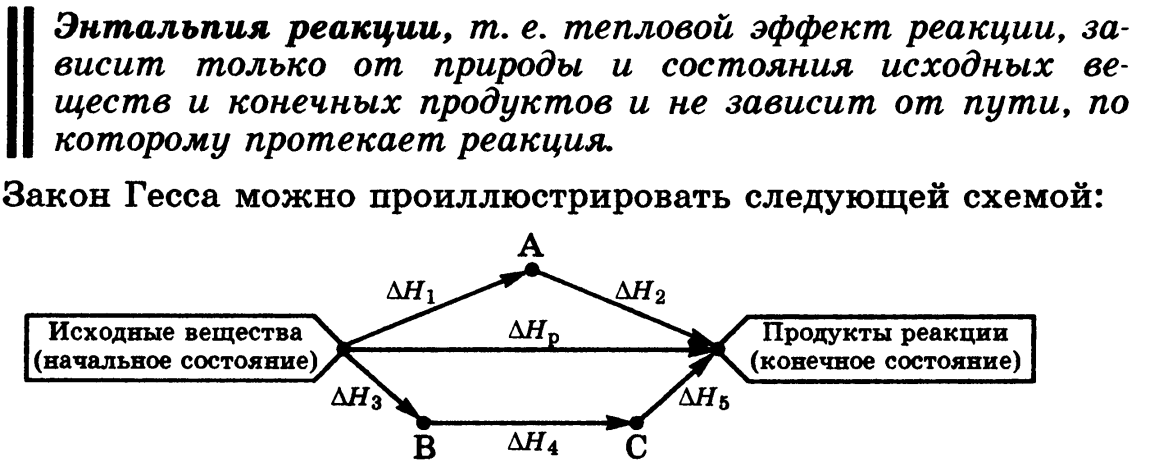
Закон Гесса

Изменение энтальпии (внутренней энергии) химической реакции зависит от вида, состояния и количества исходных веществ и продуктов реакции, но не зависит от пути процесса.

Следствия из закона Гесса

1. Изменение энтальпии реакции равно сумме энтальпий образования продуктов реакции за вычетом суммы энтальпий образования исходных веществ (суммирование проводится с учетом стехиометрических коэффициентов).
2. Изменение энтальпии реакции равно сумме энтальпий сгорания исходных веществ за вычетом суммы энтальпий сгорания продуктов реакции (суммирование проводится с учетом стехиометрических коэффициентов).

Стандартные термодинамические величины

Стандартные термодинамические величины – это такие величины, которые относятся к процессам, все ингредиенты которых находятся в стандартных состояниях.

Стандартным состоянием вещества, находящегося в конденсированной фазе (кристаллической или жидкой), является реальное состояние вещества, находящегося при данной температуре и давлении 1 атм.

Следует подчеркнуть, что стандартное состояние может иметь место при любой температуре.

Обычно тепловой эффект (изменение энтальпии) реакции приводится для температуры 25^оС (298,15 К) и давления 101,325 кПа (1 атм), т.е. указывается стандартная энтальпия ΔН^о₂₉₈.

Стандартные энтальпии образования и сгорания

Стандартная энтальпия образования ΔН^о_f,298 (или ΔН^о_обр,298) – это изменение энтальпии в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии, причем простые вещества присутствуют в наиболее термодинамически устойчивых состояниях при данной температуре.

Например, ΔН^o_f,298(Н₂О(ж)) = — 285,83 кДж/моль соответствует изменению энтальпии в процессе

Н_2(г) + ½O_2(г) = Н₂О_(ж)

при Т = 298,15 К и Р = 1 атм.

Стандартная энтальпия образования простых веществ равна нулю по определению (для наиболее устойчивых их модификаций при данной температуре).

Стандартной энтальпией сгорания ΔН^o_сгор,298 называют энтальпию сгорания вещества (обычно 1 моль), находящегося в стандартном состоянии с образованием СО_2(г), Н₂О_(ж) и других веществ, состав которых должен быть специально указан. Все продукты сгорания также должны находиться в стандартном состоянии.

Примеры решения задач

Задача 1. Используя справочные термодинамические данные вычислить ΔН^o₂₉₈ реакции:

2H₂S(г) + 3O₂(г) = 2SO₂(г) + 2H₂O(ж); ΔН^oх.р.,₂₉₈ = ?

Решение. Решим задачу, используя оба следствия из закона Гесса. Ниже для исходных веществ и продуктов реакции приведены значения энтальпий образования и сгорания в кДж/моль (энтальпия сгорания сероводорода до SO_2(г) и H₂O_(ж)):

Вещество	H2S(г)	O2(г)	SO2(г)	H2O(ж)
ΔНof,298	-20,60	0	-296,90	-285,83
ΔНoсгор,298	-562,10	0	0	0

Cогласно первому следствию закона Гесса энтальпия этой реакции ΔН^о_х.р. равна:

ΔН^о_х.р.,298 = 2ΔН^о_f,298(SO_2(г)) + 2ΔН^о_f,298(H₂O_(ж)) — 2ΔН^о_f,298(H₂S_(г)) — 3ΔН^о_f,298(O_2(г)) = 2(- 296,90) + 2(- 285,83) — 2(- 20,60) = — 1124,21 кДж.

В соответствии со вторым следствием закона Гесса получаем:

ΔН^о_х.р.,298 = 2ΔН^о_сгор,298(H₂S(г)) = 2(-562,10) = — 1124,20 кДж.

Задача 2. Вычислите ΔН^о₂₉₈ реакции N₂(г) + 3H₂(г) = 2NH₃(г), используя следующие данные:

4NH_3(г) + 3O_2(г) = 2N_2(г) + 6H₂O_(ж); ΔН^о₁ = -1531,22 кДж;

2H₂O_(ж) = O_2(г) + 2H_2(г); ΔН^о₂= 571,66 кДж.

Определите стандартную энтальпию образования NH₃(г).

Решение. Поскольку с термохимическими уравнениями можно производить все алгебраические действия, то искомое уравнение получится, если:

• • • разделить на два тепловой эффект первого уравнения и изменить его знак на противоположный, т.е:

N_2(г) + 3H₂O_(ж) = 2NH_3(г) + 3/2O_2(г); ΔН^о = 765,61 кДж;

• • • умножить на 3/2 второе уравнение и соответствующую ему величину  δН^o , изменив ее знак на противоположный:

3/2O_2(г) + 3H_2(г) = 3H₂O_(ж); ΔН^о = -857,49 кДж;

• • • сложить полученные первое и второе уравнения.

Таким образом, тепловой эффект реакции N_2(г) + 3H_2(г) = 2NH_3(г) равен:

Δ Н^о₂₉₈ = (- ΔН^о₁/2) + (- 3/2·ΔН^о₂) = 765,61 + (- 857,49) = — 91,88 кДж.

Поскольку в рассматриваемой реакции образуется 2 моль NH_3(г), то

ΔН^о_f,298(NH_3(г)) = — 91,88/2 = — 45,94 кДж/моль.

Задача 3. Определите энтальпию процесса

CuSO_4(к) + 5H₂O_(ж) = CuSO₄·5H₂O_(к)

если при 298,15 К энтальпия растворения CuSO_4(к) в n моль Н₂О с образованием раствора CuSO₄(р-р, nH₂O) равна –40, а энтальпия растворения CuSO₄·5H₂O_(к) с образованием раствора той же концентрации равна +10,5 кДж/моль.

Решение. Составляем цикл Гесса:

ΔН^о₁ = ΔН^о₂ + ΔН^о_х (по закону Гесса). Отсюда получаем:

ΔН^о_х = ΔН^о₁ – ΔН^о₂ = – 40,0 – 10,5 = -50,5 кДж.

Другой вариант решения.

CuSO_4(к) + (n H₂O) = CuSO₄(р-р, n H₂O); ΔН^о₁ = – 40,0 кДж; (1)

CuSO_4(к) + 5H₂O(ж) = CuSO₄·5H₂O(к); ΔН^о_х = Н^о₂; (2)

CuSO₄·5H₂O_(к) + (n – 5)H₂O = CuSO₄(р-р, nH₂O); ΔН^о₃ = 10,5 кДж. (3)

По закону Гесса:  ΔН^о₁ =  ΔН^о_х+  ΔН^о₃, т.е. при сложении уравнений (2) и (3) получим уравнение (1).

Задача 4. Вычислите энтальпию образования химической связи С= С в молекуле этилена, если его стандартная энтальпия образования равна 52,3 кДж/моль, энтальпия возгонки графита составляет 716,7 кДж/моль, энтальпия атомизации водорода равна +436,0 кДж/моль, энтальпия образования связи С–Н равна –414,0 кДж/моль.

Решение. Составляем цикл Гесса:

ΔН^о_f,298(С₂Н_4(г)) = 2ΔН^о_возг(С_{(графит)}) + 2ΔН^о_атом (H_2(г)) + ΔН^о_(С= С) + 4ΔН^о_(С–Н).

ΔН^о_(С = С) = 52,3 — 2·716,7 — 2·436,0 + 4·414,0 = — 597,1 кДж/моль.

Задачи для самостоятельного решения

1. Составьте уравнение реакции, для которой ΔН^о соответствует стандартной энтальпии образования ВaCl₂·2H₂O_(к).

2. Определить ΔН^о₂₉₈ реакции:

CH₃CНO_(ж) + H_2(г) = CH₃CH₂OH_(ж),

если ΔН^о_сгор,298(CH₃CНO_(ж)) = — 1193,07 кДж/моль; ΔН^о_сгор,298(CH₃CH₂OH_(ж)) = — 1370,68 кДж/моль; ΔН^о_f,298(Н₂О_(ж)) = — 285,83 кДж/моль.

10.3. Энтальпии растворения BaCl_2(к) и BaCl₂·2H₂O_(к) с образованием раствора хлорида бария (с мольным отношением BaCl₂: H₂O = 1: 500) соответственно равны –11,18 и 18,74 кДж/моль.
Определить величину ΔН^о присоединения воды к BaCl_2(к) с образованием BaCl₂·2H₂O_(к).

10.4. Рассчитать энтальпию связи в молекуле NO на основании следующих термохимических уравнений:

N_2(г) + O_2(г) = 2NO_(г); ΔН^о₂₉₈ = +182,52 кДж;

2O_(г) = O_2(г); ΔН^о₂₉₈ = — 498,34 кДж;

N_2(г) = 2N_(г); ΔН^о₂₉₈ = +945,42 кДж.

10.5. Вычислить ΔН^о₂₉₈ реакции 2C(г) + 2H₂(г) = C₂H₄(г), используя следующие термохимические уравнения:

С_{(графит)} = С_(г) ; ΔН^о₂₉₈ = +716,67 кДж;
С₂H_4(г) + 3O_2(г) = 2CO_2(г) + 2H₂O_(г); ΔН^о₂₉₈ = — 1322,94 кДж;
C_{(графит)} + O_2(г) = CO_2(г); ΔН^о₂₉₈ = — 393,51 кДж;

H_2(г) + 1/2O_2(г) = H₂O_(г); ΔН^о₂₉₈ = — 241,81 кДж.

10.6. Определите стандартную энтальпию реакции взаимодействия метана с оксидом углерода (IV), если стандартные энтальпии образования метана, оксида углерода (IV) и оксида углерода (II) при 298 К равны соответственно: -75; -393 и -111 кДж/моль.

7. Определите стандартную энтальпию образования С₂Н₅ОН_(ж), если стандартные энтальпии сгорания углерода, водорода и этанола при 298 К равны соответственно: -393; -286 и -1366 кДж/моль.

8. Вычислите энтальпию химической реакции 4KClO_3(к)=KCl_(к)+3KClO_4(к) по следующим данным:

2KClO_3(к)=2KCl_(к)+3O_2(г); ΔН^о₂₉₈ = — 95 кДж;
4KClO_4(к)=KCl_(к)+2O_2(г); ΔН^о₂₉₈ = 9 кДж/моль.

9. Вычислите среднюю энтальпию связи P-Cl в молекуле PCl₅, используя следующие термохимические уравнения:

P_{(к, бел.)}+5/2Cl_2(г)=PCl_5(г); ΔН^о₁ = — 374,8 кДж;
P_{(к, бел.)}=P_(г); ΔН^о₂ = — 17,4 кДж;
Cl_2(г)=2Cl_(г); ΔН^о₃ = 242,6 кДж.

10. Вычислите среднюю энтальпию связи N-H в молекуле NH₃, используя следующие термохимические уравнения:

1/2N_2(г)+3/2H_2(г)=NH_3(г); ΔН^о₁ = — 46,2 кДж;
N_2(г)=2N_(г); ΔН^о₂ = 945,4 кДж;
H_2(г)=2H_(г); ΔН^о₃ = 436,0 кДж.

Стандартная
энтальпия сгорания ΔH^o_сгор
–
тепловой эффект реакции сгорания одного
моля вещества до образования высших
оксидов. Для органических веществ –до
CO_2(г)
и
H₂O_(ж).
Теплота сгорания негорючих веществ
принимается равной нулю. Теплота сгорания
топлива характеризует его теплотворную
способность.

Стандартная
энтальпия образования вещества (ΔfH⁰)
– увеличение или уменьшение энтальпии,
сопровождающее образование 1 моль
вещества из простых веществ, при условии,
что все участники реакции находятся в
стандартном состоянии

Стандартная
энтальпия сгорания вещества (ΔсH⁰)
– уменьшение
энтальпии при окислении в избытке
кислорода 1 моль вещества, взятого в
стандартном состоянии, до конечных
продуктов окисления.

Закон Гесса
– энергия не создаётся и не уничтожается,
а лишь переходит из одного вида энергии
в другой.

Закон Гесса

Тепловой эффект
реакции зависит только от природы и
состояния исходных вещ-в и не зависит
от пути, по которому реакция протекает

Следствие
1.
Тепловой эффект химической реакции
равен разности сумм теплот
образования(ΔH_f)
продуктов реакции и исходных веществ,
умноженных на стехиометрическиекоэффициенты (ν):

ΔH^o_f,i
– стандартная энтальпия образование
веществ

v_i
– стехиометрические коэффициенты

Следствие
2.
Тепловой эффект химической реакции
равен разности сумм теплот
сгорания(ΔH_c)
исходных веществ и продуктов реакции,
умноженных на стехиометрические
коэффициенты (ν):

ΔH^o_с,i–
стандартная энтальпия сгорания веществ

v_i
– стехиометрические коэффициенты

Следствие
3. Энтальпия
реакции равна разности сумм энергий
связей E_св исходных
и конечных реагентов с учетом их
стехиометрических коэффициентов.

В ходе
химической реакции энергия затрачивается на
разрушение связей в исходных веществах
(ΣE_исх)
и выделяется при образовании
продуктов реакции (–ΣE_прод).
Отсюда

ΔH° = ΣEисх – ΣEпрод

Следовательно,
экзотермический эффект реакции
свидетельствует о том, что образуются
соединения с более прочными связями,
чем исходные. В случае эндотермической
реакции, наоборот, прочнее исходные
вещества.

При
определении энтальпии реакции по
энергиям связей уравнение реакции пишут
с помощью структурных формул для удобства
определения числа и характера связей.

Следствие
4. Энтальпия
реакции образования вещества равна
энтальпии реакции разложения его до
исходных веществ с обратным знаком.

Следствие
5. Энтальпия
гидратации равна разности энтальпий
растворения безводной соли (ΔH^o_{раств.б/с})и
кристаллогидрата (ΔH^o_{раств.крист})

6.Второе начало термодинамики. Формулировка. Обратимые и необратимые в термодинамическом смысле процессы. Энтропия как критерий возможности протекания самопроизвольных процессов.

Второе начало
термодинамики:
В изобарно-изотермических условиях (р,
Т = const)
в системе самопроизвольно могут протекать
только такие процессы, в результате
которых энергия Гиббса системы уменьшается
(ΔG
< 0). В состоянии равновесия G
= const,
G
= 0

Обратимый
процесс (то есть равновесный)
— термодинамический процесс, который
может проходить как в прямом, так и в
обратном направлении, проходя через
одинаковые промежуточные состояния,
причем система возвращается в исходное
состояние без затрат энергии, и в
окружающей среде не остается
макроскопических изменений. Обратимый
процесс можно в любой момент заставить
протекать в обратном направлении,
изменив какую-либо независимую переменную
на бесконечно малую величину.

Необратимым
называется процесс,
который нельзя провести в противоположном
направлении через все те же самые
промежуточные состояния. Все реальные
процессы необратимы.

Энтропия
– энтропия – функция состояния,
приращение которой ΔS
равно теплоте Qмин
подведённой к системе в обратимом
изотермическом процессе, делённой на
абсолютную температуру T,
три которой осуществляется процесс: ΔS
= Qмин/
T
или мера вероятности пребывания системы
в данном состоянии – мера неупорядоченности
системы.

7.
Энергия
Гиббса – главный критерий возможности
протекания самопроизвольных про­цессов.
Прогнозирование
направления самопроизвольно протекающих
процессов в изолированной и закрытой
системах; роль энтальпийного и энтропийного
факторов.

Критериями
направления самопроизвольного протекания
необратимых процессов являются
неравенства ΔG < 0 (для закрытых систем),
ΔS > 0 (для изолированных систем).

Если
величина ΔG
имеет отрицательный знак (ΔG
< 0),
то реакция самопроизвольно может
протекать
только в прямом направлении.
Причем абсолютное значение разности
ΔH
– TΔS
= ΔG
будет определять движущую силу данного
процесса.

Если
же ΔG
> 0,
то в условиях, для которых были измерены
ΔH
и TΔS,
в прямом
направлении данная реакция протекать
не может. Зато осуществимой окажется
обратная реакция,
для которой ΔG
будет иметь отрицательное значение.

Реакции,
для которых ΔH
< 0, а ΔS
> 0,
могут самопроизвольно протекать в
прямом
направлении при любых температурах,
т.к. ΔG
у них всегда будет меньше нуля. Примером
такой реакции может служить гидролиз
пептидов или белков.

Если
для химической реакции ΔH
> 0, а ΔS
< 0,
то ее самопроизвольное протекание в
прямом
направлении всегда неосуществимо,
т.к. энергия Гиббса в данном случае
возрастает. Примером такой реакции
может служить процесс фотосинтеза –
образование глюкозы и кислорода из
углекислого газа и воды, – который
невозможен без участия солнечной
энергии.

В
случае ΔH
> 0 и ΔS
> 0
самопроизвольному протеканию реакции
в
прямом направлении способствует
энтропийный фактор.
При низких температурах отрицательное
значение ΔH
– TΔS
может быть невозможно, но при нагревании
– оно возможно и реакция становится
осуществимой в прямом направлении.
Например, тепловая денатурация белковых
молекул.

Если
ΔH
< 0 и ΔS
< 0,
то отрицательное значение ΔG
такой химической реакции наблюдается
только при достаточно низких температурах.

При
вычислении ΔG
в химической реакции можно использовать
следствие из закона Гесса, применяемое
для расчета ее теплового эффекта
(изменения энтальпии). В данном случае
оно будет звучать следующим образом.

В ходе самопроизвольного
процесса в закрытых системах G
уменьшается до определенной величины,
принимая минимально возможное для
данной системы значение Gmin. Система
переходит в состояние химического
равновесия (ΔG= 0). Самопроизвольное
течение реакций в закрытых системах
контролируется как энтальпийным (ΔrH),
так и энтропийным (TΔrS) фактором. Для
реакций, у которых ΔrH< 0 иΔrS> 0, энергия
Гиббса всегда будет убывать, т.е.ΔrG<
0, и такие реакции могут протекать
самопроизвольно при любых температурах

В изолированных
системах энтропия
приобретает максимально возможное для
данной системы значение Smax; в состоянии
равновесияΔS= 0

Под стандартной
энергией Гиббса образования ΔG°, понимают
изменение энергии Гиббса при реакции
образования 1 моль вещества, находящегося
в стандартном состоянии. Это определение
подразумевает, что стандартная энергия
Гиббса образования простого вещества,
устойчивого в стандартных условиях,
равна нулю. В самопроизвольной реакции:

∆G<0  (G2-G1<0)

∆S>0   (S2-S1>0)
   реакция пойдет  → ∆G>0  

∆S<0   реакция
пойдет  ←

Формула для I и II
т/д: ∆Gт=∆H0хр – Т∆S

Энтальпийный и
энтропийный факторы Из приведенного
выражения следует, что самопроизвольное
течение реакции может контролироваться
как энтальпийным (∆H), так и энтропийным
фактором (T∆S). Очевидно, что для реакций,
характеризующихся ∆Hr< 0 и ∆Sr> О,
энергия Гиббса должна обязательно
убывать, т. е. ∆Gr< 0, и такие реакции
могут протекать самопроизвольно при
любых температурах, так как оба фактора
способствуют протеканию процесса.
Пример такой реакции — гидролиз белка.
Наоборот, при ∆Hr> 0 и ∆Sr< 0 самопроизвольное
течение реакций всегда невозможно, так
как энергия Гиббса должна обязательно
возрастать. Оба фактора препятствуют
протеканию реакции. Пример — фотосинтез,
т. е. образование глюкозы и кислорода
из углекислого газа и воды.

Несогласованное
действие факторов наблюдается в двух
случаях:

1) ∆Hr> 0 и ∆Sr> 0 —
самопроизвольному протеканию реакции
способствует энтропийный фактор,
отрицательное значение изменения
энергии Гиббса возможно при соотношении
|∆Sr |> |∆Hr|, т. е. при достаточно высоких
температурах. Примером процессов этого
типа является тепловая денатурация
белков;

2) ∆Hr< О и ∆Sr< О —
благоприятствующим фактором является
энтальпийный, соотношение AGT< 0
наблюдается при |∆Hr| >|∆Sr |, т. е. при
достаточно низких температурах. Пример
процессов этого типа — гидратация
белков.

8
. Термодинамические условия равновесия.
Стандартная энергия Гиббса образования
вещества, стандартная энергия Гиббса
биологического окисления вещества.
Стандартная энергия Гиббса реакции.
Примеры экзергонических и эндергонических
процессов, протекающих в организме.
Принцип энергетического сопряжения.

Под
стандартной энергией Гиббса биологического
окисления ΔG°, понимают изменение энергии
Гиббса при реакции биологического
окисления 1 моль вещества, находящегося
в стандартном состоянии.Под стандартной
энергией Гиббса образования ΔG°, понимают
изменение энергии Гиббса при реакции
образования 1 моль вещества, находящегося
в стандартном состоянии

Принцип
энергетического сопряжения:

Сопряженные
реакции – это реакции, в которых
протекание одной реакции обусловлено
протеканием другой, невозможной в
отсутствии первой. Принцип энергетического
сопряжения заключается в том, что энергия
необходимая для протекания эндергонической
реакции поступает за счет осуществление
экзэргонической реакции , причем в двух
реакциях присутствует общее веществ-
интермедиан.

1. Химическое
   равновесие. Обратимые и необратимые
   по направлению реакции. Термодинамические
   условия равновесия в изолированных и
   закрытых системах. Константа химического
   равновесия.

11.Химическая
кинетика как основа для изучения
скоростей и механизмов биохимических
процессов. Скорость реакции, средняя
скорость реакции в интервале, истинная
скорость. Факторы, влияющие на скорость
реакции.

Химическая
кинетика
изучает скорости химических реакций,
их зависимость от различных факторов
и механизмы реакций. Последо­вательность
и характер стадий химических реакций
называют меха­низмом реакции.

Факторы
влияющие на протекание реакции

В
организме человека протекают тысячи
ферментативных реакций, проходящих в
живой клетке. Однако в многостадийной
цепи процессов достаточно велика разница
между скоростями отдельных реакций.
Так, синтезу в клетке молекул белка
предшествует, по крайней мере, еще две
стадии: синтез транспортной РНК и синтез
рибосом. Но время, за которое удваивается
концентрация молекул т-РНК, составляет
1,7 мин., молекулы белка – 17 мин., а рибосом
– 170 мин. Скорость суммарного процесса
медленной (лимитирующей) стадии, в нашем
примере – скорость синтеза рибосом.
Наличие лимитирующей реакции обеспечивает
высокую надежность и гибкость управления
тысячами реакций, происходящих в клетке.
Достаточно держать под наблюдением и
регулировать лишь наиболее медленные
из них. Такой способ регулирования
скорости многостадийного синтеза носит
название принципа
минимума. Он
позволяет существенно упростить и
сделать более надежной систему
авторегулирования в клетке.

Скорость
реакций в зависимости от молекулярности
будет выражаться уравнениями: а) V = к •
С_А
– для мономолекулярной реакции; б) V = к
• С_А
• С_в
или в) V = к • С²_А
– для бимолекулярной реакции; г) V = к •
С • С_в
• С _э
д) V = к • С²_А
• С_в
или е) V
= k
• С³_А–
для тримолекулярной реакции.

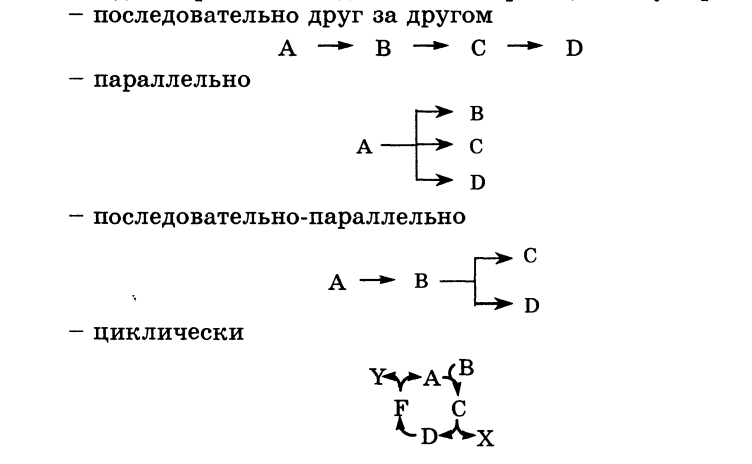
12.
Классификации реакций, применяющиеся
в кинетике: реакции, гомогенные,
гетерогенные и микрогетерогенные;
реакции простые и сложные (параллельные,
последовательные, сопряженные, цепные).
Молекулярность элементарного акта
реакции. Кинетические уравнения. Порядок
реакции. Период полупревращения

Микрогетерогенные
реакции –

Молекулярность
реакции–
это количество молекул, которые принимают
участие единовременно в одном акте
столкновений.

Молекулярность
можно определить, лишь установив механизм
реакции. В зависимости от числа реагирующих
молекул (частиц), участвующих в элементарном
акте, различают одномолекулярные
(мономолекулярные), двухмолекулярные,
тримолекулярные реакции.

К одномолекулярнымреакциям
типа А→Р относятся процессы распада
молекулы на более простые составные
части и реакции изомеризации.

Двухмолекулярными называются
элементарные реакции вида: А+В→Р и 2А→Р
(Н₂+J₂=2HJ,HJ+HJ=H₂+J₂,CH₃COOCH₃+H₂O=CH₃COOH+CH₃OHи
т.д.).

Значительно
реже встречаютсятрехмолекулярныереакции
А+2В→Р или 3А→Р. Во всех случаях вид и
количество образующихся продуктов
реакции не имеет значения, так как
молекулярность определяется только
числом молекул веществ, реагирующих в
элементарном акте.

Порядок
реакции
устанавливается экспериментально.

Молекулярность
и порядок реакции могут совпадать, а
могут и различаться. 

Молекулярность
и порядок реакции совпадаюттолько
для простых реакций, протекающих только
в одну элементарную стадию без участия
посторонних молекул.

Молекулярность
и порядок реакции не совпадают в
трех основных случаях:

1) для
сложных реакций;

2) для
гетерогенных реакций;

3) для
реакций с избытком одного из реагирующих
веществ.

Период
полупревращения–
это время, в течение которого прореагирует
половина взятого вещества.

Кинетическое
уравнение
выражает зависимость скорости хим.
реакции от концентраций компонентов
реакционной смеси

Молекулярность-число
молекул, реагирующих в в одном элементарном
химическом акте.

Молекулярность
реакции определяется числом молекул,
вступающих в химическое взаимодействие
в элементарном акте реакции. По этому
при­знаку реакции разделяются на
мономолекулярные, бимолекулярные и
тримолекулярные.

Тогда
реакции типа А —>В будут являться
мономолекулярными, например:

а) С₁₆Н₃₄
(t°C)
—>C_gH₁₈
+ С₈Н₁₆
– реакция крекинга углеводородов;

б) CaC0₃
(t°C)
—>СаО + С0₂
– термическое разложение карбоната
кальция.
Реакции типа А + В —> С или
2А —> С – являются бимолекулярными,
например:
а) С + 0₂
-> С0₂;
б) 2Н₂0₂
-> 2Н₂0
+ 0₂
и т. д.

Тримолекулярные
реакции описываются общими уравнениями
типа:

а)
А + В + С Д; б) 2А + В Д; в) 3А Д.

Например:
а) 2Н₂
+ 0₂
2Н₂0;
б) 2NO
+ Н₂N₂0
+ Н₂0.

Скорость
реакций в зависимости от молекулярности
будет выражаться уравнениями: а) V = к •
С_А
– для мономолекулярной реакции; б) V = к
• С_А
• С_в
или в) V = к • С²_А
– для бимолекулярной реакции; г) V = к •
С • С_в
• С _э
д) V = к • С²_А
• С_в
или е) V
= k
• С³_А–
для тримолекулярной реакции.

Нередко
молекулярность реакции трудно установить,
поэтому используют более формальный
признак – порядок
химической реакции.

Порядок
реакции равен сумме показателей степеней
концентраций в уравнении, выражающем
зависимость скорости реакции от
концентрации реагирующих веществ
(кинетическом уравнении).

Порядок
реакции чаще всего не совпадает с
молекулярностью ввиду того, что механизм
реакции, т. е. “элементарный акт”
реакции (см. определение признака
молекулярности), трудно установить.

Рассмотрим
ряд примеров, иллюстрирующих указанное
положение.

1. Скорость
   растворения кристаллов описывается
   уравнениями кинетики нулевого порядка,
   несмотря на мономолекулярность реакции:
   AgCl_(TB)
   —>Ag⁺
   + CI”,
   V = k
   • C(AgCl_(TBp=
   k’C(AgCl_(ra})
   – p
   – плотности и является постоянной
   величиной, т. е. скорость растворения
   не зависит от количества (концентрации)
   растворяемого вещества.

2. Реакция
   гидролиза сахарозы: СО + Н₂0
   —> С₆Н₁₂0₆(глюкоза)
   + С₆Н₁₂0₆
   (фруктоза)
   является бимолекулярной реакцией, но
   ее кинетика описывается кинетическим
   уравнением первого порядка: V=k*C_cax,
   так как в условиях опытов, в том числе
   и в организме, концентрация воды есть
   величина постоянная С(Н₂0)
   – const.

3. Реакция
   разложения водородпероксида, протекающая
   с участием катали­заторов, как
   неорганических ионов Fe³⁺,
   Cu²⁺
   металлической платины, так и био­логических
   – ферментов, например каталазы, имеет
   общий вид:

2Н₂0₂
—> 2Н₂0
+ О _э
т. е. является бимолекулярной.

Использование энтальпии позволяет сократить объем справочных данных об энергетических параметрах реакций.
Представьте, что у вас есть 100 веществ. Вообще говоря, любое вещество/комбинация может переходить в любое другой вещество/комбинацию и тогда возможно  ~2¹⁰⁰~10¹⁰  реакций с энергетическими параметрами.

А теперь представьте, что химических веществ известно около 20 млн.!

Но можно реализовать другой подход. Для каждого из 100 этих веществ определить энергию образования из исходных простейший веществ Н₂(г), О₂(г), С(гр_(афит)) , Аr(г) и т. д.

Это и называют энтальпией ∆_fH⁰₂₉₈ , где:

• ∆ – дельта – разница энергий исходных и образованного вещества
• f – formation (образование)
• верхний индекс 0 – нормальное атмосферное давление
• нижний индекс 298 – температура исходных  и конечного вещества 298^o K (25^o С)

И тогда, исходя из простого следствия закона сохранения энергии в химических реакциях (в химии он носит название закон Гесса),  энергетический выход реакции любого вещества/комбинации веществ в другое вещество/комбинацию будет простая разница суммы энтальпий исходных и конечных веществ учетом стехиометрических коэффициентов.

Звучит может страшно и непонятно, но на самом деле все просто. Например, найдем теплоту сгорания метана, используя справочные данные по энтальпии.

CH₄ + 2O₂ -> CO₂ + 2H₂O
Берем данные по энтальпии из справочника «Краткий справочник физико–химических величин» под редакцией К.П. Мищенко для конечного состояния воды в виде жидкости^

и получаем теплоту сгорания метана:

Вычисление теплоты сгорания метана через энтальпии образования высшая, кДж/моль

	CH4	O2	CO2	H2O(ж)
Энтальпия веществ	-74,85	0	-393,51	-285,83
Энтальпия с учетом стехиометрических коэффициентов	-74,85	0	-393,51	-571,66
Сумма энтальпий исходный и конечных веществ	-74,85	-965,17
Энергетическая ценность сгорания CH4 , высшая	-890,32

Сравниваем с данными, которые непосредственно приведены в этом же справочнике: -890,31 Различие на одну сотую в последнем знаке связана с ошибками округления.

Вычисляем для конечного состояния воды в виде пара:

Вычисление теплоты сгорания метана через энтальпии образования низшая, кДж/моль

	CH4	O2	CO2	H2O(г)
Энтальпия	-74,85	0	-393,51	-241,82
Энтальпия с учетом стехиометрических коэффициентов	-74,85	0	-393,51	483,64
Сумма энтальпий исходный и конечных веществ	-74,85	-877,51
Энергетическая ценность сгорания 1 моля CH4 , низшая	-802,3

Для конечного состояния воды в виде пара в справочнике уже не приводится значения. Это как раз иллюстрация того, что, с чего начиналась эта статья!))
Еще раз: добавлена энтальпия для воды в виде пара и сразу появляются энергетические значения и для метана и для пропана и тд и тд!

© Копирование и перепечатка материалов только с разрешения автора

Тепловой эффект химической реакции — изменение внутренней энергии или энтальпии системы вследствие протекания химической реакции и превращения исходных веществ (реактантов) в продукты реакции в количествах, соответствующих уравнению химической реакции (стехиометрии реакции^[1]) при следующих условиях:

• единственно возможной работой при этом является работа против внешнего давления,
• как исходные вещества, так и продукты реакции имеют одинаковую температуру^[2][3].

Теплота термохимического процесса и тепловой эффект химической реакции[править | править код]

Поясним приведённое выше определение теплового эффекта химической реакции^{[K 1]}. Для этого запишем фундаментальные уравнения Гиббса для внутренней энергии и энтальпии простой^[10] открытой однородной термодинамической системы^[11][12]:

(Фундаментальное уравнение Гиббса для внутренней энергии)

(Фундаментальное уравнение Гиббса для энтальпии)

Здесь  — абсолютная температура,  — энтропия,  — давление,  — объём,  — количество (или масса) -го составляющего систему вещества,  — химический потенциал этого вещества (см. Энтропия открытой системы).

Для бесконечно малого^[13] квазистатического изохорного процесса ()

(Изменение внутренней энергии в бесконечно малом квазистатическом изохорном процессе)

для бесконечно малого квазистатического изобарного процесса ()

(Изменение энтальпии в бесконечно малом квазистатическом изобарном процессе)

Важно понимать, что представление о теплоте химической реакции при сохранении исторически сложившегося названия (восходящего ко временам, когда любое изменение температуры связывали с поглощением или выделением теплоты) уже не имеет прямого отношения к общефизическому понятию количества теплоты. Действительно, при химической реакции в изолированной системе (например, инициируемом электрической искрой взрыве гремучего газа в герметически закрытом термосе) может иметь место изменение температуры (за счёт выделения теплоты), но не происходит обмена с окружающей средой(так как попросту это термос — изолированная система), ни изменения внутренней энергии системы. Наконец, традиционная трактовка теплоты, основанная на представлении об адиабатической изоляции системы от окружающей среды^[14] (см. Неоднозначность понятий «теплота» и «работа») к открытым системам не применима, и для них теплоту бесконечно малого квазистатического процесса полагают равной^[15][16]

(Дефиниция теплоты для любого бесконечно малого квазистатического процесса)

Таким образом, теплота бесконечно малого квазистатического изохорного процесса равна

(Теплота бесконечно малого квазистатического изохорного процесса)

а теплота бесконечно малого квазистатического изобарного процесса равна

(Теплота бесконечно малого квазистатического изобарного процесса)

Для закрытых систем изменение энергии системы за счёт изменения масс составляющих систему веществ (химическую работу^{[17][18][19][20][21]}, работу перераспределения масс составляющих систему веществ^[22]) учитывать не требуется^[23][24], и выражения для теплот ещё более упрощаются:

(Теплота бесконечно малого квазистатического изохорного процесса в простой закрытой системе)

(Теплота бесконечно малого квазистатического изобарного процесса в простой закрытой системе)

Из сказанного ясно, почему в дефиниции теплового эффекта химической реакции фигурируют внутренняя энергия, энтальпия и запрет на любые виды работ в системе, кроме работы расширения/сжатия. Уточним, что в понятии «химическая работа» термин «работа» не имеет отношения к понятию «термодинамическая работа» и использован просто как синоним словосочетания «изменение энергии». Наконец, подчеркнём, что когда речь идёт о тепловом эффекте химической реакции, то, как и во многих других случаях, касающихся термохимии, подразумевается, что речь идёт о закрытой системе и полномасштабное применение мощного, но громоздкого математического аппарата термодинамики систем переменного состава не требуется^[23][24][25].

Энергетический эффект химической реакции всегда рассматривают применительно к конкретному термохимическому уравнению, которое может не иметь отношения к реальному химическому процессу. Термохимическое уравнение лишь показывает, какие наборы начальных и конечных индивидуальных веществ, находящихся в определённых состояниях и количественных соотношениях, исчезают и образуются. В начальном состоянии должны присутствовать только исходные вещества (реактанты), а в конечном — только продукты химической реакции. Единственным условием при записи термохимического уравнения является соблюдение материального и зарядового баланса. Вещества в растворённом или адсорбированном состоянии тоже считаются индивидуальными соединениями; если растворитель или адсорбент не участвует непосредственно в химической реакции и не реагирует с растворённым веществом, то он рассматривается просто как фактор, влияющий на термодинамические свойства рассматриваемого вещества. Наконец, в термохимическом уравнении могут фигурировать частицы, не способные к самостоятельному существованию (электроны, протоны, ионы, радикалы, атомарные простые вещества)^[26].

Энергетический эффект реального процесса с химической реакцией зависит от условий проведения процесса и не может служить стандартной характеристикой конкретной химической реакции^[3]. Химическая же термодинамика нуждается в показателе, связанном с энергетикой химической реакции, но не зависящем от условий её проведения. Покажем, как может быть получен интересующий нас показатель. Для этого рассмотрим следующий мысленный эксперимент. Возьмем чистые индивидуальные исходные вещества в мольных количествах, соответствующих стехиометрическим коэффициентам интересующего нас термохимического уравнения, и находящиеся при определённых температуре и давлении. Если привести эти вещества в контакт, то энтальпия образовавшейся неравновесной системы в начальный момент времени будет равна сумме энтальпий исходных веществ. Теперь рассмотрим конечное состояние изучаемой системы в предположении, что реактанты прореагировали полностью^[27] и продукты реакции находятся при той же температуре и том же давлении, что и реактанты. Энтальпия системы (в общем случае неравновесной) из продуктов химической реакции будет равна сумме энтальпий этих веществ. Поскольку энтальпия — функция состояния, то разность энтальпий системы в конце и начале рассмотренного мысленного эксперимента не зависит от условий проведения химической реакции. Эту разность энтальпий и называют изобарным тепловым эффектом (термохимической теплотой) химической реакции, соответствующей определённому термохимическому уравнению^[28][29]. Важно, что реальная осуществимость рассмотренного мысленного эксперимента, гипотетические условия его проведения и неравновесность исходного и конечного состояний термохимической системы не сказываются на дефиниции теплового эффекта химической реакции.

Часто тепловой эффект химической реакции относят к 1 молю одного из продуктов реакции^[30].

Резюмируем сказанное: теплота процесса, связанного с фактическим протеканием химической реакции, и энергетический эффект химической реакции отнюдь не одно и то же, а дефиниция теплового эффекта химической реакции вообще не предполагает действительного осуществления реакции, соответствующей рассматриваемому термохимическому уравнению^[31].

И внутренняя энергия, и энтальпия представляют собой функции состояния, поэтому тепловой эффект химической реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, то есть от числа и характера промежуточных стадий (закон Гесса)^{[32][33][34][35]}.

Тепловой эффект химической реакции, протекающей при постоянном давлении, и равный изменению энтальпии системы в процессе, соответствующем термохимическому уравнению, называется изобарным тепловым эффектом или энтальпией химической реакции. Тепловой эффект химической реакции, протекающей при постоянном объёме, и равный изменению внутренней энергии системы в процессе, соответствующем термохимическому уравнению, называют изохорным тепловым эффектом^[2].

Для отдельных типов химических реакций вместо общего термина «тепловой эффект химической реакции» используют специальные (сокращённые) термины: теплота образования, теплота сгорания и т. п.^[1]

Дефиниции тепловых эффектов должны быть дополнены указанием на начальные точки отсчёта значений энергии и энтальпии. Для сравнения тепловых эффектов и упрощения термодинамических расчётов все величины тепловых эффектов реакций относят к стандартным условиям (все вещества находятся в стандартных состояниях)^[1]. Если реакцию — реально или гипотетически — проводят при стандартных условиях (T = 298,15 К = 25 °С и P = 1 бар = 100 кПа)^[36], то тепловой эффект называют стандартным тепловым эффектом реакции или стандартной энтальпией реакции ΔHo
r.

Химические реакции, сопровождающиеся повышением температуры, называют экзотермическими, понижением температуры — эндотермическими. В термодинамической системе знаков тепловой эффект экзотермической реакции ( или ) считают отрицательным, эндотермической ( или ) — положительным. В устаревшей и не рекомендуемой к употреблению термохимической системе знаков положительным, наоборот, считается тепловой эффект экзотермической реакции, а отрицательным — эндотермической^[37].

Тепловые эффекты химических реакций важны для теоретической химии и необходимы при расчётах равновесных составов смесей, выхода продуктов реакций, удельной тяги топлив реактивных двигателей и для решения многих других прикладных задач^[1].

Изучение тепловых эффектов химических реакций составляет важнейшую задачу термохимии^[3]. Для расчёта стандартных тепловых эффектов химических реакций используют таблицы стандартных теплот образования или сгорания^[37].

Стандартная энтальпия образования (стандартная теплота образования)[править | править код]

Под стандартной теплотой образования понимают тепловой эффект реакции образования одного моля вещества из простых веществ, его составляющих, находящихся в устойчивых стандартных состояниях.

Например, стандартная энтальпия образования 1 моля метана из углерода и водорода равна тепловому эффекту реакции:

С(тв) + 2H₂(г) = CH₄(г) + 74,9 кДж/моль.

Стандартная энтальпия образования обозначается ΔHo
f. Здесь индекс f означает formation (образование), а знак «O» в верхнем индексе указывает, что величина относится к стандартному состоянию вещества: один моль индивидуального химического соединения, взятого в чистом виде при стандартных условиях в том агрегатном состоянии, которое устойчиво в этих условиях (если нет специальной оговорки)^[38]. Иногда для обозначения стандартного состояния используют перечёркнутый символ «O» в верхнем индексе; согласно рекомендациям ИЮПАК по использованию обозначений в физической химии^[39], перечёркнутый и неперечёркнутый символ «O», используемые для обозначения стандартного состояния, одинаково приемлемы. В литературе часто встречается другое обозначение стандартной энтальпии — ΔHo
298,15, где знак «O» указывает на равенство давления одной атмосфере^[40] (или, несколько более точно, на стандартные условия^[41]), а 298,15 — температура. Иногда индекс «O» используют для величин, относящихся к чистому веществу, оговаривая, что обозначать им стандартные термодинамические величины можно только тогда, когда в качестве стандартного состояния выбрано именно чистое вещество^[42]. Стандартным также может быть принято, например, состояние вещества в предельно разбавленном растворе.

Энтальпия образования простых веществ принимается равной нулю, причем нулевое значение энтальпии образования относится к агрегатному состоянию, устойчивому при T = 298,15 K. Например, для иода в кристаллическом состоянии ΔH^o(I₂, тв) = 0 кДж/моль, а для жидкого иода ΔH^o(I₂, ж) = 22 кДж/моль. Энтальпии образования простых веществ при стандартных условиях являются их основными энергетическими характеристиками.

Тепловой эффект любой реакции находится как разность между суммой теплот образования всех продуктов и суммой теплот образования всех реагентов в данной реакции (следствие закона Гесса):

ΔH^o_{реакции} = ΣΔHo
f (продукты) — ΣΔHo
f (реагенты).

Термохимические эффекты можно включать в химические реакции. Химические уравнения в которых указано количество выделившейся или поглощенной теплоты, называются термохимическими уравнениями. Реакции, сопровождающиеся выделением тепла в окружающую среду имеют отрицательный тепловой эффект и называются экзотермическими. Реакции, сопровождающиеся поглощением тепла имеют положительный тепловой эффект и называются эндотермическими. Тепловой эффект обычно относится к одному молю прореагировавшего исходного вещества, стехиометрический коэффициент которого максимален.

Температурная зависимость теплового эффекта (энтальпии) реакции[править | править код]

Чтобы рассчитать температурную зависимость энтальпии реакции, необходимо знать мольные теплоемкости веществ, участвующих в реакции. Изменение энтальпии реакции при увеличении температуры от Т₁ до Т₂ рассчитывают по закону Кирхгофа (предполагается, что в данном интервале температур мольные теплоемкости не зависят от температуры и нет фазовых превращений):

Если в данном интервале температур происходят фазовые превращения, то при расчёте необходимо учесть теплоты соответствующих превращений, а также изменение температурной зависимости теплоемкости веществ, претерпевших такие превращения:

где ΔC_p(T₁, T_φ) — изменение теплоемкости в интервале температур от Т₁ до температуры фазового перехода;  — тепловой эффект фазового перехода; ΔC_p(T_φ, T₂) — изменение теплоемкости в интервале температур от температуры фазового перехода до конечной температуры, и T_φ — температура фазового перехода.

Стандартная энтальпия сгорания[править | править код]

Стандартная энтальпия сгорания — ΔHо
гор., тепловой эффект реакции сгорания одного моля вещества в кислороде до образования оксидов в высшей степени окисления. Теплота сгорания негорючих веществ принимается равной нулю.

Стандартная энтальпия растворения[править | править код]

Стандартная энтальпия растворения — ΔHо
раств., тепловой эффект процесса растворения 1 моля вещества в бесконечно большом количестве растворителя. Складывается из теплоты разрушения кристаллической решётки и теплоты гидратации (или теплоты сольватации для неводных растворов), выделяющейся в результате взаимодействия молекул растворителя с молекулами или ионами растворяемого вещества с образованием соединений переменного состава — гидратов (сольватов). Разрушение кристаллической решетки, как правило, эндотермический процесс — ΔH_реш. > 0, а гидратация ионов — экзотермический, ΔH_гидр. < 0. В зависимости от соотношения значений ΔH_реш. и ΔH_гидр. энтальпия растворения может иметь как положительное, так и отрицательное значение. Так растворение кристаллического гидроксида калия сопровождается выделением тепла:

ΔHо
раств.KOH = ΔHо
реш. + ΔHо
гидр.К⁺ + ΔHо
гидр.OH⁻ = −59 кДж/моль.

Под энтальпией гидратации ΔH_гидр. понимается теплота, которая выделяется при переходе 1 моля ионов из вакуума в раствор.

Стандартная энтальпия нейтрализации[править | править код]

Стандартная энтальпия нейтрализации ΔHо
нейтр. — энтальпия реакции взаимодействия сильных кислот и оснований с образованием 1 моля воды при стандартных условиях:

HCl + NaOH = NaCl + H₂O

H⁺ + OH⁻ = H₂O, ΔHо
нейтр. = −55,9 кДж/моль

Стандартная энтальпия нейтрализации для концентрированных растворов сильных электролитов зависит от концентрации ионов, вследствие изменения значения ΔHо
гидратации ионов при разбавлении.

См. также[править | править код]

• Термохимия
• Химическая термодинамика

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

• Callen H. B. Thermodynamics and an Introduction to Thermostatistics. — 2nd ed. — N. Y. e. a.: John Wiley, 1985. — XVI + 493 p. — ISBN 0471862568, 9780471862567.
• Lebon G., Jou D., Casas-Vázquez J. Understanding Non-equilibrium Thermodynamics: Foundations, Applications, Frontiers. — Berlin — Heidelberg: Springer, 2008. — XIII + 325 p. — ISBN 978-3-540-74251-7, 978-3-540-74252-4. — doi:10.1007/978-3-540-74252-4.
• Александров Н. Е., Богданов А. И., Костин К. И. и др. Основы теории тепловых процессов и машин. Часть II / Под ред. Н. И. Прокопенко. — 5-е изд. (электронное). — М.: Бином. Лаборатория знаний, 2015. — 572 с. — ISBN 978-5-9963-2613-6. (недоступная ссылка)
• Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
• Большая Советская Энциклопедия / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: Советская Энциклопедия, 1976. — Т. 25: Струнино — Тихорецк. — 600 с. Архивная копия от 5 августа 2017 на Wayback Machine
• Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М.: Инфра-М, 2017. — 868 с. — ISBN 978-5-16-104227-4.
• Бурдаков В. П., Дзюбенко Б. В., Меснянкин С. Ю., Михайлова Т. В. Термодинамика. Часть 2. Специальный курс. — М.: Дрофа, 2009. — 362 с. — (Высшее образование. Современный учебник). — ISBN 978-5-358-06140-8.
• Жариков В. А. Основы физической геохимии. — М.: Наука; Изд-во МГУ, 2005. — 656 с. — (Классический университетский учебник). — ISBN 5-211-04849-0, 5-02-035302-7.
• Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с.
• Карякин Н. В. Основы химической термодинамики. — М.: Академия, 2003. — 463 с. — (Высшее профессиональное образование). — ISBN 5-7695-1596-1. (недоступная ссылка)
• Кнорре Д. Г., Крылова Л. Ф., Музыкантов В. С. Физическая химия. — 2. — М.: Высшая школа, 1990. — 416 с. — ISBN 5-06-000655-7.
• Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
• Ляшков В. И. Теоретические основы теплотехники. — М.: Курс; Инфра-М, 2015. — 328 с. — ISBN 978-5-905554-85-8, 978-5-16-0І0639-7.
• Морачевский А. Г., Кохацкая М. С. Прикладная химическая термодинамика. — СПб.: Изд-во Политехн. ун-та, 2008. — 254 с. — ISBN 978-5-7422-2006-0.
• Морачевский А. Г., Фирсова Е. Г. Физическая химия. Термодинамика химических реакций. — 2-е изд., испр. — СПб.: Лань, 2015. — 101 с. — (Учебники

для вузов. Специальная литература). — ISBN 978-5-8114-1858-9. (недоступная ссылка)

• Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — М.: Мир, 1971. — 296 с.
• Нараев В. Н. Физическая химия. Часть 1. Химическая термодинамика. Фазовые равновесия и учение о растворах. Электрохимия. — СПб.: Санкт-Петербургский государственный технологический институт (Технический университет), 2007. — 262 с. (недоступная ссылка)
• Никольский Б. П., Смирнова Н. А., Панов М. Ю. и др. Физическая химия. Теоретическое и практическое руководство / Под ред. Б. П. Никольского. — 2-е изд., перераб. и доп. — Л.: Химия, 1987. — 880 с. — (Для высшей школы).
• Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М.: Наука, 1971. — 376 с.
• Степановских Е. И., Брусницына Л. А., Маскаева Л. Н. Химическая термодинамика в вопросах и ответах. — Екатеринбург: УИПЦ, 2014. — 221 с. — ISBN 978-5-4430-0061-9.
• Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
• Тамм М. Е., Третьяков Ю. Д. Неорганическая химия. Том 1. Физико-химические основы неорганической химии / Под. ред. акад. Ю. Д. Третьякова. — М.: Академия, 2004. — 240 с. — (Высшее профессиональное образование). — ISBN 5-7695-1446-9.
• Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.
• Химическая энциклопедия / Гл. ред. Н. С. Зефиров. — М.: Большая Российская энциклопедия, 1995. — Т. 4: Пол — Три. — 640 с. — ISBN 5-85270-092-4.
• Химический энциклопедический словарь / Гл. ред. И. Л. Кнунянц. — М.: Советская энциклопедия, 1983. — 792 с.
• Шмидт Э. Введение в техническую термодинамику / Пер. с нем. — М.—Л.: Энергия, 1965. — 392 с.
• Эткинс П. Физическая химия. — М.: Мир, 1980.

Термохимические и термодинамические расчеты

Пример 47

Рассчитать энергетический эффект химической реакции в стандартных условиях: Известны энтальпии образования участвующих в реакции соединений:

Решение:

Энтальпия этой реакции рассчитывается по формуле

Энтальпия системы в ходе реакции уменьшается, в этом случае энергия выделяется, реакция экзотермическая.

Пример 48

Рассчитать энтальпию реакции

в стандартных условиях, зная энтальпии сгорания участвующих в реакции веществ:

Энтальпии реакции можно рассчитать по формулам:

Данная реакция экзотермична.

Пример 49

Определить энтальпию образования метана, зная, что энтальпия реакции горения метана , а стандартные значения энтальпий образования равны соответственно -396 кДж/моль и -241,8 кДж/моль.

Решение:

Отсюда

Пример 50

Какое количество тепла выделяется в ходе горения 10 г серы, если стандартное значение энтальпии образования равно -296,9 кДж/моль?

Решение:

Уравнение химической реакции горения серы —

Энтальпия этой реакции определяется по формуле

реакция экзотермическая.

Определяем количество тепла, выделенное при горении 10 г серы.

Согласно уравнению реакции 1 моль дает 296,9 кДж тепла. Составляем пропорцию:

Задача № 2. Расчет энергии связи по энтальпии.

Пример 51

Определить энергию связи О-Н в молекуле воды, зная стандартное значение энтальпии образования воды в газообразном состоянии, равное -241,6 кДж/моль, и энергии связи в молекуле кислорода и в молекуле водорода.

Решение:

Уравнение реакции образования воды —

Известно, что для реакции с участием всех веществ в газообразном состоянии энтальпия может определяться по следующей формуле:

Задача № 3. Расчет энтальпии гидратации.

Пример 52

Известны энтальпии растворения безводного сульфата меди (-66,46 кДж/моль) и кристаллогидрата Определить энтальпию гидратации

Решение:

Реакция гидратации может быть представлена как алгебраическая разность двух реакций:

или в виде следующей схемы:

Согласно закону Гесса

или

Отсюда

Задача № 4. Расчет энтропии реакции.

Пример 53

Определить изменение энтропии системы в ходе следующей реакции:

Стандартные значения энтропий, участвующих в реакции веществ, следующие:

Решение:

Рассчитаем энтропию реакции по формуле

Задача № 5. Расчет изобарно-изотермического потенциала (энергии Гиббса) реакции.

Пример 54

Определить изменение изобарно-изотермического потенциала системы в стандартных условиях в ходе следующей реакции:

если изменение энтальпии системы в ходе этой реакции а изменение энтропии . Возможна ли данная реакция в стандартных условиях? Каков ее характер?

Решение:

Подставим значения в уравнение Гиббса:

если Т = 298 К, тогда

В стандартных условиях эта реакция термодинамически невозможна.

Чтобы ответить на вопрос, каков характер этой реакции и возможна ли она в каких-либо условиях, отличающихся от стандартных, необходимо изучить знаки этой реакции (табл.5).

Таким образом, исследуемая реакция, знаки которой положительны, обратимая. Высокие температуры способствуют протеканию этой реакции в прямом направлении. Реакция, являясь невозможной в стандартных условиях, становится возможной при определенных высоких температурах.

Таблица 5

Характер реакции в зависимости от значений реакции

Пример 55

Определить энергию Гиббса реакции:

зная значения стандартных изобарно-изотермических потенциалов веществ, участвующих в реакции:

Решение:

Формула для расчета энергии Гиббса (изобарноизотермического потенциала) химической реакции по значениям изобарноизотермических потенциалов, участвующих в реакции веществ,

Для изучаемой реакции

Так как значения изобарно-изотермических потенциалов простых веществ в стандартных условиях приняты равными 0,

В стандартных условиях реакция термодинамически возможна.

Пример 56

Определить приблизительно, при какой температуре реакция

становится термодинамически возможной

Примечание. Предполагается, что изменение величин незначительно с изменением температуры, поэтому принимается:

В действительности эти величины неравны, поэтому для более точных расчетов производится определение по соответствующим законам.

Известны следующие величины:

Решение:

Рассчитаем энтропию реакции в стандартных условиях:

Рассчитываем энтальпию реакции в стандартных условиях:

Энергия Гиббса реакции в стандартных условиях:

В стандартных условиях изучаемая реакция термодинамически невозможна, однако она обратима, и высокие температуры способствуют протеканию реакции в прямом направлении. Определяем приблизительно температуру, при которой реакция становится термодинамически возможной, при этом принимаем, что термодинамические функции состояния не изменяются при изменении температуры:

Задача № 6. Расчеты по химическому сродству.

Пример 57

Можно ли использовать магний для получения титана по следующей реакции:

Известны изобарно-изотермические потенциалы соединения:

Решение:

Можно подтвердить возможность реакции расчетом ее энергии Гиббса, однако более удобно использовать понятие химического сродства.

Энергия Гиббса бинарного соединения, отнесенная к единице химической связи, характеризует химическое сродство друг к другу двух химических элементов, образующих химическую связь.

Чем более отрицательна величина энергии Гиббса, отнесенная к единице химической связи одного элемента с рядом других элементов, тем выше его химическое сродство к этим элементам:

Можно заключить, что химическое сродство хлора к магнию более высокое, чем к титану. Таким образом, реакция с магнием термодинамически возможна в стандартных условиях.

Пример 58

Какой оксид среди перечисленных термически более стабилен?

Известно следующее:

Решение:

Термическая стабильность определяется отношением к реакции разложения:

Оксид является термически более стойким, если он менее склонен к реакции разложения.

Величины энергии Гиббса оксидов характеризуют именно данную реакцию (обратная реакция является реакцией образования оксида из простых веществ).

Таким образом, чем более отрицательны величины AG оксидов, тем они термически более стойки. Иначе, используем понятие химического сродства: чем более отрицательно значение энергии Гиббса оксида, отнесенной к единице связи «металл-кислород», тем больше химическое сродство металла к кислороду, а значит, оксид термически более стойкий.

В изученных оксидах число связей Ме=О одинаково, значит сравниваем величины энергий Гиббса самих оксидов.

Сравнение дает следующий результат:

• термически более стойкий оксид цинка;
• термически менее стойкий оксид ртути.

Известно, что при нагревании оксид ртути разлагается:

Эти задачи взяты со страницы решения задач по неорганической химии:

Задачи с решением по неорганической химии

Возможно эти страницы вам будут полезны: