Как найти энтропия опыта

Как найти энтропия опыта

  1. Как
    следует из формулы (4.4),

    только в двух случаях:

  • когда вероятность
    какого-либо исхода равна 1, поэтому
    вероятности остальных исходов равны
    0, то есть один из исходов достоверен,
    поэтому общий итог опыта перестает
    быть случайным;

  • все

    ,
    то есть никакие из рассматриваемых
    исходов опыта невозможны. Во
    всех остальных случаях
    .

  1. Очевидным
    следствием формулы (4.1) будет утверждение,
    что для двух независимых опытов

    и

. (4.5)

Энтропия
сложного опыта, состоящего из нескольких
независимых опытов, равна сумме энтропий
отдельных опытов.

Приведем доказательство формулы (4.5).

Пусть
опыт

имеет

исходов
,

,
…,
,
которые реализуются с вероятностями

,

,
…,
,
а опыт

имеет

исходов
,

,
…,

с вероятностями
,

,
…,
.
Сложный опыт

имеет

исходов типа
,
где
,

.
Поэтому (см. (4.4)):

. (4.6)

Поскольку
опыты
инезависимы, то независимыми окажутся
события в любой паре.
Поэтому:

,
на основании чего

Таким образом,
формулу (4.6) перепишем так:

;

;

.

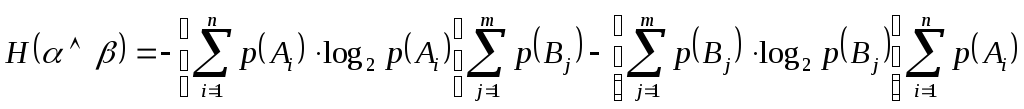
Известно, что по
условию нормировки вероятностей

и

,

Из формулы (4.4)
следует, что

и

.

Поэтому окончательно имеем:

,

что
и требовалось доказать.

Теперь
рассмотрим ситуацию, когда имеются два
опыта с одинаковым числом исходов
,
в одном случае ()
они равновероятны, а в другом ()
– нет. Каково соотношение энтропий этих
опытов? Примем без доказательства
следующее утверждение:

. (4.7)

При
прочих равных условиях наибольшую
энтропию имеет опыт с равновероятными
исходами.

Другими словами,
энтропия максимальна в опытах, где все
исходы равновероятны.

Кстати,
результат, полученный в рассмотренном
выше примере
1, иллюстрирует
справедливость формулы (4.7).

Здесь
усматривается аналогия (имеющая глубинную
первооснову!) с понятием энтропии,
используемым в физике. Впервые понятие
энтропии было введено в 1865 году немецким
физиком Рудольфом Клаузиусом: энтропия
– это функция состояния термодинамической
системы, описывающая направленность
самопроизвольных процессов в системе.
Клаузиус сформулировал II
начало термодинамики. В частности, он
показал, что энтропия достигает максимума
в состоянии равновесия системы. Позднее,
в 1872 году Людвиг Больцман, развивая
статистическую теорию, связал энтропию
системы с вероятностью ее (системы)
состояния, дал статистическое
(вероятностное) толкование II-му
началу теормодинамики. В частности,
Больцман показал, что вероятность
максимальна у полностью разупорядоченной
(равновесной) системы (аналогия с опытом,
имеющим равновероятные исходы). Энтропия
и термодинамическая вероятность тоже
связаны логарифмической зависимостью.
В физике энтропия 
мера
беспорядка в системе.
При этом беспорядок
понимается как отсутствие
знания о
характеристиках объекта (например,
координат и скорости молекулы газа); с
ростом беспорядка в системе возрастает
энтропия, то есть возрастает наше
незнание о системе, другими словами,
уменьшаются наши знания о системе.

3. Условная энтропия

Найдем
энтропию сложного опыта
в том случае, если опыты не являются
независимыми, то есть если на исход
опыта
оказывает влияние результат опыта .
Например, пусть в ящике всего два
разноцветных шара и опыт
состоит в извлечении первого, а опыт
– в извлечении второго из них. В этом
случае результат опыта
полностью снимает неопределенность
сложного опыта ,
то есть оказывается, что ,
но не .
Сумма проявляется лишь для независимых
событий!

Связь
между зависимыми опытами
и
состоит в том, что какие-то из исходов

могут оказывать влияние на исходы ,
то есть некоторые пары событий
и
не являются независимыми. Вернемся к
формуле (4.6) для энтропии сложного опыта:

.

В
случае зависимых событий: ,
где
– это вероятность наступления исхода

опыта
при условии, что в опытеимел место исход.

В этом случае по
свойству логарифма:

.

После подстановки
в формулу (4.6) получаем:

;

;

Устанавливаем
порядок суммирования, по аналогии с
интегрированием:

В этой формуле:

,
так как какое-то из событий
обязательно произойдет после того, как
произошло событие ,
поэтому:

;

,
в результате

.

,

таким образом,

;

Величины

(4.8)

имеют
смысл энтропии опыта
при условии, что в опыте
реализовался исход .
Величину
будем называть условной
энтропией.

Величина

(4.9)

имеет
смысл средней
условной энтропии опыта

при выполнении опыта
.
Окончательно получаем для энтропии
сложного опыта при условии, что в нем
могут быть зависимые исходы:

. (4.10)

Полученное
выражение представляет собой общее
правило нахождения энтропии сложного
опыта. Совершенно очевидно, что выражение
(4.5) является частным случаем формулы
(4.10) при условии независимости опытов

и .

Относительно
условной энтропии можно сделать следующие
утверждения:

  1. Условная
    энтропия является величиной
    неотрицательной.

    только в том случае, если любой
    исход опыта
    полностью определяет исход опыта
    (как в рассмотренном выше примере с
    двумя разноцветными шарами), то есть
    при .
    В этом случае .

  2. Если
    опыты
    и
    независимы, то ,
    причем

. (4.11)

Другими
словами, опыт
может либо не оказывать никакого влияния
на энтропию опыта(если опыты независимы), либо может
понижать энтропию опыта(то есть повысить определенность,
повысить наше знание об исходах опыта).
Таким образом, условная энтропия не
превосходит безусловную.

3.
Из соотношений (4.10) и (4.11) следует, что

, (4.12)

причем
равенство реализуется только при
независимости опытов
и.

Пример.
В ящике имеются 2 белых и 4 черных шара.
Из ящика извлекают последовательно два
шара без возврата. Найти энтропию,
связанную с первым и вторым извлечениями,
а также энтропию обоих извлечений.

Будем
считать опытом
извлечение первого шара. Он имеет два
исхода. Первый исход– вынут белый шар; его вероятность.
Второй исход –– вынут черный шар; его вероятность.
По формуле (4.4) сразу находим:

.

Опыт
– также имеет два исхода.– вынут белый шар,– вынут черный шар, однако вероятности
этих исходов зависят от того, каким был
исход опыта.
Именно,

При
:и;

При
:и.

Итак, энтропия,
связанная со вторым опытом, является
условной, и, согласно, формуле (4.8),
получаем:

;

.

По формуле (4.9)
получаем:

.

По формуле (4.10)
получаем:

.

Ответ:
,,
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Условная энтропия

Найдем энтропию сложного опыта %%α wedge β%% в том случае, если опыты не являются независимыми, т.е. если на исход β оказывает влияние результат опыта α. Например, если в ящике всего два разноцветных шара и α состоит в извлечении первого, а %%β%% – второго из них, то а полностью снимает неопределенность сложного опыта %%α wedge β%%, т.е. оказывается

%%Н(α wedge β) = H(α)%%, a не сумме энтропии, как следует из (2.5).

Связь между %%α%% и %%β%% состоит в том, что какие-то из исходов %%A(α)%% могут оказывать влияние на исходы из %%В(β)%%, т.е. некоторые пары событий %%A_i wedge B_j%% не являются независимыми. Но тогда в (2.6) %%p(A_i wedge B_j)%% не следует заменять произведением вероятностей:

$$p(A_i wedge B_j)=p(A_i)cdot p_{A_i}(B_j)$$

где – %%p_{A_i}(B_j)%% вероятность наступления исхода %%В%%, при условии, что в первом опыте имел место исход %%А_i%%.

Тогда %%log_2 p(A_i wedge B_j) = log_2 p(A_i)+log_2 p_{A_i}(B_j)%%

При подстановке в (2.6) получаем:

$$ H(α wedge β) = -sum^{n}_{i=1}sum^{m}_{j=1}{p(A_i)p_{A_i}(B_j)cdot (log_2 p(A_i)+log_2 p_{A_i}(B_j))}=$$
$$=-sum^{n}_{i=1}sum^{m}_{j=1}{p(A_i)p_{A_i}(B_j)cdot log_2 p(A_i)} -sum^{n}_{i=1}sum^{m}_{j=1}{p(A_i)p_{A_i}(B_j)cdot log_2 p_{A_i}(B_j)} $$

В первом слагаемом индекс %%j%% имеется только у %%B%%; изменив порядок суммирования, получим члены вида:

$$sum^{m}_{j=1}{p_{A_i}(B_j)}$$ Однако,

$$sum^{m}_{j=1}{p_{A_i}(B_j)} = p_{A_i}(B_j) (sum^{m}_{j=1}{B_j})$$

образует достоверное событие (какой-либо из исходов опыта β все равно реализуется). Следовательно, первое слагаемое оказывается равным:

$$-sum^{n}_{i=1}{p_{A_i}(B_j)log_2 p_{A_i}(B_j)}= Н_{A_i}(α)$$

Во втором слагаемом члены вида

$$sum^{m}_{j=1}{p_{A_i}(B_j)log_2 p_{A_i}(B_j)}= Н_{A_i}(β)~~~(2.8)$$

имеют смысл энтропии опыта %%β%% при условии, что в опыте %%α%% реализовался исход %%А_i%% – будем называть ее условной энтропией. Если ввести данное понятие и использовать его обозначение, то второе слагаемое будет иметь вид:

$$sum^{n}_{i=1}{p_{A_i} cdot Н_{A_i}(β)} = Н_α (β)~~~~~~~(2.9)$$

где %%H_α(β)%% есть средняя условная энтропия опыта %%β%% при условии выполнении опыта %%α%%. Окончательно получаем для энтропии сложного опыта:

$$ Н(α wedge β) = Н(α)+Н_α (β)~~~~~~~(2.10)$$

Полученное выражение представляет собой общее правило нахождения энтропии сложного опыта. Совершенно очевидно, что выражение (2.5) является частным случаем (2.10) при условии независимости опытов α и β.

Относительно условной энтропии можно высказать следующие утверждения:

  1. Условная энтропия является величиной неотрицательной. %%H_α(β) = 0%% только в том случае, если любой исход α полностью определяет исход %%β%%. В этом случае %%Н(α wedge β) = Н(α)%%.
  2. Если опыты %%α%% и %%β%% независимы, то %%Н_α(β) = Н(β)%%, причем это оказывается наибольшим значением условной энтропии. Другими словами, опыт %%α%% не может повысить неопределенность опыта %%β%%; он может либо не оказать никакого влияния (если опыты независимы), либо понизить энтропию %%β%%.

Приведенные утверждения можно объединить одним неравенством:

$$0 leqslant Н_α (β) leqslant Н (β)~~~~(2.11)$$

т.е. условная энтропия не превосходит безусловную.

3. Из соотношений (2.10) и (2.11) следует, что

$$Н(α wedge β) leqslant Н(α) +H( β)$$

причем равенство реализуется только в том случае, если опыты %%α%% и %%β%% независимы.

Пример. Имеется три тела с одинаковыми внешними размерами, но с разными массами %%х_1, х_2 и х_3%%. Необходимо определить энтропию, связанную с нахождением наиболее тяжелого из них, если сравнивать веса тел можно только попарно.

Последовательность действий достаточно очевидна: сравниваем вес двух любых тел, определяем из них более тяжелое, затем с ним сравниваем вес третьего тела и выбираем наибольший из них. Поскольку внешне тела неразличимы, выбор номеров тел при взвешивании будет случаен, однако общий результат от этого выбора не зависит. Пусть опыт ее состоит в сравнении веса двух тел, например, 1-го и 2-го. Этот опыт, очевидно, может иметь два исхода: %%А_1 – х_1 > х_2%%; его вероятность %%р(А_1) = 1/2%%; исход %%А_2 – x_1 < х_2%%; также его вероятность %%р(А_2) = 1/2%%.

$$Н(α)=-frac{1}{2} log_2 frac{1}{2}–frac{1}{2} log_2 frac{1}{2}=1 ;бит$$

Опыт %%β%% – сравнение весов тела, выбранного в опыте %%α%%, и 3-го – имеет четыре исхода: %%B_1, – х_1 > х_3, B_2 – х_1 < х_3, B_3 – х_2 > х_3, В_4 – х_2 < х_3;%% вероятности исходов зависят от реализовавшегося исхода %%α%% – для удобства представим их в виде таблицы:

– %%B_1%% %%B_2%% %%B_3%% %%B_4%%
%%A_1%% %%frac{1}{2}%% %%frac{1}{2}%% 0 0
%%A_1%% 0 0 %%frac{1}{2}%% %%frac{1}{2}%%

Вновь, воспользовавшись формулами (2.8) и (2.9) находим:

$$Н_{A_1}(β)=-frac{1}{2} log_2 frac{1}{2}–frac{1}{2} log_2 frac{1}{2}=1 ;бит$$
$$Н_{A_2}(β)=-frac{1}{2} log_2 frac{1}{2}–frac{1}{2} log_2 frac{1}{2}=1 ;бит$$
$$Н_α(β)=p(A_1)cdot Н_{A_1}(β) + p(A_2)cdot Н_{A_2}(β)=frac{1}{2}cdot 1+ frac{1}{2} cdot 1=1; бит$$

Следовательно, энтропия сложного опыта, т.е. всей процедуры испытаний:

$$Н(α wedge β) = Н(α) +H_α( β)=2;бит$$

Источник

Время на прочтение
9 мин

Количество просмотров 11K

Давно хотел сделать учебные материалы по теме Теория Информации + Machine Learning. Нашёл старые черновики и решил довести их до ума здесь, на хабре.

Теория Информации и Machine Learning мне видятся как интересная пара областей, глубокая связь которых часто неизвестна ML инженерам, и синергия которых раскрыта ещё не в полной мере.

Когда я говорю коллегам, что LogLoss на тесте и Mutual Information между прогнозом и прогнозируемой величиной связаны напрямую, и по несложной формуле можно из одного получить второе, они часто искренне удивляются. В википедии со страницы LogLoss есть ссылка на Mutual Information, но не более того.

Теория Информация может стать (а, точнее, стала) источником понимания как и почему работают разные методы ML, в частности нейронные сети, а также может дать идеи улучшения градиентных методов оптимизации.

Начнём с базовых понятий Энтропии, Информации в сообщении, Взаимной Информации (Mutual Information), пропускной способности канала. Далее будут материалы про схожесть задач максимизации Mutual Information и минимизации Loss-а в регрессионных задачах. Затем будет часть про Information Geometry: метрику Фишера, геодезические, градиентные методы, и их связь с гауссовскими процессами (движение по градиенту методом SGD — это движение по геодезической с шумом).

Также нужно затронуть AIC, Information Bottleneck, поговорить про то, как устроен поток информации в нейронных сетях – Mutual Information между слоями (Information Theory of Deep Learning, Naftali Tishby) и многое другое. Не факт, что получится всё перечисленное охватить, но попробую начать.

1. Базовые определения

Есть три более менее разных способа прийти к формуле энтропии распределения

H({p_1, ldots, p_M }) = sum_{i=1}^M p_i log(1 / p_i) ;;;;;(1)sum_{i=1}^M p_i =1, ;; p_i > 0.;;;;;;

Давайте их опишем. Начнём с базовых определений.

Опр. 1.1: Неопределенность — это логарифм по основанию 2 от числа равновероятных вариантов: H = log_2{N}. Измеряется в битах. Например, неопределенность неизвестного битового слова длины k равна k. 

Логарифм

Логарифм числа по основанию 2 – это то, сколько раз нужно делить число на 2, чтобы получить число меньше либо равно 1. Например,

log_2(1) = 0, ; log_2(2) = 1, ; log_2(4) = 2,; log_2(8) = 3,; log_2(1024) = 10.

Для не степеней двойки эта функция гладко продолжается. Например,

log_2(3) = 1.5849ldots, ; log_2(10) = 3.3219ldots

Важное свойство логарифма:

log(x) - log(y) = log(x/y)

Поробуйте вывести его из нестрогого определения выше для случая, когда xи y степени двойки.

Битовые слова

Битовые слова длины k – это последовательности нулей и единиц длины k. Каждый знак в битовом слове называется битом. Например, вот битовые слова длины 5:

00000, 00001, 00010, 00011, 00100, 00101, … , 11100, 11101, 111110, 11111

Их 32 штуки. log_2(32) = 5, то есть неопределённость слова длины 5 равна 5.
Именно столько неизвестных бит в неизвестном битовом слове длины 5.

Таким образом, каждый знак в битовом слове называется битом, но ещё бит – это единица измерения неопределённости. И из этого примера понятно почему.

Для краткости везде далее log_2 обозначается просто как log.

Опр. 1.2: Информация в сообщении — это разница неопределенностей до получения сообщения и после

I(message) = H(before) - H(after);;;;;;;(2)

Тоже измеряется в битах.

Например, Ваня загадал число от 1 до 100. Нам сообщили, что оно меньше либо равно 50. Неопределённость до сообщения равна log 100, а после — log 50. То есть в этом сообщении 1 бит информации. Умело задавая бинарные вопросы (вопросы, на которые ответ ДА или НЕТ), можно извлекать ровно 1 бит информации.

Некоторые вопросы неэффективны, например, вопрос “верно ли, что число меньше либо равно 25?” уменьшит неопределенность на log 100 - log 25 =log(100/25)= 2бита с вероятностью 0.25, а с вероятностью 0.75 только на  log(100)-log(75)=log(100/75)бит, то есть в среднем на 0.25 log(1 / 0.25) + 0.75 log(1 / 0.75) = 0.811278бит. Если вы своим вопросом разбиваете множество вариантов в пропорции x: 1 - x, то среднее количество бит информации в ответе равно  x log(1/x) + (1 - x ) log(1/(1-x)).

Это выражение будем обозначать через H({x , 1-x})или H(x). Здесь мы как программисты перегрузим функцию H так, чтобы она работала для двух случаев — когда на вход поступает пара чисел, сумма которых равна 1, и когда одно число из отрезка [0, 1].

Опр. 1.3: H({x, 1-x}) = H(x) = x log (1/x) + (1 - x ) log(1/(1-x))

График H(x)

Видно, что задавая бинарные вопросы, в можно извлекать максимум 1 бит информации в среднем (максимальное значение функции H(x). Ещё раз: да, можно сразу задавать вопросы типа “Число равно 57?” и если повезёт, получать log(100) бит информации. Но если не повезёт, вы получите лишь log(100/99) бит информации. Среднее число бит информации для такого сорта вопросов равно (1/100) cdot log(100) + (99/100) cdot log(100/99) = 0.08079...что заметно меньше 1.

В этом примере 100 вариантов, а значит начальная неопределенность равна log(100)— это то, сколько всего в среднем бинарных вопросов нужно задать Ване, чтобы выведать ответ. Правда число получается нецелое и нужно округлять вверх.

Если мы будем задавать не бинарные вопросы, а вопросы, которые подразумевают в качестве ответа натуральное число от 1 до M, то мы сможем в одном ответе получать более, чем один бит информации. Если мы задаём такой вопрос, для которого все M ответов равновероятны, то в среднем мы будем получать log Mбит. Если же вероятность ответа i равна p(i), то среднее число бит в ответе будет равно:

H({p_1, ldots, p_M}) = sum_{i=1}^M p_i log(1 / p_i).;;;;;;;;(1)

Опр. 1.4: Энтропия дискретного распределения  P={p_i}_{i=1}^Mзадаётся формулой (1) выше.

Здесь мы перегрузили функцию H для случая, когда на вход поступает дискретное распределение.

ИТАК: Первый простой способ прийти к формуле энтропии H(P)— это посчитать среднее число бит информации в ответе на вопрос с разновероятными ответами.

Давайте пойдём дальше. Пусть Ваня не загадывает число, а сэмплирует его из распределения P={p_i}_{i=1}^M. Сколько бинарных вопросов нужно задать Ване, чтобы узнать выпавшее число? Интуитивно понятно, что нужно разбить множество вариантов на два подмножества уже равных не по количеству элементов, а по суммарному значению вероятности, и спросить Ваню, в каком из двух находится выпавшее число. Получить ответ и продолжить в том же духе с новым уменьшенным множеством вариантов — снова разбить его на два с примерно равным весом, спросить в каком из двух находится выпавшее число и так далее. Идея хорошая, но не совсем рабочая. Оказывается, правильнее поступать с конца и начать строить дерево разбиений снизу, а именно, найти два самых мало вероятных варианта и объединить их в один новый вариант, тем самым уменьшив число вариантов на 1. Потом снова найти два самых маловероятных и снова объединить их в один новый, и так далее, построив конечном итоге бинарное дерево. В листьях этого дерева находятся числа. Внутренние вершины помечены множеством чисел из поддерева, корнем которого они являются. Корень дерева помечен множеством всех чисел. Это дерево и даёт алгоритм того, как нужно задавать вопросы Ване. Нужно двигаться с корня дерева и спрашивать Ваню, куда по этому дереву идти — влево или вправо (в каком из двух множеств вершин детей находится выпавшее число). Это дерево даёт не только рецепт самого быстрого в среднем метода угадывания числа, но ещё и алгоритм Хаффмана сжатия данных.

Задача 1.1: Изучите код Хаффмана. Докажите, что текст с исходной длиной символов N имеет в сжатом виде длину, ограниченную снизу величиной Ncdot H(P)бит и при удачных обстоятельствах её достигает.

ИТАК: Формула H(P) возникает при решении задачи о минимальном среднем числе бинарных вопросов, которые нужно задать, чтобы выведать выпавшее значение случайной величины с распределением P.

Это второй способ прийти к формуле (1).

Есть ещё один, третий, простой способ прийти к формуле энтропии, но нужно знать формулу Стирлинга.

Задача 1.2: Есть неизвестное битовое слово длины k (последовательность единиц и ноликов, всего k символов). Нам сообщили, что в нём 35% единичек. Чему равно I(message) / kпри больших k?

Ответ

Примерно log 2 - (p log(1 / p) + (1 - p) log(1 / (1 - p))) = log 2 - H({p, 1-p}), где p = 0.35

Задача 1.3: У Вани есть неизвестное слово длины kв алфавите длины M. Он сообщил доли всех букв в слове — P = {p_1, ..., p_M}.
Чему равно I(message) / kпри больших k?

Ответ

approx log M - sum_{i=1}^M{p_i log(1 / p_i)} = log M - H(P)

ИТАК: Задача 1.3 и есть третий способ прийти к формуле (1).

Опр. 1.5: Информация в сообщении по некоторую случайную величину — это разница энтропий: I(message) = H(P_{apriori}) - H(P_{aposteriori})

Значения случайной дискретной величины можно рассматривать как буквы, каждая следующая буква слова — это просто очередное измерение случайной величины. Вот и получается, что информация в сообщении про некоторую случайную величину — это количество бит информации про измерения этой случайной величины нормированное на число измерений.

Задача 1.4: Чему равна энтропия дискретного распределения P = {lambda ^ i cdot (1 - lambda)}_{i = 0}^{infty}?Сколько информации содержится в сообщении xi ne 0где xiимеет распределение P?

Ответ:

H(P) = H(lambda) / (1 - lambda)I(``xi ne 0'') = 0

Этот результат требует принятия. Как же так? – Нам сообщили ненулевую на первый взгляд информацию, отсекли самый вероятный вариант из возможных. Но неопределённость на множестве оставшихся вариантах осталась прежней, поэтому формула H(before) - H(after)даёт ответ 0.

Задача 1.5: Приведите пример конечного распределения и сообщения, которое не уменьшает, а увеличивает неопределённость.

Ответ:

P = {0.8, 0.1,0.1}, а сообщение message = “это не первый элемент”. Тогда P_{after} = {0, 0.5, 0.5}, H(P) = 0.9219, H(P_{after}) = 1.0

Древняя мудрость “во многих знаниях многие печали” в этом контексте получает ещё одну интересную интерпретацию: современный мир, наука и человеческая жизнь таковы, что новые “сообщения” о истории и об устройстве мира только увеличивают неопределённость.

Дискретные распределения на счётном множестве значений, которые затухают по экспоненциальному закону (геометрические прогрессии), обладают свойством неизменности неопределённости при получении информации, что среди первых элементов нет правильного ответа. Менее, чем экспоненциальные затухания (например, p_k={C / k^2}), только растят неопределённость при откидывании первых элементов.

Задача 1.6: Напишите формулу для энтропии распределения Пуассона

p_k=e^{-lambda}{lambda^k over k!}, k=0,;1,ldots,+infty.

Найдите простое приближение для больших lambda.

Ответ

H({p_k}_{k=0}^{infty})={1over 2} log (2pi e lambda) - {1over 12 lambda}-{1over 24 lambda^2}+O(1/lambda^3)

Задача 1.7: Дано распределение rho(x)вещественной случайной величины. Пусть  Q(rho,varepsilon)— это сколько бинарных вопросов в среднем нужно задать, чтобы узнать какое-то выпавшее значение случайной величины с точностью до varepsilon. Найдите приближённое выражение Q(rho,varepsilon) для малых значений varepsilon.

Ответ:

Нужно разбить ось x на корзинки длиной varepsilonпосчитать вероятности p_iкаждой корзинки и посчитать H({p_i}_i)Если значениеvarepsilonдостаточно мало, то ответ можно приблизить интегралом:

sum_i rho(x_i) cdot varepsilon cdot log (1 / (rho(x_i) cdot varepsilon) ) approx log(1/varepsilon) - int_{-infty}^{+infty} rho(x)log(rho(x))dx == log(1/varepsilon) + H(rho)

(см. определение энтропии непрерывного распределения ниже).

Опр. 1.6: Энтропия непрерывного распределения равна

H(rho) = -int_X rho(x) log(rho(x)) dx

Здесь мы ещё раз перегрузили значение символа H для случая, когда аргумент есть функция плотности вероятности (PDF).

Задача 1.8: Даны два распределения rho_1(x)и rho_2(x)двух вещественных случайных величин. К чему стремится разница Q(rho_1, varepsilon) - Q(rho_2, varepsilon)при varepsilonto0?

Ответ:

H(rho_1) - H(rho_2)

Задача 1.9: Чему равна энтропия нормального распределения mathcal{N}(mu, sigma)?

Ответ:

1/2 cdot (1 + log(2pi sigma^2))

Задача 1.10: Напишите формулу для энтропии экспоненциального распределения rho(x)=e^{-x/a}/a.

Задача 1.11: Случайная величина xiявляется смесью двух случайных величин, то есть её распределение rho(x)есть взвешенная сумма распределений:

rho(x) = w_1rho_1(x) + w_2rho_2(x),;;;;w_1 + w_2 = 1

Пусть множество значений, которые принимает xi_1, не пересекается с множеством значений xi_2, другими словами, пусть носители этих двух случайных величин не пересекаются. Найдите выражение для энтропии H(xi) через энтропии H(xi_1)и H(xi_2).

Ответ

H(rho) = -int_{X_1+X_2} rho(x) log(rho(x)) dx \=-int_{X_1+X_2} (w_1rho_1(x)+ w_2rho_2(x))log(w_1rho_1(x) + w_2rho_2(x)) dx =\ =-int_{X_1} w_1rho_1(x) log(w_1rho_1(x)) dx-int_{X_2} w_2rho_2(x) log(w_2rho_2(x)) dx

Последнее равенство тут возможно только благодаря тому, что носители X_1 и X_2двух распределений по условию задачи не пересекаются. Дальше мы это выражение преобразуем в

-w_1int_{X_1} rho_1(x) log(w_1rho_1(x))- w_2int_{X_2} rho_2(x) log(w_2rho_2(x))dx=\=w_1cdot H_1 + w_2cdot H_2 -w_1log w_1 - w_2log w_2

В этой задаче хотелось показать, что даже в простом случае непересекающихся носителей энтропии не просто складываются с соответствующими весами, а появляется добавка -(w_1log w_1 + w_2 log w_2). Если веса равны 1/2, то эта добавка равна 1.

Интерпретация формулы такая: результат измерения с вероятностью w_1находится в X_1и с вероятностью w_2 – в X_2и соответственно нам достанется неопределённость H_1значений на множестве X_1или неопределённость H_2 на множестве X_2. Но чтобы выяснить, в каком из них находится измерение мы потратим в среднем-(w_1log w_1 + w_2 log w_2)вопросов.

Из этого в частности следует, что смесь с коэффициентами 1/2 двух нормальных величин с одинаковой дисперсией, но сильно разными средними, имеет энтропию на 1 больше, чем энтропия одного нормального распределения. Носители нормальных случайных величин равны всей прямой, а значит пересекаются, но в случае сильно разных средних можно этим пренебречь.

Задача 1.12: Случайная величина xi равновероятно равна 0 или 1. Случайная величина nuзависит от xi: если xi=0, то nuсэмплируется из mathcal{N}(0, 1), а если xi=1, то nuсэмплируется из mathcal{N}(mu, 1). Сколько бит информацию про случайную величину nu содержится в сообщении ``xi=0"(как функция от mu)?

Ответ

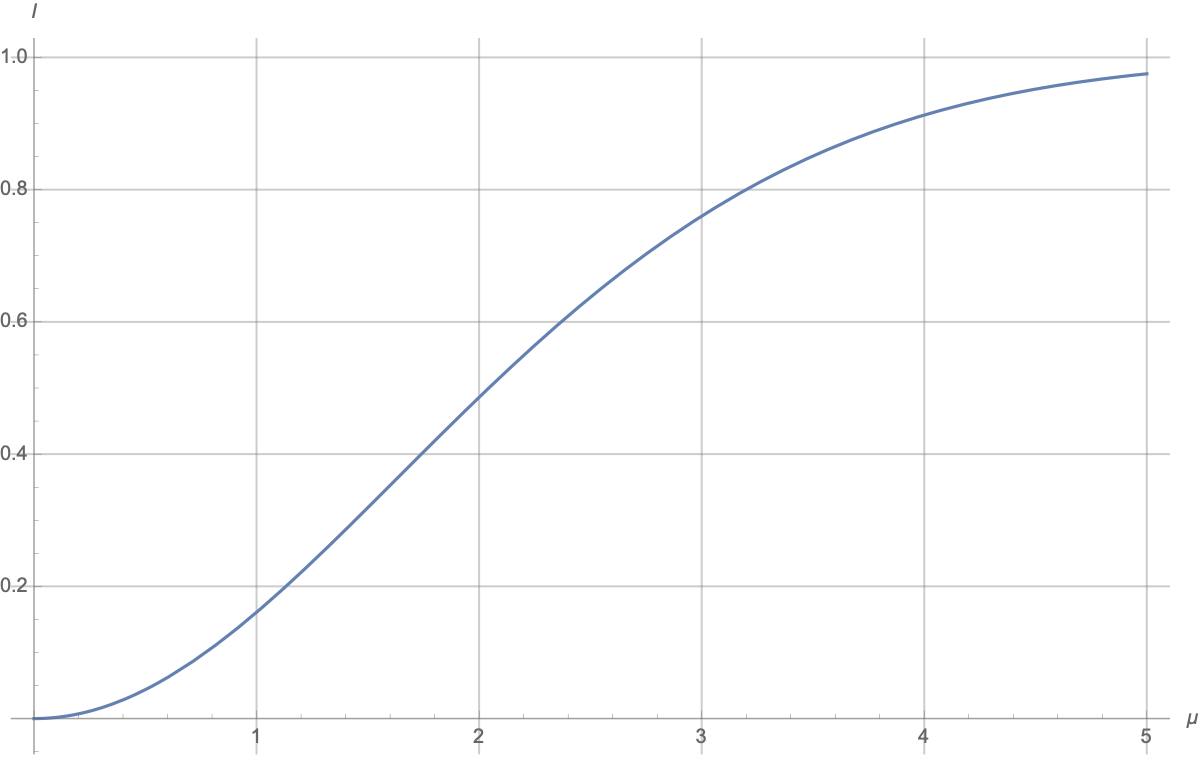
Есть такой численный ответ:

Понятно, что график начинается с 0 и стремится к 1:

  • при mu=0два гаусса одинаковые и сообщение про то, какой из них был выбран ничего не даёт;

  • при mu=5имеем смесь (mixture) двух гауссовских распределений с сильно разнесёнными центрами; сообщение про значение xiговорит, в каком из двух “гауссовских колпаков” находится ответ, и число вариантов уменьшается примерно в два раза, а неопределённость уменьшается на 1; “примерность” связана с тем, что “колпаки” перекрываются, но размер перекрытия быстро уменьшается с ростом mu.

  • в окрестности mu=0рост квадратичный, примерно (mu/2.37)^2.

  • а приближение к 1 происходит примерно по закону 1-e^{-(mu/2.74)^2 - 0.21}

Задача 1.13: Случайная величина xi устроена так: сначала сэмплируется число lambdaиз экспоненциального распределения со средним lambda_0=10, а потом сэмплируется случайное число xиз распределения Пуассона, с параметром lambda. Мы получили сообщение, что одно измерение дало x=10. Сколько бит информации мы получили про случайную величину lambda? Дайте численный ответ. Сколько бит информации даст последовательность измерений 10, 9, 11, 8, 10?

Ответ

I(``x=10") = (4861 - 2520 gamma - 252log(3628800/11))/(252 log(2)) approx 1.17.

I(``x=10, 9, 11, 8, 10") = 3.729.

Задача 1.14: Случайная величина xi устроена так: сначала один раз сэмплируется число p из бета-распределения с параметрами alpha=9, beta=1, а потом сэмплируется случайное число из биномиального распределения с параметрами n=100, ;p. Мы получили сообщение, что одно измерение xiдало 10 (то есть 10 из 100 бросаний монетки выпали орлом). Сколько бит информации мы получили про скрытую случайную величину p? Дайте численный ответ. Сколько бит информации даст последовательность измерений 10, 9, 11, 8, 10?

Задача 1.15: Случайные величины p_1,; p_2,;ldots,p_{10}сэмплированы из бета-распределения с параметрами alpha=9, beta=1. Сами p_1,; p_2,;ldots,p_{10} нам неизвестны, но нам дали 10 измерений x_1,;x_2,;ldots,x_{10}из 10 биномиальных распределений с параметрами n=100, ;p_iи это наше знание про p_1,; p_2,;ldots,p_{10}. Сколько бит информации мы получим в среднем про случайную биномиальную величину с параметрами n=100, ;p_iи когда нам назовут значение i? А если p_1,; p_2,;ldots,p_{10} известны абсолютно точно (случай n=infty)? А если 10 заменить на infty?

Эту задачу можно сформулировать на языке ML так: у нас есть категориальная фичаiдля прогноза булевой величины (‘кликнет пользователь на баннер или нет’). Насколько хорош будет наш прогноз, если в обучающих данных нам известны лишь исторические данные про количество кликов и некликов по этим 10 категориям?

Задача 1.16. Случайная величина xiимеет распределение mathcal{N}(a,varepsilon^2). Величина aнам неизвестна, но мы знаем, что она была сэмплирована из распределения mathcal{N}(0,sigma^2). Сколько информации про a мы в среднем получим от первого измерения величины xi? Как будет расти количество полученной информации с числом измерений?

Ответ

Продолжение:

  • Часть 2 – Mutual Information. В ней рассказывается про Взаимную Информацию – концепцию, которая открывает двери в помехоустойчивое кодирование, алгоритмы сжатия, а также даёт новый взгляд на задачи Машинного Обучения.

  • Часть 3 – ML & Mutual Information. Основы ML в контексте теории информации.

Источник

Добавить комментарий