Как найти энтропия в физике

Содержание:

1. Энтропия
2. Принцип существования энтропии
3. Принцип возрастания энтропии
4. Принцип действия тепловой машины
5. Цикл Карно. Максимальный КПД
6. Второе начало термодинамики

Энтропия – это физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Энтропия

Энтропия это, в широком смысле, мера хаоса в какой-либо системе. В переводе «энтропия» означает «преобразование».

Энтропия простыми словами — это то, как много информации вам не известно о системе.

В статистической физике энтропия характеризует вероятность осуществления какого-либо макроскопического состояния. Кроме физики, термин широко употребляется в математике: теории информации и математической статистике. В этих областях знания энтропия определяется статистически и называется статистической или информационной энтропией.

В широком смысле, в каком слово часто употребляется в быту, энтропия означает меру сложности, хаотичности или неопределённости системы: чем меньше элементы системы подчинены какому-либо порядку, тем выше энтропия. Величина, противоположная энтропии, именуется негэнтропией или, реже, экстропией.

Принцип существования энтропии

В середине прошлого века было сделано существенное открытие» касающееся обратимых термодинамических процессов. Оказалось, что наряду с внутренней энергией у тела имеется еще одна замечательная функция состояния — энтропия. Также, как и внутренняя энергия, энтропия определяется с точностью до произвольной постоянной. Опыт дает значение разности приращения энтропии. Если тело или система при бесконечно малом переходе из одного состояния в другое при температуре  получает тепло  то отношение  является полным дифференциалом некоторой функции  Эта функция и есть энтропия
 определяющаяся, таким образом, одним из двух эквивалентных равенств:

Утверждение о существовании функции, дифференциал которой есть носит название принципа существования энтропии и  является одним из важнейших законоз природы. Оно является существенной частью второго начала термодинамики, о чем у нас речь пойдет ниже. Открытие этого принципа, как и всего второго начала термодинамики, связано, прежде всего, с именами Карно и Клаузиу-са. Сущность принципа, несмотря на некоторую его абстрактность, легко понять: переход тела из одного состояния во второе может произойти бесчисленным количеством способов (разные кривые на графике, начинающиеся и заканчивающиеся в тех же точках); при этих переходах тело может получать самые различные количества тепла, однако во всех случаях интеграл будет иметь одинаковые значения. Отношение количества теплоты к той температуре, при которой это тепло было получено, называют иногда приведенной теплотой. Так как интеграл всегда можно представить приближенно суммой то изменение  энтропии при переходе из одного, состояния в другое равно сумме приведенных теплот. Предположим, что тело, равномерно нагреваясь от 20 до 25 °С, получает при подъеме температуры по одному джоулю тепла на каждый градус. Тогда прирост энтропии будет примерно равен

Наиболее просто выражаются изменения энтропии при изотермических процессах:
где — полученное при процессе тепло. Так, например, при таянии 1 кг льда энтропия вещества возрастает на

За нуль энтропии может быть принято значение энтропии любого состояния (кипящей воды, плавящегося льда). Однако в некоторых случаях принимают за нуль значение энтропии вещества при абсолютном нуле температуры. Для этого, впрочем, имеются некоторые теоретические основания (теорема Нернста), на которых мы останавливаться не будем.

Приняв энтропию вещества при температуре можно найти по формуле

если нагрев происходит при постоянном давлении. Как видим, чтобы знать энтропию, надо изучить ход теплоемкости с температурой.

Если известно уравнение состояния вещества, то энтропия (с точностью до произвольной постоянной) может быть вычислена  весьма просто. По определениюПодставляя значение для таким, как его дает первое начало термодинамики, получим

При помощи уравнения газового состояния исключим отсюда давление. Получим:   Если взять неопределенный интеграл, то получим выражение энтропии с точностью до произвольной постоянной

Можно также взять от определенный интеграл, пределами которого являются два состояния. Тогда получится выражение для разности энтропий двух состояний

Это — выражения для энтропии идеальных газов. Из формул видно, что энтропия возрастает при повышении температуры, а также при увеличении объема газа. Это, разумеется, полностью совпадает с общим утверждением о повышении энтропии при подводе к телу тепла.

Пример. Покажем, что энтропия действительно есть функция состояния системы. Обратимся к примеру на стр. 151 (рис. 79). Путь 1—2—3. Изменение энтропии

Изменение энтропии

Полное изменение энтропии на пути 1—2—3

Видно, что действительно, каким бы путем ни совершался переход газа из состояния 1 в состояние 3, изменение энтропии одно и то же.

Принцип возрастания энтропии

Как уже говорилось, обратимых процессов, строго говоря, не существует, хотя с точностью, доступной опыту, можно осуществить множество процессов, практически неотличимых от обратимых. Имеются, однако, примеры процессов, которые всегда односторонни и уже поэтому никоим образом не могут быть обращены. Так, например, газ может расшириться сам по себе, но не может сжиматься без приложения внешних сил. Тепло может самопроизвольно переходить от горячего тела к холодному и только при затрате работы (например, электроэнергии) может переходить от холодного тела к более нагретому. При трении кинетическая энергия макроскопического движения всегда превращается во внутреннюю энергию, но никогда не происходит самопроизвольный обратный процесс. Необратимость всех остальных процессов в конечном счете связана с тем, что в каждом из них в той или иной степени присутствует один из перечисленных односторонних процессов. В реальных процессах невозможно избежать ни самопроизвольных расширений, ни трения, ни теплового рассеяния.

Нет ли какого-нибудь общего признака у всех перечисленных односторонних процессов? Оказывается, есть: этот признак состоит в том, что во всех односторонних процессах возрастает энтропия.

В случае теплообмена между двумя телами общее (всей системы) изменение энтропии равно

где — тепло, полученное более холодным телом,— тепло, потерянное более горячим телом.

Если больше так как мы считаем положительным тепло, сообщенное телу. Значит,

т. е. при теплообмене общая энтропия системы, в которой произошел теплообмен, возрастает.

Другой случай. Внутри сосуда с газом происходит интенсивное механическое движение (скажем, вертится колесо). Объем не меняется, температура растет, поэтому энтропия изменится на

Наконец, при расширении в пустоту при неизменной температуре прирост энтропииопять-таки положительный.

Итак, во всех односторонних процессах энтропия системы возрастает.

Нетрудно понять, какое значение имеет этот вывод для всех необратимых процессов. Так как каждый необратимый процесс сопровождается односторонними явлениями, идущими с повышением энтропии,.то прирост, энтропии у необратимого процесса будет завышен против того прироста, который имел бы место при обратимом переходе. Пусть — тепло, полученное телом при температуре в интересующем нас необратимом процессе. Если бы процесс был обратимым, то прирост энтропии равнялся бы в реальном процессе прирост энтропии будет больше этой величины:

Если система теплоизолирована, то и предыдущее утверждение приобретает вид

в теплоизолированной системе возможны лишь процессы, идущие с возрастанием энтропии.

Вполне понятно, что энтропия вместе с внутренней энергией являются важнейшими функциями, определяющими термодинамический процесс. Можно сказать, что энтропия является директором-распорядителем процесса, а внутренняя энергия является его бухгалтером: энтропия (определяет направление протекания процесса, энергия «оплачивает расходы» на его проведение.

Если в предыдущие формулы ввести вместо знака  краткой формулой запишется закон энтропии как для обратимых, так и для необратимых процессов:

Эта формула передает содержание второго начала термодинамики. Для замкнутых систем второе начало говорит: энтропия теплоизолированной системы возрастает или остается неизменной.

Целесообразно объединить оба начала термодинамики одной формулой

удобной для рассмотрения всех практических задач термодинамики.

Принцип возрастания энтропии относится к закрытым системам. Если же система общается со средой, другими словами, если речь идет об открытой системе, то ее энтропия может, разумеется, и убывать.

Ниже будет показано, что процессы молекулярного упорядочения связаны с уменьшением энтропии. Живой организм из неупорядоченной системы малых молекул, получаемых в процессах питания и дыхания, конструирует высокоорганизованные постройки — биологические макромолекулы (стр. 595). При этом энтропия организма падает.

Если представить себе замкнутую систему организм+среда, энтропия которой обязана расти, то ясно, что энтропия среды должна возрастать, перекрывая уменьшение энтропии организма.

Возрастание энтропии среды происходит за счет выделений организма.

Если процесс стационарной, то

Можно сказать, что жизнедеятельность организма состоит в пропускании через себя потока энтропии вещества. При этом энтропия вещества, входящего в организм, меньше энтропии, отдаваемой среде,— организм деградирует продукты питания.

Примеры. 1. В примере на стр. 57 мы рассмотрели неупругое столкновение пули с баллистическим маятником и выяснили, что при ударе в системе пуля — маятник исчезает 3920 Дж механической энергии. Это значит, что было необратимым образом передано маятнику от пули посредством теплопроводности. Если предположить, что процесс был изотермическим (т. е. теплопроводность маятника чрезвычайно велика) и температура системы, скажем, то в этом необратимом процессе энтропия системы возросла на

2.    Детский резиновый мяч массой 0,3 кг после падения с высоты 2 м подпрыгивает на I м от пола. В этом изотермическом процессе (пустьнеобратимо передается т. е. энтропия системы мяч — пол возросла на

Если бы мяч и пол были абсолютно упругими, то энтропия не менялась бы  движение мяча продолжалось бы вечно.

3.    Рассмотрим необратимый процесс передачи тепла от парового котла к конденсатору. Пусть паровой котел находится при температуре а конденсатор — при При тепловой мощности котла 10 000 кВт и к. п. д. 25% ежесекундно от котла к конденсатору будет переноситься Для котла, теряющего теплоту, это будет отрицательным, т. е. его энтропия убывает; у конденсатора энтропия растет. Но так как то энтропия системы котел — конденсатор за каждую секунду возрастает на

Принцип действия тепловой машины

Тепловая машина превращает тепло в работу, иначе говоря, забирает тепло от одних тел и передает его другим телам в форме механической работы. Для того чтобы осуществить это превращение, надо располагать двумя различно нагретыми телами, между которыми возможен теплообмен. Для краткости будем называть более горячее тело нагревателем, а более холодное — холодильником. При наличии таких двух тел процесс превращения тепла в работу рисуется следующим образом: способное расшириться тело (рабочее тело) приводится в контакт с нагревателем. Тепло ( отбирается от нагревателя и затрачивается на работу расширения которая отдается окружающим телам. Далее, рабочее тело приводится в контакт с холодильником, которому оно отдает тепло   за счет работы совершаемой внешними силами над рабочим телом.

Чтобы получить непрерывно действующую тепловую машину, необходимо закончить такт сжатия в той точке, в которой начался такт расширения; короче, процесс должен быть циклическим. Рабочее тело по проведении каждого цикла возвращается в исходное состояние. Закон сохранения энергии требует поэтому, чтобы энергия, полученная от окружающих тел, равнялась энергии, переданной окружающим телам. От среды получено: тепло при расширении и работа при сжатии рабочего тела. Среде отдано: работа при расширении тела и тепло при сжатии. Следовательно, При проведении цикла по часовой стрелке работа сжатия меньше работы расширения. Поэтому последнее равенство выражает тот простой факт, что чистая работа, переданная рабочим телом внешней среде, равна разности теплот, полученной от нагревателя и отданной холодильнику. Соответственно коэффициент полезного действия цикла, а значит, и всей машины, будет равен

Описанный процесс действия тепловой машины является, разумеется, абстрактной схемой. Однако наиболее существенные черты каждого теплового двигателя передаются этой схемой. Рабочим телом является расширяющийся и сжимающийся газ или пар, роль холодильника играет окружающая среда. Нагревателем служит паровой котел или, в двигателях внутреннего сгорания, горючая смесь.

Те же три системы являются необходимыми и для холодильной машины, в которой цикл протекает в обратную сторону. Принцип работы этой машины заключается в следующем: расширение рабочего тела производится тогда, когда оно находится в контакте с холодильником. Этим холодное тело охлаждается еще больше, что и является задачей холодильной машины. Далее, чтобы цикл стал возможным, нужно произвести сжатие рабочего тела и передать тепло, полученное от холодильника. Это выполняется при контакте рабочего тела с нагревателем. Таким образом, более горячее тело нагревается еще больше. «Противоестественный» переход тепла от тела менее нагретого к телу более нагретому «оплачивается» работой. Действительно, при совершении цикла против часовой стрелки равенство энергии, переданной среде, и энергии, отнятой от среды где мы по-прежнему

индекс 1 относим к части процесса, протекающей при контакте с более горячим телом), имеет следующий смысл: количество тепла, отнятое от системы, должно быть скомпенсировано равным количеством механической работы.

Второе начало термодинамики накладывает некоторое условие на действие тепловой машины. Если предполагать процесс обратимым, то изменение энтропии рабочего тела после прохождения цикла должно равняться нулю. Можно сказать и иначе: изменение энтропии в процессе расширения должно равняться (с обратным знаком) изменению энтропии при сжатии, т. е.

В случае же необратимого процесса энтропия замкнутой системы, состоящей из нагревателя, холодильника и рабочего тела, возрастет и поэтому

(Напоминаем, что есть алгебраическая величина. Тепло, поступившее в систему, считается положительным.) Подсчитывая значения этих интегралов для конкретных процессов, можно в ряде случаев довольно просто найти значение максимального коэффициента полезного действия того или иного цикла тепловой машины.

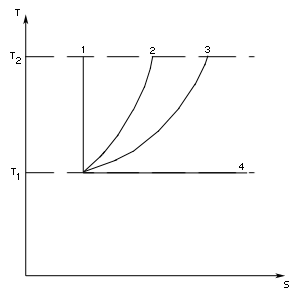
Цикл Карно. Максимальный КПД

Сейчас мы задаемся целью найти выражение предельно большого коэффициента полезного действия тепловой машины, достижимого для идеальной машины, работающей без потерь на обратимом цикле.

Прежде всего рассмотрим теоретический четырехтактный цикл Карно, изображенный на рис. 81. Цикл Карно состоит из двух изотерм (для температур и и двух адиабат. Первый  такт процесса пусть будет изотермическое расширение от состояния 1 к состоянию 2 — рабочее тело находится в контакте с нагревателем, имеющим температуру и процесс проводится весьма медленно. По достижении состояния 2 контакт с нагревателем нарушается, тело теплоизолируется и ему предоставляется возможность дополнительно расшириться. 

Работа происходит за счет внутренней энергии и температура тела пусть падает до Начиная с этой точки (состояние 3) начинается двухтактное сжатие. Тело сообщается с холодильником при температуре  и изотермически сжимается до состояния 4. Здесь опять тело теплоизолируется и сжатие продолжается уже адиабатическим путем с нагреванием рабочего тела за счет совершаемой работы до начальной температуры

Адиабатические процессы в цикле Карно носят вспомогательный характер: они помогают перейти с одной изотермы на другую. В энергетическом балансе эти процессы не участвуют, так как работа адиабатического расширения и работа сжатия компенсируют друг друга.

В адиабатическом процессе энтропия системы не меняется. При изотермическом расширении энтропия нагревателя уменьшается на величину энтропия холодильника возрастает на Энтропия  рабочего тела, вернувшегося в исходное состояние, остается неизменной. Если процесс обратим, то  В необратимых процессах энтропия всей системы, состоящей из холодильника, нагревателя и рабочего тела, возрастает и прирост энтропии больше убыли

откуда и  следовательно, максимальный коэффициент полезного действия цикла Карно равен 

К- п. д. цикла определяется температурами холодильника и нагревателя. Чем больше перепад температуры, тем выше к. п. д. машины. Нетрудно видеть, что коэффициент полезного действия цикла Карно дает оптимальное значение к. п. д. Нет лучшего цикла, чем цикл Карно, и в этом смысле он должен являться образцом для конструкторов тепловых машин, они должны стремиться как можно более приблизить реальные циклы к циклу этой идеальной машины.

Доказательство не составит труда. На рис. 82  показан произвольный цикл, вписанный в цикл

Карно. Уменьшение энтропии нагревателя может быть представлено интегралом
для которого несомненно справедливо неравенстве

так как — самое большое число из тех значений, которые пробегает при интегрировании. Увеличение энтропии холодильника выразится интегралом для которого справедливо неравенство так как — самое маленькое число из тех значений, которые пробегает при интегрировании. При обратимом процессе

следовательно,что и дает условие

Итак, из всех возможных циклических процессов максимальным к. п. д. обладает цикл Карно.
Формула максимального к. п. д. показывает причину низкого к. п. д. паровых машин. При к. п. д. равен 25%. Однако ведь это — максимальный коэффициент полезного действия, он достижим для идеальной машины, работающей обратимо без каких бы то ни было потерь энергии. Не приходится удивляться, что в реальных паровых машинах к. п. д. ниже 10%. В курсе теплотехники рассказывается о путях, которыми идет техника для увеличения коэффициента полезного действия. Ясно, что наиболее существенным является повышение температуры нагревателя, т. е. пара или горючей смеси.

Второе начало термодинамики

Как было указано выше, второе начало термодинамики состоит в утверждении, что энтропия в теплоизолированной системе возрастает. Это утверждение может показаться несколько абстрактным. Кроме того, приведенная формулировка не соответствует историческому развитию идей. Имея в виду огромную, значимость этого закона природы, надо кратко остановиться на других существующих формулировках второго начала термодинамики и показать их эквивалентность приведенной выше.

Исторически второе начало термодинамики вошло в науку в виде постулата Томсона о невозможности создания вечного двигателя второго рода. Вечным двигателем первого рода называют машину, создающую работу «из ничего», т. е. машину, работа которой нарушает первое начало термодинамики. Вечным двигателем второго  рода называют такой двигатель, который производит работу при помощи периодически действующей машины за счет одного лишь отнятия теплоты от окружающей среды. Такой двигатель, будь он возможен, был бы практически вечным, так как запас энергии в окружающей среде почти безграничен и охлаждение, скажем, воды океанов на один градус дало бы непредставимо огромную энергию. Масса воды в мировом океане по порядку величины составляет При охлаждении всей этой массы воды лишь на выделилось бы тепла, что эквивалентно полному сжиганию угля. Железнодорожный состав, нагруженный этим количеством угля, растянулся бы на расстояние что по порядку величины совпадает с размерами солнечной системы!

Вечный двигатель второго рода — это тепловая машина, работающая с нагревателем, но без холодильника. Такая машина могла бы поработать один такт — газ, находящийся в сосуде с поршнем, мог бы расшириться, но на этом работа двигателя и закончилась бы, так как для продолжения действия машины тепло, полученное газом, необходимо передать холодильнику. Формально невозможность вечного двигателя второго рода видна из формулы максимального к. п. д. При отсутствии теплового перепада максимальное значение к. п. д. равно нулю.

Невозможно осуществить периодически действующий вечный двигатель, комбинируя изотермическое расширение с адиабатическим процессом сжатия. Такой процесс невозможен, даже если бы удалось его сделать обратимым. При изотермическом расширении рабочего тела энтропия падает. Значит, процесс сжатия должен приводить к возрастанию энтропии. Этого, однако, не может сделать адиабатический процесс, так как он проходит при постоянной энтропии.

Вполне соответствует принятой здесь формулировке второго начала термодинамики также постулат Клаузиуса, который состоит в утверждении о невозможности перехода тепла от менее нагретого тела к более нагретому без компенсации. Процесс, противоречащий постулату Клаузиуса, протекает с уменьшением энтропии; это свойство энтропии было показано с самого начала.

Услуги по физике:

1. Заказать физику
2. Заказать контрольную работу по физике
3. Помощь по физике

Лекции по физике:

1. Физические величины и их измерение
2. Основные законы механики
3. Прямолинейное равномерное движение
4. Прямолинейное равнопеременное движение
5. Сила
6. Масса
7. Взаимодействия тел
8. Механическая энергия
9. Импульс
10. Вращение твердого тела
11. Криволинейное движение тел
12. Колебания
13. Колебания и волны
14. Механические колебания и волны
15. Бегущая волна
16. Стоячие волны
17. Акустика
18. Звук
19. Звук и ультразвук
20. Движение жидкости и газа
21. Молекулярно-кинетическая теория
22. Молекулярно-кинетическая теория строения вещества
23. Молекулярно – кинетическая теория газообразного состояния вещества
24. Теплота и работа
25. Температура и теплота
26. Термодинамические процессы
27. Идеальный газ
28. Уравнение состояния идеального газа
29. Изменение внутренней энергии
30. Переход вещества из жидкого состояния в газообразное и обратно
31. Кипение, свойства паров, критическое состояние вещества
32. Водяной пар в атмосфере
33. Плавление и кристаллизация
34. Тепловое расширение тел
35. Процессы перехода из одного агрегатного состояния в другое
36. Тепловое расширение твердых и жидких тел
37. Свойства газов
38. Свойства жидкостей
39. Свойства твёрдых тел
40. Изменение агрегатного состояния вещества
41. Тепловые двигатели
42. Электрическое поле
43. Постоянный ток
44. Переменный ток
45. Магнитное поле
46. Электромагнитное поле
47. Электромагнитное излучение
48. Электрический заряд (Закон Кулона)
49. Электрический ток в металлах
50. Электрический ток в электролитах
51. Электрический ток в газах и в вакууме
52. Электрический ток в полупроводниках
53. Электромагнитная индукция
54. Работа, мощность и тепловое действие электрического тока
55. Термоэлектрические явления
56. Распространение электромагнитных волн
57. Интерференционные явления
58. Рассеяние
59. Дифракция рентгеновских лучей на кристалле
60. Двойное лучепреломление
61. Магнитное поле и электромагнитная индукция
62. Электромагнитные колебания и волны
63. Природа света
64. Распространение света
65. Отражение и преломление света
66. Оптические приборы и зрение
67. Волновые свойства света
68. Действия света
69. Линзы и получение изображений с помощью линз
70. Оптические приборы и глаз
71. Фотометрия
72. Излучение и спектры
73. Квантовые свойства излучения
74. Специальная теория относительности в физике
75. Теория относительности
76. Квантовая теория и природа поля
77. Строение и свойства вещества
78. Физика атомного ядра
79. Строение атома

Энтропи́я (от др.-греч. ἐν «в» + τροπή «обращение; превращение») — широко используемый в естественных и точных науках термин (впервые введён в рамках термодинамики как функция состояния термодинамической системы), обозначающий меру необратимого рассеивания энергии или бесполезности энергии (потому что не всю энергию системы можно использовать для превращения в какую-нибудь полезную работу).
Для понятия энтропии в данном разделе физики используют название термодинамическая энтропия; термодинамическая энтропия обычно применяется для описания равновесных (обратимых) процессов.

В статистической физике энтропия характеризует вероятность осуществления какого-либо макроскопического состояния. Кроме физики, термин широко употребляется в математике: теории информации и математической статистике. В этих областях знания энтропия определяется статистически и называется статистической или информационной энтропией. Данное определение энтропии известно также как энтропия Шеннона (в математике) и энтропия Больцмана—Гиббса (в физике).

Хотя понятия термодинамической и информационной энтропии вводятся в рамках различных формализмов, они имеют общий физический смысл — логарифм числа доступных состояний системы. Взаимосвязь этих понятий впервые установил Людвиг Больцман. В неравновесных (необратимых) процессах энтропия также служит мерой близости состояния системы к равновесному: чем больше энтропия, тем ближе система к равновесию (в состоянии термодинамического равновесия энтропия системы максимальна).

Величина, противоположная энтропии, именуется негэнтропией или, реже, экстропией.

Употребление в различных дисциплинах[править | править код]

• Термодинамическая энтропия — термодинамическая функция, характеризующая меру необратимой диссипации энергии в ней.
• В статистической физике — характеризует вероятность осуществления некоторого макроскопического состояния системы.
• В математической статистике — мера неопределённости распределения вероятностей.
• Информационная энтропия — в теории информации мера неопределённости источника сообщений, определяемая вероятностями появления тех или иных символов при их передаче.
• Энтропия динамической системы — в теории динамических систем мера хаотичности в поведении траекторий системы.
• Дифференциальная энтропия — формальное обобщение понятия энтропии для непрерывных распределений.
• Энтропия отражения — часть информации о дискретной системе, которая не воспроизводится при отражении системы через совокупность своих частей.
• Энтропия в теории управления — мера неопределённости состояния или поведения системы в данных условиях.
• Технологическая энтропия — “количественная мера отставания данной технологии от наивысшего в мире уровня, принимаемого за единицу. Основным параметром, характеризующим меру технологической энтропии, является степень неопределённости получения конечного результата, а именно: объёма выпуска инновационной продукции, который может быть получен при данных объёмах вовлечённых в производство ресурсов”^[1].

В термодинамике[править | править код]

Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при замкнутых обратимых процессах, тогда как в необратимых замкнутых — её изменение всегда положительно. В открытой системе может происходить уменьшение энтропии рассматриваемой системы за счет уноса энергии, например в виде излучения, при этом полная энтропия окружающей среды увеличивается^[2].

Математически энтропия определяется как функция состояния системы, определённая с точностью до произвольного постоянного слагаемого. Разность энтропий в двух равновесных состояниях 1 и 2 по определению равна приведённому количеству тепла (), которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому пути^[3]:

.

(1)

Так как энтропия определена с точностью до произвольной аддитивной постоянной, то можно условно принять состояние 1 за начальное и положить . Тогда

,

(2)

Здесь интеграл берется для произвольного квазистатического процесса. Дифференциал функции имеет вид

.

(3)

Энтропия устанавливает связь между макро- и микросостояниями. Особенность данной характеристики заключается в том, что это единственная функция в физике, которая показывает направленность процессов. Поскольку энтропия является функцией состояния, то она не зависит от того, как осуществлён переход из одного состояния системы в другое, а определяется только начальным и конечным состояниями системы.

Физический смысл энтропии[править | править код]

Термодинамическая энтропия как физическая величина отличается своей абстрактностью, физический смысл энтропии непосредственно не вытекает из её математического выражения и не поддаётся простому интуитивному восприятию.

С физической точки зрения энтропия характеризует степень необратимости, неидеальности реального термодинамического процесса. Она является мерой диссипации (рассеивания) энергии, а также мерой оценки энергии в плане её пригодности (или эффективности) использования для превращения теплоты в работу. ^[4]
Два последних утверждения не относятся к необычным системам с отрицательной абсолютной температурой, в которых теплота самопроизвольно может полностью превращаться в работу.

В теории информации[править | править код]

Для энтропии (чаще в математике) встречается также название шенноновская информация или количество информации по Шеннону^[5].

Энтропия может интерпретироваться как мера неопределённости (неупорядоченности) или сложности некоторой системы, например, какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации^[6][7]. Таким образом, другой интерпретацией энтропии является информационная ёмкость системы. С данной интерпретацией связан тот факт, что создатель понятия энтропии в теории информации (Клод Шеннон) сначала хотел назвать эту величину информацией.

Понятие информационной энтропии применяется как в теории информации и математической статистике, так и в статистической физике (энтропия Гиббса и её упрощённый вариант — энтропия Больцмана)^[8][9]. Математический смысл информационной энтропии — это логарифм числа доступных состояний системы (основание логарифма может быть различным, но большим 1, оно определяет единицу измерения энтропии)^[10]. Такая функция от числа состояний обеспечивает свойство аддитивности энтропии для независимых систем. Причём, если состояния различаются по степени доступности (то есть не равновероятны), под числом состояний системы нужно понимать их эффективное количество, которое определяется следующим образом.

Пусть состояния системы равновероятны и имеют вероятность , тогда число состояний , а . В случае разных вероятностей состояний рассмотрим средневзвешенную величину

где  — эффективное количество состояний.
Из данной интерпретации непосредственно вытекает выражение для информационной энтропии Шеннона:

Подобная интерпретация справедлива и для энтропии Реньи, которая является одним из обобщений понятия информационная энтропия, но в этом случае иначе определяется эффективное количество состояний системы. Энтропии Реньи соответствует эффективное количество состояний, определяемое^[11] как среднее степенное взвешенное с параметром от величин .

Следует заметить, что интерпретация формулы Шеннона на основе взвешенного среднего не является её обоснованием. Строгий вывод этой формулы может быть получен из комбинаторных соображений с помощью асимптотической формулы Стирлинга и заключается в том, что комбинаторность распределения (то есть число способов, которыми оно может быть реализовано) после взятия логарифма и нормировки в пределе совпадает с выражением для энтропии в виде, предложенном Шенноном^[12][13][14].

Аксиоматическое определение энтропии[править | править код]

Выражение для информационной энтропии может быть выведено на основе некоторой системы аксиом. Одним из подходов является следующая система аксиом, известная как система аксиом Хинчина:^[15].

1. Пусть некоторая система может пребывать в каждом из доступных состояний с вероятностью , где . Энтропия является функцией только вероятностей : .

2. Для любой системы справедливо , где — система с равномерным распределением вероятностей: .

3. Если добавить в систему состояние , то энтропия системы не изменится.

4. Энтропия совокупности двух систем и имеет вид , где — средняя по ансамблю условная энтропия .

Указанный набор аксиом однозначно приводит к формуле для энтропии Шеннона.

Некоторые авторы^[16] обращают внимание на неестественность последней аксиомы Хинчина. И действительно, более простым и очевидным является требование аддитивности энтропии для независимых систем. Таким образом, последняя аксиома может быть заменена следующим условием.

4′. Энтропия совокупности двух независимых систем и имеет вид .

Оказывается, система аксиом с пунктом 4′ приводит не только к энтропии Шеннона, но и к энтропии Реньи.

f-энтропия[править | править код]

Кроме энтропии Реньи, известны и другие обобщения стандартной энтропии Шеннона, например класс f-энтропий, предложенный^[17] И. Чисаром в 1972 г. Также С. Аримото в 1971 г. предложил^[18] концепцию f-энтропии, задающую иной класс функционалов. Далее рассматривается концепция И. Чисара. Понятие f-энтропии связано^[19] с понятием f-дивергенции. Элементы этих классов образуют парное соответствие, причём каждая такая пара функционалов определяется некоторой выпуклой функцией при , удовлетворяющей условию .

Для заданной функции f-энтропия дискретного распределения определяется как

Наиболее известными частными случаями f-энтропии являются:

Энтропия Шеннона является единственной аддитивной энтропией в классе f-энтропий.

Понятие f-энтропии определяют в общем виде следующим образом. Пусть — распределение вероятностей и — любая мера на , для которой существует абсолютно непрерывная относительно функция . Тогда

Однако непрерывные версии f-энтропий могут не иметь смысла по причине расходимости интеграла.

f-энтропия является вогнутым функционалом от распределения вероятностей.

Можно заметить, что функция может быть задана с точностью до слагаемого , где — произвольная константа. Независимо от выбора функция порождает единственный функционал f-дивергенции. А функционал f-энтропии оказывается определённым с точностью до произвольной аддитивной постоянной, т.е. выбором константы можно задать начало отсчёта энтропии. При этом возникает следующий нюанс: в случае константа должна выбираться так, чтобы подынтегральное выражение не содержало ненулевых постоянных слагаемых, иначе интеграл будет всегда расходиться, т.е. перестаёт быть произвольной. В частности, в дискретной версии энтропии константа должна фиксироваться при . Поэтому для f-энтропии, чтобы не уменьшать общность определения, можно явно указывать аддитивную константу. Например, если — лебегова мера на , тогда — плотность распределения вероятности и

где — произвольная константа.

Функция может также задаваться с точностью до произвольного положительного сомножителя, выбор которого равносилен выбору единицы измерения соответствующей f-энтропии или f-дивергенции.

Сравнивая выражения для f-энтропии и f-дивергенции в общем виде, можно записать следующее связывающее их соотношение^[20]:

где — равномерное на распределение. Если положить, что аргументами энтропии и дивергенции выступают производные распределений по мере (т.е. плотности распределений), имеет место формальная запись

Данная связь носит фундаментальный характер и играет важную роль не только в классах f-энтропии и f-дивергенции. Так, данное соотношение справедливо для энтропии и дивергенции Реньи и, в частности, для энтропии Шеннона и дивергенции Кульбака—Лейблера. Обусловлено это тем, что согласно общепринятой аксиоматике энтропия достигает максимума на равномерном распределении вероятностей.

В биологии[править | править код]

Вводимая обычно как “мера неупорядоченности или неопределенности системы” энтропия часто используется в рассуждениях о направленности эволюционных процессов. Согласно этой точке зрения, биосфера – сверхсложная самоорганизующаяся структура, “питающаяся” неограниченной энтропией солнечного излучения^[21][22]. Бактериородопсин выполняет ту же функцию, что и хлорофилл (туннельный эффект) – обеспечивает преобразование электромагнитного облучения в энергию химических связей. Если говорить о порядке, то упорядочивание расположения элементов фотосинтетической электрон-транспортной цепи обеспечивается фотосинтетической мембраной (структурной единицей хлоропластов), которая определяет направленный перенос электронов и протонов, создавая и поддерживая разность электрохимических потенциалов ионов, разделяя окисленные и восстановленные продукты и препятствуя их рекомбинации^[23].

Считается, что сложность организации по-разному влияет на устойчивость в живой и неживой природе^[24][25]. В неживой природе увеличение сложности приводит к понижению устойчивости живого вещества. В противоположность этому в живой природе сложные (социальные) организации устойчивее (в смысле способности к выживанию), нежели устойчивость каждого элемента в отдельности. Например, численность организмов, состоящих из малого числа клеток (например, москитов), значительно больше численности организмов, состоящих из большого числа клеток (например, слонов). Однако это ничего не говорит об устойчивости, отнесенной к элементарной составляющей. Если бы цитолог пожелал заняться статистикой и собрал случайным образом коллекцию клеток, то он нашел бы в ней больше всего клеток, принадлежащих млекопитающим. Это говорит о том, что с усложнением живых организмов устойчивость их элементарных составляющих (клеток) значительно увеличивается^[26].

По аналогии с шенноновским определением энтропии в качестве меры организованности можно рассматривать величину

где – отношение числа связей имеющихся у элемента в данный момент, к числу всех возможных связей этого элемента. Здесь, как и в случае определения энтропии источника информации, справедливо условие однако условие выполняющееся для случая определения энтропии, здесь уже не имеет места и заменяется неравенством Для элемента не имеющего ни одной связи с любым другим элементом, Напротив, когда элемент соединен со всеми другими элементами, и

Выражение для меры относительной организованности запишется следующим образом:

Максимальная организованность находится приравниванием по всем нулю, в результате чего получается система из уравнений:

Для любого из этих уравнений справедливо

Таким образом, для достижения максимума организованности отношение связи должно быть равно (где — число Эйлера),

Данное нестохастическое толкование организованности обладает и тем преимуществом, что позволяет сделать ряд интересных выводов. Для учета в степени связи наличия связи между двумя элементами через промежуточные элементы нужно будет использовать не число связей, подходящих к элементу а число, которое определяется из выражения

где – степень родства (сила связи) между элементами и В этом случае будет представлять в формуле относительную общую силу связи (вместо числа связей, как было ранее) для элемента ^[27]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

• к.т.н. Деменок С. Л. Просто Энтропия. — Цикл изданий “Фракталы и Хаос”. — СПб.: «СТРАТА», 2019.
• Шамбадаль П. Развитие и приложение понятия энтропии. — М.: Наука, 1967. — 280 с.
• Мартин Н., Ингленд Дж. Математическая теория энтропии. — М.: Мир, 1988. — 350 с.
• Хинчин А. Я. Понятие энтропии в теории вероятностей // Успехи математических наук. — 1953. — Т. 8, вып. 3(55). — С. 3—20.
• Гленсдорф П., Пригожин И. Термодинамическая теория структуры, устойчивости и флуктуаций. — М., 1973.
• Пригожин И., Стенгерс И. Порядок из хаоса. Новый диалог человека с природой. — М., 1986.
• Брюллюэн Л. Наука и теория информации. — М., 1960.
• Винер Н. Кибернетика и общество. — М., 1958.
• Винер Н. Кибернетика или управление и связь в животном и машине. — М., 1968.
• Де Гроот С., Мазур П. Неравновесная термодинамика. — М., 1964.
• Зоммерфельд А. Термодинамика и статистическая физика. — М., 1955.
• Петрушенко Л. А. Самодвижение материи в свете кибернетики. — М., 1974.
• Эшби У. Р. Введение в кибернетику. — М., 1965.
• Яглом А. М., Яглом И. М. Вероятность и информация. — М., 1973.
• Волькенштейн М. В. Энтропия и информация. — М.: Наука, 1986. — 192 с.
• Вентцель Е. С. Теория вероятностей. — М.: Наука, 1969. — 576 с.
• Зарипов Р. Г. Новые меры и методы в теории информации. — Казань: Изд-во Казан. гос. техн. ун-та, 2005. — 364 с.
• Цыпкин Я. З. Информационная теория идентификации. — М.: Наука. Физматлит, 1995. — 336 с.
• Колмогоров А. Н. Теория информации и теория алгоритмов. — М.: Наука, 1987. — 304 с.

Ссылки[править | править код]

• Фракталы и Хаос — Проект издательства научно-популярной литературы «СТРАТА», СПб

Понятие энтропии ввел Р. Клаузиус в 1865 г.

Энтропия – функция состояния

Для того чтобы выяснить в чем состоит физический смысл энтропии, рассмотрим изотермический процесс и приведенное количество теплоты в этом процессе на очень малом участке этого процесса -$frac{delta Q}{T}$, где $delta Q$ – количество теплоты, которое получает тело, $T$ – температура тела.

Приведенное количество теплоты, которое сообщается телу в любом обратимом круговом процессе:

$oint {frac{delta Q}{T}=0left( 1 right).}$

Равенство нулю левой части выражения (1), который берут по замкнутому контуру, означает, что отношение δQ/T – это полный дифференциал некоторой функции состояния системы, которая не зависит от формы пути перехода системы из начального состояния в конечное.

Введем следующее обозначение:

$frac{delta Q}{T}=dSleft( 2 right)$.

Для обратимых процессов изменение энтропии равно нулю:

$Delta S=0left( 3 right)$.

Если выполняется необратимый процесс, то энтропия системы увеличивается:

$Delta S$>$0, left( 4 right)$.

Все реальные процессы являются необратимыми, поэтому в реальности энтропия изолированной системы способна только расти. Она становится максимальной в состоянии термодинамического равновесия.

«Энтропия простыми словами с формулами» 👇

Неравенство Клаузиуса

Выражения (3) и (4) объединяются в неравенство, которое называется неравенством Клаузиуса:

$Delta Sge left( 5 right)$.

Неравенство Клаузиуса означает, что для замкнутой системы энтропия способна увеличиваться (если процесс необратим), или не изменяется (процесс обратим).

Неравенство Клаузиуса является математической записью второго начала термодинамики.

Знак изменения энтропии указывает направление течения процесса в обратимом процессе.

Во всех ординарных термодинамических системах при стремлении температуры к бесконечности, внутренняя энергия системы безгранично растет. Абсолютная температура при равновесных процессах может только большей нуля, следовательно, если система подвергается нагреву, то:

$dS$>$0.$

При уменьшении температуры системы имеем:

$dS$

Изменение энтропии в равновесном процессе

Допустим, что термодинамическая система совершает равновесный переход из состояния 1 в состояние 2, тогда изменение энтропии найдем как:

$Delta S=S_{2}-S_{1}=intlimits_1^2 {frac{delta Q}{T}=intlimits_1^2{frac{dU+delta A}{T}left( 6 right),} }$

где $dU$ – изменение внутренней энергии в рассматриваемом процессе; $delta A$ – работа, выполняемая в этом процессе.

Выражение (6) способно определить энтропию с точностью до аддитивной константы. Это означает то, что физическим смыслом обладает не энтропия, а ее разность.

$S=intlimits_{обр} {frac{delta Q}{T}+const, left( 7 right).}$

Свойства энтропии

Свойство аддитивности имеют:

• масса;
• внутренняя энергия;
• количество теплоты.

Аддитивными не являются:

• объем,
• температура,
• давление.

Так, при обратимом адиабатном процессе мы имеем:

$delta Q=0to S=const.$

Энтропия однородной термодинамической системы – это функция пары независимых параметров, характеризующих ее состояние, например, $ p,V$ или $ T,V$ при $ m=const$.

В этой связи можно записать, что:

$left( V,T right)=intlimits_0^T {C_{V}frac{dT}{T}+S_{01, }left( 8right).}$

или

$Sleft( p,T right)=intlimits_0^T {C_{p}frac{dT}{T}+S_{02, }left( 9right),}$

где $intlimits_0^T {C_{V}frac{dT}{T},}$ – находят для обратимого изобарного процесса; $intlimits_0^T {C_{p}frac{dT}{T}}$ – вычисляют для обратимого изохорного процесса, при изменении температуры от 0К до $T$; $C_V$ – теплоемкость изохорного процесса; $C_p$ – теплоемкость при изобарном процессе; $S_{01 }=S(V,0)$ ; $S_{02 }=S(p,0).$

Статистический смысл энтропии

Допустим, что энтропия в обратимом процессе претерпевает изменения под воздействием внешних условий, которые оказывают влияние на систему. Механизм действия этих условий на энтропию можно сформулировать так:

1. Внешние условия определяют микросостояния, которые доступны системе, а также их количество.
2. В рамках доступных для системы микросостояний, она приходит в состояние равновесия.
3. Энтропия получает соответствующее значение. Получается, что величина энтропии идет за изменением внешних условий, принимая наибольшую величину, совместимую с внешними условиями.

Глубокий смысл энтропии раскрывается в статистической физике. Энтропия связана с термодинамической вероятностью состояния системы.

Термодинамическая вероятность всегда больше или равна единице.

Энтропия системы и термодинамическая вероятность связаны между собой формулой Больцмана:

$S=k ln⁡(W) (10),$

где $k$ – постоянная Больцмана.

1. Формула (10) означает, что энтропия определена натуральным логарифмом количества микросостояний, которые реализуют рассматриваемое макросостояние.
2. Согласно формуле Больцмана, энтропия – это мера вероятности состояния термодинамической системы.
3. Говорят, что энтропия – мера беспорядка системы. Это статистическая интерпретация энтропии. Большее количество микросостояний, которое осуществляет макросостояние, соответствует большей энтропии.
4. Если система находится в состоянии термодинамического равновесия, что соответствует наиболее вероятному состоянию системы, количество микросостояний наибольшее, энтропия в этом случае максимальна.
5. Поскольку при необратимых процессах энтропия увеличивается, при статистическом толковании это значит, процессы в замкнутой системе проходят в направлении роста количества микросостояний. Это означает, что процессы идут от менее вероятных к более вероятным, до достижения вероятностью максимальной величины.

Термодинамика, основы которой должны быть известны каждому ученику, наука занятная. Самым занятным для многих был вопрос – почему у термодинамики есть целых 2 начала и ни одного конца? Если с первыми 2 началами термодинамики особых непонятностей нет, то 3 вызывает немало споров даже в кругу ученых.

Для 3 начала термодинамики имеется множество формулировок — автору статьи известно 9, и он полагает наиболее доступной формулировку в виде тепловой теоремы Нернста. Она гласит – “Абсолютный нуль недостижим”. Однако в большинство учебников общей физики вошла иная формулировка – “Энтропия замкнутой системы нарастает”.

Здесь сразу начинаются проблемы — понять, что есть энтропия реально сложно. Впервые понятие энтропии ввел германский физик Рудольф Клаузиус. С помощью этой функции он описывал возможность тепла преобразовываться в иные виды энергии. Длительное время термин «энтропия» применялся исключительно в физике, позднее он перешел и в прочие науки.

Здесь сразу начинаются проблемы — понять, что есть энтропия реально сложно. Впервые понятие энтропии ввел германский физик Рудольф Клаузиус. С помощью этой функции он описывал возможность тепла преобразовываться в иные виды энергии. Длительное время термин «энтропия» применялся исключительно в физике, позднее он перешел и в прочие науки.

Энтропия в физике

Согласно термодинамике, всякая замкнутая система стремится достичь равновесного состояния — это значит перейти в положение, когда нет никакого излучения энергии или ее перехода из одного состояния в другое. Выйти из такого состояния невозможно и она характеризуется максимальным уровнем беспорядка. Таким образом – энтропия мера беспорядка. Чем он выше, тем больше и значение энтропии. Чем сложнее организована структура вещества, тем меньше уровень энтропии и выше вероятность ее распада.

Например, Останкинская телевышка весьма сложная структура, она стремится к упрощению. Если за ней не смотреть и не ремонтировать, то через определенный промежуток времени конструкция телевышки развалится на составляющие части. Беспорядок сооружения, а следовательно и энтропия, увеличатся.

Еще одним способом подачи энтропии в физике является ее определение, как разность между идеальным процессом, описываемым формулами, и процессом реальным. Чтобы не усложнять статью рассмотрим это явление на простом примере.

Человек ставит свой мобильный телефон на зарядку. Идеальным будет вариант, когда вся полученная электрическая энергия перейдет в химическую энергию аккумулятора, который затем снова будет преобразовывать ее в электроэнергию необходимую для питания сотового.

На самом деле, все далеко не так – часть энергии полученной из электросети необратимо тратится на нагрев блока питания, проводов и самого аккумулятора. В этом несложно убедиться, прикоснувшись к блоку питания или телефону в процессе подзарядки – они будут теплые. Энергия, преобразовавшаяся в тепло, и есть в данной ситуации энтропия.

Самые распространенные формулировки энтропии в физике

Многие известные физики пытались доступным для простых людей объяснить понятие энтропии. Выделим 3 наиболее известные формулировки объяснения.

Утверждение Клаузиуса

Нагрев тела с более высокой температурой невозможен посредством тела с более низкой температурой.

На примере это выглядит так — поставить чайник с водой на кусок льда можно (априори температура воды выше температуры льда), но дождаться, что вода закипит не получится. Хотя первые 2 начала термодинамики не отрицают подобной возможности.

Формулировка Томсона

В замкнутой системе невозможен процесс, единственным результатом которого была бы работа, совершаемая за счет тепловой энергии полученной от какого-либо тела.

Подобный вариант формулировки означает, что вечный двигатель построить в принципе невозможно.

Утверждение Больцмана

Уменьшение энтропии в замкнутой системе невозможно.

Эта формулировка вызывает множество споров, хотя интуитивно все понятно. В заброшенном жилище будет нарастать хаос – осядет пыль, некоторые вещи развалятся. Навести порядок можно, но только приложив внешнюю энергию, то есть работу уборщика.

Проблема в том, что Вселенная в современных представлениях является замкнутой системой. Образовалась она где-то 14-15 миллиардов лет назад. За это время ее энтропия привела бы к тому, что галактики распались, звезды погасли и никаких новых звезд не появилось бы в принципе. А ведь нашему Солнцу не больше 5 миллиардов лет, да и Вселенная в целом не пришла в состояние хаоса.

Следовательно, Вселенная получает подпитку энергией извне. Вот только откуда?

Энтропия в химии

Многие химические процессы являются необратимыми и происходят с выбросом энергии. Например, взрыв при сотрясении нитроглицерина никого не удивляет — это и есть химическая реакция сопровождаемая резким увеличением энтропии.

Экономика и энтропия

Специалистам в экономике известно понятие коэффициент энтропии. Этот коэффициент показывает изменение уровня концентрации рынка и возможность появления монополий. С ростом этого показателя вероятность захвата рынка монополистами снижается. Этот коэффициент помогает определить выгоды монопольной деятельности в том или ином сегменте рынка.

Энтропия и социология

Под энтропией в социологии полагают информационную неопределенность, которая характеризуется отклонением системы (социума), или ее частей (звеньев), от идеального (эталонного) состояния.

Пример можно взять следующий — некая организация занимается проверкой деятельности других организаций. За проверкой следует составление отчета. Если руководство требует очень подробные отчеты, то наступает момент, когда почти все время сотрудников уходит на составление этих самых отчетов. Время расходуемое на основную деятельность сотрудников (собственно проверки) становится недопустимо малым. Это положение характеризуется высоким состоянием информационной неопределенности (энтропии). Руководство в такой ситуации обязано принять меры по упрощению отчетности.

Если вам понравилась статья, то поставьте лайк и подпишитесь на канал Научпоп. Наука для всех. Оставайтесь с нами, друзья! Впереди ждёт много интересного!

Энтропия. Примеры вычисления энтропии

Энтропия
– это такая функция состояния, дифференциал
которой определяется отношением:

.

В СИ энтропия

измеряется в Дж/К.

Приведём
формулы для подсчёта изменения энтропии
в случае изопроцессов для идеального
газа:

а) Изохорический
процесс:

,
.

б) Изобарический
процесс:

,
.

в) Изотермический
процесс:

,
.

г) Адиабатический
процесс:

,
,
.

Энтропия и второе начало термодинамики

– адиабатический процесс,

– изохорический процесс,

– изобарический процесс,

– изотермический процесс.

Понятие энтропии имеет статистическое
толкование. Состояние макроскопического
тела (т.е. тела, образованного огромным
количеством молекул) может быть задано
с помощью объёма, давления, температуры,
внутренней энергии и других макроскопических
величин. Охарактеризованное таким
способом состояние называетсямакросостоянием. Состояние
макроскопического тела, охарактеризованное
настолько подробно, что оказываются
заданными состояния всех образующих
тело молекул, называетсямикросостоянием.
Всякое макросостояние может быть
осуществлено различными способами,
каждому из которых соответствует
некоторое микросостояние тела. Число
различных микросостояний, соответствующих
данному макросостоянию, называетсястатистическим весом
илитермодинамической вероятностью
макросостояния. В статистической
физике существует теорема, которая
утверждает о равновероятности всех
микросостояний данной системы. В качестве
характеристики вероятности состояния
можно было бы выбрать статистический
вес
,
однако такая характеристика не обладала
бы свойствами аддитивности. Поэтому в
качестве характеристики состояния
принимается величинаS,
пропорциональная логарифму статистического
веса
.

,
(4)

где
– постоянная Больцмана. Такую величину
называютэнтропией.

Определённая
таким образом энтропия обладает
следующими свойствами:

1. Энтропия
   изолированной системы при протекании
   необратимого процесса возрастает.
   Действительно, изолированная, т.е.
   предоставленная самой себе, система
   переходит из менее вероятных в более
   вероятные состояния, что сопровождается
   ростом величины (4).

2. Энтропия
   системы, находящейся в равновесном
   состоянии, максимальна.

Эти
утверждения и составляют содержаниевторого начала термодинамики:

Энтропия
изолированной системы может только
возрастать, (либо по достижении
максимального значения оставаться
неизменной), т.е.
.

Итак, при протекании
в изолированной системе необратимого
процесса энтропия возрастает, т.е.

.
(5)

В статистической
физике доказывается, что в ходе обратимого
процесса, сопровождающегося сообщением
системе количества теплоты
,
энтропия системы получает приращение

,
(6)

что совпадает
с принятым ранее определением энтропии

.

В определении
(6) весьма существенна обратимость
процесса, в ходе которого системе
сообщается теплота
.
Если количество теплоты
сообщается системе в ходе необратимого
процесса, энтропия возрастает как
вследствие сообщения тепла, так и
вследствие необратимости процесса.
Поэтому имеет место неравенство

.
(7)

Под
в (7) подразумевается температура
резервуара, от которого данная система
получает теплоту
.

Формулы (6) и
(7) можно объединить вместе, написав

.
(8)

Знак равенства относится
к обратимым, знак неравенства к необратимым
процессам.

Соотношение
(8), записанное в виде

,

или

,

называется
основным термодинамическим неравенством
Клаузиуса.

При абсолютном нуле температуры всякое
тело, как правило, находится в основном
состоянии, статистический вес которого
равен единице ().
Формула (4) даёт в этом случае для энтропии
значение равное нулю. Отсюда вытекает,
что энтропия всякого тела стремится к
нулю при стремлении к нулю температуры:

.

Это утверждение
представляет собой содержание третьего
начала термодинамики.

Соседние файлы в папке Физика. Лекции

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #