Как найти энтропию ансамбля

Энтропия
объединения ансамблей
используется
для вычисления энтропии совместного
появления статистических зависимых
сообщений. Например, передав сто раз
цифру 5 по каналу связи с помехами,
заметим, что цифра 5 была принята 90 раз,
цифра 6 – 8 раз и цифра 4 – 2 раза.
Неопределенность возникновения
комбинаций вида 5 – 4, 5 – 5, 5 – 6 при
передаче цифры 5 может быть описана при
помощи энтропии объединения.
– неопределенность того, что будет
посланоX,
а принято Y.

Пусть имеется
сложная система, состоящая из двух
систем X
и Y,
X=(x₁,…,
x_i,…,
x_m
)и Y=(y_1…
,y_j,
… y_n
).

Если два ансамбля
X
и Y
статистически зависимы, то совместное
распределение на ансамбле пар ()
может быть представлено в виде:

(3.12.)

В этом случае
энтропия объединения ансамблей принимает
вид

(3.13.)

В этом выражении

Поэтому

(3.14.)

Первое слагаемое
в правой части есть знакомая нам энтропия
ансамбля X.
Второе слагаемое представляет собой
усредненное по ансамблю X
выражение
.

Здесь используются
условные вероятности и это дает нам
право считать, что выделенное выражение
есть неопределенность выбора отдельного
сообщения
из ансамбляY
при условии, что известно одно сообщение

.
Другими словами, это естьчастная
условная энтропия
ансамбля Y
при условии, что известно сообщение
из ансамбляX,
который статистически связан с Y.
Обозначим эту частную условную энтропию
через
.
Усредняя частную условную энтропию по
ансамблюX,
получим среднюю
условную энтропию

(3.15.)

В результате
окончательно получим выражение для
энтропии объединения статистически
связанных ансамблей:

(3.16.)

Аналогично выводятся
следующие выражения, симметричные
этому:

H(XY)=H(YX)=H(YV)+H(X/Y).

(3.17.)

При наличии третьего
ансамбля Z,
статистически связанного с первыми
двумя, получим:

H(XYZ)=H(XY)+H(Z/XY)=H(X)+H(Y/X)+H(Z/XY).

(3.18.)

Это выражение
легко расширяется на объединение
произвольного количества статистически
связанных ансамблей:

H(XUZ…W)=H(X)+H(Y/X)+H(Z/XY)+.
. . +H(W/XYZ.
. .).

(3.19.)

В общем случае
энтропия объединенной системы

H(X,Y)≤
H(X)+H(Y),

что следует
из отношения H(Y/X)≤H(Y).

Энтропия объединенной
системы достигает максимумf,
только в случае если системы независимы.

В случае полной
зависимости систем, состояния одной
системы полностью определяют состояния
другой (они эквивалентны):

H(X,Y)=H(X)=H(Y),
так как H(Y/X)=0.

Энтропия
объединенного ансамбля H(XY)
удовлетворяет следующим соотношениям

а)
H(XY)=
H(X)+
H(Y/X)=
H(Y)+
H(X/Y)
, если X
и Y
зависимы;

б)
H(XY)=
H(X)+
H(Y),
если X
и Y
независимы.

В
случае если имеются n
– зависимых систем, энтропия объединения
будет равна:

H(Х₁;Х₂;Х₃;…;Х_n)
= Н(Х₁)+Н(Х₂/Х₁)+Н(Х₃/Х₁Х₂)
+…+Н(Х_n/Х₁Х₂…Хn).

Энтропия
первой системы входит полностью, энтропия
второй системы с
учетом того, что
первая
определена, третей – первые две определены
и т.д.

Пример 3.14. В
буфере ИС ожидают обработки 6 заданий.
2 из них запрашивают дополнительный
ресурс (например, принтер), 4 – не требуют
ресурса. Последовательно в случайном
порядке отправляются на обработку два
задания. Найти энтропию запроса
дополнительного ресурса.

Решение.
Будем считать сообщением А
– посылку первого задания на выполнение.
Ресурс потребуется с вероятностью
Р(А₁)=2/6=1/3.
Ресурс не потребуется с вероятностью
Р(А₂)=2/3.
Энтропия сообщения А
равна:

Н(А)= – Р(А₁)logР(А₁)
– Р(А₂)logР(А₂)=
-1/3 log1/3
– 2/3 log
2/3 = 0.918 бит.

Сообщение В
– посылка второго задания на выполнение.
Вероятность того, что потребуется ресурс
Р(В₁),
зависит от того, какое задание было
послано первым.

при А₁:
Р(В₁|А₁)=1/5,
Р(В₂|
А₁)=4/5;
H(B|А₁)=
-1/5∙log1/5
– 4/5∙log4/5
= 0.722;

при А₂:
Р(В₁|А₂)=2/5,
Р(В₂|А₂)=3/5;
H(B|А₂)=
-2/5∙log2/5
– 3/5∙log3/5
= 0.971.

Следовательно,
энтропия сообщения В
равна

H(B|A)=
Р(А₁)∙H(B|А₁)+Р(А₂)∙H(B|А₂)
= 1/3∙0.722 + 2/3∙0.971 = 0.888
бит.

Обратим внимание,
что энтропия сообщения В
оказалась меньше, чем сообщения А.
Это естественно, так как, получив
информацию об исходе А,
у нас уменьшилась неопределенность
относительно исхода В.
Полная совместная энтропия получается
по формуле:

H(A,B)=
0.918 + 0.888 = 1.806
бит.

Пример 3.15.
Имеется
три тела с одинаковыми внешними размерами,
но с разными массами x₁,
x₂
и x₃.
Необходимо определить энтропию, связанную
с нахождением наиболее тяжелого из них,
если сравнивать веса тел можно только
попарно.

Решение.
Последовательность действий достаточно
очевидна: сравниваем вес двух любых
тел, определяем из них более тяжелое,
затем с ним сравниваем вес третьего
тела и выбираем наибольший из них.
Поскольку внешне тела неразличимы,
выбор номеров тел при взвешивании будет
случаен, однако общий результат от этого
выбора не зависит. Пусть опыт A
состоит в сравнении веса двух тел,
например, первого и второго. Этот опыт,
очевидно, может иметь два исхода: A₁:
x₁ > x₂,
его вероятность p(A₁) = 1/2;
исход A₂:
x₁ <
x₂;
также его
вероятность p(A₂)=1/2.

H(А) = –1/2 log₂1/2
– 1/2 log₂1/2
= 1 (бит).

Опыт B
– сравнение весов тела, выбранного в
опыте A,
и третьего – имеет четыре исхода: B₁:
x₁>
x₃,
B₂:
x₁<
x₃,
B₃:
x₂>
x₃,
B₄:
x₂<
x₃;
вероятности
исходов зависят от реализовавшегося
исхода A
– для удобства представим их в виде
таблицы:

	B₁	B₂	B₃	B₄
A₁	1/2	1/2	0	0
A₂	0	0	1/2	1/2

Находим:

;
;

H(B|A)=p(A1)∙H(B|A1)+p(A2)∙H(B|A2)=1/2∙1+1/2∙1=1 бит.

Следовательно,
энтропия сложного опыта, т.е. всей
процедуры испытаний:

H(A,B)=H(A)+H(B|A)=2
(бит).

Пример 3.16.
Установленное
на предприятии оборудование в результате
эксплуатации может оказаться в одном
из трех состояний износа:

С1
– оборудование работоспособно, но
требует небольшого ремонта;

С2
– большая
часть деталей изношена, требуется
серьезный ремонт;

С3
– дальнейшая эксплуатация оборудования
невозможна.

Предыдущая практика
показывает, что вероятность состояния
С1
равна 20%,
р(С2)
= 50%, р(С3)
= 30%. Найти
неопределенность (энтропию) состояния
оборудования.

Решение.
H(C) = -(0.2∙log₂0.2+0.5∙log₂0.5+0.3∙log₂0.3)=1.48.

Пример 3.17. Для
уточнения состояния оборудования из
предыдущей задачи на предприятии
проведены испытания оборудования.
Недостаточная квалификация персонала
и отсутствие необходимой
контрольно-измерительной аппаратуры
привели к тому, что результаты испытаний
не достоверно отражают истинное состояние
оборудования. В результате испытаний
возможны 4 исхода:

Z1
– оборудование
исправно; Z2
– требуется
регулировка; Z3
– требуется замена отдельных деталей;
Z4
– оборудование не пригодно к эксплуатации.

Условные априорные
вероятности каждого исхода в зависимости
от истинного состояния оборудования
сведены в таблицу:

p(Z\|C)	Z1	Z2	Z2	Z4
C1	0.5	0.5	0	0
C2	0	0.5	0.5	0
C3	0	0	0.25	0.75

Насколько уменьшилась
неопределенность о состоянии оборудования
в результате испытаний?

Решение.
Необходимо найти общую условную энтропию
С
при условии получения сообщения Z:
H(C|Z).

Найдем вероятность
каждого исхода Zi.

p(Z1) = 0.2∙0.5+0.5∙0+0.3∙0 = 0.1;
p(Z2) = 0.2∙0.5+0.5∙0.5+0.3∙0 = 0.35;

p(Z3) = 0.2∙0+0.5∙0.5+0.3∙0.25 = 0.325;p(Z4) = 0.2∙0+0.5∙0+0.3∙0.75 = 0.225

Найдем апостериорную
вероятность состояний Cj
по формуле Байеса p(Cj|Zi) = p(Zi|Cj)∙p(Cj)/p(Zi).
Результаты сведем в таблицу

p(C\|Z)	Z1	Z2	Z3	Z4
C1	1	0.29	0	0
C2	0	0.71	0.77	0
C3	0	0	0.23	1

Наконец, вычислим
общую условную энтропию H(C|Z):

H(C|Z)
=
= 0+0.35∙0.87+0.325∙0.78+0 =0.56.

Видно, что в
результате испытаний неопределенность
уменьшилась.

Источник

Макеты страниц

Рассмотрим эргодический ансамбль функций с ограниченной полосой частот в герц. Пусть

плотности распределения вероятностей для амплитуд последовательных выборочных точках. Определим энтропию ансамбля на степень свободы как

Можно также определить энтропию в секундах, проводя деление не на а на время Т в секундах, требуемое для получения выборочных точек. Так как то

Для белого теплового шума плотность является гауссовской и имеем

При данной средней мощности белый шум имеет максимальную возможную энтропию. Это следует из отмеченных выше свойств максимальности нормального распределения.

Энтропия непрерывного вероятностного процесса имеет много свойств, аналогичных свойствам энтропии дискретных процессов. В дискретном случае энтропия была связана с логарифмом вероятности длинных последовательностей и с числом относительно вероятных последовательностей большой длительности. В непрерывном случае энтропия подобным же образом связана с логарифмом плотности вероятности для длинного ряда выборок и с объемом области сравнительно высокой вероятности в функциональном пространстве.

Более точно, если предположить, что непрерывна по всем для всех то для достаточно большого

при любом выборе значений не принадлежащих множеству, полная вероятность которого меньше чем где вид произвольно малы. Это следует из эргодического свойства, если мы разделим пространство на большое число малых ячеек.

Связь Я с объемом может быть установлена следующим образом. При тех же самых предположениях рассмотрим -мерное пространство, соответствующее . Пусть наименьший объем области в этом пространстве, имеющей полную вероятность Тогда

если только не равно 0 или 1.

Из сказанного видно, что при больших существует довольно четко определенная (по крайней мере в логарифмическом смысле) область высоких вероятностей и что внутри этой области плотность распределения вероятностей относительно равномерна (опять-таки в логарифмическом смысле).

В случае белого шума распределение задается выражением

Так как эта функция зависит только от то поверхности равной плотности распределения представляют собой сферы и все распределение обладает сферической симметрией. Областью высокой вероятности является сфера радиуса При вероятность нахождения вне сферы радиуса стремится к нулю, как бы ни было мало , а логарифма объема сферы стремится к

В непрерывном случае удобно пользоваться не энтропией ансамбля Н, а производной величиной, которую мы назовем энтропийной мощностью. Она определяется как мощность белого шума, ограниченного той же полосой частот, что и первоначальный ансамбль, и имеющего ту же самую энтропию. Другими словами, если Я — энтропия ансамбля, то его энтропийная мощность равна

В геометрической трактовке это означает измерение объема высокой вероятности квадратом радиуса сферы, имеющей такой же объем. Так как белый шум имеет максимальную энтропию при данной мощности, то энтропийная мощность любого шума меньше или равна его действительной мощности.

Источник

From Wikipedia, the free encyclopedia

A set of networks that satisfies given structural characteristics can be treated as a network ensemble.^[1] Brought up by Ginestra Bianconi in 2007, the entropy of a network ensemble measures the level of the order or uncertainty of a network ensemble.^[2]

The entropy is the logarithm of the number of graphs.^[3] Entropy can also be defined in one network. Basin entropy is the logarithm of the attractors in one Boolean network.^[4]

Employing approaches from statistical mechanics, the complexity, uncertainty, and randomness of networks can be described by network ensembles with different types of constraints.^[5]

Gibbs and Shannon entropy[edit]

By analogy to statistical mechanics, microcanonical ensembles and canonical ensembles of networks are introduced for the implementation. A partition function Z of an ensemble can be defined as:

${displaystyle Z=sum _{mathbf {a} }delta left[{vec {F}}(mathbf {a} )-{vec {C}}right]exp left(sum _{ij}h_{ij}Theta (a_{ij})+r_{ij}a_{ij}right)}$

where is the constraint, and $a_{ij}$ ( ${displaystyle a_{ij}geq {0}}$ ) are the elements in the adjacency matrix, ${displaystyle a_{ij}>0}$ if and only if there is a link between node i and node j. ${displaystyle Theta (a_{ij})}$ is a step function with ${displaystyle Theta (a_{ij})=1}$ if x>0 , and ${displaystyle Theta (a_{ij})=0}$ if x=0 . The auxiliary fields $h_{ij}$ and $r_{ij}$ have been introduced as analogy to the bath in classical mechanics.

For simple undirected networks, the partition function can be simplified as^[6]

${displaystyle Z=sum _{{a_{ij}}}prod _{k}delta ({textrm {constraint}}_{k}({a_{ij}}))exp left(sum _{i<j}sum _{alpha }h_{ij}(alpha )delta _{a_{ij},alpha }right)}$

where ${displaystyle a_{ij}in alpha }$ , alpha is the index of the weight, and for a simple network .

Microcanonical ensembles and canonical ensembles are demonstrated with simple undirected networks.

For a microcanonical ensemble, the Gibbs entropy Sigma is defined by:

${displaystyle {begin{aligned}Sigma &={frac {1}{N}}log {mathcal {N}}\&={frac {1}{N}}log Z|_{h_{ij}(alpha )=0forall (i,j,alpha )}end{aligned}}}$

where indicates the cardinality of the ensemble, i.e., the total number of networks in the ensemble.

The probability of having a link between nodes i and j, with weight alpha is given by:

${displaystyle pi _{ij}(alpha )={frac {partial log Z}{partial {h_{ij}}(alpha )}}}$

For a canonical ensemble, the entropy is presented in the form of a Shannon entropy:

${displaystyle {S}=-sum _{i<j}sum _{alpha }pi _{ij}(alpha )log pi _{ij}(alpha )}$

Relation between Gibbs and Shannon entropy[edit]

Network ensemble with given number of nodes and links , and its conjugate-canonical ensemble are characterized as microcanonical and canonical ensembles and they have Gibbs entropy Sigma and the Shannon entropy S, respectively. The Gibbs entropy in the ensemble is given by:^[7]

${displaystyle {N}Sigma =log left({begin{matrix}{cfrac {N(N-1)}{2}}\Lend{matrix}}right)}$

For ensemble,

${displaystyle {p}_{ij}=p={cfrac {2L}{N(N-1)}}}$

Inserting $p_{ij}$ into the Shannon entropy:^[6]

${displaystyle Sigma =S/N+{cfrac {1}{2N}}left[log left({cfrac {N(N-1)}{2L}}right)-log left({cfrac {N(N-1)}{2}}-Lright)right]}$

The relation indicates that the Gibbs entropy Sigma and the Shannon entropy per node S/N of random graphs are equal in the thermodynamic limit .

Von Neumann entropy[edit]

Von Neumann entropy is the extension of the classical Gibbs entropy in a quantum context. This entropy is constructed from a density matrix rho : historically, the first proposed candidate for such a density matrix has been an expression of the Laplacian matrix L associated with the network. The average von Neumann entropy of an ensemble is calculated as:^[8]

${displaystyle {S}_{VN}=-langle mathrm {Tr} rho log(rho )rangle }$

For random network ensemble , the relation between ${displaystyle S_{VN}}$ and is nonmonotonic when the average connectivity is varied.

For canonical power-law network ensembles, the two entropies are linearly related.^[6]

${displaystyle {S}_{VN}=eta {S/N}+beta }$

Networks with given expected degree sequences suggest that, heterogeneity in the expected degree distribution implies an equivalence between a quantum and a classical description of networks, which respectively corresponds to the von Neumann and the Shannon entropy.^[9]

This definition of the Von Neumann entropy can also be extended to multilayer networks with tensorial approach^[10] and has been used successfully to reduce their dimensionality from a structural point of perspective.^[11]

However, it has been shown that this definition of entropy does not satisfy the property of sub-additivity (see Von Neumann entropy’s subadditivity), expected to hold theoretically. A more grounded definition, satisfying this fundamental property, has been introduced by De Domenico and Biamonte^[12] as a quantum-like Gibbs state

${displaystyle rho (beta )={frac {e^{-beta L}}{Z(beta )}}}$

where

${displaystyle Z(beta )=Tr[e^{-beta L}]}$

is a normalizing factor which plays the role of the partition function, and beta is a tunable parameter which allows multi-resolution analysis. If beta is interpreted as a temporal parameter, this density matrix is formally proportional to the propagator of a diffusive process on the top of the network.

This feature has been used to build a statistical field theory of complex information dynamics, where the density matrix can be interpreted in terms of the super-position of streams operators whose action is to activate information flows among nodes.^[13] The framework has been successfully applied to analyze the protein-protein interaction networks of virus-human interactomes, including the SARS-CoV-2, to unravel the systemic features of infection of the latter at microscopic, mesoscopic and macroscopic scales,^[14] as well as to assess the importance of nodes for integrating information flows within the network and the role they play in network robustness.^[15]

This approach has been generalized to deal with other types of dynamics, such as random walks, on the top of multilayer networks, providing an effective way to reduce the dimensionality of such systems without altering their structure.^[16] Using both classical and maximum-entropy random walks, the corresponding density matrices have been used to encode the network states of the human brain and to assess, at multiple scales, connectome’s information capacity at different stages of dementia.^[17]

References[edit]

^ Levin, E.; Tishby, N.; Solla, S.A. (October 1990). “A statistical approach to learning and generalization in layered neural networks”. Proceedings of the IEEE. 78 (10): 1568–1574. doi:10.1109/5.58339. ISSN 1558-2256. S2CID 5254307.
^ Bianconi, Ginestra (2008). “The entropy of randomized network ensembles”. EPL (Europhysics Letters). 81 (2): 28005. arXiv:0708.0153. Bibcode:2008EL…..8128005B. doi:10.1209/0295-5075/81/28005. ISSN 0295-5075. S2CID 17269886.
^ Menichetti, Giulia; Remondini, Daniel (2014). “Entropy of a network ensemble: definitions and applications to genomic data”. Theoretical Biology Forum. 107 (1–2): 77–87. ISSN 0035-6050. PMID 25936214.
^ Krawitz, Peter; Shmulevich, Ilya (27 September 2007). “Entropy of complex relevant components of Boolean networks”. Physical Review E. 76 (3): 036115. arXiv:0708.1538. Bibcode:2007PhRvE..76c6115K. doi:10.1103/PhysRevE.76.036115. PMID 17930314. S2CID 6192682.
^ Bianconi, Ginestra (27 March 2009). “Entropy of network ensembles”. Physical Review E. 79 (3): 036114. arXiv:0802.2888. Bibcode:2009PhRvE..79c6114B. doi:10.1103/PhysRevE.79.036114. PMID 19392025. S2CID 26082469.
^ ^a ^b ^c Anand, Kartik; Bianconi, Ginestra (13 October 2009). “Entropy measures for networks: Toward an information theory of complex topologies”. Physical Review E. 80 (4): 045102. arXiv:0907.1514. Bibcode:2009PhRvE..80d5102A. doi:10.1103/PhysRevE.80.045102. PMID 19905379. S2CID 27419558.
^ Bogacz, Leszek; Burda, Zdzisław; Wacław, Bartłomiej (1 July 2006). “Homogeneous complex networks”. Physica A: Statistical Mechanics and Its Applications. 366: 587–607. arXiv:cond-mat/0502124. Bibcode:2006PhyA..366..587B. doi:10.1016/j.physa.2005.10.024. ISSN 0378-4371. S2CID 119428248.
^ Du, Wenxue; Li, Xueliang; Li, Yiyang; Severini, Simone (30 December 2010). “A note on the von Neumann entropy of random graphs”. Linear Algebra and Its Applications. 433 (11): 1722–1725. doi:10.1016/j.laa.2010.06.040. ISSN 0024-3795.
^ Anand, Kartik; Bianconi, Ginestra; Severini, Simone (18 March 2011). “Shannon and von Neumann entropy of random networks with heterogeneous expected degree”. Physical Review E. 83 (3): 036109. arXiv:1011.1565. Bibcode:2011PhRvE..83c6109A. doi:10.1103/PhysRevE.83.036109. PMID 21517560. S2CID 1482301.
^ De Domenico, Manlio; Solé-Ribalta, Albert; Cozzo, Emanuele; Kivelä, Mikko; Moreno, Yamir; Porter, Mason A.; Gómez, Sergio; Arenas, Alex (4 December 2013). “Mathematical Formulation of Multilayer Networks”. Physical Review X. 3 (4): 041022. arXiv:1307.4977. Bibcode:2013PhRvX…3d1022D. doi:10.1103/PhysRevX.3.041022. S2CID 16611157.
^ De Domenico, Manlio; Nicosia, Vincenzo; Arenas, Alex; Latora, Vito (23 April 2015). “Structural reducibility of multilayer networks” (PDF). Nature Communications. 6: 6864. Bibcode:2015NatCo…6.6864D. doi:10.1038/ncomms7864. PMID 25904309. S2CID 16776349.
^ De Domenico, Manlio; Biamonte, Jacob (21 December 2016). “Spectral Entropies as Information-Theoretic Tools for Complex Network Comparison”. Physical Review X. 6 (4): 041062. arXiv:1609.01214. Bibcode:2016PhRvX…6d1062D. doi:10.1103/PhysRevX.6.041062. S2CID 51786781.
^ Ghavasieh, Arsham; Nicolini, Carlo; De Domenico, Manlio (10 November 2020). “Statistical physics of complex information dynamics”. Physical Review E. 102 (5): 052304. arXiv:2010.04014. Bibcode:2020PhRvE.102e2304G. doi:10.1103/PhysRevE.102.052304. PMID 33327131. S2CID 222208856.
^ Ghavasieh, Arsham; Bontorin, Sebastiano; Artime, Oriol; Verstraete, Nina; De Domenico, Manlio (23 April 2021). “Multiscale statistical physics of the pan-viral interactome unravels the systemic nature of SARS-CoV-2 infections”. Communications Physics. 4 (1): 83. Bibcode:2021CmPhy…4…83G. doi:10.1038/s42005-021-00582-8.
^ Ghavasieh, Arsham; Stella, Massimo; Biamonte, Jacob; De Domenico, Manlio (10 June 2021). “Unraveling the effects of multiscale network entanglement on empirical systems”. Communications Physics. 4 (1): 129. arXiv:2008.05368. Bibcode:2021CmPhy…4..129G. doi:10.1038/s42005-021-00633-0. S2CID 221104066.
^ Ghavasieh, Arsham; De Domenico, Manlio (13 February 2020). “Enhancing transport properties in interconnected systems without altering their structure”. Physical Review Research. 2 (1): 13–15. arXiv:2001.04450. Bibcode:2020PhRvR…2a3155G. doi:10.1103/PhysRevResearch.2.013155. S2CID 210165034.
^ Benigni, Barbara; Ghavasieh, Arsham; Corso, Alessandra; D’Andrea, Valeria; De Domenico, Manlio (22 June 2021). “Persistence of information flow: a multiscale characterization of human brain”. Network Neuroscience. 5 (3): 831–850. doi:10.1162/netn_a_00203. PMC 8567833. PMID 34746629.

Источник

Энтропия источника независимых сообщений. До сих пор определялось количество информации, содержащееся в отдельных сообщениях. Вместе с тем во многих случаях, когда требуется согласовать канал с источником сообщений, таких сведений оказывается недостаточно. Возникает потребность. в характеристиках, которые, бы позволяли оценивать информационные свойства источника сообщений в целом. Одной из важных характеристик такого рода является среднее количество информации, приходящееся на одно сообщение.

В простейшем случае, когда все сообщения равновероятны, количество информации в каждом из них одинаково и, как было показано выше, определяется выражением (6.3). При этом среднее количество информации равно log т. Следовательно, при равновероятных независимых сообщениях информационные свойства источника зависят только от числа сообщений в ансамбле т.

Однако в реальных условиях сообщения, как правило, имеют разную вероятность. Так, буквы алфавита О, Е, А встречаются в тексте сравнительно часто, а буквы Щ, Ы, Ъ — редко. Поэтому знание числа сообщений т в ансамбле является недостаточным, необходимо иметь сведения о вероятностях каждого сообщения: .

Так как вероятности сообщений неодинаковы, то они несут различное количество информации J(a)=–logP(a). Менее вероятные сообщения несут большее количество информации и наоборот. Среднее количество информации, приходящееся на одно сообщение источника, определяется как математическое ожидание J(a):

(6.6)

Величину Н(а) называется энтропией. Этот термин заимствован из термодинамики, где имеется аналогичное по своей форме выражение, характеризующее неопределенность состояния физической системы. В теории информации энтропия Н(а) также характеризует неопределенность ситуации до передачи сообщения, поскольку заранее неизвестно, какое из сообщений ансамбля источника будет передано. Чем больше энтропия, тем сильнее неопределенность и тем большую информацию в среднем несет одно сообщение источника.

В качестве примера вычислим энтропию источника сообщений, который характеризуется ансамблем, состоящим из двух сообщений и с вероятностями и . На основании (6.6) энтропия такого источника будет равна:

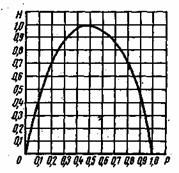
Рис. 6.1. Зависимость энтропии от вероятности р

Зависимость Н(а) от р показана на рис. 6.1. Максимум имеет место при р=1/2, т. е. когда ситуация является наиболее неопределенной. При р=1 или р⁼0, что соответствует передаче одного из сообщений или , неопределенность отсутствует. В этих случаях энтропия Н(а) равна нулю.

Среднее количество информации, содержащееся в последовательности из п сообщений, равно:

Отсюда следует, что количество передаваемой информации можно увеличить не только за счет увеличения числа сообщений, но и путем повышения энтропии источника, т. е. информационной емкости его сообщений.

Обобщая полученные выше результаты, сформулируем следующие основные свойства энтропии источника независимых сообщений (6.6):

— энтропия— величина всегда положительная, так как

— при равновероятных сообщениях, когда , энтропия максимальна и равна:

(6.7)

— энтропия равняется нулю лишь в том случае, когда все вероятности Р(a) равны нулю, за исключением одной, величина которой ,равна единице;

— энтропия нескольких независимых источников равна сумме энтропии этих источников .

Энтропия источника зависимых сообщений. Рассмотренные выше источники независимых дискретных сообщений являются простейшим типом источников. В реальных условиях картина значительно усложняется из-за наличия статистических связей между сообщениями. Примерам может быть обычный текст, где появление той или иной буквы зависит от предыдущих буквенных сочетаний. Так, например, после сочетания ЧТ вероятность следования гласных букв О, Е, И больше, чем согласных.

Статистическая связь ожидаемого сообщения с предыдущим сообщением количественно оценивается совместной вероятностью или условной вероятностью , которая выражает вероятность появления сообщения при условии, что до этого было передано сообщение аКоличество информации, содержащееся в сообщении , при условии, что известно предыдущее сообщение а согласно (6.1) будет равно:. Среднее количество информации при этом определяется условной энтропией , которая вычисляется как математическое ожидание информации по всем возможным сообщениям аи . Учитывая соотношение (2.25), .получаем

(6.8)

В тех случаях, когда связь распространяется на три сообщения , условная энтропия источника определяется аналогичным соотношением

(6.9)

В общем случае n зависимых сообщений

(6.10)

Важным свойством условной энтропии источника зависимых сообщений является то, что при неизменном количестве сообщений в ансамбле источника его энтропия уменьшается с увеличением числа сообщений, между которыми существует статистическая взаимосвязь. В соответствии с этим свойством, а также свойством энтропии источника независимых сообщений можно записать неравенства

(6.11)

Таким образом, наличие статистических связей между сообщениями всегда приводит к уменьшению количества информации, приходящегося в среднем на одно сообщение.

Избыточность источника сообщений. Уменьшение энтропии источника с увеличением статистической взаимосвязи (6.11) можно рассматривать как снижение информационной емкости сообщений. Одно и то же сообщение при наличия взаимосвязи содержит в среднем меньше информации, чем при ее отсутствии. Иначе говоря, если источник создает последовательность сообщений, обладающих статистической связью, и характер этой связи известен, то часть сообщений, выдаваемая источником, является избыточной, так как она может быть восстановлена по известным статистическим связям. Появляется возможность передавать сообщения в сокращенном виде без потери информации, содержащейся в них. Например, при передаче телеграммы мы исключаем из текста союзы, предлоги, знаки препинания, так как они легко восстанавливаются, при чтении телеграммы на основании известных правил построения фраз и слов.

Таким образом, любой источник зависимых сообщений, как принято говорить, обладает избыточностью. Количественное определение избыточности может быть получено из следующих соображений. Для того чтобы передать количество информации, источник без избыточности должен выдать в среднем сообщений, а источник с избыточностью сообщений.

Поскольку и , то для передачи одного и того же количества информации источник с избыточностью должен использовать большее количество сообщений. Избыточнее количество сообщений равно kn–k0, а избыточность определяется как отношение

(6.12)

Величина избыточности лежит в пределах и согласно (6.11) является неубывающей функцией п. Для русского языка, например, дв. ед., , , дв. ед. Отсюда на основании (6.12) для русского языка получаем избыточность порядка 50%.

Коэффициент

(6.13)

называется коэффициентом сжатия. Он показывает, до какой величины можно сжать передаваемые сообщения, если устремить избыточность. Источник, обладающий избыточностью, передает излишнее количество сообщений. Это увеличивает продолжительность передачи и снижает эффективность использования канала связи. Сжатие сообщений можно осуществить посредством соответствующего кодирования. Информацию необходимо передавать такими сообщениями, информационная емкость которых используется наиболее полно. Этому условию удовлетворяют равновероятна и независимые сообщения.

Вместе с тем избыточность источника не всегда является отрицательным свойством. Наличие взаимосвязи между буквами текста дает возможность восстанавливать его при искажении отдельных букв, т. е. использовать избыточность для повышения достоверности передачи информации.

Источник

Gibbs and Shannon entropy[edit]

Relation between Gibbs and Shannon entropy[edit]

Von Neumann entropy[edit]

See also[edit]

References[edit]

Добавить комментарий Отменить ответ

Gibbs and Shannon entropy[edit]

Relation between Gibbs and Shannon entropy[edit]

Von Neumann entropy[edit]

See also[edit]

References[edit]

Вам также может понравиться

Как составить смету на пир в эксель

Не слушается мышь на компе как исправить

Как найти все пары действительных чисел

Добавить комментарий Отменить ответ