Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Термодинамические свойства систем выражают при помощи характеристических функций и их производных. Вид характеристической функции зависит от переменных, которые используют при описании состояния системы. Так, если в качестве переменных избрать внутреннюю энергию и объем, то характеристической функцией может служить энтропия.
Функции состояния
Функции состояния – это важные характеристики, которые описывают состояние системы.
Пусть переменные $x$ и $y$ описывают состояние системы. При этом бесконечно малая величина для этих переменных:
$sigma =f_{1}left( x,y right)dx+f_{2}left( x,y right)dy, left( 1right)$,
где $f_1 (x,y)$ и $ f_2 (x,y)$ – функции от $(x,y)$,
является полным дифференциалом от функции $F$, тогда функцию $F$ считают функцией состояния. Функция состояния в заданном состоянии имеет определенное значение, при этом неважно каким путем или способом система перешла в данное состояние.

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
К функциям состояния в термодинамике, например, можно отнести:
- Внутреннюю энергию системы ($U$). Этот параметр обладает определенным значением для каждого состояния системы. $dU$- полный дифференциал.
- Теплоемкости при постоянных давлении и объеме ($C_V; C_p$).
- Энтальпию ($H$).
- Энтропию ($S$).
- Свободную энергию (функцию Гельмгольца) ($F=U-TS$).
- Термодинамический потенциал Гиббса ($G=H-TS=F+pV$).
Замечание 1
Функции состояния часто носят названия: термодинамические функции или термодинамические потенциалы.
Термодинамических функции имеется бесконечно много. Допустим, что нам известна одна термодинамическая функция, тогда функция от этой функции – термодинамический потенциал.
Энтальпия
Энтальпию, как физическую величину, предложил ввести А.У. Портер, как содержание тепла при неизменном давлении в 1922 году.
Определение 1
Энтальпией ($H$) называют функцию, которая определена равенством:
$H=U+pV (2),$
где $p$ – давление; $V$ – объем.
«Энтальпия и энтропия» 👇
При постоянном давлении можно записать, что:
${(delta Q)}_{p}=dleft( U+pV right)=dH, left( 3 right)$.
Энтальпию можно связать с теплоемкостью при постоянном давлении соотношением:
$C_{p}=left( frac{dH}{dT} right)_{p}left( 4 right),$
где $T$ – термодинамическая температура.
Полный дифференциал энтальпии ($H(S,p)$) можно записать так:
$dH=TdS+Vdp (5). $
В процессе при постоянном давлении изменение энтальпии равно:
$Delta H=Delta U+pDelta V=Delta Qleft( 6 right)$.
Замечание 2
Выражение $Delta U+pDelta V=Delta Q$ – первое начало термодинамики для изобарного процесса.
Энтальпию применяют при расчетах выделяющего тепла для процессов, происходящих при постоянном давлении.
Энтальпию сложной системы можно находить как сумму энтальпий отдельных ее компонент.
Допустим, что термодинамическая система состоит из $k$ частиц. Система является открытой и $k$ может изменяться. В таком случае полный дифференциал энтальпии запишем в виде:
$dH=TdS+Vdp+μ_k dk(7),$
где $mu_{k}=left( frac{partial H}{partial k}right)_{S,p}=frac{H-TS}{k}quad -$ химический потенциал.
Пусть термодинамическая система состоит из нескольких веществ, тогда имеем:
$dH=TdS+Vdp+sumlimits_i mu_{i} dm_{i}left( 8 right)$.
где $mu_i$- химические потенциалы каждой из компонент системы; $m_i$ – масса компоненты.
Энтальпию идеального газа можно выразить через коэффициент Пуассона этого газа (γ):
$H=frac{gamma }{gamma -1}pV, left( 9 right)$.
Энтропия
Энтропия, как и энтальпия, является функцией состояния.
Определение 2
Для обратимого процесса энтропию определяют как:
$Delta S=S_{2}-S_{1}=intlimits_1^2 {frac{delta Q}{T}=intlimits_1^2{frac{dU+delta A}{T}left( 10 right),} }$,
где $delta A$ – работа, выполняемая в термодинамическом процессе.
Формула (9) определяет энтропию с точностью до постоянной величины. Физическим смыслом обладает именно изменение энтропии, а не она сама.
Как и энтальпия, энтропия аддитивная величина:
$S=sumlimits_i S_{i} left( 11 right)$,
$S_i$ – энтропия компоненты термодинамической системы.
Процесс в замкнутой термодинамической системе, протекающий без изменения энтропии называют изоэнтропийным. Это, например, адиабатный процесс, происходящий без теплообмена системы с внешней средой.
Энтропия имеет связь с вероятностью в термодинамике.
Определение 3
Термодинамическая вероятность ($W$) – количество способов реализации данного состояния термодинамической системы. Или иначе, это число микросостояний, реализующих данное макросостояние. $W$ ≥1.
Формула Больцмана реализует связь термодинамической вероятности и энтропии:
$S=k_bln left( W right)$ (12),
где $k_b$ – постоянная Больцмана.
Смысл энтропии в том, что она является мерой беспорядка в термодинамической системе. Большее количество микросостояний, которое осуществляет макросостояние, соответствует большей энтропии.
Если система находится в состоянии термодинамического равновесия, что соответствует наиболее вероятному состоянию системы, количество микросостояний наибольшее, энтропия в этом случае максимальна.
Соотношения Максвелла
Любая из термодинамических функций может быть представлена в виде функции пары независимых переменных таких как $p,V,T,S$. Или говорят, что переменные $p,V,T,S$ связаны двумя равенствами:
- уравнением состояния термодинамической системы,
- термодинамическим тождеством.
Это означает, что только две из названных переменных являются независимыми.
Запишем полные дифференциалы от термодинамических потенциалов:
- $dU=TdS-pdV$.
- $dH=dU+pdV+Vdp=TdS+Vdp$.
- $dF=-SdT-pdV$.
- $dG=-SdT+Vdp.$
Используя выражения для дифференциалов термодинамических функций получим:
$T=left( frac{partial U}{partial S} right)_{V},, T=left(frac{partial H}{partial S} right)_{p},, -p=left( frac{partial U}{partial V} right)_{S},,$
$V=left( frac{partial H}{partial p} right)_{S},, -S=left(frac{partial F}{partial T} right)_{V},, -p=left( frac{partial F}{partial V} right)_{T} $
$-S=left( frac{partial G}{partial T} right)_{p},, V=left(frac{partial G}{partial p} right)_{T}left( 13 right).$
Получаем уравнение Максвелла:
- $left( frac{partial T}{partial V} right)_{S}=-left( frac{partial p}{partial S} right)_{V}$.
- $left( frac{partial T}{partial p} right)_{S}=left( frac{partial V}{partial S} right)_{p}$.
- $left( frac{partial S}{partial V} right)_{T}=left( frac{partial p}{partial T} right)_{V}$.
- $-left( frac{partial S}{partial p} right)_{T}=-left( frac{partial V}{partial T} right)_{p}$.
Применяя сказанное выше полный дифференциал энтальпии можно записать как:
$dH=C_{p}dT+left[ V-Tleft( frac{partial V}{partial T} right)_{p}right]dpleft( 14 right)$,
где $C_{p}=left( frac{partial H}{partial T} right)_{p}$.
Полный дифференциал энтропии:
$dS=C_{V}frac{dT}{T}+left( frac{partial p}{partial T}right)_{V}dVleft( 15 right)$.
Если в качестве независимых переменных использовать температуру и давление, тогда имеем:
$dS=C_{p}frac{dT}{T}-left( frac{partial V}{partial T}right)_{p}dpleft( 16 right)$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Расчеты изменений
энтропии в различных процессах основаны
на использовании неравенства Клаузиуса,
которое связывает изменение энтропии
![]() с количеством теплоты
с количеством теплоты![]()
![]() ,
,
которым система обменивается с окружающей
средой при температуре![]()
![]() .
.
(3.1)
В данном случае
знак равенства имеет место при обратимых,
а неравенства – при необратимых
процессах.
Величину энтропии
данной системы нельзя измерить
непосредственно на опыте, но ее можно
вычислить, пользуясь формулой
![]() .
.
(3.2)
Эта формула
позволяет найти не абсолютную величину
энтропии, а разности энтропий в двух
состояниях системы, т.е. изменение
энтропии при переходе системы из
состояния 1 в состояние 2.
Изменение энтропии
при постоянном давлении можно найти
интегрированием частной производной
энтропии по температуре при постоянном
давлении
![]() ,
,
(3.3)
где
![]()
изобарная теплоемкость системы, Дж/К.
 .
.
(3.4)
При решении
уравнения (3.4) возможно два случая.
Случай 1.
Теплоемкость вещества в интервале
температур
![]() −
−![]() не зависит от температуры. Тогда после
не зависит от температуры. Тогда после
интегрирования (3.4) имеем:
 .
.
(3.5)
Случай 2.
Теплоемкость является некоторой
функцией температуры, например для
мольной изобарной теплоемкости известны
так называемые температурные ряды
![]() ,
,
(3.6)
где
![]()
эмпирически найденные коэффициенты.
Их значения приводятся в справочной
литературе.
Подстановка
выражения (3.6) в (3.4) позволяет после
интегрирования получить следующее
выражение
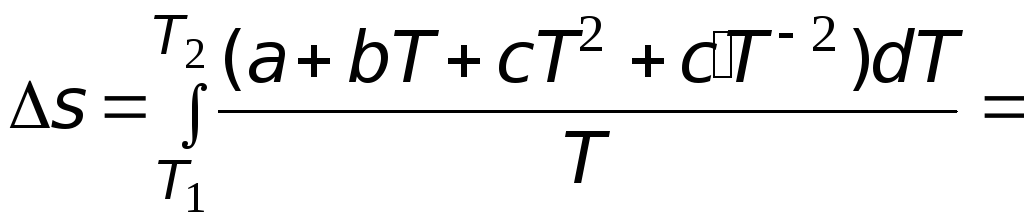
![]() .
.
(3.7)
Разность энтропий
в двух состояниях вычисляется просто,
если обратимый переход из одного
состояния в другое происходит при
постоянной температуре. Это имеет
место, например, при переходах из одного
агрегатного состояния в другое, при
фазовых переходах. Равновесные фазовые
превращения (испарение, плавление,
возгонка и т.д.) происходят в условиях
постоянства температуры и давления.
Они возможны только при подведении
(или отводе) теплоты, затрачиваемой на
проведения фазового превращения. Тогда
формула (3.4) принимает вид
![]() ,
,
(3.8)
где
![]()
скрытая теплота фазового превращения.
При постоянном
давлении скрытая теплота превращения
равна изменению энтальпии, т.е. например,
для фазового превращения
испарения − формула (3.8) примет вид
![]() ,
,
(3.9)
где
![]()
энтальпия испарения, Дж;
![]() температура
температура
кипения, К.
Если вещество в
указанном диапазоне температур
претерпевает фазовое превращение, то
общее изменение энтропии будет
складываться из нескольких слагаемых.
Например, пусть некое условное вещество
А
переходит из твердого состояния при
температуре
![]() в жидкое состояние при температуре
в жидкое состояние при температуре![]() .
.
Из условия задачи видно, что при
определенной температуре имеет место
фазовое превращение (фазовый переход)
плавление. Находим в справочнике эту
температуру, обозначим ее в общем виде
![]()
![]() .
.
Общее изменение энтропии будет равно
сумме трех слагаемых (так называемых
вкладов).
![]() .
.
(3.10)
Первый вклад в
общее изменение энтропии
это изменение энтропии при нагреве
твердого вещества от температуры
![]() до температуры плавления
до температуры плавления
 .
.
(3.11)
При температуре
плавления твердое состояние переходит
в жидкое, при этом наблюдается изменение
энтропии. Изменение энтропии при
фазовом превращении:
![]() .
.
(3.12)
И, наконец,
последний вклад в общее изменение
энтропии внесет изменение энтропии
при дальнейшем нагреве уже образовавшейся
жидкости от температуры плавления до
температуры
![]()
 .
.
(3.13)
Абсолютная мольная
энтропия газообразного вещества в
стандартном
состоянии при температуре Т
может быть найдена как сумма изменений
мольной энтропии в следующих процессах:
нагрев исследуемого вещества в твердом
состоянии от нуля до температуры
плавления; процесс плавления; нагрев
жидкого вещества до температуры кипения;
испарение жидкости; нагрев полученного
газообразного вещества до нужной
температуры.

+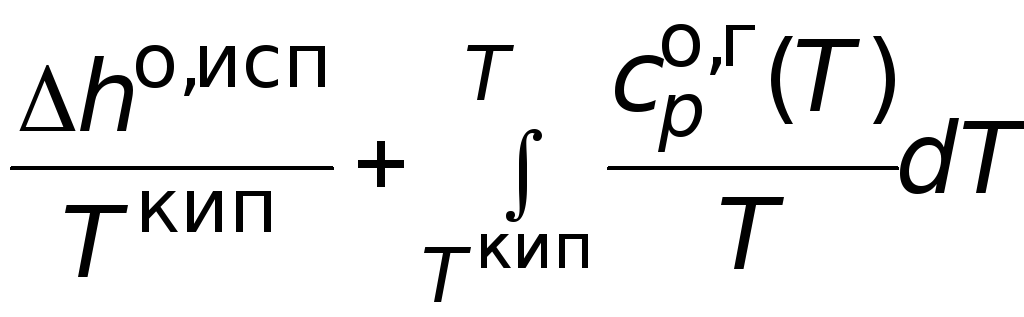 .
.
(3.14)
В справочных
термодинамических таблицах обычно
приводят значения абсолютной энтропии
в стандартном состоянии при температуре
298 К
![]() .
.
Тогда расчет абсолютного значения
энтропии при какой-либо другой температуре
можно произвести исходя из значения
энтропии при 298 К, используя формулу
(3.14) и учитывая агрегатное состояние
исследуемого вещества при 298 К.
Для расчета
изменения энтальпии системы, в которой
нет химической реакции, а только
происходит изменение температуры,
например, при постоянном давлении,
воспользуемся определительным
выражением изобарной теплоемкости
![]() ,
,
отсюда
![]() .
.
(3.15)
Так же как и при
расчете энтропии, тут возможно два
случая.
Случай 1.
Теплоемкость
вещества в интервале температур
![]() −
−![]()
не
зависит от температуры. Тогда после
интегрирования (3.15) имеем:
 .
.
(3.16)
Случай 2.
Теплоемкость является некоторой
функцией температуры. Подстановка
выражения (3.6) в (3.16) позволяет после
интегрирования получить следующее
выражение

![]() .
.
(3.17)
Если в указанном
диапазоне температур возможно фазовое
превращение, как это было рассмотрено
в вышеприведенном примере с нагревом
твердого вещества А,
то все изменение энтальпии
![]() будет равно сумме
будет равно сумме
![]() ,
,
(3.18)
где
![]()
вклад в общее изменение энтальпии за
счет процесса нагрева
твердого вещества от температуры
![]() до температуры плавления
до температуры плавления
 ,
,
(3.19)
![]() изменение
изменение
энтальпии за счет фазового превращения,
это энтальпия фазового перехода,
находится в справочниках;
![]() изменение энтальпии
изменение энтальпии
за счет дальнейшего нагрева системы
от температуры фазового перехода до
нужной температуры. Очевидно, что форма
уравнения для расчета
![]() будет аналогичной (3.19), только
будет аналогичной (3.19), только
коэффициенты температурного ряда
теплоемкости нужно брать для жидкого
вещества А.
 .
.
Для расчета
изменения энергии Гиббса чистого
вещества при переходе его из состояния
I
в состояние II
удобно использовать расчетную формулу:
![]() .
.
(3.20)
Более подробно
расчет изменения энергии Гиббса будет
рассмотрен при решении задачи.
Примеры задач
Пример 1.
Вычислите
изменение энтропии 1 кг этиленгликоля
при его нагреве от температуры 100 до
300 оС.
Решение. Используя
справочную литературу,
определим
коэффициенты температурных зависимостей
теплоемкостей жидкого и газообразного
этиленгликоля, температуру фазового
превращения
![]() и величину мольной энтропии фазового
и величину мольной энтропии фазового
превращения.
 =
=
151,0 Дж/(мольК).
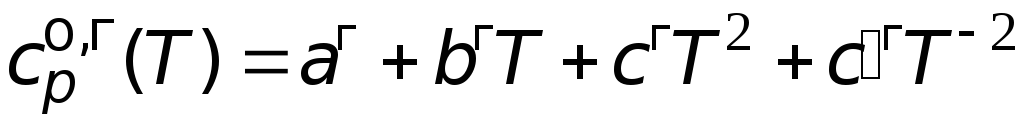 =
=
=
46,26 + 0,2005T
77,90106
T
2
Дж/(мольК).
![]() =
=
479,4 К.
Мольная энтропии
испарения
![]()
= 103,4 Дж/(моль·К).
Производим расчеты.
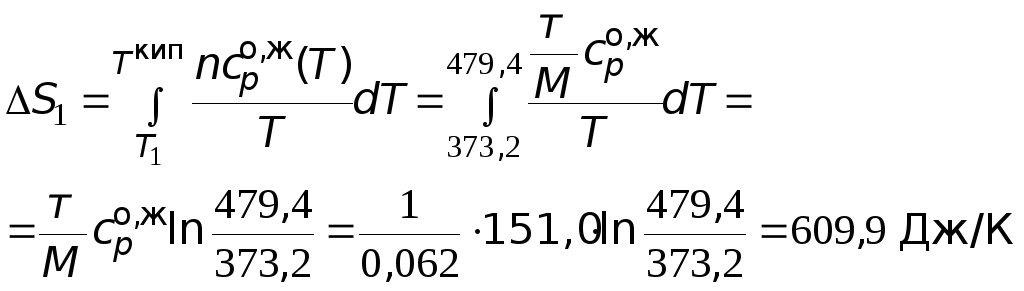
![]() =
=![]() 1667,7Дж/К.
1667,7Дж/К.

![]() =
=

![]() = 2652,2 Дж/К = 2,65
= 2652,2 Дж/К = 2,65
кДж/К.
Пример
2.
Чему
равна мольная энтропия этиленгликоля
при температуре 350 К?
Решение.
Формула
(3.14) для расчета абсолютного значения
энтропии при определенной температуре
в рассматриваемом примере упрощается.
В качестве
нижнего уровня отсчета можно использовать
абсолютное значение энтропии при 298 К
и давлении 1 атм. Это справочная величина,
она равна
![]() = 167,32 Дж/(мольК).
= 167,32 Дж/(мольК).
Выражение для расчета абсолютного
значения мольной энтропии этиленгликоля
при 350 К будет иметь вид
![]() .
.
И при 298 К, и при
350 К этиленгликоль находится в одинаковом
фазовом состоянии − жидком − т.е. в
температурном интервале 298−350 К нет
фазовых превращений. Мольная изобарная
теплоемкость жидкого этиленгликоля в
исследуемом температурном интервале
постоянна и равна
![]() =
=
151,0 Дж/(мольК).
![]() 191,6
191,6
Дж/(мольК).
Пример
3. Чему
равно изменение энтальпии при нагреве
1 моля этиленгликоля от 350 К до 500 К?
Решение.
В
указанный в условии диапазон температур
попадает температура фазового превращения
479,4 К, следовательно, до этой температуры
изменение энтальпии происходит за счет
нагревания жидкости, затем следует
изменение энтальпии при фазовом
превращении, а далее изменение энтальпии
связано с нагреванием газа. Расчет
проводим по формуле (3.18), перейдя к
мольным величинам, температурные
зависимости теплоемкости нам известны.
Мольную энтальпию фазового перехода
находим в справочной литературе, она
равна
![]() 48,6103
48,6103
Дж/моль.
![]() ;
;
 =
=
= 19 539,4 Дж/моль;
![]() 48,6103
48,6103
Дж/моль;

![]() =
=

![]() 70
70
702,2 Дж/моль = 70,7 кДж/моль.
Пример 4.
Вывести уравнение зависимости мольной
энтропии от температуры для газообразного
бензола при давлении 1 атм. Определить
величину стандартной мольной изобарной
теплоемкости бензола при 500 К двумя
способами.
Решение.
Зависимость мольной энтропии вещества
от температуры можно найти после
интегрирования выражений
 .
.
(3.21)
Слева в уравнении
(3.21) стоит разность
![]() .
.
Если в качестве первого состояния
вещества выбрать его состояние при 298
К и 1 атм, то величину мольной энтропии
(![]() )
)
этого вещества легко найти в справочнике.
Тогда из уравнения
(3.21) имеем
![]() .
.
(3.22)
Уравнения (3.22) −
это уже зависимость мольной энтропии
от температуры, но её нужно обязательно
преобразовать, учитывая, что известно
числовое значение
![]() ,
,
а также значениеТ1
= 298 К.
Необходимо учитывать, что уравнение
(3.22) написано в общем виде, поэтому
включает и эмпирический коэффициент
![]() ,
,
и эмпирический коэффициент ![]() .
.
Когда уравнение будет записано для
конкретного вещества, тогда в зависимости
от природы этого вещества в уравнении
будет слагаемое или с коэффициентом
![]()
(для органических веществ), или с
коэффициентом ![]()
(для
неорганических веществ).
В рамках данной
задачи имеем следующие данные:
|
Вещество |
кДж / моль |
Дж/(моль∙К) |
Коэффициенты уравнения
|
|||
|
а |
|
|
|
|||
|
C6H6 |
82,93 |
269,2 |
21,09 |
400,12 |
169,87 |
|
Следовательно,
энтропия газообразного бензола при
любой произвольной температуре Т
![]() .
.
После подстановки
числовых значений и преобразований
имеем выражение температурной зависимости
мольной энтропии газообразного бензола
![]() .
.
(3.23)
Используя уравнение
(3.23), можно графически изобразить
зависимость мольной энтропии газообразного
бензола от температуры (рис. 3.1), а далее
по этой зависимости определить величину
изобарной теплоемкости бензола при
температуре 500 К. Мольная изобарная
теплоемкость связана с частной
производной энтропии по температуре
![]() .
.
С
1
 ледовательно,
ледовательно,
для того чтобы графически найти
теплоемкость, нужно определить частную
производную зависимости
зависимости
энтропии от температуры в точке,
соответствующей 500 К. Графически
производную находят, проводя к
интересующей нас точке на кривой
касательную, а затем определяя угловой
коэффициента
этой касательной. Чтобы
найти угловой коэффициент касательной,
нужно взять на прямой две достаточно
удаленные друг от друга точки и определить
их координаты. Угловой коэффициент
численно равен тангенсу угла наклона
прямой (для рассматриваемого случая):
![]() .
.
Затем находим
изобарную теплоемкость
![]() .
.
Из анализа рис.
3.1 видно, что зависимость энтропии от
температуры имеет слабо выраженную
кривизну, и если точек для построения
кривой мало, то кажется, что такую
зависимость можно описать прямой
линией. Однако зависимость мольной
энтропии от температуры − это все-таки
кривая линия, и к ней можно провести
касательную. Рекомендованный шаг по
температуре для построения зависимости
составляет 50 К. В случае если какой-то
участок зависимости носит явно линейный
характер, угловой коэффициент касательной
будет совпадать с угловым коэффициентом
самой линии.
Следующий способ
определения мольной изобарной
теплоемкости газообразного бензола
расчетный, по формуле температурной
зависимости изобарной теплоемкости,
которая имеет вид:
![]() = −21,09 +
= −21,09 +
0,4T
− 0,000 169Т
2
.
По этому способу
мольная изобарная теплоемкость бензола
при 500 К равна 136,66 Дж/(моль∙К). Значения
теплоемкости,
вычисленные разными способами, должны
быть близки.
Пример 5.
Углекислый
газ массой 200 г находится в состоянии
1 при температуре 600 К и давлении 2,5 атм.
Его перевели в состояние 2, при котором
температура равна 298 К, а давление 1 атм.
Принимая
свойства углекислого газа близкими к
свойствам идеального газа, найти
изменения мольных и полных 1) объема;
2) энтропии; 3) энтальпии; 4) внутренней
энергии и 5) энергии Гиббса системы
при этом переходе.
Решение.
Из
справочных таблиц определяем форму
уравнения и значения коэффициентов
температурной зависимости мольной
изобарной теплоемкости углекислого
газа
|
Вещество |
кДж / моль |
Дж/(моль∙К) |
Коэффициенты
|
|||
|
а |
|
|
|
|||
|
CО2 |
−393,51 |
213,66 |
44,14 |
9,04 |
− |
−8,54 |
![]()
= a
+ bT
+ c’T
−2
= 44,14 + 9,04∙10−3
T
8,54∙105
T
−2
.
1. Используя
уравнение состояния идеального газа,
находим изменение мольного объема
следующим образом:
![]() =
=
= 4,74 ∙10−3
м3/моль.
Полное изменение
объёма углекислого газа при рассматриваемом
переходе составит
![]() .
.
Число молей находим
по формуле
![]() 4,55
4,55
моль.
![]() 4,55∙4,74∙10−3
4,55∙4,74∙10−3
= 2,16∙10−2
м3.
2. Расчет мольного
изменения энтропии углекислого газа
при переходе из состояния 1 в состояние
2 производится по формуле

![]()
 =
=
![]() =
=
=
−46,89 Дж/(мольК).
Полное изменение
энтропии равно
![]() −213,32 Дж/К.
−213,32 Дж/К.
3. Для идеального
газа изменение энтальпии не зависит
от давления, поэтому формула для расчета
мольного изменения энтальпии имеет
вид:
![]()
![]()
=
![]() Дж/моль.
Дж/моль.
Полное изменение
энтальпии равно
![]() =
=
4,55∙(−15998,5) = −72793,18 Дж.
4. Для идеального
газа мольное изменение внутренней
энергии связано с мольным изменением
энтальпии
![]()
Следовательно,
![]() = −15998,5−8,314(298−600)=
= −15998,5−8,314(298−600)=
−13487,7 Дж/моль.
Полное изменение
внутренней энергии найдем как
![]() =4,55(−13487,7)
=4,55(−13487,7)
= − 61369 Дж.
5. Мольное изменение
энергии Гиббса при переходе углекислого
газа из состояния 1 в состояние 2 определим
как
![]() .
.
Но известно, что
![]() ,
,
а![]() .
.
Кроме того,![]() .
.
Тогда
![]() =
=
=
![]() =
=![]() .
.
Мольные изменения
энтальпии и энтропии определены ранее,
значение мольной энтропии в состоянии
2 можно найти по справочнику, т.к. это
состояние 298 К и 1 атм:
![]() 213,66
213,66
Дж/(моль∙К).
![]() −15998,5
−15998,5
−213,66(298−600)−600∙(−46,89) =76660,8 Дж/моль.
4.
ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА РАСТВОРОВ
Для характеристики
раствора применяют следующие виды
концентраций.
![]() −мольная
−мольная
доля компонента k
(часто – молярная доля),
 .
.
![]() −массовая
−массовая
доля компонента,
 .
.
![]() −молярная
−молярная
концентрация (c),
другое название − плотность числа
молей,
![]() . [c
. [c
] = моль/м3
.
![]() −массовая
−массовая
концентрация, другое название –
плотность массы компонента k,
![]() .
.
[![]() ]
]
= кг/м3.
![]() −моляльная
−моляльная
концентрация раствора, или мольно-массовая
концентрация, другое название –
мольно-массовое отношение,
![]() . [ d
. [ d
] = моль/кг.
Состояние компонента
k
в растворе нельзя описать функциями,
отвечающими чистому компоненту k.
Для описания свойств компонента в
растворе вводится понятие
парциальных
мольных свойств
компонента.
Если обозначить полное экстенсивное
свойство раствора, образованного
компонентами в общем виде, как
![]() ,
,
то мольное экстенсивное свойство
раствора, состоящего из компонентовk,
будет
обозначаться как
![]() ,
,
причем![]() .
.
Вклад компонентаk
в любое экстенсивное свойство E
раствора определяется его парциальной
мольной (ПМ) величиной
![]() ,
,
которая равна
![]() .
.
(4.1)
Следует отметить,
что парциальные мольные величины
отражают изменение
свойств и их нельзя уподоблять
соответствующим мольным величинам.
Парциальные мольные величины могут
принимать значения, которые немыслимы
для мольных величин; например, парциальный
мольный объем может быть отрицательным.
Парциальные мольные величины могут
быть образованы от любой экстенсивной
величины. В общем случае экстенсивное
свойство Е
однородной системы, состоящей из k
компонентов,
можно представить в виде функции
температуры, давления и чисел молей
компонентов, т.е.
![]() .
.
Если зафиксировать постоянными давление
и температуру, то получим![]() .
.
Образуем полный
дифференциал этого выражения:
![]() .
.
(4.2)
С учетом (4.1) из
уравнения (4.2) можно получить
![]()
или
![]() .
.
(4.3)
Учитывая, что E
− однородная
функция первой степени от независимых
аргументов nk,
и
привлекая теорему Эйлера об однородных
функциях, получаем из (4.3) выражение
![]() .
.
(4.4)
Если раствор
двухкомпонентный, или как еще говорят,
бинарный, т.е. число компонентов k
= 2, то соотношения, получающиеся в этом
случае, имеют вид:
![]() .
.
(4.5)
При делении
выражения (4.5) на общее число молей
получим
![]() ,
,
(4.6)
с учетом
определительного выражения для мольной
доли компонента k
(4.6) можно записать как
![]() .
.
(4.7)
Используем эти
же выражения для объема
![]() .
.
![]() ,
,
![]() ,
,
где V
– полный объем раствора;
![]() 1
1
и
![]() 2
2
парциальные мольные объемы 1 и 2
компонентов раствора; n1
и n2
– числа молей компонентов 1 и 2; N1
и N2
– мольные доли компонентов 1 и 2 в
растворе;
![]() – мольный объем раствора.
– мольный объем раствора.
Способы определения
парциальных мольных величин рассмотрим
на примере определения парциальных
мольных объемов в бинарном растворе.
Первый способ.
Определение парциального мольного
объема по зависимости полного объема
раствора от числа молей одного из
компонентов.
С огласно
огласно
определительному выражению для
парциальной мольной величины (4.1),
парциальный мольный (ПМ) объем второго
компонента − это величина![]() 2
2
=![]() ,
,
а ПМ объем первого компонента − это
![]() 1
1
=![]() .
.
Если известно уравнение зависимости,
например
![]() ,
,
то для получения![]() 2
2
=![]()
нужно продифференцировать его.
Если
зависимость дана в форме таблицы или
в виде графика, то нужно определить
угловой коэффициент касательной к
кривой зависимости
![]()
в той точке, в которой нам требуется
определить ПМ объем. При графическом
определении частной производной нужно
найти угловой коэффициент касательной,
проведенной к кривой зависимости в
определенной точке (рис. 4.1).
Рис. 4.1. Зависимость
полного
объема раствора
от числа молей
второго компонента
(p,T,
n1
– const)
Частная производная
полного объема по числу молей второго
компонента в условиях постоянства
давления, температуры и остального
состава равна
![]() .
.
Угловой коэффициент
касательной находится

Второй способ.
Определение
ПМ объемов по зависимости мольного
объема раствора от состава.
Парциальные
мольные объемы компонентов бинарной
смеси следующим образом связаны с
мольным объемом смеси
![]() 1
1
=
![]()
N2
![]() .
.
(4.8)
![]() 2
2
=
![]()
+ (1 N2)![]() .
.
(4.9)
Из данных выражений
следует, что для вычисления парциальных
мольных объемов по этому методу
необходимо по зависимости мольного
объема от мольной доли второго компонента
определить частную производную мольного
объема раствора по мольной доле второго
компонента при постоянных давлении и
температуре
![]() в
в
интересующем нас растворе. Для
определения производной, например,
графическим способом, нужно к зависимости
мольного объема раствора от состава
(см. рис. 4.2, линия ВАС)
в соответствующей точке провести
касательную и определить угловой
коэффициент этой касательной по
координатам двух достаточно удаленных
друг от друга точек, лежащих на
касательной
![]()
 .
.
Далее по уравнениям
(4.8) и (4.9) вычислить парциальные мольные
объемы обоих компонентов.

Рис. 4.2. Зависимость
мольного объема раствора от состава
раствора
Третий способ.
Определение
ПМ объемов по методу Розебома
(метод отрезков).
Из анализа рис.
4.2 и уравнений (4.8−4.9) видно, что
касательная к зависимости
![]() =f
=f
(N2)
отсекает на левой оси ординат отрезок,
равный парциальному мольному объему
первого компонента в растворе концентрации
N2,
а на правой оси
отрезок, равный парциальному мольному
объему второго компонента в растворе
той же концентрации.
Примеры
задач
Пример 1
Жидкий бензол
массой 500 г занимает объем 568,8 см3
(293 К, 1 атм). Вычислить его мольный и
удельный объемы и плотность массы.
Дано:
Чистое вещество
– бензол
M
= 0,078 кг/моль
m
= 500 г = 0,5 кг
V
= 568,8 см3 =
5,688∙10−4
м3.
Найти:
![]() .
.
Решение
![]() = 8,887∙10−5
= 8,887∙10−5
м3/моль
![]() =
=
1,138∙10-4
м3/кг
![]() =
=![]() =8,787∙102
=8,787∙102
кг/м3.
Пример
2.
Общее
число молей в водно-ацетоновом растворе
составляет 12,58 моль. Плотность массы
раствора и плотность числа молей ацетона
в нем равны соответственно 916 кг/м3
и 7897 моль/м3
при 298 К и 1 атм. Определить массу и объем
раствора, его мольную массу и удельное
число молей.
Дано:
двухкомпонентный раствор. Компонент
1 – вода, H2O.
Компонент 2 – ацетон, (CH3)2CO.
M1 = 0,018
кг/моль; M2 = 0,058
кг/моль; n2
=
12,58 моль; ρ = 918 кг/м3;
c2 = 7897
моль/м3.
Найти:
m,
V,
M,
nуд.
Решение. Решение
основано на взаимосвязи между
концентрационными шкалами.
Масса раствора:
 =
=
=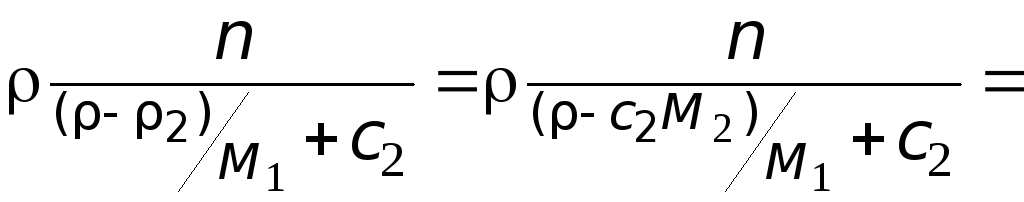
![]() .
.
Объем раствора:
![]() =
=
=![]() м3.
м3.
Мольная масса
раствора:
 =
=
=
![]() кг/моль.
кг/моль.
Удельное число
молей раствора:
![]() =
=
=
![]() моль/кг.
моль/кг.
Пример 3. Для
двухкомпонентного водно-аммиачного
раствора приведена в табличной форме
зависимость объема раствора от числа
молей аммиака при постоянных параметрах:
температуре 293 К, давлении 1 атм и числе
молей воды 5,556 моль.
|
|
0 |
0,392 |
0,682 |
1,498 |
2,521 |
|
|
1,00 |
1,10 |
1,17 |
1,34 |
1,48 |
Вычислите
парциальные мольные объемы обоих
компонентов при мольной доле аммиака,
равной 0,15.
Дано: двухкомпонентный
раствор. Компонент 1 − вода, H2O.
M1
= 0,018 кг/моль.
Компонент 2 – аммиак, NH3.
M2
= 0,017 кг/моль. n1=
5,556 моль. N2
= 0,15. Найти:
![]() .
.
Решение. Изобразим
графически данную в условии задачи
зависимость объема системы от числа
молей второго компонента.
П о
о
определению парциальный мольный объем
компонента 2 – это частная производная
полного объема по числу молей второго
компонента в условиях постоянства
температуры, давления и числа молей
первого компонента, т.е.![]() =
=![]() .
.
Полный объем
бинарного раствора может быть найден
как
![]() .
.
По рис. 4.3 найдем
частную производную объема по числу
молей второго компонента
![]() .
.
Для этого определим угловой коэффициент
касательной, проведенной к нашей
зависимости в определенной точке.
Данная точка должна показывать число
молей второго компонента в растворе
при мольной доле его, равной 0,15. Найдем
значение
n2
из
соотношения
![]() .
.
![]() =
=
![]() моль.
моль.
При числе молей
второго компонента 0,98 восстанавливаем
перпендикуляр к кривой и проводим к
точке пересечения перпендикуляра с
кривой касательную. Затем находим
угловой коэффициент касательной
![]() м3/моль,
м3/моль,
![]() = 2,210
= 2,210
−5 м3/моль.
Примечание.
Если зависимость полного объема от
числа молей второго компонента
представляет собой прямую линию, то
касательная будет совпадать с ходом
этой прямой.
Чтобы найти
![]() ,
,
воспользуемся соотношением![]() ,
,
причем значение полного объема системы
при числе молей второго компонента,
которое соответствует мольной доле
его 0,15, определим по графику.V
= 1,2510
−4
м3.
![]() =
=
![]() = 1,8610−5
= 1,8610−5
м3/моль.
|
N2 |
0,0 |
0,255 |
0,424 |
0,617 |
0,870 |
1,000 |
|
|
7,600 |
7,982 |
8,359 |
8,790 |
9,378 |
9,800 |
Пример
4.
Для
двухкомпонентного жидкого раствора
ацетон (1-й компонент)
трихлорметан (2-й компонент) представлена
в табличной форме (Т
= 298 К, р
= 1 атм) зависимость мольного объема
раствора
![]()
от мольной доли второго компонента
N2
.
Определите
для обоих компонентов парциальные
мольные объемы
![]() 1
1
и
![]() 2
2
при мольной доле второго компонента
N2
= 0,6.
Решение.
Изображаем
данные, приведенные в условии задачи,
в виде графической зависимости мольного
объема от состава (мольная доля второго
компонента). Проводим касательную к
точке на кривой, при к оторой
оторой
мольная доля трихлорметана (компонент
2) равна 0,6. Касательную проводим до
пересечения с осями ординат и по
величине, отсекаемой на каждой из осей,
находим значения парциальных мольных
объемов.
![]() 1
1
= 7,3∙10−5
м3/моль;
![]() 2
2
= 9,6∙10−5
м3/моль.
Пример
5.
Для
двухкомпонентного жидкого раствора
вода Н2О
(1-й компонент)
уксусная кислота С2Н4О2
(2-й компонент) имеется полученная на
опыте в табличной форме зависимость
изобарной теплоемкости Ср
от массы кислоты m2
(Т
= 298 К, р
= 1 атм) при постоянной массе воды m1
=
0,5 кг:
|
m2 |
0,0 |
0,057 |
0,088 |
0, 103 |
0,161 |
0,260 |
|
Сp, |
2090 |
2238 |
2314 |
2352 |
2476 |
2682 |
Удельные
изобарные теплоемкости чистых компонентов
1 и 2 (![]() )равны
)равны
4180 и 2056 Дж/(Кмоль).
Требуется
1) построить график зависимости изобарной
теплоемкости смешения раствора Срm
от числа молей кислоты n2;
2) определить для обоих компонентов их
парциальные мольные изобарные
теплоемкости смешения ср1m
и
ср2m
при мольной доле второго компонента
N2
= 0,05; 3) вычислить для тех же компонентов
при той же N2
парциальные мольные изобарные
теплоемкости ср1
и ср2.
Решение
1. Для
получения зависимости изобарной
теплоемкости смешения раствора Срm
от числа молей кислоты n2
(Срm
= f(n2))
в табличной и графической формах
необходимо преобразовать
табличные данные по зависимости
изобарной
теплоемкости Ср
от массы второго компонента
(Ср=
f
(m2))
. Используя определительные выражения
для понятий число молей и функция
смешения, получим:
![]() ;
;
![]() .
.
Пример расчета:
![]() моль;
моль;
![]() 2238
2238
− (4180∙0,5 +
2056∙0,057)
= 30,81 Дж/К.
|
n2 |
0 |
0,95 |
1,47 |
1,72 |
2,68 |
4,33 |
|
Срm, |
0 |
30,81 |
43,07 |
50,23 |
54,98 |
57,44 |
Данные расчетов
приведены ниже
Г рафический
рафический
образ зависимостиСрm
= f
(n2)
приведен на рис.4.5.
Рис.
4.5. Зависимость изобарной теплоемкости
смешения раствора Срm
от числа молей кислоты n2
2. В
основе определения
![]()
и
![]() лежит система вида
лежит система вида
![]() ,
,
 .
.
По
заданной мольной доле найдем координаты
точки на кривой Срm
=f(n2)
(рис.4.5),
к которой нужно проводить касательную):
![]() и
и
![]() (А)
(А)
в точке А
на кривой :
![]() =
=![]() =1,46
=1,46
моль.
![]() (А)
(А)
= 43 Дж/К (определили по графику при n2
=1,46 моль).
Примечание.
Следует отметить, что числовые значения,
которые в этой задаче определяются по
графику, при приближенном построении
графика, конечно, не являются точными.
При графических решениях нужно
использовать миллиметровую бумагу и
достаточно крупный масштаб, тогда
значения получатся более точными.
Определим по
угловому коэффициенту касательной
тангенсу угла наклона касательной tg
2
в точке А величину парциальной мольной
изобарной теплоемкости смешения второго
компонента
 =
=![]() Дж/(моль∙К).
Дж/(моль∙К).
Затем
можно найти
![]() :
:
![]() =
=![]() =0,496Дж/(моль∙К).
=0,496Дж/(моль∙К).
3).
Каждую из величин ср1
и ср2
находим
с помощью выражения для
![]() :
:![]() ;
;
![]() = 0,496 +4180∙ 0,018
= 0,496 +4180∙ 0,018
=75,736 Дж/(моль∙К).
![]() = 20+ 2056∙ 0,060= 143,36Дж/(моль∙К).
= 20+ 2056∙ 0,060= 143,36Дж/(моль∙К).
…
Здесь вы найдете примеры задач на вычисление таких термодинамических параметров как энтальпия, энтропия, энергия Гиббса. Определение возможности самопроизвольного протекания процесса, а также составление термохимических уравнений.
Задачи к разделу Основы термодинамики с решениями
Задача 1. Рассчитайте стандартную энтальпию и стандартную энтропию химической реакции. Определите в каком направлении при 298 °К (прямом или обратном) будет протекать реакция. Рассчитайте температуру, при которой равновероятны оба направления реакции.
Fe2O3 (к) + 3H2 = 2Fe(к) + 3H2O(г)
Показать решение »
Решение.
ΔHр-ции = ΣH0кон – ΣH0исх кДж/моль
Используя справочные данные стандартных энтальпий веществ, находим:
ΔHр-ции = 2·ΔH0Fe+3·ΔH0H2O— ΔH0Fe2O3 — 3·ΔH0H2= 2·0 + 3·(- 241,82) – (-822,16) — 3·0 = 96,7 кДж/моль
ΔSр-ции=ΣS0кон – ΣS0исх Дж/(моль·K)
Используя справочные данные стандартных энтропий веществ, находим:
ΔSр-ции = 2·ΔS0Fe + 3·ΔS0H2O — ΔS0Fe2O3 — 3·ΔS0H2= 2·27,15 + 3·188,7 – 89,96 — 3·131 = 137,44 Дж/(моль·K)
ΔG = ΔH – TΔS= 96,7 – 298 ·137,44 /1000 = 55,75 кДж/моль
При Т=298°К, ΔG > 0 – реакция не идет самопроизвольно, т.е. реакция будет протекать в обратном направлении.
Чтобы рассчитать температуру, при которой равновероятны оба направления реакции, надо ΔG приравнять к нулю:
ΔG = ΔH – TΔS = 0, тогда
T= — (ΔG – ΔH) / ΔS= — (0-96,7)/0,137 = 705,83 K
При Т = 705,83 К реакция будет идти равновероятно как в прямом так и в обратном направлении.
Задача 2. Вычислите энергию Гиббса и определите возможность протекания реакции при температурах 1000 и 3000 К.
| Cr2O3 (т) + 3C (т) = 2Cr (т) + 3CO (г) | |||||
| ΔH298, кДж/моль | — 1141 | 0 | 0 | — 110,6 | |
| ΔS298, Дж/(моль×К) | 81,2 | 5,7 | 23,6 | 197,7 |
Показать решение »
Решение.
Вычисления энергии Гиббса проводим согласно выражению:
ΔGр-ции = ΔHр-ции – TΔSр-ции
Необходимо рассчитать энтальпию и энтропию химической реакции.
ΔHр-ции = ΣH0кон – ΣH0исх кДж/моль
Используя справочные данные стандартных энтальпий веществ, находим:
ΔHр-ции= 2·ΔH0Cr + 3·ΔH0CO — ΔH0Cr2O3 — 3·ΔH0C= 2·0 + 3·(- 110,6) – (-1141) — 3·0 = 809,2 кДж/моль
ΔSр-ции=ΣS0кон – ΣS0исх Дж/моль·K
Аналогично, используя справочные данные стандартных энтропий веществ, находим:
ΔSр-ции= 2·ΔS0Cr + 3·ΔS0CO — ΔS0Cr2O3 — 3·ΔS0C= 2·23,6 + 3·197,7 – 81,2 — 3·5,7 = 542 Дж/(моль·K)
Найдем энергию Гиббса при 1000 К
ΔG1000 = ΔH – TΔS= 809,2 – 1000 ·542 /1000 = 267,2 кДж/моль
ΔG1000 > 0, следовательно, реакция самопроизвольно не идет.
Найдем энергию Гиббса при 3000 К
ΔG3000= ΔH – TΔS = 809,2 – 3000 ·542 /1000 = — 816,8 кДж/моль
ΔG3000 ˂ 0, следовательно, реакция протекает самопроизвольно.
Задача 3. Определите тепловой эффект сгорания жидкого CS2(ж) до образования газообразных СО2 и SO2. Сколько молей CS2 вступят в реакцию, если выделится 700 кДж тепла?
Показать решение »
Решение.
Уравнение реакции сгорания жидкого сероуглерода следующее:
CS2(ж) + 3O2 = СО2 + 2SO2
Тепловой эффект реакции вычислим подставляя справочные данные стандартных энтальпий веществ в выражение:
ΔHр-ции = ΣH0кон – ΣH0исх кДж/моль
ΔHр-ции= 2·ΔH0SO2 + ΔH0CO2 — ΔH0CS2 — 3·ΔH0O2 = 2·(-296,9) + 3·(- 393,5) – 87 — 3·0 = -1075,1 кДж/моль
Т.е. при сгорании 1 моля сероуглерода выделяется 1075,1 кДж тепла
а при сгорании x молей сероуглерода выделяется 700 кДж тепла
Найдем х:
x = 700·1/1075,1 = 0,65 моль
Итак, если в результате реакции выделится 700 кДж тепла, то в реакцию вступят 0,65 моль CS2
Задача 4. Вычислите тепловой эффект реакции восстановления оксида железа (II) водородом, исходя из следующих термохимических уравнений:
1. FeO (к) + CO (г) = Fe (к) + CО2 (г); ΔH1 = -18,20 кДж;
2. СO (г) + 1/2O2 (г) = СO2 (г) ΔН2 = -283,0 кДж;
3. H2 (г) + ½ O2 (г) = H2O (г) ΔН3 = -241,83 кДж.
Показать решение »
Решение.
Реакция восстановления оксида железа (II) водородом имеет следующий вид:
4. FeO (к) + H2 (г) = Fe (к) + H2O (г)
Чтобы вычислить тепловой эффект реакции необходимо применить закон Гесса, т.е. реакцию 4. можно получить, если сложить реакции 1. и 2. и вычесть реакцию 1.:
ΔHр-ции = ΔH1 + ΔH3 – ΔH2 = -18,2 – 241,3 + 283 = 23 кДж
Таким образом, тепловой эффект реакции восстановления оксида железа (II) водородом равен
ΔHр-ции = 23 кДж
Задача 5. Реакция горения бензола выражается термохимическим уравнением:
С6Н6(ж) + 7½ О2(г) = 6СО2(г) + 3Н2О(г) – 3135,6 кДж.
Вычислите теплоту образования жидкого бензола. Определите теплотворную способность жидкого бензола при условии, что стандартные условия совпадают с нормальными.
Показать решение »
Решение.
Тепловой эффект реакции равен:
ΔHр-ции = ΣH0кон – ΣH0исх кДж/моль
В нашем случае ΔHр-ции = – 3135,6 кДж, найдем теплоту образования жидкого бензола:
ΔHр-ции= 6·ΔH0СO2 + 3·ΔH0H2O — ΔH0C6H6 – 7,5·ΔH0O2
-ΔH0C6H6 = ΔHр-ции — 3·(-241,84) + 6·(- 393,51) – 7,5·0 = — 3135,6 — 3·(-241,84) + 6·(- 393,51) – 7,5·0 = — 49,02 кДж/моль
ΔH0C6H6 = 49,02 кДж/моль
Теплотворная способность жидкого бензола вычисляется по формуле:
QТ = ΔHр-ции · 1000 / М
М(бензола) = 78 г/моль
QТ = – 3135,6· 1000 / 78 = — 4,02·104 кДж/кг
Теплотворная способность жидкого бензола QТ = — 4,02·104 кДж/кг
Задача 6. Реакция окисления этилового спирта выражается уравнением:
С2Н5ОН(ж) + 3,0 О2(г) = 2СО2(г) + 3Н2О(ж).
Определить теплоту образования С2Н5ОН(ж), зная ΔН х.р. = — 1366,87 кДж. Напишите термохимическое уравнение. Определите мольную теплоту парообразования С2Н5ОН(ж) → С2Н5ОН(г), если известна теплота образования С2Н5ОН(г), равная –235,31 кДж·моль-1.
Показать решение »
Решение.
Исходя из приведенных данных, запишем термохимическое уравнение:
С2Н5ОН(ж) + 3О2(г) = 2СО2(г) + 3Н2О(ж) + 1366,87 кДж
Тепловой эффект реакции равен:
ΔHр-ции = ΣH0кон – ΣH0исх кДж/моль
В нашем случае ΔHр-ции = – 1366,87 кДж.
Используя справочные данные теплот образования веществ, найдем теплоту образования С2Н5ОН(ж):
ΔHр-ции= 2·ΔH0СO2 + 3·ΔH0H2O — ΔH0C2H5OH(ж) – 3·ΔH0O2
– 1366,87 =2·(-393,51)+ 3·(-285,84) — ΔH0C2H5OH – 3·0
ΔH0C2H5OH(ж) = -277,36 кДж/моль
ΔH0C2H5OH(г) = ΔH0C2H5OH(ж) + ΔH0парообразования
ΔH0парообразования = ΔH0C2H5OH(г) — ΔH0C2H5OH(ж)
ΔH0парообразования = — 235,31 + 277,36 = 42,36 кДж/моль
Мы определили, что теплота образования С2Н5ОН(ж) равна
ΔH0C2H5OH(ж) = -277,36 кДж/моль
и мольная теплота парообразования С2Н5ОН(ж) → С2Н5ОН(г) равна
ΔH0парообразования = 42,36 кДж/моль
Задача 7. Чем можно объяснить, что при стандартных условиях, невозможна экзотермическая реакция:
СО2 (г)+Н2 (г) ↔ СО (г)+Н2О (ж)?
Рассчитайте ΔG данной реакции. При каких температурах данная реакция становится самопроизвольной?
Показать решение »
Решение.
Рассчитаем ΔG данной реакции:
ΔG = ΔH – TΔS
Для этого сначала определим ΔH и ΔS реакции:
ΔHр-ции = ΣH0кон – ΣH0исх кДж/моль
Используя справочные данные стандартных энтальпий веществ, находим:
ΔHр-ции= ΔH0H2O(ж) + ΔH0CO — ΔH0CО2 — ΔH0Н2 = -110,5 + (-285,8) – (393,5) — 0 = -2,8 кДж/моль
ΔSр-ции=ΣS0кон – ΣS0исх Дж/(моль·K)
Аналогично, используя справочные данные стандартных энтропий веществ, находим:
ΔSр-ции= ΔS0H2O(ж) + ΔS0CO — ΔS0CО2 — ΔS0Н2 = 197,5 + 70,1 — 213,7 — 130,52 = -76,6 Дж/(моль·K)
Найдем энергию Гиббса при стандартных условиях
ΔGр-ции= ΔH – TΔS= -2,8 + 298 · 76,6 /1000 = 20 кДж/моль> 0,
следовательно, реакция самопроизвольно не идет.
Найдем при каких температурах данная реакция становится самопроизвольной.
В состоянии равновесия ΔGр-ции= 0, тогда
T = ΔH/ΔS = -2,8/(-76,6·1000) = 36,6 К
Задача 8. Рассчитав на основании табличных данных ΔG и ΔS, определите тепловой эффект реакции:
2 NO (г) + Cl2 (г) ↔ 2 NOCl(г).
Показать решение »
Решение.
При постоянных температуре и давлении, изменение энергии Гиббса связано с энтальпией и энтропией выражением:
ΔG = ΔH – TΔS
На основании табличных данных рассчитаем ΔG и ΔS
ΔG0р-ции = Σ ΔG0прод — Σ ΔG0исх
ΔGр-ции = 2·ΔG0NOCl(г) — 2·ΔG0NO(г) — ΔG0Cl2(г)
ΔGр-ции = 2· 66,37 — 2· 89,69 – 0 = — 40,64 кДж/моль
ΔGр-ции < 0, значит реакция самопроизвольна.
ΔSр-ции=ΣS0кон – ΣS0исх Дж/(моль·K)
ΔSр-ции = 2·ΔS0NOCl(г) — 2·ΔS0NO(г) — ΔS0Cl2(г)
ΔSр-ции = 2· 261,6 — 2· 210,62 – 223,0 = -121,04 Дж/(моль·K)
Найдем ΔH:
ΔH = ΔG + TΔS
ΔH = — 40,64 + 298 · (-121,04/1000) = — 76,7 кДж/моль
Тепловой эффект реакции ΔH = — 76,7 кДж/моль
Задача 9. С чем будет более интенсивно взаимодействовать газообразный хлористый водород (в расчете на 1 моль): с алюминием или с оловом? Ответ дайте, рассчитав ΔG0 обеих реакций. Продуктами реакций являются твердая соль и газообразный водород.
Показать решение »
Решение.
Рассчитаем ΔG0 для реакции взаимодействия газообразного хлористого водорода (в расчете на 1 моль) с алюминием
2Al(т) + 6HCl (г) = 2AlCl3 (т) + 3H2
ΔG0р-ции = Σ ΔG0прод — Σ ΔG0исх кДж/моль
ΔG0р-ции1 = 2·ΔG0AlCl3 (т) + 3·ΔG0H2 — 2·ΔG0Al (т) — 6·ΔG0HCl(г)
ΔG0р-ции1 = 2· (-636,8) + 3·0— 2·0— 6·(-95,27) = -701,98 кДж/моль
В реакции принимает участие 2 моль Al(т), тогда ΔGр-ции1 1 моля Al(т) равно
ΔG0р-ции 1 = -701,98 / 2 = -350,99 кДж/моль
Рассчитаем ΔG0 для реакции взаимодействия газообразного хлористого водорода (в расчете на 1 моль) с оловом:
Sn(т) + 2HCl (г) = SnCl2(т) + H2
ΔG0р-ции2 =ΔG0SnCl2 (т) + ΔG0H2 — ΔG0Sn (т) — 2·ΔG0HCl(г)
ΔG0р-ции 2 = -288,4 + 0- 0- 2·(-95,27) = -97,86 кДж/моль
Обе реакции имеют ΔG0<0, поэтому они протекают самопроизвольно в прямом направлении, но более интенсивно взаимодействовать газообразный хлористый водород будет с алюминием, т.к
ΔG0р-ции 1 ˂ ΔG0р-ции 2
Задача 10. Не прибегая к вычислениям, определите, какие знаки (>0, <0, ≅0) имеют ΔG, ΔH и ΔS для протекающей в прямом направлении реакции:
4 НBr (г) + O2(г) ↔ 2 H2O(г) + 2 Br2(г)
Как повлияет повышение температуры на направленность химической реакции?
Показать решение »
Решение.
При постоянных температуре и давлении изменение энергии Гиббса связано с энтальпией и энтропией выражением:
ΔG = ΔH – TΔS
Энтропия – мера беспорядочности системы. Значение энтропии тем больше, чем больше беспорядок в системе (больше газообразных веществ). В данной реакции количество молей газов в правой части равно – 5, а в левой – 4, значит энтропия системы уменьшается ΔS˂0.
По условию задачи реакция протекает в прямом направлении, следовательно ΔG˂0.
В обычных условиях TΔS ˂˂ ΔH, поэтому в данном случае ΔH˂0 – реакция экзотермическая.
При повышении температуры может настать момент, когда значения TΔS и ΔH станут одинаковыми, тогда система придет в равновесие ΔG=0. Если температуру повысить значительно, то будет преобладать энтропийный фактор TΔS, тогда реакция самопроизвольно протекать уже не будет ΔG>0.
Помогите, пожалуйста!) Как рассчитать энтальпию и энтропию химической реакции??? Подскажите формулы!
Ученик
(72),
на голосовании
6 лет назад
Голосование за лучший ответ
♔Lyme Life♔
Ученик
(222)
6 лет назад
В любом веществе содержится некоторое количество тепла. Это тепло называют энтальпией. Энтальпия есть величина, характеризующая энергию системы. В физике и химии она показывает теплоту реакции. Она является альтернативой внутренней энергии, и эту величину чаще всего указывают при постоянном давлении, когда система имеет некоторый запас энергии.
Как рассчитать энтальпию
Инструкция
1
В физико-химических процессах происходит передача тепла от одного тела к другому. Это возможно, как правило, при постоянном давлении и температуре. В роли постоянного давления обычно выступает атмосферное. Энтальпия, как и внутренняя энергия, является функцией состояния. Внутренняя энергия представляет собой сумму кинетической и потенциальной энергий всей системы. Она является основой для уравнения энтальпии. Энтальпия представляет собой сумму внутренней энергии и давления, умноженного на объем системы, и равна: H=U+pV, где p – давление в системе, V – объем системы. Вышеуказанная формула применяется для расчета энтальпии в том случае, когда даны все три величины: давление, объем и внутренняя энергия. Однако, далеко не всегда энтальпия рассчитывается таким образом. Помимо него, существует еще несколько способов вычисления энтальпии.
2
Зная свободную энергию и энтропию, можно вычислить энтальпию. Свободная энергия, или энергия Гиббса, представляет собой часть энтальпии системы, затраченную на превращение в работу, и равна разности энтальпии и температуры, умноженной на энтропию: ΔG=ΔH-TΔS (ΔH, ΔG, ΔS – приращения величин) Энтропия в данной формуле является мерой неупорядоченности частиц системы. Она возрастает при увеличении температуры T и давления. При ΔG<0 процесс идет самопроизвольно, при ΔG>0 – не идет.
3
Кроме того, энтальпия также рассчитывается исходя из уравнения химической реакции. Если дано уравнение химической реакции вида A+B=C, то энтальпию можно определить по формуле: dH=dU+ΔnRT, где Δn=nk-nн (nk и nн – число молей продуктов реакции и исходных веществ) При изобарном процессе энтропия равна изменению теплоты в системе: dq=dH.При постоянном давлении энтальпия равна: H=∫СpdTВ случае, если энтальпийный и энтропийный факторы уравновешивают друг друга, приращение энтальпии равно произведению температуры на приращение энтропии: ΔH=TΔS
КУРСЫ ПОВЫШЕНИЯ
КВАЛИФИКАЦИИ
Л.С.ГУЗЕЙ
Фундаментальные понятия
общей химии в школьном курсе
Учебный план курса
| № газеты | Учебный материал |
|---|---|
| 17 | Лекция № 1. Стехиометрия |
| 18 | Лекция № 2. Элементы химической кинетики |
| 19 | Лекция № 3. Элементы химической термодинамики. Kонтрольная работа № 1. Стехиометрия. Закономерности протекания химических реакций(срок выполнения – до 15 ноября 2005 г.) |
| 20 | Лекция № 4. Химическое равновесие в растворах электролитов |
| 21 | Лекция № 5. Окислительно-восстановительные процессы.Kонтрольная работа № 2. Равновесия в растворах электролитов (срок выполнения – до 15 декабря 2005 г.) |
| 22 | Лекция № 6. Строение атома и химическая связь |
| 23 | Лекция № 7. Химическая связь и строение молекул |
| 24 | Лекция № 8. Строение вещества. Дисперсные системы |
| Итоговая работа. Разработка урока для основной или старшей профильной школы. Итоговые работы, сопровождаемые справками из учебного заведения, должны быть направлены в Педагогический университет не позднее 28 февраля 2006 г. |
ЛЕКЦИЯ № 3
Элементы химической термодинамики
Требования общеобразовательного стандарта, рассмотренные
в лекции:
8–9-е классы – нет1;
10–11-е классы (базовый и профильный уровни) –
химическое равновесие и способы его смещения
(базовый уровень).
Тепловые эффекты реакций. Термохимические
уравнения. Понятие об энтальпии и энтропии.
Энергия Гиббса. Закон Гесса и следствия из него.
Обратимость реакций. Химическое равновесие.
Константа равновесия. Смещение равновесия под
действием различных факторов. Принцип Ле Шателье
(профильный уровень).
Часть I. Химическая термодинамика
1. Введение
Содержание данной лекции заметно выходит за
рамки обязательного минимума, особенно в области
определения основных понятий термодинамики –
энтальпии, энтропии, энергии Гиббса, константы
равновесия, принципа Ле Шателье.
Эти понятия в стандарте просто названы, и
многие учителя, вполне вероятно, ограничатся
лишь их формальным определением без раскрытия
физического смысла. Нагляден пример обычного
применения принципа Ле Шателье. Никогда не
объясняется, почему равновесие смещается при том
или ином воздействии на систему. Почему,
например, если при повышении температуры
ускоряются все реакции, как прямые, так и
обратные, равновесие смещается?
Ниже мы укажем и на другие часто используемые
упрощения, которые прямо граничат с ошибочными
представлениями, искажающими реальное положение
вещей. Учитель должен иметь представление о
действительном смысле используемых понятий и
определений. Тогда он сможет сознательно делать
упрощения.
В школьном курсе недопустимо использовать
приблизительные определения и вводить
приблизительные понятия, якобы всем понятные
(типичный пример: «порядок и беспорядок» — что
это такое?). Именно правильное объяснение и
применение на конкретных примерах физического
смысла вводимых понятий освобождает курс от
зубрежки и механического выучивания.
2. Определения
Предмет химии – химическая реакция2.
В результате химической реакции исчезают одни и
образуются другие вещества3.
При этом обязательно выделяется или поглощается
энергия. Таким образом, химическая реакция
состоит в изменении, во-первых, строения и,
во-вторых, энергии системы4,
испытывающей химическое превращение.
Химическая термодинамика – раздел физической
химии, использующий законы термодинамики для
описания процессов в химических системах – их
направления и степени прохождения процесса.
3. Направление химического процесса.
Энтропия
Мы живем в мире, где большинство событий
необратимо. Необратимо и большинство химических
изменений в мире, так что мир изменяется
самопроизвольно в некотором направлении5. Что значит «самопроизвольно»?
Самопроизвольным называется процесс,
происходящий без затраты работы. Наоборот, в его
результате работа может быть получена.
А что такое работа? Как видите, я даю
определения всем используемым терминам. Всякое
определение необходимо знать дословно, ибо
каждое слово в нем имеет значение, иначе его бы не
было, т. к. главное достоинство определения –
краткость.
Итак, работа — это мера упорядоченной
передачи энергии от одной системы к другой. (Это
может быть работа электрического тока,
магнитного поля, электромагнитного (светового и
др.) излучения, механического движения и др.) Иная
возможность передачи энергии — теплота — мера
передачи энергии от одного тела к другому путем
неупорядоченных, хаотических столкновений
частиц веществ, образующих эти тела, — явление
теплопроводности.
А почему самопроизвольными являются не все, а
лишь некоторые процессы? Говорят, что «всякая
система стремится перейти в состояние с
наименьшей энергией». Тем самым, во-первых,
системе приписывается человеческое устремление
к лежачему положению и, во-вторых, утверждается,
что самопроизвольно происходят только
экзотермические процессы.
Однако существование обратимых химических
реакций, которые, если они экзотермичны в одном
направлении, то эндотермичны в другом,
опровергает это утверждение. Закон сохранения
энергии гласит, что энергия Мира постоянна. Если
энергия какой-либо системы понижается, то
неминуемо в другой системе она повышается.
Если принять, что в природе отсутствует
сверхъестественная управляющая сила, то для
объяснения происходящих в мире изменений
необходимо установить физическую причину. Мы
знаем эту причину — увеличение энтропии Мира.
Миром правит энтропия! Объяснить, что такое
энтропия и почему именно ее увеличение
определяет направление процессов в природе (в
том числе химических), – цель этого раздела
лекции.
На самом деле в природе самопроизвольными
являются такие процессы (и химические реакции в
том числе), которые сопровождаются рассеянием,
диссипацией6 энергии или
вещества без изменения общего количества
энергии и вещества (в физическом смысле7)
в мире.
Что такое «рассеяние» в физическом смысле? Это
распределение энергии или вещества максимально
равномерно. При этом происходит выравнивание
интенсивных параметров системы — свойств, не
зависящих от количества вещества (молей) в
системе. Примеры интенсивных параметров:
температура (теплота переходит от более теплого
тела к менее теплому, пока их температуры не
сравняются), давление (вещество переходит из
области высокого давления в область низкого,
пока давление в разных частях системы не станет
одинаковым), электрический потенциал, а в
гомогенных системах — плотность, концентрация и
т.д.
В отличие от интенсивных экстенсивные
параметры зависят от количества вещества в
системе — это масса, объем, внутренняя энергия,
электрический заряд и др.
Разницу между интенсивными и экстенсивными
параметрами покажем на следующей модели (рис. 1).
Пусть мы имеем два сосуда, из которых первый
содержит 6 г 50%-го раствора некоторого вещества А,
а второй — 30 г 20%-го. Соединим сосуды трубкой,
которая обеспечит возможность диффузии
растворенного вещества из одного сосуда в
другой. Масса вещества (экстенсивный параметр) в
первом растворе (3 г) меньше, чем во втором (6 г). Тем
не менее вещество будет диффундировать из
первого сосуда во второй, пока не выравняется
интенсивный параметр — концентрация в обоих
растворах.
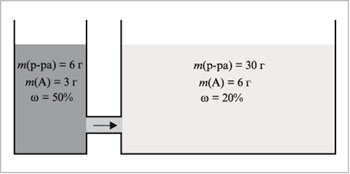 |
Рис. 1.
|
Система с интенсивными параметрами,
одинаковыми во всех ее частях, является
равновесной; в ней происходят (если вообще
происходят) только обратимые процессы, и ее
свойства не меняются во времени. Такое состояние
системы наиболее вероятно. Покажем это на
следующем примере.
Пусть мы имеем изолированную (т.е. не
обменивающуюся с внешней средой ни веществом, ни
энергией) систему, состоящую из ящика, в котором
находятся четыре одинаковые, но различимые для
нас (по номерам, цвету) молекулы, способные
свободно двигаться во всем объеме ящика, попадая
в ту или другую его половину случайным образом.
На рис. 2 показаны возможные варианты их
распределения по двум половинам сосуда (пунктир
— мысленная, но не физическая граница между
двумя половинами ящика). Этих вариантов пять.
Назовем их состояниями системы.
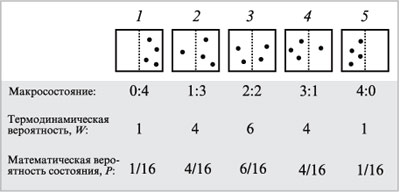 |
Рис. 2.
|
Очевидно, что состояние 1 (0:4) может
быть реализовано единственным способом,
W1 = 1 (W – число способов, которым
может быть реализовано данное состояние системы,
— так называемая термодинамическая вероятность
системы8). Для состояния 2
(1:3) возможно 4 варианта распределения молекул (в
левой половине сосуда может быть любая из
четырех молекул), W2 = 4. Для состояния 3
(2:2), как легко убедиться, W3 = 6.
Далее очевидно, W4 = W2 = 4, W5 = W1
= 1.
Всего существует W1 + W2 + W3
+W4 + W5 = 16 способов
размещения четырех молекул по двум половинам
сосуда. Какое же состояние наиболее вероятно при
случайном движении молекул? Очевидно, то, которое
возникает в большем числе случаев. Вероятности
распределения: Р(0:4) = 1/16, Р(1:3) = 4/16, Р(2:2) =
6/16, Р(3:1) = 4/16 и Р(4:0) = 1/16. Таким образом,
вероятность распределения состояния 3 (2:2) –
равномерного распределения — наибольшая.
Система самопроизвольно переходит от менее
вероятных распределений (0:4, 1:3) к более
вероятному. Вот движущая сила процесса: в
результате случайных движений происходит
направленный самопроизвольный процесс.
С увеличением числа молекул вероятность
отклонения от равномерного распределения быстро
уменьшается и становится исчезающе малой для
макроскопических систем. Если в объеме газа
0,2 мкм3 отклонение плотности от средней
на 1% происходит каждые 10–9 с, вероятность
того, что в 1 мм3 плотность будет отличаться
от средней на 1%, равна 10–60.
Для реальных веществ величина W
невообразимо велика9, так что
оперировать ею чрезвычайно неудобно. На практике
мерой вероятности существования системы в том
или другом состоянии является энтропия10
S, связанная с W уравнением Больцмана:
S = k lnW,
где k = R/NA = 1,38•10–23
Дж/К – константа Больцмана, lnW – натуральный
логарифм величины термодинамической
вероятности. С увеличением W — числа
способов, которым может быть реализовано данное
состояние вещества, – возрастает энтропия S.
Размерность энтропии определяется
размерностью константы Больцмана. Для вещества
величина энтропии обычно дается в расчете на 1
моль, тогда ее размерность Дж/(К•моль). В табл. 1
приведено несколько примеров величин W и S.
Таблица 1
Энтропия некоторых веществ в
различных
агрегатных состояниях
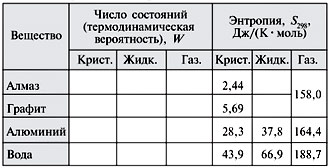
Вы видите, что наименьшая энтропия у веществ в
кристаллическом состоянии и максимальная у
газов. Жидкость в этом отношении занимает
промежуточное положение.
Чем меньшим числом способов описывается данная
система, чем меньше ее энтропия, тем, говорят,
выше в ней порядок. Действительно, строение
идеального кристалла при абсолютном нуле
градусов Кельвина совершенно однозначно, т.е. W
= 1 и в соответствии с уравнением Больцмана
S = 0. В идеально упорядоченном состоянии при
температуре абсолютного нуля энтропия вещества
равна 0.
На рис. 3 показаны двухмерные схемы строения
идеального кристалла и кристалла с одним
свободным узлом кристаллической решетки, т.е. с
одной вакансией.
Повторим, для идеального кристалла W = 1 и S =
k lnW = 0. Из рис. 3 видно, что состояние с одной
вакансией может быть реализовано не
единственным способом, как в идеальном кристалле
без дефектов, а 88 способами (сосчитайте!):
вакансия может находиться в любом из 88 узлов
решетки, W = 88 и S = k lnW =1,38•10–23•ln
88 = 1,38•10–23•4,48 = 6,18•10–23 Дж/К > 0.
Таким образом, зная структуру вещества, можно
вычислить его энтропию.
Энтропия – экстенсивный параметр системы.
Поэтому чем больше в ней вещества, тем больше ее
энтропия. Чем выше температура, тем больше число
энергетических состояний, в которых могут
находиться частицы, образующие данное вещество,
тем больше энтропия.
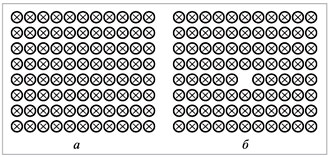 |
Рис. 3.
|
При повышении температуры от 0 К даже в
идеальном кристалле появляются молекулы (ионы,
атомы) в различных энергетических состояниях.
Следовательно, при повышении температуры, при
сообщении теплоты системе ее энтропия
возрастает. Это изменение энтропии определяется
формулой ![]() S = Q/T, где
S = Q/T, где ![]() S — изменение энтропии
S — изменение энтропии
системы, Q — количество теплоты, поглощенной
системой (тогда энтропия системы увеличивается, ![]() S > 0) или потерянной ею
S > 0) или потерянной ею
(тогда энтропия системы уменьшается, ![]() S < 0), T — абсолютная
S < 0), T — абсолютная
температура.
Например, при повышении температуры 1 л воды на
10° от 25 °С ее энтропия увеличится:
![]()
На рис. 4 показано изменение энтропии воды при
ее нагревании. Видно, что с изменением
агрегатного состояния энтропия изменяется
скачком. Обратите внимание на относительную
величину скачков при плавлении и испарении
вещества.
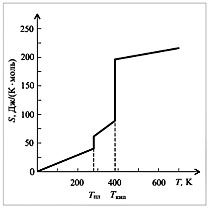 |
Рис. 4.
|
Энтропии многих веществ, во всяком
случае давно известных, вычислены или определены
экспериментально и приведены в справочниках, что
позволяет вычислять энтропии химических реакций
как разность энтропий веществ-продуктов и
веществ-реагентов. Например,
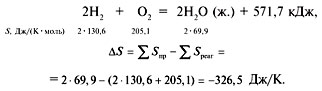
То, что изменение энтропии в этой реакции
отрицательно, т.е. энтропия уменьшается, можно
утверждать и без расчета. Действительно, в
результате реакции произошло уменьшение
количества вещества (из 3 моль образовалось 2
моль), и, кроме того, произошел переход из
газообразного в жидкое состояние, что также
ведет к уменьшению энтропии.
4. Тепловой эффект химической реакции.
Энтальпия
В результате любой химической реакции рвутся
химические связи в веществах-реагентах и
образуются новые химические связи с другой
энергией в веществах-продуктах. Поэтому любая
химическая реакция сопровождается выделением
или поглощением энергии, т. е. тепловым эффектом.
Если тепловой эффект реакции Q измерен при
постоянном давлении (а это большинство
химических процессов, которые проводятся не в
замкнутом объеме), то он называется энтальпией
реакции и обозначается ![]() H.
H.
Энтальпия (русский эквивалент этого слова –
«теплосодержание») системы возрастает в
эндотермическом процессе (когда система
поглощает теплоту), ![]() Н >
Н >
0, и убывает в экзотермическом, ![]() Н < 0 (рис. 5).
Н < 0 (рис. 5).
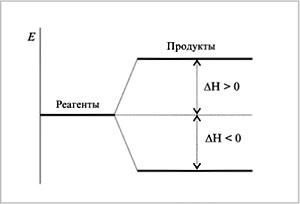 |
Рис. 5.
|
При этом выполняется закон Гесса. Если
химическая реакция проводится при постоянном
давлении или постоянном объеме, то ее тепловой
эффект не зависит от того, по какому пути (через
образование каких промежуточных соединений) она
осуществлена. Это становится очевидным при
рассмотрении рис. 2 из предыдущей лекции, на
котором показано изменение пути реакции
гидрирования этилена на разных катализаторах.
Тепловой эффект — это разница между уровнем
энергии реагентов и уровнем энергии продуктов,
которая, очевидно, зависит только от свойств
участников реакции до нее и после. А путь может
быть вообще неизвестен.
Энтальпии очень многих реакций найдены
экспериментально, часто с использованием
калориметров. Однако это осуществлено далеко не
для всех процессов. Во-первых, их слишком много,
возможно, практически бесконечное число.
Во-вторых, отнюдь не все реакции можно провести в
калориметре, например реакцию, происходящую в
зеленых растениях:
![]()
Многие реакции (можно сказать, большинство)
идут с образованием смеси веществ, так что
измеренный тепловой эффект относится не к одной
реакции, а ко всем одновременно происходившим.
Тогда откуда же известна, например, энтальпия
реакции синтеза глюкозы
(![]() rH = 2815,8 кДж),
rH = 2815,8 кДж),
уравнение которой мы только что привели?
Энтальпия реакции, как и энтропия, могла бы быть
вычислена как разность энтальпий продуктов и
реагентов. Однако это невозможно, т.к. энтальпии
веществ неизвестны. Вернее, известны, но со столь
малой точностью, что не могут быть использованы в
расчетах.
Закон Гесса позволяет обойти эти затруднения.
В расчетах энтальпий химических реакций
используются в качестве справочных данных
экспериментально определенные или рассчитанные
на основе экспериментальных данных энтальпии
образования веществ.
Энтальпией образования вещества11
![]() fH называется
fH называется
энтальпия реакции образования 1 моль этого
вещества из соответствующих простых веществ.
В табл. 2 приведено несколько примеров. Поясним
наше определение.
Таблица 2
Энтальпии образования некоторых
веществ при 298 К
| Вещество | кДж/моль |
Вещество | кДж/моль |
|---|---|---|---|
| C6Н12О6 | -1260 | H2О (ж.) | -285,8 |
| CH4 | -74,85 | H2О (кр.) | -291,8 |
| CО | -110,5 | NH3 | -46,2 |
| CО2 | -393,5 | NO | +90,25 |
| Fe2O3 | -822,2 | SO2 | -296,9 |
| FeO | -264,8 | SO3 (ж.) | -439,0 |
| H2О (г.) | -241,8 |
Рассмотрим ряд реакций (их не всегда
можно осуществить в реальности, но возможно на
бумаге), в которых может получиться карбонат
кальция. Энтальпия какой из этих реакций
является энтальпией образования карбоната
кальция?
1) Ca(OH)2 + CO2 = CaCO3![]() + H2O;
+ H2O;
2) CaO + CO2 = CaCO3;
3) 2Ca + O2 + 2CO2 = 2CaCO3;
4) Ca + 3O + С = CaCO3;
5) 2Ca + 3O2 + 2С = 2CaCO3;
6) Ca + 3/2O2 + С = CaCO3.
В реакциях 1, 2 и 3 принимают участие не только
простые вещества. В реакции 4 кислород — не
простое вещество, а находится в атомарном
состоянии. В реакции 5 образуется не 1 моль
карбоната. Таким образом, нашему определению
соответствует только реакция 6.
Следствием из закона Гесса (мы не будем это
доказывать, это математическая задача) является
то, что энтальпия любой реакции равна разности
энтальпий образования продуктов этой реакции и
реагентов. Для реакции
аА + bB = xX
сказанное будет выглядеть так:
![]()
Для реакции (обратите внимание на форму записи):
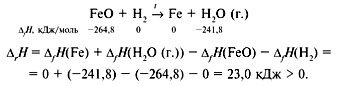
Реакция эндотермическая.
Обратите внимание на размерность чисел. Для
энтальпии образования вещества ![]() fH мы указываем величину в
fH мы указываем величину в
кДж/моль, а для энтальпии реакции ![]() rH – в кДж в соответствии с
rH – в кДж в соответствии с
уравнением реакции. Таким образом, величина
энтальпии реакции зависит от формы уравнения,
которое поэтому всегда надо приводить.
5. Энергия Гиббса
Критерий возможности самопроизвольного
процесса — ![]() S > 0. Но
S > 0. Но ![]() S чего? Системы? Нет, Мира!
S чего? Системы? Нет, Мира!
Если рассматриваемая система изолированная, то
никакие реакции внутри нее не оказывают влияния
на Мир. Поэтому в такой системе условия ![]() S > 0 достаточно для возможности
S > 0 достаточно для возможности
протекания самопроизвольного процесса.
Однако большинство реальных систем открытые,
могут обмениваться с внешней средой веществом и
энергией. В этом случае следует учесть изменение
энтропии не только системы, но и окружающей
среды. В результате химической реакции
изменилась не только система (например, водород и
кислород превратились в воду), но и окружающая
среда, в которую выделилась теплота реакции, при
этом ее (среды) энтропия тоже изменилась. Таким
образом, информации об энтропиях участвующих в
реакции веществ недостаточно для решения
вопроса о ее возможности. Должно учитываться
изменение энтропии не только системы как
разность энтропий продуктов и реагентов, но и
энтропии окружающей среды ![]() Sср,
Sср,
которая изменилась в результате рассеяния в ней
теплоты экзотермической реакции или поглощения
системой теплоты из окружающей среды в
результате эндотермической реакции ![]() Sср = Q/T. Для реакции,
Sср = Q/T. Для реакции,
проходящей при постоянном давлении (это
большинство реакций в природе), ![]() Sср =
Sср = ![]() H/T.
H/T.
Теперь критерий возможности самопроизвольного
процесса — увеличение энтропии мира ![]() Sм:
Sм:
![]() Sм =
Sм = ![]() Sсист +
Sсист + ![]() Sср > 0.
Sср > 0.
Можно записать (с учетом того, что ![]() Hср = –
Hср = –![]() Нсист):
Нсист):
![]() Sм =
Sм = ![]() Sсист +
Sсист + ![]() Sср =
Sср = ![]() Sсист
Sсист
+![]() Hср/Т =
Hср/Т =![]() Sсист –
Sсист – ![]() Hсист/Т.
Hсист/Т.
Самопроизвольный процесс в некоторой системе
(где изменения и энтропии, и энтальпии относятся
только к рассматриваемой системе) возможен, если:
![]() S –
S – ![]() H/Т > 0, или
H/Т > 0, или ![]() H – T
H – T![]() S < 0.
S < 0.
Значение этой функции (ее знак):
![]() G =
G = ![]() H – T
H – T![]() S
S
и определяет направление процесса.
Функция состояния системы G называется
энергией Гиббса12, или
изобарно-изотермическим потенциалом, или
свободной энергией (устар.) системы. В системе в
качестве самопроизвольного возможен только тот
процесс, в результате которого энергия Гиббса
системы уменьшается, ![]() G <
G <
0.
Это одно из основных уравнений химической
термодинамики, т.к. связывает возможность
протекания химической реакции в системе с
происходящими при этом изменениями H и S.
Анализ последнего уравнения показывает, что
знак изменения энергии Гиббса зависит от знаков
и относительных величин изменения энтальпии и
энтропии, а также от температуры.
При низких температурах член уравнения T![]() S мал, и величина
S мал, и величина ![]() G будет определяться величиной и
G будет определяться величиной и
знаком ![]() H. Это означает,
H. Это означает,
что при низких температурах преимущественно
самопроизвольно происходят экзотермические
реакции (![]() H < 0). А это,
H < 0). А это,
как правило, реакции соединения.
При высоких температурах член T![]() S велик, и величина
S велик, и величина ![]() G будет определяться величиной и
G будет определяться величиной и
знаком ![]() S. Это означает,
S. Это означает,
что при высоких температурах преимущественно
самопроизвольно происходят эндотермические
реакции (![]() H > 0). А это,
H > 0). А это,
как правило, реакции разложения. Поэтому при
достаточно больших температурах не могут
существовать сложные системы. Начиная с
некоторых температур, не существуют молекулы,
затем атомы… Так, на Солнце нет атомов, а есть
смесь атомных ядер, многозарядных ионов и
электронов.
Часть II. Химическое равновесие
1. Установление равновесия
Мы знаем три вида равновесия: механическое,
термодинамическое и химическое.
Механическое равновесие изучает
физика.
Термодинамическое равновесие наступает
тогда, когда интенсивные параметры системы
(температура, концентрация, давление и др.)
становятся равными во всех частях системы. При
этом ее энтропия максимальна, а энергия Гиббса
минимальна. В изолированной системе равновесное
состояние наступает всегда, если проходит
достаточно времени. Заметим, что могут
требоваться миллионы и миллиарды лет для
достижения некоторых равновесий.
При химическом равновесии скорости всех
реакций (прямых и обратных) равны между собой.
Концентрации веществ и, следовательно, все
свойства системы не меняются во времени.
Рис. 6 показывает схему возможного изменения
энергии Гиббса в некоей системе при изменении
(например, увеличении) какого-либо из ее
параметров х (например, концентрации одного
из веществ).
|
|
Рис. 6.
|
В точках 1 изменение энергии Гиббса
отрицательно (![]() G < 0), и
G < 0), и
процесс происходит самопроизвольно слева
направо (переводит в систему с бoльшим
рассматриваемым параметром и меньшей энергией
Гиббса). В точках 2 при возрастании x
энергия Гиббса увеличивается (![]() G > 0), т. е. самопроизвольно процесс
G > 0), т. е. самопроизвольно процесс
идти не может, требуется совершить над системой
работу.
В точках 3–5 свободная энергия не меняется (![]() G = 0). Эти состояния системы
G = 0). Эти состояния системы
называют равновесными. Отличием точек 3 от 4
и 5 является то, что любое изменение параметра
х сопровождается в них уменьшением G: при
любом воздействии на систему начинается
самопроизвольный процесс изменения параметра,
сопровождающийся уменьшением энергии Гиббса.
Следовательно, в точках максимумов система не
может существовать конечное время. Такое
состояние называется неустойчивым равновесием13.
В точках минимумов 4 и 5 изменения х
приводят к увеличению G, и система
самопроизвольно возвращается в исходное
положение. Отличие точки 5 в том, что в ней
система имеет наименьшую свободную энергию из
всех рассматриваемых состояний, здесь она
находится в стабильном равновесии. В
остальных точках минимумов, которые не являются
абсолютными, система находится в метастабильных
состояниях. В таких состояниях система может
находиться сколь угодно долго, т. к. для ее
перехода в стабильное состояние должен быть
преодолен некоторый энергетический барьер –
энергия активации, равная высоте ближайшего
максимума. Если бы не существовало энергии
активации, то все реакции давным-давно
закончились бы.
Таким образом, необходимое условие равновесия
— нахождение системы в состоянии с минимальным
значением энергии Гиббса.
Еще одно условие – наличие самого процесса
(обратимого!) перехода системы из одного
состояния в другое. Если отсутствует химическая
реакция, то нет химического равновесия.
В соответствии с законом действующих масс при
равновесии отношение произведения концентраций
продуктов реакции к произведению концентраций
реагентов (в степенях, равных стехиометрическим
коэффициентам) есть величина постоянная,
называемая константой равновесия.
Для реакции
aA + bB +… ![]()
xX + yY + …
выражение
с(Х)х•с(Y)y…/с(A)a•с(B)b…
= K
называется константой химического равновесия
и может быть вычислена по термодинамическим
характеристикам участников реакции.
Если K > 1, то говорят, что равновесие
реакции смещено вправо. При K < 1 говорят о
смещенности равновесия влево.
Термодинамический расчет указывает
возможность самопроизвольного перехода системы
в равновесное состояние (если расчетное ![]() G < 0, реакция может пойти только
G < 0, реакция может пойти только
слева направо; если
![]() G > 0, реакция может
G > 0, реакция может
пойти только справа налево; обратите внимание,
что знак ![]() G зависит от
G зависит от
того, какие компоненты равновесной смеси мы
считаем реагентами и какие продуктами).
Однако термодинамический расчет не сообщает
никаких сведений о скорости перехода в
равновесное состояние. Эту информацию дает
химическая кинетика (см. лекцию № 2).
Кинетика, кроме того, объясняет, как наступает
состояние равновесия.
Подойдем к рассмотренному выше примеру
взаимодействия водорода с йодом с кинетических
позиций:
H2 + I2 = 2HI.
Это бимолекулярная реакция, поэтому ее
скорость выражается уравнением
![]()
C течением времени по мере расходования
водорода и йода, т.е. уменьшении их концентраций,
скорость процесса уменьшается. Одновременно
появляется возможность обратного процесса –
распада йодоводорода:
2HI = H2 + I2,
скорость которого в течение времени
увеличивается и выражается уравнением
![]() .
.
Неминуемо наступает момент, когда ![]() и концентрации
и концентрации
веществ в системе перестанут меняться. Такое
состояние системы и называется равновесным.
Константы равновесия как характеристики
реакционных систем широко используются в
химической практике, т.к. указывают, насколько
полно может осуществиться превращение веществ в
данных условиях. Принимают, что если константа
равновесия превышает значение ~1014, то
равновесие практически полностью смещено
вправо, реакция необратима; если она меньше, чем 10–14
(величина константы диссоциации воды), то реакция
практически не идет.
2. Смещение химического равновесия
Воздействием внешних факторов можно сместить
химическое равновесие. При этом под смещением
равновесия понимают изменение концентраций
веществ в реакционной смеси. Если при некотором
воздействии в системе увеличиваются
концентрации продуктов, то говорят, что
равновесие смещается вправо, если увеличиваются
концентрации реагентов, то равновесие смещается
влево.
С термодинамических позиций смещение
химического равновесия (на самом деле вообще
любого равновесия, в том числе механического,
биологического и др.) определяется принципом Ле
Шателье: если на систему, находящуюся в
равновесии, оказывается внешнее воздействие,
смещающее это равновесие, то равновесие
смещается в сторону, указанную данным
воздействием, до тех пор, пока нарастающее в
системе противодействие не станет равно
оказанному действию.
Так, при увеличении концентрации одного из
реагентов (исходных веществ) увеличивается
содержание в системе продуктов; при увеличении
концентрации одного из продуктов увеличивается
количество исходных веществ; при повышении
давления происходит процесс, сопровождающийся
уменьшением объема; при повышении температуры
происходит процесс, сопровождающийся
поглощением теплоты (возрастанием внутренней
энергии системы). Возникающее в системе
«противодействие» обусловлено изменением
концентраций реагентов или продуктов: при
накоплении тех или других соответственно
ускоряется тот или иной процесс.
Подчеркнем два момента. Во-первых,
сформулированный принцип относится только к
равновесным (стабильным и метастабильным)
состояниям системы (в случае химического
равновесия, напомним, необходимо протекание
реакции), когда оказываемое воздействие меньше
активационного барьера. Во-вторых, не любое
воздействие смещает равновесие, эффект зависит
от специфических свойств системы.
С кинетической точки зрения воздействие на
систему по-разному сказывается на скоростях
прямой и обратной реакций, которые поэтому и
изменяются по-разному.
В качестве примера рассмотрим реакцию:
2SO2 + O2 ![]() 2SO3 + 197 кДж.
2SO3 + 197 кДж.
Ее константа равновесия
![]()
При добавлении в реакционную смесь, например,
кислорода, т.е. при возрастании концентрации
этого реагента, знаменатель в выражении для К
увеличивается, но поскольку К – константа, то
должен увеличиться и числитель. Таким образом, в
реакционной смеси возрастает количество
продукта реакции. Мы говорим о смещении
химического равновесия вправо, в сторону
продукта.
Это происходит потому, что при увеличении
концентрации реагента увеличивается скорость
прямой реакции. При этом одновременно в системе
возрастает концентрация продукта и начинает
увеличиваться скорость обратной реакции. Новое
состояние равновесия установится, когда эти
скорости опять сравняются. Но при этом в
равновесной смеси количество продукта
увеличится в сравнении с первоначальным.
По той же причине смещается равновесие реакции
при изменении давления. Снова обратимся к
реакции окисления сернистого газа. Повысим
давление, скажем, в два раза. При этом объем
газовой смеси уменьшится в два раза. Это значит,
что концентрации всех газообразных веществ
возрастут в два раза. В этом случае числитель
выражения для К увеличится в четыре раза, а
знаменатель в восемь раз, т.е. отношение
нарушится. Для его восстановления должны
возрасти концентрация оксида серы(VI) и
уменьшиться концентрации оксида серы(IV) и
кислорода. Равновесие сместится вправо.
Давление практически не влияет на следующую
реакцию (равновесие между осадком и раствором
электролита):
BaSO4 (кр.) ![]()
Ba2+ (р-р) + SO42– (р-р).
Изменение давления практически не сказывается
на объеме твердых и жидких веществ, т.е. не
изменяет их концентрацию. Следовательно,
равновесие реакций, в которых газы не участвуют,
практически не зависит от давления.
Однако если давление достаточно велико, то оно
смещает равновесие и в конденсированной фазе.
Так, степень диссоциации уксусной кислоты с
повышением давления от атмосферного до 300 МПа
возрастает в три раза. Степень диссоциации
гидроксида аммония возрастает при 1200 МПа в 500 раз.
Это объясняется существованием отрицательного
объемного эффекта сольватации ионов, в
сольватной оболочке которых происходит
уплотнение упаковки молекул воды.
Еще примеры. Равновесие реакции
С + СО2 ![]()
2СО
при повышении давления смещается влево
(концентрация С не меняется, а количество газа
увеличивается при образовании продукта).
Равновесие реакции
FeO + H2 ![]() Fe + H2O
Fe + H2O
(г.)
от давления не зависит, т.к. количества (в молях)
газообразных веществ (Н2 и H2O)
одинаковы слева и справа.
В выражение для константы равновесия не входят
концентрации веществ, которые не изменяются в
течение реакции. Поэтому, например, для последней
написанной реакции K = c(H2O)/c(H2).
В выражение для константы равновесия не входит
также концентрация вещества-растворителя, т.к.
она в течение реакции практически не изменяется.
Поэтому для реакции гидролиза
S2– + H2O ![]() HS– + OH–
HS– + OH–
K = c(HS–) • c(OH–)/c(S2–).
Следующий фактор, влияющий на химическое
равновесие, — температура. При повышении
температуры скорости всех реакций (как экзо-, так
и эндотермических) увеличиваются, но по-разному.
Чем больше энергия активации реакции, тем
сильнее ее скорость зависит от температуры (см.
лекцию № 2). Обратимся к рис. 1 и 2 предыдущей
лекции. Энергия активации прямой
(экзотермической) реакции в обоих случаях меньше,
чем обратной (эндотермической) реакции. Поэтому
при одинаковом повышении температуры прямая
реакция ускорится меньше, чем обратная, и
равновесие сместится влево.
На течение химической реакции влияют
вещества-катализаторы. Если считать, что на рис. 2
лекции № 2 изображены пути одной и той же реакции
без катализатора (а) и в его присутствии (б),
то видно, что катализатор понижает энергии
активации как прямой, так и обратной реакций на
одну и ту же величину, и поэтому равновесия не
смещает.
Вопросы и задания
1. Почему концентрация вещества в гомогенной
системе является интенсивным параметром? В
результате какого процесса происходит
выравнивание концентраций?
Ответ. Концентрация вещества в гомогенной
системе является интенсивным параметром, т.к. при
наличии различных концентраций вещества, они
самопроизвольно выравниваются в результате
диффузии растворенного вещества из области
более высокой концентрации в область более
низкой.
2. Сосчитайте энтропию двухмерного
кристалла, показанного на рис. 7.
 |
Рис. 7.
|
Ответ. В этом кристалле 9•11 – 1 = 98
атомов. Вакансия может быть в любом из 99 узлов
решетки, следовательно, W = 99. Энтропия S = k
lnW = 1,38•10–23·ln 99 = 1,38•10–23·4,60
= 6,35·10–23 Дж/К.
3. Увеличивается или уменьшается энтропия
системы, если в ней происходит испарение воды?
Ответ. Если система открытая, то водяной пар
покидает ее и энтропия оставшейся воды
уменьшается, т.к. уменьшается ее количество. Если
система закрытая и количество вещества в ней не
меняется, то ее энтропия увеличивается, т.к.
жидкая вода превращается в пар.
4. Чему равна энтальпия образования Н2?
Какого-либо другого простого вещества?
Ответ. По определению энтальпия
образования вещества есть энтальпия реакции его
образования из простых веществ, т.е. в данном
случае это энтальпия «реакции» Н2 = Н2.
Очевидно, что энтальпия такой реакции ![]() rH = 0. Отсюда следует, что в
rH = 0. Отсюда следует, что в
соответствии с принятым определением энтальпии
образования простых веществ равны нулю.
5. Больше или меньше нуля изменение энергии
Гиббса указанных ниже реакций при комнатной
температуре? Ответ дайте, не проводя расчета, но
мотивируйте.
Zn + HCl ![]() … , Cu + HCl
… , Cu + HCl ![]() … .
… .
Ответ. Реакция Zn + HCl ![]() ,
,
как мы знаем, протекает самопроизвольно.
Следовательно, ее
![]() G < 0. А реакция Cu + HCl
G < 0. А реакция Cu + HCl ![]() , как нам тоже известно, не
, как нам тоже известно, не
идет, следовательно, для нее ![]() G > 0.
G > 0.
6. Экзо- или эндотермический процесс –
растворение кислорода в воде? Ответьте, не
используя справочных данных, но мотивируйте.
Ответ. Мы знаем, что при повышении
температуры растворимость газов в воде
понижается. Следовательно, процесс их
растворения экзотермичен. Принцип Ле Шателье
может дать информацию, о которой мы порой и не
догадываемся.
7. Плотность алмаза составляет 3,5, а графита
2,3 г/см3. Какая из этих аллотропных
модификаций более стабильна при высоких
давлениях?
Ответ. При превращении алмаза в графит
объем увеличивается, следовательно, обратному
процессу соответствует повышение давления.
Алмаз стабильнее при высоких давлениях.
8. Напишите выражения для констант
равновесия следующих трех реакций:
1) 2СО + О2 ![]() 2СО2;
2СО2;
2) СаСО3 ![]() СаО + СО2;
СаО + СО2;
3) FeO + H2 ![]() Fe + H2O
Fe + H2O
(г.) – Q.
Ответ. 1) 2СО + О2 ![]() 2СО2,
2СО2,
К = [CO2]2/([CO]2•[O2]).
До сих пор для обозначения молярной
концентрации вещества мы использовали символ c,
который обычно используется в кинетических
уравнениях. В выражениях для констант равновесия
чаще используются квадратные скобки для
обозначения равновесной молярной концентрации.
В случае газов вместо концентраций чаще
используются пропорциональные им парциальные
давления газов. Тогда
Кp = p(CO2)2/(p(CO)2•p(O2)).
2) СаСО3 ![]() СаО + СО2,
СаО + СО2,
K = [CO2], или Кр = р(СО2).
Напоминаем, в выражении для константы
равновесия присутствуют формулы только тех
веществ, концентрация которых меняется во время
реакции. Концентрации твердых веществ, очевидно,
константы.
3) FeO + H2 ![]() Fe + H2O
Fe + H2O
(г.) – Q,
K = [H2O]/[H2], или Кp
= p(H2O)/(p(H2).
Концентрация жидкой воды не вошла бы в
выражение для константы.
9. Укажите, влияет ли повышение и понижение
температуры или давления на состояние
равновесия в примерах из задания 8, а если да, то
как. Ответ мотивируйте.
Ответ. Повышение давления сместит
равновесие первой реакции вправо, второй –
влево, а на третью реакцию не повлияет.
Повышение температуры сместит равновесие
первой реакции (как нам известно,
экзотермической) влево, второй (как нам известно,
эндотермической) и третьей (эндотермической, как
указано в уравнении) вправо.
10. Влево или вправо сместится при повышении
температуры равновесие реакции, энергетическая
диаграмма которой приведена на рис. 2 из лекции №
2? Как при этом изменятся скорости прямой и
обратной реакций?
Ответ. На рисунке показана экзотермическая
реакция. Следовательно, при повышении
температуры равновесие сместится влево.
Скорости как прямой, так и обратной реакций
возрастут, но сильнее возрастет скорость
обратной реакции, т. к. у нее энергия активации
больше. Да и принцип Ле Шателье действует.
1 И это удивительно. С тепловыми
эффектами химических реакций ученик
сталкивается с самых первых проводимых в классе
реакций.
2 По поводу этого определения
химии, несомненно, найдутся несогласные,
считающие, что предметом химии является также и
вещество. Но химические свойства вещества
проявляются только в химической реакции и не
существуют сами по себе. Активен ли химически
натрий? Большинство, не задумываясь, скажет: «Да!»
А по отношению к железу?
3 Кстати, эта фраза может служить
определением химической реакции в отличие от
физического превращения вещества.
4 Что такое «система» – см.
лекцию № 1.
5 При наличии обратимой реакции в
системе устанавливается равновесие и система
перестает изменяться (см. часть 2 лекции).
6 Диссипация (лат. dissipatio) —
рассеяние вещества (например, самопроизвольное
заполнение газом всего объема сосуда, в котором
он находится); термин применяется и к рассеянию
энергии, состоящему в переходе части энергии
упорядоченных процессов в энергию
неупорядоченных процессов, в конечном итоге — в
теплоту.
7 В естественно-научном смысле
вещество — вид материи, имеющий ненулевую массу
покоя, в отличие от поля, носители которого
движутся со скоростью света и имеют нулевую
массу покоя. В этом смысле веществом оказывается
и молекула, и химическое вещество, и нейтрон, и
мезон, и электрон и т. д. Химическое вещество —
это та часть материи, которая образует
окружающие нас тела. В химическом смысле вода,
железо — вещества, а молекула, электрон — нет.
8 Напомним, математическая
вероятность Р — отношение числа
благоприятных событий к общему числу возможных
событий. Ее величина заключена в пределах 0 <
P < 1. Диапазон значений
термодинамической вероятности 1 < W < ![]() .
.
9 Сравните эту величину со
следующими числами. Наша Вселенная содержит
всего около 10200 частиц (в том числе атомов,
электронов, нейтрино и др.). Число атомов, из
которых состоит Вселенная, — 1075, Солнце — 1055,
Земля — 1047.
10 Энтропия (от греч. entropia –
поворот, превращение) служит мерой вероятности
пребывания системы в том или ином состоянии.
11 Для указания, к какому
процессу относится данное изменение
термодинамической функции, после знака D
используются индексы: r (первая буква англ.
слова reaction) — для изменения функции в
результате реакции, f (formation) — для реакции
образования вещества, m (melting) — для
процесса плавления, b (boiling) — для процесса
кипения и др.
12 Дж.Гиббс (1839–1903) –
американский физик и физикохимик, один из
основоположников химической термодинамики.
13 В таком состоянии находится
карандаш, поставленный на заточенный грифель.