Как найти энтропию формулы - Сайт, где вы сможете решить свои вопросы

Екатерина Владимировна Мосина

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Понятие энтропии ввел Р. Клаузиус в 1865 г.

Энтропия – функция состояния

Для того чтобы выяснить в чем состоит физический смысл энтропии, рассмотрим изотермический процесс и приведенное количество теплоты в этом процессе на очень малом участке этого процесса -$frac{delta Q}{T}$, где $delta Q$ – количество теплоты, которое получает тело, $T$ – температура тела.

Приведенное количество теплоты, которое сообщается телу в любом обратимом круговом процессе:

$oint {frac{delta Q}{T}=0left( 1 right).}$

Равенство нулю левой части выражения (1), который берут по замкнутому контуру, означает, что отношение δQ/T – это полный дифференциал некоторой функции состояния системы, которая не зависит от формы пути перехода системы из начального состояния в конечное.

Введем следующее обозначение:

$frac{delta Q}{T}=dSleft( 2 right)$.

Определение 1

Энтропией ($S$) называют функцию состояния, дифференциал которой равен приведенному количеству тепла на малом участке термодинамического процесса, которое передано системе в этом процессе.

Для обратимых процессов изменение энтропии равно нулю:

$Delta S=0left( 3 right)$.

Если выполняется необратимый процесс, то энтропия системы увеличивается:

$Delta S$>$0, left( 4 right)$.

Все реальные процессы являются необратимыми, поэтому в реальности энтропия изолированной системы способна только расти. Она становится максимальной в состоянии термодинамического равновесия.

Замечание 1

Формулы (3) и (4) выполняются только в том случае, если система замкнута. В том случае, если термодинамическая система может обмениваться теплом с внешней средой, то поведение энтропии может быть любым.

«Энтропия простыми словами с формулами» 👇

Неравенство Клаузиуса

Выражения (3) и (4) объединяются в неравенство, которое называется неравенством Клаузиуса:

$Delta Sge left( 5 right)$.

Неравенство Клаузиуса означает, что для замкнутой системы энтропия способна увеличиваться (если процесс необратим), или не изменяется (процесс обратим).

Неравенство Клаузиуса является математической записью второго начала термодинамики.

Знак изменения энтропии указывает направление течения процесса в обратимом процессе.

Во всех ординарных термодинамических системах при стремлении температуры к бесконечности, внутренняя энергия системы безгранично растет. Абсолютная температура при равновесных процессах может только большей нуля, следовательно, если система подвергается нагреву, то:

$dS$>$0.$

При уменьшении температуры системы имеем:

$dS$

Изменение энтропии в равновесном процессе

Допустим, что термодинамическая система совершает равновесный переход из состояния 1 в состояние 2, тогда изменение энтропии найдем как:

$Delta S=S_{2}-S_{1}=intlimits_1^2 {frac{delta Q}{T}=intlimits_1^2{frac{dU+delta A}{T}left( 6 right),} }$

где $dU$ – изменение внутренней энергии в рассматриваемом процессе; $delta A$ – работа, выполняемая в этом процессе.

Выражение (6) способно определить энтропию с точностью до аддитивной константы. Это означает то, что физическим смыслом обладает не энтропия, а ее разность.

$S=intlimits_{обр} {frac{delta Q}{T}+const, left( 7 right).}$

Свойства энтропии

Замечание 2

Энтропия – аддитивная величина. Это означает, что энтропию системы можно найти как сумму энтропий тел, которые эту систему образуют.

Свойство аддитивности имеют:

масса;
внутренняя энергия;
количество теплоты.

Аддитивными не являются:

объем,
температура,
давление.

Определение 2

Термодинамический процесс, в котором энтропия остается постоянной, называется изоэнтропийным процессом.

Так, при обратимом адиабатном процессе мы имеем:

$delta Q=0to S=const.$

Энтропия однородной термодинамической системы – это функция пары независимых параметров, характеризующих ее состояние, например, $ p,V$ или $ T,V$ при $ m=const$.

В этой связи можно записать, что:

$left( V,T right)=intlimits_0^T {C_{V}frac{dT}{T}+S_{01, }left( 8right).}$

или

$Sleft( p,T right)=intlimits_0^T {C_{p}frac{dT}{T}+S_{02, }left( 9right),}$

где $intlimits_0^T {C_{V}frac{dT}{T},}$ – находят для обратимого изобарного процесса; $intlimits_0^T {C_{p}frac{dT}{T}}$ – вычисляют для обратимого изохорного процесса, при изменении температуры от 0К до $T$; $C_V$ – теплоемкость изохорного процесса; $C_p$ – теплоемкость при изобарном процессе; $S_{01 }=S(V,0)$ ; $S_{02 }=S(p,0).$

Статистический смысл энтропии

Допустим, что энтропия в обратимом процессе претерпевает изменения под воздействием внешних условий, которые оказывают влияние на систему. Механизм действия этих условий на энтропию можно сформулировать так:

Внешние условия определяют микросостояния, которые доступны системе, а также их количество.
В рамках доступных для системы микросостояний, она приходит в состояние равновесия.
Энтропия получает соответствующее значение. Получается, что величина энтропии идет за изменением внешних условий, принимая наибольшую величину, совместимую с внешними условиями.

Глубокий смысл энтропии раскрывается в статистической физике. Энтропия связана с термодинамической вероятностью состояния системы.

Определение 3

Термодинамическая вероятность ($W$) – количество способов, реализации данного состояния термодинамической системы. Или иначе, это число микросостояний, реализующих данное макросостояние.

Термодинамическая вероятность всегда больше или равна единице.

Энтропия системы и термодинамическая вероятность связаны между собой формулой Больцмана:

$S=k ln⁡(W) (10),$

где $k$ – постоянная Больцмана.

Формула (10) означает, что энтропия определена натуральным логарифмом количества микросостояний, которые реализуют рассматриваемое макросостояние.
Согласно формуле Больцмана, энтропия – это мера вероятности состояния термодинамической системы.
Говорят, что энтропия – мера беспорядка системы. Это статистическая интерпретация энтропии. Большее количество микросостояний, которое осуществляет макросостояние, соответствует большей энтропии.
Если система находится в состоянии термодинамического равновесия, что соответствует наиболее вероятному состоянию системы, количество микросостояний наибольшее, энтропия в этом случае максимальна.
Поскольку при необратимых процессах энтропия увеличивается, при статистическом толковании это значит, процессы в замкнутой системе проходят в направлении роста количества микросостояний. Это означает, что процессы идут от менее вероятных к более вероятным, до достижения вероятностью максимальной величины.

Замечание 3

Все статистические законы справедливы для систем, которые составлены из огромного количества частиц. Но эти законы могут нарушаться с небольшим числом частиц. Для систем с малым количеством частиц возможны флуктуации, это значит, что энтропия и термодинамическая вероятность состояний замкнутой системы на некотором временном отрезке могут убывать, а не расти или не изменяться.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Время на прочтение
9 мин

Количество просмотров 11K

Давно хотел сделать учебные материалы по теме Теория Информации + Machine Learning. Нашёл старые черновики и решил довести их до ума здесь, на хабре.

Теория Информации и Machine Learning мне видятся как интересная пара областей, глубокая связь которых часто неизвестна ML инженерам, и синергия которых раскрыта ещё не в полной мере.

Когда я говорю коллегам, что LogLoss на тесте и Mutual Information между прогнозом и прогнозируемой величиной связаны напрямую, и по несложной формуле можно из одного получить второе, они часто искренне удивляются. В википедии со страницы LogLoss есть ссылка на Mutual Information, но не более того.

Теория Информация может стать (а, точнее, стала) источником понимания как и почему работают разные методы ML, в частности нейронные сети, а также может дать идеи улучшения градиентных методов оптимизации.

Начнём с базовых понятий Энтропии, Информации в сообщении, Взаимной Информации (Mutual Information), пропускной способности канала. Далее будут материалы про схожесть задач максимизации Mutual Information и минимизации Loss-а в регрессионных задачах. Затем будет часть про Information Geometry: метрику Фишера, геодезические, градиентные методы, и их связь с гауссовскими процессами (движение по градиенту методом SGD — это движение по геодезической с шумом).

Также нужно затронуть AIC, Information Bottleneck, поговорить про то, как устроен поток информации в нейронных сетях – Mutual Information между слоями (Information Theory of Deep Learning, Naftali Tishby) и многое другое. Не факт, что получится всё перечисленное охватить, но попробую начать.

1. Базовые определения

Есть три более менее разных способа прийти к формуле энтропии распределения

$H({p_1, ldots, p_M }) = sum_{i=1}^M p_i log(1 / p_i) ;;;;;(1)$ $sum_{i=1}^M p_i =1, ;; p_i > 0.;;;;;;$

Давайте их опишем. Начнём с базовых определений.

Опр. 1.1: Неопределенность — это логарифм по основанию 2 от числа равновероятных вариантов: $H = log_2{N}$ . Измеряется в битах. Например, неопределенность неизвестного битового слова длины k равна k.

Логарифм

Логарифм числа по основанию 2 – это то, сколько раз нужно делить число на 2, чтобы получить число меньше либо равно 1. Например,

Для не степеней двойки эта функция гладко продолжается. Например,

Важное свойство логарифма:

Поробуйте вывести его из нестрогого определения выше для случая, когда и степени двойки.

Битовые слова

Битовые слова длины – это последовательности нулей и единиц длины . Каждый знак в битовом слове называется битом. Например, вот битовые слова длины 5:

00000, 00001, 00010, 00011, 00100, 00101, … , 11100, 11101, 111110, 11111

Их 32 штуки. , то есть неопределённость слова длины 5 равна 5.
Именно столько неизвестных бит в неизвестном битовом слове длины 5.

Таким образом, каждый знак в битовом слове называется битом, но ещё бит – это единица измерения неопределённости. И из этого примера понятно почему.

Для краткости везде далее обозначается просто как .

Опр. 1.2: Информация в сообщении — это разница неопределенностей до получения сообщения и после

Тоже измеряется в битах.

Например, Ваня загадал число от 1 до 100. Нам сообщили, что оно меньше либо равно 50. Неопределённость до сообщения равна , а после — . То есть в этом сообщении 1 бит информации. Умело задавая бинарные вопросы (вопросы, на которые ответ ДА или НЕТ), можно извлекать ровно 1 бит информации.

Некоторые вопросы неэффективны, например, вопрос “верно ли, что число меньше либо равно 25?” уменьшит неопределенность на бита с вероятностью 0.25, а с вероятностью 0.75 только на бит, то есть в среднем на бит. Если вы своим вопросом разбиваете множество вариантов в пропорции , то среднее количество бит информации в ответе равно .

Это выражение будем обозначать через или . Здесь мы как программисты перегрузим функцию H так, чтобы она работала для двух случаев — когда на вход поступает пара чисел, сумма которых равна 1, и когда одно число из отрезка [0, 1].

Опр. 1.3:

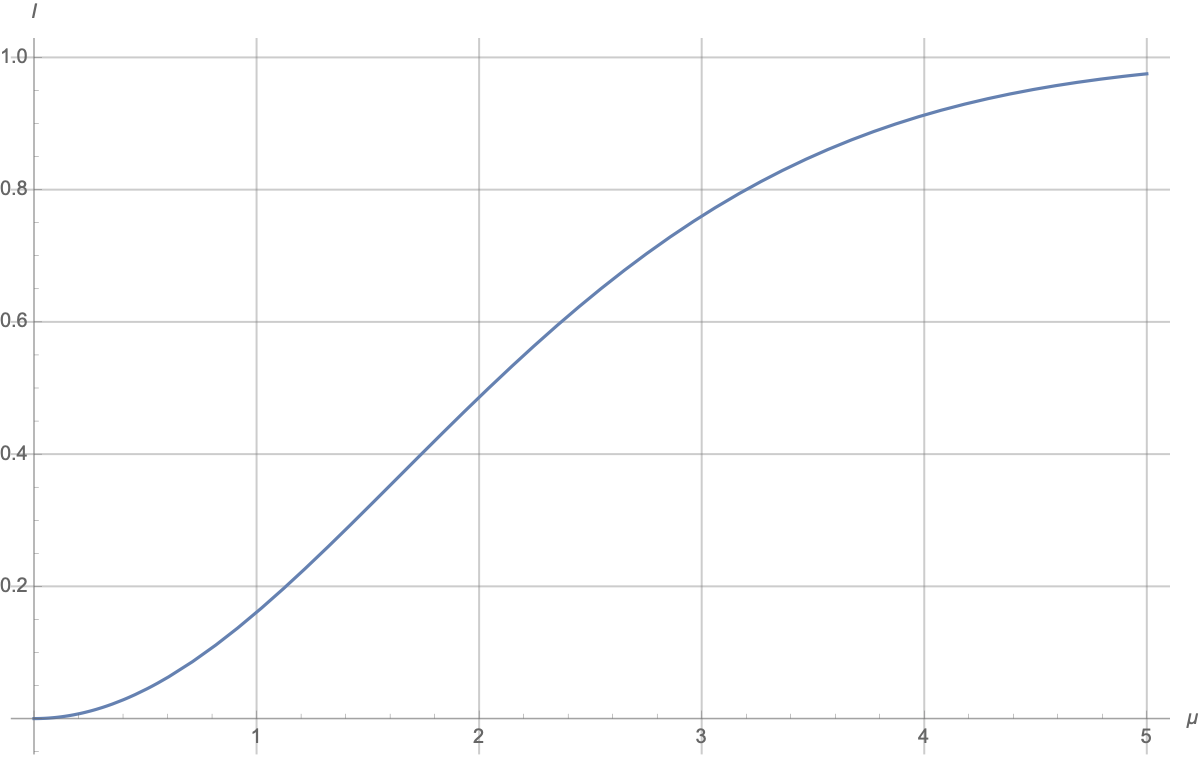
График H(x)

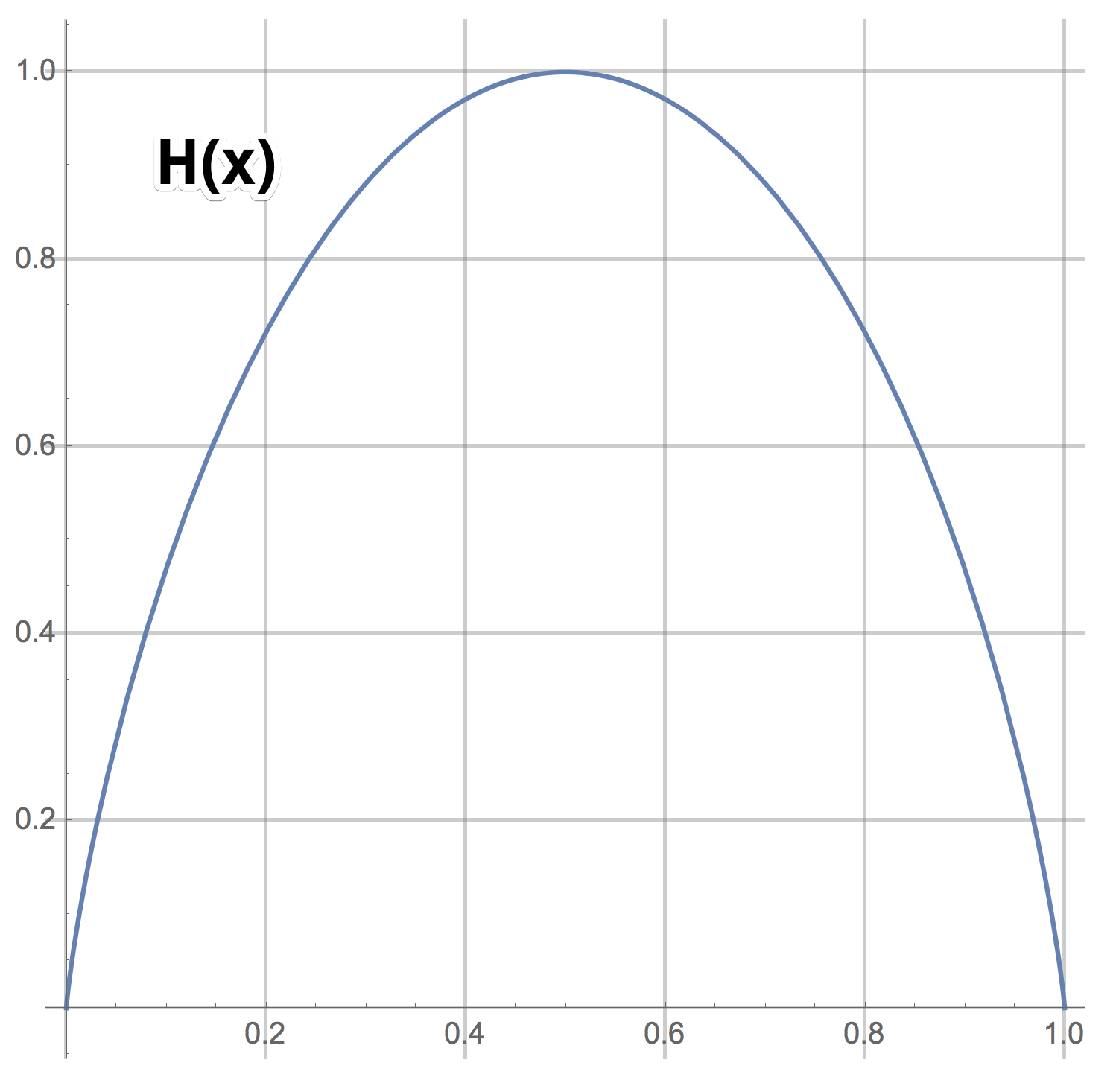
Видно, что задавая бинарные вопросы, в можно извлекать максимум 1 бит информации в среднем (максимальное значение функции . Ещё раз: да, можно сразу задавать вопросы типа “Число равно 57?” и если повезёт, получать log(100) бит информации. Но если не повезёт, вы получите лишь log(100/99) бит информации. Среднее число бит информации для такого сорта вопросов равно что заметно меньше 1.

В этом примере 100 вариантов, а значит начальная неопределенность равна — это то, сколько всего в среднем бинарных вопросов нужно задать Ване, чтобы выведать ответ. Правда число получается нецелое и нужно округлять вверх.

Если мы будем задавать не бинарные вопросы, а вопросы, которые подразумевают в качестве ответа натуральное число от 1 до M, то мы сможем в одном ответе получать более, чем один бит информации. Если мы задаём такой вопрос, для которого все M ответов равновероятны, то в среднем мы будем получать бит. Если же вероятность ответа i равна p(i), то среднее число бит в ответе будет равно:

$H({p_1, ldots, p_M}) = sum_{i=1}^M p_i log(1 / p_i).;;;;;;;;(1)$

Опр. 1.4: Энтропия дискретного распределения $P={p_i}_{i=1}^M$ задаётся формулой (1) выше.

Здесь мы перегрузили функцию H для случая, когда на вход поступает дискретное распределение.

ИТАК: Первый простой способ прийти к формуле энтропии — это посчитать среднее число бит информации в ответе на вопрос с разновероятными ответами.

Давайте пойдём дальше. Пусть Ваня не загадывает число, а сэмплирует его из распределения $P={p_i}_{i=1}^M$ . Сколько бинарных вопросов нужно задать Ване, чтобы узнать выпавшее число? Интуитивно понятно, что нужно разбить множество вариантов на два подмножества уже равных не по количеству элементов, а по суммарному значению вероятности, и спросить Ваню, в каком из двух находится выпавшее число. Получить ответ и продолжить в том же духе с новым уменьшенным множеством вариантов — снова разбить его на два с примерно равным весом, спросить в каком из двух находится выпавшее число и так далее. Идея хорошая, но не совсем рабочая. Оказывается, правильнее поступать с конца и начать строить дерево разбиений снизу, а именно, найти два самых мало вероятных варианта и объединить их в один новый вариант, тем самым уменьшив число вариантов на 1. Потом снова найти два самых маловероятных и снова объединить их в один новый, и так далее, построив конечном итоге бинарное дерево. В листьях этого дерева находятся числа. Внутренние вершины помечены множеством чисел из поддерева, корнем которого они являются. Корень дерева помечен множеством всех чисел. Это дерево и даёт алгоритм того, как нужно задавать вопросы Ване. Нужно двигаться с корня дерева и спрашивать Ваню, куда по этому дереву идти — влево или вправо (в каком из двух множеств вершин детей находится выпавшее число). Это дерево даёт не только рецепт самого быстрого в среднем метода угадывания числа, но ещё и алгоритм Хаффмана сжатия данных.

Задача 1.1: Изучите код Хаффмана. Докажите, что текст с исходной длиной символов N имеет в сжатом виде длину, ограниченную снизу величиной бит и при удачных обстоятельствах её достигает.

ИТАК: Формула возникает при решении задачи о минимальном среднем числе бинарных вопросов, которые нужно задать, чтобы выведать выпавшее значение случайной величины с распределением

Это второй способ прийти к формуле (1).

Есть ещё один, третий, простой способ прийти к формуле энтропии, но нужно знать формулу Стирлинга.

Задача 1.2: Есть неизвестное битовое слово длины k (последовательность единиц и ноликов, всего k символов). Нам сообщили, что в нём 35% единичек. Чему равно при больших k?

Ответ

Примерно , где

Задача 1.3: У Вани есть неизвестное слово длины в алфавите длины M. Он сообщил доли всех букв в слове — $P = {p_1, ..., p_M}$ .
Чему равно при больших ?

Ответ

$approx log M - sum_{i=1}^M{p_i log(1 / p_i)} = log M - H(P)$

ИТАК: Задача 1.3 и есть третий способ прийти к формуле (1).

Опр. 1.5: Информация в сообщении по некоторую случайную величину — это разница энтропий: $I(message) = H(P_{apriori}) - H(P_{aposteriori})$

Значения случайной дискретной величины можно рассматривать как буквы, каждая следующая буква слова — это просто очередное измерение случайной величины. Вот и получается, что информация в сообщении про некоторую случайную величину — это количество бит информации про измерения этой случайной величины нормированное на число измерений.

Задача 1.4: Чему равна энтропия дискретного распределения $P = {lambda ^ i cdot (1 - lambda)}_{i = 0}^{infty}$ ?Сколько информации содержится в сообщении где имеет распределение ?

Ответ:

Этот результат требует принятия. Как же так? – Нам сообщили ненулевую на первый взгляд информацию, отсекли самый вероятный вариант из возможных. Но неопределённость на множестве оставшихся вариантах осталась прежней, поэтому формула даёт ответ 0.

Задача 1.5: Приведите пример конечного распределения и сообщения, которое не уменьшает, а увеличивает неопределённость.

Ответ:

, а сообщение message = “это не первый элемент”. Тогда $P_{after} = {0, 0.5, 0.5}, H(P) = 0.9219, H(P_{after}) = 1.0$

Древняя мудрость “во многих знаниях многие печали” в этом контексте получает ещё одну интересную интерпретацию: современный мир, наука и человеческая жизнь таковы, что новые “сообщения” о истории и об устройстве мира только увеличивают неопределённость.

Дискретные распределения на счётном множестве значений, которые затухают по экспоненциальному закону (геометрические прогрессии), обладают свойством неизменности неопределённости при получении информации, что среди первых элементов нет правильного ответа. Менее, чем экспоненциальные затухания (например, $p_k={C / k^2}$ ), только растят неопределённость при откидывании первых элементов.

Задача 1.6: Напишите формулу для энтропии распределения Пуассона

$p_k=e^{-lambda}{lambda^k over k!}$ , .

Найдите простое приближение для больших .

Ответ

$H({p_k}_{k=0}^{infty})={1over 2} log (2pi e lambda) - {1over 12 lambda}-{1over 24 lambda^2}+O(1/lambda^3)$

Задача 1.7: Дано распределение вещественной случайной величины. Пусть — это сколько бинарных вопросов в среднем нужно задать, чтобы узнать какое-то выпавшее значение случайной величины с точностью до . Найдите приближённое выражение для малых значений .

Ответ:

Нужно разбить ось x на корзинки длиной посчитать вероятности каждой корзинки и посчитать $H({p_i}_i)$ Если значениедостаточно мало, то ответ можно приблизить интегралом:

$sum_i rho(x_i) cdot varepsilon cdot log (1 / (rho(x_i) cdot varepsilon) ) approx log(1/varepsilon) - int_{-infty}^{+infty} rho(x)log(rho(x))dx =$

(см. определение энтропии непрерывного распределения ниже).

Опр. 1.6: Энтропия непрерывного распределения равна

Здесь мы ещё раз перегрузили значение символа H для случая, когда аргумент есть функция плотности вероятности (PDF).

Задача 1.8: Даны два распределения и двух вещественных случайных величин. К чему стремится разница при ?

Ответ:

Задача 1.9: Чему равна энтропия нормального распределения ?

Ответ:

Задача 1.10: Напишите формулу для энтропии экспоненциального распределения $rho(x)=e^{-x/a}/a$ .

Задача 1.11: Случайная величина является смесью двух случайных величин, то есть её распределение есть взвешенная сумма распределений:

Пусть множество значений, которые принимает , не пересекается с множеством значений , другими словами, пусть носители этих двух случайных величин не пересекаются. Найдите выражение для энтропии через энтропии и .

Ответ

$H(rho) = -int_{X_1+X_2} rho(x) log(rho(x)) dx \=-int_{X_1+X_2} (w_1rho_1(x)+ w_2rho_2(x))log(w_1rho_1(x) + w_2rho_2(x)) dx =\ =-int_{X_1} w_1rho_1(x) log(w_1rho_1(x)) dx-int_{X_2} w_2rho_2(x) log(w_2rho_2(x)) dx$

Последнее равенство тут возможно только благодаря тому, что носители и двух распределений по условию задачи не пересекаются. Дальше мы это выражение преобразуем в

$-w_1int_{X_1} rho_1(x) log(w_1rho_1(x))- w_2int_{X_2} rho_2(x) log(w_2rho_2(x))dx=\=w_1cdot H_1 + w_2cdot H_2 -w_1log w_1 - w_2log w_2$

В этой задаче хотелось показать, что даже в простом случае непересекающихся носителей энтропии не просто складываются с соответствующими весами, а появляется добавка . Если веса равны 1/2, то эта добавка равна 1.

Интерпретация формулы такая: результат измерения с вероятностью находится в и с вероятностью – в и соответственно нам достанется неопределённость значений на множестве или неопределённость на множестве . Но чтобы выяснить, в каком из них находится измерение мы потратим в среднемвопросов.

Из этого в частности следует, что смесь с коэффициентами 1/2 двух нормальных величин с одинаковой дисперсией, но сильно разными средними, имеет энтропию на 1 больше, чем энтропия одного нормального распределения. Носители нормальных случайных величин равны всей прямой, а значит пересекаются, но в случае сильно разных средних можно этим пренебречь.

Задача 1.12: Случайная величина равновероятно равна 0 или 1. Случайная величина зависит от : если , то сэмплируется из , а если , то сэмплируется из . Сколько бит информацию про случайную величину содержится в сообщении (как функция от )?

Ответ

Есть такой численный ответ:

Понятно, что график начинается с 0 и стремится к 1:

при два гаусса одинаковые и сообщение про то, какой из них был выбран ничего не даёт;
при имеем смесь (mixture) двух гауссовских распределений с сильно разнесёнными центрами; сообщение про значение говорит, в каком из двух “гауссовских колпаков” находится ответ, и число вариантов уменьшается примерно в два раза, а неопределённость уменьшается на 1; “примерность” связана с тем, что “колпаки” перекрываются, но размер перекрытия быстро уменьшается с ростом .
в окрестности рост квадратичный, примерно .
а приближение к 1 происходит примерно по закону $1-e^{-(mu/2.74)^2 - 0.21}$

Задача 1.13: Случайная величина устроена так: сначала сэмплируется число из экспоненциального распределения со средним , а потом сэмплируется случайное число из распределения Пуассона, с параметром . Мы получили сообщение, что одно измерение дало . Сколько бит информации мы получили про случайную величину ? Дайте численный ответ. Сколько бит информации даст последовательность измерений 10, 9, 11, 8, 10?

Ответ

Задача 1.14: Случайная величина устроена так: сначала один раз сэмплируется число из бета-распределения с параметрами , а потом сэмплируется случайное число из биномиального распределения с параметрами . Мы получили сообщение, что одно измерение дало 10 (то есть 10 из 100 бросаний монетки выпали орлом). Сколько бит информации мы получили про скрытую случайную величину ? Дайте численный ответ. Сколько бит информации даст последовательность измерений 10, 9, 11, 8, 10?

Задача 1.15: Случайные величины $p_1,; p_2,;ldots,p_{10}$ сэмплированы из бета-распределения с параметрами . Сами $p_1,; p_2,;ldots,p_{10}$ нам неизвестны, но нам дали 10 измерений $x_1,;x_2,;ldots,x_{10}$ из 10 биномиальных распределений с параметрами и это наше знание про $p_1,; p_2,;ldots,p_{10}$ . Сколько бит информации мы получим в среднем про случайную биномиальную величину с параметрами и когда нам назовут значение ? А если $p_1,; p_2,;ldots,p_{10}$ известны абсолютно точно (случай )? А если 10 заменить на ?

Эту задачу можно сформулировать на языке ML так: у нас есть категориальная фичадля прогноза булевой величины (‘кликнет пользователь на баннер или нет’). Насколько хорош будет наш прогноз, если в обучающих данных нам известны лишь исторические данные про количество кликов и некликов по этим 10 категориям?

Задача 1.16. Случайная величина имеет распределение $mathcal{N}(a,varepsilon^2)$ . Величина нам неизвестна, но мы знаем, что она была сэмплирована из распределения $mathcal{N}(0,sigma^2)$ . Сколько информации про мы в среднем получим от первого измерения величины ? Как будет расти количество полученной информации с числом измерений?

Ответ

Продолжение:

Часть 2 – Mutual Information. В ней рассказывается про Взаимную Информацию – концепцию, которая открывает двери в помехоустойчивое кодирование, алгоритмы сжатия, а также даёт новый взгляд на задачи Машинного Обучения.
Часть 3 – ML & Mutual Information. Основы ML в контексте теории информации.

Источник

Энтропия

Размерность	${displaystyle L^{2}MT^{-2}theta ^{-1}}$
Единицы измерения
СИ	Дж/К
СГС	эрг/К

Термодинамические величины

Статья является частью серии «Термодинамика»
Энтропия Количество теплоты Термодинамическая работа Химический потенциал См. также: Термодинамические потенциалы.
Разделы термодинамики
Начала термодинамики Уравнение состояния Термодинамические величины Термодинамические потенциалы Термодинамические циклы Фазовые переходы
См. также «Физический портал»

Термодинамическая энтропия , часто именуемая просто энтропией, — физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин; энтропия и температура — сопряжённые термодинамические величины, необходимые для описания термических свойств системы и тепловых процессов в ней. Энтропия является функцией состояния и широко используется в термодинамике, в том числе технической (анализ работы тепловых машин и холодильных установок) и химической (расчёт равновесий химических реакций).

Утверждение о существовании энтропии и перечисление её свойств составляют содержание второго и третьего начал термодинамики. Значимость данной величины для физики обусловлена тем, что наряду с температурой её используют для описания термических явлений и термических свойств макроскопических объектов. Качественные представления о термическом состоянии системы связаны с тепловыми ощущениями, выражаемыми понятиями «теплее», «холоднее», «нагрев», «охлаждение», «степень нагретости». К термическим относят свойства, характеризующие поведение вещества при его нагреве или охлаждении: термические коэффициенты, теплоёмкость и другие калорические коэффициенты, постоянную Кюри, показатели термостойкости, пределы огнестойкости и т. д.; примерами термических явлений служат термическое расширение, пироэлектричество, электрокалорический эффект, теплопроводность, изменение агрегатного состояния — кристаллизация и замерзание, плавление и таяние, испарение, кипение, сублимация (возгонка), конденсация и другие процессы.

Историческая справка[править | править код]

Понятие энтропии, её обозначение и название были введены Р. Клаузиусом (1865). Абстрактность этого понятия — одного из краеугольных камней термодинамики — и разнообразие подходов к обоснованию существования энтропии как термодинамической величины привели к появлению аксиоматики термодинамики.

Термодинамическая дефиниция энтропии[править | править код]

В термодинамике энтропию вводят, обосновывая её существование, перечисляя её свойства и строя для неё шкалу измерения на основании первого, второго и третьего начал термодинамики.

В термодинамических формализмах Клаузиуса^[1] и Каратеодори^[2] энтропию вводят одновременно с абсолютной термодинамической температурой. Математический аппарат термодинамики Гиббса^[3] основан на использовании энтропии в качестве независимой термодинамической переменной, тогда как температура — естественный кандидат на эту роль, вводится как функция внутренней энергии и энтропии. Наконец, в рациональной термодинамике энтропию выражают через внутреннюю энергию и температуру, которые рассматривают как основные неопределяемые переменные теории.

Энтропия простой системы[править | править код]

Первое начало (закон) термодинамики устанавливает связь между внутренней энергией, работой и теплотой: одна из этих физических величин задаётся с помощью двух других, которые, будучи исходными объектами теории, в рамках самой этой теории определены быть не могут просто потому, что не существует понятий более общих, под которые их можно было бы подвести^[4]. Термодинамика заимствует понятия энергии и работы из других разделов физики^[5]^[6], тогда как определение количеству теплоты, наоборот, даётся только и именно в термодинамике. Согласно Клаузиусу теплоту определяют через внутреннюю энергию и работу ^[7]^[8]. При использовании термодинамического правила знаков^[9] математическое выражение для первого начала термодинамики в формулировке Клаузиуса имеет вид^[10]:

(Дефиниция теплоты по Клаузиусу)

Первое начало в этой формулировке вводит теплоту как физическую характеристику процесса, поведение которой определяется законом сохранения энергии, но не определяет её как математический объект. Детализировать дефиницию теплоты проще всего для равновесного процесса, когда работу, а следовательно и теплоту, можно выразить через переменные состояния. Для бесконечно малого^[11] равновесного процесса в простой системе^[12] возможен единственный вид работы — работа расширения/сжатия $W_{v}$ :

$delta W_{v}=-PdV,$

(Работа расширения/сжатия для равновесного процесса в простой системе)

где — давление, — объём; символ delta означает, что соответствующая величина относится к бесконечно малому процессу. Таким образом, для первого начала термодинамики в формулировке Клаузиуса получаем^[13]^[14]:

(Первое начало для равновесного процесса в простой системе)

где delta Q — элементарная (бесконечно малая) теплота процесса.

Это выражение, определяющее элементарную теплоту как математический объект, есть линейная дифференциальная форма (форма Пфаффа) для двух независимых переменных. Для данной пфаффовой формы условие интегрируемости Эйлера не выполняется, то есть delta Q есть функционал^[15], а не полный дифференциал несуществующей функции Q(U,V) ^[14]. Из теории дифференциальных форм известно, однако, что если выполняется условие Фробениуса^[16], то пфаффова форма имеет интегрирующий множитель/делитель, превращающий эту форму в полный дифференциал и представляющий собой функцию тех же независимых переменных, которые входят в форму Пфаффа^[17]. Пфаффовы формы, имеющие интегрирующий множитель/делитель называют голономными; пфаффова форма двух переменных всегда голономна (теорема Коши)^[18]^[19]. Поэтому для простых равновесных систем существует функция состояния S(U,V) , полный дифференциал которой равен

$dS~equiv ~{frac {delta Q}{T}}~=~{frac {1}{T}}dU~+~{frac {P}{T}}dV,$

(Дефиниция энтропии простой равновесной системы)

где

есть интегрирующий делитель для формы Пфаффа. Клаузиус назвал функцию состояния энтропией (от греческого ἐντροπία — изменение, превращение, преобразование). Второе начало термодинамики утверждает, что энтропия существует для любых равновесных систем, а не только простых, и что интегрирующий делитель есть абсолютная термодинамическая температура^[20]^[21]^[22]^[19]. Неравновесная термодинамика распространяет представление о локальной энтропии и локальной температуре на любые термодинамические системы.

Интегрирование уравнения для энтропии приводит к появлению в выражении для функции S(U,V) произвольной постоянной, зависящей от выбора начальной точки отсчёта энтропии. Произвол в выборе начального состояния для энтропии устраняет третий закон термодинамики.

Энтропия закрытой системы в термодинамике Клаузиуса — Каратеодори[править | править код]

Традиционный подход к построению термодинамики (аксиоматика Клаузиуса — Каратеодори) основан на использовании представления о внутренней энергии как базовом понятии теории, заимствовании формул для вычисления термодинамической работы из механики и электродинамики сплошных сред, и первом начале термодинамики в формулировке Клаузиуса.

Помимо работы расширения/сжатия система может одновременно выполнять другие виды работ, например работу по изменению площади поверхности раздела фаз, работу перемещения в поле тяготения, работу поляризации диэлектрика в электрическом поле и т. д. Объединяет все эти виды работ формальная структурная идентичность расчётных формул друг с другом и с выражением для работы расширения/сжатия^[23]^[24]^[25]:

$delta W_{i}=X_{i}dx_{i},$

где $delta W_{i}$ — элементарная работа -го типа, $x_{i}$ — обобщённая координата, сопряжённая с обобщённой силой $X_{i}.$ Каждой обобщённой координате соответствует своя обобщённая сила; физические переменные, соответствующие обобщённым координатам и силам, конкретизируют применительно к решаемой задаче^[26]^[27].

Если однородная система одновременно совершает несколько различных видов работ, то они суммируются и полная работа системы delta W равна^[23]^[28]^[29]

$delta W=sum _{i}X_{i}dx_{i},$

(Суммарная работа для равновесного процесса в однородной системе)

а для первого начала термодинамики получаем соотношение^[30]^[31]:

$delta Q=dU-sum _{i}X_{i}dx_{i},$

(Первое начало для равновесного процесса в однородной системе)

которое как и в случае простой системы представляет собой форму Пфаффа. Следствием второго начала термодинамики в любой его формулировке является вывод о том, что пфаффова форма delta Q при любом числе переменных всегда голономна^[21] и, следовательно, для любой закрытой термодинамической системы существуют энтропия

$S=S(U,{x_{i}})$

(Энтропия однородной закрытой системы)

и абсолютная термодинамическая температура

$T=T(U,{x_{i}}).$

Выражение ${x_i}$ есть сокращение для перечисления $x_{1},x_{2},...,x_{i},...$ переменных определённого типа, в данном случае — обобщённых координат.

Энтропия открытой системы[править | править код]

Принимая, что теплота и работа являются двумя единственно возможными формами передачи энергии^[32]^[33]^[34], а изменение энергии, связанное с переносом вещества в открытой системе, есть составная часть общей работы, называемая химической работой (работой перераспределения масс веществ^[35]), в случае однородной открытой системы дифференциальную форму delta Q для закрытой системы следует дополнить слагаемым, учитывающим элементарную химическую работу delta Z ^[36]^[37]^[38]^[39]^[40]:

$delta Z=sum _{j}mu _{j}dm_{j},$

(Химическая работа для равновесного процесса в открытой однородной системе)

где $m_{j}$ — масса -го компонента^[41], $mu _{j}$ — химический потенциал этого компонента.

Пфаффова форма delta Q для открытой однородной системы равна^[29]

$delta Q=dU-sum _{i}X_{i}dx_{i}-sum _{j}mu _{j}dm_{j}.$

(Первое начало для равновесного процесса в открытой однородной системе)

Дальнейшие рассуждения о существовании энтропии

$S=S(U,{x_{i}},{m_{j}})$

и абсолютной термодинамической температуры

$T=T(U,{x_{i}},{m_{j}})$

для открытой системы ничем не отличаются от соображений, высказанных при рассмотрении закрытой системы, поэтому ниже перечислены причины, по которым открытые системы потребовали отдельного рассмотрения.

Первая из этих причин состоит в том, что использование в понятийном аппарате термодинамики химической работы как части общей работы делает неэквивалентными представления об адиабатной изоляции как накладывающей запрет на обмен веществом (то есть любая адиабатно изолированная система есть система закрытая или, говоря иначе, масса есть адиабатически заторможенная величина)^[42]^[43]^[44]^[45], и адиабатной изоляции как допускающей обмен энергией только в форме работы^[46]^[47]. Восстановить эквивалентность приведённых выше формулировок об адиабатной изоляции удаётся, если модифицировать дефиницию теплоты по Клаузиусу, добавив к теплоте и работе третью форму передачи энергии — энергию переноса массы ^[48]^[49]:

(Модифицированная дефиниция теплоты для открытой системы)

где delta Z задаётся выражением для химической работы.

Вторая причина отдельного рассмотрения вопроса об энтропии открытых систем заключается в следующем. За исключением химического потенциала все входящие в пфаффову форму delta Q для открытой системы переменные в рамках термодинамического формализма представляют собой неопределяемые величины, заимствуемые из других разделов физики, что подразумевает необязательность их описания в самой термодинамике. Химический потенциал вводится в термодинамике и либо должен быть отнесён к базовым неопределяемым понятиям, для которых возможно только пояснительное описание, либо же от термодинамики требуется точная дефиниция химического потенциала. Как неопределяемую величину химический потенциал можно вводить одновременно с температурой и энтропией (более, того П. А. Жилин^[50] считает такой подход единственно правильным^[51]), но традиционно химический потенциал предпочитают вводить в рассмотрение как вторичную переменную на основе предварительно сформированного представления об энтропии открытой системы. Для этого вслед за У. Гиббсом^[52]^[45] без доказательства принимают утверждение о существовании энтропии открытой системы^[53]^[54]^[55]

$S=S(U,{x_{i}},{m_{j}})$

(Энтропия открытой однородной системы по Гиббсу; фундаментальное уравнение Гиббса в энтропийном выражении)

как функции состояния, при неизменности масс компонентов совпадающей с энтропией однородной закрытой системы. Из фундаментального уравнения Гиббса в дифференциальной форме^[55]

${displaystyle dS={frac {1}{T}}dU-{frac {1}{T}}sum _{i}X_{i}dx_{i}-{frac {1}{T}}sum _{j}mu _{j}dm_{j}}$

(Дифференциальная форма фундаментального уравнения Гиббса для энтропии)

находим значения частных производных энтропии:

$left({frac {partial S}{partial U}}right)_{{{x_{i}},{m_{j}}}}={frac {1}{T}},$

$left({frac {partial S}{partial x_{r}}}right)_{{U,{x_{{ineq r}}},{m_{j}}}}=-{frac {X_{r}}{T}},$

$left({frac {partial S}{partial V}}right)_{{x_{i}neq V,{m_{j}}}}={frac {P}{T}}.$

Химический потенциал -го компонента выразим через частную производную энтропии по массе этого компонента^[56]:

$mu _{k}equiv -Tleft({frac {partial S}{partial m_{k}}}right)_{{U,{x_{i}},{m_{{jneq k}}}}}.$

(Дефиниция химического потенциала компонента)

Энтропия в термодинамике Гиббса[править | править код]

Построение теории на основе постулирования существования энтропии как функции состояния, в состав независимых переменных которой входят массы компонентов, составляет главное содержание термодинамики Гиббса^[57], а способ, каким выполнено распространение термодинамики Клаузиуса на открытые системы, позволяет говорить об аксиоматике Гиббса^[52]^[45]. В термодинамике Гиббса вводят понятия компонента системы, фазы и многофазной гетерогенной системы, постулируют существование внутренней энергии и энтропии как аддитивных переменных состояния, постулируют связь этих величин с независимыми переменными состояния в виде фундаментальных уравнений Гиббса в энергетическом и энтропийном выражениях, постулируют аддитивность входящих в эти фундаментальные уравнения независимых переменных, постулируют, что есть термодинамическая температура, вводят химический потенциал и постулируют общее условие термодинамического равновесия в системе^[58], рассматриваемое далее в числе свойств энтропии.

Обратите внимание, что содержательную дефиницию температуры по Гиббсу^[59]^[60]^[61]

${displaystyle Tequiv left({frac {partial U}{partial S}}right)_{V,{x_{i}}}}$

(Термодинамическая температура по Гиббсу)

можно, с другой стороны, рассматривать и как описательную дефиницию энтропии. А именно, энтропия в термодинамике Гиббса есть такая экстенсивная переменная состояния, что производная внутренней энергии по энтропии представляет собой интенсивную переменную состояния, обладающую всеми положенными термодинамической температуре свойствами.

Энтропия в рациональной термодинамике[править | править код]

Рациональная термодинамика не подразделяет термодинамику на равновесную и неравновесную; обе эти дисциплины рассматриваются как единая часть физики сплошных сред^[62]^[63]^[64]^[65]. Равновесная рациональная термодинамика есть результат применения общей теории к системам в состоянии равновесия^[66]. Исходные неопределяемые понятия теории — энергия , объём и число молей компонента . По аналогии с давлением

${displaystyle P=-{frac {partial E}{partial V}}}$

при механическом равновесии имеющем одинаковое значение во всех частях системы, вводят химический потенциал

${displaystyle mu equiv {frac {partial E}{partial n}},}$

как интенсивную величину, имеющую при химическом равновесии одно и то же значение во всех частях системы^[67].
Абсолютную термодинамическую температуру вводят посредством следующей аксиомы: существует интенсивная термодинамическая величина, температура

которая характеризует степень нагретости тел и обладает следующими свойствами^[68]:

в выбранном за начало отсчёта состоянии температура равна нулю

${displaystyle T_{E=0}=0}$

;

температура монотонно растёт с увеличением энергии системы

${displaystyle {frac {partial T}{partial E}}>0}$

;

при термодинамическом равновесии имеет одно и то же значение во всех частях системы.

Энтропию в рациональной термодинамике задают как аддитивную величину, равную^[69]

${displaystyle S(E)equiv int _{0}^{E}{frac {1}{T(E)}}dE.}$

Свойства энтропии, вытекающие из этого определения^[69]:

${displaystyle S_{E=0}=S_{T=0}=0}$

;

${displaystyle {frac {partial S}{partial E}}={frac {1}{T}}>0}$

;

${displaystyle {frac {partial ^{2}S}{partial E^{2}}}=-{frac {1}{T^{2}C_{V}}}<0}$

;

где $C_{V}$ — теплоёмкость системы при постоянном объёме. Из определения энтропии и её свойств следует, что при условии постоянства энергии энтропия системы максимальна, когда все части системы имеют одинаковую температуру — вариационный принцип максимальности энтропии в состоянии равновесия^[69]. Таким образом, энтропия есть монотонная выпуклая функция энергии, достигающая максимума в состоянии термодинамического равновесия; состояние системы, принятое за начало шкалы отсчёта энергии, есть одновременно состояние для начальных точек отсчёта температуры и энтропии.

Свойства энтропии[править | править код]

Перечисление свойств энтропии дано применительно к термодинамике Гиббса; примеры, приводимые для иллюстрации перечисляемых свойств энтропии, относятся, как правило, к открытым однородным термодеформационным системам, для которых справедливо фундаментальное уравнение Гиббса в энтропийном выражении^[70]^[71]:

$S=S(U,V,{m_{j}}).$

(Фундаментальное уравнение Гиббса в энтропийном выражении для открытой термодеформационной системы)

Энтропия в фундаментальном уравнении в энтропийном выражении есть однозначная дифференцируемая функция аддитивных независимых переменных^[72]^[44]^[73] с непрерывными первыми и кусочно-непрерывными вторыми производными.
Энтропия есть величина аддитивная^[74]^[75]^[76]^[72]^[77]^[78]^[79]^[80], то есть энтропия термодинамической системы равна сумме энтропий всех её частей. Аддитивность энтропии позволяет распространить это понятие на термодинамические системы любой сложности.

Как следствие аддитивности получаем, что энтропия в фундаментальном уравнении в энтропийном выражении есть однородная функция первого порядка всех независимых переменных^[81]^[73], то есть для

${displaystyle S(lambda U,lambda V,{lambda m_{j}})=lambda S(U,V,{m_{j}}),}$

и для неё справедливо тождество (теорема) Эйлера^[82]:

${displaystyle S=Uleft({frac {partial S}{partial U}}right)_{V,{m_{j}}}~+~Vleft({frac {partial S}{partial V}}right)_{U,{m_{j}}}~+~sum _{j}m_{j}left({frac {partial S}{partial m_{j}}}right)_{U,V,{m_{jneq k}}}={frac {1}{T}}U~~+~~{frac {1}{T}}PV~~-~~{frac {1}{T}}sum _{j}mu _{j}m_{j}.}$

Для однородной системы частная производная энтропии по внутренней энергии есть величина, обратная абсолютной термодинамической температуре (термодинамическая дефиниция температуры как следствие второго начала термодинамики)^[83]^[60]^[61]^[84]:

$Tequiv left[left({frac {partial S}{partial U}}right)_{{V,{x_{i}}}}right]^{{-1}}.$

(Термодинамическая дефиниция температуры)

В соответствии с теоремой об обратных величинах^[85] это определение совпадает с дефиницией равновесной температурой по Гиббсу^[59]^[60]^[61]:

$Tequiv left({frac {partial U}{partial S}}right)_{{V,{x_{i}}}}.$

(Термодинамическая температура по Гиббсу)

Энтропия есть монотонная функция внутренней энергии , то есть абсолютная термодинамическая температура не может менять свой знак^[70]. В шкале Кельвина абсолютная термодинамическая температура всегда положительна^[86]. Использование отрицательных по шкале Кельвина температур есть удобный математический приём описания неравновесных подсистем систем с особыми свойствами^[87].
Энтропия есть величина полуограниченная. Традиционно принимают, что энтропия ограничена снизу, то есть для каждой термодинамической системы существует состояние с наименьшей энтропией^[88].
Температура есть величина полуограниченная. Абсолютная температурная шкала Кельвина построена так, что

Нуль и бесконечность допустимы в качестве пределов^[88].

Для любой термодинамической системы состояния с наименьшей энтропией и наименьшей температурой совпадают (постулат Планка)^[88]^[89]. С приближением температуры к абсолютному нулю энтропия перестаёт зависеть от температуры и приближается к определённому постоянному значению, которое можно положить равным нулю^[90] и принять за начало отсчёта энтропии, устранив тем самым упомянутый в разделе Энтропия простой системы произвол в выборе постоянной интегрирования для энтропии:

$lim limits _{{Tto ,0}}S=0.$

(Третье начало термодинамики; тепловая теорема Нернста)

Согласно постулату Тиссы внутренняя энергия ограничена и эта граница соответствует абсолютному нулю температуры^[88]^[91]. Таким образом, состояние системы при абсолютном нуле температуры, когда все термодинамические величины, характеризующие равновесное состояние, перестают зависеть от температуры^[92], наилучшим образом подходит в качестве стандартного состояния начала отсчёта основных термодинамических величин.

Энтропия изолированной системы в состоянии термодинамического равновесия имеет максимальное значение (постулат Гиббса)^[93]^[92], то есть для равновесия изолированной системы необходимо и достаточно, чтобы при всех возможных (не нарушающих постоянства внутренней энергии, обобщённых координат и масс компонентов) изменениях её состояния вариация энтропии системы не была положительной^[94]:

$(Delta S)_{{U,{x_{i}},{m_{j}}}}leqslant 0.$

(Условие равновесия изолированной системы)

Поскольку речь идёт об изолированной системе, внешнее воздействие на которую запрещено, понятие вариации в данном случае означает виртуальное изменение энтропии^[95]. Знак равенства в этом выражении относится к безразличному равновесию.

Условие равновесия Гиббса вытекает из входящего в состав второго начала термодинамики постулата Клаузиуса о неубывании энтропии адиабатно изолированной системы^[94]

Энтропия в фундаментальном уравнении в энтропийном выражении есть характеристическая функция, то есть фундаментальное уравнение содержит все термодинамические сведения о данной системе^[73].

Энтропия как характеристическая функция[править | править код]

Энтропия и теплота квазистатического (равновесного) процесса[править | править код]

Из выражения для первого начала в открытой однородной системе и дифференциальной формы фундаментального уравнения Гиббса для энтропии получаем выражение для элементарной теплоты равновесного (квазистатического) процесса^[96]^[97]:

(Теплота элементарного равновесного процесса)

(для простой равновесной системы это выражение непосредственно вытекает из дефиниции энтропии).

Данное соотношение, связывающее термодинамику Клаузиуса с термодинамикой Гиббса, представляет интерес для пользователей, которым требуется изложить материал из старой учебной и научной литературы с применением терминологии, либо вовсе не использующей понятие «теплота», либо использующей его как определяемое через энтропию и абсолютную температуру вторичное понятие.

Энтропия как характеристика изотермического процесса[править | править код]

Зависимость удельной энтропии воды от температуры

Для равновесного изотермического процесса с нулевой работой интегрирование выражения для теплоты равновесного процесса даёт следующее выражение для изменения внутренней энергии:

то есть в любом равновесном изотермическом процессе с нулевой работой энергия расходуется на увеличение энтропии системы и выделяется при уменьшении энтропии. Преобразуем это уравнение к виду

${displaystyle S_{2}-S_{1}~=~{frac {U_{2}}{T}}-{frac {U_{1}}{T}}}$

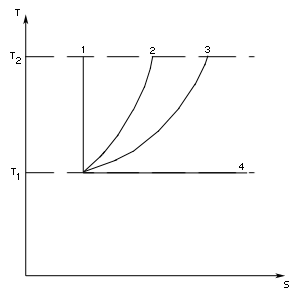
и назовём отношение ${displaystyle {frac {U}{T}}}$ приведённой внутренней энергией. Отсюда вытекает следующая трактовка — одна из нескольких существующих — физического смысла энтропии: энтропия есть приведённая внутренняя энергия изотермической системы.

Рассмотрим в качестве примера фазовые переходы в воде при атмосферном давлении (см. рисунок). При таянии льда подводимая к системе энергия расходуется на увеличение энтропии системы вследствие изменения структуры H₂O, тогда как температура системы лёд + вода остаётся близкой к 0 °C (273 К) до полного исчезновения льда. При замерзании воды имеет место обратная ситуация: энергия выделяется в окружающую среду при 0 °C. Нагрев воды, образовавшейся при таянии льда, ведёт к повышению температуры воды вплоть до её закипания при 100 °C (373 К). Кипение воды при постоянном давлении есть процесс изотермический: подводимая энергия расходуется на испарение воды и увеличение энтропии системы вода + водяной пар, тогда как температура остаётся близкой к 100 °C до полного исчезновения жидкой воды.

Статистическое определение энтропии: принцип Больцмана[править | править код]

В 1877 году Людвиг Больцман установил связь энтропии с вероятностью данного состояния. Позднее эту связь представил в виде формулы Макс Планк:

где константа 1,38⋅10⁻²³ Дж/К названа Планком постоянной Больцмана, а Omega — статистический вес состояния, является числом возможных микросостояний (способов), с помощью которых можно составить данное макроскопическое состояние. Этот постулат, названный Альбертом Эйнштейном принципом Больцмана, положил начало статистической механике, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы ( Omega ) с одним из её термодинамических свойств ().

Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых:
(I) месторасположения всех частей расположены в рамках сосуда,
(II) для получения общей энергии газа кинетические энергии атомов суммируются.

Согласно определению, энтропия является функцией состояния, то есть не зависит от способа достижения
этого состояния, а определяется параметрами этого состояния. Так как Omega может быть только натуральным числом (1, 2, 3, …), то энтропия Больцмана должна быть неотрицательной — исходя из свойств логарифма.

Понимание энтропии как меры беспорядка[править | править код]

Существует мнение, что мы можем смотреть на энтропию и как на меру беспорядка в системе. В определённом смысле это может быть оправдано, потому что мы думаем об «упорядоченных» системах как о системах, имеющих очень малую возможность конфигурирования, а о «беспорядочных» системах как об имеющих очень много возможных состояний. Собственно, это просто переформулированное определение энтропии как числа микросостояний на данное макросостояние.

Рассмотрим, например, распределение молекул идеального газа. В случае идеального газа наиболее вероятным состоянием, соответствующим максимуму энтропии, будет равномерное распределение молекул. При этом реализуется и максимальный «беспорядок», так как при этом будут максимальные возможности конфигурирования.

Получившее повсеместное распространение понимание энтропии как меры беспорядка в термодинамической системе не является, тем не менее, общепринятым^[98]: «Тождественность энтропии с беспорядком не только никем никогда не была доказана и не только не может быть доказана в принципе, но и прямо противоречит реально наблюдаемым фактам…»^[98]; «…применительно к реальным системам энтропия не является мерой беспорядка»^[99]; «…в ходе роста энтропии Вселенной общая её (Вселенной) сложность растёт, однако для составляющих Вселенную реальных (под)систем энтропия мерой беспорядка/сложности не является»^[100].

Границы применимости понимания энтропии как меры беспорядка[править | править код]

Подобное определение беспорядка термодинамической системы как количества возможностей конфигурирования системы фактически дословно соответствует определению энтропии как числа микросостояний на данное макросостояние. Проблемы начинаются в двух случаях:

когда начинают смешивать различные понимания беспорядка, и энтропия становится мерой беспорядка вообще;
когда понятие энтропии применяется для систем, не являющихся термодинамическими.

В обоих этих случаях применение понятия термодинамической энтропии совершенно неправомерно^[101].

Рассмотрим оба пункта подробнее.

Рассмотрим пример термодинамической системы — распределение молекул в поле тяготения. В этом случае наиболее вероятным распределением молекул будет распределение согласно барометрической формуле Больцмана. Другой пример — учёт электромагнитных сил взаимодействия между ионами. В этом случае наиболее вероятным состоянием, соответствующим минимуму свободной энергии, будет упорядоченное кристаллическое состояние, а совсем не «хаос», хотя в состоянии «хаоса» значение конфигурационной энтропии системы и ниже. (Термин «хаос» здесь понимается в смысле беспорядка — в наивном смысле. К хаосу в математическом смысле как сильно неустойчивой нелинейной системе это не имеет отношения, конечно.)

Рассмотрим случай с кристаллической решёткой более подробно. Кристаллическая решётка может быть и в равновесном, и в неравновесном состоянии, как и любая термодинамическая система. Скажем, возьмём следующую модель — совокупность взаимодействующих осцилляторов. Рассмотрим некоторое неравновесное состояние: все осцилляторы имеют одинаковое отклонение от положения равновесия. С течением времени эта система перейдёт в состояние ТД равновесия, в котором отклонения (в каждый момент времени) будут подчинены некоторому распределению типа Максвелла (только это распределение будет для отклонений, и оно будет зависеть от типа взаимодействия осцилляторов). В таком случае максимум энтропии будет действительно реализовывать максимум возможностей конфигурирования, то есть — беспорядок согласно вышеуказанному определению. Но данный «беспорядок» вовсе не соответствует «беспорядку» в каком-либо другом понимании, например, информационному. Такая же ситуация возникает и в примере с кристаллизацией переохлаждённой жидкости, в которой образование структур из «хаотичной» жидкости идёт параллельно с увеличением энтропии.

То есть при образовании кристалла из переохлаждённой жидкости энтропия увеличивается с одновременным ростом температуры. Если кристаллизация сопровождается отводом тепла из системы, то энтропия при этом уменьшится.

Это неверное понимание энтропии появилось во время развития теории информации, в связи с парадоксом термодинамики, связанным с мысленным экспериментом так называемый «демона Максвелла». Суть парадокса заключалась в том, что рассматривалось два сосуда с разными температурами, соединённых узкой трубкой с затворками, которыми управлял так называемый «демон». «Демон» мог измерять скорость отдельных летящих молекул, и таким образом избирательно пропускать более быстрые в сосуд с высокой температурой, а более медленные — в сосуд с низкой. Из этого мысленного эксперимента вытекало кажущееся противоречие со вторым началом термодинамики.

Парадокс может быть разрешён при помощи теории информации. Для измерения скорости молекулы «демон» должен был бы получить информацию о её скорости. Но всякое получение информации — материальный процесс, сопровождающийся возрастанием энтропии. Количественный анализ^[102] показал, что приращение энтропии при измерении превосходит по абсолютной величине уменьшение энтропии, вызванное перераспределением молекул «демоном».

Измерение энтропии[править | править код]

В реальных экспериментах очень трудно измерить энтропию системы. Техники измерения базируются на термодинамическом определении энтропии и требуют экстремально аккуратной калориметрии.

Для упрощения мы будем исследовать механическую систему, термодинамические состояния которой будут определены через её объём и давление . Для измерения энтропии определённого состояния мы должны сначала измерить теплоёмкость при постоянных объёме и давлении (обозначенную C_V и C_P соответственно), для успешного набора состояний между первоначальным состоянием и требуемым. Тепловые ёмкости связаны с энтропией и с температурой согласно формуле:

${displaystyle C_{X}=Tleft({frac {partial S}{partial T}}right)_{X},}$

где нижний индекс относится к постоянным объёму и давлению. Мы можем проинтегрировать для получения изменения энтропии:

${displaystyle Delta S=int {frac {C_{X}}{T}}dT.}$

Таким образом, мы можем получить значение энтропии любого состояния (, ) по отношению к первоначальному состоянию ( P_0 , $V_{0}$ ). Точная формула зависит от нашего выбора промежуточных состояний. Для примера, если первоначальное состояние имеет такое же давление, как и конечное состояние, то

${displaystyle S(P,V)=S(P_{0},V_{0})+int _{T(P_{0},V_{0})}^{T(P,V)}{frac {C_{P}(P,V(T,P))}{T}}dT.}$

В добавление, если путь между первым и последним состояниями лежит сквозь любой фазовый переход первого рода, скрытая теплота, ассоциированная с переходом, должна также учитываться.

Энтропия первоначального состояния должна быть определена независимо. В идеальном варианте выбирается первоначальное состояние как состояние при экстремально высокой температуре, при которой система существует в виде газа. Энтропия в этом состоянии подобна энтропии классического идеального газа плюс взнос от молекулярных вращений и колебаний, которые могут быть определены спектроскопически.

Построение графика изменения энтропии[править | править код]

Следующее уравнение может быть использовано для построения графика изменения энтропии на диаграмме для идеального газа:

${displaystyle S=n ln(P^{C_{V}}V^{C_{P}}).}$

Здесь два замечания:

«Что такое энтропия?»[править | править код]

Что сложнее: паровоз или лошадь? Когда появились первые паровозы, путеец рассказал обратившимся к нему ошеломлённым крестьянам об устройстве и действии паровой машины и закончил объяснение вопросом: «Всё понятно?» — «Всё! Кроме того, где же внутри находится лошадь?» Крестьяне с детства знают лошадь, она для них в объяснении не нуждается. С научной точки зрения лошадь несравненно более сложна, чем тепловая машина, так что наука пыталась представить лошадь как тепловую машину, а не наоборот

Однозначного ответа на этот вопрос не существует по той простой причине, что разных энтропий много — представление об энтропии используется в различных научных дисциплинах: термодинамике, статистической физике, теории информации и др. Но и внутри каждой из перечисленных дисциплин единообразия также нет и в помине: в теории информации рассматривают энтропию Шеннона, энтропию Реньи, энтропию Чисара, энтропию Хаврда — Чарват — Дароши^[103]; статистическая физика оперирует энтропиями Больцмана, Гиббса, Цаллиса; существуют различные дефиниции термодинамической энтропии. Содержательная дефиниция той или иной конкретной энтропии зависит от аксиоматики системы построения/изложения, использующей эту энтропию. По указанной причине не существует универсальной дефиниции термодинамической энтропии, ибо для различных аксиоматических систем термодинамики ответ на вынесенный в заголовок вопрос будет различен.

Студенты, приступающие к изучению термодинамики, часто жалуются на непонятность энтропии, связанную с отсутствием наглядности (рисунок иллюстрирует относительность представлений людей о наглядности, понятности и простоте термодинамических систем^{[K 1]}).

Для описания термических явлений в физике вводят новые комплементарные (взаимодополняющие) физические величины — температуру и энтропию, — содержательные дефиниции которым не дают ни в механике, ни в электродинамике. В термодинамике Клаузиуса — Каратеодори энтропию вводят как приведённую внутреннюю энергию изотермической системы, то есть разность энтропий равна приведённой теплоте изотермического процесса.

В термодинамике Гиббса и в системе А. А. Гухмана энтропия представляет собой неопределяемое базовое понятие — таков в этих системах содержательный ответ на рассматриваемый вопрос^{[K 2]}. В термодинамической аксиоматике А. А. Гухмана ^[105]^[106]^[107]^[108]^[109]^[110] и рациональной термодинамике в трактовке П. А. Жилина^[65]^{[K 3]} и температуру, и энтропию вводят как неопределяемые базовые переменные, несводимые к более простым^{[K 4]}. Пояснительное дополнение к дефиниции энтропии по Гухману разъясняет, что энтропия есть координата состояния при термическом взаимодействии (теплообмене), которое выражается в переносе энтропии от одного объекта к другому^[112].

В рациональной термодинамике в трактовке школы Трусделла в качестве базовой термической переменной используют температуру , то есть привычную и по этой причине всем понятную физическую величину. Энтропию вводят как полезную вспомогательную функцию энергии и температуры^[113]:

${displaystyle Sequiv int _{0}^{E}{frac {1}{T}}dE,}$

но, в отличие от другой функции энергии и температуры, — теплоёмкости ^[114]

${displaystyle Cequiv {frac {partial E}{partial T}},}$

в формулу, служащую дефиницией энтропии, входит не производная, а интеграл. Пояснительное дополнение к ответу, пригодное почти^{[K 5]} для любого способа изложения термодинамики, сообщает, что энтропия необходима для построения математического аппарата термодинамики и, следовательно, привлечение термодинамики к решению любой научной или практической задачи явно или неявно подразумевает использование энтропии. Польза, приносимая людям от обращения к термодинамике, есть польза от ввода энтропии в понятийный аппарат науки. Дополнительно к сказанному можно провести аналогию с теплоёмкостью: если для неизотермических процессов нагрева льда, жидкой воды и водяного пара затраты энергии равны произведению теплоёмкости на разность температур, то для изотермических процессов таяния и кипения затраты энергии равны произведению температуры на разность энтропий.

Понять энтропию и её значение для термодинамики означает, что необходимо знать происхождение этой величины, понимать её связи с другими термодинамическими переменными и уметь применять энтропию на практике^{[K 6]}^[104].

См. также[править | править код]

Аксиоматика термодинамики
Внутренняя энергия
Демон Максвелла
Негэнтропия
Стрела времени
Тепловая смерть
Температура
Термодинамика чёрных дыр
Характеристическая функция
Энтропия
Энтропия Гиббса
Энтропия Реньи
Энтропия Цаллиса
Энтропия Чисара
Энтропия Шеннона

Комментарии[править | править код]

↑ Наглядность, понятность, очевидность и простота есть суждения относительные, зависящее как от обыденности понятия, так и от уровня знаний человека. Крестьяне с детства знали лошадь, и она для них наглядна и понятна. Для теплотехников наглядна и понятна тепловая машина, а не лошадь. В. Томсон как-то на лекции спросил студентов: «Знаете ли вы, кто такой математик?» Написав на аудиторной доске: ${displaystyle int limits _{-infty }^{+infty } e^{-x^{2}}{mathrm {d} x}={sqrt {pi }}}$ , Томсон повернулся к студентам и, указывая на эту формулу, сказал: «Математик — тот, для кого это так же очевидно, как для вас то, что дважды два — четыре»^[104].
↑ Описательная характеристика энтропии как термической (тепловой) координаты состояния не отменяет того факта, что в системе Гухмана энтропия входит в число основных неопределяемых понятий теории.
↑ Вот цитата из статьи К. Трусделла, демонстрирующая совпадение его взглядов с подходом П. А. Жилина: «Я повторяю в течение уже многих лет, пренебрегая насмешками людей, наделённых физической интуицией, что температура и энтропия являются наряду с массой, положением и временем первоначальными неопределяемыми переменными. Они описываются только такими свойствами, которые можно выразить языком математики»^[111]. Эти воззрения на температуру и энтропию отличаются от тех, которые сейчас принято рассматривать как отличительную особенность «рациональной термодинамике в трактовке школы Трусделла».
↑ Чтобы дать содержательную дефиницию какому-либо понятию, нужно указать, частным случаем какого более общего понятия оно является. Если более фундаментального понятия не существует, то понятие в конце цепочки дефиниций является неопределяемым — базовым (первичным, исходным, начальным) понятием аксиоматической системы, несводимым к более простым. В любой науке имеются такие первичные понятия, те элементарные кирпичики, из которых строятся все остальные, производные понятия, и которым не даются содержательные дефиниции в самой научной дисциплине. Примерами неопределяемых базовых понятий служат: в математике — множество, в физике — пространство, время, масса, энергия и др. Невозможность дать понятию или переменной содержательной дефиниции без выхода за границы изучаемой дисциплины, во-первых, не означает запрета на использование для базового понятия/переменной описательных дефиниций, и, во-вторых, свойства базовых понятий/переменных описываются аксиомами рассматриваемой теории. Иными словами, набор базовых понятий/переменных научной дисциплины зависит от выбора системы изложения/построения этой дисциплины, а полный набор её аксиом образует систему содержательных дефиниций базовых понятий/переменных теории.
↑ Слово «почти» служит напоминанием о том, что любую систему построения/изложения термодинамики, в которой энтропия есть понятие вторичное (выводимое из понятий более общих), можно в принципе преобразовать в другую систему — «безэнтропийную термодинамику», — в которой энтропию как понятие необязательное уже не используют^[115]. В связи со сказанным упомянем, что автор третьего закона термодинамики Вальтер Нернст в своих работах не «пользовался понятием энтропии, которое он считал неясным и потому попросту не любил его»^[116] (Нернст использовал свободную энергию Гельмгольца, связанную с максимальной работой, то есть энтропию он заменял взятой со знаком «минус» производной от энергии Гельмгольца по температуре^[117]).
↑ В связи со сказанным представляют интерес воспоминания И. К. Кикоина, посещавшего в студенческие годы семинар В. А. Фока и рассказавшего историю про поиск решения сложной задачи по электростатике: «…в конце концов, получили длиннющее дифференциальное уравнение. Оно занимало всю доску. За математическими выкладками мы следили очень внимательно, так что с математикой всё было в порядке, а вот усмотреть физический смысл, скрытый за этой длинной формулой, мы не могли. Кто-то из студентов спросил Владимира Александровича: “А какой физический смысл имеет это уравнение?”. — Он на нас посмотрел с укором и сказал: “А физический смысл этого уравнения заключается в том, что оно имеет решение”»^[118].

Примечания[править | править код]

↑ Клаузиус, 1934.
↑ Каратеодори.
↑ Гиббс Дж. В., Термодинамика. Статистическая механика, 1982.
↑ Хазен, 2000, глава VI, раздел 4. Полная и замкнутая формулировка аксиоматического определения энтропии и начал термодинамики..
↑ Петров Н., Бранков Й., Современные проблемы термодинамики, 1986, с. 35.
↑ Семенченко, 1966, с. 54.
↑ Clausius, 1887, S. 33.
↑ Борн, 1964, с. 230–231.
↑ Знак или перед есть результат соглашения, какую работу считать положительной — совершаемую системой или совершаемую над системой. Встречающиеся в научной и учебной литературе варианты формулировок первого начала, отличающиеся знаками входящих в формулы величин, эквивалентны друг другу.
↑ Борн, 1964, с. 231.
↑ Элементарным (инфинитезимальным) называют процесс, для которого разница между начальным и конечным состояниями системы бесконечно мала.
↑ Простой называют закрытую термодеформационную систему, представляющую собой однородную изотропную среду (фазу) неизменного химического состава и массы, описываемую посредством переменных (давление), (объём) и (температура). Такая система обладает двумя термодинамическими степенями свободы, то есть только две переменные состояния из трёх перечисленных являются независимыми. К простым системам относятся, в частности, газы и жидкости (флюиды) в ситуации, когда поверхностными эффектами и наличием внешних силовых полей можно пренебречь. В более широкой трактовке под простой понимают любую термодеформационную систему с двумя степенями свободы, то есть такую термодинамическую систему, единственным видом работы которой является работа расширения (Сычёв В. В., Дифференциальные уравнения термодинамики, 1991, с. 9).
↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2005, с. 59.
↑ ¹ ² Радушкевич Л. В., Курс термодинамики, 1971, с. 36.
↑ Базаров И. П., Термодинамика, 2010, с. 37.
↑ Условия интегрируемости дифференциальных полиномов подробно рассмотрены в книге Белоконь Н. И., Термодинамика, 1954, с. 137—138.
↑ Кричевский И. Р., Понятия и основы термодинамики, 1970, с. 270.
↑ Сычёв, 1991, с. 22.
↑ ¹ ² Путилов К. А., Термодинамика, 1971, с. 13.
↑ Квасников, 2002, с. 43.
↑ ¹ ² Сычёв, 1991, с. 24.
↑ Радушкевич Л. В., Курс термодинамики, 1971, с. 111.
↑ ¹ ² Базаров И. П., Термодинамика, 2010, с. 27.
↑ Сычёв, 2009, с. 13.
↑ Кубо Р., Термодинамика, 1970, с. 21.
↑ Базаров И. П., Термодинамика, 2010, с. 27–29.
↑ Семенченко, 1966, с. 55.
↑ Сычёв, 2009, с. 14.
↑ ¹ ² Кубо Р., Термодинамика, 1970, с. 20.
↑ Базаров И. П., Термодинамика, 2010, с. 38.
↑ Радушкевич Л. В., Курс термодинамики, 1971, с. 38.
↑ Глазов В. М., Основы физической химии, 1981, с. 29.
↑ Путилов К. А., Термодинамика, 1971, с. 40.
↑ Сейдж Б. Х., Термодинамика многокомпонентных систем, 1969, с. 54.
↑ Тамм М. Е., Третьяков Ю. Д., Физико-химические основы неорганической химии, 2004, с. 11.
↑ Lebon, 2008, p. 14.
↑ Жариков, 2005, уравнение (2.4)..
↑ Callen, 1985, p. 36.
↑ Сычёв, 2009, с. 257.
↑ Путилов К. А., Термодинамика, 1971, с. 125.
↑ Использование масс компонентов, а не масс составляющих систему веществ в качестве обобщённых координат в выражении для химической работы означает отказ от прямого рассмотрения влияния химических реакций на массы веществ, ибо химические превращения в системе уже учтены при подсчёте числа компонентов.
↑ Квасников И. А., Молекулярная физика, 2009, с. 31.
↑ Квасников, 2002, с. 22.
↑ ¹ ² Петров Н., Бранков Й., Современные проблемы термодинамики, 1986, с. 66.
↑ ¹ ² ³ Tisza, 1966.
↑ Бэр Г. Д., Техническая термодинамика, 1977, с. 73.
↑ Залевски К., Феноменологическая и статистическая термодинамика, 1973, с. 10.
↑ Пригожин И., Кондепуди Д., Современная термодинамика, 2002, с. 52.
↑ Кубо Р., Термодинамика, 1970, с. 16.
↑ Жилин П. А., Рациональная механика сплошных сред, 2012.
↑ «…Понятия энергии, температуры, энтропии и химического потенциала вводятся одновременно и по отдельности определить их принципиально нельзя» (с. 48), «…Нельзя сначала определить внутреннюю энергию, а затем химический потенциал и энтропию. Все эти понятия могут быть введены только одновременно» (с. 140).
↑ ¹ ² Петров Н., Бранков Й., Современные проблемы термодинамики, 1986, с. 43.
↑ Воронин Г. Ф., Основы термодинамики, 1987, с. 50.
↑ Callen, 1985, p. 28—29.
↑ ¹ ² Мюнстер А., Химическая термодинамика, 1971, с. 69.
↑ Мюнстер А., Химическая термодинамика, 1971, с. 70.
↑ Мюнстер А., Химическая термодинамика, 1971, с. 67.
↑ Сам Гиббс эти постулаты в своей основной термодинамической работе «О равновесии гетерогенных веществ» формулировал по мере необходимости, как бы мимоходом, и не называл принимаемые им без доказательства утверждения ни аксиомами, ни постулатами.
↑ ¹ ² Гиббс Дж. В., Термодинамика. Статистическая механика, 1982, с. 93.
↑ ¹ ² ³ Guggenheim, 1985, p. 15.
↑ ¹ ² ³ Callen, 1985, p. 35.
↑ Трусделл К., Термодинамика для начинающих, 1970.
↑ Трусделл К., Первоначальный курс рациональной механики сплошных сред, 1975.
↑ Truesdell, 1984, 1984.
↑ ¹ ² Жилин П. А., Рациональная механика сплошных сред, 2012.
↑ Максимов, 2009.
↑ Максимов, 2009, с. 5.
↑ Максимов, 2009, с. 5—6.
↑ ¹ ² ³ Максимов, 2009, с. 7.
↑ ¹ ² Петров Н., Бранков Й., Современные проблемы термодинамики, 1986, с. 71–72.
↑ Мюнстер А., Химическая термодинамика, 1971, с. 90–91.
↑ ¹ ² Callen, 1985, p. 28.
↑ ¹ ² ³ Мюнстер А., Химическая термодинамика, 1971, с. 92.
↑ Сорокин В. С., Макроскопическая необратимость и энтропия. Введение в термодинамику, 2004, с. 55.
↑ Воронин Г. Ф., Основы термодинамики, 1987, с. 51.
↑ Петров Н., Бранков Й., Современные проблемы термодинамики, 1986, с. 67.
↑ Кубо Р., Термодинамика, 1970, с. 85—86.
↑ Buchdahl H. A., The Concepts of Classical Thermodynamics, 1966, p. 74.
↑ Зоммерфельд А., Термодинамика и статистическая физика, 1955, с. 52.
↑ В термодинамике различают аддитивность по размерам системы (длине упругого стержня или пружины, площади поверхности раздела, объёму) и аддитивность по массе. Ясно, что последнее понятие не универсально, и даже аддитивность экстенсивных переменных по объёму не гарантирует, что к этим переменным применимо представление об аддитивности по массе. Например, оно непригодно для аддитивных по объёму переменных фотонного газа — системы с нулевой массой.
↑ Петров Н., Бранков Й., Современные проблемы термодинамики, 1986, с. 62.
↑ Тер Хаар Д., Вергеланд Г., Элементарная термодинамика, 1968, с. 117.
↑ Ландау Л. Д., Лифшиц Е. М., Статистическая физика. Часть 1, 2002, с. 51.
↑ Falk, Jung, 1959, S. 156.
↑ Сычёв, 1991, с. 15.
↑ Воронин Г. Ф., Основы термодинамики, 1987, с. 53.
↑ Отрицательная температура. БСЭ, 3-е изд., 1975, т. 19.
↑ ¹ ² ³ ⁴ Петров Н., Бранков Й., Современные проблемы термодинамики, 1986, с. 68.
↑ Callen, 1985, p. 30.
↑ Базаров И. П., Термодинамика, 2010, с. 92.
↑ Tisza, 1966, p. 125.
↑ ¹ ² Новиков И. И., Термодинамика, 1984, с. 106.
↑ Базаров И. П., Термодинамика, 2010, с. 121.
↑ ¹ ² Воронин Г. Ф., Основы термодинамики, 1987, с. 102.
↑ Мысленное допустимое (не противоречащее условиям существования системы) изменение энтропии, не зависящее от времени. Встречающееся в литературе определение вариации как отклонения от равновесия, допускаемого наложенными на систему связями (условиями), означает то же самое.
↑ Базаров И. П. и др., Термодинамика и статистическая физика, 1986, с. 26.
↑ Базаров И. П., Термодинамика, 2010, с. 29.
↑ ¹ ² Хайтун С. Д., Кризис теории познания, 2014, с. 98.
↑ Хайтун С. Д., Кризис теории познания, 2014, с. 100.
↑ Хайтун С. Д., Кризис теории познания, 2014, с. 102.
↑ Lambert Frank L. A Brief Introduction to the Second Law and to Entropy for Chemistry Students
↑ Бриллюэн Л. Наука и теория информации. — М., 1960.
↑ Зарипов Р. Г., Новые меры и методы в теории информации, 2005, с. 175.
↑ ¹ ² Кричевский И. Р., Петрянов И. В. Термодинамика для многих, 1975, с. 146.
↑ Гухман, 2010, с. 11.
↑ Ляшков В. И., Теоретические основы теплотехники, 2015, с. 10.
↑ Цирлин А. М., Методы оптимизации в необратимой термодинамике и микроэкономике, 2003, с. 19.
↑ Исаев С. И., Курс химической термодинамики, 1986, с. 18.
↑ Жуковский В. С., Термодинамика, 1983, с. 11.
↑ Леонова В. Ф., Термодинамика, 1968, с. 19—20.
↑ Трусделл К., Термодинамика для начинающих, 1970, с. 117.
↑ Свиридов В. В., Свиридов А. В., Физическая химия, 2016, с. 113.
↑ Максимов, 2009, с. 7.
↑ Максимов, 2009, с. 6.
↑ Игнатович В. Н., Введение в диалектико-материалистическое естествознание, 2007, с. 411.
↑ Гельфер Я. М., История и методология термодинамики и статистической физики, 1981, с. 228.
↑ Nernst Walther, Theoretische Chemie, 1900, S. 29.
↑ Кикоин И. К. Рассказы о физике и физиках, 1986, с. 33.

Литература[править | править код]

Buchdahl H. A. The Concepts of Classical Thermodynamics. — Cambridge: Cambridge University Press, 1966. — XI + 223 p.
Callen H. B. Thermodynamics and an Introduction to Thermostatistics. — 2nd ed. — N. Y. e. a.: John Wiley, 1985. — xvi + 493 p. — ISBN 0471862568, 9780471862567.
Clausius R. Die mechanische Wärmetheorie. Band 1. — 3 Auflage. — Braunschweig: Druck und Verlag von Friedrich Vieweg und Sohn, 1887. — XVI + 403 p.
Ehrenfest-Afanassjewa T. Zur Axiomatisierung des zweiten Hauptsatzes der Thermodynamik (нем.) // Zeitschrift für Physik. — 1925. — Vol. 33, Nr. 1. — P. 933–945.
Ehrenfest-Afanassjewa T. Berichtigung zu der Arbeit: Zur Axiomatisierung des zweiten Hauptsatzes der Thermodynamik (нем.) // Zeitschrift für Physik. — 1925. — Vol. 34, Nr. 1. — P. 638.
Ehrenfest-Afanassjewa T. Die Grundlagen der Thermodynamik. — Leiden: E.J. Brill, 1956. — XII + 131 с.
Falk G., Jung H. Axiomatik der Thermodynamik (нем.) // Flügge S. (ed.). Encyclopedia of Physics / Flügge S. (Hrsg.). Handbuch der Physik. — Springer-Verlag, 1959. — Vol. III/2. Principles of Thermodynamics and Statistics / Band III/2. Prinzipien der Thermodynamik und Statistik, S. 119–175.
Guggenheim E. A. Thermodynamics: An Advanced Treatment for Chemists and Physicists. — 7th ed. — Amsterdam: North-Holland, 1985. — xxiv + 390 p. — ISBN 0 444 86951 4.
Lebon G., Jou D., Casas-Vázquez J. Understanding Non-equilibrium Thermodynamics: Foundations, Applications, Frontiers. — Berlin — Heidelberg: Springer, 2008. — xiii + 325 p. — ISBN 978-3-540-74251-7, 978-3-540-74252-4. — doi:10.1007/978-3-540-74252-4.
Nernst Walther. Theoretische Chemie vom Standpunkte der avogadro’schen Regel und der Thermodynamik. — Dritte Auflage. — Stuttgart: Verlag von Ferdinand Enke, 1900. — xiv + 710 p.
Noll W. The Foundations of Mechanics and Thermodynamics: Selected Papers. — Berlin — Heidelberg — New York: Springer-Verlag, 1974. — X + 324 p. — ISBN 978-3-642-65819-8.
Reif F. Fundamentals of statistical and thermal physics. — McGraw-Hill, 1965.
Tisza Laszlo. Generalized Thermodynamics. — Cambridge (Massachusetts) — London (England): The M.I.T. Press, 1966. — xi + 384 p.
Truesdell C. The Tragicomical History of Thermodynamics, 1822–1854. — New York — Heidelberg — Berlin: Springer-Verlag, 1980. — xii + 372 p. — (Studies in the History of Mathematics and Physical Sciences. Vol. 4). — ISBN 978-1-4613-9446-4.
Truesdell C., Bharatha S. The Concepts and Logic of Classical Thermodynamics as a Theory of Heat Engines. — New York — Heidelberg — Berlin: Springer-Verlag, 1977. — xvii + 154 p. — ISBN 3-540-07971-8.
Truesdell C. Rational Thermodynamics. — New York—Berlin—Heidelberg—Tokyo: Springer-Verlag, 1984. — xviii + 578 p. — ISBN 0-387-90874-9.
Wehrl Alfred. General properties of entropy (англ.) // Reviews of Modern Physics. — American Physical Society, 1978. — Vol. 50, no. 2. — P. 221–260. — doi:10.1103/RevModPhys.50.221.
Алексеев Г. Н. Энергия и энтропия. — М.: Знание, 1978. — 192 с. — (Жизнь замечательных идей).
Архаров А. М., Исаев С. И., Кожинов И. А. и др. Теплотехника / Под. общ. ред. В. И. Крутова. — М.: Машиностроение, 1986. — 432 с.
Ауэрбах Ф. Царица мира и её тень. — 6-е изд. — Одесса: Матезис, 1913. — VIII + 50 с.
Афанасьева-Эренфест Т. А. Необратимость, односторонность и второе начало термодинамики // Журнал прикладной физики. — 1928. — Vol. 5, № 3–4. — P. 3—30.
Базаров И. П., Геворкян Э. В., Николаев П. Н. Термодинамика и статистическая физика. Теория равновесных систем. — М.: Издательство Московского университета, 1986. — 311 с.
Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
Белоконь Н. И. Термодинамика. — М.: Госэнергоиздат, 1954. — 416 с.
Белоконь Н. И. Основные принципы термодинамики. — М.: Недра, 1968. — 112 с.
Борн М. Критические замечания по поводу традиционного изложения термодинамики // Развитие современной физики. — М.: Наука, 1964. — С. 223—256.
Бэр Г. Д. Техническая термодинамика. — М.: Мир, 1977. — 519 с.
Волькенштейн М. В. Энтропия и информация. — М.: Наука, 1986. — 192 с. — (Проблемы науки и технического прогресса).
Воронин Г. Ф. Основы термодинамики. — М.: Издательство Моск. университета, 1987. — 192 с.
Гельфер Я. М. История и методология термодинамики и статистической физики. — 2-е изд., перераб. и доп. — М.: Высшая школа, 1981. — 536 с.
Герасимов Я. И., Древинг В. П., Ерёмин Е. Н. и др. Курс физической химии / Под общ. ред. Я. И. Герасимова. — 2-е изд. — М.: Химия, 1970. — Т. I. — 592 с.
Гиббс Дж. В. Термодинамические работы / Пер. с англ. под ред. проф. В. К. Семенченко. — М. — Л.: Гостехтеориздат, 1950. — 492 с. — (Классики естествознания).
Гиббс Дж. В. Термодинамика. Статистическая механика / Отв. ред. Д. Н. Зубарев. — М.: Наука, 1982. — 584 с. — (Классики науки).
Глазов В. М. Основы физической химии. — М.: Высшая школа, 1981. — 456 с.
Гленсдорф П., Пригожин И. Термодинамическая теория структуры, устойчивости и флуктуаций. — М.: Мир, 1973. — 280 с.
Гухман А. А. Об основаниях термодинамики. — 2-е изд., испр. — М.: Издательство ЛКИ, 2010. — 384 с. — ISBN 978-5-382-01105-9.
Де Гроот С., Мазур П. Неравновесная термодинамика. — М.: Мир, 1964. — 456 с.
Жариков В. А. Основы физической геохимии. — М.: Наука; Издательство МГУ, 2005. — 656 с. — (Классический университетский учебник). — ISBN 5-211-04849-0, 5-02-035302-7.
Жилин П. А. Рациональная механика сплошных сред. — 2-е изд. — СПб.: Издательство Политехн. университета, 2012. — 584 с. — ISBN 978-5-7422-3248-3.
Жуковский В. С. Термодинамика / Под ред. А. А. Гухмана. — М.: Энергоатомиздат, 1983. — 304 с.
Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с.
Зарипов Р. Г. Новые меры и методы в теории информации. — Казань: Издательство Казан. гос. техн. университета, 2005. — 364 с.
Зоммерфельд А. Термодинамика и статистическая физика / Пер. с нем.. — М.: Издательство иностр. литературы, 1955. — 480 с.
Игнатович В. Н. Введение в диалектико-материалистическое естествознание. — Киев: Экмо, 2007. — 468 с. — ISBN 978-966-8555-78-7.
Исаев С. И. Курс химической термодинамики. — 2-е изд., перераб. и доп. — М.: Высшая школа, 1986. — 272 с.
Квасников И. А. Молекулярная физика. — М.: Эдиториал УРСС, 2009. — 232 с. — ISBN 978-5-901006-37-2.
Квасников И. А. Термодинамика и статистическая физика. Т. 1: Теория равновесных систем: Термодинамика. — 2-е изд., сущ. перераб. и доп. — М.: Едиториал УРСС, 2002. — 240 с. — ISBN 5-354-00077-7.
Каратеодори К. Об основах термодинамики (1909) // Развитие современной физики — Отв. ред. Б. Г. Кузнецов. — М.: Наука, 1964. — 331 с. — С. 223—256.
Кикоин И. К. Рассказы о физике и физиках. — Библиотечка «Квант». Выпуск 53. — М.: Наука, 1986. — 160 с.
Клаузиус Р. Механическая теория тепла // Второе начало термодинамики. — М.—Л.: Гостехиздат, 1934. — С. 70—158.
Кричевский И. Р. Понятия и основы термодинамики. — 2-е изд., пересмотр. и доп. — М.: Химия, 1970. — 440 с.
Кричевский И. Р., Петрянов И. В. Термодинамика для многих. — М.: Педагогика, 1975. — 160 с. — (Библиотечка Детской энциклопедии «Учёные — школьнику»).
Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
Ландау Л. Д., Лифшиц Е. М. Статистическая физика. Часть 1. — 5-е изд. — М.: Физматлит, 2002. — 616 с. — (Теоретическая физика в 10 томах. Том 5). — ISBN 5-9221-0054-8.
Леонова В. Ф. Термодинамика. — М.: Высшая школа, 1968. — 159 с.
Ляшков В. И. Теоретические основы теплотехники. — М.: Курс; Инфра-М, 2015. — 328 с. — ISBN 978-5-905554-85-8, 978-5-16-0І0639-7.
Максимов Л. А., Михеенков А. В., Полищук И. Я. Лекции по статистической физике. — Долгопрудный: МФТИ, 2009. — 224 с.
Морачевский А. Г., Смирнова Н. А., Пиотровская Е. М. и др. Термодинамика равновесия жидкость—пар / Под ред. А. Г. Морачевского. — Л.: Химия, 1989. — 344 с. — ISBN 5-7245-0363-8.
Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — М.: Мир, 1971. — 296 с.
Новиков И. И. Термодинамика. — М.: Машиностроение, 1984. — 592 с.
Осипов А.И., Уваров А.В. Энтропия и её роль в науке // Сетевой образовательный журнал. — 2004. — Т. 8, № 1. — С. 70—79.
Петров Н., Бранков Й. Современные проблемы термодинамики. — Пер. с болг. — М.: Мир, 1986. — 287 с.
Полянин А. Д., Полянин В. Д., Попов В. А. и др. Краткий справочник для инженеров и студентов. — М.: Международная программа образования, 1996. — 432 с. — ISBN 5-7753-0001-7.
Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур / Пер. с англ. — М.: Мир, 2002. — 462 с.
Пригожин И., Стенгерс И. Порядок из хаоса: Новый диалог человека с природой. — М.: Прогресс, 1986. — 461 с.
Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М.: Наука, 1971. — 376 с.
Радушкевич Л. В. Курс термодинамики. — М.: Просвещение, 1971. — 288 с.
Развитие современной физики. Сборник статей / Отв. ред. Кузнецов Б. Г.. — М.: Наука, 1964. — 331 с.
Свиридов В. В., Свиридов А. В. Физическая химия. — СПб.: Лань, 2016. — 597 с. — ISBN 978-5-8114-2262-3.
Свиридонов М. Н. Развитие понятия энтропии в работах Т. А. Афанасьевой-Эренфест // История и методология естественных наук. Выпуск X. Физика. — Издательство МГУ, 1971. — P. 112—129.
Сейдж Б. Х. Термодинамика многокомпонентных систем. — М.: Недра, 1969. — 304 с.
Семенченко В. К. [www.libgen.io/book/index.php?md5=FB60848D6D70A19DBF1154ECCAE49E7F Избранные главы теоретической физики]. — 2-е изд., испр. и доп. — М.: Просвещение, 1966. — 396 с. (недоступная ссылка)
Сивухин Д. В. Общий курс физики. Т. II. Термодинамика и молекулярная физика. — 5-е изд., испр. — М.: ФИЗМАТЛИТ, 2005. — 544 с. — ISBN 5-9221-0601-5.
Сорокин В. С. Макроскопическая необратимость и энтропия. Введение в термодинамику. — М.: ФИЗМАТЛИТ, 2004. — 174 с. — ISBN 5-9221-0507-8.
Сычёв В. В. Дифференциальные уравнения термодинамики. — 2-е изд., перераб. — М.: Высшая школа, 1991. — 224 с. — ISBN 5-06-002071-1.
Сычёв В. В. Дифференциальные уравнения термодинамики. — 3-е изд. — М.: Издательство МЭИ, 2010. — 256 с. — ISBN 978-5-383-00584-2.
Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп.. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
Тамм М. Е., Третьяков Ю. Д. Неорганическая химия. Том 1. Физико-химические основы неорганической химии / Под. ред. акад. Ю. Д. Третьякова. — М.: Академия, 2004. — 240 с. — (Высшее профессиональное образование). — ISBN 5-7695-1446-9.
Тер Хаар Д., Вергеланд Г. Элементарная термодинамика / Пер. с англ.. — М.: Мир, 1968. — 220 с..
Термодинамика необратимых процессов. Лекции в летней международной школе физики им. Энрико Ферми / Под ред. Д. Н. Зубарева. — М.: Издательство иностранной литературы, 1962. — 427 с.
Трайбус М. Термостатика и термодинамика. — М.: Энергия, 1971. — 503 с.
Трусделл К. Термодинамика для начинающих // Механика. Периодический сборник переводов иностранных статей. — М.: Мир, 1970. — № 3 (121), с. 116—128.
Трусделл К. Первоначальный курс рациональной механики сплошных сред / Пер. с англ. под. ред. П. А. Жилина и А. И. Лурье. — М.: Мир, 1975. — 592 с.
Фен Дж. Машины, энергия, энтропия. — М.: Мир, 1986. — 335 с.
Fermi, E., Thermodynamics, Prentice Hall (1937). — Русский перевод: Ферми, Энрико, Термодинамика, Харьков: Издательство Харьковского университета, 1969. — 140 с.
Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5. — 760 с. — ISBN 5-85270-101-7.
Хаазе Р. Термодинамика необратимых процессов. — М.: Мир, 1967. — 544 с.
Черноуцан А. И. Краткий курс физики. — М.: ФИЗМАТЛИТ, 2002. — 320 с. — ISBN 5-9921-0292-3.
Хазен А. М. Разум природы и разум человека. — М.: РИО «Мособлполиграфиздата»; НТЦ «Университетский», 2000. — 600 с. — ISBN 5-7953-0044-6.
Хайтун С. Д. [www.libgen.io/book/index.php?md5=BB7A4DF3D04E410AB163CF2D15B4501C Кризис науки как зеркальное отражение кризиса теории познания: Кризис теории познания]. — М.: Ленанд, 2014. — 448 с. — ISBN 978-5-9710-1296-2. (недоступная ссылка)
Цирлин А. М. Методы оптимизации в необратимой термодинамике и микроэкономике. — М.: Физматлит, 2003. — 416 с.
Шамбадаль П. Развитие и приложение понятия энтропии / Пер. с франц. — М.: Наука, 1967. — 279 с.

Ссылки[править | править код]

Термодинамическая энтропия
Статья «Эволюция как сопротивление энтропии»

Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист.

Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым).

Список проблемных ссылок

www.libgen.io/book/index.php?md5=BB7A4DF3D04E410AB163CF2D15B4501C
www.libgen.io/book/index.php?md5=FB60848D6D70A19DBF1154ECCAE49E7F

Источник

Энтропия. Примеры вычисления энтропии

Энтропия
– это такая функция состояния, дифференциал
которой определяется отношением:

В СИ энтропия

измеряется в Дж/К.

Приведём
формулы для подсчёта изменения энтропии
в случае изопроцессов для идеального
газа:

а) Изохорический
процесс:

,
.

б) Изобарический
процесс:

,
.

в) Изотермический
процесс:

,
.

г) Адиабатический
процесс:

,
,
.

Энтропия и второе начало термодинамики

– адиабатический процесс,

– изохорический процесс,

– изобарический процесс,

– изотермический процесс.

Понятие энтропии имеет статистическое
толкование. Состояние макроскопического
тела (т.е. тела, образованного огромным
количеством молекул) может быть задано
с помощью объёма, давления, температуры,
внутренней энергии и других макроскопических
величин. Охарактеризованное таким
способом состояние называетсямакросостоянием. Состояние
макроскопического тела, охарактеризованное
настолько подробно, что оказываются
заданными состояния всех образующих
тело молекул, называетсямикросостоянием.
Всякое макросостояние может быть
осуществлено различными способами,
каждому из которых соответствует
некоторое микросостояние тела. Число
различных микросостояний, соответствующих
данному макросостоянию, называетсястатистическим весом
илитермодинамической вероятностью
макросостояния. В статистической
физике существует теорема, которая
утверждает о равновероятности всех
микросостояний данной системы. В качестве
характеристики вероятности состояния
можно было бы выбрать статистический
вес
,
однако такая характеристика не обладала
бы свойствами аддитивности. Поэтому в
качестве характеристики состояния
принимается величинаS,
пропорциональная логарифму статистического
веса
.

,
(4)

где
– постоянная Больцмана. Такую величину
называютэнтропией.

Определённая
таким образом энтропия обладает
следующими свойствами:

Энтропия
изолированной системы при протекании
необратимого процесса возрастает.
Действительно, изолированная, т.е.
предоставленная самой себе, система
переходит из менее вероятных в более
вероятные состояния, что сопровождается
ростом величины (4).
Энтропия
системы, находящейся в равновесном
состоянии, максимальна.

Эти
утверждения и составляют содержаниевторого начала термодинамики:

Энтропия
изолированной системы может только
возрастать, (либо по достижении
максимального значения оставаться
неизменной), т.е.
.

Итак, при протекании
в изолированной системе необратимого
процесса энтропия возрастает, т.е.

.
(5)

В статистической
физике доказывается, что в ходе обратимого
процесса, сопровождающегося сообщением
системе количества теплоты
,
энтропия системы получает приращение

,
(6)

что совпадает
с принятым ранее определением энтропии

В определении
(6) весьма существенна обратимость
процесса, в ходе которого системе
сообщается теплота
.
Если количество теплоты
сообщается системе в ходе необратимого
процесса, энтропия возрастает как
вследствие сообщения тепла, так и
вследствие необратимости процесса.
Поэтому имеет место неравенство

.
(7)

Под
в (7) подразумевается температура
резервуара, от которого данная система
получает теплоту
.

Формулы (6) и
(7) можно объединить вместе, написав

.
(8)

Знак равенства относится
к обратимым, знак неравенства к необратимым
процессам.

Соотношение
(8), записанное в виде

или

называется
основным термодинамическим неравенством
Клаузиуса.

При абсолютном нуле температуры всякое
тело, как правило, находится в основном
состоянии, статистический вес которого
равен единице ().
Формула (4) даёт в этом случае для энтропии
значение равное нулю. Отсюда вытекает,
что энтропия всякого тела стремится к
нулю при стремлении к нулю температуры:

Это утверждение
представляет собой содержание третьего
начала термодинамики.

Соседние файлы в папке Физика. Лекции

Источник

Содержание:

Энтропия
Принцип существования энтропии
Принцип возрастания энтропии
Принцип действия тепловой машины
Цикл Карно. Максимальный КПД
Второе начало термодинамики

Энтропия – это физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Энтропия

Энтропия это, в широком смысле, мера хаоса в какой-либо системе. В переводе «энтропия» означает «преобразование».

Энтропия простыми словами — это то, как много информации вам не известно о системе.

В статистической физике энтропия характеризует вероятность осуществления какого-либо макроскопического состояния. Кроме физики, термин широко употребляется в математике: теории информации и математической статистике. В этих областях знания энтропия определяется статистически и называется статистической или информационной энтропией.

В широком смысле, в каком слово часто употребляется в быту, энтропия означает меру сложности, хаотичности или неопределённости системы: чем меньше элементы системы подчинены какому-либо порядку, тем выше энтропия. Величина, противоположная энтропии, именуется негэнтропией или, реже, экстропией.

Принцип существования энтропии

В середине прошлого века было сделано существенное открытие» касающееся обратимых термодинамических процессов. Оказалось, что наряду с внутренней энергией у тела имеется еще одна замечательная функция состояния — энтропия. Также, как и внутренняя энергия, энтропия определяется с точностью до произвольной постоянной. Опыт дает значение разности приращения энтропии. Если тело или система при бесконечно малом переходе из одного состояния в другое при температуре получает тепло то отношение является полным дифференциалом некоторой функции Эта функция и есть энтропия
определяющаяся, таким образом, одним из двух эквивалентных равенств:

Утверждение о существовании функции, дифференциал которой есть носит название принципа существования энтропии и является одним из важнейших законоз природы. Оно является существенной частью второго начала термодинамики, о чем у нас речь пойдет ниже. Открытие этого принципа, как и всего второго начала термодинамики, связано, прежде всего, с именами Карно и Клаузиу-са. Сущность принципа, несмотря на некоторую его абстрактность, легко понять: переход тела из одного состояния во второе может произойти бесчисленным количеством способов (разные кривые на графике, начинающиеся и заканчивающиеся в тех же точках); при этих переходах тело может получать самые различные количества тепла, однако во всех случаях интеграл будет иметь одинаковые значения. Отношение количества теплоты к той температуре, при которой это тепло было получено, называют иногда приведенной теплотой. Так как интеграл всегда можно представить приближенно суммой то изменение энтропии при переходе из одного, состояния в другое равно сумме приведенных теплот. Предположим, что тело, равномерно нагреваясь от 20 до 25 °С, получает при подъеме температуры по одному джоулю тепла на каждый градус. Тогда прирост энтропии будет примерно равен

Наиболее просто выражаются изменения энтропии при изотермических процессах:
где — полученное при процессе тепло. Так, например, при таянии 1 кг льда энтропия вещества возрастает на

За нуль энтропии может быть принято значение энтропии любого состояния (кипящей воды, плавящегося льда). Однако в некоторых случаях принимают за нуль значение энтропии вещества при абсолютном нуле температуры. Для этого, впрочем, имеются некоторые теоретические основания (теорема Нернста), на которых мы останавливаться не будем.

Приняв энтропию вещества при температуре можно найти по формуле

если нагрев происходит при постоянном давлении. Как видим, чтобы знать энтропию, надо изучить ход теплоемкости с температурой.

Если известно уравнение состояния вещества, то энтропия (с точностью до произвольной постоянной) может быть вычислена весьма просто. По определениюПодставляя значение для таким, как его дает первое начало термодинамики, получим

При помощи уравнения газового состояния исключим отсюда давление. Получим: Если взять неопределенный интеграл, то получим выражение энтропии с точностью до произвольной постоянной

Можно также взять от определенный интеграл, пределами которого являются два состояния. Тогда получится выражение для разности энтропий двух состояний

Это — выражения для энтропии идеальных газов. Из формул видно, что энтропия возрастает при повышении температуры, а также при увеличении объема газа. Это, разумеется, полностью совпадает с общим утверждением о повышении энтропии при подводе к телу тепла.

Пример. Покажем, что энтропия действительно есть функция состояния системы. Обратимся к примеру на стр. 151 (рис. 79). Путь 1—2—3. Изменение энтропии

Изменение энтропии

Полное изменение энтропии на пути 1—2—3

Видно, что действительно, каким бы путем ни совершался переход газа из состояния 1 в состояние 3, изменение энтропии одно и то же.

Принцип возрастания энтропии

Как уже говорилось, обратимых процессов, строго говоря, не существует, хотя с точностью, доступной опыту, можно осуществить множество процессов, практически неотличимых от обратимых. Имеются, однако, примеры процессов, которые всегда односторонни и уже поэтому никоим образом не могут быть обращены. Так, например, газ может расшириться сам по себе, но не может сжиматься без приложения внешних сил. Тепло может самопроизвольно переходить от горячего тела к холодному и только при затрате работы (например, электроэнергии) может переходить от холодного тела к более нагретому. При трении кинетическая энергия макроскопического движения всегда превращается во внутреннюю энергию, но никогда не происходит самопроизвольный обратный процесс. Необратимость всех остальных процессов в конечном счете связана с тем, что в каждом из них в той или иной степени присутствует один из перечисленных односторонних процессов. В реальных процессах невозможно избежать ни самопроизвольных расширений, ни трения, ни теплового рассеяния.

Нет ли какого-нибудь общего признака у всех перечисленных односторонних процессов? Оказывается, есть: этот признак состоит в том, что во всех односторонних процессах возрастает энтропия.

В случае теплообмена между двумя телами общее (всей системы) изменение энтропии равно

где — тепло, полученное более холодным телом,— тепло, потерянное более горячим телом.

Если больше так как мы считаем положительным тепло, сообщенное телу. Значит,

т. е. при теплообмене общая энтропия системы, в которой произошел теплообмен, возрастает.

Другой случай. Внутри сосуда с газом происходит интенсивное механическое движение (скажем, вертится колесо). Объем не меняется, температура растет, поэтому энтропия изменится на

Наконец, при расширении в пустоту при неизменной температуре прирост энтропииопять-таки положительный.

Итак, во всех односторонних процессах энтропия системы возрастает.

Нетрудно понять, какое значение имеет этот вывод для всех необратимых процессов. Так как каждый необратимый процесс сопровождается односторонними явлениями, идущими с повышением энтропии,.то прирост, энтропии у необратимого процесса будет завышен против того прироста, который имел бы место при обратимом переходе. Пусть — тепло, полученное телом при температуре в интересующем нас необратимом процессе. Если бы процесс был обратимым, то прирост энтропии равнялся бы в реальном процессе прирост энтропии будет больше этой величины:

Если система теплоизолирована, то и предыдущее утверждение приобретает вид

в теплоизолированной системе возможны лишь процессы, идущие с возрастанием энтропии.

Вполне понятно, что энтропия вместе с внутренней энергией являются важнейшими функциями, определяющими термодинамический процесс. Можно сказать, что энтропия является директором-распорядителем процесса, а внутренняя энергия является его бухгалтером: энтропия (определяет направление протекания процесса, энергия «оплачивает расходы» на его проведение.

Если в предыдущие формулы ввести вместо знака краткой формулой запишется закон энтропии как для обратимых, так и для необратимых процессов:

Эта формула передает содержание второго начала термодинамики. Для замкнутых систем второе начало говорит: энтропия теплоизолированной системы возрастает или остается неизменной.

Целесообразно объединить оба начала термодинамики одной формулой

удобной для рассмотрения всех практических задач термодинамики.

Принцип возрастания энтропии относится к закрытым системам. Если же система общается со средой, другими словами, если речь идет об открытой системе, то ее энтропия может, разумеется, и убывать.

Ниже будет показано, что процессы молекулярного упорядочения связаны с уменьшением энтропии. Живой организм из неупорядоченной системы малых молекул, получаемых в процессах питания и дыхания, конструирует высокоорганизованные постройки — биологические макромолекулы (стр. 595). При этом энтропия организма падает.

Если представить себе замкнутую систему организм+среда, энтропия которой обязана расти, то ясно, что энтропия среды должна возрастать, перекрывая уменьшение энтропии организма.

Возрастание энтропии среды происходит за счет выделений организма.

Если процесс стационарной, то

Можно сказать, что жизнедеятельность организма состоит в пропускании через себя потока энтропии вещества. При этом энтропия вещества, входящего в организм, меньше энтропии, отдаваемой среде,— организм деградирует продукты питания.

Примеры. 1. В примере на стр. 57 мы рассмотрели неупругое столкновение пули с баллистическим маятником и выяснили, что при ударе в системе пуля — маятник исчезает 3920 Дж механической энергии. Это значит, что было необратимым образом передано маятнику от пули посредством теплопроводности. Если предположить, что процесс был изотермическим (т. е. теплопроводность маятника чрезвычайно велика) и температура системы, скажем, то в этом необратимом процессе энтропия системы возросла на

2. Детский резиновый мяч массой 0,3 кг после падения с высоты 2 м подпрыгивает на I м от пола. В этом изотермическом процессе (пустьнеобратимо передается т. е. энтропия системы мяч — пол возросла на

Если бы мяч и пол были абсолютно упругими, то энтропия не менялась бы движение мяча продолжалось бы вечно.

3. Рассмотрим необратимый процесс передачи тепла от парового котла к конденсатору. Пусть паровой котел находится при температуре а конденсатор — при При тепловой мощности котла 10 000 кВт и к. п. д. 25% ежесекундно от котла к конденсатору будет переноситься Для котла, теряющего теплоту, это будет отрицательным, т. е. его энтропия убывает; у конденсатора энтропия растет. Но так как то энтропия системы котел — конденсатор за каждую секунду возрастает на

Принцип действия тепловой машины

Тепловая машина превращает тепло в работу, иначе говоря, забирает тепло от одних тел и передает его другим телам в форме механической работы. Для того чтобы осуществить это превращение, надо располагать двумя различно нагретыми телами, между которыми возможен теплообмен. Для краткости будем называть более горячее тело нагревателем, а более холодное — холодильником. При наличии таких двух тел процесс превращения тепла в работу рисуется следующим образом: способное расшириться тело (рабочее тело) приводится в контакт с нагревателем. Тепло ( отбирается от нагревателя и затрачивается на работу расширения которая отдается окружающим телам. Далее, рабочее тело приводится в контакт с холодильником, которому оно отдает тепло за счет работы совершаемой внешними силами над рабочим телом.

Чтобы получить непрерывно действующую тепловую машину, необходимо закончить такт сжатия в той точке, в которой начался такт расширения; короче, процесс должен быть циклическим. Рабочее тело по проведении каждого цикла возвращается в исходное состояние. Закон сохранения энергии требует поэтому, чтобы энергия, полученная от окружающих тел, равнялась энергии, переданной окружающим телам. От среды получено: тепло при расширении и работа при сжатии рабочего тела. Среде отдано: работа при расширении тела и тепло при сжатии. Следовательно, При проведении цикла по часовой стрелке работа сжатия меньше работы расширения. Поэтому последнее равенство выражает тот простой факт, что чистая работа, переданная рабочим телом внешней среде, равна разности теплот, полученной от нагревателя и отданной холодильнику. Соответственно коэффициент полезного действия цикла, а значит, и всей машины, будет равен

Описанный процесс действия тепловой машины является, разумеется, абстрактной схемой. Однако наиболее существенные черты каждого теплового двигателя передаются этой схемой. Рабочим телом является расширяющийся и сжимающийся газ или пар, роль холодильника играет окружающая среда. Нагревателем служит паровой котел или, в двигателях внутреннего сгорания, горючая смесь.

Те же три системы являются необходимыми и для холодильной машины, в которой цикл протекает в обратную сторону. Принцип работы этой машины заключается в следующем: расширение рабочего тела производится тогда, когда оно находится в контакте с холодильником. Этим холодное тело охлаждается еще больше, что и является задачей холодильной машины. Далее, чтобы цикл стал возможным, нужно произвести сжатие рабочего тела и передать тепло, полученное от холодильника. Это выполняется при контакте рабочего тела с нагревателем. Таким образом, более горячее тело нагревается еще больше. «Противоестественный» переход тепла от тела менее нагретого к телу более нагретому «оплачивается» работой. Действительно, при совершении цикла против часовой стрелки равенство энергии, переданной среде, и энергии, отнятой от среды где мы по-прежнему

индекс 1 относим к части процесса, протекающей при контакте с более горячим телом), имеет следующий смысл: количество тепла, отнятое от системы, должно быть скомпенсировано равным количеством механической работы.

Второе начало термодинамики накладывает некоторое условие на действие тепловой машины. Если предполагать процесс обратимым, то изменение энтропии рабочего тела после прохождения цикла должно равняться нулю. Можно сказать и иначе: изменение энтропии в процессе расширения должно равняться (с обратным знаком) изменению энтропии при сжатии, т. е.

В случае же необратимого процесса энтропия замкнутой системы, состоящей из нагревателя, холодильника и рабочего тела, возрастет и поэтому

(Напоминаем, что есть алгебраическая величина. Тепло, поступившее в систему, считается положительным.) Подсчитывая значения этих интегралов для конкретных процессов, можно в ряде случаев довольно просто найти значение максимального коэффициента полезного действия того или иного цикла тепловой машины.

Цикл Карно. Максимальный КПД

Сейчас мы задаемся целью найти выражение предельно большого коэффициента полезного действия тепловой машины, достижимого для идеальной машины, работающей без потерь на обратимом цикле.

Прежде всего рассмотрим теоретический четырехтактный цикл Карно, изображенный на рис. 81. Цикл Карно состоит из двух изотерм (для температур и и двух адиабат. Первый такт процесса пусть будет изотермическое расширение от состояния 1 к состоянию 2 — рабочее тело находится в контакте с нагревателем, имеющим температуру и процесс проводится весьма медленно. По достижении состояния 2 контакт с нагревателем нарушается, тело теплоизолируется и ему предоставляется возможность дополнительно расшириться.

Работа происходит за счет внутренней энергии и температура тела пусть падает до Начиная с этой точки (состояние 3) начинается двухтактное сжатие. Тело сообщается с холодильником при температуре и изотермически сжимается до состояния 4. Здесь опять тело теплоизолируется и сжатие продолжается уже адиабатическим путем с нагреванием рабочего тела за счет совершаемой работы до начальной температуры

Адиабатические процессы в цикле Карно носят вспомогательный характер: они помогают перейти с одной изотермы на другую. В энергетическом балансе эти процессы не участвуют, так как работа адиабатического расширения и работа сжатия компенсируют друг друга.

В адиабатическом процессе энтропия системы не меняется. При изотермическом расширении энтропия нагревателя уменьшается на величину энтропия холодильника возрастает на Энтропия рабочего тела, вернувшегося в исходное состояние, остается неизменной. Если процесс обратим, то В необратимых процессах энтропия всей системы, состоящей из холодильника, нагревателя и рабочего тела, возрастает и прирост энтропии больше убыли

откуда и следовательно, максимальный коэффициент полезного действия цикла Карно равен

К- п. д. цикла определяется температурами холодильника и нагревателя. Чем больше перепад температуры, тем выше к. п. д. машины. Нетрудно видеть, что коэффициент полезного действия цикла Карно дает оптимальное значение к. п. д. Нет лучшего цикла, чем цикл Карно, и в этом смысле он должен являться образцом для конструкторов тепловых машин, они должны стремиться как можно более приблизить реальные циклы к циклу этой идеальной машины.

Доказательство не составит труда. На рис. 82 показан произвольный цикл, вписанный в цикл

Карно. Уменьшение энтропии нагревателя может быть представлено интегралом
для которого несомненно справедливо неравенстве

так как — самое большое число из тех значений, которые пробегает при интегрировании. Увеличение энтропии холодильника выразится интегралом для которого справедливо неравенство так как — самое маленькое число из тех значений, которые пробегает при интегрировании. При обратимом процессе

следовательно,что и дает условие

Итак, из всех возможных циклических процессов максимальным к. п. д. обладает цикл Карно.
Формула максимального к. п. д. показывает причину низкого к. п. д. паровых машин. При к. п. д. равен 25%. Однако ведь это — максимальный коэффициент полезного действия, он достижим для идеальной машины, работающей обратимо без каких бы то ни было потерь энергии. Не приходится удивляться, что в реальных паровых машинах к. п. д. ниже 10%. В курсе теплотехники рассказывается о путях, которыми идет техника для увеличения коэффициента полезного действия. Ясно, что наиболее существенным является повышение температуры нагревателя, т. е. пара или горючей смеси.

Второе начало термодинамики

Как было указано выше, второе начало термодинамики состоит в утверждении, что энтропия в теплоизолированной системе возрастает. Это утверждение может показаться несколько абстрактным. Кроме того, приведенная формулировка не соответствует историческому развитию идей. Имея в виду огромную, значимость этого закона природы, надо кратко остановиться на других существующих формулировках второго начала термодинамики и показать их эквивалентность приведенной выше.

Исторически второе начало термодинамики вошло в науку в виде постулата Томсона о невозможности создания вечного двигателя второго рода. Вечным двигателем первого рода называют машину, создающую работу «из ничего», т. е. машину, работа которой нарушает первое начало термодинамики. Вечным двигателем второго рода называют такой двигатель, который производит работу при помощи периодически действующей машины за счет одного лишь отнятия теплоты от окружающей среды. Такой двигатель, будь он возможен, был бы практически вечным, так как запас энергии в окружающей среде почти безграничен и охлаждение, скажем, воды океанов на один градус дало бы непредставимо огромную энергию. Масса воды в мировом океане по порядку величины составляет При охлаждении всей этой массы воды лишь на выделилось бы тепла, что эквивалентно полному сжиганию угля. Железнодорожный состав, нагруженный этим количеством угля, растянулся бы на расстояние что по порядку величины совпадает с размерами солнечной системы!

Вечный двигатель второго рода — это тепловая машина, работающая с нагревателем, но без холодильника. Такая машина могла бы поработать один такт — газ, находящийся в сосуде с поршнем, мог бы расшириться, но на этом работа двигателя и закончилась бы, так как для продолжения действия машины тепло, полученное газом, необходимо передать холодильнику. Формально невозможность вечного двигателя второго рода видна из формулы максимального к. п. д. При отсутствии теплового перепада максимальное значение к. п. д. равно нулю.

Невозможно осуществить периодически действующий вечный двигатель, комбинируя изотермическое расширение с адиабатическим процессом сжатия. Такой процесс невозможен, даже если бы удалось его сделать обратимым. При изотермическом расширении рабочего тела энтропия падает. Значит, процесс сжатия должен приводить к возрастанию энтропии. Этого, однако, не может сделать адиабатический процесс, так как он проходит при постоянной энтропии.

Вполне соответствует принятой здесь формулировке второго начала термодинамики также постулат Клаузиуса, который состоит в утверждении о невозможности перехода тепла от менее нагретого тела к более нагретому без компенсации. Процесс, противоречащий постулату Клаузиуса, протекает с уменьшением энтропии; это свойство энтропии было показано с самого начала.

Услуги по физике:

Заказать физику
Заказать контрольную работу по физике
Помощь по физике

Лекции по физике:

Физические величины и их измерение
Основные законы механики
Прямолинейное равномерное движение
Прямолинейное равнопеременное движение
Сила
Масса
Взаимодействия тел
Механическая энергия
Импульс
Вращение твердого тела
Криволинейное движение тел
Колебания
Колебания и волны
Механические колебания и волны
Бегущая волна
Стоячие волны
Акустика
Звук
Звук и ультразвук
Движение жидкости и газа
Молекулярно-кинетическая теория
Молекулярно-кинетическая теория строения вещества
Молекулярно – кинетическая теория газообразного состояния вещества
Теплота и работа
Температура и теплота
Термодинамические процессы
Идеальный газ
Уравнение состояния идеального газа
Изменение внутренней энергии
Переход вещества из жидкого состояния в газообразное и обратно
Кипение, свойства паров, критическое состояние вещества
Водяной пар в атмосфере
Плавление и кристаллизация
Тепловое расширение тел
Процессы перехода из одного агрегатного состояния в другое
Тепловое расширение твердых и жидких тел
Свойства газов
Свойства жидкостей
Свойства твёрдых тел
Изменение агрегатного состояния вещества
Тепловые двигатели
Электрическое поле
Постоянный ток
Переменный ток
Магнитное поле
Электромагнитное поле
Электромагнитное излучение
Электрический заряд (Закон Кулона)
Электрический ток в металлах
Электрический ток в электролитах
Электрический ток в газах и в вакууме
Электрический ток в полупроводниках
Электромагнитная индукция
Работа, мощность и тепловое действие электрического тока
Термоэлектрические явления
Распространение электромагнитных волн
Интерференционные явления
Рассеяние
Дифракция рентгеновских лучей на кристалле
Двойное лучепреломление
Магнитное поле и электромагнитная индукция
Электромагнитные колебания и волны
Природа света
Распространение света
Отражение и преломление света
Оптические приборы и зрение
Волновые свойства света
Действия света
Линзы и получение изображений с помощью линз
Оптические приборы и глаз
Фотометрия
Излучение и спектры
Квантовые свойства излучения
Специальная теория относительности в физике
Теория относительности
Квантовая теория и природа поля
Строение и свойства вещества
Физика атомного ядра
Строение атома

Источник

Энтропия – функция состояния

Неравенство Клаузиуса

Изменение энтропии в равновесном процессе

Свойства энтропии

Статистический смысл энтропии

1. Базовые определения

Историческая справка[править | править код]

Термодинамическая дефиниция энтропии[править | править код]

Энтропия простой системы[править | править код]

Энтропия закрытой системы в термодинамике Клаузиуса — Каратеодори[править | править код]

Энтропия открытой системы[править | править код]

Энтропия в термодинамике Гиббса[править | править код]

Энтропия в рациональной термодинамике[править | править код]

Свойства энтропии[править | править код]

Энтропия как характеристическая функция[править | править код]

Энтропия и теплота квазистатического (равновесного) процесса[править | править код]

Энтропия как характеристика изотермического процесса[править | править код]

Статистическое определение энтропии: принцип Больцмана[править | править код]

Понимание энтропии как меры беспорядка[править | править код]

Границы применимости понимания энтропии как меры беспорядка[править | править код]

Измерение энтропии[править | править код]

Построение графика изменения энтропии[править | править код]

«Что такое энтропия?»[править | править код]

См. также[править | править код]

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Энтропия. Примеры вычисления энтропии

Энтропия и второе начало термодинамики

Энтропия

Принцип существования энтропии

Принцип возрастания энтропии

Принцип действия тепловой машины

Цикл Карно. Максимальный КПД

Второе начало термодинамики

Вам также может понравиться

Скажите как найти настоящих родителей

Как найти в майнкрафте стол

Как найти ошибку 300

Добавить комментарий Отменить ответ