Энтропия источника дискретных сообщений
А.
Энтропия источника независимых
сообщений
Мы
определили количество информации,
содержащееся в отдельном
сообщении. Во многих случаях, например
при согласовании канала с источником
информации, возникает необходимость в
характеристиках, позволяющих оценивать
информационные свойства источника
сообщений в
целом. Одной
из важнейших характеристик такого типа
является среднее
количество информации,
приходящееся
на одно сообщение.
В
простейшем случае, когда все сообщения
равновероятны, количество информации
в каждом из них одинаково и равно
![]()
При
этом среднее количество информации
равно
![]() .
.
Следовательно, при равновероятных
независимых сообщениях информационные
свойства источника зависяттолько
от числа сообщений
в ансамбле m.
Однако
в реальных условиях сообщения, как
правило, имеют разную вероятность.
Например, буквы О, Е и А встречаются в
тексте сравнительно часто, тогда как
Щ, Ы и Ъ – достаточно редко. Поэтому
знания числа сообщений m
в ансамбле недостаточно и требуется
иметь сведения о вероятности каждого
сообщения
![]() .
.
Так как вероятности сообщений неодинаковы,
то они несут различное количество
информации:![]()
Среднее
количество информации, приходящееся
на одно сообщение источника, определяется
как математическое ожидание
![]() :
:
![]()
Величина
![]() называетсяэнтропией.
называетсяэнтропией.
Этот термин заимствован из термодинамики,
где он характеризует неопределенность
состояния физической системы.
В
теории информации энтропия
![]() также характеризует неопределенность
также характеризует неопределенность
ситуации до передачи сообщения, поскольку
заранее неизвестно, какое из сообщений
будет передано. Важно понимать, что чем
больше энтропия, тем сильнее неопределенность
и тем большую информацию в среднем несет
одно сообщение источника.
В
качестве примера вычислим энтропию
источника сообщений, когда ансамбль
сообщений состоит лишь из двух сообщений
![]() и
и![]() , характеризуемых вероятностями
, характеризуемых вероятностями![]() .
.
Энтропия такого источника в соответствии
с (10) будет равна
![]()
Зависимость
энтропии от величины p
приведена на Рис. 1.

Рис. 1. Зависимость
энтропии от вероятности
Максимум
энтропии имеет место при
![]() ,
,
т.е. когда ситуация является наиболее
неопределенной. При![]() или
или![]() ,
,
что соответствует передаче одного из
сообщений![]() или
или![]() ,
,
неопределенностьотсутствует.
В этих случаях энтропия равна нулю.
Среднее
количество информации, содержащееся в
последовательности из n
сообщений, равно
![]()
Отсюда
следует, что количество передаваемой
информации можно увеличить не
только за счет числа сообщений,
но и путем
повышения энтропии источника,
т.е. информационной емкости его сообщений.
Обобщая
эти результаты, можно сформулировать
основные свойства энтропии источника
независимых сообщений:
-
Энтропия
– величина всегда положительная, так
как
 ;
; -
При
равновероятных сообщениях, когда
![]()
энтропия
максимальна и равна
![]()
-
Энтропия
равняется нулю лишь в тех случаях, когда
все вероятности равны нулю, за
исключением одной, величина которой
равна единице; -
Энтропия
нескольких независимых источников
равна сумме
энтропий этих источников
![]()
Б.
Энтропия источника зависимых
сообщений
Рассмотренный
нами источник независимых сообщений
является простейшим типом источника.
В реальных условиях картина значительно
усложняется из-за наличия статистических
связей
между сообщениями. Примером может
служить обычный текст, где появление
той или иной буквы зависит от предыдущих
буквенных сочетаний. Так например, после
сочетания ЧТ вероятность следования
гласных букв О, Е или И значительно
выше, чем согласных.
Статистическая
связь ожидаемого сообщения с предыдущим
сообщением количественно оценивается
совместной вероятностью
![]() или условной вероятностью
или условной вероятностью![]() ,
,
которая выражает вероятность появления
сообщенияпри
условии, что известно предыдущее
сообщение
![]() .
.
Количество информации, содержащейся в
сообщении при условии, что известно
предыдущее сообщение согласно (1)
будет равно
![]()
Среднее
количество информации при этом
определяется условной
энтропией
![]() ,
,
которая вычисляется как математическое
ожидание информации
![]() по всем возможным сообщениям
по всем возможным сообщениям![]() .
.
Важным
свойством условной энтропии источника
зависимых сообщений является то, что
при неизменном количестве сообщений в
ансамбле источника его энтропия
уменьшается с увеличением числа
сообщений, между которыми существует
статистическая взаимосвязь. В соответствии
с этим свойством, а также свойством
энтропии источника независимых сообщений
можно записать неравенства
![]()
Таким
образом, наличие статистических связей
между сообщениями всегда приводит к
уменьшению количества информации,
приходящейся в среднем на одно сообщение.
Избыточность
источника сообщений
Уменьшение
энтропии источника с увеличением
статистической взаимосвязи (14) можно
рассматривать как снижение информационной
емкости сообщений. Одно и то же сообщение
при наличии взаимосвязи содержит в
среднем меньше информации, чем при ее
отсутствии. Иначе говоря, если источник
создает последовательность сообщений,
обладающих статистической связью, и
характер этой связи известен, то часть
сообщений, выдаваемых источником,
является избыточной,
так как она может быть восстановлена
по известным статистическим связям.
Появляется возможность передавать
сообщения в сокращенном виде без потери
информации. Например при передаче
телеграммы из текста исключаются союзы,
предлоги, знаки препинания, так как они
легко восстанавливаются при чтении
телеграммы на основании известных
правил построения фраз и слов.
Говорят,
что любой источник зависимых сообщений
обладает
избыточностью.
Количественное определение избыточности
может быть получено из следующих
соображений. Для того чтобы передать
количество информации
![]() , источник без избыточности должен
, источник без избыточности должен
выдать в среднем![]() сообщений, а источник с избыточностью
сообщений, а источник с избыточностью![]() сообщений.
сообщений.
Поскольку
![]() и
и![]() , то для передачи одного и того же
, то для передачи одного и того же
количества информации источник с
избыточностью должен использоватьбольшее
количество сообщений. Избыточное
количество сообщений равно
![]() , а избыточность определяется как
, а избыточность определяется как
отношение
![]()
Величина
избыточности согласно (14) является
неубывающей функцией. Для русского
языка, например, избыточность составляет
порядка 50%.
Коэффициент
![]()
называется
коэффициентом
сжатия.
Он показывает, до какой величины можно
сжать передаваемые сообщения, если
устранить избыточность. В связи с тем,
что обладающий избыточностью источник
передает излишнее количество сообщений,
увеличивается продолжительность
передачи и снижается эффективность
использования канала связи. Требуется
проводить сжатие сообщений, которое
реализуется с помощью соответствующего
кодирования. Информацию необходимо
передавать такими сообщениями, емкость
которых используется наиболее полно.
Вместе
с тем избыточность источника далеко не
всегда является отрицательным свойством.
Наличие взаимосвязи между буквами
текста дает возможность восстановить
его при искажении отдельных букв, т.е.
использовать избыточность для повышения
достоверности
передачи информации.
Лекция
6. Пропускная способность дискретных
каналов и эффективность систем передачи
информации
Скорость
передачи информации и пропускная
способность дискретного канала без
помех
Так
как передача информации происходит во
времени, естественно ввести понятие
скорости
передачи
как количество информации, передаваемой
в среднем за единицу времени
![]()
Здесь
![]() – количество информации, содержащейся
– количество информации, содержащейся
в последовательности сообщений![]() ,
,
общая длительность которых равнаT.
Количество
информации, создаваемое источником
сообщений в среднем за единицу времени,
называется производительностью
источника
![]() .
.
Эту величину удобно выразить через
энтропию источника![]() .
.
При![]() можно считать
можно считать![]() и
и![]() ,
,
гдеn
– число сообщений, а
![]() – средняя продолжительность одного
– средняя продолжительность одного
сообщения. Подставляя в (1) значения![]() и
и![]() , получим
, получим
![]()
Величина
![]() для независимых сообщений может быть
для независимых сообщений может быть
вычислена как математическое ожидание
![]()
где
![]() – вероятность сообщения
– вероятность сообщения![]() длительностью
длительностью![]() . Если длительность всех сообщений
. Если длительность всех сообщений
одинакова и равна![]() ,
,
формула (2) принимает вид
![]()
Отсюда
следует, что наибольшей производительностью
обладает источник с максимальной
энтропией
![]() (см.
(см.
ф.(12) прошлой лекции),
т.е.
![]()
Выданная
источником информация в виде отдельных
сообщений поступает в канал связи, где
осуществляется кодирование и ряд других
преобразований, в результате которых
информация переносится уже сигналами
![]() ,
,
имеющими другую природу и в общем случае
обладающими другими статистическими
характеристиками. Для сигналов также
может быть найдена скорость передачи
по каналу связи
![]()
Высокая
скорость передачи является одним из
основных требований, предъявляемых к
системам передачи информации. В реальных
условиях всегда существует ряд причин,
ведущих к ее ограничению.
Во-первых,
в реальном канале число используемых
сигналов всегда конечно и энтропия в
соответствии с
ф.(12) прошлой лекции,
есть величина ограниченная
![]()
С
другой стороны,
уменьшение длительности сигнала приводит
к расширению спектра, что при учете
ограниченной полосы пропускания канала
ставит предел уменьшению средней
длительности .
Максимально
возможная скорость передачи информации
по каналу связи называется пропускной
способностью канала
![]()
Максимум
скорости R
здесь ищется по всем возможным ансамблям
сигналов u
.
Пусть
число используемых сигналов не превышает
m,
а их длительность не может быть меньше
секунд. Так как
![]() и
и![]() независимы, то по формуле (8) следует
независимы, то по формуле (8) следует
искать максимум![]() и минимум
и минимум![]() , что дает
, что дает
![]()
Для
двоичных сигналов m
= 2 и пропускная способность
![]()
Оптимальное
статистическое кодирование сообщений
Для
дискретных каналов
без помех
Шенноном была доказана следующая
теорема:
если производительность источника
меньше пропускной способности канала
(![]() ),
),
то всегда существует способ кодирования,
позволяющий передавать по каналу все
сообщения источника. Передачу всех
сообщений при![]() осуществить невозможно.
осуществить невозможно.
Смысл
теоремы сводится к тому, что, как бы ни
была велика избыточность источника,
все его сообщения могут быть переданы
по каналу, если
![]() .
.
Для
рационального использования пропускной
способности канала необходимо применять
соответствующие способы кодирования
сообщений.
Статистическим
или оптимальным
называется кодирование, при котором
наилучшим образом используется пропускная
способность канала без помех. При
оптимальном кодировании фактическая
скорость передачи информации по каналу
R
приближается к пропускной способности
C,
что достигается путем согласования
источника с каналом.
Сообщения источника кодируются таким
образом, чтобы они в наибольшей степени
соответствовали ограничениям, которые
накладываются на сигналы, передаваемые
по каналу связи. Поэтому структура
оптимального кода зависит как от
статистических характеристик источника,
так и от особенностей канала.
Рассмотрим
основные принципы оптимального
кодирования на примере источника
независимых сообщений, который необходимо
согласовать с двоичным каналом без
помех. Здесь процесс кодирования
заключается в преобразовании сообщений
источника в двоичные кодовые комбинации.
Поскольку существует однозначное
соответствие между сообщениями источника
и комбинациями кода, то энтропия кодовых
комбинаций равна энтропии источника
![]()
а скорость передачи
в канале определяется с помощью (6) как
![]()
Здесь
![]() – средняя длительность кодовой комбинации,
– средняя длительность кодовой комбинации,
которая в общем случае неравномерного
кода записывается по аналогии с (3) как
![]()
где
![]() – длительность одного элемента кода и
– длительность одного элемента кода и![]() – число элементов в комбинации,
– число элементов в комбинации,
присваиваемой сообщению![]() .
.
Подстановка в
формулу (12) выражений
![]()
и (13) дает

в
котором числитель определяется
исключительно статистическими свойствами
источника, а величина
![]() – характеристиками канала.
– характеристиками канала.
Возникает
вопрос: можно ли так закодировать
сообщение, чтобы скорость передачи (14)
достигала своего максимального значения,
равного пропускной способности двоичного
канала
![]() . Легко заметить, что это условие
. Легко заметить, что это условие
выполняется, если
![]()
что
соответствует минимуму
![]() и максимумуR.
и максимумуR.
Одним
из кодов, удовлетворяющих условию (33),
является код Шеннона – Фано, который
мы рассмотрим позднее.
Необходимо
подчеркнуть, что при оптимальном способе
кодирования в сигналах, передающих
сообщения источника, совершенно
отсутствует избыточность. Устранение
избыточности приводит к тому, что процесс
декодирования становится весьма
чувствительным к воздействию помех.
Это особенно сильно проявляется при
оптимальном кодировании зависимых
сообщений. Иногда одна единственная
ошибка может вызвать неправильное
декодирование всех последующих сигналов.
Поэтому оптимальные коды применимы
только для каналов с чрезвычайно низким
уровнем помех.
Скорость
передачи информации и пропускная
способность дискретных каналов с
помехами
Каналы
без помех
характеризуются тем, что количество
принятой на выходе канала информации
всегда равно
количеству информации, переданной
источником сообщений.
При
этом, если на вход канала поступил сигнал
![]() , то на выходе возникает сигнал
, то на выходе возникает сигнал![]() ,однозначно
,однозначно
определяющий
переданный сигнал
![]() . Количество информации, прошедшее по
. Количество информации, прошедшее по
каналу без помех в случае передачи![]() и приема
и приема![]() ,
,
равно количеству информации, содержащейся
в сигнале![]() :
:
![]()
Здесь
величина вероятности
![]() характеризует ту неопределенность в
характеризует ту неопределенность в
отношении сигнала![]() , которая существоваладо
, которая существоваладо
его передачи.
После приема
![]() в силу однозначного соответствия между
в силу однозначного соответствия между![]() и
и![]() неопределенность полностью устраняется.
неопределенность полностью устраняется.
Совершенно
другое положение имеет место для каналов,
где присутствуют различного рода помехи.
Воздействие
помех на передаваемый сигнал приводит
к необратимой потере части информации,
поступающей от источника сообщений.
Так как в канале с помехами принятому
сигналу
![]() может соответствовать передача
может соответствовать передача
одного из нескольких сигналов
![]() ,
,
то после приема![]() остается некоторая неопределенность
остается некоторая неопределенность
в отношении переданного сигнала. Здесь
соответствие между![]() и
и![]() носитслучайный
носитслучайный
характер, и степень неопределенности
характеризуется условной апостериорной
вероятностью
![]() . Количество информации, необходимое
. Количество информации, необходимое
для устранения оставшейся неопределенности
![]()
очевидно,
равно той части информации, которая
была потеряна вследствие помех. Количество
принятой информации определяется как
(см. ф. (9) прошлой лекции)
![]()
Для
оценки среднего количества принятой
информации при передаче одного сообщения
выражение (17) необходимо усреднить по
всему ансамблю
![]() и
и![]() :
:
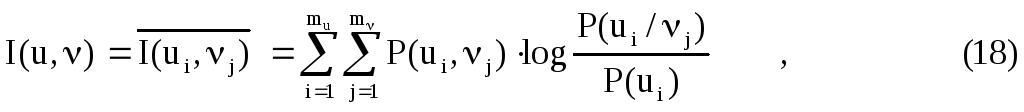
где
![]() –
–
совместная вероятность переданного и
принятого сигналов,![]() – количество сигналов в ансамбле на
– количество сигналов в ансамбле на
входе канала и![]() – количество сигналов в ансамбле на
– количество сигналов в ансамбле на
выходе канала (в общем случае![]() ).
).
Величина
![]() характеризует в среднем количество
характеризует в среднем количество
информации, которое содержит принятый
сигнал![]() относительно переданного сигнала
относительно переданного сигнала![]() и
и
называетсясредней
взаимной информацией
между
![]() и
и![]() .
.
Выражение (18) можно
представить в виде
![]()
где
![]()
представляет
энтропию источника сигналов
![]() и
и
![]()
–
условная энтропия или ненадежность.
Формула
(19) показывает, что среднее количество
принятой информации равно среднему
количеству переданной информации
![]() минус среднее количество информации
минус среднее количество информации![]() ,
,
потерянное в канале вследствие воздействия
помех.
Понятия
скорости передачи информации и пропускной
способности используются и для каналов
с помехами. В этом случае скорость
передачи информации по каналу можно
представить в виде
![]()
Пропускная
способность канала с помехами определяется
как максимально возможная скорость
передачи при ограничениях, накладываемых
на передаваемые сигналы
![]()
![]()
Для
каналов с сигналами одинаковой
длительности ,
пропускная способность равна
![]()
где
максимум ищется по всем возможным
ансамблям сигнала
![]() .
.
Выведем
выражение для пропускной способности
двоичного канала с помехами, по которому
передаются независимые дискретные
сигналы
![]() с априорными вероятностями
с априорными вероятностями![]() . На выходе канала образуются сигналы
. На выходе канала образуются сигналы![]() ,
,
при правильном приеме отражающие сигналы![]() .
.
В результате действия помех возможны
ошибки, которые характеризуются при
передаче![]() условной вероятностью
условной вероятностью![]() ,
,
а при передаче![]() – условной вероятностью
– условной вероятностью![]() .
.
Будем
полагать, что канал симметричен, т.е.
для него вероятности переходов одинаковы
![]() ,
,
а полная вероятность ошибки равна
![]()
При
этих условиях можно показать, что
пропускная способность двоичного
симметричного канала равна
![]()
На Рис. 1. приведена
зависимость пропускной способности
канала С от вероятности ошибки для
двоичного канала согласно формуле (26)

Рис.
1. Зависимость пропускной способности
двоичного канала от вероятности ошибки
![]() .
.
Видно,
что увеличение вероятности ошибки
![]() приводит к снижению пропускной
приводит к снижению пропускной
способности, которая становится равной
нулю при![]() =
=
0,5. В этом случае полностью исчезает
какая-либо зависимость между передаваемым
и принятым сигналами. Таким образом,
значение
![]() =
=
0,5 для бинарного симметричного канала
является предельным.
Теорема Шеннона
для дискретного канала с помехами
Данная
теорема имеет фундаментальное значение
для теории и техники передачи информации.
Если
производительность источника не
превышает пропускной способности
дискретного канала с помехами (![]() ),
),
то существует способ кодирования,
позволяющий передать все сообщения
источника со сколь угодно малой
вероятностью ошибки. При![]() такая передача невозможна.
такая передача невозможна.
Таким
образом, наличие помех в канале не
препятствует
передаче сообщений со сколь угодно
малой вероятностью ошибок декодирования,
а лишь ограничивает максимальную
скорость передачи информации С. Высокая
достоверность декодирования и конечная
скорость передачи не исключают друг
друга.
Вместе
с тем теорема не
указывает
конкретного способа наилучшего
кодирования. До сих пор продолжаются
поиски способов кодирования, которые
позволяли бы с аппаратурой приемлемой
сложности достигать предельных
возможностей, указанных теоремой
Шеннона.
Пропускная
способность непрерывного канала. Формула
Шеннона
Шенноном
была получена также формула для пропускной
способности непрерывного канала, в
котором помехой является аддитивный
шум
![]() .
.
Если средние мощности сигнала и шума
ограничены величинами![]() ,
,
и ширина их спектра равнаF,
то формула Шеннона имеет вид
![]()
Данная
формула очень важна, т.к. она показывает
те предельные возможности, к которым
следует стремиться при разработке
систем передачи информации. Формула
выведена для равномерных спектров
сигнала и шума, но может быть распространена
и на более реальный случай неравномерных
спектров. Оказывается, при заданных
спектрах сигнала и шума максимума
пропускной способности можно добиться
путем увеличения мощности сигнала на
тех частотах, где уменьшается мощность
шума и наоборот. Минимальная пропускная
способность соответствует равномерному
спектру шума, т.е. “белый шум” является
самым вредным
видом помех.
Эффективность
систем передачи информации
Пропускная
способность канала связи С является
тем пределом, которого можно достигнуть
при идеальном кодировании. Естественно,
что в реальных каналах скорость передачи
всегда будет меньше С. Степень отличия
R
от С зависит от того, насколько рационально
выбрана и эффективно используется та
или иная система передачи информации.
Наиболее общей оценкой эффективности
системы передачи информации является
коэффициент
использования канала
![]()
Для
дискретных систем передачи информации
справедливо соотношение
![]() ,
,
где![]() и
и![]() –
–
эффективностьсистемы
кодирования
и эффективность системы
модуляции
соответственно.
Вводя
избыточность сообщения
![]() и избыточностьсигнала
и избыточностьсигнала
![]() , можно показать, что
, можно показать, что
![]()
где
![]() –полная
–полная
избыточность
системы. Согласно этому соотношению,
эффективность системы (коэффициент
использования канала) полностью
определяется величиной ее избыточности,
т.е. задача повышения эффективности
системы передачи информации сводится
к задаче уменьшения избыточности
сообщения и сигнала.
Избыточность
сообщения
обусловлена тем, что элементы сообщения
не являются равновероятными и между
ними имеется статистическая связь. При
кодировании можно перераспределить
вероятности исходного сообщения так,
чтобы распределение вероятностей
символов кода приближалось к оптимальному.
Избыточность
сигнала
зависит от способа модуляции и вида
переносчика. Процесс модуляции обычно
сопровождается расширением полосы
частот сигнала по сравнению с полосой
частот передаваемого сообщения. Это
расширение полосы и является избыточным.
Говоря
об эффективности системы передачи
информации, нельзя забывать о ее
помехоустойчивости. Устранение
избыточности повышает эффективность
передачи, но снижает при этом
помехоустойчивость. При кодировании в
ряде случаев избыточность вводится
специально с целью повышения достоверности
передачи. Пример такого кодирования
являются корректирующие
коды,
которые мы рассмотрим позднее.
Таким
образом, имеется два основных критерия
оценки качества систем передачи
информации и наиболее совершенной
системой считается такая, которая
обеспечивает наибольшую
эффективность
при заданной
помехоустойчивости.
Энтропия источника независимых сообщений. До сих пор определялось количество информации, содержащееся в отдельных сообщениях. Вместе с тем во многих случаях, когда требуется согласовать канал с источником сообщений, таких сведений оказывается недостаточно. Возникает потребность. в характеристиках, которые, бы позволяли оценивать информационные свойства источника сообщений в целом. Одной из важных характеристик такого рода является среднее количество информации, приходящееся на одно сообщение.
В простейшем случае, когда все сообщения равновероятны, количество информации в каждом из них одинаково и, как было показано выше, определяется выражением (6.3). При этом среднее количество информации равно log т. Следовательно, при равновероятных независимых сообщениях информационные свойства источника зависят только от числа сообщений в ансамбле т.
Однако в реальных условиях сообщения, как правило, имеют разную вероятность. Так, буквы алфавита О, Е, А встречаются в тексте сравнительно часто, а буквы Щ, Ы, Ъ — редко. Поэтому знание числа сообщений т в ансамбле является недостаточным, необходимо иметь сведения о вероятностях каждого сообщения: ![]() .
.
Так как вероятности сообщений неодинаковы, то они несут различное количество информации J(a![]() )=–logP(a
)=–logP(a![]() ). Менее вероятные сообщения несут большее количество информации и наоборот. Среднее количество информации, приходящееся на одно сообщение источника, определяется как математическое ожидание J(a
). Менее вероятные сообщения несут большее количество информации и наоборот. Среднее количество информации, приходящееся на одно сообщение источника, определяется как математическое ожидание J(a![]() ):
):
![]() (6.6)
(6.6)
Величину Н(а) называется энтропией. Этот термин заимствован из термодинамики, где имеется аналогичное по своей форме выражение, характеризующее неопределенность состояния физической системы. В теории информации энтропия Н(а) также характеризует неопределенность ситуации до передачи сообщения, поскольку заранее неизвестно, какое из сообщений ансамбля источника будет передано. Чем больше энтропия, тем сильнее неопределенность и тем большую информацию в среднем несет одно сообщение источника.
В качестве примера вычислим энтропию источника сообщений, который характеризуется ансамблем, состоящим из двух сообщений ![]() и
и ![]() с вероятностями
с вероятностями ![]() и
и ![]() . На основании (6.6) энтропия такого источника будет равна:
. На основании (6.6) энтропия такого источника будет равна:
![]()
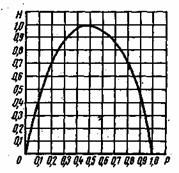
Рис. 6.1. Зависимость энтропии от вероятности р
Зависимость Н(а) от р показана на рис. 6.1. Максимум имеет место при р=1/2, т. е. когда ситуация является наиболее неопределенной. При р=1 или р=0, что соответствует передаче одного из сообщений ![]() или
или ![]() , неопределенность отсутствует. В этих случаях энтропия Н(а) равна нулю.
, неопределенность отсутствует. В этих случаях энтропия Н(а) равна нулю.
Среднее количество информации, содержащееся в последовательности из п сообщений, равно:
![]()
Отсюда следует, что количество передаваемой информации можно увеличить не только за счет увеличения числа сообщений, но и путем повышения энтропии источника, т. е. информационной емкости его сообщений.
Обобщая полученные выше результаты, сформулируем следующие основные свойства энтропии источника независимых сообщений (6.6):
— энтропия— величина всегда положительная, так как ![]()
— при равновероятных сообщениях, когда ![]() , энтропия максимальна и равна:
, энтропия максимальна и равна:
![]() (6.7)
(6.7)
— энтропия равняется нулю лишь в том случае, когда все вероятности Р(a![]() ) равны нулю, за исключением одной, величина которой ,равна единице;
) равны нулю, за исключением одной, величина которой ,равна единице;
— энтропия нескольких независимых источников равна сумме энтропии этих источников ![]() .
.
Энтропия источника зависимых сообщений. Рассмотренные выше источники независимых дискретных сообщений являются простейшим типом источников. В реальных условиях картина значительно усложняется из-за наличия статистических связей между сообщениями. Примерам может быть обычный текст, где появление той или иной буквы зависит от предыдущих буквенных сочетаний. Так, например, после сочетания ЧТ вероятность следования гласных букв О, Е, И больше, чем согласных.
Статистическая связь ожидаемого сообщения с предыдущим сообщением количественно оценивается совместной вероятностью ![]() или условной вероятностью
или условной вероятностью ![]() , которая выражает вероятность появления сообщения
, которая выражает вероятность появления сообщения ![]() при условии, что до этого было передано сообщение а
при условии, что до этого было передано сообщение а![]() Количество информации, содержащееся в сообщении
Количество информации, содержащееся в сообщении ![]() , при условии, что известно предыдущее сообщение а
, при условии, что известно предыдущее сообщение а![]() согласно (6.1) будет равно:
согласно (6.1) будет равно:![]() . Среднее количество информации при этом определяется условной энтропией
. Среднее количество информации при этом определяется условной энтропией ![]() , которая вычисляется как математическое ожидание информации
, которая вычисляется как математическое ожидание информации ![]() по всем возможным сообщениям а
по всем возможным сообщениям а![]() и
и ![]() . Учитывая соотношение (2.25), .получаем
. Учитывая соотношение (2.25), .получаем
![]() (6.8)
(6.8)
В тех случаях, когда связь распространяется на три сообщения ![]() , условная энтропия источника определяется аналогичным соотношением
, условная энтропия источника определяется аналогичным соотношением
![]() (6.9)
(6.9)
В общем случае n зависимых сообщений
![]() (6.10)
(6.10)
Важным свойством условной энтропии источника зависимых сообщений является то, что при неизменном количестве сообщений в ансамбле источника его энтропия уменьшается с увеличением числа сообщений, между которыми существует статистическая взаимосвязь. В соответствии с этим свойством, а также свойством энтропии источника независимых сообщений можно записать неравенства
![]() (6.11)
(6.11)
Таким образом, наличие статистических связей между сообщениями всегда приводит к уменьшению количества информации, приходящегося в среднем на одно сообщение.
Избыточность источника сообщений. Уменьшение энтропии источника с увеличением статистической взаимосвязи (6.11) можно рассматривать как снижение информационной емкости сообщений. Одно и то же сообщение при наличия взаимосвязи содержит в среднем меньше информации, чем при ее отсутствии. Иначе говоря, если источник создает последовательность сообщений, обладающих статистической связью, и характер этой связи известен, то часть сообщений, выдаваемая источником, является избыточной, так как она может быть восстановлена по известным статистическим связям. Появляется возможность передавать сообщения в сокращенном виде без потери информации, содержащейся в них. Например, при передаче телеграммы мы исключаем из текста союзы, предлоги, знаки препинания, так как они легко восстанавливаются, при чтении телеграммы на основании известных правил построения фраз и слов.
Таким образом, любой источник зависимых сообщений, как принято говорить, обладает избыточностью. Количественное определение избыточности может быть получено из следующих соображений. Для того чтобы передать количество информации, источник без избыточности должен выдать в среднем ![]() сообщений, а источник с избыточностью
сообщений, а источник с избыточностью ![]() сообщений.
сообщений.
Поскольку ![]() и
и ![]() , то для передачи одного и того же количества информации источник с избыточностью должен использовать большее количество сообщений. Избыточнее количество сообщений равно kn–k0, а избыточность определяется как отношение
, то для передачи одного и того же количества информации источник с избыточностью должен использовать большее количество сообщений. Избыточнее количество сообщений равно kn–k0, а избыточность определяется как отношение
![]() (6.12)
(6.12)
Величина избыточности лежит в пределах ![]() и согласно (6.11) является неубывающей функцией п. Для русского языка, например,
и согласно (6.11) является неубывающей функцией п. Для русского языка, например, ![]() дв. ед.,
дв. ед., ![]() ,
, ![]() ,
, ![]() дв. ед. Отсюда на основании (6.12) для русского языка получаем избыточность порядка 50%.
дв. ед. Отсюда на основании (6.12) для русского языка получаем избыточность порядка 50%.
Коэффициент
![]() (6.13)
(6.13)
называется коэффициентом сжатия. Он показывает, до какой величины можно сжать передаваемые сообщения, если устремить избыточность. Источник, обладающий избыточностью, передает излишнее количество сообщений. Это увеличивает продолжительность передачи и снижает эффективность использования канала связи. Сжатие сообщений можно осуществить посредством соответствующего кодирования. Информацию необходимо передавать такими сообщениями, информационная емкость которых используется наиболее полно. Этому условию удовлетворяют равновероятна и независимые сообщения.
Вместе с тем избыточность источника не всегда является отрицательным свойством. Наличие взаимосвязи между буквами текста дает возможность восстанавливать его при искажении отдельных букв, т. е. использовать избыточность для повышения достоверности передачи информации.
|
|
Макеты страниц
Энтропия источника сообщений.
Выше мы определили частное количество информации, содержащееся в некоторой последовательности а, выданной источником сообщений. Однако сам факт генерирования именно этой последовательности является случайным событием, имеющим вероятность  следовательно, случайной величиной оказывается и количество информации
следовательно, случайной величиной оказывается и количество информации  Поэтому можно поставить вопрос о среднем количестве информации, выдаваемом некоторым источником сообщений, которое можно определить как математическое ожидание случайной величины
Поэтому можно поставить вопрос о среднем количестве информации, выдаваемом некоторым источником сообщений, которое можно определить как математическое ожидание случайной величины  Если пока ограничиться лишь последовательностями длины
Если пока ограничиться лишь последовательностями длины  обозначив их
обозначив их  то в соответствии с известной формулой
то в соответствии с известной формулой  математического ожидания дискретной случайной величины, мы получаем
математического ожидания дискретной случайной величины, мы получаем

где суммирование, как видно, производится во всем возможным последовательностям длины  с элементами, взятыми из алфавита объёма К. Для того, чтобы получить исчерпывающую информационную характеристику источника сообщений, который, вообще говоря, может выдавать последовательности неограниченной длины, нужно вычислить предел среднего количества информации
с элементами, взятыми из алфавита объёма К. Для того, чтобы получить исчерпывающую информационную характеристику источника сообщений, который, вообще говоря, может выдавать последовательности неограниченной длины, нужно вычислить предел среднего количества информации  отнесённый к одному символу последовательности. Полученная величина, которую мы, следуя ещё установленной Шенноном традиции [29], обозначим через
отнесённый к одному символу последовательности. Полученная величина, которую мы, следуя ещё установленной Шенноном традиции [29], обозначим через  называется энтропией источника сообщений, т.е.
называется энтропией источника сообщений, т.е.

Если берется логарифм по основанию 2, то  измеряется в битах на символ. Выражение (6.10), очевидно, будет иметь смысл лишь тогда, когда предел в его правой части существует. Это свойство выполняется для стационарных источников. Заметим, что буква А в обозначении энтропии
измеряется в битах на символ. Выражение (6.10), очевидно, будет иметь смысл лишь тогда, когда предел в его правой части существует. Это свойство выполняется для стационарных источников. Заметим, что буква А в обозначении энтропии  указывает на определённый источник с алфавитом А, причём для краткости опускается вид вероятностного распределения
указывает на определённый источник с алфавитом А, причём для краткости опускается вид вероятностного распределения  Если источник не обладает памятью, то, используя свойство логарифмической функции, легко показать, что его энтропия будет
Если источник не обладает памятью, то, используя свойство логарифмической функции, легко показать, что его энтропия будет

где  — вероятности выдачи источником символов
— вероятности выдачи источником символов  причём они не зависят от номера элемента последовательности, так как
причём они не зависят от номера элемента последовательности, так как
источник является стационарным. Прежде чем пояснить наглядный смысл нового понятия энтропии, опишем её основные свойства.
1.  , причём
, причём  тогда и только тогда, когда одна из последовательностей имеет единичную вероятность, а все остальные – нулевую. (Это свойство очевидно из определения энтропии.)
тогда и только тогда, когда одна из последовательностей имеет единичную вероятность, а все остальные – нулевую. (Это свойство очевидно из определения энтропии.)
2. Для любого стационарного источника сообщений

Поскольку выражение в правой части (6.12) – это энтропия источника без памяти, то данное свойство означает, что память уменьшает энтропию источника. Данное свойство, хотя очевидное, требует специального доказательства [16], которое здесь не приводим.
3. Для любого стационарного источника сообщений

причём равенство имеет место тогда, и только тогда, когда источник не имеет памяти и все его символы равновероятны.
Из свойства 2 следует, что при доказательстве неравенств (6.13) мы сразу можем ограничиться источниками без памяти. Для доказательства свойства 3 рассмотрим разность

Далее воспользуемся известным неравенством 
Тогда

Равенство в (6.15) будет иметь место только при  что и доказывает данное свойство.
что и доказывает данное свойство.
Воспользовавшись свойствами 1-3, можно наглядно пояснить смысл понятия энтропии – это средняя информативность источника на один символ, определяющая “неожиданность” или “непредсказуемость” выдаваемых им сообщений. Полностью детерминированный источник, выдающий лишь одну, заранее известную последовательность, обладает нулевой информативностью. Наоборот, наиболее “хаотический” источник, выдающий взаимно независимые и равновероятные символы, обладает максимальной информативностью
Здесь уместно привести пример с обезьяной, сидящей за пишущей машинкой (в более современном варианте — за клавиатурой компьютера). Если она обучена ударять по клавишам, но, очевидно, не знает грамоты, то “обезьяний” текст окажется примером текста с взаимно независимыми и равновероятными символами. Поэтому он будет обладать наибольшей энтропией, превосходящей энтропию осмысленного текста на каком-либо языке. Несмотря на бесполезность обезьяньего текста, как мы увидим в дальнейшем, передавать его по каналам связи сложнее, чем какой-либо смысловой текст.
Энтропия источника сообщений тесно связана с понятием его избыточности, которое формально определяется следующим образом:

Как видно из выражения (6.16), чем больше энтропия источника, тем меньше его избыточность и наоборот.
Известно, что избыточность естественных языков является весьма важным свойством, позволяющим воспринимать рукописный или искажённый текст, слышать речь в больших акустических помехах и т. д. Теория информации, как мы убедимся в дальнейшем, позволяет количественно оценить эти возможности. Для экспериментального вычисления энтропии или избыточности естественных языков используются статистические данные о частости, с которой встречаются буквы текста и их сочетания (биграммы, триграммы и т.д.). Так, если воспользоваться так называемой статистикой английского языка  порядка (т.е. частостью отдельных букв), то энтропия оказывается равной 4,03 бит/букву, а если статистикой порядка, то 3.32 бит/букву. В то же время более точную оценку энтропии можно получить, воспользовавшись, например, предложенным ещё К. Шенноном “методом случайного угадывания” [29]. Такой подход даёт верхнюю оценку энтропии английского языка 2 бит/букву и нижнюю 1 бит/букву. Это позволяет сделать вывод, что основная избыточность естественного языка определяется многомерными зависимостями между буквами (корреляцией текста), и для её использования необходимо знать эти зависимости Аналогичные выводы можно сделать и относительно русского и других языков, хотя их энтропии и несколько отличаются друг от друга. (Известно, например, что одна и та же пьеса В. Шекспира идёт в Берлине дольше, чем в Лондоне.)
порядка (т.е. частостью отдельных букв), то энтропия оказывается равной 4,03 бит/букву, а если статистикой порядка, то 3.32 бит/букву. В то же время более точную оценку энтропии можно получить, воспользовавшись, например, предложенным ещё К. Шенноном “методом случайного угадывания” [29]. Такой подход даёт верхнюю оценку энтропии английского языка 2 бит/букву и нижнюю 1 бит/букву. Это позволяет сделать вывод, что основная избыточность естественного языка определяется многомерными зависимостями между буквами (корреляцией текста), и для её использования необходимо знать эти зависимости Аналогичные выводы можно сделать и относительно русского и других языков, хотя их энтропии и несколько отличаются друг от друга. (Известно, например, что одна и та же пьеса В. Шекспира идёт в Берлине дольше, чем в Лондоне.)

Рис. 6.1. Энтропия двоичного источника без памяти
Наиболее простую форму принимает энтропия в случае двоичного источника сообщений без памяти. Если для краткости обозначить  то
то

Вид этой функции показан на рис. 6.1 для основания логарифма, равного двум.
Если источник сообщений имеет фиксированную скорость  симв/с, то определим производительность источника
симв/с, то определим производительность источника  как энтропию в единицу времени, (секунду)
как энтропию в единицу времени, (секунду)

Максимум  обычно называют информационной скоростью источника.
обычно называют информационной скоростью источника.
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ОБЩИЕ СВЕДЕНИЯ О СИСТЕМАХ ЭЛЕКТРОСВЯЗИ
- 1.2. СИСТЕМЫ, КАНАЛЫ И СЕТИ СВЯЗИ
- 1.3. ПОМЕХИ И ИСКАЖЕНИЯ В КАНАЛЕ
- 1.4. КОДИРОВАНИЕ И МОДУЛЯЦИЯ
- 1.5. ДЕМОДУЛЯЦИЯ И ДЕКОДИРОВАНИЕ
- 1.6. ЦИФРОВОЕ КОДИРОВАНИЕ НЕПРЕРЫВНЫХ СООБЩЕНИЙ
- 1.7. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ СВЯЗИ
- ГЛАВА 2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СООБЩЕНИЙ, СИГНАЛОВ И ПОМЕХ
- 2.1. КЛАССИФИКАЦИЯ СООБЩЕНИЙ, СИГНАЛОВ И ПОМЕХ
- 2.2. ФУНКЦИОНАЛЬНЫЕ ПРОСТРАНСТВА И ИХ БАЗИСЫ
- 2.3. РАЗЛОЖЕНИЕ СИГНАЛОВ В ОБОБЩЁННЫЙ РЯД ФУРЬЕ
- Спектральное представление периодических колебаний.
- Спектральное представление непериодических функций.
- 2.4. ДИСКРЕТИЗАЦИЯ СИГНАЛОВ ВО ВРЕМЕНИ
- Спектральная трактовка дискретизации.
- Теорема отсчётов.
- Восстановление непрерывной функции по отсчётам.
- 2.5. СЛУЧАЙНЫЕ ПРОЦЕССЫ И ИХ ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
- Плотность вероятности и интегральная функция распределения (ИФР).
- Числовые характеристики.
- Нормальное (гауссовское) распределение.
- Равномерное распределение.
- Распределение вероятностей мгновенных значений гармонического колебания.
- Распределения вероятностей дискретных случайных величин
- Распределение Пуассона.
- Стационарные случайные процессы.
- Эргодические процессы.
- Спектральная плотность мощности случайного процесса.
- Функция корреляции случайного процесса с ограниченным спектром.
- 2.6. ПРЕДСТАВЛЕНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ РЯДАМИ И ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ
- Разложение по гармоническим функциям.
- Разложение в ряд Котельникова.
- Случайные процессы, определяемые двумерной плотностью вероятности.
- Представление случайных процессов дифференциальными уравнениями.
- 2.7. ОГИБАЮЩАЯ И ФАЗА СИГНАЛА. АНАЛИТИЧЕСКИЙ СИГНАЛ. КВАДРАТУРНЫЕ КОМПОНЕНТЫ УЗКОПОЛОСНОГО СИГНАЛА
- Корреляционная функция узкополосного случайного процесса.
- 2.8. НЕКОТОРЫЕ МОДЕЛИ НЕПРЕРЫВНЫХ И ДИСКРЕТНЫХ ИСТОЧНИКОВ (СООБЩЕНИЙ, СИГНАЛОВ И ПОМЕХ)
- Некоторые модели источников (сообщений, сигналов, помех).
- Модели речевого сообщения.
- Модель стохастического дискретного источника.
- ВЫВОДЫ
- ГЛАВА 3. ОСНОВЫ ТЕОРИИ МОДУЛЯЦИИ И ДЕТЕКТИРОВАНИЯ
- 3.1. ПРЕОБРАЗОВАНИЕ КОЛЕБАНИЙ В ПАРАМЕТРИЧЕСКИХ И НЕЛИНЕЙНЫХ ЦЕПЯХ
- 3.2. ФОРМИРОВАНИЕ И ДЕТЕКТИРОВАНИЕ СИГНАЛОВ АМПЛИТУДНОЙ МОДУЛЯЦИИ
- 3.3. ФОРМИРОВАНИЕ И ДЕТЕКТИРОВАНИЕ СИГНАЛОВ УГЛОВОЙ МОДУЛЯЦИИ
- 3.4. ФОРМИРОВАНИЕ И ДЕТЕКТИРОВАНИЕ СИГНАЛОВ ОДНОПОЛОСНОЙ МОДУЛЯЦИИ
- 3.5. ФОРМИРОВАНИЕ И ДЕТЕКТИРОВАНИЕ СИГНАЛОВ, МОДУЛИРОВАННЫХ ДИСКРЕТНЫМИ СООБЩЕНИЯМИ
- Цифровая амплитудная модуляция (ЦАМ).
- Цифровая фазовая модуляция (ЦФМ).
- Цифровая частотная модуляция (ЦЧМ).
- 3.6. МОДУЛЯЦИЯ И ДЕТЕКТИРОВАНИЕ ПРИ ИМПУЛЬСНОМ ПЕРЕНОСЧИКЕ
- 3.7. ФУНКЦИЯ КОРРЕЛЯЦИИ И СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ МОЩНОСТИ МОДУЛИРОВАННЫХ СИГНАЛОВ ПРИ МОДУЛЯЦИИ СЛУЧАЙНЫМ ПРОЦЕССОМ
- 3.8. ПОМЕХОУСТОЙЧИВОСТЬ АМПЛИТУДНОЙ И УГЛОВОЙ МОДУЛЯЦИИ
- ВЫВОДЫ
- ГЛАВА 4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ КАНАЛОВ СВЯЗИ. ПРЕОБРАЗОВАНИЕ СИГНАЛОВ В КАНАЛАХ СВЯЗИ
- 4.2. ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ МОДЕЛИ КАНАЛОВ СВЯЗИ
- 4.3. ПРЕОБРАЗОВАНИЯ СИГНАЛОВ В ЛИНЕЙНЫХ И НЕЛИНЕЙНЫХ КАНАЛАХ
- 4.3.2. ПРЕОБРАЗОВАНИЕ УЗКОПОЛОСНЫХ СИГНАЛОВ В УЗКОПОЛОСНЫХ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ КАНАЛАХ
- 4.3.3. ПРЕОБРАЗОВАНИЯ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
- 4.3.4. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ В ДЕТЕРМИНИРОВАННЫХ ЛИНЕЙНЫХ КАНАЛАХ
- 4.3.5. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ В ДЕТЕРМИНИРОВАННЫХ НЕЛИНЕЙНЫХ КАНАЛАХ
- 4.3.6. ПРОХОЖДЕНИЕ СИГНАЛОВ ЧЕРЕЗ СЛУЧАЙНЫЕ КАНАЛЫ СВЯЗИ
- 4.3.7. АДДИТИВНЫЕ ПОМЕХИ В КАНАЛЕ
- 4.3.8. КВАНТОВЫЙ ШУМ
- 4.4. МОДЕЛИ НЕПРЕРЫВНЫХ КАНАЛОВ СВЯЗИ
- 4.4.2. КАНАЛ С АДДИТИВНЫМ ГАУССОВСКИМ ШУМОМ
- 4.4.3. КАНАЛ С НЕОПРЕДЕЛЁННОЙ ФАЗОЙ СИГНАЛА И АДДИТИВНЫМ ШУМОМ
- 4.4.4. КАНАЛ С МЕЖСИМВОЛЬНОЙ ИНТЕРФЕРЕНЦИЕЙ (МСИ) И АДДИТИВНЫМ ШУМОМ
- 4.5. МОДЕЛИ ДИСКРЕТНЫХ КАНАЛОВ СВЯЗИ
- 4.5.1. НЕКОТОРЫЕ МОДЕЛИ ДИСКРЕТНЫХ КАНАЛОВ С ПАМЯТЬЮ
- 4.5.2. МОДЕЛЬ ДИСКРЕТНО-НЕПРЕРЫВНОГО КАНАЛА
- 4.6. МОДЕЛИ НЕПРЕРЫВНЫХ КАНАЛОВ СВЯЗИ, ЗАДАННЫЕ ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИМИ
- ВЫВОДЫ
- ГЛАВА 5. ТЕОРИЯ ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- 5.2. КРИТЕРИИ КАЧЕСТВА И ПРАВИЛА ПРИЁМА ДИСКРЕТНЫХ СООБЩЕНИЙ
- 5.3. ОПТИМАЛЬНЫЕ АЛГОРИТМЫ ПРИЁМА ПРИ ПОЛНОСТЬЮ ИЗВЕСТНЫХ СИГНАЛАХ (КОГЕРЕНТНЫЙ ПРИЁМ)
- 5.4. ОПТИМАЛЬНЫЙ ПРИЁМНИК С СОГЛАСОВАННЫМ ФИЛЬТРОМ
- 5.5. ПОМЕХОУСТОЙЧИВОСТЬ ОПТИМАЛЬНОГО КОГЕРЕНТНОГО ПРИЁМА
- 5.6. ОБРАБОТКА СИГНАЛОВ В КАНАЛАХ С МЕЖСИМВОЛЬНОЙ ИНТЕРФЕРЕНЦИЕЙ
- 5.7. ПРИЁМ СИГНАЛОВ С НЕОПРЕДЕЛЁННОЙ ФАЗОЙ (НЕКОГЕРЕНТНЫЙ ПРИЁМ)
- 5.8. ПРИЁМ ДИСКРЕТНЫХ СООБЩЕНИЙ В УСЛОВИЯХ ФЛУКТУАЦИИ ФАЗ И АМПЛИТУД СИГНАЛОВ
- 5.9. ПРИЁМ ДИСКРЕТНЫХ СООБЩЕНИЙ В КАНАЛАХ С СОСРЕДОТОЧЕННЫМИ ПО СПЕКТРУ И ИМПУЛЬСНЫМИ ПОМЕХАМИ
- 5.10. ПОМЕХОУСТОЙЧИВОСТЬ ПРИЁМА ДИСКРЕТНЫХ СООБЩЕНИЙ В ОПТИЧЕСКОМ ДИАПАЗОНЕ ВОЛН
- 5.11. СРАВНЕНИЕ ПОМЕХОУСТОЙЧИВОСТИ СИСТЕМ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ
- ВЫВОДЫ
- ГЛАВА 6. ПОТЕНЦИАЛЬНЫЕ ВОЗМОЖНОСТИ ПЕРЕДАЧИ СООБЩЕНИЙ ПО КАНАЛАМ СВЯЗИ (ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ)
- 6.1. ПРОБЛЕМА ОБЕСПЕЧЕНИЯ СКОЛЬ УГОДНО ВЫСОКОЙ ВЕРНОСТИ ПЕРЕДАЧИ ДИСКРЕТНЫХ СООБЩЕНИЙ В КАНАЛАХ С ПОМЕХАМИ
- 6.2. ПОТЕНЦИАЛЬНЫЕ ВОЗМОЖНОСТИ ДИСКРЕТНЫХ КАНАЛОВ СВЯЗИ
- 6.2.2. ОСНОВНОЙ ПОНЯТИЙНЫЙ АППАРАТ ТЕОРИИ ИНФОРМАЦИИ
- Энтропия источника сообщений.
- Количество информации, передаваемой по каналу связи (взаимная информация).
- 6.2.3. ТЕОРЕМЫ КОДИРОВАНИЯ ШЕННОНА ДЛЯ ДИСКРЕТНОГО КАНАЛА СВЯЗИ
- Теорема о свойстве асимптотической равновероятности (САР).
- Теорема кодирования в дискретном канале с помехами.
- 6.3. ПОТЕНЦИАЛЬНЫЕ ВОЗМОЖНОСТИ НЕПРЕРЫВНЫХ КАНАЛОВ СВЯЗИ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СООБЩЕНИЙ
- 6.3.2. КОЛИЧЕСТВО ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ ПО НЕПРЕРЫВНОМУ КАНАЛУ СВЯЗИ, РАСЧЁТ ЕГО ПРОПУСКНОЙ СПОСОБНОСТИ
- 6.3.3. ТЕОРЕМА КОДИРОВАНИЯ ДЛЯ НЕПРЕРЫВНОГО КАНАЛА СВЯЗИ
- 6.3.4. ПОТЕНЦИАЛЬНЫЕ ВОЗМОЖНОСТИ КАНАЛОВ СО МНОГИМИ ПОЛЬЗОВАТЕЛЯМИ
- ВЫВОДЫ
- ГЛАВА 7. КОДИРОВАНИЕ ИСТОЧНИКОВ И КАНАЛОВ СВЯЗИ
- 7.2. КОНСТРУКТИВНЫЕ МЕТОДЫ КОДИРОВАНИЯ ИСТОЧНИКОВ СООБЩЕНИЙ
- 7.3. ПОМЕХОУСТОЙЧИВОЕ (КАНАЛЬНОЕ) КОДИРОВАНИЕ
- 7.3.1. ВЕРОЯТНОСТЬ ОШИБКИ ОПТИМАЛЬНОГО ДЕКОДИРОВАНИЯ ДЛЯ КОДОВ С ФИКСИРОВАННОЙ ДЛИНОЙ БЛОКОВ (ЭКСПОНЕНТЫ ВЕРОЯТНОСТЕЙ ОШИБОК)
- 7.3.2. КОДЫ С ГАРАНТИРОВАННЫМ ОБНАРУЖЕНИЕМ И ИСПРАВЛЕНИЕМ ОШИБОК
- 7.3.3. ЛИНЕЙНЫЕ ДВОИЧНЫЕ КОДЫ ДЛЯ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК
- 7.3.4. ВАЖНЫЕ ПОДКЛАССЫ ЛИНЕЙНЫХ ДВОИЧНЫХ КОДОВ
- 7.3.5. КОНСТРУКТИВНЫЕ АЛГОРИТМЫ ИСПРАВЛЕНИЯ ОШИБОК ЛИНЕЙНЫМИ КОДАМИ
- 7.3.6. ОБОБЩЕНИЕ ТЕОРИИ КОДИРОВАНИЯ НА НЕДВОИЧНЫЕ КОДЫ
- 7.3.7 ИТЕРАТИВНЫЕ И КАСКАДНЫЕ КОДЫ
- 7.3.8. КОДИРОВАНИЕ В КАНАЛАХ С ПАМЯТЬЮ
- 7.3.9. СИСТЕМЫ С ОБРАТНОЙ СВЯЗЬЮ
- 7.3.10. ЗАКЛЮЧЕНИЕ ПО § 7.3. ОБЪЕДИНЕНИЕ ОПЕРАЦИЙ ДЕМОДУЛЯЦИИ И ДЕКОДИРОВАНИЯ. ДЕКОДИРОВАНИЕ С МЯГКИМ РЕШЕНИЕМ
- 7.4. СВЕРТОЧНЫЕ (РЕШЕТЧАТЫЕ) КОДЫ
- ВЫВОДЫ
- ГЛАВА 8. ТЕОРИЯ ПОМЕХОУСТОЙЧИВОСТИ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ
- 8.1. КРИТЕРИИ ПОМЕХОУСТОЙЧИВОСТИ ПРИЁМА НЕПРЕРЫВНЫХ СООБЩЕНИЙ
- 8.2. ОПТИМАЛЬНАЯ ОЦЕНКА ОТДЕЛЬНЫХ ПАРАМЕТРОВ СИГНАЛА
- 8.3. ОПТИМАЛЬНАЯ ДЕМОДУЛЯЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 8.4. ПОМЕХОУСТОЙЧИВОСТЬ СИСТЕМ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ ПРИ СЛАБЫХ ПОМЕХАХ
- 8.5. ПОРОГ ПОМЕХОУСТОЙЧИВОСТИ. АНОМАЛЬНЫЕ ОШИБКИ
- 8.6. ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ. ФИЛЬТР КОЛМОГОРОВА-ВИНЕРА
- 8.7. ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ НЕПРЕРЫВНЫХ СООБЩЕНИЙ. ФИЛЬТР КАЛМАНА
- 8.8. ТЕОРИЯ НЕЛИНЕЙНОЙ ФИЛЬТРАЦИИ
- 8.9. ОБЩИЕ СВЕДЕНИЯ О ЦИФРОВОЙ ПЕРЕДАЧЕ НЕПРЕРЫВНЫХ СООБЩЕНИЙ
- 8.10. ПОМЕХОУСТОЙЧИВОСТЬ ИМПУЛЬСНО-КОДОВОЙ МОДУЛЯЦИИ
- 8.11. КОДИРОВАНИЕ С ПРЕДСКАЗАНИЕМ
- ВЫВОДЫ
- ГЛАВА 9. ПРИНЦИПЫ МНОГОКАНАЛЬНОЙ СВЯЗИ И РАСПРЕДЕЛЕНИЯ ИНФОРМАЦИИ
- Основные положения линейной теории разделения сигналов.
- Условие линейного разделения сигналов.
- 9.2. ЧАСТОТНОЕ, ВРЕМЕННОЕ И ФАЗОВОЕ РАЗДЕЛЕНИЕ СИГНАЛОВ
- Временной способ разделения каналов.
- Разделение сигналов по фазе.
- 9.3. РАЗДЕЛЕНИЕ СИГНАЛОВ ПО ФОРМЕ. СИСТЕМЫ ПЕРЕДАЧИ С ШУМОПОДОБНЫМИ СИГНАЛАМИ
- Системы передачи с шумоподобными сигналами (ШПС).
- Примеры шумоподобных сигналов.
- 9.4. КОМБИНАЦИОННОЕ РАЗДЕЛЕНИЕ СИГНАЛОВ
- 9.5. ПРОПУСКНАЯ СПОСОБНОСТЬ СИСТЕМ МНОГОКАНАЛЬНОЙ СВЯЗИ
- Влияние взаимных помех при разделении сигналов на пропускную способность многоканальных систем.
- 9.6. ПРИНЦИПЫ ПОСТРОЕНИЯ СЕТЕЙ СВЯЗИ
- 9.6.1. СЕТЬ РАСПРЕДЕЛЕНИЯ ИНФОРМАЦИИ И ЕЁ ЭЛЕМЕНТЫ
- 9.6.2. МЕТОДЫ КОММУТАЦИИ В СЕТЯХ СВЯЗИ
- 9.6.3. МНОГОУРОВНЕВАЯ АРХИТЕКТУРА СВЯЗИ И ПРОТОКОЛЫ
- 9.6.4. ПЕРСПЕКТИВЫ РАЗВИТИЯ СЕТЕЙ СВЯЗИ
- ВЫВОДЫ
- ГЛАВА 10. ОСНОВЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ
- 10.1. СПЕКТР ДИСКРЕТНОГО СИГНАЛА
- 10.2. АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 10.3. ВРЕМЕННЫЕ И СПЕКТРАЛЬНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ ЦИФРОВЫХ ФИЛЬТРОВ
- 10.4. ИСПОЛЬЗОВАНИЕ z-ПРЕОБРАЗОВАНИЯ В ТЕОРИИ СТАЦИОНАРНЫХ ЛИНЕЙНЫХ ЦИФРОВЫХ ФИЛЬТРОВ
- 10.5. ОСНОВЫ РЕАЛИЗАЦИИ ЦИФРОВЫХ ФИЛЬТРОВ
- 10.6. УЧЁТ ПОГРЕШНОСТИ ЦИФРОВОЙ ФИЛЬТРАЦИИ ИЗ-ЗА КВАНТОВАНИЯ СИГНАЛОВ ПО УРОВНЯМ
- ВЫВОДЫ
- ГЛАВА 11. АНАЛИЗ ЭФФЕКТИВНОСТИ И ОПТИМИЗАЦИЯ СИСТЕМ СВЯЗИ
- 11.2. ХАРАКТЕРИСТИКИ И ПОКАЗАТЕЛИ ЭФФЕКТИВНОСТИ СИСТЕМ ПЕРЕДАЧИ ИНФОРМАЦИИ
- Эффективность систем передачи дискретных сообщений.
- Эффективность аналоговых систем передачи и отдельных разновидностей систем разделения сигналов.
- 11.3. ВЫБОР СИГНАЛОВ И ПОМЕХОУСТОЙЧИВЫХ КОДОВ
- Корректирующие коды.
- Сигнально-кодовые конструкции (СКК).
- 11.4. КОМПЕНСАЦИЯ ПОМЕХ И ИСКАЖЕНИЙ В КАНАЛЕ
- 11.5. СОКРАЩЕНИЕ ИЗБЫТОЧНОСТИ. СЖАТИЕ ДАННЫХ
- 11.6. ОПТИМИЗАЦИЯ СИСТЕМ СВЯЗИ
- ВЫВОДЫ
- ЗАКЛЮЧЕНИЕ
- СПИСОК ЛИТЕРАТУРЫ
Энтропия и неопределенность
Таким образом, мы выяснили, что измерение количества информации в сообщении можно проводить на основе учета изменения неопределенности. К. Шеннон ввел понятие энтропии как меры неопределенности. Энтропия H(m) определяет количество информации в сообщении m и является мерой его неопределенности.
Пусть источник сообщений может создавать n разных сообщений m 1 , m 2 , … m n с вероятностями p 1 , p 2 ,… , p n . В этом случае энтропия сообщения будет определяться формулой

Так как в данной формуле используется двоичный логарифм, то энтропия измеряется в битах, что общепринято в криптографии, теории информации и в компьютерных науках.
“Физический” смысл энтропии состоит в том, что энтропия — это количественная мера неопределенности. В качестве примера рассмотрим три источника сообщений, каждый из которых может генерировать только по два разных сообщения m1 и m2. Пусть известно, что для первого источника вероятность появления первого сообщения р(m1)=0, а вероятность второго сообщения р(m1)=1. Для второго источника вероятности сообщений равны, то есть р(m1)=0,5 и р(m2)=0,5. Для третьего источника вероятности сообщений следующие: р(m1)=0,9 и р(m1)=0,1. Определим энтропию каждого из источников сообщений. Для первого источника:
H1 = -0 * log2 0 – 1 * log2 1 = 0 – 0 = 0
Энтропия или неопределенность первого источника равна нулю. И действительно, если заранее известно, что из двух сообщений всегда генерируется только одно, то никакой неопределенности нет.
Определим энтропию второго источника:

Неопределенность оказалась равной одному биту. Найдем теперь энтропию третьего источника:

Неопределенность у третьего источника меньше, чем у второго, так как из двух возможных сообщений, генерируемых третьим источником, одно более вероятно, чем другое.
Понятие энтропии играет важную роль во многих задачах теории передачи и хранения информации. В частности, энтропия может использоваться для определения максимальной степени сжатия данных. Точнее, если источник сообщений порождает текст достаточно большой длины n с определенной предельной энтропией h на бит сообщения, то этот текст теоретически может быть сжат до величины n*h бит. Например, если h = 1/2, то текст может сжиматься вдвое и т.д. Значение n*h является пределом и на практике достигается редко.
С точки зрения криптографии, энтропия определяет количество символов, которые необходимо раскрыть, чтобы узнать содержание сообщения. Так, если некоторый 8-битовый блок данных хранит одно из двух возможных сообщений (например, ответы “Да” или “Нет” ), то достаточно правильно узнать один бит, чтобы определить значение исходного сообщения. Сколько бы бит мы не отводили для шифрования слов “Да” и “Нет”, энтропия или неопределенность всегда будет меньше или равна 1.
Норма языка и избыточность сообщений
Для каждого языка можно ввести величину, называемую нормой языка r и определяемую по формуле
где H(m) – это энтропия сообщения, а N – длина сообщения в символах используемого языка. Норму языка можно рассматривать как количество информации, приходящееся на один символ сообщения. Норма языка будет различной для разных языков, а также для сообщений с разной длиной и содержанием. Так, например, различные исследователи оценивают норму английского языка в диапазоне от 1,0 до 1,5 бит на символ. Будем считать, что норма русского языка примерно равна 1,5 бит на символ.
Абсолютной нормой языка R называют максимальное количество бит информации, которое может быть передано одним символом рассматриваемого языка, при условии, что все последовательности символов равновероятны. Абсолютная норма языка, алфавит которого состоит из L символов, может быть вычислена как
Для русского языка, алфавит которого состоит из 33 букв, абсолютная норма языка

Таким образом, видно, что абсолютная норма русского языка значительно больше, чем реальная. В этом нет ничего удивительного, так как все естественные языки обладают значительной избыточностью. Это связано с несколькими факторами. Во-первых, некоторые буквы алфавита встречаются в сообщениях чаще других. Некоторая статистика по символам русского алфавита приведена в лекции 2, где рассматривается процесс криптоанализа сообщения на основе статистических данных языка. Второй причиной избыточности является то, что некоторые сочетания букв в словах недопустимы. Например, в русском языке нет слов, в которых стояли бы подряд буквы “ц” и “й” или “я” и “ь”. Кроме того, естественные языки устроены таким образом, что иногда, зная фрагмент слова или фразы, мы может восстановить недостающую часть. Например, в приветствии
Зд.авствуй, до.огой д.уг!
мы легко сможет восстановить недостающие буквы “р”.
Избыточность языка D оценивают как
Избыточность русского языка получается равной 3,5 бит на символ. Это означает, что в среднем каждая буква русского языка содержит 3,5 бита неиспользуемой информации. Примерно такую же избыточность имеют и другие естественные языки, например, английский.
Минимальной избыточностью сообщений D = 0 обладал бы язык, в котором все символы равновероятны и могут встречаться в сообщениях независимо друг от друга в любом порядке.
Понятие совершенно секретной системы
Криптографическая система называется совершенно секретной, если анализ зашифрованного текста не может дать никакой информации об открытом тексте, кроме, возможно, его длины.
Если криптографическая система не является совершенно секретной, то знание шифротекста сообщения предоставляет некоторую информацию относительно соответствующего открытого текста. Для большинства простых систем шифрования, например, методов однократной замены или перестановки, по мере увеличения длины перехваченного зашифрованного сообщения можно делать некоторые выводы о ключе шифрования или об открытом тексте. Это связано с большой избыточностью естественных языков. Так, например, если перехвачено сообщение, зашифрованное методом перестановки, то противник может узнать, какие символы и в каком количестве встречались в исходном сообщении, а после этого может попробовать провести какой-либо более сложный анализ с целью определения правила перестановки. Если нам известно зашифрованное методом моноалфавитной замены сообщение ДКДК, мы, конечно, без дополнительной информации не сможем однозначно определить, что содержалось в исходном тексте. Однако, получив в свое распоряжение ДКДК, мы сможем сделать вывод, что
- в исходном сообщении использовалось всего две буквы алфавита
- первая и третья, а также вторая и четвертые буквы открытого текста были одинаковы.
Можно также предположить, что либо Д, либо К заменяют гласную букву. Может быть, исходное сообщение представляло собой слово МАМА, а может быть ПАПА, а может быть что-нибудь еще. Однозначно дешифровать его нельзя, однако некоторую информацию по шифротексту мы смогли определить. Таким образом, можно сделать вывод, что методы перестановки или замены не являются совершенно секретными криптографическими шифрами.
На практике возможна следующая реализация совершенно секретной системы, называемая одноразовая лента (или одноразовый блокнот, или шифр Вернама по имени американского инженера, предложившего эту систему в первой половине ХХ века). Будем предполагать, что процессу шифрования подвергаются двоичные данные. На передающей и приемной сторонах подготавливаются две одинаковые ленты, например, магнитные. Они содержат ключ шифрования. На передающей стороне лента помещается в устройство шифрования, а на принимающей стороне – в идентичное устройство, используемое для расшифрования. Когда отправитель хочет передать сообщение, он складывает по модулю два один бит исходного сообщения и один бит с магнитной ленты. После этого лента перемещается в следующее положение и можно шифровать второй бит сообщения, используя второй бит ключа. Таким образом шифруется все сообщение. На принимающей стороне лента с ключом используется аналогично.
Например, пусть исходное сообщение m содержит следующие двоичные цифры:
Предположим, в качестве ключевой используется последовательность:
Выполним шифрование по методу одноразовой ленты, сложив цифры в каждом столбике по модулю 2:
исходный текст m = 1100101110... биты ключевой послед-ти k = 1001100111... ------------------- зашифрованный текст с = 0101001001...
Этот процесс напоминает наложение гаммы на поток входных данных. Шифр с одноразовой лентой действительно является гаммированием, однако, в отличие от всех рассмотренных до этого криптосистем в нем предполагается бесконечная гамма.
В одноразовой ленте все буквы встречаются с одинаковой частотой. Поэтому, сколько бы знаков гаммы нам ни было известно, мы не сможем предсказать, какой будет следующая буква. Из этого следует, что все последовательности знаков гаммы равновероятны. Это означает, что сообщение, зашифрованное с помощью шифра Вернама, может быть “дешифровано” в любой открытый текст подходящей длины, поскольку предполагаемая последовательность знаков гаммы не имеет никаких свойств, позволяющих отличить её от любой другой.
В шифре Вернама, конечно, совсем необязательно использовать в качестве носителя ключевых данных именно ленту. Главное, чтобы у отправителя и получателя был секретный ключ размера не меньшего, чем длина исходного сообщения. Проблемы могут возникнуть при шифровании большого объема данных, так как запасы ключевых цифр должны быть заблаговременно доставлены получателю информации и храниться у него.
Совершенно секретные системы могут быть реализованы на практике. Почему же они не используются во всех случаях? Это объясняется несколькими причинами. Во-первых, как и любые системы шифрования с закрытым ключом в них существует проблема распределения ключей. Во-вторых, в совершенной секретной системе ключ шифрования должен иметь по крайней мере такую же длину, как и открытый текст. Кроме того, для шифрования каждого сообщения должен применяться свой новый ключ. Все эти факторы делают реализацию совершенно секретной системы очень дорогой и не слишком удобной. Такие системы имеет смысл использовать лишь для самых важных линий связи, например, правительственных.
Мы ежедневно работаем с информацией из разных источников. При этом каждый из нас имеет некоторые интуитивные представления о том, что означает, что один источник является для нас более информативным, чем другой. Однако далеко не всегда понятно, как это правильно определить формально. Не всегда большое количество текста означает большое количество информации. Например, среди СМИ распространена практика, когда короткое сообщение из ленты информационного агентства переписывают в большую новость, но при этом не добавляют никакой «новой информации». Или другой пример: рассмотрим текстовый файл с романом Л.Н. Толстого «Война и мир» в кодировке UTF-8. Его размер — 3.2 Мб. Сколько информации содержится в этом файле? Изменится ли это количество, если файл перекодировать в другую кодировку? А если заархивировать? Сколько информации вы получите, если прочитаете этот файл? А если прочитаете его второй раз?
По мотивам открытой лекции для Computer Science центра рассказываю о том, как можно математически подойти к определению понятия “количество информации”.
В классической статье А.Н. Колмогорова “Три подхода к определению понятия количества информации” (1965) рассматривают три способа это сделать:
-
комбинаторный (информация по Хартли),
-
вероятностный (энтропия Шеннона),
-
алгоритмический (колмогоровская сложность).
Мы будем следовать этому плану.
Комбинаторный подход: информация по Хартли
Мы начнём самого простого и естественного подхода, предложенного Хартли в 1928 году.
Пусть задано некоторое конечное множество . Количеством информации в
будем называть
.
Можно интерпретировать это определение следующим образом: нам нужно битов для описания элемента из
.
Почему мы используем биты? Можно использовать и другие единицы измерения, например, триты или байты, но тогда нужно изменить основание логарифма на 3 или 256, соответственно. В дальшейшем все логарифмы будут по основанию 2.
Этого определения уже достаточно для того, чтобы измерить количество информации в некотором сообщении. Пусть про стало известно, что
. Теперь нам достаточно
битов для описания
, таким образом нам сообщили
битов информации.
Пример
Загадано целое число
от
до
. Нам сообщили, что
делится на
. Сколько информации нам сообщили?
Воспользуемся рассуждением выше.
(Тот факт, что некоторое сообщение может содержать нецелое количество битов, может показаться немного неожиданным.)
Можно ещё сказать, что сообщение, уменшающее пространство поиска в раз приносит
битов информации. В данном примере пространство поиска уменьшилось в 1000/166 раз.
Интересно, что одного этого определения уже достаточно для того, чтобы решать довольно нетривиальные задачи.
Применение: цена информации
Загадано целое число
от
до
. Разрешается задавать любые вопросы на ДА/НЕТ. Если ответ на вопрос “ДА”, то мы должны заплатить рубль, если ответ “НЕТ” — два рубля. Сколько нужно заплатить для отгадывания числа
?
Любой вопрос можно сформулировать как вопрос о принадлежности некоторому множеству, поэтому мы будем считать, что все вопросы имеют вид “?” для некоторого множества
.
Каким образом нужно задавать вопросы? Нам бы хотелось, чтобы вне зависимости от ответа цена за бит информации была постоянной. Другими словами, в случае ответа “НЕТ” и заплатив два рубля мы должны узнать в два больше информации, чем при ответе “ДА”. Давайте запишем это формально.
Потребуем, чтобы
Пусть , тогда
. Подставляем и получаем, что
Это эквивалентно квадратному уравнению Положительный корень этого уравнения
. Таким образом, при любом ответе мы заплатим
рублей за бит информации, а в сумме мы заплатим примерно
рублей (с точностью до округления).
Осталось понять, как выбирать такие множества . Будем выбирать в качестве
непрерывные отрезки прямой. Пусть нам известно, что
принадлежит отрезку
(изначально это отрезок
). В следующего множества
возмём отрезок
, где
. Тогда за каждый заплаченный рубль текущий отрезок будет уменьшаться в
раз. Когда длина отрезка станет меньше единицы, мы однозначно определим
. Поэтому цена отгадывания не будет превосходить
Приведённое рассуждение доказывает только верхнюю оценку. Можно доказать и нижнюю оценку: для любого способа задавать вопросы будет такое число , для отгадывания которого придётся заплатить не менее
рублей.
Вероятностный подход: энтропия Шеннона
Вероятностный подход, предложенный Клодом Шенноном в 1948 году, обобщает определение Хартли на случай, когда не все элементы множества являются равнозначными. Вместо множества в этом подходе мы будем рассматривать вероятностное распределение на множестве и оценивать среднее по распределению количество информации, которое содержит случайная величина.
Пусть задана случайная величина , принимающая
различных значений с вероятностями
. Энтропия Шеннона случайной величины
определяется как
(По непрерывности тут нужно доопределить .)
Энтропия Шеннона оценивает среднее количество информации (математическое ожидание), которое содержится в значениях случайной величины.
При первом взгляде на это определение, может показаться совершенно непонятно откуда оно берётся. Шеннон подошёл к этой задаче чисто математически: сформулировал требования к функции и доказал, что это единственная функция, удовлетворяющая сформулированным требованиям.
Я попробую объяснить происхождение этой формулы как обобщение информации по Хартли. Нам бы хотелось, чтобы это определение согласовывалось с определением Хартли, т.е. должны выполняться следующие “граничные условия”:
Будем искать в виде математического ожидания количества информации, которую мы получаем от каждого возможного значения
.
Как оценить, сколько информации содержится в событии ? Пусть
— всё пространство элементарных исходов. Тогда событие
соответствует множеству элементарных исходов меры
. Если произошло событие
, то размер множества согласованных с этим событием элементарных исходов уменьшается с
до
, т.е. событие
сообщает нам
битов информации. Тут мы пользуемся тем, что количество информации в сообщении, которое уменьшает размер пространство поиска в
раз приносит
битов информации.
Примеры
Свойства энтропии Шеннона
Для случайной величины , принимающей
значений с вероятностями
, выполняются следующие соотношения.
-
.
-
распределение
вырождено.
-
.
-
распределение
равномерно.
Чем распределение ближе к равномерному, тем больше энтропия Шеннона.
Энтропия пары
Понятие энтропии Шеннона можно обобщить для пары случайных величин. Аналогично это обощается для тройки, четвёрки и т.д.
Пусть совместно распределённые случайные величины и
принимают значения
и
, соответственно. Энтропия пары случайных величин
и
определяется следующим соотношением:
Примеры
Рассмотрим эксперимент с выбрасыванием двух игральных кубиков — синего и красного.
Свойства энтропии Шеннона пары случайных величин
Для энтропии пары выполняются следующие свойства.
Условная энтропия Шеннона
Теперь давайте научимся вычислять условную энтропию одной случайной величины относительно другой.
Условная энтропия относительно
определяется следующим соотношением:
Примеры
Рассмотрим снова примеры про два игральных кубика.
Свойства условной энтропии
Условная энтропия обладает следующими свойствами
Взаимная информация
Ещё одна информационная величина, которую мы введём в этом разделе — это взаимная информация двух случайных величин.
Информация в о величине
(взаимная информация случайных величин
и
) определяется следующим соотношением
Примеры
И снова обратимся к примерам с двумя игральными кубиками.
Свойства взаимной информации
Выполняются следующие соотношения.
-
. Т.е. определение взаимной информации симметрично и его можно переписать так:
-
Или так:
.
-
и
.
-
.
-
.
Все информационные величины, которые мы определили к этому моменту можно проиллюстрировать при помощи кругов Эйлера.
Мы пойдём дальше и рассмотрим информационную величину, зависящую от трёх случайных величин.
Пусть ,
и
совместно распределены. Информация в
о
при условии
определяется следующим соотношением:
Свойства такие же как и обычной взаимной информации, нужно только добавить соответствующее условие ко всем членам.
Всё, что мы успели определить можно удобно проиллюстрировать при помощи трёх кругов Эйлера.
Из этой иллюстрации можно вывести все определения и соотношения на информационные величины.
Мы не будем продолжать дальше и рассматривать четыре случайные величины по трём причинам. Во-первых, рисовать четыре круга Эйлера со всеми возможными областями — это непросто. Во-вторых, для двух и трёх случайных величин почти все возможные соотношения можно вывести из кругов Эйлера, а для четырёх случайных величин это уже не так. И в третьих, уже для трёх случайных величин возникают неприятные эффекты, демонстрирующие, что дальше будет хуже.
Рассмотрим треугольник в пересечении всех трёх кругов ,
и
. Этот треугольник соответствуют взаимной информации трёх случайных величин
. Проблема с этой информационной величиной заключается в том, что ей не удаётся придать какой-то “физический” смысл. Более того, в отличие от всех остальных величин на картинке
может быть отрицательной!
Рассмотрим пример трёх случайных величин равномерно распределённых на . Пусть
и
будут независимы, а
. Легко проверить, что
. При этом
. В то же время
. Получается следующая картинка.
Мы знаем, что . При этом
. Получается, что
, а
, т.е. для таких случайных величин
.
Применение энтропии Шеннона: кодирование
В этом разделе мы обсудим, как энтропия Шеннона возникает в теории кодирования. Будем рассматривать коды, которые кодируют каждый символ по отдельности.
Пусть задан алфавит . Код — это отображение из
в
. Код
называется однозначно декодируемым, если любое сообщение, полученное применением
к символам некоторого текста, декодируется однозначно.
Код называется префиксным (prefix-free), если нет двух символов и
таких, что
является префиксом
.
Префиксные коды являются однозначно декодируемыми. Действительно, при декодировании префиксного кода легко понять, где находятся границы кодов отдельных символов.
Теорема [Шеннон]. Для любого однозначно декодируемого кода существует префиксный код с теми же длинами кодов символов.
Таким образом для изучения однозначно декодируемых кодов достаточно рассматривать только префиксные коды.
Задача об оптимальном кодировании.
Дан текст . Нужно найти такой код
, что
Пусть . Обозначим через
частоту, с которой символ
встречается в
. Тогда выражение выше можно переписать как
Следующая теорема могла встречаться вам в курсе алгоритмов.
Теорема [Хаффман]. Код Хаффмана, построенный по , является оптимальным префиксным кодом.
Алгоритм Хаффмана по набору частот эффективно строит оптимальный код для задачи оптимального кодирования.
Связь с энтропией
Имеют место две следующие оценки.
Теорема [Шеннон]. Для любого однозначно декодируемого кода выполняется
Теорема [Шеннон]. Для любых значений существует префиксный код
, такой что
Рассмотрим случайную величину , равномерно распределённую на символах текста
. Получим, что
. Таким образом, эти две теоремы задают оценку на среднюю длину кода символа при оптимальном кодировании, т.е. и для кодирования Хаффмана.
Следовательно, длину кода Хаффмана текста можно оценить, как
Применение энтропии Шеннона: шифрования с закрытым ключом
Рассмотрим простейшую схему шифрования с закрытым ключом. Шифрование сообщения с ключом шифрования
выполняется при помощи алгоритма шифрования
. В результате получается шифрограмма
. Зная
получатель шифрограммы восстанавливает исходное сообщение
:
.
Мы будем анализировать эту схему с помощью аппарата энтропии Шеннона. Пусть и
являются случайными величинами. Противник не знает
и
, но знает
, которая так же является случайной величиной.
Для совершенной схемы шифрования (perfect secrecy) выполняются следующие соотношения:
-
, т.е. шифрограмма однозначно определяется по ключу и сообщению.
-
, т.е. исходное сообщение однозначно восстанавливается по шифрограмме и ключу.
-
, т.е. в отсутствие ключа из шифрограммы нельзя получить никакой информации о пересылаемом сообщении.
Теорема [Шеннон]. , даже если условие
нарушается (т.е. алгоритм
использует случайные биты).
Эта теорема утверждает, что для совершенной схемы шифрования длина ключа должна быть не менее длины сообщения. Другими словами, если вы хотите зашифровать и передать своему знакомому файл размера 1Гб, то для этого вы заранее должны встретиться и обменяться закрытым ключом размера не менее 1Гб. И конечно, этот ключ можно использовать только однажды. Таким образом, самая оптимальная совершенная схема шифрования — это “одноразовый блокнот”, в котором длина ключа совпадает с длиной сообщения.
Если же вы используете ключ, который короче пересылаемого сообщения, то шифрограмма раскрывает некоторую информацию о зашифрованном сообщении. Причём количество этой информации можно оценить, как разницу между энтропией сообщения и энтропией ключа. Если вы используете пароль из 10 символов при пересылке файла размера 1Гб, то вы разглашаете примерно 1Гб – 10 байт.
Это всё звучит очень печально, но не всё так плохо. Мы ведь никак не учитываем вычислительную мощь противника, т.е. мы не ограничиваем количество времени, которое противнику потребуется на выделение этой информации.
Современная криптография строится на предположении об ограниченности вычислительных возможностей противника. Тут есть свои проблемы, а именно отсутствие математического доказательства криптографической стойкости (все доказательства строятся на различных предположениях), так что может оказаться, что вся эта криптография бесполезна (подробнее можно почитать в статье о мирах Рассела Импальяццо, которая переведена на хабре), но это уже совсем другая история.
Доказательство. Нарисуем картинку для трёх случайных величин и отметим то, что нам известно.
-
.
-
, следовательно
, а значит
.
-
(по свойству взаимной информации), следовательно
, а значит
.
-
. Таким образом,
В доказательстве мы действительно не воспользовались тем, что .
Алгоритмический подход: колмогоровская сложность
Подход Шеннона хорош для случайных величин, но если мы попробуем применить его к текстам, то выходит, что количество информации в тексте зависит только от частот символов, но не зависит от их порядка. При таком подходе получается, что в “Войне и мире” и в тексте, который получается сортировкой всех знаков в “Войне и мире”, содержится одинаковое количество информации. Колмогоров предложил подход, позволяющий измерять количество информации в конкретных объектах (строках), а не в случайных величинах.
Внимание. До этого момента я старался следить за математической строгостью формулировок. Для того, чтобы двигаться дальше в том же ключе, мне потребовалось бы предположить, что читатель неплохо знаком с математической логикой и теорией вычислимости. Я пойду более простым путём и просто буду махать руками, заметая под ковёр некоторые подробности. Однако, все утверждения и рассуждения дальше можно математически строго сформулировать и доказать.
Нам потребуется зафиксировать способ описания битовой строки. Чтобы не углубляться в рассуждения про машины Тьюринга, мы будем описывать строки на языках программирования. Нужно только сделать оговорку, что программы на этих языках будут запускаться на компьютере с неограниченным объёмом оперативной памяти (иначе мы получили бы более слабую вычислительную модель, чем машина Тьюринга).
Сложностью строки
относительно языка программирования
называется длина кратчайшей программы, которая выводит
.
Таким образом сложность “Войны и мира” относительноя языка Python — это длина кратчайшей программы на Python, которая печатает текст “Войны и мира”. Естественным образом сложность отсортированной версии “Войны и мира” относительно языка Python получится значительно меньше, т.к. её можно предварительно закодировать при помощи RLE.
Сравнение языков программирования
Дальше нам потребуется научиться любимой забаве всех программистов — сравнению языков программирования.
Будем говорить, что язык не хуже языка программирования
и обозначать
, если существует константа
такая, что для для всех
выполняется
Исходя из этого определения получается, что язык Python не хуже (!) этого вашего Haskell! И я это докажу. В качестве константы мы возьмём длину реализации интепретатора Haskell на Python. Таким образом, любая программа на Haskell переделывается в программу на Python просто дописыванием к ней интерпретатора Haskell на Python.
Соломонов и Колмогоров пошли дальше и доказали существования оптимального языка программирования.
Теорема [Соломонова-Колмогорова]. Существует способ описания (язык программирования) такой, что для любого другого способа описания
выполняется
.
И да, некоторые уже наверное догадались, что — это JavaScript. Или любой другой Тьюринг полный язык программирования.
Это приводит нас к следующему определению, предложенному Колмогоровым в 1965 году.
Колмогоровской сложностью строки будем называть её сложность относительно оптимального способа описания
и будем обозначать
.
Важно понимать, что при разных выборах оптимального языка программирования колмогоровская сложность будет отличаться, но только на константу. Для любых двух оптимальных языков программирования
и
выполняется
и
, т.е. существует такая константа
, что
Это объясняет, почему в этой науке аддитивные константы принято игнорировать.
При этом для конкретной строки и конкретного выбора колмогоровская сложность определена однозначно.
Свойства колмогоровской сложности
Начнём с простых свойств. Колмогоровская сложность обладает следующими свойствами.
Первое свойство выполняется потому, что мы всегда можем зашить строку в саму программу. Второе свойство верно, т.к. из программы, выводящей строку , легко сделать программу, которая выводит эту строку дважды.
Примеры
Несжимаемые строки
Важнейшее свойство колмогоровской сложности заключается в существовании сложных (несжимаемых строк). Проверьте себя и попробуйте объяснить, почему не бывает идеальных архиваторов, которые умели бы сжимать любые файлы хотя бы на 1 байт, и при этом позволяли бы однозначно разархивировать результат.
В терминах колмогоровской сложности это можно сформулировать так.
Вопрос. Существует ли такая длина строки
, что для любой строки
колмогоровская сложность
меньше
?
Следующая теорема даёт отрицательный ответ на этот вопрос.
Теорема. Для любого существует
такой, что
.
Доказательство. Битовых строк длины всего
. Число строк сложности меньше
не превосходит число программ длины меньше
, т.е. таких программ не больше чем
Таким образом, для какой-то строки гарантированно не хватит программы.
Верна и более сильная теорема.
Теорема. Существует такое, что для
слов длины
верно
Другими словами, почти все строки длины имеют почти максимальную сложность.
Колмогоровская сложность: вычислимость
В этом разделе мы поговорим про вычислимость колмогоровской сложности. Я не буду давать формально определение вычислимости, а буду опираться на интуитивные предствления читателей.
Теорема. Не существует программы, которая по двоичной записи числа выводит строку
, такую что
.
Эта теорема говорит о том, что не существует программы-генератора, которая умела бы генерировать сложные строки по запросу.
Доказательство. Проведём доказетельство от противного. Пусть такая программа существует и
. Тогда с одной стороны сложность
не меньше
, а с другой стороны мы можем описать
при помощи
битов и кода программы
.
Это приводит нас к противоречию, т.к. при достаточно больших значениях неизбежно станет больше, чем
.
Как следствие мы получаем невычислимость колмогоровской сложности.
Следствие. Отображение не является вычислимым.
Опять же, предположим, что это нет так и существует программа , которая по строку вычисляет её колмогоровскую сложность. Тогда на основе программы
можно реализовать программу
из теоремы выше: она будет перебирать все строки длины не более
и находить лексикографически первую, для которой сложность будет не меньше
. А мы уже доказали, что такой программы не существует.
Связь с энтропией Шеннона
Теорема. Пусть длины
содержит
единиц и
нулей, тогда
Я надеюсь, что вы уже узнали энтропию Шеннона для случайной величины с двумя значениями с вероятностями и
.
Для колмогоровской сложности можно проделать весь путь, который мы проделали для энтропии Шеннона: определить условную колмогоровскую сложность, сложность пары строк, взаимную информацию и условную взаимную информацию и т.д. При этом формулы будут повторять формулы для энтропии Шеннона с точностью до . Однако это тема для отдельной статьи.
Применение колмогоровской сложности: бесконечность множества простых чисел
Начнём с довольно игрушечного применения. С помощью колмогоровской сложности мы докажем следующую теорему, знакомую нам со школы.
Теорема. Простых чисел бесконечно много.
Очевидно, что для доказательства этой теоремы никакая колмогоровская сложность не нужна. Однако на этом примере я смогу продемонстрировать основные идеи применения колмогоровской сложности в более сложных ситуациях.
Доказательство. Проведём доказательство от обратного. Пусть существует всего простых чисел:
. Тогда любое натуральное
раскладывается на степени простых:
т.е. определяется набором степеней . Каждое
, т.е. задаётся
битами. Поэтому любое
можно задать при помощи
битов (помним, что
— это константа).
Теперь воспользуемся теоремой о существовании несжимаемых строк. Как следствие, мы можем заключить, что существуют -битовые числа
сложности не менее
(можно взять сложную строку и приписать в начало единицу). Получается, что сложное число можно задать при помощи небольшого числа битов.
Противоречие.
Применение колмогоровской сложности: алгоритмическая случайность
Колмогоровская сложность позволяет решить следующую проблему из классической теории вероятностей.
Пусть в лаборатории живёт обезьянка, которую научили печатать на печатной машинке так, что каждую кнопку она нажимает с одинаковой вероятность. Вам предлагается посмотреть на лист печатного текста и сказать, верите ли вы, что его напечатала эта обезьянка. Вы смотрите на лист и видите, что это первая страница “Гамлета” Шекспира. Поверите ли вы? Очевидно, что нет. Хорошо, а если это не Шекспир, а, скажем, текст детектива Дарьи Донцовой? Скорей всего тоже не поверите. А если просто какой-то набор русских слов? Опять же, очень сомневаюсь, что вы поверите.
Внимание, вопрос. А как объяснить, почему вы не верите? Давайте для простоты считать, что на странице помещается 2000 знаков и всего на машинке есть 80 знаков. Вы можете резонно заметить, что вероятность того, что обезьянка случайным образом породила текст “Гамлета” порядка , что астрономически мало. Это верно.
Теперь предположим, что вам показали текст, который вас устроил (он с вашей точки зрения будет похож на “случайный”). Но ведь вероятность его появления тоже будет порядка . Как же вы определяете, что один текст выглядит “случайным”, а другой — не выглядит?
Колмогоровская сложность позволяет дать формальный ответ на этот вопрос. Если у текста отстутствует короткое описание (т.е. в нём нет каких-то закономерностей, которые можно было бы использовать для сжатия), то такую строку можно назвать случайной. И как мы увидели выше почти все строки имеют большую колмогоровскую сложность. Поэтому, когда вы видите строку с закономерностями, т.е. маленькой колмогоровской сложности, то это соответствует очень редкому событию. В противоположность наблюдению строки без закономерностей. Вероятность увидеть строку без закономерностей близка к 1.
Это обобщается на случай бесконечных последовательностей. Пусть . Как определить понятие случайной последовательности?
(неформальное определение)
Последовательность случайна по Мартину–Лёфу, если каждый её префикс является несжимаемым.
Оказывается, что это очень хорошее определение случайных последовательностей, т.к. оно обладает ожидаемыми свойствами.
Свойства случайных последовательностей
-
Почти все последовательности являются случайными по Мартину–Лёфу, а мера неслучайных равна
.
-
Всякая случайная по Мартину-Лёфу последовательность невычислима.
-
Если
случайная по Мартин-Лёфу, то
Заключение
Если вам интересно изучить эту тему подробнее, то я рекомендую обратиться к следующим источникам.
-
Верещагин Н.К., Щепин Е.В. Информация, кодирование и предсказание. МЦНМО. (нет в свободном доступе, но pdf продаётся за копейки)
-
В.А. Успенский, А.Х. Шень, Н.К. Верещагин. Колмогоровская сложность и алгоритмическая случайность.
-
Курс “Введение в теорию информации” А.Е. Ромащенко в Computer Science клубе.
Если вам интересны подобные материалы, подписывайтесь в соцсетях на CS клуб и CS центр, а так же на наши каналы на youtube: CS клуб, CS центр.

