Как найти энтропию по графику

Глава VIII. ДИАГРАММА ТЕМПЕРАТУРА – ЭНТРОПИЯ

§ 39. Свойства системы координат температура — энтропия (Т — s)

При введении понятия энтропии было установлено, что эта величина является параметром состояния. Из уравнения

следует, что использовать энтропию s как параметр, характери­зующий состояние рабочего тела, удобнее всего в сочетании с абсолют­ной температурой Т.

Если энтропию и температуру рассматривать как координаты не­которой плоскостной системы коор­динат (рис. 42), то каждому сочета­нию значений s и Т на плоскости координат (точки А, В и т. д.) будут соответствовать вполне определенные состояния рабочего тела. Очевидно также, что каждый процесс в коор­динатах Т—s представляется неко­торой линией, для которой в про­стейших случаях можно установить аналитическое выражение зависимости s = f (Т).

При нанесении какого-либо процесса на координатную плос­кость sT необходимо знать абсолютное значение энтропии. Это зна­чение, вообще говоря, может быть вычислено. Но для решения тер­модинамических задач в подавляющем большинстве случаев тре­буется определять только изменение энтропии в процессе. Поэтому вместо сложного вычисления абсолютных значений энтропии выбирают условный отсчет ее от какого-либо фиксированного состо­яния. Так, для идеального газа за начало отсчета энтропии при­нимают обычно нормальные физические условия (0° С и 760 мм рт. ст.), при которых энтропия условно считается равной нулю.

93

При таком способе отсчета энтропии изменение ее в процессах останется тем же, что и разность абсолютных значений энтро­пии.

Изменение энтропии в обратимом процессе в этом случае мо­жет быть подсчитано также по общей формуле

Если взять на кривой процесса А В (рис. 42) элементарный от­резок, в котором изменение температуры будет бесконечно мало (dT), то площадь под этим элементарным процессом (заштрихован­ная площадка) будет равна произведению текущего значения тем­пературы Т на бесконечно малое приращение энтропии ds. Но, как известно, это произведение для обратимого процесса равно теплоте в обратимом процессе, т. е. dq = Tds.

Взяв бесконечно большую сумму бесконечно малых площадок по всему процессу АВ, получим площадь под кривой этого про­цесса. Аналитически эта сумма представляет собой интеграл от выражения Т ds в пределах от А до В, Этот интеграл численно ра­вен теплоте в процессе, т. е.

Следовательно, в координатах Т—s теплота представляется площадью под линией процесса. Поэтому часто диаграмму Т—s называют тепловой диаграммой.

По характеру протекания линии процесса в координатах Т—s легко определить знак теплоты в процессе.

Из соотношения dq следует, что так как температура всегда положительна, знак dq определяется знаком ds. Если энтропия в процессе возрастает, то это значит, что теплота положительная, т. е. подводится, и наоборот. Аналитически это можно записать так: ds > 0 и dq > 0, ds < 0 и dq < 0.

Следует подчеркнуть, что в системе Т—s изображают процессы изменения состояния рабочего тела, и поэтому изменение энтро­пии относится только к рабочему телу, а не к системе, в которой этот процесс осуществляется.

следовательно, работа за цикл в тепловых единицах (дж) равна

Круговые_процессы или циклы в координатах Т—s, так же как и в любой другой системе координат, где по осям отложены параметры состояния, представляются замкнутыми линиями. Так как в таких процессах изменение внутренней энергии тела u = 0, то работа за цикл определяется как алгебраическая сум­ма подводимой и отводимой теплоты:

95

разности площадей под верхней и нижней ветвями цикла, т.е. I — пл. а1А2b — пл. а1В2b (рис. 43). Эта работа соответствует площади, ограниченной линиями цикла (пл. 1А2В1). Если площадь под ли­нией процесса подвода теплоты больше площади, соответствующей отводимой теплоте, то работа цикла положительная, цикл 1А2В1 прямой. Для обратного цикла площадь, характеризующая под­веденную теплоту, будет меньше площади, представляющей собой отведенную теплоту. Значит, ра­бота за цикл отрицательная.

Очевидно, что термический к. п. д. цикла будет равен

Координаты Т—s с нанесен­ными на них графиками простей­ших процессов для данного рабочего тела называют диаграммой T—s этого тела. Простейшей тепловой диаграммой будет диаграм­ма для идеального газа. Для построения этих диаграмм необхо­димо рассмотреть основные процессы идеального газа в координатах Т—s.

§ 40. Основные процессы идеального газа в координатах Т—s

Из этого следует, что

Для процесса v — const (рис. 44) изменение энтропии в пределах от точки 1 до точки 2 выразится как

Считая, что теплоемкость в процессе остается постоянной, по­лучаем

Изохорный процесс (v = const). Для изохорного процесса бесконечно малое количество теплоты

или, переходя к десятичным логарифмам,

Изохора в координатах Т—s представляется логарифмической кривой 1—2. Площадь под линией процесса а12b соответствует теплоте в процессе

которая равна изменению внутренней энергии рабочего тела (ра­бота в процессе равна нулю):

Такой же вывод получается при рассмотрении процессов

Принимая теплоемкость в про­цессе постоянной, получаем

или

Изобарный процесс, так же как и изохорный, в координатах Т—s представляется логарифмической кривой. Площадь под ли­нией процесса а12b соответствует теплоте в процессе

эта теплота равна изменению энтальпии рабочего тела.

Рассмотрение изобары и изохоры, проходящих через одну и ту же точку (рис. 46), приводит к выводу, что изохора расположена круче, чем изобара. Это объясняется следующим образом:

Изотермический процесс (Т = const). В координатах этот про­цесс представляется прямой, параллельной оси абсцисс (рис. 47). Уравнение процесса: Т = const.

Для изотермического процесса идеального газа

изменение энтропии

Заменяя по уравнению состояния газа

получаем

97

Для процесса 1—2 (рис. 47)

или, переходя к десятичным логарифмам, получим

Отношение объемов можно заменить через обратное отношение давлений. Тогда

Для любых двух изохор v₁ = const и v₂ = const (рис. 48) легко установить, что расстояния между ними в направлении, параллель­ном оси абсцисс, одинаковы. Это следует из того, что для любой изо-

термы, расположенной между этими изохорами, изменение энтро­пии рабочего тела будет одно и то же:

Это значит, что все изохоры эквидистантны в направлении, параллельном оси абсцисс. Подобным же образом может быть по­казана эквидистантность изобар в том же направлении:

Адиабатный процесс (dq = 0)._ Для этого процесса, так же как
и для любого другого:

Теплота отводится от рабочего тела по изотерме cd. Количест­во отводимой теплоты соответствует площади

99

Для адиабатного процесса dq = 0, поэтому ds = 0. Отсюда сле­дует, что обратимый адиабатный процесс характеризуется постоян-

ством энтропии s = const. На этом основании такой процесс час­то называют изоэнтропным.

Очевидно, графиком такого процесса явится прямая, парал­лельная оси ординат (рис. 49). Такой вид графика адиабатного процесса указывает на то, что этот процесс характеризуется не только тем, что dq = 0, но и тем, что q = 0. Это находится в пол­ном соответствии со всем сказанным выше.

§ 41. Диаграмма Т —s для идеального газа

На рис. 50 приведен пример общего вида части диаграммы для газа, подчиняющегося уравнению состояния газа. Сплошными горизонтальными и вертикальными линиями нанесены соответственно изотермы и адиабаты. Начало координат по оси энтропии (ось абсцисс) выбирается условно.

Сплошные логарифми­ческие кривые представ­ляют собой изобары. При этом изобары, соответст­вующие большим давле­ниям, располагаются бли­же к оси ординат, т. е.

Рп > Р₁

Пунктирными логариф­мическими кривыми на­несены изохоры. Изохо­ры, расположенные ближе к оси ординат, соответствуют мень­шим объемам, т. е. v_n < v₁.

Такой диаграммой удобно пользоваться при исследовании процессов и циклов, протекающих в рабочих телах, которые мож­но принимать за идеальные газы. Это допустимо, например, при исследовании рабочего процесса воздушных и некоторых газовых компрессоров, двигателей внутреннего сгорания, газотурбинных установок и т. п. В качестве примера в приложении дана диаграм­ма Т—s для воздуха, который принимается за идеальный газ.

§ 42. Цикл Карно на диаграмме Т — s

Цикл Карно, состоящий из двух изотерм и двух адиабат, пред­ставится в координатах T—s в виде прямоугольника abed (рис. 51). Изотерма ab соответствует процессу подвода теплоты. Количество подводимой к рабочему телу теплоты определяется как площадь

Энтропия
Размерность
Единицы измерения
СИ	Дж/К
СГС	эрг/К

Термодинамические величины
Статья является частью серии «Термодинамика»
Энтропия Количество теплоты Термодинамическая работа Химический потенциал См. также: Термодинамические потенциалы.
Разделы термодинамики
Начала термодинамики Уравнение состояния Термодинамические величины Термодинамические потенциалы Термодинамические циклы Фазовые переходы
См. также «Физический портал»

Термодинамическая энтропия , часто именуемая просто энтропией, — физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин; энтропия и температура — сопряжённые термодинамические величины, необходимые для описания термических свойств системы и тепловых процессов в ней. Энтропия является функцией состояния и широко используется в термодинамике, в том числе технической (анализ работы тепловых машин и холодильных установок) и химической (расчёт равновесий химических реакций).

Утверждение о существовании энтропии и перечисление её свойств составляют содержание второго и третьего начал термодинамики. Значимость данной величины для физики обусловлена тем, что наряду с температурой её используют для описания термических явлений и термических свойств макроскопических объектов. Качественные представления о термическом состоянии системы связаны с тепловыми ощущениями, выражаемыми понятиями «теплее», «холоднее», «нагрев», «охлаждение», «степень нагретости». К термическим относят свойства, характеризующие поведение вещества при его нагреве или охлаждении: термические коэффициенты, теплоёмкость и другие калорические коэффициенты, постоянную Кюри, показатели термостойкости, пределы огнестойкости и т. д.; примерами термических явлений служат термическое расширение, пироэлектричество, электрокалорический эффект, теплопроводность, изменение агрегатного состояния — кристаллизация и замерзание, плавление и таяние, испарение, кипение, сублимация (возгонка), конденсация и другие процессы.

Историческая справка[править | править код]

Понятие энтропии, её обозначение и название были введены Р. Клаузиусом (1865). Абстрактность этого понятия — одного из краеугольных камней термодинамики — и разнообразие подходов к обоснованию существования энтропии как термодинамической величины привели к появлению аксиоматики термодинамики.

Термодинамическая дефиниция энтропии[править | править код]

В термодинамике энтропию вводят, обосновывая её существование, перечисляя её свойства и строя для неё шкалу измерения на основании первого, второго и третьего начал термодинамики.

В термодинамических формализмах Клаузиуса^[1] и Каратеодори^[2] энтропию вводят одновременно с абсолютной термодинамической температурой. Математический аппарат термодинамики Гиббса^[3] основан на использовании энтропии в качестве независимой термодинамической переменной, тогда как температура — естественный кандидат на эту роль, вводится как функция внутренней энергии и энтропии. Наконец, в рациональной термодинамике энтропию выражают через внутреннюю энергию и температуру, которые рассматривают как основные неопределяемые переменные теории.

Энтропия простой системы[править | править код]

Первое начало (закон) термодинамики устанавливает связь между внутренней энергией, работой и теплотой: одна из этих физических величин задаётся с помощью двух других, которые, будучи исходными объектами теории, в рамках самой этой теории определены быть не могут просто потому, что не существует понятий более общих, под которые их можно было бы подвести^[4]. Термодинамика заимствует понятия энергии и работы из других разделов физики^[5][6], тогда как определение количеству теплоты, наоборот, даётся только и именно в термодинамике. Согласно Клаузиусу теплоту определяют через внутреннюю энергию и работу ^[7][8]. При использовании термодинамического правила знаков^[9] математическое выражение для первого начала термодинамики в формулировке Клаузиуса имеет вид^[10]:

(Дефиниция теплоты по Клаузиусу)

Первое начало в этой формулировке вводит теплоту как физическую характеристику процесса, поведение которой определяется законом сохранения энергии, но не определяет её как математический объект. Детализировать дефиницию теплоты проще всего для равновесного процесса, когда работу, а следовательно и теплоту, можно выразить через переменные состояния. Для бесконечно малого^[11] равновесного процесса в простой системе^[12] возможен единственный вид работы — работа расширения/сжатия :

(Работа расширения/сжатия для равновесного процесса в простой системе)

где  — давление,  — объём; символ означает, что соответствующая величина относится к бесконечно малому процессу. Таким образом, для первого начала термодинамики в формулировке Клаузиуса получаем^[13][14]:

(Первое начало для равновесного процесса в простой системе)

где  — элементарная (бесконечно малая) теплота процесса.

Это выражение, определяющее элементарную теплоту как математический объект, есть линейная дифференциальная форма (форма Пфаффа) для двух независимых переменных. Для данной пфаффовой формы условие интегрируемости Эйлера не выполняется, то есть есть функционал^[15], а не полный дифференциал несуществующей функции ^[14]. Из теории дифференциальных форм известно, однако, что если выполняется условие Фробениуса^[16], то пфаффова форма имеет интегрирующий множитель/делитель, превращающий эту форму в полный дифференциал и представляющий собой функцию тех же независимых переменных, которые входят в форму Пфаффа^[17]. Пфаффовы формы, имеющие интегрирующий множитель/делитель называют голономными; пфаффова форма двух переменных всегда голономна (теорема Коши)^[18][19]. Поэтому для простых равновесных систем существует функция состояния , полный дифференциал которой равен

(Дефиниция энтропии простой равновесной системы)

где

есть интегрирующий делитель для формы Пфаффа. Клаузиус назвал функцию состояния энтропией (от греческого ἐντροπία — изменение, превращение, преобразование). Второе начало термодинамики утверждает, что энтропия существует для любых равновесных систем, а не только простых, и что интегрирующий делитель есть абсолютная термодинамическая температура^{[20][21][22][19]}. Неравновесная термодинамика распространяет представление о локальной энтропии и локальной температуре на любые термодинамические системы.

Интегрирование уравнения для энтропии приводит к появлению в выражении для функции произвольной постоянной, зависящей от выбора начальной точки отсчёта энтропии. Произвол в выборе начального состояния для энтропии устраняет третий закон термодинамики.

Энтропия закрытой системы в термодинамике Клаузиуса — Каратеодори[править | править код]

Традиционный подход к построению термодинамики (аксиоматика Клаузиуса — Каратеодори) основан на использовании представления о внутренней энергии как базовом понятии теории, заимствовании формул для вычисления термодинамической работы из механики и электродинамики сплошных сред, и первом начале термодинамики в формулировке Клаузиуса.

Помимо работы расширения/сжатия система может одновременно выполнять другие виды работ, например работу по изменению площади поверхности раздела фаз, работу перемещения в поле тяготения, работу поляризации диэлектрика в электрическом поле и т. д. Объединяет все эти виды работ формальная структурная идентичность расчётных формул друг с другом и с выражением для работы расширения/сжатия^[23][24][25]:

где  — элементарная работа -го типа,  — обобщённая координата, сопряжённая с обобщённой силой Каждой обобщённой координате соответствует своя обобщённая сила; физические переменные, соответствующие обобщённым координатам и силам, конкретизируют применительно к решаемой задаче^[26][27].

Если однородная система одновременно совершает несколько различных видов работ, то они суммируются и полная работа системы равна^[23][28][29]

(Суммарная работа для равновесного процесса в однородной системе)

а для первого начала термодинамики получаем соотношение^[30][31]:

(Первое начало для равновесного процесса в однородной системе)

которое как и в случае простой системы представляет собой форму Пфаффа. Следствием второго начала термодинамики в любой его формулировке является вывод о том, что пфаффова форма при любом числе переменных всегда голономна^[21] и, следовательно, для любой закрытой термодинамической системы существуют энтропия

(Энтропия однородной закрытой системы)

и абсолютная термодинамическая температура

Выражение есть сокращение для перечисления переменных определённого типа, в данном случае — обобщённых координат.

Энтропия открытой системы[править | править код]

Принимая, что теплота и работа являются двумя единственно возможными формами передачи энергии^[32][33][34], а изменение энергии, связанное с переносом вещества в открытой системе, есть составная часть общей работы, называемая химической работой (работой перераспределения масс веществ^[35]), в случае однородной открытой системы дифференциальную форму для закрытой системы следует дополнить слагаемым, учитывающим элементарную химическую работу ^{[36][37][38][39][40]}:

(Химическая работа для равновесного процесса в открытой однородной системе)

где  — масса -го компонента^[41],  — химический потенциал этого компонента.

Пфаффова форма для открытой однородной системы равна^[29]

(Первое начало для равновесного процесса в открытой однородной системе)

Дальнейшие рассуждения о существовании энтропии

и абсолютной термодинамической температуры

для открытой системы ничем не отличаются от соображений, высказанных при рассмотрении закрытой системы, поэтому ниже перечислены причины, по которым открытые системы потребовали отдельного рассмотрения.

Первая из этих причин состоит в том, что использование в понятийном аппарате термодинамики химической работы как части общей работы делает неэквивалентными представления об адиабатной изоляции как накладывающей запрет на обмен веществом (то есть любая адиабатно изолированная система есть система закрытая или, говоря иначе, масса есть адиабатически заторможенная величина)^{[42][43][44][45]}, и адиабатной изоляции как допускающей обмен энергией только в форме работы^[46][47]. Восстановить эквивалентность приведённых выше формулировок об адиабатной изоляции удаётся, если модифицировать дефиницию теплоты по Клаузиусу, добавив к теплоте и работе третью форму передачи энергии — энергию переноса массы ^[48][49]:

(Модифицированная дефиниция теплоты для открытой системы)

где задаётся выражением для химической работы.

Вторая причина отдельного рассмотрения вопроса об энтропии открытых систем заключается в следующем. За исключением химического потенциала все входящие в пфаффову форму для открытой системы переменные в рамках термодинамического формализма представляют собой неопределяемые величины, заимствуемые из других разделов физики, что подразумевает необязательность их описания в самой термодинамике. Химический потенциал вводится в термодинамике и либо должен быть отнесён к базовым неопределяемым понятиям, для которых возможно только пояснительное описание, либо же от термодинамики требуется точная дефиниция химического потенциала. Как неопределяемую величину химический потенциал можно вводить одновременно с температурой и энтропией (более, того П. А. Жилин^[50] считает такой подход единственно правильным^[51]), но традиционно химический потенциал предпочитают вводить в рассмотрение как вторичную переменную на основе предварительно сформированного представления об энтропии открытой системы. Для этого вслед за У. Гиббсом^[52][45] без доказательства принимают утверждение о существовании энтропии открытой системы^[53][54][55]

(Энтропия открытой однородной системы по Гиббсу; фундаментальное уравнение Гиббса в энтропийном выражении)

как функции состояния, при неизменности масс компонентов совпадающей с энтропией однородной закрытой системы. Из фундаментального уравнения Гиббса в дифференциальной форме^[55]

(Дифференциальная форма фундаментального уравнения Гиббса для энтропии)

находим значения частных производных энтропии:

Химический потенциал -го компонента выразим через частную производную энтропии по массе этого компонента^[56]:

(Дефиниция химического потенциала компонента)

Энтропия в термодинамике Гиббса[править | править код]

Построение теории на основе постулирования существования энтропии как функции состояния, в состав независимых переменных которой входят массы компонентов, составляет главное содержание термодинамики Гиббса^[57], а способ, каким выполнено распространение термодинамики Клаузиуса на открытые системы, позволяет говорить об аксиоматике Гиббса^[52][45]. В термодинамике Гиббса вводят понятия компонента системы, фазы и многофазной гетерогенной системы, постулируют существование внутренней энергии и энтропии как аддитивных переменных состояния, постулируют связь этих величин с независимыми переменными состояния в виде фундаментальных уравнений Гиббса в энергетическом и энтропийном выражениях, постулируют аддитивность входящих в эти фундаментальные уравнения независимых переменных, постулируют, что есть термодинамическая температура, вводят химический потенциал и постулируют общее условие термодинамического равновесия в системе^[58], рассматриваемое далее в числе свойств энтропии.

Обратите внимание, что содержательную дефиницию температуры по Гиббсу^[59][60][61]

(Термодинамическая температура по Гиббсу)

можно, с другой стороны, рассматривать и как описательную дефиницию энтропии. А именно, энтропия в термодинамике Гиббса есть такая экстенсивная переменная состояния, что производная внутренней энергии по энтропии представляет собой интенсивную переменную состояния, обладающую всеми положенными термодинамической температуре свойствами.

Энтропия в рациональной термодинамике[править | править код]

Рациональная термодинамика не подразделяет термодинамику на равновесную и неравновесную; обе эти дисциплины рассматриваются как единая часть физики сплошных сред^{[62][63][64][65]}. Равновесная рациональная термодинамика есть результат применения общей теории к системам в состоянии равновесия^[66]. Исходные неопределяемые понятия теории — энергия , объём и число молей компонента . По аналогии с давлением

при механическом равновесии имеющем одинаковое значение во всех частях системы, вводят химический потенциал

как интенсивную величину, имеющую при химическом равновесии одно и то же значение во всех частях системы^[67].
Абсолютную термодинамическую температуру вводят посредством следующей аксиомы: существует интенсивная термодинамическая величина, температура

которая характеризует степень нагретости тел и обладает следующими свойствами^[68]:

• в выбранном за начало отсчёта состоянии температура равна нулю

 ;

• температура монотонно растёт с увеличением энергии системы

 ;

• при термодинамическом равновесии имеет одно и то же значение во всех частях системы.

Энтропию в рациональной термодинамике задают как аддитивную величину, равную^[69]

Свойства энтропии, вытекающие из этого определения^[69]:

 ;

 ;

 ;

где  — теплоёмкость системы при постоянном объёме. Из определения энтропии и её свойств следует, что при условии постоянства энергии энтропия системы максимальна, когда все части системы имеют одинаковую температуру — вариационный принцип максимальности энтропии в состоянии равновесия^[69]. Таким образом, энтропия есть монотонная выпуклая функция энергии, достигающая максимума в состоянии термодинамического равновесия; состояние системы, принятое за начало шкалы отсчёта энергии, есть одновременно состояние для начальных точек отсчёта температуры и энтропии.

Свойства энтропии[править | править код]

Перечисление свойств энтропии дано применительно к термодинамике Гиббса; примеры, приводимые для иллюстрации перечисляемых свойств энтропии, относятся, как правило, к открытым однородным термодеформационным системам, для которых справедливо фундаментальное уравнение Гиббса в энтропийном выражении^[70][71]:

(Фундаментальное уравнение Гиббса в энтропийном выражении для открытой термодеформационной системы)

• Энтропия в фундаментальном уравнении в энтропийном выражении есть однозначная дифференцируемая функция аддитивных независимых переменных^[72][44][73] с непрерывными первыми и кусочно-непрерывными вторыми производными.
• Энтропия есть величина аддитивная^{[74][75][76][72][77][78][79][80]}, то есть энтропия термодинамической системы равна сумме энтропий всех её частей. Аддитивность энтропии позволяет распространить это понятие на термодинамические системы любой сложности.

Как следствие аддитивности получаем, что энтропия в фундаментальном уравнении в энтропийном выражении есть однородная функция первого порядка всех независимых переменных^[81][73], то есть для

и для неё справедливо тождество (теорема) Эйлера^[82]:

• Для однородной системы частная производная энтропии по внутренней энергии есть величина, обратная абсолютной термодинамической температуре (термодинамическая дефиниция температуры как следствие второго начала термодинамики)^{[83][60][61][84]}:

(Термодинамическая дефиниция температуры)

В соответствии с теоремой об обратных величинах^[85] это определение совпадает с дефиницией равновесной температурой по Гиббсу^[59][60][61]:

(Термодинамическая температура по Гиббсу)

• Энтропия есть монотонная функция внутренней энергии , то есть абсолютная термодинамическая температура не может менять свой знак^[70]. В шкале Кельвина абсолютная термодинамическая температура всегда положительна^[86]. Использование отрицательных по шкале Кельвина температур есть удобный математический приём описания неравновесных подсистем систем с особыми свойствами^[87].
• Энтропия есть величина полуограниченная. Традиционно принимают, что энтропия ограничена снизу, то есть для каждой термодинамической системы существует состояние с наименьшей энтропией^[88].
• Температура есть величина полуограниченная. Абсолютная температурная шкала Кельвина построена так, что

Нуль и бесконечность допустимы в качестве пределов^[88].

• Для любой термодинамической системы состояния с наименьшей энтропией и наименьшей температурой совпадают (постулат Планка)^[88][89]. С приближением температуры к абсолютному нулю энтропия перестаёт зависеть от температуры и приближается к определённому постоянному значению, которое можно положить равным нулю^[90] и принять за начало отсчёта энтропии, устранив тем самым упомянутый в разделе Энтропия простой системы произвол в выборе постоянной интегрирования для энтропии:

(Третье начало термодинамики; тепловая теорема Нернста)

Согласно постулату Тиссы внутренняя энергия ограничена и эта граница соответствует абсолютному нулю температуры^[88][91]. Таким образом, состояние системы при абсолютном нуле температуры, когда все термодинамические величины, характеризующие равновесное состояние, перестают зависеть от температуры^[92], наилучшим образом подходит в качестве стандартного состояния начала отсчёта основных термодинамических величин.

• Энтропия изолированной системы в состоянии термодинамического равновесия имеет максимальное значение (постулат Гиббса)^[93][92], то есть для равновесия изолированной системы необходимо и достаточно, чтобы при всех возможных (не нарушающих постоянства внутренней энергии, обобщённых координат и масс компонентов) изменениях её состояния вариация энтропии системы не была положительной^[94]:

(Условие равновесия изолированной системы)

Поскольку речь идёт об изолированной системе, внешнее воздействие на которую запрещено, понятие вариации в данном случае означает виртуальное изменение энтропии^[95]. Знак равенства в этом выражении относится к безразличному равновесию.

Условие равновесия Гиббса вытекает из входящего в состав второго начала термодинамики постулата Клаузиуса о неубывании энтропии адиабатно изолированной системы^[94]

• Энтропия в фундаментальном уравнении в энтропийном выражении есть характеристическая функция, то есть фундаментальное уравнение содержит все термодинамические сведения о данной системе^[73].

Энтропия как характеристическая функция[править | править код]

Энтропия и теплота квазистатического (равновесного) процесса[править | править код]

Из выражения для первого начала в открытой однородной системе и дифференциальной формы фундаментального уравнения Гиббса для энтропии получаем выражение для элементарной теплоты равновесного (квазистатического) процесса^[96][97]:

(Теплота элементарного равновесного процесса)

(для простой равновесной системы это выражение непосредственно вытекает из дефиниции энтропии).

Данное соотношение, связывающее термодинамику Клаузиуса с термодинамикой Гиббса, представляет интерес для пользователей, которым требуется изложить материал из старой учебной и научной литературы с применением терминологии, либо вовсе не использующей понятие «теплота», либо использующей его как определяемое через энтропию и абсолютную температуру вторичное понятие.

Энтропия как характеристика изотермического процесса[править | править код]

Для равновесного изотермического процесса с нулевой работой интегрирование выражения для теплоты равновесного процесса даёт следующее выражение для изменения внутренней энергии:

то есть в любом равновесном изотермическом процессе с нулевой работой энергия расходуется на увеличение энтропии системы и выделяется при уменьшении энтропии. Преобразуем это уравнение к виду

и назовём отношение приведённой внутренней энергией. Отсюда вытекает следующая трактовка — одна из нескольких существующих — физического смысла энтропии: энтропия есть приведённая внутренняя энергия изотермической системы.

Рассмотрим в качестве примера фазовые переходы в воде при атмосферном давлении (см. рисунок). При таянии льда подводимая к системе энергия расходуется на увеличение энтропии системы вследствие изменения структуры H₂O, тогда как температура системы лёд + вода остаётся близкой к 0 °C (273 К) до полного исчезновения льда. При замерзании воды имеет место обратная ситуация: энергия выделяется в окружающую среду при 0 °C. Нагрев воды, образовавшейся при таянии льда, ведёт к повышению температуры воды вплоть до её закипания при 100 °C (373 К). Кипение воды при постоянном давлении есть процесс изотермический: подводимая энергия расходуется на испарение воды и увеличение энтропии системы вода + водяной пар, тогда как температура остаётся близкой к 100 °C до полного исчезновения жидкой воды.

Статистическое определение энтропии: принцип Больцмана[править | править код]

В 1877 году Людвиг Больцман установил связь энтропии с вероятностью данного состояния. Позднее эту связь представил в виде формулы Макс Планк:

где константа 1,38⋅10⁻²³ Дж/К названа Планком постоянной Больцмана, а  — статистический вес состояния, является числом возможных микросостояний (способов), с помощью которых можно составить данное макроскопическое состояние. Этот постулат, названный Альбертом Эйнштейном принципом Больцмана, положил начало статистической механике, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы () с одним из её термодинамических свойств ().

Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых:
(I) месторасположения всех частей расположены в рамках сосуда,
(II) для получения общей энергии газа кинетические энергии атомов суммируются.

Согласно определению, энтропия является функцией состояния, то есть не зависит от способа достижения
этого состояния, а определяется параметрами этого состояния. Так как может быть только натуральным числом (1, 2, 3, …), то энтропия Больцмана должна быть неотрицательной — исходя из свойств логарифма.

Понимание энтропии как меры беспорядка[править | править код]

Существует мнение, что мы можем смотреть на энтропию и как на меру беспорядка в системе. В определённом смысле это может быть оправдано, потому что мы думаем об «упорядоченных» системах как о системах, имеющих очень малую возможность конфигурирования, а о «беспорядочных» системах как об имеющих очень много возможных состояний. Собственно, это просто переформулированное определение энтропии как числа микросостояний на данное макросостояние.

Рассмотрим, например, распределение молекул идеального газа. В случае идеального газа наиболее вероятным состоянием, соответствующим максимуму энтропии, будет равномерное распределение молекул. При этом реализуется и максимальный «беспорядок», так как при этом будут максимальные возможности конфигурирования.

Получившее повсеместное распространение понимание энтропии как меры беспорядка в термодинамической системе не является, тем не менее, общепринятым^[98]: «Тождественность энтропии с беспорядком не только никем никогда не была доказана и не только не может быть доказана в принципе, но и прямо противоречит реально наблюдаемым фактам…»^[98]; «…применительно к реальным системам энтропия не является мерой беспорядка»^[99]; «…в ходе роста энтропии Вселенной общая её (Вселенной) сложность растёт, однако для составляющих Вселенную реальных (под)систем энтропия мерой беспорядка/сложности не является»^[100].

Границы применимости понимания энтропии как меры беспорядка[править | править код]

Подобное определение беспорядка термодинамической системы как количества возможностей конфигурирования системы фактически дословно соответствует определению энтропии как числа микросостояний на данное макросостояние. Проблемы начинаются в двух случаях:

• когда начинают смешивать различные понимания беспорядка, и энтропия становится мерой беспорядка вообще;
• когда понятие энтропии применяется для систем, не являющихся термодинамическими.

В обоих этих случаях применение понятия термодинамической энтропии совершенно неправомерно^[101].

Рассмотрим оба пункта подробнее.

Рассмотрим пример термодинамической системы — распределение молекул в поле тяготения. В этом случае наиболее вероятным распределением молекул будет распределение согласно барометрической формуле Больцмана. Другой пример — учёт электромагнитных сил взаимодействия между ионами. В этом случае наиболее вероятным состоянием, соответствующим минимуму свободной энергии, будет упорядоченное кристаллическое состояние, а совсем не «хаос», хотя в состоянии «хаоса» значение конфигурационной энтропии системы и ниже. (Термин «хаос» здесь понимается в смысле беспорядка — в наивном смысле. К хаосу в математическом смысле как сильно неустойчивой нелинейной системе это не имеет отношения, конечно.)

Рассмотрим случай с кристаллической решёткой более подробно. Кристаллическая решётка может быть и в равновесном, и в неравновесном состоянии, как и любая термодинамическая система. Скажем, возьмём следующую модель — совокупность взаимодействующих осцилляторов. Рассмотрим некоторое неравновесное состояние: все осцилляторы имеют одинаковое отклонение от положения равновесия. С течением времени эта система перейдёт в состояние ТД равновесия, в котором отклонения (в каждый момент времени) будут подчинены некоторому распределению типа Максвелла (только это распределение будет для отклонений, и оно будет зависеть от типа взаимодействия осцилляторов). В таком случае максимум энтропии будет действительно реализовывать максимум возможностей конфигурирования, то есть — беспорядок согласно вышеуказанному определению. Но данный «беспорядок» вовсе не соответствует «беспорядку» в каком-либо другом понимании, например, информационному. Такая же ситуация возникает и в примере с кристаллизацией переохлаждённой жидкости, в которой образование структур из «хаотичной» жидкости идёт параллельно с увеличением энтропии.

То есть при образовании кристалла из переохлаждённой жидкости энтропия увеличивается с одновременным ростом температуры. Если кристаллизация сопровождается отводом тепла из системы, то энтропия при этом уменьшится.

Это неверное понимание энтропии появилось во время развития теории информации, в связи с парадоксом термодинамики, связанным с мысленным экспериментом так называемый «демона Максвелла». Суть парадокса заключалась в том, что рассматривалось два сосуда с разными температурами, соединённых узкой трубкой с затворками, которыми управлял так называемый «демон». «Демон» мог измерять скорость отдельных летящих молекул, и таким образом избирательно пропускать более быстрые в сосуд с высокой температурой, а более медленные — в сосуд с низкой. Из этого мысленного эксперимента вытекало кажущееся противоречие со вторым началом термодинамики.

Парадокс может быть разрешён при помощи теории информации. Для измерения скорости молекулы «демон» должен был бы получить информацию о её скорости. Но всякое получение информации — материальный процесс, сопровождающийся возрастанием энтропии. Количественный анализ^[102] показал, что приращение энтропии при измерении превосходит по абсолютной величине уменьшение энтропии, вызванное перераспределением молекул «демоном».

Измерение энтропии[править | править код]

В реальных экспериментах очень трудно измерить энтропию системы. Техники измерения базируются на термодинамическом определении энтропии и требуют экстремально аккуратной калориметрии.

Для упрощения мы будем исследовать механическую систему, термодинамические состояния которой будут определены через её объём и давление . Для измерения энтропии определённого состояния мы должны сначала измерить теплоёмкость при постоянных объёме и давлении (обозначенную и соответственно), для успешного набора состояний между первоначальным состоянием и требуемым. Тепловые ёмкости связаны с энтропией и с температурой согласно формуле:

где нижний индекс относится к постоянным объёму и давлению. Мы можем проинтегрировать для получения изменения энтропии:

Таким образом, мы можем получить значение энтропии любого состояния (, ) по отношению к первоначальному состоянию (, ). Точная формула зависит от нашего выбора промежуточных состояний. Для примера, если первоначальное состояние имеет такое же давление, как и конечное состояние, то

В добавление, если путь между первым и последним состояниями лежит сквозь любой фазовый переход первого рода, скрытая теплота, ассоциированная с переходом, должна также учитываться.

Энтропия первоначального состояния должна быть определена независимо. В идеальном варианте выбирается первоначальное состояние как состояние при экстремально высокой температуре, при которой система существует в виде газа. Энтропия в этом состоянии подобна энтропии классического идеального газа плюс взнос от молекулярных вращений и колебаний, которые могут быть определены спектроскопически.

Построение графика изменения энтропии[править | править код]

Следующее уравнение может быть использовано для построения графика изменения энтропии на диаграмме для идеального газа:

Здесь два замечания:

«Что такое энтропия?»[править | править код]

Однозначного ответа на этот вопрос не существует по той простой причине, что разных энтропий много — представление об энтропии используется в различных научных дисциплинах: термодинамике, статистической физике, теории информации и др. Но и внутри каждой из перечисленных дисциплин единообразия также нет и в помине: в теории информации рассматривают энтропию Шеннона, энтропию Реньи, энтропию Чисара, энтропию Хаврда — Чарват — Дароши^[103]; статистическая физика оперирует энтропиями Больцмана, Гиббса, Цаллиса; существуют различные дефиниции термодинамической энтропии. Содержательная дефиниция той или иной конкретной энтропии зависит от аксиоматики системы построения/изложения, использующей эту энтропию. По указанной причине не существует универсальной дефиниции термодинамической энтропии, ибо для различных аксиоматических систем термодинамики ответ на вынесенный в заголовок вопрос будет различен.

Студенты, приступающие к изучению термодинамики, часто жалуются на непонятность энтропии, связанную с отсутствием наглядности (рисунок иллюстрирует относительность представлений людей о наглядности, понятности и простоте термодинамических систем^{[K 1]}).

Для описания термических явлений в физике вводят новые комплементарные (взаимодополняющие) физические величины — температуру и энтропию, — содержательные дефиниции которым не дают ни в механике, ни в электродинамике. В термодинамике Клаузиуса — Каратеодори энтропию вводят как приведённую внутреннюю энергию изотермической системы, то есть разность энтропий равна приведённой теплоте изотермического процесса.

В термодинамике Гиббса и в системе А. А. Гухмана энтропия представляет собой неопределяемое базовое понятие — таков в этих системах содержательный ответ на рассматриваемый вопрос^{[K 2]}. В термодинамической аксиоматике А. А. Гухмана ^{[105][106][107][108][109][110]} и рациональной термодинамике в трактовке П. А. Жилина^{[65][K 3]} и температуру, и энтропию вводят как неопределяемые базовые переменные, несводимые к более простым^{[K 4]}. Пояснительное дополнение к дефиниции энтропии по Гухману разъясняет, что энтропия есть координата состояния при термическом взаимодействии (теплообмене), которое выражается в переносе энтропии от одного объекта к другому^[112].

В рациональной термодинамике в трактовке школы Трусделла в качестве базовой термической переменной используют температуру , то есть привычную и по этой причине всем понятную физическую величину. Энтропию вводят как полезную вспомогательную функцию энергии и температуры^[113]:

но, в отличие от другой функции энергии и температуры, — теплоёмкости ^[114]

в формулу, служащую дефиницией энтропии, входит не производная, а интеграл. Пояснительное дополнение к ответу, пригодное почти^{[K 5]} для любого способа изложения термодинамики, сообщает, что энтропия необходима для построения математического аппарата термодинамики и, следовательно, привлечение термодинамики к решению любой научной или практической задачи явно или неявно подразумевает использование энтропии. Польза, приносимая людям от обращения к термодинамике, есть польза от ввода энтропии в понятийный аппарат науки. Дополнительно к сказанному можно провести аналогию с теплоёмкостью: если для неизотермических процессов нагрева льда, жидкой воды и водяного пара затраты энергии равны произведению теплоёмкости на разность температур, то для изотермических процессов таяния и кипения затраты энергии равны произведению температуры на разность энтропий.

Понять энтропию и её значение для термодинамики означает, что необходимо знать происхождение этой величины, понимать её связи с другими термодинамическими переменными и уметь применять энтропию на практике^{[K 6][104]}.

См. также[править | править код]

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

• Термодинамическая энтропия
• Статья «Эволюция как сопротивление энтропии»

Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных ссылок www.libgen.io/book/index.php?md5=BB7A4DF3D04E410AB163CF2D15B4501C www.libgen.io/book/index.php?md5=FB60848D6D70A19DBF1154ECCAE49E7F

[Править] Построение графика изменения энтропии

Основная статья: адиабатический
процесс

Следующее
уравнение может быть использовано для
построения графика изменения энтропии
на диаграмме P—V:

Здесь
два замечания:

• это не определение энтропии (но выведено
  из него);

• предполагается, что C_V и
  C_P постоянные, что на самом
  деле не так.

4.5. Энтропия

Изменение
энтальпии системы не может служить
единственным критерием самопроизвольного
осуществления химической реакции,
поскольку многие эндотермические
процессы протекают самопроизвольно.
Иллюстрацией этого служит растворение
некоторых солей (например, NH₄NO₃)
в воде, сопровождающееся заметным
охлаждением раствора. Необходимо
учитывать еще один фактор, определяющий
способность самопроизвольно переходить
из более упорядоченного к менее
упорядоченному (более хаотичному)
состоянию.

Энтропия
(S) – термодинамическая функция состояния,
которая служит мерой беспорядка
(неупорядоченности) системы. Возможность
протекания эндотермических процессов
обусловлена изменением энтропии, ибо
в изолированных системах энтропия
самопроизвольно протекающего процесса
увеличивается ΔS > 0 (второй закон
термодинамики).

Модель 4.8. Энтропия и фазовые переходы

Л.
Больцман
определил энтропию как термодинамическую
вероятность состояния (беспорядок)
системы W. Энтропия связана с
термодинамической вероятностью
соотношением:

S = R · ln W

Размерность
энтропии 1 моля вещества совпадает с
размерностью газовой постоянной R и
равна Дж∙моль^–1∙K^–1.
Изменение энтропии ^*)
в необратимых и обратимых процессах
передается соотношениями ΔS > Q / T
и ΔS = Q / T. Например, изменение
энтропии плавления равно теплоте
(энтальпии) плавления ΔS_пл = ΔH_пл/T_пл.
Для химической реакции изменение
энтропии аналогично изменению энтальпии

^*)
термин энтропия был введен Клаузиусом
(1865 г.) через отношение Q / T (приведенное
тепло).

Здесь
ΔS^°
соответствует энтропии стандартного
состояния. Стандартные энтропии простых
веществ не равны нулю. В отличие от
других термодинамических функций
энтропия идеально кристаллического
тела при абсолютном нуле равна нулю
(постулат Планка),
поскольку W = 1.

Энтропия
вещества или системы тел при определенной
температуре является абсолютной
величиной. В табл. 4.1 приведены стандартные
энтропии S^°
некоторых веществ.

Соединение (Дж∙моль–1∙K–1) Соединение (Дж∙моль–1∙K–1) C(т)алмаз 2,37 NO(г) 210 C(т)графит 5,74 NO2(г) 240 H2(г) 131 N2O5(г) 342 D2(г) 145 H2O(г) 189 O(г) 161 H2O(ж) 70 O2(г) 205 D2O(ж) 79 O2(ж) 84 CH4(г) 186 O2(т) 42 C2H6(г) 229 O3(г) 237 н-C4H10(г) 310 изо-C4H10(г) 294

Таблица 4.1 Стандартные энтропии некоторых веществ

Из
табл. 4.1 следует, что энтропия зависит
от:

• агрегатного
  состояния вещества. Энтропия увеличивается
  при переходе от твердого к жидкому и
  особенно к газообразному состоянию
  (вода, лед, пар).

• изотопного
  состава (H₂O
  и D₂O).

• молекулярной
  массы однотипных соединений (CH₄,
  C₂H₆,
  н-C₄H₁₀).

• строения
  молекулы (н-C₄H₁₀,
  изо-C₄H₁₀).

• кристаллической
  структуры (аллотропии) – алмаз, графит.

Наконец,
рис. 4.3 иллюстрирует зависимость энтропии
от температуры.

Рисунок 4.3 Зависимость энтропии от температуры для свинца: ΔSпл = 8 Дж·моль–1·К–1; Tпл = 600,5 К; ΔSкип = 88 Дж·моль–1·К–1; Tкип = 2013 К

Следовательно,
стремление системы к беспорядку
проявляется тем больше, чем выше
температура. Произведение изменения
энтропии системы на температуру T ΔS
количественно оценивает эту тендецию
и называется энтропийным фактором.

Модель 4.9. Реальный газ

Энтропия.
Изменение энтропии в химических и
фазовых переходах.

Состояние любой системы может быть
охарактеризовано значениями непосредственно
измеряемых параметров (р, Т и др.). Это
характеристика макросостояния
системы.  Состояние системы
может быть описано также  
характеристиками каждой частицы системы
(атома, молекулы): координаты, частота
колебания, частота вращения и т.д. Это
характеристика микросостояния
системы.  Системы состоят из
очень большого числа частиц, поэтому
одному макросостоянию будет отвечать 
огромное число различных микросостояний.
Это число называется термодинамической
вероятностью состояния и обозначается
(W).

Термодинамическая вероятность связана
с другим свойством вещества – энтропией
(S) – формулой Больцмана

   
  (2.13)

где R –
универсальная газовая постоянная, а N_A
– постоянная Авогадро. Измеряется
энтропия в Дж/(моль^.К).

               
Физический смысл: энтропия является
мерой неупорядоченности состояния
системы. Энтропия системы
увеличивается во всех процессах, когда
возрастает неупорядоченность (нагревание,
растворение, испарение, реакции разложения
и т.п.) и уменьшается в процессах, идущих
с увеличением упорядоченности (охлаждение,
кристаллизация, сжатие и т.п.).

Энтропия является функцией состояния,
но в отличие от большинства других
термодинамических функций возможно
экспериментальное определение абсолютного
значения энтропии вещества. Эта
возможность основана на постулате
М.Планка, согласно которому «при
абсолютном нуле энтропия идеального
кристалла равна нулю» (третий закон
термодинамики).

Температурная
зависимость энтропии вещества представлена
качественно на рис.2.1.

 
   

   На рис.2.1 видно, что при нуле
Кельвина энтропия вещества равна нулю.
При повышении температуры энтропия
плавно увеличивается, а в точках фазовых
переходов   имеет место скачкообразное
увеличение энтропии, определяемое
соотношением

   
                   
       
                   
   (2.14)

где Δ _ф..п.S, Δ_ф.п.Н
и  Т_ф.п. изменение энтропии,
энтальпии и температура фазового
перехода, соответственно.

Энтропию вещества B в стандартном
состоянии обозначают .
Для многих веществ абсолютные значения
стандартных энтропий определены и
приводятся в справочных изданиях.

Энтропия, также как внутренняя энергия
и энтальпия, является функцией состояния,
поэтому изменение энтропии системы в
процессе не зависит от его пути и
определяется только начальным и конечным
состоянием системы. Изменение энтропии
в ходе химической реакции (2.10) может
быть найдено, как разность суммы энтропий
продуктов реакции и суммы энтропий
исходных веществ

  

Понятие энтропии используется в одной
из формулировок второго закона
термодинамики:  в изолированных
системах могут самопроизвольно протекать
только  процессы, идущие с увеличением
энтропии (ΔS>0).  Под изолированными
системами понимаются системы, не
обменивающиеся с окружающей средой ни
веществом, ни энергией. Системы, в которых
протекают химические процессы, к
изолированным системам не относятся,
т.к. они обмениваются с окружающей средой
энергией (тепловой эффект реакции).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

    В качестве другого примера графического дифференцирования укажем на вычисление температурного коэффициента электродвижущей силы гальванического элемента (для определения теплового эффекта или изменения энтропии в токообразующем процессе). [c.446]

Рис. П1,3. Графическое вычисление энтропии этилена.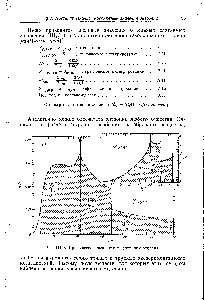

    На рис. Ill, 3, иллюстрирующем графический метод расчета энтропии на примере вычисления энтропии этилена, изображены кривые Ср/Т = ф(Т) для твердого, жидкого и газообразного этилена штриховкой показаны площади, соответствующие приростам энтропии при нагревании . (Изменения энтропии при агрегатных превращениях, естественно, не могут получить отражения на данной диаграмме.) [c.99]

    Второй и третий интегралы, которые соответственно равны изменению энтропии при нагревании двух модификаций твердого хлористого водорода, определяем графическим интегрированием. Значения второго и третьего интегралов соответственно равны 29,54 и 21,17 Дж/(моль К)- Четвертый и пятый интегралы могут быть вычислены как графическим интегрированием, так и аналитическим путем. Воспользуемся для их вычисления аналитическим методом. Зависимость теплоемкости жидкого хлористого водорода от температуры можно выразить уравнением [c.235]

    Примерами графического интегрирования служат вычисление энтальпии и энтропии вещества по температурной завнсимости теплоемкости первой — по графику С,, = / (Г), второй — по графику Ср/Т =- / (Т) нли С,, = / (1п Т). На рис. 201 приведен пример графического интегрирования для определения теплового эффекта химического процесса. [c.448]

    Величины остаточных свойств можно получить непосредственно из экспериментальных данных. Так, калориметрические измерения энтальпии и теплоемкости дают собственно остаточную энтальпию Д// и остаточную энтропию Д5. Однако количество подобных данных, особенно для смесей, ограничено. Некоторые примеры экстремального воздействия давления на теплоемкость показаны на рис. 1.3 и 1.4. На рис. 11.2 в графической форме представлен ряд измеренных величин остаточных свойств этилена. В примере 11.4 экспериментальные данные о зависимости PVT для азота применены для оценки остаточных энтальпий и энтропий результаты этих вычислений сопоставляются с результатами расчетов, выполненных на основе некоторых уравнений состояния. [c.512]

    Находя температуру, при которой давление пара твердой и жидкой фаз одинаково, мы определим точку плавления. Энтропия плавления может быть определена обычным способом как разность энтропии твердого тела и жидкости при температуре плавления. Изображая графически максимальную работу как функцию объема и находя две точки, в которых кривая имеет общую касательную, найдем объемы сосуществующих фаз (жидкость —пар), а также и соответствующие упругости паров. Однако на практике вычисления упрощаются тем, что для решения вопроса привлекают уравнение Ван-дер-Ваальса. [c.618]

    После того как вычислена теплота адсорбции по (XI.15) или теплота растворения по (XI.15а), можно приступить к вычислению энтропии адсорбции Д5а или энтропии растворения Д5а, исходя из значений В, т. е. отрезка, отсекаемого прямой графика функции Ig (Г, К) =/(1/7 ) на оси ординат [рис. XI.3 формула (XI.13)]. В этом случае AS—2,3 RB. Однако такой способ расчета энтропии ненадежен, поскольку ненадежно графическое определение константы В. [c.256]

    Третий закон используется при вычислениях абсолютных энтропий простых и сложных веществ. Абсолютной энтропией называется энтропия, отсчитанная относительно = 0. Для вычисления необходимо графическое или аналитическое интегрирование уравнения (VI.4). Однако нижним пределом интегрирования является = О К, поэтому [c.97]

    На практике вычисление энтропии часто проводят графическим спосо- [c.188]

    На рис. 31 представлена зависимость величин Гд5г, вычисленных графически, от концентрации толуола, т. е. от степени разбавления. Мы видим, что парциальная молярная энтропия каучука непрерывно возрастает с разбавлением. Полученные значения также значительно больше идеальной энтропии смешения, вычисленной по формуле = = — 1п N2. [c.117]

    Освоив технику графического интегрирования, перейдем к основному интересующему нас вопросу — вычислению энтропии из [c.164]

    Изменение энтропии в процессе, проходящем не при постоянной температуре, а при непрерывно изменяющейся, как это имеет место при нагревании вещества, можно вычислить тем же способом графического интегрирования. Площадь под кривой теплоемкости делится на элементарные площади и для каждой подсчитывается изменение энтальпии. Разделив такое элементарное изменение энтальпии на температуру, среднюю между температурами начала и конца элементарного интервала температур, получим изменение энтропии при нагревании вещества в элементарном интервале температур АТ. Просуммировав все частные от деления, получим изменение энтропии в интересующем нас интервале температуры. Проще можно поступить следующим образом разделить все теплоемкости на соответствующие им температуры и далее графическое интегрирование (в данном случае уже числовое интегрирование) проводить точно так же, как и с изменениями энтальпии. Практически для вычисления изменения энтропии при нагревании вещества от одной температуры до другой, если известен ход теплоемкости, следует поступить так разбить весь интервал на желаемое число частей по АТ градусов (5—10°), определить по графику темплоемкости, отвечающие каждой температуре, значения теплоемкости разделить на соответствующие им температуры, просуммировать частные от деления, за исключением первой и последней, сумму умножить на число градусов в АТ, к этой сумме прибавить полусумму первого и последних частных, умноженную на АТ. Если интегрирование начинается с 0°К, то на АТ умножается только половина последнего частного от деления. [c.165]

    В качестве нижнего предела в этих уравнениях можно взять любую температуру. В большинстве случаев расчет ведут относительно Т° = 273,2, причем значения энтропии и энтальпии обычно представляют в графической форме, в виде диаграмм Н — 5 и Т — S. Эти диаграммы широко применяются для технологических расчетов, так как многие вычисления могут быть сведены к простому отсчету по диаграмме. [c.164]

    Примерами графического интегрирования служат вычисление энтальпии и энтропии вещества по температурной зависимости теплоемкости первой — по графику Ср =/ (Г), второй — по графику [c.19]

    Таким образом, измеряя теплоемкости элементов и чистых соединений от комнатной температуры до возможно более низкой температуры, например до точки плавления водорода (15° К) или до точки кипения кислорода (90° К), и экстраполируя полученные величины до абсолютного нуля, возможно составить таблицу стандартных энтропий всех известных чистых веществ, которую можно затем использовать для вычисления AS любой интересующей нас xiimh-ческой реакции. Для любого процесса при заданной температуре величина AS получается вычитанием суммы энтропий веществ, составляющих начальное состояние системы, из суммы энтропий веществ в конечном состоянии. Так как при низких температурах теплоемкости очень быстро убывают и стремятся к нулю с приближением температуры к абсолютному нулю, то необходимо прибегать к графическому интегрированию уравнения (6.5). Методы этого интегрирования, описанные в деталях у Льюиса и Рендалла и у Паркса и Хаффмана [1], рассматриваются в гл. VII в связи с применением закона теплоемкостей Дебая для экстраполяции до 0° К. [c.83]

    Робинсон и Блисс [198] дали законченное аналитическое выражение для вычисления изотермического изменения U, Н и S по трем уравнениям состояния, определяющим р, а именно—по уравнениям Ван-дер-Ваальса, Воля и Битти — Бриджмена. Сравнение вычисленных данных для трех различных газов со значениями, найденными из данных p v—7 графическим методом, показывает, что уравнение Битти — Бриджмена является наилучшим по сравнению с двумя остальными, в особенности для вычисления энтальпии. Но даже с этим уравнением отклонение все же составляло 7 /д для энтропии и 12 / (а в некоторых случаях и более) — для энтальпии. [c.272]

    Изменения энтропии и изобарно-изотермического потенциала при растворении КС1 в смесях НгО—СН3ОН находились по методу [2]. Коэффициенты активности хлористого калия в смешанных растворителях вода—метиловый спирт, необходимые для вычисления АСраств, заимствованы из работы Латимера и Сланского [3]. Графические зависимости всех трех величин от моляльной концентрации электролита т для пяти составов смесей вода — метанол изображены на рис. 1. Кривая 1 для АЯраств КС1 В воде построена по данным [4]. [c.111]

    Поскольку давление паров не было измерено с достаточной точностью, коэффициенты активности ух и Уг находили из уравнений (27а) и (276), а среднюю молярную избыточную свободную энтальпию 0 вначале определяли из уравнения (22а). После этого среднюю молярную избыточную энтальпию рассчитывали по уравнению (29а). Величину устанавливали графически по тангенсу угла наклона прямой, изображающей зависимость величины функции (0 /ЯТ)х от температуры (рис. 66). Наконец, среднюю молярную избыточную энтроп ю5 находили из уравнения (30). Результаты этих вычислений представлены на рис. 67. [c.135]

    Температуры переходов определены графически (рис. 3). Энтальпия перехода kIV—>-кП1 измерена методом непрерывного ввода энергии [7] в трех опытах (табл. 3). В табл. 2 приведен средний результат и указано среднеарифметическое отклонение. Энтропия перехода вычислена по значениям энтальпии и температуры его. Оценка энтальпий переходов кП1—>-кП и кП—>-к1 выполнена путем графического интегрирования С°р по температуре в интервале указанных переходов по экспериментально полученным кривым теплоемкости и нормальным кривым °p = f (T), показанным на рис. 3 пунктиром, причем AIi°ir получалась как разность энтальпий, вычисленных по этим кривым. Энтропии переходов оценивали аналогично, но интегрировали С р = = /(1пГ). Полученные значения AH°tr и AS°tr приведены вместе с гра-( )нческой ошибкой интегрирования. Следует отметить, что энтальпии и энтропии рассмотренных переходов малы. Полученные данные не позволяют сделать однозначных выводов относительно природы переходов. Однако можно высказать предположение, что все они относятся к переходам типа порядок5= беспорядок и обусловлены изменением взаимной ориентации молекул в кристаллической решетке. В известной мере аналогичную картину переходов получили Чанг и Веструм [9] при калориметрическом изучении С°р тиомочевины. Используя полученные результаты и данные кристаллографических исследований [10], они отнесли наблюдаемые превращения к переходам типа порядок гй беспо-рядок, объяснив их появление небольшими различными поворотами молекул в кристалле. [c.25]

---

Курс физической химии Том 1 Издание 2 (1969) — [

c.95

]

Курс физической химии Том 1 Издание 2 (копия) (1970) — [

c.95

]

---

Термодинамические величины
Статья является частью серии «Термодинамика».
Энтропия
Количество теплоты
Термодинамическая работа
Химический потенциал
См. также: Термодинамические потенциалы.
Разделы термодинамики
Начала термодинамики
Уравнение состояния
Термодинамические величины
Термодинамические потенциалы
Термодинамические циклы
Фазовые переходы
править

Термодинами́ческая энтропи́я S, часто просто именуемая энтропия, в химии и термодинамике является функцией состояния термодинамической системы; её существование постулируется вторым началом термодинамики.

Термодинамическое определение энтропии

Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение изменения общего количества тепла ΔQ к величине абсолютной температуры T:

Рудольф Клаузиус дал величине S имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.

Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:

,

где – приращение (дифференциал) энтропии, а – бесконечно малое приращение количества теплоты.

Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).

Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому считать полным дифференциалом нельзя.

Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.

Статистическое определение энтропии: принцип Больцмана

В 1877 году Людвиг Больцман нашёл, что энтропия системы может относиться к количеству возможных «микросостояний» (микроскопических состояний), согласующихся с их термодинамическими свойствами. Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых:
(I) месторасположения всех частей расположены в рамках сосуда,
(II) для получения общей энергии газа кинетические энергии атомов суммируются.
Больцман постулировал, что:

где константу k=1,38•10^–23 Дж/К мы знаем теперь как постоянную Больцмана, а Ω является числом микросостояний, которые возможны в имеющемся макроскопическом состоянии (статистический вес состояния). Этот постулат, известный как принцип Больцмана, может быть оценен как начало статистической механики, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы (Ω) с одним из её термодинамических свойств (S).

Согласно определению Больцмана, энтропия является просто функцией состояния. Так как Ω может быть только натуральным числом (1,2,3,…), то энтропия Больцмана должна быть положительной — исходя из свойств логарифма.

Понимание энтропии как меры беспорядка

Существует мнение, что мы можем смотреть на Ω и как на меру беспорядка в системе. В определённом смысле это может быть оправдано, потому что мы думаем об «упорядоченных» системах как о системах, имеющих очень малую возможность конфигурирования, а о «беспорядочных» системах, как об имеющих очень много возможных состояний. Собственно, это просто переформулированное определение энтропии как числа микросостояний на данное макросостояние.

Рассмотрим, например, распределение молекул идеального газа. В случае идеального газа наиболее вероятным состоянием, соответствующим максимуму энтропии, будет равномерное распределение молекул. При этом реализуется и максимальный “беспорядок”, т.к. при этом будут максимальные возможности конфигурирования.

Границы применимости понимания энтропии как меры беспорядка

Подобное определение беспорядка термодинамической системы как количества возможностей конфигурирования системы фактически дословно соответствует определению энтропии как числа микросостояний на данное макросостояние. Проблемы начинаются в двух случаях:

• когда начинают смешивать различные понимания беспорядка, и энтропия становится мерой беспорядка вообще;
• когда понятие энтропии применяется для систем, не являющихся термодинамическими.

В обоих этих случаях применение понятия термодинамической энтропии совершенно неправомерно^[1].

Рассмотрим оба пункта более подробно.

Рассмотрим пример термодинамической системы – распределение молекул в поле тяготения. В этом случае наиболее вероятным распределением молекул будет распределение согласно барометрической формуле Больцмана. Другой пример – учёт электромагнитных сил взаимодействия между ионами. В этом случае наиболее вероятным состоянием, соответствующим максимуму энтропии, будет упорядоченное кристаллическое состояние, а совсем не “хаос”. (Термин “хаос” здесь понимается в смысле беспорядка – в наивном смысле. К хаосу в математическом смысле как сильно неустойчивой нелинейной системе это не имеет отношения, конечно.)

Рассмотрим случай с кристаллической решёткой более подробно. Кристаллическая решётка может быть и в равновесном, и в неравновесном состоянии, как и любая термодинамическая система. Скажем, возьмём следующую модель – совокупность взаимодействующих осцилляторов. Рассмотрим некоторое неравновесное состояние: все осцилляторы имеют
одинаковое отклонение от положения равновесия. С течением времени эта система перейдёт в состояние ТД равновесия, в котором отклонения (в каждый момент времени) будут подчинены некоторому распределению типа Максвелла (только это распределение будет для отклонений, и оно будет зависеть от типа взаимодействия осцилляторов). В таком случае максимум энтропии будет действительно реализовывать максимум возможностей конфигурирования, т.е. – беспорядок согласно вышеуказанному определению. Но данный “беспорядок” вовсе не соответствует “беспорядку” в каком-либо другом понимании, например, информационному. Такая же ситуация возникает и в примере с кристаллизацией переохлаждённой жидкости, в которой образование структур из “хаотичной” жидкости идёт параллельно с увеличением энтропии.

Это неверное понимание энтропии появилось во время развития теории информации, в связи с парадоксом термодинамики, связанным с мысленным экспериментом т.н. “демона Максвелла”. Суть парадокса заключалась в том, что рассматривалось два сосуда с разными температурами, соединённых узкой трубкой с затворками, которыми управлял т.н. “демон”. “Демон” мог измерять скорость отдельных летящих молекул, и т.о. избирательно пропускать более быстрые в сосуд с высокой температурой, а более медленные – в сосуд с низкой. Из этого мысленного эксперимента вытекало кажущееся противоречие со вторым началом термодинамики.

Парадокс может быть разрешён при помощи теории информации. Для измерения скорости молекулы “демон” должен был бы получить информацию о её скорости. Но всякое получение информации – материальный процесс, сопровождающийся возрастанием энтропии. Количественный анализ, проведённый, например, в ^[2] показал, что приращение энтропии при измерении превосходит по абсолютной величине уменьшение энтропии, вызванное перераспрелением молекул “демоном”.

Однако многие учёные стали отождествлять информацию с “отрицательной энтропией” ввиду совпадения выражений для этих понятий. Начало этому заблуждению положил Н. Винер ^[3] (стр. 23). На самом деле энтропия не является мерой дезорганизации, мерой беспорядка и хаоса, а информация совсем не является мерой упорядоченности, организованности, порядка.

Рассмотрим второй случай неверного применения понятия энтропии.

Рассмотрим, например, набор 10 монет, каждая из которых может находиться либо в состоянии «орёл», либо в состоянии «решка». Наиболее «упорядоченным» макроскопическим состоянием будет являться или 10 «орлов», или 10 «решек»; для каждого результата в каждом случае имеется только одна возможная конфигурация. И наоборот, наиболее «неупорядоченное» состояние содержит 5 «орлов» и 5 «решек», и здесь ¹⁰C₅ = 252 способов для получения этого результата (см. комбинаторика.)

Безусловно, этот пример также некорректен, т.к. система монет не является термодинамической системой, и поэтому термодинамическая энтропия системы в обоих случаях (как бы ни были перевёрнуты монеты) окажется, конечно, одинаковой. Т.о., разбросанные по комнате стулья не имеют отношения к термодинамической энтропии, хотя и могут иметь отношение к энтропии информационной.

Впрочем, это легко подтвердить на практике: замкнутая система 10 монет, перевёрнутых орлами вверх, самопроизвольно не перейдёт в систему хаотично перевёрнутых монет.

Энтропия в открытых системах

В силу второго начала термодинамики, энтропия замкнутой системы не может уменьшаться» (закон неубывания энтропии). Математически это можно записать так: , индекс обозначает так называемую внутреннюю энтропию, соответствующую замкнутой системе. В открытой системе возможны потоки тепла как из системы, так и внутрь неё. В случае наличия потока тепла в систему приходит количество тепла при температуре и уходит количество тепла при температуре . Приращение энтропии, связанное с данными тепловыми потоками, равно:

В стационарных системах обычно , , так что . Поскольку здесь изменение энтропии отрицательно, то часто употребляют выражение «приток негэнтропии», вместо оттока энтропии из системы. Негэнтропия определяется таким образом как обратная величина энтропии.
Суммарное изменение энтропии открытой системы будет равно:

Если всё время , то рост внутренней энтропии не компенсируется притоком внешней негэнтропии, система движется к ближайшему состоянию равновесия. Если , то мы имеем стационарный процесс с неизменной общей энтропией. В этом случае в системе осуществляется некоторая внутренняя работа с генерацией внутренней энтропии, которая преобразует, например, температуру внешнего потока тепла в температуру уходящего из системы потока тепла.

Измерение энтропии

В реальных экспериментах очень трудно измерить энтропию системы. Техники измерения базируются на термодинамическом определении энтропии и требуют экстремально аккуратной калориметрии.

Для упрощения мы будем исследовать механическую систему, термодинамические состояния которой будут определены через её объем V и давление P. Для измерения энтропии определенного состояния мы должны сперва измерить теплоёмкость при постоянных объёме и давлении (обозначенную C_V и C_P соответственно), для успешного набора состояний между первоначальным состоянием и требуемым. Тепловые ёмкости связаны с энтропией S и с температурой T согласно формуле:

где нижний индекс X относится к постоянным объёму и давлению. Мы можем проинтегрировать для получения изменения энтропии:

Таким образом, мы можем получить значение энтропии любого состояния (P,V) по отношению к первоначальному состоянию (P₀,V₀). Точная формула зависит от нашего выбора промежуточных состояний. Для примера, если первоначальное состояние имеет такое же давление, как и конечное состояние, то

В добавление, если путь между первым и последним состояниями лежит сквозь любой фазовый переход первого рода, скрытая теплота, ассоциированная с переходом, должна также учитываться.

Энтропия первоначального состояния должна быть определена независимо. В идеальном варианте выбирается первоначальное состояние как состояние при экстремально высокой температуре, при которой система существует в виде газа. Энтропия в этом состоянии подобна энтропии классического идеального газа плюс взнос от молекулярных вращений и колебаний, которые могут быть определены спектроскопически.

Построение графика изменения энтропии

Основная статья: адиабатический процесс

Следующее уравнение может быть использовано для построения графика изменения энтропии на диаграмме P-V:

Здесь два замечания: (1) это не определение энтропии (но выведено из него), (2) предполагается, что C_V и C_P постоянные, что на самом деле не так.

См. также

• Термодинамика чёрных дыр
• Тепловая смерть
• Демон Максвелла
• Термодинамические потенциалы
• Стрела времени
• Информационная энтропия
• Негэнтропия
• Энергетическое определение энтропии
• Список статей по энтропии

Литература

• Fermi, E., Thermodynamics, Prentice Hall (1937)
• Reif, F., Fundamentals of statistical and thermal physics, McGraw-Hill (1965)
• Шамбадаль П. Развитие и приложение понятия энтропии. – М.: Наука, 1967. – 280 с.
• Волькенштейн М.В. Энтропия и информация. – М.: Наука, 1986. – 192 с.

Ссылки

• Термодинамическая энтропия
• Entropy and chaos (англ.)
• Роль Термодинамики в современном мире. Второе начало термодинамики
• Статья “Эволюция как сопротивление энтропии”

---

Википедия Энтропия (в термодинамике) адрес Викисловарь — адрес Викицитатник — адрес Викиучебник — адрес Викитека — адрес Викиновости — адрес Викиверситет — адрес Викигид — адрес

Выделить Энтропия (в термодинамике) и найти в: Вокруг света (в термодинамике) адрес Академик (в термодинамике)/ru/ru/ адрес Астронет адрес Элементы (в термодинамике)+&search адрес Научная Россия (в термодинамике)&mode=2&sort=2 адрес Кругосвет (в термодинамике)&results_per_page=10 адрес Научная Сеть Традиция — адрес Циклопедия — адрес Викизнание — (в термодинамике) адрес

Google Bing Yahoo Яндекс Mail.ru Рамблер Нигма.РФ Спутник Google Scholar Апорт Онлайн-переводчик Архив Интернета Научно-популярные фильмы на Яндексе Документальные фильмы

Список ru-вики Вики-сайты на русском языке Список крупных русскоязычных википроектов Каталог wiki-сайтов Русскоязычные wiki-проекты Викизнание:Каталог wiki-сайтов Научно-популярные сайты в Интернете Лучшие научные сайты на нашем портале Лучшие научно-популярные сайты Каталог научно-познавательных сайтов НАУКА В РУНЕТЕ: каталог научных и научно-популярных сайтов

---

• Страница 0 – краткая статья
• Страница 1 – энциклопедическая статья
• Разное – на страницах: 2 , 3 , 4 , 5
• Прошу вносить вашу информацию в «Энтропия (в термодинамике) 1», чтобы сохранить ее

Комментарии читателей: