Как найти энтропию реакции при температуре

Термодинамическая
энтропия S,
часто просто именуемая энтропия,
в химии и термодинамике является функцией
состояния термодинамической
системы.

1) теплота не может
самопроизвольно переходить от менее
нагретого тела к более нагретому

2) невозможен
процесс, единственным результатом
которого является превращение теплоты
в работу

Энтропия как
критерий направления процессов. В
изолированной системе протекают только
процессы, в которых энтропия увеличивается.
Энтропия есть мера упорядоченности
системы.

Цикл Карно: состоит
из четырех участков и изображается
PV-диаграммами.
Процессы 1-2, 3-4 явл-ся изотерм., процессы
2-3, 4-1 явл-ся адиабатическими.

1-2: Пусть газ нах-ся
в точке 1 с темп Т₁,
давл Р₁
и объемом V₁.
Про изотерм. Расширении газ преходит
в состояние 2 с давл Р₂,
V₂,
но Т₁.
Темп не меняется, значит не меняется
внутр. Энергия. Чтобы газ изотерм.
Расширялся, он должен получить от нагр
Q₁.
При изотрем. Расширении Q₁=W₁

2-3: из сост 2 газ
адиабатически расширяется до сост 3.
Р₃,
V₃,
Т₂<T₁.
Падение Т связано с работой газа при
адиабатическом расширении, тепло не
подводится и газ совершает работу за
счет своей внутр энергии, в результате
газ охлаждается W₂=-ΔU

3-4: из сост 3газ
изотерм сжимается до сост 4, характеризуемого
параметрами V₄,
P₄,
T₂.
Над газом совершается работа при данном
изотерм проц ΔU=0

4-1: из сост 4 газ
адиабатно сжимается так, что он принимает
исх парметры P₁,
V₁,
T₁.
Над газом совершается работа, газ
нагревается до T₁,
т.к. теплоотдачи при адиабатическом
проц нет –ΔW=ΔU

Уравнения для
расчета энтропии для различных систем:

1. Изотермический
   процесс (Т=const):
   ΔS=
   (V=const)
   ΔS=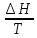
   (P=const)

2. Изобарный
   процесс (P=const):
   ΔS=;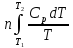
   ΔC_p=const;
   ΔS=nC_pln

3. Изохорный
   процесс (V=const):
   ΔS=;
   ΔC_v=const;
   ΔS=nC_vln

Для различных
процессов с идеальным газом

При
ΔC_v=const

ΔS=nC_vln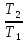
+ nRln

Если
C_p=C_v-R

ΔS=nC_pln
+ nRln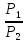

В изотермическом
процессе

ΔS=nC_pln=
nRln

В изобарном процессе

ΔS=nC_pln=
nRln

В изохорном процессе

ΔS=nC_pln=
nRln

Расчет изменения
энтропии хим. Р-ции

А₁
+
А₂
=
А₃
+
А₄

Т=298

+
––

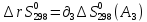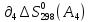T≠298

1. ΔC_p=const

1. ΔC_p
   не
   зависит от Т

для неорг. Вв

для орг. В-в

14.Изохорно-изотермический потенциал, его свойства, применение в качестве критерия направленности процесса.

Термодинамическими
потенциалами, или характеристическими
функциями, называют термодинамические
функции, посредством которых и их
производных по соответствующим
независимым переменным (естественным)
могут быть выражены в явном виде все
термодинамические свойства си-мы. Это
означает, что характеристические
функции содержат в себе всю термодинамическую
информацию о си-ме. Наибольшее значение
имеют четыре основных термодинамических
потенциала (П_ав):

1) внутренняя
энергия U(S,V),

2)Энтальпия
H(S,p)=U+pV,

3)энергия
ГельмгольцаF(T,V)=U-TS,

4)энергия
ГиббсаG(T,p)=H-TS=F+pV.

В скобках указаны
естественные переменные для
термодинамических потенциалов. Все
эти потенциалы имеют размерность
энергии и все они не имеют абсолютного
значения, поскольку определены с
точностью до постоянной, которая равна
внутренней энергии при абсолютном
нуле.

ϬQ=dU+ϬA,
ϬA=pdV+ϬA’,
ϬQ=dU+pdV+δA’
– первый закон термодинамики.

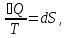ϬQ=TdS
– второй закон термодинамики.

Зависимость
термодинамических потенциалов от их
естественных переменных описывается
основным уравнением термодинамики,
которое объединяет первое и второе
начала: TdS=dU+
PdV=ϬA’
=> A’_max=
TdS-dU-
PdV.

Рассмотрим А_max
при V=const,
T=const

A’_max=
TdS
– dU
= -d(U
– TS)

U
– TS=F
– свободная энергия Гельмгольца

A’_max=
-dF
– изохорно-изотермический потенциал

В зависимости от
условия протекания процесса различают
; термодинамических потенциала

П_A,B

A’_max=-П_АВ–
т.е во всех случаях A’_max=
убыли соответствующих термодинамических
потенциалов.

A’_max=-П_АВ–
для обратимых процессов, A’_max<-П_АВ–
для необратимых процессов, A’_max>=-П_АВ–
для любых процессов.

A’_max=0,
т.е си-ма находится под влиянием давления.

∆П_АВ<0
при любом самопроизвольном процессе
термодинамический потенциал уменьшается
и его можно использовать, как критерий
направления процесса:

1. Если
   процесс идет самопроизвольно прямо,
   тогда П_АВ
   уменьшается и процесс идет в прямом
   направлении.

2. Если
   П_АВ
   уменьшается и в момент равновесия
   имеет минимальные значения или П_АВ
   равно 0, тогда процесс идет в обоих
   направлениях.

3. Если
   П_АВ
   больше 0, то процесс идет в обратную
   сторону, т.е не самопроизвольно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #

  12.05.2015367.15 Кб561.pdf

• #

  12.05.2015451.17 Кб566.pdf

• #
• #
• #

  11.05.201576.29 Кб177.doc
• #

  12.05.2015266.33 Кб277.pdf

• #

  12.05.2015126.66 Кб877.pdf

• #

Как правильно рассчитывать тепловой эффект реакции, изменение энтропии реакции, костанту равновесия реакции

Вычисление теплового эффекта реакции

Задача 67.
Вычислить тепловой эффект реакции: Al₂O_3(тв.) + 3SO₃ = Al₂(SO₄)_3(тв.) при условии, что она протекает в калориметрической бомбе при постоянном объеме и Т = 298 К.
Решение:
ΔН°Al₂O₃ = -1675,7 кДж/моль;
ΔН°Al₂(SO₄)₃ = -3441,8 кДж/моль;
ΔН°SO₃ = -395,8 кДж/моль 
ΔН = ?
Рассчитаем энтальпию реакции при стандартных условиях, используя следствие из закона Гесса:

ΔН_х.р. = ΔН_{обр.прод.} – ΔН_{обр.исх.}

Тогда 

ΔН°₂₉₈ = ΔH°Al₂(SO₄)₃  – (ΔH°Al₂O₃ – 3ΔH°SO₃) =
= -3441,8 – [-1675,7 + 3(-395,8)] = -578,7 кДж/моль.

Знак минус перед тепловым эффектом означает, что теплота выделяется в результате реакции.

 

---

Определение темпрературы начала протекания реакции

Задача 68.
Возможна ли реакция диссоциации углекислого газа при Т = 500 градусов цельсия? И при какой температуре эта реакция может начать протекать?
Уравнение реакции: 2CO₂ = 2CO +  O₂.
ΔH°CO₂ = -393,51  кДж/моль;      
ΔH°CO = -110,53   кДж/моль;
S°СО₂ = 213,66 Дж/(моль·К); 
S°СО = 197,55 Дж/(моль·К);
S°О₂ = 205,04 Дж/(моль·К); 
T =  500 °C = 773 K;       
∆G°₇₇₃ = ?
Решение:
Рассчитаем энтальпию реакции при стандартных условиях, используя следствие из закона Гесса, при этом учитываем, что для простых веществ стандартная теплота образования равна нулю.
Уравнение Гесса:

ΔН_х.р. = ΔН_{обр.прод}. – ΔН_{обр.исх.}

Тогда 

ΔН°₂₉₈ = 2ΔH°СО  – 2ΔH°CО₂) =
= 2(-110,53) – 2(-393,51) = 565,96 кДж/моль.

Знак плюс перед тепловым эффектом означает, что теплота поглощается в результате реакции.
Расчет энтропии будем вести по формуле Гесса:

∆S°_х.р. = ∑S°_{(обр.прод.)} – ∑S°_{(обр.исх.)}.

Подставив найденные значения энтропий в искомое уравнение, и произведя расчеты, получим:

∆S°х.р. = (2S°СО + S°O₂) – 2S°CO₂ = 
= [(2 ^. 197,55) + 205,04] – (2 ^. 213,66) = 172,82 Дж/(моль ^. К).

Теперь находим ∆G°773х.р., выражая ∆S°х.р. в кДж/(моль·К):

∆G°₇₇₃ = ΔН°₂₉₈ – Т∆S°_х.р.;
∆G°_773х.р. = [565,96 – 773(172,82 ^. 10-3)] = 432.37014 кДж/моль.

Т.к. ∆G°_773х.р. > 0, то реакция при 773 К не может протекать самостоятельно.

Рассчитаем температуру начала реакции, т.е. состояние равновесия её, получим.

В состоянии равновесия:

∆G = 0 и ∆H = T∆S.

Тогда

Т = ∆H/∆S;
Т = (565,96 кДж/моль)/(172,82 ^.10-3 кДж/моль·К) = 3274,85 K или приблизительно 3000 °С.

 

---

Причины изменения энтропии в ходе реакции

Задача 69.
Сколько тепла выделится при сгорании 50 г бензола в стандартных условиях? Подробно объясните причины изменения энтропии в ходе прямой реакции.
Решение:
m(С₆Н₆) = 50 г;
M(С6Н6) = 78,11 г/моль;
∆H°С₆Н_6(ж) = 49,03 кДж/моль;
∆H°СO_2(г) = -393,51 кДж/моль;
∆H°Н₂О_(ж) = -285,83 кДж/моль;
S°С₆Н_6(ж) = 172,8 Дж/(моль ^. K);
S°СO_2(г) = 213,67 Дж/(моль ^. K);
S°Н₂О_(ж) = 70,08 Дж/(моль ^. K);
S°O_2(г) = 205,04 Дж/(моль ^. K);
Q_p = ?
∆S° = ?
Уравнение реакции горения бензолы имеет вид:

С₆Н_6(ж) + 3,5О₂ =  2СО₂ + 3Н₂О_(ж), Q. 

Рассчитаем энтальпию реакции при стандартных условиях, используя следствие из закона Гесса, при этом учитываем, что для простых веществ стандартная теплота образования равна нулю.
Уравнение Гесса:

ΔН_х.р. = ΔН_{обр.прод.} – ΔН_{обр.исх.}

Тогда 

ΔН°₂₉₈ = 3ΔH°Н₂О_(ж) + 2∆H°СO₂ – ∆H°С₆Н_6(ж) =
= 3(-285,83) + 2(-393,51) – 49,03 = -1595,01 кДж/моль;
Q = -ΔН_х.р. = 1595,01 кДж.

Знак минус перед тепловым эффектом означает, что теплота выделяется в результате реакции.

Тогда

Q_p = [m(С₆Н₆) ^. (-ΔН_х.р.)]/M(С₆Н₆) = (50 ^. 1595,01)/78,11 = 1021 кДж.

Изменение энтропии химического процесса (ΔS°) определяется как разность сумм энтропий продуктов реакции и реагентов с учетом их стехиометрических коэффициентов в уравнении реакции. Расчет энтропии будем вести по формуле Гесса:

∆S°_х.р. = ∑S°_{(обр.прод.)} – ∑S°_{(обр.исх.).}

Подставив найденные значения энтропий в искомое уравнение, и произведя расчеты, получим:

∆S°_х.р. = [3S°Н₂О_(ж) + 2S°CO_2(г)] – [S°С₆Н_6(ж) + 3,5S°O2(г)] = 
= [(3 ^.70,08) + (2 ^. 213,67)] – [172,8 + (3,5 ^. 205,04] = -254.12 Дж/(моль ^. К).

Так как общее число молей газообразных веществ уменьшается (3,5VО₂) исходных газообразных веществ и (2VСО₂) газообразных продуктов), то система переходит из менее упорядоченного состояния в более упорядоченное, поэтому ∆S° < 0.
Если энтальпия ΔН° < 0 и энтропия ∆S°  < 0, то процесс возможен при условии, что член (ΔН°) в уравнении для энергии Гиббса (∆G =  ∆H – T∆S) больше по абсолютному значению, чем член (T∆S°); поскольку абсолютное значение члена(T∆S°) с ростом множителя (Т) увеличивается, то указанное условие будет осуществляться при достаточно низких температурах, возможно и в стандартных условиях. 

 

---

Расчет стандартной энтальпии образования оксида фосфора (V)

Задача 70.
При окислении 12,4 г фосфора выделилось 306 кДж теплоты. Рассчитайте стандартную энтальпию образования оксида фосфора (V).
Решение:
m(P) = 12,4 г;
Q = 306 кДж;
∆H = ?
Уравнение реакции имеет вид:

2Р + 5/2О₂ = Р₂О₅, Q

Из уравнения реакции вытекает, что при окислении 2 моль Р образуется 1 моль Р₂О₅, т.е. 2n(P) = n(Р₂О₅).
Рассчитаем количество окислившегося фосфора, получим:

n(P) = m(P)/M(P) = 12,4/31 = 0,4 моль.

Рассчитаем стандартную энтальпию образования оксида фосфора (V), получим:

0,4 моль : 306 кДж = 2 моль : х;
х = (306 кДж ^. 2 моль)/0,4 моль = 1530 кДж;
Q_р = 1530 кДж;
∆H = -Q_р = 11530 кДж/моль.

---

Расчет константы равновесия реакции (н.у.), зная значение энергии Гиббса

Задача 71.
Определите возможность протекания реакции при стандартных условиях. Если реакция возможна, то рассчитайте константу её равновесия. Как нужно изменить температуру проведения реакции, чтобы увеличить выход продуктов реакции. Дайте обоснованный ответ. Уравнение реакции имеет вид:
4HCl_(г) + O_2(г) = 2H₂O_(ж) + 2Cl_2(г).
Решение:
∆H°HC_l(г) = -92,31 кДж/моль;
∆H°H₂O_(ж) = -285,83 кДж/моль;
S°HCl_(г) = 186,79 Дж/(моль ^. К);
S°H₂O_(ж) = 70,08;
S°O_2(г) = 205,04 Дж/(моль ^. К);
S°Cl_2(г) = 222,98 Дж/(моль ^. К);
Кр = ?
Рассчитаем энтальпию реакции при стандартных условиях, используя следствие из закона Гесса, при этом учитываем, что для простых веществ стандартная теплота образования равна нулю.
Уравнение Гесса:

ΔН_х.р. = ΔН_{обр.прод.} – ΔН_{обр.исх.}

Тогда 

ΔН°₂₉₈ = 2ΔH°Н₂О_(ж) – 4∆H°HCl_(г) =
= 2(-285,83) – 4(-92,31) = -202,42 кДж/моль.

Знак минус перед тепловым эффектом означает, что теплота выделяется в результате реакции.
Согласно 3-му следствию из закона Гесса, изменение энтропии химического процесса (ΔS°) определяется как разность сумм энтропий продуктов реакции и реагентов с учетом их стехиометрических коэффициентов в уравнении реакции. Расчет энтропии будем вести по формуле Гесса:

∆S°_х.р. = ∑S°_{(обр.прод.)} – ∑S°_{(обр.исх.)}.

Подставив найденные значения энтропий в искомое уравнение, и произведя расчеты, получим:

∆S°_х.р. = [2S°Н₂О_(ж) + 2S°Cl_2(г)] – [4S°HCl_(г) + S°O_2(г)] = 
= [(2 ^. 70,08) + (2 ^. 222,98)] – [(4^. 186,79) + 205,04] = -366,08 Дж/(моль ^. К).

Отрицательное значение изменения энтропии (уменьшение энтропии) свидетельствует о невозможности осуществления указанного процесса самопроизвольно в стандартных условиях.
Теперь находим ∆G°₂₉₈, выражая ∆S°_х.р. в кДж/(моль·К):

∆G°₂₉₈ = ΔН°₂₉₈ – Т∆S°_х.р.;
∆G°₂₉₈ = [-202,42 – 298(-366,08 ^. 10^-3)] кДж/моль = -93,38816 кДж/моль.

Т.к. ∆G°_250х.р. < 0, то реакция при 298 К может протекать самостоятельно.

Рассчитаем константу равновесия реакции (н.у.) по формуле:

lgK = ∆G°₂₉₈/-5,69.

Тогда

lgK = ∆G°₂₉₈/-5,69 = -202,42/-5,69 = 35,57;
К = 3,7 ^. 10^35.

Так как процесс идес с выделением температуры, то для увеличения выхода продукта нужно понизить температуру в системе, т.е. отводить тепло.

---

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Понятие энтропии

Абсолютная энтропия веществ и изменение энтропии в процессах

Стандартная энтропия

Стандартная энтропия образования

Энергия Гиббса

Стандартная энергия Гиббса образования

Энтальпийный, энтропийный фактор и направление процесса

Примеры решения задач

Задачи для самостоятельного решения

Понятие энтропии

Энтропия S – функция состояния системы. Энтропия характеризует меру неупорядоченности (хаотичности) состояния системы. Единицами измерения энтропии являются Дж/(моль·К).

Абсолютная энтропия веществ и изменение энтропии в процессах

При абсолютном нуле температур (Т = 0 К) энтропия идеального кристалла любого чистого простого вещества или соединения равна нулю. Равенство нулю S при 0 К позволяет вычислить абсолютные величины энтропий веществ на основе экспериментальных данных о температурной зависимости теплоемкости.

Изменение энтропии в процессе выражается уравнением:

ΔS = S_(прод.) – S_(исх.)

где S_(прод.) и S_(исх.) – соответственно абсолютные энтропии продуктов реакции и исходных веществ.

На качественном уровне знак S реакции можно оценить по изменению объема системы ΔV в результате процесса. Знак ΔV определяется по изменению количества вещества газообразных реагентов Δn_г. Так, для реакции

CaCO₃(к) = CaO(к) + CO₂(г)

(Δn_г = 1) ΔV > 0, значит, ΔS > 0.

Для реакции:

С(графит) + 2Н₂(г) = СН₄(г)

(Δn_г = -1) ΔV < 0, следовательно и ΔS < 0.

Стандартная энтропия

Величины энтропии принято относить к стандартному состоянию. Чаще всего значения S рассматриваются при Р = 101,325 кПа (1 атм) и температуре Т = 298,15 К (25^оС). Энтропия в этом случае обозначается S^о₂₉₈ и называется стандартной энтропией при Т = 298,15 К. Следует подчеркнуть, что энтропия вещества S (S^о) увеличивается при повышении температуры.

Стандартная энтропия образования

Стандартная энтропия образования ΔS^о_f,298 (или ΔS^о_обр,298) – это изменение энтропии в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии.

Энергия Гиббса

Энергия Гиббса G – функция состояния системы. Энергия Гиббса равна:

G = Н – ТS.

Абсолютное значение энергии Гиббса определить невозможно, однако можно вычислить изменение δG в результате протекания процесса.

Критерий самопроизвольного протекания процесса: в системах, находящихся при Р, Т = const, самопроизвольно могут протекать только процессы, сопровождающиеся уменьшением энергии Гиббса (ΔG < 0). При достижении равновесия в системе ΔG = 0.

Стандартная энергия Гиббса образования

Стандартная энергия Гиббса образования δG^о_f,298 (или δG^о_обр,298) – это изменение энергии Гиббса в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии, причем простые вещества пристутствуют в наиболее термодинамически устойчивых состояниях при данной температуре.

Для простых веществ, находящихся в термодинамически наиболее устойчивой форме, δG^о_f,298 = 0.

Энтальпийный, энтропийный фактор и направление процесса

Проанализируем уравнение ΔG^о_Т = ΔН^о_Т — ΔТS^о_Т. При низких температурах ТΔS^о_Т мало. Поэтому знак ΔG^о_Т определяется в основном значением ΔН^о_Т (энтальпийный фактор). При высоких температурах ТΔS^о_Т – большая величина, знак Δ G^о_Т определяется и энтропийным фактором. В зависимости от соотношения энтальпийного (ΔН^о_Т) и энтропийного (ТΔS^о_Т) факторов существует четыре варианта процессов.

• • 1. Если ΔН^о_Т < 0, ΔS^о_Т > 0, то ΔG^о_Т < 0 всегда (процесс может протекать самопроизвольно при любой температуре).
    2. Если ΔН^о_Т > 0, ΔS^о_Т < 0, то ΔG^о_Т > 0 всегда (процесс не протекает ни при какой температуре).
    3. Если ΔН^о_Т < 0, ΔS^о_Т < 0, то ΔG^о_Т < 0 при Т < ΔН^о/ΔS^о (процесс идет при низкой температуре за счет энтальпийного фактора).
    4. Если ΔН^о_Т > 0, ΔS^о_Т > 0, то ΔG^о_Т < 0 при Т > ΔН^о/ ΔS^о (процесс идет при высокой температуре за счет энтропийного фактора).

Примеры решения задач

Задача 1. Используя термодинамические справочные данные, вычислить при 298,15 К изменение энтропии в реакции:

4NH_3(г) + 5O_2(г) = 4NО_(г) + 6H₂O_(ж)

Объяснить знак и величину ΔS^о.

Решение. Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	NH3(г)	O2(г)	NО(г)	H2O(ж)
Sо298, Дж/(моль·К)	192,66	205,04	210,64	69,95

ΔS^о_х.р.,298 = 4S^о₂₉₈(NО_(г) ) + 6S^о₂₉₈(H₂O_(ж)) — 4S^о₂₉₈(NH_3(г)) — 5S^о₂₉₈(O_2(г)) = 4× 210,64 + 6× 69,95 — 4× 192,66 — 5× 205,04 = — 533,58 Дж/К

В данной реакции ΔV < 0 (Δn_г = — 5), следовательно и ΔS^o_х.р.,298 < 0, что и подтверждено расчетом.

Задача 2. Используя справочные термодинамические данные, рассчитать стандартную энтропию образования NH₄NO_3(к). Отличается ли стандартная энтропия образования NH₄NO_3(к) от стандартной энтропии этого соединения?

Решение. Стандартной энтропии образования NH₄NO₃ отвечает изменение энтропии в процессе:

N_(г) + 2H_2(г) + 3/2O_2(г) = NH₄NO_3(к); δS^о_f,298(NH₄NO_3(к)) = ?

Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	N2(г)	H2(г)	O2(г)	NH4NO3(к)
Sо298, Дж/(моль·К)	191,50	130,52	205,04	151,04

ΔS^о_х.р.,298 = ΔS^о_f,298(NH₄NO_3(к)) = S^о₂₉₈(NH₄NO_3(к)) — S^о₂₉₈(N_2(г)) — 2S^о₂₉₈(H_2(г)) – 3/2S^о₂₉₈(O_2(г)) = 151,04–191,50 —— 2× 130,52–3/2× 205,04 = — 609,06 Дж/(моль·К).

Стандартная энтропия образования NH₄NO₃(к), равная — 609,06 Дж/(моль·К), отличается от стандартной энтропии нитрата аммония S^о₂₉₈(NH₄NO_3(к)) = +151,04 Дж/(моль·К) и по величине, и по знаку. Следует помнить, что стандартные энтропии веществ S^о₂₉₈ всегда больше нуля, в то время как величины ΔS⁰_f,298, как правило, знакопеременны.

Задача 3. Изменение энергии Гиббса реакции:

2Н_2(г) + О_2(г) = 2 Н₂О_(ж)

равно δG^о₂₉₈= –474,46 кДж. Не проводя термодинамические расчеты, определить, за счет какого фактора (энтальпийного или энтропийного) протекает эта реакция при 298 К и как будет влиять повышение температуры на протекание этой реакции.

Решение. Поскольку протекание рассматриваемой реакции сопровождается существенным уменьшением объема (из 67,2 л (н.у.) исходных веществ образуется 36 мл жидкой воды), изменение энтропии реакции ΔS^о<0. Поскольку ΔG^о₂₉₈ реакции меньше нуля, то она может протекать при температуре 298 К только за счет энтальпийного фактора. Повышение температуры уменьшает равновесный выход воды, поскольку ТΔS^о<0.

Задача 4. Используя справочные термодинамические данные, определить может ли при 298,15 К самопроизвольно протекать реакция:

С₄Н_10(г) = 2С₂Н_4(г) + Н_2(г)

Если реакция не будет самопроизвольно протекать при 298,15 К, оценить возможность ее протекания при более высоких температурах.

Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	С4Н10(г)	С2Н4(г)	Н2(г)
ΔGоf,298× , кДж/моль	— 17,19	68,14	0
Sо298, Дж/(моль·К)	310,12	219,45	130,52

ΔG^о_х.р.,298 = 2ΔG^о_f,298(С₂Н_4(г)) + ΔG^о_f,298(Н_2(г)) — ΔG^о_f,298(С₄Н_10(г)) = 2× 68,14 + 17,19 = 153,47 кДж.

ΔG^о_х.р.,298 > 0, следовательно, при Т = 298,15 К реакция самопроизвольно протекать не будет.

ΔS^о_х.р.,298 = 2S^о₂₉₈(С₂Н_4(г)) + S^о₂₉₈(Н_2(г)) — S^о₂₉₈(С₄Н_10(г)) = 2× 219,45 + 130,52 – 310,12 = +259,30 Дж/К.

Поскольку ΔS^о_х.р.,298 > 0, то при температуре Т>ΔН^о/ΔS^о величина ΔG^о_х.р.,298 станет величиной отрицательной и процесс сможет протекать самопроизвольно.

Задача 5. Пользуясь справочными данными по ΔG^о_f,298 и S^о₂₉₈, определите ΔH^о₂₉₈ реакции:

N₂O_(г) + 3H_2(г) = N₂H_4(г) + H₂O_(ж)

Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	N2O(г)	H2(г)	N2H4(г)	H2O(ж)
ΔGоf,298, кДж/моль	104,12	0	159,10	-237,23
Sо298, Дж/(моль·К)	219,83	130,52	238,50	69,95

ΔG^о_х.р.,298 = ΔG^о_f,298(N₂H₄(г)) + ΔG^о_f,298(H₂O(ж)) – ΔG^о_f,298(N₂O(г)) – 3ΔG^о_f,298(H₂(г)) = 159,10 + (–237,23) – 104,12 – 0 = –182,25 кДж.

ΔS^о_х.р.,298 = S^о₂₉₈(N₂H₄(г)) + S^о₂₉₈(H₂O(ж)) – S^о₂₉₈(N₂O(г)) — 3S^о₂₉₈(H₂(г)) = 238,50 + 69,95 – 219,83 –3× 130,52 = –302,94 Дж/К.

ΔG^о₂₉₈ = ΔН^о₂₉₈ – ТΔS^о₂₉₈. Подставляя в это уравнение величины ΔН^о₂₉₈ и ТΔS^о₂₉₈, получаем:

ΔН^о₂₉₈ = –182,25× 10³ + 298·(–302,94) = –272526,12 Дж = – 272,53 кДж.

Следует подчеркнуть, что поскольку ΔS^о₂₉₈ выражена в Дж/(моль× К), то при проведении расчетов ΔG⁰₂₉₈ необходимо также выразить в Дж или величину ΔS⁰₂₉₈ представить в кДж/(мольK).

Задачи для самостоятельного решения

1. Используя справочные данные, определите стандартную энтропию образования ΔS^о_f,298 NaHCO_3(к).

2. Выберите процесс, изменение энергии Гиббса которого соответствует стандартной энергии Гиббса образования NO_2(г):

а) NO_(г) + 1/2O_2(г) = NO_2(г);

б) N_2(г) + 2O_2(г) = 2NO_2(г);

в) 1/2N_2(г) + O_2(г) = NO_2(г);

г) N_(г) + O_2(г) = NO_2(г).

3. Используя справочные данные, вычислите при 298,15 К изменение энтропии в реакции:

2NH₄NO_3(к) = 2N_2(г) + 4H₂O_(г) + О_2(г).

Объясните знак и величину  ΔSº реакции.

• .

δSох.р.,298 =1040,84 Дж/К. В данной реакции δV > 0 (D nг = 7), следовательно и δSох.р.,298 > 0, что и подтверждено расчетом.

4. Используя справочные данные, определите принципиальную возможность протекания реакции при 298,15 К:

NiO_(к) + C_{(графит)} = Ni_(к) + CO_(г)

Если реакция не будет самопроизвольно протекать при 298,15 К, оценить возможность ее протекания при более высоких температурах.

ΔGох.р.,298 = 74,45 кДж > 0, следовательно, при Т = 298,15 К реакция самопроизвольно протекать не будет. Поскольку ΔSох.р.,298 = 183,69 Дж/К, то есть больше нуля, то при достаточно высоких температурах ΔGох.р.,298 изменит знак на обратный.

5. Рассчитайте стандартную энергию Гиббса образования ΔG^о_f,298 C₂H₅OH_(ж), используя справочные данные о величинах ΔН^о_f,298 и S^о₂₉₈.

6. Используя справочные данные, определите стандартную энтропию образования ΔS^о_f,298 K₂Cr₂O_7(к).

7. На основе расчетов термодинамических величин покажите, чем эффективнее восстанавливать при 298 К Cr₂O_3(к) до металла — алюминием или магнием:

1) Cr₂O_3(к) + 3Mg_(к) = 3MgO_(к) + 2Cr_(к); ΔG^о₁;
2) Cr₂O_3(к) + 2Al_(к) = Al₂O_3(к) + 2Cr_(к); ΔG^о₂.

ΔGо1=-648,9 кДж; ΔGо2=-523,3 кДж. Таким образом, самопроизвольно протекают два процесса. Так как значение ΔGо1 более отрицательное, то эффективнее при 298 К будет протекать процесс восстановления магнием.

8. Используя справочными данными по величинам S^о₂₉₈, определите возможность самопроизвольного протекания в изолированной системе при 298 К процесса:

KClO_3(к) = KCl_(к) + 3/2O_2(к)

ΔSо298=247,1 Дж/К. ΔSо298 больше 0, следовательно данный процесс будет протекать самопроизвольно в изолированной системе при 298 К.

9. Используя справочные данные, вычислите при 298 К изменение энтропии в процессе:

Н_2(г) + 1/2О_2(г) = Н₂О_(г)

10. На основе справочных данных оценить температуру восстановления WO_3(к) водородом:

WO_3(к) + 3H_2(г) = W_(к) + 3H₂O_(г).

ЭЛЕМЕНТЫ ТЕРМОХИМИИ      

Термохимия – раздел химии, в котором рассматриваются тепловые явления, происходящие в процессе химических реакций.

Нужен репетитор по химии? Записывайтесь на занятия в каталоге TutorOnline!

Все химические реакции можно разделить на два типа: реакции, идущие с выделением теплоты, их называют экзотермические, и реакции, идущие с поглощением теплоты эндотермические. Критерием таких процессов является тепловой эффект реакции. 

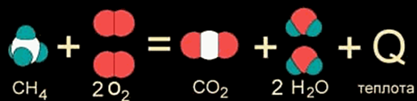
Как правило, к экзотермическим реакциям относятся реакции окисления, т.е. взаимодействия с кислородом, например сгорание метана

СН₄ + 2O₂   = СО₂ + 2Н₂О + Q   (1)

а к эндотермическим реакциям – реакции разложения. Знак Q в конце уравнения указывает на то, выделяется ли теплота в процессе реакции (+ Q) или поглощается (- Q):

СаCO₃ = СаO + CO₂ -Q   (2)

При химических процессах может выделяться или поглощаться не только тепловая, но и другие виды энергии: электрическая, световая, механическая и др.

Тепловые эффекты прямой и обратной реакций одинаковы по числу, но противоположны по знаку, например, оксид кальция (СаО) при взаимодействии с водой образует гидроксид кальция (Са(ОН)₂). Процесс сопровождается выделением большого количества теплоты:

СаО + Н₂О = Са(ОН) + 108 кДж   (3)

А реакция разложения гидроксида кальция (Са(ОН)₂) осуществляется с поглощением такого же количества теплоты извне

Са(ОН)₂ = СаО + Н₂О – 108 кДж   (4)

Если тепловой эффект реакции определяется при постоянном давлении, температуре, то он будет соответствовать стандартной энтальпии реакции, обозначаемой ∆Н, которая противоположна   по знаку величине теплового эффекта реакции. Например, если в процессе экзотермической реакции во взаимодействие вступают алюминий (Аl) и оксид железа (Fe₂O₃), то в конце уравнения это обозначится следующим образом:

2Аl + Fe₂O₃ = 2Fe + Al₂O₃ (+Q) или (-∆Н)   (5) 

А в случае эндотермической реакции значения этих тепловых величин будут иметь противоположные знаки:

С + СО₂ = 2СО (-Q) или (+∆Н)   (6)

Это объясняется тем, что выделяющаяся в процессе экзотермической реакции теплота как энергия, теряется системой (-∆Н), а при эндотермических процессах, наоборот – приобретается (+∆Н). Величина (Н) называется энтальпией системы. Часто её называют так же теплосодержанием или теплотой образования ∆Н данного вещества. В расчётах применяют справочные значения тепловых эффектов образования (или сгорания) одного моля вещества, отнесённые к 298К (25⁰С) и Р = 101,325 кПа (1 атм). Эти условия считаются стандартными и поэтому используемые значения тепловых эффектов называют стандартными теплотами образования(или сгорания) вещества и обозначают как ∆Н⁰₂₉₈. Например, тепловой эффект реакции взаимодействия графита с кислородом, выраженный через изменение энтальпии, следует записать как ∆Н⁰₂₉₈ = – 393,6 кДж, а так как при этом из простых веществ образуется 1 моль СО₂, то данный тепловой эффект является теплотой образования СО₂, выраженной в кДж/моль. Главной характеристикой топлив являются их теплоты сгорания. Тепловой эффект реакции горения одного моля вещества называется теплотой сгорания данного вещества. Следовательно, исходя из вышеприведённых положений, теплота сгорания одного моля графита (12 г) составляет 393,6 кДж/моль.

Уравнение химической реакции, в котором указан тепловой эффект, называется термохимическим уравнением.

На практике это имеет большое значение. При строительстве тепловых трасс, доменных печей, котельных и т.п. теплотопотребляющих промышленных объектов, необходимо предусмотреть или приток энергии для поддержания процессов, или наоборот, отвод избытка теплоты, чтобы не было перегрева вплоть до взрыв                                                                                                              

Расчёт теплового эффекта реакции между простыми веществами не предоставляется затруднительным. Например, для реакции образования хлористого водорода:

Н₂ + Cl₂ = 2НCl    (7)

Энергия затрачивается на разрыв двух химических связей Н–Н и Cl – Cl. При этом энергия выделяется при образовании двух химических связей Н- Cl. Значения энергий этих связей можно найти в справочных таблицах и по разности между ними определить тепловой эффект (Q) реакции (7):

 Е_Н–Н = 436 кДж/моль, Е_Cl–Cl = 240 кДж/моль,

 Е_Н–Cl = 240 кДж/моль,

 Q = 2 х 430 – ( 1 х 436 – 1 х 240 ) = 184 кДж.

Приведённая в качестве примера термохимическая реакция (7) является экзотермической. Теплоты образования простых веществ при стандартных условиях приняты равными нулю.           

Термохимические уравнения имеют особую форму записи. Они отличаются от обычных уравнений тем, что:

1). В термохимических уравнениях обязательно указывают агрегатные состояния веществ (жидкое, твёрдое, газообразное) Это связано с тем, что одна и та же реакция может иметь различный тепловой эффект в зависимости от фазового состояния вещества

2). Коэффициенты в термохимическом уравнении равны количеству веществ ( в молях), вступивших в реакцию. Например, дана реакция сгорания ацетилена:

2С₂Н₂(г) + 5О₂(г) = 4СО₂(г) + 2Н₂О (+Q)   (8)

При сгорании одного моль ацетилена С₂Н₂ выделяется 1257кДж теплоты. Поэтому, относительно одного моль С₂Н₂ необходимо все коэффициенты перед реагентами поделить на 2, тогда получим следующую запись термохимического уравнения:

С₂Н₂ + 5/2О₂ = 2СО₂ + Н₂О + 1257 кДж    (9)

Или другая тождественная запись:

С₂Н₂ + 2,5О₂ = 2СО₂ + Н₂О + 1257 кДж   (10)

Например, дано термохимическое уравнение сгорания метана:

СН₄ + 2О₂ = СО₂ + 2Н₂О + 802 кДж    (11)

Необходимо вычислить, какое количество теплоты выделится при сгорании 20 г метана?

Поскольку 1 моль метана имеет массу 16 г, а 20 г метана соответственно составляют

n = m/Mr = 20:12 = 1,25 моль,

то, составив пропорцию: при сгорании

1 моль СН₄ выделяется 802 кДж теплоты

1,25    СН₄   ——–«——-Х кДж теплоты

Определим, что на сгорание 20г метана потребуется                              

Х = 1,25 х 802 / 1 = 1002,5 кДж

Приведём другой пример . Дано уравнение реакции сгорания оксида азота(+4):

4NО₂(г) + O₂(г) + 2H₂O(г) = 4НNО₃(ж) + 448 кДж   (12)

Необходимо составить термохимическое уравнение относительно сгорания одного моль оксида азота. Определить: какой объём оксида азота потребуется на образование 4258 кДж теплоты в процессе данной реакции?

Для составления термохимического уравнения относительно одного моль оксида азота(+4) необходимо все коэффициенты, стоящие перед реагентами, разделить на коэффициент, стоящий перед NО₂, т.е. на «4», тогда уравнение примет вид:

NО₂(г) + 1/4O₂(г) + 1/2H₂O(г) = НNО₃(ж) +112 кДж   (13)

В уравнении изменится количество выделяющейся теплоты, оно станет   равным 112, т.е. в четыре раза меньше, чем в приведённом уравнении. В соответствии с уравнением (13) 1 моль оксида азота(NО₂) или 22,4 л в данной реакции образует 112 кДж теплоты, а Х л соответственно 4258 кДж:                

22,4 моль NО₂ при сгорании образуют 112 кДж теплоты.

           Х л  —————-«————-4258 кДж теплоты.

            Хг = 22,4 х 4258 / 112 = 851,6 кДж

Важнейшим законом термохимии является закон Г.И.Гесса (1840): тепловой эффект реакции зависит только от начального и конечного состояния веществ и не зависит от промежуточных стадий процесса. При помощи закона Гесса можно рассчитывать такие тепловые эффекты реакции, которые измерить трудно или невозможно. Например, теплоту образования угарного газа(СО) можно вычислить, если полное сгорание углерода

С (графит) + О₂ = СО₂ (∆Н₁)   (14)

разбить на стадии:

С (графит) + 0,5О₂ = СО (∆Н₂)   (15)

СО + 0,5О₂ = СО₂ (∆Н₃)   (16)

Зная, что ∆Н₁ = -393,6 кДж/моль и ∆Н₃ = – 283,1 кДж/моль, из равенства ∆Н₁ = ∆Н₂ + ∆Н₃

находим, что ∆Н₂ = – 110,5 кДж/моль.    

В качестве другого примера можно привести образование сульфата алюминия при сгорании алюминия и серы ромбической согласно реакции:

2Al(к) + 3S(ромб) + 6О₂(г) = Al₂(SO₄)₃(к)   (17)

∆Н может быть найдена по тепловым эффектам отдельных стадий:

2Al + 1,5О₂ = Al₂O₃        ∆Н₁= -1670,2 кДж/моль   (18)

3S + 1,5О₂ = SO₃               ∆Н₂= -395,3 кДж/моль    (19)

Al₂O₃ + 3SO₃  = Al₂(SO₄)₃   ∆Н₃= -579,7 кДж/моль   (20)

Тогда ∆Н = ∆Н₁ + 3∆Н₂ + ∆Н₃  = (- 1670,2) – 3х (-395,3) – (579,7) = – 3435,8 кДж/моль.

На основании закона Гесса термохимические уравнения можно разбивать на отдельные стадии независимо от того, осуществимы они на практике или нет. Из закона Гесса вытекает важное следствие: тепловой эффект химической реакции равен сумме теплот образования получающихся веществ за вычетом суммы теплот образования исходный веществ:                                                                              

∆Н = ∑ (𝘮 ∆Н) продукты – ∑ (𝘯 ∆Н) реагенты,

где 𝘮 и 𝘯 – число молей каждого вещества в уравнении реакции. Например, теплоту сгорания ацетилена (10) можно рассчитать, зная теплоты образования  С₂Н₂ , СО₂   и Н₂О (∆Н⁰₀₂ = 0), как ∆Н⁰ = 2 ∆Н _СО2 + ∆Н_Н2О – ∆Н_С2Н2 = -2 х 393,6 – 281 – (+226,8) = -1295 кДж/моль.

НАЧАЛА ТЕРМОДИНАМИКИ

 Среди многообразия химических реакций, термохимические занимают особое положение. Если рассуждать с точки зрения эволюции жизни на Земле, то в конечном итоге, действительно, от этих процессов зависит жизнь на нашей планете. А что касается человеческой цивилизации в целом, то здесь мы имеем прямую зависимость её развития от термохимических явлений. Ведь благодаря именно данным процессам произошёл отрыв человечества в развитии от всех других видов живых организмов, населяющих нашу планету. С древнейших времён, начиная от пассивного использования огня в качестве средства для согревания и приготовления примитивной пищи, человечество пришло к активному использованию этого явления (изготовление гончарных изделий – плавка меди, железа и других металлов – паровые двигатели – двигатели внутреннего сгорания – управление ядерными реакциями)

Если можно было бы предложить создать проект монумента человеческому прогрессу, то на его фронтоне надо было бы начертать уравнение химической реакции

С + О₂ = СО₂

Именно со сгорания дров, угля, торфа начался отсчёт человеческой цивилизации. В настоящее время наше с вами существование просто немыслимо без тепловых процесов. Но кроме приведённой выше реакции существует великое множество других термодинамических процессов. Почему именно углероду дано такое предпочтение? Может быть его собрату по IV-й группе – кремнию более выгоден данный процесс?

Si + О₂ = SiО₂ 

Тем более, что кремний по массе составляет 27,6% земной коры. Это несравненно больше, чем запасы древесины и её ископаемых на нашей планете. Чего же проще? Кидай в топку кремнезём! Его ведь целая планета! Правда надо оговорить тот факт, что чистого кремния в природе не существует. В наличии только его оксид – SiО₂. Но на то и химики, чтобы придумать что-нибудь? А может быть для более сильного окислителя, чем кислород – фтору окисление углерода более выгодно термодинамически?

C + 2F₂ = СF₄

Как во всём этом разобраться? И возможно ли вообще предсказать осуществления того или иного процесса, ведь на бумаге можно написать уравнение любой химической реакции, а возможна ли она практически? Придётся начинать всё по порядку.

  Одним из самых важных и очевидных законов природы является закон сохранения энергии: энергия не возникает из ничего и не исчезает бесследно, она только переходит из одной формы в другую. Аналогичным является закон сохранения массы вещества: массы веществ вступивших в реакцию равны массам веществ, образовавшихся в процессе данной реакции.

Поэтому и при экзотермической и при эндотермической обратимых реакциях одного и того же процесса как количество затрачиваемой и расходуемой энергии равны, но противоположны по знаку, так и массы веществ распадающихся и вновь образующихся равны:

СаО + Н₂О = Са(ОН)₂ + 108 кДж

Mr=56     Mr=18          Mr=74

Са(ОН)₂ = СаО + Н₂О – 108 кДж

Mr=74          Mr=56        Mr=18

Но всё дело в том, что в приведённых выше двух реакциях уже указано, какая из них экзотермическая, а какая эндотермическая. А можно ли так, как говорится «на вскидку» по одному только уравнению реакции определить: какая это реакция? В принципе, в большинстве случаев, возможно. К экзотермическим реакциям, в основном, относятся реакции соединения и как их разновидность – реакции окисления.(8,11,12,14). А к реакциям эндотермическим, соответственно – реакции разложения (2,4). Ещё раз уточним: в большинстве случаев. Поскольку реакция окисления:

0,5N₂ + 0,5O₂ = NО  – 90 кДж

требует расхода энергии и является эндотермической, а реакция разложения нитрата натрия

2NaNO₃ = 2NaNO₂ + O₂ (+Q)

осуществляется с выделением большого количества теплоты и является экзотермической.

Значит, принцип «на вскидку» не годится. Но каким же принципом тогда следует руководствоваться в определении реакций данного типа? В приводимых выше примерах (10), (14-20) указывалось, что стандартные теплоты образования веществ (∆Н) являются справочными данными. Такие данные скрупулёзно составлялись на протяжении десятилетий для многочисленных термодинамических реакций. С этой целью использовался прибор калориметр. Именно по этим данным в настоящее время мы можем установить, какой является та или иная реакция: экзотермической или эндотермической.

  Теперь попробуем заглянуть как бы внутрь термохимической реакции. Как она начинается? Что способствует её осуществлению? В качестве примера приведём ещё раз две реакции (14) и (2):

С(графит) + О₂ = СО₂ + 393,3 кДж

СаСО₃ = СаО + СО₂  (-Q)

Представим себе, что химическими символами (С) и (О₂) будут обозначаться не элемент «углерод» и простое вещество «кислород», а дрова (или уголь, торф) и воздух (атмосфера). А в качестве соединения СаСО₃ – не карбонат кальция, а известное всем вещество: мел (или известняк). Первую реакцию будем проводить для того, чтобы нагреть печь и вскипятить чайник, а вторую – чтобы получить негашёную известь (СаО) в дальнейшем используемую для побелки садовых деревьев. Для разжигания печи приготовим щепки и, поместив сверху них дрова, зажжём огонь спичками.

Во втором случае, поместим в металлическое ведро мелко накрошенный мел, поставим на плиту и такими же действиями, как в случае разжигания огня в печи, разведём костёр под ведром.

Стоп! Тут что-то не так! Ведь мы установили, что первая реакция экзотермическая, протекает с выделением теплоты, а вторая реакция – эндотермическая, протекает с поглощением теплоты. А мы в обоих случаях разводим огонь, т.е. передаём этим процессам извне тепловую энергию. Значит, обе реакции эндотермические – идут с поглощением теплоты! Да, идут с поглощением теплоты, но это только на первом этапе. Некоторым экзотермическим реакциям требуется небольшой «толчок» – первоначальная подача энергии, а спустя некоторое время, когда загорятся дрова, процесс будет сопровождаться с выделением энергии в окружающую среду и во многие сотни, тысячи раз превзойдёт по величине первоначальное значение этой энергии. А второй процесс ка был так и останется эндотермическим. Ведь с прекращением подачи тепловой энергии мел перестанет разлагаться: реакция остановится. И всё-таки, почему в одних случаях процесс окисления (горения) является экзотермическим, а в других – эндотермическим процессом? И что является движущей силой эндотермических реакций, в ходе которых тепловая энергия поступает из окружающей среды? Ни у кого не вызывает удивление такое явление, как остывание со временем горячего чайника. Это нормально. А почему бы этому же чайнику, уже остывшему, холодному, взять, да и нагреться самому по себе? Вот это уже вызовет удивление.

Так вот, эта самая сила связана со стремлением любой системы к наиболее вероятному состоянию, характеризующимся максимальным беспорядком, называемым энтропией. Это одно из важнейших понятий в термодинамике. Энтропия обозначается символом «S». К примеру, при экзотермических реакциях, при проведении процессов плавления, кипения, переходов из жидкостей к газообразному состоянию, энтропия приобретает максимальное значение, поскольку при тепловых явлениях кинетическая энергия атомов, молекул, ионов возрастает, усиливаются беспорядочные колебания этих частиц. И наоборот, самый большой порядок в химических системах – в идеальном кристалле при температуре абсолютного нуля. Энтропия в данном случае равна нулю

Энтропия имеет численные значения, единицей её измерения является Дж/(моль ^. К); К примеру энтропия алмаза равна 2,4 Дж/(моль ^. К), пропана – 269,9 Дж/(моль ^. К). Энтропия газов значительно превышает энтропию жидких и тем более твёрдых тел. Поскольку в газообразных веществах постоянно происходит беспорядочное распределение молекул по всему объёму.

Существуют экспериментальные и теоретические методы определения энтропий различных химических соединений. Используя их, можно количественно рассчитать изменения энтропии при протекании конкретной реакции аналогично тому, как это делается для теплового эффекта реакции. Составлены специальные справочные данные, которые включают сравнительную характеристику этих величин с учётом температуры.          

Подтянуть знания по химии можно записавшись на урок к онлайн-репетиторам TutorOnline

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Энтропия. Энергия Гиббса

Понятие энтропии

Абсолютная энтропия веществ и изменение энтропии в процессах

Стандартная энтропия

Стандартная энтропия образования

Энергия Гиббса

Стандартная энергия Гиббса образования

Энтальпийный, энтропийный фактор и направление процесса

Примеры решения задач

Задачи для самостоятельного решения

Понятие энтропии

Энтропия S – функция состояния системы. Энтропия характеризует меру неупорядоченности (хаотичности) состояния системы. Единицами измерения энтропии являются Дж/(моль·К).

Абсолютная энтропия веществ и изменение энтропии в процессах

При абсолютном нуле температур (Т = 0 К) энтропия идеального кристалла любого чистого простого вещества или соединения равна нулю. Равенство нулю S при 0 К позволяет вычислить абсолютные величины энтропий веществ на основе экспериментальных данных о температурной зависимости теплоемкости.

Изменение энтропии в процессе выражается уравнением:

где S_(прод.) и S_(исх.) – соответственно абсолютные энтропии продуктов реакции и исходных веществ.

На качественном уровне знак S реакции можно оценить по изменению объема системы ΔV в результате процесса. Знак ΔV определяется по изменению количества вещества газообразных реагентов Δn_г. Так, для реакции

(Δn_г = 1) ΔV > 0, значит, ΔS > 0.

Стандартная энтропия

Величины энтропии принято относить к стандартному состоянию. Чаще всего значения S рассматриваются при Р = 101,325 кПа (1 атм) и температуре Т = 298,15 К (25 о С). Энтропия в этом случае обозначается S о ₂₉₈ и называется стандартной энтропией при Т = 298,15 К. Следует подчеркнуть, что энтропия вещества S (S о ) увеличивается при повышении температуры.

Стандартная энтропия образования

Стандартная энтропия образования ΔS о _f,298 (или ΔS о _обр,298) – это изменение энтропии в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии.

Энергия Гиббса

Энергия Гиббса G – функция состояния системы. Энергия Гиббса равна:

Абсолютное значение энергии Гиббса определить невозможно, однако можно вычислить изменение δG в результате протекания процесса.

Критерий самопроизвольного протекания процесса: в системах, находящихся при Р, Т = const, самопроизвольно могут протекать только процессы, сопровождающиеся уменьшением энергии Гиббса (ΔG

Стандартная энергия Гиббса образования

Стандартная энергия Гиббса образования δG о _f,298 (или δG о _обр,298) – это изменение энергии Гиббса в процессе образования данного вещества (обычно 1 моль), находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартном состоянии, причем простые вещества пристутствуют в наиболее термодинамически устойчивых состояниях при данной температуре.

Для простых веществ, находящихся в термодинамически наиболее устойчивой форме, δG о _f,298 = 0.

Энтальпийный, энтропийный фактор и направление процесса

Проанализируем уравнение ΔG о _Т = ΔН о _Т — ΔТS о _Т. При низких температурах ТΔS о _Т мало. Поэтому знак ΔG о _Т определяется в основном значением ΔН о _Т (энтальпийный фактор). При высоких температурах ТΔS о _Т – большая величина, знак Δ G о _Т определяется и энтропийным фактором. В зависимости от соотношения энтальпийного (ΔН о _Т) и энтропийного (ТΔS о _Т) факторов существует четыре варианта процессов.

• • 1. Если ΔН о _Т о _Т > 0, то ΔG о _Т
    2. Если ΔН о _Т > 0, ΔS о _Т о _Т > 0 всегда (процесс не протекает ни при какой температуре).
    3. Если ΔН о _Т о _Т о _Т о /ΔS о (процесс идет при низкой температуре за счет энтальпийного фактора).
    4. Если ΔН о _Т > 0, ΔS о _Т > 0, то ΔG о _Т ΔН о / ΔS о (процесс идет при высокой температуре за счет энтропийного фактора).

Примеры решения задач

Задача 1. Используя термодинамические справочные данные, вычислить при 298,15 К изменение энтропии в реакции:

Объяснить знак и величину ΔS о .

Решение. Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	NH3(г)	O2(г)	NО(г)	H2O(ж)
S о 298, Дж/(моль·К)	192,66	205,04	210,64	69,95

В данной реакции ΔV o _х.р.,298

Задача 2. Используя справочные термодинамические данные, рассчитать стандартную энтропию образования NH₄NO_3(к). Отличается ли стандартная энтропия образования NH₄NO_3(к) от стандартной энтропии этого соединения?

Решение. Стандартной энтропии образования NH₄NO₃ отвечает изменение энтропии в процессе:

Значения стандартных энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	N2(г)	H2(г)	O2(г)	NH4NO3(к)
S о 298, Дж/(моль·К)	191,50	130,52	205,04	151,04

Стандартная энтропия образования NH₄NO₃(к), равная — 609,06 Дж/(моль·К), отличается от стандартной энтропии нитрата аммония S о ₂₉₈(NH₄NO_3(к)) = +151,04 Дж/(моль·К) и по величине, и по знаку. Следует помнить, что стандартные энтропии веществ S о ₂₉₈ всегда больше нуля, в то время как величины ΔS 0 _f,298, как правило, знакопеременны.

Задача 3. Изменение энергии Гиббса реакции:

равно δG о ₂₉₈= –474,46 кДж. Не проводя термодинамические расчеты, определить, за счет какого фактора (энтальпийного или энтропийного) протекает эта реакция при 298 К и как будет влиять повышение температуры на протекание этой реакции.

Решение. Поскольку протекание рассматриваемой реакции сопровождается существенным уменьшением объема (из 67,2 л (н.у.) исходных веществ образуется 36 мл жидкой воды), изменение энтропии реакции ΔS о о ₂₉₈ реакции меньше нуля, то она может протекать при температуре 298 К только за счет энтальпийного фактора. Повышение температуры уменьшает равновесный выход воды, поскольку ТΔS о

Задача 4. Используя справочные термодинамические данные, определить может ли при 298,15 К самопроизвольно протекать реакция:

Если реакция не будет самопроизвольно протекать при 298,15 К, оценить возможность ее протекания при более высоких температурах.

Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	С4Н10(г)	С2Н4(г)	Н2(г)
ΔG о f,298× , кДж/моль	— 17,19	68,14	0
S о 298, Дж/(моль·К)	310,12	219,45	130,52

ΔG о _х.р.,298 > 0, следовательно, при Т = 298,15 К реакция самопроизвольно протекать не будет.

Поскольку ΔS о _х.р.,298 > 0, то при температуре Т>ΔН о /ΔS о величина ΔG о _х.р.,298 станет величиной отрицательной и процесс сможет протекать самопроизвольно.

Задача 5. Пользуясь справочными данными по ΔG о _f,298 и S о ₂₉₈, определите ΔH о ₂₉₈ реакции:

Решение. Значения стандартных энергий Гиббса и энтропий исходных веществ и продуктов реакции приведены ниже:

Вещество	N2O(г)	H2(г)	N2H4(г)	H2O(ж)
ΔG о f,298, кДж/моль	104,12	0	159,10	-237,23
S о 298, Дж/(моль·К)	219,83	130,52	238,50	69,95

ΔG о ₂₉₈ = ΔН о ₂₉₈ – ТΔS о ₂₉₈. Подставляя в это уравнение величины ΔН о ₂₉₈ и ТΔS о ₂₉₈, получаем:

ΔН о ₂₉₈ = –182,25× 10 3 + 298·(–302,94) = –272526,12 Дж = – 272,53 кДж.

Следует подчеркнуть, что поскольку ΔS о ₂₉₈ выражена в Дж/(моль× К), то при проведении расчетов ΔG 0 ₂₉₈ необходимо также выразить в Дж или величину ΔS 0 ₂₉₈ представить в кДж/(мольK).

Задачи для самостоятельного решения

1. Используя справочные данные, определите стандартную энтропию образования ΔS о _f,298 NaHCO_3(к).

2. Выберите процесс, изменение энергии Гиббса которого соответствует стандартной энергии Гиббса образования NO_2(г):

Энергия Гиббса. Энергия Гельмгольца. Направление процесса.

Чтобы дать ответ на вопрос о возможности протекания той или иной реакции, о ее направлении и глубине необходимо снова воспользоваться II – законом термодинамики, который может быть сформулирован следующим образом: любой самопроизвольно протекающий процесс, а также и химическая реакция, идет в том направлении, которое сопровождается уменьшением свободной энергии в системе (при постоянных температуре и давлении) или энергии Гельмгольца (при постоянных температуре и объеме).

Свободная энергия или Энергия Гиббса G – это та часть всей энергии системы, которую можно использовать для совершения максимальной работы.

Энергия Гельмгольца A — это та часть внутренней энергии системы, также определяющая работоспособность и может быть применена для совершения максимальной работы.

При протекании химических реакций единовременно совершаются два направления: стремление простых частиц объединиться в более сложные, а также стремление сложных частиц к распаду на более простые.

Они не зависят друг от друга и их величины противоположны, и процесс идет в сторону той реакции, при которой изменение величины больше. Разность между этими величинами определяет свободную энергию реакции (при постоянных температуре и давлении). Ее изменение в реакции определяется разностью сумм энергий Гиббса конечных продуктов реакции и исходных веществ:

При постоянных температуре и давлении изменение энергии Гиббса связано с энтальпией и энтропией следующим выражением:

Здесь изменение энергии Гиббса учитывает одновременно изменение энергетического запаса системы и степень ее беспорядка (самопроизвольность протекания процесса).

Т.к. энергия Гиббса является мерой самопроизвольности протекания процесса, то между знаком ΔG для любой реакции и ее самопроизвольным протеканием (при постоянных температуре и давлении) существуют такие зависимости:

1. Если ΔG отрицательно (ΔG 0), то реакция протекать самопроизвольно в прямом направлении не может. Однако обратная реакция идет самопроизвольно.

Энтальпийный и энтропийный факторы и направление процесса

Выясним, как функция свободной энергии зависит от изменений энтропии и энтальпии идущего процесса. Вернемся к выражению, связывающему энергию Гиббса с энтальпией и энтропией:

Без энтропийных факторов все экзотермические реакции (ΔH˂0) должны были быть самопроизвольными. Но энтропийный фактор, который определяется величиной – TΔS, может привести к росту или, наоборот, к падению способности самопроизвольного протекания.

Так, при ΔS>0, член – TΔS вносит отрицательный вклад в общую величину ΔG, следовательно он повышает возможность реакции протекать самопроизвольно.

А при при ΔS 0
Всегда ˂0
Реакция самопроизвольна при любых температурах, обратная реакция всегда несамопроизвольна

>0
˂0
Всегда >0
Реакция несамопроизвольна при любых температурах, обратная реакция самопроизвольна

˂0
˂0
При низких температурах ˂0, при высоких температурах >0
Реакция самопроизвольна при низких температурах, обратная реакция становится самопроизвольной при высоких температурах

>0
>0
При низких температурах >0, при высоких температурах ˂0
Реакция несамопроизвольна при низких температурах, но при высоких температурах становится самопроизвольной

Изменение энергии Гиббса. Для удобства принято сравнивать значения ΔG при стандартных условиях – концентрации равны 1 моль/л, парциальное давление газообразных веществ равно 101,3 кПа, температура 298,15 К. Тогда свободную энергию обозначают через ΔG 0 , на основе значений которой можно вычислить изменение энергии Гиббса химической реакции:

Величина ΔG 0 _р-ции позволяет определить, будет ли данная реакция, находящаяся в стандартных условиях, протекать самопроизвольно в прямом или обратном направлении. Аналогично теплоте образования, энергии Гиббса образования простых веществ равны нулю.

Энергия Гельмгольца системы с определенной внутренней энергией (U), энтропией (S) при абсолютной температуре (Т) определяется уравнением:

Изменение энергии Гельмгольца для процессов (при постоянных температуре и объеме) можно определить соотношением:

ΔA — величина, которая не зависит от пути, а зависит только от исходного и конечного состояния системы, т.е. ΔA также, как и другие рассмотренные термодинамические величины, является функцией состояния.

Энергия Гельмгольца подобно энергии Гиббса связана с самопроизвольностью протекания процесса. Если допустить, что система изолирована, а объем и температура постоянны, то самопроизвольно будут протекать только те процессы, при которых А уменьшается.

Таким образом, при ΔA 0 – в обратном направлении,

а при ΔA=0 система находится в состоянии равновесия.

Энергию Гельмгольца и энергию Гиббса в стандартных состояниях можно связать с константой равновесия:

Где R– универсальная газовая постоянная, K – константа равновесия, Т – абсолютная температура.

Если K>>1, т.е. реакция идет в прямом направлении, то ΔG 0 ˂˂0.

Если K 0 >>0

Если K=1, то ΔG 0 =0

В случае химической реакции, протекающей в гальваническом элементе при стандартных условиях ΔG 0 можно связать с ЭДС гальванического элемента следующим соотношением:

ΔG 0 =-nFE 0 , где

nF – количество прошедшего электричества

E 0 – электродвижущая сила, при условии что все вещества, принимающие участие в реакции, находятся в стандартном состоянии.

При самопроизвольном протекании процесса, его ΔG 0.

Порог реакционной способности веществ для большинства реакций имеет значение ΔG 0 ≈41 кДж/моль.

То есть, если ΔG 0 0 >+41 кДж/моль, то процесс неосуществим в любых реальных и стандартных условиях.

Уравнение зависимости энергии гиббса от температуры

Термодинамическими потенциалами, или характеристическими функциями, называют термодинамические функции, которые содержат в себе всю термодинамическую информацию о системе. Наибольшее значение имеют четыре основных термодинамических потенциала:

В скобках указаны термодинамические параметры, которые получили название естественных переменных для термодинамических потенциалов. Все эти потенциалы имеют размерность энергии и все они не имеют абсолютного значения, поскольку определены с точностью до постоянной, которая равна внутренней энергии при абсолютном нуле.

Зависимость термодинамических потенциалов от их естественных переменных описывается основным уравнением термодинамики, которое объединяет первое и второе начала. Это уравнение можно записать в четырех эквивалентных формах:

Эти уравнения записаны в упрощенном виде – только для закрытых систем, в которых совершается только механическая работа.

Зная любой из четырех потенциалов как функцию естественных переменных, можно с помощью основного уравнения термодинамики найти все другие термодинамические функции и параметры системы (см. пример 5-1).

Другой важный смысл термодинамических потенциалов состоит в том, что они позволяют предсказывать направление термодинамических процессов. Так, например, если процесс происходит при постоянных температуре и давлении, то неравенство, выражающее второй закон термодинамики:

эквивалентно неравенству dG_p,T 0 (мы учли, что при постоянном давлении Q_p = dH), где знак равенства относится к обратимым процессам, а неравенства – к необратимым. Таким образом, при необратимых процессах, протекающих при постоянных температуре и давлении, энергия Гиббса всегда уменьшается. Минимум энергии Гиббса достигается при равновесии.

Аналогично, любой термодинамический потенциал в необратимых процессах при постоянстве естественных переменных уменьшается и достигает минимума при равновесии:

Потенциал

Естественные
переменные

Условие само-произвольности

Условия
равновесия

S = const, V = const

dU 2 U > 0

S = const, p = const

dH 2 H > 0

T = const, V = const

dF 2 F > 0

T = const, p = const

dG 2 G > 0

Наибольшее значение в конкретных термодинамических расчетах имеют два последние потенциала – энергия Гельмгольца F и энергия Гиббса G , т.к. их естественные переменные наиболее удобны для химии. Другое (устаревшее) название этих функций – изохорно-изотермический и изобарно-изотермический потенциалы. Они имеют дополнительный физико-химический смысл. Уменьшение энергии Гельмгольца в каком-либо процессе при T = const, V = const равно максимальной механической работе, которую может совершить система в этом процессе:

Таким образом, энергия F равна той части внутренней энергии (U = F + TS), которая может превратиться в работу.

Аналогично, уменьшение энергии Гиббса в каком-либо процессе при T = const, p = const равно максимальной полезной (т.е., немеханической) работе, которую может совершить система в этом процессе:

Зависимость энергии Гельмгольца (Гиббса) от объема (давления) вытекает из основного уравнения термодинамики (5.3), (5.4):

. (5.5)

Зависимость этих функций от температуры можно описать с помощью основного уравнения термодинамики:

(5.6)

или с помощью уравнения Гиббса-Гельмгольца:

(5.7)

Расчет изменения функций F и G в химических реакциях можно проводить разными способами. Рассмотрим два из них на примере энергии Гиббса.

1) По определению, G = H – TS. Если продукты реакции и исходные вещества находятся при одинаковой температуре, то стандартное изменение энергии Гиббса в химической реакции равно:

, (5.8)

где тепловой эффект можно рассчитать с помощью стандартных энтальпий образования, а стандартное изменение энтропии – по абсолютным энтропиям участников реакции.

2) Аналогично тепловому эффекту реакции, изменение энергии Гиббса можно рассчитать, используя энергии Гиббса образования веществ:

. (5.9)

В термодинамических таблицах обычно приводят абсолютные энтропии и значения термодинамических функций образования соединений из простых веществ при температуре 298 К и давлении 1 бар (стандартное состояние). Для расчета _rG и _rF при других условиях используют соотношения (5.5) – (5.7).

Все термодинамические потенциалы являются функциями состояния. Это свойство позволяет найти некоторые полезные соотношения между частными производными, которые называют соотношениями Максвелла.

Рассмотрим выражение (5.1) для внутренней энергии. Т.к. dU – полный дифференциал, частные производные внутренней энергии по естественным переменным равны:

Если продифференцировать первое тождество по объему, а второе – по энтропии, то получатся перекрестные вторые частные производные внутренней энергии, которые равны друг другу:

(5.10)

Три другие соотношения получаются при перекрестном дифференцировании уравнений (5.2) – (5.4).

(5.11)

(5.12)

(5.13)

ПРИМЕРЫ

Пример 5-1. Внутренняя энергия некоторой системы известна как функция энтропии и объема, U(S,V). Найдите температуру и теплоемкость этой системы.

Решение. Из основного уравнения термодинамики (5.1) следует, что температура – это частная производная внутренней энергии по энтропии:

.

Изохорная теплоемкость определяет скорость изменения энтропии с температурой:

.

Воспользовавшись свойствами частных производных, можно выразить производную энтропии по температуре через вторую производную внутренней энергии:

.

Пример 5-2. Используя основное уравнение термодинамики, найдите зависимость энтальпии от давления при постоянной температуре: а) для произвольной системы; б) для идеального газа.

Решение. а) Если основное уравнение в форме (5.2) поделить на dp при постоянной температуре, получим:

.

Производную энтропии по давлению можно выразить с помощью соотношения Максвелла для энергии Гиббса (5.13):

.

б) Для идеального газа V(T) = nRT / p. Подставляя эту функцию в последнее тождество, получим:

.

Энтальпия идеального газа не зависит от давления.

Пример 5-3. Выразите производные и через другие термодинамические параметры.

Решение. Основное уравнение термодинамики (5.1) можно переписать в виде:

,

представив энтропию как функцию внутренней энергии и объема. Коэффициенты при dU и dV равны соответствующим частным производным:

.

Пример 5-4. Два моля гелия (идеальный газ, мольная теплоемкость C_p = 5/2 R) нагревают от 100 о С до 200 о С при p = 1 атм. Вычислите изменение энергии Гиббса в этом процессе, если известно значение энтропии гелия, = 131.7 Дж/(моль . К). Можно ли считать этот процесс самопроизвольным?

Решение. Изменение энергии Гиббса при нагревании от 373 до 473 К можно найти, проинтегрировав частную производную по температуре (5.6):

.

Зависимость энтропии от температуры при постоянном давлении определяется изобарной темлоемкостью:

.

Интегрирование этого выражения от 373 К до T дает:

.

Подставляя это выражение в интеграл от энтропии, находим:

Процесс нагревания не обязан быть самопроизвольным, т.к. уменьшение энергии Гиббса служит критерием самопроизвольного протекания процесса только при T = const и p = const.

Ответ. G = -26850 Дж.

Пример 5-5. Рассчитайте изменение энергии Гиббса в реакции

при температуре 500 K и парциальных давлениях 3 бар. Будет ли эта реакция самопроизвольной при данных условиях? Газы считать идеальными. Необходимые данные возьмите из справочника.

Решение. Термодинамические данные при температуре 298 К и стандартном давлении 1 бар сведем в таблицу:

Вещество

Энтальпия образования
, кДж/моль

Энтропия
, Дж/(моль . К)

Теплоемкость
, Дж/(моль . К)

Реакция

, кДж/моль

, Дж/(моль . К)

, Дж/(моль . К)

CO + ЅO₂ =
= CO₂

Примем, что C_p = const. Изменения термодинамических функций в результате реакции рассчитаны как разность функций реагентов и продуктов:

f = f(CO₂) – f(CO) – Ѕ f(O₂).

Стандартный тепловой эффект реакции при 500 К можно рассчитать по уравнению Кирхгофа в интегральной форме (3.8):

Стандартное изменение энтропии в реакции при 500 К можно рассчитать по формуле (4.9):

Стандартное изменение энергии Гиббса при 500 К:

Для расчета изменения энергии Гиббса при парциальных давлениях 3 атм необходимо проинтегрировать формулу (5.5) и использовать условие идеальности газов ( V = n RT / p, n – изменение числа молей газов в реакции):

Эта реакция может протекать самопроизвольно при данных условиях.

Ответ. G = -242.5 кДж/моль.

ЗАДАЧИ

5-1. Выразите внутреннюю энергию как функцию переменных G, T, p.

5-2. Используя основное уравнение термодинамики, найдите зависимость внутренней энергии от объема при постоянной температуре: а) для произвольной системы; б) для идеального газа.

5-3. Известно, что внутренняя энергия некоторого вещества не зависит от его объема. Как зависит давление вещества от температуры? Ответ обоснуйте.

5-4. Выразите производные и через другие термодинамические параметры и функции.

5-5. Напишите выражение для бесконечно малого изменения энтропии как функции внутренней энергии и объема. Найдите частные производные энтропии по этим переменным и составьте соответствующее уравнение Максвелла.

5-6. Для некоторого вещества известно уравнение состояния p(V, T). Как изменяется теплоемкость C_v с изменением объема? Решите задачу: а) в общем виде; б) для какого-либо конкретного уравнения состояния (кроме идеального газа).

5-7. Докажите тождество: .

5-8. Энергия Гельмгольца одного моля некоторого вещества записывается следующим образом:

где a, b, c, d – константы. Найдите давление, энтропию и теплоемкость C_V этого тела. Дайте физическую интерпретацию константам a, b, d.

5-9. Нарисуйте график зависимости энергии Гиббса индивидуального вещества от температуры в интервале от 0 до T > T_кип.

5-10. Для некоторой системы известна энергия Гиббса:

5-11. Зависимость мольной энергии Гельмгольца некоторой системы от температуры и объема имеет вид:

,

где a, b, c, d – константы. Выведите уравнение состояния p(V,T) для этой системы. Найдите зависимость внутренней энергии от объема и температуры U(V,T). Каков физический смысл постоянных a, b, c?

5-12. Найдите зависимость мольной внутренней энергии от объема для термодинамической системы, которая описывается уравнением состояния (для одного моля)

,

где B(T) – известная функция температуры.

5-13. Для некоторого вещества зависимость теплоемкости от температуры имеет вид: C_V = aT 3 при температуре 0 – 10 К. Найдите зависимость энергии Гельмгольца, энтропии и внутренней энергии от температуры в этом диапазоне.

5-14. Для некоторого вещества зависимость внутренней энергии от температуры имеет вид: U = aT 4 + U₀ при температуре 0 – 10 К. Найдите зависимость энергии Гельмгольца, энтропии и теплоемкости C_V от температуры в этом диапазоне.

5-15. Выведите соотношение между теплоемкостями:

.

5-16. Исходя из тождества , докажите тождество:

.

5-17. Один моль газа Ван-дер-Ваальса изотермически расширяется от объема V₁ до объема V₂ при температуре T. Найдите U, H, S, F и G для этого процесса.

5-18. Вычислите изменение H, U, F, G, S при одновременном охлаждении от 2000 К до 200 К и расширении от 0.5 м 3 до 1.35 м 3 0.7 молей азота (C_V = 5/2 R). Энтропия газа в исходном состоянии равна 150 Дж/(моль . К), газ можно считать идеальным.

5-19. Вычислите изменение энергии Гиббса при сжатии от 1 атм до 3 атм при 298 К: а) одного моля жидкой воды; б) одного моля водяного пара (идеальный газ).

5-20. Изменение энергии Гиббса в результате испарения воды при 95 о С и 1 атм равно 546 Дж/моль. Рассчитайте энтропию паров воды при 100 о С, если энтропия жидкой воды равна 87.0 Дж/(моль . К). При каком давлении изменение энергии Гиббса в результате испарения воды будет равно 0 при 95 о С?

5-21*. Давление над одним молем твердой меди при температуре 25 о С увеличили от 1 до 1000 атм. Найти U, H, S, F. Медь считать несжимаемой, плотность 8.96 г/см 3 , изобарический коэффициент теплового расширения = 5.01 . 10 -5 К -1 .

5-22. Вычислите стандартную энергию Гиббса образования () жидкой и газообразной воды, если известны следующие данные: (H₂O_(г)) = -241.8 кДж/моль, (H₂O_(ж)) = -285.6 кДж/моль, (H₂) = 130.6 Дж/(моль . К), (O₂) = 205.0 Дж/(моль . К), (H₂O_(г)) = 188.5 Дж/(моль . К), (H₂O_(ж)) = 69.8 Дж/(моль . К).

5-23. Рассчитайте G o при 25 о С для химической реакции:

Стандартные значения энтальпии образования и абсолютной энтропии при 25 о С равны: _fH o (HСl) = -22.1 ккал/моль, _fH o (H₂O_(ж)) = -68.3 ккал/моль; S o (HCl) = 44.6 кал/(моль . K), S o (O₂) = 49.0 кал/(моль . K), S o (Сl₂) = 53.3 кал/(моль . K), S o (H₂O_(ж)) = 16.7 кал/(моль . K).

5-24. Рассчитайте G o при 25 о С для химической реакции:

Стандартные значения энтальпии образования и абсолютной энтропии при 25 о С равны: _fH o (СO₂) = -94.1 ккал/моль, _fH o (СH₄) = -17.9 ккал/моль, _fH o (H₂O_(ж)) = -68.3 ккал/моль; S o (СO₂) = 51.1 кал/(моль . K), S o (H₂) = 31.2 кал/(моль . K), S o (СH₄) = 44.5 кал/(моль . K), S o (H₂O_(ж)) = 16.7 кал/(моль . K).

5-25. Рассчитайте стандартные энергии Гиббса и Гельмгольца G o и F o при 300 о С для химической реакции:

Может ли эта реакция протекать самопроизвольно при данной температуре? Теплоемкости веществ считать постоянными.

5-26. Найдите энергию Гиббса образования NH₃ при температурах 298 и 400 K, если известны следующие данные: (NH₃) = -46.2 кДж/моль,

NH₃

C_p,298, Дж/(моль . К)

35.7

, Дж/(моль . К)

Считать, что теплоемкости в указанном интервале температур постоянны.

5-27. Рассчитайте стандартные энергии Гиббса и Гельмгольца G o и F o при 60 о С для химической реакции:

Может ли эта реакция протекать самопроизвольно при данной температуре? Теплоемкости веществ считать постоянными.

5-28. Рассчитайте стандартные энергии Гиббса и Гельмгольца G o и F o при 700 о С для химической реакции:

Может ли эта реакция протекать самопроизвольно при данной температуре? Теплоемкости веществ считать постоянными.

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

[spoiler title=”источники:”]

http://zadachi-po-khimii.ru/obshaya-himiya/energiya-gibbsa-energiya-gelmgolca-napravlenie-processa.html

http://www.chem.msu.su/rus/teaching/eremin1/1-5.html

[/spoiler]