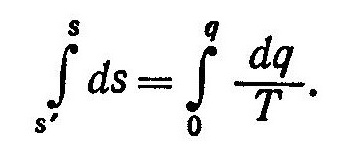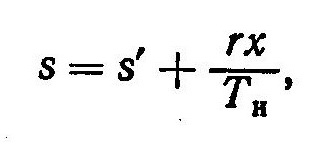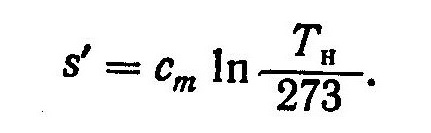Как найти энтропию водяного пара

Энтропия пара

Энтропия
водяного пара отсчитывается от условного
нуля, за каковой принимают энтропию
воды при 0°С и при давлении насыщения,
соответствующем этой температуре, т.е.
при давлении 0,0062 ата.

Энтропия жидкости
определяется из выражения

S’ = С ln,(9.14)

где
С – теплоемкость воды, Т_н
– температура кипения жидкости в °К.

Энтропия
сухого насыщенного пара S” определяется
из уравнения

S”
= S’ +
,
(9.15)

где r
– теплота парообразования.

Энтропия
влажного насыщенного пара S_х
равна

S_х
= S’ +
∙х
(9.16)

или на основании
формулы (7.15)

S_х
= S’ + (S” – S’)∙х, (9.17)

где х – степень
сухости пара.

Значения
энтропии S’ и S” приведены в приложениях
Б иВ.

Значения
можно
получить из этих таблиц как разность
S” – S’.

Энтропия
перегретого пара может быть найдена из
уравнения

S
= S” +
.
(9.18)

Значения S приводятся
в таблицах перегретого пара.

При определении
состояния пара заданных параметров
необходимо исходить из следующего.

Для перегретого
и сухого насыщенного пара одинакового
давления

υ > υ” и t > t_н;

при одной и той же
температуре перегретого и сухого
насыщенного пара

υ
> υ” и р < р_н.

При помощи
водяного пара и этих соотношений легко
определить состояние пара.

Таблица 9.2 – Формулы
для расчета теплоты и работы в процессах

водяного пара

Процесс	Теплота	Работа
Изохорический	q = U2 – U1 q = (h2 – h1) – υ (Р2 – Р1)	ι = 0
Изобарический	q = U2 – U1 + Р(υ2 – υ1) q = h2 – h1	ι = q – ΔU
Изотермический	q = Т (S2 – S1)	ι = q – ΔU
Адиабатический	q = 0	ι = U2 – U1 ι = (h1 – Р1υ1) – (h1 – Р1υ1)
Х = соnst	q =	ι = q – ΔU

ЗАДАЧИ

9.1 Сухой насыщенный
пар имеет давление 10,2 МПа. Определить
все остальные параметры пара.

Решение. По таблицам
[6] находим: t_н
= 312,42 °С;
S″
= 5,6019 кДж/кг; υ″=0,01756
м³/кг;
ρ″ = 59,648 кг/м³;
h″ = 2720,8 кДж/кг; r = 1303,5 кДж/кг;

U″ = h″ – Рυ″
= 2720,8 – 10,2 ∙ 0,01756 = 929,68 кДж/кг.

9.2 Определить
состояние водяного пара, если температура
его 300°С, а давление 6,0 МПа.

9.3 Определить
состояние водяного пара, если его
давление 4,5 МПа, а удельный объем 0,0707
м³/кг.

9.4 Состояние
водяного пара характеризуется давлением
9 МПа и влажностью 20%. Найти удельный
объем, внутреннюю энергию, энтропию и
энтальпию пара.

Решение. При Р = 9
МПа υ′
= 0,0014179 м³/кг;
υ″
= 0,02046 м³/кг;
h′ = 1363,2кДж; h″ = 2741,8 кДж/кг; S′ = 3,2875
кДж/кг∙К; S″ = 5,6773 кДж/кг∙К; r = 1377, 6 кДж/кг;
υ′_х
= υ′ +
х (υ″
– υ′)
= 0,0014179 + 0,8 ( 0,02046 – 0,0014179 ) = =0,016645 м³/кг;

hх = h′ + х ( h″ – h′
) = h′ + rх = 1364,2 + 0,8 ∙ 1377,6 = 2466,3 кДж/кг;

Uх = hх – Рυх = 2466,8 –
9 ∙ 103 ∙ 0,016645 = 2317,0 кДж/кг.

9.5 Вода нагрета до
150,96 °С (при давлении 1,2 МПа). На сколько
градусов еще нагреть воду, чтобы началось
кипение?

9.6 Определить
состояние водяного пара, если его
температура 363,37 °С, а давление 2,0 МПа.

Решение. При
давлении 2,0 МПа температура насыщения
пара 212,37 °С, следовательно, пар перегрет;
перегрев составляет 263,37 – 212,37 = 51 °С.

9.7 Определить
состояние водяного пара, если его
давление 7,5 МПа, а удельный объем 0,019
м³/кг.

9.8 В верхней половине
барабана парового котла находится сухой
насыщенный пар, а в нижней вода в состоянии
насыщения. Во сколько раз масса воды
больше массы пара, если давление пара
в барабане Р = 11,5 МПа?

9.9 Состояние
водяного пара определяется давлением
14 МПа и температурой 813 К. Найти значения
остальных параметров состояния по
таблицам приложения Б и В.

9.10 Внутри трубы
под давлением 11 МПа происходит
парообразование за счет теплового
потока 75 кВт, подводимого от внешних
источников. Вода в трубу поступает при
температуре насыщения; расход 0,5 кг/с.
Определить плотность пароводяной смеси
на выходе из трубы.

Решение. Количество
образующегося пара

G =
=
75/1254,2 = 0,059 кг/с.

Степень сухости
пара на выходе

Х = 0,0598/0,5 = 0,1196.

Удельный объем
смеси

υ_х
= υ″
х + (1 – х)υ′
= 0,01597 ∙ 0,1196 +
(1 – 0,1196) ∙ 0,1489 ∙ 10
^-2 =

= 0,3221 ∙ 10 ^–
2 м³/кг.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #

Размер: 3070х3995 пикселей

Форматы: .PDF, .JPG

Диаграмма цветная — степени сухости, температура, давление и объем выделены разными цветами, что делает работу с диаграммой очень удобной.

Большой размер позволит распечатать диаграмму на формате А3 и больше.

is-диаграмма применяется для практических расчетов процессов водяного пара. На ней теплота и энтальпия измеряются линейными отрезками.

is-диаграмма обладает рядом важных свойств: по ней можно быстро определить параметры пара и разность энтальпий в виде отрезков, наглядно изобразить адиабатный процесс, и решать другие задачи.

Так же вы можете использовать очень удобную и наглядную программу.

Описание is-диаграммы

На is-диаграмме изображены термодинамические процессы:

• Изобарный процесс (p = const) — фиолетовые линии (изобары),
• Изотермический процесс (t = const) — зеленые линии (изотермы),
• Изохорный процесс (v = const) — красные линии (изохоры).

Степень сухости и паросодержание (х) — розовые линии. Жирная розовая линия — степень сухости х=1. Все что ниже этой линии — зона влажного пара.

Подробнее о термодинамических процессах читайте в статье «Основные термодинамические процессы»

Ось «Х» — энтропия, ось «Y» — энтальпия.

Семейство изобар в области насыщения представляет собой пучок расходящихся прямых, начинающихся на нижней и оканчивающихся на верхней пограничной кривой. Чем больше давление, тем выше лежит соответствующая изобара. Переход изобар из области влажного насыщенного в область перегретого пара происходит без перелома на верхней пограничной кривой.

В i, s-диаграмме водяного пара наносятся также линии постоянного паросодержания (x = const) и линии постоянного удельного объема (v = const). Изохоры идут несколько круче, чем изобары.

Состояние перегретого пара обычно определяется в технике давлением p и температурой t. Точка, изображающая это состояние, находится на пересечении соответствующей изобары и изотермы. Состояние влажного насыщенного пара определяется давлением p и паросодержанием x.

Точка, изображающее это состояние, определяется пересечением изобары и линии x = const.

Как пользоваться is-диаграммой

Для описания воспользуемся небольшой задачей. Возьмем с потолка условие.

Пусть начальные параметры пара будут: давление пара р = 120 бар, температура пара t = 550°С. Пар адиабатно расширяется в турбине до температуры, например, 400 °С.

Для примера этого будет достаточно.

Адиабатный процесс на is-диаграмме — это вертикальная линия (горизонтальная линия — дросселирование). Это для справки.

Итак, начальное давление и температура у нас есть. Найдем эту точку на is-диаграмме:

Нам нужна изобара, соответствующая давлению 120 бар и изотерма, соответствующая температуре 550 °С. На их пересечении и будет точка, соответствующая начальным параметрам пара в нашей задаче.

Найдя эту точку, мы уже можем определить в ней энтальпию и энтропию. Опустив на оси проекции найденной точки, узнаем значения энтальпии (ось «Y») и энтропии (ось «Х»).

i = ~3480 кДж/кг, S = 6,65 кДж/(кг•К)

Далее нам нужно узнать параметры пара после адиабатного расширения. Мы знаем, что по поставленным нами условиям, пар расширился и его температура в точке 2 = 400 °С. Я уже упоминал, что на is-диаграмме адиабатный процесс изображается в виде вертикальной линии. Проведем эту линию из точки 1 (начальные параметры) до пересечения с изотермой 400 °С.

Получена точка 2. Через эту точку проходит изобара. Она соответствует давлению 50 бар. Энтропия у нас не изменилась, так как процесс адиабатный, а вот энтальпия стала равна i = 3200 кДж/кг. 

Вот и все. Дальше остаются только расчеты: определение изменения внутренней энергии (Δu), работы (l, l’) и т. д. Все это считается по формулам (формулы можете найти в статье «Основные термодинамические процессы»), а значения и график процесса расширения пара у вас уже есть.

      Здравствуйте! Водяной пар может быть трех видов: влажным насыщенным, сухим насыщенным, перегретым. Рассмотрим все три вида. 

Влажный насыщенный пар. Удельный объем влажного насыщенного пара находится из выражения

υ = υ”x+υ'(1— х),

где υ” — удельный объем сухого насыщенного пара; υ’ — удельный объем воды при температуре парообразования и том же давлении, что и объем υ”.

     Двумя штрихами в технической термодинамике принято обозначать параметры и функции состояния сухого насыщенного пара, а одним штрихом — величины, характеризующие состояние воды при температуре парообразования.

     При небольших давлениях (p < 3 МПа) удельный объем υ’ воды очень мал по сравнению с удельным объемом υ” сухого насыщенного пара. Поэтому при х>0,8 объем жидкости υ'(1—х) можно не учитывать и приближенно определять удельный объем влажного насыщенного пара из соотношения υ ≈ υ”x. В процессе парообразования при постоянном давлении для получения 1 кг влажного насыщенного пара к 1 кг кипящей жидкости необходимо подвести количество теплоты

q=rx (1)

Так как в процессе при р = const количество теплоты равно изменению энтальпии, то величину энтальпии i влажного насыщенного пара можно определить из выражения

q = rx = i—i’ или i=i’+rx. (2)

Энтальпия i’ кипящей воды при температуре парообразования и теплота парообразования г соответствуют тому же давлению, что и энтальпия i. Так как величина энтальпии при 273 К принимается за нуль, то энтальпию i’ кипящей воды можно найти из выражения

(3)

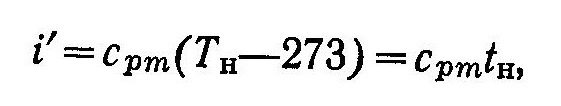
где сm — средняя массовая теплоемкость воды в интервале температур от 273 К до Тн.

     Энтальпия i’ кипящей воды, как следует из выражения (3), численно равна количеству теплоты, которая затрачивается для нагревания 1 кг воды от 0° С до температуры кипения tн при р = const.

     В соответствии с уравнением первого закона термодинамики q = ∆u+l имеем

r = u” — u’ + p*(u” — υ’).

Анализ этого выражения показывает, что теплота парообразования r складывается из внутренней теплоты парообразования u”- u’, затрачиваемой на изменение внутренней энергии (преодоление сил притяжения между молекулами), и внешней теплоты парообразования p (u”- u’), равной работе против внешних сил. Для давлений меньше 20 МПа внешняя теплота парообразования незначительна и не превышает 13% от величины r.

     Энтропию влажного насыщенного пара найдем из выражения

Так как в процессе парообразования при p=const T=const, то с учетом уравнения (1) получим

где s’— энтропия воды при температуре парообразования и том же давлении, что и величины s, г и Tн.
Величину s’ можно определить из соотношения

(4)

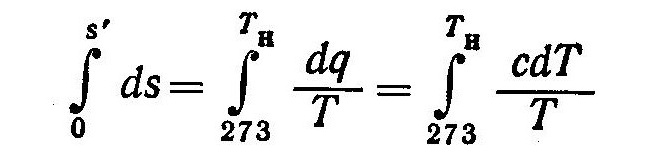
или

Пределы интегрирования в выражении (4) приняты в соответствии с условием, что при 273 К энтропия равна нулю.

Сухой насыщенный пар.

     Состояние сухого насыщенного пара определяется значением одного параметра, например давления или температуры парообразования, так как другой параметр состояния — степень сухости — имеет определенное значение х=1. Параметры и функции состояния сухого насыщенного пара можно определить по выведенным выше формулам (1), (2) для влажного пара при условия х = 1.

Перегретый пар.

     Для получения перегретого пара в котельном агрегате устанавливают специальный теплообменник (пароперегреватель), в котором происходит перегрев влажного насыщенного пара. Для характеристики состояния перегретого пара должны быть известны два любых параметра состояния пара, например давление и температура. Вместо параметров могут быть заданы функции состояния (энтальпия или энтропия).

Энтальпия перегретого пара находится из выражения

(5)

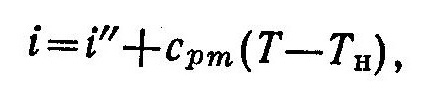
где сpm—массовая средняя изобарная теплоемкость пара в интервале температур от Tн до Т.

Энтропия перегретого пара определяется следующим образом

(6)

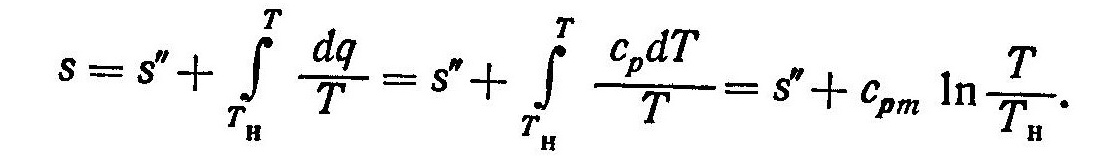
В уравнения (5) и (6) необходимо подставлять значения величин i”, s” и cpm при том же давлении, для которого определяются энтальпия i и энтропия s. Исп.литература: 1) Теплотехника и теплотехническое оборудование предприятий промышленности строительных материалов и изделий, Н.М. Никифорова, Москва, «Высшая школа», 1981. 2) Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,”Вышейшая школа”, 1976.

Пример б. Определить энтропию водяного пара в гипотетическом состоянии идеального газа при 25 °С и 1 атм. По данным Герцберга [22], длина связи Н—О в молекуле воды равна 0,958 А и угол между связями Н—О—Н равен 104°27. Частота колебания вдоль связи Н—О приблизительно равна 3700 см и частота колебания, изменяющая угол И—О—Н, равна около 1600 см (рис. 16).  [c.141]

Энтропия водяного пара отсчитывается от условного нуля, в качестве которого принимают энтропию воды при 0,01° С н при давлении насыщения, соответствующем этой температуре, т. е. при давлении 0,0006108 МПа.  [c.174]

Формулы (10.11) и (Ю.12) используются для расчета адиабатного процесса в перегретом водяном паре. Блок-схема программы вычисления энтальпий в начале и конце обратимого адиабатного процесса по заданным ри Т1 и рг аналогична схеме, изображенной на рис. 10.4,а (рис. 10.5). Следующие за вводом исходных параметров два прямоугольника блок-схемы — расчет энтальпии и энтропии водяного пара в начале адиабатного процесса по  [c.249]

Все три программы условно делятся на две половины в первой рассчитываются энтальпия и энтропия водяного пара. в начале процесса (Ль Х ), а во второй — энтальпия влажного пара Лг по известной энтропии зз и давлению Р2.  [c.252]

Удельные энтальпия и энтропия являются функциями состояния, определяемыми с точностью до постоянной их отсчет производится от условно принимаемого состояния. В частности, удельные энтальпия и энтропия водяного пара принимаются равными нулю для жидкой фазы в тройной точке.  [c.161]

Напомним, что при вычислении удельной энтропии водяного пара ее условно принимают равной нулю (sj —0) в тройной точке для жидкой фазы (7/ = 273,16 К для воды). Следовательно, в системе координат Ts тройная точка находится на оси температур при значении Т/г =273,16 К (0,0ГС) (рис. 11.9). Приращение удельной энтропии жидкости при повышении его температуры вдоль пограничной кривой от температуры Т /7 = 273,16 к до температуры Ts можно определить по формуле  [c.165]

Уравнения (32) и (33) определяют теплосодержание, удельный объем и энтропию водяного пара.  [c.33]

Отклонение теплосодержания и энтропии водяного пара в идеально-газовом состоянии от теплосодержания и энтропии водяного пара, полученных опытом, будет  [c.34]

ТеплоемкостЬ энтальпия и энтропия водяного пара Н%0 (4)  [c.31]

SI. Теплоемкость, энтальпия и энтропия водяного пара Н 0 4  [c.33]

Рис. 1-2. Изменение энтропии водяного пара при переходе через пограничную кривую.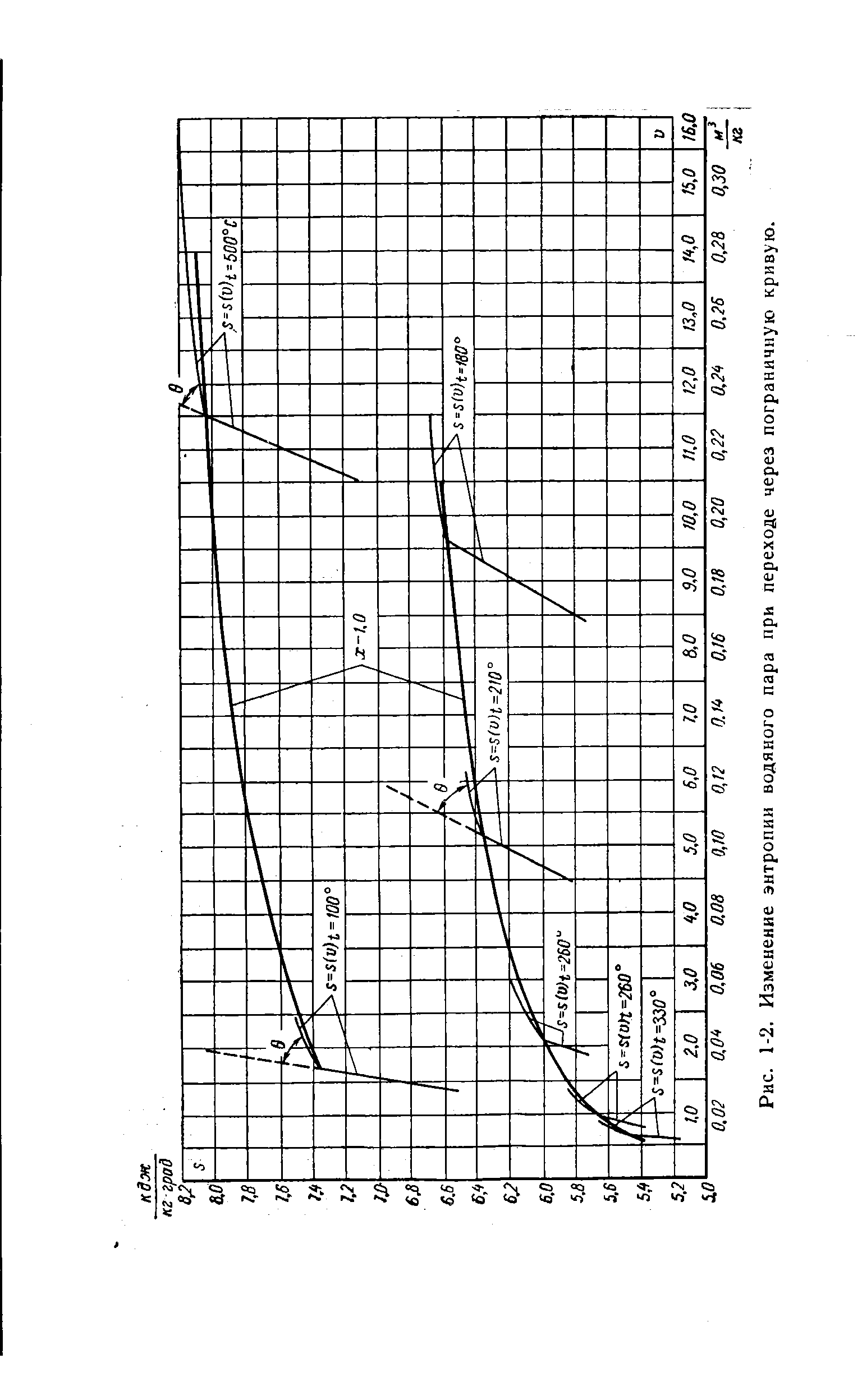

Вследствие необратимости рабочего процесса в реальной паровой турбине (наличие трения, внутренних утечек пара по ступеням и т. д.), в действительном рабочем процессе внутри турбины энтропия водяного пара возрастает, а используемое теплопадение уменьшается. При этом теплосодержание отработавшего пара турбины выше, чем в идеальном цикле Ренкина, на величину = = = —где Q, и -соот-  [c.30]

I, 54. ЭНТРОПИЯ ВОДЯНОГО ПАРА. ДИАГРАММЫ Т и is ДЛЯ водяного ПАРА  [c.131]

Если в температурно-энтропийной диаграмме построен цикл для 1 кг водяного перегретого пара (площадка 5—6—7—8—9 по рис. 14) при каком-то масштабе энтропии водяного пара, то пограничные кривые для ртутного пара должны строиться с масштабом энтропии в т раз большим.  [c.34]

Поскольку за точку отсчёта эксергии принято состояние влажного воздуха в окружающей среде, то изобарно-изотермический потенциал водяного пара в среде следует приравнять к нулю. Последнее условие и определяет выбор точки отсчёта энтальпии и энтропии водяного пара она должна быть такой, чтобы изобарно-изотермический потенциал (функция Гиббса) водяного пара при параметрах среды равнялся нулю. Этому условию, в частности, удовлетворяет точка с параметрами t = 0°С и /> = 100 кПа [24].  [c.113]

Условно за нуль энтропии водяного пара (sq — 0) принимают состояние при 0°С и давлении р = 0,006228 ama. Изменение энтропии для процесса изобарного нагрева 1 кг воды от 0°С до температуры кипения t равно  [c.87]

Величиной 5о исходя из уравнения (7.42) можно пренебречь. Примером изменения энтропии может служить система НгО. От 0° до 273° К НгО при нормальном давлении сохраняется в виде кристаллического льда. До 373° К эта система существует как вода, а выше 373° К находится в парообразном состоянии. Для приращения энтропии получается зависимость, изображенная на рис. 7.1. Зная температурную зависимость молярной теплоемкости льда и воды, можно представить энтропию водяного пара как сумму следующих величин (если пренебречь энтропией при абсолютном нуле)  [c.112]

Если требуется найти изменение энтропии водяного пара в процессе превращения кипящей воды в сухой насыщенный пар, в выражении (8-18) следует положить величину х равной единице (сухость сухого насыщенного пара) и тогда  [c.130]

Пусть пар с начальными параметрами Pi, / вытекает в среду с давлением р2-Если потери энергии на трение при движении водяного пара по каналу и теплоотдача к стенкам сопла пренебрежимо малы, то процесс истечения протекает при постоянной энтропии и изображается на /I, -диаграмме вертикальной прямой 1-2 (рис. 5.5).  [c.50]

Чтобы изобразить описанные процессы в Т,. ч-диаграмме водяного пара в одном масштабе, отложенные на ней значения энтропии воды и пара отнесены к I кг, а энтропии греющих газов — к их количеству, приходящемуся на 1 кг пара, т. е. si =.siг m,/0, S2 = S2, m,ID, где Sr — удельная энтропия газа. Для удобства сравнения принято также общее начало отсчета энтропии, т. е.. S2r/Иг/О = s i. В таком случае площадь 1-Г- 2 -2. представляющая собой количество отданной газом теплоты, и площадь 2 -3-4-5-6-в эквивалентная количеству теплоты, воспринятой паром, равны друг другу.  [c.57]

Значения энтальпии, энтропии и удельного объема перегретого пара берутся по. таблицам водяного пара.  [c.182]

Энтропия воды и водяного пара  [c.182]

Практически энтропию воды сухого насыщенного и пер( гретого пара берут из таблиц водяного пара.  [c.184]

При построении г5-диаграммы по оси ординат откла/ ывается энтальпия пара, а по оси абсцисс — энтропия. За начало координат принято состояние воды в тройной точке, где so = О, /о = 0. По данным таблиц водяного пара на диаграмму прежде всего наносят нижнюю и верхнюю пограничные кривые, сходящиеся в критической точке К. Нижняя пограничная кривая выходит из начала координат, так как в этой точке энтальпию и энтропию принимают равной нулю (рис. 11-9). Состояние воды изображается точками па соответствующих изобарах, которые практически сливаются с нижней пограничной кривой. Линии изобар в области влажного пара являются прямыми наклонными линиями, расходящимися веером от нижней пограничной кривой. В изобарном процессе  [c.186]

Решение задач, связанных с термодинамическими процессами в области насыш,енных и перегретых паров, можно производить или с помощью таблиц воды и водяного пара, или с помощью -диаграммы. В этих задачах обычно определяются начальные и конечные параметры пара, изменения внутренней энергии, энтальпии и энтропии, степень сухости, работа и количество теплоты, участвующей в процессе.  [c.190]

Процесс дросселирования является необратимым процессом, который сопровождается увеличением энтропии. Из предыдуш,их глав известно, что с ростом энтропии всегда понижается работоспособность газа или пара, что наглядно видно из диаграммы (рис. 14-3). Пусть водяной пар дросселируется от состояния а до с. От точки а до давления разность энтальпий выражается отрезком аЬ] от точки с разность энтальпий выражается отрезком d, который значительно меньше отрезка аЬ, т. е. работоспособность пара резко падает. Чем больше мятие пара, тем меньше его работоспособность.  [c.226]

Определить состояние водяного пара, если давление его р = 0,9 МПа, а энтропия s = 6,52 кДж/(кг-К).  [c.178]

Рассмотрим 7—5-диаграмму водяного пара (рис. 7.3). Общие свойства этой диаграммы были описаны ранее (см. 18). Т—5-диаграмма строится по данным специальных таблиц, содержащих параметры Т, 5 и 5″, полученные на основании опытов и теоретических исследований. Так как энтропия воды в тройной точке, т. е. при = 0,01°С (7 = 273,16 К), обычно принимается равной нулю, это состояние в 7—5-диаграмме соответствует точке М. Откладывая для разных температур 7 значения 5 и 5″, получим нижнюю (х = 0) и верхнюю (х=1) пограничные кривые с критической точкой К, соединяющей их.  [c.85]

Смесь выхлопных газов реактивного самолета состоит из углекислого газа, водяного пара, кислорода и азота и находится при давлении 98 кПа и температуре 469 °С. Массовые доли компонентов 0,18, Ян,о = 0,17, go, — 0,182 и gn, = 0,468. Определить энтропию I кг газовой смеси, предполагая, что энтропия газов равна нулю при давлении 10 кПа и температуре О °С. При решении воспользоваться понятием энтропии смешения.  [c.55]

Состояние водяного пара характеризуется давлением 9 МПа и влажностью 20 %. Найти удельный объем, внутреннюю энергию, энтропию и энтальпию пара.  [c.62]

Уравнения для энтальпии (10.11) и энтропии (10.12) водяного пара получены на основе вириального уравнения состояния (10.10), в котором вириальные коэффициенты представлены в виде ряда по обратным степеням температуры. Используя более сложные функциональные зависимости вириальных коэффициентов от температуры, можно уменьшить число эмпирических коэффициентов вириального уравнения состояния. В частности, такое уравнение было предложено в [51]  [c.249]

Рассмотрим Ts-диаграмму для водяного пара (рис. 3-3). За начало отсчета принимают состояние воды при t = = 0° С = 273° К. Давление при этом не имеет значения, если исходить из того, что вода несжимаема энтропию  [c.118]

Чаще всего приходится при помощи гз-диаграммы исследовать адиабатный процесс, так как расширение пара в паровых двигателях в первом приближении рассматривают как обратимый адиабатный процесс. В этой диаграмме задачи, относящиеся к адиабатному процессу изменения состояния, решаются легко и с достаточной степенью точности. Действительно, если начальное состояние задано параметрами Pi и 1, то оно найдется на is-диаграмме пересечением соответствующих изобары и изотермы (рис. 3-5). Точка 1 изображает начальное состояние. Проектируя эту точку на ось ординат, находим t l, проектируя ее на ось абсцисс, находим чтобы найти конечное состояние, следует провести адиабату, которая для обратимого адиабатного процесса будет линией постоянной энтропии и поэтому изобразится в виде прямой, параллельной оси ординат. Если задано конечное давление, конечная точка процесса определится пересечением заданной конечной изобары с адиабатой. На рис. 3-5 точка 2 характеризует конечное состояние водяного пара Б адиабатном процессе. Энтальпия в этой точке может быть  [c.122]

Значения удельной энтропии воды s (учетом переменного значения удельной теплоемкости с1) и сухого насыщенного пара s” приведены в таблице насыщенного водяного пара.  [c.166]

При помощи этого уравнения легко определяется температура в точках 7 и 3″, а следовательно, и положение конечных точек 7 изобарического нагревания воды и 3″ — изобарического охлаждения газообразных. продуктов сгорания на Т—s диаграмме. Разность энтропий в точках 7 и 5 представляет собой приращение энтропии системы из-за необратимости процесса теплообмена. После смешения состояние водяных паров изображается точкой 1 р fi), а газообразных продуктов сгорания— точкой 3 р ii). Парциальные давления pi, р , могут быть определены по известным значениям р и из соотношения р = р + ру, уравнений состояния водяных паров и газообразных продуктов сгорания  [c.463]

Очевидно, что живая ткань растения более высоко структурно организована, чем поступающие из воздуха питательные вещества. Поэтому при образовании такой ткани (с массой ДМо) ее энтропия будет несомненно меньше, чем суммарная энтропия исходных веществ (СОз, Н2О и питательных веществ почвы). В этом смысле образование и накопление живой ткани растения и поддержание ее существования будет несомненно ан-тиэнтропийным процессом. Но никак нельзя забывать, что одновременно неизбежно меняется энтропия потоков вещества и энергии, проходящих через контрольную поверхность. Здесь получается обратная картина (рис. 4.3) суммарная энтропия выходящих потоков (3 и 6) неизбежно оказывается много большей, чем входящих (/, 2, 4 и 5). Это объясняется тем, что энтропия поглощаемого солнечного излучения сравнительно невелика, так же как и поступающих из почвы минеральных солей энтропии газов — кислорода и СО2 — близки по значениям. Зато энтропия водяного пара, отдаваемого листьями, относительно велика (примерно в 3 раза больше, чем у воды). В результате энтропия потоков, проходящих через контрольную поверхность, возрастает намного больше, чем снижается энтропия веш еств, превраш ающихся в органическую ткань.  [c.152]

С другой стороны, величина A=il,3 для водяного пара, тогда как для воздуха А=1,4 поэтому энтропия водяного пара в состояниях, со-ответствующих состоянию смеси, изменяется, в то время как энтропия смеси остается неизменной. Определим направление изменения энтропии водяиого пара. Из соотношения  [c.118]

Остаточную энтропию при 0° К можно вычислить, сравнивая калориметрически измеренную энтропию водяного пара, определяемую соотношением г (пар)  [c.318]

На диаграмму наносят изобары, изохоры и линии постоянной степени сухости, для чего каждую изобару а а” делят на одинаковое число частей и соединяют соответствующие точки линиями x = onst. Область диаграммы, лежащая ниже нулевой изотермы, отвечает различным состояниям смеси пар + лед, h, s-диаграмма водяного пара. Если за независимые параметры, определяющие состояние рабочего тела, принять энтропию S и энтальпию Л, то каждое состояние можно изобразить точкой на Л, 5-диаграмме.  [c.37]

Энтальпию воды после сжатия в пасосе находим из условия, что процесс 2 -3 является адиабатным. При давлении щ /л == 160 бар и энтропии S3 = S2- = 0,4764 кдж1кг-град по таблицам водяного пара определяем /3 = 152,8 кдж/кг. Разность г з — i 2 = 152,8—137,79 = 15,0 кдж кг представляет собой теоретическую работу насоса, отсюда Цоу == 0,389.  [c.318]

Найти массу, внутреннюю энергию, энтальпию и энтропию 6 м насыщенного водяного пара при давлевти р — 1,2 МПа н сухости пара х =- 0,9.  [c.179]

Построим, пользуясь данными таблиц водяного пара, изобары в Ts-диа-грамме если подводить к рабочему телу тепло при р — onst, изменение энтропии жидкости при изменении температуры изобразится близкой к логарифмическому виду кривой. На диаграмме эта кривая изображается линией аЬ. В точке Ь, соответствующей температуре кипения при выбранном давлении, прекращается повышение температуры и начинается кипение воды. При дальнейшем подводе тепла энтропия увеличивается, а температура остается постоянной конец процесса парообразования характеризуется точкой с таким образом, процесс парообразования изображается линией Ьс, параллельной оси абсцисс. Дальнейший подвод тепла при постоянном давлении опять сопровождается повышением температуры, и процесс перегрева пара при р = onst изображается близкой к логарифмическому виду кривой се.  [c.118]

По решению VI Международной конференции по свойствам водяного пара за начало отсчета внутренней энергии и энтропии принята внутренняя энергия и энтропия жидкой фазы воды в тройной точке, т. е. и = О и s = 0. Так как температура в тройной точке у воды и большинства жидкостей близка к температуре плавления, то представляется в химической технологии более целесообразным вести отсчет этих параметров от температуры плавления, т. е. принять i/o = О и So = О при to и р . Тогда ho = Uo + PmVo = Pml o-  [c.34]

---

Физико-химическая кристаллография (1972) — [
c.113
]

Справочник машиностроителя Том 2 (1955) — [
c.31
]

---