- Информация о материале
- Категория: Лабораторные работы
-
Опубликовано: 11 октября 2016
-
Обновлено: 29 января 2019
-
Просмотров: 4572
Лабораторная работа № 5
Тема: Измерение ЭДС и внутреннего сопротивления источника тока.
Цель работы: научиться измерять ЭДС (E) источника тока и косвенными измерениями определять его внутреннее сопротивление.
Оборудование:
- аккумулятор или батарейка для карманного фонаря;
- вольтметр;
- амперметр;
- реостат;
- ключ.
Теоретическая часть
При разомкнутом ключе (рисунок) ЭДС источника тока равна напряжению на внешней цепи. В эксперименте источник тока 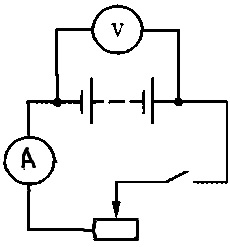 замкнут на вольтметр, сопротивление которого Rв должно быть много больше внутреннего сопротивления источника тока г. Обычно сопротивление источника тока достаточно мало, поэтому для измерения напряжения можно использовать школьный вольтметр со шкалой 0-6 В и сопротивлением Rв = 900 Ом (см. надпись под шкалой прибора). Так как Rв » г, отличие E от U не превышает десятых долей процента, а потому погрешность измерения ЭДС равна погрешности измерения напряжения.
замкнут на вольтметр, сопротивление которого Rв должно быть много больше внутреннего сопротивления источника тока г. Обычно сопротивление источника тока достаточно мало, поэтому для измерения напряжения можно использовать школьный вольтметр со шкалой 0-6 В и сопротивлением Rв = 900 Ом (см. надпись под шкалой прибора). Так как Rв » г, отличие E от U не превышает десятых долей процента, а потому погрешность измерения ЭДС равна погрешности измерения напряжения.
Внутреннее сопротивление источника тока можно измерить косвенным путем, сняв показания амперметра и вольтметра при замкнутом ключе. Действительно, из закона Ома для замкнутой цепи (см. § 108) получаем E = U + Ir, где U = IR – напряжение на внешней цепи (R – сопротивление реостата). Поэтому гпр = (Eпр – Uпр)/Iпр. Для измерения силы тока в цепи можно использовать школьный амперметр со шкалой 0-2 А. Максимальные погрешности измерений внутреннего сопротивления источника тока определяются по формулам εпр = (ΔE + ΔU)/(Eпр – Uпр) + ΔI/Iпр, Δr = rпрεr
Указания к работе
1. Подготовьте бланк отчета со схемой электрической цепи и таблицей для записи результатов измерений и вычислений.
| № | Измерено | Вычислено | |||||||
| Uпр, В | Iпр, А | Eпр, В | ΔиU, В | ΔоU, В | ΔU, В | εU, % | εE, % | rпр, Ом |
|
| Измерение E | |||||||||
| Измерение r | |||||||||
| Вычислено | |||||||||
| Измерение E | ΔиI, А | ΔоI, А | ΔI, А | εI, % | εr, % | Δr, Ом | |||
| Измерение r |
2. Соберите электрическую цепь согласно рисунку. Проверьте надежность электрических контактов, правильность подключения амперметра и вольтметра.
3. Проверьте работу цепи при разомкнутом и замкнутом ключе.
4. Измерьте ЭДС источника тока.
5. Снимите показания амперметра и вольтметра при замкнутом ключе и вычислите rпр. Вычислите абсолютную и относительную погрешности измерения ЭДС и внутреннего сопротивления источника тока, используя данные о классе точности приборов.
6. Запишите результаты измерений ЭДС и внутреннего сопротивления источника тока:
E = Eпр ± ΔE, εE = …%
r = rпр ± Δr, εr = …%
Если заметили ошибку, выделите фрагмент текста и нажмите Ctrl+Enter
Инфоурок
›
Физика
›Презентации›Лабораторная работа по физике. Измерение ЭДС источника тока.
Лабораторная работа по физике. Измерение ЭДС источника тока.
Скачать материал
без ожидания

Скачать материал
без ожидания


- Сейчас обучается 43 человека из 25 регионов


- Сейчас обучается 478 человек из 71 региона


- Сейчас обучается 107 человек из 45 регионов


Описание презентации по отдельным слайдам:
-

1 слайд
Лабораторная работа.
Измерение ЭДС и внутреннего сопротивления источника тока -

2 слайд
Цель работы: проверить закон Ома для полной цепи, измерить ЭДС и внутреннее сопротивление источника тока.
Оборудование: источник тока, реостат, ключ, соединительные нити, амперметр, вольтметр.
Примечание: при сборке электрической цепи ползунок реостата установите в среднее положение. -

3 слайд
Тренировочные задания и вопросы.
Электрический ток – _____________
Напишите формулу закона для участка цепи:I = ________
ЭДС источника тока – ___________ -

4 слайд
Определите напряжение участка цепи постоянного тока, если через резистор сопротивление 20 Ом проходит ток силой 250 мА.Дано: Решение. I = R =
U
– ?
Ответ: ____________ -

5 слайд
Закон Ома для полной цепи: ______________
-

6 слайд
ЭДС источника равна 12 В, а внутреннее сопротивление r = 2 Ом. Найдите сопротивление внешней цепи, если сила тока в цепи равна 2 А. Дано:Решение. ℰ = r = I =
R
– ?
Ответ: __________ -

7 слайд
Закон Ома для полной цепи записан в виде ℰ = U + U₀. Что определяют величины U и U₀ ? U = _______ U₀ = _______
ЭДС источника равна 6 В. Сила тока цепи равна 250 мА, внешнее сопротивление цепи R = 20 Ом.Дано: Решение. ℰ = I = R =r
– ?
Ответ: __________ -

8 слайд
Ход работы.
Соберите электрическую цепь согласно схеме на рис. 3.
Проверьте работу ползунка реостата.
Проверьте работу цепи при разомкнутом и замкнутом ключе, при перемещении ползунка реостата.
V
A
Рис. 3
+
– -

9 слайд
При разомкнутом ключе измерьте ЭДС источника тока. ℰпр = ____________
При разомкнутом ключе измерьте силу тока в цепи и напряжение внешней цепи. Iпр =________, Uпр = ____________
Результаты измерений запишите в таблицу. -

10 слайд
Вычислите внутреннее сопротивление источника тока. r пр = ℰпр – Uпр=______________ Iпрr пр = _______________
Вычислите абсолютную погрешность измерения ЭДС источника.∆ℰ ≈ ∆U ( т.к. R >> r ) ∆U = ∆иU + ∆₀U ∆иU = 0,15 В ∆₀U = 0,1 В ∆ℰ = ∆U = _________ -

11 слайд
Вычислите относительную погрешность измерения ЭДС источника. εℰ = ∆ℰ · 100%= _________ℰ εℰ = __________
Вычислите относительную погрешность измерения внутреннего сопротивления. εr = 2∆U + ∆I , ℰпр – Uпр Iпргде ∆I = Dи I + ∆₀I , ∆I = 0,05 А + 0,05 А = 0,1 А εr = _________ εr = ___________ -

12 слайд
Вычислите абсолютную погрешность измерения внутреннего сопротивления. ∆r = εr · rпр = ___________ ∆r = _________
Результаты вычислений занесите в таблицу.
Запишите результаты измерений ЭДС и внутреннего сопротивления источника тока в виде:ℰ = ℰпр ± ∆ℰℰ = _______ ,εℰ = ________% r = r пр ± ∆r r = ________,εr = ________% -

13 слайд
Дополнительное задание.
Соберите электрическую цепь по рис. 4.
Снимите показания амперметра и вольтметр при двух различных положениях ползунка реостата.
Занесите результаты измерений в таблицу.
+
–
A
V -

14 слайд
Вычислите:r = U₂ – U₁ = ________ I₁ – I₂
Вычислите:ℰ = U₁ + I₁· r = __________
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 251 750 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы



- 22.04.2018
- 1670
- 6

Рейтинг:
1 из 5
- 22.04.2018
- 2817
- 16


Опыт Юнга + – слайды для урока
- Учебник: «Физика (базовый и профильный уровни)», Тихомирова С.А., Яворский Б.М.
- Тема: § 50. Электродинамическая картина мира
- 22.04.2018
- 1236
- 3


Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
-
Курс профессиональной переподготовки «Организация и предоставление туристских услуг»
-
Курс повышения квалификации «Введение в сетевые технологии»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС педагогических направлений подготовки»
-
Курс повышения квалификации «История и философия науки в условиях реализации ФГОС ВО»
-
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
-
Курс профессиональной переподготовки «Организация системы менеджмента транспортных услуг в туризме»
-
Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»
-
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
-
Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»
-
Курс повышения квалификации «Информационная этика и право»
-
Курс профессиональной переподготовки «Управление качеством»
-
Скачать материал (медленно)
Настоящий материал опубликован пользователем Чирва Лилия Сергеевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-

- На сайте: 7 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 49304
-
Всего материалов:
31
Определение электрической прочности диэлектриков
Для
вычисления электрической прочности
диэлектрика необходимо измерить его
Uпр.
Для сопоставимости результатов,
полученных разными лабораториями,
введены стандарты (ГОСТы) на условия
испытаний (форму,
размеры и материал электродов; вид и
длительность приложения напряжения;
параметры окружающей среды и пр.)
Длительность
приложения напряжения.
Установлены
методы определения Uпр
при переменном (промышленной и повышенной
частоты), импульсном и постоянном токе.
По длительности приложения напряжения
различают импульсные,
кратковременные и длительные
испытания на пробой.
Импульсное
воздействие применяют для оценки
стойкости изоляции к перенапряжениям,
а также с целью изучения физического
механизма быстро протекающих процессов
электрического пробоя.
При
кратковременных
испытаниях переменное или постоянное
напряжение повышают автоматически
(либо плавно – с фиксированной скоростью,
либо ступенями – за время от нескольких
секунд до минут). Момент пробоя диэлектрика
фиксируют по резкому увеличению тока
или спаду напряжения, определяя величину
кратковременного пробивного напряжения
Uпр
кр.
В
случае длительных
испытаний, применяемых для исследования
надежности изоляции и изучения процессов
электрического старения, оценивают
время жизни от момента подачи напряжения
(Uисп
< Uпр)
до пробоя диэлектрика.
Форма
электродов.
Пробивное
напряжение пропорционально напряженности
электрического поля только при условии
его однородности, степень которой
определяет форма электродов. Электрическое
поле является наиболее однородным в
случае применения так называемых
электродов
Роговского,
поверхности которых описываются
уравнениями Роговского и соответствуют
форме эквипотенциальных линий поля. На
практике, особенно для сравнительных
испытаний, используют электроды более
простой формы: диски с закругленными
краями или шары. Если размер сфер много
больше длины разрядного промежутка
(толщины диэлектрика), то получают
относительно однородное (или слабо
неоднородное) поле.
В
неоднородном поле (например: электроды
типа шар-игла или игла-игла) Uпр
всегда меньше, чем в однородном поле,
при прочих равных условиях, так как в
этом случае на элемент диэлектрика
приходится большая электрическая
нагрузка. Именно поэтому технологические
нарушения типа складок при намотке
ленточной изоляции, пылинок и пр.
повышают вероятность пробоя. При
вычислении электрической прочности в
условиях неоднородного поля вводят
поправочный коэффициент а>1.
Тогда: Епр
= (аUпр)
/ d
.
(22)
Величина
коэффициента а
зависит от
формы, размера электродов и расстояния
между ними. Отмечено и влияние материала,
из которого сделаны электроды. Поэтому
значение поправочного коэффициента
должно указываться в стандарте на
материал.
Обработка
результатов измерения.
Величина пробивного напряжения
диэлектрика определяется электрической
прочностью наиболее слабого участка.
Величина Епр
электроизоляционного материала
существенно зависит от местных изменений
толщины диэлектрика, наличия дефектных
мест (неоднородностей, полупроводящих
включений, пустот и пр.), а также от
состояния поверхности электродов.
Поскольку перечисленные факторы
случайны, то и электрическая прочность
диэлектрика также является случайной
величиной, при определении которой
наблюдается значительный разброс
значений. Поэтому испытания на пробой
производят путем многократных измерений
на больших партиях образцов (выборках)
с последующей статистической обработкой
экспериментальных результатов.
Установлено,
что распределение кратковременной
электрической прочности диэлектрических
материалов подчиняется нормальному
закону,
реже – экстремальному
закону Вейбулла.
В соответствии с нормальным законом
распределения по результатам измерения
Uпр
выборки из n
образцов рассчитывают значения их Епр,
а затем – среднюю величину электрической
прочности диэлектрика
![]()
[ кВ/мм
] :

(23)
Разброс значений электрической прочности
характеризуют среднеквадратическим
отклонением:

(24)
Если
испытания проводились на одних и тех
же электродах при постоянном расстоянии
между ними (или при одной и той же толщине
диэлектрика), то о степени однородности
материала можно судить по величине
коэффициента
вариации
Квар
(тем точнее, чем больше выборка):
![]()
(25)
Согласно
стандарту, при Квар
< 15% материал
считается относительно
(более) однородным,
а результаты измерения –
достоверными.
При Квар
> 15% качество диэлектрика неудовлетворительно
(материал
неоднороден)
и для получения достоверных результатов
необходимо увеличивать выборку.
Однако
в любом случае ограниченное число
измерений приводит к тому, что найденные
Епр
и S
будут случайными величинами. Известно,
что отклонение средних значений от
истинного
или генерального
среднего подчиняется распределению
Стьюдента (t-распределение).
Тогда отклонение от средней величины
электрической прочности при данной
доверительной вероятности p
определяется, как:
![]()
(26)
где
t
– величина
критерия Стьюдента для n
измерений.
Для
вероятности p
= 95% имеем:
|
n |
5 |
6 |
7 |
8 |
9 |
10 |
|
t |
2,78 |
2,57 |
2,45 |
2,37 |
2,31 |
2,26 |
Окончательное
значение электрической прочности
(определенное, например, по 5 пробоям) с
вероятностью 95% будет находиться в
пределах:
![]()
(27)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
21.03.201614.11 Mб13МЕТОДИЧКА ЭТМ №2.rtf
- #
- #
- #
1. Измерение ускорения тела при равноускоренном движении
Цель работы: измерить ускорение шарика, скатывающегося по наклонному желобу.
Оборудование: металлический желоб, стальной шарик, металлический цилиндр, измерительная лента, секундомер или часы с секундной стрелкой. (Для устойчивости к концам желоба можно приклеить кусочки ластика.)
Описание работы
Движение шарика, скатывающегося по желобу, можно приблизительно считать равноускоренным. При равноускоренном движении без начальной скорости модуль перемещения s, модуль ускорения a и время движения t связаны соотношением s = (at2)/2. Поэтому, измерив s и t, мы можем найти ускорение a по формуле a = (2s)/t2. Чтобы повысить точность измерения, ставят опыт несколько раз, а затем вычисляют средние значения измеряемых величин.
Ход работы
1. Положите желоб на стол, подложив под один из его концов одну или несколько тетрадей. Изменяя угол наклона желоба, добейтесь, чтобы шарик катился по нему достаточно медленно: движение вдоль всего желоба должно занимать не менее 3 с.
Положите в желоб у его нижнего конца металлический цилиндр. Когда шарик, скатившись, ударится о цилиндр, звук удара поможет точнее определить время движения шарика.
2. Отметьте на желобе начальное положение шарика, а также его конечное положение – верхний торец металлического цилиндра.
3. Измерьте расстояние между верхней и нижней отметками на желобе (модуль перемещения шарика s) и результат измерения запишите в таблицу, заголовок которой приведен ниже.

4. Отпустите шарик у верхней отметки без толчка и измерьте время t до удара шарика о цилиндр.
Повторите опыт 5 раз, записывая в таблицу результаты измерений. В каждом опыте пускайте шарик из одного и того же начального положения, а также следите за тем, чтобы верхний торец цилиндра находился у соответствующей отметки.
5. Вычислите tср = (t1 + t2 + t3 + t4 + t5) / 5 и результат запишите в таблицу.
6. Вычислите ускорение, с которым скатывался шарик: a ≈ (2s)/tср2. Результат вычислений запишите в таблицу.
7. Запишите выводы из эксперимента.
2. Изучение движения тела, брошенного горизонтально
Цели работы: 1) убедиться на опыте, что тело, брошенное горизонтально, движется по параболе; 2) измерить начальную скорость тела, брошенного горизонтально.
Оборудование: штатив с муфтой и зажимом, изогнутый желоб, металлический шарик, лист бумаги, лист копировальной бумаги, отвес, измерительная лента.
Описание работы
Шарик скатывается по изогнутому желобу, верхняя часть которого наклонная, а нижняя – горизонтальная (рис. 1). Оторвавшись от желоба, шарик под действием силы тяжести движется по параболе. Вершина этой параболы находится в точке, где шарик оторвался от желоба.
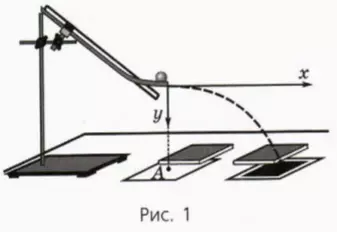
Выберем систему координат, как показано на рисунке.
При движении по параболе высота h, с которой падает шарик, и дальность полета l связаны соотношением h = (gl2)/(2v02). Отсюда следует, что при одинаковых начальных скоростях отношение высот, с которых падает шарик, должно быть равно отношению квадратов дальности полета.
Измерив h и l, можно найти скорость шарика в момент отрыва от желоба по формуле v0 = l√(g/(2h)).
Ход работы
1. Соберите установку, изображенную на рисунке Л-1. Нижний участок желоба должен быть горизонтальным, а расстояние h от нижнего края желоба до стола должно равняться 40 см. Лапки зажима расположите около верхнего конца желоба.
2. Положите под желобом лист бумаги, придавив его книгой, чтобы он не сдвигался при проведении опытов. Отметьте на этом листе с помощью отвеса точку А, находящуюся на одной вертикали с нижним концом желоба.
3. Поместите шарик в желоб так, чтобы он касался зажима штатива, и отпустите шарик без толчка. Заметьте (примерно) место на столе, куда упадет шарик. На отмеченное место положите лист бумаги, а на него – лист копировальной бумаги рабочей стороной вниз. Придавите эти листы книгой, чтобы они не сдвигались при проведении опытов.
4. Снова поместите шарик в желоб так, чтобы он касался зажима штатива, и отпустите без толчка. Повторите этот опыт 5 раз, следя за тем, чтобы лист копировальной бумаги и находящийся под ним лист не сдвигались. Снимите лист копировальной бумаги, не сдвигая листа под ним, и отметьте точку, расположенную наиболее близко ко всем отпечаткам (выбор этой точки означает усреднение результатов пяти опытов).
Учтите при этом, что некоторые отпечатки могут быть расположены очень близко друг к другу.
5. Измерьте расстояние l от отмеченной точки до точки А.
6. Опустите желоб так, чтобы его нижний край находился на высоте 10 см над столом, и повторите пункты 1–5. Измерьте соответствующее значение дальности полета и вычислите отношения h1/h2 и l1/l2.
7. Результаты измерений и вычислений запишите в таблицу, заголовок которой приведен ниже.

8. Проверьте, выполняется ли соотношение h1/h2 = l12/l22. Запишите расчет и сделайте вывод.
9. По результатам первого опыта вычислите значение v0, используя формулу v0 = l√(g/(2h)). Запишите расчет.
10. Запишите выводы из эксперимента.
3. Измерение жесткости пружины
Цели работы: 1) проверить справедливость закона Гука для пружины динамометра; 2) измерить жесткость этой пружины.
Оборудование: штатив с муфтой и зажимом, динамометр с заклеенной шкалой, набор грузов массой по 100 г, прозрачная линейка.
Описание работы
Согласно закону Гука модуль F силы упругости и модуль x удлинения пружины связаны соотношением F = kx. Измерив для конкретного случая F и x, можно найти коэффициент жесткости k по формуле k = F/x.
Ход работы
1. Закрепите динамометр в штативе на достаточно большой высоте над столом.
2. Подвешивая от одного до четырех грузов, вычислите для каждого случая значение силы упругости. Напомним, что в состоянии равновесия действующая на груз со стороны пружины сила упругости уравновешивается силой тяжести: F = mg. Измерьте также соответствующее удлинение пружины x.
3. Результаты измерений и вычислений запишите в таблицу, заголовок которой приведен ниже.
4. Начертите оси координат x и F, выбрав такой масштаб: 1 см удлинения пружины – 2 клетки и 1 Н силы упругости – 2 клетки. Нанесите полученные экспериментальные точки на координатную сетку.
5. С помощью прозрачной линейки проведите отрезок прямой, проходящий через начало координат как можно ближе к каждой из поставленных вами точек.
6. На основании этого построения определите, как зависит сила упругости от удлинения пружины. Запишите вывод.
7. По графику зависимости силы упругости от удлинения пружины найдите жесткость пружины. Для наибольшей точности расчета следует взять точку на графике, наиболее удаленную от начала координат. Запишите расчет и результат.
8. Запишите выводы из эксперимента.
4. Определение коэффициента трения скольжения
Цели работы: 1) исследовать, от каких параметров зависит сила трения скольжения; 2) измерить коэффициент трения скольжения.
Оборудование: деревянная доска (или линейка), брусок, набор грузов массой по 100 г, динамометр.
Описание работы
Если равномерно тянуть брусок с грузом по горизонтальной поверхности, то прикладываемая к бруску горизонтальная сила будет равна по модулю силе трения скольжения Fтр, действующей на брусок со стороны поверхности. Модуль силы трения Fтр связан с модулем силы нормальной реакции N соотношением Fтр = μN. Измерив Fтр и N, можно найти коэффициент трения μ по формуле μ = Fтр/N.
Ход работы
1. Измерьте вес бруска.
2. Положите брусок на горизонтальную деревянную поверхность так, чтобы с этой поверхностью соприкасалась самая большая грань бруска. Поставьте на брусок один груз и равномерно тяните брусок по поверхности с помощью динамо- метра, как показано на рисунке 1.
Запишите значение модуля силы нормальной реакции N и соответствующее ему значение модуля силы трения Fтр в таблицу, заголовок которой приведен ниже.
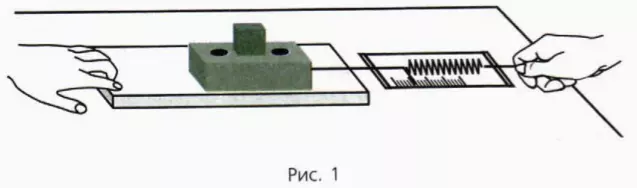
3. Повторите опыт, поставив на брусок два и затем три груза. Запишите результаты в таблицу.
4. Вычислите коэффициент трения между бруском и горизонтальной поверхностью во всех трех случаях (в пределах погрешности опыта результаты должны совпадать). Результаты опыта с тремя грузами обеспечивают наибольшую точность вычисления коэффициента трения. Расчет и результат запишите.
5. Запишите выводы из эксперимента.
5. Изучение закона сохранения энергии в механике
Цель работы: сравнить изменение потенциальной энергии груза с изменением потенциальной энергии пружины.
Оборудование: штатив с муфтой и зажимом, динамометр с фиксатором, груз, прочная нить, измерительная лента или линейка с миллиметровыми делениями.
Описание работы
Груз весом P прикрепляют с помощью нити к крючку пружины динамометра. Затем его поднимают на такую высоту h1 над поверхностью стола, чтобы нить провисала (рис. 3). Когда груз отпускают, он движется вниз и растягивает пружину. Измеряют высоту груза h2 над поверхностью стола, а также удлинение пружины x в тот момент, когда оно максимально (в этот момент скорость груза и, следовательно, его кинетическая энергия равны нулю).
При движении груза вниз его потенциальная энергия уменьшается на |∆Eгр| = P(h1 – h2), зато потенциальная энергия пружины увеличивается на Eпр = (kx2)/2, где k – жесткость пружины, x – максимальное удлинение пружины.
При движении груза вниз часть его потенциальной энергии переходит во внутреннюю вследствие трения в динамометре и сопротивления воздуха, поэтому Eпр < |∆Eгр|.
Потенциальная энергия деформированной пружины Eпр = (Fx)/2; где x – максимальное удлинение пружины, а F – соответствующая ему сила упругости. (При выводе формулы для потенциальной энергии деформированной пружины надо учесть, что среднее значение силы упругости при растяжении пружины равно F/2.) Таким образом, чтобы найти отношение Eпр/|∆Eгр|, надо измерить P, h1, h2, F и x.
Для измерения F, x и h2 необходимо отметить максимальное удлинение пружины. Для этого на стержень динамометра около ограничительной скобы надевают кусочек картона (фиксатор), который может перемещаться вдоль стержня с небольшим трением. При движении груза вниз ограничительная скоба динамометра переместит фиксатор вверх по стержню динамометра. Чтобы измерить максимальную силу упругости, надо затем растянуть динамометр рукой так, чтобы фиксатор оказался снова у ограничительной скобы. По значению максимальной силы упругости F можно определить значения x и h2.
Ход работы
1. Соберите установку, изображенную на рисунке 2.
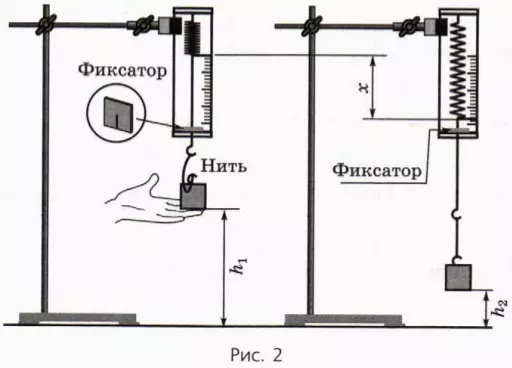
2. Привяжите груз на нити длиной 12–15 см к крючку динамометра. Закрепите динамометр в зажиме штатива на такой высоте, чтобы груз при максимальном растяжении пружины динамометра не доставал до стола.
3. Приподняв груз так, чтобы нить провисала, установите фиксатор на стержне динамометра около ограничительной скобы (рис. 3, а). Отпустив груз, убедитесь в том, что при максимальном растяжении пружины она не достает до ограничительной скобы (в противном случае при неупругом ударе пружины об ограничительную скобу произойдет превращение значительной части ее механической энергии во внутреннюю). Если это условие не выполняется, уменьшите начальную высоту груза.
4. Поднимите груз и измерьте высоту h1, на которой находится нижняя грань груза.
5. Отпустите груз без толчка. Падая, груз растянет пружину, и фиксатор переместится по стержню вверх. Затем, растянув рукой пружину так, чтобы фиксатор оказался у ограничительной скобы, измерьте F, x и h2.
6. Вычислите: а) вес груза P = mg; б) увеличение потенциальной энергии пружины Eпр = (Fx)/2; в) модуль уменьшения потенциальной энергии груза |∆Eгр| = P(h1 – h2).
7. Результаты измерений и вычислений запишите в таблицу, заголовок которой приведен ниже.

8. Найдите значение отношения Eпр/|∆Eгр| и сравните его с единицей. Расчет и результат запишите.
9. Запишите выводы из эксперимента.
Как найти пробивное напряжение формула
Пробой диэлектрика (нарушение электрической прочности) — это потеря изоляционных свойств материала при его нахождении в электрическом поле. При этом в диэлектрике образуется канал проводимости. При пробое газообразного или жидкого диэлектрика в результате подвижности молекул после снятия напряжения «пробитый» участок восстанавливает свои первоначальные свойства.
Электрическая прочность — это минимальная напряженность однородного электрического поля, при которой происходит пробой диэлектрика.
где Eпр, В/м; Uпр – пробивное напряжение, В; d – толщина диэлектрика, м.
Кроме в В/м электрическую прочность часто выражают в МВ/м или кВ/мм. Соотношение между этими единицами таково: 1 МВ/м=10 6 В/м=1 кВ/мм.
Минимальное напряжение Uпр, приложенное к диэлектрику, и приводящее к образованию в нем проводящего канала, называется пробивным напряжением.
Различают следующие виды пробоя:
Ø полный пробой — канал проводимости проходит через всю толщу диэлектрика от одного электрода к другому;
Ø неполный пробой (например, коронный разряд ) — канал проводимости не достигает одного из электродов;
Ø частичный пробой происходит только в газовых или жидкостных включениях (порах) твердой изоляции.
При совместном использовании диэлектриков, находящихся в различных агрегатных состояниях, пробой может произойти не сквозь толщу одного из них, а по границе раздела фаз. Такой пробой называют поверхностным (поверхностным разрядом, или поверхностным перекрытием). Практически чаще всего изоляционная среда состоит из твердого диэлектрика и воздуха. В этом случае разряд происходит вдоль поверхности твердого диэлектрика в прилегающих слоях воздуха, и напряжение поверхностного разряда U р будет ниже, чем Unp воздуха ( U пр> U р). При этом повреждается поверхность материала, образуя на органических диэлектриках науглероженный след-трекинг.
Отношение импульсного пробивного напряжения к его статическому значению больше единицы и называется коэффициентом импульса.
Зависимость пробивного напряжения от времени приложения напряжения называют кривой жизни электрической изоляции.
Снижение Uпр от времени происходит из-за электрического старения изоляции — необратимых процессов под действием тепла и электрического поля.
Источник
Пробой диэлектриков
При напряженности электрического поля, превосходящей предел электрической прочности диэлектрика, наступает пробой. Пробой представляет собой процесс разрушения диэлектрика, в результате чего диэлектрик теряет электроизоляционные свойства в месте пробоя.
Величину напряжения, при котором происходит пробой диэлектрика, называют пробивным напряжением 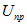 , а соответствующее значение напряженности электрического поля называется электрической прочностью диэлектрика
, а соответствующее значение напряженности электрического поля называется электрической прочностью диэлектрика 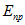 .
.
Для равномерного электрического поля электрическая прочность (пробивная напряженность) диэлектрика определяется по формуле
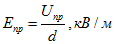
где d — толщина диэлектрика в месте пробоя, м.
Пробой жидких диэлектриков — явление сложное, что объясняется сложным составом жидких диэлектриков и сильным влиянием загрязнений на развитие пробоя. На рис. 5-13 показана зависимость изменения электрической прочности трансформаторного масла от содержания влаги. Наиболее резкое снижение электрической прочности жидких диэлектриков вызывает эмульсионная вода. С повышением температуры эмульсионная вода переходит в растворенную; при этом жидкий диэлектрик становится более однородным и электрическая прочность его повышается.
Рис. 5-13. Изменение электрической прочности трансформаторного масла от содержания в нем воды.
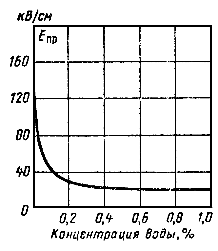
Другие загрязнения (волокна, смолистые вещества и др.) подобно воде понижают электрическую прочность жидких диэлектриков.
Чистота поверхности электродов оказывает существенное влияние на электрическую прочность жидких диэлектриков.
Большая продолжительность воздействия электрического поля на жидкий диэлектрик вызывает резкое снижение пробивного напряжения (рис. 5-14).
Рис. 5-14. Зависимость пробивного напряжения жидкого диэлектрика от времени воздействия на него электрического поля.
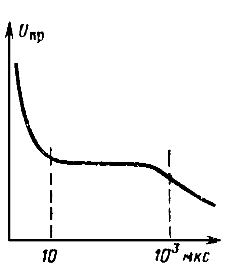
Конфигурация электрического поля и полярность электродов также вызывают изменение пробивных характеристик жидких диэлектриков (рис. 5-15 и 5-16).
Рис. 5-15. Зависимость пробивного напряжения трансформаторного масла от расстояния между электродами.
1 — плоскость против шара диаметром 125 мм; 2 — плоскость против острия.
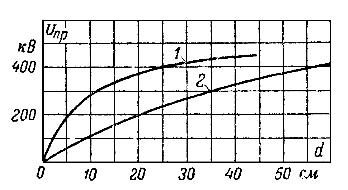
Рис. 5-16. То же, что рис. 5-15, но для постоянного напряжения. Электроды острие — плоскость:
1 — острие отрицательное; 2 — острие положительное.
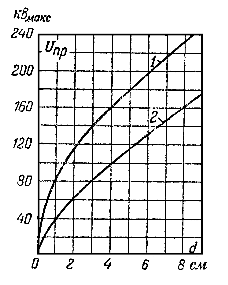
Пробивное напряжение жидких диэлектриков повышается с увеличением давления (рис. 5-17). Зависимость пробивного напряжения от давления заметно уменьшается с повышением степени очистки электроизоляционных жидкостей, что указывает на большое влияние газообразных примесей.
Рис. 5-17. Зависимость пробивного напряжения трансформаторного масла от давления при 50 Гц.1-невакуумированное масло; 2-вакуумированное масло.
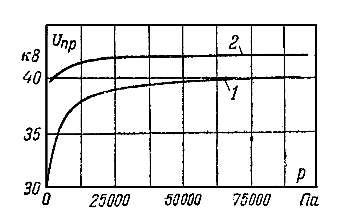
При импульсных воздействиях напряжения на слой жидкого диэлектрика зависимости пробивного напряжения от давления практически не наблюдается. С увеличением плотности жидкого диэлектрика его электрическая прочность линейно возрастает.
Влияние температуры на пробивные характеристики жидких диэлектриков различно в зависимости от их химического состава и степени загрязнения примесями. Заметные изменения электрической прочности с температурой наблюдаются у электроизоляционных жидкостей сложного химического состава, особенно при наличии в них загрязнений (влага, газы и др.). По мере приближения к температуре кипения электрическая прочность жидких диэлектриков резко понижается.
Наибольший практический интерес представляют теории, посвященные процессам пробоя технических электроизоляционных жидкостей. В большинстве этих теорий (авторы Н. Н. Семенов и А. Ф. Вальтер, Эдлер и др.) пробой жидких диэлектриков рассматривается как тепловой процесс, в результате которого в слое жидкого диэлектрика образуются газовые или паровые каналы. Паровая и газовая фазы в жидком диэлектрике возникают при нагреве его токами проводимости, повышенные значения которых наблюдаются в наиболее загрязненных частях диэлектрика. При критических значениях напряженности электрического поля в газовых и паровых каналах начинает развиваться процесс ударной ионизации газа, завершающийся пробоем.
Пробой твердых диэлектриков представляет собой или чисто электрический процесс (электрическая форма пробоя), или тепловой процесс (тепловая форма пробоя). В основе электрического пробоя лежат явления, в результате которых в твердых диэлектриках имеет место лавинное возрастание электронного тока, подобно тому как это наблюдается в процессе ударной ионизации в газообразных диэлектриках.
Характерными признаками электрического пробоя твердых диэлектриков являются:
- Независимость или очень слабая зависимость электрической прочности диэлектрика от температуры и длительности приложенного напряжения (до
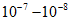 с).
с). - Электрическая прочность твердого диэлектрика в однородном поле не зависит от толщины диэлектрика (до толщин
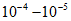 см).
см). - Электрическая прочность твердых диэлектриков находится в сравнительно узких пределах:
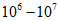 В/см; причем она больше, чем при тепловой форме пробоя.
В/см; причем она больше, чем при тепловой форме пробоя. - Перед пробоем ток в твердом диэлектрике увеличивается по экспоненциальному закону, а непосредственно перед наступлением пробоя наблюдается скачкообразное возрастание тока.
- При наличии неоднородного поля электрический пробой происходит в месте наибольшей напряженности поля (краевой эффект).
Тепловой пробой имеет место при повышенной проводимости твердых диэлектриков и больших диэлектрических потерях, а также при подогреве диэлектрика посторонними источниками тепла или при плохом теплоотводе. Процесс теплового пробоя твердого диэлектрика состоит в следующем. Вследствие неоднородности состава отдельные части объема диэлектрика обладают повышенной проводимостью. Они представляют собой тонкие каналы, проходящие через всю толщину диэлектрика. Вследствие повышенной плотности тока в одном из таких каналов будут выделяться значительные количества тепла. Это повлечет за собой еще большее нарастание тока вследствие резкого уменьшения сопротивления этого участка в диэлектрике. Процесс нарастания тепла будет продолжаться до тех пор, пока не произойдет тепловое разрушение материала (расплавление, науглероживание) по всей его толщине — по ослабленному месту.
Характерными признаками теплового пробоя твердых диэлектриков являются:
- Пробой наблюдается в месте наихудшего теплоотвода от диэлектрика в окружающую среду.
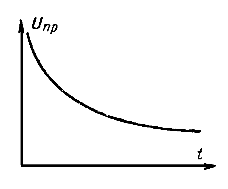
- Пробивное напряжение диэлектрика снижается с повышением температуры окружающей среды (рис. 5-18).
Рис. 5-18. Зависимость пробивного напряжения твердого диэлектрика от температуры (при тепловом пробое).
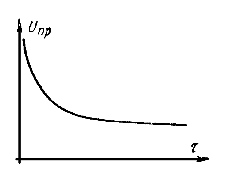
Пробивное напряжение снижается с увеличением длительности приложенного напряжения (рис. 5-19).
Рис. 5-19. Зависимость пробивного напряжения твердого диэлектрика от длительности приложенного напряжения (при тепловом пробое).
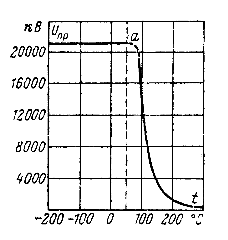
При пробое твердых диэлектриков часто наблюдаются случаи, когда до определенной температуры имеет место электрический пробой, а затем в связи с дополнительным нагревом диэлектрика наступает процесс теплового пробоя диэлектрика (рис. 5-20).
Рис. 5-20. Зависимость пробивного напряжения от температуры для электротехнического фарфора (а — точка перехода к тепловому пробою).
Аналогичный переход электрической формы пробоя в тепловую происходит в зависимости от времени выдержки твердого диэлектрика под напряжением.
Согласно выводам теории теплового пробоя твердых диэлектриков (В. А. Фок, Н. Н. Семенов) можно подсчитать величину пробивного напряжения для простых электроизоляционных конструкций (пластины) по формулам
а) для постоянного напряжения
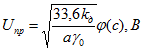
б) для переменного напряжения
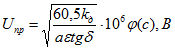
где 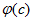 — функция величины,
— функция величины,
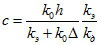
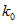 — коэффициент теплоотдачи в окружающую среду;
— коэффициент теплоотдачи в окружающую среду; 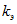 — коэффициент теплопроводности электродов, Дж/(с м °С);
— коэффициент теплопроводности электродов, Дж/(с м °С); 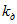 — коэффициент теплопроводности диэлектрика Дж/(с м °С); h — половина толщины диэлектрика, м;
— коэффициент теплопроводности диэлектрика Дж/(с м °С); h — половина толщины диэлектрика, м; 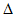 — толщина электрода, м; а — постоянная, характеризующая рост проводимости диэлектрика с температурой;
— толщина электрода, м; а — постоянная, характеризующая рост проводимости диэлектрика с температурой; 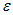 — диэлектрическая проницаемость твердого диэлектрика (при температуре окружающей среды);
— диэлектрическая проницаемость твердого диэлектрика (при температуре окружающей среды); 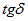 — тангенс угла диэлектрических потерь твердого диэлектрика (при температуре окружающей среды); f — частота, Гц.
— тангенс угла диэлектрических потерь твердого диэлектрика (при температуре окружающей среды); f — частота, Гц.
По известным значениям 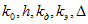 вычисляют величину с и, воспользовавшись графиком (рис. 5-21), находят
вычисляют величину с и, воспользовавшись графиком (рис. 5-21), находят 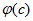 .
.
Рис. 5-21. Значения функции. К расчету пробивного напряжения твердого диэлектрика при тепловом пробое (по В. А. Фоку).
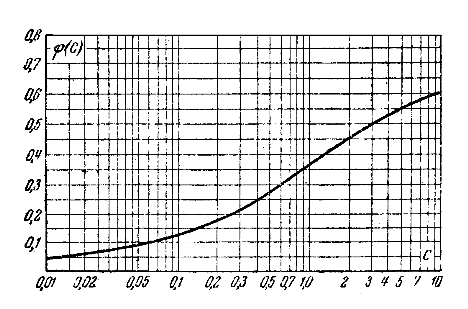
При неограниченном возрастании с величина 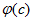 стремится к пределу, равному 0,66.
стремится к пределу, равному 0,66.
Источник
Основные расчетные выражения и необходимые пояснения
Электрическая прочность диэлектриков
Основные расчетные выражения и необходимые пояснения
Электрической прочностью, Eпр называется средняя напряженность электрического поля, при которой происходит электрический пробой изоляционного промежутка. Напряжение, при котором происходит электрический пробой, называют «пробивным напряжением», Uпр.
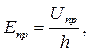 (6.1.)
(6.1.)
где h- толщина диэлектрика (изоляционный промежуток между электродами, разрядный промежуток).
Пробивное напряжение зависит от размера разрядного промежутка. При увеличении промежутка пробивное напряжение возрастает, а электрическая прочность снижается.
Электрическим пробоем диэлектрика называют скачкообразное увеличение электропроводности материала при воздействии высокого напряжения, вплоть до образования электропроводящего плазменного канала. Явление электрического пробоя в газах или жидкостях часто называют «электрическим разрядом», что говорит о разряде емкости через этот канал.
Механизмы развития разряда в газообразных, жидких и твёрдых диэлектриках различны
При электрическом пробое большого газового промежутка последовательно развиваются следующие явления:
I. Появление свободного электрона в газовом промежутке (случайного, из металлического электрода, в результате фотоионизации молекулы газа и т.п.)
II. Разгон свободного электрона электрическим полем до энергии, достаточной для того, чтобы при соударении с нейтральным атомом ионизировать последний (ударная ионизация).
III. Развитие электронной лавины как следствие множественных актов ударной ионизации.
IV. Рост стримера – проводящего плазменного канала, формирующегося из положительных ионов, оставшихся после прохождения лавины, и отрицательных зарядов, втягиваемых в положительную плазму.
V. Преобразование стримера в лидер за счет термоионизации, вызываемой прохождением емкостного тока по стримеру.
VI. Главный разряд происходит при замыкании каналом разряда разрядного промежутка.
При малых промежутках процесс пробоя может завершиться на стадиях III (лавинный пробой) и IV (стримерный пробой, искра).
Электрическая прочность газов зависит:
А) от давления. (При увеличении давления уменьшаются расстояния между молекулами. Разгоняющемуся электрону необходимо на более коротком пути разгона (называемого длиной свободного пробега) получить ту же энергию, достаточную для ионизации атома. Эта энергия определяется в первую очередь конечной (в момент соударения) скоростью электрона. Большего ускорения электрон может достичь за счет увеличения действующей на него силы – напряженности электрического поля. Экспериментальная зависимость пробивного напряжения газового промежутка от произведения давления «р» на величину промежутка «h» называется законом Пашẻна. Минимальное значение пробивного напряжения для воздуха при ph=0,7Па×м составляет примерно 330 В. Левее указанного значения ph электрическая прочность возрастает из-за малой вероятности столкновения электронов с молекулами газа.); кривая Пашена представлена на рис. 6.1
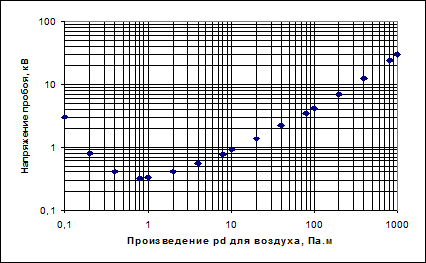
Рис 6.1.Кривая Пашẻна для лавинного пробоя воздушного промежутка
10 Па·м и более можно пользоваться следующей приближенной формулой для расчета пробивного напряжения
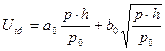 (6.2.)
(6.2.)
где параметры a0 и b0 зависят от сорта газа:
| Постоянные коэффициенты | Воздух | O2 | N2 | H2 | Ar | He | Ne | SF6 |
| a0, МВ/м | 2,45 | 2,6 | 2,35 | 1,26 | 0,57 | 0,57 | 0,201 | 8,93 |
| b0, МВ/м 1/2 | 0,064 | 0,0635 | 0,0955 | 0,0437 | 0,226 | 0,0153 | 0,0157 |
Здесь предполагается давление p0 =101,3 кПа, температура T0 = 293 К.
При изменении температуры и давления предыдущая формула слегка модифицируется
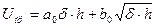 , где
, где 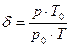 (6.3.)
(6.3.)
Б) От сродства молекулы газа к электрону, электроотрицательности газа. (Сродство к электрону – это способность некоторых нейтральных атомов и молекул присоединять добавочные электроны, превращаясь в отрицательные ионы. В электроотрицательных газах, состоящих из атомов с высоким сродством к электрону, требуется бǒльшая энергия разгона электронов полем для образования электронной лавины).
Электрическая прочность жидкого диэлектрика не связана непосредственно с химическим строением жидкостей. Из-за близкого расположения молекул в жидком диэлектрике не реализуется механизм ударной ионизации.
На значение электрической прочности влияет в первую очередь количество газа в жидкости, состояние и площадь поверхности электродов
Электрический пробой жидкого диэлектрика начинается, как правило, с пробоя микроскопических газовых пузырьков. Из-за низкой диэлектрической проницаемости газа напряженность в пузырьке выше, чем в жидкости. А электрическая прочность газа – ниже.
Частичные разряды в пузырьках приводят к росту последних, что в итоге завершается пробоем жидкого диэлектрика.
Электрическая прочность жидкого диэлектрика повышается при:
— очистке от твердых проводящих микрочастиц (сажа, уголь и т.п.);
— сушке жидкости (удалении воды);
— дегазации жидкости (вакууммировании);
Для учета давления Р и площади электродов S используется обобщение эмпирических зависимостей в виде формулы Мартина.
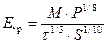 (6.4.)
(6.4.)
где постоянная M зависит от сорта жидкости и имеет размерность МВ/см. В этом выражении длительность импульса τ следует подставлять в микросекундах, давление в атм., а площадь электродов S — в см 2 . Постоянная М составляет 0,7 МВ/см для гексана и трансформаторного масла, 0,6 МВ/см для глицерина, 0,5 МВ/см для этилового спирта, 0,6 МВ/см для воды (в случае пробоя с катода) и 0,3 МВ/см (в случае пробоя с анода).
Механизмы пробоя твердых диэлектриков зависят от времени воздействия напряжения (с момента подачи до пробоя), определяющим физические процессы, происходящие при этом воздействии. Различают:
— электрический пробой (время воздействия – доли секунды);
— тепловой пробой (время воздействия от секунд до часов);
— пробой под действием частичных разрядов (время воздействия от нескольких часов до года и более).
При электрическом пробое твёрдого диэлектрика под действием приложенного напряжения разрываются химические связи, и вещество перерабатывается в плазму. Электрическая прочность твердого диэлектрика пропорциональна энергии химических связей.
Причиной теплового пробоя является разогрев диэлектрика, чаще всего за счет диэлектрических потерь, когда мощность потерь превышает мощность, отводимую от диэлектрика.
При повышении температуры увеличиваются электропроводность (за счет увеличения числа носителей) и угол диэлектрических потерь, что приводит к дополнительному росту энерговыделения, и снижению электрической прочности.
Частичным разрядом, ЧР называют разряд, проходящий в какой-либо ограниченной области изоляционного промежутка, и не замыкающий весь промежуток. Одним из примеров частичного разряда является коронный разряд в газах в неравномерном электрическом поле, когда стримером пробивается лишь область вблизи электрода с напряженностью поля выше электрической прочности газа (например, у провода высоковольтной линии электропередачи). В твердых телах ЧР – это локальный многолавинный разряд в газовой поре диэлектрика.
Для возникновения частичного разряда в твердом диэлектрике необходимы два условия:
— наличие воздушного включения, напряженность поля в котором выше, чем в самом диэлектрике;
— напряжение, приложенное к диэлектрику, должно быть достаточным для того, чтобы напряженность поля в воздушном включении превысила пробивную.
При переменном поле, приложенном к диэлектрику, частичные разряды возникают на каждом полупериоде при достижении напряжением пробивного значения. Длительные периодические ЧР химически разрушают диэлектрик, увеличивают диэлектрические потери, что в конечном итоге приводит к пробою диэлектрика.
Для определения напряжённости поля, изоляции коаксиального кабеля можно использовать выражение:
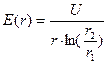 (6.5.)
(6.5.)
где r – расстояние от оси кабеля до точки в изоляции, r2 — радиус внешнего электрода, r1 – радиус внутреннего электрода.
Источник
