Скажите чему равен эпсилон нулевое??
Знаток
(374),
закрыт
13 лет назад
Игорь Елькин
Ученик
(118)
6 лет назад
На самом деле …-эпсилон- это уровень электрической эмпиданции среды. Если очень просто – конденсатор. Чем меньше кластер воды – тем меньше заряд который он может сакуммулировать. Эпсилон воды деминерализованой равен- 80, а дистилированной – 60 и это константы вписанные в учебники. На самом деле это глупость, как и теории Энштейна. Вода с ледников гренландии имеет эпстилон 4 и она лечит рак и Паркинсона. Вода, имеющая эпсилон 4 растворяер в 3000 раз большше кислорода и в 1600 раз больше углекислого газа …и в 7000раз больше азота.
Leximilian Luteriansky
Ученик
(114)
2 года назад
Странная штука что Ацюковский эту величину приводит в качестве плотности эфира в околоземном пространстве – 8.86*10(^-12) кгм^3. Вобщем даже и не странно, что под это понятием и завуалировали реально эфир. Если движение этого же эфира в проводнике и есть то что называют электричеством.
Электрическая постоянная (ранее также носила название диэлектрической постоянной) — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона, при записи их в рационализованной форме, соответствующей Международной системе единиц (СИ)[1].
Иногда, используя устаревшую терминологию, называют электрической (или диэлектрической) проницаемостью вакуума[2]. Измеряется в фарадах, делённых на метр.
Определение[править | править код]
По определению в СИ электрическая постоянная 


Численное значение[править | править код]
В Международной системе единиц[править | править код]
До изменения СИ 2018—2019 годов[править | править код]
Поскольку в СИ для магнитной постоянной было справедливо точное равенство 
м/Гн,[3]
также являвшееся точным.
Учитывая, что скорости света в СИ приписано точное значение, по определению равное 299 792 458 м/с, из последнего соотношения следует численное значение 
Ф/м ≈ 8,85418781762039 · 10−12 Ф·м−1.
Или, выражая то же через основные единицы СИ,
- ε0 ≈ 8,85418781762039 · 10−12 м−3·кг−1·с4·А2.
После изменений СИ 2018—2019 годов[править | править код]
С 2019 года вступили в силу изменения в СИ, включающие, в частности, переопределение ампера на основе фиксации численного значения элементарного заряда. Это привело к тому, что значение электрической постоянной стало экспериментально определяемой величиной, хотя численно её значение осталось прежним с высокой точностью. Значение электрической постоянной, рекомендованное CODATA[4]:
- ε0 = 8,8541878128(13) · 10−12 м−3·кг−1·с4·А2, или Ф·м−1.
В системе СГС[править | править код]
В системе СГС электрическая постоянная как коэффициент, связывающий напряжённость и индукцию электрического поля в вакууме, также может быть введена. При этом в различных вариантах системы СГС электрическая постоянная имеет разную размерность и значение. Конкретно, Гауссова система единиц и система СГСЭ построены так, что электрическая постоянная безразмерна и равна 1, а в системе СГСМ она равна ε0 = 1/c2 ≈ 1,11265005605362 · 10−21 с2·см−2.
Некоторые уравнения электродинамики в СИ[править | править код]
В материальных уравнениях, в вакууме, через электрическую постоянную связаны вектор электрической индукции 

Она также входит в запись закона Кулона (тоже в вакууме):
,
где 



При использовании СИ произведение электрической постоянной на относительную диэлектрическую проницаемость называют абсолютной диэлектрической проницаемостью.
См. также[править | править код]
- Магнитная постоянная
- Скорость света
- Уравнения Максвелла
Примечания[править | править код]
- ↑ 1 2 Электрическая постоянная — статья в Физической энциклопедии
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 213. — 240 с. — ISBN 5-7050-0118-5.
- ↑ Размерность м/Гн у численного коэффициента — из размерности магнитной постоянной.
- ↑ CODATA Internationally recommended values of the Fundamental Physical Constants (англ.). Дата обращения: 20 мая 2019.
физическая постоянная ε0(произносится как «эпсилон ноль» или «эпсилон ноль»), обычно называемая диэлектрической проницаемостью вакуума, диэлектрической проницаемостью свободное пространство или электрическая постоянная или распределенная емкость вакуума, является идеальной (базовой) физической постоянной, которая представляет собой значение абсолютной диэлектрической проницаемости из классический вакуум. Его значение CODATA составляет
- ε0= 8,8541878128 (13) × 10 Фм (фарад на метр ) с относительной погрешностью 1,5 × 10.
| Значение ε 0 | Единица |
|---|---|
| 8,8541878128 (13) × 10 | F ⋅m |
| 55,26349406 | e ⋅ГэВ ⋅fm |
Это способность электрического поля проникать в вакуум. Эта постоянная связывает единицы измерения электрического заряда с механическими величинами, такими как длина и сила. Например, сила между двумя разделенными электрическими зарядами со сферической симметрией (в вакууме классического электромагнетизма ) задается законом Кулона :
- FC = 1 4 π ε 0 q 1 q 2 r 2 { displaystyle F _ { text {C}} = { frac {1} {4 pi varepsilon _ {0}}} { frac {q_ {1} q_ {2}} {r ^ {2 }}}}
Значение постоянной дроби, 1/4 π ε 0 { displaystyle 1/4 pi varepsilon _ {0}}
Содержание
- 1 Значение
- 1.1 Новое определение единиц СИ
- 2 Терминология
- 3 Историческое происхождение параметра ε 0
- 3.1 Рационализация единиц
- 3.2 Определение значения ε 0
- 4 Диэлектрическая проницаемость реальной среды
- 5 См. Также
- 6 Примечания
Значение
Значение ε 0 определяется по формуле
- ε 0 = 1 μ 0 c 2 { displaystyle varepsilon _ {0} = { frac {1} { mu _ {0} c ^ {2}}}}
, где c – определенное значение для скорость света в классическом вакууме в единицах СИ, а μ 0 – параметр, который международные организации по стандартизации называют «магнитной постоянной. “(обычно называемая вакуумной проницаемостью или проницаемостью свободного пространства). Поскольку μ 0 имеет приблизительное значение 4π × 10 H /m, а c имеет определенное значение 299792458 м⋅с, отсюда следует, что ε 0 может быть выражено численно как
- ε 0 = 1 (4 π × 10–7 N / A 2) (299792458 м / с) 2 = 625000 22468879468420441 π F / м ≈ 8,85418781762039 × 10–12 F ⋅ м – 1 { displaystyle varepsilon _ {0} = { frac {1} {(4 pi times 10 ^ {- 7} , { textrm {N / A}} ^ {2}) (299792458 , { textrm {m / s}}) ^ {2}}} = { frac {625000} {22468879468420441 pi}} , { textrm {F / m}} приблизительно 8.85418781762039 times 10 ^ {- 12} , { textrm {F}} { cdot} { textrm {m}} ^ {- 1}}
(или A ⋅s ⋅kg ⋅m в базовых единицах СИ, или C ⋅N ⋅m или C ⋅V ⋅m с использованием других единиц СИ
Историческое происхождение электрической постоянной ε 0 и ее значения более подробно объясняются ниже.
Новое определение единиц СИ
С 20 мая 2019 года ампер был изменен путем определения элементарного заряда как точного количества кулонов, в результате чего электрическая диэлектрическая проницаемость вакуума больше не имеет точно определенного значения в единицах СИ. Величина заряда электрона стала численно определенной величиной, а не измеренной, что сделало μ 0 измеряемой величиной. Следовательно, ε 0 не является точным. Как и прежде, он определяется уравнением ε 0 = 1 / (μ 0 c) и, таким образом, определяется значением μ 0, магнитная проницаемость вакуума, которая, в свою очередь, определяется экспериментально определенной безразмерной постоянной тонкой структуры α:
- ε 0 = 1 μ 0 c 2 = e 2 2 α hc, { Displaystyle varepsilon _ {0} = { frac {1} { mu _ {0} c ^ {2}}} = { frac {e ^ {2}} {2 alpha hc}} ,}
, где e – это элементарный заряд, h – постоянная Планка, а c – скорость света в вакууме, каждый с точно определенными значениями. Таким образом, относительная неопределенность значения ε 0 такая же, как и для безразмерной постоянной тонкой структуры, а именно 1,5 × 10.
Терминология
Исторически параметр ε 0 был известен под множеством разных имен. Термины «диэлектрическая проницаемость вакуума» или ее варианты, такие как «диэлектрическая проницаемость в вакууме / в вакууме», «диэлектрическая проницаемость пустого пространства» или «диэлектрическая проницаемость свободного пространства » широко распространены. Организации по стандартизации во всем мире теперь используют термин «электрическая постоянная» как единообразный термин для этой величины, и официальные документы по стандартам приняли этот термин (хотя они продолжают перечислять старые термины как синонимы). В новой системе СИ диэлектрическая проницаемость вакуума будет больше не постоянной, а измеряемой величиной, связанной с (измеренной) безразмерной постоянной тонкой структуры.
Другим историческим синонимом была «диэлектрическая проницаемость вакуума», поскольку «диэлектрическая постоянная» в прошлом иногда использовалась для обозначения абсолютной диэлектрической проницаемости. Однако в современном использовании «диэлектрическая постоянная» обычно относится исключительно к относительной диэлектрической проницаемости ε / ε 0, и даже это использование считается «устаревшим» некоторыми органами по стандартизации в пользу относительная статическая диэлектрическая проницаемость. Следовательно, термин «диэлектрическая проницаемость вакуума» для электрической постоянной ε 0 считается устаревшим большинством современных авторов, хотя иногда можно найти примеры продолжающегося использования.
Что касается обозначений, константа может быть обозначена как ε 0 { displaystyle varepsilon _ {0} ,}

Историческое происхождение параметра ε 0
Как указано выше, параметр ε 0 является постоянной системой измерения. Его присутствие в уравнениях, которые сейчас используются для определения электромагнитных величин, является результатом так называемого процесса «рационализации», описанного ниже. Но метод присвоения ему значения является следствием того, что уравнения Максвелла предсказывают, что в свободном пространстве электромагнитные волны движутся со скоростью света. Чтобы понять, почему ε 0 имеет такое значение, требуется краткое понимание истории.
Рационализация единиц
Эксперименты Кулона и других показали, что сила F между двумя равными точечными «количествами» электричества, расположенными на расстоянии r друг от друга в свободное пространство, должно быть задано формулой, имеющей вид
- F = ke Q 2 r 2, { displaystyle F = k _ { text {e}} { frac {Q ^ {2}} {r ^ {2}}},}
где Q – количество, которое представляет количество электричества, присутствующего в каждой из двух точек, а k e – постоянная Кулона. Если начинается без ограничений, то значение k e может быть выбрано произвольно. Для каждого различного выбора k e существует своя «интерпретация» Q: во избежание путаницы каждой другой «интерпретации» должно быть присвоено отличительное имя и символ.
В одной из систем уравнений и единиц, согласованных в конце 19 века, которая называется «электростатическая система единиц сантиметр – грамм – секунда» (система cgs esu), константа k e было принято равным 1, и величина, теперь называемая «гауссовский электрический заряд » q s, была определена полученным уравнением
- F = qs 2 r 2. { displaystyle F = { frac {{q _ { text {s}}} ^ {2}} {r ^ {2}}}.}
Единица гауссовского заряда, статкулон, такова, что две единицы, расположенные на расстоянии 1 сантиметра друг от друга, отталкиваются друг от друга с силой, равной единице силы cgs, dyne. Таким образом, единица гауссовского заряда также может быть записана как 1 дин см. «Гауссов электрический заряд» – это не та же математическая величина, что современный (MKS и впоследствии SI ) электрический заряд, и не измеряется в кулонах.
Впоследствии возникла идея, что в ситуациях сферической геометрии было бы лучше включить множитель 4π в уравнения, подобные закону Кулона, и записать его в форме:
- F = ke ′ qs ′ 2 4 π r 2. { displaystyle F = k ‘_ { text {e}} { frac {{q’ _ { text {s}}} ^ {2}} {4 pi r ^ {2}}}.}
Эта идея называется «рационализация». Величины q s ′ и k e ′ не такие же, как в более раннем соглашении. Если положить k e ′ = 1, генерируется единица электроэнергии другого размера, но она все еще имеет те же размеры, что и система cgs esu.
Следующим шагом было рассматривать величину, представляющую «количество электричества», как самостоятельную фундаментальную величину, обозначенную символом q, и записать закон Кулона в его современной форме:
- F = 1 4 π ε 0 q 2 r 2. { displaystyle F = { frac {1} {4 pi varepsilon _ {0}}} { frac {q ^ {2}} {r ^ {2}}}.}
Система Сгенерированные таким образом уравнения известны как рационализированная система уравнений метр – килограмм – секунда (rmks) или система уравнений «метр – килограмм – секунда – ампер (mksa)». Это система, используемая для определения единиц СИ. Новая величина q получила название «rmks электрический заряд» или (в настоящее время) просто «электрический заряд». Ясно, что величина q s, используемая в старой системе cgs esu, связана с новой величиной q соотношением
- q s = q 4 π ε 0. { displaystyle q _ { text {s}} = { frac {q} { sqrt {4 pi varepsilon _ {0}}}}.}
Определение значения ε 0
One теперь добавлено требование, согласно которому сила должна измеряться в ньютонах, расстояние в метрах, а заряд измеряться в практической единице инженеров, кулонах, которые определяются как заряд, накопленный при протекании тока силой 1 ампер в течение одной секунды.. Это показывает, что параметру ε 0 следует присвоить единицу C⋅N⋅m (или эквивалентные единицы – на практике «фарады на метр»).
Чтобы установить числовое значение ε 0, используют тот факт, что если использовать рационализированные формы закона Кулона и закона силы Ампера ( и другие идеи) для разработки уравнений Максвелла, то обнаруживается, что указанная выше связь существует между ε 0, μ 0 и c 0. В принципе, у каждого есть выбор – сделать кулон или ампер фундаментальной единицей электричества и магнетизма. Было принято решение использовать ампер во всем мире. Это означает, что значение ε 0 определяется значениями c 0 и μ 0, как указано выше. Краткое объяснение того, как определяется значение μ 0, см. В статье о μ0.
Диэлектрической проницаемости реальных сред
По соглашению, электрическая постоянная ε 0 появляется в соотношении, которое определяет поле Dэлектрического смещения в терминах электрического поля Eи классической электрической плотности поляризации Pсреды. В общем, это соотношение имеет вид:
- D = ε 0 E + P. { displaystyle mathbf {D} = varepsilon _ {0} mathbf {E} + mathbf {P}.}
Для линейного диэлектрика P предполагается пропорциональным E, но разрешен отклик с задержкой и пространственно нелокальный ответ, поэтому мы имеем:
- D (r, t) = ∫ – ∞ tdt ′ ∫ d 3 r ′ ε (r, t ; r ′, t ′) E (r ′, t ′). { displaystyle mathbf {D} ( mathbf {r}, t) = int _ {- infty} ^ {t} dt ‘ int d ^ {3} mathbf {r}’ varepsilon ( mathbf {r}, t; mathbf {r} ‘, t’) mathbf {E} ( mathbf {r} ‘, t’).}
В случае нелокальности и задержки ответ не важен, результат:
- D = ε E = ε р ε 0 E { displaystyle mathbf {D} = varepsilon mathbf {E} = varepsilon _ { text {r}} varepsilon _ {0} mathbf {E}}
где ε – диэлектрическая проницаемость, а ε r – относительная статическая диэлектрическая проницаемость. В вакууме классического электромагнетизма поляризация P= 0, поэтому ε r = 1 и ε = ε 0.
См. Также
- Эффект Казимира
- Относительная диэлектрическая проницаемость
- Закон Кулона
- Уравнение электромагнитной волны
- ISO 31-5
- Математическое описание электромагнитного поля
- Синусоидальные плоские волновые решения уравнения электромагнитной волны
- Волновое сопротивление
Примечания
В физическая постоянная ε0 (произносится как «эпсилон ноль» или «эпсилон ноль»), обычно называемый диэлектрическая проницаемость вакуума, диэлектрическая проницаемость свободного пространства или же электрическая постоянная или распределенная емкость вакуума, – идеальная (базовая) физическая константа, которая является значением абсолютная диэлектрическая проницаемость из классический вакуум. Его CODATA ценность
- ε0 = 8.8541878128(13)×10−12 F⋅m−1 (фарады на метр ), с относительной неопределенностью 1.5×10−10.[1]
| Значение ε0 | Единица измерения |
|---|---|
| 8.8541878128(13)×10−12 | F ⋅м−1 |
| 55.26349406 | е2⋅ГэВ−1⋅FM−1 |
Это способность электрическое поле проникнуть в вакуум. Эта константа связывает единицы измерения электрический заряд к механическим величинам, таким как длина и сила.[2] Например, сила между двумя разделенными электрическими зарядами сферической симметрии (в вакуум классического электромагнетизма ) дан кем-то Закон Кулона:
Значение постоянной дроби, 
Ценить
Значение ε0 является определенный по формуле[3]
куда c определенное значение для скорость света в классический вакуум в Единицы СИ,[4] и μ0 это параметр, который международные организации по стандартизации называют “магнитная постоянная “(обычно называется проницаемостью вакуума или проницаемостью свободного пространства). Поскольку μ0 имеет приблизительное значение 4π × 10−7 ЧАС /м,[5] и c имеет определенный ценить 299792458 мес−1,[6] следует, что ε0 можно численно выразить как
(или же А2⋅s4⋅кг−1⋅м−3 в Базовые единицы СИ, или же C2⋅N−1⋅м−2 или же C ⋅V−1⋅м−1 с использованием других когерентных единиц СИ).[7][8]
Историческое происхождение электрической постоянной ε0, и его значение более подробно описаны ниже.
Новое определение единиц СИ
В ампер было переопределено путем определения элементарный заряд как точное количество кулонов по состоянию на 20 мая 2019 г.,[9] в результате чего электрическая диэлектрическая проницаемость вакуума больше не имеет точно определенного значения в единицах СИ. Величина заряда электрона стала численно определенной величиной, а не измеренной, что сделало μ0 измеренное количество. Как следствие, ε0 не совсем. Как и прежде, он определяется уравнением ε0 = 1/(μ0c2), и, таким образом, определяется значением μ0, то магнитная вакуумная проницаемость что в свою очередь определяется экспериментально определенным безразмерным постоянная тонкой структуры α:
с е будучи элементарный заряд, час будучи Постоянная Планка, и c будучи скорость света в вакуум, каждый с точно определенными значениями. Относительная неопределенность значения ε0 поэтому такой же, как и для безразмерного постоянная тонкой структуры, а именно 1.5×10−10.[10]
Терминология
Исторически параметр ε0 был известен под разными именами. Термины «диэлектрическая проницаемость вакуума» или ее варианты, такие как «диэлектрическая проницаемость в вакууме / в вакууме»,[11][12] «диэлектрическая проницаемость пустого пространства»,[13] или “диэлектрическая проницаемость свободное место “[14] широко распространены. Организации по стандартизации во всем мире теперь используют термин «электрическая постоянная» как единый термин для этой величины,[7] и официальные документы по стандартам приняли этот термин (хотя они продолжают перечислять старые термины как синонимы).[15][16] В новой системе СИ диэлектрическая проницаемость вакуума больше не будет постоянной, а будет измеряемой величиной, связанной с (измеренным) безразмерным постоянная тонкой структуры.
Другим историческим синонимом была «диэлектрическая проницаемость вакуума», поскольку «диэлектрическая постоянная» иногда использовалась в прошлом для обозначения абсолютной диэлектрической проницаемости.[17][18] Однако в современном использовании термин «диэлектрическая проницаемость» обычно относится исключительно к относительная диэлектрическая проницаемость ε/ε0 и даже это использование считается “устаревшим” некоторыми органами по стандартизации в пользу относительная статическая диэлектрическая проницаемость.[16][19] Следовательно, термин «диэлектрическая проницаемость вакуума» для электрической постоянной ε0 считается устаревшим большинством современных авторов, хотя время от времени можно найти примеры продолжающегося использования.
Что касается обозначений, то константу можно обозначать либо 

Историческое происхождение параметра ε0
Как указано выше, параметр ε0 – постоянная измерительной системы. Его присутствие в уравнениях, которые сейчас используются для определения электромагнитных величин, является результатом так называемого процесса «рационализации», описанного ниже. Но метод присвоения ему значения является следствием результата, который уравнения Максвелла предсказывают, что в свободном пространстве электромагнитные волны движутся со скоростью света. Понимание почему ε0 имеет ценность, требует краткого понимания истории.
Рационализация единиц
Эксперименты Кулон и другие показали, что сила F между двумя равными точечными «количествами» электричества, расположенными на расстоянии р в свободном пространстве, должна задаваться формулой, имеющей вид
куда Q – величина, которая представляет количество электричества, присутствующего в каждой из двух точек, и kе это Кулоновская постоянная. Если кто-то начинает без ограничений, то значение kе могут быть выбраны произвольно.[20] Для каждого другого выбора kе есть иная “интерпретация” Q: чтобы избежать путаницы, каждой «интерпретации» следует присвоить отличительное имя и символ.
В одной из систем уравнений и единиц, согласованных в конце 19 века, называемой «электростатическая система единиц сантиметр – грамм – секунда» (система cgs esu), константа kе было принято равным 1, и теперь величина называется “гауссовский электрический заряд ” qs определялась полученным уравнением
Единица гауссовского заряда, статкулон, такое, что две единицы, расположенные на расстоянии 1 сантиметра друг от друга, отталкиваются друг от друга с силой, равной единице силы cgs, Дайн. Таким образом, единица гауссовского заряда также может быть записана 1 дин.1/2 см. «Гауссов электрический заряд» – это не та же математическая величина, что и современный (МКС и впоследствии SI ) электрический заряд и не измеряется в кулонах.
Впоследствии возникла идея, что в ситуациях сферической геометрии было бы лучше включить множитель 4π в уравнения, подобные закону Кулона, и записать его в форме:
Эта идея называется «рационализация». Количество qs‘ и kе′ Не такие, как в старом соглашении. Положив kе′ = 1 генерирует единицу электроэнергии разного размера, но все равно имеет те же размеры, что и система cgs esu.
Следующим шагом было рассматривать количество, представляющее «количество электричества», как самостоятельную фундаментальную величину, обозначенную символом qи записать закон Кулона в его современной форме:
Созданная таким образом система уравнений известна как рационализированная система уравнений метр – килограмм – секунда (rmks) или система уравнений «метр – килограмм – секунда – ампер (mksa)». Это система, используемая для определения единиц СИ.[21]Новое количество q получил название «рмкс электрический заряд», или (в настоящее время) просто «электрический заряд». Ясно, что количество qs использованный в старой системе cgs esu связан с новым количеством q к
Определение стоимости ε0
Теперь добавляется требование о том, чтобы сила измерялась в ньютонах, расстояние в метрах, а заряд измерялся в практической единице инженеров, кулонах, которые определяются как заряд, накопленный, когда ток в 1 ампер протекает на одного человека. второй. Это показывает, что параметр ε0 следует выделить блок C2⋅N−1⋅m−2 (или эквивалентные единицы – на практике «фарады на метр»).
Чтобы установить числовое значение ε0, используется тот факт, что если использовать рационализированные формы закона Кулона и Закон силы Ампера (и другие идеи) для развития Уравнения Максвелла, то обнаруживается, что указанная выше связь существует между ε0, μ0 и c0. В принципе, у каждого есть выбор: сделать кулон или ампер фундаментальной единицей электричества и магнетизма. В международном масштабе было принято решение использовать ампер. Это означает, что значение ε0 определяется значениями c0 и μ0, как указано выше. Для краткого объяснения того, как ценность μ0 решено, см. статью о μ0.
Разрешимость реальных медиа
Условно электрическая постоянная ε0 появляется в отношениях, определяющих электрическое поле смещения D с точки зрения электрическое поле E и классическая электротехника плотность поляризации п среды. В общем, это отношение имеет вид:
Для линейного диэлектрика п считается пропорциональным E, но разрешен отложенный ответ и пространственно нелокальный ответ, поэтому мы имеем:[22]
В случае, если нелокальность и задержка ответа не важны, результатом будет:
куда ε это диэлектрическая проницаемость и εр в относительная статическая диэлектрическая проницаемость. в вакуум классического электромагнетизма поляризация п = 0, так εр = 1 и ε = ε0.
Смотрите также
- Эффект Казимира
- Относительная диэлектрическая проницаемость
- Закон Кулона
- Уравнение электромагнитной волны
- ISO 31-5
- Математические описания электромагнитного поля
- Синусоидальные плоско-волновые решения уравнения электромагнитной волны
- Волновое сопротивление
Примечания
- ^ «2018 CODATA Value: вакуумная диэлектрическая проницаемость». Справочник NIST по константам, единицам и неопределенности. NIST. 20 мая 2019. Получено 20 мая 2019.
- ^ «электрическая постоянная». Электропедия: Международный электротехнический словарь (IEC 60050). Женева: Международная электротехническая комиссия. Получено 26 марта 2015..
- ^ Приблизительное числовое значение находится по адресу:«Электрическая постоянная, ε0“. Ссылка NIST на константы, единицы измерения и неопределенность: основные физические константы. NIST. Получено 22 января 2012. Эта формула, определяющая точное значение ε0 находится в таблице 1, с. 637 из П. Дж. Мор; Б.Н. Тейлор; Д.Б. Ньюэлл (апрель – июнь 2008 г.). “Таблица 1: Некоторые точные количества, относящиеся к корректировке 2006 г. в CODATA рекомендуемые значения фундаментальных физических констант: 2006 г. ” (PDF). Rev Mod Phys. 80 (2): 633–729. arXiv:0801.0028. Bibcode:2008РвМП … 80..633М. Дои:10.1103 / RevModPhys.80.633.
- ^ Цитата из NIST: «Символ c – условное обозначение скорости света в вакууме. ” Видеть NIST Специальная публикация 330, п. 18
- ^ См. Последнее предложение NIST определение ампера.
- ^ См. Последнее предложение Определение метра NIST.
- ^ а б Мор, Питер Дж .; Тейлор, Барри Н .; Ньюэлл, Дэвид Б. (2008). “CODATA Рекомендуемые значения фундаментальных физических констант: 2006 г.” (PDF). Обзоры современной физики. 80 (2): 633–730. arXiv:0801.0028. Bibcode:2008РвМП … 80..633М. Дои:10.1103 / RevModPhys.80.633. Архивировано из оригинал (PDF) 1 октября 2017 г.Прямая ссылка на значение..
- ^ Краткое изложение определений c, μ0 и ε0 содержится в отчете CODATA 2006 г .: Отчет CODATA, стр. 6–7
- ^ «Резолюция 1 24-го заседания Генеральной конференции по мерам и весам». О возможном будущем пересмотре Международной системы единиц СИ (PDF). Севр, Франция: Международное бюро мер и весов. 21 октября 2011 г.
- ^ «Значение CODATA 2018: постоянная тонкой структуры». Справочник NIST по константам, единицам и неопределенности. NIST. 20 мая 2019. Получено 20 мая 2019.
- ^ SM Sze & Ng KK (2007). «Приложение E». Физика полупроводниковых приборов (Третье изд.). Нью-Йорк: Wiley-Interscience. п. 788. ISBN 978-0-471-14323-9.
- ^ Р.С. Мюллер, Каминс Т.И. и Чан М. (2003). Электроника для интегральных схем (Третье изд.). Нью-Йорк: Вили. Внутренняя передняя крышка. ISBN 978-0-471-59398-0.
- ^ FW Sears, Zemansky MW и Young HD (1985). Колледж физики. Ридинг, Массачусетс: Эддисон-Уэсли. п. 40. ISBN 978-0-201-07836-7.
- ^ Б. Е. А. Салех и М. К. Тейч, Основы фотоники (Wiley, 1991).
- ^ Международное бюро мер и весов (2006). «Международная система единиц (СИ)» (PDF). п. 12.
- ^ а б Браславский, С. (2007). «Глоссарий терминов, используемых в фотохимии (рекомендации IUPAC 2006 г.)» (PDF). Чистая и прикладная химия. 79 (3): 293–465, см. С. 348. Дои:10.1351 / pac200779030293. S2CID 96601716.
- ^ “Натурконстантен”. Freie Universität Berlin.
- ^ Кинг, Ронольд В. П. (1963). Фундаментальная электромагнитная теория. Нью-Йорк: Дувр. п. 139.
- ^ IEEE Совет по стандартам (1997). Стандартные определения терминов IEEE для распространения радиоволн. п. 6. Дои:10.1109 / IEEESTD.1998.87897. ISBN 978-0-7381-0580-2.
- ^ Для введения в тему выбора независимых единиц см.Джон Дэвид Джексон (1999). «Приложение по агрегатам и размерам». Классическая электродинамика (Третье изд.). Нью-Йорк: Вили. стр.775 и далее. ISBN 978-0-471-30932-1.
- ^ Международное бюро мер и весов. «Международная система единиц (СИ) и соответствующая система величин».
- ^ Jenö Sólyom (2008). «Уравнение 16.1.50». Основы физики твердого тела: Электронные свойства. Springer. п. 17. ISBN 978-3-540-85315-2.
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
- ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
-
- ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
-
(e0) (по старой терминологии — диэлектрич. проницаемость вакуума), физ. постоянная, входящая в ур-ния законов электрич. поля (см. КУЛОНА ЗАКОН) при записи этих ур-ний в рационализованной форме, в соответствии с к-рой образованы электрич. и магн. ед. Международной системы единиц. e0=(m0с2)-1=(107/4pc2) Ф•м-1=8,85418782(7) •10-12 Ф•м-1, где m0— магнитная постоянная. В отличие от диэлектрич. проницаемости e (зависящей от типа в-ва, темп-ры, давления и др. параметров), e0 зависит только от выбора системы ед. В СГС системе единиц (гауссовой) e0=1.
Физический энциклопедический словарь. — М.: Советская энциклопедия.
.
1983.- ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
-
(e0) -физ постоянная, входящая в ур-ния законов электрич. поля (напр., в Кулона закон )при записи этих ур-ний в рационализованной форме, в соответствии с к-рой образованы электрич. и магн. единицы Международной системы единиц; по старой терминологии Э. п. называется диэлектрич. проницаемостью вакуума.
где m0 – магнитная постоянная. В отличие от диэлектрич. проницаемости e, зависящей от типа вещества, темп-ры, давления и др. параметров, Э. п. e0 зависит только от выбора системы единиц. Напр., в гауссовой СГС системе единиц
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
1988.
.
Полезное
Смотреть что такое “ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ” в других словарях:
-
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — коэффициент пропорциональности ?о в законе Кулона определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q1 и q2; ?о = (?оc2) 1 Ф/м = 8,854187817.10 12 Ф/м, где ?о магнитная постоянная.… … Большой Энциклопедический словарь
-
электрическая постоянная — Коэффициент, применяемый при записи ряда соотношений в СИ, равный величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. Примечание — Электрическая постоянная приблизительно равна 8,85419 • 10 12 Ф/м … Справочник технического переводчика
-
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (см.) … Большая политехническая энциклопедия
-
электрическая постоянная — электрическая постоянная; отрасл. диэлектрическая проницаемость пустоты Скалярная величина, характеризующая электрическое поле в пустоте, равная отношению суммарного электрического заряда, заключенного внутри некоторой замкнутой поверхности, к… … Политехнический терминологический толковый словарь
-
Электрическая постоянная — 14. Электрическая постоянная Постоянная, равная в системе СИ величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. П .р и м е ч а н и е. Электрическая постоянная приблизительно равна 8,35*4 • 10 12 Ф/м Источник … Словарь-справочник терминов нормативно-технической документации
-
электрическая постоянная — коэффициент пропорциональности ε0 в законе Кулона , определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q1 и q2; ε0 = (μ0c2) 1Ф/м = 8,854187817·10 12Ф/м, где μ0 магнитная постоянная … Энциклопедический словарь
-
Электрическая постоянная — (ранее также носила название диэлектрической постоянной) физическая константа, скалярная величина, определяющая напряжённость электрического поля в вакууме; входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона … Википедия
-
электрическая постоянная — elektrinė konstanta statusas T sritis automatika atitikmenys: angl. electric constant; permittivity constant; permittivity of free space; permittivity of vacuum vok. dielektrische konstante, f; Dielektrizitätskonstante, f; elektrische… … Automatikos terminų žodynas
-
электрическая постоянная — elektrinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. electric constant; permittivity of vacuum vok. absolute Dielektrizitätskonstante, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
-
электрическая постоянная — elektrinė konstanta statusas T sritis fizika atitikmenys: angl. permittivity constant; permittivity of free space; permittivity of vacuum vok. Dielektrizitätskonstante, f; elektrische Feldkonstante, f; Verschiebungskonstante, f rus. абсолютная… … Fizikos terminų žodynas







 (или A ⋅s ⋅kg ⋅m в базовых единицах СИ, или C ⋅N ⋅m или C ⋅V ⋅m с использованием других единиц СИ
(или A ⋅s ⋅kg ⋅m в базовых единицах СИ, или C ⋅N ⋅m или C ⋅V ⋅m с использованием других единиц СИ








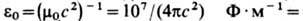
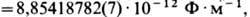 где m0 – магнитная постоянная. В отличие от диэлектрич. проницаемости e, зависящей от типа вещества, темп-ры, давления и др. параметров, Э. п. e0 зависит только от выбора системы единиц. Напр., в гауссовой СГС системе единиц
где m0 – магнитная постоянная. В отличие от диэлектрич. проницаемости e, зависящей от типа вещества, темп-ры, давления и др. параметров, Э. п. e0 зависит только от выбора системы единиц. Напр., в гауссовой СГС системе единиц