Как найти эпсилон от времени

Как найти эпсилон от времени

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с  точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

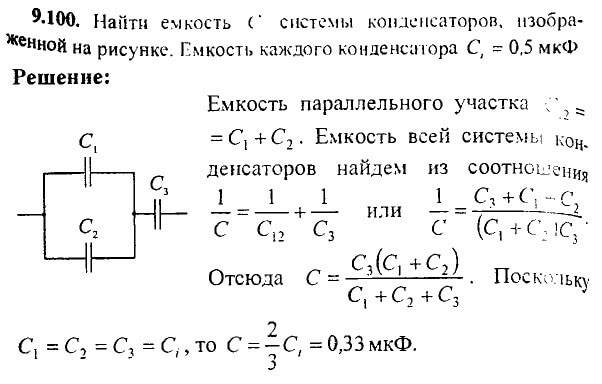
Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением 
шкалы линейки совпадает второй край стола  (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Точность измерений и погрешности в физике - определение и формулы с примерами

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать
Точность измерений и погрешности в физике - определение и формулы с примерами

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.  

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения 
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: Точность измерений и погрешности в физике - определение и формулы с примерами.  То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой  (эпсилон): 

Точность измерений и погрешности в физике - определение и формулы с примерами     (5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения –  плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 Точность измерений и погрешности в физике - определение и формулы с примерами 0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.

На точность измерения влияет много факторов, в частности:

  1. При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» – смотреть можно под разными углами.
  2. Не вполне ровно установили рулетку.
  3. Наша рулетка является копией эталона и может несколько отличаться от оригинала.

Все это необходимо учитывать при проведении измерений.

Итоги:

  • Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
  • Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора. 
  • Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:  Точность измерений и погрешности в физике - определение и формулы с примерами и указывает на качество измерения. Ее можно выразить в процентах.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Точность измерений и погрешности в физике - определение и формулы с примерами

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

Точность измерений и погрешности в физике - определение и формулы с примерами

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Точность измерений и погрешности в физике - определение и формулы с примерами

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

  1. выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
  2. подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
  3. вычесть из большего значения меньшее (4 см – 3 см = 1 см) и результат разделить на число делений.

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

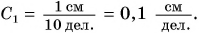
  • Для линейки 1: Точность измерений и погрешности в физике - определение и формулы с примерами
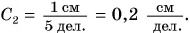
  • Для линейки 2: Точность измерений и погрешности в физике - определение и формулы с примерами
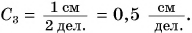
  • Для линейки 3: Точность измерений и погрешности в физике - определение и формулы с примерами

Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Точность измерений и погрешности в физике - определение и формулы с примерами

Цена деления шкалы мензурки 2: 

Точность измерений и погрешности в физике - определение и формулы с примерами

Точность измерений и погрешности в физике - определение и формулы с примерами

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше Точность измерений и погрешности в физике - определение и формулы с примерами Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы Точность измерений и погрешности в физике - определение и формулы с примерами), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления Точность измерений и погрешности в физике - определение и формулы с примерами). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Точность измерений и погрешности в физике - определение и формулы с примерами

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

  1. Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
  2. Цена деления шкалы равна значению наименьшего деления шкалы.
  3. Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

  • Заказать решение задач по физике

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Точность измерений и погрешности в физике - определение и формулы с примерами

Решение:

1) Цена деления нижней шкалы:

Точность измерений и погрешности в физике - определение и формулы с примерами

Цена деления средней шкалы: 

Точность измерений и погрешности в физике - определение и формулы с примерами

Цена деления верхней шкалы:

2) Определенный но нижней шкале с точностью до 10° Точность измерений и погрешности в физике - определение и формулы с примерами определенный по средней шкале с точностью до 5° Точность измерений и погрешности в физике - определение и формулы с примерами определенный по верхней шкале с точностью до 1° Точность измерений и погрешности в физике - определение и формулы с примерами

  • Определение площади и объема
  • Связь физики с другими науками
  • Макромир, мегамир и микромир в физике
  • Пространство и время
  • Как зарождалась физика 
  • Единая физическая картина мира
  • Физика и научно-технический прогресс
  • Физические величины и их единицы измерения
Источник

Всё содержание этой статьи является следствием решения задачи уровня первого года институтского курса математического анализа.

Здесь мы вводим новое произведение для решетчатых функций (мы будем называть его эпсилон-умножением), что дает нам возможность увидеть интересную связь между интегрально-дифференциальными уравнениями (в том числе и нелинейными) и рекуррентными соотношениями. Это позволяет с необычного ракурса взглянуть на некоторые методы их решения.

Но, что мне показалось особенно интересным, это то, что новое произведение также позволяет нам «порассуждать» о таких фундаментальных вещах, как непрерывность пространства-времени. Это рассуждение, конечно, нужно рассматривать, скорее, как интеллектуальное упражнение.

Мне показалось, что этот математический ребус или, если хотите, небольшое математическое путешествие на уровне знаний первого-второго курса технического ВУЗа может заинтересовать читателей Хабра, интересующихся математикой.

Замечание

  • вы не увидите никаких ссылок и, вообще, всё это результат размышлений отдельно взятого человека
  • возможно (и даже скорее всего), всё это и не ново, и, возможно, некоторые термины, которые я использую не соответствуют математической традиции, но так как это не научная публикация, здесь нет претензии на новизну и всё это довольно просто, то это терминологическое отличие, на мой взгляд, не является чем-то действительно важным

Краткое изложение

В этой статье речь будет идти о двух типах функций (определенных в области действительных чисел): аналитических и решетчатых.

Замечание 1

Точнее речь будет идти об аналитических справа от нуля функциях, которые мы будем обозначать заглавными буквами

$F(x), G(x), ...$ и о решетчатых функциях, определенных на множестве целых неотрицательных чисел ($N_0$), для обозначения которых мы будем использовать строчные буквы $ f_n, g_n, ...$. Множество таких решетчатых функций мы будем обозначать как $A^epsilon $. Точные определения этих функций будут приведены ниже в данной статье

Замечание 2

Иногда, в примерах мы будем расширять наш подход и на область комплексных чисел. Строго говоря, это должно быть обосновано. Но я опускаю это обоснование (как и доказательства некоторых других утверждений), чтобы не перегружать и так длинную статью

Мы установим взаимно однозначное соответствие между функциями из этих двух классов. Мы также введем новые операции для решетчатых функций. Эти операции будут аналогичны «обычным» операциям над «обычными» функциями. Мы будем отличать эти новые операции добавлением приставки «эпсилон». Так «обычной» производной будет соответствовать эпсилон-производная, обычному произведению — эпсилон-произведение, обычному интегрированию — эпсилон-интегрирование и т.д. При этом, если операция остается неизменной (как в случае суммирования и вычитание) название меняться не будет.

Одна из основных целей введения этих операций проста — сохранить свойства производной произведения функций:

$(F(x)G(x))' = F'(x)G(x) + F(x)G'(x)$

Что в случае решетчатых функций (

$in A^epsilon$) будет выглядеть как

$overset{displaystyleepsilon}{nabla} (f_n overset{displaystyleepsilon}{*}g_n) = overset{displaystyleepsilon}{nabla} f_n overset{displaystyleepsilon}{*}g_n + f_n overset{displaystyleepsilon}{*}overset{displaystyleepsilon}{nabla} g_n$

где

$overset{displaystyleepsilon}{nabla}$ — левый оператор эпсилон-производной

$overset{displaystyleepsilon}{*}$ — эпсилон-умножение

Это позволит нам (по аналогии, например, с преобразованием Лапласа) ввести новое преобразование, которое мы будем называть эпсилон-преобразованием. Это даст нам возможность преобразовывать в общем случае нелинейные интегрально-дифференциальные уравнения в рекуррентные выражения и решать их (численно или аналитически), соответственно, рекуррентными методами.

Замечание

Также справедливо и обратное: мы получаем возможность решать рекуррентные соотношения методами интегрально-дифференциальных уравнений

Важным фактом при этом является то, что при стремлении шага решетчатой функции к нулю (

$epsilon to 0$), все наши эпсилон-функции, эпсилон-операции и рекуррентные уравнения стремятся к «обычным» функциям (аналитическим справа от нуля), обычным операциям между ними и обычным интегрально-дифференциальным уравнениям.

Но тогда, это наводит на фундаментальный вопрос: а не является ли эпсилон-умножение «истинным» умножением в нашем физическом мире (по крайней мере там, где речь идет о пространстве или о времени)?

Так, например, говоря о времени, при достаточно малом шаге (например, порядка Планковского времени

$t_p sim 10^{-43}$ сек) эпсилон-уравнение Шредингера c

$epsilonsim t_p$ для временных процессов с характерным временем

$t gg t_p$ (или в области частот с частотами

$omega ll 1/epsilon$) будет давать тот же результат, что и обычное уравнение Шредингера, но при этом, естественным образом вводится квантование времени.

В принципе, аналогичное рассуждение возможно и для пространства.

Обозначения, используемые в статье

$f_n, g_n, p_n ...$ — строчными буквами мы будем обозначать решетчатые функции, определенные на множестве

${0,epsilon,2epsilon,ldots}$, где

$epsilon in R$,

$epsilon>0$. В зависимости от контекста

$f_n$ (или подобное, например,

$g_n,p_n$) может быть или обозначением самой решетчатой функции или значением этой функции в точке

$nepsilon$

$A^epsilon$ — множество всех функций

$f_n$ определенных выше

$f$ — иногда, для обозначения функции

$f_n$ для простоты будем писать просто

$f$

$F(x), G(x), ..$ — заглавными буквами мы будем обозначать «обычные» функции. Все подобные функции в данной статье будут аналитическими справа от нуля функциями (определение будет дано ниже в статье)

$epsilon$ — шаг решетчатой функции:

$f_k = f(kepsilon)$. В зависимости от контекста

$f_n$ может быть или обозначением самой решетчатой функции или значением этой функции в точке

$nepsilon$

$nabla$ — левый оператор, обозначающий производную дифференцируемой функции:

$nabla F(x) = F ^{'}(x)$

$overset{displaystyleepsilon}{nabla}$ — левый оператор, обозначающий эпсилон-производную решетчатой функции:

$overset{displaystyleepsilon}{nabla}{f_n} = f_n^overset{displaystyleepsilon}{'}$

$nabla_F$ — левый оператор, введенный для удобства записи некоторых выражений, и обозначающий производную дифференцируемой функции, применяемый только к функции

$F(x) $ (или к производной функции

$F(x)$ любого порядка) в произведении функций, например,

$nabla_F(F(x)G(x)) = G(x)nabla F(x) = G(x) F^{'}(x)$

$nabla^2_F(F(x)G(x)) = G(x)nabla^2 F(x) = G(x) F^{''}(x)$

$overset{wedge}{I}$ — единичный левый оператор для решетчатой функции:

$overset{wedge}{I} f_n = f_n$

$overset{displaystyleepsilon}{'}$ — эпсилон-производная решетчатой функции:

$f_k^overset{displaystyleepsilon}{'} = (f_{k+1} - f_k)/epsilon$

$overset{displaystyleepsilon}{nabla}_f$ — левый оператор, введенный для удобства записи некоторых выражений, и обозначающий эпсилон-производную решетчатой функции, применяемый только к решетчатой функции

$f$ (или эпсилон-производной функции

$f$ любого порядка) в произведении (обычном) решетчатых функций, например,

$overset{displaystyleepsilon}{nabla}_f{(f_n g_n)} = g_noverset{displaystyleepsilon}{nabla}f_n$

$overset{displaystyleepsilon}{nabla^2}_f{(f_n g_n)} = g_noverset{displaystyleepsilon}{nabla^2}f_n$

$overset{displaystyleepsilon}{*}$ — эпсилон произведение

$f^{overset{displaystyleepsilon}{displaystyle i}}$ —

$i$-ая эпсилон-степень функции

$f$. Так, например,

$f^{overset{displaystyleepsilon}{ 2}} = fdisplaystyleoverset{displaystyleepsilon}{*}{f}$

$f^{overset{displaystyleepsilon}{displaystyle (i)}}$ —

$i$-ая эпсилон-производная функции

$f$. Так, например,

$f^{overset{displaystyleepsilon}{ (2)}} = (fdisplaystyleoverset{displaystyleepsilon}{'})displaystyleoverset{displaystyleepsilon}{'}$

$overset{epsilon}{rightarrow}$ — эпсилон-преобразование (прямое)

Если

$F(x) overset{epsilon}{rightarrow} f_n$, то

$F(x)$ и

$f_n$ являются эпсилон-сопряженными, при этом

$f_n$ является эпсилон-образом

$F(x)$ и

$F(x) $ — эпсилон-прообразом

$f_n$

$overset{epsilon}{leftarrow}$ — обратное эпсилон-преобразование

Краткая логика статьи

Здесь изложена логическая структура статьи. Кому-то этого будет достаточно для понимания всей статьи и таким образом сохранит его время.

  • Мы будем рассматривать решетчатые функции $f_n, g_n,p_n$,…, определенные на множестве ${0,epsilon,2epsilon,ldots}$, где $epsilon in R$, $epsilon>0$.

    Замечание

    При этом

    $epsilon$ может быть любым положительным действительным числом. Поэтому иногда в примерах, в тех случаях, когда мы не используем стремление $epsilon to 0$, мы принимаем для простоты $epsilon = 1$

  • Назовем эпсилон дифференцированием следующий левый оператор:
    $overset{displaystyleepsilon}{nabla}{f_n} = (f_{n+1} - f_n)/epsilon$, где $epsilon$ — шаг решетчатой функции
  • Введем новое произведение, которое будем называть эпсилон-произведением и обозначать как $f_n overset{displaystyleepsilon}{*} g_n $.

    Здесь три эквивалентные формулы для эпсилон-произведения:

    $p_k=(fdisplaystyleoverset{displaystyleepsilon}{*}{g})_k=(epsilon({{overset{displaystyleepsilon}{nabla}}_{f}}+{{overset{displaystyleepsilon}{nabla}}_{g}})+{overset{wedge}{I}})^k (f g)|_0$$p_k = (fdisplaystyleoverset{displaystyleepsilon}{*}{g})_k=sum_{j=0}^{k}C_{k}^{j}sum_{i=0}^{j}C_{j}^{i}{f^{overset{displaystyleepsilon}{(i)}}}|_0{g^{overset{displaystyleepsilon}{(j-i)}}}|_0$$p_k=(fdisplaystyleoverset{displaystyleepsilon}{*}{g})_k=sum_{j+i+l=k}C_k^{j,i}f_ig_j(-1)^{l}$

    где

    $C_{k}^{j,i}$ — биномиальный коэффициент Ньютона: $C_{k}^{j,i}=displaystylefrac{k!}{j!i!l!}$, ($l+j+i=k$)
    Его основные свойства:

  • Вводим эпсилон-ряд Тейлора. Он будет аналогичен обычному ряду Тейлора, но произведение, возведение в степень и производные должны быть заменены на эпсилон-произведение, эпсилон-степень и эпсилон-производные:$f_k=f_0+displaystylefrac{(kepsilon)^{overset{displaystyleepsilon}{1}}}{1!}{foverset{displaystyleepsilon}{'}}_0+displaystylefrac{(kepsilon)^{overset{displaystyleepsilon}{2}}}{2!}{f^{overset{displaystyleepsilon}{(2)}}}_0+displaystylefrac{(kepsilon)^{overset{displaystyleepsilon}{3}}}{3!}{f^{overset{displaystyleepsilon}{(3)}}}_0+ldots+displaystylefrac{(kepsilon)^{overset{displaystyleepsilon}{k}}}{k!}{f^{overset{displaystyleepsilon}{(k)}}}_0 $
  • Введение эпсилон-ряда Тейлора позволяет нам ввести эпсилон-функции, аналогичные аналитическим функциям (например, эпсилон-тригонометрические функции). Для этого потребуем, чтобы эпсилон-производные в нуле (всех порядков) для этих эпсилон-функций равнялись производным в нуле (справа) для обычных функций. Для обозначения эпсилон-функции мы будем добавлять приставку $epsilon$. Так, например, для эпсилон-экспоненты получим:$epsilon exp(kepsilon)=1+displaystylefrac{(kepsilon)^{overset{displaystyleepsilon}{1}}}{1!}+displaystylefrac{(kepsilon)^{overset{displaystyleepsilon}{2}}}{2!} +displaystylefrac{(kepsilon)^{overset{displaystyleepsilon}{3}}}{3!}+ldots+displaystylefrac{(kepsilon)^{overset{displaystyleepsilon}{k}}}{k!}$
  • Введем понятие эпсилон преобразования. Суть этого преобразования заключается в замене всех операций (производная, умножение, возведение в степень) на эпсилон-операции а всех функций на эпсилон-функции. При данном преобразовании тождества будут сохраняться. Так, например, для эпсилон-тригонометрических функций все тождества будут аналогичны обычным тригонометрическим тождествам. Например, $epsilon cos^{overset{displaystyleepsilon}{2}}(kepsilon) +epsilon sin^{overset{displaystyleepsilon}{2}}(kepsilon) = 1$

    Если эпсилон преобразование обозначить через

    $overset{displaystyleepsilon}{rightarrow}$, то этот факт можно записать, как$cos^2(x) + sin^2(x) = 1$ $overset{displaystyleepsilon}{rightarrow}$ $epsilon cos^{overset{displaystyle epsilon}{2}}(kepsilon) +epsilon sin^{overset{displaystyleepsilon}{2}}(kepsilon) = 1$

    Эпсилон-функцию мы также будем называть эпсилон-образом. Так эпсилон-косинус является эпсилон-образом косинуса. При этом сам косинус является эпсилон-прообразом для эпсилон-косинуса. При этом эти две функции (например, эпсилон-косинус и косинус) являются эпсилон-сопряженными.

  • Соответственно, обратное эпсилон-преобразование — это преобразование обратное (прямому) эпсилон-преобразованию. Будем обозначать его, как $overset{displaystyleepsilon}{leftarrow}$.
  • Таким образом, через прямые и обратные эпсилон-преобразования мы устанавливаем соответствие между дифференциальными уравнениями (ДУ) (в том числе и нелинейными) и рекуррентными соотношениями (РС).

    Теперь для решения нелинейных дифференциальных уравнений мы можем применить следующую схему:

    ДУ

    $overset{displaystyleepsilon}{rightarrow}$ РС $rightarrow$ $f_n $(решение РС) $overset{displaystyleepsilon}{leftarrow}$ $ F(x)$ (решение ДУ)

    То есть, мы делаем эпсилон-преобразование исходного ДУ, получаем РC, решаем его и делаем обратное эпсилон-преобразование, получая таким образом решение дифференциального уравнения. Важно понимать, что таким образом будут найдены лишь решения, являющиеся функциями, аналитическими справа от нуля. Это тот же подход, что применяется при решении, например, линейных дифференциальных уравнений с помощью преобразований Лапласа.

  • Аналогично, рекуррентные уравнения можно привести к дифференциальным и решать их соответствующими методами. В этом случае мы имеем следующую схему:

    РC

    $overset{displaystyleepsilon}{leftarrow}$ ДУ $rightarrow$ $ F(x)$ (решение ДУ) $overset{displaystyleepsilon}{ rightarrow}$ $f_n$ (решение РC)

  • Также легко можно ввести и дополнительные операции, и преобразования, например, эпсилон-интегрирование и эпсилон-преобразование Лапласа
  • В статье приводятся три примера
    • решение линейного дифференциального уравнения гармонических колебаний
    • решение нелинейного дифференциального уравнения (Бесселя)
    • решение линейного рекуррентного уравнения (формула для чисел Фибоначчи)
  • При стремлении $epsilon rightarrow 0$ (шаг решетчатой функции) эпсилон-функции и эпсилон-операторы стремятся к своим прообразам. Так, например, при стремлении $epsilon rightarrow 0$ эпсилон произведение стремится к обычному произведению, эпсилон-производная — к обычной производной,… эпсилон-косинус — к обычному косинусу, эпсилон-синус к обычному синусу… Это значит, что обратное эпсилон-преобразование может быть выполнено обычным стремлением $epsilon rightarrow 0$. Этот факт позволяет нам рассматривать дифференциально-интегральные уравнения (в том числе и нелинейные) с решениями аналитическими справа от нуля, как предельный случай рекуррентных уравнений с шагом $epsilon rightarrow 0$.
  • Это наводит на мысль о том, а не является ли эпсилон-умножение «истинным» умножением (во всяком случае в некоторых случаях) в нашем физическом мире? Так, например, рассмотрим одномерное уравнение Шредингера:$ihbarfrac{partial}{partial t}Psi(x,t)=-frac{hbar^2}{2m}frac{partial^2}{partial x^2}Psi(x,t) + U(x,t )Psi(x,t)$

    Это уравнение предполагает непрерывность пространства времени и возможность бесконечно малой величины

    $Delta x$ и $Delta t$ (что заложено в том факте, что мы используем дифференцирование), что в случае квантовой механики подразумевает бесконечную энергию, что невозможно.

    Но давайте рассмотрим эпсилон-преобразование этого уравнения (заменив производные на эпсилон-производные, функции на решетчатые эпсилон-функции, произведение — на эпсилон-произведение, …). При достаточно малом

    $epsilon$ мы получим решения очень близкие к тем, которые мы бы получили при решении изначального уравнения Шредингера. При этом естественным образом вводится дискретность пространства-времени, что устраняет проблему бесконечной энергии.

  • Это в свою очередь ставит вопрос о том, как можно проверить, а какое же умножение является «истинным» в нашем физическом мире, обычное или эпсилон-умножение? Возможно ли поставить мыслительный или физический эксперимент для ответа на этот вопрос?

Далее каждый из этих пунктов рассматривается более детально

Решетчатые функции и эпсилон-производная

Решетчатая функция и множество

$A^epsilon$

Решетчатые функции — это функции, определенные на дискретном множестве действительных чисел с постоянным шагом. Мы будем рассматривать только функции, определенные на множестве

${0,epsilon,2epsilon,3epsilon,ldots}$, где

$epsilon in R$,

$epsilon>0$. Так, например, такой функцией будет

$cos(0.1kpi)$, где

$k$ — целое неотрицательное число. При этом

$epsilon = 0.1pi$. Будем обозначать множество таких функций через

$A^epsilon$. Все решетчатые функции, которые мы будем рассматривать ниже будут принадлежать этому множеству

$A^epsilon $.

Пример решетчатой функции $in A^epsilon $

Функция

$cos(0.1kpi)$, где

$k in N_0$:

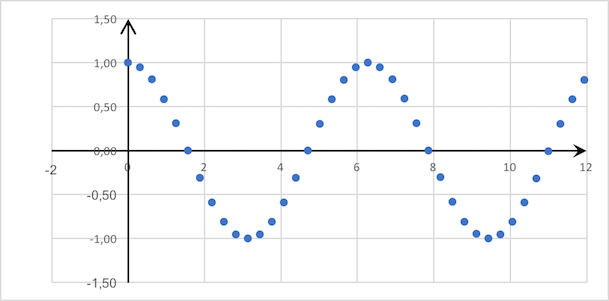
Эпсилон-производная

Будем называть эпсилон-производной функции

$f in A^epsilon$ в

$k$ следующую величину:

$foverset{displaystyleepsilon}{'}_k = overset{displaystyleepsilon}{nabla}{f_k} = (f_{k+1} - f_k)/epsilon$

Соответственно, функцию, значение которой в

$k$ для любого

$k$ равно эпсилон-производной функции

$f_n $ в

$k$, мы будем называть эпсилон-производной функции

$f_n$ и обозначать как

$f_noverset{displaystyleepsilon}{'}$ (или просто

$foverset{displaystyleepsilon}{'}$).

Очевидно, что функция

$f^{overset{displaystyleepsilon}{'}}in$

$A^epsilon$ и поэтому по отношению к ней можно еще раз применить эпсилон дифференцирование, и т.д. Мы будем обозначать символом

$^{overset{displaystyleepsilon}{(n)}}$

$n$-ю

$epsilon$-производную функции. По индукции легко доказывается, что

$f^{overset{displaystyleepsilon}{(n)}}_k=displaystylefrac{1}{epsilon^n}sumlimits_{j=0}^{n}C_{n}^{j}f_{k+j}(-1)^{n-j}$

Эпсилон-интегрирование

Процедуру, обратную эпсилон-дифференцированию, назовем соответственно эпсилон-интегрированием. Функцию

$g_nin A^epsilon$, значение которой в

$k$ для любого

$k$

$g_k=epsilonsumlimits^{k-1}_{i=0}f_i+C$

будем называть эпсилон-первообразной функции

$f$.

Эпсилон производная произведения

К сожалению, эпсилон-производная не обладает свойствами обычной производной. Так, например, очевидно, что в общем случае

$(f_n g_n)^{overset{displaystyleepsilon}{'}} = f_n^{overset{displaystyleepsilon}{'}}g_n+g_n^{overset{displaystyleepsilon}{'}}f_n +epsilon f_n^{overset{displaystyleepsilon}{'}} g_n^{overset{displaystyleepsilon}{'}}neq f_n^{overset{displaystyleepsilon}{'}}g_n+g_n^{overset{displaystyleepsilon}{'}}f_n $

Часть

$epsilon f_n^{overset{displaystyleepsilon}{'}} g_n^{overset{displaystyleepsilon}{'}}$ отличает эту «производную» от обычной производной произведения дифференцируемых функций. В случае решения численными методами нелинейных дифференциальных уравнений это дает дополнительную погрешность в вычислениях.

Замечание

Это дополнительное слагаемое приводит также, в частности, к тому, что мы не можем применить обычную формулу Тейлора для разложения решетчатой функции в ряд

Теперь давайте представим, что у нас не было бы этого дополнительного члена. Чтобы нам это могло дать?

По крайней мере, мы могли бы применять некоторые методы решения дифференциальных уравнений для решения рекуррентных уравнений (уравнений с функциями из множества

$A^epsilon $). Например, мы имели бы разложение в ряд Тейлора, мы смогли бы пользоваться интегрированием (эпсилон-интегрированием) по частям, применять преобразования (эпсилон-преобразование) Лапласа. Но в действительности все даже интереснее, и этому и посвящена данная статья.

Но как избавиться от этого дополнительного элемента? Мы можем создать, например, другое умножение (эпсилон-умножение).

Базовая задача

Это именно та задача, следствием решения которой и является вся эта статья.

Мы хотим найти такую формулу для эпсилон-произведения

$p_k=(fdisplaystyleoverset{displaystyleepsilon}{*}{g})_k$, чтобы удовлетворялись следующие требования:

  • выполнялись бы свойства обычного умножения, такие, как коммутативность, ассоциативность, дистрибутивность, существование единицы (единственной) и нулевого элемента (единственного)
  • для эпсилон-производной эпсилон-произведения решетчатых функций мы должны иметь ту же формулу, что и для производной произведения (обычных) дифференцируемых функций, то есть$overset{displaystyleepsilon}{nabla} (f_n overset{displaystyleepsilon}{*}g_n) = overset{displaystyleepsilon}{nabla} f_n overset{displaystyleepsilon}{*}g_n + f_n overset{displaystyleepsilon}{*}overset{displaystyleepsilon}{nabla} g_n $
  • при стремлении $epsilon rightarrow 0$ (шаг решетчатой функции) эпсилон-произведение должно стремиться к обычному произведение $F(x)G(x)$, где $F(x)$ и $G(x)$ соответственно функции, к которым стремятся решетчатые функции $f_n$ и $g_n$ при $epsilon rightarrow 0$, то есть:$F(x) = limlimits_{epsilon rightarrow 0, kepsilon = x} f_k$
    $G(x) = limlimits_{epsilon rightarrow 0, kepsilon = x} g_k $

Эпсилон-умножение

Всем этим свойствам удовлетворяет функция

$p_k$, определяемая как (все три формулы эквивалентны):

$p_k=(fdisplaystyleoverset{displaystyleepsilon}{*}{g})_k=(epsilon({{overset{displaystyleepsilon}{nabla}}_{f}}+{{overset{displaystyleepsilon}{nabla}}_{g}})+{overset{wedge}{I}})^k (f g)|_0$

$p_k = (fdisplaystyleoverset{displaystyleepsilon}{*}{g})_k=sum_{j=0}^{k}C_{k}^{j}sum_{i=0}^{j}C_{j}^{i}{f^{overset{displaystyleepsilon}{(i)}}}|_0{g^{overset{displaystyleepsilon}{(j-i)}}}|_0$

$p_k=(fdisplaystyleoverset{displaystyleepsilon}{*}{g})_k=sum_{j+i+l=k}C_k^{j,i}f_ig_j(-1)^{l}$,
где

$C_{k}^{j,i}$ — биномиальный коэффициент Ньютона:

$C_{k}^{j,i}=displaystylefrac{k!}{j!i!l!}$, (

$l+j+i=k$)

Замечание

Чтобы не перегружать статью мы не будем приводить доказательства, но первые два свойства доказываются легко, последнее — не так очевидно

Чтобы немного освоиться с новым произведением, рассмотрим несколько примеров.

Пример 1. (умножение на число)

Если для некоторой функции

$f_nin A^{epsilon}$ все элементы

$f_k = lambda$, где

$lambda$ — любое действительное число, то для любой функции

$g_k in A^{epsilon}$ элементы эпсилон-произведения

$p =fdisplaystyleoverset{displaystyleepsilon}{*}g$ равны

$p_k = lambda g_k$.

Это легко можно увидеть из первой формулы эпсилон-умножения.

Как результат мы получаем, что единичным элемент эпсилон-умножения является функция

$f_n in A^epsilon $ все элементы которой равны 1, а нулевым элементом — со всеми элементами равными 0.

Пример 2. (эпсилон степень)

Из определения эпсилон-произведения легко найти эпсилон-степень

$f_k = (kepsilon)^{overset{displaystyleepsilon}{i}}$, которая является эпсилон-аналогом (в следующей главе будет введено определение эпсилон-образа) функции

$F(x) = x^i$:

$x^{overset{displaystyleepsilon}{i}} = (kepsilon)^{overset{displaystyleepsilon}{i}}=i!C_k^iepsilon^i$

Таким образом получаем, что эпсилон-аналог (далее будет введено понятие эпсилон-образа) функции

$x^i=(kepsilon)^i$ является функция

$i!C_k^iepsilon^i$

Так, например,

$x^{overset{displaystyleepsilon}{2}} = (kepsilon)^{overset{displaystyleepsilon}{2}}=k(k-1)epsilon^2$

$x^{overset{displaystyleepsilon}{3}} = (kepsilon)^{overset{displaystyleepsilon}{3}}=k(k-1)(k-2)epsilon^3$

Очевидно, что

$(kepsilon)^{overset{displaystyleepsilon}{i}}$ равна нулю для

$i>k$

Теперь формула для эпсилон-производных эпсилон-степени находится в полном соответствии с обычной производной обычной степени, так например,

$ (k^{overset{displaystyleepsilon}{i}})^{overset{displaystyleepsilon}{'}}=ik^{overset{displaystyleepsilon}{i-1}}$

Замечание

В последней формуле пропущено

$epsilon$, что не является проблемой, т.к. $epsilon$ может быть любым ($epsilon >0$, $epsilon in R$), в том числе и 1. Конечно, мы не должны забывать про $epsilon$, если исследуется зависимость от него, например, при $epsilon to 0 $

Эпсилон-ряд Тейлора

Теперь мы имеем полный аналог разложения Тейлора:

$ f_k=f_0+displaystylefrac{(kepsilon)^{overset{displaystyleepsilon}{1}}}{1!}{foverset{displaystyleepsilon}{'}}_0+displaystylefrac{(kepsilon)^{overset{displaystyleepsilon}{2}}}{2!}{f^{overset{displaystyleepsilon}{(2)}}}_0+displaystylefrac{(kepsilon)^{overset{displaystyleepsilon}{3}}}{3!}{f^{overset{displaystyleepsilon}{(3)}}}_0+ldots+displaystylefrac{(kepsilon)^{overset{displaystyleepsilon}{k}}}{k!}{f^{overset{displaystyleepsilon}{(k)}}}_0 $

Будем называть этот ряд эпсилон-рядом Tейлора, а само разложение — эпсилон-разложением в ряд Tэйлора.

Эпсилон преобразование

Определение. (Эпсилон преобразование)

Пусть

$exists x_0 >0$ такое, что на множестве

$[0,x_0)$ ряд Tэйлора функции

$F(x)$ в правой окрестности нуля сходится к самой функции. Тогда функцию

$F(x)$ мы будем называть аналитической функцией в нуле справа. Тогда функции

$F$ и

$fin A^epsilon$ будем называть эпсилон-сопряженными, если для любого целого или нулевого

$i$

$i$-ая производная справа функции

$F$ в нуле равняется

$i$-ой эпсилон-производной функции

$f$ в нуле.

$F^{(i)}|_{+0}=f^{overset{displaystyleepsilon}{(i)}}_0, forall i in N_0$

Функцию

$f$ тогда будем называть эпсилон-образ

$F$ или в случае, если эта функция имеет название (например, cos), то будем называть просто эпсилон-‘название функции’ (например, эпсилон-косинус) и обозначать как

$epsilon$”обозначение функции” (

$epsilon$cos). Функцию

$F$ будем называть эпсилон-прообраз функции

$f$.

Пример 1. (Эпсилон-экспонента)

Найдем формулу для эпсилон-экспоненты, которую мы в соответствии с оговоренным правилом будем обозначать

$epsilon{exp}$. Пусть

$sigma$ произвольное комплексное число. Найдем функцию эпсилон-сопряженную функции

$exp(sigma x)$

$epsilon exp(sigma x)_k=1+C_k^1sigma epsilon+C_k^2(sigma epsilon)^2+ldots+C_k^k(sigmaepsilon)^k=(1+sigma epsilon)^k$

Заметим, что

$(1+ sigma x/k)^koverset{ktoinfty}{to}exp(sigma x)$

При этом очевидно, что

$epsilon = x/k to 0$, поэтому предыдущее равенство мы будем записывать в виде (хотя эта запись и не совсем корректна):

$epsilon exp(sigma x) overset{epsilonto 0}{to} exp(sigma x) $

Такой вид записи мы будем использовать и для других эпсилон-функций.

Пример 2. (Эпсилон-косинус, эпсилон-синус)

Найдем формулу для эпсилон-косинуса и эпсилон-синуса.
Пусть

$lambda$ — действительное число. Tогда

$epsilon{cos(lambda x)}_k=frac{1}{2}((1+ilambdaepsilon)^k+(1-ilambdaepsilon)^k)$

$epsilon{cos(lambda x)}overset{epsilonto0}{to}cos{(lambda x)}$

$epsilon{sin(lambda x)}_k=frac{1}{2i}((1+ilambda epsilon)^k-(1-ilambda epsilon)^k)$

$epsilon{sin(lambda x)}overset{epsilonto0}{to}sin{(lambda x)}$

Пример 3. (Эпсилон-умножение на икс в эпсилон-степени)

Найдем эпсилон-ряд Тейлора для

$f_n overset{displaystyle epsilon}{*} x^{overset{displaystyleepsilon}{lambda}}$

где

$lambda$ — неотрицательное целое число

Найдем производные в нуле справа для функции

$x^lambda F(x)$

$(x^lambda F(x))^{(n)}|_{x = 0} = sumlimits_{j=0}^{infty}C^j_n (x^lambda)^{(j)}F^{(n-j)}(x) |_{x = 0} = C_n^lambda lambda! F^{(n-lambda)}(x) |_{x = 0} $

Тогда эпсилон-ряд Тейлора для эпсилон-сопряженной функции можно записать как

$f_n overset{displaystyle epsilon}{*} x^{overset{displaystyleepsilon}{lambda}} = f_{n - lambda } x^{overset{displaystyleepsilon}{lambda}} $

В дальнейшем будет показано, что эта формула справедлива также и для отрицательных целых

$lambda$, что значит, что эта формула справедлива для любых целых

$lambda$

Эпсилон-преобразования операций

В данной таблице и в следующей функции

$F(x)$ и

$f_n$, а также

$G(x)$ и

$g_n$ — попарно эпсилон-сопряженные, то есть

$F(x) overset{epsilon}to f_n$

$G(x) overset{epsilon}to g_n$

Тогда операции преобразовываются (в результате эпсилон-преобразования) следующим образом:

$F(x) equiv G(x)$

$overset{epsilon} {to}$

$f_n equiv g_n$

$F(x) + G(x)$

$overset{epsilon} {to}$

$f_n + g_n$

$F(x) G(x)$

$overset{epsilon} {to}$

$f_n displaystyleoversetepsilon{*} g_n$

$F'(x) $

$overset{epsilon} {to}$

$f displaystyleoversetepsilon{'}_n$

$int F(x)dx$

$overset{epsilon} {to}$

$epsilonsumlimits^{k-1}_{i=0}f_i$ (эпсилон-первообразная)

Эпсилон-преобразование некоторых аналитических функций

$F(x) equiv lambda$

$overset{epsilon} {to}$

$f_n equiv lambda$

$lambda F(x)$

$overset{epsilon} {to}$

$lambda f_n$

$x^i$

$overset{epsilon} {to}$

$(kepsilon)^{overset{displaystyleepsilon}{i}}=i!C_k^iepsilon^i$

$exp(lambda x)$

$overset{epsilon} {to}$

$epsilon exp(lambda x)_k=(1+lambda epsilon)^k$

$cos(lambda x)$

$overset{epsilon} {to}$

$epsilon{cos(lambda x)}_k=frac{1}{2}((1+ilambdaepsilon)^k+(1-ilambdaepsilon)^k)$

$sin(lambda x)$

$overset{epsilon} {to}$

$epsilon{sin(lambda x)}_k=frac{1}{2i}((1+ilambda epsilon)^k-(1-ilambda epsilon)^k)$

$(1 + lambda x)^{-1}$

$overset{epsilon} {to}$

$(1+lambda x)^{overset{displaystyleepsilon}{-1}}=1-lambda x +lambda^2 x^{overset{displaystyleepsilon}{2}}-lambda^3x^{overset{displaystyleepsilon}{3}}+...$ (для

$|lambda x| < 1$)

Разложение в эпсилон-ряд Тейлора

$f_k = (1 + epsilon overset{epsilon}{nabla})^k f|_{k=0}=f_0+displaystylefrac{(epsilon k)^{overset{displaystyleepsilon}{1}}}{1!}{foverset{displaystyleepsilon}{'}}_0+displaystylefrac{(epsilon k)^{overset{displaystyleepsilon}{2}}}{2!}{f^{overset{displaystyleepsilon}{(2)}}}_0+displaystylefrac{(epsilon k)^{overset{displaystyleepsilon}{3}}}{3!}{f^{overset{displaystyleepsilon}{(3)}}}_0+ldots+displaystylefrac{(epsilon k)^{overset{displaystyleepsilon}{k}}}{k!}{f^{overset{displaystyleepsilon}{(k)}}}_0$

Эта формула становится очевидной, если мы заметим, что оператор

$(1 + epsilon overset{epsilon}{nabla})^i$ является оператором смещения на

$i$ шагов:

$(1 + epsilon overset{epsilon}{nabla})^i f_k = f_{k+i}$

Эпсилон-преобразование Лапласа

Мы можем также ввести эпсилон-преобразование Лапласа и пользоваться им также, как и обычным преобразованием Лапласа но применительно к решетчатым функциям

$in A^epsilon$, но это выходит за рамки целей данной статьи.

Примеры эпсилон-преобразований для тригонометрических формул

В силу вышесказанного мы можем записать, например, аналоги тригонометрических формул

${epsilon{cos(x)}}^{overset{displaystyleepsilon}{2}}+{displaystyleepsilon{sin(x)}}^{overset{displaystyleepsilon}{2}}equiv 1$

${epsilon{cos(x)}}{overset{displaystyleepsilon}{'}}equiv-epsilon{sin(x)}$

${epsilon{sin(x)}}{overset{displaystyleepsilon}{'}}equivepsilon{cos(x)}$

${epsilon{cos(alpha+beta)}}equiv{epsilon{cos(alpha)}}displaystyleoverset{displaystyleepsilon}{*}{epsilon{cos(beta)}}-{epsilon{sin(alpha)}}displaystyleoverset{displaystyleepsilon}{*}{epsilon{sin(beta)}}$

${epsilon{cos(alpha-beta)}}equiv{epsilon{cos(alpha)}}displaystyleoverset{displaystyleepsilon}{*}{epsilon{cos(beta)}}+{epsilon{sin(alpha)}}displaystyleoverset{displaystyleepsilon}{*}{epsilon{sin(beta)}}$

${epsilon{sin(alpha+beta)}}equiv{epsilon{sin(alpha)}}displaystyleoverset{displaystyleepsilon}{*}{epsilon{cos(beta)}}+{epsilon{cos(alpha)}}displaystyleoverset{displaystyleepsilon}{*}{epsilon{sin(beta)}}$

${epsilon{sin(alpha-beta)}}equiv{epsilon{sin(alpha)}}displaystyleoverset{displaystyleepsilon}{*}{epsilon{cos(beta)}}-{epsilon{cos(alpha)}}displaystyleoverset{displaystyleepsilon}{*}{epsilon{sin(beta)}}$

Но все же эпсилон-косинус и эпсилон-синус не обладают в отличии от обычного косинуса и синуса одной важной чертой — они не периодичны. Действительно,

$epsilon{cos(omega t)}_k=frac{1}{2}((1+iomega epsilon)^k+(1-iomega epsilon)^k)=left({sqrt{1+(omega epsilon)^2}}right)^k cos{(k(arctg(omega epsilon)))}$

$epsilon{cos(omega t)}_{frac{t}{epsilon}}=left({{1+omega^2 epsilon^2}}right)^{frac{t}{2epsilon}}cos{(t displaystyle frac{arct(omega epsilon)}{ epsilon})}$

Также

$epsilon{sin(omega t)}_{frac{t}{epsilon}}=left({{1+omega^2 epsilon^2}}right)^{frac{t}{2epsilon}}sin{(t displaystyle frac{arctg(omega epsilon)}{ epsilon})}$

при этом функции

$sin( t(arctg(omega epsilon)/epsilon))$ и

$cos(t(arctg(omegaepsilon/)epsilon))$ — периодические функции с периодом

$2piepsilon/arctg(omega epsilon)$. Поэтому функции

$epsilon{cos(x)}$ и

$epsilon{sin(x)}$ — не периодические функции, с нулями в точках

$(pi/2+pi n)epsilon/arctg(omega epsilon)$ и

$pi nepsilon/arctg(omega epsilon)$ соответственно, при этом ”размах” между минимумами и максимумами при увлечении

$t$ возрастает как

$({1+omega^2epsilon^2})^{frac{t}{2epsilon}}$.

Замечание

Соответственно для эпсилон-экспоненты имеем

$epsilon{exp(iomega t)}_{frac{t}{epsilon}}=left({{1+omega^2 epsilon^2}}right)^{frac{t}{2epsilon}}exp{(i displaystyle frac{arctg(omega epsilon)}{ epsilon}t)}$

Примеры решения дифференциальных уравнений методом эпсилон-отображения

Пример 1. Гармонические колебания

Давайте начнем с решения линейных дифференциальных уравнений и в качестве примера возьмем уравнение гармонических колебаний:

$F^{''}(t) + omega^2 F(t) = 0 $

Распишем процедуру решения по шагам.

Шаг 1. (Эпсилон преобразование)

$epsilon^2 f^overset{displaystyleepsilon}{(2)} + epsilon^2omega^2 f = f_{k+2} - 2f_{k+1} + (1+ epsilon^2omega^2)f_{k} = f_{k+2} - 2f_{k+1} + lambda f_{k}equiv 0$

Где

$lambda = 1+epsilon^2 omega^2$.

Получили рекуррентное уравнение.

Далее, в зависимости от того, хотим ли мы найти приблизительное решение численными методами или хотим найти точное аналитическое решение, последовательность шагов может быть разной.

Если мы ищем точное решение, выраженное формулой, то последовательность шагов может быть следующей.

Шаг 2. Аналитическое решение. (Эпсилон-производные функций в нуле всех порядков)

Находим формулу для

$n$-ой эпсилон-производной для нашего рекуррентного выражения и находим рекуррентное выражение для всех эпсилон-производных в нуле.

$(f^{overset{displaystyleepsilon}{(2)}}+ omega^2 f)^{overset{displaystyleepsilon}{(n)}} = f^{overset{displaystyleepsilon}{(n+2)}} + omega^2 f^{overset{displaystyleepsilon}{(n)}} equiv 0$

Берем значение в нуле

$f^{overset{displaystyleepsilon}{(n+2)}}|_0 + omega^2 f^{overset{displaystyleepsilon}{(n)}}|_0 = 0$

Шаг 3. Аналитическое решение. (Коэффициенты ряда Тейлора)

Заметим, что

$f_0 = F(0)$,

$(f_1 - f_0)/epsilon = F'(t)|_{t=0}$.

Будем для определенности считать, что начальное смещение

$F(0) = 0$, а начальная скорость

$F'(0) = 1$. Тогда имеем:

$f^{overset{displaystyleepsilon}{(2k)}}|_0 = 0$

$f^{overset{displaystyleepsilon}{(2k+1)}}|_0 = (-1)^komega^{2k}$

Шаг 4. Аналитическое решение. (Ряд Тейлора для искомой функции)

Но тогда

$F(x) = sumlimits_{k=0}^{infty} (-1)^kdisplaystyle{frac{omega^{2k}t^{2k+1}}{(2k+1)!}} = displaystylefrac{1}{omega}sin(omega t)$

Если же мы хотим решать численным методом (приблизительное решение), то

Шаг 2. Численное решение. (Находим значения $f_k$)

Замечание

Для наглядности в данном примере мы будем сохранять

$epsilon$ и $lambda$ в наших формулах, но в реальном численном расчёте вместо $lambda$ должно быть подставлено его численное значение, а вместо $epsilon$ может быть подставлено любое положительное число $in R$, например, $epsilon = 1$

Решаем последовательно для значений

$k$, начиная с 0. Чем больше значений будет найдено, тем больше коэффициентов ряда Тейлора нам будет известно, и, соответственно, тем точнее будет результат.

Для определенности, как и в предыдущем случае, будем считать, что начальное смещение

$F(0) = 0$, а начальная скорость 1. Имеем:

$f_0 = 0$

$f_1 = epsilon$

$f_2 = 2f_1 - lambda f_0 = 2epsilon$

$f_3 = 2f_2 - lambda f_1 = epsilon(4 -lambda)$

$f_4 = 2f_3 - lambda f_2 = 2epsilon(4 -lambda) -2 epsilonlambda = epsilon(8 - 4lambda)$

$f_5 = 2f_4 - lambda f_3 = epsilon(2(8 -4lambda) -lambda (4- lambda)) = epsilon(lambda^2 - 12lambda +16)$

…

Шаг 3. Численное решение. (Эпсилон-производные в нуле)

$f_0 = 0$

$f^overset{displaystyleepsilon}{'}|_0 = (f_1 -f_0)/epsilon = 1$

$f^overset{displaystyleepsilon}{(2)}|_0 = f_2 - 2f_1 +f_0 = 0$

$f^overset{displaystyleepsilon}{(3)}|_0 =epsilon(f_3 -3f_2 + 3f_1 - f_0)/epsilon^3 = (4 - lambda - 6 + 3 - 0)/epsilon^2 = (1 - lambda)/epsilon^2 = - omega^2$

$f^overset{displaystyleepsilon}{(4)}|_0 =(f_4 - 4f_3 +6f_2 - 4f_1 + f_0)/epsilon^4 = (8 - 4lambda - 4(4-lambda) + 12 - 4)/epsilon^3 = 0$

$f^overset{displaystyleepsilon}{(5)}|_0 = ... = omega^4$

…

Шаг 4. Численное решение. (Ряд Тейлора для искомой функции)

Имея необходимое для точности наших вычислений количество (или все, если получилось найти аналитическую формулу) эпсилон производных в нуле, мы можем построить ряд Тейлора для эпсилон-сопряженной функции, что и будет решением:

$F(x) = f_0 + displaystylefrac{f^{overset{displaystyleepsilon}{(1)}}|_0}{1!}x + displaystylefrac{f^{overset{displaystyleepsilon}{(2)}}|_0}{2!}x^2 + displaystylefrac{f^{overset{displaystyleepsilon}{(3)}}|_0}{3!}x^3 + displaystylefrac{f^{overset{displaystyleepsilon}{(4)}}|_0}{4!}x^4 + displaystylefrac{f^{overset{displaystyleepsilon}{(5)}}|_0}{5!}x^5 + ... $

Подставляя значения эпсилон производных для нашего случай получим

$F(x) = t - displaystylefrac{omega^2}{3!}t^3 + displaystylefrac{omega^4}{5!}t^5 + ...$

Таким образом мы можем с точностью до любого члена разложения в ряд Тейлора найти нашу искомую функцию.

Замечание

В данном случае, конечно, не было особого смысла использовать эпсилон-преобразование, и мы привели это лишь, как пример, чтобы продемонстрировать подход

Пример 2. Уравнение Бесселя

Теперь давайте применим этот метод для решения для чего-то более интересного. Рассмотрим нелинейное дифференциальное уравнение, например, уравнения Бесселя.

$x^2F''+xF'+(x^2-mu^2)Fequiv 0$

Шаг 1. (Эпсилон преобразование)

$x^{overset{displaystyleepsilon}{2}}overset{displaystyleepsilon}{*}f^{overset{displaystyleepsilon}{(2)}}+xoverset{displaystyleepsilon}{*}f^{overset{displaystyleepsilon}{(1)}}+(x^{overset{displaystyleepsilon}{2}}-mu^2)overset{displaystyleepsilon}{*}fequiv0$

$x^{overset{displaystyleepsilon}{2}}f_{n-2}^{overset{displaystyleepsilon}{(2)}}+xf_{n-1}^{overset{displaystyleepsilon}{(1)}}+x^{overset{displaystyleepsilon}{2}}f_{n-2}- mu^2 fequiv0$

Шаг 2. Аналитическое решение. (Эпсилон-производные функций в нуле)

Будем считать

$epsilon =1$

Берем

$n$-ую эпсилон-производную в нуле. Получаем формулу

$2displaystylefrac{n(n-1)}{2!}f_0^{overset{displaystyleepsilon}{(n)}}+nf_0^{overset{displaystyleepsilon}{(n)}}+2frac{n(n-1)}{2!}f_0^{overset{displaystyleepsilon}{(n-2)}}-mu^2f_0^{overset{displaystyleepsilon}{(n)}} =0$

$(n^2-mu^2)f_0^{overset{displaystyleepsilon}{(n)}}=-n(n-1)f_0^{overset{displaystyleepsilon}{(n-2)}}$

Шаг 3. Аналитическое решение. (Коэффициенты ряда Тейлора)

Будем последовательно находить значения эпсилон-производных

$f$ в нуле:

$mu^2f_0 = 0$

$f^{overset{displaystyleepsilon}{(1)}}= f_0displaystylefrac{mu^2}{1 - mu^2}$

$f^{overset{displaystyleepsilon}{(2)}}= - f_0displaystylefrac{2}{(4-mu^2)}$

…

$f_0^{overset{displaystyleepsilon}{(n)}}=- f_0^{overset{displaystyleepsilon}{(n-2)}}displaystylefrac{n(n-1)}{n^2-mu^2}$

Пусть

$b_n$ —

$n$-ый коэффициент эпсилон-ряда Тейлора. Тогда предыдущее равенство можно записать в виде

$b_n =- displaystylefrac{b_{n-2}}{n^2-mu^2}$

Мы видим, что если

$mu$ не целое число и не 0, то все коэффициенты ряда Tейлора равны 0. Если

$mu$ целое или ноль, то это говорит о том, что

$mu$-тый коэффициент эпсилон-ряда Tейлора может быть не равен нулю и его выбор произволен и определяется требованиями нормировки. При этом для

$n = 2k+mu$ коэффициенты эпсилон-ряда Тейлора также не равны 0, а для

$n = 2k -1 +mu$ (

$k$ — натуральное) — равны 0.

Найдем

$2k+mu$ — ые коэффициенты эпсилон-ряда Тейлора.
Подставляя

$2k + mu $ вместо

$n$ получим

$b_{2k+mu} =- displaystylefrac{b_{2(k-1) +mu}}{4k(k+mu)}$

Тогда легко получить, что

$2k+mu$-ый член разложения в эпсилон-ряд Tэйлора имеет вид

$b_{2k+mu}=Cdisplaystyle{frac{(-1)^k}{k!(k+mu)!2^{2k+mu}}}$

где

$mu$-неотрицательное целое число, C-произвольное комплексное неравное нулю, определяемое требованиями нормировки

Шаг 4. Аналитическое решение. (Ряд Тейлора для искомой функции)

Тогда для неотрицательных целых

$mu$, принимая

$C = 1$ получим формулу

$F(x)=sum_limits{k=0}^{infty}{displaystyle{frac{(-1)^k}{k!(k+mu)!}left(frac{x}{2}right)^{2k+mu}}}$

что соответствует известной формуле функции Бесселя первого рода для целых, неотрицательных

$mu$.

Для всех других решений — не существует разложения в ряд Tэйлора в нуле.

Пример 3. Числа Фибоначчи

Теперь рассмотрим, как можно решать рекуррентные уравнения с помощью эпсилон-преобразования.

Рассмотрим числа Фибоначчи, которые задаются следующим рекуррентным соотношением:

$f_{k+2}=f_k+f_{k+1}$,
при этом,

$f_0=0$,

$f_1=1$, откуда следует, что

$f_0overset{displaystyleepsilon}{'}=1/epsilon$

Это можно записать как

$f_k+2epsilon f_k^{overset{displaystyle{epsilon}}{(1)}}+epsilon^2f_k^{overset{displaystyle{epsilon}}{(2)}}=f_k+f_k+epsilon f_k^{overset{displaystyle{epsilon}}{(1)}}$ или

$f-epsilon f^{overset{displaystyle{epsilon}}{(1)}}-epsilon^2f^{overset{displaystyle{epsilon}}{(2)}}=0$

Будем считать, что

$epsilon=1$. Tогда получим

$f-f^{overset{displaystyle{epsilon}}{(1)}}-f^{overset{displaystyle{epsilon}}{(2)}}=0$,

при этом

$f_0=0$ и

$f_0overset{displaystyleepsilon}{'}=1$

Шаг 1. (Обратное эпсилон-преобразование)

Выполняя обратное эпсилон-преобразование получим

$F-F'-F''=0$
при этом

$F(+0)=0$,

$F'(+0)=1$

Шаг 2. (Решаем дифференциальное уравнение)

Мы можем решить это уравнение через преобразование Лапласа. Применим преобразование Лапласа. Получим

$p^2L(p)-0-1+p L(p)+0-L(p)=0$

$L(p)=displaystyle{frac{1}{(p^2+p-1)}}=displaystyle{frac{1}{(p_1-p_2)} left[frac{1}{p-p_1}-frac{1}{p-p_2}right]}$,

где

$p_1$,

$p_2$ — корни уравнения

$p^2+p-1=0$ и соответственно равны:

$p_1=(-1+sqrt{5})/2$

$p_2=(-1-sqrt{5})/2$.

Но тогда

$F(x)=displaystyle{frac{1}{sqrt{5}}}(exp{(p_1x)}-exp{(p_2x)})$.

Шаг 3. (Производим прямое эпсилон-преобразование)

Теперь запишем функцию, являющуюся эпсилон-образом

$F$.

Это будет

$f_k=displaystyle{frac{1}{sqrt{5}}}(epsilon{exp{(p_1x)}}-epsilon{exp{(p_2x)}})=displaystyle{{frac{left((1+epsilonfrac{-1+sqrt{5}}{2})^k-left(-1+epsilonfrac{1-sqrt{5}}{2}right)^kright)}{sqrt{5}}}}$

Соответственно, при

$epsilon=1$ получаем известную формулу

$f_k=displaystyle{{frac{left(left(frac{1+sqrt{5}}{2}right)^k-left(frac{1-sqrt{5}}{2}right)^kright)}{sqrt{5}}}}$

Свойства эпсилон-отображения при ε → 0

Обратное эпсилон-преобразование можно осуществить просто устремив

$epsilon to 0$

Это можно сформулировать более строго в виде теоремы, которую я приведу без доказательства.

Теорема

Пусть функции

$F$ и

$f$ — эпсилон-сопряженные для любого

$epsilon$. Тогда, при стремлении

$epsilon to 0 $, при условии, что

$kepsilon=const=ain(0,x_0)$ (где

$x_0$ имеет тот же смысл, что и в определении эпсилон-отображения ), значение

$f_k$ на множестве

$(0,x_0)$ стремится к

$F(a)$, то есть

$limlimits_{epsilon to0, kepsilon=a}f(kepsilon)=F(a)$

Не аналитические функции

деление на икс в эпсилон-степени

До сих пор мы говорили только об аналитических (справа от нуля) функциях.

Можно ли «расширить» этот подход и на другие функции?

В качестве примера, попробуем найти эпсилон-образ для функции

$displaystylefrac{1}{x^lambda}$, где

$lambda$ — натуральное число. Для этой функции нет разложения в ряд Тейлора в 0. Обозначим этот эпсилон-образ в соответствии с нашим подходом как

$x^overset{displaystyleepsilon}{-lambda}$. Пусть

$g_n = x^overset{displaystyleepsilon}{-lambda} overset{displaystyleepsilon}{*} f_n$

Тогда

$x^{overset{displaystyleepsilon}{lambda}} overset{displaystyleepsilon}{*} g_n = f_n$

$x^{overset{displaystyleepsilon}{lambda}} overset{displaystyleepsilon}{*} g_n = x^overset{displaystyleepsilon}{lambda}g_{n-lambda} $

$g_{n-lambda} = f_n/x^overset{displaystyleepsilon}{lambda} =displaystylefrac {f_n}{n(n-1)..(n-lambda + 1)}$

$g_n = x^overset{displaystyleepsilon}{-lambda} overset{displaystyleepsilon}{*} f_n =displaystylefrac {n!f_{n + lambda}}{(n+lambda)!}$

Если

$f_n = overset{wedge}{I}$, то получим, что

$x^overset{displaystyleepsilon}{-lambda} = displaystylefrac {n!}{(n+lambda)!}$, таким образом получаем, что

$x^overset{displaystyleepsilon}{lambda} = displaystylefrac {n!}{(n-lambda)!}$ для любого целого

$lambda $ (а не только для

$lambda in N_0$)

Эпсилон-произведение и дискретность пространства-времени

Все сказанное выше наводит на фундаментальный вопрос: a не является ли эпсилон-умножение «истинным» умножением в нашем физическом мире (по крайней мере там, где речь идет о пространстве или о времени)?

Рассмотрим, например, одномерное уравнение Шредингера:

$ihbarfrac{partial}{partial t}Psi(x,t)=-frac{hbar^2}{2m}frac{partial^2}{partial x^2}Psi(x,t) + U(x,t)Psi(x,t)$

Это уравнение предполагает непрерывность пространства-времени и возможность бесконечно малой величины

$Delta x$ и

$Delta t$ (это неявно принимается, если мы используем дифференцирование). Если говорить о времени, то это подразумевает бесконечную энергию, что противоречит современным представлениям о вселенной.

Чтобы не усложнять рассуждения, давайте рассмотрим случай когда

$U$ не зависит от

$t$. В этом случае

$Psi(x,t)$ можно записать в виде:

$Psi(x,t) = psi(x)exp(-iEt/hbar)$

Но ведь

$exp(-iEt/hbar)$ — это аналитическая функция, значит мы можем применить к ней наш подход, то есть мы можем сделать эпсилон-преобразование (относительно времени) нашего исходного уравнения Шредингера и мы получим

$ihbaroverset{displaystyleepsilon}{nabla}overset{displaystyleepsilon}Psi(x,t)=-frac{hbar^2}{2m}frac{partial^2}{partial x^2}overset{displaystyleepsilon}Psi(x,t) + U(x)overset{displaystyleepsilon}Psi(x,t)$

$overset{displaystyleepsilon}Psi(x,t) = psi(x)epsilon exp(-iEt/hbar)$

При этом

$overset{displaystyleepsilon}Psi(x,t) overset{epsilon to 0}{to}Psi(x,t)$

То есть при очень меленьком шаге времени (кванте времени)

$epsilon$ не существенном для наших расчетов, мы не увидим разницы между решением (обычного) уравнения Шредингера и решением эпсилон-уравнения Шредингера.

Но тогда это значит, что мы не можем в действительности сказать, какое произведение является «истинным» («используется» природой) — наше обычное или эпсилон-произведение (с достаточно малым квантованием времени).

При этом в случае эпсилон-произведения (и соответственно эпсилон-уравнения Шредингера и его эпсилон-волнового решения), мы имеем очевидный плюс — квантование времени становится естественным, и мы не сталкиваемся с требованием бесконечной энергии. Фактически мы имеем все то же уравнение, с теми же решениями, но при этом естественным образом устраняем необходимость допущения непрерывности времени.

Замечание

Когда мы говорим о дискретности какой-либо измеряемой сущности, имеется ввиду то, что существуют четко отграниченные, неделимые элементы, из которых эта сущность состоит. Но когда мы говорим о дискретности пространства или о времени, то возможна также и иная интерпретация. Например, возможно, при достаточно малых значениях

$Delta x ll delta_x$ или/и $Delta t ll delta_t $ уже нет смысла говорить о времени или о пространстве. Время и пространство, возможно, перестают существовать для этих величин. Таким образом мы получаем некие «размытое пятна» вместо точек, которые можно рассматривать как точки при $Delta x gg delta_x$ или/и $Delta t gg delta_t $. В данном случае нельзя выделить кванты, но также нельзя говорить и о непрерывности. Но даже в этом случае мы также можем использовать описанный здесь эпсилон-подход, предполагая, что $epsilon$ — это те минимальные $Delta x$ или/и $Delta t$, когда еще имеет смысл говорить о времени или/и пространстве (грубо говоря, это усредненный размер «пятна»).

Как проверить?

Итак, если время дискретно с «шагом»

$epsilon$, а ”истинным” умножением является эпсилон-умножение с шагом дискретности времени, то как это может проявиться? Можно ли поставить мысленный или реальный эксперимент и понять, какое произведение является «истинным» и какой шаг (квант) при этом используется?

Можно привести некоторые оценки, для понимания насколько сильно изменились бы наши представления о мире, если «истинным» было бы именно «эпсилон-умножение» (а не обычное умножение).

Вспомним, что

$epsilon{exp(iomega_0 t)}_{frac{t}{epsilon}}=left({{1+omega_0^2 epsilon^2}}right)^{frac{t}{2epsilon}}exp{(i displaystyle frac{arctg(omega_0 epsilon)}{ epsilon}t)}$

Тогда для

$omega_0epsilon ll 1$ имеем:

  • частота будет отличаться от частоты синусоидального колебания $omega_0$ и будет равняться$omega = displaystyle frac{arctg(omega_0 epsilon)}{ epsilon} approx omega_0(1 - displaystylefrac{omega_0^2epsilon^2}{3})$
  • амплитуда будет расти как$(1+(omega_0epsilon)^2))^{frac{t}{2epsilon}} approx 1 + displaystylefrac{tomega^2_0epsilon}{2}$

Давайте грубо оценим, способны ли мы заметить это отличие?

Пример 1. Изменения за время жизни вселенной

Предположим, что наша временная дискретность сравнима с Планковским временем:

$t_p approx 10^{−43 }$ сек.

Время жизни вселенной:

$t_{u} approx 10^{17} $ сек.

Найдем для каких частот

$omega_0$ за время жизни вселенной амплитуда колебаний могла измениться, например, на 0,5%.

$t_u t_pomega^2_0 = 10^{-2}$

$omega_0 = displaystylefrac{10^{-1}}{sqrt{t_ut_p}} = 10^{-1}10^{13} = 10^{12}$ рад/сек

Это значит, что для частот порядка 1 TГц (или для частиц с энергией

$10^6$ эВ) за время жизни вселенной амплитуда (волновой функции) изменилась бы на порядка один процент (порядок). То есть понятно, что как минимум в обычной жизни мы никак не можем это увидеть.

Пример 2. Изменения за секунду

Давайте оценим во сколько раз изменится амплитуда волновой функции частицы с ультравысокой энергией порядка

$ 10^{18}$ эВ за одну секунду.

$10^{18}$ эв по порядку соответствует

$10^{24}$ Гц

$(1+(omega_0 t_p)^2))^{frac{1}{2t_p}} approx 10^{48}10^{-43} = 10 ^5$

То есть за секунду амплитуда волновой функции такой частицы увеличится в 100 тысяч раз (порядок).

Выглядит существенным. Но как это обнаружить? Дело в том, что физический смысл имеет не сама волновая функция, а

$PsiPsi^*$, а в случае эпсилон-образа это будет

$overset{epsilon}Psi displaystyleoverset{displaystyle epsilon}{*}overset{epsilon}Psi$. Но

$epsilon exp(-iEt/hbar) overset{displaystyleepsilon}{*} epsilon exp(iEt/hbar) = 1$

Что говорит о том, что как раз величина, которая имеет физический смысл меняться не будет, и данный подход не позволит нам ответить на поставленный вопрос.

Источник

На чтение 9 мин Просмотров 1.9к. Опубликовано 11.09.2022 Обновлено 11.09.2022

Содержание

  1. Понятие ЭДС и единица измерения
  2. Где и как образуется электродвижущая сила
  3. Виды ЭДС
  4. Законы и формулы
  5. ЭДС аккумуляторной батареи
  6. ЭДС индукции
  7. Внутреннее сопротивление источника ЭДС
  8. Закон Ома для полной цепи
  9. Как найти мощность ЭДС

Чтобы в какой-либо среде (металле, растворе, ионизированном газе и т.п.) протекал электрический ток в течение продолжительного времени, недостаточно наличия свободных носителей заряда и электрического поля. Еще потребуется сила, которая будет разделять заряды в направлении, противоположном направлению электрического поля.

Понятие ЭДС и единица измерения

Если имеется заряженный предмет и соединить его с электрически нейтральным (или противоположно заряженным предметом), некоторое время в цепи будет существовать ток. Как только все свободные электроны перейдут от одного тела к другому, и заряды уравняются, ток прекратится.

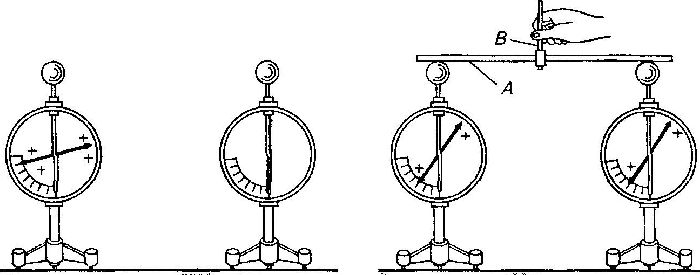
В чем суть ЭДС: единица измерения, виды и формулы для расчета

Опыт с двумя электроскопами

Это можно увидеть на примере школьного опыта с двумя электроскопами. Один из них заряжен (например, положительно), а другой заряда не имеет. Если их соединить металлическим стержнем, то заряды перейдут от одного прибора к другому. Количество зарядов уравновесится, потенциалы электроскопов станут равными, электрическое поле прекратит действие на электроны, и ток перестанет течь.

Чтобы ток продолжался, надо носители зарядов из второго электроскопа перенести обратно в первый. Для этого нужна сторонняя сила, действующая против направления электрического поля. Такая сила называется ЭДС. Расшифровка этого сокращения – электродвижущая сила.

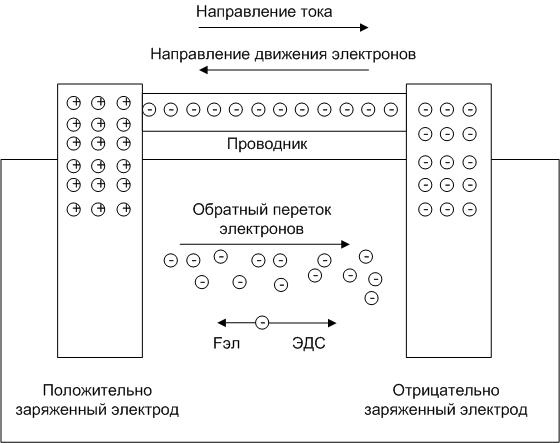
В чем суть ЭДС: единица измерения, виды и формулы для расчета

Перенос зарядов посредством ЭДС

Можно провести аналогию с водой. Если есть два бассейна, один из которых находится выше другого, то вода может перетекать из верхнего водоема в нижний. Но как только запас воды закончится, переток прекратится. Чтобы он продолжался, надо воду из нижнего бассейна перекачивать обратно в верхний (например, с помощью насоса).

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Необходимость наличия ЭДС на примере перетока воды

ЭДС обозначается греческой буквой ε (эпсилон), а иногда E. Измеряется ЭДС, как и напряжение, в вольтах (1 В). Понятие электродвижущей силы является не очень удачным – сила не измеряется в вольтах. Но этот термин укоренился и широко применяется.

Из-за сходства единиц измерения часто происходит путаница ЭДС и напряжения. Эти термины регулярно подменяются друг с другом. В некоторых случаях действительно принципиальной разницы нет, но в целом эти понятия различны.

В видео простыми словами объясняется чем отличаются ЭДС и напряжение

Где и как образуется электродвижущая сила

Электродвижущая сила образуется в источнике питания. Это необходимое условие существования разности потенциалов на выходных клеммах такого источника. Образовываться ЭДС может по-разному, в зависимости от устройства источника.

Виды ЭДС

Электродвижущая сила может быть различной природы (но всегда неэлектрической). В зависимости от типа источника питания ЭДС может быть:

  • фотоэлектрического характера – возникает в полупроводниковых переходах при облучении видимым светом или ультрафиолетом (на этом эффекте основана работа солнечных батарей);
  • электрохимической природы – всем известные гальванические элементы и аккумуляторы;
  • термоэлектрической ЭДС – возникает при разности температур между холодным и горячим спаем металлов (термопары для генерации электроэнергии и измерения температуры);
  • пьезоэлектрической природы (возникает при деформации некоторых материалов) – применяется в пьезозажигалках;
  • ЭДС электромагнитного характера – генераторы электростанций, автомобилей и т.п.

В технике встречаются и некоторые другие виды ЭДС, но реже.

Законы и формулы

Электродвижущая сила совершает работу по переносу заряда, а движущийся заряд представляет собой электрический ток/ Этот ток равен I=qt, где q – заряд, перенесенный полем за время t. За это время поле совершает работу A=ε*q= ε*I*t.

Можно определить ЭДС, как отношение работы по переносу заряда к величине этого заряда:

ε=A/q=A/(I*t)

ЭДС аккумуляторной батареи

ЭДС аккумуляторной батареи определяется типом электрохимических реакций, протекающих внутри элемента. Для различных технологий батарей наибольшая электродвижущая сила составит:

  1. Свинцово-кислотные элементы – 2,17 вольта.
  2. Никель-кадмиевые батареи – 1,37 вольта.
  3. Никель-металлогидридные элементы – 1,37 вольта.
  4. Щелочные аккумуляторы – 1,45 вольта.
  5. Литий-ионные элементы – 4,2 вольта.

Электродвижущая сила химических источников тока не зависит от размеров и площади пластин. Чтобы повысить выходное напряжение, единичные аккумуляторы соединяют в батареи последовательно.

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Последовательно соединенные элементы автомобильной батареи

ЭДС индукции

Основной источник получения электроэнергии на Земле – генераторы постоянного и переменного тока. Их принцип действия основан на создании ЭДС индукции.

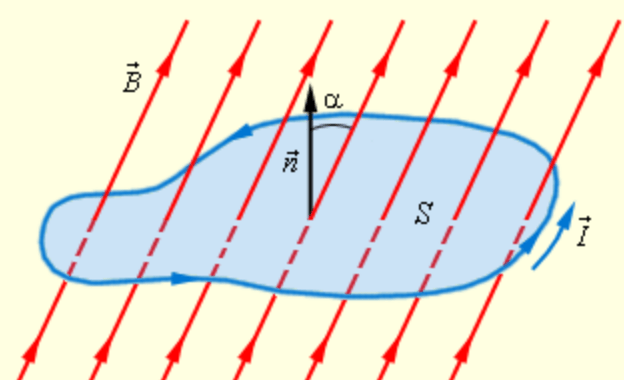
Если замкнутый контур находится в магнитном поле, и его пронизывает магнитный поток Ф, и этот поток изменяется во времени (по направлению или по величине), то в контуре возникает ЭДС. Ее величина равна:

ε=∆Ф/∆t, где Ф – магнитный поток, а t – время его изменения.

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Ток в замкнутом контуре, вызываемый ЭДС индукции под действием внешнего магнитного поля

В свою очередь магнитный поток зависит от величины магнитной индукции и площади поверхности, охватываемой контуром. Следовательно, чтобы увеличить ЭДС, надо усиливать магнитное поле (повышением тока возбуждения), или увеличивать площадь витка (при разработке или изготовлении генератора), или заставить магнитный поток изменяться быстрее (например, увеличивая скорость вращения ротора генератора). Каждый путь имеет определенные технические ограничения, поэтому в генераторах делают большое количество витков, соединяя их последовательно. При этом электродвижущие силы всех контуров складываются.

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Статор автомобильного генератора – витки соединяются последовательно

Внутреннее сопротивление источника ЭДС

Пусть имеется источник тока — например, аккумулятор — с напряжением на разомкнутых клеммах (в отсутствие нагрузки) 12 вольт. Если его нагрузить на сопротивление в 5 Ом, напряжение на клеммах упадет (например, до 11,5 вольт). Если нагрузить аккумулятор на сопротивление 1 Ом, на его выходных терминалах напряжение снизится до 9,86 вольт.

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Снижение выходного напряжения аккумулятора при уменьшении сопротивления нагрузки

Это явление легко объяснить, если ввести понятие внутреннего сопротивления источника питания. При разделении зарядов они движутся к соответствующим полюсам, но при этом взаимодействуют с кристаллической решеткой вещества, с ионами электролитов и отдают часть своей энергии. Движение носителей заряда замедляется, ток уменьшается, его ограничивает внутреннее сопротивление источника.

Это сопротивление включается последовательно с нагрузкой, и часть выходного напряжения падает на нем. Чем меньше сопротивление нагрузки, тем больше ток, тем больше потеря напряжения на внутреннем сопротивлении источника.

Внутреннее сопротивление определяется его конструкцией и типом ЭДС. Например, в аккумуляторе внутреннее сопротивление зависит от электрохимических реакций, протекающих в источнике тока.

В чем суть ЭДС: единица измерения, виды и формулы для расчета

Внутреннее сопротивление в виде резистора внутри источника тока

Для анализа электрических цепей внутреннее сопротивление рисуется на схеме в виде резистора, подключенного внутри источника параллельно его выходным клеммам. На самом деле, конечно, никакого резистора там нет, но это удобно для рассмотрения процессов, протекающих в цепи.

Для наглядности рекомендуем видео-урок.

Закон Ома для полной цепи

Один из фундаментальных законов электротехники – закон Ома для участка цепи. Согласно ему, ток на участке цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению.

Ток в полной цепи, в которую кроме нагрузки входит еще и источник, определяется величиной ЭДС, приложенной к внутреннему сопротивлению r и сопротивлению внешней нагрузки R, включенными последовательно. Общее значение сопротивления равно r+R. Следовательно, ток определяется соотношением I=ε/(R+r).

Как найти мощность ЭДС

Идеальный источник имеет нулевое внутреннее сопротивление. В нем напряжение под нагрузкой не уменьшается и всегда равно ЭДС. На практике таких источников не бывает.

Согласно закону Ома для полной цепи, формула ЭДС источника выглядит, как ε=I*R+I*r (в таком виде формулируется второй закон Кирхгофа). В этом выражении:

  • I*R=Uвнеш – напряжение на внешней нагрузке;
  • i*r=Uвнутр – падение напряжения на внутреннем сопротивлении источника.

Если источник идеален, то r=0 и вся ЭДС прикладывается к нагрузке. Чем выше r и выше ток, тем меньше напряжения достается потребителю, тем меньшая мощность выделяется на нем. Отсюда очевидно, что с ростом внутреннего сопротивления r, при равном токе, снижается напряжение на внешней нагрузке.

Внутреннее сопротивление источника можно рассчитать по результатам измерений напряжения на терминалах источника ЭДС по итогам двух замеров. Для этого надо воспользоваться законом Ома для полной цепи. Так, в рассмотренном примере, в первом случае падение напряжения на резисторе в 5 Ом составляет 11,5 вольт. Тогда можно найти ток в цепи по формуле:

I=U/R=11,5/5=2,3 А.

Выражение для ЭДС примет вид:

ε= 2,3*5+2,3*r=11,5+2,3*r.

Для второго замера на сопротивлении 1 Ом ток составит:

I=U/R=9,86/1=9,86 ампер

Следовательно,

ε= 9,86 *1+9,86 *r=9,86 +9,86 *r.

Левые части уравнений равны, тогда можно приравнять правые:

11,5+2,3*r=9,86 +9,86 *r

Путем несложных вычислений получается, что r=0,217 Ом. Если источник имеет меньшее внутреннее сопротивление, то при подключении той же нагрузки на ней будет большее напряжение. Напряжение на разомкнутых клеммах (на холостом ходу) в отсутствие ток будет примерно равно значению величины ЭДС. Таким образом, чем меньше внутреннее сопротивление, тем большее напряжение способен выдавать источник в нагрузку и тем больше мощность ЭДС.

Если же идеальный источник тока замкнуть накоротко, ток короткого замыкания будет бесконечным, так как R=r=0. На самом деле этого не происходит – в реальном источнике ток КЗ при R=0 ограничивается внутренним сопротивлением r.

Электродвижущая сила является одним из основополагающих понятий в физике. Ее суть и значение надо четко осознавать, в противном случае дальнейшее освоение электротехники будет затруднено.

Источник

Макеты страниц

Для приближенного вычисления величины ем удобно пользоваться следующим определением. Машинное эпсилон — это минимальное из представимых на ЭВМ чисел для которых

Величину ем можно оценить непосредственно в ходе вычислительного процесса. Для этого достаточно включить в программу фрагмент, реализующий следующий метод. Полагая следует вычислять последовательно проверяя каждый раз выполнение неравенства Как только при некотором окажется, что следует положить и перейти к следующему этапу вычислений. Хотя полученное таким способом значение может отличаться от в 2 раза, обычно оно используется так, что эта погрешность не имеет значения.

Пример 2.19. Покажем, что машинное эпсилон для ЭВМ из примера 2.17. В самом деле, и после округления имеем Если же к единице добавить любое положительное то в седьмом разряде результата будет стоять нуль и после округления получим

Всюду в дальнейшем, приводя конкретные числовые примеры, мы откажемся от использования двоичной арифметики. Десятичная арифметика привычнее, а основные закономерности поведения ошибок округления не зависят от основания используемой системы. В большинстве расчетов, которые будут приведены для иллюстрации поведения ошибок округления, имитируется выполнение вычислений на гипотетической вычислительной машине, имеющей десятичных разрядов мантиссы и производящей округление по дополнению. Будем называть эту машину -разрядной десятичной ЭВМ. Для нее так что по точности она сравнима с компьютером типа IBM PC (при вычислениях на ФОРТРАНЕ с обычной точностью).

Источник

Содержание

  1. Расчет емкости конденсатора
  2. Тема: Как рассчитать параметры воздушного конденсатора ?
  3. Как рассчитать параметры воздушного конденсатора ?
  4. Формула емкости конденсатора, С
  5. От чего зависит емкость и заряд конденсатора
  6. Сопротивления конденсатора в зависимости от
  7. Частоты и сдвига фаз
  8. Номинала конденсатора
  9. Видео
  10. Формулы для вычисления
  11. Электрической ёмкости в фарадах, посредством математических выражений
  12. Ёмкости конденсатора в зависимости от диэлектрической проницаемости среды, заполняющей пространство между его пластинами
  13. Формула электрической емкости цилиндрического конденсатора
  14. Физика ёмкостных характеристик
  15. Практические измерения
  16. Конденсаторы постоянной и переменной емкости
  17. Виды конденсаторов
  18. Электроемкость плоского конденсатора
  19. Цилиндрический конденсатор
  20. Примеры решения задач по теме Емкость конденсатора

Расчет емкости конденсатора

Емкость C есть способность конденсатора принять (накопить и удержать) количество электричества Q в ампер-секундах или заряд Q в кулонах. Если сообщить какому-либо телу, например шару, электрический заряд (количество электричества) Q, то электроскоп, включенный между этим телом и землей, покажет напряжение U (рис. 1). Это напряжение пропорционально заряду и зависит также от формы и размеров тела.

Зависимость между зарядом Q и напряжением U выражается формулой Q=C∙U.

Постоянная пропорциональности C называется емкостью тела. В случае, если тело имеет форму шара, емкость тела пропорциональна радиусу шара r.

Единицей измерения емкости является фарада (Ф).

Емкостью 1 Ф обладает тело, когда при заряде 1 к между ним и землей получается напряжение 1 В. Фарада – очень большая единица измерения, а потому на практике используют более мелкие единицы: микрофарады (мкФ), нанофарады (нФ) и пикофарады (пФ).

Эти единицы связаны следующими соотношениями: 1 Ф =10^6 мкФ; 1 мкФ =10^6 пФ; 1 нФ =10^3 пФ.

Емкость шара радиусом 1 см равна 1,1 пФ.

Накапливать заряд может не только изолированное тело, но и специальное устройство, называемое конденсатором. Конденсатор состоит из двух или более пластин (обкладок), которые разделены диэлектриком (изоляцией).

На рис. 2 показана схема с источником постоянного тока, включенным на конденсатор. При включении на правой пластине конденсатора образуется положительный заряд +Q, а на левой пластине отрицательный заряд –Q. Во время заряда конденсатора по цепи протекает ток, который после окончания заряда прекращается; тогда напряжение на конденсаторе будет равно э. д. с. источника U. Заряд на обкладке конденсатора, напряжение и емкость связаны соотношением Q=C∙U. В диэлектрике конденсатора при этом образуется электростатическое поле.

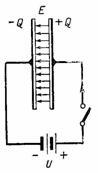
Емкость конденсатора с диэлектриком из воздуха можно подсчитать по формуле C=S/(4∙π∙d)∙1,11, пФ, где S – площадь одной обкладки, см2; d – расстояние между обкладками, см; C – емкость конденсатора, пФ.

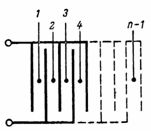
Емкость конденсатора, состоящего из n пластин (рис. 3), равна: C=(n-1)∙ S/(4∙π∙d)∙1,11, пФ.

Если пространство между пластинами заполнить другим диэлектриком – например бумагой, емкость конденсатора увеличится в ε раз. При применении бумажной изоляции емкость увеличится в 3 раза, при слюдяной изоляции – в 5–8 раз, при стеклянной – в 7 раз и т. д. Величина ε называется диэлектрической проницаемостью диэлектрика.

Общая формула для определения емкости конденсатора с диэлектрической проницаемостью ε (эпсилон) имеет вид: C=ε∙S/(4∙π∙d)∙1,11, пФ.

Эта формула удобна для расчетов небольших переменных конденсаторов для радиоприемников. Эта же формула может быть представлена в виде: C=(ε_0∙ε∙S)/d, где ε_0 – диэлектрическая постоянная, или диэлектрическая проницаемость, вакуума (ε_0=8,859∙10^(-12) Ф/м); ε – диэлектрическая проницаемость диэлектрика.

В этой формуле размеры подставляются в метрах, а емкость получается в фарадах.

1. Какую емкость имеет планета Земля, радиус которой r=6378 км?

Так как емкость шара радиусом 1 см равна 1,11 пФ, то емкость Земли равна: C=637,8∙10^6∙1,11=707,95∙10^6 пФ =708 мкФ. (Емкость шара, равного по величине нашей планете, сравнительно невелика. Такую емкость имеют небольшие по размерам электролитические конденсаторы).

2. Определить емкость конденсатора, состоящего из двух пластин, каждая из которых имеет площадь S=120 см 2 .

Пластины разделены слоем воздуха толщиной d=0,5 см, C=S/(4∙π∙d)∙1,11= (120∙1,11)/(4∙π∙0,5)=21,20 пФ.

3. Определить емкость конденсатора с данными, указанными в предыдущем примере, если пространство между пластинами будет заполнено парафинированной бумагой с диэлектрической проницаемостью ε=4, стеклом (ε=7), электротехническим картоном (ε=2), слюдой (ε=8).

Конденсатор с парафинированной бумагой имеет емкость C=ε∙(S∙1,11)/(4∙π∙d)=4∙21,2=84,8 пФ.

Емкость конденсатора со стеклом C=7∙21,2=148,4 пФ.

Емкость конденсатора с картоном C=2∙21,2=42,3 пФ.

Емкость конденсатора со слюдой C=8∙21,2=169,6 пФ.

4. Какова емкость воздушного поворотного конденсатора для радиоприемника, состоящего из 20 пластин площадью 20 см2, если расстояние между пластинами 0,06 см (рис. 149)?

Конденсатор, изображенный на рис. 3, состоит из отдельных простейших конденсаторов с двумя обкладками, число которых равно n-1.

5. Бумажный конденсатор емкостью C=2 мкФ состоит из двух полос станиоля C и двух полос диэлектрика из парафинированной бумаги Б с диэлектрической проницаемостью ε=6. Толщина парафинированной бумаги d=0,1 мм. Сложенные полосы сворачиваются в рулон, от станиолевых обкладок делаются выводы. Определить длину станиолевой полосы конденсатора, если ее ширина 4 см (рис. 4).

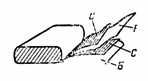
Сначала определим площадь S одной полосы по формуле C=ε∙S/(4∙π∙d)∙1,11, откуда S=(C∙4∙π∙d)/(ε∙1,11)=(2∙4∙π∙0,01∙10^6)/(6∙1,11); S=2000000/(6∙1,11)∙4∙π∙0,01=37680 см2.

Длина каждой полосы l=37680/4=9420 см =94,2 м.

Телеграмм канал для тех, кто каждый день хочет узнавать новое и интересное: Школа для электрика

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Тема: Как рассчитать параметры воздушного конденсатора ?

Обратные ссылки
Опции темы

Как рассчитать параметры воздушного конденсатора ?

Если все знают, как конденсатор пропускает ток, то может быть они мне помогут рассчитать параметры воздушного конденсатора — бабочки? Требуется найти максимальную и минимальную емкость, а также узнать напряжение пробоя.

1) Максимальную емкость можно определить по формуле показанной на втором изображении (уравнение международной системы измерения СИ)
S – площадь поверхности одной пластины (меньшей, если они не равны)
d – расстояние между пластинами
E – относительная диэлектрическая проницаемость среды между пластинами (для воздуха численно равна одному)
E0 — Что это такое, кто подскажет.

б. Или по формуле приведенной на третьем изображении с необъясненным коэффициентом 1.8.

в. Уравнение нахождения максимальной емкости по гауссовой системе (СГС). Рисунок четыре.

г. Заряд конденсатора, формула на пятом изображении.

2) Как определить минимальную емкость? Как я себе представляю, если роторные и статорные пластины разведены, то связь между ними отсутствует и тогда следует учесть только площадь статорных пластин и расстояние между ними, а рассчет будет выполняться по той же формуле, что и для максимальной емкости?

3) Чтобы узнать напряжение пробоя надо знать параметры диэлектрической среды, в данном случае воздуха. Наиболее важный параметр диэлектрика — это электрическая прочность. По данной ссылке — http://sermir.narod.ru/lec/lect10.htm с названием «лекции по курсу Электротехнические материалы» находим такую строчку — «Воздух при нормальных условиях имеет электрическую прочность 30 кВ/см.«

Напряженность поля плоского конденсатора. Шестое изображение — уравнение системы СИ, седьмое изображение — уравнение системы СГС.

Последний раз редактировалось Neo; 09.01.2009 в 18:10 .

Источник

Формула емкости конденсатора, С

От чего зависит емкость и заряд конденсатора

Емкость конденсатора это физическая величина по которой производится оценка его возможностей выполнять свои функциональные задачи.

Практическое значение емкости выражается в способности электрического устройства к накоплению заряда.

Величина напряжения на пластинах в прямой пропорции влияет на количественные характеристики заряда на обкладках. Формула определения емкости выглядит как

где С — емкость конденсатора,

q — означает количество заряда на одной из пластин,

U — разница потенциалов на обкладках. Приведенная формула расчета имеет в большей степени теоретический характер.

Существует иное определение емкости, которое полезнее в практическом смысле.

В формуле C = єS/d обозначена ее связь с площадью S обкладок, расстоянием между пластинами d и свойствами диэлектрика є.

Из формулы следует, что чем больше площадь обкладок, тем больший заряд может на них разместиться и чем больше расстояние между пластинами, тем слабее заряженные частицы будут притягиваться друг к другу, увеличивая их шансы покинуть обкладку.

Максимальная диэлектрическая проницаемость материала, расположенного между пластинами, увеличивает емкость конденсатора без изменения габаритных характеристик.

Сопротивления конденсатора в зависимости от

Сопротивление конденсатора зависит от частоты подаваемого на него напряжения и показателя емкости.

Частоты и сдвига фаз

Устройство накопления зарядов одинаковой емкости на разных частотах оказывает различный уровень сопротивления. Оно растет или уменьшается.

При повышении частоты входного напряжения сопротивление (его также называют емкостным) уменьшается.

На низких частотах имеется в наличии сдвиг по фазе входного напряжения и напряжения на нагрузке.

С увеличением частоты сдвиг по фазе уменьшается.

При достижении частоты определенного уровня фазовый сдвиг стремиться к нулю.

где ω — круговая частота, равная произведению 2πf,

С—емкость цепи в фарадах.

Номинала конденсатора

Емкость конденсатора влияет на процесс зарядки и разрядки при прохождении через него переменного тока.

Устройство с меньшей емкостью будет быстрее отдавать заряд и вновь заряжаться.

Сопротивление переменному току будет выше, чем при медленной зарядке и разрядке.

Отсюда вывод: емкостное сопротивление находится в обратной зависимости от номинала конденсатора.

Видео

Формулы для вычисления

Электрической ёмкости в фарадах, посредством математических выражений

Ёмкость, которую может накапливать и хранить конденсатор, как потенциальную электрическую энергию – величина постоянная. Она пропорциональна заряду и обратно пропорциональна приложенному напряжению. Математическое выражение фарада выглядит так:

  • C – ёмкость конденсатора,
  • Q – заряд,
  • U – приложенное напряжение.

Из приведённого выражения следует, что, изменяя прикладываемое напряжение, можно регулировать величину самого заряда.

Единица измерения электрической ёмкости – фарад – может выражаться (рассчитываться) и через иные единицы измерения, действующие в системе СИ:

Здесь: F – фарад, C – кулон, V – вольт, A – ампер, s – секунда, J – джоуль, N – ньютон, m – метр, W – ватт, kg – килограмм, Ω – ом, Hz – герц, H – генри.

Ёмкости конденсатора в зависимости от диэлектрической проницаемости среды, заполняющей пространство между его пластинами

Диэлектрическая проницаемость среды характеризует изоляционные свойства материала. В нашем случае – изолятора, определяющего ёмкость конденсатора. Из приведённых выше формул для расчёта ёмкостей плоского, сферического и цилиндрического конденсаторов видно, что ёмкость всегда прямо пропорциональна величине проницаемости используемого диэлектрического материала – ε.

Из практических соображений при расчёте ёмкостей конденсаторов употребляется относительная диэлектрическая проницаемость, равная:

  • 3-10 для стекла;
  • 5-7 для слюды;
  • 2,5-3,5 для бумаги;
  • 1,0006 для воздуха.

Формула электрической емкости цилиндрического конденсатора

Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляется как:

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.

Физика ёмкостных характеристик

Устройства, обладающие способностью хранения энергии в форме электрического заряда и производящие при этом разность потенциалов, называют конденсаторами. В простейшем виде они состоят из двух или более параллельных проводящих пластин, находящихся на небольшом расстоянии друг от друга, но электрически разделённых либо воздухом, либо каким-либо другим изоляционным материалом, например, вощёной бумагой, слюдой, керамикой, пластмассой или специальным гелем.

Вам это будет интересно Принцип работы, назначение и сферы применения триггеров

Практические измерения

Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.

Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.

Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.

Вам это будет интересно Устройство и применение резистора в электрической цепи

Измерение емкости конденсаторов на плате. Возможно ли это?

Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.

Конденсаторы постоянной и переменной емкости

Эра накопителей электричества началась с воздушных конденсаторов. Благодаря плоскому конденсатору с большой площадью обкладок физики смогли понять, как взаимная емкость регулируется площадями пластин, что позволило им создать конденсаторы с переменной емкостью (см. рис. 5).

Рис. 5. Конденсатор переменной емкости

Идея изменения емкости состояла в том, чтобы путем поворота плоской обкладки изменять площадь поверхности, которая располагается напротив другой пластины. Если обкладки располагались точно друг против друга, то напряженность поля между ними была максимальной. При смещении одной из пластин на некоторый угол, напряженность уменьшалась, что приводило к изменению емкости. Таким образом, можно было плавно управлять накопительной способностью конденсатора.

Детали с переменной емкостью нашли применение в первых радиоприемниках для поиска частоты нужной станции. Данный принцип используется по сегодняшний день в различных аналоговых электрических схемах.

Большую популярность приобрели электролитические конденсаторы. В качестве одной из обкладок у них используется электролит, обладающий высокими показателями диэлектрической проницаемости. Благодаря диэлектрическим свойствам электролитов такие конденсаторы обладают большими емкостями.

Главные их преимущества электролитического конденсатора:

  • высокие показатели емкости при малом объеме;
  • применение в цепях с постоянным током.

Недостатки:

  • необходимо соблюдать полярность;
  • ограниченный срок службы;
  • чувствительность к повышенным напряжениям.

Высокую электрическую прочность имеют плоские конденсаторы, у которых в качестве диэлектрического материала применяется керамика. Они используются в цепях с переменным током и выдерживают большие напряжения.

Сегодня промышленность поставляет на рынок множество конденсаторов различных типов, с высокими показателями проницаемости диэлектриков.

Конденсаторы различных типов

Виды конденсаторов

Особенность электроемкости в том, что она зависит от формы проводника. Для каждого вида проводников есть своя формула расчета электроемкости.

Проще всего вычислить электроемкость плоского конденсатора. Плоский конденсатор состоит из двух металлических пластин, между которыми помещают диэлектрическое вещество.

Электроемкость плоского конденсатора

— относительная диэлектрическая проницаемость среды [—]

— площадь пластин [м 2 ]

— расстояние между пластинами [м]

Самый популярный конденсатор — цилиндрический. Он состоит из двух металлических цилиндров, вложенных друг в друга, и диэлектрика, которым заполнено пространство между ними. Рассмотрим формулу электроемкости такого конденсатора.

Электроемкость цилиндрического конденсатора

— относительная диэлектрическая проницаемость среды [—]

— длина цилиндров [м]

— радиусы цилиндров [м]

— функция натурального логарифма, которая зависит от радиусов цилиндров

Сферический конденсатор состоит из двух проводящих сфер, вложенных друг в друга, и непроводящей жидкости, которой заполнено пространство между ними.

Электроемкость сферического конденсатора

— относительная диэлектрическая проницаемость среды [—]

Подытожим все, что узнали, на картинке-шпаргалке:

Электроемкость плоского конденсатора

Плоским конденсатором обычно называют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Благодаря простоте конструкции такого конденсатора легко рассчитывать его емкость и получать значения, подтверждаемые опытами. Для этого достаточно знать его геометрические параметры и электрические свойства диэлектрика между его пластинами. Зависимость электроемкости плоского конденсатора от указанных параметров можно исследовать в школьной лаборатории.

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равняется:

C = 2 πεε l ln R 2 R 1 , где l — высота цилиндров, R 1 и R 2 — радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3 .

Важной характеристикой конденсаторов считается пробивное напряжение — напряжение, при котором происходит электрический разряд через слой диэлектрика.

U m a x находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.

Примеры решения задач по теме Емкость конденсатора

Задание Какова электрическая емкость плоского двуслойного конденсатора? Один из слоев диэлектрика – фарфор с толщиной =2мм; второй слой – эбонит ( мм). Площадь пластин конденсатора равна 0,01 м2. Решение Для решения этой задачи проще всего применить формулу для расчета емкости слоистого плоского конденсатора, учитывая, что мы имеем всего два слоя: Перед тем, как провести расчет электрической емкости, в справочниках найдем диэлектрические проницаемости веществ, которые применены в нашем конденсаторе. Так, фарфор имеет диэлектрическую проницаемость равную ; диэлектрическая проницаемость эбонита равна Электрическая постоянная равна Толщину слоев диэлектрика переведем в метры. м; м. Получим: Ответ Ф

Задание Сферический конденсатор состоит из двух концентрических металлических сфер, имеющих радиусы м и м. Пространство между этими сферами заполняет парафин. Какова емкость этого конденсатора? Решение Сделаем рисунок. В качестве основы для решения задачи следует применить формулу для вычисления электрической емкости сферического конденсатора: Прежде чем перейти к вычислениям в справочнике следует найти диэлектрическую проницаемость парафина. Она равна приблизительно двум . Найдем величину C: Ответ С=46,68 пФ

Источник

Источник

Добавить комментарий