Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.
Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!
Что же давай приступим к изучению!
Построение эпюры продольных сил
В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.
Что такое эпюра?
Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.
Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.
Что такое продольная сила?
Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.
Расчёт эпюры продольных сил
Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.
То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.
Правило знаков для продольных сил
Правило знаков для продольных сил следующее:
- если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
- если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках
На первом участке сила F1 растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F1, также действует сила F2, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:
Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке
Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.
Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.
Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:
То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.
Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:
А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.
Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.
Построение эпюры нормальных напряжений
В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.
Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.
Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A1=2 см2, а на втором и третьем A2 = A3 = 4 см2.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.
Построение эпюры осевых перемещений поперечных сечений
Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.
Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:
Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.
Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:
А также удлинения (или укорочения) участка между расчетными сечениями:
В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).


Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.
Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.
Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину WD (т. к. значение WD — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.
Учёт распределённой нагрузки
А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил
На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:
Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:
Рассчитываем продольную силу на третьем участке:
Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений
Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений
Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче:


Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):


Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.



Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.
То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.
Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:


Отмечаем найденное значение на эпюре перемещений:


Пример решения задачи на расчет и построение эпюры перемещений сечений стержня при растяжении и сжатии.
Задача
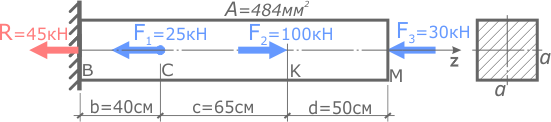
Рассчитать перемещения характерных сечений стержня постоянного сечения и построить их эпюру.
Другие примеры решений >
Помощь с решением задач >
Пример решения
Предыдущие пункты решения задачи:
- Расчет опорной реакции стержня,
- Расчет внутренних сил с построением эпюры,
- Подбор размеров поперечного сечения,
- Построение эпюры напряжений,
- Расчет деформаций участков стержня.
Под действием внешних сил стержень деформируется, вследствие чего его поперечные сечения перемещаются (в данном случае влево либо вправо).
Для расчета величины и направления перемещений воспользуемся соответствующей формулой:
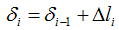
где δi – перемещение рассматриваемого сечения,
δi-1 – перемещение предыдущего сечения,
Δli – деформация участка расположенного между указанными сечениями (рассчитаны ранее).
По расчетной схеме видно, что сечение, расположенное в заделке (сечение B) перемещаться не может, следовательно, его перемещение равно нулю, т.е.
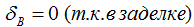
Перемещение остальных сечений рассчитывается последовательно от него.
Следующим рассматриваем сечение C.
Его перемещение δC будет складываться из двух составляющих:
- изменения дины участка BC,
- перемещения предыдущего сечения B с которым связан их общий участок.
Так как сечение В неподвижно, сечение C переместится ровно на ту величину, на которую растянется III участок BC.
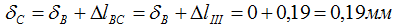
Перемещения остальных сечений рассчитываются аналогично:
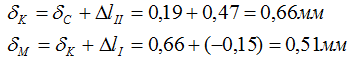
По этим данным строится эпюра перемещений δ. Для этого рассчитанные значения в выбранном масштабе откладываются от базовой линии под соответствующим сечением стержня.
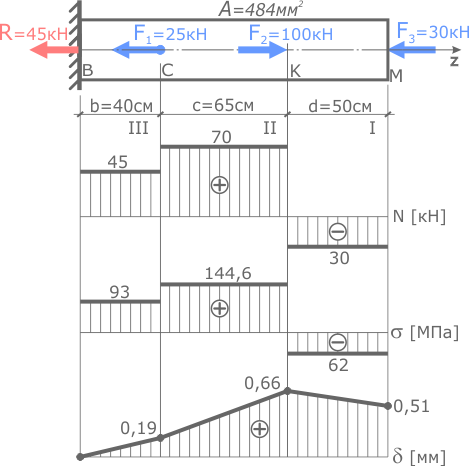
Эпюра наглядно показывает, что в результате деформации стержня наибольшее перемещение получило сечение K, которое переместилось вправо на 0,66 мм, а общая длина всего стержня увеличилась на 0,51 мм.
На участках, где нормальные напряжения положительны линия эпюры перемещений идет на возрастание (при условии, что заделка слева) и, наоборот. При этом, чем больше величина напряжений, тем больше угол наклона линии эпюры δ к базовой линии.
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее

И. В. Богомаз. Механика
При сжатии вдоль волокон древесина работает сначала упруго, затем упруго пластически (рис. 11.8, б). Разрушение происходит с образованием характерной складки (рис. 11.8, в) в результате потери местной устойчивости рядом волокон.
При сжатии поперек волокон до небольшой нагрузки (точка В) существует линейная зависимость между силой и деформацией. Затем деформации сильно увеличиваются, а нагрузка растет незначительно. В результате образец спрессовывается – уплотняется (рис. 11.8, г). Разрушающая нагрузка определяется условно и соответствует сжатию образца на 1/3 высоты. Сопротивление древесины сжатию вдоль волокон в 8–10 раз больше, чем поперек.
Коши Огюстен Луи
(1789–1857)
Английский ученый Роберт Гук в 1678 г. на основе экспериментов с проволокой и пружинами сформулировал закон «Ut tensio, sic vis», т. е. «Каково удлинение, такова и сила».
В 1822 г. французский математик Луи Коши ввел понятия «напряжение» и «деформация». В современном виде закон Гука форму-
лируется так: «Относительная продольная деформация прямо пропорциональна соответствующему нормальному напряжению»:
|
ε = |
σ |
. |
(11.8) |
|
E |
Перейдем к вычислению деформаций (удлинения) стержня. Со-
гласно (11.3), (11.4) и (11.9) имеем
ε = AA, σ = NA , ε = Eσ ,
откуда
E = σε = AN AA .
240

11. Осевое растяжение и сжатие в пределах упругости
|
Тогда абсолютное удлинение участка |
Aстержня длиной A при |
|||
|
A = const и E = const будет равно |
||||
|
A = |
NA |
, |
(11.9) |
|
|
EA |
||||
где EA – жесткость стержня при растяжении (сжатии).
Формула (11.9) выражает закон Гука для абсолютной продольной деформации, ее называют формулой жесткости при растяжении и сжатии.
Для бруса, имеющего несколько участков,
|
A = ∑ Ai . |
(11.10) |
|
Удлинение, связанное с температурным воздействием, |
|
|
A°t = A α t , |
(11.11) |
|
где α – коэффициент температурного расширения материала; |
t – из- |
|
менение температуры. |
При растяжении (сжатии) поперечные сечения стержня перемещаются в продольном направлении; перемещения поперечных сечений – это следствие деформации. При осевом нагружении бруса длиной A и с постоянной площадью поперечного сечения A перемещение
|
δ(zi) любого i-го сечения |
||||||||||
|
δ(z ) = zi |
N (z)dz |
= |
1 zi |
N (z)dz , |
(11.12) |
|||||
|
EA ∫ |
||||||||||
|
i |
∫ |
EA |
||||||||
|
0 |
0 |
|||||||||
|
а при одинаковой по длине силе N вычисляется по формуле |
||||||||||
|
δ(z ) = |
N zi |
. |
(11.12’) |
|||||||
|
i |
EA |
|||||||||
Эпюру перемещений δ(z) начинают строить от защемленного конца бруса, вычисляя перемещения в характерных сечениях (как правило, это границы участков).
241

И. В. Богомаз. Механика
Абсолютная деформация стержня при одинаковой по длине силе N ис постоянной площадью поперечного сечения A равна
|
A = |
N |
A dz |
i |
= |
NA |
. |
(11.13) |
|
E A ∫ |
E A |
||||||
|
0 |
В том случае, когда продольная сила и поперечное сечение не постоянные, то абсолютное удлинение участка длиной Ai вычисляет-
ся по формуле
|
Ai = |
Ai |
N( z )dz |
. |
(11.13’) |
|
|
∫ |
E A( z ) |
||||
|
0 |
Если стержень имеет k участков нагружения, то полное (абсолютное) удлинение всего стержня вычисляют как алгебраическую сумму удлинений отдельных участков по формуле
|
k |
k Ai |
N (zi )dzi |
|
|
A = ∑ |
Ai = ∑∫ |
||
|
. |
(11.14) |
||
|
E A(z ) |
|||
|
i=1 |
i=1 0 |
i i |
Общая формула для вычисления количества потенциальной энергии упругой деформации U, накопленной при растяжении и сжатии, имеет вид
|
k Ai |
N |
2 (z )dz |
i |
||
|
U = ∑∫ |
i |
. |
(11.15) |
||
|
2E A(z ) |
|||||
|
i=1 0 |
i |
Для стержня, растянутого или сжатого силами F, F′, приложенными по концам вдоль оси (рис. 11.1, а), потенциальную энергию можно вычислить как работу внешних сил:
Дифференциальная зависимость между перемещением i-го сечения δz и продольной силой N(z) имеет вид
|
dδz = |
1 |
N (z)dz . |
(11.17) |
|
|
E A(z) |
||||
242
11. Осевое растяжение и сжатие в пределах упругости
Зависимость (11.17) можно использовать для контроля эпюры δz: На участке, где Nz = const, перемещение δz изменяется по линей-
ному закону.
1.На участке, где N(z) изменяется по линейному закону, δz изменяется как квадратичная функция.
2.Если на участке N(z) > 0, то δz возрастает; если N(z) < 0, то δz убывает.
3.В сечении, где N(zO) = 0 (эпюра пересекает базисную линию), перемещение δz имеет экстремальное значение.
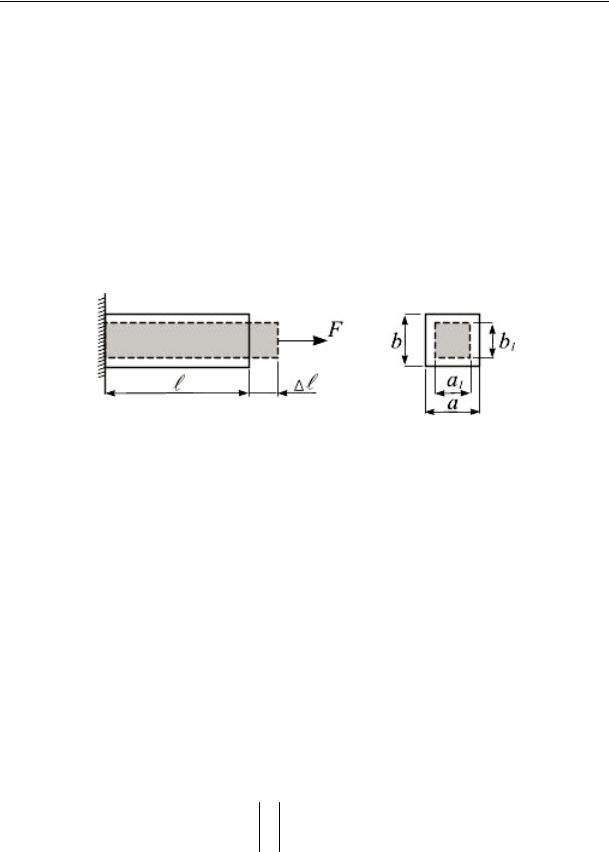
Растяжение (сжатие) сопровождается изменением поперечных размеров (рис. 11.9).
Рис. 11.9
Абсолютная поперечная деформация определяется как разность размеров после деформации и до нее:
Относительная поперечная деформация для изотропных материалов по всем направлениям одинакова.
ε′ = aa = bb .
Между поперечной и продольной относительными деформациями, которые всегда противоположны по знаку, в пределах закона Гука существует постоянное отношение
|
ν = |
ε′ |
′ |
|||
|
ε или ε |
= −νε, |
(11.18) |
|||
где v – коэффициент поперечной деформации (коэффициент Пуассона) – безразмерная величина, упругая постоянная материала, опреде-
243
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача. Для балки определить перемещения в т. А, В, С, D, подобрать сечение из двух швеллеров из условия прочности, проверить жесткость, показать изогнутую ось балки. Материал — сталь Ст3, допускаемое перемещение  .
.

- Определим опорные реакции.


Наносим значение опорных реакций на расчетную схему

2. Строим эпюру моментов от заданной нагрузки – грузовую эпюру МF.

Т.к. под равномерно распределенной нагрузкой линия параболическая кривая, то для её проведения потребуется дополнительная точка – поставим т.К в середине нагрузки.
![]()
Строим эпюру МF от заданной нагрузки.

3. Подберем сечение из двух швеллеров:

Подбираем 2 швеллера №33 см3.
![]()
Проверим прочность подобранного сечения.

Прочность обеспечена.
4. Определим перемещения в заданных точках. Снимаем с балки всю нагрузку. Для определения линейных перемещений (прогибов) прикладываем единичную силу (F=1), а для определения угловых перемещений — единичный момент ![]() .
.
Точки А и В – это опоры, и по граничным условиям в шарнирных опорах прогиб невозможен, а угловое перемещение присутствует. В точках С и D будут и линейные (прогибы), и угловые (углы поворота) перемещения.
Определим угловое перемещение в т.А. Прикладываем в А единичный момент (рис. б). Строим эп ![]() , определяем в ней необходимые ординаты. (рис. в).
, определяем в ней необходимые ординаты. (рис. в).
Ординаты эп.МF – все положительные, эп.![]() – тоже.
– тоже.

Перемещения будем определять методом Мора по формуле Симпсона.

Определим момент инерции Iх для сечения.
![]()
Модуль продольной упругости Е для Ст3 Е = 2·105 МПа = 2·108 кПа. Тогда:

Угол поворота φА получился положительным, это значит, что угол поворота сечения совпадает с направлением единичного момента.
Определим угол поворота φВ. (рис.г,д )


Теперь определим перемещения в т. С (линейное и угловое). Прикладываем единичную силу (рис. е), определяем опорные реакции и строим эп. ![]() от единичной силы (рис.ж).
от единичной силы (рис.ж).

Рассмотрим рис. е.

Строим эп. ![]() :
:
![]()
Определим прогиб в т. С.

Для определения угла поворота в т. С приложим единичный момент (рис. з), определим опорные реакции и построим эпюру единичных моментов (рис. и).

(знак “— “ говорит о том, что реакция RА направлена в обратную сторону. Показываем это на расчетной схеме – рис.з).
Строим эп. ![]() ,
, ![]()
Поскольку m=1 приложен в т. С пролета балки, то момент в т. С определим как от левых, так и от правых сил.
![]()
Определим прогиб в точке С.

(знак «-» говорит о том, что угол поворота направлен противоположно направлению единичного момента)
Аналогично определим линейное и угловое перемещения в т. D.
Определим уD . (рис. к).


Строим эп. ![]() (рис.л) :
(рис.л) :

Определим φD (рис. м):

Строим эп. ![]() — (рис.н).
— (рис.н).
Определим угол поворота:

(угол поворота направлен в сторону, противоположную единичному моменту).
Теперь покажем изогнутую ось балки (упругую линию), которой стала прямолинейная ось под действием нагрузки. Для этого зарисуем первоначальное положение оси и в масштабе отложим вычисленные перемещения (рис.о).

Проверим жесткость балки ![]() , где f – максимальный прогиб.
, где f – максимальный прогиб.

Максимальный прогиб ![]() — жесткость не обеспечена.
— жесткость не обеспечена.
Т.о. в данной задаче мы убедились в том, что не всегда сечения, подобранные из условия прочности (в данном случае – сечение из двух швеллеров) удовлетворяют условиям жесткости.
Задача. Определить горизонтальное перемещение свободного конца рамы по интегралу Мора

1. Составляем выражение изгибающего момента MF от действующей нагрузки.

2. Снимаем с балки все нагрузки, и в точке, где необходимо определить перемещение, прикладываем единичную силу (если определяем линейное перемещение) либо единичный момент (если определяем угловое перемещение) по направлению искомого перемещения. В нашей задаче прикладываем горизонтальную единичную силу. Составляем выражение изгибающего момента.

Определяем моменты от единичной нагрузки F=1

По интегралу Мора вычисляем горизонтальное перемещение:

Перемещение имеет положительное значение. Это значит, что оно соответствует направлению единичной силы.
Интеграл Мора, формула Мора. В криволинейном брусе определить горизонтальное перемещение точки А. Жесткость в пределах всей длины бруса постоянна. 
Ось бруса очерчена по параболе, уравнение которой:

Учитывая, что брус безраспорный и достаточно пологий (f/ι = 3/15 = 0,2), влиянием продольных и поперечных сил пренебрегаем. Поэтому для определения перемещения воспользуемся формулой:
 Так как жесткость EJ постоянна, то:
Так как жесткость EJ постоянна, то:
Составим выражение M1 для действительного состояния бруса (1-го состояния) (рис. а):
Снимаем с бруса все нагрузки и прикладываем в точке А горизонтальную единичную силу (2-е состояние) (рис. б). Составляем выражение для ![]() :
:
![]()
Вычисляем искомое перемещение в точке А:
Знак минус указывает на то, что перемещение точки А противоположно направлению единичной силы, т.е. это точка смещается по горизонтали влево.
Интеграл Мора, формула Мора.Определить угол поворота шарнирной опоры D для рамы с определенными опорными реакциями, Жесткости элементов указаны на расчетной схеме.

Составим выражение М1, используя схему системы в 1-м состоянии. М1 – функция внутреннего изгибающего момента на силовом участке для заданной балки или рамы от действия заданных нагрузок 1-го состояния.
Освобождаем раму от нагрузок, прикладываем единичный момент на опоре D, получаем систему второго состояния.
 Составляем выражения
Составляем выражения ![]() – это функция внутреннего изгибающего момента на силовом участке для вспомогательной системы 2- го состояния, нагруженной единичным усилием:
– это функция внутреннего изгибающего момента на силовом участке для вспомогательной системы 2- го состояния, нагруженной единичным усилием: Находим искомое перемещение — угол поворота по формуле (интегралу) Мора:
Находим искомое перемещение — угол поворота по формуле (интегралу) Мора:
 Значение угла поворота положительно, значит направление соответствует выбранному направлению единичного момента.
Значение угла поворота положительно, значит направление соответствует выбранному направлению единичного момента.
Интеграл Мора (формула Мора). Для рамы определить горизонтальное перемещение точки C. Жесткости элементов указаны на рисунке. Назовем заданную систему системой первого состояния. . Составляем для каждого элемента выражение М₁, пользуясь схемой 1-го состояния системы:
Назовем заданную систему системой первого состояния. . Составляем для каждого элемента выражение М₁, пользуясь схемой 1-го состояния системы:![]()
Снимаем с рамы все нагрузки и получим 2-е состояние рамы, приложив по направлению искомого перемещения горизонтальную единичную силу.  Составляем выражение единичных моментов
Составляем выражение единичных моментов ![]() :
:  . Вычисляем по формуле (интегралу) Мора искомое перемещение:
. Вычисляем по формуле (интегралу) Мора искомое перемещение:
Тогда получим:
Знак минус указывает, что направление перемещения противоположно направлению единичной силы.
Для стальной балки подобрать размеры поперечного сечения, состоящего из двух двутавров, на основе условия прочности по нормальным напряжениям, построить эпюры линейных и угловых перемещений. Дано: ![]()

Расчет опорных реакций и значений грузовой эпюры (эпюры изгибающих моментов) приводить не будем, покажем без расчетов. Итак, грузовая эпюра моментов:

При этом на эпюре М у значений изгибающих моментов отсутствуют знаки, указываются волокна, испытывающие сжатие. Как видно из эпюры, в опасном сечении: МС=Мmax=86,7кНм.
Подберем сечение из двух двутавров. Из условия прочности: 
Согласно сортаменту прокатной стали выбираем двутавр №27а, у которого Ix1=5500см3, h=27см. Фактическое значение осевого момента сопротивления всего сечения Wx=2Ix1/(h/2)=2·5500/(27/2)=815см3.
Вычисляем линейные и угловые перемещения сечения балки методом О.Мора, применяя формулу Симпсона. Выбор количества сечений, необходимого для построения эпюр линейных и угловых перемещений в балке, зависит от числа участков и характера эпюры изгибающих моментов. В рассматриваемой балке к таким можно отнести сечения А, B, C, D (принадлежат границам силовых участков) и сечения 1, 2, 3 – в середине участков (определение перемещений в этих сечениях повышает точность построения эпюр).
Сечение А. Как известно, линейное перемещение сечения в шарнирной опоре yA=0.
Для вычисления углового перемещения θа загружаем вспомогательную систему единичной парой сил -моментом, равным единице Уравнения равновесия
Уравнения равновесия
Решая уравнения равновесия, получим:

Определяем значения моментов в характерных сечениях
Участок АD: ![]()
В середине участка АВ значение изгибающего момента грузовой эпюры MF равно f=73,3·1- 80·12/2=33,3кНм
Определяем угловое перемещение сечения А по формуле Симпсона:
Угловое перемещение сечения А направлено против часовой стрелки (противоположно действию единичного момента).
Сечение В
Прикладываем в сечении В силу, равную единице, для определения линейного перемещения, и строим единичную эпюру моментов
Уравнения равновесия:
Из решения уравнений равновесия следует:

Определяем значения моментов в характерных сечениях:
Определяем линейное перемещение yВ.
Линейное перемещение yВ=3,65×10-3м направлено вверх (противоположно действию единичной силы).
Для определения углового перемещения в сечении В прикладываем единичный момент и строим единичную эпюру моментов.
В результате «перемножения» единичной эпюры и грузовой эпюры получим угловое перемещение:
Угловое перемещение направлено против часовой стрелки.
Сечение С.

Линейное перемещение:
Линейное перемещение yС=5,4 ×10-3 м направлено вверх.
Угловое перемещение:

Угловое перемещение направлено по часовой стрелке.
Сечение D. Линейное перемещение в данном сечении равно нулю.
Угловое перемещение:


Угловое перемещение направлено по часовой стрелке.
Дополнительные сечения:
Сечение 1 (z=0,5ℓ)


Линейное перемещение y1=1,34×10-3м направлено вверх;
Угловое перемещение:

Угловое перемещение направлено против часовой стрелки.
Аналогично строим единичные эпюры для сечения 2 (z=1,5ℓ) и сечения 3 (z=2,5ℓ),находим перемещения.
Применяя правило знаков для линейных перемещений вверх — плюс, вниз — минус, а для угловых перемещений против часовой стрелки — плюс, по часовой стрелке – минус, строим эпюры линейных и угловых перемещений y и θ.

Для балки определить максимальный прогиб и максимальный угол поворота.

Ввиду симметрии нагрузки опорные реакции А=В=ql/2
Дифференциальное уравнение изогнутой оси балки:

Интегрируем данное уравнение дважды. После первого интегрирования получаем уравнение углов поворота:
 (а)
(а)
После второго интегрирования получаем уравнение прогибов:
 (б)
(б)
Необходимо определить значение постоянных интегрирования — С и Д. Определим их из граничных условий. В сечениях А и В балка имеет шарнирные опоры, значит прогибы в них равны нулю. Следовательно, имеем граничные условия:
1) z = 0, y = 0.
2) z = l, y = 0.
Используем первое граничное условие: z = 0, y = 0.
Тогда из (б) имеем:
![]()
Второе граничное условие при z =l дает:
 , откуда:
, откуда:

Окончательно получаем.
Уравнение углов поворота:

Уравнение прогибов:

При  угол поворота
угол поворота ![]() равен нулю, а прогиб будет максимальным:
равен нулю, а прогиб будет максимальным:

Знак минус говорит о том, что при принятом положительном направлении оси вверх, прогиб будет направлен вниз.
Наибольшее значение угол поворота ![]() имеет на опорных сечениях, например, при
имеет на опорных сечениях, например, при
z = 0:

Знак минус говорит о том, что угол поворота при z = 0 направлен по часовой стрелке.
Для рамы требуется определить угол поворота сечения 1 и горизонтальное перемещение сечения 2.
Дано: L=8 м, F=2 кН, q=1 кН/м, h=6 м, моменты инерции I1=I, I2=2I

1. Определяем опорные реакции и строим грузовую эпюру:
а) Определяем опорные реакции:

Проверка сошлась. Вертикальные реакции определены верно. Для определения горизонтальных реакций нужно использовать свойство шарнира, а именно — записать уравнение моментов относительно шарнира от всех сил, расположенных с одной стороны рамы.

Проверка сошлась, значит, горизонтальные реакции определены верно.
б) Строим грузовую эпюру — эпюру от заданной нагрузки. Грузовую эпюру будем строить на растянутых волокнах.
Разбиваем раму на участки. На каждом участке намечаем сечения в начале и конце участка, а на участках с распределенной нагрузкой дополнительное сечение в середине. В каждом сечении определяем значение внутреннего изгибающего момента по правилу: изгибающий момент равен алгебраической сумме моментов всех внешних сил, расположенных с одной стороны от сечения, относительно центра этого сечения. Правило знаков для изгибающего момента: момент считается положительным, если он растягивает нижние волокна.

Строим грузовую эпюру.

2.Определяем угол поворота сечения (1)
а) Для того, чтобы определить угол поворота указанного сечения, нужно зарисовать исходную раму без внешней нагрузки и к заданному сечению приложить единичный момент.

Сначала определяем реакции:

Строим единичную эпюру моментов.


б) Определяем угол поворота по формуле Симпсона, подставив I1=I, I2=2I:

Знак « — » означает, что поворот сечения происходит против направления единичного момента, т.е. по часовой стрелке.
3. Определяем горизонтальное перемещение сечения (2).
а) Для того, чтобы определить горизонтальное перемещение в указанном сечении, нужно зарисовать исходную раму без внешней нагрузки и к заданному сечению приложить в горизонтальном направлении единичную силу.

Определяем реакции:

Строим единичную эпюру моментов


б) Определяем горизонтальное перемещение сечения (2) по формуле Симпсона:

Результат получился с «+», значит точка (2) перемещается по направлению единичной силы, т.е. вправо.
Для балки определить линейные и угловые перемещения в точках A, B, C, предварительно подобрав сечение двутавра из условия прочности.
Дано: a=2 м, b=4 м, с=3 м, F=20 кН, М=18 кНм, q=6 кН/м, σadm=160 МПа, Е=2 105 МПа



1) Вычерчиваем схему балки, определяем опорные реакции. В жёсткой заделке возникает 3 реакции — вертикальная и горизонтальная, а так же опорный момент. Поскольку горизонтальных нагрузок нет – соответствующая реакция равна нулю. Для того, чтобы найти реакции в точке E, составим уравнения равновесия.
∑Fy= 0 q7-F+RE=0
RE=-q7+F=-67+20=-22кН (знак говорит о том, что реакция направлена в обратную сторону, показываем это на схеме)
Найдем опорный момент в жесткой заделке, для чего решим уравнение моментов относительно любой выбранной точки.
∑MC: -ME-RE9-F6-q77/2-M=0
ME=-18-229+649/2=-18-198+147=-69кНм (знак говорит о том, что реакция направлена в обратную сторону, показываем это на схеме)
Далее требуется выполнить проверку правильности определения реакций, составив уравнение равновесия относительно любой точки, к примеру, точки Е, ∑MЕ = 0.
2) Строим грузовую эпюру MF– эпюру моментов от заданной нагрузки.
Для построения эпюр моментов найдем моменты в характерных точках. В точке В определяем моменты как от правых, так и от левых сил, поскольку в этой точке приложен момент.

Для построения эпюры момента на линии действия распределенной нагрузки (участки АВ и ВС) нам нужны дополнительные точки для построения кривой. Определим моменты в серединах этих участков. Это моменты в серединах участков АВ и ВС 15,34 кНм и 23,25кНм. Строим грузовую эпюру.
3) Для определения линейных и угловых перемещений в точке необходимо приложить в этой точке, в первом случае, единичную силу (F=1) и построить эпюру моментов, во втором случае, единичный момент (M=1) и построить эпюру моментов. Строим эпюры от единичных нагрузок для каждой точки – А, В и С.
4) Для нахождения перемещений мы используем формулу Симпсона.

где li – длина участка;
EIi – жесткость балки на участке;
MF – значения изгибающих моментов с грузовой эпюры, соответственно в начале, в середине и в конце участка;
![]() – значения изгибающих моментов с единичной эпюры, соответственно в начале, в середине и в конце участка.
– значения изгибающих моментов с единичной эпюры, соответственно в начале, в середине и в конце участка.
Если ординаты эпюр расположены с одной стороны от оси балки, то при перемножении учитывается знак «+», если с разных, то знак «-».
Если результат получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением соответствующего единичного силового фактора.
Рассмотрим применение формулы Симпсона на примере определения перемещений в точке А.
Определим прогиб, перемножив грузовую эпюру на эпюру от единичной силы.

Прогиб получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением единичной силы (направлено вверх).
Определим угол поворота, перемножив грузовую эпюру на эпюру от единичного момента.

Угол поворота получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением соответствующего единичного момента (направлен против часовой стрелки).
5) Для определения конкретных значений перемещений требуется подобрать сечение. Подберем сечение двутавра


где Mmax – это максимальный момент на грузовой эпюре моментов
Подбираем по сортаменту двутавр №30 с Wx=472см3 и Ix= 7080см4
6) Определяем перемещения в точках, раскрывая жесткость сечения: E – модуль продольной упругости материала или модуль Юнга (2 105 МПа), Jx – осевой момент инерции сечения
Прогиб в точке А (вверх)

Угол поворота (против часовой стрелки)

Если требуется построить изогнутую ось балки, то балка вычерчивается без нагрузки, и в точках откладываются прогибы в соответствующие стороны — строится плавная кривая – изогнутая ось балки.
Определить прогиб и угол поворота в сечении В

Сначала построим грузовую эпюру от заданной нагрузки. Площадь грузовой эпюры имеет криволинейное очертание и равна:

Теперь снимем с балки нагрузку и приложим в точке, где необходимо определить перемещение единичную силу для определения прогиба и единичный момент для определения угла поворота. Строим эпюры от единичных нагрузок.
Центр тяжести грузовой эпюры находится на расстоянии одной четверти (см. эпюру)
Ординаты единичных эпюр напротив центра тяжести грузовой эпюры :

Теперь по формуле правила Верещагина  определяем:
определяем:
сначала прогиб

затем угол поворота:

В знаменателе формулы – жесткость сечения.
