Эпюрами внутренних усилий в балках называют геометрические образы, применяемые для графического изображения изменения в элементе какого-либо силового фактора либо иных данных.
Примеры построения эпюр
Эпюры внутренних усилий (поперечных сил и изгибающих моментов) для простейших систем показаны на рисунке 3.1.
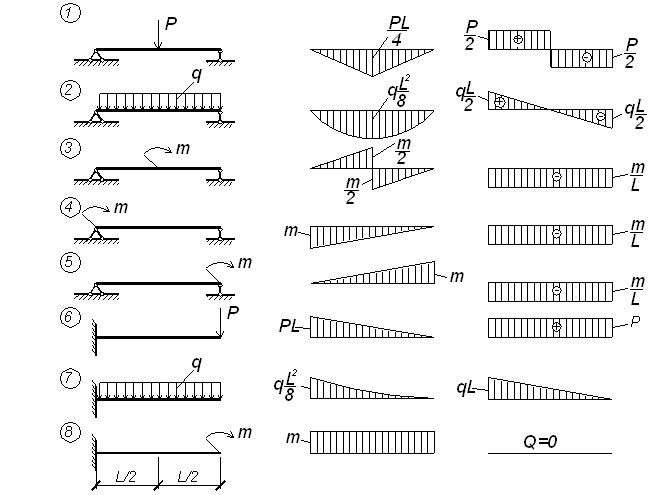
Рисунок 3.1 – Эпюры внутренних усилий для простейших балок
Отметим, что в строительной механике, на эпюре изгибающих моментов знак, как правило, не ставится, и в отличие от сопромата, она строится со стороны растянутых волокон.
Эпюры для однопролетных балок с консолями строят в следующем порядке:
- сначала строят эпюры на консолях, используя таблицы изгибающих моментов для консольных балок (рисунок 3.1), фиксируя при этом консольные моменты;
- отмечая опорные моменты, проводят так называемую линию опорных моментов. Это прямая, соединяющая ординаты моментов над опорами;
- на линию опорных моментов накладывают пролетную балочную эпюру (табличная эпюра М для однопролетной балки) от соответствующего вида загружения;
- все эпюры М строят со стороны растянутых волокон.
Между выражениями для изгибающего момента, поперечной силы и интенсивностью распределенной нагрузки в пределах расчетного силового участка существуют известные из курса “Сопротивление материалов” дифференциальные зависимости.
Они легко выводятся с помощью уравнений равновесия, составленных для вырезанного бесконечно малого элемента (рисунок 3.2):
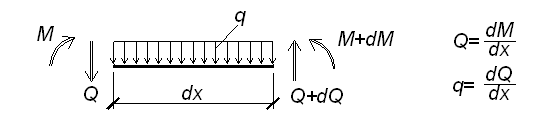
Рисунок 3.2 – Определение значений поперечной силы
Внутренние силы в основных типах элементов систем:
Понятие о расчетном силовом участке
Расчетным силовым участком называется участок элемента системы с постоянным законом изменения всех внутренних силовых факторов.
В расчетной практике силовые участки определяются их границами.
Граница силового участка − это место приложения какой-либо сосредоточенной нагрузки (силы или момента), начало или конец распределенной нагрузки, место изменения геометрии, механических характеристик конструкции, интенсивности распределенной нагрузки.
В курсе «Строительная механика» принята следующая последовательность определения внутренних усилий (построения эпюр).
Первоначально с помощью уравнений статики в требуемых сечениях определяются изгибающие моменты.
Далее посредством дифференциальной зависимости осуществляется переход к поперечным силам. Последние дают возможность оценить и продольные силы.
Построение эпюры моментов производится по силовым участкам. При этом за расчетный модуль принимается консольная балка (рисунок 3.3).
За начало (В) принимается тот конец силового участка, на котором все внутренние и внешние воздействия определены.
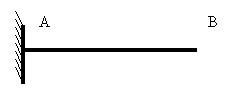
Рисунок 3.3 – Консольная балка
Они (воздействия) легко (принцип независимости действия сил) приводятся к алгебраической сумме результатов простейших воздействий.
При построении эпюр внутренних усилий в многопролетных балках, рамах и других конструкциях используются эпюры М и Q в простых однопролетных и консольных балках, которые чаще всего называют табличными эпюрами моментов и поперечных сил (рисунок 3.1).
Последовательность построения эпюр внутренних усилий М, Q, N в статически определимых системах:
1) Кинематический анализ. Напомним, что нас интересуют лишь геометрически неизменяемые системы с нулевым количеством степеней свободы и правильной расстановкой связей.
2) Определение опорных реакций и реакций связи. При этом используются уравнения равновесия, составленные как для всей системы в целом, так и для любого элемента или группы элементов.
3) Построение эпюры изгибающих моментов − М.
По эпюре изгибающих моментов с помощью дифференциальной зависимости Журавского строится эпюра поперечных сил (Q).
На участке с линейной эпюрой изгибающих моментов величина поперечной силы равна тангенсу угла наклона эпюры М.
Q = |tga| — где a угол наклона касательной на эпюре М к оси балки.
Знак Q определяется по направлению кратчайшего совмещения оси участка с эпюрой. Если оно происходит по направлению движения часовой стрелки, поперечную силу считают положительной.
Если же против часовой стрелки, то отрицательной.
При построении эпюры поперечных сил для участков с криволинейной (изменяющейся только по закону квадратной параболы) эпюрой изгибающих моментов пользуются следующей зависимостью:
Q = Qо + (Мпр – Мл)/L
где Qо − поперечная сила от внешней нагрузки, приложенной на рассматриваемый участок, определенная для балки на двух опорах пролета равного L;
Мп, Мл − алгебраические величины изгибающих моментов, соответственно на правом и левом торцах рассматриваемого участка.
Вышеуказанное выражение (3.1) легко получить самостоятельно (рисунок 3.4):
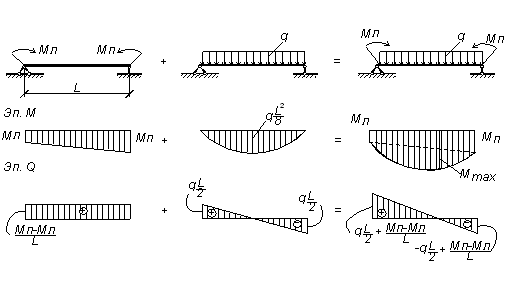
Рисунок 3.4 – Вывод выражения (3)
4) По эпюре поперечных сил строится эпюра продольных сил. При этом рассматривается равновесие всех узлов системы под действием внутренних (продольных и поперечных) и внешних (узловых) сил.
5) Проводится статическая проверка правильности построения эпюр М, Q, N.
Правила для проверки правильности построенных эпюр внутренних усилий:
а) На прямолинейном ненагруженном участке эпюра моментов прямолинейна.
б) В сечении, где приложен сосредоточенный внешний момент, эпюра получает скачок на величину этого момента (рисунок 3.5), а линии эпюры моментов примыкающие к скачку идут параллельно друг другу.
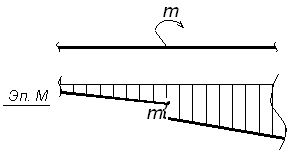
Рисунок 3.5 – Эпюра М на участке с приложенным сосредоточенным моментом
в) В точке приложения сосредоточенной внешней силы Р, перпендикулярной оси стержня, эпюра моментов имеет перелом, направленный острием в сторону действия силы (рисунок 3.6).
Изменение тангенсов углов наклона эпюры в точке ее перелома равно силе Р. На эпюре Q в этой точке — скачок на величину Р в направлении ее действия.
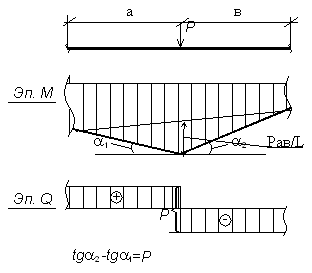
Рисунок 3.6 – Эпюра М на участке с приложенной сосредоточенной силой Р
г) На участке, где приложена равномерно распределенная нагрузка, эпюра моментов очерчена по параболе второй степени с выпуклостью в сторону действия нагрузки и со стрелкой равной q×L2/8 (рисунок 3.7).
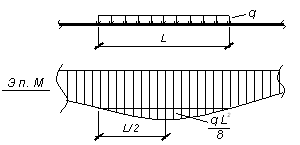
Рисунок 3.7 – Эпюра М на участке с равномерно распределенной нагрузкой
д) В сечениях, где нет сосредоточенной нагрузки, эпюра моментов не имеет перелома.
е) Поперечная сила в сечении стержня положительна, если она стремится вращать разделенные данным сечением части стержня по часовой стрелке (рисунок 3.8).
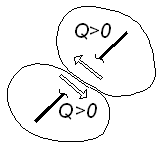
Рисунок 3.8 – Правило знаков для поперечной силы
Расчет внутренних усилий в рамах >
Примеры решения задач >
Эпюрой
называется
графическое изображение закона изменения
внутренних усилий по длине стержня.
Эпюры
внутренних усилий строят для того, что
бы определить опасные сечения стержня,
т.е. сечения, в которых внутренние усилия
достигают наибольших значений, поскольку
существует большая вероятность
наступления разрушения в этих сечениях.
2.1 Построение эпюры продольной силы
Под
действием внешних нагрузок, направленных
вдоль оси стержня, или нагрузок,
равнодействующая которых направлена
также вдоль продольной оси, в поперечных
сечениях возникает только один внутренний
силовой фактор – продольная
сила (N).
Такая деформация стержня называется
осевое
растяжение (сжатие).
Эпюрой
продольной силы N
называется графическое изображение
закона её изменения по длине бруса.
Правило знаков:
Растягивающая
продольная сила, т.е. направленная от
сечения, считается положительной, а
сжимающая, т.е. направленная к сечению
– отрицательной.

Рис.2.1
Правило знаков
Величина
и направление продольной силы в сечениях
стержня определяются с помощь метода
сечений (см.
п. 1.3) .
Продольная
сила в поперечных сечениях стержня
численно равна алгебраической сумме
проекций внешних сил на ось стержня,
приложенных к рассматриваемой отсеченной
части.
![]()
.
(2.1)
Порядок построения эпюры продольной силы (n)
1.
Изображается расчетная схема бруса с
указанием численных значений приложенных
нагрузок и геометрических размеров
бруса.
2.
Брус разбивается на участки, границами
которых являются точки приложения
сосредоточенных сил, а так же начало и
конец распределенной нагрузки.
3.
Для каждого участка из уравнения
равновесия записывается аналитическое
выражение продольной силы согласно
(2.1) и вычисляются все её значения,
необходимые для построения эпюры, обычно
в начале и конце участка.
4.
Проводится ось (база) эпюры, параллельно
оси бруса. Значения продольной силы для
каждого участка откладываются
перпендикулярно оси в масштабе.
Положительные значения выше оси,
отрицательные – ниже.
5.
На эпюре ставятся её знаки: «+» или «»,
она штрихуется прямыми параллельными
линиями, перпендикулярными оси.
6.
Проводится проверка правильности
построения эпюры.
Для
исключения ошибки при составлении
уравнения равновесия следует неизвестное
внутреннее усилие принимать всегда
положительным, так как знак усилия,
полученный из решения, позволяет
установить, правилен ли был сделан выбор
направления силы N,
и какой вид деформации при этом возникает
– растяжение, если значение N
положительно, или сжатие, если отрицательно.
Пример
№2.1: Построить
эпюру продольной силы для бруса жестко
закрепленного левым концом, на который
действуют осевые силы F1
, F2
, F3
(рис 2.2).

Рис.
2.2 Расчетная схема бруса
Внешние
осевые нагрузки делят брус на три
участка. Пронумеруем участки со свободного
конца. Определим величину продольной
силы с помощью метода сечений, а
направление в соответствии с правилом
знаков.


![]()
![]()
![]()

![]()
Эпюра
строится под расчетной схемой. Проводится
проверка правильности построения эпюры.

Рис.
2.3 К примеру №2.1. Эпюра продольной силы.
Пример
№2.2. Построить
эпюру продольной силы для бруса жестко
закрепленного левым концом, на который
действуют сосредоточенные силы F1
и F2,
а так же равномернораспределенная
нагрузка интенсивностью q1
и q2.

Рис.
2.4 К примеру №2.2
Внешние
нагрузки делят брус на три участка.
Начнем рассматривать участки со
свободного конца. Применяем метод
сечений и для каждого участка составляем
уравнение равновесия отсеченной части
бруса (в данном случае правой), находим
значение продольной силы в крайних
точках : начало и конец участка.


![]()
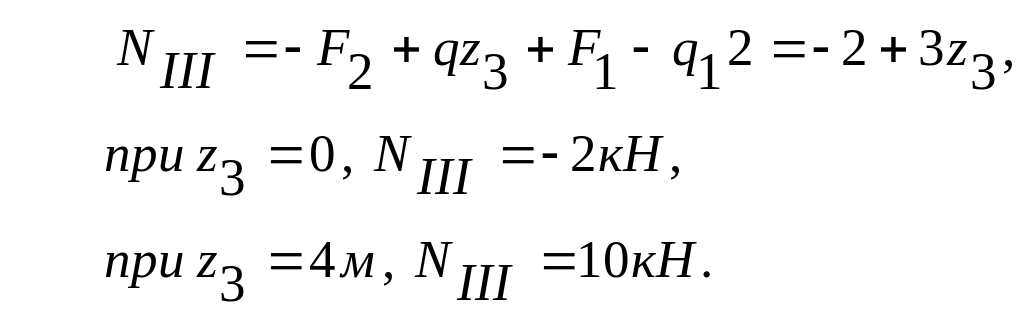
По
полученным значениям строим эпюру
продольной силы (рис. 2.4). Проводим
проверку правильности построения эпюры.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача. Расчет рамы. Для рамы построить эпюры продольных сил N, поперечных сил Q и изгибающих моментов М.

- Определим опорные реакции


Нанесем значения опорных реакций на расчетную схему.

2. Строим эпюру продольных сил N методом сечений. Имеем три характерных участка и три сечения на них.

Правило знаков продольных сил – продольная сила считается положительной, если сила растягивает стержень, и отрицательной, если сила сжимает стержень. Положительные значения откладываем влево от стойки и вверх от ригеля.

Строим эпюру продольных сил.

3. Строим эпюру поперечных сил Q методом сечений. Правило знаков – если сила относительно сечения направлена по часовой стрелке, то поперечная сила считается положительной и наоборот. Положительные значения откладываются влево от стоек и вверх от ригеля.

Строим эпюру поперечных сил

4. Строим эпюру изгибающих моментов М методом характерных точек. Расставляем точки: А – опора, В,С, — узлы рамы, D – свободный конец, К – середина равномерно распределенной нагрузки (точки экстремума при построении эп.Q не обнаружено). Эпюру М строим на сжатых волокнах (для машиностроительных специальностей), знак не ставим.

Строим эпюру моментов.

5. Вырезаем узлы С и В и проверяем их равновесие.

Узлы находятся в равновесии, значит эпюры построены верно.
Для балки с жесткой заделкой построить эпюры Q и М.

Расставляем сечения от свободного конца балки — в этом случае можно построить эпюры, не определяя опорных реакций. Рассматривать в каждом случае будем правую часть — справа от сечения. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 2 участка, 2 сечения.

Сечение 2-2 проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z2 вправо от сечения до начала участка. Определяем поперечные силы в сечениях. Правило знаков см. — здесь.

Строим эпюру Q.

Построим эпюру М методом характерных точек. Расставляем точки на балке — это точки начала и конца балки (D,A), сосредоточенного момента (B), а также отметим в качестве характерной точки середину равномерно распределенной нагрузки (K) — это дополнительная точка для построения параболической кривой.

Определяем изгибающие моменты в точках. Правило знаков см. — здесь.
![]()
Момент в т. В будем определять следующим образом. Сначала определим:
![]()
Теперь:
![]()
Точку К возьмем в середине участка с равномерно распределенной нагрузкой.

Строим эпюру M. Участок АВ – параболическая кривая (правило «зонтика»), участок ВD – прямая наклонная линия.

Для балки определить опорные реакции и построить эпюры изгибающих моментов (М) и поперечных сил (Q).

- Обозначаем опоры буквами А и В и направляем опорные реакции RА и RВ.

Составляем уравнения равновесия.

Проверка

Записываем значения RА и RВ на расчетную схему.
2. Построение эпюры поперечных сил методом сечений. Сечения расставляем на характерных участках (между изменениями). По размерной нитке – 4 участка, 4 сечения.

сеч. 1-1 ход слева.
Сечение проходит по участку с равномерно распределенной нагрузкой, отмечаем размер z1 влево от сечения до начала участка. Длина участка 2 м. Правило знаков для Q — см. здесь.

Строим по найденным значением эпюру Q.
сеч. 2-2 ход справа.
Сечение вновь проходит по участку равномерно распределенной нагрузкой, отмечаем размер z2 вправо от сечения до начала участка. Длина участка 6 м.

Строим эпюру Q.
сеч. 3-3 ход справа.

сеч. 4-4 ход справа.

Строим эпюру Q.

3. Построение эпюры М методом характерных точек.
Характерная точка – точка, сколь-либо заметная на балке. Это точки А, В, С, D, а также точка К, в которой Q=0 и изгибающий момент имеет экстремум. Также в середине консоли поставим дополнительную точку Е, поскольку на этом участке под равномерно распределенной нагрузкой эпюра М описывается кривой линией, а она строится, как минимум, по 3 точкам.

Итак, точки расставлены, приступаем к определению в них значений изгибающих моментов. Правило знаков — см. здесь.
Участки NA, AD – параболическая кривая (правило «зонтика» у механических специальностей или «правило паруса» у строительных ), участки DС, СВ – прямые наклонные линии.

Момент в точке D следует определять как слева, так и справа от точки D. Сам момент в эти выражения не входит. В точке D получим два значения с разницей на величину m – скачок на его величину.

Теперь следует определить момент в точке К (Q=0). Однако сначала определим положение точки К, обозначив расстояние от нее до начала участка неизвестным х.

Т. К принадлежит второму характерному участку, его уравнение для поперечной силы (см. выше)

Но поперечная сила в т. К равна 0, а z2 равняется неизвестному х.
Получаем уравнение:

Теперь, зная х, определим момент в точке К с правой стороны.

Строим эпюру М. Построение выполним для механических специальностей, откладывая положительные значения вверх от нулевой линии и используя правило «зонтика».

Для заданной схемы консольной балки требуется построить эпюры поперечной силы Q и изгибающего момента M, выполнить проектировочный расчет, подобрав круглое сечение.
Материал — дерево, расчетное сопротивление материала R=10МПа, М=14кН·м,q=8кН/м
Строить эпюры в консольной балке с жесткой заделкой можно двумя способами — обычным, предварительно определив опорные реакции, и без определения опорных реакций, если рассматривать участки, идя от свободного конца балки и отбрасывая левую часть с заделкой. Построим эпюры обычным способом.
1. Определим опорные реакции.
Равномерно распределенную нагрузку q заменим условной силой Q= q·0,84=6,72 кН
В жесткой заделке три опорные реакции — вертикальная, горизонтальная и момент, в нашем случае горизонтальная реакция равна 0.
Найдем вертикальную реакцию опоры RA и опорный момент МA из уравнений равновесия.
2. Строим эпюру поперечных сил.
На первых двух участках справа поперечная сила отсутствует. В начале участка с равномерно распределенной нагрузкой (справа) Q=0, в заделеке — величине реакции RA. 3. Для построения эпюры изгибающих моментов M составим выражения для их определения на участках. Эпюру моментов построим на растянутых волокнах, т.е. вниз.
3. Для построения эпюры изгибающих моментов M составим выражения для их определения на участках. Эпюру моментов построим на растянутых волокнах, т.е. вниз. 
4.Проектировочный расчет, то есть подбор размеров поперечного сечения.
Максимальный изгибающий момент с эпюры М=14 кН·м. Определим осевой момент сопротивления сечения

Таким образом, подбираем сечение с диаметром 25 см.
Требуется построить эпюры Q и M и подобрать стальную балку двутаврового поперечного сечения при расчетном сопротивлении R=160 МПа.

1.Определение реакций:
Сумма моментов относительно опор:
Опора А: 
Опора В:

Сумма проекций всех сил на ось У (проверка):
![]()
2.Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.
1) Первый участок:

2) Второй участок:

3) Третий участок:

3.Проектировочный расчет, то есть подбор размеров поперечного сечения.
Подобрать стальную балку двутаврового поперечного сечения при R=160 МПа:
С эпюры берем максимальный момент:

По сортаменту подбираем двутавр № 20 с ![]()
Двутавр можно взять чуть меньше, при условии, что перенапряжение составляет меньше 5%:

Для заданной балки требуется построить эпюры Q и M, найти Mmax и сделать проектировочный расчет — подобрать деревянную балку круглого поперечного сечения. Расчетное сопротивление материала Ru=10 МПа.

1.Определение реакций:
Сумма проекций всех сил на ось z: ![]()
Сумма проекций всех сил на ось y: ![]()
Сумма моментов относительно точки А: 
После нахождения опорных реакций следует выполнить проверку, использовав уравнение равновесия (сумма моментов относительно любой выбранной точки должна быть равна нулю).
2. Записываем уравнения Q и M для каждого из участков в общем виде, при этом учитываем знаки.
Q — поперечная сила, считается положительной, если стремится повернуть рассматриваемую часть балки по часовой стрелке.
M— изгибающий момент, считается положительным, если растягивает нижние волокна.
1)Первый участок:

2) Второй участок:

3) Третий участок:

Следует отметить ,что на втором и третьем участке для построения плавной кривой потребуются дополнительные точки, в которых следует посчитать значение изгибающего момента.
3.Проектировочный расчет, то есть подбор размеров поперечного сечения.
Подберем деревянную балку круглого поперечного сечения при Ru=10 МПа
С эпюры берем максимальный момент и рассчитываем требуемый осевой момент сопротивления, после чего вычисляем необходимый диаметр балки.
Задача 1. Построить эпюры Q и M в балке с шарниром.

1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.
Если рассмотреть левую часть, то в уравнении ![]() будут присутствовать две неизвестные RА и МА. Значит, следует рассмотреть правую часть (из него найдем RВ).
будут присутствовать две неизвестные RА и МА. Значит, следует рассмотреть правую часть (из него найдем RВ).

Теперь ![]() из него найдем МА
из него найдем МА

Следующее уравнение ![]() из него найдем RА
из него найдем RА

2. Строим эпюру Q.
Участок первый — АС, смотрим левую часть
Участок второй — СВ, смотрим правую часть

3. Строим эпюру М

Определим момент в точке, где Q=0 (момент имеет экстремум), это момент в точке К, т.е. МК , для этого определим положение точки К.
![]() Это уравнение первого участка, на котором находится точка К
Это уравнение первого участка, на котором находится точка К
в точке К 
Строим эпюры. Задача решена.
Задача 2. Построить эпюры Q и M в балке с шарниром.

1. Определим опорные реакции. Для определения опорных реакций используем свойство шарнира – момент в нем как от левых, так и от правых сил равен 0.
Если рассмотреть правую часть, то в уравнении ![]() будут присутствовать две неизвестные Rд и Rв. Значит, следует рассмотреть левую часть.
будут присутствовать две неизвестные Rд и Rв. Значит, следует рассмотреть левую часть.

Знак «-» говорит о том, что реакция RВ направлена в обратную сторону.
Проверка:
2. Построение эпюры Q.
Участок первый – ЕА, смотрим левую часть
Участок второй – АС, смотрим левую часть
Участок третий – СВ, смотрим левую часть
Участок четвертый – ВД, смотрим правую часть

3. Построение эпюры М

Т.к. точки экстремума на эп.Q не наблюдается, определяем изгибающий момент в середине участка ВД

Строим эпюры, задача решена.
Задача 1. Построить эпюры внутренних усилий для рамы ( рис.а).
Дано: F=30кН, q=40 кН/м, М=50кНм, а=1,8м, h=2м.

Решение.
Для рассматриваемой рамы опорные реакции можно не определять, поскольку будем рассматривать участки, идя от свободных концов рамы к заделке.
Вычислим значения внутренних усилий N, Q и М в характерных сечениях рамы. Правило знаков для поперечных сил Q и изгибающих моментов М такие же,как в балках. Эпюры моментов построим на сжатых волокнах. Для продольной N, силы правило знаков: растягивающая сила – положительна, сжимающая – отрицательна.
Участок ВС: ![]() (сжаты нижние волокна).
(сжаты нижние волокна).
![]() (сжаты нижние волокна).
(сжаты нижние волокна).
Участок DC:  (сжаты верхние волокна).
(сжаты верхние волокна).
Участок СК: ![]() (сжаты левые волокна)
(сжаты левые волокна)
![]() (сжаты левые волокна)
(сжаты левые волокна)
На рисунке – эпюры нормальных (продольных) сил — (б), , поперечных сил — (в) и изгибающих моментов — (г).
Проверка равновесия узла С:

Задача 2 Построить эпюры внутренних усилий для рамы (рис. а).
Дано: F=30кН, q=40 кН/м, М=50кНм, а=3м, h=2м.

Определим опорные реакции рамы:

Из этих уравнений найдем:

Поскольку значения реакции RK имеет знак минус, на рис. а изменяется направление данного вектора на противоположное, при этом записывается RK=83,33кН.
Определим значения внутренних усилий N, Q и М в характерных сечениях рамы:
Участок ВС:
(сжаты правые волокна).
Участок CD: 
(сжаты правые волокна);
![]()
(сжаты правые волокна).
Участок DE: 
(сжаты нижние волокна);

(сжаты нижние волокна).
Участок КС

(сжаты левые волокна).
Построим эпюры нормальных (продольных) сил (б), поперечных сил (в) и изгибающих моментов (г).
Рассмотрим равновесие узлов D и Е

Из рассмотрения узлов Dи Е видно, что они находятся в равновесии.
Задача 3. Для рамы с шарниром построить эпюры внутренних усилий.
Дано: F=30кН, q=40 кН/м, М=50кНм, а=2м, h=2м.

Решение. Определим опорные реакции. Следует отметить ,что в обеих шарнирно-неподвижных опорах по две реакции. В связи с этим следует использовать свойство шарнира С — момент в нем как от левых ,так и от правых сил равен нулю. Рассмотрим левую часть.
Уравнения равновесия для рассматриваемой рамы можно записать в виде:

Из решения данных уравнений следует:

На схеме рамы направление действия силы НВ изменяется на противоположное (НB=15кН).
Определим усилия в характерных сечениях рамы.
Участок BZ: 
(сжаты левые волокна).
Участок ZC:

(сжаты левые волокна);

Участок КD: ![]()
(сжаты левые волокна);

(сжаты левые волокна).
Участок DС:

(сжаты нижние волокна);

Определение экстремального значения изгибающего момента на участке CD :

(сжаты верхние волокна).
Строим эпюры внутренних усилий. Проверяем равновесие узлов рамы.
Узлы C и D находятся в равновесии.
Построение эпюр М и Q в балке с жесткой заделкой с определенными опорными реакциями. Построение методом характерных точек.

1. Построение эпюры поперечных сил. Для консольной балки (рис. а) характерные точки: А – точка приложения опорной реакции VA; С – точка приложения сосредоточенной силы; D, B– начало и конец распределенной нагрузки. Для консоли поперечная сила определяется аналогично двухопорной балке. Итак, при ходе слева:

Для проверки правильности определения поперечной силы в сечениях пройдите балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Помните, что правило знаков при этом изменятся. Результат должен получиться тот же. Строим эпюру поперечной силы (рис,б).
2. Построение эпюры моментов
Для консольной балки эпюра изгибающих моментов строится аналогично предыдущему построению.Характерные точки для этой балки (см. рис. а) следующие: А – опора; С — точка приложения сосредоточенного момента и силы F; D и В — начало и конец действия равномерно распределенной нагрузки. Поскольку эпюра Qx на участке действия распределенной нагрузки нулевую линию не пересекает, для построения эпюры моментов на данном участке (параболическая кривая) следует выбрать произвольно дополнительную точку для построения кривой, к примеру в середине участка.
Ход слева:

Ходом справа находим MB = 0.
По найденным значениям строим эпюру изгибающих моментов (см. рис. в).
Построение эпюр М и Q в балке на двух опорах с определенными опорными реакциями. Построение методом характерных точек.

1. Построение эпюры Qу. Из теоретического курса известно, что на участке балки с равномерно распределенной нагрузкой эпюра Qу ограничивается наклонной прямой, а на участке, на котором нет распределенной нагрузки, — прямой, параллельной оси, поэтому для построения эпюры поперечных сил достаточно определить значения Qу в начале и конце каждого участка. В сечении, соответствующем точке приложения сосредоточенной силы, поперечная сила должна быть вычислена чуть левее этой точки (на бесконечно близком расстоянии от нее) и чуть правее ее; поперечные силы в таких местах обозначаются соответственно ![]() .
.
Строим эпюру Qу методом характерных точек, ходом слева. Для большей наглядности отбрасываемую часть балки на первых порах рекомендуется закрывать листом бумаги. Характерными точками для двухопорной балки (рис. а) будут точки C и D – начало и конец распределенной нагрузки, а также A и B – точки приложения опорных реакций, E– точка приложения сосредоточенной силы. Проведем мысленно ось y перпендикулярно оси балки через точку С и не будем менять ее положение, пока не пройдем всю балку от C до E. Рассматривая левые отсеченные по характерным точкам части балки, проецируем на ось y действующие на данном участке силы с соответствующими знаками. В результате получаем:
Для проверки правильности определения поперечной силы в сечениях можно пройти балку аналогичным образом, но с правого конца. Тогда отсеченными будут правые части балки. Результат должен получиться тот же. Совпадение результатов может служить контролем построения эпюры Qу. Проводим нулевую линию под изображением балки и от нее в принятом масштабе откладываем найденные значения поперечных сил с учетом знаков в соответствующих точках. Получим эпюру Qу (рис. б).
Построив эпюру, обратите внимание на следующее: эпюра под распределенной нагрузкой изображается наклонной прямой, под ненагруженными участками — отрезками, параллельными нулевой линии, под сосредоточенной силой на эпюре образуется скачок, равный значению силы. Если наклонная линия под распределенной нагрузкой пересекает нулевую линию, отметьте эту точку, то это точка экстремума, и она является теперь для нас характерной, согласно дифференциальной зависимости между Qу и Мx, в этой точке момент имеет экстремум и его нужно будет определить при построении эпюры изгибающих моментов. В нашей задаче это точка К. Сосредоточенный момент на эпюре Qу себя никак не проявляет, так как сумма проекций сил, образующих пару, равна нулю.
2. Построение эпюры моментов.Строим эпюру изгибающих моментов, как и поперечных сил, методом характерных точек, ходом слева. Известно, что на участке балки с равномерно распределенной нагрузкой эпюра изгибающих моментов очерчивается кривой линией (квадратичной параболой), для построения которой надо иметь не менее трех точек и, следовательно, должны быть вычислены значения изгибающих моментов в начале участка, конце его и в одном промежуточном сечении. Такой промежуточной точкой лучше всего взять сечение, в котором эпюра Qу пересекает нулевую линию, т.е. где Qу= 0. На эпюре М в этом сечении должна находиться вершина параболы. Если же эпюра Qу не пересекает нулевую линию, то для построения эпюры М следует на данном участке взять дополнительную точку, к примеру, в середине участка (начала и конца действия распределенной нагрузки), помня, что выпуклостью парабола всегда обращена вниз, если нагрузка действует сверху вниз (для строительных специальностей). Существует правило «дождя», которое очень помогает при построении параболической части эпюры М. Для строителей это правило выглядит следующим образом: представьте, что распределенная нагрузка — это дождь, подставьте под него зонт в перевернутом виде, так чтобы дождь не стекал, а собирался в нем. Тогда выпуклость зонта будет обращена вниз. Точно так и будет выглядеть очертание эпюры моментов под распределенной нагрузкой. Для механиков существует так называемое правило «зонта». Распределенная нагрузка представляется дождем, а очертание эпюры должно напоминать очертания зонтика. В данном примере эпюра построена для строителей.
Если требуется более точное построение эпюры, то должны быть вычислены значения изгибающих моментов в нескольких промежуточных сечениях. Условимся для каждого такого участка изгибающий момент сначала определить в произвольном сечении, выражая его через расстояние х от какой-либо точки. Затем, давая расстоянию х ряд значений, получим значения изгибающих моментов в соответствующих сечениях участка. Для участков, на которых нет распределенной нагрузки, изгибающие моменты определяют в двух сечениях, соответствующих началу и концу участка, так как эпюра М на таких участках ограничивается прямой. Если к балке приложен внешний сосредоточенный момент, то обязательно надо вычислять изгибающий момент чуть левее места приложения сосредоточенного момента и чуть правее его.
Для двухопорной балки характерные точки следующие: C и D – начало и конец распределенной нагрузки; А – опора балки; В – вторая опора балки и точка приложения сосредоточенного момента; Е – правый конец балки; точка К, соответствующая сечению балки, в котором Qу = 0.
Ход слева. Правую часть до рассматриваемого сечения мысленно отбрасываем (возьмите лист бумаги и прикройте им отбрасываемую часть балки). Находим сумму моментов всех сил, действующих слева от сечения относительно рассматриваемой точки. Итак,

Прежде чем определить момент в сечении К, необходимо найти расстояние х=АК. Составим выражение для поперечной силы в данном сечении и приравняем его к нулю (ход слева):

Это расстояние можно найти также из подобия треугольников KLN и KIG на эпюре Qу (рис.б).
Определяем момент в точке К:

Пройдем оставшуюся часть балки ходом справа.

Как видим, момент в точке D при ходе слева и справа получился одинаковый – эпюра замкнулась. По найденным значениям строим эпюру. Положительные значения откладываем вниз от нулевой линии, а отрицательные – вверх (см. рис. в).
