Как найти эталон килограмма

Килограмм
кг, kg
Компьютерное изображение международного прототипа килограмма, рядом изображена дюймовая линейка. По размерам он сопоставим с мячом для гольфа, края имеют фаски для минимизации износа материала
Величина	Масса
Система	СИ
Тип	основная
См. Приставки СИ
Медиафайлы на Викискладе

Килогра́мм (русское обозначение: кг; международное: kg) — единица массы, одна из семи основных единиц Международной системы единиц (СИ). Кроме того, является единицей массы и относится к числу основных единиц в системах МКС, МКСА, МКСК (МКСГ), МКСЛ^[1]. Килограмм — единственная из основных единиц СИ, используемая с приставкой («кило», обозначение «к»).

XXVI Генеральная конференция по мерам и весам (13—16 ноября 2018 года) одобрила^[2] определение килограмма, основанное на фиксации численного значения постоянной Планка. Решение вступило в силу 20 мая 2019 года.

Килограмм, обозначение кг, является единицей массы в СИ; его величина устанавливается фиксацией численного значения постоянной Планка h равной в точности 6,62607015⋅10^-34, когда она выражена единицей СИ Дж⋅с, которая эквивалентна кг⋅м²⋅с⁻¹, где метр и секунда определены через c и Δν_Cs.^[3][4]

Действовавшее до мая 2019 года определение килограмма было принято III Генеральной конференцией по мерам и весам (ГКМВ) в 1901 году и формулировалось так^[5][6]:

Килограмм — единица массы, равная массе международного прототипа килограмма.

До 20 мая 2019 года килограмм оставался последней единицей СИ, определённой на основе изготовленного человеком объекта. После принятия нового определения с практической точки зрения величина килограмма не изменилась, но существующий «прототип» (эталон) более не определяет килограмм, а является очень точной гирькой с потенциально измеримой погрешностью.

Прототип килограмма[править | править код]

Международный прототип (эталон) килограмма хранится в Международном бюро мер и весов (расположено в Севре близ Парижа) и представляет собой цилиндр диаметром и высотой 39,17 мм из платино-иридиевого сплава (90 % платины, 10 % иридия).

Современный международный эталон килограмма был выпущен Генеральной конференцией по мерам и весам (ГКМВ) в 1889 году на основе Метрической конвенции (1875) и передан на хранение Международному бюро мер и весов (МБМВ), действующему от имени ГКМВ. Международный эталон килограмма практически не подвергается какому-либо перемещению или использованию. Его копии хранятся в национальных метрологических учреждениях по всему миру. В 1889, 1948, 1989 и 2014 годах проводились верификации копий с эталоном с целью обеспечить единство измерений массы относительно эталона^[7]. Поскольку были обнаружены изменения масс копий эталона, Международный комитет мер и весов (МКМВ) рекомендовал переопределить килограмм с помощью фундаментальных физических свойств.

Килограмм и постоянная Планка[править | править код]

Связь между массой и постоянной Планка с теоретической точки зрения определяется двумя формулами^[8]. Эквивалентность массы и энергии связывает энергию и массу :

где  — скорость света в вакууме. Постоянная Планка связывает квантовое и традиционное понятия энергии:

где  — частота.

Эти две формулы, найденные в начале XX века, устанавливают теоретическую возможность измерения массы через энергию индивидуальных фотонов, но практические эксперименты, позволяющие связать массу и постоянную Планка, появились лишь в конце XX века.

Весы Киббла использовались с середины 1970-х годов для измерения величины постоянной Планка. Сотрудники Национального института стандартов США П. Мор (англ. Peter Mohr) и Б. Тэйлор (англ. Barry Taylor) в 1999 году предложили, наоборот, зафиксировать величину постоянной Планка и определять с помощью этих весов массу. Посмертно названные в честь изобретателя, Б. Киббла  (англ.) (рус., весы Киббла — это усовершенствование токовых весов, они представляют собой электромеханический инструмент, где масса вычисляется через электрическую мощность:

где  — произведение электрического тока во время балансирования массы и напряжения в процессе калибровки,  — произведение ускорения свободного падения и скорости катушки во время калибровки весов. Если независимо замерено с высокой точностью (практические особенности эксперимента также требуют высокоточного замера частоты^[9]), предыдущее уравнение по сути определяет килограмм в зависимости от величины ватта (или наоборот). Индексы у и введены с тем, чтобы показать, что это виртуальная мощность (замеры напряжения и тока делаются в разное время), избегая эффектов от потерь (которые могли бы быть вызваны, например, наведёнными токами Фуко)^[10].

Связь между ваттом и постоянной Планка использует эффект Джозефсона и квантовый эффект Холла^[9][11]:

поскольку , где  — электрическое сопротивление, ;

эффект Джозефсона: ;

квантовый эффект Холла: ,

где и  — целые числа (первое связано со ступенькой Шапиро, второе — фактор заполнения плато квантового эффекта Холла),  — частота из эффекта Джозефсона,  — заряд электрона. После подстановки выражений для и в формулу для мощности и объединения всех целочисленных коэффициентов в одну константу , масса оказывается линейно связанной с постоянной Планка:

.

Поскольку все остальные величины в этом уравнении могут быть определены независимо от массы, оно смогло быть принято за определение единицы массы после фиксации значения 6,62607015×10⁻³⁴ Дж·с для постоянной Планка.^[12]

Этимология и употребление[править | править код]

Слово «килограмм» произошло от французского слова «kilogramme», которое в свою очередь образовалось из греческих слов «χίλιοι» (хилиои), что означает «тысяча», и «γράμμα» (грамма), что означает «маленький вес»^[13]. Слово «kilogramme» закреплено во французском языке в 1795 году^[14]. Французское написание слова перешло в Великобританию, где впервые оно было использовано в 1797 году^[15], в то время как в США слово стало использоваться в форме «kilogram», позднее ставшее популярным и в Великобритании^{[16][К 1]} Положение о мерах и весах (англ. Weights and Measures Act) в Великобритании не запрещает использование обоих написаний^[17].

В XIX веке французское сокращение «kilo» было заимствовано в английский язык, где стало применяться для обозначения как килограммов^[18], так и километров^[19].

История[править | править код]

Идея использовать заданный объём воды для определения единицы измерения массы была предложена английским философом Джоном Уилкинсом в его эссе 1668 года как способ связать массу и длину^[20][21].

7 апреля 1795 года грамм был принят во Франции как «абсолютный вес объёма чистой воды, равного кубу [со стороной] в сотую часть метра, и при температуре тающего льда»^[22][23]. В это же время была поручена работа с необходимой точностью определить массу кубического дециметра (литра) воды^{[К 2][22]}.

Поскольку торговля и коммерция обычно имеют дело с предметами, чья масса намного значительней одного грамма, и поскольку стандарт массы, изготовленный из воды, был бы неудобен в обращении и сохранении, было предписано отыскать способ практической реализации такого определения. В связи с этим был изготовлен временный эталон массы в виде металлического предмета в тысячу раз тяжелее, чем грамм, — 1 кг.

Французский химик Луи Лефёвр-Жино (англ. Louis Lefèvre-Gineau) и итальянский натуралист Джованни Фабброни (англ. Giovanni Fabbroni) после нескольких лет исследований решили переопределить наиболее устойчивую точку воды: температура, при которой вода имеет наибольшую плотность, которая была определена в 4 °C^{[К 3][24]}.
Они решили, что 1 дм³ воды при своей максимальной плотности эквивалентен 99,9265 % массы временного эталона килограмма, изготовленного четыре года назад^{[К 4]}. Интересно, что масса 1 м³ дистиллированной воды при 4 °C и атмосферном давлении, принятая за ровно 1000 килограммов в историческом определении 1799 года, согласно современному определению тоже составляет приблизительно 1000,0 килограммов^[25].

Временный эталон был изготовлен из латуни и постепенно покрылся бы патиной, что было нежелательно, поскольку его масса не должна была меняться. В 1799 году под руководством Лефёвра-Жено и Фабброни был изготовлен постоянный эталон килограмма из пористой платины, которая химически инертна. С этого момента масса эталона стала основным определением килограмма. Сейчас этот эталон известен как kilogramme des Archives (с фр. — «архивный килограмм»)^[25].

За XIX век технологии измерения массы значительно продвинулись. В связи с этим, а также в преддверии создания в 1875 году Международного бюро мер и весов, специальная международная комиссия запланировала переход к новому эталону килограмма. Этот эталон, называемый «международный прототип килограмма», был изготовлен из платиново-иридиевого сплава (более прочного, чем чистая платина) в виде цилиндра высотой и диаметром 39 мм^[26], и с тех пор он хранится в Международном бюро мер и весов. В 1889 году было принято международное определение килограмма как массы международного прототипа килограмма^[25]; это определение действовало до 2019 года.

Были изготовлены также копии международного прототипа килограмма: шесть (на данный момент) официальных копий; несколько рабочих эталонов, используемых, в частности, для отслеживания изменения масс прототипа и официальных копий; и национальные эталоны, калибруемые по рабочим эталонам^[25]. Две копии международного эталона были переданы России^[26], они хранятся во ВНИИ метрологии им. Менделеева.

За время, прошедшее с изготовления международного эталона, его несколько раз сравнивали с официальными копиями. Измерения показали рост массы копий относительно эталона в среднем на 50 мкг за 100 лет^[27][28]. Хотя абсолютное изменение массы международного эталона не может быть определено с помощью существующих методов измерения, оно определённо должно иметь место^[27]. Для оценки величины абсолютного изменения массы международного прототипа килограмма приходилось строить модели, учитывающие результаты сравнений масс самого прототипа, его официальных копий и рабочих эталонов (при этом, хотя обычно участвующие в сравнении эталоны обычно предварительно промывали и чистили, но не всегда), что дополнительно усложнялось отсутствием полного понимания причин изменений масс. Это привело к пониманию необходимости ухода от определения килограмма на основе материальных предметов^[25].

В 2011 году XXIV Генеральная конференция по мерам и весам приняла Резолюцию, в которой предложено в будущей ревизии Международной системы единиц (СИ) продолжить переопределение основных единиц таким образом, чтобы они были основаны не на созданных человеком артефактах, а на фундаментальных физических постоянных или свойствах атомов^[29]. В частности предлагалось, что «килограмм останется единицей массы, но его величина будет установлена путём фиксации численного значения постоянной Планка в точности равным 6,626 06X⋅10⁻³⁴, когда она выражается единицей СИ м²·кг·с⁻¹, которая равна Дж·с». В Резолюции отмечается, что сразу после предполагаемого переопределения килограмма масса его международного прототипа будет равна 1 кг, но это значение приобретёт погрешность и впоследствии будет определяться экспериментально. Такое определение килограмма стало возможным благодаря прогрессу физики в XX веке.

В 2014 году было проведено внеочередное сравнение масс международного прототипа килограмма, его официальных копий и рабочих стандартов; на результатах этого сравнения основаны рекомендованные значения фундаментальных постоянных CODATA 2014 и 2017 годов, на которых, в свою очередь, основывается новое определение килограмма.

Рассматривалось также альтернативное определение килограмма, основанное на результатах работы проекта «Авогадро» (англ. The Avogadro Project). Команда проекта, создав шар из кристалла моноизотопного кремния ²⁸Si массой 1 кг и рассчитав количество атомов в ней, предполагает описать килограмм как определённое количество атомов данного изотопа кремния^[30]. Однако Международное бюро мер и весов не стало использовать такой вариант определения килограмма^[29][31].

XXVI Генеральная конференция по мерам и весам в ноябре 2018 года одобрила^[2] новое определение килограмма, основанное на фиксации численного значения постоянной Планка. Решение вступило в силу во Всемирный день метрологии 20 мая 2019 года.

На практике взвешивание на весах Киббла — это чрезвычайно сложный эксперимент, и потому Генеральная конференция по мерам и весам в 2011 году рекомендовала создать набор вторичных стандартов в виде привычных гирек, включая как существующие платино-иридиевые эталоны, так и новые шары из кремния, которые будут далее использоваться для распространения эталона по миру^[9].

Кратные и дольные единицы[править | править код]

По историческим причинам название «килограмм» уже содержит десятичную приставку «кило», поэтому кратные и дольные единицы образуют, присоединяя стандартные приставки СИ к названию или обозначению единицы измерения «грамм» (которая в системе СИ сама является дольной: 1 г = 10⁻³ кг).

Вместо мегаграмма (1000 кг), как правило, используют единицу измерения «тонна».

В определениях мощности атомных бомб в тротиловом эквиваленте вместо гигаграмма применяется килотонна, вместо тераграмма — мегатонна.

Кратные	Дольные
величина	название	обозначение	величина	название	обозначение
101 г	декаграмм	даг	dag	10−1 г	дециграмм	дг	dg
102 г	гектограмм	гг	hg	10−2 г	сантиграмм	сг	cg
103 г	килограмм	кг	kg	10−3 г	миллиграмм	мг	mg
106 г	мегаграмм	Мг	Mg	10−6 г	микрограмм	мкг	µg
109 г	гигаграмм	Гг	Gg	10−9 г	нанограмм	нг	ng
1012 г	тераграмм	Тг	Tg	10−12 г	пикограмм	пг	pg
1015 г	петаграмм	Пг	Pg	10−15 г	фемтограмм	фг	fg
1018 г	эксаграмм	Эг	Eg	10−18 г	аттограмм	аг	ag
1021 г	зеттаграмм	Зг	Zg	10−21 г	зептограмм	зг	zg
1024 г	иоттаграмм	Иг	Yg	10−24 г	иоктограмм	иг	yg
1027 г	роннаграмм	Рг	Rg	10−27 г	ронтограмм	рг	rg
1030 г	кветтаграмм	Квг	Qg	10−30 г	квектограмм	квг	qg
рекомендовано к применению      применять не рекомендуется      не применяются или редко применяются на практике

Копии[править | править код]

№ 12, 26 — СССР^[32] (Россия)

№ 20 — США^[32]

См. также[править | править код]

• Килограмм-сила
• Центнер

Примечания[править | править код]

Комментарии

Источники

Литература[править | править код]

• Richard S. Davis, Pauline Barat and Michael Stock. A brief history of the unit of mass: continuity of successive definitions of the kilogram // Metrologia. — 2016. — Vol. 53. — P. A12–A18. — doi:10.1088/0026-1394/53/5/A12.
• Ernst O. Goebel, Uwe Siegner. Quantum Metrology: Foundation of Units and Measurements (англ.). — John Wiley & Sons, 2015.
• Смирнова Н. А. Единицы измерений массы и веса в Международной системе единиц. — М., 1966.
• Эллиотт, Л., Уилкокс, У. Физика / пер. с англ. под ред. А. И. Китайгородского. — 3-е, исправленное. — Москва: Наука, 1975. — 736 с. — 200 000 экз.
• Historic Vote Ties Kilogram and Other Units to Natural Constants (англ.). NIST. Дата обращения: 17 ноября 2018. Архивировано 29 мая 2019 года.

Ссылки[править | править код]

• Kilogram: Mass and Planck’s Constant (англ.). NIST. Дата обращения: 18 ноября 2018. Архивировано 19 ноября 2018 года.
• New Measurement Will Help Redefine International Unit of Mass (англ.). News. NIST (30 июня 2017). Дата обращения: 6 июля 2017. Архивировано 18 июля 2017 года.

Итак, решение развенчать килограмм принято, и с  20 мая 2019  никому уже не отвертеться от нового эталона. Давайте разберемся аккуратно, как теперь ученый мир будет измерять единицу массы.

Почему новый килограмм был нужен

Старый килограмм действительно имеет почтенный возраст: Метрическая конвенция назначила его задающим единицу массы еще в 1875 году. То есть именно тогда метрологическое сообщество провозгласило килограмм массой международного прототипа килограмма (ИПК, от английского — International Prototype of the Kilogram, IPK). Роль ИПК все еще играет платино-иридиевый цилиндр высотой и диаметром 39 миллиметров, который изготовили в 1889-м. Тогда же сделали еще 42 точных копий — их разделили между странами-участниками конвенции, чтобы там могли следить за единством измерений, периодически обращаясь напрямую к французскому цилиндру.

За годы службы эталонов проводились неоднократные сличения с ИПК — в 1889, 1948, 1989 и 2014 годах. Сверка показала, что эталоны «расползлись» за сто с небольшим лет на 20–50 микрограммов. Несмотря на высокую химическую устойчивость платино-иридиевого сплава, эталоны все равно подвергаются испарению и диффузии (они не только «худеют»). В современном мире с растущими требованиями к точности измерений набег расхождений масс эталонов тревожен: такое непостоянство — на грани утраты функциональности, ведь накапливающаяся неточность грозит потерей первоцели эталонов — обеспечения единства измерений.

Метрологи давно предлагали перевести все основные величины на определения через фундаментальные физические константы (ФФК). Некоторые величины (секунда, метр, ампер, кандела) обрели свои квантовые «фамилии» еще давно, а на последней конференции в ноябре 2018 года пришел черед килограмма и его брата — моля, который был определен, по сути, через массу (а теперь завязан на ФФК — постоянной Планка и числе Авогадро).

Новое определение и сфера вместо цилиндра

До 26-й Генеральной конференции по мерам и весам килограмм был привязан к физическому объекту, а не природной константе. На конференции все изменилось кардинально: всем известная мера массы теперь определяется через постоянную Планка, значение которой фиксированное и равно 6.62607015×10^-34 кг*м²/с. Секунда и метр определены в терминах значений скорости света и частоты квантового перехода в цезии, которые, в свою очередь, так же, как и постоянная Планка, являются фиксированными ФФК. Другими словами, новый «килограмм» теперь не отождествляется с массой эталонного цилиндра, а завязывается на значениях достаточно точно измеренных постоянных.

Новое определение отрывает единицу массы от физического объекта, что тут же вызвало множество вопросов, ведь миру по-прежнему надо взвешивать объекты, измерять их массы и уточнять измерительные приборы. Метрологический мир нашел два решения.

Во-первых, можно создать более «абсолютный» эталон. То есть такой, который максимально точно мог бы воспроизводить единицу массы, но при этом и сам был бы воспроизводимым. И ученые создали такой объект — это сфера из кремния-28 максимально технологически возможной «чистоты», которую  проверяли исследователи из Национального института метрологических исследований (Италия) и Австралийской организации ядерной физики и технологий с помощью нейтронно-активационного анализа. Метод позволяет очень точно определять элементный состав образца. В результате была подтверждена высокая степень чистоты: концентрация примесей порядка от фемтограммов до нанограммов на грамм кремния.

Кремний был избран в качестве основного материала для нового «физического» килограмма, так как благодаря развитию полупроводниковых технологий в мире освоены способы получения «чистого» кремния. Основным фиксированным параметром для кремниевого эталонозаменителя является число атомов. Структура кремния известна, и у любой достаточно оснащенной лаборатории есть возможность воссоздать сферический килограмм (в вакууме, безусловно). Способ не самый бюджетный (каждая такая сфера стоит 3,2 миллиона долларов), но он смещает фокус от конкретного объекта в сторону его точного определения и потенциальной заменимости.

Интересно, что создатели кремниевой сферы — коллаборация «Международный проект Авогадро» — по сути, занимались более точным определением числа Авогадро (N_A). То есть логически-метрологическая цепочка такова: есть 1 кг (цилиндр), делаем точную копию по массе (сфера из кремния), хорошенько ее исследуем самыми современными методами (определяем радиус сферы, кристаллическую структуру), зная точную массу каждого атома кремния-28, считаем, сколько в сфере атомов, и таким образом определяем число Авогадро. Уточненное значение константы оказалось равно 6.02214076 x 10²³, неточность 20 частей на миллиард. В таком виде теперь постоянную фиксируют для переопределения единицы моля. А далее применим обратный подход: зная точное число атомов, структуру, размеры и состав сферы, мы имеем возможность воспроизвести килограмм, пользуясь постоянной Авогадро, — все снова через ФФК.

Взвесим по-новому

Вторая возможная реализация нового определения единицы массы — так называемый электронный килограмм. Чтобы понять, как такой килограмм работает, давайте сначала рассмотрим прибор, который единицу массы воспроизводит, — весы Киббла (the Kibble balance).

Аппарат был разработан в Национальной физической лаборатории в Великобритании в 1975 году и известен под несколькими именами — его называют ватт-весами с движущейся катушкой, или весами Киббла. Первое название отражает физическую и техническую суть устройства, второе имя весы приобрели после смерти своего разработчика Брайана Киббла в 2016 году.

Весы Киббла и функционируют в двух основных режимах: взвешивания и движения.

Представим классические ручные весы, в них измерение массы происходит за счет уравновешивания двух сил — силы тяжести измеряемого объекта и упругости проградуированной пружины.

В режиме взвешивания на весах Киббла гравитационная сила уравновешивается электромагнитной. Взвешиваемый образец помещается в специальную чашку, а ток через катушку подбирается таким образом, чтобы действующие силы уравновесили друг друга.

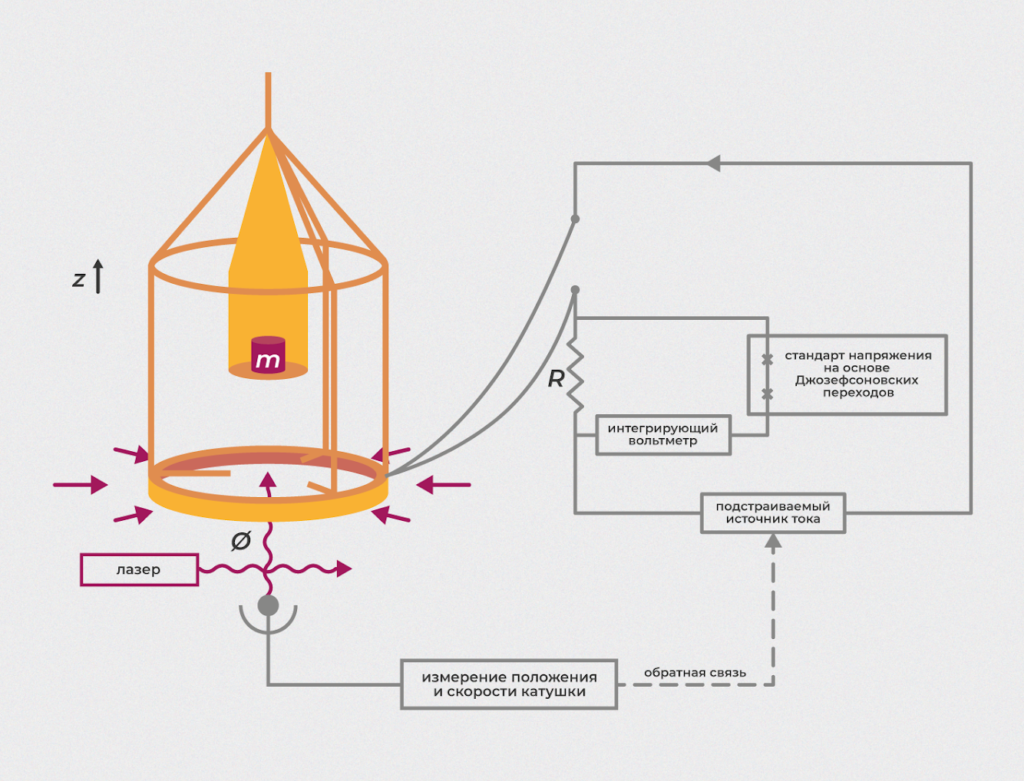
Режим движения основан на явлении электромагнитной индукции. Измеряемый объект удаляется за ненужностью, а катушка движется в магнитном поле. Цель такого дополнительного измерения проста: косвенно и с меньшей погрешностью измерить параметр магнитного поля – плотность магнитного потока в зазоре постоянного магнита — необходимый для итогового вычисления массы.

Гонка за точностью

Чтобы обеспечить точное измерение или воспроизведение массы, необходимо выполнить ряд вещей, уменьшающих неточности. Один из шагов — упомянутая выше калибровка, устраняющая неопределенность измерения индукции магнитного поля и линейного размера катушки. Следующий шаг — наиболее точно определить значения всех входящих в уравнение ватт-баланса величин.

Скорость движения катушки измеряется с помощью лазерного интерферометра, а благодаря открытию в 1980 году квантового эффекта Холла и ранее известному к тому времени эффекту Джозефсона появилась возможность точной и стабильной реализации единиц ома и вольта соответственно.

Также в устройство ватт-весов входит гравиметр. Он измеряет точное значение ускорения свободного падения (которое входит в уравнение для вычисления массы) в том месте, где находится измеряемая масса. Сегодня несколько существующих весов Киббла воспроизводят единицу массы в диапазоне от миллиграммов до килограммов с точностью 2 на 10^-8.

Приключения нового килограмма в России

Наш отечественный килограмм «увольнять» в 2019-м никто не планирует. Результаты сверки с МПК действуют до 2024-го года. А наш килограмм к тому же еще вел себя хорошо: по словам хранителя государственного эталона Виктора Снегова, сотрудника  ВНИИМ им. Д.И.Менделеева  (организации Росстандарта), отклонился только на 1 микрограмм за 20 лет. Хранитель говорит, что еще лет 10 наш эталон должен держаться в рамках требуемой точности. К этому сроку российские метрологи планируют реализовать независимый килограмм с необходимой точностью.

«В рамках национального проекта будут создаваться отечественные весы Киббла на основе многолетнего опыта других стран, но пока непонятно, кто конкретно будет реализовывать новое определение килограмма у нас», — говорит Виктор Снегов.

Но все реформы касаются первичных метрологических уровней. Госэталон должен будет со временем воспроизводить единицу массы с точностью, заданной определением. Передаваться килограмм на второй уровень должен будет в условиях вакуума, то есть в условиях калибровки первичного эталона. А далее — уже передача единицы массы в условиях атмосферы другим измерительным приборам (вплоть до бытовых весов) не будет никак отличаться от того, что было раньше.

Кстати, передача единицы осуществляется с помощью еще одних специальных весов — компаратора массы. Работает эта машина на принцип электромагнитной компенсации — так же, как и ватт-весы в режиме взвешивания, когда измеряемая масса уравновешивается током. Компаратор при этом, конечно же, дает гораздо меньшую точность.

Детальное описание принципа работы весов

Ученые любят формулы, и на формальном языке принцип работы ватт-весов демонстрируется очень наглядно. Привлечем силы школьной физики. Весу объекта Mg сопоставляется вертикальная составляющая магнитной силы BIL, действующая на проволочную катушку с током в сильном магнитном поле B c известной скоростью v. Такое движение по закону электромагнитной индукции Фарадея индуцирует разность потенциалов U=BLv на концах катушки. Так как и магнитное поле, и сама катушка те же, что и в первом случае, величина плотности магнитного потока BL остается прежней, а режим движения является калибровочным шагом, позволяющим избавиться от неопределенности измерения значения BL.

То есть с одной стороны мы имеем равенство сил Мg=BIL, c другой — соотношение U=BLv (закон индукции Фарадея). Итоговое уравнение после исключения произведения BL имеет вид: Mgv=UI. Размерность обеих сторон уравнения — единицы мощности, поэтому весы Киббла изначально назывались ватт-весами, а итоговое выражение сопоставляет электрическую и механическую мощности.

Внимательный читатель может задать вопрос: если работа весов определяется уравнением Mgv=UI, то какое во всей этой истории место занимают постоянная Планка и определение килограмма через ФФК? А ответ кроется в технической реализации точных измерений электрического тока и напряжения.

Эффект Джозефсона заключается в следующем: если два сверхпроводника разделить тонким слоем изолятора и через полученный «сэндвич» пропустить электромагнитное излучение микроволнового диапазона, то разность потенциалов на концах конструкции будет пропорциональна частоте излучения, а коэффициент пропорциональности равен h/2e, где h — постоянная Планка, а e — заряд электрона. Конструкция сверхпроводник-диэлектрик-сверхпроводник называется «Джозефсоновский контакт», именно она лежит в основе воспроизведения единицы вольта в системе СИ через ФФК — заряд электрона и постоянную Планка.

Все для того же уменьшения неопределенности ток в уравнении баланса не измеряют прямо, а поставляют эквивалентное выражение по закону Ома I=U/R. Напряжение мы умеем точно воспроизводить, сопротивление — тоже, но на основе уже другого эффекта — квантового эффекта Холла. Благодаря открытию Клауса фон Клитцинга в 1980 году у инженеров-микроэлектроников появилась возможность создавать стандарты с точно заданным значением сопротивления с неопределенностью на уровне миллиардной доли Ома. Математически говоря, благодаря вышеописанным квантовым эффектам электрическую мощность можно сопоставить с частотой, постоянной Планка и зарядом электрона и, соответственно, через уравнение ватт-баланса связать постоянную Планка, секунду и заряд электрона с килограммом.

Необходимо будет немного преобразовать уравнение ватт-баланса так, чтобы в левой части была только масса, а в правой — все остальные величины. Напряжение представляется в виде U(n)= hf/2e, где n — квантовое число. Сопротивление, соответственно, R(p)=h/pe². Электрическая мощность выражается через квантовые величины как UI=U*U/R=(hf/2e)²*h/pe². Из уравнения баланса мощностей мы получим: m=p*n²*f²*h/(4gv).

Это и есть то самое выражение массы через фундаментальные константы природы. Точное вычисление параметров правой части уравнения обеспечивает вычисление массы, а подбор этих параметров — воспроизведение.

Среди работников Всероссийского научно-исследовательского института метрологической службы прошел научный рэп-баттл «За новый килограмм».  Александр представлял международный прототип килограмма, Денис —  постоянную Планка. Как отметил руководитель Росстандарта Алексей Абрамов, освещение метрологии в таком формате сделает ее более доступной обществу и заинтересует современную молодежь.

Просмотров:
16 404

Время на прочтение
2 мин

Количество просмотров 55K

Международный прототип без защитного чехла

В сентябре 2014 года исполняется 125 лет с момента появления на свет международного прототипа килограмма. Решение о создании эталона было принято на Генеральной конференции мер и весов 7-9 сентября 1889 года в Париже.

Он хранится в Международном бюро мер и весов около Парижа и представляет собой цилиндр диаметром и высотой 39,17 мм из платино-иридиевого сплава (90% платины, 10% иридия). Такой состав выбран из-за высокой плотности платины, так что эталон можно сделать относительно маленького размера: меньше спичечного коробка по высоте.

Национальный прототип килограмма Великобритании в защитном корпусе, 18-я копия международного прототипа

Масса международного прототипа примерно соответствует 1 литру воды при температуре 4°C, а его вес зависит от высоты над уровнем моря и силы гравитации.

Когда изготовляли международный прототип, вместе с ним сделали 40 копий из того же платино-иридиевого сплава. Их разослали по национальным бюро мер и весов в разных странах, чтобы учёным не приходилось обращаться к основному эталону каждый раз для проведения измерений.

Национальные прототипы сверяют с основным прототипом каждые 40 лет. Последняя проверка проходила в 1989 году, и тогда максимальная разница в весе составила 50 микрограммов. Эти девиации беспокоят учёных. Они понимают, что масса конкретного образца изменяется со временем из-за физических повреждений и появления прочих артефактов.

Национальный прототип хранится в сейфе Национальной физической лаборатории

К сожалению, для международного прототипа нынешний юбилей, скорее всего, станет последним. Сейчас подходят к завершению два эксперимента по созданию более точных эталонов массы. Их цель — определить массу через естественную природную константу, а не через эталонный образец.

Один из экспериментов предполагает определение килограмма через постоянную Планка. Для этого измеряют ток, проходящий через [проводную] катушку в магнитном поле, по отношению к силе гравитации, действующей на килограмм, объясняют специалисты Национальной физической лаборатории Великобритании, где в честь 125-летия килограмма открыли праздничный раздел на сайте. Именно в Великобритании в 1975 году начали эксперимент по ватт-балансу, который сейчас продолжают в Канаде.

Другой метод предлагают немецкие специалисты: в рамках проекта Авогадро создают кремниевую сферу размером с грейпфрут, которая содержит около 50 септиллионов атомов кремния-28.

Кремниевая сфера Авогадро

Поскольку известны масса кремния и плотность вещества, то эталонное значение килограмма можно привязать к объёму сферы и, соответственно, к постоянной Авогадро.

Измерение массы сферы Авогадро

Килограмм остался последней единицей СИ, которая выражается через физический эталон. Это указывает на то, что 125 лет назад физики очень грамотно выбрали материал для изготовления прототипа. И даже если скоро его выведут из использования, он сослужил хорошую службу за эти годы.

С 20 мая 2019 года слиток платины и иридия, хранящийся в Международном бюро мер и весов, перестал обозначать килограмм. Теперь эту единицу массы будут определять через постоянную Планка, используя уже имеющиеся эталонные значения длины и времени. Решение об этом приняли на XXVI Генеральной конференции мер и весов.

С 1901 года килограммом считалась масса, равная массе прототипа, хранящегося в Международном бюро мер и весов в городке Севр недалеко от Парижа. Когда-то этот эталон создали для того, чтобы по всему миру привести меру массы к единому стандарту. Со временем, как оказалось, слиток, хранящийся под тремя герметичными колпаками, все-таки менялся, теряя примерно по 50 микрограммов за 100 лет.

Из-за того, что эталон оказался непостоянным, XXVI Генеральная конференция мер и весов, которая прошла в ноябре 2018 года, решила использовать для определения килограмма не материальный предмет, а постоянную Планка. Эта физическая константа определяет связь энергии квантов излучения с частотой.

Читайте также: Бородатая секунда и радиоактивные бананы. Необычные единицы измерения, которые используются для смеха и всерьез

Теперь килограмм должен быть таким, чтобы постоянная Планка составляла 6,626069 * 10⁻³⁴ джоулей на секунду. Джоули выводятся через килограммы, метры и секунды. Для секунд и метра эталон уже есть — секунда, это время, равное 9 192 631 770 периодам излучения охлажденного атома цезия, а свет проходит за секунду 299 792 458 метров. Для измерения постоянной Планка метрологи используют так называемые весы Киббла. Этот прибор определяет, какой ток нужен для того, чтобы создать электромагнитное поле, способное уравновесить чашу с образцом.

муниципальное
бюджетное общеобразовательное учреждение

города
Ростова-на-Дону

«Школа
№ 60 имени пятого гвардейского Донского казачьего кавалерийского
Краснознаменного Будапештского корпуса» 

 (МБОУ «Школа № 60»)

«ЭТАЛОН КИЛОГАММА»

Секция:
Физика

Работа
выполнена:

Учащимися
9 «Б» класса

Казачковой
Вероникой и

Титаренко
Андреем

Под
руководством учителя физики

Тыквинской  О.В.

г.
Ростов-на-Дону

Оглавление:

1.     Актуальность
темы

2.     Определение
килограмма

3.     26-ая
Генеральная конференция по мерам и весам

4.     Весы
Киббла

5.     Вывод
формул

6.     Старые
эталоны

7.     Ссылки
на источники

Актуальность
работы

В 21-м веке все единицы измерения, кроме единицы
массы, в соответствии с Международной системой единиц (СИ) определяются с
помощью фундаментальных физических свойств и законов. Но все еще используется
предмет, созданный людьми в 1889 году – «эталонный килограмм» или LeGrand K,
который хранится в Париже в Международном бюро мер и весов.

В
конце прошлого века ученые обнаружили, что эталон килограмма постепенно теряет
массу. С момента создания цилиндра всего потеряно около 50 микрограмм
(приблизительно вес одной ресницы). «Так как эталон – это определение
килограмма, он технически не может потерять или набрать вес. Вместо этого,
более точно сказать, что остальной мир стал немного тяжелее», – объясняет
издание. Точная причина изменения веса эталона неизвестна. Милтон предполагает,
что вес эталона изменился между 1940 и 1990 гг. .

 Очевидно, что в современном высокотехнологичном
мире даже такие, казалось бы, минимальные отклонения от эталона могут привести
к неприятным, а то и к катастрофическим последствиям.

Изменение
расчета эталона килограмма будет иметь практическую важность в области
вычислительной техники, производства, фармацевтики, климатических исследований
и других наук, где требуются точные измерения.

«Фармацевтические
компании скоро захотят использовать ингредиенты, которые нужно будет измерять с
точностью до нескольких миллионных или даже миллиардных долей грамма. Мы должны
быть готовы взвешивать вещества с такой точностью», — говорит Приор.

Определение килограмма

Килограмм-единица измерения массы, одна из
семи основных единиц Международной системы единиц (СИ).

Действующее
до мая 2019 года определение килограмма принято III Генеральной конференцией по
мерам и весам (ГКМВ) в 1901 году и формулируется так

Килограмм
— единица массы, равная массе международного прототипа килограмма.

Международный
прототип (эталон) килограмма хранится в Международном бюро мер и весов и
представляет собой цилиндр диаметром и высотой 39,17 мм из платино-иридиевого
сплава (90 % платины, 10 % иридия).

XXVI
Генеральная конференция по мерам и весам

Генеральные
конференции по мерам и весам созываются для принятия решений в Международном
бюро мер и весов для принятия решений по стандартам измерения и вопросам измерительной
науки. На ГКВМ присутствуют делегаты правительств членов и наблюдатели
ассоциированных членов. Под руководством такой каждой Конференции Международный
комитет мер и весов руководит бюро. Комитет подаёт на каждую Конференцию доклад
о проделанной работе: меры по популяризации и улучшении СИ, поддержка новых
фундаментальных метрологических определений, научные резолюции международного
характера.

Конференции
созываются обычно раз каждые 4 года, заседания проходят в Севре. Открывающая
сессия Конференций открывается председателем Французской академии наук.

XXVI
Генеральная конференция по мерам и весам (13 — 16 ноября 2018 года) одобрила
новое определение килограмма, основанное на фиксации численного значения
постоянной Планка. Решение вступит в силу 20 мая 2019 года.

Новым
эталоном килограмма стала универсальная формула, основанная на принципах
квантовой физики

Килограмм
– одна из семи единиц Международной системы единиц (СИ). На конференции в
Версале были выбраны новые эталоны еще для трех единиц измерения системы –
ампера (единица измерения силы электрического тока), кельвина (единица
измерения температуры) и моля (единица измерения количества вещества). Эти
единицы теперь привязаны к фундаментальным физическим константам.

Директор
Международного бюро мер и весов Мартин Милтон назвал принятые решения
«исторической вехой». «Фактически принимается новая система единиц, которая
будет использоваться почти во всех странах мира», – заявил он.

Ожидается,
что это изменение будет иметь важное практическое значение во многих отраслях и
науках, требующих сверхточных измерений массы. И это также будет означать конец
для так называемого «великого килограмма» – эталона, которым мы пользовались
еще с 1889 года. Изготовленный из стойкого к коррозии сплава, на 90 %
состоящего из платины и на 10 % – из иридия, международный прототип килограмма
редко видел свет. Однако его роль была просто огромной – ведь этот эталон
служил основой для общепринятой в мире системы измерения массы, от которой
зависят такие вещи, как, скажем, международная торговля.

Весы
Киббла

Весы
Киббла— прибор для установления соотношения между массой и электрической
мощностью. Использовались с середины 1970-х годов для измерения величины
постоянной Планка, в XXI веке используются для определения нового эталона
килограмма, основанного исключительно на природных величинах. Посмертно
названные в честь изобретателя, Б. Киббла.

Весы
Киббла — это усовершенствование токовых весов и представляют собой
электромеханический инструмент, где масса вычисляется через электрическую
мощность.

Этот
сложный и точный прибор предназначен для взвешивания без гирь. Весы названы в
честь британского ученого Киббла, предложившего такой метод.

В
обычных весах есть две чашки, на одну кладут взвешиваемый объект, например,
сахар, на вторую калиброванные гирьки, то есть известной массы. С точки зрения
физики в гравитационном поле Земли мы уравновешиваем две силы тяжести, действующие
на гирьку и на сахар.

Но
силу тяжести можно уравновесить с помощью другой силы. И весы Киббла — это тоже
весы, очень сложной конструкции, но весы. На одной чашке размещается груз, и на
него действует сила тяжести. А вместо второй чаши весов — электромагнитная
катушка, которая создает магнитную силу. Магнитное поле катушки взаимодействует
с полем постоянного магнита, и эта магнитная сила уравновешивает силу тяжести,
действующую на взвешиваемый объект.

Это
очень похоже на токовые весы (ампер-весы), когда измеряют величину
электрического тока в катушке и определяют магнитную силу. Однако в весах
Киббла (ватт-весах) сделан важный шаг к повышению точности. Для того чтобы
исключить погрешность, обусловленную геометрией катушки, измеряют напряжение
электромагнитной индукции при движении катушки с постоянной скоростью в том же
самом магнитном поле, что и при «взвешивании». Скорость катушки при этом
измеряют при помощи высокоточного интерферометра. Напряжение и ток сейчас
ученые умеют очень точно измерять, используя квантовые эффекты: квантовый
эффект Холла и эффект Джозефсона.

Дальше
нужен абсолютный гравиметр, чтобы знать ускорение свободного падения в том
месте, где размещается установка. Произведение массы и ускорения свободного
падения — это действующая сила тяжести в данной точке.

В
итоговой формуле расчета массы по весам Киббла кроме измеренных (см. выше)
величин входит одна фундаментальная константа — постоянная Планка

Когда
килограмм был определен через эталонную гирю, весы Киббла использовали для
наиболее точного измерения постоянной Планка. Теперь же, приняв (зафиксировав)
значение постоянной Планка равным 6,62607015×10−34 Дж·сек, можно использовать
весы Киббла для взвешивания.

Вывод
формул

Связь
между массой и постоянной Планка с теоретической точки зрения определяется
двумя формулами. Эквивалентность массы и энергии связывает энергию E и массу m:
Эквивале́нтностьма́ссы и эне́ргии — физическая концепция теории
относительности, согласно которой полная энергия физического объекта
(физической системы, тела) равна его (её) массе, умноженной на размерный
множитель квадрата скорости света в вакууме:

E=mc^2

где
c — скорость света в вакууме.

E=hu

где
h-постоянная планка,u-частота из этих формул следует,что h=mc^2/u

Отсюда
фиксируем значение h=6,62607015*10^-34

Принцип
работы ампер-весов основан на действии силы Лоренца: на провод длиной L с
протекающим по нему электрическим током I при внесении его в магнитное поле с
индукцией B, будет действовать сила величиной BLI. Если провод нагрузить массой
m, то при установлении равновесия появится соответствие между силой тока и
массой m:

mg=BLI

где
g — это ускорение свободного падения.

Точность
ампер-весов на практике ограничена точностью измерения константы BL в уравнении
выше. Киббл предложил оригинальное решение, позволяющее избежать измерения BL.
В весах Киббла измерение производится в два шага. На одном из них масса
уравновешивается током точно так же, как и в ампер-весах. На втором шаге
происходит «калибровка»: ток в проводнике (на практике, в обмотке) отключается,
проводник протягивается через то же магнитное поле с постоянной и точно
замеренной скоростью v. При этом по закону Фарадея на концах проводника
образуется напряжение:

U=BLv

Поскольку
величина BL на обоих шагах одинакова, то получаем равенство:

U/v=BL=mg/I
откуда в свою очередь:

U[1]I[2]=mgv[1]
Также это уравнение можно доказать через мощность:

P=UI

где
U-напряжение,I-сила тока.

P=A/t

где
A-работа,t-время

A=FS

где
F-сила притяжения,S-расстояние

из
этого следует,что

P=FS/t

S=vt

где
v-скорость

P=Fvtt
P=Fv F=mg

где
m-масса,g-ускорение свободного падения

P=mgv

Следовательно
U[1]I[1]=mgv[1]

где
U[1]I[2]- произведение электрического тока I[2] во время балансирования массы и
напряжения U[1] в процессе калибровки,gv[1] — произведение ускорения свободного
падения и скорости катушки v[1] во время калибровки весов. Если gv[1]
независимо замерено с высокой точностью , предыдущее уравнение по сути
определяет килограмм в зависимости от величины ватта (или наоборот).Индексы у
U[1],I[2] введены с тем, чтобы показать, что это виртуальная мощность (замеры
напряжения и тока делаются в разное время), избегая эффектов от потерь.

1)Английский
физик Б. Джозефсон в 1962 году на основе теории сверхпроводимости Бардина —
Купера — Шриффера предсказал стационарный и нестационарный эффекты в контакте
сверхпроводник-диэлектрик-сверхпроводник. Экспериментально стационарный эффект
был подтвержден американскими физиками П. Андерсоном и Дж. Роуэллом в 1963
году. Различают стационарный и нестационарный эффекты Джозефсона. В нашем
случае понадобится нестационарный.

При
пропускании через контакт тока, величина которого превышает критическую, на
контакте возникает падение напряжения U, и контакт при этом начинает излучать
электромагнитные волны. При этом частота такого излучения определяется как
w=2eU/h

где
e-заряд электрона,h-постоянная планка.

Возникновение
излучения связано с тем, что объединённые в пары электроны, создающие
сверхпроводящий ток, при переходе через контакт приобретают избыточную по
отношению к основному состоянию сверхпроводника энергию 2eU. Единственная
возможность для пары электронов вернуться в основное состояние — это излучить
квант электромагнитной энергии hw=2eU

2)Квантовый
эффект Холла (КЭХ) был открыт Клаусом фон Клитцингом в 1980 году, за что
впоследствии в 1985 году он получил Нобелевскую премию. Сам эффект состоит в
том, что на зависимости поперечного сопротивления (отношения возникающего
поперечного напряжения к протекающему току) от магнитного поля (или от
концентрации при фиксированном поле) наблюдаются плато, причем значения
сопротивления на этих плато равно

R
= h/e2,

деленное
на целые числа (называемых фактором заполнения). Фон Клитцинг обнаружил так
называемый нормальный(или целочисленный) квантовый эффект Холла. В 1982 году
Цуи и Штёрмер открыли дробный квантовый эффект Холла (фактор заполнения при
этом становится меньше единицы).

Из
эффекта Джозефсона следует, что

E=eU

где
E-энэргия,e-заряд электрона,U-напряжение

отсюда
U[1]=hu[1]/e т.к. E=hu

U[2]=hu[2]/e

По
закону Ома: I[2]=U[2]/R[2]

Из
квантового эффекта Холла следует,что R[2]=h/e^2

I[2]=e^2hu[2]/eh=u[2]e

следовательно
т.к. UI=mgv[1]

hu[1]/e*u[2]e=mgv[1]

Выразим
массу: m=hu[1]u[2]/g[1]

Поскольку
все остальные величины в этом уравнении могут быть определены независимо от
массы, оно может быть принято за определение единицы массы после фиксации значения
6,62607015×10^−34 для постоянной Планка.

Старые
эталоны

Может
показаться, что существующие сейчас эталоны, включая государственный первичный
эталон, станут не нужны. Это не так. Переход к новым определениям единиц СИ
позволяет изменить конструкцию первичных эталонов, сделав их точнее и избавив
от «артефакта», произведенного человеком. Теперь любая квалифицированная
лаборатория, обладающая достаточными финансами, может воспроизвести единицу с
высокой точностью на самом передовом уровне. Однако если точность отдельных
элементов и узлов не будет достаточной, то установка, построенная по принципу
весов Киббла, не обеспечит ожидаемую «высшую точность». Поэтому для обеспечения
единства измерений в стране, для того чтобы все измерения проводились в одних
единицах с ожидаемой точностью, требуется сохранять и совершенствовать систему
эталонов. Кроме того, весы Киббла — очень недешевое удовольствие, и для
калибровки массово применяемых рабочих средств измерений подойдут эталоны
попроще, которые используются и сегодня. А «высшая точность» окажется
востребована современными высокими технологиями в науке и промышленности.

Возникает
вопрос: если каждый может сделать эталон, по точности не уступающий первичному,
то как быть в ситуации, когда результаты воспроизведения килограмма на двух
эталонах получатся различными?

Для
этой цели метрологи всего мира проводят международные сличения, когда один и
тот же объект «взвешивают» на первичных эталонах разных государств и сравнивают
результаты. Если у кого-то результат слишком сильно отклоняется от общего
среднего, скорее всего, в работе этого эталона есть неточности и он требует
настройки. Государства, успешно завершившие международные сличения, начинают
признавать измерительные и калибровочные возможности друг друга по данному виду
измерений, а сведения об этом заносятся в базу данных Международного бюро по
мерам и весам.

Это значит, что
короля килограмма скоро будет свергнут и он займет свое место в музее рядом с
эталонами времен Людовика XVI и Французской революции. Трудно представить, что
в эпоху космических кораблей и искусственного интеллекта человечество все еще
использует изготовленный в XIX веке металлический брусок как отправную точку
для измерения массы всех предметов на Земле.

Ссылки
на источники

1.     https://www.vedomosti.ru/technology/news/2018/11/16/786696-vo–frantsii

2.     https://nag.ru/articles/article/102601/injeneram–na–zametku–utverdili–novyie–etalonyi–ampera–i–kilogramma.html

3.     http://www.vniiftri.ru/ru/news–ru/item/607-nachala–svoyu–rabotu-26-ya–generalnaya–konferentsiya–po–meram–i–vesam

4.     https://ru.wikipedia.org/wiki/Весы_Киббла

5.    
https://elementy.ru/nauchno–populyarnaya_biblioteka/434478/Rossiya_vzvesit_sama

6.     http://fb.ru/news/journalism/2018/11/15/34744