Как найти эталонный ряд

РЯДЫ

Числовой ряд
— бесконечная сумма вида

.
(1)

(необходимый
признак сходимости ряда).
Пусть ряд

сходится,
тогда

.

Замечания:
1. То есть,
если

,
то ряд (1) расходится.

2.
Этот признак необходимый, но не
достаточный.

Расходящийся
ряд с общим членом, стремящимся к нулю.

(гармонический ряд) ТЕОРЕМА
2 (признак
сравнения). Пусть ряды

(1)
и

(2)
с положительными членами удовлетворяют
условию

.
Тогда:

1.
Из сходимости ряда (2) следует сходимость
ряда (1).

2.
Из расходимости ряда (1) следует
расходимость ряда (2).

ТЕОРЕМА
3 (предельный
признак сравнения). Пусть ряды (1) и (2) с
положительными членами удовлетворяют
условию

.
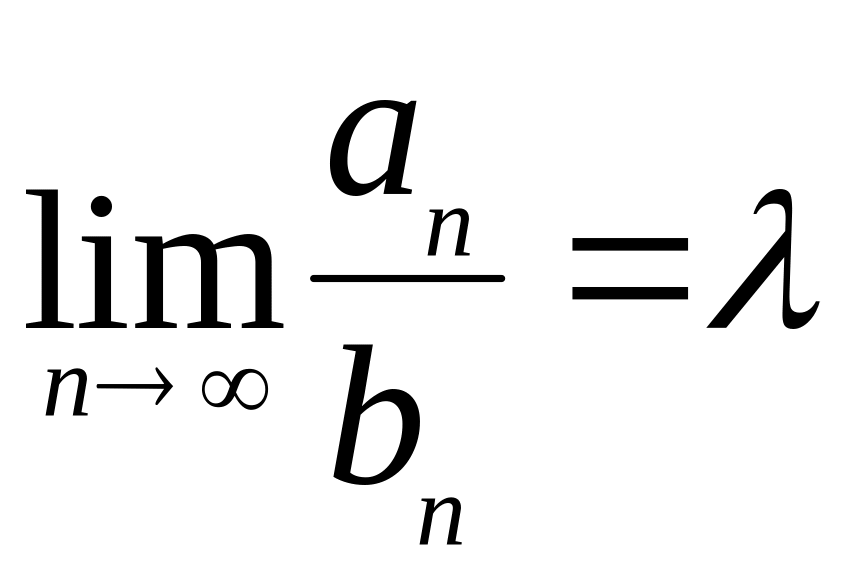
Тогда: если

,
то (1) и (2) сходятся или расходятся
одновременно. Если

,
то:

сходится
(2)

сходится (1)

расходится
(1)

расходится (2)

ТЕОРЕМА
4 (признак
Даламбера). Пусть дан ряд

с положительными членами и

,
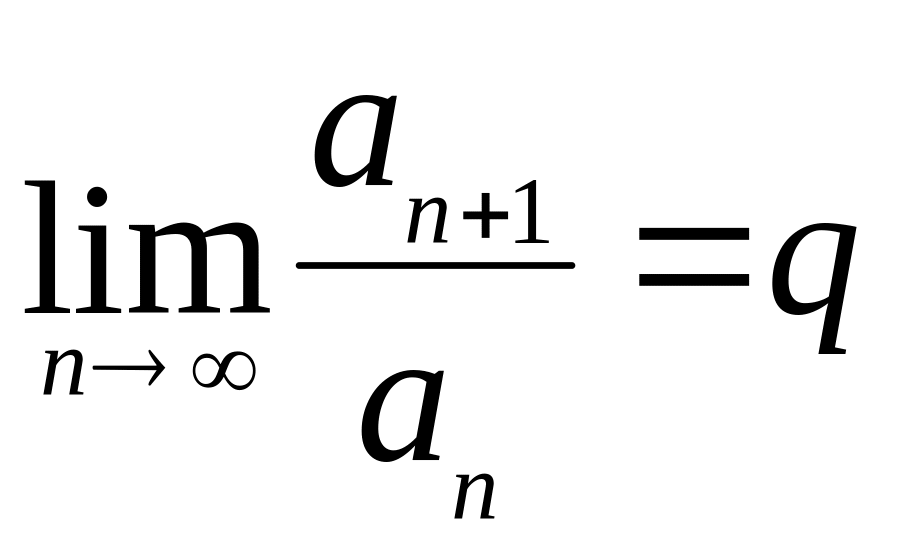
тогда: а.
при

ряд сходится;

б.
при

ряд расходится;

в.
при

признак не даёт информации о сходимости.

ТЕОРЕМА
5 (радикальный
признак Коши). Пусть дан ряд

с положительными членами и существует

,
тогда:

а.
при

ряд сходится;

б.
при

ряд расходится;

в.
при

признак не даёт информации о сходимости.

ТЕОРЕМА
6 (интегральный
признак Коши). Пусть

,
где

определена и монотонно убывает на

,
а также интегрируема на каждом конечном
промежутке из L.
Тогда: для сходимости ряда

необходима и достаточна сходимость
интеграла

.

Эталонные ряды

1.
Геометрический ряд.

2.
Обобщенный гармонический ряд.

3.
Ряд

:
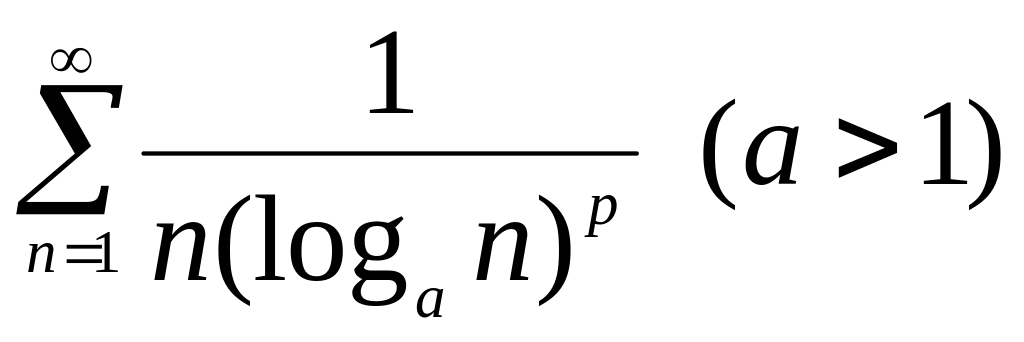
сходится при

и расходится при

.

§3. Знакопеременные ряды. Абсолютная и условная сходимости. Знакочередующиеся ряды. Признак Лейбница.

Определение.
Ряд называется знакочередующимся,
если каждые два соседние его слагаемые
имеют разный знак:

Сформируем
достаточный признак сходимости такого
ряда.

ТЕОРЕМА
1 (признак
Лейбница). Пусть ряд

знакочередующийся, последовательность

монотонно убывает и

.
Тогда ряд (1) сходится, его сумма

.

Следствие.

,
то есть погрешность приближённого
вычисления знакочередующегося ряда по
частичной сумме не превосходит абсолютной
величины первого отброшенного члена.

Пример
1. Сколько
слагаемых нужно взять, чтобы вычислить

с точностью до 0,001?

Решение.
Можно записать два неравенства:

Найдём

:

.
Ответ: 31 слагаемое.

Ряды
с произвольным членами, абсолютная и
условная сходимости.

Определение.
Ряд называется знакопеременным,
если его общий член может быть как
положительным, так и отрицательным.

Определение.
Ряд

сходится
абсолютно,
если сходится ряд

.

Определение.
Сходящийся ряд, который не сходится
абсолютно, называется условно
сходящимся.

ТЕОРЕМА
2. Из сходимости
ряда

следует сходимость ряда

.

Абсолютная
сходимость

сходимость,
сходимость

абсолютная сходимость.

Замечание.
Каждый из рассмотренных нами признаков
сходимости знакоположительных рядов
может рассматриваться как достоверный
признак абсолютной сходимости.

Члены
абсолютно сходящегося ряда можно менять
местами произвольным образом. Для
условно сходящегося — это неверно.

ТЕОРЕМА
3 (Дирихле).
Пусть ряд

сходится абсолютно и его сумма равна

.
Тогда ряд

,
полученный из

произвольной перестановкой его членов
также сходится абсолютно, причём к той
же сумме

(без доказательства).

ТЕОРЕМА
4 (Римана).
Пусть ряд

сходится условно,

. Тогда члены ряда можно переставить
так, что его сумма будет равна

.

§4 Функциональные ряды.

Определение.
Пусть

— функции, заданные на

.
Тогда ряд .

называется функциональным
рядом.

Определение.
Ряд называется

сходящимся
на множестве

,
если в каждой точке

ряд сходится как числовой.

Определение.
Функциональный ряд

равномерно
сходится на
множестве

,
если

и

.
Здесь

,

.

Пример
1. Геометрический
ряд

— сходится, если

,
расходится при

.
Рассмотрим функциональный ряд:

.
Этот ряд сходится, если

(расходится при

)
и его сумма

при

.

Определение:
Функциональный ряд

мажорируется
на множестве

сходящимся числовым рядом

,
если

ТЕОРЕМА
1 ((Достаточный)
признак Вейерштрасса равномерной
сходимости функционального ряда). Пусть
ряд

(1)
мажорируется на

сходящимся числовым рядом

(2).
Тогда ряд равномерно сходится на

.

Примеры
2-3: Функциональные
ряды

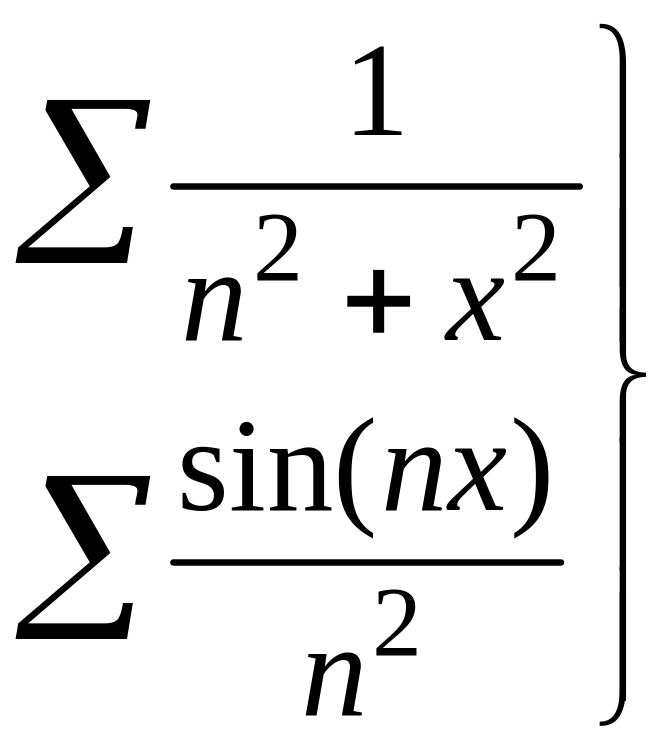
равномерно сходятся на

,
так как они мажорируются

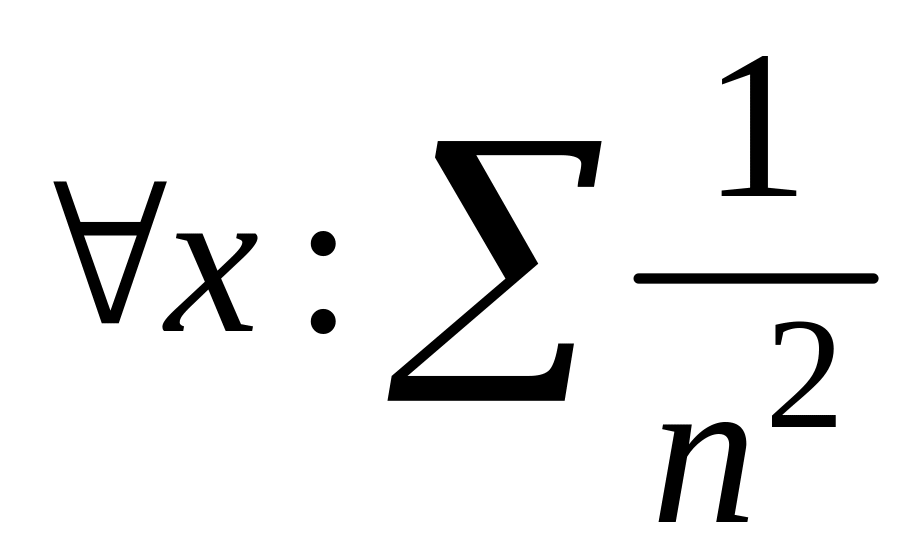
§5 Степенные ряды.

Определение.
Функциональный ряд вида

(1) называется степенным.
Здесь

—
коэффициенты,

—
центр степенного ряда. Определение:
множество

точек числовой оси, где сходится ряд
(1), называются его областью сходимости.

ТЕОРЕМА
1 (Абеля): 1)
Если степенной ряд (1) сходится в точке

,
то он сходится, причём абсолютно,

.

1. Если
   ряд расходится в точке
   
   ,
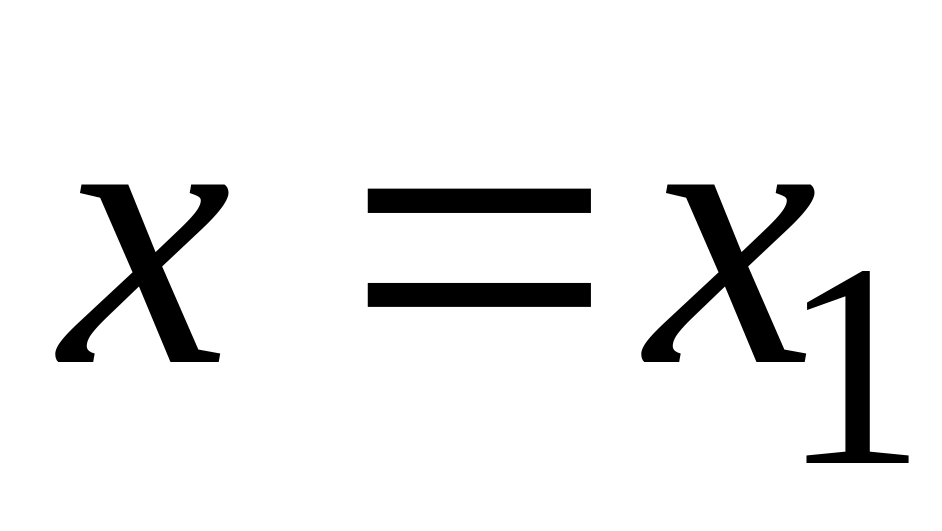
   то он расходится,
   
   .

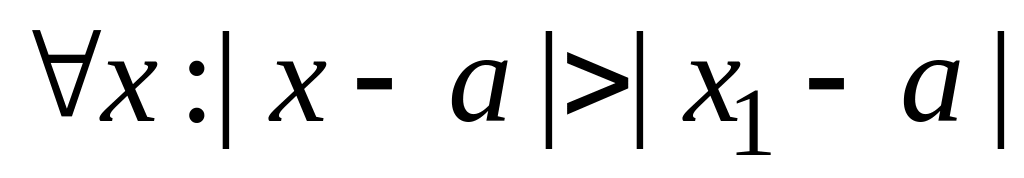
Область
сходимости степенного ряда всегда –
промежуток с центром в точке , причём
этот промежуток может являться интервалом
или полуинтервалом или отрезком.

Определение:
радиусом
сходимости
степенного ряда (1) называется число

:
при

ряд сходится, а вне этого интервала —
расходится. Если

,
то интервал вырождается в точку

(в своём центре сходится любой степенной
ряд!);

— интервал сходимости представляет
собой всю числовую ось. Сформулируем
результаты, позволяющие вычислить
радиус сходимости степенного ряда.

ТЕОРЕМА
2 (Коши-Адамар):
Пусть существует

.

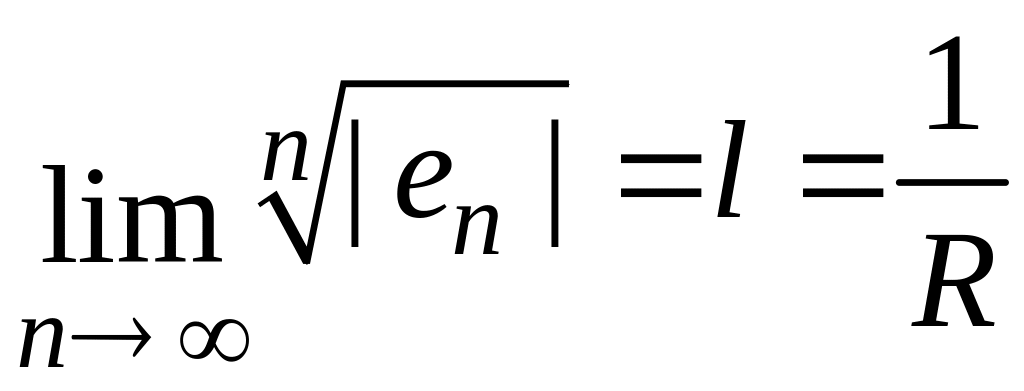
Тогда
ряд сходится при

и расходится вне этого интервала. Если

,
то

,
если

,
то

.

ТЕОРЕМА
3 (Даламбера).
Пусть

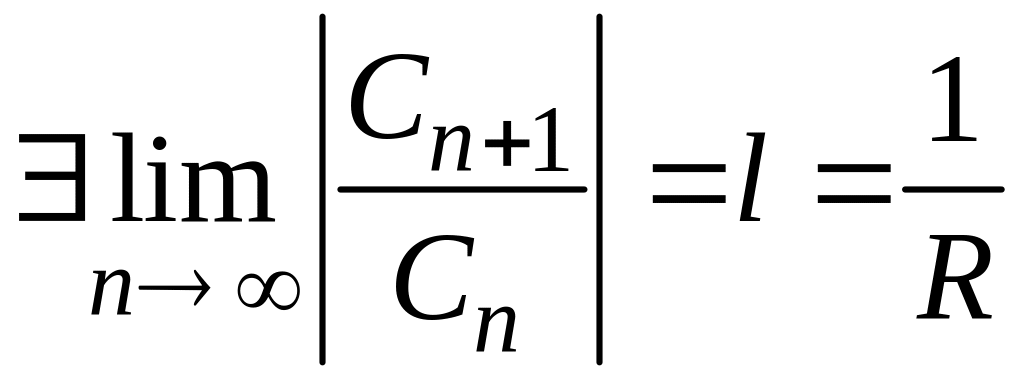
Тогда
степенной ряд (1) сходится внутри интервала

и расходится вне его.

Замечания:

1. При
   
   ,
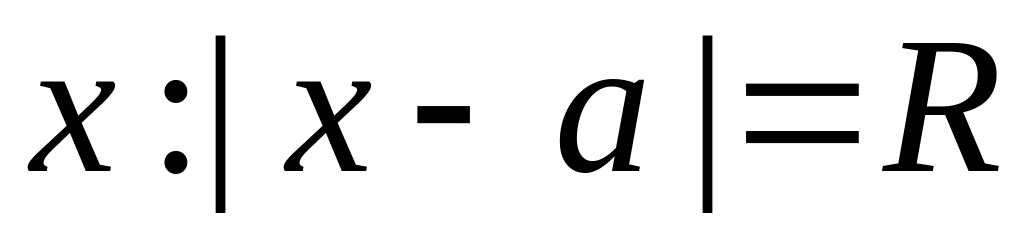
   то есть на концах интервала, теоремы 2
   и 3 ответа на вопрос о сходимости не
   дают. В этих точках требуется отдельное
   исследование.

2. В
   каждой из этих точек, как показывают
   примеры ниже, ряд может как сходиться,
   так и расходиться.

Пример
1: степенной
ряд:

.
Его

сходимости

,
при

ряд расходится как гармонический;

, сходится как ряд Лейбница. Таким образом

Определение:
интервалом
сходимости
принято называть

.

ТЕОРЕМА
4: Пусть
степенной ряд (1) сходится на интервале

.
Тогда

ряд равномерно сходится на отрезке

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Числовым рядом называется бесконечная последовательность чисел 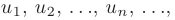формально соединенных знаком сложения:

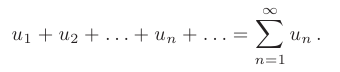
Числа 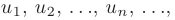называются членами ряда, а выражение 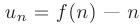-ым или общим членом ряда.

Сумма 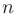первых членов ряда называется 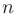-ой частичной суммой ряда:

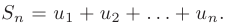
Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, являющийся суммой ряда:

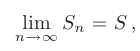
и расходящимся, если указанный предел расходится или не существует

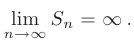
Расходящийся ряд суммы не имеет.

В качестве примеров приведем следующие числовые ряды:

• Гармонический ряд

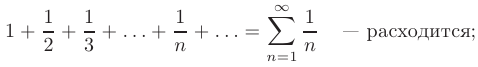
• Обобщенный гармонический ряд

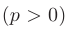
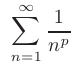
сходится при 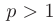, расходится при .

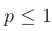• Геометрический ряд

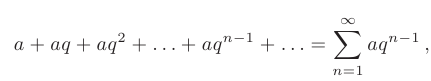
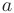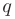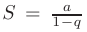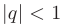где — начальный член; — знаменатель геометрической прогрессии. Геометрический ряд сходится к сумме при и расходится при .

Знакоположительные числовые ряды

Знакоположительным рядом называется ряд 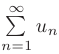, члены которого неотрицательны: .

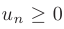Необходимый признак сходимости. Если числовой ряд сходится, то предел его общего члена 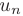при 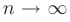равен нулю:

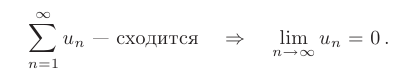
Следствие. Если предел общего члена ряда при 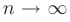не равен нулю, то ряд расходится:

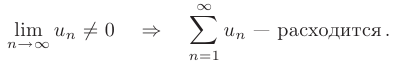
Пример:

Проверить, выполняется ли необходимый признак сходимости для числового ряда

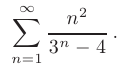
► Для проверки необходимого признака сходимости выпишем и найдем предел общего члена данного числового ряда

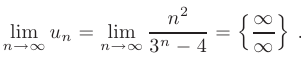
Для раскрытия неопределенности такого типа воспользуемся правилом Лопиталя:

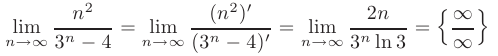
Применяя правило Лопиталя повторно, получим:

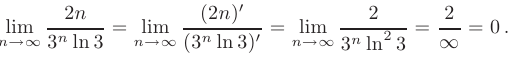
Необходимый признак сходимости для данного числового ряда выполняется, следовательно, расходимость ряда не доказана.

Признак сравнения. Пусть даны два положительных ряда 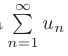и 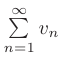. Если члены ряда 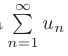не превосходят соответствующих членов ряда 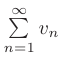т. е. 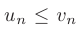при всех 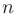, то из сходимости ряда 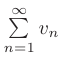следует сходимость ряда 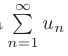, а из расходимоси ряда 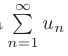следует расходимость ряда .

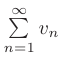Пример:

Используя признак сравнения, исследовать на сходимость числовой ряд

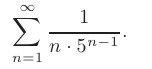
► Сравним данный ряд с рядом 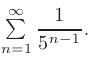Последний является геометрической прогрессией со знаменателем

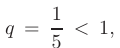
т. е. сходящимся рядом. Так как

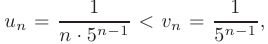
то по признаку сравнения данный числовой ряд сходится.

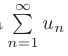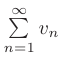Предельный признак сравнения. Если для двух знакоположительных рядов и существует конечный, отличный от нуля предел отношения их общих членов

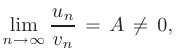
то оба ряда сходятся или расходятся одновременно.

Пример:

Используя предельный признак сравнения, исследовать на сходимость числовой ряд

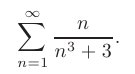
► Если общий член ряда представляет собой отношение двух многочленов, то при подборе эталонного обобщенного гармонического ряда значение 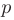выбирают равным разности наибольших показателей степеней знаменателя и числителя. Так как в нашем случае 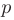= 3 — 1 = 2. то для сравнения возьмем обобщенный гармонический

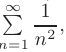
который сходится. Применяя предельный признак, найдем

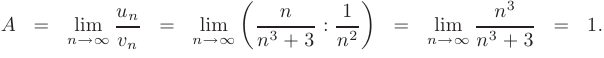
Поскольку предел 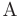конечен и отличен от нуля, то исследуемый ряд также является сходящимся.

Признак сходимости Даламбера. Если для знакоположительного ряда существует предел отношения 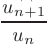при , то в зависимости от значения этого предела возможны три случая:

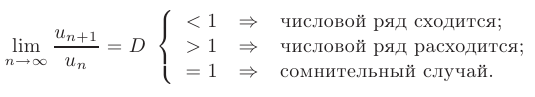
Пример:

Используя признак сходимости Даламбера, исследовать на сходимость числовой ряд

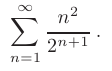
► Для проверки сходимости с помощью признака Даламбера запишем предел отношения ( + 1)-го члена к -му:

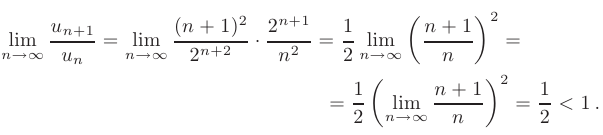
Так как предел полученного выражения меньше единицы, следовательно, данный числовой ряд сходится.

Интегральный признак Коши. Пусть члены знакоположительного числового ряда 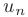соответствуют при 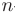= 1,2,3,… значениям некоторой функции 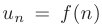, положительной, непрерывной, монотонно убывающей на интервале 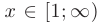. Тогда несобственный интеграл 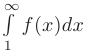и соответствующий числовой ряд 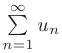сходятся или расходятся одновременно.

Пример:

Используя интегральный признак сходимости Коши, исследовать на сходимость числовой ряд

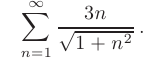
► Для проверки сходимости с помощью интегрального признака Коши запишем формулу общего члена ряда в виде функции натурального аргумента

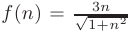
и составим соответствующую ей функцию действительного аргумента

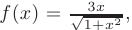
а затем вычислим несобственный интеграл от полученной функции:

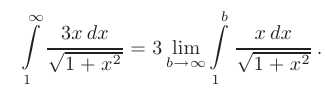
Определенный интеграл, стоящий под знаком предела, вычисляется с помощью подстановки :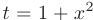

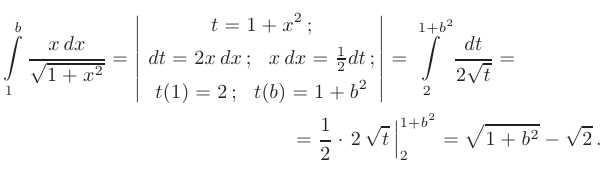
Вычисляя предел полученного выражения, приходим к выводу, что заданный числовой ряд расходится:

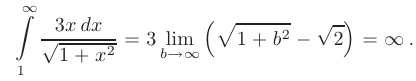
Знакопеременные ряды

Зпакочередующимся числовым рядом называется ряд

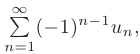
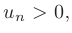
в котором любые два соседних члена имеют разные знаки.

Признак Лейбница. Пусть для знакочередующегося ряда

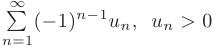
выполнены условия:

1. Члены ряда монотонно убывают по абсолютной величине:
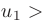
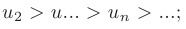
2. Общий член ряда стремится к нулю:

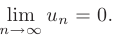
Тогда ряд сходится, причем его сумма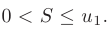

Знакопеременным числовым рядом называется ряд 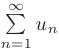, который содержит как положительные, так и отрицательные члены.

Заметим, что знакочередующийся числовой ряд является частным случаем знакопеременного числового ряда.

Ряд 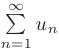называется абсолютно сходящимся, если сходится числовой ряд 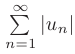— составленный из абсолютных величин его членов. Сходимость ряда 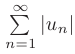влечет за собой сходимость ряда .

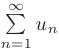Ряд 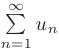называется условно сходящимся, если ряд 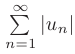расходится, а исходный ряд 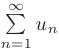сходится.

Пример:

Используя признак Лейбница, исследовать на сходимость знакочередующийся ряд. В случае сходимости ряда, определить тип сходимости.

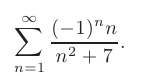
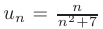► Для проверки сходимости с помощью признака Лейбница заметим, что при члены данного ряда монотонно убывают по абсолютной величине:

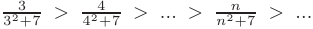
и

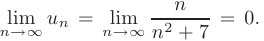
Отбрасывание конечного числа членов не влияет на его сходимость, поэтому по признаку Лейбница ряд сходится.

Определим тип сходимости ряда. Для этого исследуем сходимость ряда, составленного из абсолютных величин его членов:

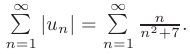
Применяя предельный признак сравнения, возьмем в качестве эталонного ряда гармонический ряд

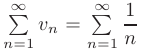
и вычислим предел

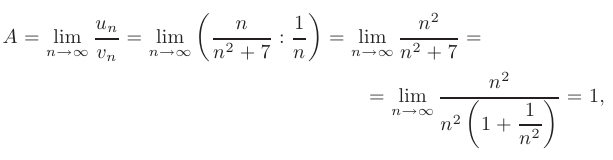
т.е. предел 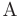конечен и отличен от нуля. Следовательно, исследуемый ряд ведет себя так же, как и эталонный ряд. Из расходимости эталонного ряда следует расходимость исследуемого ряда.

Таким образом, сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится, т.е. ряд сходится условно.

Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:

Онлайн помощь по математике

Возможно эти страницы вам будут полезны:

Признаки сравнения числовых рядов. Вторая часть.

В первой части этой темы мы начали разбирать примеры применения признаков сравнения для исследования вопроса сходимости положительных рядов. Вот два этих признака:

Первый признак сравнения

Второй признак сравнения

Пусть заданы два положительных ряда $sumlimits_{n=1}^{infty}u_n$ и $sumlimits_{n=1}^{infty}v_n$. Если при условии $v_nneq 0$ существует предел
$$lim_{ntoinfty}frac{u_n}{v_n}=K,$$
где $0 < K < infty$, то ряды $sumlimits_{n=1}^{infty}u_n$ и $sumlimits_{n=1}^{infty}v_n$ сходятся либо расходятся одновременно.

И вот два ряда, с которыми мы и будем сравнивать исследуемые в задачах ряды: обобщённый гармонический ряд

$$
begin{equation}
sumlimits_{n=1}^{infty}frac{1}{n^alpha}
end{equation}
$$

который сходится если $alpha > 1$ и расходится при $alpha ≤ 1$, а также сумма геометрической прогрессии

$$
begin{equation}
sumlimits_{n=1}^{infty}aq^n
end{equation}
$$

Ряд (2) сходится если $|q| < 1$ и расходится если $|q|≥ 1$.

На этой странице поговорим о рядах, у которых выражение общего члена ряда включает в себя некий “несущественный” элемент: $arcsin x$, $arccos x$, $arctg x$, $arcctg x$, $cos x$ или $sin x$. В вопросе исследования сходимости таких рядов нам помогут записанные ниже неравенства. Для начала отметим, что при любом $xin R$ верны такие неравенства:

$$
begin{equation}
-1≤sin x≤ 1
end{equation}
$$

$$
begin{equation}
-1≤cos x≤ 1
end{equation}
$$

$$
begin{equation}
-frac{pi}{2}<arctg x<frac{pi}{2}
end{equation}
$$

$$
begin{equation}
0<arcctg x<pi
end{equation}
$$

Если $-1≤ x≤ 1$, то:

$$
begin{equation}
-frac{pi}{2}≤arcsin x≤frac{pi}{2}
end{equation}
$$

$$
begin{equation}
0≤arccos x≤pi
end{equation}
$$

На неравества с арксинусом и арккосинусом стоит обратить особое внимание. Дело в том, что их можно применять только когда $-1≤ x≤ 1$. Поэтому перед применением неравенств (7) и (8) нужно проверить выполнение условия $-1≤ x≤ 1$. Да и вообще, если в записи общего члена ряда указан арксинус или арккосинус, то нелишне проверить его аргумент: лежит ли этот аргумент в положенном ему интервале $-1≤ x≤ 1$ или нет? То же самое касается, кстати, и иных выражений. Например, ряд $sumlimits_{n=1}^{infty}frac{5n}{n-9}$ записан с ошибкой. Посудите сами: если $n=9$, то $n-9=0$ и значит значение выражения $frac{5n}{n-9}$ будет попросту неопределено, – мы же не можем делить на ноль! Подобного рода ошибками часто страдают стандартные типовые расчёты и контрольные работы. Поэтому предварительная (пусть и устная) проверка не помешает.

В первой части мы решали все примеры двумя способами: с помощью первого и второго признаков сравнения. В этой части станем решать примеры с помощью какого-либо одного признака, – так как все эти решения, по сути, однотипны. Хотя есть примеры, где нужно применять какой-то один признак, ибо применение иного признака сравнения будет невозможным (см. пример №7) или нецелесообразным (см. пример №8).

Для вычисления пределов будем использовать методы, изложенные в теме “Пределы с иррациональностями”, а также “Предел отношения двух многочленов”.

Пример №5

Исследовать сходимость ряда $sumlimits_{n=1}^{infty}frac{arcsinfrac{7n-1}{9n}}{sqrt[6]{4n^2-3}}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{arcsinfrac{7n-1}{9n}}{sqrt[6]{4n^2-3}}$. Сразу обратим внимание, что общий член ряда записан корректно. Ноль в знаменателе или отрицательное число под корнем невозможны так как $4n^2-3 > 0$. Так как $0<7n-1<9n$, то выражение $frac{7n-1}{9n}$, которое является аргументом арксинуса, удовлетворяет неравенству $0<frac{7n-1}{9n}<1$. Т.е. аргумент арксинуса не выходит за пределы отрезка $[-1;1]$, что говорит о корректности выражения общего члена ряда. В дальнейшем такие рассуждения будем пропускать, однако проводить их (хотя бы устно) всё-таки желательно.

Ну, и так как и числитель и знаменатель общего члена ряда положительны, то $u_n > 0$, т.е. наш ряд положительный.

Выполнение необходимого условия сходимости проверять не будем. В принципе, очевидно, что так арксинус в числителе ограничен (см. формулу (7)), а знаменатель стремится к бесконечности, то $lim_{ntoinfty}u_n=0$. Обычно дело и ограничивается устной проверкой, после которой переходят к одному из признаков сходимости. В данном случае переходим к применению признаков сравнения.

Выберем ряд для сравнения. Для этого сначала проведём пару неформальных рассуждений. Если $ntoinfty$, то выражение в знаменателе общего члена ряда будет стремиться к бесконечности, т.е. $sqrt[6]{4n^2-3}toinfty$. Но что будет с числителем? А в числителе мы имеем арксинус, который удовлетворяет неравенству (7):

$$-frac{pi}{2}≤arcsinfrac{7n-1}{9n}≤frac{pi}{2}$$

В принципе, так как $0<frac{7n-1}{9n}<1$, то указанное выше неравенство можно записать более точно:

$$0<arcsinfrac{7n-1}{9n}<frac{pi}{2}$$

Иными словами, если $ntoinfty$, то арксинус не сможет выйти даже за пределы $frac{pi}{2}$, в то время как знаменатель будет уходить в бесконечность. Мысленно отбросим арксинус в числителе. А в знаменателе оставим лишь наибольшую степень $n$ (как это делалось с предыдущих примерах). Дробь $frac{arcsinfrac{7n-1}{9n}}{sqrt[6]{4n^2-3}}$ после таких преобразований примет вид $frac{1}{sqrt[6]{n^2}}=frac{1}{sqrt[3]{n}}$. Именно с рядом $sumlimits_{n=1}^{infty}frac{1}{sqrt[3]{n}}$ мы и станем сравнивать наш ряд. Так как $sumlimits_{n=1}^{infty}frac{1}{sqrt[3]{n}}=sumlimits_{n=1}^{infty}frac{1}{n^frac{1}{3}}$ и $frac{1}{3}≤ 1$, то ряд $sumlimits_{n=1}^{infty}frac{1}{sqrt[3]{n}}$ расходится. А значит будет расходиться и наш ряд. Остаётся лишь формально провести доказательство этого утверждения.

В этот раз применим признак сравнения в предельной форме. Сравнивать станем с рядом $sumlimits_{n=1}^{infty}frac{1}{sqrt[3]{n}}$. Оба общих члена сравниваемых рядов не равны нулю, поэтому в знаменателе можем размещать общий член любого ряда. В предыдущих примерах общий член “эталонного” ряда попадал всегда в знаменатель, а здесь, сугубо для разнообразия, поместим его в числитель:

$$
lim_{ntoinfty}frac{frac{1}{sqrt[3]{n}}}{frac{arcsinfrac{7n-1}{9n}}{sqrt[6]{4n^2-3}}}=lim_{ntoinfty}frac{sqrt[6]{4n^2-3}}{sqrt[3]{n}cdotarcsinfrac{7n-1}{9n}}=left|frac{infty}{infty} right|
=lim_{ntoinfty}frac{sqrt[6]{4-frac{3}{n^2}}}{arcsinfrac{7n-1}{9n}}=
frac{sqrt[6]{4-0}}{arcsinfrac{7}{9}}=frac{sqrt[3]{2}}{arcsinfrac{7}{9}}.
$$

Так как $0<frac{sqrt[3]{2}}{arcsinfrac{7}{9}}<infty$, то ряды $sumlimits_{n=1}^{infty}frac{arcsinfrac{7n-1}{9n}}{sqrt[6]{4n^2-3}}$ и $sumlimits_{n=1}^{infty}frac{1}{sqrt[3]{n}}$ сходятся либо расходятся одновременно. Так как ряд $sumlimits_{n=1}^{infty}frac{1}{sqrt[3]{n}}$ расходится, то одновременно с ним будет расходиться и ряд $sumlimits_{n=1}^{infty}frac{arcsinfrac{7n-1}{9n}}{sqrt[6]{4n^2-3}}$.

Ответ: ряд расходится.

Пример №6

Исследовать сходимость ряда $sumlimits_{n=1}^{infty}frac{arctg^2sqrt{2n^3-1}}{sqrt[4]{3n^5-2}}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{arctg^2sqrt{n^3-1}}{sqrt[4]{3n^5-2}}$. При этом и числитель и знаменатель положительны, т.е. $u_n > 0$. Следовательно, заданный нам ряд – положительный. Так как арктангенс в числителе ограничен (см. формулу (5)), а $sqrt[4]{3n^5-2}toinfty$ при $ntoinfty$, то при проверке необходимого условия сходимости мы получим, что $lim_{ntoinfty}u_n=0$. Так как эта проверка нам ничего нового не даёт (ряд может как сходиться, так и расходиться), то переходим к использованию признака сравнения.

Начнём с неформальных рассуждений для выбора ряда, с которым станем сравнивать. Если $ntoinfty$, то выражение в знаменателе общего члена ряда будет стремиться к бесконечности, т.е. $sqrt[4]{3n^5-2}toinfty$. Но что будет с числителем? А в числителе мы имеем арктангенс. Согласно формуле (5) можно записать такое неравенство:

$$
-frac{pi}{2}<arctgsqrt{2n^3-1}<frac{pi}{2}
$$

А для $arctg^2sqrt{2n^3-1}$ получим:

$$
0≤arctg^2sqrt{2n^3-1}<left(frac{pi}{2}right)^2
$$

Данное неравенство можно и уточнить. Начальное значение $arctg^2sqrt{2n^3-1}$ при $n=1$ равно

$$arctg^2sqrt{2n^3-1}=arctg^2sqrt{2-1}=arctg^21=left(frac{pi}{4}right)^2.$$

Так как арктангенс – возрастающая функция, то записанное выше неравенство станет таким:

$$
left(frac{pi}{4}right)^2≤arctg^2sqrt{2n^3-1}<left(frac{pi}{2}right)^2
$$

Итак, что мы имеем? Знаменатель стремится в бесконечность, а числитель не может превысить даже $left(frac{pi}{2}right)^2$. Мысленно отбросим арктангенс в числителе. В знаменателе оставим под корнем лишь $n^5$. Тогда дробь $frac{arctg^2sqrt{n^3-1}}{sqrt[4]{3n^5-2}}$ станет такой: $frac{1}{sqrt[4]{n^5}}$. Именно с рядом $sumlimits_{n=1}^{infty}frac{1}{sqrt[4]{n^5}}$ мы и станем сравнивать заданный ряд. Так как $sumlimits_{n=1}^{infty}frac{1}{sqrt[4]{n^5}}=sumlimits_{n=1}^{infty}frac{1}{n^frac{5}{4}}$ и $frac{5}{4} > 1$, то ряд $sumlimits_{n=1}^{infty}frac{1}{sqrt[4]{n^5}}$ сходится. Значит, и наш ряд будет сходиться. Осталось лишь строго доказать эту сходимость.

Здесь можно применять как первый, так и второй признаки сравнения. Мне удобнее применить признак сравнения в предельной форме (т.е., второй признак). Однако я укажу и решение с помощью первого признака сравнения, только скрою его под примечание в конце решения этого примера. Сравнивать станем с рядом $sumlimits_{n=1}^{infty}frac{1}{sqrt[4]{n^5}}$. Оба общих члена сравниваемых рядов не равны нулю, поэтому в знаменателе можем размещать общий член любого ряда.

$$
lim_{ntoinfty}frac{frac{arctg^2sqrt{2n^3-1}}{sqrt[4]{3n^5-2}}}{frac{1}{sqrt[4]{n^5}}}=
lim_{ntoinfty}frac{sqrt[4]{n^5}cdotarctg^2sqrt{2n^3-1}}{sqrt[4]{3n^5-2}}=left|frac{infty}{infty}right|=
lim_{ntoinfty}frac{arctg^2sqrt{2n^3-1}}{sqrt[4]{3-frac{2}{n^5}}}=frac{left(frac{pi}{2}right)^2}{sqrt[4]{3}}=
frac{pi^2}{4cdotsqrt[4]{3}}.
$$

При вычислении предела был использован тот факт, что $lim_{tto +infty}arctg t=frac{pi}{2}$. Так как $0<frac{pi^2}{4cdotsqrt[4]{3}}<infty$, то ряды $sumlimits_{n=1}^{infty}frac{arctg^2sqrt{2n^3-1}}{sqrt[4]{3n^5-2}}$ и $sumlimits_{n=1}^{infty}frac{1}{sqrt[4]{n^5}}$ сходятся либо расходятся одновременно. Так как ряд $sumlimits_{n=1}^{infty}frac{1}{sqrt[4]{n^5}}$ сходится, то одновременно с ним будет сходиться и ряд $sumlimits_{n=1}^{infty}frac{arctg^2sqrt{2n^3-1}}{sqrt[4]{3n^5-2}}$.

Как решить этот пример с помощью первого признака сравнения? показатьскрыть

Ответ: ряд сходится.

Пример №7

Исследовать сходимость ряда $sumlimits_{n=1}^{infty}frac{1}{n}sinleft(frac{2+(-1)^n}{6}cdotpiright)$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{1}{n}sinleft(frac{2+(-1)^n}{6}cdotpiright)$.

Посмотрим, какие значения может принимать $sinleft(frac{2+(-1)^n}{6}cdotpiright)$. Если $n$ – чётное число, то $(-1)^n=1$, поэтому:

$$
sinleft(frac{2+(-1)^n}{6}cdotpiright)=sinleft(frac{2+1}{6}cdotpiright)=sinfrac{pi}{2}=1.
$$

Если же $n$ – нечётное число, то $(-1)^n=-1$, тогда синус станет таким:

$$
sinleft(frac{2+(-1)^n}{6}cdotpiright)=sinleft(frac{2-1}{6}cdotpiright)=sinfrac{pi}{6}=frac{1}{2}.
$$

Как видите, синус в данной ситуации выступает как простой числовой коэффициент, который равен то 1, то $frac{1}{2}$. Кстати, отсюда следует, что наш ряд положительный и мы можем применить признаки сравнения. Выберем ряд для сравнения. Отбросив синус, который, по сути, является простым числовым коэффициентом, получим ряд для сравнения: $sumlimits_{n=1}^{infty}frac{1}{n}$. Это гармонический ряд. Он расходится, поэтому и наш ряд будет расходиться. Однако применить второй признак сравнения (предельный признак) мы в этой ситуации не можем. Судите сами:

$$
lim_{ntoinfty}frac{frac{1}{n}sinleft(frac{2+(-1)^n}{6}cdotpiright)}{frac{1}{n}}=
lim_{ntoinfty}sinleft(frac{2+(-1)^n}{6}cdotpiright)
$$

Полученный предел не существует, так как при $ntoinfty$ синус для четных $n$ принимает значение 1, а для нечётных – значение $frac{1}{2}$. Значит ли это, что наш ряд расходится? Вовсе нет, – это говорит лишь о том, что нужно применять первый признак сравнения. Так как $sinleft(frac{2+(-1)^n}{6}cdotpiright)≥frac{1}{2}$, то:

$$
frac{1}{n}sinleft(frac{2+(-1)^n}{6}cdotpiright)≥frac{1}{2}cdotfrac{1}{n}.
$$

Так как ряд $sumlimits_{n=1}^{infty}frac{1}{n}$ расходится, то будет расходиться и ряд $sumlimits_{n=1}^{infty}left(frac{1}{2}cdotfrac{1}{n}right)$. Так как ряд $sumlimits_{n=1}^{infty}left(frac{1}{2}cdotfrac{1}{n}right)$ расходится и $frac{1}{n}sinleft(frac{2+(-1)^n}{6}cdotpiright)≥frac{1}{2}cdotfrac{1}{n}$, то согласно первому признаку сравнения (пункт №1) ряд $sumlimits_{n=1}^{infty}frac{1}{n}sinleft(frac{2+(-1)^n}{6}cdotpiright)$ расходится.

Ответ: ряд расходится.

Пример №8

Исследовать сходимость ряда $sumlimits_{n=1}^{infty}frac{2^{3n}+cos n!}{5^{2n+1}-n}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{2^{3n}+cos n!}{5^{2n+1}-n}$. Так как согласно формуле (4) имеем $-1≤cos n!≤ 1$, то $2^{3n}+cos n!≥ 1$. Так как $5^{2n+1}-n > 0$ (это легко доказать, например, методом математической индукции), то наш ряд – положительный, т.е. $u_n≥ 0$.

С каким рядом станем сравнивать заданный ряд? Давайте отбросим все “несущественные” элементы для дроби $frac{2^{3n}+cos n!}{5^{2n+1}-n}$. В числителе выкинем косинус, а в знаменателе отбросим $n$. Дело в том, что порядок роста $n$ меньше, чем $5^{2n+1}$. Например, если $n=5$, то $5^{2n+1}=48,828,125$. После всех “отбрасываний” у нас останется $frac{2^{3n}}{5^{2n+1}}=frac{left(2^3right)^n}{5cdot left(5^2right)^n}=frac{1}{5}left(frac{8}{25}right)^n$. В принципе, и множитель $frac{1}{5}$ можно смело убрать, так как на сходимость он не повлияет.

Итак, мы станем сравнивать наш ряд с рядом $sumlimits_{n=1}^{infty}left(frac{8}{25}right)^n$. Это ряд вида (2), т.е. сумма элементов геометрической прогрессии с знаменателем $frac{8}{25}$. Так как $left|frac{8}{25}right|< 1$, то ряд $sumlimits_{n=1}^{infty}left(frac{8}{25}right)^n$ сходится.

Здесь можно применять как первый признак сравнения, так и второй. Однако проще использовать неравенства, т.е. применить первый признак сравнения (если есть необходимость рассмотреть применение второго признака сравнения, то отпишите об этом на форум). Если мы вместо $cos n!$ в числителе напишем $2^{3n}$, то увеличим данную дробь:

$$
frac{2^{3n}+cos n!}{5^{2n+1}-n} < frac{2^{3n}+2^{3n}}{5^{2n+1}-n}=2cdotfrac{2^{3n}}{5^{2n+1}-n}.
$$

Так как $n < frac{1}{2}5^{2n+1}$ (это можно доказать методом математической индукции, если есть необходимость рассмотреть здесь это доказательство, то отпишите об этом на форум), то $5^{2n+1}-n > 5^{2n+1}-frac{1}{2}5^{2n+1}=frac{1}{2}5^{2n+1}$. Уменьшая знаменатель мы увеличиваем дробь:

$$
frac{2^{3n}+cos n!}{5^{2n+1}-n} < 2cdotfrac{2^{3n}}{5^{2n+1}-n} < 2cdotfrac{2^{3n}}{frac{1}{2}cdot 5^{2n+1}}=4cdot frac{2^{3n}}{5^{2n+1}}=frac{4}{5}cdotleft(frac{8}{25}right)^n.
$$

Так как ряд $sumlimits_{n=1}^{infty}left(frac{4}{5}cdotleft(frac{8}{25}right)^nright)$ сходится и $frac{2^{3n}+cos n!}{5^{2n+1}-n} < frac{4}{5}cdotleft(frac{8}{25}right)^n$, то согласно первому признаку сравнения (пункт №2) ряд $sumlimits_{n=1}^{infty}frac{2^{3n}+cos n!}{5^{2n+1}-n}$ сходится.

Ответ: ряд сходится.

Продолжение темы исследования сходимости рядов с помощью признаков сравнения рассмотрим в третьей части.