- Понятие ренты
- Формы земельной ренты
- Абсолютная
- Монопольная
- Дифференциальная
- Факторы земельной ренты
- Виды ренты
- Отличие от аренды и купли-продажи
- Договор ренты
- Риски договора
- Как оформить земельную ренту
Многие мечтают получать пассивные поступления. Кто-то формирует их за счет накоплений на банковских вкладах и живет на проценты. Однако есть и те, кто пользуется рентой: передает свою недвижимость в собственность в обмен на гарантированное материальное обеспечение.
Особого внимания заслуживает земельная рента. Разбираемся с данным понятием в материале.

Понятие ренты
Понятие «рента» предстает в разных значениях. Так называют пассивные поступления, к примеру, с ценных бумаг или недвижимости. Также есть и другие значения термина.
- Ресурсная предполагает зависимость государства от поступлений с добычи полезных ископаемых.
- Правоотношения, в которых актив переходит от одного лица к другому в обмен на обязательные выплаты.
Выделение земельной ренты как самостоятельной категории – условное. Оно связано лишь с тем, что передаваемым объектом выступает земельный участок. Это доход, уплачиваемый в обмен на получение собственности на землю.
Формы земельной ренты
Форма предполагает тот или иной характер взаимоотношений между плательщиком и получателем земельной ренты. Выделяют абсолютную, монопольную и дифференциальную.
Абсолютная
Абсолютная рента предполагает выплаты независимо от уровня использования участка, а также плодородности земли. Плательщику нужно зарабатывать с участка столько, сколько хватит для покрытия обязательных платежей.
Монопольная
Данный формат возникает, если на участке выращивают уникальные культуры или добывают полезные ископаемые, продать которые можно по нерыночной цене. Условия договора здесь привязывают к итоговой стоимости.
Дифференциальная
Дифференциальная предполагает, что размер платежей зависит не только от площади и расположения участка, но и от дополнительных затрат, которые влияют на итоговый размер прибыли.
Рента предполагает ежемесячные выплаты в обмен на передачу права собственности на ваш актив. Часто ее оформляют из-за нехватки средств на текущие расходы. Однако с вещью можно не расставаться, а начать экономить грамотно с помощью карты «Халва». Подайте заявку онлайн и оформляйте беспроцентную рассрочку, получайте кешбэк и процент на остаток.
Халва знает, как заставить цвести ваше «денежное дерево» в любых условиях: покупать в беспроцентную рассрочку товары в более чем 250 000 магазинах-партнерах на сумму до 500 000 рублей, получать кешбэк до 10% и приумножать сбережения в удобной онлайн-копилке до 8% годовых. Оформите карту и получите «золотой ключик» финансового благополучия!
Факторы земельной ренты
Факторы влияют на итоговый размер. Среди них выделяют:
- климатические условия (почва, осадки и проч.);
- степень плодородности земли;
- локация (насколько далеко или близко расположена земля к месту сбыта продукции. Также, к примеру, ценность расположения может повышаться за счет приближенности водоемов).
Необходимо отметить, что обязательства могут исполняться в нескольких формах:
- денежная – выплаты и периодичность определяются договором;
- натуральная – выплачивается продукцией;
- отработочная – встречно выполняют работы или оказывают услуги.
Виды ренты
Законом предусмотрено несколько категорий.
- Постоянная.
Предполагает уплату платежей на бессрочной основе. Может передаваться по наследству физическим лицам, а также при реорганизации юридического лица. Получатели — те, кто передает землю — физические лица или НКО.
В экономическом смысле использование конструкции уместно, если потенциальная доходность объекта недвижимости, то есть земли, выше, чем платежи по договору.
Остановить рентные платежи можно, если плательщик примет решение ее выкупить и согласует цену.

- Пожизненная.
Ограничена сроком жизни получателя, передавшего имущество. Учитывая данное обстоятельство, точную сумму выплат по ренте определить невозможно. Поэтому плательщик сталкивается с риском получить убыток от такого приобретения.
Учитывая, что период платежей ограничен сроком жизни гражданина, очевидно, что пожизненная форма не предполагает наследования.
- Пожизненное содержание с иждивением.
Предполагает не только периодические платежи до конца жизни, но и обеспечение потребности в жилище, питании, одежде, лечении и уходе за гражданином. В рамках данных выплат законодательство предусматривает даже оплату ритуальных услуг при погребении гражданина.
Пожизненное содержание с иждивением часто реализуется так, что получатель остается на своем участке или в квартире. Поэтому эффективное полезное использование имущества при жизни рентополучателя невозможно. Но выгода заключается в цене объекта. После смерти ее можно будет выгодно продать.
Отличие от аренды и купли-продажи
Купля-продажа предполагает переход права собственности на земельный участок или иную недвижимость в обмен за денежную плату от нового собственника. Точная цена соглашения определена, чего нельзя сказать о договоре ренты, стоимость которого зависит от момента выкупа или момента смерти прежнего собственника.
Также разница заключается в форме сделки: договор предполагает удостоверение у нотариуса, тогда как сделку купли-продажи не обязательно удостоверять. Переход права собственности на недвижимость по ренте требует регистрации, аналогично купле-продаже — это сходство данных сделок.
Сделки по купле-продаже более привычны рядовым гражданам, особенно для крупных покупок вроде квартиры. Часто их оформляют с помощью кредитных средств. В Совкомбанке можно оформить ипотеку на привлекательных условиях. Рассчитайте платежи на калькуляторе, выберете оптимальную программу и оставьте заявку на сайте банка.

Аренда — обязательственные отношения. Она предполагает владение и пользование участком, но не распоряжение им. Также соглашения по аренде носят срочный характер, тогда как рента прекращается с наступлением события, которое может случиться в любой момент.
Из общих черт можно выделить то, что есть регулярные платежи: рента или арендная плата. Также отметим, что ее получают граждане и некоммерческие организации, тогда как по аренде нет ограничений среди сторон соглашения.
Договор ренты
Договор содержит следующие существенные условия:
- Стороны.
Плательщик ренты — физическое или юридическое лицо, может быть как коммерческая, так и некоммерческая организация. По пожизненной ренте или пожизненному содержанию с иждивением — только физическое лицо, по постоянной — физическое лицо или НКО.
- Предмет.
Может выступать не только земельный участок, но и иное имущество, включая денежные средства, ценные бумаги и иные активы. Главное, чтобы предмет был индивидуально определен.
В случае с участком должны быть описаны его площадь, кадастровый номер, местоположение, целевое назначение использования, например, земли населенных пунктов.
Ограничение по предмету в соглашении о пожизненном содержании с иждивением. Здесь предметом выступает строго недвижимое имущество.
- Обеспечение обязательств.
Если передается недвижимость, то в силу ст. 587 ГК РФ у рентополучателя появляется право залога на эту недвижимость. Это означает обременение, когда рентополучатель не может в полной мере распоряжаться полученным имуществом без согласия плательщика.
Кроме того, залог предполагает право требования земельного участка или иного объекта в том случае, если рентоплательщик нарушает свои обязательства.
К примеру, Георгий Иванович заключил договор пожизненной ренты и передал землю Алексею. Алексей обязался вносить платежи по 50 000 рублей ежемесячно. Если Алексей пропустил два платежа, то Георгий Иванович, согласно условиям соглашения, может потребовать землю назад.
При передаче другого имущества плательщик ренты должен обеспечить исполнение обязательств поручительством, неустойкой, страхованием.
Помните о необходимости удостоверить соглашение у нотариуса, иначе оно будет признано недействительным.
Уместно детализировать в договоре ренты ее стоимость, порядок уплаты платежей, порядок выкупа, условия для одностороннего отказа от сделки, условия о конфиденциальности, права, обязанности, обстоятельствах непреодолимой силы и проч.
Риски договора
Договор ренты, поскольку его срок определяется наступлением или не наступлением события, — рисковый или алеаторный. К этой же группе соглашений, к примеру, относятся обязательства из игр и пари.
Среди основных рисков стоит выделить:
- Несоблюдение формы.
Если нотариальная форма не была соблюдена или не было государственной регистрации перехода права собственности, то сделку признают недействительной. Стороны вернутся в первоначальное положение: то есть отдадут все, что передали по сделке. Только не факт, что у рентополучателя будут эти деньги.
- Претензии родственников.
У рентополучателя могут быть наследники. Они не заинтересованы в том, чтобы его участок уходил третьему лицу, пусть и под выплаты ренты. Поэтому стоит ждать признания этой сделки недействительной. Если перед вами пожилой человек, и такой риск возможен, то запросите справку из психоневрологического диспансера, полученного незадолго до сделки.
- Расторжение договора.
Плательщику нужно письменно (чеки, расписки, квитанции) фиксировать факт выполнения обязанностей. Иначе есть риск, что получатель ренты обратится в суд с целью расторгнуть соглашение из-за нарушений его условий плательщиком.
- Снижение привлекательности земли.
Стоимость земли не всегда идет в гору, она снижается в силу экономических потрясений: кризисов, военных конфликтов и т.д. Поэтому сделка для рентоплательщика станет нецелесообразной.
- Неопределенность по срокам и сумме.
В теории платежи в пользу прежнего собственника могут превысить стоимость недвижимости. Также в теории плательщик может прожить меньше рентополучателя. Тогда его обязательства переходят наследнику.

Как оформить земельную ренту
- Выбрать вид.
- Согласовать условия сделки, включая размер и вид платежей, порядок расторжения соглашения.
- Обратиться к нотариусу за удостоверением соглашения. Если это недвижимость, то действие происходит по месту ее нахождения. Нотариус не только удостоверит договор, но и проверит стороны сделки (удостоверение личности, дееспособность), а также разъяснит смысл договора, зачитает его содержание. При удостоверении делается соответствующая надпись нотариуса.
- Далее следует этап оформления смены собственника. Для этого нотариус обращается в Росреестр с электронным заявлением.
Земельная рента — это действенный механизм, используемый в экономике, особенно для тех, кто хочет быстро стать собственником недвижимости. Однако не стоит забывать о рисках.
Соблюдайте форму сделки и максимально подробно фиксируйте факт выполнения обязательств по нему, тогда у вас появится шанс заработать на рентных отношениях.
Получатели
поступлений оценивают свой доход
суммарной величиной за полный срок
действия платежа, разумеется, с учетом
временной неравноценности денег.
Наращенная
сумма
– сумма всех платежей с начисленными
на них процентами к концу срока ренты.
Это может быть обобщенная сумма
задолженности, итоговый объем инвестиций
и т.п.
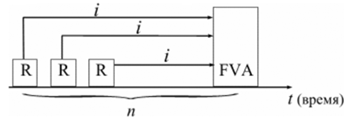
Логика
финансовой операции наращения финансовой
ренты
Наращенные
отдельные платежи представляют собой
члены геометрической прогрессии с
первым членом равным R
и множителем равным (1 + i).
Рассмотрим
определение наращенной суммы на примере
наиболее простого случая, – годовой
постоянной обычной ренты:

где
FVA
– наращенная сумма ренты;
R
– размер члена ренты, т.е. размер
очередного платежа;
i
– годовая процентная ставка, по которой
на платежи начисляются сложные проценты;
n
– срок ренты в годах,
s
n;i
– коэффициент наращения ренты.
Пример.
На счет в банке в течении пяти лет в
конце каждого года будут вноситься
суммы в размере 500 руб., на которые будут
начисляться проценты по ставке 30%.
Определить сумму процентов, которую
банк выплатит владельцу счета.
Решение:
Поскольку
период ренты равен одному году, то это
годовая
рента; проценты начисляются один раз в
год; взносы будут в конце периода ренты,
постнумерандо, значит это обычная
рента; сумма платежа постоянна на
протяжении всего срока ренты, что
характерно для постоянной
ренты; число членов ренты пять, т.е.
конечно, следовательно, ограниченная
рента; а выплаты носят безусловный
характер, таким образом, это верная
рента.
Сумма
всех взносов с начисленными процентами
будет равна:
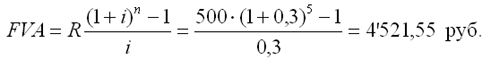
Расчет современной
стоимости постоянной годовой ренты
ПОСТНУМЕРАНДО при начислении % один раз
в год.
Помимо
наращенной суммы обобщающей характеристикой
потока платежей является современная
величина. Современная
(текущая) величина потока платежей
(капитализированная или приведенная
величина) – это сумма платежей,
дисконтированных на момент начала ренты
по ставке начисляемых сложных процентов.
Это важнейшая характеристика финансового
анализа, т.к. является основой для
измерения эффективности различных
финансово-кредитных операций, сравнения
условий контрактов и т.п. Данная
характеристика показывает, какую сумму
следовало бы иметь первоначально, чтобы,
разбив ее на равные взносы, на которые
начислялись бы установленные проценты
в течение всего срока, можно было бы
получить указанную наращенную сумму.

Логика
финансовой операции определения
современной величины потока платежей
В
этом случае реализуется схема
дисконтирования: все элементы с помощью
дисконтных множителей приведены к
одному моменту времени, что позволяет
их суммировать.
В
простейшем случае, для годовой обычной
ренты с выплатами в конце каждого года,
когда момент оценки совпадает с началом
ренты, современная величина финансовой
ренты равна:
![]()
Дробь
в формуле – коэффициент
приведения ренты
(an;i),
значения которого табулированы для
широкого круга значений, поскольку
зависят от ставки процентов (i)
и от числа лет (n)
(Приложение
5).
Пример.
Определить по данным примера современную
величину ренты.
Решение:
Современная
величина ренты составит:
![]()
Таким
образом, все производимые в будущем
платежи оцениваются в настоящий момент
в размере 1’217,78 руб.
16.
Расчет
наращенной суммы постоянной p-срочной
ренты ПОСТНУМЕРАНДО при начислении % m
раз в год (p=m)
Бывают
случаи, когда рентные платежи вносятся
несколько раз в год равными суммами
(срочная рента), а начисление процентов
производится только раз в году. Тогда
наращенная величина ренты будет
определяться по формуле:

Также
нередки случаи, когда рентные платежи
вносятся несколько раз в году и начисление
процентов также происходит несколько
раз в год, но число рентных платежей не
равно числу периодов начисления
процентов, т.е. p
≠ m.
Тогда формула по которой можно определить
наращенную величину финансовой ренты
примет вид:

На
практике большее распространение
получил поток постнумерандо, поскольку
согласно общим принципам учета принято
подводить итоги и оценивать финансовый
результат операции или иного действия
по окончании очередного отчетного
периода. Что же касается поступления
денежных средств в счет оплаты, то на
практике они чаще всего распределены
во времени неравномерно и поэтому для
удобства все поступления относят к
концу периода, что позволяет использовать
формализованные алгоритмы оценки.
Поток
пренумерандо имеет значение при анализе
различных схем накопления денежных
средств для последующего их инвестирования.
Рента
пренумерандо отличается от обычной
ренты числом периодов начисления
процентов. Поэтому наращенная сумма
ренты пренумерандо будет больше
наращенной суммы обычной ренты в (1 + i)
раз.
Для
годовой ренты пренумерандо с начислением
процентом один раз в год формула примет
вид:

Для
годовой ренты пренумерандо с начислением
процентов несколько раз в год:

Расчет современной
стоимости постоянной p-срочной
ренты ПОСТНУМЕРАНДО при начислении % m
раз в год (p=m).
Рассмотрим
расчет современной величины ренты для
различных ее видов:
-
годовая
рента с начислением процентов несколько
раз в год:

-
срочная
рента при начислении процентов один
раз в год:

-
срочная
рента с неоднократным начислением
процентов в течение года, при условии,
что число выплат не равно числе
начислений, т.е. p
≠ m
:

17. Определение
размера очередного платежа постоянной
финансовой ренты ПОСТНУМЕРАНДО (p=m=1)
Последовательные
платежи в виде постоянной обычной
годовой ренты определяются основными
параметрами:
R
– размер платежа;
n
– срок ренты в годах;
i
– годовая ставка процентов.
Однако
при разработке условий финансовой
операции могут возникать ситуации,
когда заданной величиной является одна
из двух обобщающих характеристик и
неполный набор параметров ренты. В таких
случаях находят недостающий параметр.
При
определении члена
ренты
возможны два варианта, зависящие от
того, какая величина является исходной:
а)
наращенная
сумма.
Если сумма долга определена на какой-либо
момент в будущем (FVA),
тогда величину последующих взносов в
течение n
лет при начислении на них процентов по
ставке i можно определить по формуле:

Пример.
Для покупки автомобиля через 5 лет
потребуется 50 тыс. руб. Определите размер
ежегодных взносов, вносимых в конце
каждого года в банк, который начисляет
проценты по ставке 40%.
Решение:
В
данном случае известна наращенная
величина постоянной финансовой ренты,
поэтому размер ежегодных взносов будет
равен:

Таким
образом, чтобы накопить на счете
необходимую сумму для покупки автомобиля
следует в конце каждого года в течении
пяти лет откладывать 4’568 руб.
б)
современная величина финансовой ренты,
тогда, исходя из ставки процента и срока
ренты, разовый платеж находится по
формуле:

Пример.
Сумма 10 тыс. долларов предоставлена в
долг на 5 лет под 8% годовых. Определить
ежегодную сумму погашения долга.
Решение:
Известна
современная величина долга, отсюда:

Таким
образом, ежегодно необходимо будет
возвращать сумму 2’504,56 руб.
Можно
произвести проверку: сумма долга с
начисленными на нее процентами к концу
пятого года будет составлять:
FV
= 10’000 • (1 + 0,08)5
= 14’693,28 руб.
Наращенная
сумма для потока платежей размером
2’504,56 руб. составит:

Следовательно,
величина члена финансовой ренты
определена верно. Незначительное
расхождение вызвано округлением
расчетов.
Современная
величина ренты пренумерандо рассчитывается
путем умножения современной величины
обычной ренты на соответствующий
множитель наращения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача 1
Родители планируют, что их ребенок через 8 лет поступит в
университет, где за обучение надо платить в течение 5 лет по 700 у.е. каждое
полугодие. Какую сумму должны сегодня родители положить в банк под 6% годовых, начисляемых
ежемесячно, чтобы оплатить обучение?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Кредит 10000 руб. на 5 лет
под 10% погашается разовым платежом в конце срока. Рассчитать размер взноса в
погасительный фонд, если банковская ставка 15%.
Задача 3
Какова приведенная
стоимость аннуитета постнумерандо с изменяющимся денежным потоком общей
продолжительностью 10 лет, имеющего нулевые поступления в первые три года и
равные поступления в 1000 долл. в оставшиеся годы, если рыночная норма прибыли
равна 8% для первых трех лет и 10% для оставшихся семи лет?
Задача 4
Родители планируют, что их
ребенок через 6 лет поступит в колледж, где за обучение надо платить по 1200
д.е. в год. Какую сумму должны сегодня родители положить в банк, под 6,5%
годовых, начисляемых ежемесячно, чтобы оплатить обучение в течение 4 лет?
Задача 5
Найти приведенную
стоимость “А” ренты постнумерандо, выплачиваемой в течение
лет с
годовыми аннуитетами
при
годовой процентной ставе
. (“А” рассчитать с точностью до
копеек).
Задача 6
Вам предлагают вложить 250
тыс. руб. в некий проект, рассчитанный
на 15 лет. Ожидаемые доходы по проекту таковы: в течение первых четырёх лет по
24 тыс. руб. в год, в последующие годы- 30 тыс. руб. в год (схема постнумерандо).
Стоит ли принимать это предложение и почему, если приемлемая норма прибыли- 8%
(в ответе привести значение критерия)?
Задача 7
В конце каждого полугодия
учебного года в течение следующих пяти лет студенту университете придется
платить за обучение по 2250 евро. Сколько нужно иметь денег в наличии на начало
поступления в университет, чтобы покрыть эту сумму. Процентная ставка по
депозитам в евро составляет 5,8%.
Задача 8
Клиент предложил оплатить
выполненную работу одним из двух способов: а) единовременно получить 5000 долл.
или б) два года спустя получать бесконечно долго по 500 долл. ежегодно в конце
каждого года. Какой вариант более предпочтителен, если приемлемая норма прибыли
8%?
Задача 9
На счет в банке в течение двух лет в конце каждого года будут
вноситься суммы в размере 3000 руб., на которые ежеквартально будут начисляться
проценты по ставке 16% годовых. Определить современную стоимость аннуитета.
Задача 10
При аварии на химическом
заводе в Индии корпорация «Union carbide» первоначально предложила в качестве
компенсации пострадавшим 200 млн. дол., выплачиваемых в течение 35 лет
ежемесячно. Правительство Индии требовало 85 млн. дол. Имело ли смысл принимать
предложение корпорации, если банковская процентная ставка 6%.
Задача 7
Ожидается, что доходы от
эксплуатации месторождения полезных ископаемых составят 0,8 млрд. руб. в год,
продолжительность разработки 12 лет. Отгрузка и реализация продукции непрерывны
и равномерны. Есть ли необходимость осваивать это месторождение, если оно
потребует вложений в 4,4 млрд. руб., а доходность по государственным
безрисковым ценным бумагам 12%.
Задача 8
В конце каждого полугодия
учебного года в течение следующих пяти лет студенту университета придется
платить за обучение 2250 евро. Сколько нужно иметь денег в наличии на начало
поступления в университет, чтобы покрыть эту сумму. Процентная ставка по
депозитам в евро составляет 5,8%.
Задача 9
Семья имела на банковском
счете 500 000 р., на который ежемесячно начислялся 1%. Отбыв в трехлетнюю
командировку, она доверила банку потратить весь счет на содержание сына.
Сколько в месяц будет получать сын?
Задача 10
Кредит в сумме 4 млн. р,
взятый на покупку квартиры, выплачивается в течение 15 лет ежемесячными
выплатами
при
годовой ставке 10% с ежеквартальной капитализацией процентов. Найти
.
Задача 11
Какую сумму нужно положить
в банк под 9% мужчине 47 лет, чтобы по достижении им возраста 60 лет получать в
конце каждого месяца 10 тыс. руб. в течение 10 лет при ежеквартальной
капитализации процентов?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 12
Найти цену ежегодной ренты, выплачиваемой в конце каждого года в
течение 10 лет с ежегодной суммой 150 у.д.е., если процентная ставка равна 12
%.
Задача 13
Найти цену ежегодной пожизненной ренты с правом наследования,
выплачиваемой в конце каждого года суммой 350 у.д.е., если годовая учётная
ставка равна 8%.
Задача 14
Определить современную стоимость потока ренты пренумерандо, если
ставка 23% годовых, период ренты квартал, срок ренты 1 год. Платежи 1500, 2000,
2500 у.е.
Задача 13
При заключении нового договора было решено заменить единовременный
платеж в размере 110 000 руб. (который должен был быть выплачен в день
заключения нового договора) на 5 одинаковых ежеквартальных (в конце периода)
платежей начиная с момента заключения нового договора. Найдите размер
ежеквартального платежа, используя сложную годовую ставку 7,00 % с начислением
процентов 1 раз в год.
Задача 14
Предприятие создает инвестиционный фонд. Ежегодно для создания
фонда в банк вносится 250 тыс. руб. под 9% годовых. Найти наращенную сумму
ренты, если фонд создается в течении 7 лет, при условии что:
а) рентные платежи осуществляются один раз в году, начисление
процентов производится один раз в конце периода начисления;
б) рентные платежи осуществляются один раз в году, а проценты
начисляются ежеквартально;
в) рентные платежи осуществляются ежеквартально, а проценты
начисляются один раз в году;
г) рентные платежи осуществляются два раза в году, и проценты
начисляются два раза в год.
д) рентные платежи осуществляются каждые два месяца в году, а
проценты начисляются ежемесячно.
Определить срок, для каждого варианта, который необходим для
создания инвестиционного фонда, если процентная ставка снизится в полтора раза.
Определить современную величину постоянной ренты для каждого
варианта.
Задача 15
Известны параметры ренты с выплатами постнумерандо. Член ренты –
200 тыс у.е. Срок ренты – 4 года. При расчетах принять ставку (схема сложных
процентов) 15% годовых. Найти
современную стоимость данной ренты.
Задача 16
Кредит 4000000 д.е. выплачивается в течении 25-ти лет (300
платежей). Посчитайте величину ежегодных взносов, если на долг начисляется
сложные проценты по процентной по
годовой ставке 19 % постнумерандо.
Задача 17
Предпринимателю предлагают либо взять в безвременную аренду
земельный участок за R = 100 тыс. руб. в год, либо выкупить этот участок за S =
2000000 руб. Что выгоднее при сложной годовой ставке i %?
Задача 18
Условия аренды предусматривают месячные платежи в 100000 рублей в
течение 2 лет. За какую цену можно купить площади сегодня, чтобы расходы
компании оказались одинаковыми, если ставка альтернативной доходности
составляет 12% годовых?
Задача 19
Кредит в размере 50 млн.р., выданный под 80% годовых, должен
погашаться равными суммами в течение 5 лет.
Определите размеры ежегодных срочных уплат и сумму выплаченных
процентов, если погасительные платежи осуществляются: 1) 1 раз в конце года; б)
каждые полгода.
Задача 20
Кредит в сумме 5 млн.р. погашается 12 равномерными ежемесячными
взносами. Процентная ставка по кредиту установлена в размере 24% годовых.
Найдите сумму ежемесячного взноса при платеже по схеме
постнумерандо.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 21
Вы заняли на 5 лет $10000 под 8% годовых, начисляемых по схеме
сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в
конце каждого года. Определите общую сумму процентов к выплате.
Задача 22
Определить размер ежегодных платежей по сложной ставке 17% годовых
для погашения кредита размером 300000 руб. в течение 5 лет.
Задача 23
В течение 20 лет на расчетный счет в конце каждого года поступает
по 10000 руб. Ежегодное дисконтирование производится по сложной ставке 10%
годовых. Определить современную стоимость ренты.
Задача 24
Предположим, Вам предлагают
два варианта оплаты: сразу заплатить 500 000 руб. или вносить по 115 000 руб. в
конце каждого следующего месяца в течение полугода. Вы могли бы обеспечить
вложениям 8 % годовых. Какой вариант предпочтительнее?
Задача 25
Определить размер ежегодных платежей по сложной ставке 20% годовых
для погашения кредита размером 300000 руб. в течение 5 лет.
Задача 26
Кредит в сумме 500000 руб. погашается 12 равномерными ежемесячными
взносами. Процентная ставка по кредиту установлена в размере 12% годовых. Найти
сумму ежемесячного взноса при платеже по схеме пренумерандо.
Задача 27
Трехлетний кредит в 3*100 тыс. руб. под 3% годовых погашается
выплатами в конце каждого месяца по (3+5) тыс. руб. Найдите сумму, которую
необходимо заплатить при подписании контракта.
Задача 28
Какую сумму Вам нужно положить в банк под 3%, чтобы по достижении
Вами возраста 60 лет получать в конце каждого месяца 10 тыс. руб. в течении 3
лет при ежеквартальной капитализации процентов.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 29
Фирма взяла кредит в банке 100 млн. руб. сроком на три года под 20%
годовых. Определить размер ежегодных платежей.
Задача 30
Страховая компания, заключив на 4 года договор с некоторой фирмой,
получает от нее страховые взносы по 20 тыс. руб. в конце каждого полугодия. Эти
взносы компания помещает в банк под 12% годовых.
Найдите современную стоимость суммы, которую получит страховая
компания по данному контракту, если проценты начисляются ежемесячно.
Задача 31
Компания гарантирует
выплату дивидендов в размере 1000 руб. на акцию в конце каждого года в течение
неопределенного долгого времени. Имеет ли смысл покупать акции этой компании по
цене 9000 руб., если можно поместить деньги на депозит под 10% годовых?
Задача 32
Фирма собирается вложить
средства в приобретение нового оборудования, стоимость которого вместе с
доставкой и установкой составит 1 млн. руб. Ожидается, что внедрение
оборудование обеспечит получение в течение 6 лет чистых доходов, равных 260
тыс. руб. в год. Оценить эффективность проекта, если денежные средства для его
реализации можно занять в банке под 10% годовых (сложные проценты).
Задача 33
Фирма
взяла кредит в банке 100 млн. руб. сроком на три года под 35% годовых.
Определить размер ежегодных платежей.
Задача 34
Какие одинаковые платежи в
конце каждого квартала в течении 20 лет обеспечили бы приобретение дома,
которые стоит 200 тысяч рублей наличными, если процентная ставка j4=5%
Задача 35
Оформляется контракт, по
которому выплачивается 500тыс.руб. в конце каждого полугодия в течение семи с
половиной лет и дополнительно 10 тыс. руб. в конце этого срока. Чему равна
стоимость контракта, если деньги стоят j=5%?
Задача 36
Потоки платежей.
Для постоянной годовой
ренты пренумерандо с разовым платежом 100000 рублей, сложной годовой ставки
18%. Начисления процентов раз в году в течение пяти лет определить сумму всех
платежей на начало выплат.
Задача 37
Некто
желает приобрести аннуитет с ежегодными выплатами, равными 12000 д.е., в течение
последующих 15 лет. Если на сумму вклада ежеквартально начисляются сложные
проценты по годовой процентной ставке 0,08, какова стоимость этого аннуитета?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 38
Мэри
получила наследство 30000 д. е., которые она вложила под ежеквартальное
начисление сложных процентов по годовой процентной ставке 0,08 для приобретения
аннуитета. Мэри желает в конце каждого года брать сумму
для отдыха на Гавайях. Определите величину
, если последняя
выплата использована через 10 лет.
Задача 39
Банк
предлагает ренту постнумерандо на 10 лет с квартальной выплатой 4 тыс. руб.
Годовая процентная ставка в течение всего периода остается постоянной, и
сложные проценты начисляются ежеквартально. По какой цене можно приобрести эту
ренту сейчас, если выплаты начнут осуществляться немедленно, а сложная
процентная ставка равна 32% годовых?
Задача 40
Клиент
обратился в банк с просьбой о предоставлении кредита на покупку автомобиля,
сроком на 1,5 года, уведомив банк, что ежемесячно может перечислять 1000
долларов. На какую сумму кредита может рассчитывать клиент, если процентная
ставка, предложенная банком, составляет 9%. Определить издержки клиента по
кредиту.
Задача 41
Определите
текущую стоимость обязательных ежемесячных платежей размером 150 тыс. денежных
единиц в течение 10 лет, если процентная ставка составляет 14,2% годовых.
Задача 42
Определите
современную стоимость обычных ежеквартальных платежей размером 64 тыс. ден. ед.
в течение 2 лет, если учетная ставка 18,5% годовых.
Задача 43
Инвестиции
производятся на протяжении 4 лет один раз в конце года по 2 млн. руб. Ставка
сложных процентов 17% годовых. Найти современную стоимость инвестиций.
Задача 44
Найти
современную стоимость годовой ренты, если проценты начисляются по номинальной
ставке 16% ежемесячно, член ренты 50 000 руб., срок ренты 4 года.
Задача 45
Для
формирования фонда ежеквартально делаются взносы по 100 000 руб., Проценты
начисляются один раз в год по ставке 17%. Найти современную стоимость фонда,
который будет накоплен к концу пятилетнего срока.
Задача 46
Для
формирования фонда ежеквартально делаются взносы по 100 000 руб., Проценты
начисляются ежемесячно по номинальной ставке 17%. Найти современную стоимость
фонда, накопленного к концу пятилетнего срока. Полученную сумму сравните с
результатом предыдущей задачи.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 47
Определите
размер равных ежегодных взносов, которые необходимо делать для погашения в
течение 3 лет текущего долга в размере 1 млн. руб., если ставка сложных
процентов 17% годовых.
Задача 48
За
счет привлеченных средств сделаны инвестиции в размере 10 млн. руб. расчетная
отдача от них составляет по 2,2 млн. руб. в конце каждого года. За какой срок
окупятся инвестиции, если на долг начисляются проценты по квартальной ставке
4%?
Задача 49
Для
создания фонда развития фирма помещает в банк ежегодно 43,4 млн. р. в течение пяти лет под 17,5% годовых (сложные
проценты начисляются раз в квартал). Определите современную величину ренты.
Задача 50
Каждый
член ренты 2000 д.е., выплачиваемый в конце года, дисконтируется сложными
процентами по годовой процентной ставке 0,08. Определите современную величину
ренты при условии, что срок ренты равен 10 годам.
Задача 51
Фирма
предлагает покупателю свою продукцию на сумму 2000 тыс. руб. с условием ее
оплаты в рассрочку в течение двух лет под 14% годовых (проценты сложные).
Платежи должны вноситься в конце каждого квартала, проценты начисляются один
раз в конце года. Определить величину квартального платежа.
Задача 52
Вам предлагают сдать в
аренду участок земли на пять лет, выбрав один из двух вариантов оплаты аренды:
а) 10 тыс. руб. в конце каждого года; б) 80 тыс. руб. в конце пятилетнего
периода. Какой вариант более предпочтителен, если банк предлагает 15% годовых
по вкладам.
Задача 53
Вам предложено
инвестировать 500 тыс. руб. на срок пять лет при условии возврата этой суммы
частями (ежегодно по 100 тыс. руб. в конце года). По истечении пяти лет
выплачивается дополнительное вознаграждение в размере 100 тыс. руб. Принимать
ли это предложение, если можно разместить деньги в банке из расчета 14%
годовых?
Калькулятор стоимости будущей ренты
О Калькулятор стоимости будущей ренты
Будущая стоимость калькулятора аннуитета используется для расчета обычных будущих значений аннуитета. Будущая стоимость аннуитета (FVA) — это будущая стоимость потока равных платежей (аннуитетов), при условии, что платежи инвестируются по заданной процентной ставке.
формула
Формула расчета будущей стоимости ренты выглядит следующим образом:
![]()
в:
FVA = будущая стоимость аннуитета
C = эквивалентная сумма
r = процентная ставка за период
n = количество периодов
Таблица будущей стоимости аннуитета
Следующая таблица будущих значений аннуитета (1 доллар США за период (n), r% из n% периодов) также поможет вам рассчитать обычные будущие значения аннуитета.
| Ожидать | 1% | 2% | 3% | 4% | 5% |
|---|---|---|---|---|---|
| 1 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2 | 2.0100 | 2.0200 | 2.0300 | 2.0400 | 2.0500 |
| 3 | 3.0301 | 3.0604 | 3.0909 | 3.1216 | 3.1525 |
| 4 | 4.0604 | 4.1216 | 4.1836 | 4.2465 | 4.3101 |
| пять | 5.1010 | 5.2040 | 5.3091 | 5.4163 | 5.5256 |
| 6 | 6.1520 | 6.3081 | 6.4684 | 6.6330 | 6.8019 |
| 7 | 7.2135 | 7.4343 | 7.6625 | 7.8983 | 8.1420 |
| 8 | 8.2857 | 8.5830 | 8.8923 | 9.2142 | 9.5491 |
| 9 | 9.3685 | 9.7546 | 10.1591 | 10.5828 | 11.0266 |
| 10 | 10.4622 | 10.9497 | 11.4639 | 12.0061 | 12.5779 |
| 11 | 11.5668 | 12.1687 | 12.8078 | 13.4864 | 14.2068 |
| 12 | 12.6825 | 13.4121 | 14.1920 | 15.0258 | 15.9171 |
| 13 | 13.8093 | 14.6803 | 15.6178 | 16.6268 | 17.7130 |
| 14 | 14.9474 | 15.9739 | 17.0863 | 18.2919 | 19.5986 |
| 15 | 16.0969 | 17.2934 | 18.5989 | 20.0236 | 21.5786 |
| 16 | 17.2579 | 18.6393 | 20.1569 | 21.8245 | 23.6575 |
| 17 | 18.4304 | 20.0121 | 21.7616 | 23.6975 | 25.8404 |
| 18 | 19.6147 | 21.4123 | 23.4144 | 25.6454 | 28.1324 |
| 19 | 20.8109 | 22.8406 | 25.1169 | 27.6712 | 30.5390 |
| 20 | 22.0190 | 24.2974 | 26.8704 | 29.7781 | 33.0660 |
| 21 | 23.2392 | 25.7833 | 28.6765 | 31.9692 | 35.7193 |
| 22 | 24.4716 | 27.2990 | 30.5368 | 34.2480 | 38.5052 |
| 23 | 25.7163 | 28.8450 | 32.4529 | 36.6179 | 41.4305 |
| 24 | 26.9735 | 30.4219 | 34.4265 | 39.0826 | 44.5020 |
| 25 | 28.2432 | 32.0303 | 36.4593 | 41.6459 | 47.7271 |
| 26 | 29.5256 | 33.6709 | 38.5530 | 44.3117 | 51.1135 |
| 27 | 30.8209 | 35.3443 | 40.7096 | 47.0842 | 54.6691 |
| 28 | 32.1291 | 37.0512 | 42.9309 | 49.9676 | 58.4026 |
| 29 | 33.4504 | 38.7922 | 45.2189 | 52.9663 | 62.3227 |
| тридцать | 34.7849 | 40.5681 | 47.5754 | 56.0849 | 66.4388 |
| 31 | 36.1327 | 42.3794 | 50.0027 | 59.3283 | 70.7608 |
| 32 | 37.4941 | 44.2270 | 52.5028 | 62.7015 | 75.2988 |
| 33 | 38.8690 | 46.1116 | 55.0778 | 66.2095 | 80.0638 |
| 34 | 40.2577 | 48.0338 | 57.7302 | 69.8579 | 85.0670 |
| 35 | 41.6603 | 49.9945 | 60.4621 | 73.6522 | 90.3203 |
| 36 | 43.0769 | 51.9944 | 63.2759 | 77.5983 | 95.8363 |
| 37 | 44.5076 | 54.0343 | 66.1742 | 81.7022 | 101.6281 |
| 38 | 45.9527 | 56.1149 | 69.1594 | 85.9703 | 107.7095 |
| 39 | 47.4123 | 58.2372 | 72.2342 | 90.4091 | 114.0950 |
| 40 | 48.8864 | 60.4020 | 75.4013 | 95.0255 | 120.7998 |
| 41 | 50.3752 | 62.6100 | 78.6633 | 99.8265 | 127.8398 |
| 42 | 51.8790 | 64.8622 | 82.0232 | 104.8196 | 135.2318 |
| 43 | 53.3978 | 67.1595 | 85.4839 | 110.0124 | 142.9933 |
| 44 | 54.9318 | 69.5027 | 89.0484 | 115.4129 | 151.1430 |
| 45 | 56.4811 | 71.8927 | 92.7199 | 121.0294 | 159.7002 |
| 46 | 58.0459 | 74.3306 | 96.5015 | 126.8706 | 168.6852 |
| 47 | 59.6263 | 76.8172 | 100.3965 | 132.9454 | 178.1194 |
| 48 | 61.2226 | 79.3535 | 104.4084 | 139.2632 | 188.0254 |
| 49 | 62.8348 | 81.9406 | 108.5406 | 145.8337 | 198.4267 |
| 50 | 64.4632 | 84.5794 | 112.7969 | 152.6671 | 209.3480 |
| Ожидать | 6% | 7% | 8% | 9% | 10% |
| 1 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2 | 2.0600 | 2.0700 | 2.0800 | 2.0900 | 2.1000 |
| 3 | 3.1836 | 3.2149 | 3.2464 | 3.2781 | 3.3100 |
| 4 | 4.3746 | 4.4399 | 4.5061 | 4.5731 | 4.6410 |
| пять | 5.6371 | 5.7507 | 5.8666 | 5.9847 | 6.1051 |
| 6 | 6.9753 | 7.1533 | 7.3359 | 7.5233 | 7.7156 |
| 7 | 8.3938 | 8.6540 | 8.9228 | 9.2004 | 9.4872 |
| 8 | 9.8975 | 10.2598 | 10.6366 | 11.0285 | 11.4359 |
| 9 | 11.4913 | 11.9780 | 12.4876 | 13.0210 | 13.5795 |
| 10 | 13.1808 | 13.8164 | 14.4866 | 15.1929 | 15.9374 |
| 11 | 14.9716 | 15.7836 | 16.6455 | 17.5603 | 18.5312 |
| 12 | 16.8699 | 17.8885 | 18.9771 | 20.1407 | 21.3843 |
| 13 | 18.8821 | 20.1406 | 21.4953 | 22.9534 | 24.5227 |
| 14 | 21.0151 | 22.5505 | 24.2149 | 26.0192 | 27.9750 |
| 15 | 23.2760 | 25.1290 | 27.1521 | 29.3609 | 31.7725 |
| 16 | 25.6725 | 27.8881 | 30.3243 | 33.0034 | 35.9497 |
| 17 | 28.2129 | 30.8402 | 33.7502 | 36.9737 | 40.5447 |
| 18 | 30.9057 | 33.9990 | 37.4502 | 41.3013 | 45.5992 |
| 19 | 33.7600 | 37.3790 | 41.4463 | 46.0185 | 51.1591 |
| 20 | 36.7856 | 40.9955 | 45.7620 | 51.1601 | 57.2750 |
| 21 | 39.9927 | 44.8652 | 50.4229 | 56.7645 | 64.0025 |
| 22 | 43.3923 | 49.0057 | 55.4568 | 62.8733 | 71.4027 |
| 23 | 46.9958 | 53.4361 | 60.8933 | 69.5319 | 79.5430 |
| 24 | 50.8156 | 58.1767 | 66.7648 | 76.7898 | 88.4973 |
| 25 | 54.8645 | 63.2490 | 73.1059 | 84.7009 | 98.3471 |
| 26 | 59.1564 | 68.6765 | 79.9544 | 93.3240 | 109.1818 |
| 27 | 63.7058 | 74.4838 | 87.3508 | 102.7231 | 121.0999 |
| 28 | 68.5281 | 80.6977 | 95.3388 | 112.9682 | 134.2099 |
| 29 | 73.6398 | 87.3465 | 103.9659 | 124.1354 | 148.6309 |
| тридцать | 79.0582 | 94.4608 | 113.2832 | 136.3075 | 164.4940 |
| 31 | 84.8017 | 102.0730 | 123.3459 | 149.5752 | 181.9434 |
| 32 | 90.8898 | 110.2182 | 134.2135 | 164.0370 | 201.1378 |
| 33 | 97.3432 | 118.9334 | 145.9506 | 179.8003 | 222.2515 |
| 34 | 104.1838 | 128.2588 | 158.6267 | 196.9823 | 245.4767 |
| 35 | 111.4348 | 138.2369 | 172.3168 | 215.7108 | 271.0244 |
| 36 | 119.1209 | 148.9135 | 187.1021 | 236.1247 | 299.1268 |
| 37 | 127.2681 | 160.3374 | 203.0703 | 258.3759 | 330.0395 |
| 38 | 135.9042 | 172.5610 | 220.3159 | 282.6298 | 364.0434 |
| 39 | 145.0585 | 185.6403 | 238.9412 | 309.0665 | 401.4478 |
| 40 | 154.7620 | 199.6351 | 259.0565 | 337.8824 | 442.5926 |
| 41 | 165.0477 | 214.6096 | 280.7810 | 369.2919 | 487.8518 |
| 42 | 175.9505 | 230.6322 | 304.2435 | 403.5281 | 537.6370 |
| 43 | 187.5076 | 247.7765 | 329.5830 | 440.8457 | 592.4007 |
| 44 | 199.7580 | 266.1209 | 356.9496 | 481.5218 | 652.6408 |
| 45 | 212.7435 | 285.7493 | 386.5056 | 525.8587 | 718.9048 |
| 46 | 226.5081 | 306.7518 | 418.4261 | 574.1860 | 791.7953 |
| 47 | 241.0986 | 329.2244 | 452.9002 | 626.8628 | 871.9749 |
| 48 | 256.5645 | 353.2701 | 490.1322 | 684.2804 | 960.1723 |
| 49 | 272.9584 | 378.9990 | 530.3427 | 746.8656 | 1057.1896 |
| 50 | 290.3359 | 406.5289 | 573.7702 | 815.0836 | 1163.9085 |
| Ожидать | 11% | 12% | 13% | 14% | 15% |
| 1 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2 | 2.1100 | 2.1200 | 2.1300 | 2.1400 | 2.1500 |
| 3 | 3.3421 | 3.3744 | 3.4069 | 3.4396 | 3.4725 |
| 4 | 4.7097 | 4.7793 | 4.8498 | 4.9211 | 4.9934 |
| пять | 6.2278 | 6.3528 | 6.4803 | 6.6101 | 6.7424 |
| 6 | 7.9129 | 8.1152 | 8.3227 | 8.5355 | 8.7537 |
| 7 | 9.7833 | 10.0890 | 10.4047 | 10.7305 | 11.0668 |
| 8 | 11.8594 | 12.2997 | 12.7573 | 13.2328 | 13.7268 |
| 9 | 14.1640 | 14.7757 | 15.4157 | 16.0853 | 16.7858 |
| 10 | 16.7220 | 17.5487 | 18.4197 | 19.3373 | 20.3037 |
| 11 | 19.5614 | 20.6546 | 21.8143 | 23.0445 | 24.3493 |
| 12 | 22.7132 | 24.1331 | 25.6502 | 27.2707 | 29.0017 |
| 13 | 26.2116 | 28.0291 | 29.9847 | 32.0887 | 34.3519 |
| 14 | 30.0949 | 32.3926 | 34.8827 | 37.5811 | 40.5047 |
| 15 | 34.4054 | 37.2797 | 40.4175 | 43.8424 | 47.5804 |
| 16 | 39.1899 | 42.7533 | 46.6717 | 50.9804 | 55.7175 |
| 17 | 44.5008 | 48.8837 | 53.7391 | 59.1176 | 65.0751 |
| 18 | 50.3959 | 55.7497 | 61.7251 | 68.3941 | 75.8364 |
| 19 | 56.9395 | 63.4397 | 70.7494 | 78.9692 | 88.2118 |
| 20 | 64.2028 | 72.0524 | 80.9468 | 91.0249 | 102.4436 |
| 21 | 72.2651 | 81.6987 | 92.4699 | 104.7684 | 118.8101 |
| 22 | 81.2143 | 92.5026 | 105.4910 | 120.4360 | 137.6316 |
| 23 | 91.1479 | 104.6029 | 120.2048 | 138.2970 | 159.2764 |
| 24 | 102.1742 | 118.1552 | 136.8315 | 158.6586 | 184.1678 |
| 25 | 114.4133 | 133.3339 | 155.6196 | 181.8708 | 212.7930 |
| 26 | 127.9988 | 150.3339 | 176.8501 | 208.3327 | 245.7120 |
| 27 | 143.0786 | 169.3740 | 200.8406 | 238.4993 | 283.5688 |
| 28 | 159.8173 | 190.6989 | 227.9499 | 272.8892 | 327.1041 |
| 29 | 178.3972 | 214.5828 | 258.5834 | 312.0937 | 377.1697 |
| тридцать | 199.0209 | 241.3327 | 293.1992 | 356.7868 | 434.7451 |
| 31 | 221.9132 | 271.2926 | 332.3151 | 407.7370 | 500.9569 |
| 32 | 247.3236 | 304.8477 | 376.5161 | 465.8202 | 577.1005 |
| 33 | 275.5292 | 342.4294 | 426.4632 | 532.0350 | 664.6655 |
| 34 | 306.8374 | 384.5210 | 482.9034 | 607.5199 | 765.3654 |
| 35 | 341.5896 | 431.6635 | 546.6808 | 693.5727 | 881.1702 |
| 36 | 380.1644 | 484.4631 | 618.7493 | 791.6729 | 1014.3457 |
| 37 | 422.9825 | 543.5987 | 700.1867 | 903.5071 | 1167.4975 |
| 38 | 470.5106 | 609.8305 | 792.2110 | 1030.9981 | 1343.6222 |
| 39 | 523.2667 | 684.0102 | 896.1984 | 1176.3378 | 1546.1655 |
| 40 | 581.8261 | 767.0914 | 1013.7042 | 1342.0251 | 1779.0903 |
| 41 | 646.8269 | 860.1424 | 1146.4858 | 1530.9086 | 2046.9539 |
| 42 | 718.9779 | 964.3595 | 1296.5289 | 1746.2358 | 2354.9969 |
| 43 | 799.0655 | 1081.0826 | 1466.0777 | 1991.7088 | 2709.2465 |
| 44 | 887.9627 | 1211.8125 | 1657.6678 | 2271.5481 | 3116.6334 |
| 45 | 986.6386 | 1358.2300 | 1874.1646 | 2590.5648 | 3585.1285 |
| 46 | 1096.1688 | 1522.2176 | 2118.8060 | 2954.2439 | 4123.8977 |
| 47 | 1217.7474 | 1705.8838 | 2395.2508 | 3368.8380 | 4743.4824 |
| 48 | 1352.6996 | 1911.5898 | 2707.6334 | 3841.4753 | 5456.0047 |
| 49 | 1502.4965 | 2141.9806 | 3060.6258 | 4380.2819 | 6275.4055 |
| 50 | 1668.7712 | 2400.0182 | 3459.5071 | 4994.5213 | 7217.7163 |
| Ожидать | 16% | 17% | 18% | 19% | 20% |
| 1 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2 | 2.1600 | 2.1700 | 2.1800 | 2.1900 | 2.2000 |
| 3 | 3.5056 | 3.5389 | 3.5724 | 3.6061 | 3.6400 |
| 4 | 5.0665 | 5.1405 | 5.2154 | 5.2913 | 5.3680 |
| пять | 6.8771 | 7.0144 | 7.1542 | 7.2966 | 7.4416 |
| 6 | 8.9775 | 9.2068 | 9.4420 | 9.6830 | 9.9299 |
| 7 | 11.4139 | 11.7720 | 12.1415 | 12.5227 | 12.9159 |
| 8 | 14.2401 | 14.7733 | 15.3270 | 15.9020 | 16.4991 |
| 9 | 17.5185 | 18.2847 | 19.0859 | 19.9234 | 20.7989 |
| 10 | 21.3215 | 22.3931 | 23.5213 | 24.7089 | 25.9587 |
| 11 | 25.7329 | 27.1999 | 28.7551 | 30.4035 | 32.1504 |
| 12 | 30.8502 | 32.8239 | 34.9311 | 37.1802 | 39.5805 |
| 13 | 36.7862 | 39.4040 | 42.2187 | 45.2445 | 48.4966 |
| 14 | 43.6720 | 47.1027 | 50.8180 | 54.8409 | 59.1959 |
| 15 | 51.6595 | 56.1101 | 60.9653 | 66.2607 | 72.0351 |
| 16 | 60.9250 | 66.6488 | 72.9390 | 79.8502 | 87.4421 |
| 17 | 71.6730 | 78.9792 | 87.0680 | 96.0218 | 105.9306 |
| 18 | 84.1407 | 93.4056 | 103.7403 | 115.2659 | 128.1167 |
| 19 | 98.6032 | 110.2846 | 123.4135 | 138.1664 | 154.7400 |
| 20 | 115.3797 | 130.0329 | 146.6280 | 165.4180 | 186.6880 |
| 21 | 134.8405 | 153.1385 | 174.0210 | 197.8474 | 225.0256 |
| 22 | 157.4150 | 180.1721 | 206.3448 | 236.4385 | 271.0307 |
| 23 | 183.6014 | 211.8013 | 244.4868 | 282.3618 | 326.2369 |
| 24 | 213.9776 | 248.8076 | 289.4945 | 337.0105 | 392.4842 |
| 25 | 249.2140 | 292.1049 | 342.6035 | 402.0425 | 471.9811 |
| 26 | 290.0883 | 342.7627 | 405.2721 | 479.4306 | 567.3773 |
| 27 | 337.5024 | 402.0323 | 479.2211 | 571.5224 | 681.8528 |
| 28 | 392.5028 | 471.3778 | 566.4809 | 681.1116 | 819.2233 |
| 29 | 456.3032 | 552.5121 | 669.4475 | 811.5228 | 984.0680 |
| тридцать | 530.3117 | 647.4391 | 790.9480 | 966.7122 | 1181.8816 |
| 31 | 616.1616 | 758.5038 | 934.3186 | 1151.3875 | 1419.2579 |
| 32 | 715.7475 | 888.4494 | 1103.4960 | 1371.1511 | 1704.1095 |
| 33 | 831.2671 | 1040.4858 | 1303.1253 | 1632.6698 | 2045.9314 |
| 34 | 965.2698 | 1218.3684 | 1538.6878 | 1943.8771 | 2456.1176 |
| 35 | 1120.7130 | 1426.4910 | 1816.6516 | 2314.2137 | 2948.3411 |
| 36 | 1301.0270 | 1669.9945 | 2144.6489 | 2754.9143 | 3539.0094 |
| 37 | 1510.1914 | 1954.8936 | 2531.6857 | 3279.3481 | 4247.8112 |
| 38 | 1752.8220 | 2288.2255 | 2988.3891 | 3903.4242 | 5098.3735 |
| 39 | 2034.2735 | 2678.2238 | 3527.2992 | 4646.0748 | 6119.0482 |
| 40 | 2360.7572 | 3134.5218 | 4163.2130 | 5529.8290 | 7343.8578 |
| 41 | 2739.4784 | 3668.3906 | 4913.5914 | 6581.4965 | 8813.6294 |
| 42 | 3178.7949 | 4293.0169 | 5799.0378 | 7832.9808 | 10577.3553 |
| 43 | 3688.4021 | 5023.8298 | 6843.8646 | 9322.2472 | 12693.8263 |
| 44 | 4279.5465 | 5878.8809 | 8076.7603 | 11094.4741 | 15233.5916 |
| 45 | 4965.2739 | 6879.2907 | 9531.5771 | 13203.4242 | 18281.3099 |
| 46 | 5760.7177 | 8049.7701 | 11248.2610 | 15713.0748 | 21938.5719 |
| 47 | 6683.4326 | 9419.2310 | 13273.9480 | 18699.5590 | 26327.2863 |
| 48 | 7753.7818 | 11021.5002 | 15664.2586 | 22253.4753 | 31593.7436 |
| 49 | 8995.3869 | 12896.1553 | 18484.8251 | 26482.6356 | 37913.4923 |
| 50 | 10435.6488 | 15089.5017 | 21813.0937 | 31515.3363 | 45497.1908 |
| Ожидать | 21% | 22% | 23% | 24% | 25% |
| 1 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2 | 2.2100 | 2.2200 | 2.2300 | 2.2400 | 2.2500 |
| 3 | 3.6741 | 3.7084 | 3.7429 | 3.7776 | 3.8125 |
| 4 | 5.4457 | 5.5242 | 5.6038 | 5.6842 | 5.7656 |
| пять | 7.5892 | 7.7396 | 7.8926 | 8.0484 | 8.2070 |
| 6 | 10.1830 | 10.4423 | 10.7079 | 10.9801 | 11.2588 |
| 7 | 13.3214 | 13.7396 | 14.1708 | 14.6153 | 15.0735 |
| 8 | 17.1189 | 17.7623 | 18.4300 | 19.1229 | 19.8419 |
| 9 | 21.7139 | 22.6700 | 23.6690 | 24.7125 | 25.8023 |
| 10 | 27.2738 | 28.6574 | 30.1128 | 31.6434 | 33.2529 |
| 11 | 34.0013 | 35.9620 | 38.0388 | 40.2379 | 42.5661 |
| 12 | 42.1416 | 44.8737 | 47.7877 | 50.8950 | 54.2077 |
| 13 | 51.9913 | 55.7459 | 59.7788 | 64.1097 | 68.7596 |
| 14 | 63.9095 | 69.0100 | 74.5280 | 80.4961 | 86.9495 |
| 15 | 78.3305 | 85.1922 | 92.6694 | 100.8151 | 109.6868 |
| 16 | 95.7799 | 104.9345 | 114.9834 | 126.0108 | 138.1085 |
| 17 | 116.8937 | 129.0201 | 142.4295 | 157.2534 | 173.6357 |
| 18 | 142.4413 | 158.4045 | 176.1883 | 195.9942 | 218.0446 |
| 19 | 173.3540 | 194.2535 | 217.7116 | 244.0328 | 273.5558 |
| 20 | 210.7584 | 237.9893 | 268.7853 | 303.6006 | 342.9447 |
| 21 | 256.0176 | 291.3469 | 331.6059 | 377.4648 | 429.6809 |
| 22 | 310.7813 | 356.4432 | 408.8753 | 469.0563 | 538.1011 |
| 23 | 377.0454 | 435.8607 | 503.9166 | 582.6298 | 673.6264 |
| 24 | 457.2249 | 532.7501 | 620.8174 | 723.4610 | 843.0329 |
| 25 | 554.2422 | 650.9551 | 764.6054 | 898.0916 | 1054.7912 |
| 26 | 671.6330 | 795.1653 | 941.4647 | 1114.6336 | 1319.4890 |
| 27 | 813.6759 | 971.1016 | 1159.0016 | 1383.1457 | 1650.3612 |
| 28 | 985.5479 | 1185.7440 | 1426.5719 | 1716.1007 | 2063.9515 |
| 29 | 1193.5129 | 1447.6077 | 1755.6835 | 2128.9648 | 2580.9394 |
| тридцать | 1445.1507 | 1767.0813 | 2160.4907 | 2640.9164 | 3227.1743 |
| 31 | 1749.6323 | 2156.8392 | 2658.4036 | 3275.7363 | 4034.9678 |
| 32 | 2118.0551 | 2632.3439 | 3270.8364 | 4062.9130 | 5044.7098 |
| 33 | 2563.8467 | 3212.4595 | 4024.1287 | 5039.0122 | 6306.8872 |
| 34 | 3103.2545 | 3920.2006 | 4950.6783 | 6249.3751 | 7884.6091 |
| 35 | 3755.9379 | 4783.6447 | 6090.3344 | 7750.2251 | 9856.7613 |
| 36 | 4545.6848 | 5837.0466 | 7492.1113 | 9611.2791 | 12321.9516 |
| 37 | 5501.2787 | 7122.1968 | 9216.2969 | 11918.9861 | 15403.4396 |
| 38 | 6657.5472 | 8690.0801 | 11337.0451 | 14780.5428 | 19255.2994 |
| 39 | 8056.6321 | 10602.8978 | 13945.5655 | 18328.8731 | 24070.1243 |
| 40 | 9749.5248 | 12936.5353 | 17154.0456 | 22728.8026 | 30088.6554 |
| 41 | 11797.9250 | 15783.5730 | 21100.4761 | 28184.7152 | 37611.8192 |
| 42 | 14276.4893 | 19256.9591 | 25954.5856 | 34950.0469 | 47015.7740 |
| 43 | 17275.5521 | 23494.4901 | 31925.1403 | 43339.0581 | 58770.7175 |
| 44 | 20904.4180 | 28664.2779 | 39268.9225 | 53741.4321 | 73464.3969 |
| 45 | 25295.3458 | 34971.4191 | 48301.7747 | 66640.3758 | 91831.4962 |
| 46 | 30608.3684 | 42666.1312 | 59412.1829 | 82635.0660 | 114790.3702 |
| 47 | 37037.1257 | 52053.6801 | 73077.9850 | 102468.4818 | 143488.9627 |
| 48 | 44815.9221 | 63506.4897 | 89886.9215 | 127061.9174 | 179362.2034 |
| 49 | 54228.2658 | 77478.9175 | 110561.9135 | 157557.7776 | 224203.7543 |
| 50 | 65617.2016 | 94525.2793 | 135992.1536 | 195372.6442 | 280255.6929 |
| Ожидать | 26% | 27% | 28% | 29% | 30% |
| 1 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2 | 2.2600 | 2.2700 | 2.2800 | 2.2900 | 2.3000 |
| 3 | 3.8476 | 3.8829 | 3.9184 | 3.9541 | 3.9900 |
| 4 | 5.8480 | 5.9313 | 6.0156 | 6.1008 | 6.1870 |
| пять | 8.3684 | 8.5327 | 8.6999 | 8.8700 | 9.0431 |
| 6 | 11.5442 | 11.8366 | 12.1359 | 12.4423 | 12.7560 |
| 7 | 15.5458 | 16.0324 | 16.5339 | 17.0506 | 17.5828 |
| 8 | 20.5876 | 21.3612 | 22.1634 | 22.9953 | 23.8577 |
| 9 | 26.9404 | 28.1287 | 29.3692 | 30.6639 | 32.0150 |
| 10 | 34.9449 | 36.7235 | 38.5926 | 40.5564 | 42.6195 |
| 11 | 45.0306 | 47.6388 | 50.3985 | 53.3178 | 56.4053 |
| 12 | 57.7386 | 61.5013 | 65.5100 | 69.7800 | 74.3270 |
| 13 | 73.7506 | 79.1066 | 84.8529 | 91.0161 | 97.6250 |
| 14 | 93.9258 | 101.4654 | 109.6117 | 118.4108 | 127.9125 |
| 15 | 119.3465 | 129.8611 | 141.3029 | 153.7500 | 167.2863 |
| 16 | 151.3766 | 165.9236 | 181.8677 | 199.3374 | 218.4722 |
| 17 | 191.7345 | 211.7230 | 233.7907 | 258.1453 | 285.0139 |
| 18 | 242.5855 | 269.8882 | 300.2521 | 334.0074 | 371.5180 |
| 19 | 306.6577 | 343.7580 | 385.3227 | 431.8696 | 483.9734 |
| 20 | 387.3887 | 437.5726 | 494.2131 | 558.1118 | 630.1655 |
| 21 | 489.1098 | 556.7173 | 633.5927 | 720.9642 | 820.2151 |
| 22 | 617.2783 | 708.0309 | 811.9987 | 931.0438 | 1067.2796 |
| 23 | 778.7707 | 900.1993 | 1040.3583 | 1202.0465 | 1388.4635 |
| 24 | 982.2511 | 1144.2531 | 1332.6586 | 1551.6400 | 1806.0026 |
| 25 | 1238.6363 | 1454.2014 | 1706.8031 | 2002.6156 | 2348.8033 |
| 26 | 1561.6818 | 1847.8358 | 2185.7079 | 2584.3741 | 3054.4443 |
| 27 | 1968.7191 | 2347.7515 | 2798.7061 | 3334.8426 | 3971.7776 |
| 28 | 2481.5860 | 2982.6443 | 3583.3438 | 4302.9470 | 5164.3109 |
| 29 | 3127.7984 | 3788.9583 | 4587.6801 | 5551.8016 | 6714.6042 |
| тридцать | 3942.0260 | 4812.9771 | 5873.2306 | 7162.8241 | 8729.9855 |
| 31 | 4967.9527 | 6113.4809 | 7518.7351 | 9241.0431 | 11349.9811 |
| 32 | 6260.6204 | 7765.1207 | 9624.9810 | 11921.9456 | 14755.9755 |
| 33 | 7889.3817 | 9862.7033 | 12320.9756 | 15380.3098 | 19183.7681 |
| 34 | 9941.6210 | 12526.6332 | 15771.8488 | 19841.5997 | 24939.8985 |
| 35 | 12527.4424 | 15909.8242 | 20188.9665 | 25596.6636 | 32422.8681 |
| 36 | 15785.5774 | 20206.4767 | 25842.8771 | 33020.6960 | 42150.7285 |
| 37 | 19890.8276 | 25663.2254 | 33079.8826 | 42597.6978 | 54796.9471 |
| 38 | 25063.4428 | 32593.2963 | 42343.2498 | 54952.0302 | 71237.0312 |
| 39 | 31580.9379 | 41394.4863 | 54200.3597 | 70889.1190 | 92609.1405 |
| 40 | 39792.9817 | 52571.9976 | 69377.4604 | 91447.9635 | 120392.8827 |
| 41 | 50140.1570 | 66767.4369 | 88804.1494 | 117968.8729 | 156511.7475 |
| 42 | 63177.5978 | 84795.6449 | 113670.3112 | 152180.8460 | 203466.2718 |
| 43 | 79604.7732 | 107691.4690 | 145498.9983 | 196314.2913 | 264507.1533 |
| 44 | 100303.0142 | 136769.1656 | 186239.7178 | 253246.4358 | 343860.2993 |
| 45 | 126382.7979 | 173697.8403 | 238387.8388 | 326688.9022 | 447019.3890 |
| 46 | 159243.3254 | 220597.2572 | 305137.4337 | 421429.6838 | 581126.2058 |
| 47 | 200647.5900 | 280159.5166 | 390576.9151 | 543645.2922 | 755465.0675 |
| 48 | 252816.9634 | 355803.5861 | 499939.4514 | 701303.4269 | 982105.5877 |
| 49 | 318550.3739 | 451871.5544 | 639923.4978 | 904682.4207 | 1276738.2640 |
| 50 | 401374.4711 | 573877.8741 | 819103.0771 | 1167041.3227 | 1659760.7433 |
Другие сопутствующие инструменты:
-
Калькулятор будущей стоимости предоплаченного аннуитета
-
Калькулятор будущей стоимости ренты роста
-
калькулятор будущей стоимости
-
Калькулятор текущей стоимости аннуитета
-
калькулятор фактора будущей стоимости
-
Калькулятор будущей стоимости паушальной суммы
-
Калькулятор текущей стоимости предоплаченного аннуитета
-
Калькулятор приведенной стоимости ренты роста
Общие инструменты
-
Калькулятор среднего балла (GPA)
-
дробь в десятичный калькулятор
-
футы дюймы в сантиметры
-
калькулятор ИМТ
-
инструмент подсчета слов
-
счетчик символов
-
калькулятор времени удвоения
-
конвертер фунтов в кг
-
калькулятор десятичной дроби
-
калькулятор сложных процентов
-
калькулятор даты
-
калькулятор площади параллелограмма
-
Калькулятор комплексных чисел
-
конвертер футов в метры
-
калькулятор натуральных логарифмов
-
Калькулятор Гугл Адсенс
-
калькулятор скидок
-
Калькулятор коэффициента вариации
-
процентный калькулятор
-
Конвертер градусов в радианы
-
двоичный калькулятор
-
Калькулятор числа судьбы
-
Калькулятор площади поверхности цилиндра (Высокая точность)
-
Калькулятор площади равностороннего треугольника
-
калькулятор возраста
-
Калькулятор объема пирамиды (Высокая точность)
-
Калькулятор рентабельности инвестиций
-
калькулятор дисперсии (Высокая точность)
-
Акры в Квадратные ярды Конвертер
-
Калькулятор гамма-функции
При увеличении периода начислений Т, но при сохранении процентной ставки, происходит увеличение текущей стоимости единицы обычного аннуитета.
- Авансовый аннуитет – поступление потоков платежей в начале каждого периода.
Первый платеж происходит одновременно с начальным поступлением денежных средств, поэтому его называют “авансовым аннуитетом” или “причитающимся аннуитетом”. Первый платеж не дисконтируется, а все последующие платежи дисконтируются по фактору обычного аннуитета, а последующие поступления дисконтируются в обычном порядке. Формула расчета авансового аннуитета имеет вид:
PVAа = PMT x {[1 – (1 + R)-(n – 1)] : R + 1}.
Выражение в фигурных скобках характеризует фактор текущей стоимости авансового аннуитета:
Аап = {[1 – (1 + R)-(n – 1)] : R + 1}.
Значение Аап показывает текущую стоимость единицы денежных средств при равномерном поступлении ее в начале каждого единичного периода, входящего в период Т.
Примеры расчета фактора текущей стоимости авансового аннуитета приведены ниже:
-
R = 15%; T = 4 года; Aaп1 = [1 – (1 + 0,15)-(4 – 1)] : 0,15 + 1 = 3,28.
Текущая стоимость единицы денежных средств в конце 4-го года при равномерном поступлении в будущем единицы ДС в начале каждого года при ставке 15% годовых будет соответствовать 3,28%;
-
R = 25%; T = 4 года; Aaп2 = [1 – (1 + 0,25)-(4 – 1)] : 0,25 + 1 = 2,95.
При увеличении процентной ставки R, но при том же периоде поступлений, происходит уменьшение текущей стоимости денежной единицы авансового аннуитета;
-
R= 15%; T = 5 лет; Aaп3 = [1 – (1 + 0,15)-(5 – 1)] : 0,15 + 1 = 3,85.
При увеличении Т, но при сохранении процентной ставки, происходит увеличение текущей стоимости единицы авансового аннуитета.
Фактор текущей стоимости авансового аннуитета может быть определен как сумма фактора обычного аннуитета для предыдущего периода (Ап – 1) и единицы:
Аап = Ап – 1 + 1.
Например. Фактор текущей стоимости авансового аннуитета, возникающего 5 раз при годовой ставке 15%, можно определить:
- Аап = {[1 – (1 + R)-(n – 1)] : R + 1} = {[1 – (1 + 0,15)-(5 – 1)] : 0,15 + 1} = 3,85;
- вычисляем фактор текущей стоимости аннуитета для предпоследнего периода (5 – 1):
Ап = {[1 – 1 : (1 + R)n] : R}; А4 = {[1 – 1 : (1 + 0,15)4] : 0,15} = 2,85.
К полученному результату прибавляем 1:
Ап + 1 = А4 + 1 = 2,85 +1 = 3,85.
Результаты расчетов одинаковые.
Использование функции “текущая стоимость аннуитета” PVA на практике позволяет принимать обоснованные управленческие решения при оценке стоимости активов организации.
Пример 61. Владелец предприятия, специализирующегося на оказании услуг населению, предполагает в течение 5 лет получать ежегодный доход в размере 2000 тыс. руб., а затем в конце 5 года продать предприятие за 3500 тыс. руб., расходы по ликвидации предприятия составят 12% от продажной цены. Определить доход от деятельности и продажи, учитывая ставку дисконта по деятельности – 14%, а от продажи предприятия – 23%.
Решение:
- Определим значение фактора обычного аннуитета:
Ап = {[1 – 1 : (1 + R)n] : R}; А5 = [1 – 1 : (1 + 0,14)5] : 0,14 = 3,4331.
- Определим текущую стоимость потока доходов от деятельности по формуле текущей стоимости обычного аннуитета:
PVA = PMT x Ап = 2000 x 3,4331 = 6866,2 (тыс. руб.).
- Определим текущую стоимость от продажи предприятия в конце 5-го года деятельности, учитывая дисконт – 23%, а также расходы на ликвидацию в размере 12%, используя формулу дисконтирования:
PV = S x (1 – Рл) x [1 : (1 + d)n],
где
PV – текущая стоимость предприятия;
S – продажная цена предприятия;
Рл – доля расходов на продажу предприятия;
d – ставка дисконтирования при продаже предприятия;
n – число периодов начисления процентов.
PV = 3500 x (1 – 0,12) x [1 : (1 + 0,23)5] = 3500 x 0,88 x 0,36 = 1108,8 (тыс. руб.).
- Определим текущую сумму доходов владельца предприятия:
Д = PVA + PV = 6866,2 + 1108,8 = 7975 (тыс. руб.)
Таким образом, владелец предприятия получит доход от деятельности и последующей продажи предприятия в размере 7975 тыс. руб.
Пример 62. Фирма сдает свободные площади в аренду. Определить текущую стоимость совокупного дохода от сдачи в аренду площадей в течение 4 лет, если сдача в аренду торговых помещений может принести ежегодный доход в размере 6700 тыс. руб., сдача в аренду складских помещений позволяет ежегодно получать 2300 тыс. руб. Ставка дисконта по каждому виду соответственно 21 и 17%.
Решение:
- Определим значение фактора обычного аннуитета:
Ап = {[1 – 1 : (1 + R)n] : R}.
Значение фактора обычного аннуитета для аренды торговых площадей:
А4(т.пл) = [1 – 1 : (1 + 0,21)4] : 0,21 = 2,5404.
Значение фактора обычного аннуитета для аренды складских площадей:
А4(ск.пл) = [1 – 1 : (1 + 0,17)4] : 0,17 = 2,7432.
- Определим значение текущей стоимости дохода от аренды торговых площадей (округление до целых):
PVA(т.пл) = 6700 x 2,5404 = 17021 (тыс. руб.);
PVA(ск.пл) = 2300 x 2,7432 = 6309 (тыс. руб.).
- Текущая стоимость совокупного дохода:
PVA = 17021 + 6309 = 23330 (тыс. руб.).
Совокупный текущий доход фирмы от сдачи в аренду помещений в течение 4 лет составит 23 330 тыс. руб.
Пример 63. Определить текущую стоимость совокупного дохода от сдачи помещения в аренду, если по прогнозу предполагается, что в течение первых 2 лет ежегодный доход составит 2000 тыс. руб., в следующие 3 года ежегодный доход может увеличиваться на 200 тыс. руб. в год. Ставка дисконта – 13%.
Решение:
В данной ситуации ежегодные выплаты различные.
- Определим текущую стоимость потока платежей за первые 2 года.
Определим значение фактора обычного аннуитета:
Ап = {[1 – 1 : (1 + R)n] : R},
А2 = [1 – 1 : (1 + 0,13)2] : 0,13 = 1,6681.
Значение текущей стоимости дохода от аренды за первые два года (округление до целых):
PVA2 = 2000 x 1,6681 = 3336 (тыс. руб.).
- Определим текущую стоимость потока платежей за последующие 3 года.
Значение фактора обычного аннуитета за эти годы как разность между факторами, соответствующими значению фактора в расчете за 5 лет (2 + 3) и за 2 года:
ΔА = А5 – А2 = {[1 – 1 : (1 + 0,13)5] : 0,13} – {[1 – 1 : (1 + 0,13)2] : 0,13} = 3,5172 – 1,6681 = 1,8491.
Текущая стоимость аренды с конца второго года по конец 5 года аренды будет равна:
PVA5 – 2 = 2200 x 1,8491 = 4068 (тыс. руб.).
- Суммарная текущая стоимость арендной платы за 5 лет составит:
PVA5 = 3336 + 4068 = 7404 (тыс. руб.).
Пример 64. Определить текущую стоимость совокупного дохода от сдачи помещения в аренду, если в течение первых 3 лет ежегодный доход может составить 4500 тыс. руб., ставка дисконта – 15 %. В следующие 5 лет ежегодный доход от сдачи помещения в аренду из-за физического износа может уменьшиться на 15 %, а ежегодная ставка дисконта увеличится на 2%.
Решение:
- Определим текущую стоимость потока платежей за первые 3 года, учитывая, что ставка дисконтирования 15%.
Значение фактора обычного аннуитета:
А3 = [1 – 1 : (1 + 0,15)3] : 0,15 = 2,2832.
Значение текущей стоимости дохода от аренды за первые три года (округление до целых):
PVA3 = 4500 x 2,2832 = 10 274 (тыс. руб.).
Таким образом, текущая стоимость совокупного дохода, полученного в будущем, от сдачи помещения в аренду за первые 3 года, при ставке дисконтирования 15%, составит 10 274 тыс. руб. (без учета фактора времени – 13 500 тыс. руб. (4500 x 3)).
- Определим значение фактора текущей стоимости потока платежей в следующие 5 лет, учитывая, что ставка дисконтирования 17%.
ΔА = А8 – А3 = {[1 – 1 : (1 + 0,17)8] : 0,17} – {[1 – 1 : (1 + 0,17)3] : 0,17} = 4,2072 – 2,2096 = 1,9976.
Текущая стоимость аренды с конца третьего года по конец 8 года аренды будет равна:
PVA8 – 3 = 4500 x (1 – 0,15) x 1,9976 = 7641 (тыс. руб.).
- Суммарная текущая стоимость арендной платы за 8 лет, которая будет получена в будущем, составит:
PVA = 10 274 + 7641 = 17 915 (тыс. руб.).
Размер совокупного дохода от сдачи помещения в аренду с учетом фактора времени составит 17 915 тыс. руб., без учета фактора времени – 32 625 тыс. руб. (13 500 + 5 x 4500 x 0,85).
Функция “Будущая стоимость аннуитета” FVA.
С помощью функции FVA определяют величину накопленных равновеликих взносов при заданной ставке дохода. Если взносы осуществляются в конце периода, то используется формула:
FVA = PMT x {[(1 + R)n – 1] : R},
где
FVA – будущая стоимость накопленных денежных средств,
PMT – периодический взнос;
R – периодическая ставка процента;
n – число периодов начисления (лет).
Выражение в фигурных скобках представляет собой фактор “будущей стоимости обычного аннуитета”:
Абт = [(1 + R)n – 1] : R.
Значение Абт показывает, какой по истечению всего срока будет стоимость денежной единицы периодических равных взносов, депонированных в конце каждого периода:
- R = 15%; T = 4 года; Aбт1 = [(1 + 0,15)4 – 1] : 0,15 = 4,99.
Стоимость единицы денежных средств, депонированной в конце каждого года, в течение 4 лет при годовой ставке 15% будет равна 4,99 единиц ДС;
- R = 25%; T = 4 года; Aбт2 = [(1 + 0,25)4 – 1] : 0,25 = 5,77;
- R = 15%; T = 5 лет; Aбт3 = [(1 + 0,15)5 – 1] : 0,15 = 6,74.
При увеличении R и начислений Т, но при том же периоде поступлений, происходит увеличение накопления будущей стоимости денежной единицы обычного аннуитета.
Пример 65. Определить размер денежных средств, накопленных на счете в течение 3 лет, если ежегодно вносить 280 тыс. руб., а банк начисляет на вклад 9% годовых.
Решение:
- Определим значение фактора “будущей стоимости обычного аннуитета” за 3 периода при ставке 9% годовых:
Абт = [(1 + R)n – 1] : R = [(1 + 0,09)3 – 1] : 0,09 = 3,2781.
- Определим величину накопленных на счете денежных средств к концу 3 года:
FVA = PMT x {[(1 + R)n – 1] : R} = 280 x 3,2781 = 918 (тыс. руб.)
Таким образом, если ежегодно на счет перечислять 280 тыс. руб., то сумма накоплений за 3 года составит 918 тыс. руб. Разница между суммой накоплений и возрастающей суммой вклада – 840 тыс. руб. (280 x 3) в размере 78 тыс. руб. представляет собой величину процентов, начисленных на возрастающую сумму.
Если взносы (платежи) осуществляются в начале периода, то используют формулу:
FVAа = PMT x {[(1 + R)n + 1 – 1] : R}.
Выражение в фигурных скобках представляет собой фактор “будущей стоимости авансового аннуитета”:
Аба = [(1 + R)n + 1 – 1] : R.
Значение Аба показывает, какой по истечению всего срока будет стоимость денежной единицы периодических равных взносов, депонированных в начале каждого единичного периода:
- R = 15%; T = 4 года; Aба1 = [(1 + 0,15)4 + 1 – 1] : 0,15 = 6,74.
Стоимость единицы денежных средств, депонированной в начале каждого года, в течение 4 лет при годовой ставке 15% будет равна 6,74 единиц ДС;
- R = 25%; T = 4 года; Aба2 = [(1 + 0,25)4 + 1 – 1] : 0,25 = 8,21;
- R = 15%; T = 5 лет; Aба3 = [(1 + 0,15)5 + 1 – 1] : 0,15 = 8,75.
При увеличении R и начислений Т, но при том же периоде поступлений, происходит увеличение накопления будущей стоимости денежной единицы авансового аннуитета.
Пример 66. Предприятие сдало в аренду оборудование сроком на 15 месяцев. Ежемесячные арендные платежи должны по договору поступать в начале каждого месяца в размере 180 тыс. руб. Какова будущая стоимость платежей к концу 15-го месяца, если ставка дисконтирования – 14% годовых?
Решение:
- Определим ставку дисконтирования в месяц:
Rm = 14% : 12 = 1,17%.
- Определим значение фактора “будущей стоимости авансового аннуитета”:
Аба = [(1 + Rm)n + 1 – 1] : Rm = [(1 + 0,0117)15 – 1] : 0,0117 = 16,29302854.
- Определим стоимость аренды за 15 месяцев:
FVAа = PMT x {[(1 + Rm)n + 1 – 1] : Rm} = 180 x 16,293 = 2933 (тыс. руб.).
Без учета ставки дисконтирования суммарные арендные платежи составят 2700 тыс. руб. (15 x 180), с учетом ставки дисконтирования – 2933 тыс. руб. Разность между ними в размере 233 тыс. руб. представляет величину процентов, начисленных на возрастающую сумму платежей.
Функция “периодический взнос на погашение кредита” (РМТ).
С помощью данной функции определяется величина самого аннуитета, если известны текущая стоимость, число взносов и ставка дисконтирования. Эта функция является обратной текущей стоимостью обычного аннуитета.
Из формулы PVA = PMT x Ап = РМТ x {[1 – 1 : (1 + R)n] : R} следует, что:
РМТ = PVA : Ап = PVA : [1 – 1 : (1 + R)n] : R} = PVA x {1 : [1 – 1 : (1 + R)n] : R}.
Величина, обратная фактору обычного аннуитета, представляет собой фактор взноса на погашение кредита:
Акр = 1 : Ап = 1 : [1 – 1 : (1 + R)n] : R, или
Акр = R : [1 – 1 : (1 + R)n]
Значение Акр показывает равновеликий периодический платеж единицы ДС, необходимый для погашения единицы кредита ДС:
-
R = 15%; T = 4 года; Aкр1 = 0,15 : [1 – 1 : (1 + 0,15)4] = 0,35.
Если сегодня положить единицу денежных средств сроком на 4 года под 15% годовых, то в конце каждого года можно снимать 0,35 единицы ДС;
-
R = 25%; T = 4 года; Aкр2 = 0,25 : [1 – 1 : (1 + 0,25)4] = 0,42.
Если сегодня положить единицу денежных средств, сроком на 4 года под 25% годовых, то в конце каждого года можно снимать 0,42 единицы ДС.
Увеличение годовой процентной ставки, при том же периоде, приводит к увеличению суммы, снимаемой в конце каждого года;
-
R = 15%; T = 5 лет; Aбт3 = 0,15 : [1 – (1 + 0,15)5] = 0,30.
Если сегодня положить единицу денежных средств, сроком на 5 лет под 15% годовых, то в конце каждого года можно снимать лишь 0,30 единицы ДС.
Увеличение периода кредитования, при той же годовой процентной ставке, приводит к уменьшению суммы, снимаемой в конце каждого года.
Пример 67. Организации предоставлен кредит в размере 9000 тыс. руб. сроком на 5 лет под 16% годовых. Какие должны быть ежегодные равновеликие выплаты по погашению кредита?
Решение:
- Рассчитаем величину обычного аннуитета, учитывая, что срок кредита 5 лет, а годовая ставка дисконтирования 16%:
Ап = [1 – 1 : (1 + R)n] : R = [1 – 1 : 1,165] : 0,16 = 3,2743.
Фактор взноса на погашение кредита:
Акр = 1 : Ап = 1 : 3,2743 = 0,3054.
- Определим ежегодные выплаты, если размер их должен быть один и тот же:
