Как найти фактическое значение критерия фишера - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 октября 2017 года; проверки требуют 8 правок.

F-тест или критерий Фишера (F-критерий, φ*-критерий) — статистический критерий, тестовая статистика которого при выполнении нулевой гипотезы имеет распределение Фишера (F-распределение).

Статистика теста так или иначе сводится к отношению выборочных дисперсий (сумм квадратов, деленных на «степени свободы»). Чтобы статистика имела распределение Фишера, необходимо, чтобы числитель и знаменатель были независимыми случайными величинами и соответствующие суммы квадратов имели распределение Хи-квадрат. Для этого требуется, чтобы данные имели нормальное распределение. Кроме того, предполагается, что дисперсия случайных величин, квадраты которых суммируются, одинакова.

Тест проводится путём сравнения значения статистики с критическим значением соответствующего распределения Фишера при заданном уровне значимости. Известно, что если , то . Кроме того, квантили распределения Фишера обладают свойством $F_{1-alpha}=1/F_{alpha}$ . Поэтому обычно на практике в числителе участвует потенциально большая величина, в знаменателе — меньшая и сравнение осуществляется с «правой» квантилью распределения. Тем не менее тест может быть и двусторонним, и односторонним. В первом случае при уровне значимости alpha используется квантиль $F_{alpha/2}$ , а при одностороннем тесте — $F_{alpha}$ ^[1].

Более удобный способ проверки гипотез — с помощью p-значения p(F) — вероятностью того, что случайная величина с данным распределением Фишера превысит данное значение статистики. Если p(F) (для двустороннего теста — 2p(F )) меньше уровня значимости alpha , то нулевая гипотеза отвергается, в противном случае принимается.

Примеры F-тестов[править | править код]

F-тест на равенство дисперсий[править | править код]

Две выборки[править | править код]

Пусть имеются две выборки объёмом m и n соответственно случайных величин X и Y, имеющих нормальное распределение. Необходимо проверить равенство их дисперсий. Статистика теста

$F=frac {hat{sigma}^2_X}{hat{sigma}^2_Y}~ sim ~F(m-1,n-1)$

где ${hat{sigma}^2}$ — выборочная дисперсия.

Если статистика больше критического значения, соответствующего выбранному уровню значимости, то дисперсии случайных величин признаются не одинаковыми.

Несколько выборок[править | править код]

Пусть выборка объёмом N случайной величины X разделена на k групп с количеством наблюдений $n_{i}$ в i-ой группе.

Межгрупповая («объяснённая») дисперсия: $hat{sigma}^2_{BG}=sum^k_{i=1} n_i (overline {x_i}-overline {x})^2/(k-1)$

Внутригрупповая («необъяснённая») дисперсия: $hat{sigma}^2_{WG}=sum^k_{i=1}sum^{n_i}_{j=1} (x_{ij}-overline {x}_i)^2/(N-k)$

$F=frac {hat{sigma}^2_{BG}}{hat{sigma}^2_{WG}}~sim~F(k-1,N-k)$

Данный тест можно свести к тестированию значимости регрессии переменной X на фиктивные переменные-индикаторы групп. Если статистика превышает критическое значение, то гипотеза о равенстве средних в выборках отвергается, в противном случае средние можно считать одинаковыми.

Проверка ограничений на параметры регрессии[править | править код]

Статистика теста для проверки линейных ограничений на параметры классической нормальной линейной регрессии определяется по формуле:

${displaystyle F={frac {(RSS_{S}-RSS_{L})/q}{RSS_{L}/(n-k_{L})}}={frac {(R_{L}^{2}-R_{S}^{2})/q}{(1-R_{L}^{2})/(n-k_{L})}}~sim ~F(q,n-k_{L})}$

где -количество ограничений, n-объём выборки, k-количество параметров модели, RSS-сумма квадратов остатков модели, R^2 -коэффициент детерминации, индексы S и L относятся соответственно к короткой и длинной модели (модели с ограничениями и модели без ограничений).

Замечание[править | править код]

Описанный выше F-тест является точным в случае нормального распределения случайных ошибок модели. Однако F-тест можно применить и в более общем случае. В этом случае он является асимптотическим. Соответствующую F-статистику можно рассчитать на основе статистик других асимптотических тестов — теста Вальда (W), теста множителей Лагранжа(LM) и теста отношения правдоподобия (LR) — следующим образом:

$F=frac {n-k}{q} W/n ~,~ F=frac {n-k}{q} frac {LM} {n-LM} ~,~F=frac {n-k}{q}(e^{LR/n}-1)$
Все эти статистики асимптотически имеют распределение F(q, n-k), несмотря на то, что их значения на малых выборках могут различаться.

Проверка значимости линейной регрессии[править | править код]

Данный тест очень важен в регрессионном анализе и по существу является частным случаем проверки ограничений. В данном случае нулевая гипотеза — об одновременном равенстве нулю всех коэффициентов при факторах регрессионной модели (то есть всего ограничений k-1). В данном случае короткая модель — это просто константа в качестве фактора, то есть коэффициент детерминации короткой модели равен нулю. Статистика теста равна:

$F=frac {R^2/(k-1)}{(1-R^2)/(n-k)}~sim ~F(k-1,n-k)$

Соответственно, если значение этой статистики больше критического значения при данном уровне значимости, то нулевая гипотеза отвергается, что означает статистическую значимость регрессии. В противном случае модель признается незначимой.

Пример[править | править код]

Пусть оценивается линейная регрессия доли расходов на питание в общей сумме расходов на константу, логарифм совокупных расходов, количество взрослых членов семьи и количество детей до 11 лет. То есть всего в модели 4 оцениваемых параметра (k=4). Пусть по результатам оценки регрессии получен коэффициент детерминации ${displaystyle R^{2}=41.2366%}$ . По вышеприведенной формуле рассчитаем значение F-статистики в случае, если регрессия оценена по данным 34 наблюдений и по данным 64 наблюдений:
$F_1=frac {0.412366/(4-1)}{(1-0.412366)/(34-4)}=0,70174*10=7,02$

$F_2=frac {0.412366/(4-1)}{(1-0.412366)/(64-4)}=0,70174*20=14.04$

Критическое значение статистики при 1 % уровне значимости (в Excel функция FРАСПОБР) в первом случае равно ${displaystyle F_{1%}(3,30)=4,51}$ , а во втором случае ${displaystyle F_{1%}(3,60)=4,13}$ . В обоих случаях регрессия признается значимой при заданном уровне значимости. В первом случае P-значение равно 0,1 %, а во втором — 0,00005 %. Таким образом, во втором случае уверенность в значимости регрессии существенно выше (существенно меньше вероятность ошибки в случае признания модели значимой).

Проверка гетероскедастичности[править | править код]

См. Тест Голдфелда-Куандта

См. также[править | править код]

Проверка статистических гипотез
Статистический критерий
Тест Вальда
Тест отношения правдоподобия
Тест множителей Лагранжа
Тест Голдфелда-Куандта

Примечания[править | править код]

↑ F-Test for Equality of Two Variances (англ.). NIST. Дата обращения: 29 марта 2017. Архивировано 9 марта 2017 года.

Источник

Критерий Фишера и Стьюдента

С помощью критерия Фишера оценивают качество регрессионной модели в целом и по параметрам.

Для этого выполняется сравнение полученного значения F и табличного F значения. F-критерия Фишера. F фактический определяется из отношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

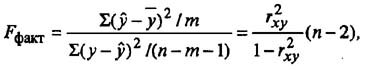
где n — число наблюдений;

m — число параметров при факторе х.

F табличный — это максимальное значение критерия под влиянием случайных факторов при текущих степенях свободы и уровне значимости а.

Уровень значимости а — вероятность не принять гипотезу при условии, что она верна. Как правило а принимается равной 0,05 или 0,01.

Если Fтабл > Fфакт то признается статистическая незначимость модели, ненадежность уравнения регрессии.

Таблицы по нахождению критерия Фишера и Стьюдента

Таблицы значений F-критерия Фишера и t-критерия Стьюдента Вы можете посмотреть здесь.

Табличное значение критерия Фишера вычисляют следующим образом:

Определяют k1, которое равно количеству факторов (Х). Например, в однофакторной модели (модели парной регрессии) k1=1, в двухфакторной k=2.
Определяют k2, которое определяется по формуле n — m — 1, где n — число наблюдений, m — количество факторов. Например, в однофакторной модели k2 = n — 2.
На пересечении столбца k1 и строки k2 находят значение критерия Фишера

Для нахождения табличного значения критерия Стьюдента определяют число степеней свободы, которое определяется по формуле n — m — 1 и находят его значение при определенном уровне значимости (0,10, 0,05, 0,01).

Критерии Стьюдента

Для оценки статистической значимости модели по параметрам рассчитывают t-критерии Стьюдента.

Оценка значимости модели с помощью критерия Стьюдента проводится путем сравнения их значений с величиной случайной ошибки:

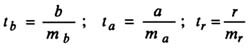
Случайные ошибки коэффициентов линейной регрессии и коэффициента корреляции определяются по формулам:

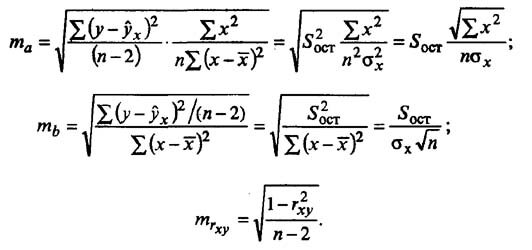
Сравнивая фактическое и табличное значения t-статистики и принимается или отвергается гипотеза о значимости модели по параметрам.

Зависимость между критерием Фишера и значением t-статистики Стьюдента определяется так

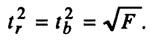
Как и в случае с оценкой значимости уравнения модели в целом, модель считается ненадежной если tтабл > tфакт

Видео лекциий по расчету критериев Фишера и Стьюдента

Для более подробного изучения расчетов критериев Фишера и Стьюдента советуем посмотреть это видео

Лекция 1. Критерии и Гипотезы

Лекция 2. Критерии и Гипотезы

Лекция 3. Критерии и Гипотезы

Определение доверительных интервалов

Для построения доверительного интервала определяется предельная ошибка А для обоих показателей:

Формулы для нахождения доверительных интервалов выглядят так

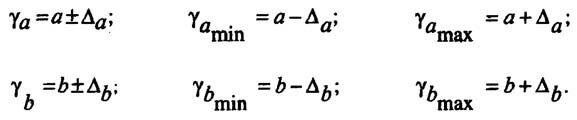
Прогнозное значение у определяется с помощью подстановки в
уравнение регрессии прогнозного значения х. Вычисляется средняя стандартная ошибка прогноза

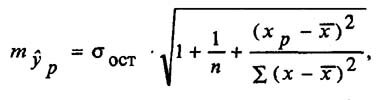
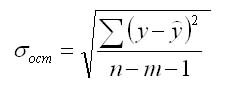
и находится доверительный интервал

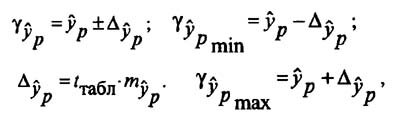
Задача регрессионного анализа в предмете эконометрика состоит в анализе дисперсии изучаемого показателя y:

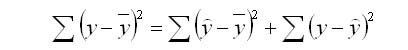
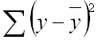общая сумма квадратов отклонений (TSS)

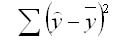сумма квадратов отклонений, обусловленная регрессией (RSS)

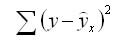остаточная сумма квадратов отклонений (ESS)

Долю дисперсии, обусловленную регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R, который должен превышать 50% (R² > 0,5). В контрольных по эконометрике в ВУЗах этот показатель рассчитывается всегда.

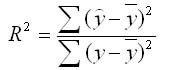
Любые задачи по эконометрике решаются здесь

Источник

Критерий фишера таблица как пользоваться пример?

kafedra meis

23 октября 2018 · 15,9 K

Образование Высшее – закончил в 2000г ВГАСУ. Слушаю рок, панк, рок как русский так и… · 23 окт 2018

Для определения критерия Фишера сначала нужно определиться какая таблица нам нужна, то есть нужно знать уровень значимости (0.1, 0.05 или 0.01).

Зная уровень значимости, выбираем Таблицу значений F-критерия Фишера при уровне значимости (здесь уровень значимости, например, 0.05).

Затем определяем k1 (равно количеству факторов). Например, в однофакторной модели k1=1, а в четыхфакторной k1=4.

После нам нужно определить k2 по формуле: k2=n-m-1, где n – число наблюдений, m – количество факторов. Например для четырехфакторной модели k2 = n – 5.

И в заключении, когда известны k1 и k2, на пересечении столбца k1 и строки k2 находится значение критерия Фишера.

Для нашего примера (четырехфакторная модель, пусть будет при 10 измерениях, при уровне значимости 0.05) на пересечении k1 = 4 и k2 = 10 – 5 = 5 в Таблице значений F-критериев Фишера при уровне значимости 0.05 находится значение 4.53. Это и есть нужное нам значение критерия Фишера для заданных условий.

13,6 K

А если k1 = 15 и этого значения нет в таблице?

Комментировать ответ…Комментировать…

Источник

Критерий
Фишера позволяет
сравнивать величины выборочных
дисперсий двух независимых выборок.
Для вычисления F_эмп нужно
найти отношение дисперсий двух выборок,
причем так, чтобы большая по величине
дисперсия находилась бы в числителе, а
меньшая – в знаменателе. Формула
вычисления критерия Фишера такова:

(8)

где –
дисперсии первой и второй выборки
соответственно.

Так
как, согласно условию критерия, величина
числителя должна быть больше или равна
величине знаменателя, то значение
F_эмп всегда
будет больше или равно единице.

Число
степеней свободы определяется также
просто:

k₁=n_l–
1 для
первой выборки (т.е. для той выборки,
величина дисперсии которой больше)
и k₂=n₂–
1 для
второй выборки.

В
Приложении 1 критические значения
критерия Фишера находятся по
величинам k₁ (верхняя
строчка таблицы) и k₂ (левый
столбец таблицы).

Если t_эмп>t_крит,
то нулевая гипотеза принимается, в
противном случае принимается
альтернативная.

Пример
3. В
двух третьих классах проводилось
тестирование умственного развития по
тесту ТУРМШ десяти учащихся.[3] Полученные
значения величин средних достоверно
не различались, однако психолога
интересует вопрос — есть ли различия
в степени однородности показателей
умственного развития между классами.

Решение.
Для критерия Фишера необходимо сравнить
дисперсии тестовых оценок в обоих
классах. Результаты тестирования
представлены в таблице:

Таблица
3.

№№ учащихся	Первый класс	Второй класс
1	90	41
2	29	49
3	39	56
4	79	64
5	88	72
6	53	65
7	34	63
8	40	87
9	75	77
10	79	62
Суммы	606	636
Среднее	60,6	63,6

Рассчитав
дисперсии для переменных X и Y, получаем:

s_x²=572,83; s_y²=174,04

Тогда
по формуле (8) для расчета по F критерию
Фишера находим:

По
таблице из Приложения 1 для F критерия
при степенях свободы в обоих случаях
равных k=10
– 1 = 9 находим F_крит=3,18
(<3.29), следовательно, в терминах
статистических гипотез можно утверждать,
что Н₀ (гипотеза
о сходстве) может быть отвергнута на
уровне 5%, а принимается в этом случае
гипотеза Н₁.
Иcследователь
может утверждать, что по степени
однородности такого показателя, как
умственное развитие, имеется различие
между выборками из двух классов.

6.2 Непараметрические критерии

Сравнивая
на глазок (по процентным соотношениям)
результаты до и после какого-либо
воздействия, исследователь приходит к
заключению, что если наблюдаются
различия, то имеет место различие в
сравниваемых выборках. Подобный подход
категорически неприемлем, так как для
процентов нельзя определить уровень
достоверности в различиях. Проценты,
взятые сами по себе, не дают возможности
делать статистически достоверные
выводы. Чтобы доказать эффективность
какого-либо воздействия, необходимо
выявить статистически значимую тенденцию
в смещении (сдвиге) показателей. Для
решения подобных задач исследователь
может использовать ряд критериев
различия. Ниже будет рассмотрены
непараметрические критерии: критерий
знаков и критерий хи-квадрат.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Примеры F-тестов[править | править код]

F-тест на равенство дисперсий[править | править код]

Две выборки[править | править код]

Несколько выборок[править | править код]

Проверка ограничений на параметры регрессии[править | править код]

Замечание[править | править код]

Проверка значимости линейной регрессии[править | править код]

Пример[править | править код]

Проверка гетероскедастичности[править | править код]

См. также[править | править код]

Примечания[править | править код]

Критерий Фишера и Стьюдента

Таблицы по нахождению критерия Фишера и Стьюдента

Критерии Стьюдента

Видео лекциий по расчету критериев Фишера и Стьюдента

Определение доверительных интервалов

Критерий фишера таблица как пользоваться пример?

6.2 Непараметрические критерии

Вам также может понравиться

Как найти промокод в биглионе

Будь послушным как найти

Что делать если нашел айфон как вернуть

Добавить комментарий Отменить ответ