Как найти фактор множества

Приветствую Вас, уважаемые Читатели! Пару недель назад я уже писал о таком понятии как “отношение эквивалентности”. Ознакомьтесь с этим материалом, потому что это – ключевой момент к теоретико-множественному пониманию определения “фактормножество”.

Формул в этом материале не будет, так что смело листайте дальше. Материал на понимание.

Почему я в заглавии написал, что каждый из нас постоянно использует это понятие? Всё просто: мы делим людей на мужчин и женщин (надеюсь, в нашей стране по-другому никогда и не будет), яблоки на желтые, красные и зелёные, граждан на российских, украинских, американских и т.д. Реализуя эти мыслительные операции, мы каждый раз, сами того не понимая, строим фактормножество. Давайте разберемся подробнее в этом простом, но важном понятии. Поехали!

Итак, для начала определим на множестве людей “отношение эквивалентности” в виде согражданства. Мы называем его эквивалентностью потому, что оно удовлетворяет трем свойствам:

1. Симметричность. Если первый человек согражданин второго, то и второй – согражданин первого.

2. Рефлексивность. Любой человек является согражданином для самого себя

3. Транзитивность. Если первый и второй, второй и третий – сограждане, то первый и третий – тоже сограждане.

Теперь, обладая таким отношением, мы можем разделить всех людей на планете на т.н. “классы эквивалентности”, в каждом из которых находятся лишь люди, имеющие одно гражданство. Иными словами мы имеем некий классифицирующий признак, отправляющий людей в одну и ту же “корзину”:

Давайте будем считать, что каждый человек может иметь только одно гражданство.

Множество самих классов эквивалентности называется фактормножеством по отношению эквивалентности для данного множества и обозначается X/~.

Отображение X –> X/~ называется каноническим отображением и является сюръекцией (отображением “на”). Иными словами у каждого элемента фактормножества X/~ есть хотя бы один прообраз в множестве X.

Надеюсь, что данный материал станет полезным для тех, кто только начинает разбираться в теории множеств. В дальнейшем я расскажу о факторгруппах, факторкольцах, а, может быть, и о фактортопологиях. Спасибо за внимание!

Читайте также:

Фактормножество — множество всех классов эквивалентности для заданного отношения эквивалентности на множестве , обозначается . Разбиение множества на классы эквивалентных элементов называется его факторизацией.

Отображение из в множество классов эквивалентности называется факторотображением. Благодаря свойствам отношения эквивалентности, разбиение на множества единственно. Это означает, что классы, содержащие , либо не пересекаются, либо совпадают полностью.
Для любого элемента однозначно определён некоторый класс из , иными словами существует сюръективное отображение из в . Класс, содержащий , иногда обозначают .

Если множество снабжено структурой, то часто отображение можно использовать, чтобы снабдить фактормножество той же структурой; например классы эквивалентности топологического пространства можно снабдить индуцированной топологией (факторпространство), классы эквивалентности алгебраической системы снабдить теми же операциями и отношениями (факторсистема).

Применения и примеры[править | править код]

Если задано сюръективное отображение , тогда на множестве задаётся отношение . Можно рассмотреть фактормножество . Функция задаёт естественное взаимно-однозначное соответствие между и .

Факторизацию множества разумно применять для получения нормированных пространств из полунормированных, пространств со скалярным произведением из пространств с почти скалярным произведением и пр. Для этого вводится соответственно норма класса, равная норме произвольного его элемента, и скалярное произведение классов как скалярное произведение произвольных элементов классов. В свою очередь отношение эквивалентности вводится следующим образом (например для образования нормированного факторпространства): вводится подмножество исходного полунормированного пространства, состоящее из элементов с нулевой полунормой (кстати, оно линейно, то есть является подпространством) и считается, что два элемента эквивалентны, если разность их принадлежит этому самому подпространству.

Если для факторизации линейного пространства вводится некоторое его подпространство и считается, что если разность двух элементов исходного пространства принадлежит этому подпространству, то эти элементы эквивалентны, то фактормножество является линейным пространством и называется факторпространством.

Проективную плоскость можно определить как факторпространство двумерной сферы, задав отношение эквивалентности .

Бутылку Клейна можно представить как факторпространство цилиндра по отношению эквивалентности ( — угловая координата на окружности).

Свойства[править | править код]

Факторотображения q : X → Y описывается среди сюръективных отображений следующим свойством: если Z является каким-либо топологическим пространством и f : Y → Z является какой-либо функцией, то f является непрерывным тогда и только тогда, когда f ∘ q непрерывна.

Факторпространство X/~ вместе с факторотображением q : X → X/~ описывается следующим универсальным свойством: если g : X → Z является непрерывным отображением, таким что если из a ~ b следует g(a) = g(b) для всех a и b из X, то существует единственное отображение f : X/~ → Z, такое что g = f ∘ q. Мы говорим, что g спускается до факторотображения.

Непрерывные отображения, определённые на X/~ поэтому являются в точности такими отображениями, которые возникают из непрерывных отображений, определённых на X, которые удовлетворяют отношению эквивалентности (в смысле, что они переводят эквивалентные элементы в один и тот же образ). Этот критерий обширно используется при изучении факторпространств.

Если дана непрерывная сюръекция q : X → Y, полезно иметь критерий, по которому можно определить, является ли q факторотображением. Два достаточных условия — q является открытым^[en] или закрытым отображением^[en]. Заметим, что эти условия являются лишь достаточными, но не необходимыми. Легко построить примеры факторотображений, которые не являются ни открытыми, ни закрытыми. Для топологических групп факторотображение является открытым.

Совместимость с другими топологическими понятиями[править | править код]

• Отделимость
  • В общем случае факторпространства плохо себя ведут относительно аксиом отделимости. Свойства отделимости множества X не обязательно наследуются при X/~ и X/~ могут иметь свойства отделимости, не существующие в X.
  • X/~ является пространством T₁^[en] тогда и только тогда, когда любой класс эквивалентности ~ замкнут в X.
  • Если факторотображение открыто^[en], то X/~ является хаусдорфовым пространством тогда и только тогда, когда ~ является замкнутым подмножеством произведения пространств X×X.
• Связность
  • Если пространство связно или линейно связно, то таковыми являются все его факторпространства.
  • Факторпространство односвязного или стягиваемого пространства не обязательно будет обладать этими свойствами.
• Компактность
  • Если пространство компактно, таковыми будут и все его факторпространства.
  • Факторпространство локально компактного пространства не обязательно локально компактно.
• Размерность пространства
  • Топологическая размерность факторпространства может быть больше (а может быть и меньше) размерности исходного пространства; заполняющие пространство кривые дают такие примеры.

2.1. Отношения
(См. также [4], §§1.2, 1.5; [5], §1.5).
n–местным
отношением
или n–местным
предикатом
P
на множествах
A₁,
A₂,
…, A_n
называется любое подмножество прямого
произведения A₁A₂…,A_n.
При этом, если (a₁,
a₂,
…, a_n)P,
то говорят что a₁,
a₂,
…, a_n
находятся
в отношении
Р.
Отношение РAⁿ
называется n–местным
отношением
(или n–местным
предикатом)
на множестве
А.

При n=1
отношение называется унарным
или свойством.
При n=2
отношение называется бинарным
или соответствием.
При этом если РAB,
то говорят о соответствии между
множествами A
и B,
причем, если (a,
b)Р,
то говорят, что элементу
a
ставится
в соответствие элемент
b.
В этом случае также пишут aРb.

Пример
2.1. Пусть А=1,
2, 3, 4, 5.
Определим бинарное отношение P
на А:
Р=(a,
b)|
a
меньше b.
Тогда Р=(1,
2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5),
(4, 5).
Обратно, задав множество Р
перечислением, мы задаём отношение
«быть меньше» на множестве А.

Пример
2.2. Пусть А=1,
2, 3, 4, 5,
B={a,
b}.
Определим бинарное отношение P
на множествах А
и B:
Р=(1,
a),
(2, b),
(3, a),
(4, b),
(5, a).
При этом бинарном отношении каждому
нечётному числу из А
ставится в соответствие буква a,
а чётному числу 
буква b.

Бинарные отношения
на А
и B
можно изобразить графически.

Первый способ
графического изображения назовём
декартовым.
Он заключается в том, что на двух взаимно
перпендикулярных осях отмечаются
элементы А
и B:
на горизонтальной 
оси Ох,

элементы А,
на вертикальной 
оси Оy,

элементы B.
Отметив точки с координатами (a,
b)
такими, что (a,
b)Р,
получим графическое декартово изображение
отношения Р.

Второй способ
основан на диаграммах Эйлера-Венна, и
заключается в том, что если (a,
b)Р,
то из a
к b
проводится стрелка. При этом условимся,
что если одновременно (a,
b)Р
и (b,
a)Р,
то две стрелки из a
к b
и из b
к a
изображать в виде одной двойной (то есть
стрелка идёт в обе стороны) (см. рис. 8
ниже)

На рисунках 6 и 7
приведены графические изображения
отношений из примеров 2.1 и 2.2.

Тождественным
отношением
на множестве А
называется отношение id_A=(х,
х)
хА.
Универсальным
отношением
называется отношение U_A=A².

Областью
определения
бинарного отношения Р
называется множество _Р=х(х,
y)Р
для некоторого у.
Областью
значений
бинарного отношения Р
называется множество _Р=у(х,
y)Р
для некоторого х.

Обратным
отношением к
бинарному отношению
Р называется
множество
=(у,
х)(х,
y)Р.

Образом
множества Х
относительно предиката Р
называется множество Р(Х)=у(х,
y)Р
для некоторого хХ.
Прообразом
множества Y=Р(Х)
относительно предиката Р
называется множество
(Y)=х(х,
y)Р
для некоторого уР(Х).

Пример
2.3. Пусть Р

бинарное отношение примера 2.1. Тогда
_Р=1,
2, 3, 4=А{5},
_Р=2,
3, 4, 5=А{1},
=(2,
1), (3, 1), (4, 1), (5, 1), (3, 2), (4, 2), (5, 2), (4, 3), (5, 3),
(5, 4).
Пусть Х=3,
4, 5.
Тогда Р(Х)=4,
5.
Прообразом множества 2,
3
является
(2,
3)=1,
2.

Произведением
бинарных
отношений PAB
и QBC
(или композицией)
называется множество PQ={(x,
z)|
xA,
zC,
и существует такой элемент уB
что (x,
y)P
и (y,
z)Q}.
Произведение PQ
также обозначается через PQ.

Пример
2.4. Пусть
А=1,
2, 3, 4, 5,
B={a,
b,
с},
С=,
,
,
,
Р=(1,
a),
(2, b),
(3, a),
(4, b),
(5, a),
Q
=(a,
),
(b,
).
Тогда
PQ
=(1,
),
(2, ),
(3, ),
(4, ),
(5, ).

Для любых бинарных
отношений
PAB,
QBC,
RCD
выполняются
следующие свойства:

1) PQAC;

2)
=P;

3) (PQ)=QP;

4) (PQ)R=P(QR)
(ассоциативность
произведения);

5) id_AP
=P;

6) Qid_BQ
=Q;

7)
PP=id_A.

Свойство 4) обобщается
на произведение любого числа предикатов.
Именно, если Р₁А₁А₂,
Р₂А₂А₃,
…, Р_nА_nА_n+1

предикаты, то в произведении вида
(…((Р₁Р₂)
Р₃)…)Р_n
скобки можно проставлять произвольным
образом, это произведение не зависит
от расстановки скобок. В связи с этим в
произведениях вида (PQ)R
и (…((Р₁Р₂)Р₃)…)Р_n
скобки принято опускать: (PQ)R=PQR,
(…((Р₁Р₂)Р₃)…)Р_n=Р₁Р₂Р₃…Р_n.

Пусть даны два
множества А=a₁,
a₂,
…, a_n,
B=b₁,
b₂,
…, b_m
и бинарное отношение PAB.
Свяжем с Р
матрицу [Р]=(p_ij)_mn,
элементы которой определены по следующему
правилу:

(p_ij)_mn=

Эта матрица
называется матрицей
бинарного отношения
Р.
Она однозначно определяет бинарное
отношение.

Пример
2.5. Матрицы бинарных отношений Р
и Q
из примера 2.4 следующие:

[Р]=,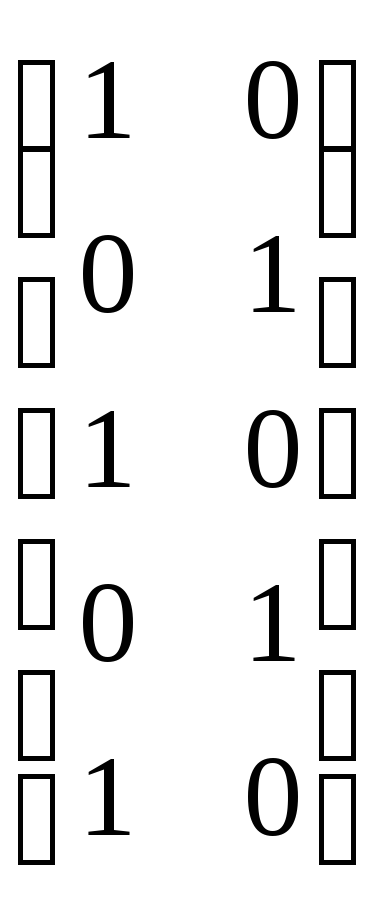
[Q]=.

Матрица бинарного
отношения обладает следующими свойствами:

1. Если
Р,
QAB,
[Р]=(p_ij)_mn,
[Q]=(q_ij)_mn,
то
[РQ]=[Р][Q]=(p_ijq_ij)_mn
и
[РQ]=[Р]+[Q],
где сложение производится по правилам
0+0=0, 1+0=0+1=1+1=1, а умножение 
по обычным правилам 00=10=01=0,
11=1
(Здесь и далее XY
будет означать матрицу, полученную
умножением соответствующих элементов
матриц X
и Y).

2. Если
PAB,
QBC,
то
[РQ]=[Р][Q].
Здесь умножение матриц производится
по обычным правилам, а произведение и
сумма элементов матриц 
по правилам, определённым в пункте 1.

3.
=[Р]^Т.

4. Если
PQ,
[Р]=(p_ij)_mn,
[Q]=(q_ij)_mn,
то
[Р][Q]
(то есть p_ijq_ij
для всех i=1,
…, m
и j=1,
…, n).

5. [id_А]=Е

единичная
матрица.

2.2. Свойства
отношений. Отношение эквиваленции.
Фактор-множество
(См. также [4], §§1.5,
1.6; [5], §1.7).
Пусть Р

бинарное отношение на А:
РА².
Отношение называется рефлексивным,
если (х,
х)Р
для всех хА.
Это означает, что id_АР,
а диагональные
элементы матрицы такого отношения равны
1: [Р]=.

Отношение называется
симметричным,
если для любых х,
yА
из (х,
y)Р
следует (y,
х)Р.
Это означает, что P=Р,
то есть [Р]^Т=Р
(матрица
отношения является симметричной).

Отношение называется
антисимметричным,
если из (х,
y)Р
и (y,
х)Р
следует х=y.
Это означает, что РPid_А,
то есть в матрице [РP]=[Р][P]^T
все элементы,
стоящие вне
главной диагонали являются нулевыми.

Отношение называется
транзитивным,
если из (х,
y)Р
и (y,
z)Р
следует (х,
z)Р.
Это означает, что РРР,
то есть [РР]=[Р][Р][Р].

Пример
2.6. Отношение Р
из примера 2.1 не является ни рефлексивным,
ни симметричным, ни антисимметричным,
но является транзитивным. Докажем
последнее. Так как Р=(1,
2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5),
(4, 5),
то из (1, 2)Р
и (2, 3)Р
следует (1, 3)Р,
из (1, 3)Р
и (3, 4)Р
следует (1, 4)Р,
из (1, 4)Р
и (4, 5)Р
следует (1, 5)Р,
из (2, 3)Р
и (3, 4)Р
следует (2, 4)Р,
из (2, 4)Р
и (4, 5)Р
следует (2, 5)Р,
из (3, 4)Р
и (4, 5)Р
следует (3, 5)Р.

Это можно увидеть
и из соответствующих свойств матрицы
отношения. Имеем

[Р]=.

Как видим, не все
диагональные элементы равны 1 (точнее,
равных 1 среди них вообще нет), что
означает не рефлексивность отношения.
Далее, матрица отношения не является
симметричной, то есть отношение
несимметрично. Так как не все элементы
вне главной диагонали равны 0, то отношение
не является антисимметричным. Наконец,

[РР]=[Р][Р]==,

то есть [РР][Р],
и отношение транзитивно.

Отношение, обладающее
одновременно свойствами рефлексивности,
симметричности и транзитивности,
называется отношением эквивалентности
(или эквивалентностью).
Отношение эквивалентности будем
обозначать также через 
(знак «тильда»). При этом, если xy,
то будем говорить, что x
и y
эквивалентны.

Пример
2.7. Отношение равенства на множестве
чисел является отношением эквивалентности.
Действительно, это отношение рефлексивно
(для любого хR
х=х),
симметрично (для любых x,
yR
из x=y
следует y=x)
и транзитивно (из x=y
и y=z
следует x=z).

Пусть на множестве
А
введено отношение эквивалентности .
Тогда множество
А
разбивается
на непересекающиеся между собой
подмножества,
каждое из
которых состоит из эквивалентных между
собой элементов,
причем неэквивалентные
между собой элементы попадают в разные
подмножества.
Эти подмножества называются классами
эквиваленции.
Множество всех классов эквиваленции
множества А
относительно отношения эквивалентности

называется фактор–множеством
множества А
по 
и обозначается через А/.
Если отношение эквиваленции обозначить
через Р,
то соответствующее фактор-множество
обозначается через А/Р.
Класс, содержащий элемент х,
будем обозначать через
.

Пример
2.8. Определим на множестве Z
целых чисел бинарное отношение по
правилу для x,
yZ
положим x~y
тогда и только тогда, когда x
и y
имеют одинаковую чётность. Это отношение
является отношением эквиваленции
(проверьте!),
и множество Z
разбивается на два класса целых чисел

класс четных чисел и класс нечётных
чисел.

Если А

множество с конечным числом элементов,
на котором введено отношение эквиваленции
~, то элементы А
можно пронумеровать таким образом, что
матрица отношения ~ будет иметь
блочно-диагональный вид с блоками,
состоящими из единиц:

[~]=.

Пример
2.9. Рассмотрим отношение Р
на множестве А=1,
2, 3, 4, 5,
изображённое на рисунке 8: Р=(1,
1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3),
(4, 4), (4, 5), (5, 4), (5, 5).
Оно является одновременно рефлексивным,
симметричным и транзитивным (проверьте!),
то есть отношение Р

эквиваленция. Её матрица отношений 
блочно-диагональноая с двумя блоками
из 1:

[Р]=.

2.3. Отношения
порядка (См. также [4], §1.7;
[5], §1.8).
Бинарное отношение РА²=A×A,
обладающее свойством рефлексивности
и транзитивности, называется отношением
предпорядка.
Бинарное отношение РА²,
обладающее свойством рефлексивности,
транзитивности и антисимметричности,
называется отношением частичного
порядка.
Таким образом, отношение частичного
порядка 
это антисимметричный предпорядок. Как
правило, отношение частичного порядка
обозначается через .
Непустое множество А,
на котором определён частичный порядок,
называется частично
упорядоченным.

Частичный порядок
А²
(напоминаем, что если отношение P

это отношение ,
то А²
означает PА²)
называется линейным
порядком,
если для любых х,
yА
либо хy,
либо yх
(то есть любые два элемента х
и y
из А
сравнимы).
Непустое множество А,
на котором определён линейный порядок,
называется линейно
упорядоченным.
Частично упорядоченное и линейно
упорядоченное множества сокращённо
обозначаются соответственно через ЧУМ
и ЛУМ.

Пример
2.10. Отношение P={(a,
a),
(b,
b),
(c,
c),
(a,
b),
(b,
a),
(b,
c),
(a,
c)}
на множестве a,
b,
c
обладает свойствами рефлексивности и
транзитивности (проверьте!).
Значит, это P
отношение предпорядка.

Пример
2.11. Отношение P={(a,
a),
(b,
b),
(c,
c),
(b,
c)}
на множестве А=a,
b,
c
обладает свойствами рефлексивности и
транзитивности (проверьте!). Далее,
одновременно условия (х,
у)Р
и (у,
х)Р
выполняются только для пар (a,
a),
(b,
b),
(c,
c).
Поэтому, если (х,
у)Р
и (у,
х)Р,
то х=у.
Это означает, что Р
удовлетворяет условию антисимметричности.
Таким образом, Р
рефлексивно, транзитивно и антисимметрично,
то есть Р

отношение частичного порядка. При этом
оно не является отношением линейного
порядка, так как не все элементы множества
А
сравнимы, а именно, элементы a
и b,
и элементы a
и c.
Отношение P={(a,
a),
(b,
b),
(c,
c),
(a,
b),
(a,
c),
(b,
c)}
является отношением линейного порядка.

Пример
2.12. Линейным порядком является любое
подмножество действительных чисел
относительно обычного отношения .
Отношение 
на булеане P(А)
является частичным порядком, но не
линейным (почему?).

Отношение <,
определённое по правилу: a<b
тогда и только тогда, когда a≤b
и a≠b,
называется строгим
порядком.

Элемент a
частично упорядоченного множества A
называется максимальным,
если для всех xA,
сравнимых с a,
из a≤x
следует, что x=a.
Аналогично, элемент a
частично упорядоченного множества A
называется минимальным,
если для всех xA,
сравнимых с a,
из x≤a
следует, что x=a.

Элемент a
частично упорядоченного множества A
называется наибольшим,
если a
сравним со всеми элементами из А,
и для любого xA
имеет место x≤a.
Элемент a
частично упорядоченного множества A
называется наименьшим,
если a
сравним со всеми элементами из А,
и для любого aA
имеет место a≤x.

Разница между
максимальным и наибольшим элементами
(соответственно, между минимальным и
наименьшим элементами) очевидна:
наибольший
элемент является также максимальным,
а максимальный
элемент, в
силу того, что он не обязан быть сравнимым
со всеми элементами множества А,
вообще говоря, не
обязательно наибольший в
А.
Он является
наибольшим только в
некотором подмножестве B
из A,
а именно, в
подмножестве тех
(и только
тех) элементов
из A,
которые
сравнимы с данным максимальным.
Ясно, что наибольший
элемент во множестве обязан быть
единственным:
если a
и b

наибольшие в A,
то с одной стороны, a≤b
(так как b

наибольший в A),
с другой стоороны b≤a
(так как a

наибольший в A),
то есть одновременно выполнены условия
a≤b
и b≤a;
но отношение ≤ обладает свойством
антисимметричности, и поэтому a=b.

Аналогично,
наименьший
элемент является минимальным,
но обратное,
вообще говоря, неверно,
и наименьший
элемент в частично упорядоченном
множестве единствен
(докажите!).

Ясно, что в
линейно упорядоченном множестве
максимальный и наибольший элементы
совпадают
(соответственно, минимальный
и наименьший элементы совпадают).

Максимальный и
минимальный элементы не обязательно
единственны
(почему?).

Максимальный и
минимальный элементы множества A
будем обозначать через maxA,
minA,
соответственно. Если их по несколько,
то через max₁A,
max₂A,
…, min₁A,
min₂A,
….

Пусть A

ЧУМ и BA.
Элемент aA
называется верхней
гранью
множества B,
если b≤a
для всех bB.
Элемент aA
называется нижней
гранью
множества B,
если a≤b
для любого bB.
Из определений верхней и нижней граней
множества следует, что они не обязаны
принадлежать самому множеству.

Наименьшая из
верхних граней множества называется
точной
верхней гранью
(супремумом)
данного множества. Наибольшая из нижних
граней множества называется его точной
нижней гранью
(инфимумом).
Точная верхняя и нижняя грани множества
B
обозначаются через supB
и infB,
соответственно.

Пример
2.13. Рассмотрим интервал [a,
b)
(a<b)
на числовой прямой. Тогда inf
[a,
b)=a,
sup
[a,
b)=b.
Кроме того, для любого c<a
имеем, что c

нижняя грань интервала, и для любого d
c
условием b<d
d

верхняя грань.

Пример
2.14. Рассмотрим множество A={,
{1}, {2}, {1, 2}} (множество всех подмножеств
множества {1, 2}, то есть A=P({1,
2}). Отношение ≤ между элементами введём
по правилу a≤b
тогда и только тогда, когда ab.
Тогда 
и {1, 2} 
соответственно наименьший и наибольший
элементы. В подмножестве B={,
{1}, {2}} существует наименьший элемент 
это ,
наибольшего нет; minB=,
max₁B={1}
и max₂B={2},
то есть в B
имеется два максимальных элемента;
наконец, infB=,
supB={1,
2}.

Аналогично можно
рассмотреть minC,
maxC,
infC,
supC,
наибольший и наименьший элементы
подмножества A={{1},
{2}, {1, 2}} (что предоставляется читателю
в качестве несложного упражнения).

2.4.
Упражнения.
1. Пусть А=a
aN,
1a20.
Задать отношение PA²
перечислением элементов:

а) (х,
у)Р
тогда и только тогда, когда х
делит у;

б) (х,
у)Р
тогда и только тогда, когда у=х²;

в) (х,
у)Р
тогда и только тогда, когда х+у=20;

г) (х,
у)Р
тогда и только тогда, когда ху
делится на 3;

д) (х,
у)Р
тогда и только тогда, когда ху
делится на 5;

е) (х,
у)Р
тогда и только тогда, когда х+3=у.

Решение.
б) В Р
включаются такие пары (х,
у),
что у=х².
Например, 4=2².
Поэтому (2, 4)P.
Так как 83²,
то (3, 8)P.
Окончательно имеем P={(1,
1), (2, 4), (3, 9), (4, 16)}.

Ответ:
б) P={(1,
1), (2, 4), (3, 9), (4, 16)}.

2.
Пусть A={a,
b,
c},
B={1,
2, 3, 4}. Изобразить отношения PAB
и QB²
графически. Найти _Р,
_Q,
_Р,
_Q
и РQ:

а)
P={(b,
1), (b,
3), (c,
1), (c,
2), (c,
3), (c,
4)}, Q={(1,
1), (2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4), (4, 2), (4, 3),
(4, 4)};

б)
P={(a,
1), (a,
2), (a,
4), (b,
3), (c,
1), (c,
4)}, Q={(1,
3), (1, 2), (2, 3), (3, 2), (3, 4), (4, 1)};

в) P={(a,
1),(a,
4), (b,
2), (b,
3), (c,
1), (c,
4)}, Q={(1,
1), (1, 4), (2, 1), (3, 4), (4, 3), (4, 1)}.

3.
Найти матрицы отношений P,
Q
из упражнения 2, а также (PQ),
и по матрице отношений найти (PQ).
С помощью матрицы отношения проверить,
является ли отношение Q
рефлексивным, симметричным, транзитивным,
антисимметричным.

Решение.
а) Имеем

[Р]=,
[Q]=.

Поэтому по свойствам
композиций отношений и их матриц получаем

[(PQ)]=[QP]=[Q][P]=[Q]^T[P]^T==.

В частности,
(PQ)=(1,
b),
(2, b),
(3, b),
(4, b),
(1, с),
(2, с,
(3, с),
(4, с).

Матрица [Q]
отношения Q
обладает тем свойством, что по главной
диагонали стоят единицы. Следовательно,
отношение Q
рефлексивно.

Далее, матрица [Q]
симметрична, [Q]^Т=[Q].
Поэтому отношение Q
симметрично.

Так как

[Q][Q]===[Q]

(напоминаем, что
умножение матриц и чисел производится
обычным образом, а сложение чисел 
по правилу 0+0=0, 1+0=0+1=1+1=1, см. свойства
матриц бинарных отношений, стр. 12), то
отношение Q

транзитивно.

Наконец, вне главной
диагонали [Q]
имеются ненулевые элементы. Поэтому
отношение Q
не является антисимметричным.

Таким образом,
отношение Q
рефлексивно, симметрично, транзитивно
(в частности, Q

эквиваленция), не антисимметрично.

Ответ:
[Р]=,
[Q]=,
[(PQ)]=.
ОтношениеQ
является рефлексивным, симметричным,
транзитивным, но не является
антисимметричным. (PQ)=(1,
b),
(2, b),
(3, b),
(4, b),
(1, с),
(2, с,
(3, с),
(4, с).

4.
Проверить отношения из упражнения 1 на
рефлексивность, симметричность,
транзитивность, антисимметричность.
Если на множестве А
отношение Р
является эквиваленцией, то найти
фактор-множество .

Решение.
г) Так как 0=хх
делится на 3 для любого х,
то для любого х
(х,
х)Р,
и отношение
Р
рефлексивно. Далее, для любых х,
у
из того, что ху
делится на 3 следует, что ух=(ху)
делится на 3. Поэтому из (х,
у)Р
следует (у,
х)Р,
и отношение симметрично. Пусть ху
делится на 3 и уz
делится на 3. Тогда (в силу того, что сумма
чисел, делящихся на 3 тоже делится на 3)
хz
=(ху)+(уz)
делится на 3. Поэтому из (х,
y)Р
и (y,
z)Р
следует (х,
z)Р,
и отношение транзитивно. Следовательно,
отношение Р
рефлексивно, симметрично, транзитивно,
и Р

эквиваленция.

Из того, что ху
делится на 3 и ух
делится на 3 не следует, что х=у.
Поэтому отношение не является
антисимметричным.

Найдем фактор-множество
по отношению Р.
Классами эквиваленции являются
=1,
4, 7, 10, 13, 16, 19,
=2,
5, 8, 11, 14, 17, 20,
=3,
6, 9, 12, 15, 18.
Поэтому А/Р=,,.

Ответ:
Отношение Р
является рефлексивным, симметричным,
транзитивным, но не является
антисимметричным. А/Р=,,.

5.
Найдите область определения, область
значений отношения РR².
Является ли отношение Р
рефлексивным, симметричным, антисимметричным,
транзитивным?

а) (x,
y)P
тогда и только тогда, когда y=|x|;

б) (x,
y)P
тогда и только тогда, когда xy>1;

в) (x,
y)P
тогда и только тогда, когда x²+y²=1.

Решение.
а) Элемент х
может принимать любое действительное
значение, то есть хR,
и _Р=R.
Так как y=|x|0,
то _Р=R
₊=у
уR,
у0

множество всех неотрицательных чисел.
Вообще говоря, х|x|
(например, 1|1|,
и отношение нерефлексивно. Далее, из
y=|x|
не следует, что х=|у|
(это не так, если х

отрицательно), и поэтому отношение
несимметрично. Из y=|x|
и z=|у|
следует z=|x|,
так как z=|у|=у=|x|
(|у|=у
так как y=|x|≥0).
Поэтому отношение транзитивно. Наконец,
из y=|x|
и х=|у|
следует х=у,
то есть отношение антисимметрично.

Ответ:
_Р=R,
_Р=R₊=у
уR,
у0.
Отношение нерефлексивно, несимметрично,
транзитивно, антисимметрично.

6.
Пусть
a,
b,
c,
d,
e,
f

такие
числа,
что
a<b<c<d<e<f,
A=[c,
d),
B=[c,
d)(e,
f
), C=[a,
b)[c,
d),
D=[c,
d)(e,
+),E=(,d)[c,
d).
Найти (в
случае наличия) minX,
maxX,
infX,
supX,
наименьшее и наибольшее значения
множеств X=A,
B,
C,
D,
E.

Решение.
Решим упражнение для X=B.

Покажем, что minB=с,
maxB
не существует. Действительно,

B=[c,
d)(e,
f
)={x|c≤x<d}{x|e<x<f
}.

Поэтому для xB
из x≤c
следует, что x=c,
так как x
удовлетворяет системе неравенств

Следовательно,
c=minB.
Далее, так как для любого xB
имеет место неравенство x<d,
то нет такого aB,
что для любого xB
имело бы место x≤a.
Действительно, aB
означает, что a<d
и тогда существует x
такой, что a<x<d,
то есть xB
и a<x.
Следовательно, maxB
не существует.

Покажем, что infB=с
и supB=f.
Будем рассматривать B
как подмножество R:
BR.
Тогда для любого xR
с условием x≤y,
где y

произвольный элемент из B,
является нижней гранью B.
Из нижних граней B
наибольшим является c,
то есть infB=с.
Аналогично, любой xR
с условием y≤x,
где yB,
является верхней гранью B.
Наименьшая из них 
это d,
то есть supB=f.

Наконец, в ЛУМ minX
и maxX
являются одновременно наибольшим и
наименьшим элементами, соответственно.
Так как B

ЛУМ (как числовое множество) и minB=c,
a
c=maxB
не существует, то наименьшим элементом
B
является c,
а наибольшего элемента не существует.

7.
Пусть A={1,
2, 3} (A={1,
2, 3, 4}) и P(A)

его булеан.

а) Доказать, что
P(A)
имеет наименьший и наибольший элементы
относительно отношения .
Найти все минимальные и максимальные
элементы в P(A).

б) Для B=P(A){{2,
3}, {1, 2, 3}} найти наибольший и наименьший
элементы, minB,
maxB,
infB,
supB
(если указанные элементы существуют).

в) Изобразить
графически отношение 
на A,
B.

Отношения эквивалентности на множестве

Разбиение множества

Пусть — произвольное множество. Семейство непустых и попарно не пересекающихся множеств называют разбиением множества , если объединение множеств семейства равно , то есть

Сами множества называют элементами (или членами) разбиения .

Например, множества и образуют разбиение отрезка . Тривиальными разбиениями являются, по определению, разбиение , состоящее только из самого , и разбиение, состоящее из всех одноэлементных подмножеств множества .

Пусть — эквивалентность на множестве и . Множество всех элементов , эквивалентных , т.е. множество , называют классом эквивалентности по отношению и обозначают . Отметим, что в силу рефлексивности для любого элемента класс эквивалентности не пуст, так как .

Теорема 1.4. Для любого отношения эквивалентности на множестве множество классов эквивалентности образует разбиение множества . Обратно, любое разбиение множества задает на нем отношение эквивалентности, для которого классы эквивалентности совпадают с элементами разбиения.

Покажем, что отношение эквивалентности на множестве определяет некоторое разбиение этого множества. Убедимся вначале, что любые два класса эквивалентности по отношению либо не пересекаются, либо совпадают.

Пусть два класса эквивалентности и имеют общий элемент . Тогда и . В силу симметричности отношения имеем , и тогда и . В силу транзитивности отношения получим . Пусть , тогда . Так как , то и, следовательно, .

Обратно, если , то в силу симметричности получим и в силу транзитивности — , то есть . Таким образом, .

Итак, любые два не совпадающих класса эквивалентности не пересекаются. Так как для любого справедливо (поскольку ), т.е. каждый элемент множества принадлежит некоторому классу эквивалентности по отношению , то множество всех классов эквивалентности по отношению образует разбиение исходного множества . Таким образом, любое отношение эквивалентности однозначно определяет некоторое разбиение.

Теперь пусть — некоторое разбиение множества . Рассмотрим отношение , такое, что имеет место тогда и только тогда, когда и принадлежат одному и тому же элементу данного разбиения:

Очевидно, что введенное отношение рефлексивно и симметрично. Если для любых и имеет место и , то и в силу определения отношения принадлежат одному и тому же элементу разбиения. Следовательно, и отношение транзитивно. Таким образом, — эквивалентность на .

---

Фактор-множество

Теорема 1.4 позволяет отождествлять отношения эквивалентности и разбиения: любая эквивалентность определяет единственное разбиение и наоборот.

Множество всех классов эквивалентности по данному отношению эквивалентности на множестве называют фактор-множеством множества по отношению и обозначают .

Пример 1.14. а. На множестве целых чисел определим отношение равенства по модулю , где . Положим , если и только если делится на .

Легко проверяется, что это отношение эквивалентности. Действительно, рефлексивность следует из того, что для любо и делится на ; симметричность — из того, что если делится на , то и делится на . Для доказательства транзитивности заметим, что если делится на и делится на , то и их сумма делится на . Другими словами, для любых целых из и следует , что доказывает транзитивность отношения .

Равенство чисел и по модулю означает, что при делении на эти числа дают одинаковые остатки. Действительно, для каждого имеем , где — остаток от деления на . Следовательно, , то есть . Таким образом, каждое число попадает в тот же класс эквивалентности по отношению , что и остаток от деления его на . Поскольку всего различных остатков может быть ровно , получаем ровно попарно различных классов эквивалентности по данному отношению:

где класс состоит из всех целых чисел, дающих при делении на остаток .

Отметим, что мы установили взаимно однозначное соответствие между фактор-множеством и множеством , состоящим из чисел .

Второе множество дает нам как бы wнаглядный образ” построенного фактор-множества. Нельзя считать, что фактор-множество равно множеству . Нет, указанное фактор-множество состоит из элементов, каждый из которых есть не число, а множество всех целых чисел, при делении на дающих фиксированный остаток. Но каждому такому классу эквивалентности однозначно сопоставляется целое число от 0 до , и, наоборот, каждому целому числу от 0 до соответствует единственный класс эквивалентности по отношению . Заметим, что в математике часто используется прием сопоставления фактор-множеству такого находящегося с ним во взаимно однозначном соответствии множества, которое легко представить и описать.

б. На множестве действительных чисел зададим отношение , полагая, что числа и равны по модулю 1 тогда и только тогда, когда число является целым. Из определения следует, что каждое число по модулю 1 равно своей дробной части.

Примечание. Под дробной частью числа понимается число из полуинтервала , такое, что для некоторого целого . Поэтому дробной частью отрицательного числа , где , будет число . Так, Дробной частью будет не , а .

Так как отношение определено через равенство, то легко понять, что все свойства отношения эквивалентности для него выполняются. Каждый класс эквивалентности будет содержать числа с равными дробными частями. Это значит, что каждый класс эквивалентности по данному отношению однозначно определяет некоторое число из полуинтервала и, наоборот, каждому числу однозначно сопоставляется класс эквивалентности, состоящий из всех действительных чисел, дробная часть которых равна . Таким образом, фактор-множество и полуинтервал на числовой прямой находятся во взаимно однозначном соответствии. Этот полуинтервал можно рассматривать как представление определенного выше фактор-множества.

---

Связь между понятиями эквивалентности и отображения

Установим теперь связь между понятиями эквивалентности и отображения. Заметим, что для любого отношения эквивалентности на множестве можно определить отображение , положив , т.е. сопоставив каждому содержащий его класс эквивалентности. Это отображение сюръективно, так как каждый элемент множества принадлежит некоторому классу эквивалентности, т.е. для каждого справедливо .

Отображение определенное таким образом, называют канонической сюръекцией множества .

Покажем, что любое отображение однозначно определяет некоторое отношение эквивалентности.

Теорема 1.5. Пусть — произвольное отображение. Отношение на множестве , для которого , если и только если , является отношением эквивалентности, причем существует биекция фактор-множества на множество .

Доказательство. Рефлексивность, симметричность и транзитивность отношения следуют непосредственно из его определения, т.е. — эквивалентность.

Зададим отображение фактор-множества в множество следующим образом: . Из способа задания отношения следует, что отображение определено корректно, т.е. каждому классу эквивалентности поставлен в соответствие единственный элемент .

Докажем, что — биекция, для чего убедимся в том, что это инъекция и сюръекция одновременно. Пусть классы эквивалентности и не совпадают. В силу теоремы 1.4 это означает, что они не пересекаются, т.е. не эквивалентно . Из определения отношения следует, что . Таким образом, — инъекция. Если элемент , то найдется такой элемент , что , то есть — сюръекция фактор-множества на множество . Итак, — биекция.

---

Следовательно, в силу доказанных теорем 1.4 и 1.5 существует связь между тремя понятиями — отображением множества, отношением эквивалентности на множестве и разбиением множества. Но неверно, что существует взаимно однозначное соответствие между отображениями и отношениями эквивалентности (заметим, что теорема 1.5 этого и не утверждает). Два разных отображения могут определять одно и то же разбиение отображаемого множества, тем самым задавая на нем одно и то же отношение эквивалентности. Так, например, любое биективное отображение задает на одно и то же разбиение — тривиальное разбиение на одноэлементные множества.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Макеты страниц