Как найти факториал больших чисел – Сайт, где вы сможете решить свои вопросы

Find the factorial of a large number.

What is Factorial of a number?

Factorial of a non-negative integer, is the multiplication of all integers smaller than or equal to n.

Factorial of a number

Examples:

Input: 100
Output: 933262154439441526816992388562667004-
907159682643816214685929638952175999-
932299156089414639761565182862536979-
208272237582511852109168640000000000-
00000000000000

Input: 50
Output: 3041409320171337804361260816606476884-
4377641568960512000000000000

We have discussed a simple program for factorial.

Why conventional way of computing factorial fails for large numbers?

A factorial of 100 has 158 digits. It is not possible to store these many digits even if we use long int.

The idea is to use basic mathematics for multiplication.

Illustration:

Example to show working of multiply(res[], x)

A number 5189 is stored in res[] as following: res[] = {9, 8, 1, 5}

let x = 10
Initialize carry = 0

At i = 0, prod = res[0]*x + carry = 9*10 + 0 = 90.
res[0] = 0, carry = 9

At i = 1, prod = res[1]*x + carry = 8*10 + 9 = 89
res[1] = 9, carry = 8

At i = 2, prod = res[2]*x + carry = 1*10 + 8 = 18
res[2] = 8, carry = 1

At i = 3, prod = res[3]*x + carry = 5*10 + 1 = 51
res[3] = 1, carry = 5

res[4] = carry = 5
res[] = {0, 9, 8, 1, 5}

Follow the steps below to solve the given problem:

Create an array res[] of MAX size where MAX is a number of maximum digits in output.
Initialize value stored in res[] as 1 and initialize res_size (size of ‘res[]’) as 1.
Multiply x with res[] and update res[] and res_size to store the multiplication result for all the numbers from x = 2 to n.
To multiply a number x with the number stored in res[], one by one multiply x with every digit of res[].
To implement multiply function perform the following steps:
- Initialize carry as 0.
- Do following for i = 0 to res_size – 1
  - Find value of res[i] * x + carry. Let this value be prod.
  - Update res[i] by storing the last digit of prod in it.
  - Update carry by storing the remaining digits in carry.
- Put all digits of carry in res[] and increase res_size by the number of digits in carry.

Below is the implementation of the above algorithm.

NOTE: In the below implementation, the maximum digits in the output are assumed as 500. To find a factorial of a much larger number ( > 254), increase the size of an array or increase the value of MAX. This can also be solved using Linked List instead of using res[] array which will not waste extra space.

C++

#include <iostream>

using namespace std;

#define MAX 500

int multiply(int x, int res[], int res_size);

void factorial(int n)

{

int res[MAX];

res[0] = 1;

int res_size = 1;

for (int x = 2; x <= n; x++)

res_size = multiply(x, res, res_size);

cout << "Factorial of given number is n";

for (int i = res_size - 1; i >= 0; i--)

cout << res[i];

}

int multiply(int x, int res[], int res_size)

{

int carry = 0;

for (int i = 0; i < res_size; i++) {

int prod = res[i] * x + carry;

res[i] = prod % 10;

carry = prod / 10;

}

while (carry) {

res[res_size] = carry % 10;

carry = carry / 10;

res_size++;

}

return res_size;

}

int main()

{

factorial(100);

return 0;

}

Java

class GFG {

static void factorial(int n)

{

int res[] = new int[500];

res[0] = 1;

int res_size = 1;

for (int x = 2; x <= n; x++)

res_size = multiply(x, res, res_size);

System.out.println("Factorial of given number is ");

for (int i = res_size - 1; i >= 0; i--)

System.out.print(res[i]);

}

static int multiply(int x, int res[], int res_size)

{

int carry = 0;

for (int i = 0; i < res_size; i++) {

int prod = res[i] * x + carry;

res[i] = prod % 10;

carry = prod / 10;

}

while (carry != 0) {

res[res_size] = carry % 10;

carry = carry / 10;

res_size++;

}

return res_size;

}

public static void main(String args[])

{

factorial(100);

}

Python3

import sys

def factorial(n):

res = [None]*500

res[0] = 1

res_size = 1

x = 2

while x <= n:

res_size = multiply(x, res, res_size)

x = x + 1

print("Factorial of given number is")

i = res_size-1

while i >= 0:

sys.stdout.write(str(res[i]))

sys.stdout.flush()

i = i - 1

def multiply(x, res, res_size):

carry = 0

i = 0

while i < res_size:

prod = res[i] * x + carry

res[i] = prod % 10

carry = prod//10

i = i + 1

while (carry):

res[res_size] = carry % 10

carry = carry // 10

res_size = res_size + 1

return res_size

factorial(100)

C#

using System;

class GFG {

static void factorial(int n)

{

int[] res = new int[500];

res[0] = 1;

int res_size = 1;

for (int x = 2; x <= n; x++)

res_size = multiply(x, res, res_size);

Console.WriteLine("Factorial of "

+ "given number is ");

for (int i = res_size - 1; i >= 0; i--)

Console.Write(res[i]);

}

static int multiply(int x, int[] res, int res_size)

{

int carry = 0;

for (int i = 0; i < res_size; i++) {

int prod = res[i] * x + carry;

res[i] = prod % 10;

carry = prod / 10;

}

while (carry != 0) {

res[res_size] = carry % 10;

carry = carry / 10;

res_size++;

}

return res_size;

}

static public void Main() { factorial(100); }

}

PHP

<?php

$MAX = 500;

function factorial($n)

{

global $MAX;

$res = array_fill(0, $MAX, 0);

$res[0] = 1;

$res_size = 1;

for ($x = 2; $x <= $n; $x++)

$res_size = multiply($x, $res, $res_size);

echo "Factorial of given number is n";

for ($i = $res_size - 1; $i >= 0; $i--)

echo $res[$i];

}

function multiply($x, &$res, $res_size)

{

$carry = 0;

for ($i = 0; $i < $res_size; $i++)

{

$prod = $res[$i] * $x + $carry;

$res[$i] = $prod % 10;

$carry = (int)($prod / 10);

}

while ($carry)

{

$res[$res_size] = $carry % 10;

$carry = (int)($carry / 10);

$res_size++;

}

return $res_size;

}

factorial(100);

?>

Javascript

<script>

function factorial(n)

{

let res = new Array(500);

res[0] = 1;

let res_size = 1;

for (let x=2; x<=n; x++)

res_size = multiply(x, res, res_size);

document.write("Factorial of given number is " + "<br>");

for (let i=res_size-1; i>=0; i--)

document.write(res[i]);

}

function multiply(x, res, res_size)

{

let carry = 0;

for (let i=0; i<res_size; i++)

{

let prod = res[i] * x + carry;

res[i] = prod % 10;

carry = Math.floor(prod/10);

}

while (carry)

{

res[res_size] = carry%10;

carry = Math.floor(carry/10);

res_size++;

}

return res_size;

}

factorial(100);

</script>

Output

Factorial of given number is 
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000

Time Complexity: O(N log (N!)), where O(N) is for loop and O(log N!) is for nested while loop
Auxiliary Space: O(max(digits in factorial))

Find the Factorial of a large number using Basic BigInteger

This problem can be solved using the below idea:

Big Integer can also be used to calculate the factorial of large numbers.

Illustration:

N = 5

ans = 1

At i = 2: ans = ans x i = 1 x 2 = 2
At i = 3: ans = ans x i = 2 x 3 = 6
At i = 4: ans = ans x i = 6 x 4 = 24
At i = 5: ans = ans x i = 24 x 5 = 120

Hence factorial of N is 120

Follow the steps below to solve the given problem:

Declare a BigInteger f with 1 and perform the conventional way of calculating factorial
Traverse a loop from x = 2 to N and multiply x with f and store the resultant value in f

Below is the implementation of the above idea :

C++

#include <bits/stdc++.h>

using namespace std;

#define ull unsigned long long

ull factorial(int N)

{

ull f = 1;

for (ull i = 2; i <= N; i++)

f *= i;

return f;

}

int main()

{

int N = 20;

cout << factorial(N) << endl;

}

Java

import java.math.BigInteger;

import java.util.Scanner;

public class Example {

static BigInteger factorial(int N)

{

BigInteger f

= new BigInteger("1");

for (int i = 2; i <= N; i++)

f = f.multiply(BigInteger.valueOf(i));

return f;

}

public static void main(String args[]) throws Exception

{

int N = 20;

System.out.println(factorial(N));

}

Python3

def factorial(N):

f = 1

for i in range(2, N + 1):

f *= i

return f;

N = 20;

print(factorial(N));

C#

using System;

using System.Collections.Generic;

using System.Numerics;

public class Example {

static BigInteger factorial(int N)

{

BigInteger f

= new BigInteger(1);

for (int i = 2; i <= N; i++)

f = BigInteger.Multiply(f, new BigInteger(i));

return f;

}

public static void Main(string[] args)

{

int N = 20;

Console.WriteLine(factorial(N));

}

Javascript

function factorial(N)

{

let f = BigInt(1);

for (var i = 2; i <= N; i++)

f *= BigInt(i);

return f;

}

let N = 20;

console.log(factorial(N));

Output

2432902008176640000

Time Complexity: O(n)
Auxiliary Space: O(1)

Method 3:

1. Define a function factorial(n) that takes an integer n as input.
2. Check if n is 0 or 1. If it is, return 1.
3. If n is greater than 1, call the function recursively with input n-1 and store the result in a variable called sub_result.
4. Multiply sub_result with n and return the product as the final result.

C++

#include <iostream>

#include <vector>

using namespace std;

vector<int> multiply(vector<int>& digits, int factor) {

int carry = 0;

for (int i = 0; i < digits.size(); i++) {

int prod = digits[i] * factor + carry;

digits[i] = prod % 10;

carry = prod / 10;

}

while (carry) {

digits.push_back(carry % 10);

carry /= 10;

}

return digits;

}

void print(vector<int>& digits) {

for (int i = digits.size() - 1; i >= 0; i--) {

cout << digits[i];

}

int main() {

int n = 100;

vector<int> digits;

digits.push_back(1);

for (int i = 2; i <= n; i++) {

digits = multiply(digits, i);

}

print(digits);

return 0;

}

Java

import java.math.BigInteger;

public class Main {

public static void main(String[] args) {

int n = 100;

BigInteger result = BigInteger.valueOf(1);

for (int i = 1; i <= n; i++) {

result = result.multiply(BigInteger.valueOf(i));

}

System.out.println(result);

}

Python3

import math

n = 100

result = math.factorial(n)

print(result)

Javascript

function factorial(n) {

let result = BigInt(1);

for (let i = 2; i <= n; i++) {

result *= BigInt(i);

}

return result;

}

const n = 100;

const result = factorial(n);

console.log(result);

C#

using System;

using System.Collections.Generic;

class MainClass {

static List<int> Multiply(List<int> digits, int factor)

{

int carry = 0;

for (int i = 0; i < digits.Count; i++) {

int prod = digits[i] * factor + carry;

digits[i] = prod % 10;

carry = prod / 10;

}

while (carry > 0) {

digits.Add(carry % 10);

carry /= 10;

}

return digits;

}

static void Print(List<int> digits)

{

for (int i = digits.Count - 1; i >= 0; i--) {

Console.Write(digits[i]);

}

static void Main()

{

int n = 100;

List<int> digits = new List<int>();

digits.Add(1);

for (int i = 2; i <= n; i++) {

digits = Multiply(digits, i);

}

Print(digits);

}

Output

93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000

Time Complexity: O(n)

The time complexity of the code is O(n), where n is the value of the input parameter. This is because the math.factorial() function internally uses a loop to calculate the product of all integers from 1 to n, and the loop iterates n times. Therefore, the time taken by the function is proportional to n.
Auxiliary Space: O(1)

The auxiliary space complexity of the code is O(1), because the code uses only a constant amount of additional memory to store the result of the factorial calculation. Specifically, the memory required to store the result is proportional to the number of digits in the result, which is roughly log10(n!), or O(log n), but this is negligible compared to the input size for large values of n.

Last Updated :
09 Apr, 2023

Like Article

Save Article

Источник

Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала.

Это очень просто, вот пример:

7! = 1 * … * 7 = 5040.

Факторизация – разложение функции на множители.

Таблица факториалов

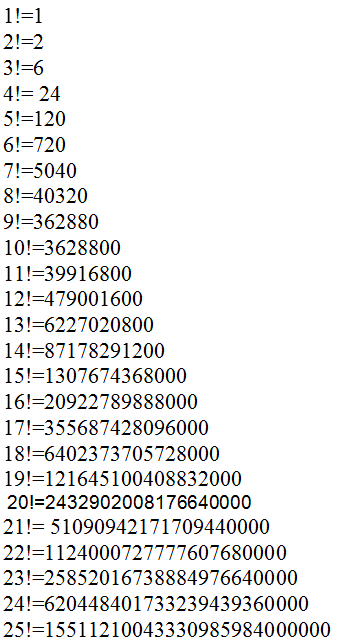
Свойства факториалов

Рекуррентная формула

251

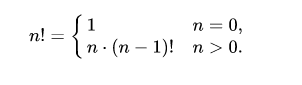
Комбинаторная интерпретация

Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.

Формула Стирлинга

Позволяет не перемножать большие числа. Обычно необходим только главный член:

252

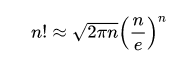
Можно ли вычислить 0,5 или -3,217? Нет, нельзя. Но можно использовать нечто под названием «Гамма-функция», что намного сложнее.

Расчет по предыдущему значению

Функцию легко вычислить из предыдущего значения:

3! = 3 × 2! = 6;
41160 = 5! +8! + 6!

А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.

Однако было решено, что в случае 0 результат будет равен 1.

Свойства факториала

Некоторые очень большие значения

Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.

Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.

Примеры вычисления факториалов больших чисел:

70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);
100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;
200! это примерно 7 88657867867364479050355236321393 x 103743.

Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.

Программа на языке Паскаль:

Факториал на Паскале

На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.

Факториал дроби (½) – это половина квадратного корня pi = (½)√π.

Примеры задач с решениями

Задание 1

254

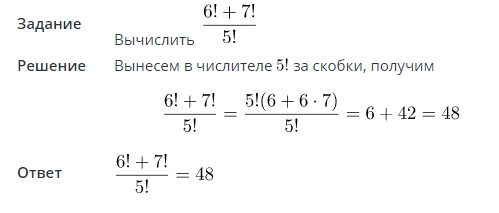
Задание 2

255

Использование факториалов

Математика и многие ее области используют функцию. В комбинаторике функция была введена именно для расчета перестановки. Также понятие тесно связано с биномом ньютона (формула бинома Ньютона необходима для разложения степени (x + y) n в многочлен).

Источник

Какие есть алгоритмы вычисления факториалов больших чисел без калькуляторов?

ПрограммированиеМатематика+3

521

В целом, конечно, согласен. Но вычисление гамма-функции ручками — не выглядит упрощением 🙂

Комментировать ответ…Комментировать…

Кандидат физико-математических наук, выпускник ШАД · 14 мая 2022

Некий Г. С. Улер с помощью допотопных средств годами вычислял число 1000! и в 1955 году опубликовал-таки все его 2568 цифр. Сработал на совесть: все они оказались верными.

Факториалы больших чисел и записывать-то затруднительно без вычислительной техники, не то что вычислять. Да и зачем, если компьютеры делают это за доли секунды?

7,3 K

Дело в том, что я недавно узнал о том, что иногда такое задание может встретиться на экзаменах учителей… Читать дальше

Комментировать ответ…Комментировать…

к.ф.м.н., доцент МФТИ, с.н.с. Института Проблем Управления. · 14 мая 2022

Ну без вычислительной техники вряд-ли удастся обойтись, уже 10! — довольно солидное число. Но в целом, можно использовать скажем формулу Стирлинга: Читать далее

1,0 K

Ответ считаю вкратце правильным. Если точность не требуется, то для условно “порядка роста” достаточно формулы… Читать дальше

Комментировать ответ…Комментировать…

Закончил физфак Новосибирского университета. Занимался теор. физикой и преподаванием… · 14 мая 2022

584

Непонятно, зачем снова постить тот же самый кривоватый ответ с теми же грамматическими ошибками и невразумительными… Читать дальше

Комментировать ответ…Комментировать…

Закончил физфак Новосибирского университета. Занимался теор. физикой и преподаванием… · 12 мая 2022

560

Если Вы уж хотите вставить ссылку, то наверное следует дать её не на кустарное исследование, а на более точную форм… Читать дальше

Комментировать ответ…Комментировать…

Написал только для того что бы “далее” нажать · 16 мая 2022

Без калькуляторов, конечно не просто. Я бы предложил очень приближенный способ- из упрощенной ф-лы Стирлига, для счета “в уме”

2.51*sqrt(n)*10^(n(lgn-0.43))
Например, n=10000
2.51*100*10^(10000*3.57)=2.51*10^35702, ошибка на три порядка, при 36 тыс дес.знаков

Для продвинутых счетчиков, можно добавить поправку.

492

действительно без калькулятора

Комментировать ответ…Комментировать…

О сообществе

Источник

Факториа́л — функция, определённая на множестве неотрицательных целых чисел. Название происходит от лат. factorialis — действующий, производящий, умножающий; обозначается $n!$ , произносится эн факториа́л. Факториал натурального числа $n$ определяется как произведение всех натуральных чисел от 1 до $n$ включительно:

${displaystyle n!=1cdot 2cdot ldots cdot n=prod _{k=1}^{n}k}$ .

Например,

$5 ! = 1 cdot 2 cdot 3 cdot 4 cdot 5 = 120$ .

Для $n=0$ принимается в качестве соглашения, что

$0!=1$ .

Факториалы всех чисел составляют последовательность A000142 в OEIS; значения в научной нотации округляются

n	n!
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800
11	39916800
12	479001600
13	6227020800^[1]
14	87178291200^[2]
15	1307674368000^[3]
16	20922789888000^[4]
17	355687428096000^[5]
18	6402373705728000^[6]
19	121645100408832000^[7]
20	2432902008176640000^[8]
25	15511210043330985984000000^[9]
50	30 414 093 201 713 378 043 612 608 166 064 768 844 377 641 568 960 512 000 000 000 000^[10]
70	11 978 571 669 969 891 796 072 783 721 689 098 736 458 938 142 546 425 857 555 362 864 628 009 582 789 845 319 680 000 000 000 000 000^[11]
100	≈9,332621544⋅10¹⁵⁷
450	≈1,733368733⋅10¹⁰⁰⁰
1000	≈4,023872601⋅10²⁵⁶⁷
3249	≈6,412337688⋅10¹⁰⁰⁰⁰
10000	≈2,846259681⋅10³⁵⁶⁵⁹
25206	≈1,205703438⋅10¹⁰⁰⁰⁰⁰
100000	≈2,824229408⋅10⁴⁵⁶⁵⁷³
205023	≈2,503898932⋅10^1000004
1000000	≈8,263931688⋅10^5565708
10¹⁰⁰	≈10^{9,956570552⋅10¹⁰¹}
10¹⁰⁰⁰	≈10^10¹⁰⁰³
10^10 000	≈10^{10^10 004}
10^100 000	≈10^{10^100 005}
10^10¹⁰⁰	≈10^{10^10¹⁰⁰}

Факториал активно используется в различных разделах математики: комбинаторике, математическом анализе, теории чисел, функциональном анализе и др.

Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем любая показательная функция или любая степенная функция, а также быстрее, чем любая сумма произведений этих функций. Однако степенно-показательная функция ${displaystyle n^{n}}$ растёт быстрее факториала, так же как и большинство двойных степенных, например $e^{{e^{n}}}$ .

Свойства[править | править код]

Рекуррентная формула[править | править код]

Факториал может быть задан следующей рекуррентной формулой:

$n!= begin{cases} 1 & n = 0,\ n cdot (n-1)! & n > 0. end{cases}$

Комбинаторная интерпретация[править | править код]

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов.

Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала подтверждает целесообразность соглашения $0!=1$ — количество перестановок пустого множества равно единице. Кроме того, формула для числа размещений из $n$ элементов по $m$

${displaystyle A_{n}^{m}={frac {n!}{(n-m)!}}}$

при $n=m$ обращается в формулу для числа перестановок из $n$ элементов (порядка $n$ ), которое равно $n!$ .

Связь с гамма-функцией[править | править код]

Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением

${displaystyle n!=Gamma (n+1)}$ .

Это же выражение используют для обобщения понятия факториала на множество вещественных чисел. Используя аналитическое продолжение гамма-функции, область определения факториала также расширяют на всю комплексную плоскость, исключая особые точки при $n=-1,-2,-3ldots$ .

Непосредственным обобщением факториала на множества вещественных и комплексных чисел служит пи-функция ${displaystyle Pi (z)=Gamma (z+1)}$ , которая при ${displaystyle mathrm {Re} (z)>-1}$ может быть определена как

$Pi (z)=int _{0}^{infty }t^{{z}}e^{{-t}},{mathrm {d}}t$ (интегральное определение).

Пи-функция натурального числа или нуля совпадает с его факториалом: ${displaystyle Pi (n)=n!}$ . Как и факториал, пи-функция удовлетворяет рекуррентному соотношению ${displaystyle Pi (z)=zPi (z-1)}$ .

Формула Стирлинга[править | править код]

Формула Стирлинга — асимптотическая формула для вычисления факториала:

$n!={sqrt {2pi n}}left({frac {n}{e}}right)^{n}left(1+{frac {1}{12n}}+{frac {1}{288n^{2}}}-{frac {139}{51840n^{3}}}-{frac {571}{2488320n^{4}}}+{frac {163879}{209018880n^{5}}}+{frac {5246819}{75246796800n^{6}}}+Oleft(n^{{-7}}right)right),$

см. O-большое^[12].

Во многих случаях для приближённого вычисления факториала достаточно рассматривать только главный член формулы Стирлинга:

$n! approx sqrt{2pi n}left(frac{n}{e}right)^n.$

При этом можно утверждать, что

$sqrt{2pi n}left(frac{n}{e}right)^n e^{1/(12n+1)}< n! < sqrt{2pi n}left(frac{n}{e}right)^n e^{1/(12n)}.$

Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Например, с помощью формулы Стирлинга легко подсчитать, что

100! ≈ 9,33×10¹⁵⁷;
1000! ≈ 4,02×10²⁵⁶⁷;
10 000! ≈ 2,85×10^35 659.

Разложение на простые множители[править | править код]

Каждое простое число p входит в разложение n! на простые множители в степени определяемой следующей формулой:

$leftlfloor frac{n}{p}rightrfloor + leftlfloor frac{n}{p^2}rightrfloor + leftlfloor frac{n}{p^3}rightrfloor + ldots.$

Таким образом,

$n! = prod_{p} p^{lfloor frac{n}{p}rfloor + lfloor frac{n}{p^2}rfloor +ldots},$

где произведение берётся по всем простым числам. Можно заметить, что для всякого простого p большего n соответствующий множитель в произведении равен 1; следовательно, произведение можно брать лишь по простым p, не превосходящим n.

Связь с производной от степенной функции[править | править код]

Для целого неотрицательного числа n:

$left(x^{n}right)^{{(n)}}=n!$

Например:

$left( x^5 right)^{(5)} = left( 5 cdot x^4 right)^{(4)} = left( 5 cdot 4 cdot x^3 right)''' = left( 5 cdot 4 cdot 3 cdot x^2 right)'' = left( 5 cdot 4 cdot 3 cdot 2 cdot x right)' = {5 cdot 4 cdot 3 cdot 2 cdot 1} = 5!$

Другие свойства[править | править код]

Для натурального числа $n$ :

$n!^{2}geqslant n^{n}geqslant n!geqslant n$

Для любого $n>1$ :

$n!$ не является квадратом целого числа;

Для любого $n>4$ :

$n!$ оканчивается на 0;

Для любого ${displaystyle n>9}$ :

$n!$ оканчивается на 00.

Если $n$ простое число:

${displaystyle (n-1)!+1}$ делится на $n$ (теорема Вильсона)

История[править | править код]

Факториальные выражения появились ещё в ранних исследованиях по комбинаторике, хотя компактное обозначение $n!$ предложил французский математик Кристиан Крамп только в 1808 году^[13]. Важным этапом стало открытие формулы Стирлинга, которую Джеймс Стирлинг опубликовал в своём трактате «Дифференциальный метод» (лат. Methodus differentialis, 1730 год). Немного ранее почти такую же формулу опубликовал друг Стирлинга Абрахам де Муавр, но в менее завершённом виде (вместо коэффициента ${sqrt {2pi }}$ была неопределённая константа)^[14].

Стирлинг подробно исследовал свойства факториала, вплоть до выяснения вопроса о том, нельзя ли распространить это понятие на произвольные вещественные числа. Он описал несколько возможных путей к реализации этой идеи и высказал мнение, что:

${displaystyle left({1 over 2}right)!={frac {sqrt {pi }}{2}}}$

Стирлинг не знал, что годом ранее решение проблемы уже нашёл Леонард Эйлер. В письме к Кристиану Гольдбаху Эйлер описал требуемое обобщение^[15]:

${displaystyle x!=lim _{mto infty }{frac {m^{x}m!}{(x+1)(x+2)dots (x+m)}}}$

Развивая эту идею, Эйлер в следующем, 1730 году, ввёл понятие гамма-функции в виде классического интеграла. Эти результаты он опубликовал в журнале Петербургской академии наук в 1729—1730 годах.

Обобщения[править | править код]

Двойной факториал[править | править код]

Двойной факториал числа n обозначается n‼ и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность, что и n.

Для чётного n:

$n!! = 2 cdot 4 cdot 6 cdot ldots cdot n = prod_{i=1}^{frac{n}{2}} 2i = 2^{{color{white}1}^{!!!! frac{n}{2}}} cdot left ( frac{n}{2} right )!$

Для нечётного n:

$n!!={1cdot 3cdot 5cdot ldots cdot n}=prod _{{i=0}}^{{{frac {n-1}{2}}}}(2i+1)={frac {n!}{2^{{{color {white}1}^{{!!!!{frac {n-1}{2}}}}}}cdot left({frac {n-1}{2}}right)!}}$

Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.

$n!!={frac {n!}{(n-1)!!}}$

Осуществив замену $n=2k$ для чётного n и $n=2k+1$ для нечётного n соответственно, где $k$ — целое неотрицательное число, получим:

для чётного числа:

$(2k)!!=2cdot 4cdot 6cdot ldots cdot 2k=prod _{{i=1}}^{{k}}2i=2^{k}cdot k!$

для нечётного числа:

$(2k+1)!!=1cdot 3cdot 5cdot ldots cdot (2k+1)=prod _{{i=0}}^{{k}}(2i+1)={frac {(2k+1)!}{2^{k}cdot k!}}$

По договорённости: $0!! = 1$ . Также это равенство выполняется естественным образом:

$0!! = 2^0 cdot 0! = 1 cdot 1 = 1$

Двойной факториал, так же, как и обычный факториал, определён только для целых неотрицательных чисел.

Последовательность значений n!! начинается так^[16]:

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, …

Кратный факториал[править | править код]

m-кратный факториал числа n обозначается $textstyle nunderbrace{!!ldots !}_m$ и определяется следующим образом. Пусть число n представимо в виде $n=mk-r,$ где $kin {mathbb {Z}},$ $r in {0,1,ldots ,m-1}.$ Тогда^[17]

$nunderbrace{!!ldots !}_m = prod_{i=1}^k (mi-r)$

Обычный и двойной факториалы являются частными случаями m-кратного факториала для m = 1 и m = 2 соответственно.

Кратный факториал связан с гамма-функцией следующим соотношением^[18]:

$nunderbrace {!!ldots !}_{m}=prod _{{i=1}}^{{k}}(mi-r)=m^{k}cdot {frac {Gamma left(k-{frac {r}{m}}+1right)}{Gamma left(1-{frac {r}{m}}right)}}.$

Также кратный факториал $textstyle nunderbrace{!!ldots !}_m$ возможно записывать в сокращенном виде ${displaystyle n!_{(m)}}$ .

Неполный факториал[править | править код]

Убывающий факториал[править | править код]

Убывающим факториалом называется выражение

$(n)_k = n^{underline{k}} = n^{[k]}= ncdot (n-1)cdot ldotscdot (n-k+1) = frac{n!}{(n-k)!} = prod_{i=n-k+1}^n i$ .

Например:

n = 7; k = 4,

(n − k) + 1 = 4,

n^k = 7 • 6 • 5 • 4 = 840.

Убывающий факториал даёт число размещений из n по k.

Возрастающий факториал[править | править код]

Возрастающим факториалом называется выражение

$n^{(k)} = n^{overline{k}} = ncdot (n+1)cdot ldotscdot (n+k-1) = frac{(n+k-1)!}{(n-1)!}=prod_{i=n}^{(n+k)-1} i.$

Праймориал или примориал[править | править код]

Праймориал или примориал (англ. primorial) числа n обозначается p_n# и определяется как произведение n первых простых чисел. Например,

$p_{5}#=2times 3times 5times 7times 11=2310$ .

Иногда праймориалом называют число $n#$ , определяемое как произведение всех простых чисел, не превышающих заданное n.

Последовательность праймориалов (включая ${textstyle{1# equiv 1}}$ ) начинается так^[19]:

1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 400, 32 589 158 477 190 046 000, 1 922 760 350 154 212 800 000, …

Фибонориал или фибоначчиал[править | править код]

Произведение нескольких первых чисел Фибоначчи. Записывается n!_F.

Например, : 6!_F = ${displaystyle 1times 1times 2times 3times 5times 8=240}$ .

Суперфакториалы[править | править код]

Нейл Слоан и Симон Плуффэ^[en] в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырёх равен

${displaystyle operatorname {sf} (4)=1!times 2!times 3!times 4!=288}$

(поскольку устоявшегося обозначения нет, используется функциональное).

В общем

$operatorname{sf}(n) =prod_{k=1}^n k! =prod_{k=1}^n k^{n-k+1} =1^ncdot2^{n-1}cdot3^{n-2}cdots(n-1)^2cdot n^1.$

Последовательность суперфакториалов чисел $n geqslant 0$ начинается так^[20]:

1, 1, 2, 12, 288, 34 560, 24 883 200, 125 411 328 000, 5 056 584 744 960 000, 1 834 933 472 251 084 800 000, 6 658 606 584 104 737 000 000 000 000, 265 790 267 296 391 960 000 000 000 000 000 000, 127 313 963 299 399 430 000 000 000 000 000 000 000 000 000, …

Идея была обобщена в 2000 году Генри Боттомли^[en], что привело к гиперфакториалам (англ. Hyperfactorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел $n geqslant 0$ начинается так^[21]:

1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 745 453 331 864 786 800 000 000 000, 3 769 447 945 987 085 600 000 000 000 000 000 000 000 000, 6 916 686 207 999 801 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000, …

Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение (m − 1)-уровневых факториалов чисел от 1 до n, то есть

$operatorname {mf}(n,m)=operatorname {mf}(n-1,m)operatorname {mf}(n,m-1)=prod _{{k=1}}^{n}k^{{n-k+m-1 choose n-k}},$

где $operatorname{mf}(n,0)=n$ для $n>0$ и $operatorname{mf}(0,m)=1.$

Субфакториал[править | править код]

Субфакториал !n определяется как количество беспорядков порядка n, то есть перестановок n-элементного множества без неподвижных точек.

См. также[править | править код]

Факторион

Примечания[править | править код]

↑ Шесть миллиардов двести двадцать семь миллионов двадцать тысяч восемьсот
↑ Восемьдесят семь миллиардов сто семьдесят восемь миллионов двести девяносто одна тысяча двести
↑ Один триллион триста семь миллиардов шестьсот семьдесят четыре миллиона триста шестьдесят восемь тысяч
↑ Двадцать триллионов девятьсот двадцать два миллиарда семьсот восемьдесят девять миллионов восемьсот восемьдесят восемь тысяч
↑ Триста пятьдесят пять триллионов шестьсот восемьдесят семь миллиардов четыреста двадцать восемь миллионов девяносто шесть тысяч
↑ Шесть квадриллионов четыреста два триллиона триста семьдесят три миллиарда семьсот пять миллионов семьсот двадцать восемь тысяч
↑ Сто двадцать один квадриллион шестьсот сорок пять триллионов сто миллиардов четыреста восемь миллионов восемьсот тридцать две тысячи
↑ Два квинтиллиона четыреста тридцать два квадриллиона девятьсот два триллиона восемь миллиардов сто семьдесят шесть миллионов шестьсот сорок тысяч
↑ Пятнадцать септиллионов пятьсот одиннадцать секстиллионов двести десять квинтиллионов сорок три квадриллиона триста тридцать триллионов девятьсот восемьдесят пять миллиардов девятьсот восемьдесят четыре миллиона
↑ Тридцать вигинтиллионов четыреста четырнадцать новемдециллионов девяносто три октодециллиона двести один септдециллион семьсот тринадцать седециллионов триста семьдесят восемь квиндециллионов сорок три кваттуордециллиона шестьсот двенадцать тредециллионов шестьсот восемь додециллионов сто шестьдесят шесть ундециллионов шестьдесят четыре дециллиона семьсот шестьдесят восемь нониллионов восемьсот сорок четыре октиллиона триста семьдесят семь септиллионов шестьсот сорок один секстиллион пятьсот шестьдесят восемь квинтиллионов девятьсот шестьдесят квадриллионов пятьсот двенадцать триллионов
↑ Одиннадцать дуотригинтиллионов девятьсот семьдесят восемь антригинтиллионов пятьсот семьдесят один тригинтиллион шестьсот шестьдесят девять новемвигинтиллионов девятьсот шестьдесят девять октовигинтиллионов восемьсот девяносто один септемвигинтиллион семьсот девяносто шесть сексвигинтиллионов семьдесят два квинвигинтиллиона семьсот восемьдесят три кватторвигинтиллиона семьсот двадцать один тревигинтиллион шестьсот восемьдесят девять дуовигинтиллионов девяносто восемь анвигинтиллионов семьсот тридцать шесть вигинтиллионов четыреста пятьдесят восемь новемдециллионов девятьсот тридцать восемь октодециллионов сто сорок два септдециллиона пятьсот сорок шесть седециллионов четыреста двадцать пять квиндециллионов восемьсот пятьдесят семь кваттуордециллионов пятьсот пятьдесят пять тредециллионов триста шестьдесят два додециллиона восемьсот шестьдесят четыре ундециллиона шестьсот двадцать восемь дециллионов девять нониллионов пятьсот восемьдесят два октиллиона семьсот восемьдесят девять септиллионов восемьсот сорок пять секстиллионов триста девятнадцать квинтиллионов шестьсот восемьдесят квадриллионов
↑ Коэффициенты этого разложения дают A001163 (числители) и A001164 (знаменатели)
↑ Крамп, Кристиан. Дата обращения: 19 сентября 2016. Архивировано 19 сентября 2016 года.
↑ Pearson, Karl (1924), Historical note on the origin of the normal curve of errors, Biometrika Т. 16: 402–404 [p. 403], DOI 10.2307/2331714: «Стирлинг лишь показал, что арифметическая константа в формуле Муавра равна ${sqrt {2pi }}$ . Я считаю, что это не делает его автором теоремы»
↑ Дональд Кнут. Искусство программирования, том I. Основные алгоритмы. — М.: Мир, 1976. — С. 79—81. — 736 с.
↑ Последовательность A006882 в OEIS
↑ «Энциклопедия для детей» Аванта+. Математика.
↑ wolframalpha.com Архивная копия от 1 ноября 2013 на Wayback Machine.
↑ Последовательность A002110 в OEIS
↑ Последовательность A000178 в OEIS
↑ Последовательность A055462 в OEIS

Источник

Факториал неотрицательного целого числа — это умножение всех целых чисел, меньших или равных n. Например, факториал 6 равен 6 * 5 * 4 * 3 * 2 * 1, что равно 720.

Мы обсудили простую программу для факториала .

Как вычислить факториал из 100, используя программу на C / C ++?
Факториал 100 имеет 158 цифр. Невозможно сохранить эти много цифр, даже если мы используем long long int.

Примеры :

Input : 100
Output : 933262154439441526816992388562667004-
         907159682643816214685929638952175999-
         932299156089414639761565182862536979-
         208272237582511852109168640000000000-
         00000000000000

Input :50
Output : 3041409320171337804361260816606476884-
         4377641568960512000000000000

Ниже приводится простое решение, в котором мы используем массив для хранения отдельных цифр результата. Идея состоит в том, чтобы использовать базовую математику для умножения.

Ниже приведен подробный алгоритм поиска факториала.

факториала (п)
1) Создайте массив ‘res []’ размера MAX, где MAX — количество максимальных цифр в выводе.
2) Инициализируйте значение, сохраненное в ‘res []’ как 1, и инициализируйте ‘res_size’ (размер ‘res []’) как 1.
3) Выполните следующие действия для всех чисел от x = 2 до n.
…… а) Умножьте x на res [] и обновите res [] и res_size, чтобы сохранить результат умножения.

Как умножить число ‘x’ на число, сохраненное в res []?
Идея состоит в том, чтобы использовать простую школьную математику. Мы по одному умножаем x на каждую цифру res []. Здесь важно отметить, что цифры умножаются с крайней правой цифры на самую левую. Если мы храним цифры в том же порядке в res [], тогда становится трудно обновить res [] без лишнего пробела. Вот почему res [] поддерживается в обратном порядке, т. Е. Сохраняются цифры справа налево.

умножить (res [], x)
1) Инициализируйте перенос как 0.
2) Выполните следующие действия для i = 0 до res_size — 1
… .A) Найти значение res [i] * x + carry. Пусть это значение будет прод.
… .B) Обновите res [i], сохранив в нем последнюю цифру prod.
… .C) Обновите перенос, сохранив оставшиеся цифры в переносе.
3) Поместите все цифры переноса в res [] и увеличьте res_size на количество цифр в переносе.

Example to show working of multiply(res[], x)
A number 5189 is stored in res[] as following.
res[] = {9, 8, 1, 5}
x = 10

Initialize carry = 0;

i = 0, prod = res[0]*x + carry = 9*10 + 0 = 90.
res[0] = 0, carry = 9

i = 1, prod = res[1]*x + carry = 8*10 + 9 = 89
res[1] = 9, carry = 8

i = 2, prod = res[2]*x + carry = 1*10 + 8 = 18
res[2] = 8, carry = 1

i = 3, prod = res[3]*x + carry = 5*10 + 1 = 51
res[3] = 1, carry = 5

res[4] = carry = 5

res[] = {0, 9, 8, 1, 5}

Ниже приведена реализация вышеуказанного алгоритма.

C ++

#include<iostream>

using namespace std;

#define MAX 500

int multiply(int x, int res[], int res_size);

void factorial(int n)

{

int res[MAX];

res[0] = 1;

int res_size = 1;

for (int x=2; x<=n; x++)

res_size = multiply(x, res, res_size);

cout << "Factorial of given number is n";

for (int i=res_size-1; i>=0; i--)

cout << res[i];

}

int multiply(int x, int res[], int res_size)

{

int carry = 0;

for (int i=0; i<res_size; i++)

{

int prod = res[i] * x + carry;

res[i] = prod % 10;

carry = prod/10;

}

while (carry)

{

res[res_size] = carry%10;

carry = carry/10;

res_size++;

}

return res_size;

}

int main()

{

factorial(100);

return 0;

}

Джава

class GFG {

static void factorial(int n)

{

int res[] = new int[500];

res[0] = 1;

int res_size = 1;

for (int x = 2; x <= n; x++)

res_size = multiply(x, res, res_size);

System.out.println("Factorial of given number is ");

for (int i = res_size - 1; i >= 0; i--)

System.out.print(res[i]);

}

static int multiply(int x, int res[], int res_size)

{

int carry = 0;

for (int i = 0; i < res_size; i++)

{

int prod = res[i] * x + carry;

res[i] = prod % 10;

carry = prod/10;

}

while (carry!=0)

{

res[res_size] = carry % 10;

carry = carry / 10;

res_size++;

}

return res_size;

}

public static void main(String args[])

{

factorial(100);

}

питон

import sys

def factorial( n) :

res = [None]*500

res[0] = 1

res_size = 1

x = 2

while x <= n :

res_size = multiply(x, res, res_size)

x = x + 1

print ("Factorial of given number is")

i = res_size-1

while i >= 0 :

sys.stdout.write(str(res[i]))

sys.stdout.flush()

i = i - 1

def multiply(x, res,res_size) :

carry = 0

i = 0

while i < res_size :

prod = res[i] *x + carry

res[i] = prod % 10;

carry = prod/10;

i = i + 1

while (carry) :

res[res_size] = carry % 10

carry = carry / 10

res_size = res_size + 1

return res_size

factorial(100)

C #

using System;

class GFG

{

static void factorial(int n)

{

int []res = new int[500];

res[0] = 1;

int res_size = 1;

for (int x = 2; x <= n; x++)

res_size = multiply(x, res,

res_size);

Console.WriteLine("Factorial of " +

"given number is ");

for (int i = res_size - 1; i >= 0; i--)

Console.Write(res[i]);

}

static int multiply(int x, int []res,

int res_size)

{

int carry = 0;

for (int i = 0; i < res_size; i++)

{

int prod = res[i] * x + carry;

res[i] = prod % 10;

carry = prod / 10;

}

while (carry != 0)

{

res[res_size] = carry % 10;

carry = carry / 10;

res_size++;

}

return res_size;

}

static public void Main ()

{

factorial(100);

}

PHP

<?php

$MAX = 500;

function factorial($n)

{

global $MAX;

$res = array_fill(0, $MAX, 0);

$res[0] = 1;

$res_size = 1;

for ($x = 2; $x <= $n; $x++)

$res_size = multiply($x, $res, $res_size);

echo "Factorial of given number is n";

for ($i = $res_size - 1; $i >= 0; $i--)

echo $res[$i];

}

function multiply($x, &$res, $res_size)

{

$carry = 0;

for ($i = 0; $i < $res_size; $i++)

{

$prod = $res[$i] * $x + $carry;

$res[$i] = $prod % 10;

$carry = (int)($prod / 10);

}

while ($carry)

{

$res[$res_size] = $carry % 10;

$carry = (int)($carry / 10);

$res_size++;

}

return $res_size;

}

factorial(100);

?>

Выход :

Factorial of given number is
9332621544394415268169923885626670049071596826438162146859296389
5217599993229915608941463976156518286253697920827223758251185210
916864000000000000000000000000

Вышеуказанный подход может быть оптимизирован многими способами. Мы скоро будем обсуждать оптимизированное решение для того же.

Эта статья предоставлена Харшитом Агравалом . Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по обсуждаемой теме

Рекомендуемые посты:

Найти последнюю цифру, когда факториал А делит факториал Б
Сумма делителей факториала числа
Программа для факториала ряда
C Программа для факториала числа
Первая цифра в факториале числа
Наименьшее число с не менее n цифрами в факториале
Рассчитать MDAS Факториал данного числа
Количество цифр в N, факториальное к степени N
Программа Python для факториала числа
Java программа для факториала числа
Функция одной строки для факториала числа
Найти сумму цифр в факториале числа
Наименьшее число S такое, что N является фактором S факториала или S!
Подсчет конечных нулей в факториале числа
Максимальное количество с одинаковой цифрой факториала

Факториал большого числа

0.00 (0%) 0 votes

Источник

What is Factorial of a number?

Why conventional way of computing factorial fails for large numbers?

C++

Java

Python3

C#

PHP

Javascript

Find the Factorial of a large number using Basic BigInteger

C++

Java

Python3

C#

Javascript

Method 3:

C++

Java

Python3

Javascript

C#

Таблица факториалов

Свойства факториалов

Рекуррентная формула

Комбинаторная интерпретация

Формула Стирлинга

Расчет по предыдущему значению

Некоторые очень большие значения

Примеры задач с решениями

Задание 1

Задание 2

Использование факториалов

Какие есть алгоритмы вычисления факториалов больших чисел без калькуляторов?

О сообществе

Свойства[править | править код]

Рекуррентная формула[править | править код]

Комбинаторная интерпретация[править | править код]

Связь с гамма-функцией[править | править код]

Формула Стирлинга[править | править код]

Разложение на простые множители[править | править код]

Связь с производной от степенной функции[править | править код]

Другие свойства[править | править код]

История[править | править код]

Обобщения[править | править код]

Двойной факториал[править | править код]

Кратный факториал[править | править код]

Неполный факториал[править | править код]

Убывающий факториал[править | править код]

Возрастающий факториал[править | править код]

Праймориал или примориал[править | править код]

Фибонориал или фибоначчиал[править | править код]

Суперфакториалы[править | править код]

Субфакториал[править | править код]

См. также[править | править код]

Примечания[править | править код]

Вам также может понравиться

Raw формат hdd дисков как исправить chkdsk

Как найти наименьшую величину угла

Курсор мыши стал круглым как исправить

Добавить комментарий Отменить ответ