Коротеев Александр
Высший разум
(112987)
15 лет назад
1. Взвешиваем 27 и 27. Если одна чаша легче – значит на ней, если равны – значит в третьей. Если в третьей, добавим туда одну настоящую – чтобы 27 было (для простоты дальнейшего изложения) .
2. Взвешиваем 9 и 9. Если одна чаша легче – значит на ней. Иначе в третьей.
3. Аналогично 3 и 3.
4. Аналогично 1 и 1.
Источник: Короче говоря – делением на 3 кучи.
КОРеец
Знаток
(495)
15 лет назад
Сначало 1)взвесить по 20 монет. ту стопку из 20 монет которая легче, 2)взвесить по 5 монет, Ту стопку из 5 монет Которая легче, 3)взвесить по 2монеты (пятую отложить) . Если на весах равенство, то фальшивая пятая! Если неравный вес, То 4)взять две монеты которые легче и положить на весы, та которая легче и будет фальшивая!
Анна Уродкова
Просветленный
(20602)
15 лет назад
В таких задачах обычно монеты делят на 3 группы – 27, 27 и 26
1. 27 монет и 27 монет укладывают на весы. Если весы уравновешены, значит поддельная в отложенной стопке из 26 монет. Если весы не уравновешены, то поддельная в той стопке, где весы показывают легче вес.
если весы все таки равны, то:
2. 26 монет делим на 9, 9 и 8
взвешиваем 9 и 9 монет и аналогично п. 1 определяем, в какой группе монет находится поддельная
3. 9 монет делим на 3, 3 и 3 монеты (Ну а если монет восемь, то делим 8 монет на 3, 3 и 2 монеты)
и определяем с помощью взвешивания в какой группе из трех монет (или из 2х) находится поддельная монета – на весы ложим 3 и 3 монеты:
Если чаши весов уравновешены, то поддельная монета находится среди отложенных трех (двух) монет,
Если весы не уравновешены, то поддельная монета на той чаше весов, которая легче!!! !
4. последнее взвешивание – определяем поддельную монету из трех (двух) монет с помощью взвешивания путем укладывания на весы с обоих сторон по одной монете (третья монета, если есть-отложенная) .
Если весы равны, то поддельная монета – та, которая отложена!!! !
Если весы не равны, то поддельная монета на той чаше весов, которая показывает меньший вес!! !
ну и если после п. 1 весы не равны:
2. рассматриваем монеты с той чаши весов, которая показывает меньший вес (а монеток там 27 штуков будет) и делим их на три группы по 9 монет в каждой и укладываем на весы по 9 монет, и 9 монет остаются на столе, определяем, в какой стопке поддельная.
далее смотрим пп. 3и4.
Надеюсь, что разобрались!! ! мы с сыном (6класс) такие задачи влегкую делаем!!!!
Источник: и вам того же желаем!
Время на прочтение
3 мин
Количество просмотров 74K
Дано: 12 монет, одна из них фальшивая, отличается только весом. Неизвестно легче или тяжелее. Даны рычажные весы, которые показывают, что груз с одной из сторон тяжелее. За 3 взвешивания необходимо найти фальшивую монетку.
Из опыта советую не спешить, решать письменно. Головоломка «12 монет, 3 взвешивания» несколько раз возникала в моей жизни. Первый раз ее задал мне мой товарищ-олимпиадник, решил я ее после олимпиады и пришлось пару часиков поломать голову. И через несколько лет она далось мне не сразу. Если желаете решить самим — делайте на листочке.
Ниже будет разбор и этапы решения. Этапы проведут по универсальной методике решения задач, которая применима как к программированию, так и к жизни. Благодаря подходу решение головоломки станет простым.
Предлагаю вам, прежде чем читать предложить решение. У вас есть ответ? Проверенный?
Если бы это было программного обеспечения вопросы были бы следующие: «Вы запрограммировали, протестировали алгоритм? Рассмотрели тестовые случаи и проверили их?».
Как показывает опыт, чтобы решить требуется нарисовать дерево решений и проверить все 12 случаев.

1. Подсказки
В процессе решения поможет:
1) Понижение энтропии (меры неопределенности) и ответы на вопросы:
- Что узнали на предыдущем шаге?
- Что снижает неопределённость?
- Какой информацией располагаем?
- Что еще нужно узнать?
Вопросы подходят для любой задачи, проектов. Ответы на них помогают в снижении рисков срыва сроков, перерасхода бюджета и получения нагоняя от начальства.
2) Декомпозиция. Подход от простого к сложному. Если подготовить решение простейших случаев, затем использовать их для решения задачи (алгоритм разделяй и властвуй) то, будет проще, чем представлять всю ситуацию в голове.
Алгоритмы «разделяй и властвуй» разбивают задачу на две или более подзадачи того же типа, но меньшего размера до элементарных задач и объединяют их решения для получения ответа к исходной задаче.
Составьте вопросы для декомпозиции. Какие бы вы предложили?
2. Декомпозиция
Какие вопросы вы сформулировали для декомпозиции? Есть совпадения?
1) Какая ситуация самая элементарная? Что можем сделать за одно взвешивание?
За одно взвешивание можем определить, какая монета тяжелее, равен ли вес монет.
2) Если у нас 2 монеты, и, известно, фальшивая тяжелее или легче. Как за одно взвешивание определить фальшивую?
Необходимо взвесить монеты, и в зависимости от стрелки весов определить фальшивую.
3) Если у нас 2 монеты, и, не известно, фальшивая тяжелее или легче, как за одно взвешивание определить фальшивую?
Взвесив одну из 2-х представленных монет с третьей монетой, про которую известно, что она подлинная.
4) Если у нас 3 монеты, и, известно, фальшивая тяжелее или легче. Как за одно взвешивание определить фальшивую?
Необходимо сравнить любые две из этих монет, если они равны, фальшивой является третья монета.
5) Если у нас 3 монеты, и, неизвестно, фальшивая тяжелее или легче. Можно ли определить фальшивую за одно взвешивание?
К сожалению, нет.
6) Если у нас 4 монеты, и, неизвестно фальшивая тяжелее или легче, можно определить фальшивую за одно взвешивание?
К сожалению, нет.
7) Если у нас 4 монеты, и, неизвестно, фальшивая тяжелее или легче, за сколько взвешиваний можно определить фальшивую?
За два взвешивания.
Далее из элементарных случаев соберем ситуации из 8, 9, 10, 11 и 12 монет. Как вы видите решение?
Ниже полное решение.
3. Решение
Первый шаг: разделим монеты на 3 группы по 4: 1 2 3 4, 5 6 7 8, 9 10 11 12.
Сравним первые две группы. Возможны три варианта:
- первая группа тяжелее;
- вторая группа тяжелее;
- равны.

1) Если группы равны, то фальшивая монета находится в третьей группе. Необходимо найти фальшивую монету из 4 монет за два взвешивания.
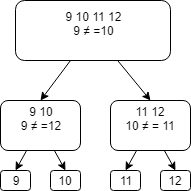
Делим третью группу на две: 9 10 11 12
Сравниваем 9 и 10:
- если они равны, то фальшивая монета во второй группе – сравниваем 9 и 11. Если 9 и 11 равны — то фальшивая – 12, если нет -11
- если они не равны, то фальшивая в первой группе – сравниваем 10 и 12. Если 10 и 12 равны – фальшивая – 9, если нет – 10.
Таким образом мы нашли фальшивую монету.
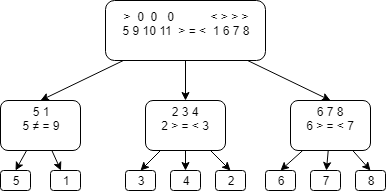
2) Рассмотрим второй случай. Если первая группа тяжелее второй, то присваиваем первой группе знак «>», второй группе знак «<», третьей группе – «0».

Делим монеты на группы 1 9 10 11 и 5 2 3 4, взвешиваем. Возможны три варианта:
- Равны. Фальшивая монета находится среди чисел: 6 7 8. Сравниваем 6 и 7, если равны – фальшивая — 8, если 6 больше, то фальшивая – 7, если 7 больше, то фальшивая – 6, так как в данном случае фальшивая монета легче.
- Первая группа тяжелее, то фальшивая монета либо 1, либо 5. Сравниваем 1 и 9, если они равны – фальшивая монета — 5, если нет — 1.
- Первая группа легче, то фальшивая среди монет 2 3 4, так как известно, что 9, 10 и 11 настоящие, и перевесить вторая группа может только за счет монет 2, 3 и 4. Сравниваем 2 и 3, если равны – фальшивая 4, если 2 тяжелее, то фальшивая – 2, иначе 3-я является фальшивой.
3) Случай когда вторая группа тяжелее первой, аналогичен второму.
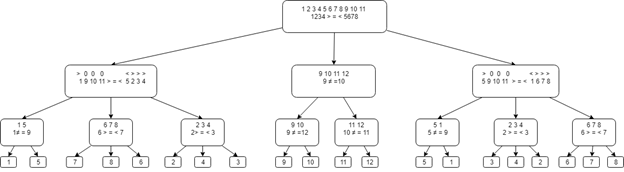
Общая диаграмма «Дерева решений» представлена ниже.
Заключение
При поступлении задачи на доработку или отладку хорошо применить рассмотренный выше подход:
- Определиться, что дано?
- На какие элементарные случаизадачи можно разложить?
- Что неизвестно для решения задачи? Какие эксперименты нужно провести, чтобы снизить энтропию?
- Выполнить.
- Задача решена? Нет? Вернуться к шагу 1.
Успешных решений.
|
4816 / 2276 / 287 Регистрация: 01.03.2013 Сообщений: 5,944 Записей в блоге: 27 |
|
|
1 |
|
|
13.06.2016, 01:09. Показов 4648. Ответов 5
Если кому эта задачка покажется излишне простой, то просто скажите что знаете решение, не обязательно его озвучивать – вдруг найдутся те кому будет интересно порешать. Я со своей стороны хочу узнать степень ее легкости, чтобы знать на какой уровень предлагать. Условие просто донельзя – есть 38 внешне неотличимых монет, рычажные весы, одна монета фальшивая – отличается от других по весу. Надо за 4 взвешивания найти фальшивую монету. Добавлено через 2 часа 41 минуту
0 |
|
Регистрация: 23.10.2013 Сообщений: 5,076 Записей в блоге: 8 |
|
|
13.06.2016, 17:30 |
2 |
|
_Ivana
0 |
|
4816 / 2276 / 287 Регистрация: 01.03.2013 Сообщений: 5,944 Записей в блоге: 27 |
|
|
13.06.2016, 21:12 [ТС] |
3 |
|
geh, ну например я хочу составить по этой задаче задание на одном сайте компьютерных задачек. Разумеется для произвольного количества взвешиваний. И написать тесты, только продумаю как защититься от читерства и ограничить взвешивания. ЗЫ кстати, чисто для проформы, можете написать ваше решение для 40 монет?
0 |
|
Регистрация: 23.10.2013 Сообщений: 5,076 Записей в блоге: 8 |
|
|
15.06.2016, 07:38 |
4 |
|
_Ivana
0 |
|
4816 / 2276 / 287 Регистрация: 01.03.2013 Сообщений: 5,944 Записей в блоге: 27 |
|
|
15.06.2016, 14:18 [ТС] |
5 |
|
Уровень сложности можно определить только статистически Правильно. Поэтому ваше категоричное самонадеянное заяввление
Я знаю решение вашей задачи. в сочетании с
При данных условиях решения нет. подтверждает мою первоначальную догадку [удалено]. Поэтому удачи вам в
К сожалению/счастью моя голова занята другими, но к вашим словам здесь у меня отношение однозначное и соответствующее
0 |
|
4816 / 2276 / 287 Регистрация: 01.03.2013 Сообщений: 5,944 Записей в блоге: 27 |
|
|
17.06.2016, 23:51 [ТС] |
6 |
|
я хочу составить по этой задаче задание на одном сайте компьютерных задачек Собственно, вот: https://www.codewars.com/kata/false-coin/haskell
0 |
Задача абсолютно стандартная. Разобрана в миллиарде книг. Мне кажется, даже каждый школьный учитель её рассказывает в какой-то момент своим ученикам. Тем не менее задача встречается на олимпиадах в разных классах едва ли не чаще остальных. И все равно находятся люди, которые не понимают что к чему. Даже среди взрослых.
Давайте разберем одну из таких задач. Имеется 12 монет. Одна из которых фальшивая. Она отличается от подлинных только по весу (но заранее не известно в меньшую или в большую сторону). Как на чашечных весах определить фальшивку за 3 взвешивания и понять легче она или тяжелее, чем остальные? Как вы понимаете количество монет и взвешиваний может быть разным. От этого суть не изменится.
В любом случае нам надо будет разбить монеты на кучки, чтобы взвешивать их группами. В данной задаче удобно разбить монеты на 3 кучки по 4 монеты в каждой.
В какой-то момент в одном из случаев вам может показаться, что для некоторых случаев трех взвешиваний мало и надо бы четвертое. Ну или не получится определить легче или тяжелее фальшивка. Если так, то вы ошибаетесь, надо думать снова. Трех взвешиваний достаточно в любом случае. И в любом случае получится узнать легче фальшивка или тяжелее.
Для наглядности пронумеруем монеты: {1,2, 3, 4}; {5, 6,7, 8}; {9,10, 11, 12} и приступим к решению.
Первое взвешивание
Сравниваем первые две кучки монет {1,2, 3, 4} и {5, 6,7, 8}. Если весы находятся в равновесии, значит фальшивка в третьей кучке. Переходим к пункту а) во втором взвешивании.
Если весы не в равновесии, то фальшивка в одной из этих двух кучек, а в третьей все монеты настоящие. Запоминаем, какая кучка перевесила [я для примера буду считать, что перевесила кучка {1,2,3,4}, но если нет, то решение будет симметричным] и переходим к пункту б) во втором взвешивании.
Второе и третье взвешивания
а) Фальшивка среди монет {9,10, 11, 12}. Взвешиваем {1, 2, 3} и {9,10, 11}. Если весы в равновесии, значит фальшивая монета под номером 12. третьим взвешиванием узнаем, легче она или тяжелее.
Если не равны, значит, фальшивка среди монет 9, 10, 11. При этом уже после второго взвешивания мы будем точно знать легче фальшивка или тяжелее. Третьим взвешиванием однозначно находим фальшивку: взвешиваем монеты 9 и 10. Если они равны, то фальшивка – 11. Если не равны, то фальшивка либо 9, либо 10 в зависимости от того, какая монета легче (оригинал или фальшивка), ведь эту информацию мы узнали после второго взвешивания.
б) Фальшивка в одной из первых двух кучек. Для того, чтобы понять в какой, взвесим {1, 2, 5} и {3, 4, 9} [опечатки нет, монета 9 заведомо настоящая]. Если весы в равновесии, значит, фальшивка среди 6, 7, 8, причем одна из них легче остальных [это потому что мы для ясности рассматриваем случай, когда первое взвешивание показало, что первая кучка тяжелее]. Третьим взвешиванием сравниваем монеты 6 и 7. Если они равны, то фальшивка – 8. Если нет, то фальшивка та, которая весит меньше.
Если весы после второго взвешивания оказались не в равновесии, возникает два случая
б.1) Если перевесила кучка {1, 2, 5}, то фальшивка среди монет 1 и 2. Третьим взвешиванием мы узнаем, какая из них тяжелее и это и есть фальшивка.
б.2) Если перевесила кучка {3, 4, 9}, то фальшивка среди монет 3, 4 и 5. Если фальшивка – 5, то она будет легче других. А если 3 или 4, то фальшивка тяжелее настоящих. Третьим взвешиванием сравниваем монеты 3 и 4. Если одна из них тяжелее, то это фальшивка. Если они равны, то фальшивка – 5 и она легче.
Всё. Как вам задачка? Как видите, рассмотрены все случаи и трех взвешиваний достаточно даже для того, чтобы определить не только фальшивку, но и её относительный вес.
Ещё интересно:
Задача
Имеется 8 монет одинакового достоинства, одна из которых фальшивая. Фальшивая монета легче настоящей. Как с помощью всего лишь двух взвешиваний найти фальшивую монету? В вашем распоряжении аптекарские весы без гирь, которые показывают только легче-тяжелее.
Решение этой задачи состоит в том, что исходный набор монет надо разделить на три кучки, в двух из которых число монет обязательно должно быть равным.

Если мы взвесим на весах с двумя чашами две кучки с одинаковым числом монет одинакового достоинства и одна из них окажется легче, значит фальшивая монета в этой кучке, и уже её надо разделить на три части, в двух из которых число монет обязательно должно быть равным.
Если же у взвешенных двух кучек монет одинаковый вес, значит фальшивая монета в третьей кучке.
Покажем схему взвешивания для наших 8 монет:
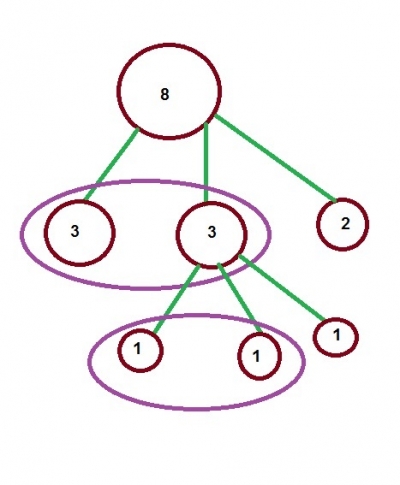
Вначале у нас есть 8 монет. Мы делим их на кучки по 3, 3 и 2 монеты.
Взвешиваем две кучки по 3 монеты. Предположим, что одна из этих кучек оказалась легче. Значит, фальшивая монета в ней. Теперь делим эту кучку на три по 1 монете в каждой.
Теперь нам достаточно взвесить любые две монеты, чтобы определить, где фальшивая – она окажется или на весах, или это будет третья монета.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Задача
Имеется 10 монет одинакового достоинства, одна из которых фальшивая. Фальшивая монета легче настоящей. За какое минимально гарантированное количество взвешиваний можно найти фальшивую монету? В вашем распоряжении аптекарские весы без гирь, которые показывают только легче-тяжелее.
Это точно такая же задача, как и предыдущая, но в ней на 2 монеты больше, и взвешиваний будет на одно больше.
Вот схема взвешивания:
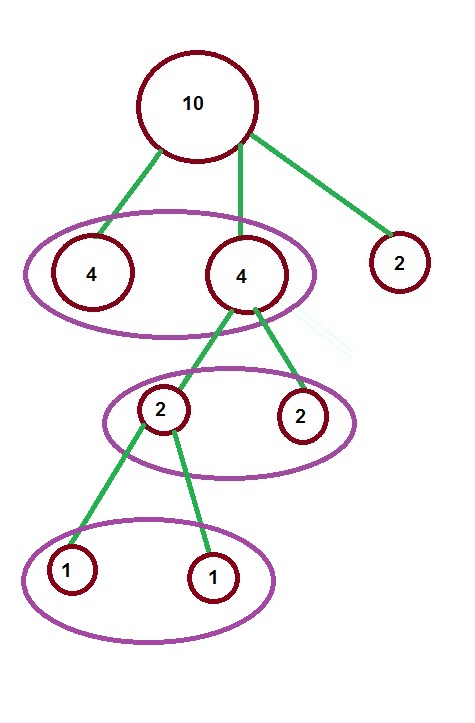
Как видим, на втором взвешивании у нас образовались кучки по две монеты, поэтому, когда мы определили, в какой из этих кучек находится фальшивая, то дальше смогли разделить её только на две “кучки” по 1 монете в каждой.
Дата публикации
17.04.2020


