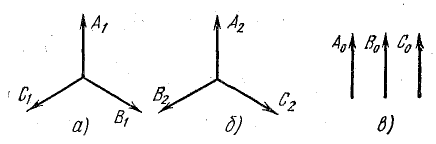
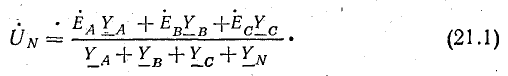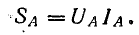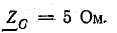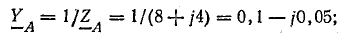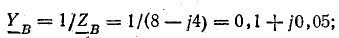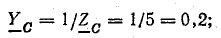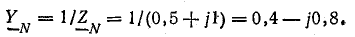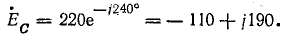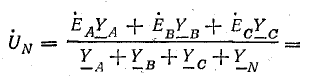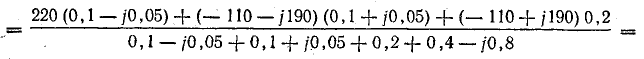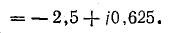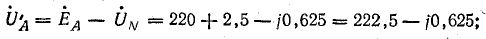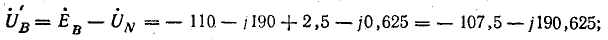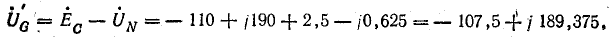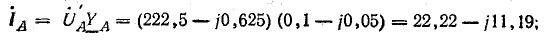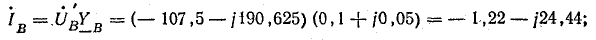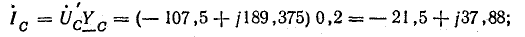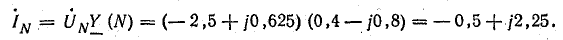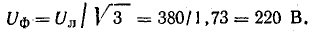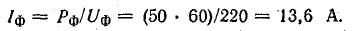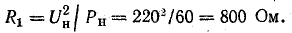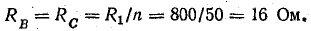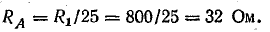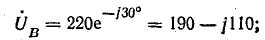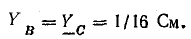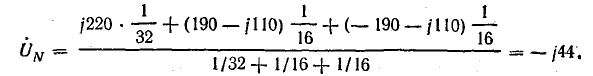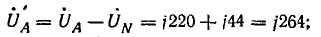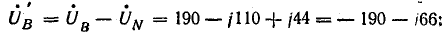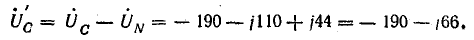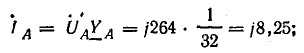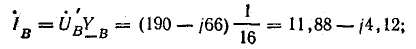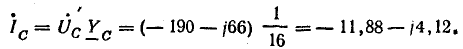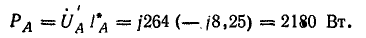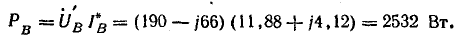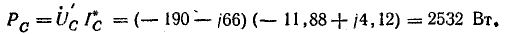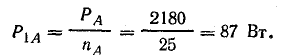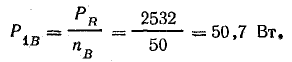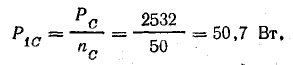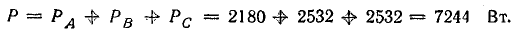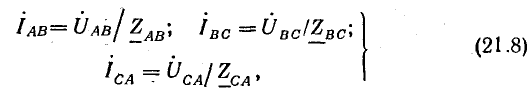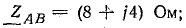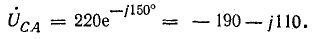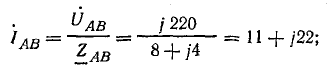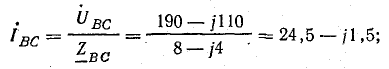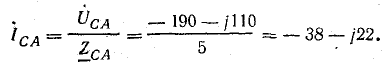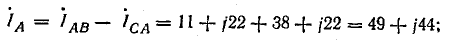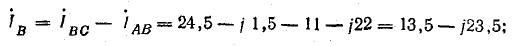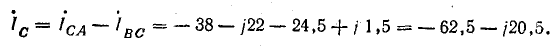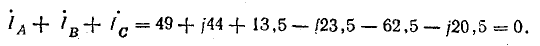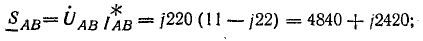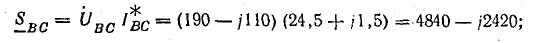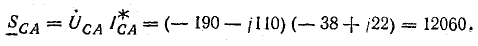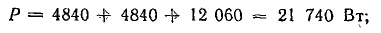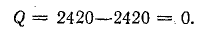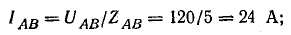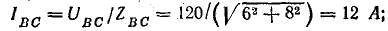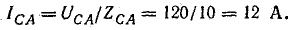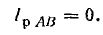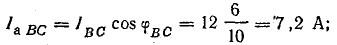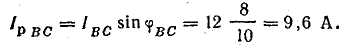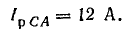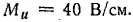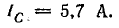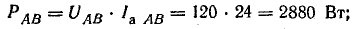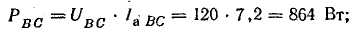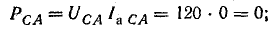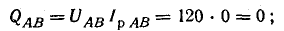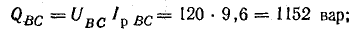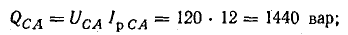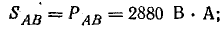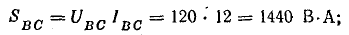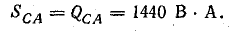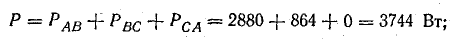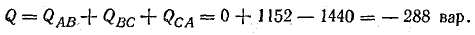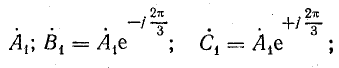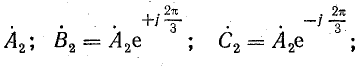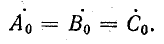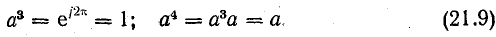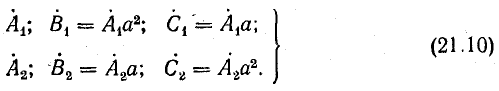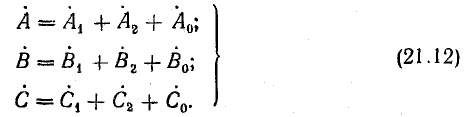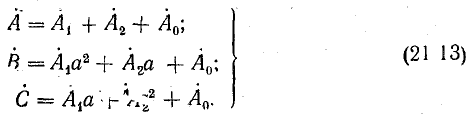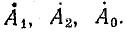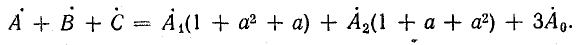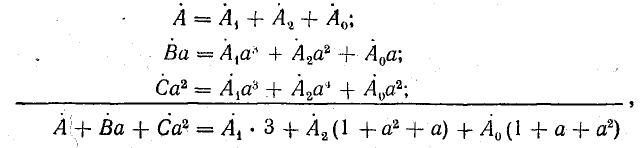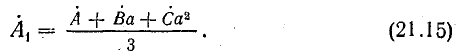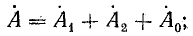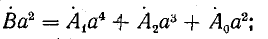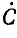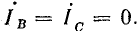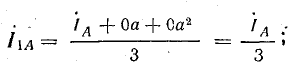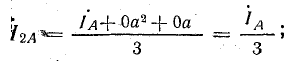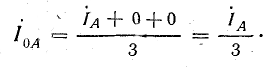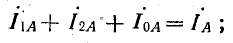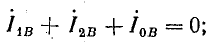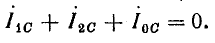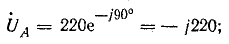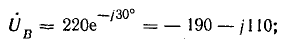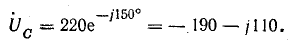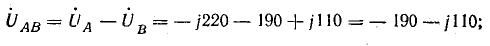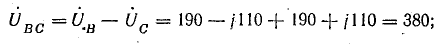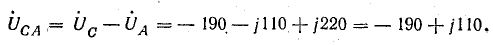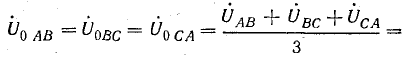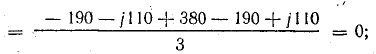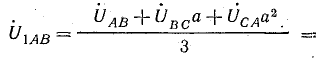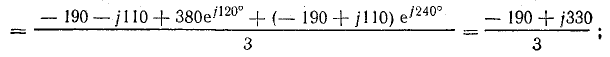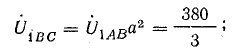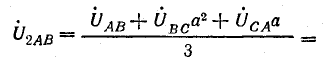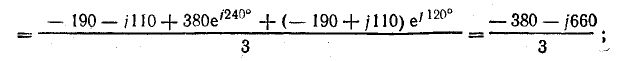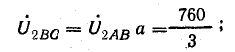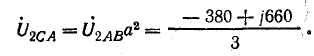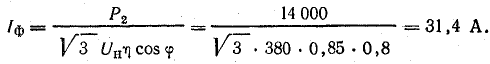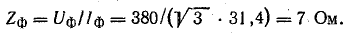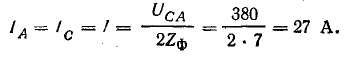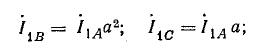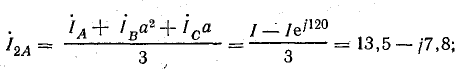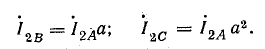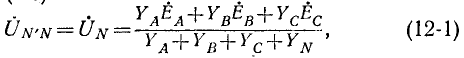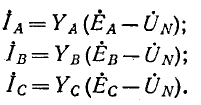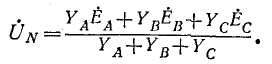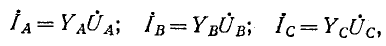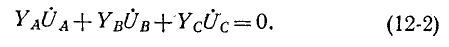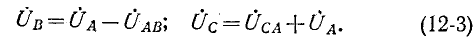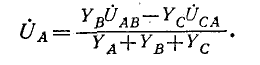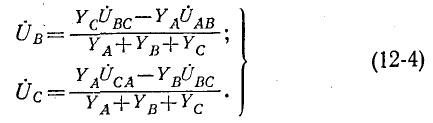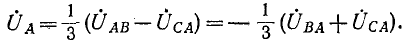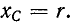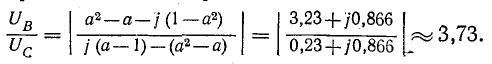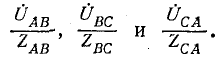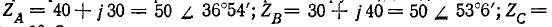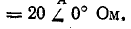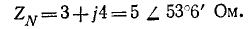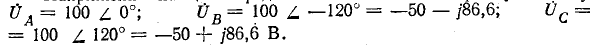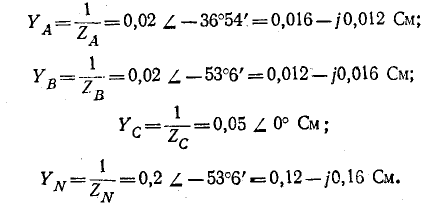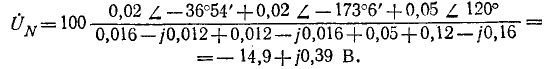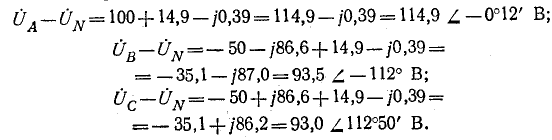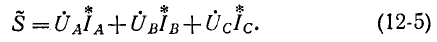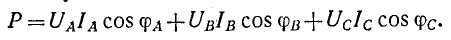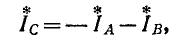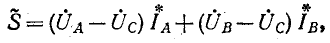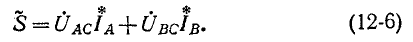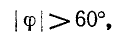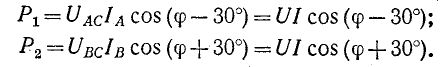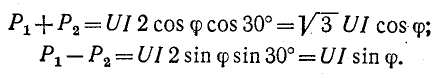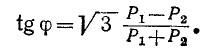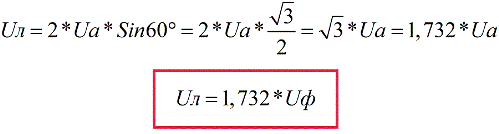Напряжение на
каждой фазе нагрузки
нагр.
является
разностью фазного напряжения источника
питания
и напряжения смещения нейтрали
0
нагр.
=
–
0
(4.4.3)
Напряжения на
фазах нагрузки
а) при наличии
нулевого провода
А
нагр. =А
–
0
= 380 – 39,45 + j37,75
= 340,5 + j37,75
= 348 еВ;
В
нагр.
=В
–0=
-190 – j328
– 39,45 + j37,75=
-229,45 – j290,25=370еВ;
С
нагр.=С
–
0
= -190 + j328
– 39,45 + j37,75
= -229,45 + j365,75=433
еВ.
б) при обрыве
нулевого провода
А
нагр. =А
–
0
= 380 – 270 + j258
= 110 + j258
= 280 еВ;
В
нагр.
=
В
–
0
= -190 – j328
– 270 + j258
= – 460 – j70
= 464 еВ;
С
нагр.
=
С
–
0
= -190 + j
328 – 270 + j258
= – 460 + j586
= 745 еВ.
3) Определение фазных и линейных токов, тока в нулевом проводе
При соединении
звездой фазные и линейные токи равны,
т.е. Iф.А
= Iл.А;
Iф.В
= Iл.В;
Iф.С
= Iл.С;
Если известны
напряжения
и проводимости Y
участков,
токи через них
можно определить
по закону Ома
=
Y
(4.4.4)
а) Фазные и линейные
токи при наличии нулевого провода
ф.А
=л.А
=
А
нагр. YА
= 348 е0,1
е=
34,8 е=
= (30 – j17,8)
А;
ф.В
=
л.В
=
В
нагр. YВ
= 370 е0,1
е=
37 е=
= (9,35 – j35,7)
А;
ф.С
=
л.С
=
С
нагр. YС
= 433 е0,0362
е=
15,7 е=
= (0,45 + j15,6)
А
Ток в нулевом
проводе
0
=
0
Y0
= 54 е1
= 54 еА.
Этот же ток может
быть найден по второму закону Кирхгофа
0
=
ф.А
+
ф.В
+
ф.С
= 30 – j17,8
+ 9,35 – j35,7
+ 0,45 + j15,6
= 39,8 – j37,9
= 54 еА.
Совпадение
результатов подтверждает правильность
выполнения расчетов.
б) Фазные и линейные
токи при обрыве нулевого провода
ф.А
=
л.А =А
нагр.YА
= 280 е0,1
е=
28 е=
= (24,2 + j13,95)
А;
ф.В
=
л.В
=В
нагр.YВ
=464е0,1
е=
46,4 е=
(- 21,9 – j40,9)
А;
ф.С
=
л.С
=
нагр. YС
= 745 е0,0362
е=
27 е=
= (- 2,3 + j26,95)
А
Ток в нулевом
проводе
0
=0
Y0
= 0, т.к. при обрыве нулевого провода его
проводимость равна
нулю.
4А) Определение мощностей
Полные мощности
фаз Sф.
находятся как произведение комплексов
фазных напряжений
ф.
на сопряженные комплексы фазных токов
ф.
S
=
ф.
ф.
(4.4.5)
Сопряженный
комплекс какой-либо величины – комплекс
этой величины, в котором знак мнимой
части заменен на противоположный.
Например: для
комплекса фазного тока
ф.В
= 9,35 – j35,7
= 37
е
его
сопряженный комплекс имеет вид:
ф.В
= 9,35 + j35,7
= 37
е
А.
Сопряженные
комплексы величин принято обозначать
звездочками над их буквенными символами.
Полная мощность
каждой фазы по (4.4.5)
SА=
А
ф.А
= 348 е34,8
е=
11696 е=
(9357 +j7017)
ВА;
SВ=
В
ф.В
= 370 е37
е=
13690 е=
(8214 –j10952)
ВА;
SС=
С
ф.С
= 433 е15,7
е=
6785 е=
(5647 +j3757)
ВА.
Полная мощность
всей нагрузки
S
=SА+SВ+
SС
= 9357 + j7017
+ 8214 – j10952
+ 5647 + j3757
= (23218 – j178)ВА.
Активная и реактивная
мощности фаз и всей нагрузки находятся
как действительная и мнимая части
соответствующих комплексов полных
мощностей, т.е.
активная мощность
фаз
РА
= 9357 Вт;
РВ
= 8214 Вт;
РС
= 5647 Вт;
активная мощность
всей нагрузки
Р = РА
+ РВ
+ РС
= 9357 + 8214 + 5647 = 23218 Вт;
реактивная мощность
фаз
QА
= 7017 вар;
QВ
= -10952 вар;
QС
= 3757 вар;
реактивная мощность
всей нагрузки
Q
= QА
+ QВ
+ QС
= 7017 -10952 + 3757 = -178 вар.
Активная мощность
каждой фазы может быть также найдена
по выражению
Рф.
= Iф.
Rф.
, (4.4.6)
где Iф.
– действующее значение фазного тока;
Rф.
– активное сопротивление фазы.
Тогда
РА
= Iф.А
Rф.А
=(34,8)8
= 9357 Вт;
РВ
=
Iф.В
Rф.В
= (37)6
= 8214 Вт;
РС
= Iф.С
Rф.С
=
(15,7)23
= 5647 Вт.
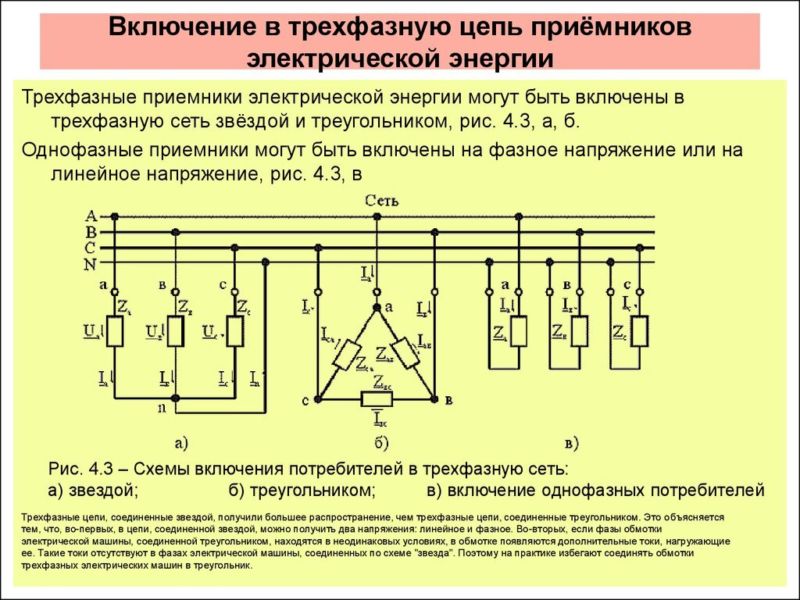
Содержание:
Трехфазные несимметричные цепи:
Трехфазная цепь несимметрична, если комплексы сопротивлений ее фаз неодинаковы.
Несимметричной может быть действующая в цепи система э. д. с. (не равны модули э. д. с. или фазовые сдвиги между каждой парой э. д. с.). .
Для расчета несимметричной цепи применяются различные методы в зависимости от ее схемы и вида несимметрии.
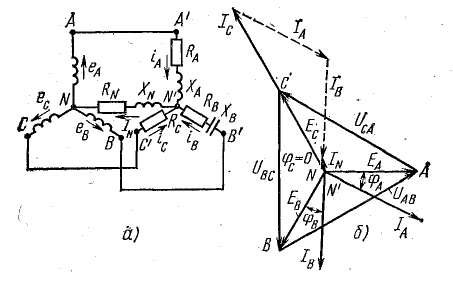
Расчет несимметричной трехфазной цепи при соединении источника и приемника звездой
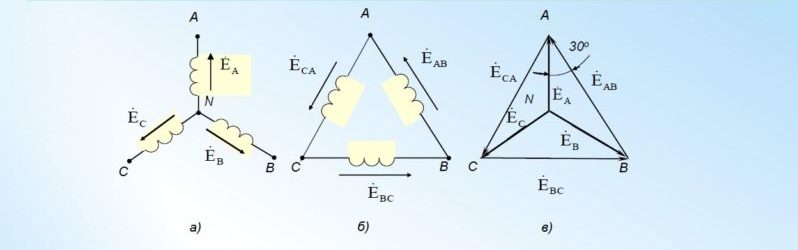
На схеме (см. рис. 20.4) видно, что при соединении звездой трехфазная система представляет собой электрическую цепь с двумя узлами — нейтральными точками N и N’. Наиболее удобным методом расчета в данном случае является метод узлового напряжения.
Определение токов
Рассмотрим сначала общий случай расчета цепи с нулевым проводом, сопротивление которого ZN. При этом сделаем некоторые упрощения: сопротивления линейных проводов и фаз источников будем полагать равными нулю. Если указанные сопротивления нельзя считать равными нулю, их можно отнести к приемнику, прибавив к сопротивлениям последнего по правилам сложения комплексов.
При таком упрощении потенциалы линейных зажимов источника и приемника (например, точек А и А’) можно считать одинаковыми.
Напряжение между нулевыми точками N и N’, или узловое напряжение
Смещение нейтрали
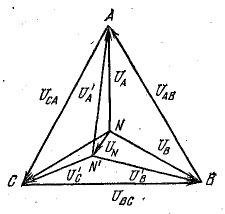
На рис. 21.1 изображена топографическая диаграмма цепи рис. 20.4, а при несимметричной нагрузке.
При наличии сопротивления в нулевом проводе (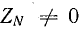
Рис. 21.1. Топографическая диаграмма при несимметричной нагрузке (соединение звездой)
Из формулы (21.1) видно, что симметрия фазных напряжений на нагрузке, когда UN = 0, достигается в двух частных случаях.
1. При симметричной нагрузке, когда комплексы проводимостей фаз равны: 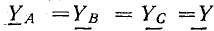
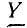
2. В четырехпроводной системе, когда сопротивление нулевого провода равно нулю (YN = ∞.)
Роль нулевого провода
Нулевой провод является уравнительным. Потенциалы нейтрали источника и приемника с помощью этого провода принудительно уравнены, а поэтому звезда векторов фазных напряжений приемника точно совпадает со звездой фазных напряжений источника.
Четырехпроводная система применяется в электрических сетях с напряжением 380/220 В при электроснабжении от общего источника силовой (электродвигатели) и осветительной (электролампы) нагрузки.
При несимметричной нагрузке обрыв нулевого провода (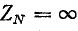
Определение мощности
При несимметричной нагрузке нужно определить мощность каждой фазы. Например, для фазы А:
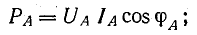
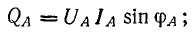
Аналогично определяются мощности других фаз.
Активная мощность всей трехфазной цепи равна сумме мощностей фаз:
Реактивная мощность цепи равна алгебраической сумме реактивных мощностей фаз:
В этой сумме реактивная мощность катушки считается положительной, а реактивная мощность конденсатора — отрицательной.
Задача 21.1.
При соединении звездой с нулевым проводом определить фазные напряжения и токи в приемнике энергии, сопротивления которого заданы комплексами:
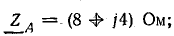
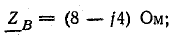
Действующая величина симметричной трехфазной системы э. д. с. 220 В. Сопротивление нулевого провода 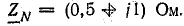
Построить векторную диаграмму.
Сопротивлениями линейных проводов и внутренними сопротивлениями источника э. д. с. пренебречь.
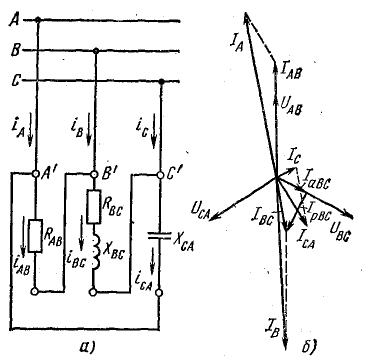
Решение. Схема, соответствующая условию задачи, показана на рис. 21.2, а.
Проводимости ветвей между узловыми точками NN’:
Рис. 21.2. К задаче 21.1
Комплексы э. д. с. источника:
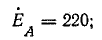
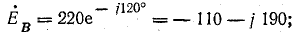
Узловое напряжение
Фазные напряжения приемника:
Токи в фазах и нулевом проводе:
Векторная диаграмма напряжений и токов показана на рис. 21.2, б.
Задача 21.3.
Электрические лампы включены звездой в трехфазную сеть с линейным напряжением 380 В. В каждую фазу включены по 50 ламп с номинальной мощностью 60 Вт каждая, номинальным напряжением 220 В. Как изменяются фазные напряжения и токи при изменении нагрузки одной фазы от холостого хода до короткого замыкания при обрыве нулевого провода?
В каждом выбранном случае нагрузки построить векторную диаграмму, определить мощность всей трехфазной цепи.
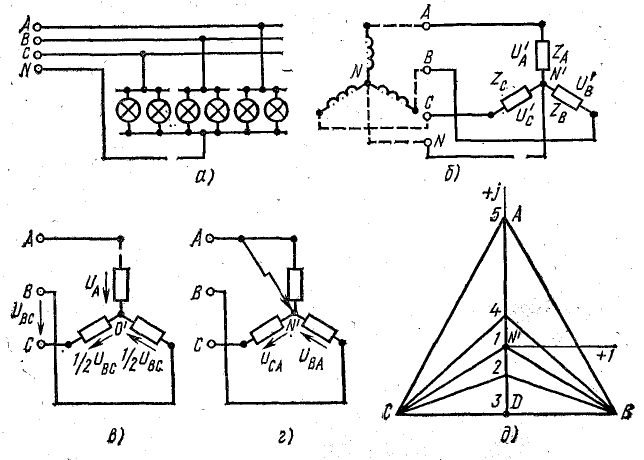
Решение. Условию задачи соответствует схема рис. 21.3, а, на которой группа ламп в каждой фазе условно показана двумя лампами.
Оставляя постоянным число ламп в фазах В и С, будем менять его в фазе А. Подсчеты по условию задачи выполним для таких нагрузок в фазе А: 50, 25, 100 ламп, короткое замыкание, холостой ход.
1. При включении в каждую фазу по 50 одинаковых ламп нагрузка симметрична. Поэтому фазные напряжения на нагрузке равны фазным напряжениям в сети:
Напряжение на лампах равно номинальному. В этом случае лампы работают с номинальной мощностью.
Это даёт право определить фазные токи по заданной мощности ламп:
При соединении звездой IФ = IЛ, поэтому Iл = 13,6 А. Общая мощность трехфазной цепи
Р = ЗРФ = 3 • 60 • 50 = 9000 Вт.
2. В фазе А включено 25 ламп.
При несимметричной нагрузке напряжения на лампах отличаются от фазных напряжений в сети. Поэтому определить токи по заданной мощности ламп нельзя, так как действительная мощность ламп и фазные напряжения их неизвестны. При решении задачи будем считать, что сопротивление ламп в накаленном состоянии нити практически не меняется при некотором изменении их мощности.
Сопротивление лампы в номинальном режиме
Сопротивление фаз В и С при включении 50 ламп
Сопротивление фазы А
Комплексы фазных напряжений в сети:
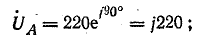
Проводимости ветвей:
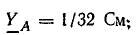
Смещение нейтрали
Напряжения фаз:
Токи в фазах:
Мощность всех ламп в фазах:
Мощность одной лампы:
Общая мощность в трехфазной системе
Векторная диаграмма напряжений для различной нагрузки фазы А показана на рис. 21.3, д.
Положение нулевой точки на диаграмме соответствует такой нагрузке фазы А: 1 — симметричная нагрузка (во всех фазах по 50 ламп); 2 — в фазе А 25 ламп; 3 — фаза А разомкнута (холостой ход); 4 — в фазе А 100 ламп; 5 — в фазе А короткое замыкание.
Выполните расчет трехфазной цепи для случаев нагрузки 3, 4, 5 подобно приведенному расчету для случая нагрузки 2, проверьте соответствие результатов расчета векторной диаграмме рис. 21.3, д.
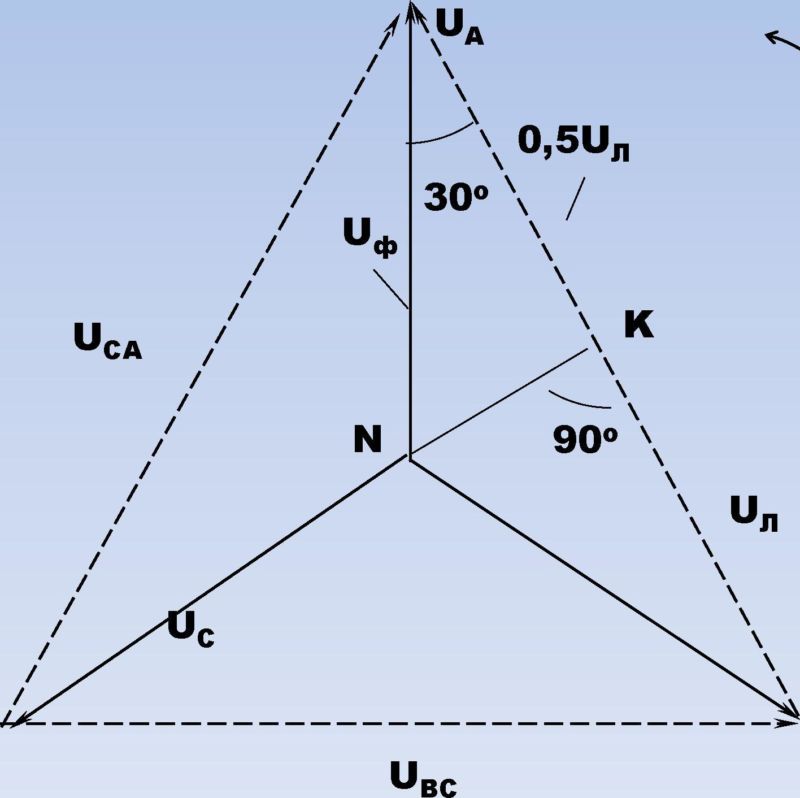
Как видно, нулевая точка нагрузки при изменении проводимости фазы А перемещается на прямой АD, которая является перпендикуляром, опущенным из точки А к вектору линейного напряжения UBC. При холостом ходе фазы А (обрыв линейного провода в этой фазе) нулевая точка перемещается в точку D и напряжения на двух других фазах UB и UC по величине оказываются равными половине линейного напряжения UBC (рис. 21.3, б).
Рис. 21.3. К задаче 21.3
То же следует из схемы рис. 21.3, в. В рассматриваемом случае сопротивления фаз В и С оказываются включенными последовательно на линейное напряжение UBC.
Сопротивления эти равны, поэтому линейное напряжение делится между двумя фазами поровну.
При коротком замыкании фазы А линейный провод этой фазы подводится непосредственно к нулевой точке нагрузки (рис. 21.3, г). Поэтому лампы, включенные в фазы В и С, оказываются под линейным напряжением.
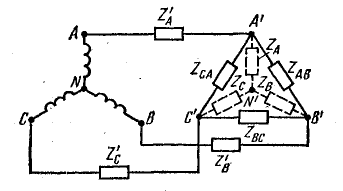
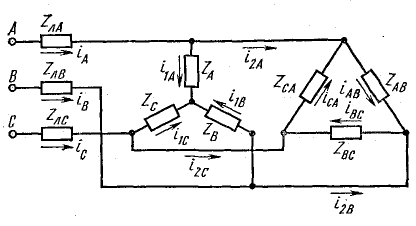
Расчет несимметричной трехфазной цепи при соединении треугольником
Трехфазная цепь при соединении приемника треугольником и любой схеме соединения фаз источника имеет разветвленную многоконтурную схему (см., например, рис. 20.8, а; 21.5).
Расчет такой цепи выполняется одним из известных методов с учетом состава ее элементов и схемы соединения.
Соединение источника и приемника треугольником
Расчет сложной цепи (см. рис. 20.8, а) значительно упрощается, если не принимать во внимание сопротивление проводов. В этом случае напряжения на фазах приемника равны соответствующим напряжениям источника и, как правило, представляют собой симметричную систему.
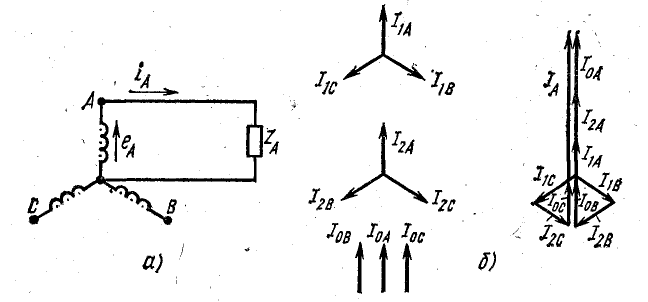
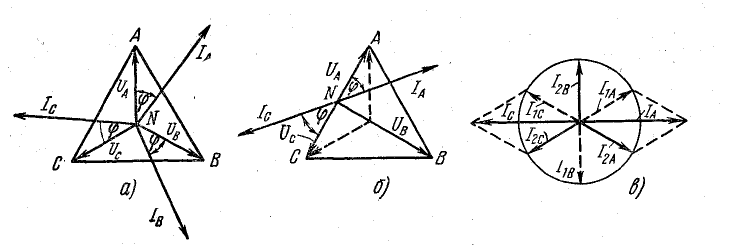
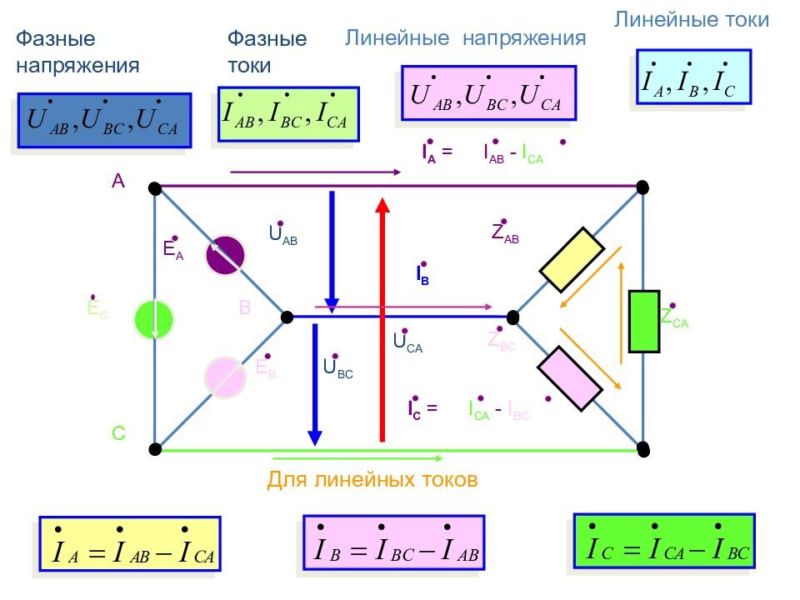
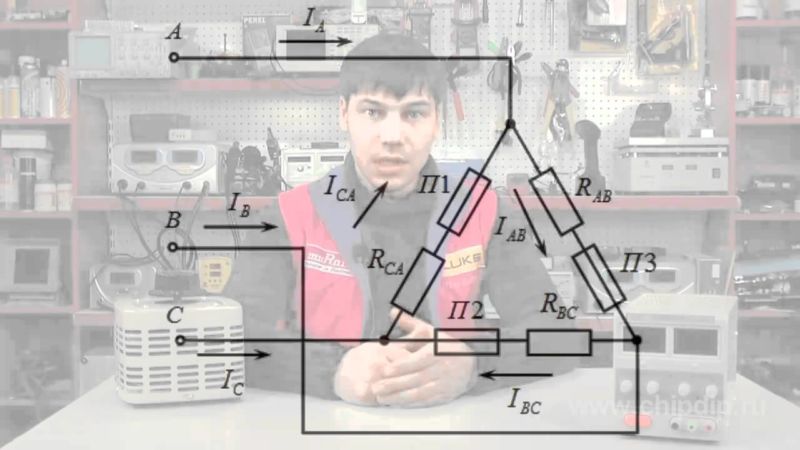
Если трехфазная система напряжений, приложенных к приемнику, известна, то фазные токи
где 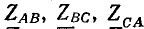
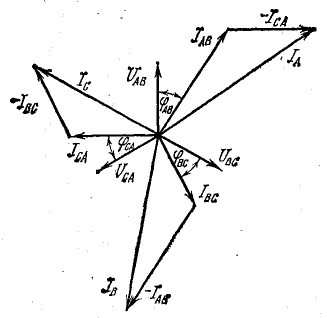
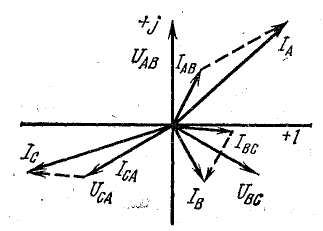
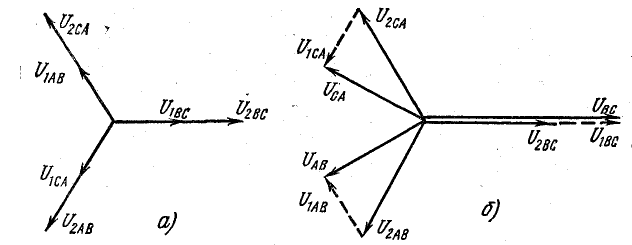
Линейные токи можно определить графически, как показано на рис. 21.4. Если задача решается в комплексной форме, линейные токи находят по формулам (20.7).
Мощность в несимметричной трехфазной цепи при соединении треугольником определяют по тем же формулам, что и при соединении звездой (21.6), (21.7).
Рис. 21.4. Векторная диаграмма токов при несимметричной нагрузке (соединение треугольником)
Рис. 21.5. К вопросу о преобразовании треугольника сопротивлений в эквивалентную звезду в трехфазной цепи
Преобразование звезды и треугольника сопротивлений в трехфазных цепях
Расчет трехфазных цепей при смешанном соединении (звездой и треугольником), с учетом сопротивлений проводов линии представляет значительные трудности.
В этих случаях упрощения достигаются благодаря применению метода взаимного преобразования звезды и треугольника.
На рис. 21.5 приемник энергии соединен треугольником. С учетом сопротивлений проводов линии (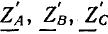
Если в ходе расчета схемы со смешанным соединением приемников — звездой и треугольником (рис. 21.6) — необходимо определить общее сопротивление фазы, это делается преобразованием звезды в треугольник или треугольника в звезду.
При симметричной нагрузке можно преобразовать треугольник в звезду, а затем две звезды заменить одной. Последняя операция возможна только при симметричной нагрузке, когда фазные напряжения у этих «звезд» одинаковы (смещение нейтрали отсутствует). При несимметричной нагрузке звезду следует преобразовать в эквивалентный треугольник, а затем сложением соответствующих проводимостей определить общую проводимость каждой фазы.
Рис. 21.6. к расчету трехфазной цепи при соединении приемников звездой и треугольником
Если в последнем случае требуется учесть сопротивление проводов, то общий треугольник еще раз приходится преобразовать в звезду и к сопротивлениям звезды прибавить сопротивления проводов линии.
Задача 21.4.
Сопротивления фаз приемника 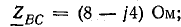
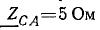
Решение. Схема рис. 20.8, а соответствует условию задачи. Если сопротивления линейных проводов и обмоток генератора считать равными нулю, то фазные напряжения приемника равны соответствующим э. д. с.:
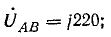
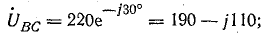
Фазные токи в приемнике:
Линейные токи:
Сумма линейных токов
Равенство нулю суммы линейных токов является общим свойством трехфазных трехпроводных цепей при соединении звездой и треугольником при симметричной и несимметричной нагрузках.
Рис. 21.7. К задаче 21.4
Рис. 21.8. К задаче 21.5
Мощности фаз:
Общая мощность системы:
активная
реактивная
Векторная диаграмма построена на рис. 21.7.
Задача 21.5.
Приемник электрической энергии, соединенный треугольником, включен в сеть с линейным напряжением 120 В. Сопротивления фаз: 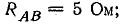
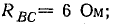
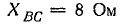
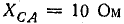
Начертить схему по условию задачи. Определить фазные и линейные токи, активную, реактивную и полную мощности в каждой фазе и всей цени. Построить векторную диаграмму.
Решение. Схема цепи изображена на рис. 21.8, а.
Решим задачу без применения комплексных чисел. Токи в фазах:
Линейные токи определим графически с помощью векторной диаграммы. Для этого найдем активные и реактивные токи фаз.
В фазе АВ включено активное сопротивление, поэтому
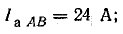
В фазе ВС последовательно соединены R и ХL, поэтому
В фазе CA включено емкостное сопротивление, следовательно,
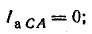
Векторная диаграмма цепи показана на рис. 21.8, б. Для определения линейных токов постройте векторную диаграмму на листе миллиметровой бумаги в масштабах: 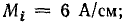
Линейные токи: 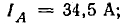
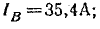
Мощности фаз:
активные
реактивные
полные
Мощность всей цепи:
активная
реактивная
Знак минус указывает на емкостный характер реактивной мощности цепи.
Симметричные составляющие несимметричной трехфазной системы
Несимметричную трехфазную систему токов (напряжений или других синусоидальных величин) можно представить в виде суммы трех симметричных систем.
Разложение несимметричной системы векторов на симметричные составляющие применяется для расчета и анализа несимметричных режимов в трехфазных цепях: при симметричной нагрузке, но несимметричной системе э. д. с., при однофазных и двухфазных коротких замыканиях, при обрыве линейных проводов в цепях с симметричной системой э. д. с.
Комплексы симметричных составляющих
Первая симметричная система имеет прямую последовательность фаз (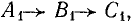
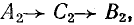
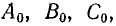
Рис. 21.9. Симметричные составляющие несимметричной системы
Система величин:
прямой последовательности
обратной последовательности
нулевой последовательности
Умножение на 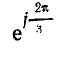
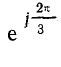
Поворот вектора против часовой стрелки на 240° можно выразить умножением его на а2.
Умножение вектора на а3 не меняет его положения:
С помощью поворотного множителя а системы прямой и обратной последовательности можно записать так:
Сумма синусоидальных величин симметричной системы равна нулю, поэтому
Разложение несимметричной системы на симметричные составляющие
Выразим комплексы несимметричной системы через симметричные составляющие:
Если из этой системы уравнений можно однозначно определить симметричные составляющие через известные величины 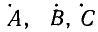
Используя выражения (21.10), запишем систему уравнений (21.12) в таком виде:
Решение системы уравнений (21.13) позволяет найти симметричные составляющие
Сложим уравнения:
Учитывая формулу (21.11), найдем
Умножим второе уравнение в системе (21.13) на 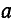
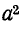
откуда
Умножим второе уравнение в системе (21.13) на 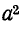
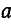
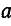
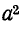
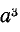
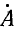
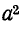
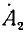
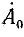
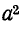
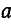
откуда
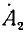
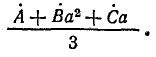
Свойства трехфазных цепей
Отметим некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений.
Степень несимметрии линейных напряжений оценивается коэффициентом несимметрии, т.е. отношением составляющей обратной последовательности напряжений к составляющей прямой последовательности.
ε = 100 • Uоп/Uпп.
Отсюда следует, что ток в нулевом проводе можно найти, если утроить величину составляющей тока нулевой последовательности.
В трехпроводной системе сумма линейных токов равна нулю. Из формулы (21.14) следует, что линейные токи в этом случае не содержат составляющей нулевой последовательности. Это справедливо и для линейных напряжений трехфазной системы, сумма которых тоже равна нулю.
Рис. 21.10. Симметричные составляющие токов трехфазной цепи при разомкнутых двух фазах
Отсутствие тока в одной или двух фазах при несимметричном режиме означает, что сумма трех симметричных составляющих токов в этих фазах равна нулю.
Например, на схеме рис. 21.10, а фазы В и С разомкнуты. Поэтому
Согласно формулам (21.14) — (21.16), симметричные составляющие токов имеют следующие выражения:
прямой последовательности
обратной последовательности
нулевой последовательности
На рис. 21.10, б показаны симметричные составляющие прямой, обратной и нулевой последовательности и их геометрическое сложение; в результате сложения получаем:
Задача 21.8.
В результате неправильной маркировки концов обмоток трехфазного трансформатора (начало фазы А вторичной обмотки помечено как конец) система линейных напряжений несимметрична. Определить симметричные составляющие линейных напряжений при соединении звездой, если фазные напряжения во вторичной обмотке 220 В.
Решение. Запишем комплексы фазных напряжений во вторичной обмотке:
Вектор напряжения 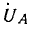
Комплексы линейных напряжений:
Составляющие:
нулевой последовательности
прямой последовательности
обратной последовательности
Рис. 21.11. К задаче 21.8
На рис. 21.11, а, б показаны векторы систем прямой и обратной последовательности и их сумма — система трех исходных векторов линейных напряжений.
Задача 21.9.
Трехфазный электродвигатель, включенный в сеть с линейным напряжением 380 В при соединении звездой, имеет мощность на валу Р2 = 14 кВт; соsφ = 0,8; к. п. д. η = 0,85.
Определить симметричные составляющие токов в обмотке двигателя при обрыве линейного провода в фазе В.
Решение. При нормальной работе ток в фазе двигателя
При симметричной системе напряжений токи в фазах двигателя образуют симметричную систему (рис. 21.12, а). При обрыве линейного провода В векторная диаграмма фазных напряжений и токов показана на рис. 21.12, б.
Ток в фазах В равен нулю (IB = 0).
Токи в фазах А и С равны по величине, но находятся в противофазе: IА = IC.
Для определения величины токов IА и IC найдем расчетное сопротивление фазы двигателя при нормальном режиме, которое будем считать неизменным:
При обрыве линейного провода фазы В обмотки двух других фаз двигателя с одинаковым сопротивлением включены последовательно на линейное напряжение UCA. Поэтому ток в фазах А и С
Рис. 21.12. к задаче 21.9
Выразим токи в комплексной форме, полагая ток IA совпадающим с положительным направлением действительной оси:
Токи:
нулевой последовательности
прямой последовательности
обратной последовательности
На рис. 21.12, в изображены симметричные составляющие токов в двигателе при обрыве фазы.
Несимметричный режим работы трехфазной цепи
Несимметрия в трехфазной цепи может быть вызвана различными причинами: 1) неодинаковым сопротивлением фаз (несимметричная нагрузка); 2) несимметричным коротким замыканием (например, между двумя фазами или фазой и нейтралью); 3) размыканием фазы; 4) неравенством э. д. с. и т. п.
Расчет токов и напряжений в трехфазной цепи при несимметричном режиме может производиться теми же
методами, которые применяются для расчета однофазных цепей.
Рассмотрим несколько простейших вариантов (без взаимной индукции между фазами).
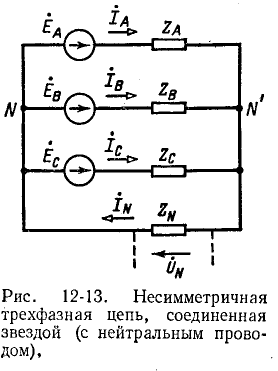
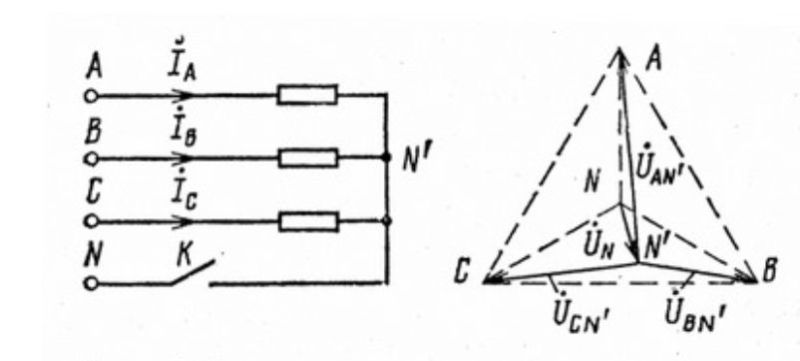
1. Несимметричная трехфазная цепь, соединенная звездой, с нейтральным проводом (рис. 12-13).
Несимметричная трехфазная цепь, показанная на рис. 12-13, может рассматриваться как трехконтурная цепь с тремя э. д. с. Такая цепь может быть рассчитана методами контурных токов, узловых напряжений и другими. Поскольку в схеме имеются только два узла, наиболее целесообразно в данном случае определить узловое напряжение (напряжение смещения) между нейтральными точками N’ и N по формуле,
где 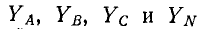
После этого найдем токи:
В симметричной трехфазной цепи 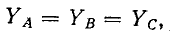
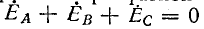
Стучаю размыкания какой-либо фазы или нейтрального провода соответствует равенство нулю проводимости данной фазы или нейтрального провода. j
При отсутствии нейтрального провода, полагая в (12-1)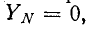
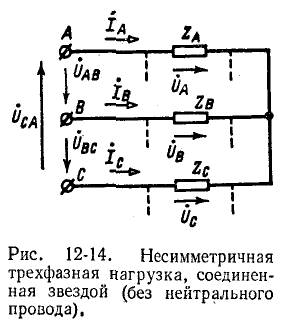
2. Несимметричная трехфазная нагрузка, соединенная звездой (без нейтрального провода), с заданными линейными напряжениями на выводах (рис. 12-14).
Если заданы линейные напряжения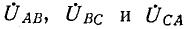
Обозначив фазные напряжения на выводах нагрузки через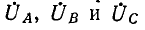
где 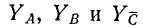
Равенство нулю суммы токов трех фаз записывается в виде:
Фазные напряжения 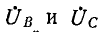
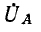
Подстановка (12-3) в (12-2) дает:
Круговой заменой индексов (с порядком следования АВСА и т. д.) находятся:
По фазным напряжениям нагрузки находятся фазные токи.
В Случае симметричной нагрузки 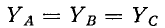
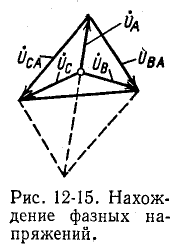
На рис. 12-15 построение сделано для фазы А по формуле (12-4)1
В качестве примера рассмотрим схему фазоуказателя, используемую для определения чередования фаз по времени, состоящую из конденсатора и двух одинаковых электрических ламп, соединенных звездой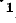
Положим, что конденсатор присоединен к фазе А, лампы — к фазам В и С; емкостное сопротивление конденсатора берется равным по модулю сопротивлению лампы, т. е. 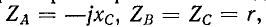
Неравенство напряжений на лампах проявится в том, что накал ламп будет разным.
1 Для определения чередования фаз на практике обычно пользуются специальным прибором, в котором создается вращающееся магнитное поле, увлекающее за собой диск в ту или другую сторону.
Отношение напряжений согласно выведенным выше выражениям (12-4) равно при симметрии линейных напряжений:
Следовательно, лампа, присоединенная к фазе В (т. е. к фазе, опережающей ту, к которой присоединена вторая лампа), будет светить ярко, а лампа, присоединенная к отстающей фазе, — тускло.
Вместо конденсатора можно применить индуктивную катушку, подобрав ее индуктивное сопротивление приблизительно равным по модулю сопротивлению лампы. В этом случае ярче будет светить лампа, присоединенная к отстающей фазе. Эти соотношения также могут быть получены непосредственно из векторной диаграммы.
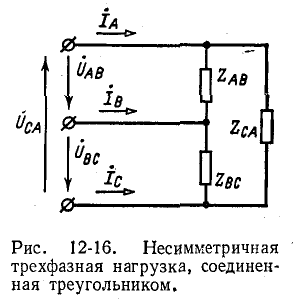
3. Несимметричная трехфазная нагрузка, соединенная треугольником, с заданными напряжениями на выводах Рис. 12-16. Несимметричная (рис. 12-16). Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы линейные напряжения 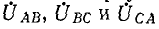
Токи в линии определяются как разности соответствующих токов нагрузки, например: 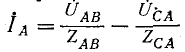
Если на выводах несимметричной трехфазной нагрузки, соединенной треугольником, заданы фазные напряжения 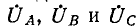
Пример 12-2. Сопротивления фаз нагрузки, соединенной звездной
Сопротивление нейтрального провода
Напряжения на цепи представляют собой симметричную звезду:
Требуется определить фазные напряжения нагрузки.
Проводимости фаз нагрузки и нейтрального провода
На основании формулы (12-1)
Искомые фазные напряжения нагрузки:
Мощность несимметричной трехфазной цепи
Пользуясь комплексной формой записи мощности, можно написать общее выражение для мощности трехфазной цепи:
Действительная часть этого выражения представляет собой активную мощность
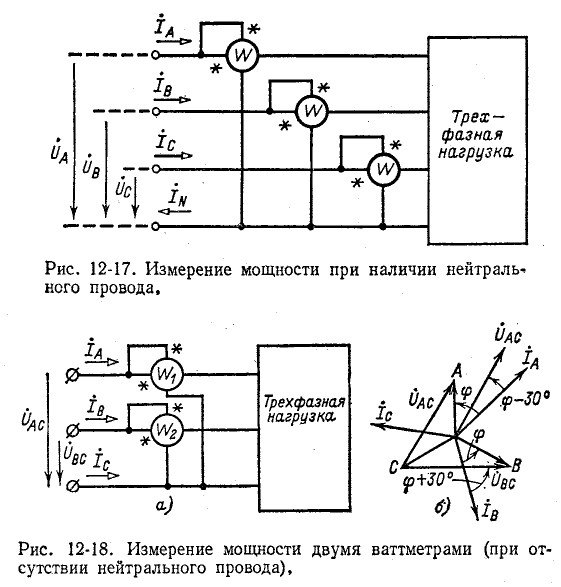
Суммарная активная мощность, потребляемая несимметричной трехфазной цепью, может быть в соответствии с этим измерена при помощи трех ваттметров, включенных на подведенные к данной цепи фазные напряжения относительно нейтрали и одноименные с ними токи. Активная мощность равна сумме показаний трех ваттметров. Такой метод измерения применяется при наличии нейтрального провода (рис. 12-17) или искусственно созданной нейтральной точки.
В случае отсутствия нейтрального провода измерение может быть произведено с помощью двух ваттметров
(рис. 12-18). В этом случае выражение (12-5) преобразуется следующим образом: исключая ток 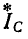
получаем:
или
В соответствии с (12-6) при измерении активной мощности двумя ваттметрами к одному из них подводятся напряжение 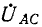
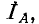
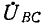
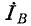
Круговой заменой А, В. и С в выражении (12-6) можно получить выражения для других равноценных вариантов включения двух ваттметров.
Следует иметь в виду’, что если стрелка одного ваттметра отклоняется по шкале в обратную сторону, то, изменив направление напряжения или тока, подводимого к данному ваттметру, записывают полученное показание со знаком минус. При симметричном режиме работы трехфазной цепи такое положение имеет место при
что видно непосредственно из векторной диаграммы (рис. 12-18, б).
При симметричном режиме показания двух ваттметров в схеме рис. 12-18, б будут следующие:
Сумма и разность показаний ваттметров соответственно равны:
Следовательно, при симметричном режиме работы трехфазной цепи тангенс угла сдвига фаз может быть вычислен по формуле
- Вращающееся магнитное поле
- Электрические цепи синусоидального тока
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Метод симметричных составляющих
- Цепи периодического несинусоидального тока
- Резонанс токов
- Трехфазные симметричные цепи
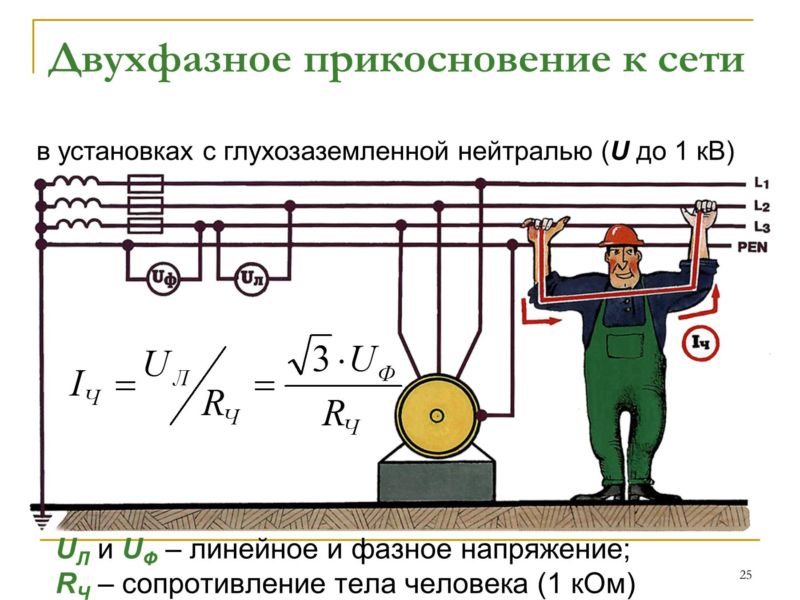
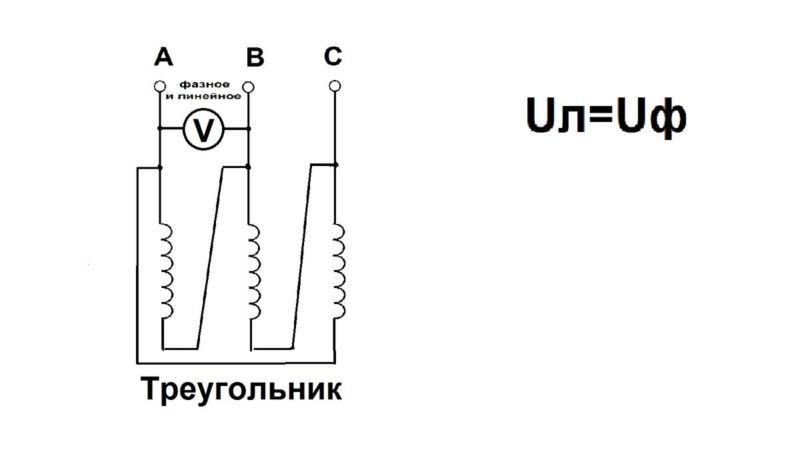
Линейное и фазное напряжения — определение, измерение, схемы и описание типов
Без электричества сегодня представить жизнь современного человека крайне сложно. Вот только в тонкостях, которые касаются непосредственно процесса снабжения городов, предприятий и домов, разбираются лишь единицы.
И это большое упущение. Поскольку в жизни может возникнет ситуация, когда подобные знания действительно пригодятся. Поэтому попробуем разобраться в данном вопросе.
Содержание
Особенности напряжения в трехфазных сетях
Для того чтобы снабдить объекты электричеством, используются сети из 3-х фаз. Конечно, существуют и другие генераторы. Например, шестифазные. Но их применяют крайне редко.
Объясняется подобное необходимостью минимизировать затраты, которые возникают в процессе создания вращающегося магнитного поля. Эти затраты в любом случае возникают во время генерации электричества.
Хотя избежать их невозможно, но свести к минимуму вполне реально. И поэтому предпочтение отдается именно сетям с 3-х фазных напряжением.
В трехфазной сети выделяют три основных элемента:
- генератор;
- линии электропередач;
- нагрузка.
Под термином «нагрузка» принято подразумевать непосредственно потребителя. Фаза же представляет собой одну электрическую цепь в многофазной системе электрических цепей.
Важно! Данный вид подключения предоставляет возможность использовать сразу два вида напряжения.
Теперь поговорим о том, что представляют собой фазное и линейное напряжение. Ведь именно эти два термина в данном случае играют ключевую роль.
Итак, фазное напряжение должно определяться непосредственно между началом и концом фазы. Линейное напряжение измеряют между 2-мя фазами. То есть, между выводами разных фаз.
В этом заключается основное отличие этих двух понятий. И о нем ни в коем случае нельзя забывать. Особенно тем, кто в будущем все-таки планирует устроиться на работу по специальности электрик.
Поскольку фазное и линейное напряжения отличаются на 60%, то появляется возможность при линейном напряжении в 380 вольт, получить 220 вольт фазного напряжения. Именно по этой причине делать разводку сетей достаточно просто.
Необходимость сделать это часто возникает в случае, когда на первых этажах многоквартирных домов компания начинает оборудовать собственные офисы. Ведь тогда напряжения, доступного для рядовых потребителей, оказывается недостаточно.
Соотношение линейного и фазного напряжения
Универсальным и приемлемым соотношением этих двух видов напряжения является такая цепь – 380/220 вольт нулевым проводом.
Если приборам для нормального функционирования требуется напряжение 220 вольт, то их необходимо подсоединить к двум проводам фазного напряжения, которые будут питаться от линейного напряжения.
Следует отметить тот факт, что приборы, которые запитываются от 3-х фазной сети, могут функционировать исключительно в том случае, если они были подсоединены к трем выводам разных фаз.
Важно! Использовать заземление в таком случае вовсе необязательно. Однако, если изоляционный материал, покрывающий провод, будет поврежден, то вероятность удара током возрастет.
Как определить линейное и фазное напряжение
Чтобы правильно определить эти два вида напряжения, нужно вспомнить о некоторых тонкостях.
Ведь зачастую эти два понятия многие попросту путают. И поэтому правильно определить их величину становятся сложно.
Во-первых, линейное напряжение следует определять исключительно между двумя фазами.
Во-вторых, фазное напряжение по определению нужно вычислять непосредственно между фазой и нулем. Поэтому нельзя пытаться определить фазное напряжение между двумя фазами.
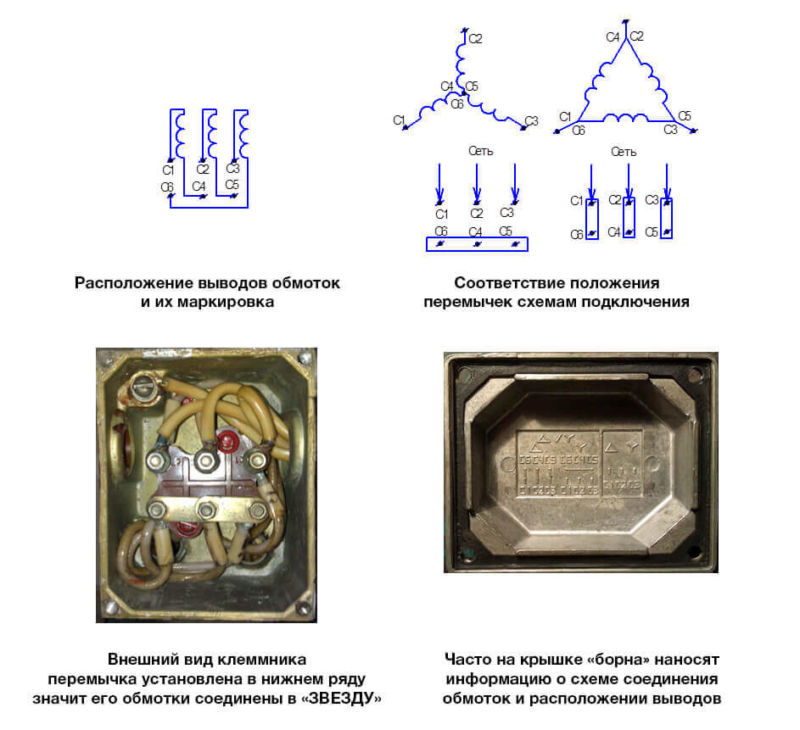
Типы соединения
Чтобы запустить генератор, часто используют именно линейное и фазное напряжение. Если говорить о запуске именно трехфазного генератора, то следует отметить один важный факт.
Состоит такой прибор не только из первичных, но и вторичных обмоток. Эти обмотки нужно правильно соединить и для этого существует два самых распространенных способа.
Только благодаря тому, что все обмотки будут правильно соединены, можно добиться определенных улучшений:
- Увеличение мощности передачи – это важнейшая задача, которую нужно решить, но сделать это следует без увеличения напряжения. И сделать это можно благодаря использованию определенных типов соединений.
- Снижение пульсаций напряжения – если в блоках питания наблюдаются постоянные колебания напряжения, это может стать причиной выхода из строя, подключенных к ней приборов. Поэтому устранение данного недочета с помощью разных соединений является первостепенной задачей.
- Уменьшение количества проводов – при подключении к сети нужно минимизировать количество соединений, чтобы улучшить качество работы приборов. Именно по этой причине использование двух упрощенных схем для подключения настолько важно.
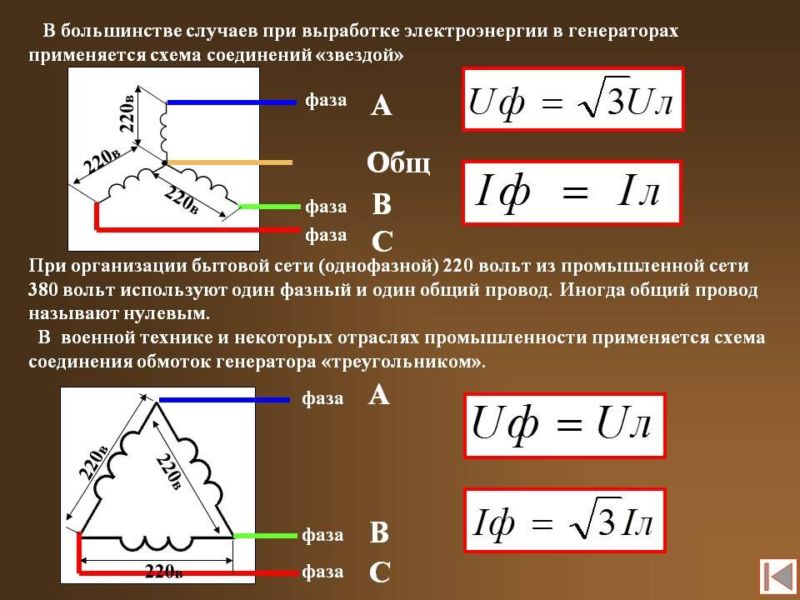
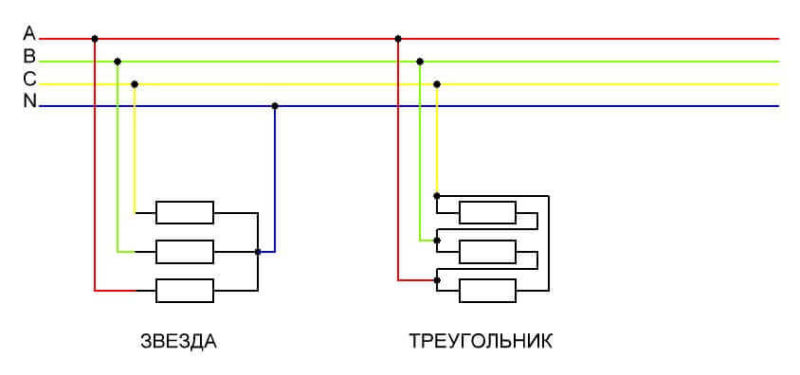
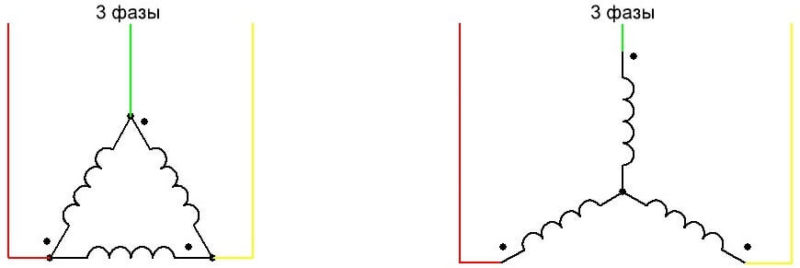
Звезда
Сначала рассмотрим данный тип подключения. Чтобы его выполнить, нужно соединить начало всех мотков в одной точке.
Эту точку принято называть нулевой. В некоторых печатных руководствах упоминается другое обозначение – нейтральная точка.
Иногда встречается соединение нулевой точки и нулевым источником питания. И поэтому ошибочно юные и начинающие электрики считают его обязательным. Но это не так, такое соединение могут использовать в некоторых случаях, и оно не является обязательным.
Важно! Если такое соединение присутствует, то систему правильно называть 4-проводной. В том случае, если оно отсутствует, то соединение считается трехпроводным.
Треугольник
Для выполнения соединения используют схему, отличную от той, которая была описана выше. Ведь нужно соединить одну обмотку с другой.
Свое название соединение получило из-за внешнего сходства с треугольником.
Его особенностью является то, что все обмотки соединяются в строгой последовательности. А поскольку общая точка соприкосновения отсутствует, такая система может быть только одного вида, а именно – трехпроводная.
Нюансы выбора типа соединения
В настоящее время оба типа соединения, звезда и треугольник, активно используются. Однако, подобное вовсе не означает, что можно по собственному усмотрению выбрать тот способ, который больше понравится.
Существуют определенные требования и общие рекомендации, следуя которым можно избежать ошибок.
Нужно запомнить, что при линейном напряжении в 220 вольт подключение двигателя по схеме звезда невозможно.
Для такого напряжения идеально подходит схема треугольник.
С другой стороны, если в сети напряжение выше 220 вольт, к примеру 380, то оптимальным вариантом станет использование именно звезды.
Если запомнить это простое правило, удастся в будущем избежать ошибок при подключении генераторов и других приборов.
Фото схем и формул измерения линейного и фазного напряжения

Об авторе: эксперт в области электроники и деревообработки
Задать вопрос
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно,
все рассмотренные ранее методы расчета и анализа в символической форме в полной
мере распространяются на них. Анализ трехфазных систем удобно осуществлять с
использованием векторных диаграмм, позволяющих достаточно просто определять
фазовые сдвиги между переменными. Однако определенная специфика многофазных
цепей вносит характерные особенности в их расчет, что, в первую очередь, касается
анализа их работы в симметричных режимах.
Расчет симметричных режимов работы трехфазных систем
Многофазный приемник и вообще многофазная цепь называются симметричными,
если в них комплексные сопротивления соответствующих фаз одинаковы, т.е.
если . В противном случае они являются
несимметричными. Равенство модулей указанных сопротивлений не является
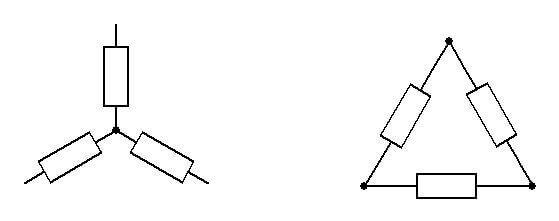
достаточным условием симметрии цепи. Так, например трехфазный приемник на рис.
1,а является симметричным, а на рис. 1,б – нет даже при условии: .

Если к симметричной трехфазной цепи приложена симметричная трехфазная система
напряжений генератора, то в ней будет иметь место симметричная система токов.
Такой режим работы трехфазной цепи называется симметричным. В этом режиме
токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг
по отношению к другу на угол . Вследствие указанного расчет
таких цепей проводится для одной – базовой – фазы, в качестве которой
обычно принимают фазу А. При этом соответствующие величины в других фазах получают
формальным добавлением к аргументу переменной фазы А фазового сдвига при сохранении неизменным ее модуля.
Так для симметричного режима работы цепи на рис. 2,а при известных линейном
напряжении и сопротивлениях фаз можно записать

где
определяется характером нагрузки .
Тогда на основании вышесказанного
;
.

Комплексы линейных токов можно найти с использованием векторной диаграммы на
рис. 2,б, из которой вытекает:

При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется
с помощью двух основных приемов:
Все треугольники заменяются эквивалентными звездами. Поскольку треугольники
симметричны, то в соответствии с формулами преобразования «треугольник-звезда»

Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы
их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи
их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется
базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам
которого определяются соответствующие величины в других фазах.
Пусть, например, при заданном фазном напряжении необходимо определить линейные
токи и
в схеме на рис. 3, все сопротивления
в которой известны.
В соответствии с указанной методикой выделим расчетную фазу А, которая представлена
на рис. 4. Здесь ,
.
Тогда для тока 

и соответственно .


Расчет несимметричных режимов работы трехфазных систем
Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет
место несимметричный режим работы. Такие режимы при наличии в цепи только статической
нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для
всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные
напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить,
что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес
также потенциалы узлов, чаще других для расчета сложных схем применяется метод
узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей
с электрическими машинами в основном применяется метод симметричных составляющих,
который будет рассмотрен далее.
При заданных линейных напряжениях наиболее просто рассчитываются трехфазные
цепи при соединении в треугольник. Пусть в схеме на рис. 2,а . Тогда при известных комплексах
линейных напряжений в соответствии с законом Ома



По найденным фазным токам приемника на основании первого закона Кирхгофа определяются
линейные токи:
.
Обычно на практике известны не комплексы линейных напряжений, а их модули.
В этом случае необходимо предварительное определение начальных фаз этих напряжений,
что можно осуществить, например, графически. Для этого, приняв , по заданным модулям напряжений,
строим треугольник (см. рис.5), из которого (путем замера) определяем значения
углов a и b.
Тогда

Искомые углы a и b могут быть также найдены аналитически
на основании теоремы косинусов:

При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода
с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям
на фазах источника. В этом случае фазные токи легко определяются по закону Ома,
т.е. путем деления известных напряжений на фазах потребителя на соответствующие
сопротивления. Однако, если сопротивление нейтрального провода велико или он
отсутствует, требуется более сложный расчет.
Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной
нагрузке ей в общем случае будет соответствовать
векторная диаграмма напряжений (см. рис. 6,б), на которой нейтральные точки
источника и приемника занимают разные положения, т.е. .
Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением
смещения нейтральной точки (обычно принимается, что ) или просто напряжением смещения
нейтрали. Чем оно больше, тем сильнее несимметрия фазных напряжений на нагрузке,
что наглядно иллюстрирует векторная диаграмма на рис. 6,б.
Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали.
Если оно известно, то напряжения на фазах нагрузки равны:
.

Тогда для искомых токов можно записать:
.
Соотношение для напряжения смещения нейтрали, записанное на основании метода
узловых потенциалов, имеет вид
 . . |
(1) |
При наличии нейтрального провода с нулевым сопротивлением , и из (1)
. В случае отсутствия нейтрального
провода . При симметричной нагрузке
с учетом того, что
, из (1) вытекает
.
В качестве примера анализа несимметричного
режима работы цепи с использованием соотношения (1) определим, какая из ламп
в схеме на рис. 7 с прямым чередованием фаз источника будет гореть ярче, если
.
Запишем выражения комплексных сопротивлений фаз нагрузки:

Тогда для напряжения смещения нейтрали будем иметь

Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника
опускается)

Таким образом, наиболее ярко будет гореть лампочка в фазе С.
В заключение отметим, что если при соединении в звезду задаются линейные напряжения
(что обычно имеет место на практике), то с учетом того, что сумма последних
равна нулю, их можно однозначно задать с помощью двух источников ЭДС, например,
и
. Тогда, поскольку при этом
, соотношение (1) трансформируется
в формулу
 . . |
(2) |
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Какой многофазный приемник является симметричным?
- Какой режим работы трехфазной цепи называется симметричным?
- В чем заключается специфика расчета симметричных режимов работы трехфазных
цепей? - С помощью каких приемов трехфазная симметричная схема сводится к расчетной
однофазной? - Что такое напряжение смещения нейтрали, как оно определяется?
- Как можно определить комплексы линейных напряжений, если заданы их модули?
- Что обеспечивает нейтральный провод с нулевым сопротивлением?
- В цепи на рис. 6,а
;
;
;
. Линейное напряжение равно 380
В. - В схеме предыдущей задачи
;
. Остальные параметры те же.
- В задаче 8 нейтральный провод оборван.
- В задаче 9 нейтральный провод оборван.
Определить ток в нейтральном проводе.
Ответ: .
Определить ток в нейтральном проводе.
Ответ: .
Определить фазные напряжения на нагрузке.
Ответ: ;
;
.
Определить фазные напряжения на нагрузке.
Ответ: ;
;
.
Линейное и фазное напряжение — отличие и соотношение
В этой краткой статье, не вдаваясь в историю сетей переменного тока, разберемся в соотношениях между фазными и линейными напряжениями. Ответим на вопросы о том, что такое фазное напряжение и что такое линейное напряжение, как они соотносятся между собой и почему эти соотношения именно таковы.
Ни для кого не секрет, что сегодня электроэнергия от генерирующих электростанций подается к потребителям по высоковольтным линиям электропередач с частотой 50 Гц. На трансформаторных подстанциях высокое синусоидальное напряжение понижается, и распределяется по потребителям на уровне 220 или 380 вольт. Где-то сеть однофазная, где-то трехфазная, однако давайте разбираться.
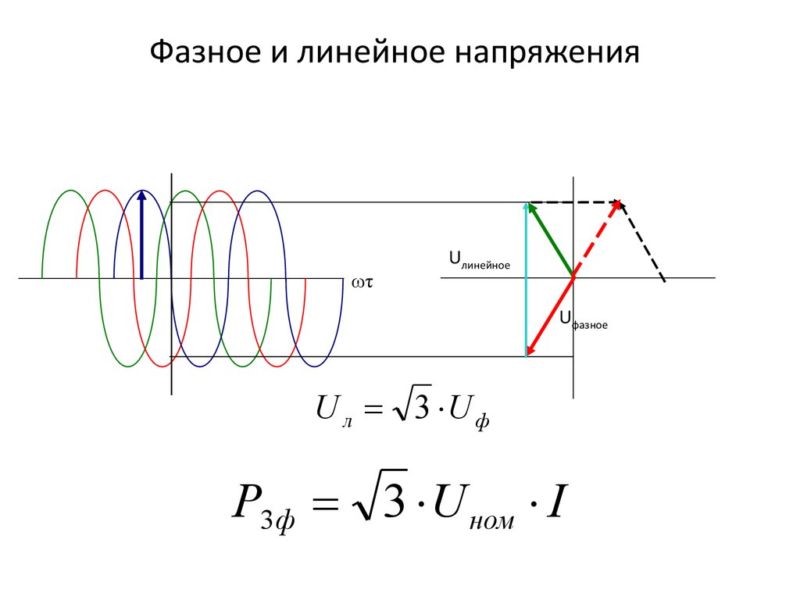
Действующее значение и амплитудное значение напряжения
Прежде всего отметим, что когда говорят 220 или 380 вольт, то имеют ввиду действующие значения напряжений, выражаясь математическим языком — среднеквадратичные значения напряжений . Что это значит?
Это значит, что на самом деле амплитуда Um (максимум) синусоидального напряжения, фазного Umф или линейного Umл, всегда больше этого действующего значения. Для синусоидального напряжения его амплитуда больше действующего значения в корень из 2 раз, то есть в 1,414 раза.
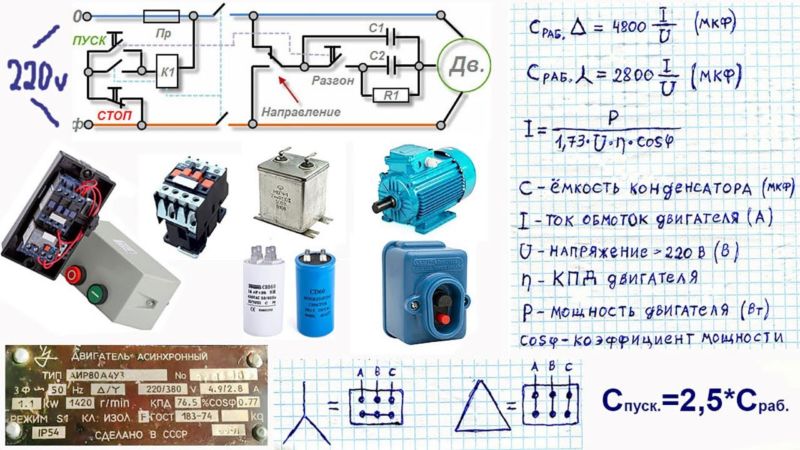
Так что для фазного напряжения в 220 вольт амплитуда равна 310 вольт, а для линейного напряжения в 380 вольт амплитуда окажется равной 537 вольт. А если учесть, что напряжение в сети никогда не бывает стабильным, то эти значения могут быть как ниже, так и выше. Данное обстоятельство всегда следует учитывать, например выбирая конденсаторы для трехфазного асинхронного электродвигателя.
Фазное сетевой напряжение
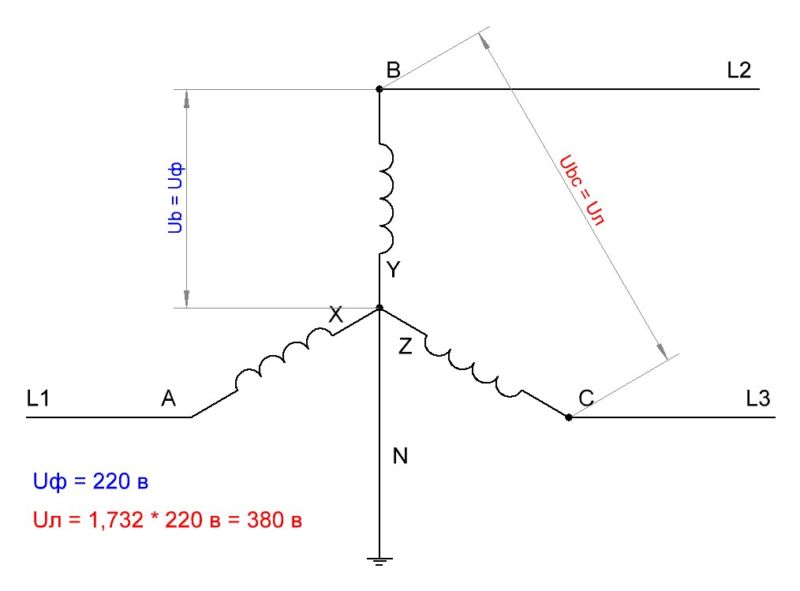
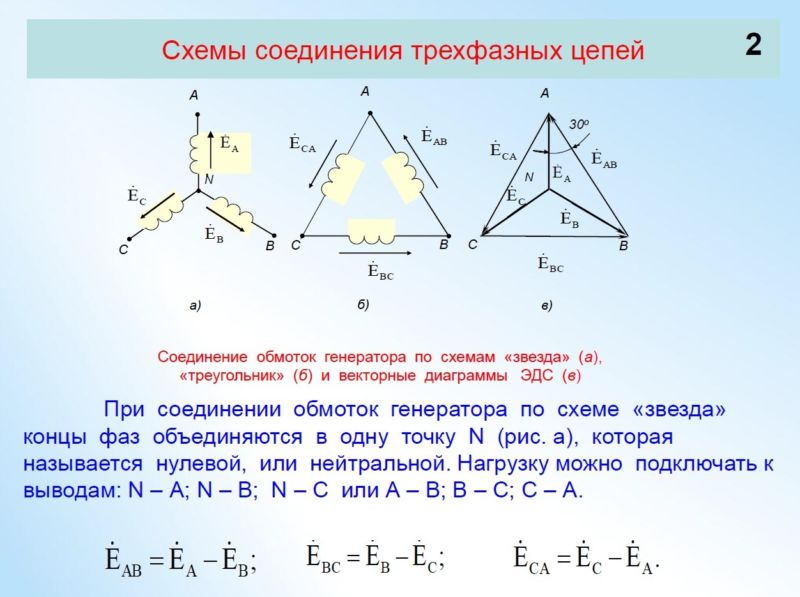
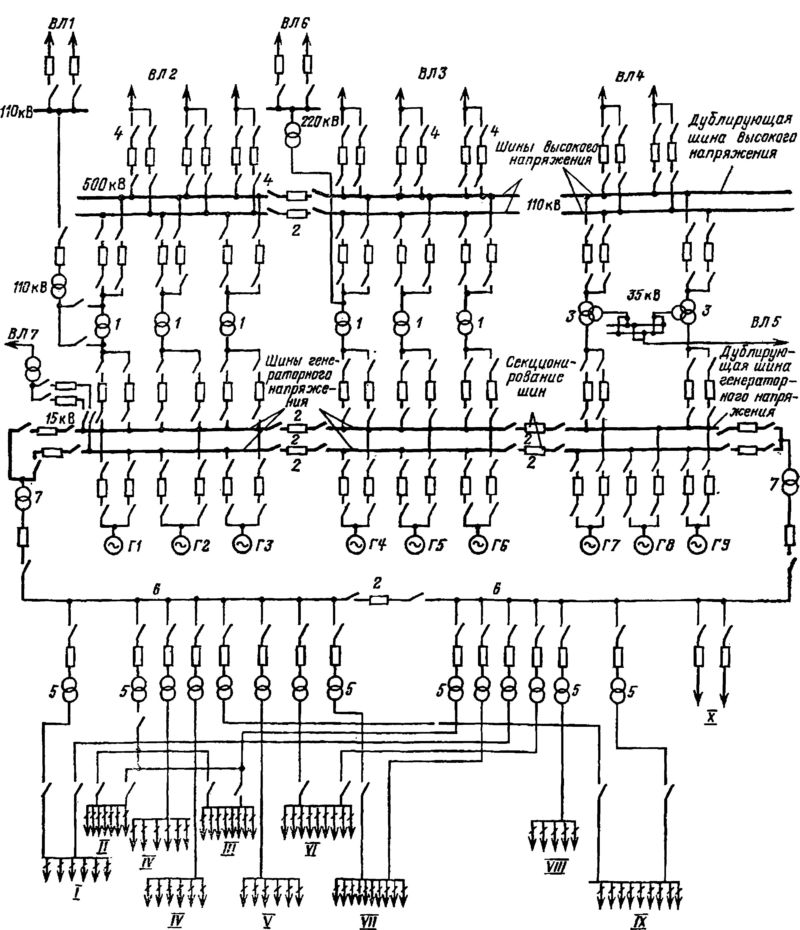
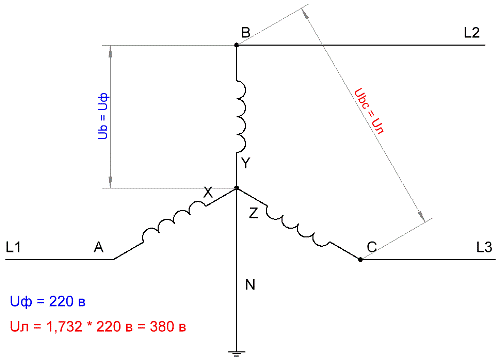
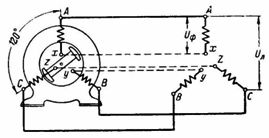
Обмотки генератора соединены по схеме «звезда», и объединены концами X, Y и Z в одной точке (в центре звезды), которая называется нейтралью или нулевой точкой генератора. Это четырехпроводная трехфазная схема. К выводам обмоток A, B и C присоединяются линейные провода L1, L2 и L3, а к нулевой точке — нейтральный провод N.
Напряжения между выводом A и нулевой точкой, B и нулевой точкой, С и нулевой точкой, — называются фазными напряжениями, их обозначают Ua, Ub и Uc, ну а поскольку сеть симметрична, то можно просто написать Uф — фазное напряжение.
В трехфазных сетях переменного тока большинства стран стандартное фазное напряжение равно приблизительно 220 вольт — напряжение между фазным проводом и нейтральной точкой, которая обычно заземляется, и ее потенциал принимается равным нулю, потому она и называется еще нулевой точкой .
Линейное напряжение трехфазной сети
Напряжения между выводом A и выводом B, между выводом B и выводом C, между выводом C и выводом A, — называются линейными напряжениями, то есть это напряжения между линейными проводниками трехфазной сети. Их обозначают Uab, Ubc, Uca, или можно просто написать Uл.
Стандартное линейное напряжение в большинстве стран равно приблизительно 380 вольт. Легко заметить в данном случае, что 380 больше 220 в 1,727 раза, и, пренебрегая потерями, ясно, что это квадратный корень из 3, то есть 1,732. Безусловно, напряжение в сети все время в ту или другую сторону колеблется в зависимости от текущей загруженности сети, но соотношение между линейными и фазными напряжениями именно таково.
Откуда взялся корень из 3
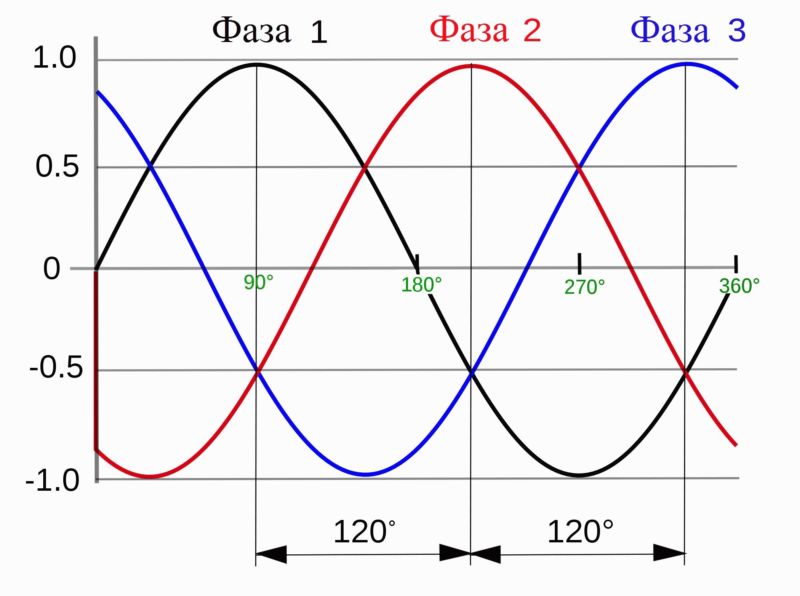
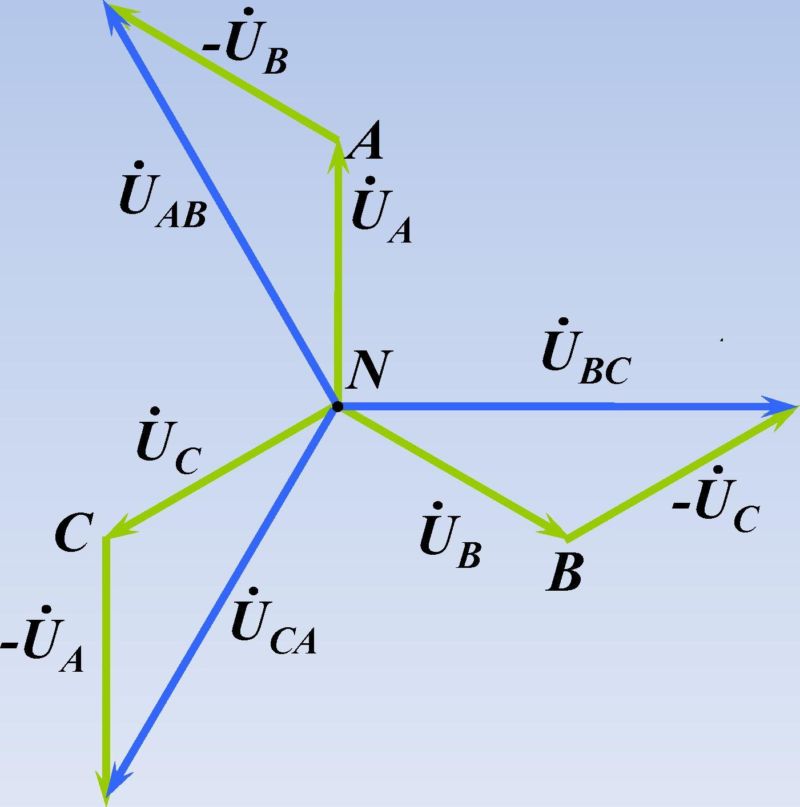
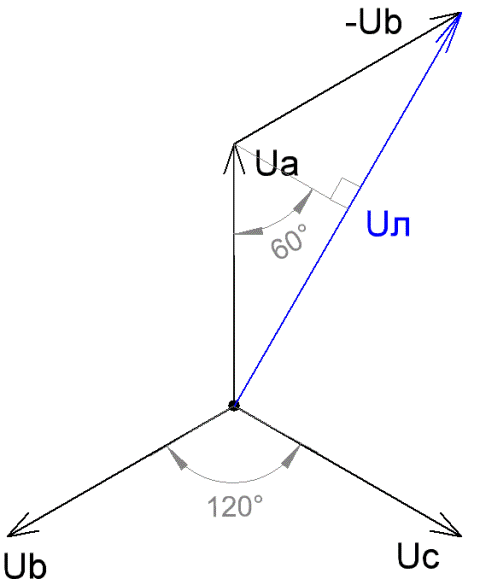
В электротехнике часто применяют векторный метод изображения синусоидально изменяющихся во времени величин напряжений и токов.
График зависимости величины проекции от времени есть синусоида. И если амплитуда напряжения — это длина вектора U, то проекция, которая меняется со временем — это текущее значение напряжения, а синусоида отражает динамику напряжения.
Так вот, если теперь изобразить векторную диаграмму трехфазных напряжений, то получится, что между векторами трех фаз одинаковые углы по 120°, и тогда если длины векторов — это действующие значения фазных напряжений Uф, то чтобы найти линейные напряжения Uл, необходимо вычислить РАЗНОСТЬ любой пары векторов двух фазных напряжений. Например Ua – Ub.
Выполнив построение методом параллелограмма, увидим, что вектор Uл = Uа + (-Ub), и в результате Uл = 1,732Uф. Отсюда и получается, что если стандартные фазные напряжения равны 220 вольт, то соответствующие линейные будут равны 380 вольт.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Расчет фазных и линейных величин трехфазного тока
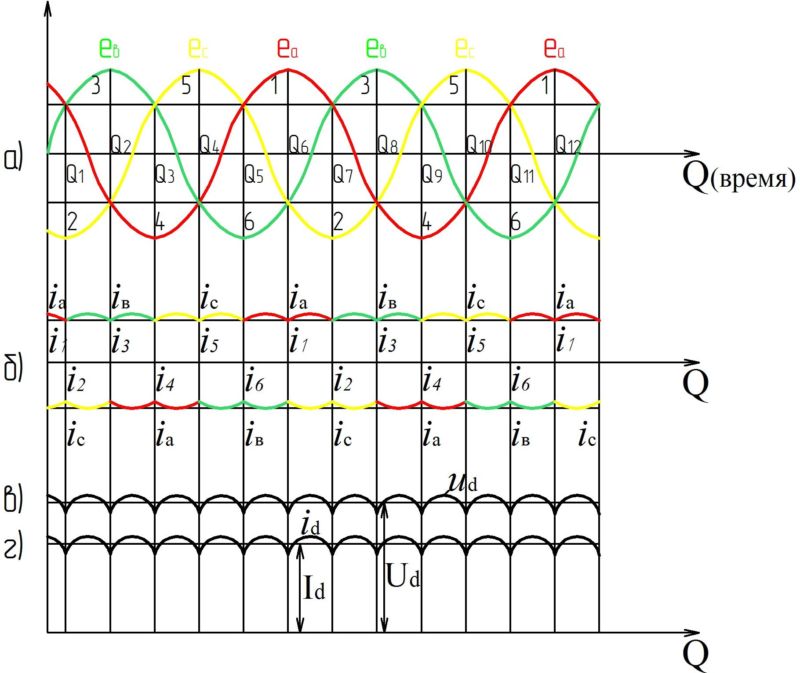
Трехфазный генератор имеет на статоре три однофазные самостоятельные обмотки, начала и концы которых сдвинуты соответственно на 120 эл. град, или на 2/3 полюсного деления, т. е на 2/3 расстояния между серединами разноименных полюсов (рис. 1). В каждой из трех обмоток возникает однофазный переменный ток. Однофазные токи обмоток взаимно сдвинуты на 120 эл. град, т. е. на 2/3 периода. Таким образом, трехфазный ток представляет собой три однофазных тока, сдвинутых во времени на 2/3 периода (120°).
В любой момент времени алгебраическая сумма всех трех мгновенных: значений а. д. с. отдельных фаз равна нулю. Поэтому у генератора вместо шести выводов (для трех самостоятельных однофазных обмоток) делают только три вывода или четыре, когда выводится нулевая точка. В зависимости от того, как соединить отдельные фазы и как их подключить к сети, можно получить соединение в звезду или треугольник.
Начала обмоток обозначаются в дальнейшем буквами A, B, C, а концы их – буквами X, Y, Z.
Рис. 1. Трехфазный генератор
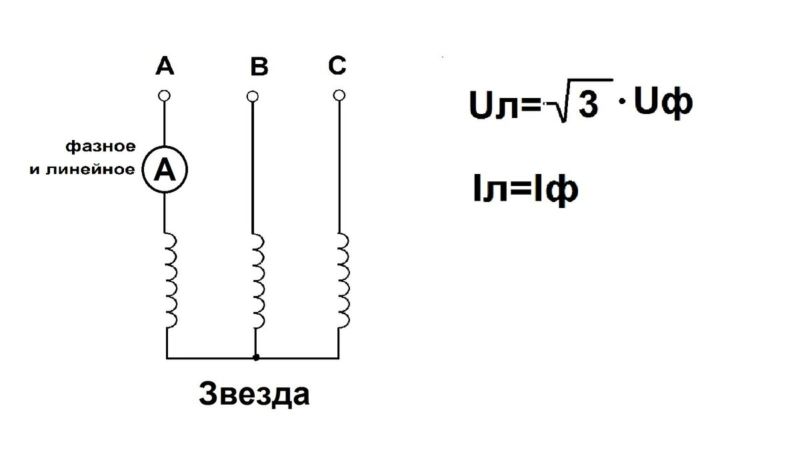
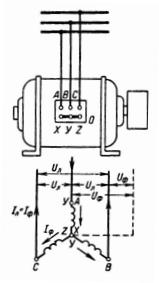
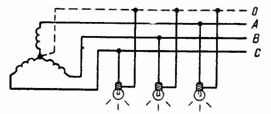
При соединении в звезду концы фаз X, Y, Z (рис. 2) соединяют и узел соединения называют нулевой точкой. Узел может иметь вывод – так называемый нулевой провод (рис. 272), показанный пунктиром, или быть без вывода.
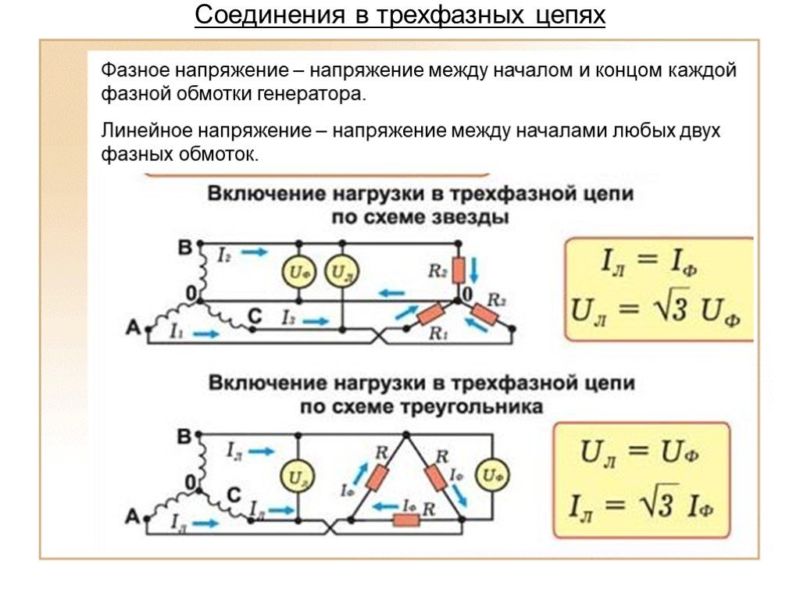
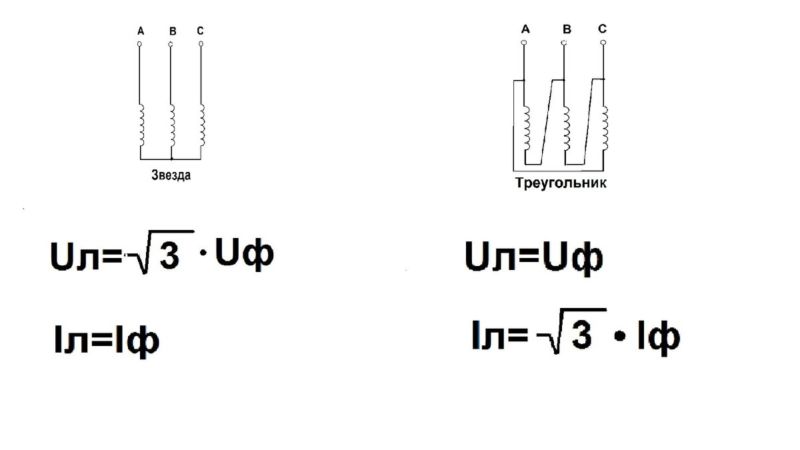
При соединении в звезду с нулевым проводом можно получить два напряжения: линейное напряжение Uл между проводами отдельных фаз и фазное напряжение Uф между фазой и нулевым проводом (рис. 2). Соотношение между линейным и фазным напряжениями выражается следующим образом: Uл=Uф∙√3.
Рис. 2. Соединение в звезду
Ток, который проходит в проводе (сети), проходит и по обмотке фазы (рис. 2), т. е. Iл=Iф.
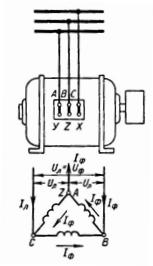
б) Соединение в треугольник.
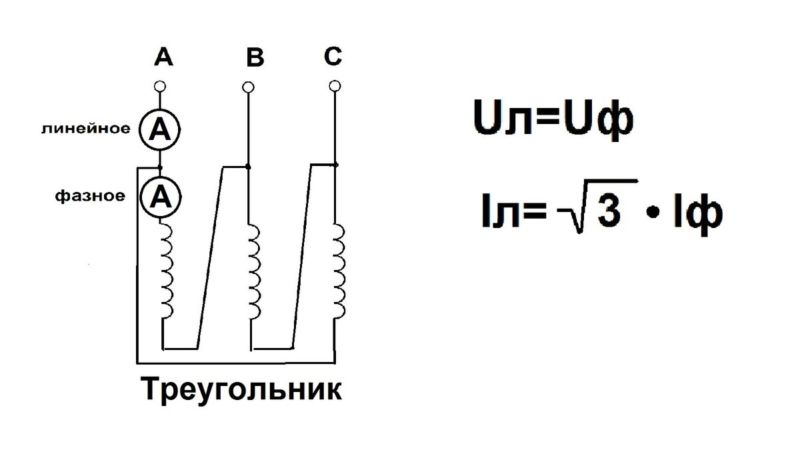
Соединение фаз в треугольник получается при соединении концов и начал фаз согласно рис. 3, т. е. AY, BZ, CX. При таком соединении нет нулевого провода и напряжение на фазе равно линейному напряжению между двумя проводами линии Uл=Uф. Однако ток в линии Iл (сети) больше, чем ток в фазе Iф, а именно: Iл=Iф∙√3.
Рис. 3. Соединение в треугольник
При трехфазной системе в каждое мгновение, если ток в одной обмотке идет от конца к началу, то в двух других он направлен от начала к концу. Например, на рис. 2 в средней обмотке AX проходит от A к X, а в крайних – от Y к B и от Z к C.
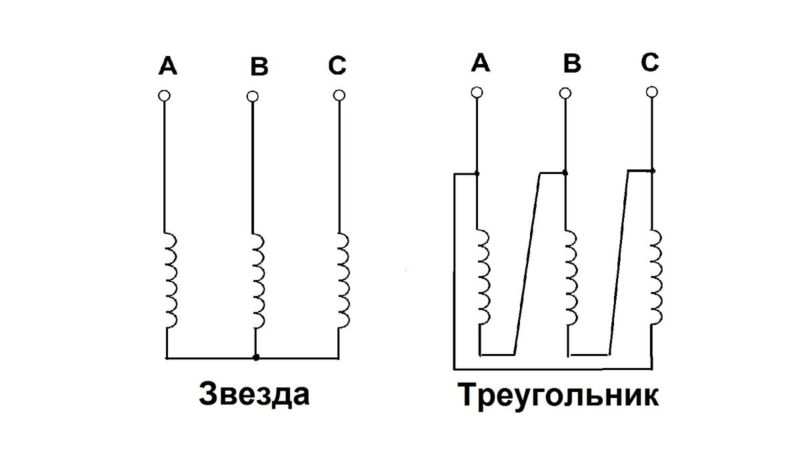
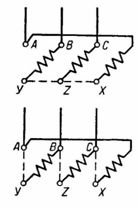
На схеме (рис. 4) показано, как три одинаковые обмотки соединяются с зажимами двигателя в звезду или треугольник.
Рис. 4. Соединение обмоток в звезду и треугольник
1. Генератор с обмоткой статора, соединенной по представленной на рис. 5 схеме, при линейном напряжении 220 В питает током три одинаковые лампы сопротивлением по 153 Ом. Какие напряжение и ток имеет каждая лампа (рис. 5)?
Согласно включению лампы имеют фазное напряжение Uф=U/√3=220/1,732=127 В.
Ток лампы Iф=Uф/r=127/153=0,8 А.
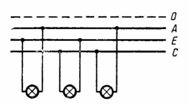
2. Определить схему включения трех ламп на рис. 6, напряжение и ток каждой лампы сопротивлением по 500 Ом, подключенных к питающей сети с линейным напряжением 220 В.
Ток в лампе I=Uл/500=220/500=0,45 А.
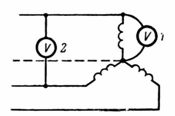
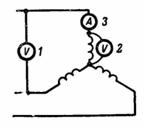
3. Сколько вольт должен показывать вольтметр 1, если вольтметр 2 показывает напряжение 220 В (рис. 7)?
Фазное напряжение Uф=Uл/√3=220/1,73=127 В.
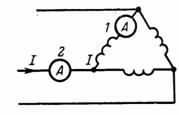
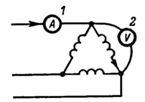
4. Какой ток показывает амперметр 1, если амперметр 2 показывает ток 20 А при соединении в треугольник (рис. 8)?
При соединении в треугольник ток в фазе потребителя меньше, чем в линии.
5. Какие напряжение и ток будут показывать измерительные приборы 2 и 3, включенные в фазу, если вольтметр 1 показывает 380 В, а сопротивление фазы потребителя 22 Ом (рис. 9)?
Вольтметр 2 показывает фазное напряжение Uф=Uл/√3=380/1,73=220 В. а амперметр 3 – фазный ток Iф=Uф/r=220/22=10 А.
6. Сколько ампер показывает амперметр 1, если сопротивление одной фазы потребителя 19 Ом с падением напряжения на нем 380 В, которое показывает вольтметр 2, включенный согласно рис. 10.
Ток в фазе Iф=Uф/r=Uл/r=380/19=20 А.
Ток потребителя по показанию амперметра 1 Iл=Iф∙√3=20∙1,73=34,6 А. (Фаза, т. е. сторона треугольника, может представлять собой обмотку машины, трансформатора или другое сопротивление.)
7. Асинхронный двигатель на рис. 2 имеет обмотку, соединенную в звезду, и включается в трехфазную сеть с линейным напряжением Uл=380 В. Каким будет фазное напряжение?
Фазное напряжение будет между нулевой точкой (зажимы X, Y, Z) и любыми из зажимов A, B, C:
8. Обмотку асинхронного двигателя из предыдущего примера замкнем в треугольник, соединив зажимы на щитке двигателя согласно рис. 3 или 4. Амперметр, включенный в линейный провод, показал ток Iл=20 А. Какой ток проходит по обмотке (фазе) статора?
Линейный ток Iл=Iф∙√3; Iф=Iл/√3=20/1,73=11,56 А.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Источник
Как найти линейные токи?
Как найти линейный ток в трехфазной цепи?
На фазах нагрузки находят линейные напряжения источника питания. Фазные токи в нагрузке определяют с помощью закона Ома для участка цепиIф = Uф/zф, где Uф – фазное напряжение на нагрузке (соответствующее линейное напряжение источника питания); zф – полное сопротивление соответствующей фазы нагрузки.
Как найти ток в трехфазной цепи?
На практике применяется формула, в которой ток и напряжение обозначают линейные величины и для соединения в звезду и в треугольник. В первое уравнение подставим Uф=U/1,73, а во второе Iф=I/1,73, получим общую формулу P=1,73·U·I·cosфи.
Как определить линейные токи?
При соединении в звезду с нулевым проводом можно получить два напряжения: линейное напряжение Uл между проводами отдельных фаз и фазное напряжение Uф между фазой и нулевым проводом (рис. 2). Соотношение между линейным и фазным напряжениями выражается следующим образом: Uл=Uф∙√3.
Что такое линейный ток?
Линейный ток — ток, протекающий по линейному проводу. При соединении звездой линейный ток равен фазному. При работе по нулевому проводу протекает ток, равный векторной сумме трех линейных токов: IА, IB и IC.
Как найти фазное напряжение?
При соединении в звезду с нулевым проводом можно получить два напряжения: линейное напряжение Uл между проводами отдельных фаз и фазное напряжение Uф между фазой и нулевым проводом (рис. 2). Соотношение между линейным и фазным напряжениями выражается следующим образом: Uл=Uф∙√3.
Что такое фазное напряжение?
Uф — фазное напряжение — это напряжение между началом и концом фазной обмотки или приемника энергии. Другими словами можно сказать: фазное напряжение — это напряжение между ли-нейным и нулевым проводами. При симметричной нагрузке нулевой провод практически не нужен, т.
Что такое косинус фи?
Коэффициент мощности cos фи (φ) определяется как отношение полезной мощности к полной. Математически это определение часто записывают в виде кВт/кВА, где числитель – активная (действительная) мощность, а знаменатель – кажущаяся (активная + реактивная, полная) мощность.
Как узнать ток двигателя по мощности?
Зная номинальную мощность двигателя (из паспорта) можно определить его номинальный ток. При включении двигателя в трехфазную сеть 380 В номинальный ток можно посчитать по следующей формуле: Iн = Pн/(√3Uн х η х сosφ), где Pн — номинальная мощность двигателя в кВт, Uн — напряжение в сети, в кВ (0,38 кВ).
Как рассчитать мощность трехфазного автомата?
Расчет мощности трехфазного автомата
- Для расчета мощности номинала трехфазного автомата необходимо суммировать всю мощность электроприборов, которые будут подключены через него. …
- L1 5000 W + L2 5000 kW + L3 5000W = 15000 W.
- Полученные ваты переводим в киловатты:
- 15000 W / 1000 = 15 kW.
- Полученное число умножаем на 1,52 и получаем рабочий ток А.
Какой из токов в схеме линейный какой фазный?
Так, токи, протекающие в каждой фазе, именуют фазными и условно обозначают IА, IB, IC либо условно Iф. Токи в ветвях нагрузки именуют линейными. … При сугубо активной нагрузке токи идентичны с напряжениями по фазе, а при индуктивной либо емкостной нагрузке, токи могут опережать или отставать от напряжения.
Как измерить линейные и фазные напряжения?
КРАТКО: Линейное напряжение измеряется между фазой и фазой, а фазное между фазой и нулём. Линейное напряжение больше фазного в √3 или в 1,73 раза. Нагрузка к трёхфазной сети может быть подключена по трём или четырем проводам.
В каком соотношении находятся линейные и фазные напряжения?
больше фазных, а при соединении треугольником равны. Этот фактор необходимо учитывать при подключении нагрузки, чтоб не произошло аварийных ситуаций и выхода оборудования из строя. Линейные напряжения тоже сдвинуты друг относительно друга на угол 1200 или 2π/3.
Что такое звезда в электрике?
В трехфазных цепях применяют два вида соединений генераторных обмоток – в звезду и треугольник (рис. 1). При соединении в звезду все концы фазных обмоток соединяют в один узел, называемый нейтральной или нулевой точкой, и обозначают, как правило, буквой O.
Чему равно фазное напряжение в треугольнике?
180, линейное напряжение создает каждая фазная обмотка. У потребителя, соединенного треугольником, линейное напряжение подключается к зажимам фазного сопротивления. Следовательно, при соединении треугольником фазное напряжение равно линейному: Uл = Uф.
Источник