Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
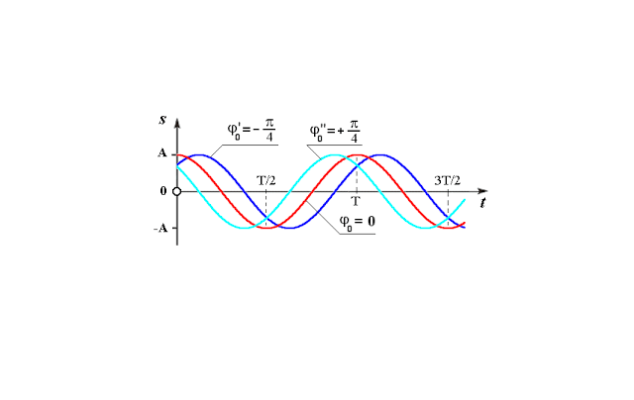
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
У этого термина существуют и другие значения, см. Фаза.
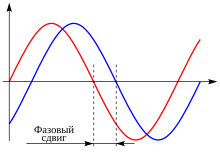
Графики двух периодических функций (колебаний) одинаковой частоты задержаны (сдвинуты) один относительно другого. Задержка во времени эквивалентна соответствующей разности фаз
Фа́за колеба́ний полная или мгновенная — аргумент периодической функции, описывающей колебательный или волновой процесс.
Фаза колебаний начальная — значение фазы колебаний (полной) в начальный момент времени, то есть при 
(для колебательного процесса), а также в начальный момент времени в начале системы координат, то есть при в точке с координатами 
(для волнового процесса).
Фаза колебания (в электротехнике) — аргумент синусоидальной функции (напряжения, тока), отсчитываемый от точки перехода значения через нуль к положительному значению[1].
Определения[править | править код]
Фаза колебания — гармоническое колебание 
Величину 
входящую в аргумент функций косинуса или синуса, называют фазой колебаний описываемой этой функцией:
Как правило, о фазе говорят применительно к гармоническим колебаниям или монохроматическим волнам. При описании величины, испытывающей гармонические колебания, используется, например, одно из выражений:
Аналогично, при описании волны, распространяющейся в одномерном пространстве, например, используются выражения вида:
для волны в пространстве любой размерности (например, в трехмерном пространстве):
Фаза колебаний (полная) в этих выражениях — аргумент функции, то есть выражение, записанное в скобках; фаза колебаний начальная — величина 
являющаяся одним из слагаемых полной фазы. Говоря о полной фазе, слово полная часто опускают.
Колебания с одинаковыми амплитудами и частотами могут различаться фазами. Так как:
то
Отношение 
указывает, сколько периодов прошло от момента начала колебаний. Любому значению времени 
выраженному в числе периодов 
соответствует значение фазы выраженное в радианах. Так, по прошествии времени 
(четверти периода) фаза будет 
по прошествии половины периода — 
по прошествии целого периода 
и т. д.
Поскольку функции синус и косинус совпадают друг с другом при сдвиге аргумента (то есть фазы) на 
то во избежание путаницы лучше пользоваться для определения фазы только одной из этих двух функций, а не той и другой одновременно. По обычному соглашению фазой считают аргумент косинуса, а не синуса[2][3].
То есть, для колебательного процесса (см. выше) фаза (полная):
для волны в одномерном пространстве:
для волны в трехмерном пространстве или пространстве любой другой размерности:
- ,
- где — угловая частота (величина, показывающая, на сколько радиан или градусов изменится фаза за 1 с; чем величина выше, тем быстрее растет фаза с течением времени);
- — время;
- — начальная фаза (то есть фаза при
- — волновое число;
- — координата точки наблюдения волнового процесса в одномерном пространстве;
- — волновой вектор;
- — радиус-вектор точки в пространстве (набор координат, например, декартовых).
В приведенных выше выражениях фаза имеет размерность угловых единиц (радианы, градусы). Фазу колебательного процесса по аналогии с механическим вращательным также выражают в циклах, то есть долях периода повторяющегося процесса:
- 1 цикл = радиан = 360 угловых градусов.
В аналитических выражениях (в формулах) преимущественно (и по умолчанию) используется представление фазы в радианах, представление в градусах также встречается достаточно часто (по-видимому, как предельно явное и не приводящее к путанице, поскольку знак градуса не принято никогда опускать ни в устной речи, ни в записях). Указание фазы в циклах или периодах (за исключением словесных формулировок) в технике сравнительно редко.
Иногда (в квазиклассическом приближении, где используются квазимонохроматические волны, то есть близкие к монохроматическим, но не строго монохроматические, а также в формализме интеграла по траекториям, где волны могут быть и далекими от монохроматических, хотя всё же подобны монохроматическим) рассматривается фаза, являющаяся нелинейной функцией времени 
и пространственных координат 
в принципе — произвольная функция[4]:
Связанные термины[править | править код]
Рассматривая два колебательных процесса одинаковой частоты, говорят о постоянной разности полных фаз (о сдвиге фаз) этих процессов. В общем случае сдвиг фаз может меняться во времени, например, из-за угловой модуляции одного или обоих процессов.
Если два колебательных процесса происходят одновременно (например, колеблющиеся величины достигают максимума в один и тот же момент времени), то говорят, что они находятся в фазе (колебания синфазны). Если моменты максимума одного колебания совпадают с моментами минимума другого колебания, то говорят, что колебания находятся в противофазе (колебания противофазны). Если разность фаз составляет ±90°, то говорят, что колебания находятся в квадратуре или что одно из этих колебаний — квадратурное по отношению к другому колебанию (опорному, «синфазному», то есть служащему для условного определения начальной фазы).
Если амплитуды двух противофазных монохроматических колебательных процессов одинаковы, то при сложении таких колебаний (при их интерференции) в линейной среде происходит взаимное уничтожение колебательных процессов.
Действие[править | править код]
Действие – одна из наиболее фундаментальных физических величин, на которой построено современное описание практически любой достаточно фундаментальной физической системы[5] — по своему физическому смыслу является фазой волновой функции.
Примечания[править | править код]
- ↑ ГОСТ Р 52002-2003. Электротехника. Термины и определения основных понятий. ГОСТ даёт определение: «Фаза (синусоидального электрического) тока — аргумент синусоидального электрического тока, отсчитываемый от точки перехода значения тока через нуль к положительному значению»
- ↑ Хотя нет принципиальной причины не сделать противоположный выбор, что иногда и делается некоторыми авторами.
- ↑ Таким образом, обычно, в соответствии с этим соглашением начальная фаза колебания вида считается равной (синус отстает от косинуса по фазе)
- ↑ Хотя в части случаев с наложением условий на скорость изменения и т. п., несколько ограничивающих произвольность функции.
- ↑ Существуют системы, формализм действия к которым применять неудобно и даже такие, к которым он по сути неприменим, однако в современном понимании такие системы делятся на два класса: 1) не фундаментальные (то есть описываемые неточно, и предполагается, что будучи описана более точно такая система может быть — в принципе — описана через действие), 2) относящиеся к далеко не общепризнанным теоретическим построениям
Литература[править | править код]
- Стрелков С. П. Введение в теорию колебаний. Учебник для вузов. 4-е изд., стер.. — М.: Лань-Пресс, 2021. — 440 с.
Начальная фаза колебаний, теория и онлайн калькуляторы
Начальная фаза колебаний
Определение
Начальная фаза колебаний – это параметр, который совместно с амплитудой колебаний определяет начальное состояние колебательной системы.
Величину начальной фазы задают в начальных условиях, то есть при $t=0$ c.
Рассмотрим гармонические колебания некоторого параметра $xi $. Гармонические колебания описываются уравнением:
[xi =A{cos ({omega }_0t+varphi ) } left(1right),]
где $A={xi }_{max}$ – амплитуда колебаний; ${omega }_0$ – циклическая (круговая) частота колебаний. Параметр $xi $ лежит в пределах $-Ale xi le $+A.
Определение фазы колебаний
Весь аргумент периодической функции (в данном случае косинуса:$ ({omega }_0t+varphi )$), описывающей колебательный процесс, называют фазой колебаний. Величина фазы колебаний в начальный момент времени, то есть при $t=0$, ($varphi $)- носит название начальной фазы. Устоявшегося обозначения фазы нет, у нас начальная фаза обозначена $varphi $. Иногда, чтобы подчеркнуть, что начальная фаза относится к моменту времени $t=0$ к букве, обозначающей начальную фазу, добавляют индекс 0, пишут, например, ${varphi }_0.$
Единицей измерения начальной фазы является единица измерения угла – радиан (рад) или градус.
Начальная фаза колебаний и способ возбуждения колебаний
Допустим, что при $t=0$ смещение системы от положения равновесия равно ${xi }_0$, а начальная скорость ${dot{xi }}_0$. Тогда уравнение (1) принимает вид:
[xi left(0right)=A{cos varphi = }{xi }_0left(2right);;]
[ frac{dxi }{dt}=-A{omega }_0{sin varphi = }{dot{xi }}_0to -A{sin varphi =frac{{dot{xi }}_0}{{omega }_0} } left(3right).]
Возведем в квадрат оба уравнения (2) и сложим их:
[{xi }^2_0+{left(frac{{dot{xi }}_0}{{omega }_0}right)}^2=A^2left(4right).]
Из выражения (4) имеем:
[A=sqrt{{xi }^2_0+{left(frac{{dot{xi }}_0}{{omega }_0}right)}^2 }left(5right).]
Разделим уравнение (3) на (2), получим:
[tg varphi =-frac{{dot{xi }}_0}{{{xi }_0omega }_0}left(6right).]
Выражения (5) и (6) показывают, что начальная фаза и амплитуда зависят от начальных условий колебаний. Это значит, что амплитуда и начальная фаза зависят от способа возбуждения колебаний. Например, если груз пруженного маятника отклоняют от положения равновесия и на расстояние $x_0$ и отпускают без толчка, тогда уравнением движения маятника является уравнение:
[x=A{cos left({omega }_0t+varphi right) }(7)]
с начальными условиями:
[xleft(0right)=x_0;; dot{x}left(0right)=0 left(8right).]
При таком возбуждении колебания пружинного маятника можно описывать выражением:
[x=x_0{cos left({omega }_0tright)left(9right). }]
Сложение колебаний и начальная фаза
Тело, совершающее колебания, способно принимать участие в нескольких колебательных процессах одновременно. В таком случае возникает необходимость выяснить, каким будет результирующее колебание.
Допустим, что два колебания с равными частотами происходят по одной прямой. Уравнением результирующих колебаний будет выражение:
[xi ={xi }_1+{xi }_2=A{cos left({omega }_0t+varphi right), }]
тогда амплитуда суммарного колебания равна:
[A=sqrt{A^2_1+A^2_2+2A_1A_2{cos left({varphi }_2-{varphi }_1right) }left(10right),}]
где $A_1$; $A_2$ – амплитуды складывающихся колебаний; ${varphi }_2;;{varphi }_1$ – начальные фазы суммирующихся колебаний. При этом начальную фазу полученного колебания ($varphi $) вычисляют, применяя формулу:
[tg varphi =frac{A_1{sin {varphi }_1+A_2{sin {varphi }_2 } }}{A_1{cos {varphi }_1+A_2{cos {varphi }_2 } }}left(11right).]
Уравнение траектории точки, которая принимает участие в двух взаимно перпендикулярных колебаниях с амплитудами $A_1$и $A_2$ и начальными фазами ${varphi }_2и{varphi }_1$:
[frac{x^2}{A^2_1}+frac{y^2}{A^2_2}-frac{2xy}{A_1A_2}{cos left({varphi }_2-{varphi }_1right) }={sin}^2left({varphi }_2-{varphi }_1right)left(12right).]
В случае равенства начальных фаз составляющих колебаний уравнение траектории имеет вид:
[y=frac{A_2}{A_1}x или y=-frac{A_2}{A_1}x left(13right),]
что говорит о движении точки по прямой линии.
Если разность начальных фаз складываемых колебаний составляет $Delta varphi ={varphi }_2-{varphi }_1=frac{pi }{2},$ уравнением траектории становится формула:
[frac{x^2}{A^2_1}+frac{y^2}{A^2_2}=1left(14right),]
что означает, траектория движения эллипс.
Примеры задач с решением
Пример 1
Задание. Колебания пружинного осциллятора возбуждены толчком из положения равновесия, при этом грузу сообщают мгновенную скорость, равную $v_0$. Запишите начальные условия для такого колебания и функцию $x(t)$, описывающую данные колебания.
Решение. Сообщение грузу пружинного маятника мгновенной скорости равной $v_0$ означает, что при описании его колебаний с помощью уравнения:
[x=A{cos left({omega }_0t+varphi right) }(1.1)]
начальными условиями будут:
[xleft(0right)=0;; dot{x}left(0right)=v_0left(1.2right).]
Подставим в выражение (1.1) $t=0$, имеем:
[x=A{cos left(varphi right) }=0 left(1.3right).]
Так как $Ane 0$, то ${cos left(varphi right) }=0to varphi =pm frac{pi }{2}.$
Возьмем первую производную $frac{dx}{dt}$ подставим момент времени $t=0$:
[dot{x}left(0right)=-A{omega }_{0 }{sin left(varphi right) }=v_0to A=frac{v_0}{{omega }_{0 }} left(1.4right).]
Из (1.4) следует, что начальная фаза получается $varphi =-frac{pi }{2}.$ Подставим, полученную начальную фазу и амплитуду в уравнение (1.1):
[x=frac{v_0}{{omega }_{0 }}{cos left({omega }_0t-frac{pi }{2}right) }=frac{v_0}{{omega }_{0 }}{sin ( }{omega }_0t).]
Ответ. $x(t)=frac{v_0}{{omega }_{0 }}{sin ( }{omega }_0t)$
Пример 2
Задание. Два колебания одного направления складываются. Уравнения этих колебаний имеют вид: $x_1={cos pi (t+frac{1}{6}) };; x_2=2{cos pi (t+frac{1}{2}) }$. Какова начальная фаза полученного колебания?
Решение. Запишем уравнение гармонических колебаний по оси X:
[x=A{cos left({omega }_0t+varphi right) }left(2.1right).]
Преобразуем заданные в условии задачи уравнения к этому же виду:
[x_1={rm cos}left[pi t+frac{pi }{6}right];; x_2=2{cos left[pi t+frac{pi }{2}right](2.2). }]
Сравнивая уравнения (2.2) с (2.1) получим, что начальные фазы колебаний равны:
[{varphi }_1=frac{pi }{6};; {varphi }_2=frac{pi }{2}.]
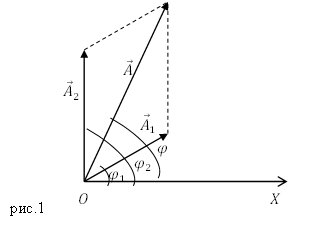
Изобразим на рис.1 векторную диаграмму колебаний.
$tg varphi $ суммарных колебаний можно найти из рис.1:
[tg varphi =frac{A_1{sin {varphi }_1+A_2{sin {varphi }_2 } }}{A_1{cos {varphi }_1+A_2{cos {varphi }_2 } }}=frac{{sin left(frac{pi }{6}right)+2{sin (frac{pi }{2}) } }}{{cos left(frac{pi }{6}right)+2{cos (frac{pi }{2}) } }}=2,87.]
[varphi =arctg left(2,87right)approx 70,9{}^circ ]
Ответ. $varphi =70,9{}^circ $
Читать дальше: начальная фаза.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Фаза колебаний
4.6
Средняя оценка: 4.6
Всего получено оценок: 233.
4.6
Средняя оценка: 4.6
Всего получено оценок: 233.
Любой колебательный процесс, который изучается физикой, имеет ряд параметров, одним из которых является фаза. Кратко рассмотрим, что это такое, каков физический смысл фазы, в чем измеряется фаза, приведем формулу фазы колебаний.
Параметры гармонического колебания
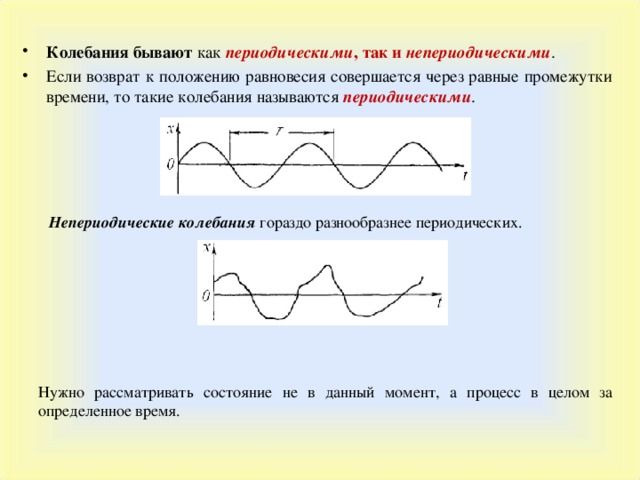
Любой колебательный процесс — это изменения некоторого параметра около среднего значения. Колебания бывают периодическими (маятник) и непериодическими (флаг на ветру). Если построить график колебательного процесса, то среднее значение на нём будет представлено горизонтальной прямой, а значение колеблющегося параметра — кривой, постоянно возвращающейся к среднему. При этом для непериодического колебания возвраты будут хаотичными, а для периодического — строго через одинаковый промежуток времени. Этот промежуток называется периодом колебания $T$.
Простейшим периодическим колебанием является колебание, которое совершается по закону круговых функций (синуса или косинуса). Оно называется гармоническим. Поскольку в высшей математике доказывается, что любое колебание (в том числе непериодическое) можно представить в виду бесконечной суммы гармонических колебаний, то в первую очередь изучаются именно они. А по определению любое гармоническое колебание можно представить в виде функции:
$$A=A_0sin Bigg ( {2piover T} t +varphi_0 Bigg ),$$
где:
- $A_0$ — амплитуда колебания, максимальное отклонение мгновенного значения функции от нуля;
- $T$ — период колебаний;
- $t$ — свободная переменная — момент времени, для которого находится мгновенное значение амплитуды;
- $varphi_0$ — начальная фаза колебаний.
Коэффициент ${2piover T}=omega$ при свободной переменной $t$ называется угловой частотой. Его физический смысл состоит в том, что это угол, проходимый гармонической функцией за единицу времени. Значение выражения ${2piover T} t +varphi_0=varphi$, которое является аргументом функции синуса, называется полной фазой колебания.
Фаза гармонического колебания
Из формулы гармонического колебания можно понять физический смысл фазы. Поскольку аргументом функции $sin(x)$ является угол поворота единичного вектора на координатной плоскости, выраженный в радианах, и его период равен $2pi$, то фаза — это часть периода колебания, соответствующая моменту $t$. Она еще выражается в радианах и тоже имеет период $2pi$.
Из формулы также можно видеть, что если $t=0$, то $varphi=varphi_0$ (полная фаза в начальный момент равна начальной фазе).
Разность фаз
Для одного колебательного процесса фаза не играет большой роли. В самом деле, если брать разные моменты времени за начальные, мы можем получать любое значение фазы, колебательный процесс при этом никак не изменится. Однако, когда речь идет о нескольких колебательных процессах, то значение фазы существенно возрастает. Именно фазой определяется разница мгновенных значений двух колебаний.
Если частоты колебаний неодинаковы, то каждый момент времени фазы будут различны, их разность также будет изменяться. Если же частоты колебаний одинаковы, то несмотря на изменение со временем фазы каждого колебания, разность фаз этих двух колебаний будет постоянной. Это может приводить к интересным ситуациям.
Например, если мы возьмем два колебания с одинаковыми амплитудами и частотами, но у первого начальная фаза будет равна нулю, а у второго — $pi$, то эти два колебания никогда не будут иметь одинаковых ненулевых значений. Более того, если эти колебания сложить, то их сумма всегда будет равна нулю. Говорят, что такие процессы происходят в противофазе.
Что мы узнали?
Фаза колебания — это часть периода колебания, соответствующая текущему моменту времени. Единица измерения фазы — радиана, она имеет период $2pi$. Особо важное значение имеет разность фаз двух и более колебаний. Если частота этих колебаний одинакова, то и разность фаз будет всегда постоянной.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 233.
А какая ваша оценка?
Фаза колебаний
- Подробности
- Обновлено 21.07.2018 11:46
- Просмотров: 994
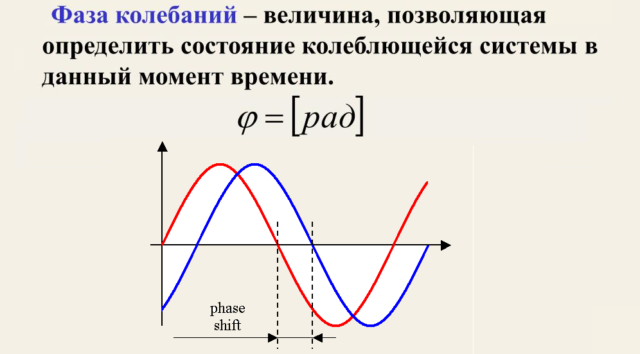
Фаза колебаний (φ) характеризует гармонические колебания.
Выражается фаза в угловых единицах — радианах.
При заданной амплитуде колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса: φ = ω0t.
Фаза колебаний определяет при заданной амплитуде состояние колебательной системы (значение координаты, скорости и ускоренияв) любой момент времени.
Колебания с одинаковыми амплитудами и частотами могут различаться фазами.
Отношение 
указывает, сколько периодов прошло от момента начала колебаний.
График зависимости координаты колеблющейся точки от фазы.
Гармонические колебания можно представить как с помощью функции синуса, так и косинуса, т.к.
синус отличается от косинуса сдвигом аргумента на 
.
Поэтому вместо формулы
х = хm cos ω0t
можно для описания гармонических колебаний использовать формулу
Но при этом начальная фаза, т. е. значение фазы в момент времени t = 0, равна не нулю, а .
В разных ситуациях удобно использовать синус или косинус.
Какой формулой пользоваться при расчетах?
1. Если в начале колебаний выводят маятник из положения равновесия, то удобнее пользоваться формулой с применением косинуса.
2. Если координата тела в начальный момент была бы равна нулю, то удобнее пользоваться формулой с применением синуса х = хm sin ω0t, т.к. при этом начальная фаза равна нулю.
3. Если в начальный момент времени (при t — 0) фаза колебаний равна φ, то уравнение колебаний можно записать в виде х = хm sin (ω0t + φ).
Сдвиг фаз
Колебания, описываемые формулами через синус и косинус, отличаются друг от друга только фазами.
Разность фаз (или сдвиг фаз) этих колебаний составляет .
Графики зависимости координат от времени для двух гармонических колебаний, сдвинутых по фазе на :
где
график 1 – колебания, совершающиеся по синусоидальному закону,
график 2 — колебания, совершающиеся по закону косинуса.
Для определения разности фаз двух колебаний надо колеблющиеся величины выразить через одну и ту же тригонометрическую функцию — косинус или синус.
Источник: «Физика – 11 класс», учебник Мякишев, Буховцев, Чаругин
Механические колебания. Физика, учебник для 11 класса – Класс!ная физика
Свободные, затухающие и вынужденные колебания —
Условия возникновения свободных колебаний. Математический маятник —
Динамика колебательного движения. Уравнение движения маятника —
Гармонические колебания —
Фаза колебаний —
Превращение энергии при гармонических колебаниях —
Вынужденные колебания. Резонанс —
Примеры решения задач —
Краткие итоги главы
