Фазовый сдвиг – что это? А фаза звукового сигнала? Попробуем немного разобраться в этом вопросе. Не факт, что смогу ясно разъяснить этот вопрос, но примерное понятие должно получиться.
Пролог
Музыканты, меломаны, а так же, любители “хай-эндовского” звука, в разговорах между собой, часто используют, вроде бы всем понятные термины – спектр, фаза, частота, меандр, глубина и локализация сцены, и прочие узкозначимые слова. Но зачастую, даже некоторые из “знатоков”, до конца не могут понять, что же это на самом деле такое.
Такие понятия как – “Фазовый сдвиг” очень часто упоминаются при проектировании кроссоверов для акустики. Подробно про кроссоверы мы уже поговорили чуть ранее.
При наличии интернета выяснить тот или иной вопрос не составляет проблем. В отсутствии такового – можно сходить в библиотеку, найти пару реально научных книжек и почитать саму теорию. Но все нынче стали на столько занятые, что даже выуживать информацию из интернета – времени нет. Попробуем найти простое объяснение – что же такое “фазовый сдвиг”?
Что означают эти термины на самом деле? Можно ли “пощупать” их истинное значение? Да, однозначно, можно. Сейчас мы попробуем разобраться в вопросе – “Что такое – фазовый сдвиг?”
Фаза сигнала
Для начала порассуждаем, что такое – “фаза сигнала”. Фаза сигнала никогда не существует сама по себе. Это виртуальное понятие. Вообще, можно сказать так: Фаза – это уровень сигнала в текущий момент времени, или иначе, – это уровень звукового давления в текущий момент времени в измеряемой точке пространства (к примеру, это место, где находится слушатель).
Вот картинка, изображающая звуковые волны в фазе. К примеру, звуковые сигналы двух каналов нашей акустики совпадают. В этом случае, музыка звучит чётко, без каких либо искажений. В музыкальном произведении можно услышать все задействованные инструменты, которые звукорежиссер слышал при записи. Имеется некая область звукового давления, где ощущается “эффект присутствия” – это то, о чем спорят меломаны и аудиофилы. Иными словами – получаем ожидаемый звук и впечатления.
На следующей картинке ниже, фаза смещена на 90 градусов, или на четверть фазы. Этот эффект можно услышать в виде небольшого эха. Это может и не связано с оборудованием самой комнаты. Эффект звуковой задержки с небольшим смещением фазы вносит некую сумятицу в музыку, теряется “картинка”, исполнители “уходят в разные стороны”, появляется ощущение, что находишься в огромном зале с каменными стенами. Звуки становятся не естественными, искаженными.
Далее, мы наблюдаем смещение фаз на 180 градусов. То есть, акустика в этом случае играет в противофазе. Чуть ниже подробно об этом. В данном случае, общая “звуковая картина” на столько становится не понятной, что слушать музыку становится просто не интересно и противно. Звуки становятся “ватные”, многие часты просто могут отсутствовать, хотя они и воспроизводятся колонками. Может сложиться такое впечатление, что слушаешь музыку в завязанной шапке-ушанке.
Далее, немного теории без научных выкладок.
К примеру, слушая, сидя у себя дома, свои акустические системы, мы слышим, как они порождают в районе дивана те или иные переменные звуковые давления. Звуковые волны складываются друг с другом. Эти волны имеют разные частоты и амплитуду. Они то нарастают, то убывают.
Противофаза
А теперь предположим, что давления от обоих колонок (звуковые волны) изменяются одинаково, но имеют противоположную направленность. То есть, одна колонка излучает “плюсовые” волны, а другая колонка – “минусовые”. Это может случиться, когда слушатель, случайно, перепутал клеммы подключения одного из каналов (левый канал например).
Немного проще. Динамики правой колонки играют вперёд, а динамики в левой колонке играют назад, одновременно пытаясь воспроизводить одну и туже частоту. Одна колонка создаёт давление, скажем, 1 Паскаль, а другая – минус 1 Паскаль. Такой эффект называется – противофаза.
Общая громкость звука в том месте, где находится слушатель, теоретически, должна стремится к нулю, но это не означает, что какой либо звук вообще будет не слышно. В этом случае, может сильно поломаться “звуковая сцена”, “картинка” музыкального произведения, а в каком либо месте помещения звук реально будет затухать, но не совсем. Звук станет “смазанным” и исчезнут некоторые частотные составляющие из общего звукового сигнала.
Не будем вдаваться в непростую научную формулировку, приводя формулы. Можно сказать так, что из второй колонки звук доходит к слушателю, но с задержкой по времени (не забываем, что сигнал на колонки подаётся одинаковый!). И задержка в этом случае получается именно 180 градусов. Почему так? Попробуем разобраться на картинке, нагляднее – понятнее.
360 градусов – длина периода сигнала (Фаза), 180 градусов – половина периода сигнала.
Фазовый сдвиг
А теперь, мы дошли до момента, когда можно уже разобрать вопрос – “Что такое – фазовый сдвиг?”
Фаза — это временная связь двух сигналов. И в течении периода колебания меняется от 0 до 360 градусов. Потом опять – от 0 до 360, и так далее. Можно сказать, что это мгновенный уровень сигнала в определенной точке времени внутри периода. Саму фазу мы не слышим, но слышим фазовый сдвиг одного сигнала относительно другого.
Вики про это говорит так: Сдвиг фаз — это разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.
Фазовый сдвиг является безмерной величиной и измеряется в градусах или долях периода.
Вывод
Предположим, вы подключили два динамика к выходу усилителя (пусть физически это будут ваши акустические системы). Один динамик как положено – плюс на плюс, минус на минус. А второй, перепутали и он получился подключенным плюс на минус и минус на плюс. Включив усилитель, что мы услышим? Вероятнее всего – жалкое подобие звука. Один динамик будет как-бы гасить сигнал другого своими звуковыми волнами.
На картинках ниже будет нагляднее. Представим, что это мы видим на экране осциллографа, который измеряет сигналы левого и правого каналов вашего усилителя.
Вторая картинка демонстрирует осциллограмму полного не совпадения. “Горб” левого канала по времени совпадает с “ямой” правого. Чисто по школьной физике – в результате сложения таких колебаний, в идеале, получится ноль. Эти сигналы будут взаимно подавлять друг друга. Сигналы в противофазе.
Фазовый сдвиг подразумевает запаздывание первого сигнала по времени относительно второго.
При двух гармонических колебаниях одной частоты результатом сдвига фаз будет частичное ослабление сигнала. Степень ослабления результирующего сигнала будет зависеть как раз от этого самого сдвига фаз. В предельном случае (в противофазе), на выходе получится абсолютный ноль.
Все эти картинки и рассуждения, о физических свойствах звуковых волн, отдаленно относятся к практике, к реальности. Звуки любого музыкального инструмента нельзя назвать – “одночастотным сигналом” (как осциллограмма на картинках). Частичный сдвиг фаз может ослаблять одни частоты по сравнению с другими. А иногда, усиливать некоторые из них.
Форум РадиоКот • Просмотр темы – Фаза сигнала
Сообщения без ответов | Активные темы
| ПРЯМО СЕЙЧАС: |
| Автор | Сообщение |
|---|---|
|
|
Заголовок сообщения: Фаза сигнала
|
|
Вымогатель припоя
Зарегистрирован: Сб фев 19, 2011 18:04:08 Рейтинг сообщения: 0
|
Здравствуйте уважаемые форумчане. Пытаюсь сделать фазовый пеленгатор. Но пока застрял на теории. |
| Вернуться наверх |
Профиль
|
| Реклама | |
|
|
|
|
rustot |
Заголовок сообщения: Re: Фаза сигнала
|
|
Поставщик валерьянки для Кота
Карма: 5 Рейтинг сообщения: 0
|
да там чистая тригонометрия. по простому sin(w*t)*sin(w*t+fi) = cos(fi)/2 – cos(2*w*t+fi)/2, теперь если интегрировать за период, то второй член обращается в ноль, и остается только первый, косинус фазы в чистом виде. поскольку из косинуса вблизи нуля фаза определяется с большими погрешностями, то тем же способом на втором сумматоре можно получить sin(fi) |
| Вернуться наверх | |
| Реклама | |
|
|
|
|
phanis |
Заголовок сообщения: Re: Фаза сигнала
|
|
Зарегистрирован: Сб фев 19, 2011 18:04:08 Рейтинг сообщения: 0
|
rustot писал(а): да там чистая тригонометрия. по простому sin(w*t)*sin(w*t+fi) = cos(fi)/2 – cos(2*w*t+fi)/2, теперь если интегрировать за период, то второй член обращается в ноль, и остается только первый, косинус фазы в чистом виде. поскольку из косинуса вблизи нуля фаза определяется с большими погрешностями, то тем же способом на втором сумматоре можно получить sin(fi) Спасибо за быстрый ответ, только я совсем не понял, как это будет работать. Наверное не правильно задал вопрос .. Цитата: Нужно взять 180 значений синуса и косинуса для углов от 0 до 358 с шагом 2. На самом деле там реально разных значений всего 45, остальное повторы и повторы со знаком минус. И посчитать сумму произведений входного сигнала с АЦП в 180 точках круга на соответствующие синусы и косинусы. Получим 2 числа: A = sum(U_k*cos(Alfa_k)), Alfa_k = 2*k град., k=0..179 Эти числа – ни что иное, как действительная и мнимая части первого коэффициента преобразования Фурье входного сигнала – соответствующего основной гармонике, т.е. частоте “вращения” антенного переключателя. По ним легко определить азимут – это просто фаза этой гармоники, то есть arg(A+i*B), считается обычно через арктангенс (его тоже задают таблицей на отрезке от -1 до 1): если А>B и A>-B, то Phi = arctg(B/A); Попроще никак?? |
| Вернуться наверх | |
|
rustot |
Заголовок сообщения: Re: Фаза сигнала
|
|
Поставщик валерьянки для Кота
Карма: 5 Рейтинг сообщения: 0
|
сдвиг фаз же относительно чего-то, допустим относительно сигнала который вы отправляете. вот этот сигнал обозначим через sin(w*t). одновременно сгенерим сдвинутый по фазе cos(w*t). обратно приняли сигнал sin(w*t+fi). подаем sin(w*t+fi) и sin(w*t) на умножитель, суммируем полученное произведение в течение периода, получаем N*cos(fi)/2 подаем sin(w*t+fi) и cos(w*t) на умножитель, суммируем полученное произведение в течение периода, получаем N*sin(fi)/2 делим второе на первое и получаем tg(fi), тангенс того сдвига фаз что мы искали. если охота в градусах, то берете арктангенс и умножаете на 180/pi но тангенс обычно более полезен. допустим тобы нарисовать на бумажке tg(fi)=0.9 не нужно транспортиров, 10 клеток вправо, 9 клетов вверх – получится линия под искомым углом |
| Вернуться наверх | |
| Реклама | |

|
Выбираем источники питания MEAN WELL в открытом исполнении для промышленных устройств В номенклатуре продукции MEAN WELL в Компэл можно легко найти требуемую модель стандартного источника питания практически для всех отраслей применения. Рассмотрим преимущества, эксплуатационные характеристики, схемотехнику и конструктивные решения трех наиболее характерных представителей класса источников питания в открытом исполнении семейств EPS, EPP и RPS, которые могут использоваться для индустриальных устройств. Подробнее>> |
|
phanis |
Заголовок сообщения: Re: Фаза сигнала
|
|
Зарегистрирован: Сб фев 19, 2011 18:04:08 Рейтинг сообщения: 0
|
rustot писал(а): но тангенс обычно более полезен. допустим тобы нарисовать на бумажке tg(fi)=0.9 не нужно транспортиров, 10 клеток вправо, 9 клетов вверх – получится линия под искомым углом Да вот теперь не много проясняется. Понимаю, хочется сказать нафига этим занялся, если даже основных тригонометрических понятий нет. |
| Вернуться наверх | |
| Реклама | |
|
|
|
| Реклама | |

|
RSDH-150/300 – новые DC/DC-преобразователи со сверхшироким входом от MEAN WELL
Компания MEAN WELL разработала две серии монтируемых на шасси DC/DC-преобразователей со сверхшироким входным диапазоном 250…1500 В (6:1) мощностью 150 и 300 Вт (RSDH-150; RSDH-300). Изделия могут эксплуатироваться при температурах -40…80°С. Подробнее>> |
|
rustot |
Заголовок сообщения: Re: Фаза сигнала
|
|
Поставщик валерьянки для Кота
Карма: 5 Рейтинг сообщения: 0
|
ну в обратную сторону. cos вправо, -cos влево, sin вверх, -sin вниз |
| Вернуться наверх | |
|
phanis |
Заголовок сообщения: Re: Фаза сигнала
|
|
Зарегистрирован: Сб фев 19, 2011 18:04:08 Рейтинг сообщения: 0
|
Спасибо разобрался,и сделал именно так ..Все заработало правильно. Кстати там есть еще вариант, когда делитель равен нулю..А на ноль, лучше не делить. Это я тоже учел.. Как можно округлять углы например если скачет в районе 350 – 10 градусов среднее должно быть примерно 0 градусов?? простая арифметика не подходит, например (350 + 10 )/2=180 совсем в другую сторону. Грубый пример но тем не менее. |
| Вернуться наверх | |
|
Shr1mpy |
Заголовок сообщения: Re: Фаза сигнала
|
|
Зарегистрирован: Вт июн 14, 2011 16:50:56 Рейтинг сообщения: 0
|
phanis писал(а): Как можно округлять углы например если скачет в районе 350 – 10 градусов среднее должно быть примерно 0 градусов?? простая арифметика не подходит, например (350 + 10 )/2=180 совсем в другую сторону. Грубый пример но тем не менее. Для простой арифметики тебе для начала надо было бы представить 350 как “-(минус) 10” |
| Вернуться наверх | |
|
phanis |
Заголовок сообщения: Re: Фаза сигнала
|
|
Зарегистрирован: Сб фев 19, 2011 18:04:08 Рейтинг сообщения: 0
|
Все разобрался, спасибо всем кто помогал.. Усреднение сделал не по градусам, а средне арифметически получаемых Сумм синусов и сумм косинусов , Sum(sin(U[0..N]* t))/ Количество сложений Sum(cos(Y[0..N] *t))/ Количество сложений Код: function TForm1.GET_PHASE( freq : real; input_buffer : array of smallint; input_buffer_size : integer): integer; begin SUMM_COS :=0; Temp_real :=(360/(const_freq/(freq+trackbar1.Position))); for i:=0 to input_buffer_size div 4 -1 do SUMM_COS := SUMM_COS+( input_buffer[i*2] * cos( Gradus(i*Temp_real)) ) ; end; SUMM_SIN:=SUMM_SIN/(input_buffer_size/2); GLOBAL_SUMM_COS[GLOBAL_COUNT] := SUMM_COS; SUMM_COS :=0; SUMM_COS := SUMM_COS+GLOBAL_SUMM_COS[i]; end; SUMM_SIN:=SUMM_SIN/100; if ((SUMM_SIN=0) and (SUMM_COS=0)) then TEMP_UGOL := 0 else if (SUMM_SIN=0) then if (SUMM_COS=0) then end; end; RESULT := ROUND(TEMP_UGOL); end; function TForm1.Gradus(c:real):real; result:=c*pi/180-pi/2; |
| Вернуться наверх | |
|
rustot |
Заголовок сообщения: Re: Фаза сигнала
|
|
Поставщик валерьянки для Кота
Карма: 5 Рейтинг сообщения: 0
|
вы значительно повысите точность, если урежете обрабатываемый буфер до точно кратного половине периода, отбросив лишний хвост. допустим если вы просуммируете данные за _ровно_ 1 период то получится более точное значение, чем если просуммируете за 100 с четвертью периодов после умножителя у вас синусоида удвоенной частоты с постоянной составляющей, чтобы полностью изничтожить эту синусоиду и оставить только нужную постоянную составляющую нужно усреднять сигнал ровно за период этой синусоиды |
| Вернуться наверх | |
|
phanis |
Заголовок сообщения: Re: Фаза сигнала
|
|
Зарегистрирован: Сб фев 19, 2011 18:04:08 Рейтинг сообщения: 0
|
Вроде так и сделал. Частота дискретизации 44100 Гц размер буфера 256 (значений), значит частота должна быть кратная 44100/256=172,265625 Гц Далее получаю сумму синусов и сумму косинусов всего буфера , делим (сумму синусов и сумму косинусов) на количество периодов синусоид(в одном буфере здесь 10) и получаем среднеарифметическое средн(sin) средне(cos). Среднеарифметические (sin) и (cos) с каждого буфера складываю необходимое количество раз к примеру 100(буферов) и делю на 100 получается среднеарифметическое значение уже на 1000 периодов нахожу угол через arctg(средее за 1000 периодов синуса / средее за 1000 периодов косинуса) (+/- sin +/-cos)для определения четверти окружности и все. Теперь даже если скачет в районе 350 10 градусов показывает 0 градусов. |
| Вернуться наверх | |
|
B@R5uk |
Заголовок сообщения: Re: Фаза сигнала
|
||
Карма: 28 Рейтинг сообщения: 0
|
Если заранее известно, что сигналом является чистый синус и обработка ведётся на компе, то нет необходимости подстраивать длину буфера под частоту сигнала и наоборот. Достаточно сигнал обработать методом наименьших квадратом взяв в качестве базовых функций синус и косинус частоты, которую, правда, перед этим необходимо определить. Но в любом случае это гораздо удобнее, чем подгонять количество семплов под частоту. Ещё более продвинутый метод обработки может выдать относительную девиацию частоты (ну или фазы, не принципиально при малых значениях) на промежутке, а так же амплитуды, когда сигнал записан на достаточно большом промежутке времени (в сравнении с периодом дискретизации). Правда тут двумя базовыми функциями не обойдёшься. За то точность определения частоты и фазы (за счёт большой статистики) будет просто заоблачной, единственная погрешность, в ней содержащаяся будет только систематическая — погрешность частоты кварца звуковой карты. Я кстати такого рода частотометр хотел замутить для компа (чтобы непрерывно мерял частоту и дисплеил девиацию в реальном времени), просчитал всю математику и метод расчёта, даже немного DirectSound освоил, но так до конца и ниасилил :,-(( |
||
| Вернуться наверх | |||
Кто сейчас на форуме |
|
Сейчас этот форум просматривают: HochReiter и гости: 13 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |

Фаза сигнала переменного тока
Добавлено 13 октября 2019 в 00:23
Всё начинает усложняться, когда нам нужно связать два или более напряжения или тока переменного тока, которые «не идут в ногу» друг с другом. Под «не идут в ногу» я подразумеваю, что два сигнала не синхронизированы: их пики и нулевые точки не попадают в одни и те же моменты времени. График на рисунке ниже иллюстрирует пример этого.
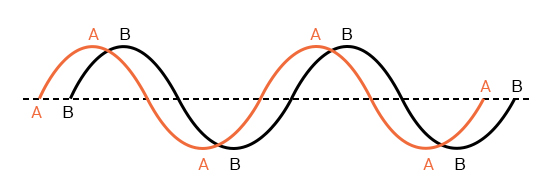
Две волны, показанные выше (А и В), имеют одинаковую амплитуду и частоту, но «не идут в ногу» друг с другом. Техническими терминами это называется сдвигом фазы. Ранее мы видели, как можно построить «синусоидальную волну», рассчитав тригонометрическую функцию синуса для углов в диапазоне от 0 до 360 градусов, полный круг. Начальная точка синусоидальной волны была нулевой амплитуды при нулевых градусах, продвигающейся до полной положительной амплитуды при 90 градусах, до нулевой амплитуды при 180 градусах, до полной отрицательной амплитуды при 270 градусах и обратно в начальную точку с нулем при 360 градусах. Мы можем использовать эту шкалу углов на горизонтальной оси графика, чтобы определить, насколько сигналы различаются по фазе. Рисунок ниже.
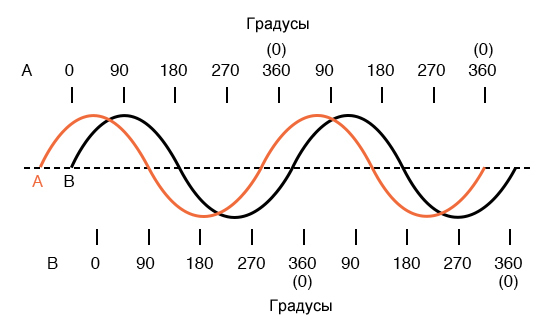
Сдвиг фазы между этими двумя сигналами составляет около 45 градусов, волна “А” опережает волну “В”. Чтобы лучше проиллюстрировать эту концепцию, на следующих графиках приведен ряд примеров сдвигов фаз.
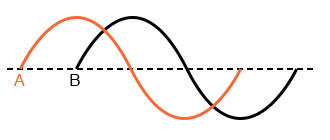
“A” опережает “B”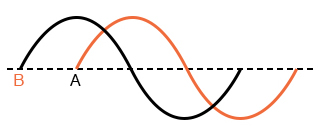
“B” опережает “A”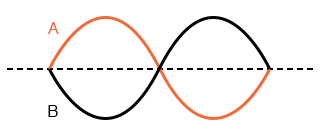
“A” и “B” представляют собой зеркальные отражения друг друга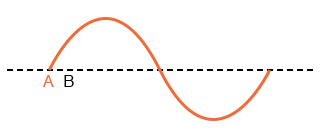
“A” и “B” идеально синхронизированы друг с другом
Поскольку сигналы в приведенных выше примерах имеют одинаковую частоту, они будут расходиться по фазе на одну и ту же величину в любой момент времени. По этой причине мы можем выразить сдвиг фазы для двух или более сигналов одной и той же частоты как постоянную величину для всей волны, а не просто как значение сдвига между двумя любыми конкретными точками на формах сигналов. То есть можно с уверенностью сказать что-то вроде: «напряжение “A” отличается по фазе от напряжения “B” на 45 градусов». Про ту волну, которая находится впереди, можно сказать что она «опережает», а про ту волну, которая находится позади, можно сказать что она «отстает».
Сдвиг фазы, как и напряжение, всегда является относительным измерением, то есть между двумя сигналами. На самом деле не существует такого понятия, как сигнал с абсолютным значением фазы, потому что не известен универсальный эталон для фазы. Обычно при анализе цепей переменного тока в качестве эталона фазы используется сигнал напряжения источника питания, причем это напряжение указывается как «ххх вольт при 0 градусах». Любое другое напряжение или ток переменного тока в этой цепи будет иметь свой сдвиг фазы, выраженный относительно этого источника напряжения.
Это то, что делает вычисления цепей переменного тока более сложными, чем цепей постоянного тока. При применении закона Ома и законов Кирхгофа величины переменного напряжения и тока должны отражать как амплитуду, так и сдвиг фазы. Математические операции сложения, вычитания, умножения и деления должны оперировать этими величинами амплитуды, а также сдвига фазы. К счастью, существует математическая система счисления, называемая комплексными числами, идеально подходящая для этой задачи представления амплитуды и фазы.
Поскольку тема комплексных чисел настолько важна для понимания цепей переменного тока, следующая глава будет посвящена только этой теме.
Резюме
- Сдвиг фазы – это когда два или более сигналов не синхронизированы друг с другом.
- Величина сдвига фазы между двумя волнами может быть выражена в градусах, и это значение в градусах может быть определено по горизонтальной оси графика формы волны, используемого при построении тригонометрической функции синуса.
- Опережающий сигнал определяется как один сигнал, опережающий другой по нарастанию. Отстающий сигнал – тот, который позади другого. Пример:

Рисунок 7 – Сдвиг фазы = 90°.
“A” опережает “B”, “B” отстает от “A” - Расчеты для анализа цепей переменного тока, чтобы быть полностью точными, должны учитывать как амплитуду, так и сдвиг фазы сигналов напряжения и тока. Это требует использования математической системы, называемой комплексными числами.
Теги
Для начинающихСдвиг фазы
Исследование фазы сигнала
-

Бахурин Сергей
- Администратор
- Сообщения: 1108
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: Исследование фазы сигнала
Сообщение
Бахурин Сергей » 26 апр 2011, 12:29
у вас есть сигнал
Вы хотите выделить из него фазу я правильно понял?
Если да то делаете так:
далее фнч устраняет удвоенную частоту и ваша фаза находится как арктангенс
никакого бпф и прочего всего не требуется. Единственное что потребуется это unwrap функция для раскрытия периодичности арктангенса, и то если девиация фазы больше pi радиан.
-
Dmitri Seva
- Сообщения: 30
- Зарегистрирован: 07 дек 2010, 09:29
Re: Исследование фазы сигнала
Сообщение
Dmitri Seva » 26 апр 2011, 12:52
Да именно требуется определить изменение фазы во времени. Как я понял это геометрическое определение фазы через прямоугольный треугольник ![]() Надо будет попробовать, хотя я сомневаюсь что данная методика применима если в сигнале присутствуют шумы и другие гармоники.
Надо будет попробовать, хотя я сомневаюсь что данная методика применима если в сигнале присутствуют шумы и другие гармоники.
-

Бахурин Сергей
- Администратор
- Сообщения: 1108
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: Исследование фазы сигнала
Сообщение
Бахурин Сергей » 26 апр 2011, 13:01
понимаете в чем дело. Как только ваша перестала быть постоянной величиной, ваш сигнал
это уже сигнал с фазовой модуляцией, состоящий не из одной гармоники а занимающий определенную полосу. То что я вам написал это ничто иное, как фазовый детектор позволяющий выделить из вашего фазомодулированного сигнала . ФНЧ который вы поставите после квадратурного преобразования позволит отфильтровать шумы. Чем уже полоса ФНЧ тем меньше будет влияние шумов.
-
Dmitri Seva
- Сообщения: 30
- Зарегистрирован: 07 дек 2010, 09:29
Re: Исследование фазы сигнала
Сообщение
Dmitri Seva » 26 апр 2011, 13:09
Задаваемый сигнал чисто вещественный а не квадратурный. Т.е. получается вначале ставится узкополосный фильтр а затем уже фазовый детектор? (С фазовыми детекторами пока не общался близко ![]() )
)
-

Бахурин Сергей
- Администратор
- Сообщения: 1108
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
-
Dmitri Seva
- Сообщения: 30
- Зарегистрирован: 07 дек 2010, 09:29
Re: Исследование фазы сигнала
Сообщение
Dmitri Seva » 26 апр 2011, 19:10
Прочитал статью, ФНЧ-фильтр как я понял нужен с линейной фазой, желательно с нулевой. Т.е. подойдет оконный симметричный КИХ-фильтр. Мат. модель в статье приведена для непрерывных сигналов. Точность задаваемой частоты несущей я так понимаю все же зависит от частоты дискретизации (или я мудрю и она просто ограничена Fs/2 ?). Я имею ввиду если частота дискретизации скажем 25 Гц, несущую можно задать 10.367 Гц ?
-

Бахурин Сергей
- Администратор
- Сообщения: 1108
- Зарегистрирован: 05 окт 2010, 19:55
- Контактная информация:
Re: Исследование фазы сигнала
Сообщение
Бахурин Сергей » 26 апр 2011, 20:26
релизуемых фильтров с нулевой фчх не бывает возьмите с линейной фазой ких. Точность оценки частоты не зависит от частоты дискретизации
Dmitri Seva писал(а): Я имею ввиду если частота дискретизации скажем 25 Гц, несущую можно задать 10.367 Гц ?
Можно
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.

Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):

Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):

Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.

Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина (large varphi_{0} ) — в радианах. Значит, нужно связать формулой кусочек времени (large Delta t) и соответствующий ему начальный угол (large varphi_{0} ).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.

Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.

Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.


