Фигу́рные чи́сла — числа, которые можно представить с помощью геометрических фигур. Это историческое понятие восходит к пифагорейцам, которые развивали алгебру на геометрической основе и представляли любое положительное целое число в виде набора точек на плоскости[1]. Отголоском этого подхода остались выражения «возвести число в квадрат» или «в куб»[2].
Традиционно различают два основных класса фигурных чисел[3]:
- плоские многоугольные числа — числа, связанные с определённым многоугольником. Они делятся на классические[⇨] и центрированные[⇨];
- пространственные многогранные числа — числа, связанные с определённым многогранником[⇨].
В свою очередь, каждый класс фигурных чисел делится на разновидности, каждая из которых связана с определённой геометрической фигурой: треугольником, квадратом, тетраэдром и т. д.
Существуют также обобщения фигурных чисел на многомерные пространства[⇨]. В древности, когда арифметика не отделялась от геометрии, рассматривались ещё несколько видов фигурных чисел, в настоящее время не используемых[⇨].
В теории чисел и комбинаторике фигурные числа связаны с многими другими классами целых чисел[⇨] — биномиальными коэффициентами, совершенными числами, числами Мерсенна, Ферма, Фибоначчи, Люка и другими[4].
Классические многоугольные числа[править | править код]
Для краткости в этом разделе классические многоугольные числа называются просто «многоугольными числами».
Геометрическое определение[править | править код]
Геометрическое построение семиугольных чисел
Многоугольные числа — это последовательность, указывающая число точек, построенную согласно правилам, которые проиллюстрируем на примере семиугольника. Ряд семиугольных чисел начинается с 1 (базовая точка), затем следует 7, потому что 7 точек образуют правильный семиугольник, 6 точек добавились. Третье число соответствует семиугольнику, у которого стороны содержат уже не по две, а по три точки, причём все точки, построенные на предыдущих шагах, также учитываются. Из рисунка видно, что третья фигура содержит 18 точек, прибавка (Пифагор называл её «гномон») составила 11 точек. Нетрудно видеть, что прибавки образуют арифметическую прогрессию, в которой каждый член на 5 больше, чем предыдущий[5].
Переходя к общему 

Алгебраическое определение[править | править код]
Общее определение k-угольного числа для любого 
Например, треугольные числа получаются как частичные суммы ряда 

Последовательность k-угольных чисел имеет вид[7]:
Общую формулу для явного подсчёта 

 . .
|
(ОКФ) |
В некоторых источниках последовательность фигурных чисел начинают с нуля (например, в A000217):
В этом случае в общей формуле для 

Существует также рекуррентная формула для вычисления многоугольного числа[8]:
.
При увеличении числа сторон 
Поскольку 

, где
.
Другими словами, каждое многоугольное число есть среднее арифметическое для равноотстоящих от него по 
Если 


.
Доказательство: пусть 



Ряды из обратных многоугольных чисел
сходятся. Их сумма 



Исторический очерк[править | править код]
Фигурные числа, по мнению пифагорейцев, играют важную роль в структуре мироздания. Поэтому их изучением занимались многие видные математики античности: Эратосфен, Гипсикл, Диофант Александрийский, Теон Смирнский и другие. Гипсикл (II век до н. э.) дал общее определение 




Если взять сколько-нибудь чисел, начиная с единицы, имеющих одинаковые разности, то сумма их, если разность единица, будет треугольником, если же двойка, то четырёхугольником, а если тройка — пятиугольником. Количество углов определяется разностью, увеличенной на двойку, а сторона — количеством взятых чисел, считая и единицу.
О фигурных числах много говорится в пифагорейских учебниках арифметики, созданных Никомахом Геразским и Теоном Смирнским (II век), которые установили ряд зависимостей между фигурными числами разных размерностей. Большой интерес к фигурным числам проявили индийские математики и первые математики средневековой Европы (Фибоначчи, Пачоли, Кардано и др.)[14][4].
В Новое время многоугольными числами занимались Ферма, Валлис, Эйлер, Лагранж, Гаусс и другие. В сентябре 1636 года[15] Ферма сформулировал в письме Мерсенну теорему, которая сегодня называется теоремой Ферма о многоугольных числах[14]:
Я первым открыл очень красивую и совершенно общую теорему о том, что каждое число является либо треугольным, либо суммой двух или трёх треугольных чисел; каждое число или квадратное, или является суммой двух, трёх или четырёх квадратов; или пятиугольное, или является суммой двух, трёх, четырёх или пяти пятиугольных чисел, и т. д. до бесконечности, будь то для шестиугольных, семиугольных или любых многоугольных чисел. Я не могу дать здесь доказательство, которое зависит от многочисленных и запутанных тайн чисел, ибо я намерен посвятить этой теме целую книгу и получить в этой части арифметики удивительные достижения по сравнению с ранее известными пределами.
Вопреки обещанию, Ферма так и не опубликовал доказательство этой теоремы, которую в письме Паскалю (1654) назвал своим главным достижением в математике[15]. Проблемой занимались многие выдающиеся математики — в 1770 году Лагранж доказал теорему для квадратных чисел (теорема Лагранжа о сумме четырёх квадратов), в 1796 году Гаусс дал доказательство для треугольных. Полное доказательство теоремы сумел дать Коши в 1813 году[16][17].
Разновидности классических многоугольных чисел[править | править код]
Треугольные числа[править | править код]
Последовательность треугольных чисел:
- 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210 …,
… (последовательность A000217 в OEIS)
Свойства[18]:
Чётность элемента последовательности меняется с периодом 4: нечётное, нечётное, чётное, чётное. Никакое треугольное число не может (в десятичной записи) оканчиваться цифрами 2, 4, 7, 9[19].
Обозначим для краткости 

-
;
.
Формула Баше де Мезириака: общую формулу многоугольного числа можно преобразовать так, что она покажет выражение любого многоугольного числа через треугольные:
 . .
|
(Баше) |
Сумма двух последовательных треугольных чисел образует квадратное число
Сумма двух последовательных треугольных чисел даёт полный квадрат (квадратное число):
-
.
Из теоремы Ферма о многоугольных числах следует, что любое натуральное число представимо в виде суммы не более трёх треугольных чисел.
Сумма конечного ряда треугольных чисел вычисляется по формуле:
-
.
Ряд из чисел, обратных треугольным (телескопический ряд), сходится[20]:
.
Удвоенные треугольные числа дают последовательность (определённых ниже[⇨]) прямоугольных чисел.
Натуральное число 

Известное в мистике «число зверя» (666) является 36-м треугольным. Оно является наименьшим треугольным числом, которое представимо в виде суммы квадратов треугольных чисел[22]: 
Треугольные числа образуют третью диагональную линию треугольника Паскаля[⇨].
Квадратные числа[править | править код]
Квадратные числа представляют собой произведение двух одинаковых натуральных чисел, то есть являются полными квадратами:
- 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400 …,
… (последовательность A000290 в OEIS).
Каждое квадратное число, кроме единицы, есть сумма двух последовательных треугольных чисел[23]:
-
. Примеры:
и т. д.
Сумма квадратного числа с предшествующим ему по номеру треугольным числом даёт пятиугольное число:
.
Эта теорема была впервые опубликована Никомахом («Введение в арифметику», II век)[24].
Сумма квадратов первых 
.
Ряд обратных квадратных чисел сходится[26]:
-
.
Каждое натуральное число может быть представлено как сумма не более четырёх квадратов (теорема Лагранжа о сумме четырёх квадратов).
Тождество Брахмагупты — Фибоначчи: произведение суммы двух квадратных чисел на любую другую сумму двух квадратных чисел само представимо в виде суммы двух квадратных чисел.
Поскольку второе слагаемое справа может быть равно нулю, здесь следует рассматривать расширенный ряд квадратных чисел, начинающийся не с 1, а с нуля (см. A000290).
Пример:
.
Пятиугольные числа[править | править код]
Последовательность пятиугольных чисел имеет вид:
- 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590 …,
… (последовательность A000326 в OEIS).
Пятиугольные числа тесно связаны с треугольными[24]:
.
Как уже упоминалось выше, пятиугольное число, начиная со 2-го номера, можно представить как сумму квадратного и треугольного числа:
.
Если в формуле 

.
то получатся обобщённые пятиугольные числа:
- 0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126, 145, 155… (последовательность A001318 в OEIS).
Леонард Эйлер обнаружил обобщённые пятиугольные числа в следующем тождестве:
.
Степени 
Шестиугольные числа[править | править код]
- 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, 630, 703, 780 …,
… (последовательность A000384 в OEIS).
Последовательность шестиугольных чисел получается из последовательности треугольных чисел вычёркиванием элементов с чётными номерами[28]: 
Натуральное число 

Семиугольные числа[править | править код]
Восьмиугольные числа[править | править код]
Двенадцатиугольные числа[править | править код]
Двенадцатиугольные числа вычисляются по формуле 
- 1, 12, 33, 64, 105, 156, 217, 288, 369, 460, 561, 672, 793, 924, 1065, 1216, 1377, 1548, 1729, 1920 … (последовательность A051624 в OEIS).
В десятичной системе 



Определение, является ли заданное число многоугольным[править | править код]
Задача 1 (задача Диофанта): дано натуральное число 



Решение задачи сводится к решению «диофантова уравнения» (см. общую формулу):
или:
.
Перепишем полученное уравнение в виде: 
Знаменатели дробей справа взаимно просты; сумма или разность таких дробей может быть целым числом только если каждая дробь есть целое число[30], поэтому 



В результате алгоритм решения приобретает следующую форму[29]:
- Выписать все натуральные делители числа
(включая
и само
).
- Выписать все натуральные делители числа
.
- Отобрать из первого набора те числа, которые на
больше какого-либо числа из второго набора. Эти числа соответствуют
.
- Для каждого отобранного
подсчитать
.
- Вычеркнуть пары
, в которых
.
Тогда все соответствующие оставшимся парам числа 

Пример[29]. Пусть 
- Делители
.
- Делители
.
- Отбор
.
- Соответственно
. Последнее значение следует отбросить.
Ответ: 

Задача 2: дано натуральное число 



Для решения можно использовать тождество Диофанта[31]:
Это тождество получается из приведённой выше общей формулы для 







.
Пример[31]. Определим, является ли число 




Производящая функция[править | править код]
Степенной ряд, коэффициенты которого — 

.
Выражение справа является производящей функцией для последовательности 
Аппарат производящих функций позволяет применять в теории чисел и комбинаторике методы математического анализа. Приведённая формула также объясняет появление 
- При
:
;
- При
:
;
- При
:
и т. д.
Для некоторых классов многоугольных чисел существуют свои, специфические производящие функции. Например, для квадратных треугольных чисел 
; ряд сходится при
.
Классические многоугольные числа из более чем одной разновидности[править | править код]
Существует бесконечное количество «многофигурных» (или «мультимногоугольных»)[34] чисел, то есть чисел, которые относятся одновременно к нескольким различным разновидностям фигурных чисел. Например, существуют треугольные числа, которые одновременно являются квадратными («квадратные треугольные числа»)[35]:
(последовательность A001110 в OEIS).
Треугольное число может также быть одновременно
- пятиугольным (последовательность A014979 в OEIS):
- 1, 210, 40755, 7906276, 1533776805, 297544793910, 57722156241751, 11197800766105800, 2172315626468283465…;
- шестиугольным (все треугольные числа с нечётным номером);
- семиугольным (последовательность A046194 в OEIS):
- 1, 21, 11781, 203841, 113123361, 1957283461, 1086210502741, 18793835590881, 10429793134197921, 180458407386358101…
и т. д. Неизвестно, существуют ли числа, одновременно треугольные, квадратные и пятиугольные; проверка на компьютере чисел, меньших 
Квадратное число может быть одновременно
- пятиугольным (последовательность A036353 в OEIS):
- 1, 9801, 94109401, 903638458801, 8676736387298001, 83314021887196947001, 799981229484128697805801…,
- шестиугольным (последовательность A046177 в OEIS):
- 1, 1225, 1413721, 1631432881, 1882672131025, 2172602007770041, 2507180834294496361, 2893284510173841030625…,
- семиугольным (последовательность A036354 в OEIS):
- 1, 81, 5929, 2307361, 168662169, 12328771225, 4797839017609, 350709705290025, 25635978392186449…
и т. д.
Пятиугольное число может одновременно быть:
- шестиугольным (последовательность A046180 в OEIS):
- 1, 40755, 1533776805, 57722156241751, 2172315626468283465, 81752926228785223683195, 3076689623521787481625080301…,
- семиугольным (последовательность A048900 в OEIS):
- 1, 4347, 16701685, 64167869935, 246532939589097, 947179489733441251, 3639063353022941697757…
и т. д.
Шестиугольное число обязательно является также треугольным; оно также может одновременно быть семиугольным (последовательность A48903 в OEIS):
- 1, 121771, 12625478965, 1309034909945503, 135723357520344181225, 14072069153115290487843091…
Возможны и другие сочетания трёх и более разновидностей фигурных чисел. Например, как доказано выше[⇨], число 

Сводная таблица[править | править код]
| k | Разновидность фигурных чисел |
Общая формула | n | Сумма обратных значений[36] | Номер OEIS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||
| 3 | треугольное | 12(n2 + n) | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | 2 | A000217 |
| 4 | квадратное | 12(2n2 − 0n) = n2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |  26 26
|
A000290 |
| 5 | пятиугольное | 12(3n2 − n) | 1 | 5 | 12 | 22 | 35 | 51 | 70 | 92 | 117 | 145 | 
|
A000326 |
| 6 | шестиугольное | 12(4n2 − 2n) | 1 | 6 | 15 | 28 | 45 | 66 | 91 | 120 | 153 | 190 | 2 ln 2 | A000384 |
| 7 | семиугольное | 12(5n2 − 3n) | 1 | 7 | 18 | 34 | 55 | 81 | 112 | 148 | 189 | 235 |  
|
A000566 |
| 8 | восьмиугольное | 12(6n2 − 4n) | 1 | 8 | 21 | 40 | 65 | 96 | 133 | 176 | 225 | 280 | 34 ln 3 +  √312 √312
|
A000567 |
| 9 | девятиугольное | 12(7n2 − 5n) | 1 | 9 | 24 | 46 | 75 | 111 | 154 | 204 | 261 | 325 |   
|
A001106 A244646 |
| 10 | десятиугольное | 12(8n2 − 6n) | 1 | 10 | 27 | 52 | 85 | 126 | 175 | 232 | 297 | 370 | ln 2 +  6 6
|
A001107 |
| 11 | 11-угольное | 12(9n2 − 7n) | 1 | 11 | 30 | 58 | 95 | 141 | 196 | 260 | 333 | 415 | A051682 | |
| 12 | 12-угольное | 12(10n2 − 8n) | 1 | 12 | 33 | 64 | 105 | 156 | 217 | 288 | 369 | 460 | A051624 | |
| 13 | 13-угольное | 12(11n2 − 9n) | 1 | 13 | 36 | 70 | 115 | 171 | 238 | 316 | 405 | 505 | A051865 | |
| 14 | 14-угольное | 12(12n2 − 10n) | 1 | 14 | 39 | 76 | 125 | 186 | 259 | 344 | 441 | 550 | 25 ln 2 + 310 ln 3 +  √310 √310
|
A051866 |
| 15 | 15-угольное | 12(13n2 − 11n) | 1 | 15 | 42 | 82 | 135 | 201 | 280 | 372 | 477 | 595 | A051867 | |
| 16 | 16-угольное | 12(14n2 − 12n) | 1 | 16 | 45 | 88 | 145 | 216 | 301 | 400 | 513 | 640 | A051868 | |
| 17 | 17-угольное | 12(15n2 − 13n) | 1 | 17 | 48 | 94 | 155 | 231 | 322 | 428 | 549 | 685 | A051869 | |
| 18 | 18-угольное | 12(16n2 − 14n) | 1 | 18 | 51 | 100 | 165 | 246 | 343 | 456 | 585 | 730 | 47 ln 2 − √214 ln (3 − 2√2) +  (1 + √2)14 (1 + √2)14
|
A051870 |
| 19 | 19-угольное | 12(17n2 − 15n) | 1 | 19 | 54 | 106 | 175 | 261 | 364 | 484 | 621 | 775 | A051871 | |
| 20 | двадцатиугольное | 12(18n2 − 16n) | 1 | 20 | 57 | 112 | 185 | 276 | 385 | 512 | 657 | 820 | A051872 | |
| 21 | 21-угольное | 12(19n2 − 17n) | 1 | 21 | 60 | 118 | 195 | 291 | 406 | 540 | 693 | 865 | A051873 | |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 1000 | 1000-угольное | 12(998n2 − 996n) | 1 | 1000 | 2997 | 5992 | 9985 | 14976 | 20965 | 27952 | 35937 | 44920 | A195163 | |
| 10000 | 10000-угольное | 12(9998n2 − 9996n) | 1 | 10000 | 29997 | 59992 | 99985 | 149976 | 209965 | 279952 | 359937 | 449920 | A167149 |
Центрированные многоугольные числа[править | править код]
Определение[править | править код]
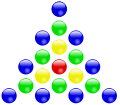
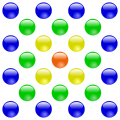
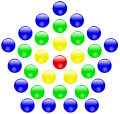
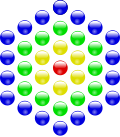
Центрированные 




Примеры построения центрированных многоугольных чисел:
| Треугольные | Квадратные | Пятиугольные | Шестиугольные |
|---|---|---|---|
|
|
|
|
Из построения видно, что центрированные многоугольные числа получаются как частичные суммы следующего ряда: 








Из приведённой выше формулы для треугольных чисел можно выразить общую формулу для 



|
(ОЦФ) |
Производящая функция для центрированных многоугольных чисел имеет вид[39]:
.
Разновидности центрированных многоугольных чисел[править | править код]
Центрированные треугольные числа[править | править код]
Центрированные треугольные числа

.
Следствие (при 

Первые элементы последовательности центрированных треугольных чисел:
- 1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, 235, 274, 316, 361, 409, 460, 514, 571 …,
(последовательность A005448 в OEIS).
- Некоторые свойства[40]
- Каждое центрированное треугольное число, начиная с 10, является суммой трёх последовательных классических треугольных чисел:
- Из следствия общей формулы видно, что каждое центрированное треугольное число
при делении на 3 даёт остаток 1, а частное (если оно положительно), есть классическое треугольное число
.
- Некоторые центрированные треугольные числа являются простыми[10]: 19, 31, 109, 199, 409 … (последовательность A125602 в OEIS).
Центрированные квадратные числа[править | править код]
| 1 | 5 | 13 | 25 | |||
|---|---|---|---|---|---|---|

.
Первые элементы последовательности центрированных квадратных чисел:
- 1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, 761 …,
(последовательность A001844 в OEIS).
- Некоторые свойства[41]
- Как видно из общей формулы, центрированное квадратное число есть сумма двух последовательных квадратов.
- Все центрированные квадратные числа нечётны, и последняя цифра в их десятичном представлении меняется в цикле: 1-5-3-5-1.
- Все центрированные квадратные числа и их делители дают остаток 1 при делении на 4, а при делении на 6, 8 или 12 дают остаток 1 или 5.
- Все центрированные квадратные числа, за исключением 1, представляют длину гипотенузы в одной из пифагоровых троек (например, 3-4-5, 5-12-13). Таким образом, каждое центрированное квадратное число равно числу точек внутри данного расстояния в кварталах от центральной точки на квадратной решётке.
- Разность между двумя последовательными классическими восьмиугольными числами есть центрированное квадратное число.
- Некоторые центрированные квадратные числа являются простыми (как показано выше, классические квадратные числа, начиная с третьего по порядку, заведомо составные). Примеры простых центрированных квадратных чисел:
-
- 5, 13, 41, 61, 113, 181, 313, 421, 613, 761, 1013, 1201, 1301, 1741, 1861, 2113, 2381, 2521, 3121, 3613 … (последовательность A027862 в OEIS).
Центрированные пятиугольные числа[править | править код]
Центрированные пятиугольные числа

.
Несколько первых центрированных пятиугольных чисел:
- 1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526, 601, 681, 766, 856, 951 …,
… (последовательность A005891 в OEIS)
Чётность центрированных пятиугольных чисел меняется по правилу: чётное-чётное-нечётное-нечётное, и последняя десятичная цифра меняется в цикле: 6-6-1-1.
Некоторые центрированные пятиугольные числа являются простыми[10]: 31, 181, 331, 391, 601 . . . (последовательность A145838 в OEIS).
Центрированные шестиугольные числа[править | править код]
Представление формулы в виде 



.
Несколько первых центрированных шестиугольных чисел:
- 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919 …
… (последовательность A003215 в OEIS).
- Некоторые свойства[42]
- Последний десятичный знак центрированных шестиугольных чисел меняется в цикле 1-7-9-7-1.
- Сумма первых n центрированных шестиугольных чисел равна «кубическому числу»
.
- Справедливо рекуррентное равенство:
.
- Некоторые центрированные шестиугольные числа являются простыми[10]: 7, 19, 37, 61, 127 … (последовательность A002407 в OEIS).
Центрированные семиугольные числа[править | править код]



Несколько первых центрированных семиугольных чисел:
- 1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, 547, 638, 736, 841, 953 …,
… (последовательность A069099 в OEIS).
Чётность центрированных семиугольных чисел меняется в цикле нечётный-чётный-чётный-нечётный.
Некоторые центрированные семиугольные числа являются простыми[10]:
- 43, 71, 197, 463, 547, 953, 1471, 1933, 2647, 2843, 3697 … (последовательность A144974 в OEIS).
Существуют также центрированные семиугольные числа, входящие в пары простых чисел-близнецов:
- 43, 71, 197, 463, 1933, 5741, 8233, 9283, 11173, 14561, 34651 … (последовательность A144975 в OEIS).
Центрированные восьмиугольные числа[править | править код]


Несколько первых центрированных восьмиугольных чисел:
- 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089.
- Некоторые свойства[43]
- Все центрированные восьмиугольные числа нечётны, и их последняя десятичная цифра меняется в цикле 1-9-5-9-1.
- Центрированное восьмиугольное число совпадает с классическим квадратным числом с нечётным номером:
Другими словами, нечётное число является центрированным восьмиугольным числом тогда и только тогда, когда оно является квадратом целого числа.
- Из предыдущего свойства следует, что все центрированные восьмиугольные числа, кроме 1, составные.
Центрированные девятиугольные числа[править | править код]


Умножая 


Первые центрированные девятиугольные числа:
- 1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946 … (последовательность A060544 в OEIS).
За исключением 6, все чётные совершенные числа являются также центрированными девятиугольными числами. В 1850-м году математик-любитель Фредерик Поллок высказал предположение, которое до сих пор не доказано и не опровергнуто, что любое натуральное число есть сумма максимум одиннадцати центрированных девятиугольных чисел[44].
Из общей формулы следует, что все центрированные девятиугольные числа, кроме 1, составные.
Центрированные десятиугольные числа[править | править код]


Первые представители центрированных десятиугольных чисел:
- 1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, 781, 911, 1051 …
(последовательность A062786 в OEIS).
Подобно другим k-угольным числам, 


Часть центрированных десятиугольных чисел являются простыми, например:
- 11, 31, 61, 101, 151, 211, 281, 661, 911, 1051, 1201, 1361, 1531, 1901, 2311, 2531, 3001, 3251, 3511, 4651, 5281… (последовательность A090562 в OEIS).
Многоугольные числа, одновременно классические и центрированные[править | править код]
Некоторые центрированные многоугольные числа совпадают с классическими, например: 
- 1. Двойные числа с общим параметром
(число углов): имеет место тождество[45]:
.
- 2. Двойные треугольные числа с разными
Пример:
(последовательность A128862 в OEIS). Для их нахождения надо решить диофантово уравнение:
тогда
. Некоторые решения:
(последовательность A133161 в OEIS), соответственно:
(последовательность A102871 в OEIS).
- 3. Классические квадратные, являющиеся центрированными треугольными числами. Их определяет диофантово уравнение:
Тогда
.
- Решения:
(последовательность A129445 в OEIS), соответственно
- Первые такие числа:
- 4. Классические треугольные, являющиеся центрированными шестиугольными числами. Первые такие числа:
(последовательность A006244 в OEIS). Их определяет диофантово уравнение:
Тогда
.
- Решения:
(последовательность A031138 в OEIS);
(последовательность A087125, в OEIS).
- 5. Классические квадратные, являющиеся центрированными шестиугольными числами. Первые такие числа:
(последовательность A006051 в OEIS). Их определяет диофантово уравнение:
Тогда
.
- Решения:
(последовательность A001570 в OEIS);
(последовательность A001921, в OEIS).
Пространственные фигурные числа[править | править код]
Наряду с рассмотренными выше фигурными числами для плоских фигур, можно определить пространственные или даже многомерные их аналоги. Уже античные математики исследовали тетраэдральные и квадратные пирамидальные числа. Несложно определить числа, связанные с пирамидами, в основании которых лежит любой другой многоугольник, например:
- Пятиугольное пирамидальное число[en].
- Шестиугольное пирамидальное число[en].
- Семиугольное пирамидальное число[en].
Другие разновидности пространственных фигурных чисел связаны с классическими многогранниками.
Пирамидальные числа[править | править код]
Геометрическое представление квадратного пирамидального числа:
Пирамидальные числа определяются следующим образом:
Геометрически пирамидальное число 


По индукции нетрудно доказать общую формулу для пирамидального числа, известную ещё Архимеду[46]:
 . .
|
(ОПФ) |
Правую часть этой формулы можно также выразить через плоские многоугольные числа:
.
Существует трёхмерный аналог формулы Никомаха для пирамидальных чисел[47]:
.
Производящая функция пирамидальных чисел имеет вид[48]:
.
Треугольные пирамидальные (тетраэдральные) числа[править | править код]
Тетраэдр с длиной стороны 5 содержит 35 сфер. Каждый слой представляет одно из первых пяти треугольных чисел
Треугольные пирамидальные числа, называемые также тетраэдральными — это фигурные числа, которые представляют тетраэдр, то есть пирамиду, в основании которой лежит треугольник. Согласно приведенному выше общему определению пирамидальных чисел, 

Общая формула для тетраэдрального числа: 
Несколько первых тетраэдральных чисел:
- 1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969 … (последовательность A000292 в OEIS).
Интересно, что пятое число равно сумме всех предыдущих.
Существует трёхмерный аналог формулы Баше де Мезириака, а именно разложение произвольного пирамидального числа по тетраэдральным[47]:
.
Пять тетраэдральных чисел одновременно являются треугольными (последовательность A027568 в OEIS):
- 1, 10, 120, 1540, 7140.
Только три тетраэдральных числа являются квадратными числами (последовательность A003556 в OEIS):
,
,
.
Одна из «гипотез Поллока» (1850 год): каждое натуральное число представимо как сумма не более пяти тетраэдральных чисел. До сих пор не доказана, хотя проверена для всех чисел, меньших 10 миллиардов[49][50].
Квадратные пирамидальные числа[править | править код]
Квадратные пирамидальные числа часто кратко называют просто пирамидальными. Для них пирамида имеет квадратное основание. Начальная последовательность:
- 1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819… (последовательность A000330 в OEIS).
Общая формула для квадратного пирамидального числа: 
Квадратное пирамидальное число 

Между квадратными и треугольными пирамидальными числами существует следующая зависимость[52]:
.
Выше было отмечено, что сумма последовательных треугольных чисел есть квадратное число; аналогично сумма последовательных тетраэдральных чисел есть квадратное пирамидальное число[52]:

Многогранные числа[править | править код]
По аналогии с квадратными можно ввести «кубические числа» 
- Октаэдральное число
- Додекаэдральное число
- Икосаэдральное число
Предусмотрены также их центрированные варианты.
Кубические числа[править | править код]
Кубические числа 

- 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000 . . . (последовательность A000578 в OEIS).
Кубическое число можно выразить как разность квадратов последовательных треугольных чисел[53]:
,
.
Следствие: сумма первых 

.
Разность между двумя соседними кубическими числами есть центрированное шестиугольное число. Следствие: сумма первых 

Выражение кубического числа через тетраэдральные[53]:
, где
.
Одна из «гипотез Поллока» (1850 год): каждое натуральное число представимо как сумма не более девяти кубических чисел. Доказана в начале XX века. Обычно достаточно семи кубов, но 15 чисел требуют восьми (15, 22, 50, 114, 167, 175, 186, 212, 231, 238, 303, 364, 420, 428, 454, последовательность A018889 в OEIS), а двум числам нужны все девять: 23 и 239. Если, кроме сложения, допускать вычитание, то достаточно и пяти кубов (возможно, что даже четырёх, но это пока не доказано)[54].
Производящая функция кубических чисел имеет вид[53]:
;
.
Октаэдральные числа[править | править код]
Додекаэдральные числа[править | править код]
Икосаэдральные числа[править | править код]
Многомерные обобщения[править | править код]
Описанные выше трёхмерные конструкции можно обобщить на четыре и более измерений. Аналогом тетраэдральных чисел в 
.
Их частным случаем выступают:
Другие разновидности многомерных чисел — гиперкубические: ![{displaystyle Q_{n}^{[d]}=n^{d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/994da48a0b29edfff10ede51a2387ff370b62a11)

Числа из более чем одной разновидности[править | править код]
Некоторые фигурные числа могут принадлежать более чем одной разновидности плоских и/или многомерных чисел, примеры для плоских чисел уже приводились выше[⇨][⇨]. Для многомерных чисел это довольно редкая ситуация[56].
Никакое натуральное число, кроме 1, не может быть одновременно[58][56]:
- треугольным и кубическим;
- треугольным и биквадратным[59];
- треугольным и пятой степенью целого числа[58];
- центрированным шестиугольным и кубическим.
В 1988 году Ф. Бейкерс и Дж. Топ доказали, что никакое число, кроме 1, не может быть одновременно тетраэдральным и квадратным пирамидальным[60]. Доказано также, что не существует чисел, которые одновременно[56]:
- тетраэдральные и кубические;
- квадратные пирамидальные и кубические;
- тетраэдральные и биквадратные;
- квадратные пирамидальные и биквадратные.
Архаичные виды фигурных чисел[править | править код]
В античные времена, когда арифметика не отделялась от геометрии, пифагорейцы (VI век до н. э.) различали ещё несколько видов фигурных чисел[61].
- Линейные числа — числа, «измеряемые только единицей», то есть, в современной терминологии, простые числа (у Евклида используется термин «первые числа», др.-греч. πρώτοι αριθμοί).
- Плоские (или плоскостные) числа — числа, представимые в виде произведения двух сомножителей, бо́льших единицы, то есть составные.
- Частным случаем являются прямоугольные числа (в источниках иногда называются «продолговатыми», англ. oblong), представляющие собой произведение двух последовательных целых чисел[62], то есть имеющие вид
- Частным случаем являются прямоугольные числа (в источниках иногда называются «продолговатыми», англ. oblong), представляющие собой произведение двух последовательных целых чисел[62], то есть имеющие вид
- Телесные числа — числа, представимые произведением трёх сомножителей:, бо́льших единицы.
Комментатор Евклида Д. Д. Мордухай-Болтовской поясняет[63]:
Термины «плоскостное» и «телесное» число являются, вероятно, пережитком более раннего периода математической мысли, когда число и геометрический образ были ещё теснее связаны, когда произведение числа
предметов на абстрактное число
мыслилось как расположение этих предметов в
рядах по
предметов в каждом, с заполнением площади прямоугольника. То же следует сказать и о произведении трёх чисел, являющемся, согласно евклидовской терминологии, телесным числом.
В настоящее время простые числа не относят к фигурным, а термины «плоское число» и «телесное число» вышли из употребления[63].
Роль в теории чисел[править | править код]
Треугольник Паскаля[править | править код]
Числа из треугольника Паскаля обнаруживают связь со многими разновидностями фигурных чисел.
Тетраэдральные числа в треугольнике Паскаля (выделены красным)
На третьей линии в треугольнике Паскаля находятся треугольные числа, а на четвёртой — тетраэдральные числа (см. рисунок). Это объясняется тем, что 

Таким образом, все внутренние элементы треугольника Паскаля являются фигурными числами, причём представлены различные их разновидности. Вдоль каждой строки, слева направо, идут гипертетраэдральные числа возрастающей размерности. Известно, что сумма всех чисел 



Другие применения[править | править код]
Многие теоремы теории чисел допускают формулировку в терминах фигурных чисел. Например, гипотеза Каталана утверждает, что среди гиперкубических чисел произвольных размерностей только одна пара отличается на 1: 
Всякое чётное совершенное число является треугольным[66] (и одновременно шестиугольным, причём номер шестиугольного числа есть степень двойки). Такое число не может одновременно быть квадратным, кубическим или иным гиперкубическим числом[67].
Гипотеза Лежандра (1808 год, она же третья проблема Эдмунда Ландау): между последовательными квадратными числами всегда найдётся простое число. До сих пор не доказана.
Сумма первых 





Число Мерсенна, большее 1, не может быть квадратным, кубическим или иным гиперкубическим, но может быть треугольным. Треугольных чисел Мерсенна всего четыре: 




Получение чисел Фибоначчи из треугольника Паскаля
Число Ферма также не может быть квадратным, кубическим или иным гиперкубическим, но в единственном случае может быть треугольным: 
Среди чисел Фибоначчи имеются только три квадратных числа (0, 1 и 144) и четыре треугольных (1, 3, 21, 55, последовательность A039595 в OEIS). Если повернуть треугольник Паскаля, как показано на рисунке, то числа Фибоначчи можно получить как суммы вдоль восходящих диагоналей; этот факт даёт разложение числа Фибоначчи по гипертетраэдральным числам[69].
Среди чисел Люка квадратных чисел два (1 и 4), а треугольных три (1, 3, 5778)[69].
Числа Каталана 
.
Ещё один класс чисел, тесно связанных с фигурными — числа Стирлинга второго рода 



![{displaystyle Q_{2}^{[n]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8afaed0172274299d068445d247c03a3c1c16c9a)


.
Примечания[править | править код]
- ↑ Деза Е., Деза М., 2016, с. 9.
- ↑ История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 68. — 352 с.
- ↑ Фигурные числа // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 607. — 847 с.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 10.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 12—13.
- ↑ Ожигова Е. П. Что такое теория чисел. — М.: Знание, 1970. — С. 56—57.
- ↑ Арифметический ряд // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 1. Архивная копия от 13 ноября 2013 на Wayback Machine
- ↑ 1 2 Деза Е., Деза М., 2016, с. 15.
- ↑ За страницами учебника математики, 1996, с. 50.
- ↑ 1 2 3 4 5 Деза Е., Деза М., 2016, с. 217.
- ↑ Sameen Ahmed Khan. Sums of the powers ofreciprocals of polygonal numbers (формула 23)
- ↑ Деза Е., Деза М., 2016, с. 14.
- ↑ Диофант Александрийский. Арифметика и Книга о многоугольных числах / Пер. И. Н. Веселовского; Ред. и коммент. И. Г. Башмаковой. — М.: Наука, 1974. — С. 48. — 328 с. Архивная копия от 24 апреля 2007 на Wayback Machine
- ↑ 1 2 Матвиевская Г. П. Учение о числе на средневековом Ближнем и Среднем Востоке. — Ташкент: ФАН, 1967. — С. 22—23. — 344 с. Вопреки названию, книга прослеживает историю понятия числа с самых древних времён.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 237.
- ↑ Виленкин Н. Я. Популярная комбинаторика. — М.: Наука, 1975. — С. 10—11. — 208 с. Архивная копия от 5 июня 2016 на Wayback Machine
- ↑ Деза Е., Деза М., 2016, с. 10.
- ↑ Деза Е., Деза М., 2016, с. 19—24.
- ↑ Dickson, 2005, p. 27.
- ↑ Weisstein, Eric W. Telescoping Sum (англ.) на сайте Wolfram MathWorld.
- ↑ Dickson, 2005, p. 3.
- ↑ Деза Е., Деза М., 2016, с. 225.
- ↑ Деза Е., Деза М., 2016, с. 19.
- ↑ 1 2 Dickson, 2005, p. 2.
- ↑ Некоторые конечные числовые ряды. Math24.ru. Дата обращения: 14 июня 2019. Архивировано 14 июня 2019 года.
- ↑ Кохась К. П. Сумма обратных квадратов // Математическое просвещение. — 2004. — Вып. 8. — С. 142—163.
- ↑ Вайнштейн Ф. В. Разбиение чисел. : [арх. 9 августа 2019] // Журнал «Квант». — 1988. — № 11.
- ↑ Деза Е., Деза М., 2016, с. 22.
- ↑ 1 2 3 Деза Е., Деза М., 2016, с. 37—38.
- ↑ В самом деле, пусть
(все числа целые) есть целое
, причём
,
— взаимно просты. Умножая обе части на
, получим:
. Справа — целое число, поэтому
делит
, и, согласно обобщённой лемме Евклида,
делит
.
- ↑ 1 2 3 Деза Е., Деза М., 2016, с. 38—39.
- ↑ Деза Е., Деза М., 2016, с. 17—19.
- ↑ Деза Е., Деза М., 2016, с. 33.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 34—37.
- ↑ Деза Е., Деза М., 2016, с. 25—34.
- ↑ Lawrence Downey, Boon W. Ong. Beyond the Basel Problem: Sums ofReciprocals of Figurate Numbers Архивная копия от 29 декабря 2019 на Wayback Machine
- ↑ Деза Е., Деза М., 2016, с. 39—40.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 40—41.
- ↑ Деза Е., Деза М., 2016, с. 42.
- ↑ Деза Е., Деза М., 2016, с. 43.
- ↑ Деза Е., Деза М., 2016, с. 44—46.
- ↑ Деза Е., Деза М., 2016, с. 45—46.
- ↑ Деза Е., Деза М., 2016, с. 46.
- ↑ Dickson, 2005, p. 23.
- ↑ Деза Е., Деза М., 2016, с. 48.
- ↑ Деза Е., Деза М., 2016, с. 70—71.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 76.
- ↑ Деза Е., Деза М., 2016, с. 74—75.
- ↑ Деза Е., Деза М., 2016, с. 239.
- ↑ Frederick Pollock. On the extension of the principle of Fermat’s theorem on the polygonal numbers to the higher order of series whose ultimate differences are constant. With a new theorem proposed, applicable to all the orders (англ.) // Abstracts of the Papers Communicated to the Royal Society of London : journal. — 1850. — Vol. 5. — P. 922—924. — JSTOR 111069.
- ↑ Robitaille, David F. Mathematics and chess // The Arithmetic Teacher. — 1974. — Vol. 21, no. 5 (май). — P. 396—400. — JSTOR 41190919.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 75.
- ↑ 1 2 3 4 Деза Е., Деза М., 2016, с. 78—81.
- ↑ Деза Е., Деза М., 2016, с. 231—232.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 126—134.
- ↑ 1 2 3 Деза Е., Деза М., 2016, с. 77—78.
- ↑ Watson G. N. The Problem of the Square Pyramid // Messenger. Math. 1918. Vol. 48. P. 1-16.
- ↑ 1 2 The Penguin Dictionary of Curious and Interesting Numbers (англ.). Дата обращения: 9 марта 2021.
- ↑ Dickson, 2005, p. 8.
- ↑ Beukers F., Top J. On oranges and integral points on certain plane cubic curves // Nieuw Archief voor Wiskunde (4). — 1988. — Vol. 6, no. 3. — P. 203—210.
- ↑ Гайденко П. П. Эволюция понятия науки (становление и развитие первых научных программ) Архивная копия от 19 августа 2014 на Wayback Machine, глава 1. М.: Наука, 1980.
- ↑ Ben-Menahem, Ari. Historical Encyclopedia of Natural and Mathematical Sciences, Volume 1 : [арх. 11 ноября 2021]. — Springer-Verlag, 2009. — С. 161. — (Springer reference). — ISBN 9783540688310.
- ↑ 1 2 Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.—Л.: ГТТИ, 1948. — Т. 2. — С. 10, 268—270. — (Классики естествознания).
- ↑ 1 2 3 Деза Е., Деза М., 2016, с. 203—205.
- ↑ Деза Е., Деза М., 2016, с. 196—197.
- ↑ За страницами учебника математики, 1996, с. 51.
- ↑ Деза Е., Деза М., 2016, с. 200—201.
- ↑ Деза Е., Деза М., 2016, с. 222—223.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 208.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 214—215.
Литература[править | править код]
- Виленкин Н. Я., Шибасов Л. П. Шибасова 3. Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия. — М.: Просвещение, 1996. — С. 48—52. — 320 с. — ISBN 5-09-006575-6.
- Глейзер Г. И. История математики в школе (4—6 классы). — М.: Просвещение, 1964. — С. 84—86. — 376 с.
- Деза Е. Специальные числа натурального ряда: Учебное пособие.. — М.: Книжный дом «ЛИБРОКОМ», 2011. — 240 с. — ISBN 978-5-397-01750-3.
- Деза Е., Деза М. Фигурные числа. — М.: МЦНМО, 2016. — 349 с. — ISBN 978-5-4439-2400-7.
- Депман И. Я. История арифметики. Пособие для учителей. — Изд. второе. — М.: Просвещение, 1965. — С. 150—155.
- Матвиевская Г. П. Заметки о многоугольных числах в записных книжках Эйлера // Историко-математические исследования. — М.: Наука, 1983. — № 27. — С. 27—49.
- Серпинский В. Пифагоровы треугольники. — М.: Учпедгиз, 1959. — 111 с.
- Стиллвелл Д. Глава 3. Греческая теория чисел // Математика и её история. — Москва-Ижевск: Институт компьютерных исследований, 2004.
- Dickson L. E. Polygonal. pyramidal and figurate numbers // History of the Theory of Numbers. — New York : Dover, 2005. — Vol. 2: Diophantine Analysis. — P. 22—23.
Ссылки[править | править код]
- Фигурные числа. Издательская группа ОСНОВА. Дата обращения: 10 февраля 2021.
- Weisstein, Eric W. Figurate Number (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Centered Polygonal Numbe (англ.) на сайте Wolfram MathWorld.
Государственное бюджетное общеобразовательное учреждение
школа-интернат № 1 имени К. К. Грота
Красногвардейского района Санкт-Петербурга
Исследовательская работа
Как найти фигурные числа?
Математика
Владимирова Вера
ученица 6б класса
Руководитель:
Сергеева Вилора Вячеславовна,
учитель надомного обучения
ГБОУ школы-интерната
№ 1 им. К.К.Грота
Санкт-Петербург
2018
ОГЛАВЛЕНИЕ
Введение 3
1. Информационная часть 4
1.1. Из истории возникновения фигурных чисел 4
1.2. Натуральный ряд чисел 5
1. 3.Фигурные числа 6
2. Исследовательская часть 7
2.1 Треугольные числа 7
2.2. Квадратные числа 8
2.3. Прямоугольные числа 19
2.4. Кубические числа 10
2.5 Формулы для нахождения фигурных чисел 11
2.6 Фигурные числа в математике 12
Заключение 13
Источники информации 14
Приложения 15
ВВЕДЕНИЕ
В учебнике по математике есть рассказы об истории возникновения и развития математики. В одном из них числа 10 и 16 представлены, как фигурные. Там же содержатся задание и вопросы:
«…попробуйте найти ещё несколько треугольных и квадратных чисел. Какими свойствами обладают эти числа? Подумайте, как можно находить треугольные и квадратные числа, используя ряд натуральных чисел».
Мне стало интересно, что же это за числа, смогу ли я справиться с заданием и ответить на предложенные вопросы.
Сначала я попробовала сама составлять треугольные и квадратные числа, ставя точки на листе бумаги. Увидела некоторые закономерности. Потом я нашла информацию об истории возникновения и свойствах фигурных чисел. Узнала о том, что есть и другие виды фигурных чисел, и тоже решила научиться их составлять.
Гипотеза: Фигурные числа можно находить не только выкладывая однородные мелкие предметы, но и по формуле, используя ряд натуральных чисел.
Объект исследования: фигурные числа.
Предмет исследования: свойства фигурных чисел и закономерности их составления.
Цель исследования: найти способы нахождения фигурных чисел,
Задачи:
1.Составить несколько первых фигурных чисел разных видов.
2.Определить некоторые свойства этих видов фигурных чисел.
3.Найти информацию об истории возникновения этих чисел.
4.Изучить доступные свойства фигурных чисел.
5.Описать способы составления фигурных чисел.
Методы исследования:
поисковый метод: работа с источниками информации;
практический метод: практическая работа, поиск фигурных чисел;
анализ полученной информации.
1. ИНФОРМАЦИОННАЯ ЧАСТЬ
Как возникли фигурные числа? Какую роль они играли в древности и какое значение имеют сейчас? Какими свойствами обладают? Что такое натуральные числа и какими они бывают?
1.1. Из истории возникновения фигурных чисел
Давным-давно люди считали на пальцах рук и ног. Было придумано немало хитроумных способов счета при помощи пальцев и их суставов. С развитием хозяйственной деятельности появились «большие» числа. Для удобства подсчета стали использовать однородные мелкие предметы: камешки, ракушки, бобы… Эти предметы раскладывали на специальной доске и пересчитывали. Можно было заметить, что некоторые количества предметов при раскладывании образуют уже известные к тому времени геометрические фигуры.
Людям в Древнем Египте и Вавилоне надо было строить каналы, возводить плотины и валы, восстанавливать границы земельных участков после разливов рек. Так что простые геометрические фигуры, их свойства, способы вычисления площадей были известны уже народам Древнего Востока. Их умения строить громадные здания тоже это подтверждают. Так возникла геометрия, оттуда она перешла в Грецию.
Итак, первоначально фигурные числа выкладывались при счете, как математический объект возникли из связи чисел (количеств) с геометрическими фигурами: отрезок, треугольник, прямоугольник, квадрат.
Пифагор создал одну из самых известных философских школ в Древней Греции. «Музыка и астрономия были сведены пифагорейцами к анализу числовых закономерностей, то есть к арифметике и геометрии. Все четыре дисциплины стали называться одним словом «математа».[2,стр.123] Прежде размышлений над глубокими тайнами Вселенной его ученики как можно больше занимались математикой.
Объясняя устройство мира, Пифагор опирался на математику. «Все вещи – суть числа», – считали последователи Пифагора и повсюду искали числа для объяснения сути вещей. Они составляли фигуры, которые содержали определенное число предметов, изображали числа точками. Числа разделили на группы. В каждую группу входили числа, которые имеют одну и ту же форму: треугольник, квадрат, пятиугольник и так далее. Такие числа стали называть фигурными.
С помощью фигурных чисел и их свойств пифагорейцы описывали устройство Вселенной, земного мира и человека.
1.2. Натуральный ряд чисел
В пятом классе я узнала, что числа, которые мы используем при счете предметов, называются натуральными. Если их записать по порядку так, как мы их называем при счете, то получится ряд натуральных чисел.
Этот ряд начинается с единицы и не имеет конца, а каждое следующее число ряда на 1 больше предыдущего.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, …
Все числа натурального ряда могут быть распределены на два ряда, на числа четные и нечетные.
Четные числа: 2, 4, 6, 8, …
Нечетные числа: 1, 3, 5, 7, 9, …
Если пронумеровать числа в этих рядах по порядку, то можно заметить, что четное число в 2 раза больше своего номера n: 2n .
Нечетное число может быть найдено путем умножения номера на 2 и вычитания единицы: 2n–1.
В шестом классе я узнала, что все числа натурального ряда могут быть распределены и на два других ряда, на числа простые и составные, и 1 (1 не является ни простым, ни составным числом):
Простые числа: 2, 3, 5, 7, 11, 13, 17, 19, 29, …
Составные числа:4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, …
Любое натуральное число либо простое, либо может быть представлено как произведение простых чисел.
1. 3.Фигурные числа
Любое целое число, которое является произведением двух целых чисел, можно назвать прямоугольным числом. Когда две стороны прямоугольника имеют одну и ту же длину, то такое число является квадратным числом, или квадратом.
Некоторые числа можно представлять в виде прямоугольных чисел только в виде цепочки точек, лежащих в одном ряду. Такие числа греки называли простыми числами.
Число 1 – «кирпич», из которого строились все остальные числа. Можно рассматривать точки, равномерно заполняющие не только прямоугольники и квадраты, но и другие геометрические фигуры, например, треугольники.
Эти построения позволяли математикам объединить геометрию и арифметику, считать, открывать законы чисел, использовать свойства фигурных чисел для построения математических моделей.
2.ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ
Выкладывание фигурных чисел; связь между фигурными числами и рядом натуральных чисел; запись формул и вычисления по ним.
2.1 Треугольные числа
Я выкладывала треугольники из кубиков. Приложение 1.
1 2 3 4 5
Рисунок 1.
Можно заметить, что треугольные числа получаются при сложении натуральных чисел по порядку.
«Таблица1–Треугольные числа»
|
n |
число |
|
1 |
1 |
|
2 |
1+2=3 |
|
3 |
1+2+3=6 |
|
4 |
1+2+3+4=10 |
|
5 |
1+2+3+4+5=15 |
|
6 |
1+2+3+4+5+6=21 |
|
7 |
1+2+3+4+5+6+7=28 |
|
8 |
1+2+3+4+5+6+7+8=36 |
|
9 |
1+2+3+4+5+6+7+8+9=45 |
|
10 |
1+2+3+4+5+6+7+8+9+10=55 |
2.2. Квадратные числа
Я выкладывала квадраты из кубиков. Приложение 2.
1 2 3 4 5
Рисунок 2.
Можно заметить, что квадратные числа получаются при сложении нечетных чисел по порядку.
«Таблица2–Квадратные числа»
|
n |
число |
|
1 |
1 |
|
2 |
1+3=4 |
|
3 |
1+3+5=9 |
|
4 |
1+3+5+7=16 |
|
5 |
1+3+5+7+9=25 |
|
6 |
1+3+5+7+9+11=36 |
|
7 |
1+3+5+7+9+11+13=49 |
|
8 |
1+3+5+7+9+11+13+15=64 |
|
9 |
1+3+5+7+9+11+13+15+17=81 |
|
10 |
1+3+5+7+9+11+13+15+17+19=100 |
2.3. Прямоугольные числа
Я выкладывала прямоугольники из кубиков. Приложение 3.
1 2 3 4 5
Рисунок 3.
Можно заметить, что прямоугольные числа получаются при сложении четных чисел по порядку.
«Таблица3–Прямоугольные числа»
|
n |
число |
|
1 |
2 =1*2 |
|
2 |
2+4=6 =2*3 |
|
3 |
2+4+6=12 =3*4 |
|
4 |
2+4+6+8=20 =4*5 |
|
5 |
2+4+6+8+10=30 =5*6 |
|
6 |
2+4+6+8+10+12=42 =6*7 |
|
7 |
2+4+6+8+10+12+14=56 =7*8 |
|
8 |
2+4+6+8+10+12+14+16=72 =8*9 |
|
9 |
2+4+6+8+10+12+14+16+18=90 = 9*10 |
|
10 |
2+4+6+8+10+12+14+16+18+20=110 =10*11 |
2.4. Кубические числа
Я выкладывала кубические числа из кубиков. Приложение 4.
«Таблица4–Кубические числа»
|
n |
число |
|
1 |
1 |
|
2 |
2*2*2=8 |
|
3 |
3*3*3=27 |
|
4 |
4*4*4=64 |
|
5 |
5*5*5=125 |
|
6 |
6*6*6=216 |
|
7 |
7*7*7=343 |
|
8 |
8*8*8=512 |
|
9 |
9*9*9=729 |
|
10 |
10*10*10=1000 |
2.5 Формулы для нахождения фигурных чисел
Слово «формула» в переводе с латинского означает «правило», форма».
n – ные по счету фигурные числа могут быть вычислены по формулам:
1. Кубическое: n*n*n
«Таблица5–Ряд кубических чисел»
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
8 |
27 |
64 |
125 |
216 |
343 |
512 |
729 |
1000 |
|
|
1*1*1 |
2*2*2 |
3*3*3 |
4*4*4 |
5*5*5 |
2. Квадратное: n*n
«Таблица6–Ряд квадратных чисел»
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
|
|
1*1 |
2*2 |
3*3 |
4*4 |
5*5 |
3.Прямоугольное: n*(n+1)
«Таблица7–Ряд прямоугольных чисел»
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
2 |
6 |
12 |
20 |
30 |
42 |
56 |
72 |
90 |
100 |
|
|
1*2 |
2*3 |
3*4 |
4*5 |
5*6 |
4.Треугольное:
«Таблица7–Ряд треугольных чисел»
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
55 |
|
|
2/2 |
6/2 |
12/2 |
20/2 |
30/2 |
42/2 |
56/2 |
72/2 |
90/2 |
110/2 |
Можно заметить, что треугольное число составляет половину от прямоугольного числа.
Запишем формулу для прямоугольного числа и разделим её на 2
n*( n+1)/2
Найдем десятые фигурные числа по формулам:
1. Кубическое: n*n*n, n = 10 10*10*10=1000.
2. Квадратное: n*n, n = 10 10*10=100.
3.Прямоугольное n*(n+1), n = 10 10*(10+1)=110.
4.Треугольное: n*( n+1)/2, n = 10 10*(10+1)/2=55.
Те же числа были получены при выкладывании фигурных чисел, при сложении натуральных чисел по порядку.
2.6 Фигурные числа в математике
Фигурные числа помогают «увидеть» свойства действий с рациональными числами.
а + в = в + а
а*в = в*а
( а + в) *с = а*с + в*с
От фигурных чисел произошли выражения:
«квадрат числа»,
«куб числа»,
«возвести в квадрат»,
«возвести в куб».
ЗАКЛЮЧЕНИЕ
Я составила по 10 треугольных, квадратных, прямоугольных и кубических чисел и заметила их особенности.
Я изучила и обобщила информацию об истории возникновения фигурных чисел, проверила некоторые свойства, нашла связь между фигурными числами и натуральным рядом:
треугольные числа получаются при сложении натуральных чисел по порядку,
прямоугольные числа получаются при сложении четных чисел по порядку,
квадратные числа получаются при сложении нечетных чисел по порядку.
Фигурные числа можно находить разными способами:
1. выкладывать мелкие предметы по форме и пересчитывать,
2. последовательно складывать числа натуральные, четные или нечетные.
3. вычислять по формулам.
Таким образом, задачи исследования выполнены, гипотеза подтвердилась.
Я смогла выполнить дополнительное задание из учебника. Фигурные числа помогли мне «увидеть» законы действий с числами, обобщить знания о натуральных числах.
Я узнала, что эти числа математики и физики используют до сих пор.
Что–то о фигурных числах я пока понять не смогла, с чем–то я встречусь еще в старших классах.
ИСТОЧНИКИ ИНФОРМАЦИИ
1. Виленкин Н.Я. Математика.6 класс.– М.: «Мнемозина»,2013.
2.Волошинов А.В. Математика и искусство.– М.: Просвещение, 2000.
3.Свечников А.А. Путешествие в историю математики, или как люди учились считать.– М.: Педагогика–Пресс, 1995.
4. Я познаю мир: Детская энциклопедия: Математика/ Составитель Савин А.П.– М.: ООО «Издательство АСТ– ЛТД»,1998.
ПРИЛОЖЕНИЕ 1
Составление треугольных чисел.
ПРИЛОЖЕНИЕ 2
Составление квадратных чисел
ПРИЛОЖЕНИЕ 3
Составление прямоугольных чисел.
ПРИЛОЖЕНИЕ 4
Составление кубических чисел.
Фигурные числа – общее название чисел, связанных с той или иной геометрической фигурой.
Предполагают, что впервые они появились в VI веке до нашей эры – в школе Пифагора. В дальнейшем многие математики интересовались этими числами.
Согласно пифагорейскому учению, в основе мира лежат числа (натуральные).
Числа древними греками, а вместе с ними Пифагором и пифагорейцами мыслились зримо, в виде камешков, разложенных на песке или на счетной доске – абаке. По этой причине греки не знали нуля, т.к. его невозможно было “увидеть”.
Арифметика пифагорейцев была поэтому тесно связана с геометрией: они выделяли классы чисел, имеющих одну и ту же форму, а именно: треугольные, квадратные, пятиугольные и так далее.
Линейные числа
Линейные числа (т.е. простые числа) – числа, которые делятся только на единицу и на самих себя и, следовательно, представимы в виде последовательности точек, выстроенных в линию:
1,2,3,5,7,11,13,17,19,23
Плоские числа
Плоские числа – числа, представимые в виде произведения двух сомножителей:
4,6,8,9,10,12,14,15
Телесные числа
Телесные числа — числа, выражаемые произведением трёх сомножителей
(8,12,18,20,24,27,28,…) и т. д.
Треугольные числа
Треугольные числа — это такие числа, из которых (имея столько камушков) можно выложить правильные треугольники.
1, 1+2= 3 , 1+2+3= 6 , 1+2+3+4= 10 ,
1+2+3+4+5= 15 , 1 +2+3+4+5+6= 21
Квадратные числа
квадратные числа получаются при выкладывании из камушков квадратов. Вот они какие: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 и т. д.
Второй- это два ряда, каждый из двух камушков: 2*2=4. Третий – три ряда по три камушка: 3*3=9. Четвертый- 4 ряда по 4 камня: 4*4=16. Неспроста про числа 2*2, 3*3, 4*4 говорят ” два в квадрате”, “три в квадрате”, “четыре в квадрате”!
Пятиугольные числа
Можно рассматривать и шестиугольные, и семиугольные числа, и вообще, числа, возникающие при складывании разнообразных многоугольников, с разными сторонами или с одинаковыми.
Кубические числа
Очень интересны кубические числа, возникающие при складывании кубиков: 1, 2*2*2=8 (два этажа из квадратов 2*2). 3*3*3=27 (три этажа из квадратов 3*3) 4*4*4=64 (четыре этажа из квадратов 4*4) 5*5*5=125, 6*6*6=216, 7*7*7=343, 8*8*8=512, 9*9*9=729, 10*10*10= 1000 и так далее. Теперь понятно, почему про такие числа говорят: “два в кубе”, “три в кубе”, “десять в кубе “?
Пирамидальные числа
Фигурное представление чисел помогало пифагорейцам открывать законы арифметических операций. Так, представляя число 10 в двух формах: 5*2=2*5, легко “увидеть” переместительный закон умножения: a*b=b*a.
Если “камешки”, образующие фигурные числа, мыслить в виде равных по площади квадратиков, то, укладывая их в прямоугольное число ab : автоматически получаем формулу для вычисления площади прямоугольника: S= ab .
Счет на камушках оставил глубокий след в истории математики. Древние греки, когда им приходилось умножать числа, рисовали прямоугольники; результатом умножения трех на пять был прямоугольник со сторонами три и пять. Это- развитие счета на камушках. Множество закономерностей, возникающих при действиях с числами, были обнаружены древнегреческими учеными при изучений чертежей. И долгие века лучшим подтверждением справедливости таких соотношений считался способ геометрический, с прямоугольниками, квадратами, пирамидами и кубами.
В Новое время многоугольными числами занимались Ферма , Эйлер, Гаусс и другие. Ферма сформулировал ( 1670 ) так называемую «золотую теорему»:
Всякое натуральное число — либо треугольное, либо сумма двух или трёх треугольных чисел;
Всякое натуральное число — либо квадратное, либо сумма двух, трёх или четырёх квадратных чисел;
Всякое натуральное число — либо пятиугольное, либо сумма от двух до пяти пятиугольных чисел:
и т. д.
Этой теоремой занимались многие выдающиеся математики, полное доказательство сумел дать Коши в 1813 году .
Почему числа 2*2*2*2=16, 3*3*3*3=81, 4*4*4*4=256 и т.д. не имеют своего названия, хотя у квадратов и кубов чисел такие названия есть? А дело в том, что мы живем в мире трех измерений (длина, широта и высота). Квадрат получился, когда мы выложили фигуру с одинаковой длиной и шириной: куб – фигура с одинаковыми длиной, шириной и высотой. Но нет четвертого измерения, чтобы выложить такую же красивую фигуру из 2*2*2*2 камушков.
Квадратное число находится по формуле:
N кв.=п х п
Треугольное число находится по формуле:
N тр.=п(п-1):2
Пятиугольные числа находятся по формуле:
N пят.=п+3п(п-1):2
Использовано:
https://ru.wikipedia.org/wiki/ Фигурные_числа
http://totangens.ru/figurnye-chisla.html
|
МУНИЦИПАЛЬНОЕ |
|
|
Проект в номинации № 2 |
|
|
Тема проекта: |
|
|
«Фигурные числа» |
|
|
Автор: |
|
|
Панин Илья Игоревич |
|
|
Класс: |
|
|
Научный |
|
|
Товстоног Елена Анатольевна |
|
|
«Общеобразовательная |
|
|
(полная) |
|
|
г. |
|
|
учитель |
|
|
Белоярский |
|
|
2013 – 2014 учебный год |
Содержание
|
ВВЕДЕНИЕ |
|
|
ОСНОВНАЯ ЧАСТЬ |
4 |
|
1.1. Из истории фигурных чисел |
4 |
|
1.2. Формулы плоских фигурных чисел |
7 |
|
1.3. Свойства фигурных чисел |
8 |
|
1.4. Применение фигурных чисел в |
13 |
|
ЗАКЛЮЧЕНИЕ |
14 |
|
СПИСОК ЛИТЕРАТУРЫ |
15 |
|
ПРИЛОЖЕНИЯ |
16 |
ВВЕДЕНИЕ
Давным – давно, помогая себе при
счёте камушками, люди обращали внимание на правильные фигуры, которые можно
выложить из камушков. Можно просто класть камушки в ряд: один, два, три. Если
класть их в два ряда, получались прямоугольники. Можно выкладывать камни в три
ряда: получаются числа, делящиеся на три и т.д. Числа – камушки можно
раскладывать в виде правильных геометрических фигур, так возникли числа,
которые сегодня называют фигурными.
Во время изучения обыкновенных дробей
обратил внимание на то, что в учебнике математики есть небольшая историческая
сводка о фигурных числах. Это и подтолкнуло меня к исследованию темы, целью
которой, стало изучить свойства фигурных чисел и их использование в
повседневной жизни.
В своей исследовательской работе я
рассмотрел использование фигурных чисел не только в математике, но и в
окружающей жизни.
Чтобы достичь этой цели, я исследовал
дополнительную литературу и другие источники.
Цель работы: более глубоко изучить и
исследовать одно из понятий математики – фигурное число, выявить его свойства
и использование в повседневной жизни.
Задачи:
1.
Собрать по различным научным и учебным
источникам материал по данной проблеме и проанализировать его.
2.
Рассмотреть историю возникновения фигурных
чисел, их свойства и применение в жизни человека.
ОСНОВНАЯ
ЧАСТЬ
1.1.
Из истории фигурных
чисел.
Фигурные числа — общее название
чисел, геометрическое представление которых связано с той или иной
геометрической фигурой. Понятие фигурного числа было введено древнегреческими
математиками, последователями учения Пифагора (пифагорейцами) в VI—IV вв. до н.
э.
Они предпочитали думать о числах, как
о геометрических величинах. Произведение ab рассматривалось как площадь
прямоугольника со сторонами a и b. В случае, если a и b
– натуральные, произведение ab выражало число точек в прямоугольной
таблице с a точками в строке и b точками в столбце. Например,
число 20 выражает число точек в таблице с пятью строками и четырьмя столбцами
(рис. 1).
Рис. 1. Произведение
чисел 5 и 4.
Числа, выражающие число точек в
квадратной таблице, назывались квадратными. Например, квадратными числами
являются 1, 4, 9, 16, 25, 36,…(рис. 2).
|
|
|
|
|
|
|
|
1 |
4 |
9 |
16 |
25 |
36 |
Рис. 2. Квадратные числа.
Таблицы могут быть не только
прямоугольными или квадратными, но и иметь форму других геометрических фигур.
Например, на рисунке 3 изображены треугольные числа, выражающие числа точек в
треугольных таблицах.
|
|
|
|
|
|
|
|
1 |
3 |
6 |
10 |
15 |
21 |
Рис. 3. Треугольные
числа.
На рисунках 4 и 5 изображены
пятиугольные и шестиугольные числа. Из этих рисунков видно, что пятиугольными
числами являются 1, 5, 12, 22, 35, … , а шестиугольными – 1, 6, 15, 28, 45, 66,…
|
|
|
|
|
|
|
|
1 |
5 |
12 |
22 |
35 |
51 |
Рис. 4. Пятиугольные
числа.
Рис. 5. Шестиугольные
числа.
Уложив камешки в пространственную
фигуру можно получить телесные фигурные числа (рис. 6).
Именно от фигурных чисел пошло
выражение: «Возвести в квадрат или куб».
Множество закономерностей, возникших
при действиях с числами, были обнаружены древнегреческими учёными при изучении
чертежей. И долгие века лучшим подтверждением справедливости таких соотношений
считался способ геометрический, с прямоугольниками, квадратами, пирамидами и
кубами. Древнегреческие учёные, комбинируя натуральные числа, составляли из них
затейливые ряды, придавая элементам этих рядов то или иное геометрическое
истолкование.
|
|
|
Рис. 6. Кубическое и
квадратное пирамидальное числа.
1.2.
Формулы плоских фигурных
чисел.
Рассматривая ряд, образованный
треугольными числами легко заметить, что:
T1=1; Т2=3=1+2;
T3=6=(1+2)+3,…, Tn=(1+2+…+(n–1))+n=
Tn-1+n (1),
где Tn
– значение треугольного числа с номером n,
Tn-1. – значение треугольного числа с номером
(n-1).
Т.е. каждое следующее число получаем из предыдущего, увеличивая предыдущее на
номер нового числа (таблица 1).
Таблица 1. Зависимость значения
треугольного числа от его номера
|
число |
|
|
|
|
|
… |
|
|
Номер |
1 |
2 |
3 |
4 |
5 |
… |
n |
|
Значение |
1 |
3 |
6 |
10 |
15 |
… |
Tn-1+n |
Дополним Тn
до квадратного числа (рис. 7).
Рис. 7. Красным цветом
обозначено исходное число Tn,
зеленым его дополнение до квадратного (Tn-1).
Тогда (согласно рис. 7 и формуле (1)):
.
Поэтому:
Тогда: (2) – формула
треугольного n – го треугольного числа.
Эту формулу открыли еще древние
греки, а потом, независимо от них, согласно легенде, Карл Гаусс в возрасте 9
лет.
Для вывода формул других n – x
многоугольных чисел, древние греки, разбивали их на треугольные.
Рассмотрим вывод формулы для
произвольного пятиугольного числа
Если разбить n – е
пятиугольное число на три (n–1) треугольных, то останутся еще n камешков
(см. таблицу 2).
Таблица 2. Зависимость Pn
от Tn–1.
|
Номер (n) |
Tn |
Pn |
|
1 |
1 |
1 |
|
2 |
3 |
|
|
3 |
6 |
|
|
4 |
10 |
|
|
5 |
15 |
|
|
6 |
21 |
|
|
… |
… |
… |
|
n–1 |
|
… |
|
n |
|
|
Т.е.: .
Аналогичным образом, используя только
геометрические соображения можно получить формулы, для:
·
квадратных: ;
·
пятиугольных: ;
·
шестиугольных:
·
семиугольных:
·
и произвольных k-угольных: , чисел.
Где, – n–e
квадратное число, – n–e
пятиугольное число, – n–e
шестиугольное число, – n–e k-угольное
число.
1.3.
Свойства фигурных чисел
Между фигурными числами имеется много
интересных зависимостей. Так, например, древнегреческий математик Диофант (III
век до н. э.) нашел зависимость между треугольными (Тn)
и квадратными (K2n+1)
числами: .
Доказательство Диофанта приведено на
рисунке 8, для квадратных чисел K7
и K9.
|
|
|
Рис. 8. Связь между
треугольными и квадратными числами.
Выделим среди точек каждого
квадратного числа центральную, а остальные точки разобьем на группы, образующие
восемь треугольных чисел T3
для K7
и T4
для K9.
В результате получаем равенства 8T3+1=K7
и 8T4+1=K9.
В общем случае имеет место равенство:
.
Следствие: Если n
– нечетное число, то делится на 8.
Пьер Ферма обобщил формулу Диофанта и
сформулировал, в 1637, так называемую
«золотую теорему»:
·
Всякое натуральное число — либо
треугольное, либо сумма двух или трёх треугольных чисел.
·
Всякое натуральное число — либо
квадратное, либо сумма двух, трёх или четырёх квадратных чисел.
·
Всякое натуральное число — либо
пятиугольное, либо сумма от двух до пяти пятиугольных чисел, и т.д.
Используя геометрический метод,
разработанный древнегреческими учеными, можно доказать и формулы сокращенного
умножения.
Докажем, что Для этого построим
квадрат со стороной, и выделим в построенном квадрате, квадраты со стороной a
и стороной b (рис. 9).
Рис. 9. Доказательство
тождества .
Тогда (согласно рис. 9): , что и требовалось
доказать.
Изучая фигурные числа, греки окрыли
очень много свойств числовых последовательностей.
Рассмотрим произвольное квадратное
число (рис. 10):
Рис. 10. Разбиение
квадратного числа на сумму нечетных чисел.
«Уголки» выделенные на рисунке одним
цветом образуют ряд последовательных нечетных чисел, очевидно: 1+3+5+7+9+11=62.
Обобщив полученную зависимость
получим:
(3) – формулу для суммы
последовательных нечетных чисел.
Следовательно, квадрат любого
натурального числа можно представить в виде суммы последовательных нечетных чисел,
начиная с единицы.
Аналогичным образом можно получить
формулу для суммы четных чисел. Для этого рассмотрим прямоугольную таблицу
(рис. 11):
Рис. 11. Разбиение
прямоугольного числа на сумму четных чисел.
«Уголки» выделенные на рисунке одним
цветом образуют ряд последовательных четных чисел, очевидно: .
Обобщив полученную зависимость
получим:
(4) – формулу для
суммы последовательных четных чисел.
Следствие: Произведение двух
последовательных натуральных чисел можно представить в виде суммы
последовательных четных чисел, начиная с двух.
Великие математики затратили немало
усилий на изучение свойств фигурных чисел.
Обобщением «золотой теоремы» стала
Великая (или Последняя) теорема Ферма:
·
Для любого натурального числа уравнение
не имеет решений в целых
не нулевых числах a, b, c.
Которая на протяжении более трех
веков будоражила умы математиков во всем мире, и только в 1995 году была
окончательно доказана английским математиком Эндрю Джоном Уайлсом.
1.4.
Применение фигурных
чисел в жизни человека
Мы не задумываемся о том, что
ежедневно встречаемся с фигурными числами. А ведь это так просто и интересно.
·
При изучении формулы площади
прямоугольника используется понятие плоского числа, которое представляется виде
произведения двух сомножителей – длины и ширины.
·

вычислении объёма прямоугольного параллелепипеда применяется понятие телесного
числа, выражаемого произведением трёх сомножителей – длины, ширины и высоты.
·
Упаковка конфет в форме линейного числа
·
На параде солдаты стоят правильными
рядами, образуя квадраты или прямоугольники (плоские числа). (Приложение 1)
·
Во время различных праздников мы видим
показательные выступления лётчиков. Самолёты в воздухе образуют треугольные или
другие фигурные числа. (Приложение 2)
·
Треугольные числа можно встретить в самых
обычных местах (Приложение 3)
·
Фигурные числа встречаются при упаковке
различных товаров в коробки и другие ёмкости.
·
Телесные числа используются при упаковке
конфет, консервных банок, блокнотов, тетрадей, ручек и др. в различные ёмкости.
(Приложение 4)
·
Плоские числа тоже часто используются при
упаковке конфет, растительного масла, лимонадных бутылок … (Приложение 5)
·
К фигурным числам можно отнести
пирамидальные числа, которые получаются, если шарики складывать пирамидкой. Как
раньше складывались ядра у около пушки. (Приложение 6)
·
Используя различные фигурные числа как
телесные, так и пирамидальные , укладывают товар на прилавке, конфеты в
различные упаковки, украшают праздничный стол и т.д. (Приложение 7)
ЗАКЛЮЧЕНИЕ
А зачем все это? И действительно —
зачем? Чему автор хотел научить, какие проблемы поднял?
Могу ответить лишь в духе Ноздрева:
очень уж интересные подробности открылись! Да и так ли уж обязательно
непременно чему-то учить? Нужна ведь и просто «гимнастика ума», а если она
может немного развлечь — тем лучше!
В процессе работы по данной проблеме
я добился цели, поставленной в начале исследования: изучил и исследовал
фигурные числа.
Подводя итог работы, пришёл к выводу
об актуальности данной темы. Невозможно представить современную жизнь без
фигурных чисел, они вокруг нас, мы живем среди них. Значит – это кому-нибудь
нужно.
СПИСОК ЛИТЕРАТУРЫ
1.
Виленкин Н.Я. Математика. 6 класс: учебник
для общеобразовательных учреждений.- М.: Мнемозина, 2008.
2.
Волошинов А.В. Пифагор: Союз истины, добра
и красоты. – М.: Просвещение, 1993.
3.
Энциклопедический словарь юного
математика/ Составитель А.П.Савин. – М.: Педагогика, 1985
ПРИЛОЖЕНИЯ
Приложение 1
Приложение
2
Приложение
3
Приложение 4
Приложение 5
Приложение 6
Приложение
7

Фигурные числа — числа, которые можно представить с помощью геометрических фигур. Это историческое понятие восходит к пифагорейцам, которые развивали алгебру на геометрической основе и представляли любое положительное целое число в виде набора точек на плоскости. Отголоском этого подхода остались выражения «возвести число в квадрат или в куб».
В теории чисел и комбинаторике фигурные числа связаны с многими другими классами целых чисел — биномиальными коэффициентами, совершенными числами, числами Мерсенна, Ферма, Фибоначчи, Люка и другими.
Виды фигурных чисел
Со времён пифагорейцев (VI век до н. э.) традиционно различают следующие виды фигурных чисел (они определены, например, в VII книге «Начал» Евклида):
- Линейные числа — числа, не разлагающиеся на сомножители, большие единицы, то есть это ряд простых чисел, дополненный единицей (у Евклида используется термин «первые числа», πρώτοι αριθμοί): 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271 … (последовательность A008578 в OEIS)
- Плоские числа — числа, представимые в виде произведения двух сомножителей, больших единицы, то есть составные: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88 … (последовательность A002808 в OEIS)
- Частным случаем являются прямоугольные числа (в источниках называются также «продолговатыми»), являющиеся произведением двух последовательных целых чисел, то есть имеющие вид n ( n + 1 ) . {displaystyle n(n+1).}
- Телесные числа — числа, представимые произведением трёх сомножителей: 8, 12, 16, 18, 20, 24, 27, 28, 30, 32, 36, 40, 42, 44, 45, 48, 50, 52, 54, 56, 60, 63, 64, 66, 68, 70, 72, 75, 76, 78, 80, 81, 84, 88, 90, 92, 96, 98, 99, 100, 102, 104, 105, 108, 110, 112, 114, 116, 117, 120, 124, 125, 126, 128, 130, 132, 135, 136, 138, 140, 144 … (последовательность A033942 в OEIS)
- Многоугольные числа — числа, связанные с определённым многоугольником, определение см. ниже.
- Пространственные многогранные числа — числа, связанные с определённым многогранником, определение см. ниже.
Классические многоугольные числа
Определение и общий вид
Общее определение k-угольного числа для любого k ⩾ 3 {displaystyle kgeqslant 3} можно сформулировать следующим образом:
Например, треугольные числа получаются как частичные суммы ряда 1 + 2 + 3 + 4 … {displaystyle 1+2+3+4dots } , а четырёхугольным (квадратным) числам соответствует ряд 1 + 3 + 5 + 7 … {displaystyle 1+3+5+7dots }
Последовательность k-угольных чисел имеет вид:
1 , k , 3 k − 3 , 6 k − 8 , 10 k − 15 , 15 k − 24 , 21 k − 35 , 28 k − 48 , 36 k − 63 , 45 k − 80 … {displaystyle 1,k,3k-3,6k-8,10k-15,15k-24,21k-35,28k-48,36k-63,45k-80dots }
Общую формулу для явного подсчёта n {displaystyle n} -го по порядку k-угольного числа P n ( k ) {displaystyle P_{n}^{(k)}} легко получить, найдя по стандартным правилам сумму арифметической прогрессии. Эту формулу можно представить в нескольких вариантах, получаемых один из другого простыми преобразованиями:
Можно также использовать рекуррентную формулу:
P n + 1 ( k ) = P n ( k ) + ( k − 2 ) n + 1 ; P 1 ( k ) = 1 {displaystyle P_{n+1}^{(k)}=P_{n}^{(k)}+(k-2)n+1; P_{1}^{(k)}=1}
При увеличении числа сторон k {displaystyle k} на единицу соответствующие фигурные числа изменяются согласно формуле Никомаха:
Поскольку P n ( k ) {displaystyle P_{n}^{(k)}} линейно зависит от k , {displaystyle k,} справедлива формула:
P n ( k + s ) + P n ( k − s ) = 2 P n ( k ) {displaystyle P_{n}^{(k+s)}+P_{n}^{(k-s)}=2P_{n}^{(k)}} , где s = 0 , 1 , 2 … k − 3. {displaystyle s=0,1,2dots k-3.}
Другими словами, каждое многоугольное число есть среднее арифметическое для равноотстоящих от него по k {displaystyle k} многоугольных чисел с тем же номером.
Если k {displaystyle k} — простое число, то второе k-угольное число, равное k , {displaystyle k,} также простое; это единственная ситуация, когда многоугольное число является простым. В самом деле, запишем общую формулу в следующем виде:
P n ( k ) = 2 + ( n − 1 ) ( k − 2 ) 2 n {displaystyle P_{n}^{(k)}={frac {2+(n-1)(k-2)}{2}}n}
Пусть n > 2. {displaystyle n>2.} Если n {displaystyle n} чётно, то фигурное число делится на n / 2 , {displaystyle n/2,} а если нечётно, то делится на ( 2 + ( n − 1 ) ( k − 2 ) ) / 2. {displaystyle (2+(n-1)(k-2))/2.} В обоих случаях фигурное число оказывается составным.
Исторический очерк
Фигурные числа, по мнению пифагорейцев, играют важную роль в структуре мироздания. Поэтому их изучением занимались многие математики античности: Эратосфен, Гипсикл, Диофант Александрийский и другие. Гипсикл (II век до н. э.) дал общее определение k-угольного числа P n ( k ) {displaystyle P_{n}^{(k)}} как суммы n {displaystyle n} членов арифметической прогрессии, у которой первый член есть 1, а разность равна k − 2 ; {displaystyle k-2;} определение Гипсикла приводится в книге Диофанта в следующем виде:
Если взять сколько-нибудь чисел, начиная с единицы, имеющих одинаковые разности, то сумма их, если разность единица, будет треугольником, если же двойка, то четырёхугольником, а если тройка — пятиугольником. Количество углов определяется разностью, увеличенной на двойку, а сторона — количеством взятых чисел, считая и единицу.
Диофант написал большое исследование о свойствах многоугольных чисел, фрагменты которого дошли до наших дней. О фигурных числах много говорится в пифагорейских учебниках арифметики, созданных Никомахом Геразским и Теоном Смирнским (II век), которые установили ряд зависимостей между фигурными числами разных размерностей. Большой интерес к фигурным числам проявили индийские математики и первые математики средневековой Европы (Фибоначчи, Пачоли, Кардано и др.).
В Новое время многоугольными числами занимались Ферма, Валлис, Эйлер, Лагранж, Гаусс и другие. В сентябре 1636 года Ферма сформулировал в письме Мерсенну замечательную теорему, которая сегодня называется теоремой Ферма о многоугольных числах:
Я первым открыл очень красивую и совершенно общую теорему о том, что каждое число является либо треугольным, либо суммой двух или трёх треугольных чисел; каждое число или квадратное, или является суммой двух, трёх или четырёх квадратов; или пятиугольное, или является суммой двух, трёх, четырёх или пяти пятиугольных чисел, и т. д. до бесконечности, будь то для шестиугольных, семиугольных или любых многоугольных чисел. Я не могу дать здесь доказательство, которое зависит от многочисленных и запутанных тайн чисел, ибо я намерен посвятить этой теме целую книгу и получить в этой части арифметики удивительные достижения по сравнению с ранее известными пределами.
Вопреки обещанию, Ферма так и не опубликовал доказательство этой теоремы, которую в письме Паскалю (1654) назвал своим главным достижением в математике. Проблемой занимались многие выдающиеся математики — в 1770 году Лагранж доказал теорему для квадратных чисел (теорема Лагранжа о сумме четырёх квадратов), в 1796 году Гаусс дал доказательство для треугольных. Полное доказательство теоремы сумел дать Коши в 1813 году.
Треугольные числа
Последовательность треугольных чисел:
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946, 990, 1035, 1081, 1128, 1176, 1225, 1275, 1326, 1378, 1431 …, n ( n + 1 ) 2 {displaystyle {frac {n(n+1)}{2}}} … (последовательность A000217 в OEIS)
Свойства:
- Чётность элемента последовательности меняется с периодом 4: нечётное, нечётное, чётное, чётное.
- Обозначим для краткости n {displaystyle n} -е треугольное число: T n = P n ( 3 ) = n ( n + 1 ) 2 . {displaystyle T_{n}=P_{n}^{(3)}={frac {n(n+1)}{2}}.} Тогда справедливы рекуррентные формулы:
T 2 n = 3 T n + T n − 1 {displaystyle T_{2n}=3T_{n}+T_{n-1}} T 2 n + 1 = 3 T n + T n + 1 {displaystyle T_{2n+1}=3T_{n}+T_{n+1}}
- Формула Баше де Мезириака: общую формулу многоугольного числа можно преобразовать так, что она покажет выражение любого многоугольного числа через треугольные:
- Сумма двух последовательных треугольных чисел даёт полный квадрат (квадратное число):
T n + T n + 1 = ( n + 1 ) 2 = P n + 1 ( 4 ) . {displaystyle T_{n}+T_{n+1}=(n+1)^{2}=P_{n+1}^{(4)}.} .
- Сумма конечного ряда треугольных чисел вычисляется по формуле:
S m − 1 = 1 + 3 + 6 + ⋯ + ( m − 1 ) m 2 = m 3 − m 6 {displaystyle S_{m-1}=1+3+6+dots +{frac {(m-1)m}{2}}={frac {m^{3}-m}{6}}} .
- Ряд из чисел, обратных треугольным, сходится:
1 + 1 3 + 1 6 + 1 10 + 1 15 + ⋯ = 2 ∑ n = 1 ∞ ( 1 n − 1 n + 1 ) = 2 {displaystyle 1+{1 over 3}+{1 over 6}+{1 over 10}+{1 over 15}+dots =2sum _{n=1}^{infty }left({1 over n}-{1 over n+1}
ight)=2}
- Удвоенные треугольные числа дают последовательность (определённых выше ) прямоугольных чисел.
- Натуральное число N {displaystyle N} является треугольным тогда и только тогда, когда число 8 N + 1 {displaystyle 8N+1} является полным квадратом. Это несложно доказать непосредственно, но проще вывести из общей методики (задача 2)..
- Существует бесконечно много треугольных чисел, которые одновременно являются квадратными («квадратные треугольные числа»): 1 , 36 , 1225 , 41616 , 1413721 … {displaystyle 1,36,1225,41616,1413721dots } (последовательность A001110 в OEIS).
- Известное в мистике «число зверя» (666) является 36-м треугольным. Оно является наименьшим треугольным числом, которое представимо в виде суммы квадратов треугольных чисел: 666 = 15 2 + 21 2 . {displaystyle 666=15^{2}+21^{2}.}
- Треугольные числа образуют третью диагональную линию треугольника Паскаля; см. подробнее ниже.
Квадратные числа
Квадратные числа представляют собой произведение двух одинаковых натуральных чисел, то есть являются полными квадратами:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500 …, n 2 {displaystyle n^{2}} … (последовательность A000290 в OEIS)
Каждое квадратное число, кроме единицы, есть сумма двух последовательных треугольных чисел:
n 2 = T n − 1 + T n {displaystyle n^{2}=T_{n-1}+T_{n}} . Примеры: 4 = 1 + 3 ; 9 = 3 + 6 ; 16 = 6 + 10 {displaystyle 4=1+3;quad 9=3+6;quad 16=6+10} и т. д.
Сумма квадратов первых n {displaystyle n} натуральных чисел вычисляется по формуле:
1 2 + 2 2 + 3 2 + . . . + n 2 = n ( n + 1 ) ( 2 n + 1 ) 6 {displaystyle 1^{2}+2^{2}+3^{2}+…+n^{2}={frac {n(n+1)(2n+1)}{6}}}
Ряд обратных квадратов сходится:
∑ n = 1 ∞ 1 n 2 = 1 1 2 + 1 2 2 + ⋯ + 1 n 2 + ⋯ = π 2 6 {displaystyle sum _{n=1}^{infty }{frac {1}{n^{2}}}={frac {1}{1^{2}}}+{frac {1}{2^{2}}}+dots +{frac {1}{n^{2}}}+dots ={frac {pi ^{2}}{6}}}
Каждое натуральное число может быть представлено как сумма не более четырёх квадратов (теорема Лагранжа о сумме четырёх квадратов).
Тождество Брахмагупты — Фибоначчи: произведение суммы двух квадратных чисел на любую другую сумму двух квадратных чисел само представимо в виде суммы двух квадратных чисел, причём двумя способами.
( a 2 + b 2 ) ( c 2 + d 2 ) = ( a c − b d ) 2 + ( a d + b c ) 2 = ( a c + b d ) 2 + ( a d − b c ) 2 . {displaystyle (a^{2}+b^{2})(c^{2}+d^{2})=(ac-bd)^{2}+(ad+bc)^{2}=(ac+bd)^{2}+(ad-bc)^{2}.}
Пример:
( 1 2 + 4 2 ) ( 2 2 + 7 2 ) = 26 2 + 15 2 = 30 2 + 1 2 . {displaystyle (1^{2}+4^{2})(2^{2}+7^{2})=26^{2}+15^{2}=30^{2}+1^{2}.}
Пятиугольные числа
1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001, 1080, 1162, 1247, 1335, 1426, 1520, 1617, 1717, 1820, 1926, 2035, 2147, 2262, 2380, 2501, 2625, 2752, 2882, 3015, 3151 …, n ( 3 n − 1 ) 2 {displaystyle {frac {n(3n-1)}{2}}} … (последовательность A000326 в OEIS)
Если в формуле n ( 3 n − 1 ) 2 {displaystyle {frac {n(3n-1)}{2}}} указать для n {displaystyle n} более общую последовательность:
n = 0 , 1 , − 1 , 2 , − 2 , 3 , − 3 … {displaystyle n=0,1,-1,2,-2,3,-3dots }
то получатся так называемые обобщённые пятиугольные числа:
0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126, 145, 155, 176, 187, 210, 222, 247, 260, 287, 301, 330, 345, 376, 392, 425, 442, 477, 495, 532, 551, 590, 610, 651, 672, 715, 737, 782, 805, 852, 876, 925, 950, 1001, 1027, 1080, 1107, 1162, 1190, 1247, 1276, 1335… (последовательность A001318 в OEIS)
Леонард Эйлер обнаружил обобщённые пятиугольные числа в следующем тождестве:
( 1 − x ) ( 1 − x 2 ) ( 1 − x 3 ) … = 1 − x − x 2 + x 5 + x 7 − x 12 − x 15 + x 22 + x 26 − x 35 − x 40 + … {displaystyle (1-x)(1-x^{2})(1-x^{3})ldots =1-x-x^{2}+x^{5}+x^{7}-x^{12}-x^{15}+x^{22}+x^{26}-x^{35}-x^{40}+ldots }
Степени x {displaystyle x} в правой части тождества образуют последовательность обобщённых пятиугольных чисел, См. подробнее: Пентагональная теорема Эйлера.
Шестиугольные числа
1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, 630, 703, 780, 861, 946, 1035, 1128, 1225, 1326, 1431, 1540, 1653, 1770, 1891, 2016, 2145, 2278, 2415, 2556, 2701, 2850, 3003, 3160, 3321, 3486, 3655, 3828, 4005, 4186, 4371, 4560 …, 2 n 2 − n {displaystyle 2n^{2}-n} … (последовательность A000384 в OEIS)
Очевидно, последовательность шестиугольных чисел получается из последовательности треугольных чисел вычёркиванием элементов с чётными номерами: P n ( 6 ) = P 2 n − 1 ( 3 ) . {displaystyle P_{n}^{(6)}=P_{2n-1}^{(3)}.}
Натуральное число N {displaystyle N} является шестиугольным тогда и только тогда, когда число 8 N + 1 + 1 4 {displaystyle {frac {{sqrt {8N+1}}+1}{4}}} является натуральным. Это несложно доказать непосредственно, но проще вывести из общей методики (задача 2)..
Двенадцатиугольные числа
Двенадцатиугольные числа вычисляются по формуле 5 n 2 − 4 n {displaystyle 5n^{2}-4n} :
1, 12, 33, 64, 105, 156, 217, 288, 369, 460, 561, 672, 793, 924, 1065, 1216, 1377, 1548, 1729, 1920, 2121, 2332, 2553, 2784, 3025, 3276, 3537, 3808, 4089, 4380, 4681, 4992, 5313, 5644, 5985, 6336, 6697, 7068, 7449, 7840, 8241, 8652, 9073, 9504, 9945 … (последовательность A051624 в OEIS)
В десятичной системе n {displaystyle n} -ое двенадцатиугольное число заканчивается на ту же цифру, что и само число n {displaystyle n} .
Определение, является ли заданное число многоугольным
Задача 1 (часто называемая задачей Диофанта): дано натуральное число N > 2 , {displaystyle N>2,} требуется определить, является ли оно многоугольным числом P n ( k ) {displaystyle P_{n}^{(k)}} и если да, то для каких значений k , n . {displaystyle k,n.} Диофант сформулировал эту проблему так: «выяснить, сколько раз данное число встречается среди всевозможных многоугольных чисел». Алгоритм решения этой задачи следующий.
Тогда все соответствующие оставшимся парам P n ( k ) {displaystyle P_{n}^{(k)}} равны N . {displaystyle N.}
Пример. Пусть N = 105. {displaystyle N=105.} .
- Делители 2 N = 210 : 1 , 2 , 3 , 5 , 6 , 7 , 10 , 14 , 15 , 21 , 30 , 35 , 42 , 70 , 105 , 210. {displaystyle 2N=210colon quad 1,2,3,5,6,7,10,14,15,21,30,35,42,70,105,210.}
- Делители 2 N − 2 = 208 : 1 , 2 , 4 , 8 , 13 , 16 , 26 , 52 , 104 , 208. {displaystyle 2N-2=208colon quad 1,2,4,8,13,16,26,52,104,208.}
- Отбираем n = 2 , 3 , 5 , 14 , 105. {displaystyle n=2,3,5,14,105.}
- Соответственно k = 105 , 36 , 12 , 14 , 2. {displaystyle k=105,36,12,14,2.} Последнее значение отбросим.
Ответ: 105 {displaystyle 105} встречается как P 2 ( 105 ) , P 3 ( 36 ) , P 5 ( 12 ) , P 14 ( 14 ) , {displaystyle P_{2}^{(105)},P_{3}^{(36)},P_{5}^{(12)},P_{14}^{(14)},} то есть как 2-е 105-угольное, 3-е 36-угольное, 5-е 12-угольное и 14-е 14-угольное число.
Задача 2: дано натуральное число N > 2 , {displaystyle N>2,} требуется определить, является ли оно k-угольным числом P n ( k ) {displaystyle P_{n}^{(k)}} . В отличие от задачи 1, здесь k {displaystyle k} задано.
Для решения можно использовать тождество Диофанта:
8 ( k − 2 ) P n ( k ) + ( k − 4 ) 2 = ( 2 n ( k − 2 ) − ( k − 4 ) ) 2 {displaystyle 8(k-2)P_{n}^{(k)}+(k-4)^{2}=(2n(k-2)-(k-4))^{2}}
Это тождество без труда получается из приведенной выше общей формулы для P n ( k ) {displaystyle P_{n}^{(k)}} и равносильно ей. Из тождества вытекает решение поставленной задачи 2: если N {displaystyle N} есть k-угольное число, то есть N = P n ( k ) {displaystyle N=P_{n}^{(k)}} для некоторого n , {displaystyle n,} то 8 ( k − 2 ) N + ( k − 4 ) 2 {displaystyle 8(k-2)N+(k-4)^{2}} есть некоторое квадратное число R 2 {displaystyle R^{2}} , и обратно. При этом номер n {displaystyle n} находится по формуле:
n = R + k − 4 2 k − 4 {displaystyle n={frac {R+k-4}{2k-4}}}
Пример. Определим, является ли число 1540 {displaystyle 1540} 10-угольным. Значение 8 ( k − 2 ) N + ( k − 4 ) 2 {displaystyle 8(k-2)N+(k-4)^{2}} здесь равно 98596 = 314 2 , {displaystyle 98596=314^{2},} поэтому ответ утвердительный. n = 20 , {displaystyle n=20,} следовательно, 1540 {displaystyle 1540} является 20-м 10-угольным числом.
Производящая функция
Степенной ряд, коэффициенты которого — k-угольные числа, сходится при | x | < 1 {displaystyle |x|<1} :
P 1 ( k ) x + P 2 ( k ) x 2 + P 3 ( k ) x 3 + ⋯ = x ( 1 + ( k − 3 ) x ) ( 1 − x ) 3 {displaystyle P_{1}^{(k)}x+P_{2}^{(k)}x^{2}+P_{3}^{(k)}x^{3}+dots ={frac {x(1+(k-3)x)}{(1-x)^{3}}}}
Выражение справа является производящей функцией для последовательности k-угольных чисел.
Аппарат производящих функций позволяет применять в теории чисел и комбинаторике методы математического анализа. Приведенная формула также объясняет появление k-угольных чисел среди коэффициентов ряда Тэйлора для различных рациональных дробей. Примеры:
При k = 3 {displaystyle k=3} : x ( 1 − x ) 3 = P 1 ( 3 ) x + P 2 ( 3 ) 3 x 2 + P 3 ( 3 ) x 3 + ⋯ + P n ( 3 ) x n + … {displaystyle qquad {frac {x}{(1-x)^{3}}}=P_{1}^{(3)}x+P_{2}^{(3)}3x^{2}+P_{3}^{(3)}x^{3}+dots +P_{n}^{(3)}x^{n}+dots } При k = 4 {displaystyle k=4} : x ( x + 1 ) ( 1 − x ) 3 = P 1 ( 4 ) x + P 2 ( 4 ) 3 x 2 + P 3 ( 4 ) x 3 + ⋯ + P n ( 4 ) x n + … {displaystyle qquad {frac {x(x+1)}{(1-x)^{3}}}=P_{1}^{(4)}x+P_{2}^{(4)}3x^{2}+P_{3}^{(4)}x^{3}+dots +P_{n}^{(4)}x^{n}+dots } При k = 5 {displaystyle k=5} : x ( 2 x + 1 ) ( 1 − x ) 3 = P 1 ( 5 ) x + P 2 ( 5 ) 3 x 2 + P 3 ( 5 ) x 3 + ⋯ + P n ( 5 ) x n + … {displaystyle qquad {frac {x(2x+1)}{(1-x)^{3}}}=P_{1}^{(5)}x+P_{2}^{(5)}3x^{2}+P_{3}^{(5)}x^{3}+dots +P_{n}^{(5)}x^{n}+dots }
и т. д.
Для некоторых классов многоугольных чисел существуют свои, специфические производящие функции. Например, для квадратных треугольных чисел 1 , 36 , 1225 , 41616 , 1413721 … {displaystyle 1,36,1225,41616,1413721dots } производящая функция имеет следующий вид:
x ( 1 + x ) ( 1 − x ) ( 1 − 34 x + x 2 ) = x + 36 x 2 + 1225 x 3 + … {displaystyle {frac {x(1+x)}{(1-x)(1-34x+x^{2})}}=x+36x^{2}+1225x^{3}+dots } ; ряд сходится при | x | < 17 − 12 2 {displaystyle |x|<17-12{sqrt {2}}}
Сводная таблица
Центрированные многоугольные числа
Определение
Центрированные k-угольные числа ( k ⩾ 3 {displaystyle kgeqslant 3} ) — это класс фигурных чисел, получаемый следующим геометрическим построением. Сначала на плоскости фиксируется некоторая центральная точка. Затем вокруг неё строится правильный k-угольник с k {displaystyle k} точками вершин, каждая сторона содержит две точки (см. рисунок). Далее снаружи строятся новые слои k-угольников, причём каждая их сторона на новом слое содержит на одну точку больше, чем в предыдущем слое, то есть начиная со второго слоя каждый следующий слой содержит на k {displaystyle k} больше точек, чем предыдущий. Общее число точек внутри каждого слоя и принимается в качестве центрированного многоугольного числа (точка в центре считается начальным слоем).
Примеры построения центрированных многоугольных чисел:
Из построения видно, что центрированные многоугольные числа получаются как частичные суммы следующего ряда: 1 + k + 2 k + 3 k + 4 k + … {displaystyle 1+k+2k+3k+4k+dots } (например, центрированные квадратные числа, для которых k = 4 , {displaystyle k=4,} образуют последовательность: 1 , 5 , 13 , 25 , 41 … {displaystyle 1,5,13,25,41dots } ) Этот ряд можно записать как 1 + k ( 1 + 2 + 3 + 4 + … ) . {displaystyle 1+k(1+2+3+4+dots ).} , откуда видно, что в скобках — порождающий ряд для классических треугольных чисел (см. выше ). Следовательно, каждая последовательность центрированных k-угольных чисел, начиная со 2-го элемента, может быть представлена как k T n + 1 , {displaystyle kT_{n}+1,} где T n ( n = 1 , 2 , 3 … ) {displaystyle T_{n}(n=1,2,3dots )} — последовательность треугольных чисел. Например, центрированные квадратные числа — это учетверённые треугольные числа плюс 1, порождающий ряд для них имеет вид: 1 + 4 + 8 + 12 … {displaystyle 1+4+8+12dots }
Из приведенной выше формулы для треугольных чисел получаем общую формулу для n {displaystyle n} -го центрированного k-угольного числа C n ( k ) {displaystyle C_{n}^{(k)}} :
Производящая функция для центрированных многоугольных чисел имеет вид:
f ( x ) = x ( 1 + ( k − 2 ) x + x 2 ) ( 1 − x ) 3 ; | x | < 1 {displaystyle f(x)={frac {x(1+(k-2)x+x^{2})}{(1-x)^{3}}};quad |x|<1}
Типы центрированных многоугольных чисел
Центрированные треугольные числа
n {displaystyle n} -е по порядку центрированное треугольное число задаётся формулой:
C n ( 3 ) = 3 n 2 − 3 n + 2 2 {displaystyle C_{n}^{(3)}={frac {3n^{2}-3n+2}{2}}} .
Первые элементы последовательности центрированных треугольных чисел:
1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, 235, 274, 316, 361, 409, 460, 514, 571, 631, 694, 760, 829, 901, 976, 1054, 1135, 1219, 1306, 1396, 1489, 1585, 1684, 1786, 1891, 1999, 2110, 2224, 2341, 2461, 2584, 2710, 2839, 2971 …, 3 n 2 − 3 n + 2 2 {displaystyle {frac {3n^{2}-3n+2}{2}}} (последовательность A005448 в OEIS) Некоторые свойства
Центрированные квадратные числа
n {displaystyle n} -е по порядку центрированное 4-угольное (квадратное) число задаётся формулой:
C n ( 4 ) = ( 2 n − 1 ) 2 + 1 2 = 2 n 2 − 2 n + 1 = ( n − 1 ) 2 + n 2 {displaystyle C_{n}^{(4)}={(2n-1)^{2}+1 over 2}=2n^{2}-2n+1=(n-1)^{2}+n^{2}}
Первые элементы последовательности центрированных квадратных чисел:
1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, 761, 841, 925, 1013, 1105, 1201, 1301, 1405, 1513, 1625, 1741, 1861, 1985, 2113, 2245, 2381, 2521, 2665, 2813, 2965, 3121, 3281, 3445, 3613, 3785, 3961, 4141, 4325 …, n 2 + ( n − 1 ) 2 … {displaystyle n^{2}+(n-1)^{2}dots } (последовательность A001844 в OEIS) Некоторые свойства
5, 13, 41, 61, 113, 181, 313, 421, 613, 761, 1013, 1201, 1301, 1741, 1861, 2113, 2381, 2521, 3121, 3613 … (последовательность A027862 в OEIS).
Центрированные пятиугольные числа
n {displaystyle n} -е по порядку центрированное пятиугольное число задается формулой:
C n ( 5 ) = 5 ( n − 1 ) 2 + 5 ( n − 1 ) + 2 2 {displaystyle C_{n}^{(5)}={frac {5(n-1)^{2}+5(n-1)+2}{2}}} .
Несколько первых центрированных пятиугольных чисел:
1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526, 601, 681, 766, 856, 951, 1051, 1156, 1266, 1381, 1501, 1626, 1756, 1891, 2031, 2176, 2326, 2481, 2641, 2806, 2976 …, 5 ( n − 1 ) 2 + 5 ( n − 1 ) + 2 2 {displaystyle {frac {5(n-1)^{2}+5(n-1)+2}{2}}} … (последовательность A005891 в OEIS)
Чётность центрированных пятиугольных чисел меняется по правилу: чётное-чётное-нечётное-нечётное, и последняя десятичная цифра меняется в цикле: 6-6-1-1.
Некоторые центрированные пятиугольные числа являются простыми: 31, 181, 331, 391, 601 . . . (последовательность A145838 в OEIS)
Центрированные шестиугольные числа
n {displaystyle n} -е по порядку центрированное шестиугольное число задаётся формулой:
C n ( 6 ) = n 3 − ( n − 1 ) 3 = 3 n ( n − 1 ) + 1 {displaystyle C_{n}^{(6)}=n^{3}-(n-1)^{3}=3n(n-1)+1} .
Несколько первых центрированных шестиугольных чисел:
1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919 … 1 + 3 n ( n − 1 ) {displaystyle 1+3n(n-1)} … (последовательность A003215 в OEIS) Некоторые свойства
Центрированные семиугольные числа
n {displaystyle n} -е по порядку центрированное семиугольное число задаётся формулой 7 n 2 − 7 n + 2 2 {displaystyle {frac {7n^{2}-7n+2}{2}}} . Его можно также вычислить умножением треугольного числа ( n − 1 ) {displaystyle (n-1)} на 7 с добавлением 1.
Несколько первых центрированных семиугольных чисел:
1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, 547, 638, 736, 841, 953 …, 7 n 2 − 7 n + 2 2 {displaystyle {frac {7n^{2}-7n+2}{2}}} … (последовательность A069099 в OEIS)
Чётность центрированных семиугольных чисел меняется в цикле нечётный-чётный-чётный-нечётный.
Некоторые центрированные семиугольные числа являются простыми:
43, 71, 197, 463, 547, 953, 1471, 1933, 2647, 2843, 3697 … (последовательность A144974 в OEIS)
Существуют также центрированные семиугольные числа, входящие в пары простых чисел-близнецов:
43, 71, 197, 463, 1933, 5741, 8233, 9283, 11173, 14561, 34651 … (последовательность A144975 в OEIS)
Центрированные восьмиугольные числа
n {displaystyle n} -е по порядку центрированное восьмиугольное число задаётся формулой ( 2 n − 1 ) 2 = 4 n 2 − 4 n + 1. {displaystyle (2n-1)^{2}=4n^{2}-4n+1.}
Несколько первых центрированных восьмиугольных чисел:
1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089. Некоторые свойства
Центрированные девятиугольные числа
n {displaystyle n} -е по порядку центрированное девятиугольное число определяется общей формулой ( 3 n − 2 ) ( 3 n − 1 ) 2 . {displaystyle {frac {(3n-2)(3n-1)}{2}}.}
Умножая ( n − 1 ) {displaystyle (n-1)} -ое треугольное число на 9 и добавляя 1, получим n {displaystyle n} -ое центрированное девятиугольное число, но имеется и более простая связь с треугольными числами — каждое третье треугольное число (1-е, 4-е, 7-е, и т. д.) также является центрированным девятиугольным числом, и так можно получить все центрированные девятиугольные числа. Формальная запись: C n ( 9 ) = P 3 n − 2 ( 3 ) . {displaystyle C_{n}^{(9)}=P_{3n-2}^{(3)}.}
Первые центрированные девятиугольные числа:
1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946 … (последовательность A060544 в OEIS)
За исключением 6, все чётные совершенные числа являются также центрированными девятиугольными числами. В 1850-м году математик-любитель Фредерик Поллок (Sir Frederick Pollock) высказал предположение, которое до сих пор не доказано и не опровергнуто, что любое натуральное число есть сумма максимум одиннадцати центрированных девятиугольных чисел.
Из общей формулы следует, что все центрированные девятиугольные числа, кроме 1, составные.
Центрированные десятиугольные числа
n {displaystyle n} -е по порядку центрированное десятиугольное число задаётся формулой 5 ( n 2 − n ) + 1 {displaystyle 5(n^{2}-n)+1} .
Первые представители центрированных десятиугольных чисел:
1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, 781, 911, 1051 … 5 ( n 2 − n ) + 1 {displaystyle 5(n^{2}-n)+1} (последовательность A062786 в OEIS)
Подобно другим k-угольным числам, n {displaystyle n} -ое центрированное десятиугольное число можно вычислить, умножая ( n − 1 ) {displaystyle (n-1)} -ое треугольное число на k {displaystyle k} , в нашем случае 10, затем добавляя 1. Как следствие, центрированные десятиугольные числа могут быть получены просто добавлением 1 к десятичному представлению числа. Таким образом, все центрированные десятиугольные числа нечётны и всегда оканчиваются на 1 в десятичном представлении.
Часть центрированных десятиугольных чисел являются простыми, например:
11, 31, 61, 101, 151, 211, 281, 661, 911, 1051, 1201, 1361, 1531, 1901, 2311, 2531, 3001, 3251, 3511, 4651, 5281… (последовательность A090562 в OEIS)
Многоугольные числа, одновременно классические и центрированные
Некоторые центрированные многоугольные числа совпадают с классическими, например: 1 , 10 , 25 , 51 ; {displaystyle 1,10,25,51;} для краткости будем называть такие многоугольные числа двойными.
1. Двойные числа с общим параметром k {displaystyle k} (число углов): имеет место тождество: C k ( k ) = P k + 1 ( k ) {displaystyle C_{k}^{(k)}=P_{k+1}^{(k)}quad } 2. Двойные треугольные числа с разными k . {displaystyle k.} Пример: 1 , 10 , 136 , 1891 , 26335 … {displaystyle 1,10,136,1891,26335dots } (последовательность A128862 в OEIS). Для их нахождения надо решить диофантово уравнение: m 2 + m = 3 n 2 − 3 n + 2 , {displaystyle m^{2}+m=3n^{2}-3n+2,} тогда P m ( 3 ) = C n ( 3 ) . {displaystyle P_{m}^{(3)}=C_{n}^{(3)}.} Некоторые решения: m = 1 , 4 , 16 , 61 , 229 … {displaystyle m=1,4,16,61,229dots } (последовательность A133161 в OEIS), соответственно: n = 1 , 3 , 10 , 36 , 133 … {displaystyle n=1,3,10,36,133dots } (последовательность A102871 в OEIS) 3. Классические квадратные, являющиеся центрированными треугольными числами. Их определяет диофантово уравнение: m 2 = 3 n 2 − 3 n + 2 2 . {displaystyle m^{2}={frac {3n^{2}-3n+2}{2}}.quad } Тогда C m ( 3 ) = P n ( 4 ) . {displaystyle C_{m}^{(3)}=P_{n}^{(4)}.} Решения: m = 1 , 2 , 8 , 19 , 79 … {displaystyle m=1,2,8,19,79dots } (последовательность A129445 в OEIS), соответственно n = 1 , 2 , 7 , 16 , 65 … {displaystyle n=1,2,7,16,65dots } Первые такие числа: 1 , 4 , 64 , 361 , 6241 … {displaystyle 1,4,64,361,6241dots } 4. Классические треугольные, являющиеся центрированными шестиугольными числами. Первые такие числа: 1 , 91 , 8911 , 873181 , 85562821 … {displaystyle 1,91,8911,873181,85562821dots } (последовательность A006244 в OEIS). Их определяет диофантово уравнение: m ( m + 1 ) 2 = 3 n 2 + 3 n + 1. {displaystyle {frac {m(m+1)}{2}}=3n^{2}+3n+1.quad } Тогда P m ( 3 ) = C n + 1 ( 6 ) {displaystyle P_{m}^{(3)}=C_{n+1}^{(6)}} Решения: m = 1 , 13 , 133 , 1321 , 13081 … {displaystyle m=1,13,133,1321,13081dots } (последовательность A031138 в OEIS) n = 0 , 5 , 54 , 539 , 5340 … {displaystyle n=0,5,54,539,5340dots } (последовательность A087125, в OEIS) 5. Классические квадратные, являющиеся центрированными шестиугольными числами. Первые такие числа: 1 , 169 , 32761 , 6355441 , 1232922769 … {displaystyle 1,169,32761,6355441,1232922769dots } (последовательность A006051 в OEIS). Их определяет диофантово уравнение: m 2 = 3 n 2 + 3 n + 1. {displaystyle m^{2}=3n^{2}+3n+1.quad } Тогда P m ( 4 ) = C n + 1 ( 6 ) {displaystyle P_{m}^{(4)}=C_{n+1}^{(6)}} Решения: m = 1 , 13 , 181 , 2521 , 35113 … {displaystyle m=1,13,181,2521,35113dots } (последовательность A001570 в OEIS) n = 0 , 7 , 104 , 1455 , 20272 … {displaystyle n=0,7,104,1455,20272dots } (последовательность A001921, в OEIS)
Пространственные фигурные числа
Наряду с рассмотренными выше фигурными числами для плоских фигур, можно определить пространственные или даже многомерные их аналоги. Уже античные математики исследовали тетраэдральные и квадратные пирамидальные числа. Несложно определить числа, связанные с пирамидами, в основании которых лежит любой другой многоугольник, например:
- Пятиугольное пирамидальное число.
- Шестиугольное пирамидальное число.
- Семиугольное пирамидальное число.
Другие классы пространственных фигурных чисел связаны с классическими многогранниками.
Пирамидальные числа
Пирамидальные числа определяются следующим образом.
Геометрически пирамидальное число Π n ( k ) {displaystyle Pi _{n}^{(k)}} можно представить как пирамиду из n {displaystyle n} слоёв (см. рисунок), каждый из которых содержит от 1 (верхний слой) до P n ( k ) {displaystyle P_{n}^{(k)}} (нижний) шаров.
По индукции нетрудно доказать общую формулу для пирамидального числа, известную ещё Архимеду:
Правую часть этой формулы можно также выразить через плоские многоугольные числа:
Π n ( k ) = ( k − 2 ) n − k + 5 3 P n ( 3 ) = n + 1 6 ( 2 P n ( k ) + n ) {displaystyle Pi _{n}^{(k)}={frac {(k-2)n-k+5}{3}}P_{n}^{(3)}={frac {n+1}{6}}(2P_{n}^{(k)}+n)}
Существует трёхмерный аналог формулы Никомаха для пирамидальных чисел:
Π n ( k + 1 ) = Π n ( k ) + Π n − 1 ( 3 ) {displaystyle Pi _{n}^{(k+1)}=Pi _{n}^{(k)}+Pi _{n-1}^{(3)}}
Производящая функция пирамидальных чисел имеет вид:
f ( x ) = x ( 1 + ( k − 3 ) x ) ( 1 − x ) 4 ; | x | < 1 {displaystyle f(x)={frac {x(1+(k-3)x)}{(1-x)^{4}}};quad |x|<1}
Треугольные пирамидальные (тетраэдральные) числа
Треугольные пирамидальные числа, называемые также тетраэдральными — это фигурные числа, которые представляют тетраэдр, то есть пирамиду, в основании которой лежит треугольник. Несколько первых тетраэдральных чисел:
1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969 … (последовательность A000292 в OEIS)
Интересно, что пятое число равно сумме всех предыдущих.
Общая формула для тетраэдрального числа: Π n ( 3 ) = n ( n + 1 ) ( n + 2 ) 6 . {displaystyle Pi _{n}^{(3)}={frac {n(n+1)(n+2)}{6}}.}
Существует трёхмерный аналог формулы Баше де Мезириака, а именно разложение произвольного пирамидального числа по тетраэдральным:
Π n ( k ) = Π n ( 3 ) + ( k − 3 ) Π n − 1 ( 3 ) {displaystyle Pi _{n}^{(k)}=Pi _{n}^{(3)}+(k-3)Pi _{n-1}^{(3)}}
Пять тетраэдральных чисел одновременно являются треугольными (последовательность A027568 в OEIS):
1, 10, 120, 1540, 7140
Только три тетраэдральных числа являются квадратными числами:
1 2 = 1 {displaystyle 1^{2}=1} , 2 2 = 4 {displaystyle 2^{2}=4} , 140 2 = 19 600 {displaystyle 140^{2}=19,600} .
Одна из «гипотез Поллока» (1850 год): каждое натуральное число представимо как сумма не более пяти тетраэдральных чисел. До сих пор не доказана, хотя проверена для всех чисел, меньших 10 миллиардов.
Квадратные пирамидальные числа
Квадратные пирамидальные числа часто кратко называют просто пирамидальными. Для них пирамида имеет квадратное основание. Начальная последовательность:
1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819… (последовательность A000330 в OEIS).
Общая формула для квадратного пирамидального числа: Π n ( 4 ) = n ( n + 1 ) ( 2 n + 1 ) 6 . {displaystyle Pi _{n}^{(4)}={frac {n(n+1)(2n+1)}{6}}.}
Квадратное пирамидальное число Π n ( 4 ) {displaystyle Pi _{n}^{(4)}} также выражает общее количество квадратов в квадратной сетке n × n {displaystyle n imes n} .
Между квадратными и треугольными пирамидальными числами существует следующая зависимость:
4 Π n ( 4 ) = Π 2 n ( 3 ) {displaystyle 4Pi _{n}^{(4)}=Pi _{2n}^{(3)}}
Выше было отмечено, что сумма последовательных треугольных чисел есть квадратное число; аналогично сумма последовательных тетраэдральных чисел есть квадратное пирамидальное число: Π n ( 4 ) = Π n ( 3 ) + Π n − 1 ( 3 ) {displaystyle Pi _{n}^{(4)}=Pi _{n}^{(3)}+Pi _{n-1}^{(3)}}
Многогранные числа
По аналогии с квадратными можно ввести «кубические числа» Q n = n 3 , {displaystyle Q_{n}=n^{3},} а также числа, соответствующие другим правильным и неправильным многогранникам — например, платоновым телам:
- Октаэдральное число
- Додекаэдральное число
- Икосаэдральное число
Предусмотрены также их центрированные варианты.
Кубические числа
Кубические числа Q n {displaystyle Q_{n}} представляют собой произведение трёх одинаковых натуральных чисел и имеют общий вид Q n = n 3 . {displaystyle Q_{n}=n^{3}.} Начальные значения:
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000 . . . (последовательность A000578 в OEIS)
Кубическое число можно выразить как разность квадратов последовательных треугольных чисел:
Q n = ( T n ) 2 − ( T n − 1 ) 2 , n ⩾ 2 {displaystyle Q_{n}=(T_{n})^{2}-(T_{n-1})^{2},ngeqslant 2}
Следствие: сумма первых n {displaystyle n} кубических чисел равна квадрату n {displaystyle n} -го треугольного числа:
Q 1 + Q 2 + Q 3 + ⋯ + Q n = ( T n ) 2 {displaystyle Q_{1}+Q_{2}+Q_{3}+dots +Q_{n}=(T_{n})^{2}}
Разность между двумя соседними кубическими числами есть центрированное шестиугольное число. Следствие: сумма первых n {displaystyle n} центрированных шестиугольных чисел есть кубическое число Q n {displaystyle Q_{n}} .
Выражение кубического числа через тетраэдральные:
Q n = Π n ( 3 ) + 4 Π n − 1 ( 3 ) + Π n − 2 ( 3 ) {displaystyle Q_{n}=Pi _{n}^{(3)}+4Pi _{n-1}^{(3)}+Pi _{n-2}^{(3)}} , где n > 2. {displaystyle n>2.}
Одна из «гипотез Поллока» (1850 год): каждое натуральное число представимо как сумма не более девяти кубических чисел. Доказана в начале XX века. Обычно достаточно семи кубов, но 15 чисел требуют восьми (15, 22, 50, 114, 167, 175, 186, 212, 231, 238, 303, 364, 420, 428, 454, последовательность A018889 в OEIS), а двум числам нужны все девять: 23 и 239. Если, кроме сложения, допускать вычитание, то достаточно и пяти кубов (возможно, что даже четырёх, но это пока не доказано).
Производящая функция кубических чисел имеет вид:
f ( x ) = x ( x 2 + 4 x + 1 ) ( x − 1 ) 4 ; | x | < 1 {displaystyle f(x)={frac {x(x^{2}+4x+1)}{(x-1)^{4}}};quad |x|<1}
Октаэдральные числа
Додекаэдральные числа
Икосаэдральные числа
Многомерные обобщения
Описанные выше трёхмерные конструкции можно обобщить на четыре и более измерений. Аналогом тетраэдральных чисел в d {displaystyle d} -мерном пространстве служат «симплексные числа», называемые также гипертетраэдральными:
S n [ d ] = ( n − 1 + d ) ! ( n − 1 ) ! d ! {displaystyle S_{n}^{[d]}={frac {(n-1+d)!}{(n-1)! d!}}}
Их частным случаем выступают:
- S n [ 2 ] {displaystyle S_{n}^{[2]}} — треугольные числа.
- S n [ 3 ] {displaystyle S_{n}^{[3]}} — тетраэдральные числа.
- S n [ 4 ] {displaystyle S_{n}^{[4]}} — пентатопные числа
Другой класс многомерных чисел — гиперкубические: Q n [ d ] = n d . {displaystyle Q_{n}^{[d]}=n^{d}.} Четырёхмерные гиперкубические числа ( d = 4 {displaystyle d=4} ) называются биквадратными.
Числа из более чем одного класса
Некоторые фигурные числа могут входить более чем в один класс плоских и/или многомерных чисел, примеры для плоских чисел уже приводились выше. Для многомерных чисел это довольно редкая ситуация.
- Пять чисел 1 , 10 , 120 , 1540 , 7140 {displaystyle 1,10,120,1540,7140} (и только они) одновременно треугольные и тетраэдральные (последовательность A027568 в OEIS).
- Четыре числа 1 , 55 , 91 , 208335 {displaystyle 1,55,91,208335} одновременно треугольные и квадратные пирамидальные (последовательность A039596 в OEIS).
- Три числа 1 , 4 , 19600 {displaystyle 1,4,19600} одновременно плоские квадратные и тетраэдральные (последовательность A003556 в OEIS).
- Два числа 1 , 4900 {displaystyle 1,4900} одновременно квадратные плоские и квадратные пирамидальные. Это утверждение получило известность как «гипотеза Люка» или «задача о пушечных ядрах» (1875 год). Полное решение дал в 1918 году Джордж Невилл Ватсон.
- Никакое натуральное число, кроме 1, не может быть одновременно:
- треугольным и кубическим;
- центрированным шестиугольным и кубическим.
В 1988 году Ф. Бейкерс и Дж. Топ доказали, что никакое число, кроме 1, не может быть одновременно тетраэдральным и квадратным пирамидальным. Доказано также, что не существует чисел, которые одновременно:
- тетраэдральные и кубические;
- квадратные пирамидальные и кубические;
- тетраэдральные и биквадратные;
- квадратные пирамидальные и биквадратные.
Роль в теории чисел
Треугольник Паскаля
Числа из треугольника Паскаля обнаруживают связь со многими типами фигурных чисел.
На третьей линии в треугольнике Паскаля находятся треугольные числа, а на четвёртой — тетраэдральные числа (см. рисунок). Это объясняется тем, что n {displaystyle n} -е тетраэдральное число есть сумма первых n {displaystyle n} треугольных чисел, которые расположены на третьей линии. Аналогично на пятой линии расположены четырёхмерные пентатопные числа и т. д. Все они, как и прочие числа внутри треугольника Паскаля, являются биномиальными коэффициентами.
Таким образом, все внутренние элементы треугольника Паскаля являются фигурными числами, причём представлены различные их типы. Вдоль каждой строки, слева направо, идут гипертетраэдральные числа возрастающей размерности. Известно, что сумма всех чисел n {displaystyle n} -й строки равна 2 n , {displaystyle 2^{n},} отсюда следует, что сумма всех чисел первых n {displaystyle n} строк равна числу Мерсенна M n . {displaystyle M_{n}.} Следовательно, число Мерсенна можно представить как сумму гипертетраэдральных чисел.
Другие применения
Многие теоремы теории чисел допускают формулировку в терминах фигурных чисел. Например, гипотеза Каталана утверждает, что среди гиперкубических чисел произвольных размерностей только одна пара отличается на 1: 3 2 = 2 3 + 1 {displaystyle 3^{2}=2^{3}+1} (доказано в 2002 году).
Всякое чётное совершенное число является треугольным (и одновременно шестиугольным, причём номер шестиугольного числа есть степень двойки). Такое число не может одновременно быть квадратным, кубическим или иным гиперкубическим числом.
Гипотеза Лежандра (1808 год, она же третья проблема Эдмунда Ландау): между последовательными квадратными числами всегда найдётся простое число. До сих пор не доказана.
Сумма первых n {displaystyle n} центрированных треугольных чисел ( n > 2 ) {displaystyle (n>2)} есть «магическая константа» для магического квадрата размерности n × n {displaystyle n imes n} . Другие способы получить эту же константу — через треугольное число T n 2 n , {displaystyle {frac {T_{n^{2}}}{n}},} или сложить все натуральные числа от T n − 1 {displaystyle T_{n-1}} до T n {displaystyle T_{n}} включительно.
Число Мерсенна, большее 1, не может быть квадратным, кубическим или иным гиперкубическим, но может быть треугольным. Треугольных чисел Мерсенна всего четыре: 1 , 3 , 5 , 4095 , {displaystyle 1,3,5,4095,} их поиск эквивалентен решению в натуральных числах уравнения Рамануджана — Нагеля: 2 n − 7 = x 2 . {displaystyle 2^{n}-7=x^{2}.} Как оказалось, решение этого уравнения существует только при n = 3 , 4 , 5 , 7 , 15 {displaystyle n=3,4,5,7,15} (последовательность A060728 в OEIS), и при n > 3 {displaystyle n>3} соответствующее число Мерсенна M n − 3 {displaystyle M_{n-3}} будет тогда треугольным.
Число Ферма также не может быть квадратным, кубическим или иным гиперкубическим, но в единственном случае может быть треугольным: F 0 = 3. {displaystyle F_{0}=3.} Число Ферма также не может быть тетраэдральным и гипертетраэдральным любой размерности выше 2-й.
Среди чисел Фибоначчи имеются только три квадратных числа (0, 1 и 144) и четыре треугольных (1, 3, 21, 55, последовательность A039595 в OEIS). Если повернуть треугольник Паскаля, как показано на рисунке, то числа Фибоначчи можно получить как суммы вдоль восходящих диагоналей; этот факт даёт разложение числа Фибоначчи по гипертетраэдральным числам.
Среди чисел Люка квадратных чисел два (1 и 4), а треугольных три (1, 3, 5778).
Числа Каталана C a t n {displaystyle Cat_{n}} выражаются через гипертетраэдральные числа следующим образом:
C a t n = S n + 1 [ n ] − S n + 2 [ n − 1 ] {displaystyle Cat_{n}=S_{n+1}^{[n]}-S_{n+2}^{[n-1]}}
Ещё один класс чисел, тесно связанных с фигурными — числа Стирлинга второго рода S ( n , m ) . {displaystyle S(n,m).} Этот класс включает все треугольные числа: T n = S ( n + 1 , n ) , {displaystyle T_{n}=S(n+1,n),} а выражение S ( n , 2 ) + 1 {displaystyle S(n,2)+1} равно 2-му по порядку n {displaystyle n} -мерному гиперкубическому числу Q 2 [ n ] . {displaystyle Q_{2}^{[n]}.} Наконец, всякое n {displaystyle n} -мерное гиперкубическое число разлагается по S ( n , m ) {displaystyle S(n,m)} следующим образом:
Q n [ d ] = ∑ m = 0 d S ( d , m ) x ( x − 1 ) … ( x − m + 1 ) {displaystyle Q_{n}^{[d]}=sum _{m=0}^{d}{S(d,m)x(x-1)dots (x-m+1)}}
Комментариев пока еще нет. Вы можете стать первым!
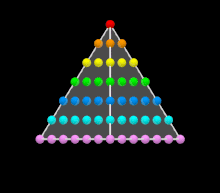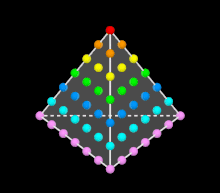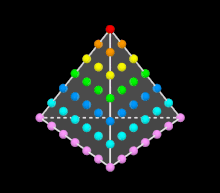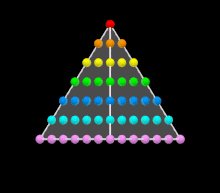




































































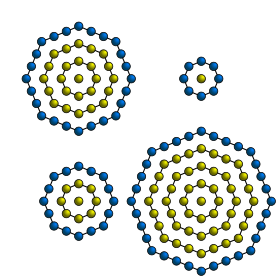










































![{displaystyle S_{n}^{[d]}={frac {(n-1+d)!}{(n-1)! d!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28a47962c7f0baec91883adc82aeda56e4695839)





![{displaystyle Cat_{n}=S_{n+1}^{[n]}-S_{n+2}^{[n-1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e303a9fc2b2d32f4a8e53599babb6e2ada6ef0e9)
![{displaystyle Q_{n}^{[d]}=sum _{m=0}^{d}{S(d,m)n(n-1)dots (n-m+1)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52d9f9637833e09aa2d6a5d27d278891ea9a0ee9)














































