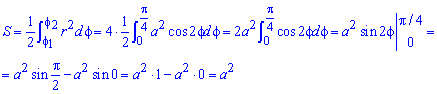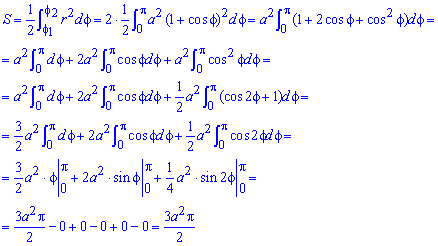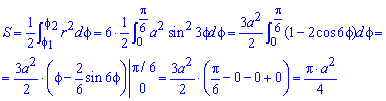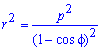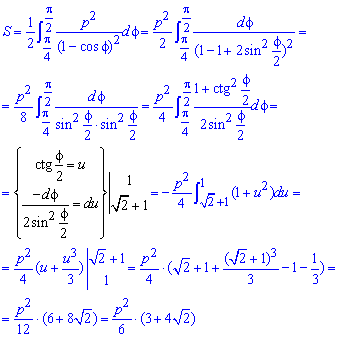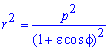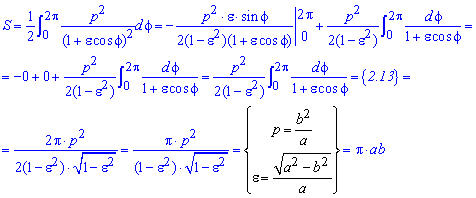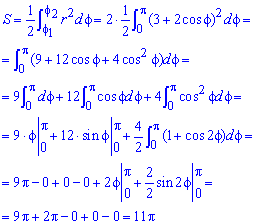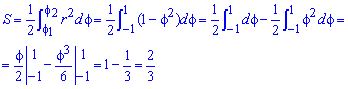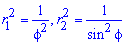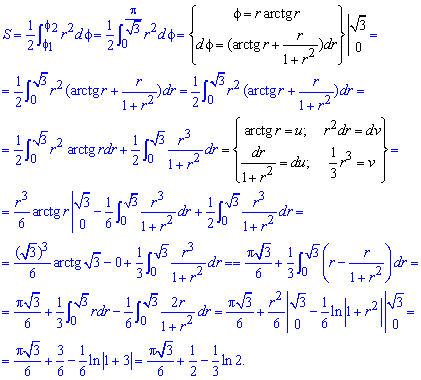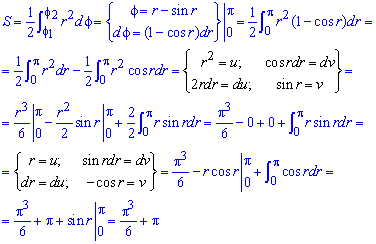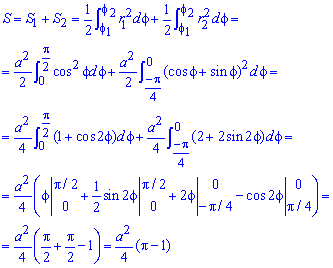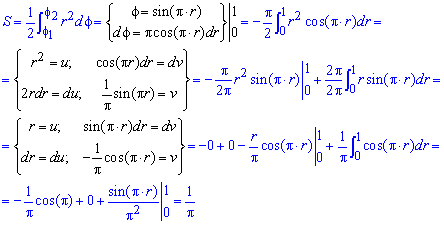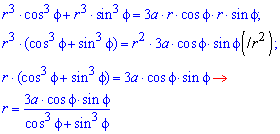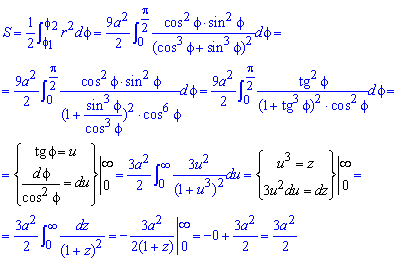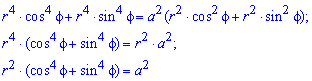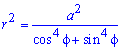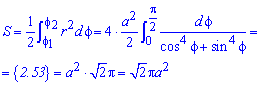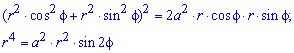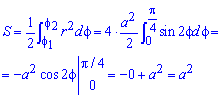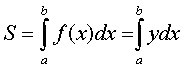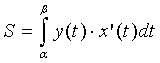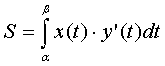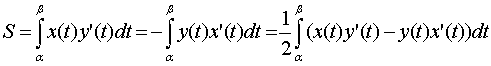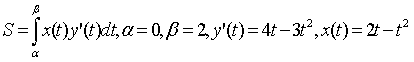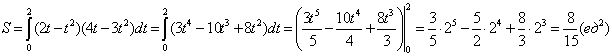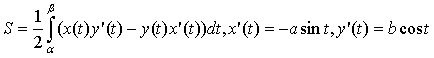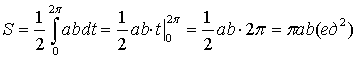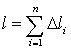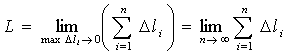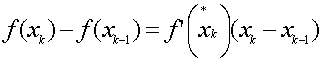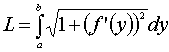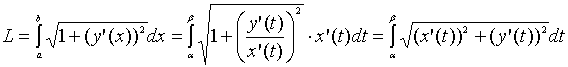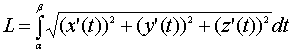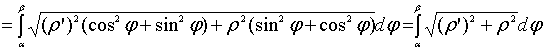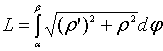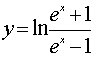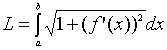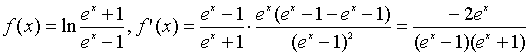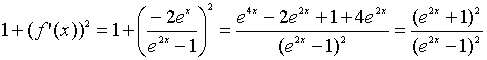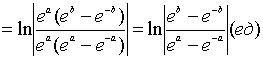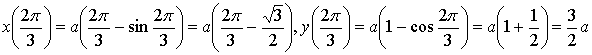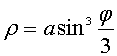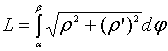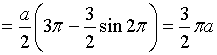Когда мы выясняли геометрический смысл определенного интеграла, у нас получилась формула, с помощью которой можно найти площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми x=a, x=b, а также непрерывной (неотрицательной или неположительной) функцией y=f(x). Иногда удобнее задавать функцию, ограничивающую фигуру, в параметрическом виде, т.е. выражать функциональную зависимость через параметр t. В рамках данного материала мы покажем, как можно найти площадь фигуры, если она ограничена параметрически заданной кривой.
После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.
Основная формула для вычисления
Допустим, что у нас имеется криволинейная трапеция, границами которой являются прямые x=a, x=b, ось Ox и параметрически заданная кривая x=φ(t)y=ψ(t), а функции x=φ(t) и y=ψ(t) являются непрерывными на интервале α; β, α<β, x=φ(t) будет непрерывно возрастать на нем и φ(α)=a, φ(β)=b.
Чтобы вычислить площадь трапеции при таких условиях, нужно использовать формулу S(G)=∫αβψ(t)·φ'(t)dt.
Мы вывели ее из формулы площади криволинейной трапеции S(G)=∫abf(x)dx методом подстановки x=φ(t)y=ψ(t):
S(G)=∫abf(x)dx=∫αβψ(t)d(φ(t))=∫αβψ(t)·φ'(t)dt
Учитывая монотонное убывание функции x=φ(t) на интервале β; α, β<α, нужная формула принимает вид S(G)=-∫βαψ(t)·φ'(t)dt.
Если функция x=φ(t) не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.
Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой
В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.
Условие: найдите площадь фигуры, которую образует линия, заданная уравнениями вида x=2cos ty=3sin t.
Решение
У нас есть параметрически заданная линия. Графически ее можно отобразить в виде эллипса с двумя полуосями 2 и 3. См на иллюстрацию:
Попробуем найти площадь 14 полученной фигуры, которая занимает первый квадрант. Область находится в интервале x∈a; b=0; 2. Далее умножим полученное значение на 4 и найдем площадь целой фигуры.
Вот ход наших вычислений:
x=φ(t)=2cos ty=ψ(t)=3sin tφα=a⇔2cos α=0⇔α=π2+πk, k∈Z,φβ=b⇔2cos β=2⇔β=2πk, k∈Z
При k, равном 0, мы получим интервал β; α=0; π2. Функция x=φ(t)=2cos t на нем будет монотонно убывать (подробнее см. статью об основных элементарных функциях и их свойствах). Значит, можно применить формулу вычисления площади и найти определенный интеграл, используя формулу Ньютона-Лейбница:
-∫0π23 sin t·2cos t’dt=6∫0π2sin2t dt=3∫0π2(1-cos(2t)dt==3·t-sin(2t)20π2=3·π2-sin2·π22-0-sin2·02=3π2
Значит, площадь фигуры, заданной исходной кривой, будет равна S(G)=4·3π2=6π.
Ответ: S(G)=6π
Уточним, что при решении задачи выше можно было взять не только четверть эллипса, но и его половину – верхнюю или нижнюю. Одна половина будет расположена на интервале x∈a; b=-2; 2. В этом случае у нас бы получилось:
φ(α)=a⇔2cos α=-2⇔α=π+πk, k∈Z,φ(β)=b⇔2cos β=2⇔β=2πk, k∈Z
Таким образом, при k равном 0, мы получили β; α=0; π. Функция x=φ(t)=2cos t на этом интервале будет монотонно убывать.
После этого вычисляем площадь половины эллипса:
-∫0π3sin t·2cos t’dt=6∫0πsin2t dt=3∫0π(1-cos(2t)dt==3·t-sin(2t)20π=3·π-sin2·π2-0-sin2·02=3π
Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.
Можно составить параметрическое уравнение данного эллипса, центр которого будет расположен в начале координат. Оно будет иметь вид x=a·cos ty=b·sin t. Действуя так же, как и в примере выше, получим формулу для вычисления площади эллипса Sэлипса=πab.
Задать окружность, центр которой расположен в начале координат, можно с помощью уравнения x=R·cos ty=R·sin t, где t является параметром, а R – радиусом данной окружности. Если мы сразу воспользуемся формулой площади эллипса, то то у нас получится формула, с помощью которой можно вычислить площадь круга с радиусом R: Sкруга=πR2.
Разберем еще одну задачу.
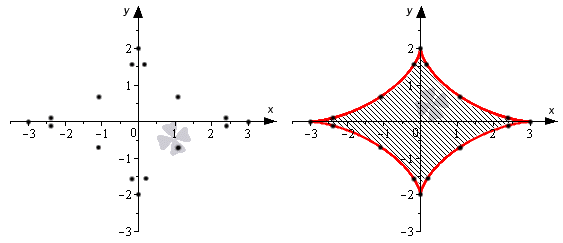
Условие: найдите, чему будет равна площадь фигуры, которая ограничена параметрически заданной кривой x=3cos3ty=2sin3t.
Решение
Сразу уточним, что данная кривая имеет вид вытянутой астроиды. Обычно астроида выражается с помощью уравнения вида x=a·cos3ty=a·sin3t.
Теперь разберем подробно, как построить такую кривую. Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.
У нас x=φ(t)=3cos3t, y=ψ(t)=2sin3t.
Данные функции являются определенными для всех действительных значений t. Для sin и cos известно, что они являются периодическими и их период составляет 2 пи. Вычислив значения функций x=φ(t)=3cos3t, y=ψ(t)=2sin3t для некоторых t=t0∈0; 2π π8, π4, 3π8, π2,…, 15π8, получим точки x0; y0=(φ(t0); ψ(t0)).
Составим таблицу итоговых значений:
| t0 | 0 | π8 | π4 | 3π8 | π2 | 5π8 | 3π4 | 7π8 | π |
| x0=φ(t0) | 3 | 2.36 | 1.06 | 0.16 | 0 | -0.16 | -1.06 | -2.36 | -3 |
| y0=ψ(t0) | 0 | 0.11 | 0.70 | 1.57 | 2 | 1.57 | 0.70 | 0.11 | 0 |
| t0 | 9π8 | 5π4 | 11π8 | 3π2 | 13π8 | 7π4 | 15π8 | 2π |
| x0=φ(t0) | -2.36 | -1.06 | -0.16 | 0 | 0.16 | 1.06 | 2.36 | 3 |
| y0=ψ(t0) | -0.11 | -0.70 | -1.57 | -2 | -1.57 | -0.70 | -0.11 | 0 |
После этого отметим нужные точки на плоскости и соединим их одной линией.
Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее x∈a; b=0; 3:
φ(α)=a⇔3cos3t=0 ⇔α=π2+πk, k∈Z,φ(β)=b⇔3cos3t=3⇔β=2πk, k∈Z
Если k равен 0, то у нас получится интервал β; α=0; π2, и функция x=φ(t)=3cos3t на нем будет монотонно убывать. Теперь берем формулу площади и считаем:
-∫0π22sin3t·3cos3t’dt=18∫0π2sin4t·cos2tdt==18∫0π2sin4t·(1-sin2t)dt=18∫0π2sin4tdt-∫0π2sin6tdt
У нас получились определенные интегралы, которые можно вычислить с помощью формулы Ньютона-Лейбница. Первообразные для этой формулы можно найти, используя рекуррентную формулу Jn(x)=-cos x·sinn-1(x)n+n-1nJn-2(x), где Jn(x)=∫sinnxdx.
∫sin4tdt=-cos t·sin3t4+34∫sin2tdt==-cos t·sin3t4+34-cos t·sin t2+12∫sin0tdt==-cos t·sin3t4-3cos t·sin t8+38t+C⇒∫0π2sin4tdt=-cos t·sin3t4-3cos t·sin t8+38t0π2=3π16∫sin6tdt=-cos t·sin5t6+56∫sin4tdt⇒∫0π2sin6tdt=-cos t·sin5t60π2+56∫0π2sin4tdt=56·3π16=15π96
Мы вычислили площадь четверти фигуры. Она равна 18∫0π2sin4tdt-∫0π2sin6tdt=183π16-15π96=9π16.
Если мы умножим это значение на 4, получим площадь всей фигуры – 9π4.
Точно таким же образом мы можем доказать, что площадь астроиды, заданной уравнениями x=a·cos3ty=a·sin3t, можно найти по формуле Sастроиды=3πa28, а площадь фигуры, которая ограничена линией x=a·cos3ty=b·sin3t, считается по формуле S=3πab8.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Площадь S криволинейного сектора, ограниченного непрерывной кривой r=r(f) и двумя лучами f=f1 и f=f2, где f1<f2 равняется половине определенного интегралу от квадрата радиуса кривой, проинтегрированного в пределах изменения угла
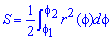
Для запоминания основных моментов схема интегрирования и нахождения площадей из примера в пример будет повторяться. Сами ррешеня по возможности будут проиллюстрированы графиками исследуемых кривых.
Найти площади фигур, ограниченных кривыми, заданными в полярных координатах
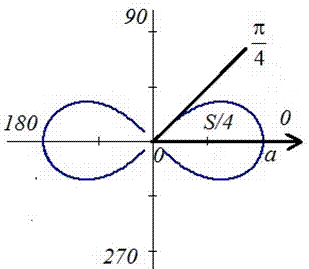
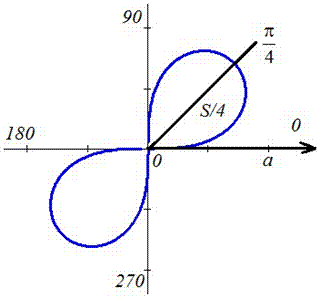
Пример 2.106 (2418) Вычислить площадь фигуры, ограниченной кривыми r2=a2*cos(2f) (лемниската Бернулли).
Вычисление: Лемниската Бернулли – геометрическое место точек, произведение расстояний от которых до двух фиксированных точек (фокусов) остается постоянным и равняется квадрату половины расстояния между фокусами.
Запишем подинтегральную функцию: r2=a2*cos(2f) (известна за условием).
Найдем пределы интегрирования:
задана кривая замкнутая, симметричная относительно прямых r*cos(f)=0 и r*sin(f)=0.
Наведем график лемнискаты Бернулли
Поскольку заданная функция осями координат делится на четыре равных части и достигает своих критических значений при f1=0 (r=a) и f2=p/4 (r=0), то площадь фигуры вычислим для одной части лемнискаты, а результат умножим на 4.
Найдем площадь фигуры интегрированиям по углу
Площадь измеряется в единицах квадратных, однако в этом и следующих примерах размерности наводить не будем, хотя о них помним.
Пример 2.107 (2419) Найти площадь фигуры, ограниченной кривыми r=a* (1+cos(f)) – кардиоида.
Вычисление: Кардиоида – плоская линия, которая описывается фиксированной точкой круга, который катится по неподвижному кругу с таким же радиусом a.
Записываем подинтегральную функцию: r2=a2*(1+cos(f))2.
Находим пределы интегрирования: кривая замкнутая, симметричная относительно прямой r*sin(f) =0.
Поскольку заданная функция осями координат делится на две равных части и достигает своих критических значений при f1=0 (r=2a) и f2=p (r=0), то площадь фигуры вычислим для половины кардиоиды, а результат умножим на 2.
График кардиоиды имеет вид
Вычислим площадь фигуры, которая ограничена заданной кривой, интегрированием:
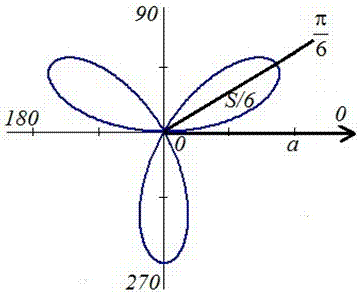
Пример 2.108 (2420) Найти площадь фигуры, ограниченной кривой r=a*sin(f) -трилисник.
Вычисление: Подносим функцию к квадрату, чтобы получить подинтегральную функцию:
r2=a2*sin2(f).
График трилистника в полярной системе координат
Установим пределы интегрирования:
Поскольку заданный график функции делится на шесть равных частей (полупелюсток) и достигает своих критических значений при f1=0 (r=0) и f2=p/6 (r=a/2) то площадь фигуры вычислим для одной его части, а результат умножим на 6.
Находим площадь фигуры интегрированием по углу
Получили простую для вычислений формулу площади трилистника S=Pi*a2/4.
Пример 2.109 ( 2421) Вычислить площадь фигуры, ограниченной кривой 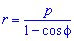
Вычисление: Подносим к квадрату уравнения кривой в полярной системе коринат (СК).
Пределы интегрирования известны f1=p/4, f2=p/2 за условием.
График фигуры, площадь которой нужно найти имеет вид
Интегрированием вычисляем площадь фигуры, которая ограничена параболой:
Для вычисления интеграла следует выполнить замену переменных, не забывая при этом , что изменяются пределы интегрирования.
Пример 2.110 ( 2422) Найти площадь фигуры, ограниченной кривой 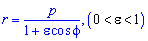
Вычисление: Запишем подинтегральную функцию:
Пределы интегрирования: f1=0, f2=2p (начало и конец кривой эллипса).
График эллипса имеет вид
Находим площадь елипса, воспользовавшись следующей формулой интегрирования
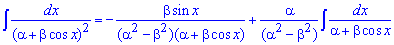
При выведении этой формулы пользовались методом интегрирования частями!
Напоследок превращаем конечную формула с помощью известных формул.
Как видим, ответы задач 2.110 и 2.87 совпадают, то есть площадь эллипса S=Pi*a*b вычислена правильно.
Пример 2.111 (2422.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r=3+2*cos(f).
Вычисление: Сначала находим подинтегральную функцию: r2=(3+2*cos(f))2.
Дальше пределы интегрирования: задана кривая замкнутая, симметричная относительно прямой r*sin(f)=0.
Ее график приведен на рисунку ниже
Поскольку задана кривая осями координат делится на две равных части и достигает своих критических значений при углах f1=0 (r=5) и f2=p (r=1), то вычислим половину площади фигуры, а результат умножим на 2.
Находим площадь фигуры через определенный интеграл
Интеграл в данном случае не тяжелый и, возведя в квадрат подинтегральную функцию и понизив квадрат косинуса, в результате вычислений получим, что площадь равна S=11*Pi.
Пример 2.112 (2424.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r2+f2=1.
Вычисление: Выражаемый подинтегральную функцию: r2=1-f2 .
Найдем пределы интегрирования.
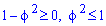
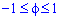
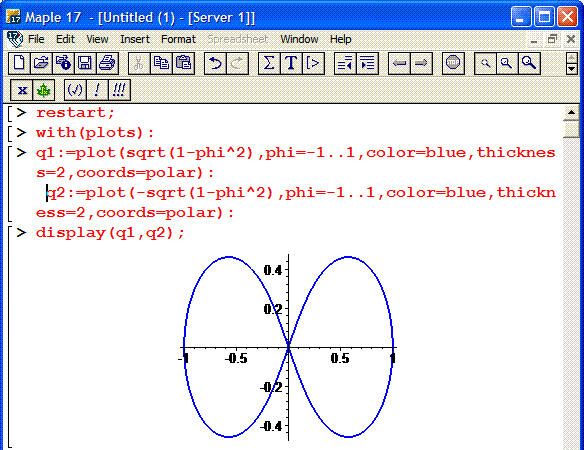
Построим график кривой в математическом пакете Maple17.
Кривая состоит из двух веток корневой функции, поэтому для корректного ее отображения используем следующий код:
> restart;
> with (plots) :
> q1:=plot(sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
q2:=plot(-sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
> display (q1, q2);
Фрагмент программы Maple приведен ниже
Находим площадь фигуры, которая ограничена кривой:
Интеграл в этом задании простей всех, что рассматривались.
Пример 2.113 ( 2422.2) Вычислить площадь фигуры, ограниченной кривыми 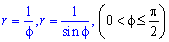
Вычисление: Выписываем подинтегральные функции:
Поскольку на промежутке интегрирования 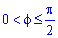
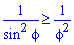
Найдем пределы интегрирования: f1=0 – особенная точка (функция направляется к безграничности) f1=p/2 (известны за условием).
Находим площадь фигуры через предел от интеграла:
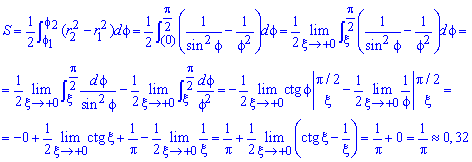
Данный пример хорошо разберите, чтобы не иметь трудностей на экзамене или модуле с подобными.
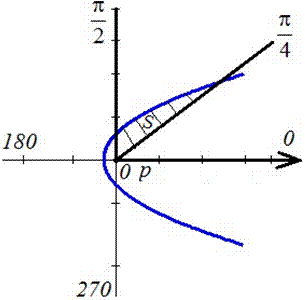
Пример 2.114 ( 2424) Вычислить площадь фигуры, ограниченной кривой 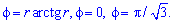
Вычисление: Запишем подинтегральную функцию: r2.
Запишем пределы интегрирования:
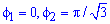
График функций имеет вид
Вычислим площадь фигуры, что приведена на графике.
Для этого сначала находим дифференциал угла f и переходим к интегрированию по радиусу.
Для нахождения интеграла применяем интегрирование частями
Интеграл достаточно трудно находится, поэтому все что содержит формула внимательно проанализируйте.
Пример 2.116 (2424.4) Найти площадь фигуры, ограниченной полярными кривыми f=r-sin(r), f=p.
Вычисление: Подинтегральную функция следующая: r2.
Пределы интегрирования: f1=0, (r=0) начало; f1=p (известно за условием).
График функции имеет вид
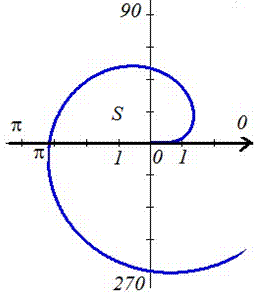
Находим площадь фигуры, применяя дважды интегрирование частями
Интеграл не слишком сложен, все переходы просьба проанализировать самостоятельно.
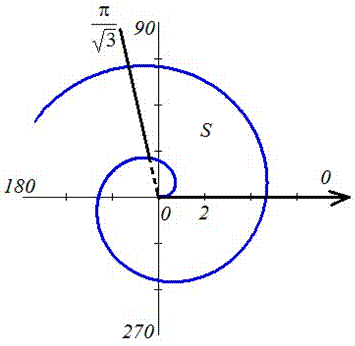
Пример 2423 Вычислить площадь фигуры, ограниченной полярными кривыми r=a*cos(f), r=a(cos(f)+sin(f)), M (a/2;0)єS.
Вычисление: Для представления фигуры, площадь которой нужно найти предварительно выполняем построение графика заданных функций
Поскольку точка M (a/2;0)єS делит искомую площадь на две части, то имеем два интеграла
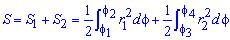
Записываем уравнение подинтегральных функций:
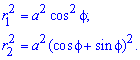
Определяем пределы интегрирования:
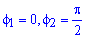
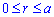
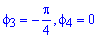
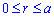
Вычисляем площадь изображенной фигуры интегрированием
Здесь воспользовались известные тригонометрические формулы для понижения степени косинусов и синусов под интегралом. Все остальное сводятся к применению простых формул интегрирования, и нахождения их значений.
Пример 2424.2 Найти площадь фигуры, ограниченной полярными кривыми f=sin(p*r), r пренадлежит [0;1].
Вычисление: Запишем подинтегральную функцию: r2.
Запишем пределы интегрирования: При росте r от 0 к 1/2 угол f растет от 0 к 1, при росте r от 1/2 к 1 угол f спадает от 1 к 0, поэтому величина интеграла в пределах r пренадлежит [0;1] имеет знак “минус”.
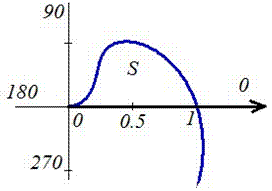
Находим площадь фигуры, предварительно перейдя к новой переменной под интегралом:
Перед интегралом (после замены переменных) поставили знак “минус”, поскольку интеграл является отрицательным на этом промежутке, а площадь должна быть положительной.
Перейти к полярным координатам и найти площади фигур, ограниченных кривыми
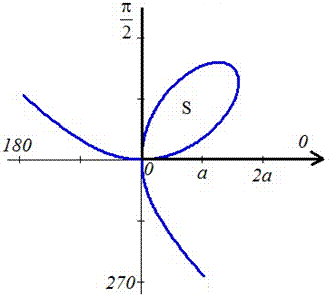
Пример 2426 Перейти к полярным координатам и найти площадь фигуры x3+y3=3a*x*y (лист Декарта)
Вычисление: Перейдем от прямоугольной системы координат к полярной системе координат за формулами перехода:
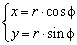
При подстановке в уравнение получим
Поднесем к квадрату, чтобы получить подинтегральную функцию:
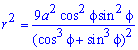
Выпишем пределы интегрирования:
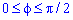
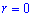
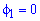
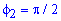
График функции имеет вид
Найдем площадь фигуры интегрированиям:
Для получения конечной формулы площади дважды применяли замену переменных под интегралом.
Внимательно разберите, как при этом изменяются пределы и эффективность методики.
Пример 2427 Перейти к полярным координатам и найти площадь фигуры x4+y4=3a2(x2+y2)
Вычисление: Переходим от прямоугольной к полярной системе координат:
Выражаемый подинтегральную функцию делением:
Запишем пределы интегрирования:
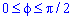
Ее график изображен на рисунку
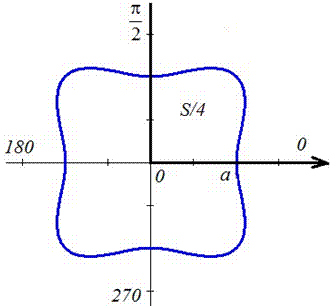
Оси прямоугольной системы координат являются осями симметрии для фигуры, которая ограничена заданной линией, поэтому площадь найдем для симметричной части и результат умножим на 4.
Находим площадь фигуры через интеграл:
Пример 2428 Перейти к полярным координатам и найти площадь фигуры (x2+y2)2=2a2*x*y (лемниската).
Вычисление: Выполняем переход от прямоугольной к полярной системе координат:
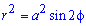
График исследуемой кривой следующий
Запишем пределы интегрирования: учитывая симметрию точек лемнискаты относительно прямой r*sin(f) =r*cos (f) и относительно начала координат, то площадь фигуры будем искать в пределах 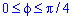
Находим площадь фигуры интегрированием:
Вычислений в этом задании минимум.
В следующих публикациях Вы найдете больше примеров на применение определенного интеграла при вычислении длины дуги, объемов фигур вращения и площадей поверхностей.
Вычисление площади фигуры, ограниченной кривой, заданной в параметрическом виде.
Пусть x=x(t), y=y(t),
где
–
параметрические уравнения кусочно-гладкой
кривой. Если данные уравнения определяют
некоторую функцию y=f(x)
на отрезке [a,b]
(без ограничения общности будем считать,
что
на
отрезке [a,b]),
то площадь криволинейной трапеции,
ограниченной осью OX,
кривой y=f(x)
и прямыми x=a и x=b,
может быть найдена по формуле
.
Вводя
замену переменной y=y(t), x=x(t), dx= x’(t)dt,
получим формулу для вычисления площади
фигуры при параметрическом задании
границы:
.
Аналогично
может быть получена формула
.
Таким
образом, вычисление площади фигуры,
ограниченной кривой в параметрической
форме, может быть рассмотрено как замена
переменной при вычислении площади в
декартовых координатах.
Если x=x(t), y=y(t),
–
параметрические уравнения кусочно-гладкой
замкнутой кривой, пробегаемой в
положительном направлении (то есть
таким образом, что фигура, ограниченная
заданным контуром остается слева), то
площадь S этой
фигуры равна:
,
где
–
значения параметра, соответствующие
началу и концу обхода контура фигуры в
положительном направлении.
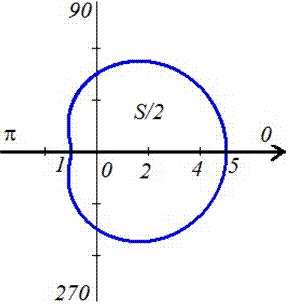
Пример
1. Найти площадь фигуры, ограниченной
кривой, заданной параметрически:
.
Решение.
Выясним, какую фигуру ограничивает
заданная кривая. Функции x=x(t)
и y=y(t)
определены, непрерывны и дифференцируемы
при любом действительном значении
параметра
.
Если
,
то
,
а если
,
то
.
Наибольшее
значение x принимает
при x’(t)=0,
2-2t=0; t=1, x(1)=1; y(1)=1.
Если x=0,
то t=2
или t=0.
При этих же значениях параметра y=0.
Таким образом, точка с координатами
(0;0) является точкой самопересечения.
Следовательно, искомая площадь ограничена
петлей кривой, расположенной в первом
квадранте, и соответствует изменению
параметра от t=0
до t=2
при положительном направлении обхода
(рисунок 7).
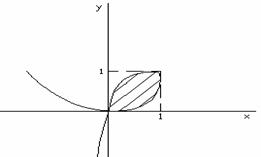
Рисунок
7.
Площадь
искомой фигуры можно вычислить по
формуле
,
.
Поскольку
некоторые кривые могут быть заданы
простыми параметрическими уравнениями,
то вычисление площади фигуры, ограниченной
замкнутой кривой, в декартовых координатах
зачастую удобнее проводить, перейдя к
параметрической форме записи.
Пример
2. Вычислить площадь фигуры ограниченной
эллипсом
.
Решение.
Запишем уравнение эллипса в параметрической
форме: x=a×cost, y=b×sint,
.
Возрастание параметра от 0 до
2p соответствует
положительному направлению обхода.
Наиболее простой вид подынтегральное
выражение примет, если воспользоваться
формулой
;
;
.
Вычисление длины дуги кривой.
Пусть
в декартовой системе координат на
плоскости дана кривая, являющаяся
графиком непрерывной дифференцируемой
функции y=f(x)
с непрерывной производной на отрезке
[a,b].
Разобьем отрезок [a,b]
произвольным образом на n частей
точками
.
Найдем значения функции f(x)
в точках разбиения. Тогда дуга кривой f(x)
на [a,b]
разобьется на n частей
точками
.
Проведем хорды
и
обозначим их длины
соответственно.
Полученная ломаная
имеет
длину
.
Определение. Длиной
дуги кривой y=f(x)
на отрезке [a,b]
называется предел, к которому стремится
длина вписанной ломаной при стремлении
к нулю длины ее наибольшего звена (или,
что то же самое, при неограниченном
увеличении числа точек деления)
.
Длина
отдельного звена ломаной может быть
найдена как длина отрезка
:
.
Поскольку
функция f(x)
непрерывна и дифференцируема на всем
промежутке [a,b],
то, по теореме Лагранжа о дифференцируемых
функциях, найдется такая точка
на
отрезке
,
что
.
Если
обозначить
,
то формулу для
можно
переписать в виде
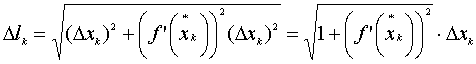
Таким
образом, длина дуги y=f(x)
на отрезке [a,b]
определяется формулой
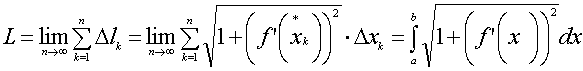
в
силу непрерывности f’(x)
и определения интегральной суммы.
Выражение
называется
дифференциалом дуги.
Если
кривая задана уравнением x=f(y), yÎ[a,b],
то, рассуждая аналогично, можно получить
формулу
,
.
Если
кривая на плоскости задана
параметрически: x=x(t), y=y(t),
;
,
где x(t), y(t)
– дифференцируемые функции, имеющие
на отрезке
непрерывную
производную, то, выполнив замену
переменной в предыдущих формулах,
получим:
,
.
Если
задана пространственная кривая
параметрическими
уравнениями x=x(t), y=y(t), z=z(t),
,
где x(t), y(t), z(t)
– дифференцируемые на отрезке
функции
с непрерывной производной, то длина
кривой вычисляется по формуле
,
.
Пусть
в полярных координатах кривая задана
уравнением
,
где
–
дифференцируемая функция с непрерывной
на
производной
.
Запишем формулы перехода от декартовой
системы координат к полярной:
.
Если в эти формулы подставить
,
то получится параметрическое задание
кривой, где параметр
–
полярный угол. Тогда по формуле для
параметрически заданной функции можно
найти длину дуги кривой:
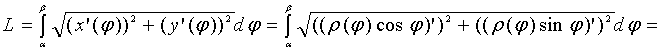
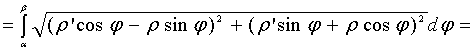
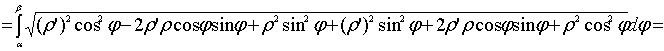
.
,
.
Рассмотрим
некоторые примеры вычисления длины
дуги кривой.
Пример
1. Вычислить длину дуги кривой
от
точки
до
точки
,
(b>a).
Решение.
Воспользуемся формулой
:
;
;
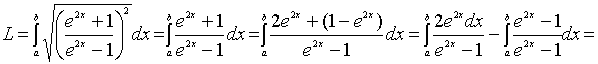
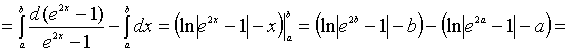
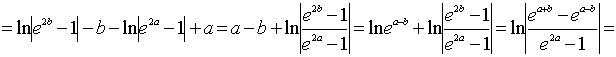
.
Пример
2. На циклоиде x=a(t-sint), y=a(1-cost), a>0,
найти точку, которая делит первую арку
циклоиды по длине в отношении 1:3.
Решение.
Первая арка циклоиды соответствует
изменению параметра t от t=0
до t=2p.
Вычислим длину первой арки циклоиды.
;
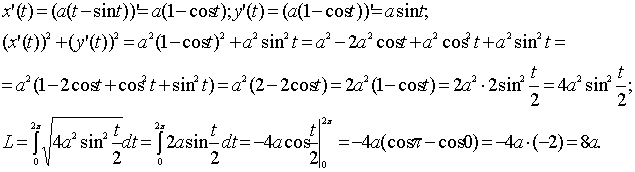
Таким
образом, искомая точка, соответствующая
значению параметра
,
определяет часть кривой, имеющую длину
2а, то есть
.
Найдем
из этого равенства значение
:
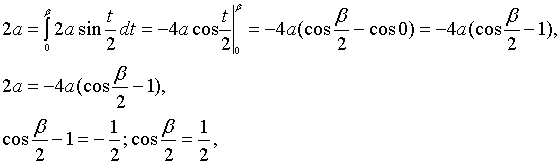
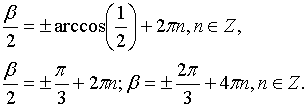
Исходя
из условий задачи, следует выбрать
значение
.
Если
,
то
.
Искомая
точка имеет координаты:
.
Пример
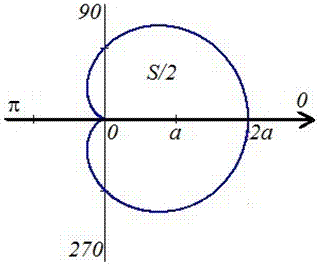
3. Найти длину дуги кривой, заданной в
полярных координатах уравнением
, a>0.
Решение.
Уравнение
, a>0,
определяет замкнутую кривую, соответствующую
изменению j от
0 до 3p (рисунок
8).
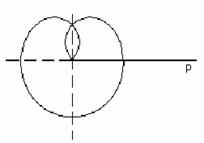
Рисунок
8.
Воспользуемся
формулой
:
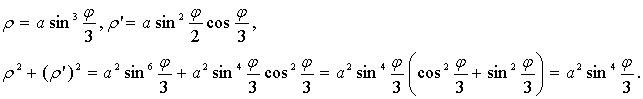
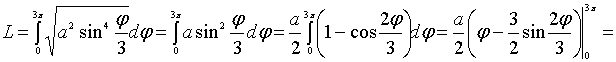
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вычисление площади фигуры – это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур. Именно при решении таких задач очень удобно использовать интегральное исчисление.
Определение.
Криволинейной трапецией называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1). Площадь криволинейной трапеции можно обозначить S(G).
Определенный интеграл ʃаb f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.
То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл ʃаb f(x)dx.
Таким образом, S(G) = ʃаb f(x)dx.
В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле S(G) = -ʃаb f(x)dx.
Пример 1.
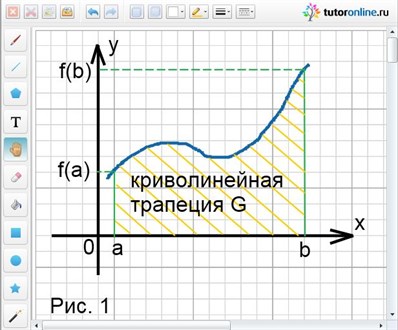
Вычислить площадь фигуры, ограниченной линиями у = х3; у = 1; х = 2.
Решение.
Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.
Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.
Используя формулу S = ʃаb f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:
{у = х3,
{у = 1.
Таким образом, имеем х1 = 1 – нижний предел и х = 2 – верхний предел.
Итак, S = SDACE – SDABE = ʃ12 x3 dx – 1 = x4/4|12 – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).
Ответ: 11/4 кв. ед.
Пример 2.
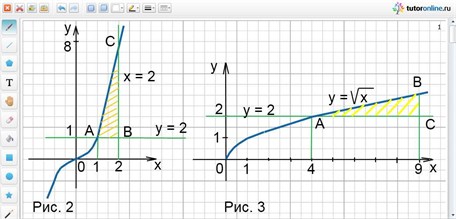
Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.
Решение.
Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции
у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.
Искомая площадь равна S = ʃаb(√x – 2). Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:
{у = √х,
{у = 2.
Таким образом, имеем, что х = 4 = а – это нижний предел.
Итак, S = ∫49 (√x – 2)dx = ∫49 √x dx –∫49 2dx = 2/3 x√х|49 – 2х|49 = (18 – 16/3) – (18 – 8) = 2 2/3 (кв. ед.).
Ответ: S = 2 2/3 кв. ед.
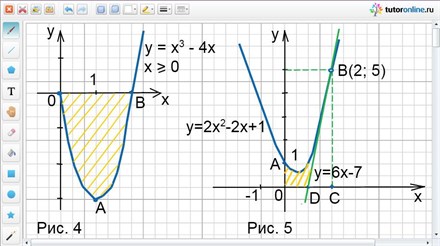
Пример 3.
Вычислить площадь фигуры, ограниченной линиями у = х3 – 4х; у = 0; х ≥ 0.
Решение.
Построим график функции у = х3 – 4х при х ≥ 0. Для этого найдем производную у’:
y’ = 3x2 – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.
Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности. Тогда х = 2/√3 – точка минимума, минимальное значение функции уmin = -16/(3√3) ≈ -3.
Определим точки пересечения графика с осями координат:
если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;
если у = 0, то х3 – 4х = 0 или х(х2 – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х1 = 0, х2 = 2, х3 = -2 (не подходит, т.к. х ≥ 0).
Точки А(0; 0) и В(2; 0) – точки пересечения графика с осью Ох.
Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.
Так как функция у = х3 – 4х принимает на (0; 2) отрицательное значение, то
S = |ʃ02 (x3 – 4x)dx|.
Имеем: ʃ02 (x3 – 4х)dx =(x4/4 – 4х2/2)|02= -4, откуда S = 4 кв. ед.
Ответ: S = 4 кв. ед.
Пример 4.
Найти площадь фигуры, ограниченной параболой у = 2х2 – 2х + 1, прямыми х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х0 = 2.
Решение.
Сначала составим уравнение касательной к параболе у = 2х2 – 2х + 1 в точке с абсциссой х₀ = 2.
Так как производная y’ = 4x – 2, то при х0 = 2 получим k = y’(2) = 6.
Найдем ординату точки касания: у0 = 2 · 22 – 2 · 2 + 1 = 5.
Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.
Построим фигуру, ограниченную линиями:
у = 2х2 – 2х + 1, у = 0, х = 0, у = 6х – 7.
Гу = 2х2 – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение 2х2 – 2х + 1 = 0 не имеет решений (D < 0). Найдем вершину параболы:
xb = -b/2a;
xb = 2/4 = 1/2;
yb = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).
Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.
Имеем: SОAВD = SOABC – SADBC.
Найдем координаты точки D из условия:
6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.
Площадь треугольника DBC найдем по формуле SADBC = 1/2 · DC · BC. Таким образом,
SADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.
Далее:
SOABC = ʃ02(2x2 – 2х + 1)dx = (2x3/3 – 2х2/2 + х)|02 = 10/3 (кв. ед.).
Окончательно получим: SОAВD = SOABC – SADBC = 10/3 – 25/12 = 5/4 = 1 1/4 (кв. ед).
Ответ: S = 1 1/4 кв. ед.
Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями. Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Как найти площадь фигуры ограниченной линиями онлайн
Предлагаем Вашему вниманию онлайн калькулятор для нахождения площади фигуры ограниченной кривыми линиями. Калькулятор в автоматическом режиме составляет интеграл, находит границы интегрирования, а также рисует саму фигуру на координатной плоскости. Как частный случай, калькулятор находит площадь криволинейной трапеции.
1). Как найти площадь криволинейной трапеции онлайн.
Площадь криволинейной трапеции, ограниченной кривой y=f(x) [f(x)≥0], прямыми x=a, x=b и отрезком [a,b] оси Ox находим по формуле
Пример. Найти площадь криволинейной трапеции ограниченной кривой y=2x^2+1 и прямыми x=1,x=2.
Решение. Вставляем в калькулятор функции в виде y=2x^2+1,x=1,x=2, нажимаем «Ok», получаем ответ.
2). Как найти площадь фигуры ограниченной линиями онлайн
Площадь фигуры, ограниченной кривыми y=f1(x) и y=f2(x) [f1(x) ≤ f2(x)] и прямыми x=a, x=b вычисляется по формуле y=f1(x) и y=f2(x) [f1(x) ≤ f2(x)] и прямыми x=a, x=b вычисляется по формуле
Пример. Найти площадь фигуры ограниченной линиями y=4x-x^2, y=4-x
Решение. Вставляем функции y=4x-x^2, y=4-x в калькулятор, нажимаем «Ok», получаем ответ.
141,479 просмотров всего, 20 просмотров сегодня