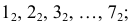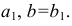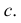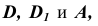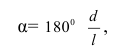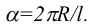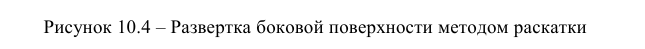Содержание:
Развертки поверхностей:
Развертыванием поверхности называется такое преобразование, в результате которого поверхность всеми точками совмещается с плоскостью. Полученная при этом плоская фигура называется разверткой.
Поверхности делятся на развертываемые и неразвертываемые.
Разветываемые поверхности совмещаются с плоскостью без разрывов и складок. Признаком развертываемости является пересечение соседних образующих или их параллельность. К развертываемым поверхностям относятся многогранные, цилиндрические, конические, торсовые. Развертки многогранников строятся точно, учитываются лишь погрешности инструмента и графических построений. Развертки цилиндрических, конических и торсовых поверхностей получаются приближенно, так как эти поверхности заменяются вписанными в них или описанными около них многогранными поверхностями, которые и развертываются.
Неразвертываемые поверхности с плоскостью не совмещаются, т.е. теоретически они разверток не имеют, так как образующие их скрещиваются. К неразвертываемым относятся поверхности с плоскостью параллелизма (цилиндроид, коноид, косая плоскость), криволинейные (сфера, тор и т.п.) и графические.
В инженерной практике строятся условные развертки неразверты-ваемых поверхностей. Для этого неразвертываемая поверхность делится на части (доли), которые заменяются развертываемыми поверхностями.
Если рассматривать поверхность и ее развертку как множество точек, то между этими множествами устанавливается взаимооднозначное соответствие, т.е. каждой точке на поверхности соответствует единственная точка на развертке и наоборот.
Свойства развертки
1. Прямая на поверхности переходит в прямую на развертке.
2. Параллельные прямые на поверхности будут параллельными прямыми на развертке.
3. На развертке сохраняются:
- – длина линии, лежащей на поверхности;
- – величина угла между линиями поверхности;
- – величина площади фигуры на поверхности.
Развертки прямых круговых цилиндра и конуса
Развертка боковой поверхности прямого кругового цилиндра представляет собой прямоугольник, высота которого равна высоте цилиндра, а длина – длине окружности основания
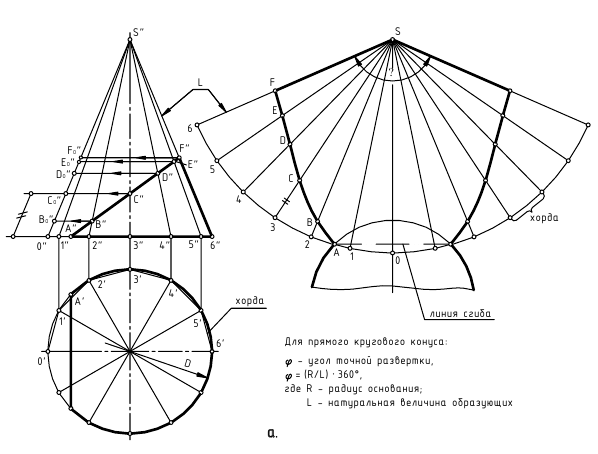
Развертка боковой поверхности прямого кругового конуса (рис. 241) представляет собой круговой сектор. Длина дуги
откуда
Отложив центральный угол 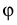
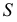
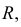
Развертки линейчатых поверхностей
Способ триангуляции
Способ триангуляции (треугольников) универсален, его можно применять для построения разверток любых поверхностей, в том числе и криволинейных (например, подвесные сферические своды). Однако способ триангуляции не всегда является рациональным. Для каждой группы поверхностей рекомендуется соответствующий графический способ построения разверток. Все линейчатые поверхности, включая и неразвертываемые (цилиндроид, коноид, косая плоскость), можно развернуть способом триангуляции.
Сущность способа заключается в следующем:
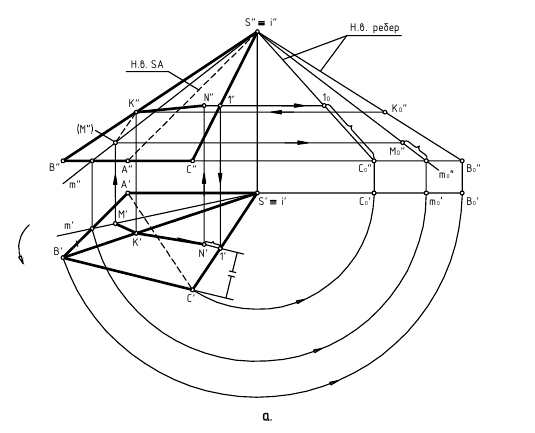
1. Криволинейная поверхность заменяется вписанной в нее многогранной поверхностью. Так, на рис. 242 в наклонный эллиптический конус (нормальное сечение – эллипс) с круговым основанием вписана двенадцатигранная пирамида. Для этого основание конуса разбивается па 12 равных частей.
Исследование точности построения разверток показало, что оптимально деление окружности на 12 частей. При делении на 8 и менее частей длина кривой на развертке получается значительно короче длины окружности основания. При делении более чем на 12 частей, увеличивается величина графических неточностей. Полученные после деления окружности дуги заменяются стягивающими хордами. Затем проводятся образующие 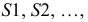
2. Определяются натуральные величины сторон каждого треугольника 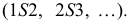
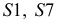
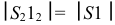
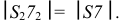
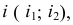
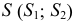
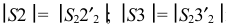
Третьей стороной у каждого треугольника являются хорды, которые на горизонтальную плоскость проекций проецируются без искажения. Натуральные величины хорд
3. Развертка выполняется последовательным построением всех треугольников. Каждый треугольник строят по трем сторонам, натуральные величины которых известны. Если отсек поверхности симметричен, то развертку следует выполнять также симметричной и построение начинать с оси симметрии. Допускается строить половину развертки, которая с одной стороны должна быть ограничена осевой линией. Рекомендуется поверхность разрезать по самой короткой образующей, чтобы длина соединительных “швов” была наименьшей.
Осевая линия располагается на чертеже вертикально или горизонтально. На ней откладывается отрезок 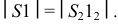
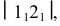
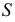
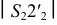
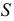
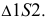
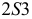
На развертках часто приходится строить линии, расположенные на поверхностях. К ним относятся линии пересечения двух поверхностей и сечения поверхности плоскостью.
Для построения на развертке точки выполняют следующее:
- через данную точку проводят линию, лежащую на поверхности и удобную для построения (чаще всего это прямая или окружность). На рис. 242 точка
принадлежит образующей
- определяют натуральную величину этой линии и на нее переносят рассматриваемую точку. На рис. 242
– натуральная величина образующей и точка
- на развертке строят соответствующую линию. Образующая
располагается между образующими
и
Отрезок
равен хорде, а расстояние
берется равным натуральной величине –
Способ нормального сечения
Способ применяется для построения разверток призматических и цилиндрических поверхностей.
При построении развертки призматической поверхности необходимо все ее грани последовательно совместить с плоскостью. В общем случае (наклонная призма с непараллельными основаниями) боковые грани призмы – трапеции. Чтобы построить натуральные величины этих граней, необходимо определить натуральные величины ребер призмы, которые являются основаниями трапеций – отрезки 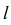
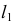
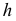
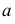
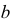
В зависимости от того, высота или боковые стороны применяются при построении разверток, различают два способа: нормального сечения и раскатки. В первом способе расстояние между образующими определяется при помощи нормального сечения. В способе раскатки используются натуральные величины сторон основания призмы.
Развертка призматической поверхности строится точно, не считая графических погрешностей. При построении развертки цилиндрической поверхности необходимо сначала вписать в нее призматическую поверхность, которую затем развернуть. Следовательно, развертка цилиндрической поверхности является приближенной.
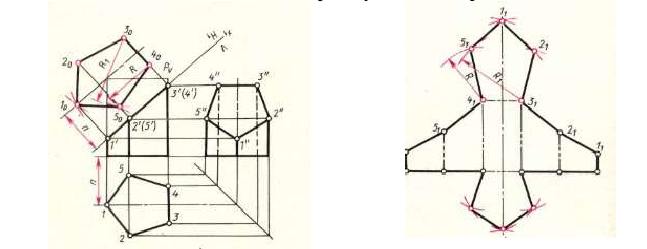
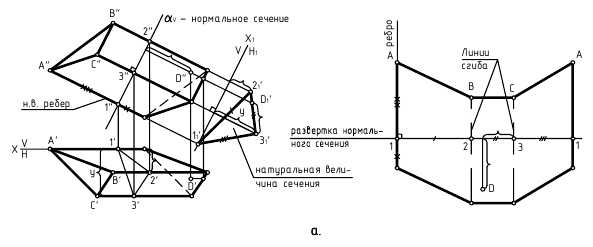
На рис. 244 показано построение развертки наклонной призмы способом нормального сечения. При помощи нормального сечения, перпендикулярного к образующим, определяют расстояния между ними. Способ целесообразно применять в тех случаях, когда основания призмы или цилиндра заданы в общем положении.
Последовательность построений:
1) определяются натуральные величины образующих, если они заданы в общем положении (см. рис. 244). Натуральные величины ребер определяются проецированием на дополнительную плоскость проекций 
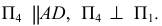
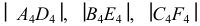
2) строится нормальное сечение перпендикулярно ребрам призмы. Так как ребра параллельны плоскости 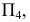
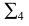
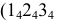
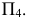
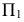
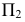
3) определяется натуральная величина нормального сечения любым способом. В данном примере она определена проецированием на плоскость 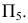
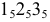
4) строится развертка следующим образом:
а) периметр нормального сечения “развертывается” в прямую линию, на которой 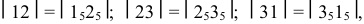
б) через точки 1, 2, 3 проводятся образующие, перпендикулярные развертке нормального сечения;
в) на этих линиях откладываются натуральные величины образующих: 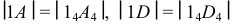
г) полученные точки соединяются ломаной линией.
На рис. 244 показано построение на развертке точки 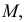
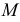
Развертки криволинейных поверхностей вращения
Криволинейные поверхности вращения (сфера, тор и др.) относятся к неразвертываемым, их нельзя совместить с плоскостью без разрывов и складок, поэтому при выполнении их из листового материала строятся условные развертки.
Последовательность построений:
- поверхность разрезается по меридианам или параллелям на ряд частей;
- каждая такая часть заменяется вписанной или описанной развертываемой поверхностью (цилиндрической или конической);
- строятся развертки отдельных частей, из которых затем собирается заданная поверхность.
При разрезании по меридианам каждая доля заменяется описанной цилиндрической поверхностью. Такой прием называется способом вспомогательных цилиндров.
При разрезании по параллелям поверхность разбивается на ряд поясов, которые заменяются вписанными коническими поверхностями. Этот прием называется способом вспомогательных конусов.
Способ вспомогательных цилиндров
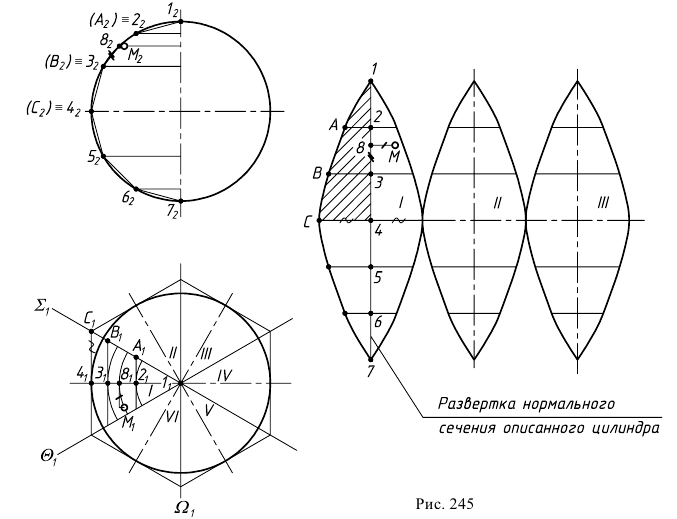
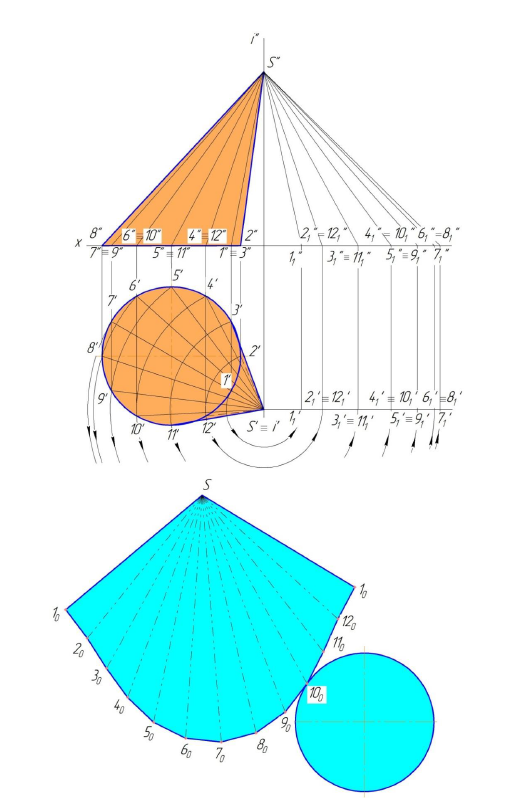
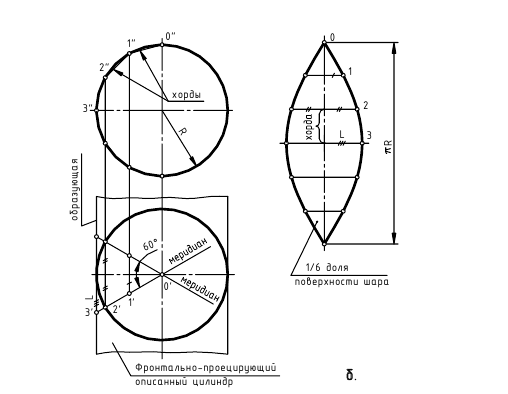
Построение развертки сферы способом вспомогательных цилиндров показано на рис. 245:
- поверхность сферы меридиональными плоскостями
и
разрезают на равные части (доли). Рекомендуется разбивать ее не менее чем на 12 частей. В примере принято 6 долей для того, чтобы отрезки были крупнее и чертеж более четким;
- каждую такую долю заменяют описанной цилиндрической поверхностью, касающейся ее по линии симметрии доли.
Цилиндрическая поверхность касается доли I по главному меридиану. Разделив его на 6 равных частей, через точки 2, 3, 4, 5, 6 проводят параллели – окружности. Затем строят образующие цилиндра, касающиеся параллелей в точках 2, 3, 6. Образующие 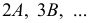
3) строят развертку каждого описанного цилиндра способом нормального сечения:
а) нормальным сечением доли 1 является главный меридиан, который развертывается в отрезок 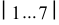
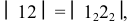
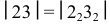
б) через полученные точки 2, 3, 4, 5, 6 проводят образующие цилиндра перпендикулярно ”развертке” нормального сечения. Размеры образующих берут с горизонтальной проекции 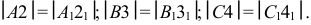
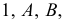
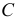
Местоположение точки 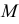
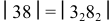
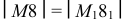
Способ вспомогательных конусов
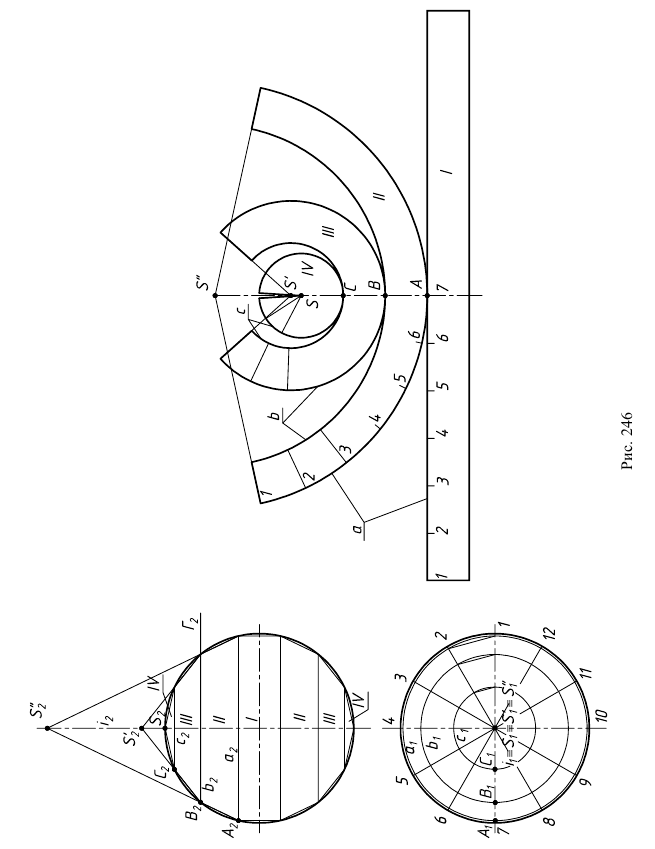
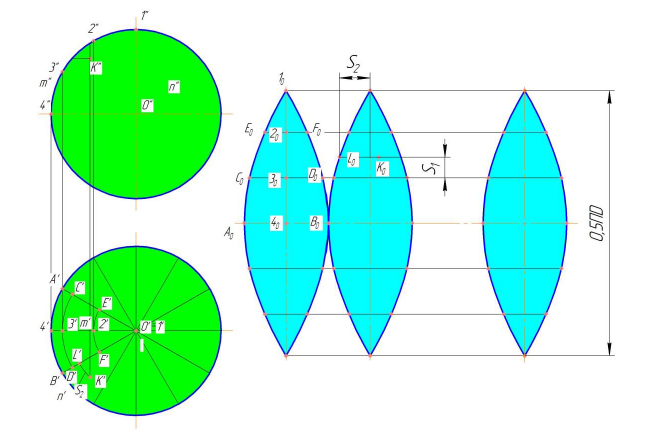
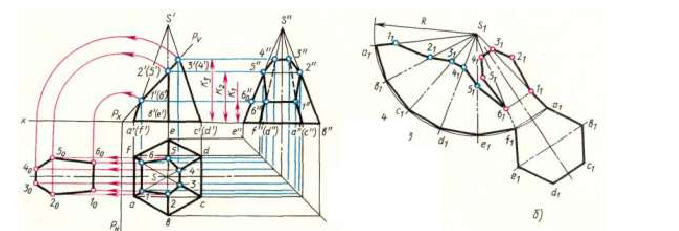
Построение развертки сферы этим способом показано на рис. 246:
1) поверхность сферы разрезается по параллелям горизонтальными плоскостями на ряд поясов и два сегмента;
2) в полученные шаровые пояса и сегменты вписываются поверхности вращения, оси которых совпадают с осью 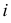
В шаровой сегмент IV вписывается полный конус вращения, вершина которого совпадает с точкой 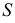
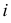
В шаровые пояса III и II вписываются усеченные конусы вращения. Образующие конусов совпадают с хордами 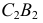
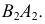
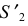
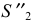
В экваториальный пояс I вписывается цилиндр вращения;
3) строятся развертки вписанных поверхностей.
Разверткой конуса является сектор, радиус которого равен образующей конуса. Для пояса II – образующая 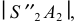
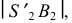
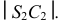
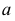
Построенные части I и II соединяются между собой по линиям 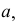
Примеры построения разверток некоторых поверхностей
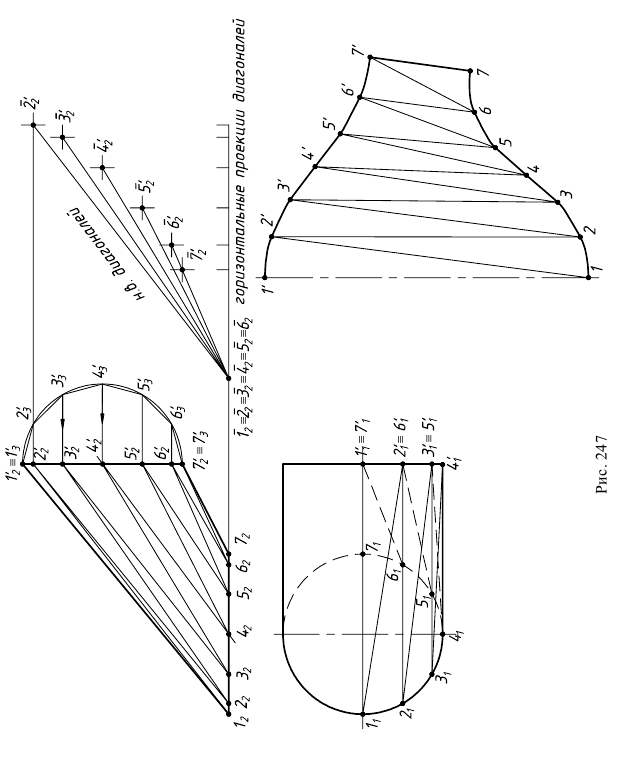
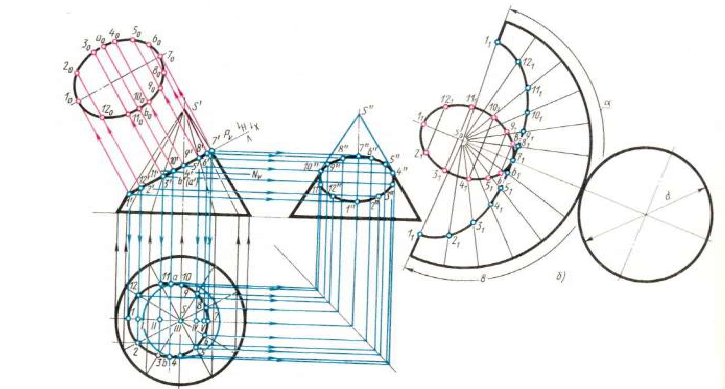
Задача 1 (рис. 247). Дано: поверхность цилиндроида, плоскостью параллелизма которой является плоскость проекций
Требуется: построить развертку способом триангуляции.
Решение:
1. В заданную поверхность вписывается многогранная поверхность. Окружность нижнего основания разбивается на 12 равных частей. Окружность верхнего основания лежит в профильной плоскости уровня, поэтому дополнительно строится полуокружность, соответствующая его профильной проекции. Полуокружность разбивается на 6 равных частей. Полученные дуги заменяются стягивающими хордами, точки деления переносят на фронтальную и горизонтальную проекции верхнего основания. Затем проводятся образующие 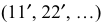
В результате получается многогранная поверхность, ограниченная треугольниками
2. Определяются натуральные величины диагоналей (способом плоскопараллельного перемещения). У образующих натуральными величинами являются их фронтальные проекции, т.к. все они параллельны 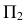
3. Строится развертка. Заданная поверхность имеет плоскость симметрии, поэтому развертка будет симметричной и достаточно построить ее половину.
Поверхность разрезается по наименьшей образующей 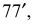
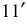
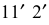
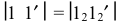
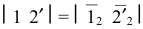
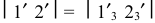
На стороне 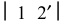
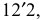
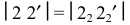
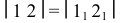
Аналогично продолжается построение следующих треугольников. Полученные точки нижнего основания (1, 2, 3,…, 7) и верхнего основания 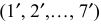
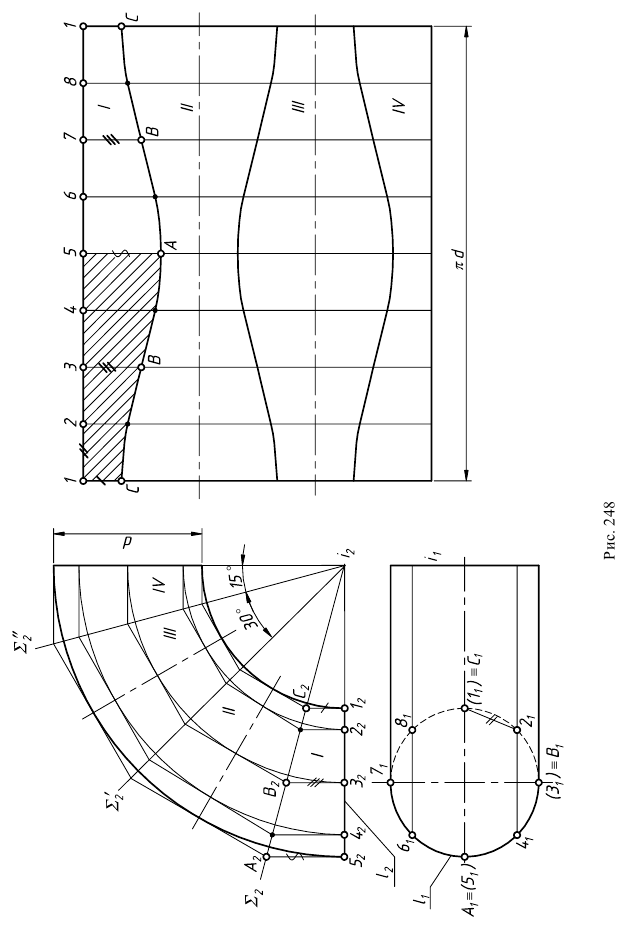
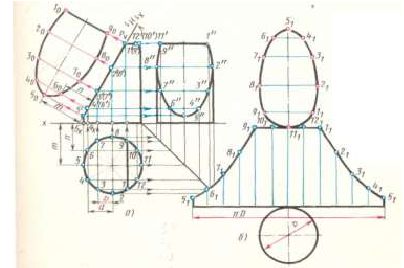
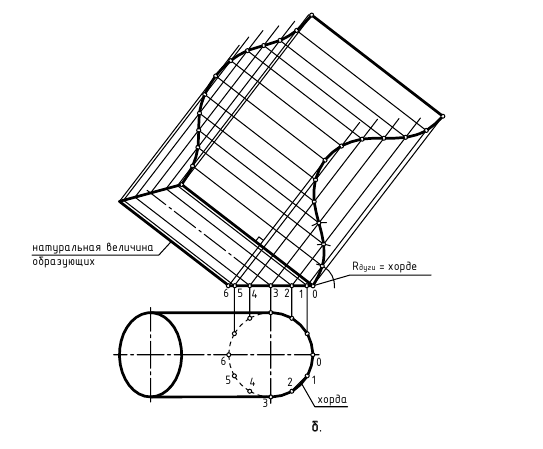
Задача 2 (рис. 248). Дано: отвод под углом 90° (1/4 часть тора).
Требуется: построить развертку поверхности тора способом описанных цилиндров.
Решение:
1. Поверхность тора проецирующими меридиональными плоскостями 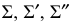
2. Все звенья кругового кольца заменяются описанными цилиндрами. Нормальным сечением этих цилиндров является окружность /, образующая тор. Эта окружность делится на 8 (или 12) частей. Через точки деления 2, 3…8 проводятся параллели (на фронтальной проекции это четверти окружностей радиусами 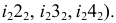
3. Строятся развертки описанных цилиндров способом нормального сечения. Нормальное сечение каждой части (сечение, перпендикулярное образующим цилиндров) есть окружность 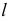
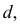
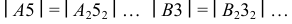
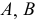
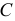
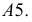
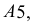
Весь тор можно раскроить из единого листа без обрезков. Для этого развертки звеньев надо разместить на листе так, как показано на рис. 248. Из чертежа видно, что звенья разрезаются попеременно, то по образующей 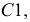
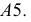
В практике при раскрое даются припуски на швы в соответствии с типом соединения.
Развертка поверхностей
Разверткой поверхности называется плоская фигура, полученная путем совмещения элементов поверхности с плоскостью.
Если для поверхности можно построить её развертку точно без складок и разрывов, то поверхность называется развертываемой, в противном случае – неразвертываемой.
К развертываемым поверхностям относятся все гранные, а из линейчатых только -цилиндрические, конические и поверхности е ребром возврата.
Построение разверток развертываемых поверхностей
Существуют следующие способы построения разверток развертываемых поверхностей:
- Способ триангуляции (треугольников);
- Способ раскатки;
- Способ нормального сечения.
Способ триангуляции (треугольников) применяется для построения разверток пирамидальных и конических поверхностей. Они выполняются по одному принципу. Каждая грань пирамиды представляет треугольник и для построения развертки необходимо определить натуральные величины всех сторон треугольника. По найденным натуральным величинам сторон вычерчиваются последовательно треугольные грани. Коническая поверхность, заменяется вписанной в нее, пирамидальной и решение задачи ведется аналогично пирамиде.
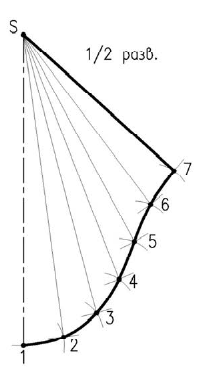
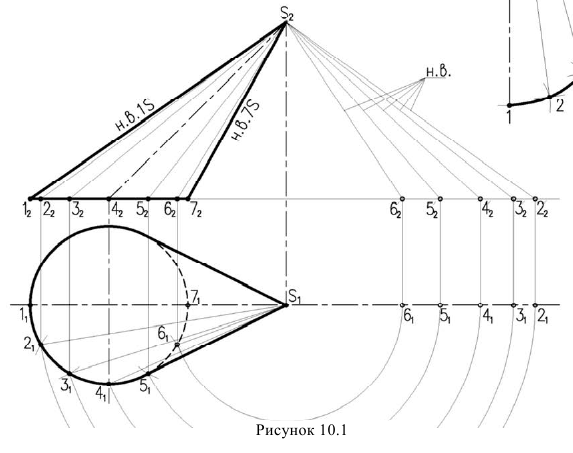
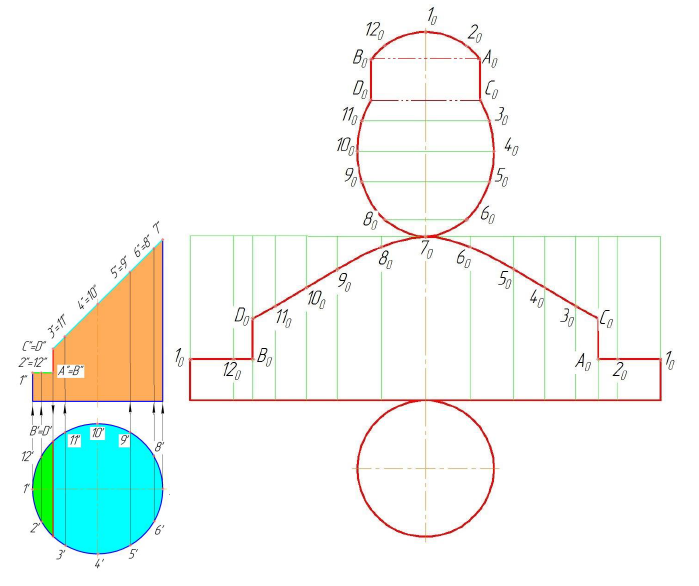
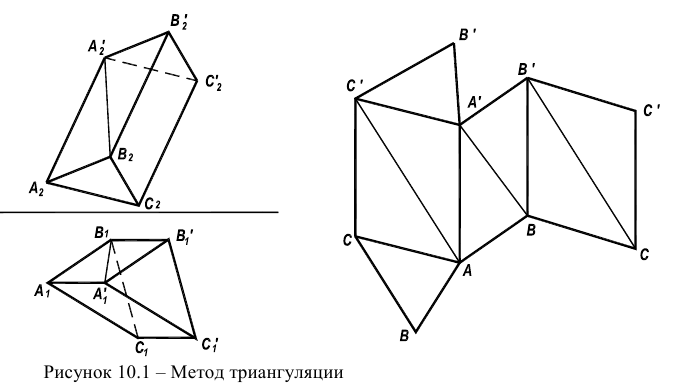
Рассмотрим пример, построения развертки, конической поверхности (рисунок 10.1)
Для построения развертки в конус вписываем двенадцатигранную пирамиду. Т.к. по условию конус расположен симметрично относительно оси, построим половину развертки.
Образующие конуса имеют разную длину, поэтому натуральную величину определяем вращением до положения параллельного фронтальной плоскости проекций. Только образующие 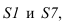
Способ раскатки применяется для построения разверток призматической и цилиндрической поверхности. И если поверхность цилиндрическая, то в нее вписывается призматическая поверхность. Поэтому принцип построения этих разверток одинаков.
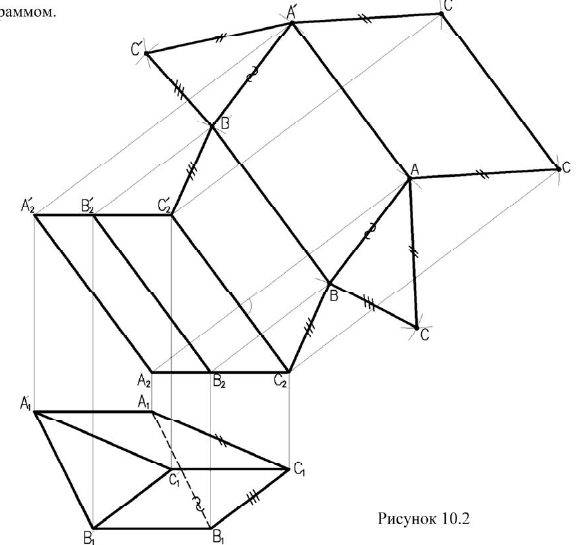
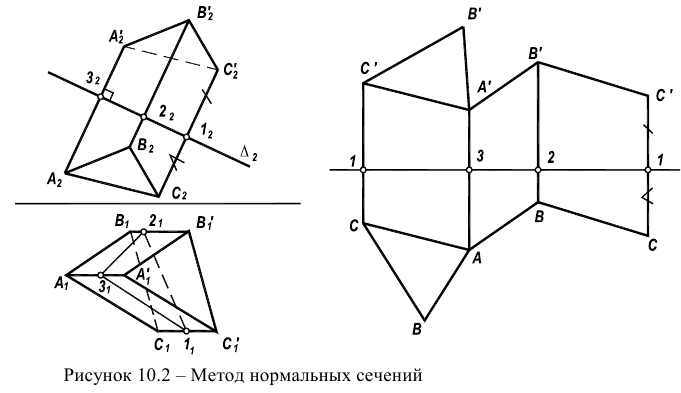
Рассмотрим пример построения развертки наклонной треугольной призмы
Развертку можно выполнять только в том случае, если боковые ребра призмы параллельны плоскости проекций, как на рисунке 10.2. В противном случае, сначала выполняется преобразование (методом замены строится новая проекция на плоскость параллельную ребрам). При выполнении развертки методом раскатки точки 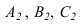
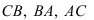
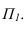
Способ нормального сечения используется также для построения разверток призматической и цилиндрической поверхностей.
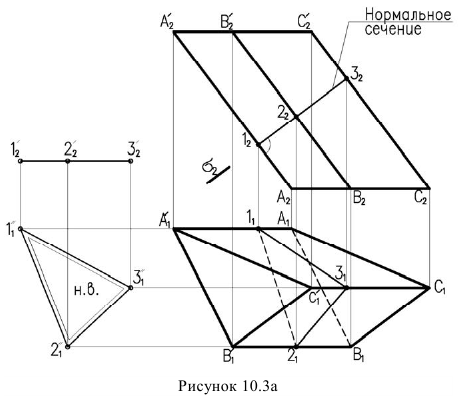
Рассмотрим построение развертки призмы изображенной на рисунке 10.3а. Для этого построим нормальное сечение – сечение перпендикулярное боковым ребрам призмы 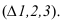
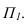
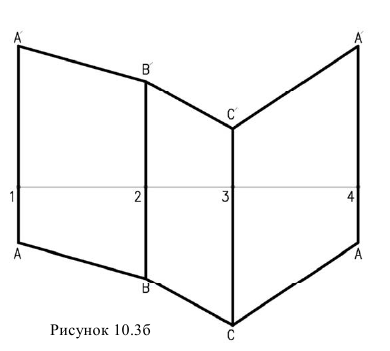
Соединив построенные точки, получим развертку боковой поверхности данной призмы (рисунок 10.36).
Построение приближенной развертки неразвёртываемых поверхностей
Когда надо развернуть неразвертывающуюся поверхность ее заменяют развертывающейся (цилиндрической, конической, одной или несколькими), имеющей общие линии е данной.
Такая замена называется аппроксимацией, а полученная развертка – условной или приближенной.
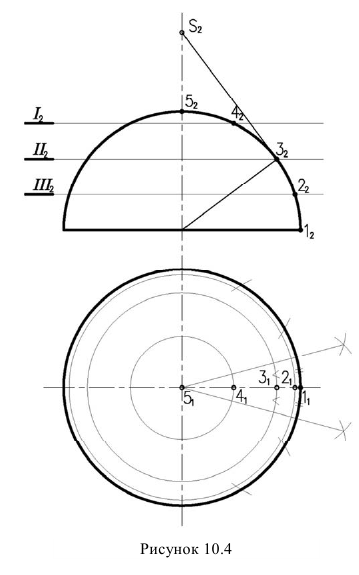
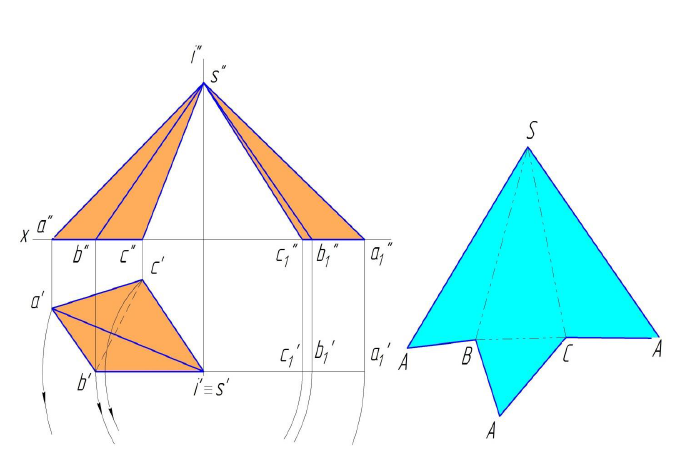
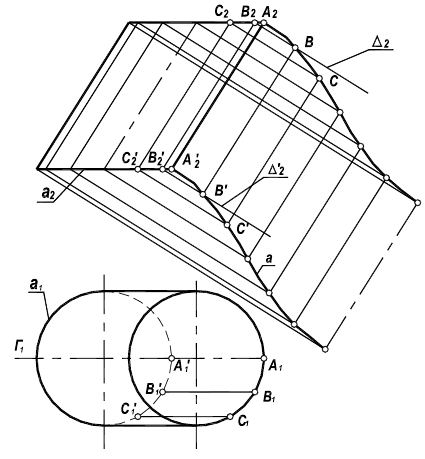
Рассмотрим построение такой развертки на примере полусферы (рисунок 10.4).
Полусферическую поверхность разделим меридиональными плоскостями на дольки (на 12 частей). По высоте сферу делим на несколько частей параллелями. Возьмем одну дольку, ось которой параллельна фронтальной проекции и развернем ее в плоскую фигуру, ось которой будет равна 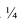
Через точки 1,2,3,4 проводим перпендикуляры к оси дольки и на них откладываем от оси в обе стороны половину ширины каждой дольки измеренную на горизонтальной проекции. Полная развертка составит двенадцать таких долек.
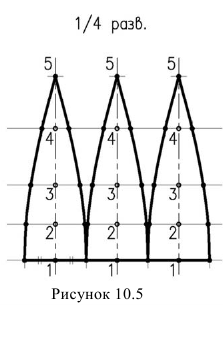
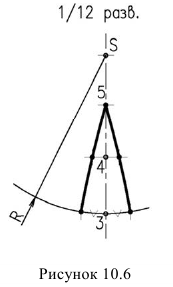
Если развертывающаяся долька начинается с экватора, то на развертке линия экватора изобразится прямой (рисунок 10.5). Если же долька начинается какой-то параллелью, то на развертке эта параллель изобразится окружностью. Например, параллель, проходящая через точку 3. Для нахождения радиуса этой окружности на фронтальной проекции необходимо провести касательную прямую в точке 5, к окружности до пересечения с осью сферы 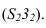
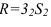
Решение задач
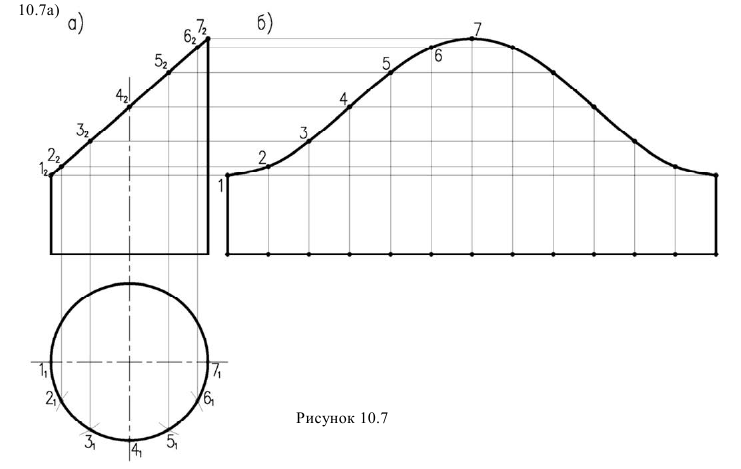
Задача 1. Построить развертку усеченного прямого кругового цилиндра (рисунок
Развертка боковой поверхности цилиндра строится фактически методом нормального сечения, т.к. основание цилиндра перпендикулярно оси. Окружность основания развертывается в прямую линию равную длине окружности 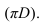
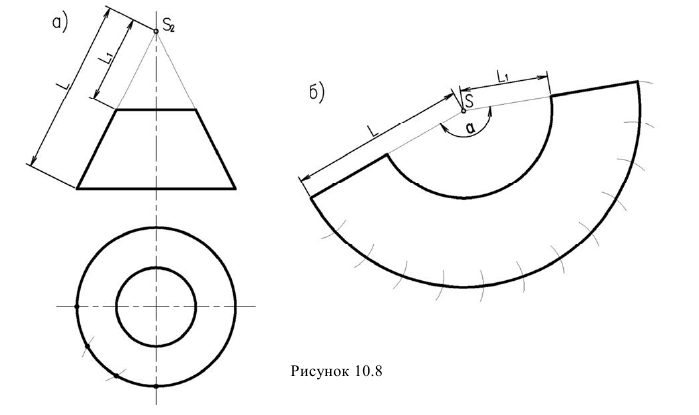
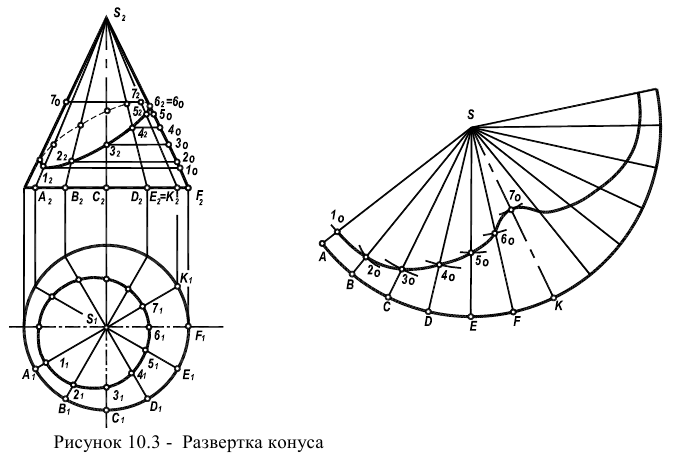
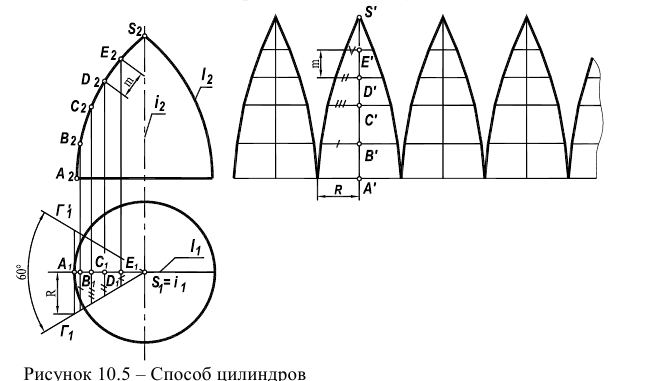
Задача 2. Построить развертку усеченного прямого кругового конуса (рисунок
10.8а).
Так как в прямом круговом конусе все образующие одинаковой длины, развертка представляет собой сектор окружности с радиусом равным длине образующей конуса 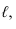
Угол а также можно определить по формуле:
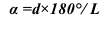
Что такое развертка поверхности
Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).
Приступая к изучению развертки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью.
Если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой.
Свойства развёртки
Длины двух соответствующих линий поверхности и ее развертки равны между собой;
Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке;
Прямой на поверхности соответствует также прямая на развертке;
Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке;
Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической.
Способы построения развёртки
Существует три способа построения развертки многогранных поверхностей:
- Способ треугольника
- Способ нормального сечения
- Способ раскатки
К развертывающим поверхностям относятся все поверхности гранные, то есть поверхности, состоящие из отсеков плоскостей. Из кривых поверхностей к ним относятся только те линейчатые поверхности. У которых касательная плоскость касается поверхности о всех точках ее прямолинейной образующей. Этому условию удовлетворяют три типа линейчатых поверхностей: цилиндрическая, коническая, торсовая [1].
Все остальные поверхности относятся к неразвёртывающимся или косым.
Развертки могут быть точными. Это развертки прямого кругового цилиндра и конуса. Если пренебречь графическими ошибками, то к точным развёрткам можно отнести развертки многогранников.
Развертки всех других поверхностей как развертывающихся, так и неразвёртывающихся, которые, как правило, строятся графически, являются приближенными.
Любая конструкция рассматривается как комбинация простейших геометрических поверхностей.
Рассмотрим наиболее простую гранную поверхность.
Развертки гранных поверхностей
Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.
Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины истинных размеров и формы отдельных граней поверхности – плоских многоугольников и вычерчиванию их в том порядке, в каком они следуют друг за другом на самой поверхности.
Рассмотрим на примере решение задачи
Развертка поверхности прямой призмы
Представим, что поверхности призмы разрезана по ребру АА1.
Развернем ее боковую поверхность и совместим се грани с плоскостью чертежа (рис.10.1) [1].
Так как призма прямая, то ее основание развернется в прямую линию. Поэтому на свободном поле чертежа проведем прямую линию, на которой произвольно выберем точку А. От этой точки развернем основание призмы. Поскольку основание данной призмы проецируется на горизонтальную плоскость проекций в натуральную величину, на прямой от точки А последовательно отложим отрезки, равные соответствующим сторонам основания.
Рисунок 10.1- Развертка поверхности прямой призмы
Учитывая, что призма прямая и ее ребра проецируются на фронтальную плоскость проекций в натуральную величину, к прямой – развёртке основания в точках 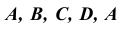
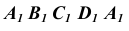
Полная развертка призмы состоит из развертки ее боковой поверхности и двух оснований – верхнего и нижнего.
Так как призма прямая, и ее основание проецируется на горизонтальную плоскость проекций в натуральную величину, к боковой развертке в любом месте пристраиваем два четырехугольника 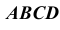
Развертка поверхности наклонной призмы
Построение развёртки может быть выполнено способом нормального (перпендикулярного) сечения. Способом раскатки и способом треугольников (триангуляция). Рассмотрим каждый способ в раздельности [1].
Построение развертки способом нормального сечения (рис.10.2).
Рисунок 10.2 – Построение развертки призмы способом нормального сечения
Если разрезать боковую поверхность наклонной призмы по любому ребру и совместить с плоскостью чертежа, то очевидно, что основание такой призмы развернется не в прямую, а в ломаную линию.
Если же призму пересечь плоскостью, перпендикулярной рёбрам, то полученное при этом сечение при развертывании даст прямую линию. Поэтому для решения задачи необходимо:
- Пересечь призму плоскостью, перпендикулярной ее ребрам;
- Найти проекции сечения вспомогательной плоскости с призмой;
- Определить истинную величину нормального сечения;
- Развернуть полученный четырехугольник сечения прямую линию;
- Отложить вверх и вниз от этой линии истинные величины отрезков ребер относительно сечения призмы.
Проведем плоскость Р, перпендикулярную ребрам призмы (рис.10.2 а).
Эта плоскость Р – фронтально проецирующая и следы ее будут перпенди-кулярны соответствующим проекциям ребер.
Найдем проекции сечения призмы плоскостью Р. Фронтальные проекции 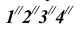
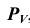
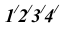
Истинную величину фигуры (четырёхугольника) сечения определяем любым способом, например. Способом замены плоскостей проекций.
На свободном поле чертежа (рис.10.2 б) проведём горизонтальную прямую, на которой последовательно отложим от точки 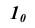
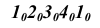
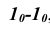
Развертка призмы способом раскатки
Так как основание призмы на горизонтальной плоскости проекций изображается в натуральную величину, ее развертку можно построить более удобным способом, чем способ нормального сечения.
Построения развертки призмы способом раскатки показано на рис 10.3.
Поскольку ребра призмы параллельны фронтальной плоскости проек-ций, то каждую грань можно повернуть вокруг бокового ребра (как вокруг фронтали) до положения, при котором грань будет параллельна плоскости V и спроецируется на эту плоскость без искажения. Разворачивая таким образом одну грань за другой по порядку, получим развертку боковой поверхности.
Практически такое построение выполняется следующим образом [1] .
Так как при повороте грани 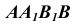
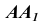
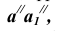
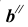
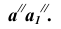
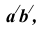
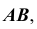
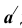
Таким образом, находим точку 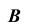
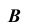
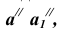
Рисунок 10.3 – Построение развертки призмы способом раскатки
Из точки 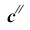
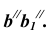
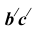
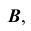
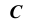
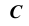
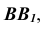
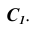
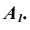
Следует отметить, что если ребра призмы не параллельны плоскости проекций, а развертку необходимо выполнить раскаткой, то предварительно меняют плоскости проекций новой системой, в которой ребра окажутся параллельными одной из плоскостей проекций.
Построение развертки пирамиды (способ треугольника)
Так как боковые грани наклонной призмы являются парраллелограммами, для построение их истиной величины недостаточно иметь только истинные значения ребер и сторон основания призмы. Для этого необходима еще одна величина – диагонали, что и положено в основу построения развертки боковой поверхности призмы способом треугольника [1].
При построении развертки следует:
- Разбить каждую из граней призмы диагоналями на треугольники;
- Определить длину неизвестных сторон треугольника (например, методом плоскопараллельного перемещения);
- Построить треугольники в плоскости чертежа в той последователь-ности, в которой они расположены в многограннике.
Задача. Построить развертку поверхности пирамиды SABC (рис.10.4).
Развернутая поверхность пирамиды состоит из треугольника – ее боковых граней, расположенных в определенной последовательности, и основания.
Для построения боковых граней – треугольника развертки, необходимо определить истинные длины боковых ребер с учетом того, что основание пирамиды на горизонтальной проекции изображается в натуральную величину. Используем наиболее простой способ – способ вращения. Выберем ось вращения I, перпендикулярную плоскости H и проходящую через вершину пирамиды S. Поворачивая вокруг оси горизонтальные проекции ребер до положения, параллельного оси X, получим на фронтальной проекции отрезки 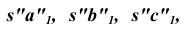
Каждая боковая грань строится как треугольник по трем известным сторонам, и развертка получается в виде примыкающих друг к другу в соответствующем порядке треугольников с общей вершиной S.
Рисунок 10.4 – Построение развертки пирамиды
Развертывание поверхностей вращения
Как было упомянуто ранее, развертки кривых поверхностей, как правило, строятся приближенные. Даже для таких развертывающихся поверхностей как цилиндрическая и коническая, которые имеют теоретические точные развертки, на практике строят их приближенными, заменяя (аппроксимируя) эти поверхности гранными, вписывая или описывая их вокруг заданной поверхности.
Надо иметь в виду, что если развертываемый элемент имеет плоскость симметрии, то линию разреза поверхности лучше выбирать так, чтобы развертка получалась в виде симметричной фигуры. При этом предпочтительнее выбирать наиболее короткую линию разреза.
Развёртка цилиндрической поверхности
Развертка цилиндрической поверхности выполняется аналогично развертке призмы. Предварительно в заданный цилиндр вписывают n-угольную призму. Чем больше углов в призме, тем точнее развертка ( при n → ∞ призма преобразуется в цилиндр).
На рис. 10.6. приведено построение полной развёртки усечённого цилиндра (см. условия задания рис. 8.2) стр. 61.
Для построения развертки боковой поверхности на горизонтальной прямой откладывают длину окружности основания πd и делят ее на 12 равных частей (с определенной степенью точности вместо 1/12 длины окружности можно откладывать длину соответствующей хорды) [5]. Из точек деления проводят перпендикуляры к отрезку πd и на них откладывают длины образующих от основания до секущих плоскостей α , β, χ. Для построения точек А, В, С, D на развертке использовано расположение этих точек на горизонтальной проекции цилиндра (от точек деления откладывают длины дуг 2А и 12В) Точки 1, А, С и 1, В, D соединены прямыми линиями.
Точки С, 3…11, D соединяют плавной линией.
Рисунок 10.6 – Полная развёртка поверхности усечённого цилиндра.
К прямой линии πd (развертка нижнего основания цилиндра) присоединяют окружность основания, а к верхней части боковой развертки натуральные фигуры сечения плоскостями (часть эллипса, прямоугольник, сегмент окружности).
Развертка поверхности конуса
Развертка боковой поверхности прямого кругового конуса с радиусом снованием r представляет собой круговой сектор, радиус которого равен длине образующей конуса L, а центральный угол φ=Пr/L.
Чтобы избежать вычислений, связанных с определением длины дуги сектора или угла, вначале в основанием конуса вписывают правильный 12-угольник. Затем на свободном поле чертежа из точки S проводят дугу радиусом l. От произвольно выбранной начальной точки по дуге последо-вательно засекают 12 дуг, хорды которых равны стороне 12-угольника.
Таким образом, построение развертки боковой поверхности конуса заменяют построением развертки, вписанной в него правильной 12-гранной пирамиды [1] (рис. 10.7).
Рисунок 10.7 – Построение развертки боковой поверхности конуса
На рисунке 10.7 построена развертка боковой поверхности конуса и нанесена ней линия сечения плоскостью P.
В конус впишем правильную 12-гранную пирамиду. Для этого основание конуса разбиваем на 12 равных частей (рис. 7 а). На фронтальной плоскости проекций получим фронтальные проекции (на оси X) точек деления 1″, 2″ ,3″ и т.д. и соединим их с точкой S′ (1″s″, 2″s″, 3″s″, 4″s″ и т.д. – фронтальные проекции образующих конуса, т.е. ребер вписанной пирамиды).
На свободном поле чертежа из произвольно выбранной точки S, проведем угу радиусом L и отложим на ней 12 дуг, хорды которых равны сторонам основания пирамиды (рис. 10.7). Полученные точки соединим с вершиной S, в результате чего образуется развертка боковой поверхности конуса.
Затем на ней строим линию сечения. Для этого найдем истинные величины отрезков образующих, или ребер пирамиды, от вершины до плоскости сечения. Истинные величины можно найти любым способом. Найденные отрезки отложим на соответствующих образующих на развертке. Полученные точки соединим плавной кривой. Последняя и будет линией сечения.
Развертка наклонных тел вращения
Развертки наклонных тел вращения строятся аналогично предыдущим задачам, т.е. поверхность вращения аппроксимируется гранной ( пирамидой или призмой) соответственно с максимально возможным числом граней, а затем используются все те же методы решения, что и при развертке гранных поверхностей.
На рис.10.8 приведено построение полной равертки наклонного конуса [1].
Рисунок 10.8 – Построение полной развертки наклонного конуса
Построение условной развертки сферы
На рисунке 10.9 показано построение условной развертки сферы [5].
Так как сферическая поверхность принадлежит к числу не развертывающихся, то возможна лишь ее приближенная (условная) развертка. Способ построения состоит в том, что сферу разбивают с помощью меридианов на узкие равные между собой доли (клинья). Каждую такую долю заменяют описанной цилиндрической поверхностью, которая касается сферы по среднему меридиану доли. Этот средний меридиан будет нормальным сечением цилиндрической поверхности. Границами цилиндрической поверхности будут плоскости меридианов, ограничивающих рассматриваемую долю.
Рисунок 10.9 – Построение условной развертки сферы.
Горизонтальную проекцию n’ экватора n разбиваем на 12 равных частей и через полученные точки проводим горизонтальные проекции меридианов ( рис. 10.9 а).
Рассмотрим построение приближенной развертки 1/12 части (доли) сферы, средним меридианом которой является меридиан
Заменим часть сферы цилиндрической поверхностью. Описанной около нее. Образующие этой поверхности будут фронтально-проецирующими прямыми. Для построения развертки элемента цилиндрической поверхности половину фронтального меридиана разбиваем на 6 равных частей (отмечены точками 1, 2, 3, 4 только половина симметричной части). На горизонтальной прямой (рис. 8.14,б) откладываем отрезок 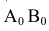
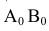
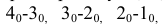
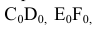
Для придания каждой доли развертки сферической поверхности кроме изгибания проводят растяжение и сжатие материала.
Положение произвольной точки К принадлежащей поверхности сферы, может быть определено на развертке с помощью двух «координат» – длин дуг 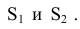
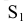
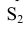
Построение развёрток поверхностей
Развёрткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга.)
Развертка усеченной призмы
Развертку боковой поверхности с основанием и фигурой сечения призмы строят следующим образом. Проводят прямую, на которой откладывают пять отрезков, равных длинам сторон пятиугольника, лежащего в основании призмы. Из полученных точек проводят перпендикуляры, на которых откладывают действительные длины ребер усеченной призмы, беря их с фронтальной или профильной проекции, получают развертку боковой поверхности призмы.
К развертке боковой поверхности пристраивают фигуру нижнего основания — пятиугольник и фигуру сечения. При этом используют метод триангуляции (метод засечек). На рисунке показано построение вершины 5 методом триангуляции. Линии сгиба по ГОСТ 2.303—68 показывают на развертке штрих-пунктирной линией с двумя точками.
- Заказать чертежи
Развертка усеченного цилиндра
Для построения развертки на горизонтальной прямой откладывают длину окружности основания, равную 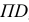
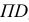
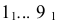
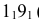
Развертка усеченной пирамиды
Сначала строят развертку неусеченной пирамиды, все грани которой, имеющие форму треугольника, одинаковы. На плоскости намечают точку 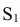
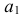
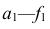
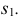
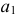
На профильной проекции усеченной пирамиды имеются действительные длины только двух отрезков — 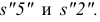
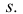
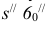
Полученные точки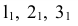
Развертка усеченного конуса
Построение развертки поверхности конуса начинают с проведения дуги окружности радиусом, равным длине образующей конуса из точки л». Длина дуги определяется углом а:
где d — диаметр окружности основания конуса в мм;
l — длина образующей конуса в мм.
Дугу делят на 12 частей и полученные точки соединяют с вершиной л>. От вершины 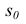
Действительные длины этих отрезков находят, как и в примере с пирамидой, способом вращения около вертикальной оси, проходящей через вершину конуса. Так, например, чтобы получить действительную длину отрезка S2, надо из 2′ провести горизонтальную прямую до пересечения в точке 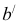
К развертке конической поверхности пристраивают фигуры сечения и основания конуса.
Развертки поверхностей
Фигура, получающаяся при совмещении всех точек поверхности с плоскостью (без складок и разрывов), получила название развертки. Поверхности же, допускающие такую операцию, называют развертывающимися.
Построение разверток является важной практической задачей, что связано с изготовлением множества изделий из листового материала (резервуары и трубы, изделия швейной и кожевенной промышленности и т.п.).
Из физической модели процесса развертывания поверхности на плоскость следует, что площадь отсека поверхности должна быть равна площади отсека плоскости на развертке.
Свойство сохранения площади влечет за собой справедливость следующих двух утверждений: длины соответственных линий поверхности и ее развертки равны, углы, образованные линиями поверхности, равны углам, составленным их образами на развертке. Углом между двумя линиями поверхности в их точке пересечения называют угол, составленный касательными, проведенными к кривым в точке.
Это в свою очередь приводит к следующему: прямая поверхности отображается на прямую развертки; параллельные прямые поверхности, отображаются на параллельные прямые развертки.
На этих свойствах и базируются графические и машинные алгоритмы построения разверток.
Из дифференциальной геометрии известно, что к развертывающимся поверхностям относятся только поверхности нулевой кривизны (состоящие только из параболических точек). У этих (линейчатых) поверхностей касательные плоскости, проведенные во всех точках одной образующей, совпадают.
Изо всего множества линейчатых поверхностей развернуты на плоскость могут быть только цилиндрические, конические и торсовые. Развертки для них строятся приближенно. В процессе построения развертки эти поверхности аппроксимируются (заменяются) многогранными поверхностями. Последнее вызвано тем, что спрямление кривых линий базируется на замене их ломаными. Точные развертки аппроксимирующих многогранных поверхностей принимают за приближенные развертки развертываемых поверхностей.
Развертки гранных поверхностен
Процесс получения развертки гранной поверхности сводится к совмещению с плоскостью ее граней. Для гранной поверхности всегда можно построить развертку.
К наиболее распространенным многогранным поверхностям следует отнести призмы и пирамиды.
Развертка поверхности призмы строится в основном двумя способами, с помощью треугольников (триангуляции) и нормальных сечений.
первом способе каждая грань призмы разбивается на два треугольника, для которых определяются натуральные длины сторон. Затем на плоскости последовательно строят треугольники в натуральную величину. Способ основан на свойстве «жесткости» треугольника — три отрезка определяют единственный треугольник.
По способу нормальных сечений призма пересекается плоскостью 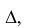
Через точки, соответствующие положению вершин, проводятся прямые, перпендикулярные к развертке ломаной. На построенных перпендикулярах откладываются натуральные длины соответствующих отрезков ребер. Концы ребер последовательно соединяются отрезками прямых.
При необходимости к построенной развертке боковой поверхности призмы пристраиваются натуральные фигуры оснований призмы.
Способ нормальных сечений эффективен, если ребра призмы являются линиями уровня. Если же при этом основания призмы расположены в плоскостях уровня, то реализуется частный случай этого способа — способ раскатки (рисунок 10.4).
Построение развертки поверхности пирамиды сводится к отысканию истинных величин граней этой пирамиды и последующему совмещению их с плоскостью. Для нахождения истинных величин граней необходимо (каким-либо способом) найти натуральные длины всех ребер пирамиды (рисунок 11.33).
Приближенное построение разверток
Выше было отмечено, что для всех поверхностей строятся приближенные развертки. Однако для таких поверхностей, как цилиндрическая и коническая поверхности вращения, могут быть вычислены все параметры необходимые для точной развертки.
Отсек цилиндра вращения радиуса R и высоты h развертывается в прямоугольник 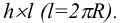
Отсек конуса вращения с высотой h и радиусом основания R развертывается в круговой сектор, радиус которого равен длине образующей отсека конической поверхности 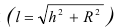
Построение разверток поверхностей начинается с аппроксимации их многогранными поверхностями, базирующейся на линейной аппроксимации направляющих. Как правило, кривая заменяется вписанной ломаной. Проиллюстрируем все выше сказанное примерами.
Развертка боковой поверхности усеченного конуса вращения представлена на рисунке 10.3.
Развертывание боковой поверхности усеченного конуса, в общем случае, производится по схеме развертывания поверхности пирамиды.
Коническая поверхность заменяется вписанной в нее поверхностью пирамиды. Построение развертки будет тем точнее, чем больше граней имеет пирамида, заменяющая коническую поверхность.
Истинные величины отрезков образующих 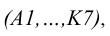
Развертка боковой поверхности наклонного кругового цилиндра показана на рисунке 10.4.
На первом этапе в цилиндрическую поверхность вписывается призма, основанием которой служит многоугольник с n сторонами. Достаточная точность аппроксимации может быть получена при длине стороны равной четверти радиуса окружности. В силу того, что рассматриваемая поверхность симметрична относительно фронтальной плоскости уровня, достаточно построить развертку лишь одной ее половинки.
Развертка вписанной призмы выполняется по способу раскатки. Некоторая фронтальная плоскость совмещается с ребром 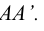
Вращением вокруг ребра 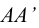
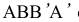
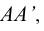
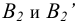
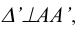
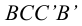
Условные развертки поверхностей
Для неразвертывающихся поверхностей строят условные развертки. Для этого, исходя из требуемой точности развертки, исходную поверхность разрезают на несколько равных частей. Затем полученные отсеки аппроксимируются отсеками развертывающихся поверхностей, для которых (по рассмотренной выше методике) и выполняют развертки. Последние и принимают за условную развертку исходной поверхности.
Рассмотрим построение разверток поверхностей вращения по описанной выше методике на примерах, приведенных на рисунках 10.5 и 10.6.
Условные развертки поверхностей вращения выполняют в основном двумя способами: способом цилиндров и способом конусов.
При построении условной развертки способом цилиндров исходная поверхность разрезается плоскостями, проходящими через ее ось вращения (рисунок 10.5).
Каждый выделенный отсек заменяется отсеком цилиндрической поверхности, которая касается исходной поверхности по ее среднему меридиану. Образующие отсека цилиндра ограничены плоскостями меридианов, ограничивающих отсек исходной поверхности.
При этом дуги параллелей исходной поверхности аппроксимируются отрезками образующих соответствующих цилиндров.
Для построения развертки поверхности вращения способом конусов исходная поверхность разрезается плоскостями перпендикулярными ее оси вращения, на несколько частей — «поясов». Каждый из поясов аппроксимируется отсеком конуса вращения.
Таким образом, задача сводится к построению разверток отсеков аппроксимирующих конусов.
Выбор способа построения условной развертки поверхности вращения, в реальном проектировании, во многом зависит от конкретных размеров поверхности и технологии изготовления изделия.
Развертки поверхностей
Разверткой называется плоская фигура, в которую преобразуется поверхность предмета при ее совмещении с плоскостью. При этом подразумевается, что поверхность – это гибкая, но нерастяжимая и несжимаемая пленка и при ее развертке не происходит разрывов и образования складок.
Поверхности, которые допускают такое преобразование, называются развертывающимися.
К развертывающимся поверхностям относятся многогранники и некоторые линейчатые поверхности – цилиндрические, конические и поверхности с ребром возврата (торсы – развертка торсов не рассматривается).
Развертки можно построить точные и приближенные.
Точные развертки можно строить для гранных поверхностей призмы и пирамиды (не считая графических погрешностей построения), для круговых цилиндров (развертка – прямоугольник с размерами (π·d)×H) и круговых конусов (круговой сектор с углом φ = R·360o/L, где R – радиус основания конуса; L – длина его образующей).
Развертки, которые можно построить графически, заменяя (аппроксимируя) заданные поверхности участками развертывающихся призматических, пирамидальных или цилиндрических поверхностей, называются приближенными. К поверхностям, развертку которых можно построить приближенно, относятся круговые наклонные конуса, эллиптические цилиндры с круговыми сечениями, сферические, торовые, а также комбинированные поверхности, участки которых состоят из развертывающихся поверхностей.
Каждой точке на поверхности соответствует единственная точка на развертке, т. е. между поверхностью и ее разверткой существует взаимно однозначное соответствие, которое обладает следующими основными свойствами:
- а) длины соответствующих линий на поверхности и на развертке равны;
- б) линии, параллельные на поверхности, сохраняют параллельность на развертке;
- в) углы между соответствующими пересекающимися линиями на поверхности и на развертке равны;
- г) площади соответствующих фигур на поверхности и на развертке, ограниченные замкнутыми линиями, равны.
Развертки многогранников
Построение развертки многогранников сводится к определению натуральных величин боковых граней или ребер этих поверхностей. Натуральные величины граней (плоскостей) или ребер (прямых) могут быть определены любым из рассмотренных выше способов преобразования чертежа (см. тему «Преобразование чертежа»).
Развертка поверхности призмы
Построение развертки поверхности призмы можно выполнить несколькими способами:
- Способ нормального сечения.
- Способ раскатки.
- Способ треугольников (триангуляции) – здесь не рассматривается.
Рассмотрим на примерах построение развертки поверхности призмы первыми двумя способами.
1-й способ. Способ нормального сечения (нормальное сечение перпендикулярно ребрам призмы).
Этот способ развертки боковой поверхности призмы можно применить, если на чертеже:
- – ребра призмы являются прямыми уровня, то есть имеют на одной из заданных проекций натуральную величину,
- – на проекциях нет натуральных величин оснований призмы.
!!! Если на чертеже ребра призмы являются прямыми общего положения, то следует изменить положение призмы относительно плоскостей проекций, преобразовав ребра в прямые уровня, например, способом замены плоскостей проекций.
Построение развертки боковой поверхности призмы способом нормального сечения выполняется по следующему графическому алгоритму:
1-е действие. Провести на проекции призмы, на которую ребра призмы проецируются в натуральную величину, плоскость нормального сечения, перпендикулярную ее ребрам (в произвольном месте по длине ребер).
2-е действие. Построить натуральную величину многоугольника нормального сечения (например, способом замены плоскостей проекций).
3-е действие. Развернуть на свободном поле чертежа натуральный многоугольник сечения в прямую и через точки его вершин провести перпендикулярные прямые
- – направления ребер.
4-е действие. Отложить на направлениях ребер в обе стороны от линии нормального сечения натуральные отрезки соответствующих ребер.
5-е действие. Соединить построенные конечные точки ребер отрезками прямых и достроить плоскую фигуру развертки боковой поверхности призмы.
6-е действие. Оформить чертеж развертки, проведя линии сгиба в местах расположения ребер тонкими штрихпунктирными линиями с двумя короткими пунктирами.
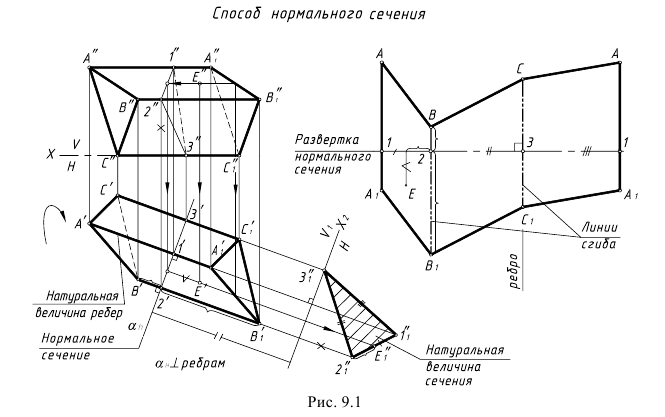
На рис. 9.1 показан пример построения развертки поверхности треугольной призмы способом нормального сечения, так как на чертеже призмы ее ребра являются горизонтальными прямыми уровня, а основания являются плоскостями общего положения, т. е. не имеют натуральной величины.
Поверхность призмы «разрезана» по ребру А и развернута по часовой стрелке.
Для построения развертки выполнены графические действия предложенного алгоритма.
1-е действие. Провести горизонтально-проецирующую плоскость нормального сечения α(αh) перпендикулярно горизонтальным проекциям ребер призмы (произвольно по длине ребер).
2-е действие. Способом замены плоскостей проекций построить натуральную величину нормального сечения
- – треугольник 11“-21“-31“, стороны которого определяют ширину каждой грани призмы.
3-е действие. На свободном поле чертежа треугольник 11“-21“-31” нормального сечения развернуть в горизонтальную линию и отметить натуральные величины его сторон; из отмеченных на линии сечения точек 1, 2, 3 и 1 провести перпендикулярные прямые – направления ребер.
4-е действие. Отложить на проведенных направлениях ребер вверх и вниз отрезки натуральных величин ребер (см. ребро B’-B’1), взятых с заданной горизонтальной проекции призмы, где ребра имеют натуральную величину.
5-е действие. Соединить отрезками прямых построенные конечные точки ребер и достроить плоскую фигуру развертки.
6-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам призмы тонкими штрихпунктирными линиями с двумя короткими штрихами.
На этом же рис. 9.1 показано также построение на развертке точки Е(Е”,Е’), лежащей на грани АВ призмы.
2-й способ. Способ раскатки
Этот способ развертки применяется, если на чертеже:
- – ребра призмы являются прямыми уровня;
- – основания призмы (или одно из оснований) лежат в плоскости уровня, т. е. имеют на чертеже натуральную величину.
Суть способа в том, что, «разрезав» поверхность призмы по одному из ее ребер, вращением призмы (раскаткой) вокруг этого ребра ближайшая грань призмы совмещается с плоскостью развертки (за плоскость развертки принимается плоскость проекций, которой параллельны ребра призмы). Затем последовательным вращением призмы вокруг следующих ребер с плоскостью развертки совмещаются все прочие грани призмы, т. е. выполняется полная раскатка ее боковой поверхности.
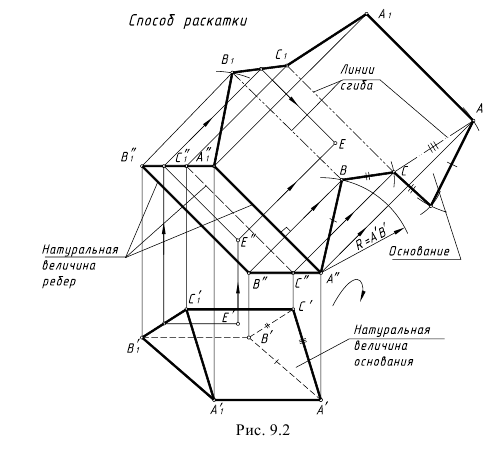
На рис. 9.2 показан пример построения развертки способом раскатки, так как на чертеже ребра призмы являются фронтальными прямыми, а оба основания лежат в горизонтальных плоскостях уровня и на горизонтальной проекции призмы имеют натуральную величину. За плоскость развертки принята фронтальная плоскость проекций, так как ребра призмы фронтальные прямые.
Построение развертки способом раскатки выполняется по следующему графическому алгоритму:
1-е действие. «Разрезать» поверхность призмы по очерковому ребру A-A1(A”-A1“) и повернуть вокруг этого ребра грань АВ призмы до совмещения с плоскостью развертки, построив ребро В-B1; чтобы построить на развертке это ребро, нужно провести из вершин оснований В(B”) и B1(B1“) перпендикуляры к ребру A-A1(A”-A1“) и на пересечении этих перпендикуляров с дугой-засечкой, равной стороне основания AВ(A’B’), построить точки B и B1, определяющие положение ребра В-B1 на развертке (ребро В-B1 параллельно ребру А-A1).
2-е действие. Повторить последовательное вращение каждой грани вокруг следующего ребра и совместить каждую грань с плоскостью развертки, построив конечные точки каждого ребра с помощью дуг-засечек, равных следующим сторонам основания BC(B’C’) и CА(C’А’).
3-е действие. Соединить построенные конечные точки ребер отрезками прямых и достроить плоскую фигуру развертки (достроено также одно основание призмы).
4-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам тонкими штрихпунктирными линиями с двумя короткими пунктирами.
На этом же рисунке показано построение на развертке точки E, лежащей на грани BC призмы.
Развертка поверхности пирамиды
Построение развертки боковой поверхности пирамиды по натуральным величинам ее ребер выполняется по следующему графическому алгоритму.
1-е действие. Построить на заданных проекциях пирамиды натуральные величины всех ее боковых ребер (например, способом вращения вокруг проецирующей прямой) и натуральные величины сторон многоугольника основания пирамиды (если основание лежит в плоскости уровня, то натуральные величины даны на одной из проекций).
2-е действие. Построить на свободном поле чертежа последовательно грани пирамиды по натуральным величинам ребер и натуральным величинам сторон основания (с помощью дуг-засечек) так, чтобы они имели общую вершину S и примыкали друг к другу.
3-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам пирамиды тонкими штрихпунктирными линиями.
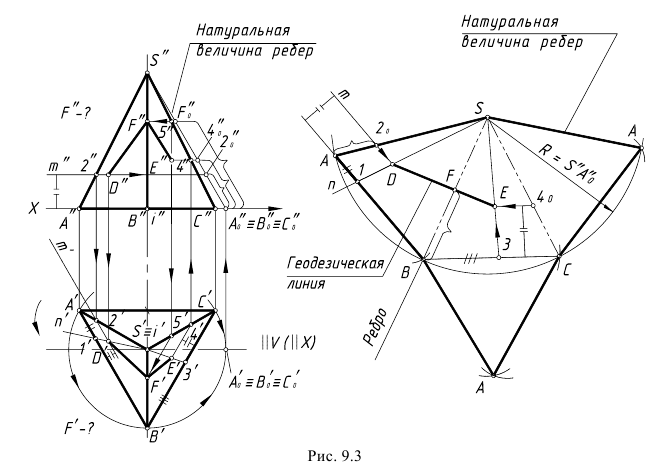
На рис. 9.3 показан пример построения развертки поверхности правильной треугольной пирамиды, основание которой треугольник АВС на горизонтальной проекции имеет натуральные величины сторон, так как лежит в горизонтальной плоскости уровня.
Для построения развертки выполнены графические действия предложенного алгоритма.
1-е действие. Построить на заданной фронтальной проекции натуральные величины ребер пирамиды способом вращения вокруг горизонтально-проецирующей оси i(i’), проходящей через вершину пирамиды точку S (S’) и совпадающую с ее высотой. Напоминаем графические действия этого способа преобразования:
1.1. Повернуть горизонтальные проекции ребер S’А’, S’В’ и S’С’ вокруг оси i(i’) так, чтобы они расположились параллельно фронтальной плоскости проекций V (все ребра правильной пирамиды равны по длине), и получить совмещенные проекции точек Ao‘≡Bo‘≡Co‘.
1.2. На фронтальной проекции пирамиды конечные точки А”, В” и С” ребер перемещаются по горизонтальной линии, перпендикулярной оси i(i”), и на пересечении с линией связи от точек Ao‘(Bo‘≡Co‘) построить точки Ao“(Bo“≡Co“).
1.3. Соединить вершину пирамиды S(S”) с совпадающими точками Ao“(Bo≡Co“)
– полученный отрезок S”A”(S”B”≡S”C”) и есть натуральная величина всех ребер пирамиды.
2-е действие. На свободном поле чертежа построить последовательно (например, против часовой стрелки) от ребра SA, по которому «разрезается» поверхность, треугольники граней пирамиды с общей вершиной S следующим образом:
2.1. Провести дугу радиусом R равным натуральной величине ребер S”Ao” пирамиды из произвольной точки S плоскости чертежа.
2.2. На дуге отметить (произвольно) вершину основания точку A, то есть построить ребро SA пирамиды.
2.3. На проведенной дуге засечками, равными длине сторон основания пирамиды A’В’=В’C’=C’A’ отметить следующие точки вершин основания
– B, C и точку A.
2.4. Построить треугольники граней пирамиды, соединив вершину S с вершинами основания и достроить основание пирамиды к стороне, например, ВС грани SBC.
3-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам пирамиды тонкими штрихпунктирными линиями с двумя короткими пунктирами.
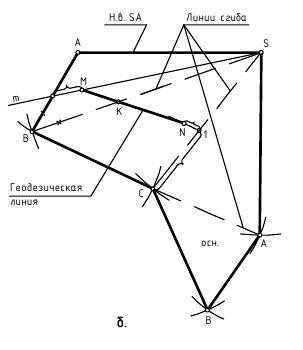
Геодезическая линия
Геодезическая линия – это линия кратчайшего расстояния между двумя точками на поверхности. На развертке этой линии соответствует прямая. Геодезическая линия строится на развертке по двум ее конечным точкам, заданным на проекциях предмета, а затем достраивается на заданных проекциях по дополнительным промежуточным точкам, взятым на построенной развертке.
На рис. 9.3 показано построение проекций геодезической линии на поверхности пирамиды по двум заданным на проекциях конечным точкам D(D”,D’-?) и E(E’,E”-?). Порядок графических действий для построения геодезической линии:
1-е действие. Построить полную развертку поверхности (в данном примере развертка пирамиды уже построена).
2-е действие. Построить на развертке геодезическую линию.
2.1. Построить на развертке заданные точки D(D”,D’) и E(E’,E”):
– точка D определяется на развертке на пересечении вспомогательной линии m, проведенной параллельно стороне АВ основания на расстоянии А-2o, равным отрезку Ao“-2o“, взятому на построенной натуральной величине ребер и отложенному по ребру SA развертки, и линии, проведенной через точку S и точку 1, построенную на стороне АВ развертки по отрезку A’-1′, взятому на горизонтальной проекции А’В’ стороны основания;
- – точка E определяется на пересечении аналогично построенных линий 4o-Е и S-3;
2.2. Соединить построенные на развертке точки геодезической линией D-E, которая пересекает ребро SB в точке F.
3-е действие. Достроить фронтальную и горизонтальную проекции геодезической линии D-F-E на проекциях пирамиды по промежуточной точке F с учетом видимости линии на поверхности (на проекциях пирамиды проекции геодезической линии – ломаные линии):
3.1. Отрезок B-F, взятый на развертке (отмечен скобкой), отложить на натуральной величине ребер, построенных на фронтальной проекции, и определить положение точки Fо“.
3.2. Провести через точку Fо” линию, параллельную основанию пирамиды, и на пересечении с проекцией ребра SB(S”B”) построить фронтальную проекцию точки F(F”) геодезической линии.
3.3. Достроить горизонтальную проекцию точки F(F’) по вспомогательной точке 5(5′), лежащей на ребре SC.
3.4. Соединить на проекциях пирамиды заданные проекции точек D и E с построенной точкой F, определив видимость участков ломаной геодезической линии.
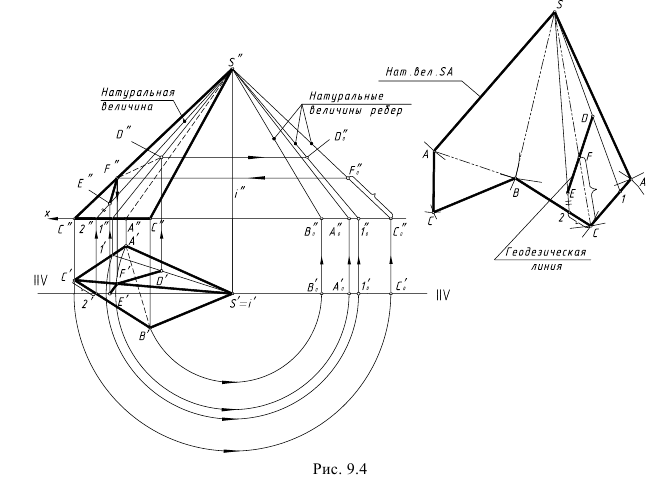
На рис. 9.4 показан пример построения развертки неправильной треугольной пирамиды SABC и геодезической линии D-E-F на развертке и на проекциях пирамиды по заданным конечным точкам D и E. Основание пирамиды лежит в горизонтальной плоскости и на горизонтальной проекции пирамиды стороны основания имеют натуральную величину.
Построение развертки поверхности пирамиды выполнено по приведенному выше алгоритму с дополнительными графическими действиями по построению геодезической линии:
1-е действие. Построить на фронтальной проекции пирамиды способом вращения вокруг горизонтально-проецирующей оси i(i’), проходящей через вершину пирамиды S(S’), натуральные величины всех ребер пира-миды и вспомогательной линий S-1, проведенной на грани пирамиды SAC через заданную точку D, и определить проекцию Dо” точки D на натуральной величине S”-1o” вспомогательной линии S-1: вспомогательная линия S-2, проведенная через точку E(E’,E”), является фронтальной (//V), и проекция S”-2″ есть ее натуральная величина, которую можно использовать для построения точки E на развертке.
2-е действие. Построить на свободном поле чертежа последовательно от ребра SA по часовой стрелке треугольники граней пирамиды с общей вершиной S по натуральным величинам ее ребер и сторон основания дугами-засечками соответствующей величины и достроить основание пирамиды к стороне АВ.
3-е действие. Оформить чертеж развертки, проведя линии сгиба.
4-е действие. Построить геодезическую линию на развертке и заданных проекциях пирамиды.
4.1. Построить на развертке конечные точки D и E на вспомогательных линиях S-1 и S-2 по натуральным величинам отрезков 1-D(1o“-Dо“) и 2-E(2″-E”) и соединить эти точки прямой геодезической линией D-E, которая пересекает ребро SC в точке F.
4.2. Достроить фронтальную и горизонтальную проекции ломаной геодезической линии D-F-E на проекциях пирамиды с учетом ее видимости, определив проекции точки F(F’,F”) на ребре SC(S’C’,S”C”) по ее положению на развертке (по отрезку C-F).
Приближенные развертки цилиндрических и конических поверхностей
Развертки цилиндрических и конических поверхностей выполняются аналогично разверткам призматических и пирамидальных поверхностей. При этом цилиндрическая поверхность заменяется (аппроксимируется) вписанной многоугольной призматической поверхностью (обычно 12-угольной), а коническая поверхность заменяется вписанной многоугольной пирамидальной поверхностью, т. е. строятся приближенные развертки.
Развертка кругового цилиндра
Развертку поверхности прямого кругового цилиндра можно выполнять следующими способами:
- – способом нормального сечения на свободном поле чертежа, если образующие являются прямыми уровня, а основания не перпендикулярны образующим;
- – способом раскатки при тех же условиях (развертка является при этом продолжением проекции).
Развертка эллиптического цилиндра (нормальное сечение – эллипс) выполняется способом раскатки, если образующие являются прямыми уровня, и на проекциях есть круговое основание (не рассматривается).
Графические алгоритмы для построения разверток поверхности цилиндра этими способами аналогичны вышеприведенным графическим алгоритмам для построения разверток призмы такими же способами.
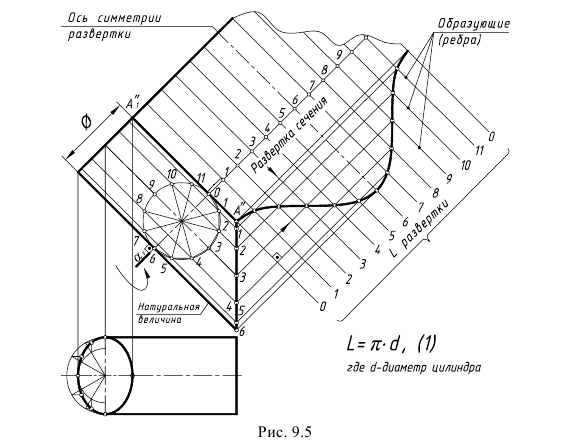
На рис. 9.5 показан пример построения развертки боковой поверхности прямого кругового цилиндра, наклоненного относительно горизонтальной плоскости проекций H и срезанного по одному торцу профильной плоскостью.
Поскольку по условию задачи образующие являются фронтальными прямыми уровня, а нормальным сечением кругового цилиндра является окружность, то здесь для построения развертки можно объединить и способы построения, и графические действия алгоритмов.
Развертка выполняется по предлагаемому графическому алгоритму.
1-е действие. Провести на фронтальной проекции цилиндра фронтально-проецирующую плоскость нормального сечения α(αV) перпендикулярно фронтальным проекциям образующих (в произвольном месте по длине образующих) и построить окружность нормального сечения, повернув плоскость этой окружности вокруг линии сечения.
1.1. Окружность нормального сечения разделить на двенадцать частей и точки деления пронумеровать от точки O на очерковой образующей А”-A1“, то есть цилиндр заменить (аппроксимировать) двенадцатиугольной вписанной призмой; из точек деления окружности сечения провести на фронтальной проекции образующие до их пересечения с проекциями оснований.
2-е действие. На продолжении линии нормального сечения отметить двенадцать отрезков – сторон двенадцатиугольника (хорды окружности), которым заменяется окружность сечения, и провести направления ребер (образующих), перпендикулярно линии сечения (линии пронумеровать), то есть выполнить от ребра А”-A1” последовательную раскатку граней призмы, заменившей цилиндр.
3-е действие. Построить конечные точки каждой образующей (ребра) на пересечении образующих с линиями, проведенными перпендикулярно образующим из одноименных точек нижнего основания.
4-е действие. Оформить чертеж развертки боковой поверхности цилиндра, соединив построенные конечные точки образующих плавными кривыми линиями (в примере развертка оборвана из-за недостатка места). Для построения более точной развертки следует по формуле (1) (рис. 9.5, где L – диаметр цилиндра) вычислить длину развертки и разделив эту длину на 12 равных частей, провести образующие и далее выполнить 3 и 4 действия алгоритма.
Развертка кругового конуса
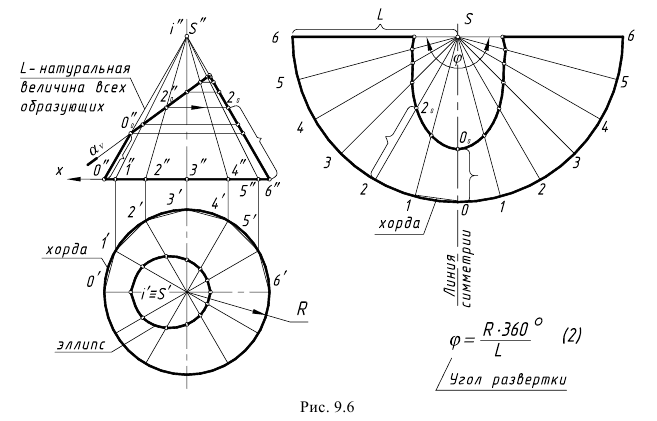
На рис. 9.6 показан пример построения развертки боковой поверхности прямого кругового конуса со срезом фронтально-проецирующей плоскостью α(αV), которая пересекает его поверхность по эллипсу.
Построение развертки боковой поверхности конуса выполняется по алгоритму, приведенному выше для построения развертки пирамиды, с некоторыми дополнениями.
Развертка выполняется по предлагаемому алгоритму.
1-е действие. Заменить прямой круговой конус вписанной правильной 12-угольной пирамидой с ребрами-образующими.
2-е действие. Построить развертку боковой поверхности пирамиды по натуральным величинам ребер (образующих) и сторон основания, выполнив следующие графические действия:
2.1. Отметить на свободном поле чертежа точку S и провести дугу радиусом L, равным натуральной величине всех образующих конуса (ребер пирамиды).
2.2. Отметить на дуге точку O на вертикальной линии симметрии развертки и построить вправо и влево на дуге засечками, равными сторонам-хордам 12-угольника, точки, соответствующие вершинам этого многоугольника; пронумеровать эти точки и соединить их с вершиной развертки, построив таким образом вспомогательные ребра-образующие (грани пирамиды).
3-е действие. Достроить на развертке линию среза конуса фронтально-проецирующей плоскостью α(αV), выполнив следующие графические действия:
3.1. На фронтальной проекции конуса перенести горизонтально на натуральную величину образующей S”-6″ точки сечения, отмеченные на вспомогательных образующих, то есть вращением вокруг оси i(i”,i’) построить натуральные величины отрезков образующих-ребер сечения.
3.2. Отложить на соответствующих образующих развертки натуральные величины отрезков образующих-ребер до точек сечения (отмечены на фронтальной проекции и на развертке фигурными скобками отрезки O”-Oo” образующей для точки Oo и 2″-2o” образующей для точки 2o) и соединить построенные точки сечения на развертке плавной кривой линией.
4-е действие. Оформить чертеж развертки, проведя сплошными толстыми линиями контур построенной развертки.
Для построения более точной развертки следует вычислить по формуле (2) (рис. 9.6, где R – радиус основания конуса; L – длина образующей конуса) угол развертки и разделить дугу развертки на 12 равных частей, провести образующие и далее выполнить 3 и 4 действия алгоритма.
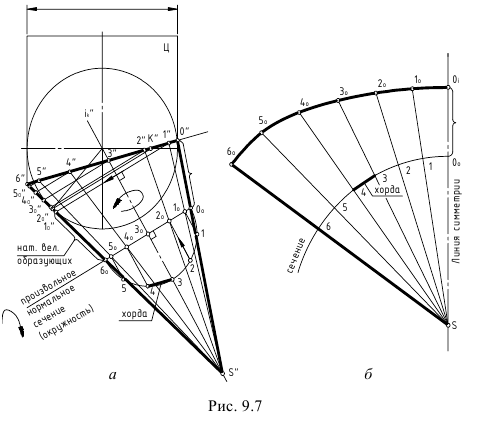
На рис. 9.7, а дан чертеж поверхностей кругового цилиндра и кругового конуса, описанных вокруг сферы, и построена линия пересечения этих поверхностей по теореме Г. Монжа.
На рис. 9.7, б построена развертка конической части этой конструкции по следующему графическому алгоритму:
1-е действие. Провести произвольное сечение, перпендикулярное оси конуса, и повернуть половину окружности сечения в очерковую плоскость конуса.
2-е действие. Разделить окружность сечения на 6 частей и перенести точки 1-6 параллельно оси конуса на линию сечения (проекцию окружности), то есть построить точки 1o-6o.
3-е действие. Через вершину конуса S(S”) и точки 1o-6o провести образующие конуса до пересечения с проекцией линии пересечения с проекцией линии пересечения цилиндра и конуса О1“-6”.
4-е действие. Вращением построенных образующих вокруг оси конуса перенести точки 1o“-5o” на очерковую образующую S”-6″, имеющую на чертеже натуральную величину.
5-е действие. На свободном поле чертежа провести радиусом R=S”Oo дугу и отложить на этой дуге шесть отрезков-хорд, на которые было поделено сечение конуса.
6-е действие. Через точку S на развертке и построенные точки Oo-6 провести семейство образующих.
7-е действие. Отложить от точек Oo-6 на каждой образующей развертки соответствующие натуральные величины образующих, взятые с чертежа, то есть отрезки 6o-1o, 6o-2o и т. д.
8-е действие. Построенные на концах семейства образующих точки соединить плавной кривой и оформить чертеж развертки (построена половина развертки).
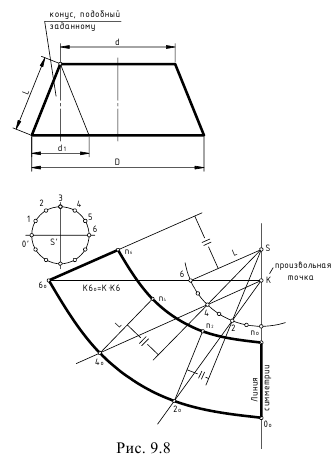
На рис. 9.8 показано построение развертки боковой поверхности боковой поверхности усеченного конуса (если вершину конуса на чертеже достроить нельзя) с основаниями, равными d и D.
Предварительно на чертеже усеченного конуса строится вспомогательный неусеченный конус подобный заданному так, чтобы отношение диаметра D исходного конуса к диаметру вспомогательного конуса d, было целым число, то есть K = D/d1 – целое число, где K – коэффициент кратности оснований конусов.
Примем K = 3 и впишем в заданный конус вспомогательный конус с вершиной S”.
Достроим горизонтальную проекцию вспомогательного конуса и разделим половину окружности основания d1 на 6 частей (1-6).
Далее приступаем к построению развертки половины усеченного конуса по следующему графическому алгоритму:
1-е действие. На свободном поле чертежа построить развертку вспомогательного конуса с вершиной S (см. рис. 9.8), то есть построить точки 0-2-4-6 на дуге развертки.
2-е действие. На оси симметрии развертки (биссектриса полной развертки) выбрать произвольную точку К и провести семейство лучей, соединяющих соответственно произвольную точку К с точками 0-2-4-6 развертки вспомогательного конуса.
3-е действие. Отложить на проведенных лучах отрезки, величины которых определяются произведениями:
- KOo = K×KO;
- K2o = K×K2;
- K4o = K×K4;
- K6o = K×K6,
где К – принятый коэффициент пропорциональности, а величины KO, K2, K4 и K6 следует измерить на строящейся развертке. На концах лучей определяются точки Oo, 2o, 4o и 6o.
4-е действие. Через построенные точки на концах лучей провести прямые n0-n6, каждая из которых должна быть соответственно параллельна образующим вспомогательного конуса на его развертке.
5-е действие. На проведенных прямых n0-n6 отложить натуральную величину длин образующих заданного усеченного конуса L.
6-е действие. Оформить чертеж развертки, соединив построенные точки развертки лекальными прямыми.
Условные развертки поверхностей
Условные развертки можно выполнить для некоторых неразвертывающихся поверхностей.
Рассмотрим построение условных разверток неразвертывающихся поверхностей сферы и открытого тора (кругового кольца).
Развертка сферической поверхности
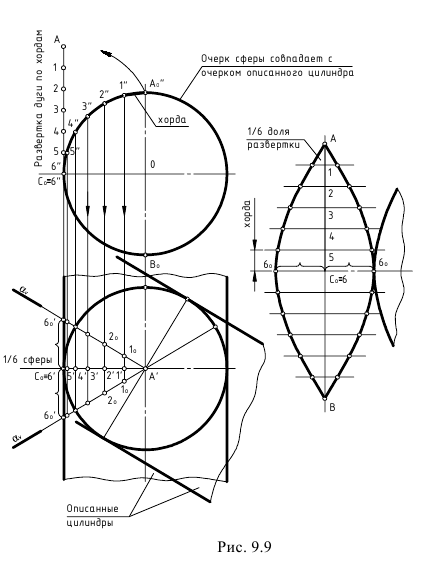
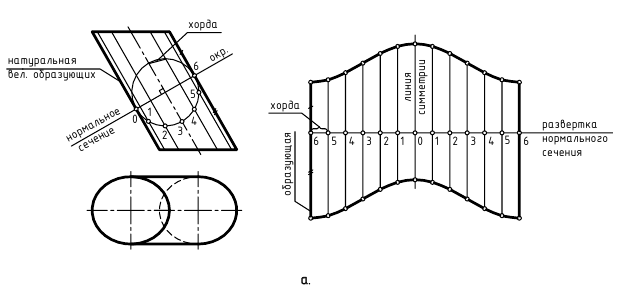
На рис. 9.9 показано построение условной развертки сферической поверхности.
Поверхность сферы условно разрезают на какое-то количество частей (6, 12 и более) и каждую часть заменяют (аппроксимируют) цилиндрической описанной поверхностью, фронтальная проекция которой совпадает с фронтальным очерком сферы – окружностью.
Далее выполнятся развертка одной доли поверхности сферы как сектора цилиндрической поверхности по следующему графическому алгоритму:
1-е действие. На горизонтальной проекции разрезать поверхность сферы на 6 частей и рассмотреть эту 1/6 часть (сектор) как фронтально-проецирующий цилиндр, описанный вокруг сферы.
2-е действие. Разделить дугу очерковой окружности A0B0 сферы, которая совпадает с окружностью описанного цилиндра, на 12 частей (поскольку есть симметрия, рассматриваем дугу A0С0) и заменить участки хордами (то есть вписать 12-угольную призму) – A0“-1″, 1″-2” и т. д.
3-е действие. Спроецировать точки 1″-6″ на стороны взятого сектора его горизонтальной проекции.
4-е действие. Свободном поле чертежа провести вертикальную линию и отложить от точки C0 вверх и вниз по 6 отрезков, равных величине хорд (точки пронумеровать).
5-е действие. Через каждую построенную точку А-6 провести горизонтальные линии и на каждой отложить величину соответствующей образующей: 10-10, 20-20 и т. д.
6-е действие. Конечные точки соединить лекальной кривой.
Таким образом построена 1/6 доля условной поверхности сферы, а 6 таких долей составят развертку всей поверхности.
С увеличением количества долей (1/12, 1/24 и т. д.) точность развертки увеличивается.
Развертка поверхности открытого тора
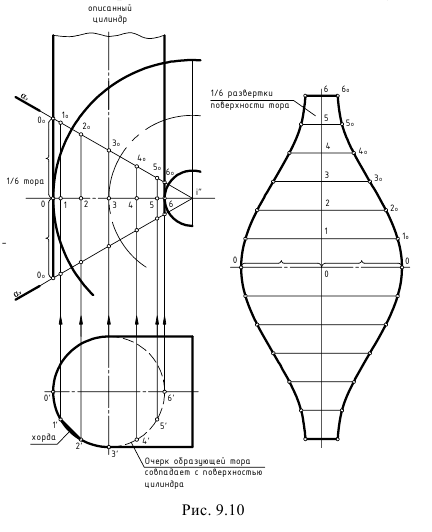
На рис. 9.10 показана условная развертка поверхности открытого тора.
Поверхность кольца разрезают на какое-то количество долей (6, 12 и более) плоскостями, проходящими через его ось i”, и заменяют каждую долю (сектор) поверхности описанной цилиндрической поверхностью.
Далее выполняют развертку одной доли поверхности по графическому алгоритму, приведенному для построения развертки одной доли поверхности сферы.
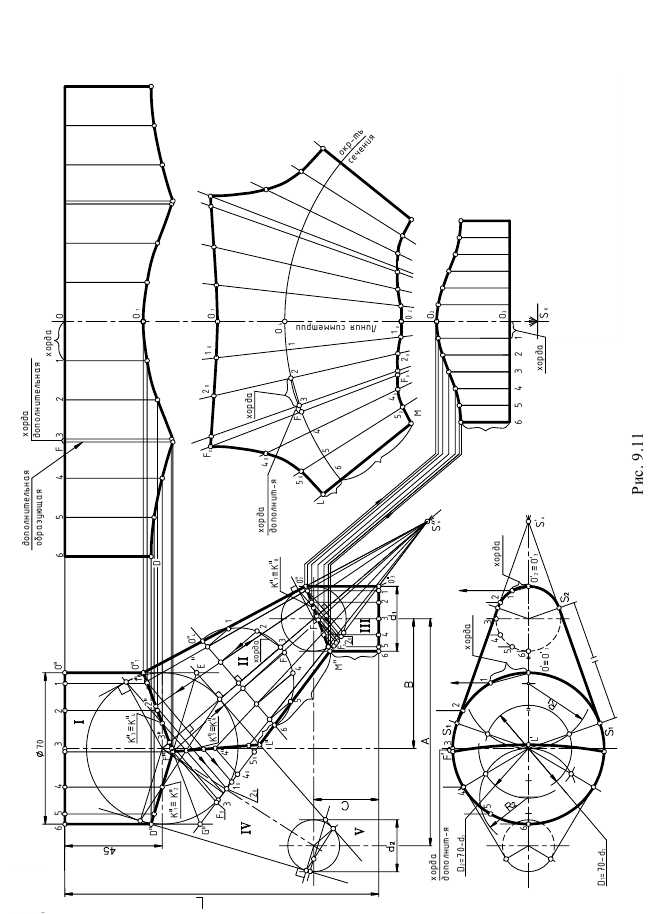
На рис. 9.11 приведен чертеж построения части (правой) развертки комбинированной геометрической поверхности, состоящей из трех полых цилиндров, сообщенных двумя коническими рукавами, в котором подытоживается изученный материал данной темы. Показано, что развертка каждой части комбинированной поверхности строится отдельно.
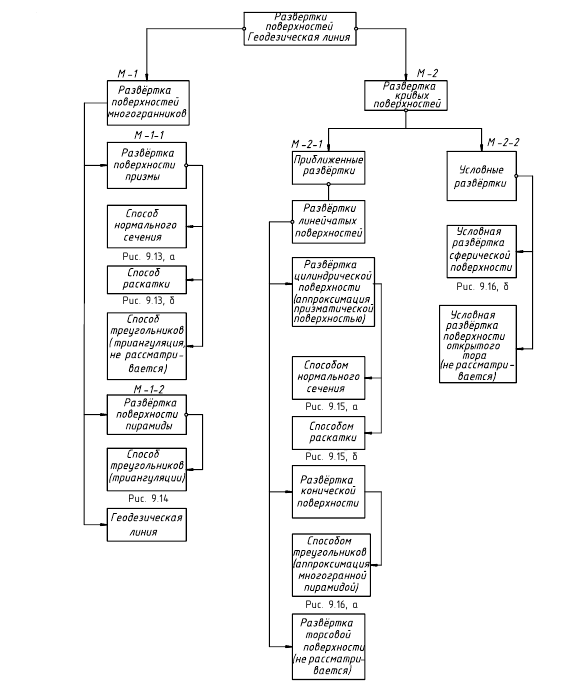
Структуризация материала девятой лекции в рассмотренном объеме схематически представлена на рис. 9.12 (лист 1). На последующих листах 2–5 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 9.13–9.16).
Развертки поверхностей:
Развертка – плоская фигура, в которую преобразовывается поверхность при ее совмещении с плоскостью без разрывов и складок.
Геодезическая линия – кратчайшее расстояние между двумя точками на поверхности. На развертке этой линии соответствует прямая.
Развертка гранных поверхностей
Развертка призмы.
а. Способ нормального сечения (применяется, если на чертеже ребра призмы являются прямыми уровня)
Графический алгоритм:
1. Построить натуральную величину нормального сечения, перпендикулярного к ребрам призмы.
2. Развернуть стороны сечения в линию и из вершин, провести направления ребер перпендикулярно к линии развертки.
3. Отложить вверх и вниз от точек вершин натуральные отрезки ребер и соединить построенные вершины; провести линии сгиба на месте ребер тонкими штрихпунктирными линиями с двумя штрихами.
б. Способ раскатки (применяется, если на чертеже ребра являются прямыми уровня и есть натуральная величина основания) Графический алгоритм построения на чертеже геодезической линии:
1. Построить развертку поверхности призмы.
2. Построить на развертке заданные на поверхности точки (M и N) и соединить прямой геодезической линией, которая пересекает ребро A в т.K.
3. Вернуть построенную т.K на проекции призмы и соединить с заданными точками M и N ломаной линией с учетом ее видимости на поверхности.
Развертка поверхности пирамиды.
Графический алгоритм построения развертки поверхности пирамиды:
1. Построить натуральные величины всех ребер пирамиды (способом вращения вокруг проецирующей оси).
2. Выполнить развертку поверхности, построив по натуральным величинам ребер треугольники граней и основание.
3. Соединить отрезками построенные на развертке вершины и оформить линии сгиба.
Развертка цилиндрических поверхностей
1. Способ нормального сечения
2. Способ раскатки
- Способы преобразования проекций
- Взаимное положение прямой и плоскости
- Решение метрических задач
- Тени в ортогональных проекциях
- Преобразование чертежа
- Кривые линии
- Образование и задание поверхности на чертеже
- Пересечение поверхности плоскостью и прямой
Содержание:
- Свойства развёрток
- Развёртывание поверхности многогранника
- Способ натуральных граней
- Способ нормального сечения
- Способ раскатки
- Развёртывание поверхностей тел вращения
- Приближённое и условное развёртывание кривых поверхностей
- Способ аппроксимирующих поверхностей
- Способ призматических поверхностей
- Способ пирамидальных поверхностей
- Способ цилиндрических поверхностей
- Способ конических поверхностей
- Метод триангуляции
Развертывание цилиндров и конусов основывается на способах развертки гранных поверхностей приведенных выше. В общем случае поверхность цилиндра аппроксимируется призматической поверхностью, а конус – пирамидой и затем строится приближенная развертка кривой поверхности.
Свойства развёрток
Развёрткой криволинейной поверхности Ф называется плоская фигура 
Развёртывание поверхностей тел широко применяется в технике, поскольку большое количество технических конструкций изготавливается из листового материала. Заготовки таких конструкций, которые являются развёртками, используются для изготовления тонкостенных ёмкостей, воздуходувов, промышленной вентиляции и пневмотранспорта, фасонных частей пылеулавливателей, деталей подъёмно – транспортных приборов и т.д. (рис. 5.2).


Поверхности Ф, которые можно совместить с плоскостью Σ без разрывов и складок, являются, развёртывающимися. К ним принадлежат все многогранники (см. п. 4.1), цилиндрические и конические поверхности (см. п. 3.2.1.3, рис. 3.55 б – в), торсы (см. п. 3.2.1.3, рис. 3.57). Все другие кривые поверхности не развёртываются на плоскость, поэтому при их изготовлении из листового материала они приближённо заменяются развёртывающимися поверхностями (призмами, пирамидами, цилиндрами, конусами). В этих случаях имеют место так называемые условные развёртки (см. п. 5.4.1.3 – 5.4.1.4).
Основные свойства развёрток:
а) прямая l на поверхности Ф отвечает прямой 
б) параллельные прямые 

в) длина (натуральная величина) любой линии s на поверхности Ф равна длине линии 
г) угол α между линиями r, s на поверхности Ф равен углу между линиями 
д) площадь S фигуры на поверхности Ф равна плоскости соответствующей фигуры на развёртке
е) если прямая 

Описанные свойства геометрически интерпретированы на рис. 5.3.

Геодезическая линия (от греческого γεωδαισία – разделение Земли) – линия минимальной длины, проведенная через две точки криволинейной поверхности. На развёртке поверхности эта линия – прямая.
Геодезическая линия широко применяется в неэвклидовой геометрии, теоретических и практических задачах геодезии – науки, которая изучает измерения пространства, в том числе размеры и форму Земли, её гравитационное поле и т.д.
Развёртывание поверхности многогранника
Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью. Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.
Способ натуральных граней
Согласно свойствам развёртки (см. п. 5.1) все грани многогранника Ф сохраняют на развёртке свою длину, для определения которой используются способы начертательной геометрии.
На рис. 5.4 построены горизонтальная и фронтальная проекции треугольной пирамиды SABC. Основа АВС является плоскостью горизонтального уровня, поэтому проецируется на П1 в натуральную величину А1В1С1. Для определения натуральных величин граней SAB, SBC, SCA используется способ вращения вокруг горизонтально-проецирующей оси і, которая проходит через вершину S пирамиды. Отрезки 

Для определения на развёртке произвольной точки D пирамиды применяется способ вспомогательного отрезка. Точка D принадлежит грани SАС. Через вершину S и точку D проводится отрезок S-1, точка 1 которого принадлежит основе АВС пирамиды. Определяется натуральная величина



Способ нормального сечения
Способ нормального сечения применяется для построения развёртки призм, ребра которых являются прямыми уровня.
Суть способа нормального сечения
Призма пересекается в произвольном месте плоскостью Σ, перпендикулярной рёбрам. Определяется натуральная величина линии 1 – 2 – … нормального сечения. Эта линия является плоским многоугольником, количество сторон которого равно количеству граней призмы. Линия 1 – 2 – … разворачивается до формы прямого отрезка 

На рис. 5.5 заданы две проекции треугольной призмы ABCDEF с рёбрами AD, BE, CF горизонтального уровня. Вводится секущая плоскость Σ, перпендикулярная рёбрам призмы (горизонтальный след Σ1 перпендикулярен горизонтальным проекциям рёбер призмы). Плоскость Σ пересекает призму по треугольнику 1 – 2 – 3, точки которого принадлежат, соответственно, рёбрам AD, BE, CF. Способом замены плоскостей проекций определяется натуральная величина 









Для определения на развёртке произвольной точки G призмы применяется способ вспомогательных отрезков. Точка G принадлежит грани ABDE. Через точку G проводится отрезок 4 – 5, параллельный рёбрам призмы. Точка 4 принадлежит отрезку АВ, точка 5 – отрезку DE. Определяется точка 6 пересечения отрезка 4 – 5 с плоскостью Σ. Точка 6 принадлежит отрезку 1 – 2. Определяется проекция 








Способ раскатки
Способ раскатки применяется для развёртывания призмы, основа которой параллельна одной плоскости проекций, а боковые рёбра параллельны другой плоскости проекций.
Из точек 1, 2, … основы 




На рис. 5.6 заданы две проекции треугольной призмы 







Для определения на развёртке произвольной точки А призмы применяется способ вспомогательного луча. Точка А принадлежит грани 







Развёртывание поверхностей тел вращения
По развертыванию поверхности делятся на два класса: развертываемые, которые можно совместить с плоскостью без разрывов и складок, и неразвертываемые, которые невозможно совместить с плоскостью без разрывов и складок. Развертываются все многогранные поверхности, из кривых поверхностей – только линейчатые, у которых смежные образующие параллельны между собой (цилиндрические) или пересекаются по одной точке (конические).
Из всего разнообразия поверхностей тел вращения точное развёртывание осуществляется только для прямых круговых цилиндра и конуса (рис. 5.7 – 5.8).
Поверхность прямого кругового цилиндра разворачивается в прямоугольник, одна сторона которого равна длине 



Поверхность прямого кругового конуса разворачивается в сектор окружности с центром в вершине S конуса. Радиус сектора равен длине l образующей линии конуса; угол φ = 180°·d/l, где d – диаметр основы конуса (рис. 5.8). Развёртка конуса при необходимости дополняется основой – окружностью диаметром d. Для определения точки А на развёртке прямого кругового конуса применяется способ образующей линии. Определяется угол α и строится образующая линия на развёртке, положение которой определяется углом β = 0,5αd/l. Точка 



Приближённое и условное развёртывание кривых поверхностей
При построении приближенных и условных разверток используют ап-проксимацию (от approximare (лат.) – приближаться) одной поверхности к другой. Аппроксимацией называют замену одной поверхности другой – аппроксимирующей, которая приближается к заданной по каким-то опре-деленным свойствам (форма, площадь, кривизна) с той или иной степенью точности.
Способ аппроксимирующих поверхностей
Развёртка любой развёртывающейся поверхности (кроме прямых круговых конуса и цилиндра) строится приближённо. Это происходит вследствие того, что при развёртывании кривой поверхности её аппроксимируют гранями вписанных многогранников(рис. 5.9).
Способ призматических поверхностей
Например, цилиндрическая поверхность условно заменяется призмой (рис. 5.9 а), коническая поверхность – пирамидой (рис. 5.9 б).

Для построения приближённой развёртки цилиндрической поверхности используется способ призматических поверхностей
Суть способа призматических поверхностей
В цилиндрическую поверхность вписывается призма, количество граней которой прямо влияет на точность построения развёртки цилиндра. Строится развёртка этой призмы способом нормального сечения или раскатки (см. п. 5.2.2 – 5.2.3). Через точки на развёртке призмы проводятся плавные кривые, являющиеся контуром приближённой развёртки цилиндра. При необходимости развёртка цилиндра дополняется нижней и верхней основами.
На рис. 5.10 изображен комплексный чертёж эллиптического цилиндра, поверхность которого аппроксимируется двенадцатигранной призмой. Развёртка последней строится способом раскатки. Через точки 
Способ пирамидальных поверхностей
Способ пирамидальных поверхностей используется для построения развёртки боковой поверхности конуса.
Суть способа пирамидальных поверхностей
В коническую поверхность вписывается пирамида. Строится приближённая развёртка этой пирамиды способом натуральных граней (см. п. 5.2.1). Через точки на развёртке пирамиды проводится плавная кривая, являющаяся контуром развёртки конуса. По необходимости развёртка конуса дополняется его основой.
Аппроксимация (от англ. approximation – приближение) – научный метод, состоящий в замене одних объектов другими, более простыми, приближёнными к оригиналу.
Необходимо различать такие понятия, как приближённая и условная развёртка. Приближённая развёртка касается развёртывающихся поверхностей. Условная развёртка строится для поверхностей, которые не развёртываются.

На рис. 5.11 изображен комплексный чертёж эллиптического конуса, поверхность которого аппроксимируется двенадцатигранной пирамидой. Развёртка последней строится способом натуральных граней. Через точки 

Способ цилиндрических поверхностей
Для поверхностей, которые не развёртываются. в том числе нелинейчатых, строятся условные развёртки. Основные способы построения условных развёрток такие:
а) способ цилиндрических поверхностей;
б) способ конических поверхностей;
в) метод триангуляции.
Суть способа цилиндрических поверхностей
Кривая поверхность описывается совокупностью цилиндрических поверхностей, которые в дальнейшем развёртываются и совмещаются по точкам и линиям. Полученная развёртка является условной развёрткой кривой поверхности.
На рис. 5.12 построена условная развёртка сферы. Вокруг её поверхности описываются шесть одинаковых цилиндрических поверхностей. Одна из таких поверхностей имеет образующие линии 





На рис. 5.13 построена условная развёртка открытого тора. Вокруг его поверхности описываются двенадцать одинаковых цилиндрических поверхностей. Одна из таких поверхностей имеет образующие линии 



Способ конических поверхностей
Способ конических поверхностей используется для построения условных развёрток закрытых тел вращения (эллипс, параболоид, эллипсоид, двуполостной гиперболоид, закрытый тор и т.д.).
Суть способа конических поверхностей
Сегменты поверхности описываются совокупностью конических поверхностей, которые развёртываются и совмещаются по точкам и линиям. Полученная развёртка является условной развёрткой кривой поверхности.
На рис. 5.14 построена условная развёртка сферы. Вокруг её поверхности описывается одна цилиндрическая и шесть конических поверхностей с разными вершинами 



На рис. 5.15 построена условная развёртка эллипсоида. Вокруг его поверхности описываются одна цилиндрическая и шесть конических поверхностей с разными вершинами 


Метод триангуляции
Метод триангуляции (от англ. triangle – треугольник) применяется для развёртывания многогранников, приближенного развёртывания цилиндрических и конических поверхностей и поверхностей с ребром поворота (торсов), а также условного развёртывания поверхностей которые не развёртываются.
Суть метода триангуляции
Кривая поверхность разбивается на треугольники с общими сторонами. Натуральные величины этих треугольников сочетаются по общим сторонам. Внешний контур полученной плоской фигуры является приближенной или условной развёрткой заданной кривой поверхности.
На рис. 5.16 построена приближённая развёртка торса Ф. Последний разбивается совокупностью треугольников с вершинами 1, 2, …, принадлежащими ребру возврата 

На рис. 5.17 построена приближённая развёртка поверхности произвольного пространственного тела. Его поверхность разбивается на треугольники, стороны которых построены по точкам 1, 2, …, А, В, …, принадлежащим соответственно верхней и нижней основам тела. Натуральные величины сторон треугольников определяются способом вращения вокруг горизонтально-проецирующих осей, проходящих через точки В, С. По найденным отрезкам строятся натуральные величины треугольников, которые сочетаются по общим сторонам. Контур полученной плоской фигуры является приближенной развёрткой поверхности тела.

Примеры и образцы решения задач:
- Решение задач по инженерной графике
- Решение задач по начертательной геометрии
Услуги по выполнению чертежей:
- Заказать чертежи
- Помощь с чертежами
- Заказать чертеж в компасе
- Заказать чертеж в автокаде
- Заказать чертежи по инженерной графике
- Заказать чертежи по начертательной геометрии
- Заказать черчение
Учебные лекции:
- Инженерная графика
- Начертательная геометрия
- Оформление чертежей
- Чертеж общего вида и сборочный чертеж
- Техническое рисование
- Машиностроительные чертежи
- Геометрические построения
- Деление окружности на равные части
- Сопряжение линий
- Коробовые кривые линии
- Построение уклона и конусности
- Лекальные кривые
- Параллельность и перпендикулярность
- Методы преобразования ортогональных проекций
- Поверхности
- Способы проецирования
- Метрические задачи
- Способы преобразования чертежа
- Кривые линии
- Кривые поверхности
- Трёхгранник Френе
- Проецирование многогранников
- Проецирование тел вращения
- Проекционное черчение
- Проецирование
- Проецирование точки
- Проецирование отрезка прямой линии
- Проецирование плоских фигур
- Способы преобразования проекций
- Аксонометрическое проецирование
- Проекции геометрических тел
- Сечение геометрических тел плоскостями и развертки их поверхностей
- Взаимное пересечение поверхностей тел
- Сечение полых моделей
- Разрезы
- Требования к чертежам деталей
- Допуски и посадки
- Шероховатость поверхностей и обозначение покрытий
- Разъемные и неразъемные соединения деталей
- Передачи и их элементы
Мы этого не замечаем, но вокруг нас существует огромное количество объемных геометрических фигур. Практически все технические устройства, дома, мебель и автомобили созданы с их применением. Именно поэтому знакомство с многогранниками начинается еще в школе. Представление тел в 3D — измерении лишь только кажется сложным и скучным. Рассмотрим доступные инструкции, как сделать из бумаги объемные фигуры геометрической формы, а также интересные примеры поделок из них.
Содержание
- 1. Как правильно сделать объемные фигуры из бумаги и картона
- 2. Развертки простых объемных геометрических фигур
- 2.1. Шаблон для склеивания параллелепипеда
- 2.2. Правильная четырехгранная пирамида
- 2.3. Правильна многогранная пирамида
- 2.4. Непростая развертка усеченной пирамиды
- 2.5. Развертка шестигранной призмы
- 2.6. Как правильно сделать круглый конус
- 2.7. Развертка цилиндра
- 3. Шаблоны и схемы правильных выпуклых многогранников
- 3.1. Тетраэдр или фигура из четырех равносторонних треугольников
- 3.2. Куб или гексаэдр, то есть фигура из шести квадратов
- 3.3. Фигура октаэдра состоит из 8 равносторонних треугольников
- 3.4. Додекаэдр, то есть фигура из 12 правильных пятиугольников
- 3.5. Икосаэдр, то есть фигура из 20 равносторонних треугольников
- 4. Забавные приключения объемных геометрических фигур: модели, фигурки животных, декор
- 5. Комментарии посетителей по теме статьи
Как правильно сделать объемные фигуры из бумаги и картона
Удобнее всего выполнить задание, используя плотную бумагу или картон. Разумеется, необходимо знать, как выглядит требуемая фигура в 3D – формате. Кроме того, необходимо начертить или распечатать схему развертки многогранника. Чаще всего макет склеивают, и для этого чертеж должен иметь соответствующие припуски материала. Впрочем, многие геометрические фигуры дети могут сделать своими руками в технике оригами из нескольких листов бумаги, то есть без клея.
Имея навыки черчения, схему несложно начертить на бумаге самостоятельно. Грани фигур состоят из треугольника, квадрата, ромба, круга, трапеции или другого многоугольника. При этом ребра многогранников должны иметь точный одинаковый размер, иначе фигуру не получится собрать. В случае одинаковых граней можно подготовить шаблон одной из них, а затем его обвести, формируя полный чертеж развертки.
Чтобы грани были аккуратными, ровными, рекомендуется подготовить линии изгибов, прочертив их тупой стороной иглы по металлической линейке. Таким образом, в общей сложности для работы потребуются:
- тонкий картон или плотная бумага;
- карандаш и линейка;
- клей для бумаги и канцелярские ножницы.
Из цветного материала получится веселая и привлекательная фигурка. Лучший вариант клея – ПВА.
Развертки простых объемных геометрических фигур
Грани объемных фигур вовсе не обязаны быть одинаковыми. Получается большое разнообразие возможных вариантов, и мы рассмотрим основные из них.
Шаблон для склеивания параллелепипеда
Тривиальный параллелепипед встречается повсюду. Фигура имеет шесть граней в виде параллелограммов. Если его грани прямоугольные, значит и параллелепипед – прямоугольный.
При вычерчивании шаблона для изготовления фигуры необходимо обеспечить углы 90°, а прямоугольники должны быть попарно одинаковые. В следующем примере грани фигуры образуют ромбы, а не параллелограммы. Удобно изготовить шаблон одного из них, а затем обвести 6 раз.
Это видео поможет изготовить параллелепипед из бумаги или картона.
Правильная четырехгранная пирамида
Такая пирамида называется правильной не потому, что хорошо себя ведет, а потому, что в ее основании — равносторонняя геометрическая фигура. В данном случае это квадрат. Чертеж выполнить очень просто: сначала изображаем квадрат, а к нему пристыковываем 4 одинаковых треугольника. К ним добавляем 4 припуска на склейку.
Можно распечатать шаблон с формулами расчета параметров фигуры. Очень поможет на уроке!
Это видео поможет изготовить пирамиду из бумаги.
Кстати, из правильной четырехгранной пирамиды получается оригинальная коробочка для подарка. Ее лучше изготовить из плотной цветной бумаги. Другой вариант – сделать упаковку из картона и оклеить бумагой с рисунком. В верхней части треугольников нужно пробить отверстия дыроколом и пропустить через низ красивый шнурок с бантом.
Правильна многогранная пирамида
Непростая развертка усеченной пирамиды
Шаблон усеченной пирамиды — не самый простой. Его чертеж достаточно точно можно выполнить с помощью циркуля и линейки.
Для склейки фигуры следует оставить припуски в соответствии с рисунком.
Чертеж шаблона с конкретными размерам представлен на следующем фото.
Это видео поможет изготовить четырехгранную усеченную пирамиду своими руками.
Развертка шестигранной призмы
Это видео поможет изготовить четырехгранную призму своими руками.
Как правильно сделать круглый конус
Проще всего шаблон для изготовления круглого конуса распечатать на принтере.
Припуски на склейку можно предусмотреть либо на круглом основании, либо на боковой поверхности конуса.
Это видео поможет правильно вырезать шаблон и склеить конус.
Развертка цилиндра
Добавляем припуски на склейку и получаем полноценный шаблон для изготовления цилиндра. Следующее видео поможет правильно вырезать шаблон и склеить цилиндр.
Шаблоны и схемы правильных выпуклых многогранников
Тетраэдр или фигура из четырех равносторонних треугольников
Другой вариант разметки шаблона – разделить пополам две противоположные стороны параллелограмма.
Грани тетраэдра можно раскрасить в разные цвета. Фигура станет веселее и поможет ребенку запомнить названия цветов.
Еще один вариант оформления тетраэдра – наклеить на его грани веселые детские картинки.
Грани тетраэдра можно отметить цифрами, чтобы упростить ребенку их запоминание.
Это видео поможет правильно вырезать и склеить тетраэдр.
Это видео поможет собрать 3D — фигуру в технике оригами, то есть без клея.
Куб или гексаэдр, то есть фигура из шести квадратов
Его развертку можно построить из квадратов, добавим припуски на склейку.
Грани гексаэдра можно отметить цифрами, чтобы упростить ребенку их запоминание.
Куб небольших размеров превращается в игральный кубик, если на его грани нанести маркером соответствующее количество точек.
Это видео поможет правильно вырезать и склеить куб.
Фигура октаэдра состоит из 8 равносторонних треугольников
Составляем параллелограмм из 3-х ромбов с углами 60° и добавляем короткие диагонали. Достраиваем снизу и сверху по треугольнику, а также добавляем припуски на склейку. Получаем шаблон для вырезания октаэдра.
Грани поделки можно оклеить веселыми картинками для детей.
Еще один вариант оформления – распечатать шаблон с формулами расчета параметров фигуры. Это поможет на уроке!
Далее видео изготовления звездчатого октаэдра.
Додекаэдр, то есть фигура из 12 правильных пятиугольников
Развертка додекаэдра состоит из 2-х одинаковых групп пятиугольников.
Грани фигуры можно украсить занимательными детскими картинками.
Это видео поможет собрать 3D — фигуру додекаэдра в технике оригами, то есть без клея.
Икосаэдр, то есть фигура из 20 равносторонних треугольников
Составляем параллелограмм из 5-ти ромбов с углами 60° и проводим короткие диагонали. Достраиваем снизу и сверху по 5 треугольников, а также добавляем припуски на склейку. Получаем шаблон для вырезания икосаэдра.
Есть еще один вариант шаблона, который удобен для вырезания из квадратного листа бумаги.
Возможно, такая схема шаблона покажется более понятной.
Это видео поможет правильно вырезать шаблон и склеить икосаэдр.
Если по заданию учителя изготовить не один, а два икосаэдра, можно собрать композицию снеговика и гарантированно рассчитывать на 5 баллов!
Один икосаэдр должен быть чуть больше другого. Склеиваем их вместе и подрисовываем фломастерами глаза, щеки и пуговички у снеговика. Нос – маленькая пятигранная пирамида, которую нужно сделать из красной бумаги.
Забавные приключения объемных геометрических фигур: модели, фигурки животных, декор
Освоив изготовление объемных геометрических фигур по заданию учителя, самое время сделать теперь что-то повеселее. Используя полученные навыки, можно создать своими руками 3Д — фигурки животных и героев мультфильмов, коробочки для подарков, сами праздничные подарки, элементы украшения комнаты и прочие поделки для детей. Рассмотрим наиболее интересные пошаговые инструкции для учащихся и дошкольников.
Так, шестигранная призма превращается в карандаш, если ее увенчать шестигранной же пирамидой. Шаблон следует раскрасить в соответствии с фото, и тогда получится полная аналогия.
Дети очень любят фигурки животных. Используя приведенную выкройку, можно изготовить очаровательную таксу.
С помощью такого шаблона можно изготовить игрушечный домик. В следующем видео Вы найдете еще один вариант домика из бумаги.
Таким образом из объемных геометрических фигурок можно построить целый город.
Как известно, из цветной бумаги делают самые разные цветы. При этом, даже если бутоны представляют из себя объемные геометрические фигуры, из них можно сформировать очаровательный букет.
Один из вариантов сборки красочных бутонов представлен в следующем мастер-классе. Шаблон представляет из себя восьмиконечную звезду.
В итоге получаются вот такие фигуры. Их собирают с помощью клея ПВА.
Объемные геометрические фигуры, изготовленные из цветной бумаги и картона, удивительным образом подходят для оформления интерьера.
Достаточно подвесить их на нитях к потолку, и необычное оформление комнаты к празднику обеспечено.
Впрочем, и на столе они произведут неизгладимое впечатление. Подобные украшения легко изготовить к празднику, так же просто и выбросить их после окончания торжества.
Как Вам такая вазочка с набором желаний, которые размещены внутри уже знакомых фигур? Просто и со вкусом.
Собирайте своими руками объемные геометрические фигуры и радуйтесь их прямой и правильной красоте!
- Авторы
- Научный руководитель
- Файлы
- Литература
Ляховский К.С.
1
1 г. Котлас, ЧЧОУ «Школа-интернат № 1 среднего общего образования ОАО «Российские железные дороги», 4 класс
Бубнова Н.И. (Котлас, ЧОУ «Школа-интернат № 1 ;среднего общего образования ОАО «Российские железные дороги»)
1. Моро М.И., Волкова С.И. Для ;тех, кто любит математику. 4 ;класс ;/ Просвещение, 2017.
2. Волкова С.И. Математика и ;конструирование. 4 ;класс, 2014.
3. Атанасян Л.С., Бутузов В.Ф. Геометрия 7–9 ;классы: учеб. для ;образовательных учреждений. 5-е изд. – М.: Просвещение.
4. http://uslide.ru/geometriya/18852–razvyortki-kuba.html.
5. http://easyen.ru/load/m/3_klass/kub_ehlementy_kuba_grani_rebra_vershiny/377–1–0–13873.
6. https://ru.wikipedia.org/wiki.
Математика изучает объекты, явления, процессы окружающего мира во всех его проявлениях и взаимодействиях. Обустраивая окружающее пространство, человек всегда старается его упорядочить. Одна из часто встречаемых форм бытовых предметов – это прямоугольный параллелепипед. Его форму имеют: шкаф, телевизор, детские кубики, кусочки сахара… Длину, ширину и высоту прямоугольного параллелепипеда называют его измерением. Если все три измерения равны, то его называют кубом.
Знания о площади поверхности куба, его развертках, объёме полезны при расчётах количества обоев, паркета, краски при ремонте квартиры, кубометров леса при постройке дома… Поэтому тема «Куб и его развёртки» является актуальной.
Актуальность применения правил замощения плоскости подтверждает сказ о мастерах.
Двум мастерам было дано задание из одинаковых листов железа изготовить максимальное количество кубов, используя предложенную развертку куба. У первого мастера получилось 5 штук, второй же мастер, применив принципы замощения плоскости, сумел сделать в два раза больше кубов, тем самым показав возможность рационального использования материала
Цель исследования: получение новых знаний о кубе, его развертках и их практических применениях.
Задачи исследования:
1. Изучить элементы куба.
2. Исследовать развёртки куба.
3. Изготовить модели куба.
4. Выполнить замощение плоскости развёртками куба.
5. Изготовить пазлы.
Предмет исследования: куб.
Объект исследования: развёртки куба.
Гипотеза: знания о кубе и его развёртках помогают решать практические задачи.
Методы исследования: практический, наблюдение, опрос, анализ, обобщение, измерения, расчёты, изучение литературы и материалов сайтов.
Теоретический этап исследования
1. Куб и его элементы
По другому куб называют шестигранником или гексаэдром [6]. Куб имеет 6 граней Каждая грань куба – квадрат. У куба 8 вершин. Вершина куба – это самая отдалённая от центра куба точка, которая лежит на пересечении трёх его граней. Каждая вершина принадлежит только трём граням и только трём рёбрам. Куб имеет 12 рёбер. Ребро куба – это отрезок, образованный пересечением двух граней куба. Рёбра имеют одинаковую длину. Каждый конец ребра соединен с двумя соседними рёбрами под прямым углом [3].
Поверхность куба состоит из шести граней. Площадь поверхности куба – это сумма площадей всех граней.
Площадь одной грани куба при длине ребра «а» равна а2. Площадь поверхности куба можно выразить формулой S=6a2.
Площадь одной грани этого куба: 1 дм2, тогда площадь поверхности куба будет равна 6 дм2. Если разбить 1 дм2 на см2 и мм2, мы получим, что площадь поверхности данного куба будет равна 600см2 и 60 000мм2 соответственно.
Объём куба – это совокупность всех точек в пространстве, ограниченных гранями куба. Объём куба при длине ребра «а» можно выразить формулой V=a3.
Кубы с одинаковым размером граней, но сделанные из разных материалов имеют одинаковый объем, одинаковую площадь, но разную массу. Соответственно, кубы, изготовленные из разных материалов, но имеющие одинаковую массу, будут отличаться размерами.
Игральная кость – это популярный источник случайности, который широко применяется в азартных, настольных и ролевых играх.
Традиционная игральная кость – это кубик, который используется как средство генерирования случайных чисел. На каждую грань кубика нанесены числа от 1 до 6. Их принято располагать так, чтобы сумма чисел на противоположных гранях была равна семи. Целью кубика является демонстрация случайно определённого целого числа от одного до шести. Выпадение каждого числа является равновозможным благодаря правильной геометрической форме кубика.
2. Развёртки куба
Развёртка куба – это оболочка, позволяющая увидеть куб со всех сторон. Развертка куба состоит из 6 равных квадратов.
Изучение возможных вариантов развёртки куба, показало, что их всего 11 видов [4].
3. Замощение
Замощение – это покрытие всей плоскости или заполнение всего пространства неперекрывающимися фигурами [5].
Изучение куба показало, что плоскость можно покрыть целиком без пробелов его реберными развёртками одного вида. При этом несколько развёрток одного типа складываются в симметричный элемент орнамента, называемый плиткой, с помощью которой происходит замощение плоскости [2].
Выполнено замощение плоскости различными развёртками куба. Замощение плоскости развертками куба можно использовать при изготовлении пазлов.
Пазл – это увлекательная головоломка очень популярная у взрослых и незаменимый элемент в жизни каждого ребёнка. Пазлы для детей – это увлекательная игра, позволяющая развивать мелкую моторику, логическое мышление, воображение, память, усидчивость, терпение, целеустремленность.
Практический этап исследования
Практическая работа №1
Сделать модель куба из дерева с рёбрами 1 дм, из бумаги с ребром 1 дм. Из бумаги с ребром 1 см.
Заполнить таблицу.
|
Ребро |
Площадь поверхности |
Объём |
Масса |
|
|
Куб из дерева |
1 дм |
6 дм2 |
1 дм3 |
650 г |
|
Куб из бумаги |
1 дм |
6 дм2 |
1 дм3 |
50 г |
|
Куб из бумаги |
1 см |
6 см2 |
1 см3 |
0,5 г |
Вывод: площадь поверхности и объёма куба зависит от величины ребра и не зависит от материала. Масса куба зависит от размеров куба и материала, из которого он изготовлен (Приложение 1).
Практическая работа №2
Изготовить тренажёр по переводу единиц измерения площади. На бумажной модели куба разбить одну грань на квадратные сантиметры, на противоположной сделать надпись 100см2, другую грань разбить на квадратные миллиметры, на противоположной грани сделать надпись 10000 мм2. На пятой грани сделать надпись 1 дм2.
Результат: изготовлен тренажёр по переводу единиц измерения площади (Приложение 2).
Практическая работа №3
Изготовить 11 различных развёрток куба с длиной ребра 1дм. Обёртыванием бумажной модели куба убедиться, что все они являются развёртками куба.
Результат: даны названия развёрткам куба: «Буква Т», «Крестик», «Лежачая собачка», «Ружьё», «Стоячая собачка», «Пушка», «Загадочная», «Лесенки».
Проверено, что все 11 многоугольников являются развёртками куба (Приложение 3).
Практическая работа №4
Изготовить модель игральной кости с ребром 5 см. Подбрасыванием кости убедиться, что выпадение очков происходит с равной вероятностью.
|
№ опыта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Выпадение очков |
5 |
1 |
4 |
5 |
6 |
3 |
3 |
1 |
2 |
6 |
3 |
5 |
6 |
4 |
2 |
1 |
6 |
2 |
4 |
5 |
Вывод: выпадение очков происходит с равной вероятностью (Приложение 4).
Практическая работа №5
Замостить плоскость различными развёртками куба. Сделать пазлы.
Результаты:
1. Выполнены рисунки по замощению плоскости развёртками куба.
2. Изготовлены пазлы (Приложение 5).
Задача о нахождении кратчайшего расстояния по поверхности куба
В точке А на поверхности куба находится паук, в точке В муха. Найти кратчайшее расстояние по поверхности куба от паука к мухе.
Развертки куба помогают при решении различных задач. Одна из таких задач была предложена для решения воспитанникам нашей школы. Необходимо было указать кратчайший путь от паука, сидящего в точке А, к мухе, находящейся в точке В.
Был проведён опрос воспитанников по нахождению самого короткого пути по поверхности куба.Предложенные варианты ответов изображены цифрами.
|
№ опыта |
Длина линии |
|
1 |
25 см |
|
2 |
23 см |
|
3 |
21 см 5 мм |
|
4 |
20 см 5 мм |
|
5 |
21 см 4 мм |
Произвели измерения и вычислили длины путей, самый короткий путь оказался четвёртый. Это подтверждает развёртка куба. Самый короткий путь на развёртке – это отрезок АВ. Двигаться надо к точке на ребре куба, отстоящей от нижней грани на четверть ребра (Приложение 6).
Заключение
В результате работы были сделаны следующие выводы:
1. Куб – это геометрическое тело, являющееся правильным шестигранником, каждая грань которого представляет собой квадрат.
2. Куб небольшого размера, на каждую грань которого нанесены числа от 1 до 6, используется как средство генерирования случайных чисел.
3. Развёртки куба позволяют находить решения различных задач.
4. Применение различных развёрток куба и правил замощения плоскости способствуют созданию разнообразных орнаментов и рациональному использованию материала.
5. Замощение плоскости развертками куба можно использовать при изготовлении пазлов для детей, способствующих их полноценному и всестороннему развитию.
Приложения
Приложение 1
Модели куба
Приложение 2
Поверхность куба

Приложение 3
Развёртки куба


Приложение 4
Игральная кость
Приложение 5
Замощение плоскости

Приложение 6
Нахождение кратчайшего пути

Библиографическая ссылка
Ляховский К.С. КУБ И ЕГО РАЗВЁРТКИ // Старт в науке. – 2018. – № 5-6.
;
URL: https://science-start.ru/ru/article/view?id=1223 (дата обращения: 23.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Скачать материал

Скачать материал




- Сейчас обучается 30 человек из 12 регионов


- Сейчас обучается 97 человек из 36 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
УМК «Начальная школа 21 века»
Урок математики № 104 в 4 классе
Тема: «Практическая работа. Сопоставление фигур и развёрток: выбор фигуры, имеющей соответствующую развёртку.»
Автор презентации:
Т. И. Туран,
учитель начальных классов
г. Новокузнецк, 2020
МБОУ «Средняя общеобразовательная школа № 6 -
2 слайд
Актуализация опорных знаний
Устный счет
Сумма двух чисел равна 22. Одно из них оканчивается нулём. Если этот нуль отбросить, то получится другое число.
Ответ: 20 и 2. -
3 слайд
Актуализация опорных знаний
Интеллектуальная разминка
Догадайтесь, какие это числа?
В корзине 6 яблок. Как разделить их между тремя мальчиками, чтобы каждому досталось по 2 яблока и чтобы 2 яблока осталось в корзине?
– Один мальчик берёт яблоки вместе с корзиной.
– Два ученика договорились сесть в четвёртый вагон электрички. Но один ученик сел в четвертый вагон от начала электрички, а другой – в четвёртый вагон от конца. В одном ли вагоне едут ученики, если всего в поезде 8 вагонов?
– В соседних. -
4 слайд
Актуализация опорных знаний
Геометрический материал
– Утром проснулась белочка, позавтракать решила она. На березке – грибочки, на сосне – шишки. Собрала запасы, вернулась в дупло.
– Найдите весь путь белочки, если от ели до березки 15 м, от березы до сосны 4 м, а от сосны до ели – 20 м.– Как называется фигура?
– Треугольник.
– Докажите, что это треугольник.
– У треугольника 3 угла, 3 стороны.
– Что нужно найти?
– Весь путь белочки.
– Как по-другому сказать, что нужно найти?
– Весь путь белочки – это периметр треугольника.
– Что такое периметр?
– Периметр – сумма длин всех сторон.
Р = 15 + 4 + 20 = 39 (м).
Ответ: Р = 39 м. -
5 слайд
Открытие нового знания, способа действия С. 69, № 2
– Какие предметы или их части имеют форму цилиндра?
– Бревно, стакан, ведро, бидон, консервная банка имеют форму цилиндра. -
6 слайд
Открытие нового знания, способа действия С. 69, № 3
– Возьмите модель цилиндра и рассмотрите её основания, боковую поверхность. Какую фигуру представляет каждое из двух оснований цилиндра?
– Каждое из двух оснований цилиндра представляет круг. -
7 слайд
Открытие нового знания, способа действия С. 69, № 4
– Возьмите стакан, в основании которого круг (см. задание 2), и налейте в него воду. Какую форму принимает вода в стакане? -
8 слайд
Открытие нового знания, способа действия С. 69, № 4
– Форму стакана (цилиндра) принимает вода в стакане. -
9 слайд
Открытие нового знания, способа действия С. 69, № 4
– Развёртка конуса состоит из круга (основание конуса) и сектора (боковая поверхность). Длина окружности и длина дуги сектора равны. Выкройка модели конуса дополняется выступами для склейки. -
10 слайд
Открытие нового знания, способа действия С. 69, № 4
Выполняют модель цилиндра и конуса.
Конус -
11 слайд
Открытие нового знания, способа действия С. 69, № 4
Развёртка цилиндра состоит из двух кругов
(основания цилиндра) и прямоугольника (боковая поверхность). Длины окружностей равны длине прямоугольника. Выкройка модели цилиндра дополняется выступами для склейки -
12 слайд
Открытие нового знания, способа действия С. 69, № 4
Выполняют модель цилиндра и конуса.
Цилиндр -
13 слайд
Включение нового в активное использование в сочетании с ранее изученным, освоенным.
С. 71, № 10
– Масса курантов, установленных на Спасской башне Московского Кремля, равна 25000000 г, диаметр каждого из четырех циферблатов – 6120 мм, длина часовой стрелки – 2970 мм, а минутной – 3280 мм.
Выразите массу в тоннах, а длины – в метрах и сантиметрах.
25 000 000 г = 25 т
6120 мм = 612 см = 6 м 12 см
2 970 мм = 297 см = 2 м 97 см
3 280 мм = 328 см = 3 м 28 см -
14 слайд
Включение нового в активное использование в сочетании с ранее изученным, освоенным.
С. 71, № 11
– Найдите и объясните ошибки, которые допустил Миша при умножении чисел.
– В первом произведении Миша допустил ошибки в переходе через разряд, в третьем – при записи третьего неполного произведения. -
15 слайд
Включение нового в активное использование в сочетании с ранее изученным, освоенным.
С. 71, № 12
– Какие из утверждений неверны?
– Неверно утверждение «Это не конус». -
16 слайд
Включение нового в активное использование в сочетании с ранее изученным, освоенным.
С. 72, № 13
– Запишите в таблицу значения данных выражений, подставляя вместо буквы t числа: 10, 20, 30, 60, 150. -
17 слайд
Включение нового в активное использование в сочетании с ранее изученным, освоенным.
С. 72, № 13 -
18 слайд
Итог урока. Рефлексия
– Что особенно заинтересовало вас во время урока?
– Что нового узнали на уроке?
– Оцените свои достижения на уроке. Кто доволен своей работой, нарисуйте красный смайлик, синий – если некоторые вопросы вызвали затруднения. -
19 слайд
Домашнее задание
С. 72, № 14, 15.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 261 144 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы

- 25.03.2020
- 329
- 12

- 25.03.2020
- 437
- 22


- 25.03.2020
- 218
- 1




Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
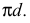
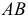
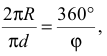
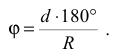
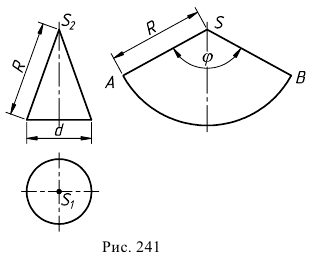
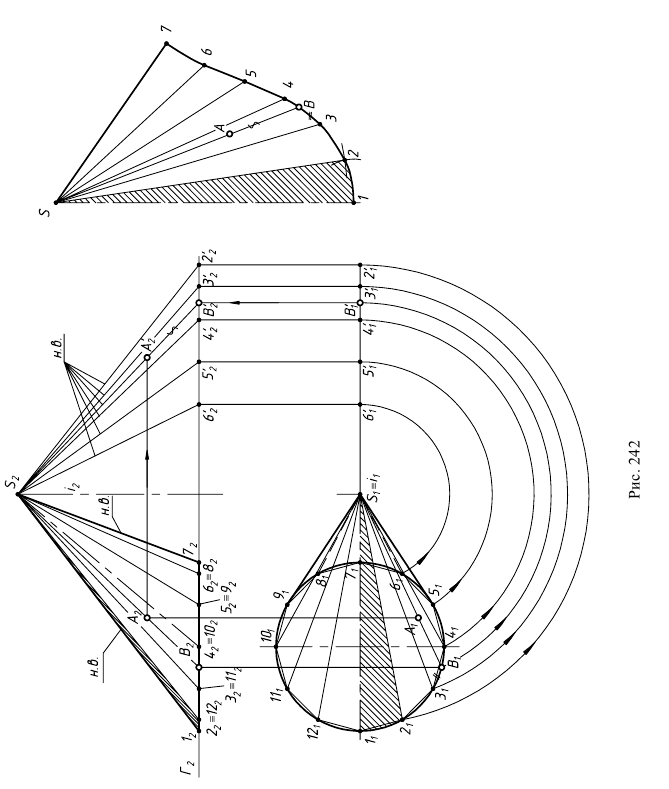
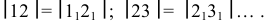
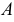 принадлежит образующей
принадлежит образующей 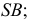
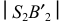 – натуральная величина образующей и точка
– натуральная величина образующей и точка 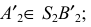
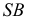 располагается между образующими
располагается между образующими 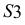 и
и 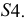 Отрезок
Отрезок 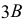 равен хорде, а расстояние
равен хорде, а расстояние 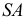 берется равным натуральной величине –
берется равным натуральной величине – 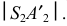
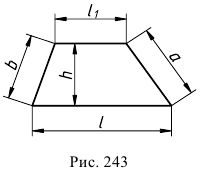
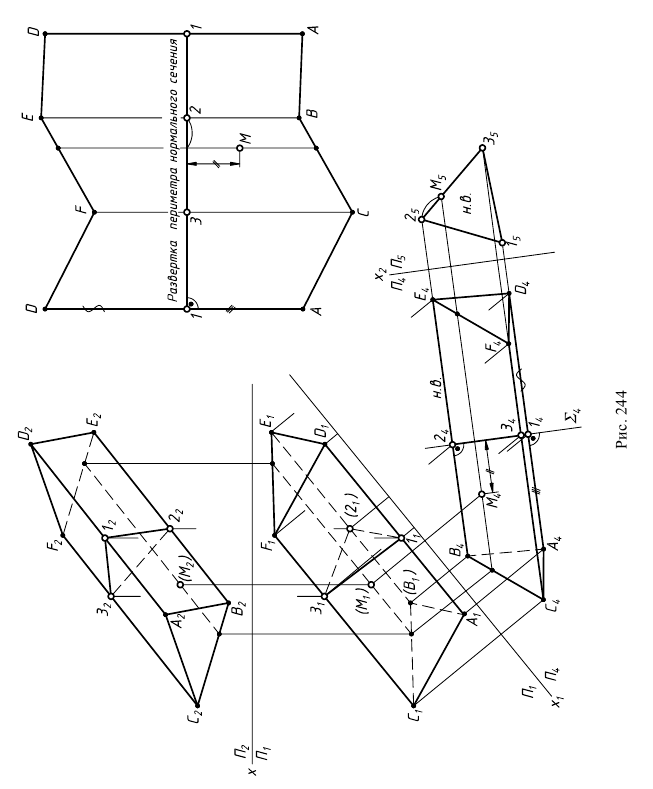
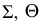 и
и  разрезают на равные части (доли). Рекомендуется разбивать ее не менее чем на 12 частей. В примере принято 6 долей для того, чтобы отрезки были крупнее и чертеж более четким;
разрезают на равные части (доли). Рекомендуется разбивать ее не менее чем на 12 частей. В примере принято 6 долей для того, чтобы отрезки были крупнее и чертеж более четким;