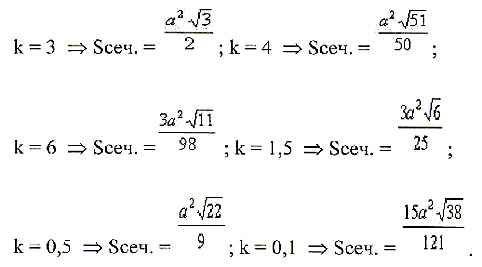Определение
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Замечание
Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве”.
Важные определения
1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.
2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.
3. Прямая и плоскость параллельны, если они не имеют общих точек.
4. Две плоскости параллельны, если они не имеют общих точек.
5. Две прямые в пространстве называются перпендикулярными, если угол между ними равен (90^circ).
6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
7. Две плоскости называются перпендикулярными, если угол между ними равен (90^circ).
Важные аксиомы
1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Важные теоремы
1. Если прямая (a), не лежащая в плоскости (pi), параллельна некоторой прямой (p), лежащей в плоскости (pi), то она параллельна данной плоскости.
2. Пусть прямая (p) параллельна плоскости (mu). Если плоскость (pi) проходит через прямую (p) и пересекает плоскость (mu), то линия пересечения плоскостей (pi) и (mu) — прямая (m) — параллельна прямой (p).
3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.
4. Если две параллельные плоскости (alpha) и (beta) пересечены третьей плоскостью (gamma), то линии пересечения плоскостей также параллельны:
[alphaparallel beta, alphacap gamma=a, betacapgamma=b Longrightarrow aparallel b]
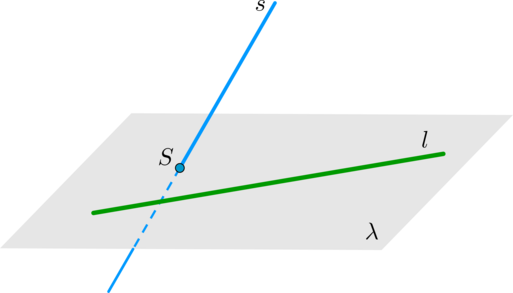
5. Пусть прямая (l) лежит в плоскости (lambda). Если прямая (s) пересекает плоскость (lambda) в точке (S), не лежащей на прямой (l), то прямые (l) и (s) скрещиваются.
6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
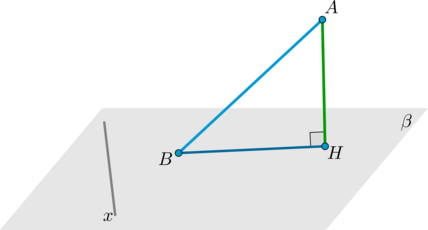
7. Теорема о трех перпендикулярах.
Пусть (AH) – перпендикуляр к плоскости (beta). Пусть (AB, BH) – наклонная и ее проекция на плоскость (beta). Тогда прямая (x) в плоскости (beta) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.
8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.
Замечание
Еще один важный факт, часто использующийся для построения сечений:
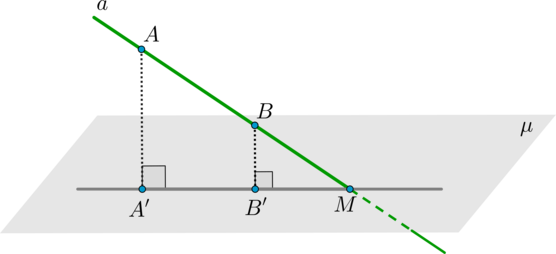
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.
Для этого из двух произвольных точек (A) и (B) прямой (a) проведем перпендикуляры на плоскость (mu) – (AA’) и (BB’) (точки (A’, B’) называются проекциями точек (A,B) на плоскость). Тогда прямая (A’B’) – проекция прямой (a) на плоскость (mu). Точка (M=acap
A’B’) и есть точка пересечения прямой (a) и плоскости (mu).
Причем заметим, что все точки (A, B, A’, B’, M) лежат в одной плоскости.
Пример 1.
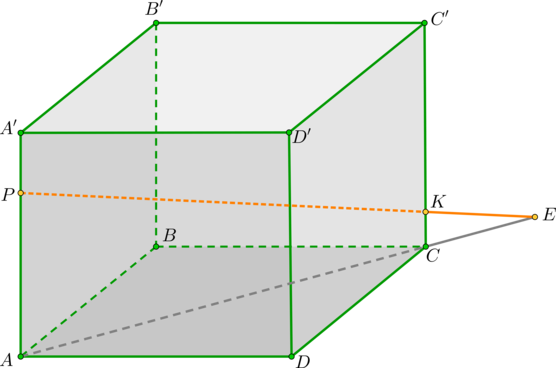
Дан куб (ABCDA’B’C’D’). (A’P=dfrac 14AA’, KC=dfrac15 CC’). Найдите точку пересечения прямой (PK) и плоскости (ABC).
Решение
1) Т.к. ребра куба (AA’, CC’) перпендикулярны ((ABC)), то точки (A) и (C) — проекции точек (P) и (K). Тогда прямая (AC) – проекция прямой (PK) на плоскость (ABC). Продлим отрезки (PK) и (AC) за точки (K) и (C) соответственно и получим точку пересечения прямых – точку (E).
2) Найдем отношение (AC:EC). (triangle PAEsim triangle KCE) по двум углам ((angle A=angle C=90^circ, angle E) – общий), значит, [dfrac{PA}{KC}=dfrac{EA}{EC}]
Если обозначить ребро куба за (a), то (PA=dfrac34a, KC=dfrac15a,
AC=asqrt2). Тогда:
[dfrac{frac34a}{frac15a}=dfrac{asqrt2+EC}{EC} Rightarrow
EC=dfrac{4sqrt2}{11}a Rightarrow AC:EC=4:11]
Пример 2.
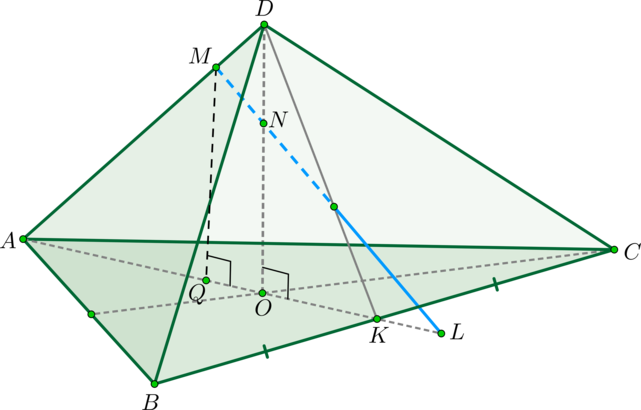
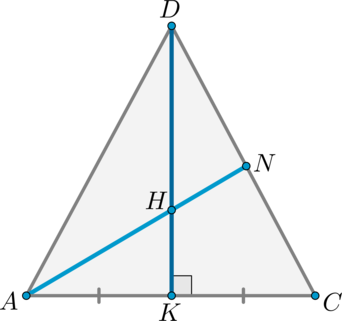
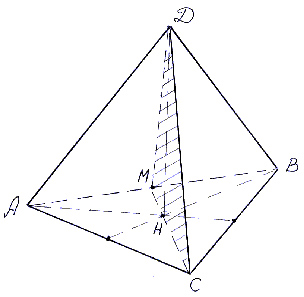
Дана правильная треугольная пирамида (DABC) с основанием (ABC), высота которой равна стороне основания. Пусть точка (M) делит боковое ребро пирамиды в отношении (1:4), считая от вершины пирамиды, а (N) – высоту пирамиды в отношении (1:2), считая от вершины пирамиды. Найдите точку пересечения прямой (MN) с плоскостью (ABC).
Решение
1) Пусть (DM:MA=1:4, DN:NO=1:2) (см. рисунок). Т.к. пирамида правильная, то высота падает в точку (O) пересечения медиан основания. Найдем проекцию прямой (MN) на плоскость (ABC). Т.к. (DOperp (ABC)), то и (NOperp (ABC)). Значит, (O) – точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр (MQ) из точки (M) на плоскость (ABC). Точка (Q) будет лежать на медиане (AK).
Действительно, т.к. (MQ) и (NO) перпендикулярны ((ABC)), то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки (M, N, O) лежат в одной плоскости (ADK), то и точка (Q) будет лежать в этой плоскости. Но еще (по построению) точка (Q) должна лежать в плоскости (ABC), следовательно, она лежит на линии пересечения этих плоскостей, а это – (AK).
Значит, прямая (AK) и есть проекция прямой (MN) на плоскость (ABC). (L) – точка пересечения этих прямых.
2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки (L) (например, на нашем чертеже точка (L) лежит вне отрезка (OK), хотя она могла бы лежать и внутри него; а как правильно?).
Т.к. по условию сторона основания равна высоте пирамиды, то обозначим (AB=DO=a). Тогда медиана (AK=dfrac{sqrt3}2a). Значит, (OK=dfrac13AK=dfrac 1{2sqrt3}a). Найдем длину отрезка (OL) (тогда мы сможем понять, внутри или вне отрезка (OK) находится точка (L): если (OL>OK) – то вне, иначе – внутри).
а) (triangle AMQsim triangle ADO) по двум углам ((angle Q=angle
O=90^circ, angle A) – общий). Значит,
[dfrac{MQ}{DO}=dfrac{AQ}{AO}=dfrac{MA}{DA}=dfrac 45
Rightarrow MQ=dfrac 45a, AQ=dfrac 45cdot dfrac 1{sqrt3}a]
Значит, (QK=dfrac{sqrt3}2a-dfrac 45cdot dfrac
1{sqrt3}a=dfrac7{10sqrt3}a).
б) Обозначим (KL=x).
(triangle LMQsim triangle LNO) по двум углам ((angle Q=angle O=90^circ, angle L) – общий). Значит,
[dfrac{MQ}{NO}=dfrac{QL}{OL} Rightarrow dfrac{frac45 a}{frac 23a}
=dfrac{frac{7}{10sqrt3}a+x}{frac1{2sqrt3}a+x} Rightarrow
x=dfrac a{2sqrt3} Rightarrow OL=dfrac a{sqrt3}]
Следовательно, (OL>OK), значит, точка (L) действительно лежит вне отрезка (AK).
Замечание
Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что (x) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки (L) (то есть, что она находится внутри отрезка (AK)).
Пример 3
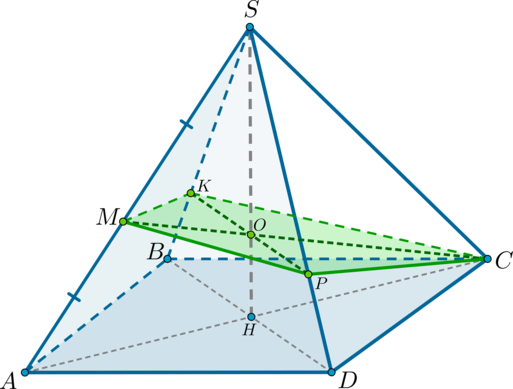
Дана правильная четырехугольная пирамида (SABCD). Найдите сечение пирамиды плоскостью (alpha), проходящей через точку (C) и середину ребра (SA) и параллельной прямой (BD).
Решение
1) Обозначим середину ребра (SA) за (M). Т.к. пирамида правильная, то высота (SH) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость (SAC). Отрезки (CM) и (SH) лежат в этой плоскости, пусть они пересекаются в точке (O).
Для того, чтобы плоскость (alpha) была параллельна прямой (BD), она должна содержать некоторую прямую, параллельную (BD). Точка (O) находится вместе с прямой (BD) в одной плоскости – в плоскости (BSD). Проведем в этой плоскости через точку (O) прямую (KPparallel
BD) ((Kin SB, Pin SD)). Тогда, соединив точки (C, P, M, K), получим сечение пирамиды плоскостью (alpha).
2) Найдем отношение, в котором делят точки (K) и (P) ребра (SB) и (SD). Таким образом мы полностью определим построенное сечение.
Заметим, что так как (KPparallel BD), то по теореме Фалеса (dfrac{SB}{SK}=dfrac{SD}{SP}). Но (SB=SD), значит и (SK=SP). Таким образом, можно найти только (SP:PD).
Рассмотрим (triangle ASC). (CM, SH) – медианы в этом треугольнике, следовательно, точкой пересечения делятся в отношении (2:1), считая от вершины, то есть (SO:OH=2:1).
Теперь по теореме Фалеса из (triangle BSD): (dfrac{SP}{PD}=dfrac{SO}{OH}=dfrac21).
3) Заметим, что по теореме о трех перпендикулярах (COperp BD) как наклонная ((OH) – перпендикуляр на плоскость (ABC), (CHperp BD) – проекция). Значит, (COperp KP). Таким образом, сечением является четырехугольник (CPMK), диагонали которого взаимно перпендикулярны.
Пример 4
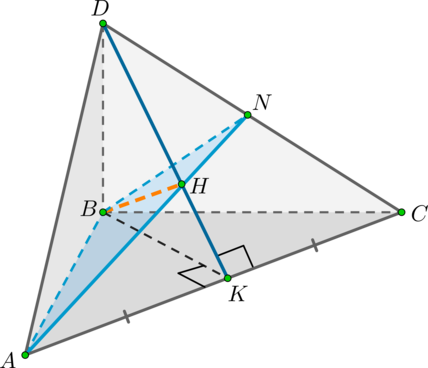
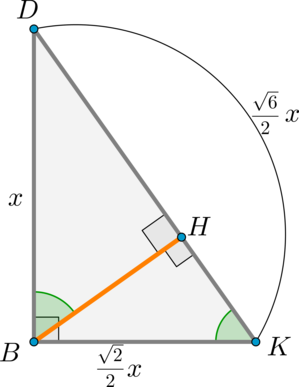
Дана прямоугольная пирамида (DABC) с ребром (DB), перпендикулярным плоскости (ABC). В основании лежит прямоугольный треугольник с (angle B=90^circ), причем (AB=DB=CB). Проведите через прямую (AB) плоскость, перпендикулярную грани (DAC), и найдите сечение пирамиды этой плоскостью.
Решение
1) Плоскость (alpha) будет перпендикулярна грани (DAC), если она будет содержать прямую, перпендикулярную (DAC). Проведем из точки (B) перпендикуляр на плоскость (DAC) — (BH), (Hin DAC).
Проведем вспомогательные (BK) – медиану в (triangle ABC) и (DK) – медиану в (triangle DAC).
Т.к. (AB=BC), то (triangle ABC) – равнобедренный, значит, (BK) – высота, то есть (BKperp AC).
Т.к. (AB=DB=CB) и (angle ABD=angle CBD=90^circ), то (triangle
ABD=triangle CBD), следовательно, (AD=CD), следовательно, (triangle DAC) – тоже равнобедренный и (DKperp AC).
Применим теорему о трех перпендикулярах: (BH) – перпендикуляр на (DAC); наклонная (BKperp AC), значит и проекция (HKperp AC). Но мы уже определили, что (DKperp AC). Таким образом, точка (H) лежит на отрезке (DK).
Соединив точки (A) и (H), получим отрезок (AN), по которому плоскость (alpha) пересекается с гранью (DAC). Тогда (triangle
ABN) – искомое сечение пирамиды плоскостью (alpha).
2) Определим точное положение точки (N) на ребре (DC).
Обозначим (AB=CB=DB=x). Тогда (BK), как медиана, опущенная из вершины прямого угла в (triangle ABC), равна (frac12 AC), следовательно, (BK=frac12 cdot sqrt2 x).
Рассмотрим (triangle BKD). Найдем отношение (DH:HK).
Заметим, что т.к. (BHperp (DAC)), то (BH) перпендикулярно любой прямой из этой плоскости, значит, (BH) – высота в (triangle DBK). Тогда (triangle DBHsim triangle DBK), следовательно
[dfrac{DH}{DB}=dfrac{DB}{DK} Rightarrow DH=dfrac{sqrt6}3x
Rightarrow HK=dfrac{sqrt6}6x Rightarrow DH:HK=2:1]
Рассмотрим теперь (triangle ADC). Медианы треугольника точной пересечения делятся в отношении (2:1), считая от вершины. Значит, (H) – точка пересечения медиан в (triangle ADC) (т.к. (DK) – медиана). То есть (AN) – тоже медиана, значит, (DN=NC).
На этой странице вы узнаете
- Как дракон с помощью сечений разрушал город?
- Чем вода похожа на сечение?
- Что общего у следа на снегу и следа в сечении?
Заглянем в кинотеатр имени Математики. Какой фильм сейчас будут показывать? Располагайтесь поудобнее, приятного просмотра…
Сечения
Как дракон с помощью сечений разрушал город?
…В далеком будущем, на одной из недавно открытых планет, люди построили новую цивилизацию. Они возвели новые дома для комфортной жизни разных необычных форм.
Но внезапно с другой, темной стороны планеты, появился дракон, коренной обитатель планеты. Ему не понравилось вторжение людей, и решил он стереть в пыль все строения.
Он прилетал к домам, раскрывал свою пасть и стрелял страшным красным лучом. И каждая поверхность и каждый объем, которого касался этот луч, разрезался по прямой линии.

Прилетел дракон к пирамиде и разрезал ее. Ахнули люди: верхушка пирамиды съехала, осталась лишь прямоугольная плоскость.
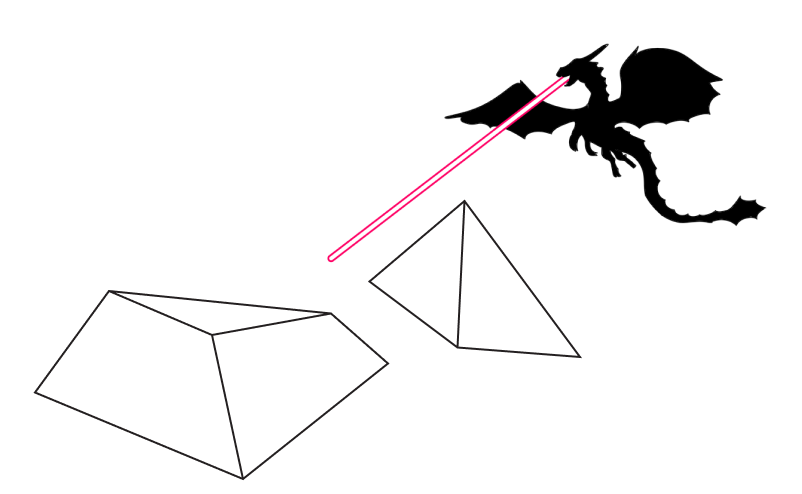
Увидел дракон обычный дом — в форме параллелепипеда, — и снова луч разрезал здание. Осталась вместо крыши дыра в форме четырехугольника.
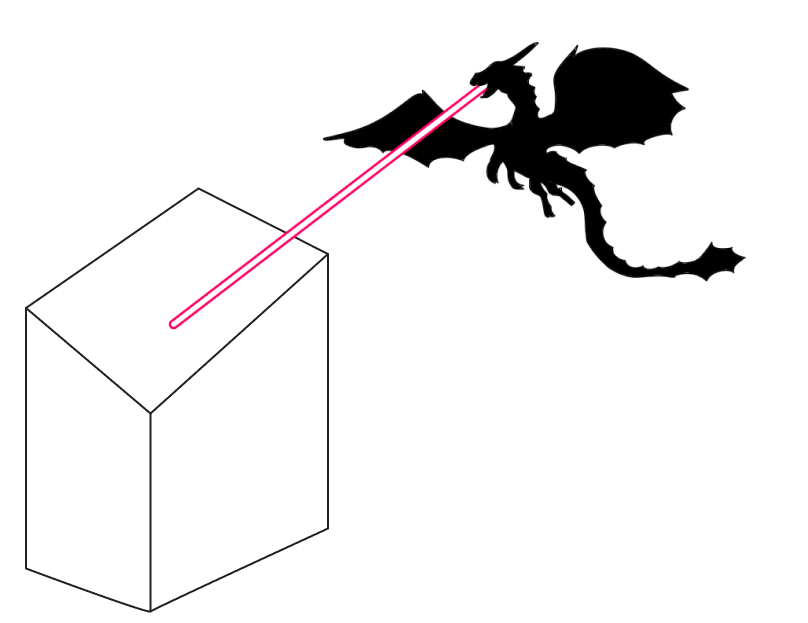
Долетел змей до памятника того народа: “треугольной” башни. Разрушил и это здание. Раскололось здание на две половинки, а в месте их раскола остались треугольные дыры.
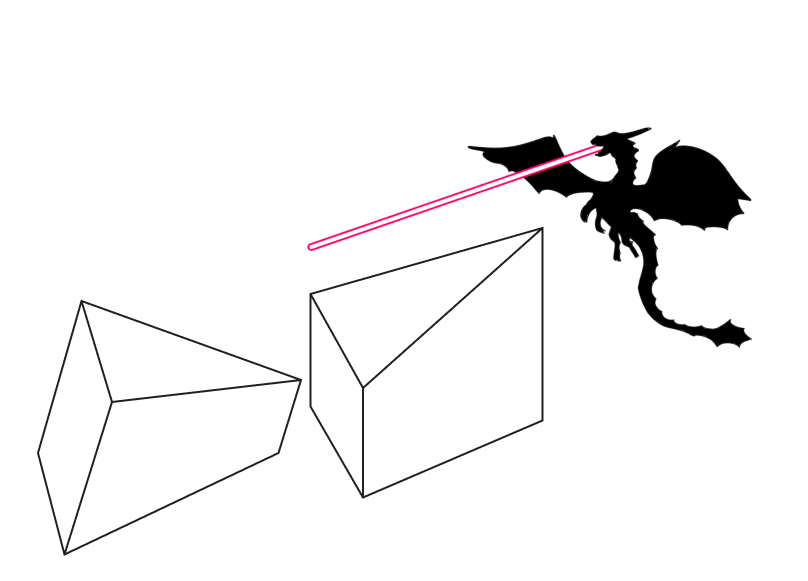
Поняли люди: нет сил это терпеть! Собрали межгалактические войска и победили дракона. А после восстанавливали город и удивлялись: как интересно были разрезаны здания.
Так что же делал дракон? Он разрезал геометрические тела, а на месте их разреза оставались сечения.
Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью.
Разумеется, никакой дракон не прилетает и не рассекает наши рисунки в тетради. Все сечения чертятся отдельно, а представляются мысленно.
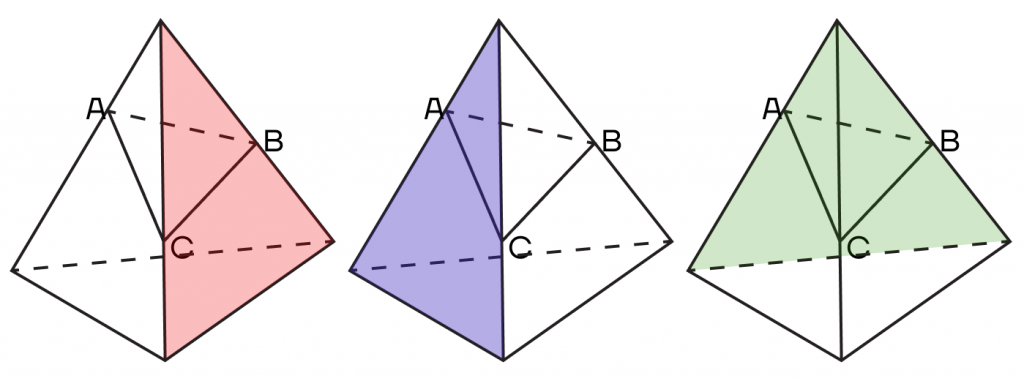
Заметим, что в многогранниках сечение получается в форме многоугольника, вершины которого лежат на ребрах многогранника, а стороны на гранях. Обратим внимание, что две соседние вершины будут принадлежать одной и той же грани, то есть одной плоскости.
Рассмотрим сечение пирамиды АВС: вершины А, В и С лежат точно на ребрах.
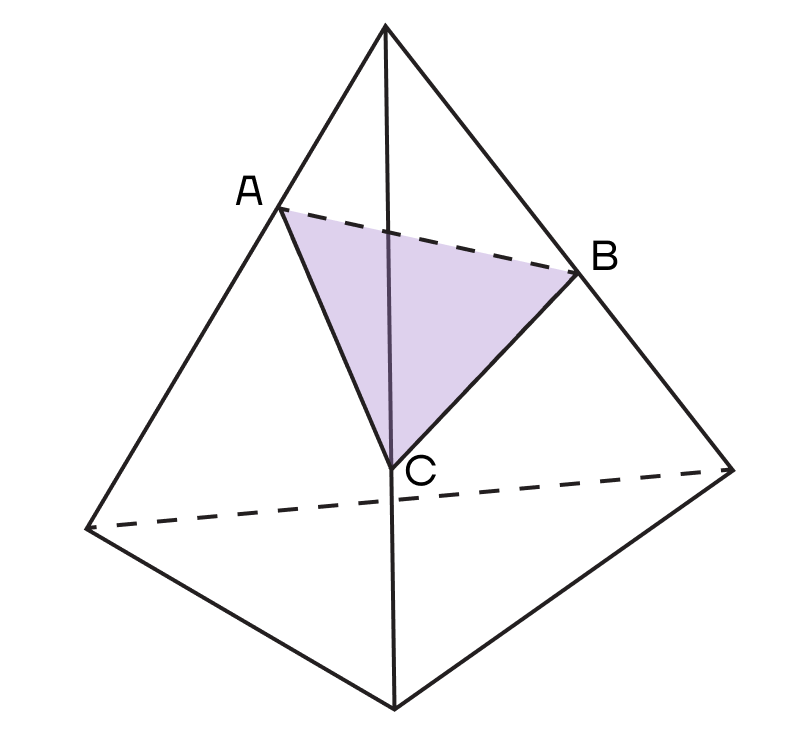
При этом пары вершин А и В, В и С, А и С лежат в одной грани и принадлежат одной плоскости.
Сечение геометрических тел является очень интересным разделом стереометрии. Поскольку это раздел стереометрии, в нем действуют все ее законы, в том числе и аксиомы стереометрии. В этой статье мы не будем заострять на них внимание, прочитать подробнее можно в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве».
Зачем может потребоваться сечение?
Мы сталкиваемся с ними намного чаще, чем думаем. Они бывают не только в задачах, но и встречаются в жизни.
Что мы делаем, когда нарезаем салат? Рассекаем овощи. Каждый разрез — это сечение.

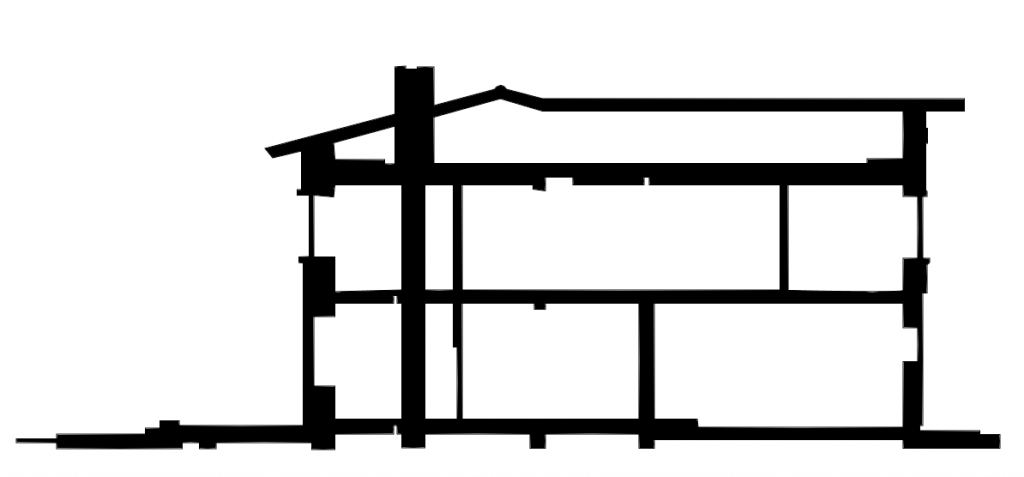
А что делают архитекторы, когда чертят разрезы? Мысленно рассекают здание и показывают его “внутренности”.
Посмотрим на бутылку с водой. Верхний уровень воды можно принять за плоскость, которая рассекает тело бутылки. Наклоняя бутылку и меняя положение воды, можно увидеть различные сечения, которые могут в ней появиться.

Сечения окружают нас, и в них совсем нет ничего сверхъестественного. А поэтому и разобраться в сечениях в стереометрии не составит для нас труда.
Методы построения сечений
Однако сечения нужно правильно построить. Для их построения существует несколько методов:
- Метод следов;
- Метод внутреннего проектирования;
- Комбинированный метод.
Разберем их по порядку.
Зимой очень интересно гулять по лесу и разглядывать следы животных: вот пробежал заяц, а это, кажется, была маленькая лисица. Здесь просто снег упал с веток дерева.

Все эти тела оставляют след на снегу.
Сечение так же, как и любое животное на снегу, оставляет след на гранях многогранника. И этот след — это сторона многоугольника, который образовывает сечение.
Если мы возьмем карандаш и проведем прямую на листе, он оставит след. Также и плоскость сечения как бы проводит карандашом по граням фигур, оставляя после себя следы.
След плоскости а в плоскости основания многогранника — прямая, по которой секущая плоскость пересекает плоскость основания многогранника.
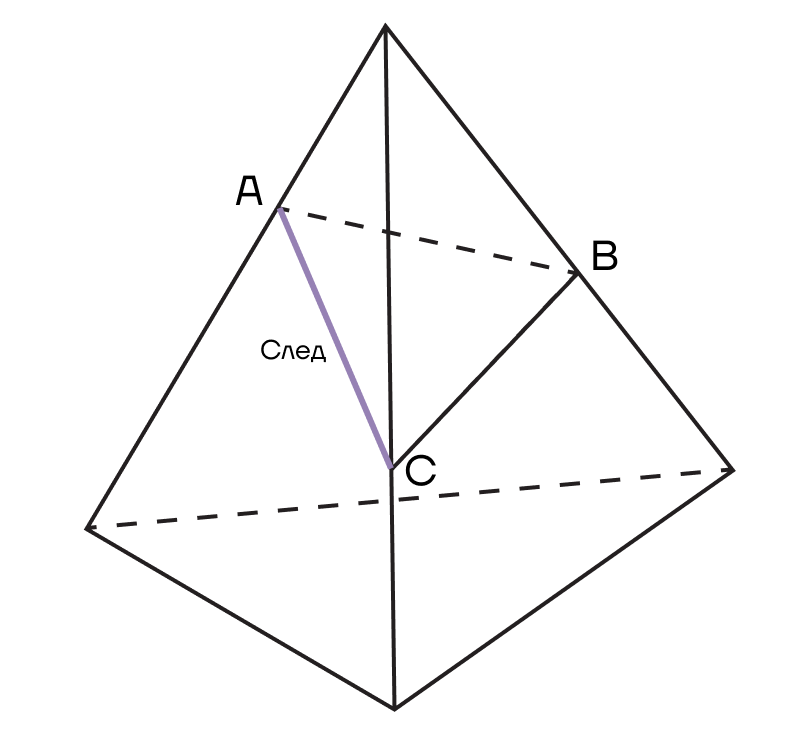
Вспомним, что плоскость бесконечна, значит, и след можно продолжать в разные стороны бесконечно.
Однако для построения сечений необходимости бесконечно его продолжать нет: достаточно до пересечения с ребром многогранника или продолжением ребра.
Построим сечение куба, которое проходит через точки К, М и Т, чтобы чуть подробнее разобраться в методе следов.
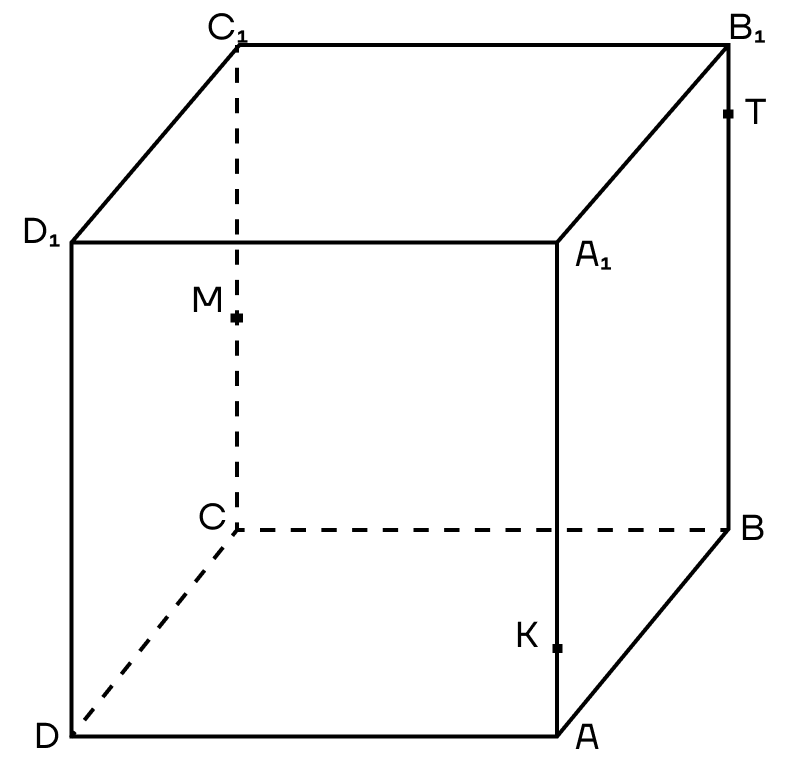
При построении сечений существует очень важный лайфхак: если точки лежат в одной плоскости (то есть в одной грани), то их можно соединить.
1. Заметим, что в нашем кубе это точки К и Т в плоскости (АВВ1) и точки М и Т в плоскости (ВСС1). Поэтому мы можем их соединить.
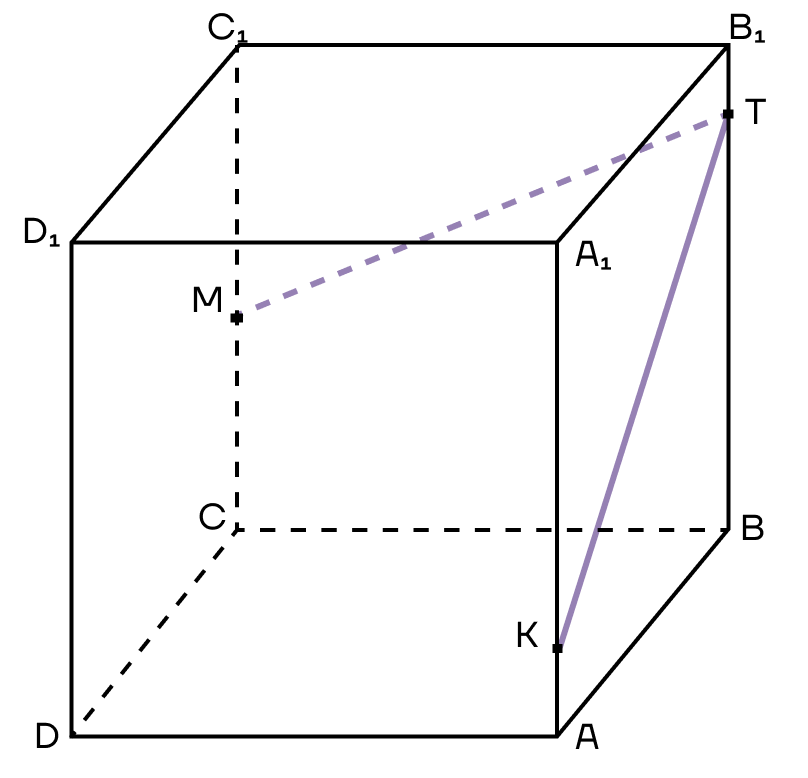
2. КТ и МТ в нашем случае — это следы плоскости сечения. Продолжим их за точку К и за точку М. Аналогично продолжим стороны АВ и ВС до тех пор, пока их продолжения не пересекутся со следами.
Пусть продолжения прямых АВ и ТК пересекутся в точке Н, а продолжения прямых ТМ и ВС пересекутся в точке F.
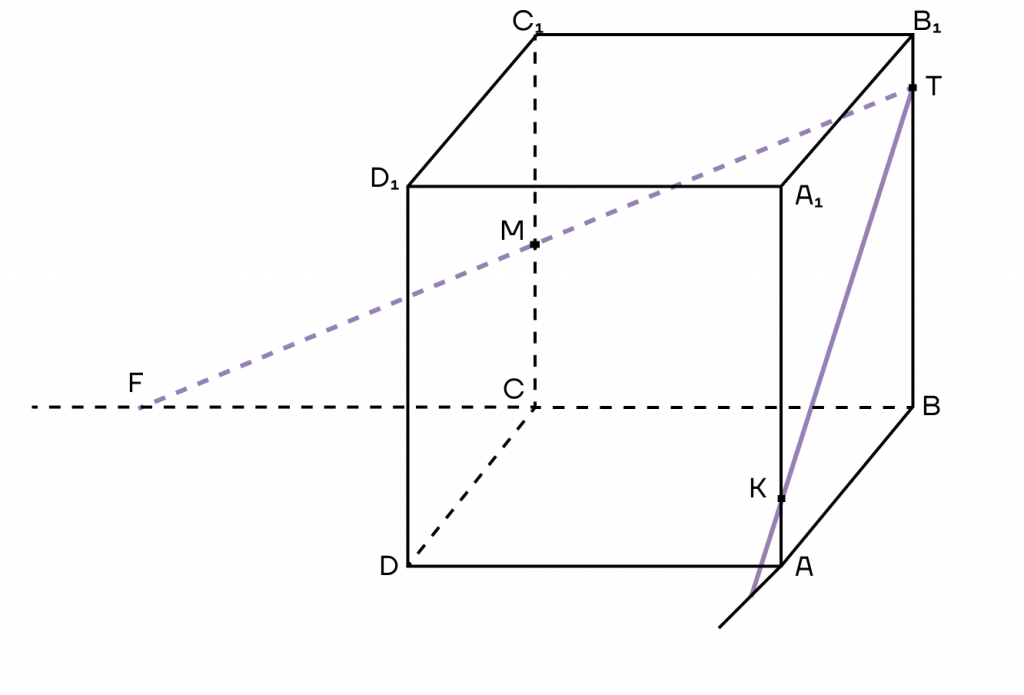
3. Обратим внимание, что точки Н и F лежат на продолжении ребер основания, а значит, лежат в плоскости основания куба. Пользуясь лайфхаком, их можно соединить. Таким образом, получим треугольник, который как бы разрезает наш куб.
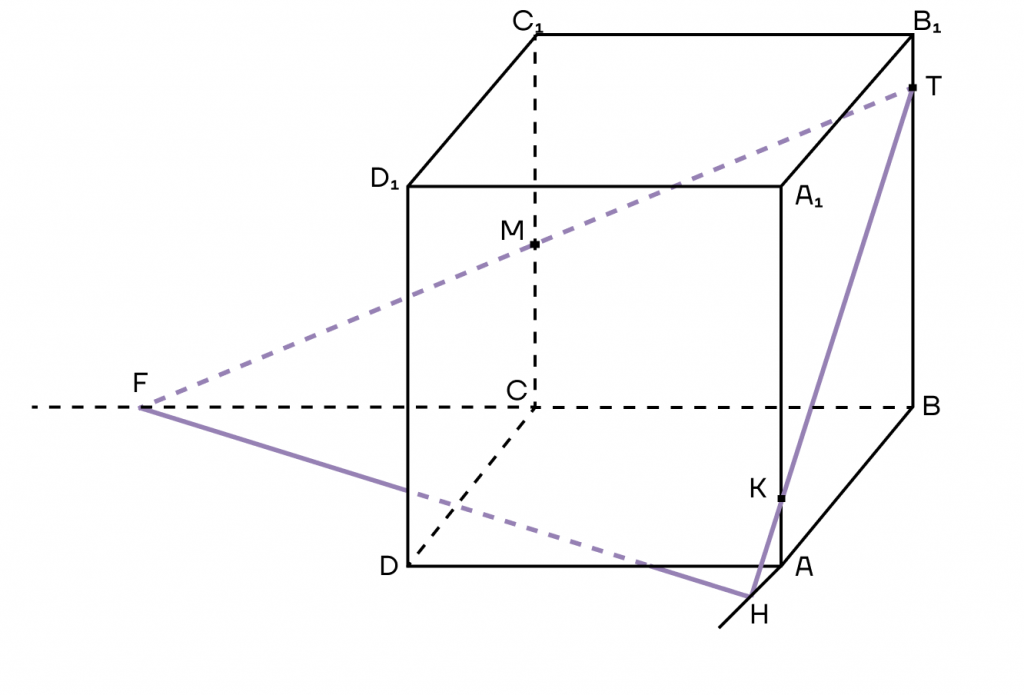
4. Однако наше сечение не закончено. Вспомним, что все вершины многоугольника должны лежать на ребрах куба, то есть точки Н и F не подходят. Но на самом деле осталось совсем немного закончить построение.
5. Заметим, что прямая HF пересекает ребра AD, DC, назовем точки этих пересечений как N и L.
А также соединим все точки, которые окажутся в одной плоскости.
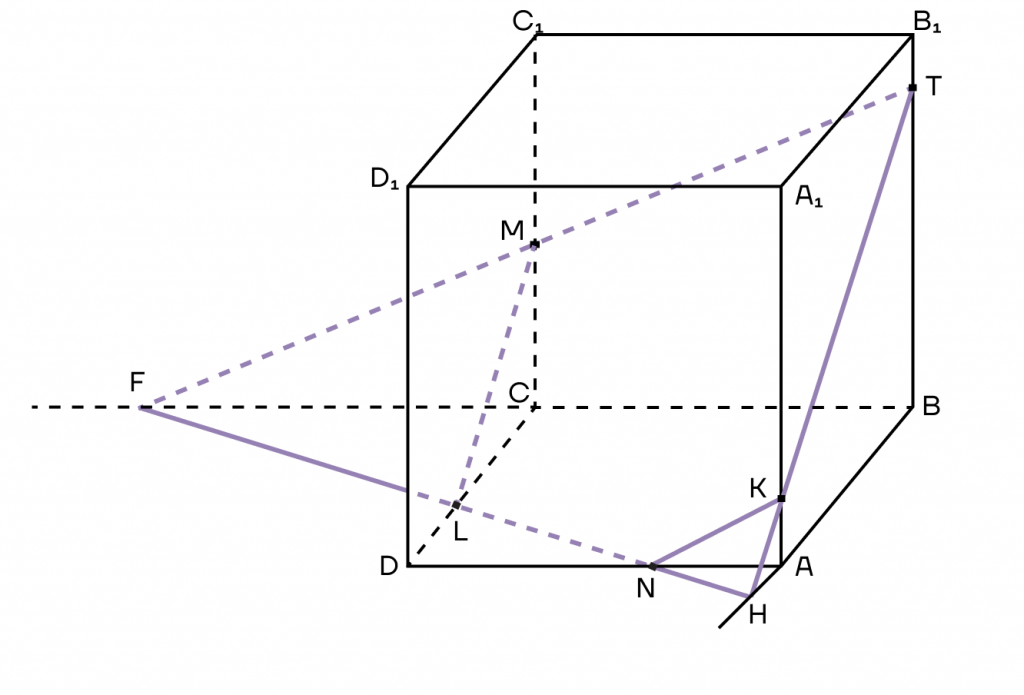
6. И вот мы получили сечение. Многоугольник TKNLM — сечение куба.
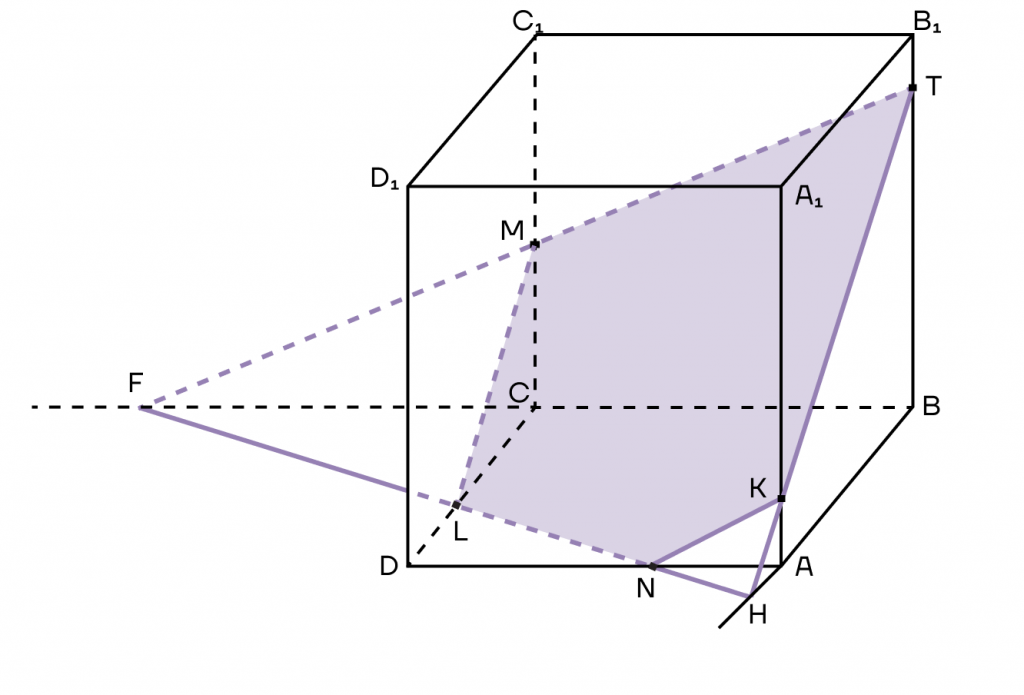
Итак, основной способ построить сечение методом следов — продолжить след сечения до его пересечения с ребрами многогранника или продолжениями его ребер.
А также пользоваться лайфхаком: точки в одной плоскости можно соединять.
Рассмотрим метод внутреннего проектирования.
Иногда метод следов может не помочь: след будет идти параллельно ребру или пересекаться с его продолжением далеко за пределами листа.
В таких случаях часто используется следующее свойство: параллельные плоскости пересекаются другой плоскостью по параллельным прямым. Подробнее про это свойство можно прочесть в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве».
Польза этого свойства в том, что если сечение пройдет через параллельные плоскости, то оно пересечет их по параллельным линиям. А значит, зная сторону сечения в одной из этих плоскостей и точку в другой плоскости, мы можем просто параллельно перенести прямую и достроить сторону сечения во второй плоскости.
Но будем разбираться на практике. Построим сечение треугольной призмы, проходящее через точки К, М, Т.
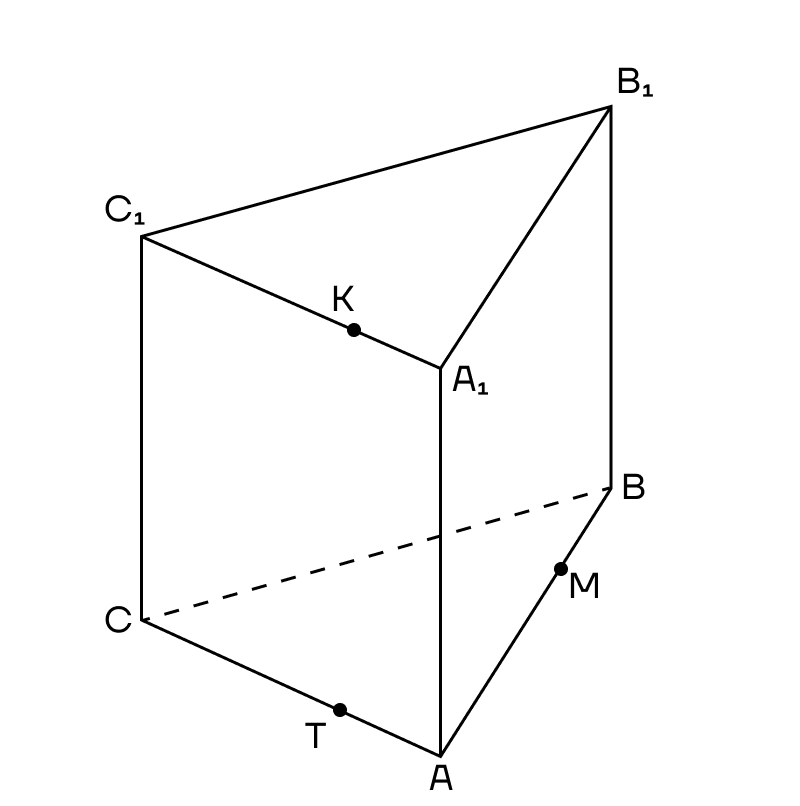
1. Первым делом соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС1) и точки Т и М в плоскости (АВС).
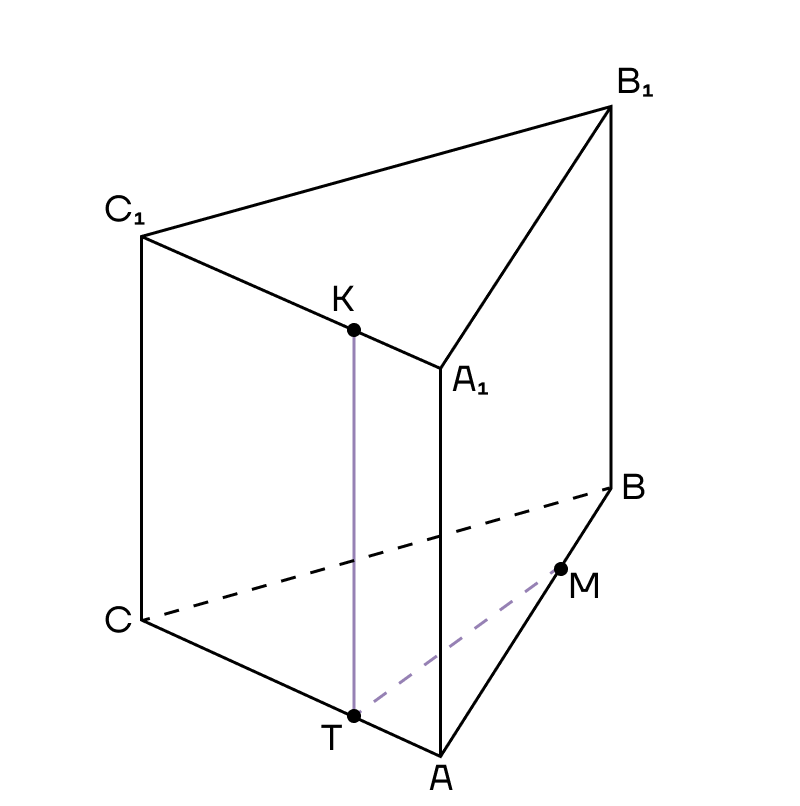
2. КТ проходит почти параллельно ребру АА1, следовательно, использовать метод следов не рационально.
3. Теперь посмотрим на плоскости (АВС) и (А1В1С1) — они параллельные. А значит прямую сечения можно параллельно перенести в одну из них.
В плоскости (АВС) лежит прямая ТМ, а в плоскости (А1В1С1) лежит точка К, которая является вершиной сечения. Тогда из точки К в плоскости верхнего основания нам нужно провести прямую, параллельную ТМ до пересечения с ребром призмы. Назовем эту точку Е.
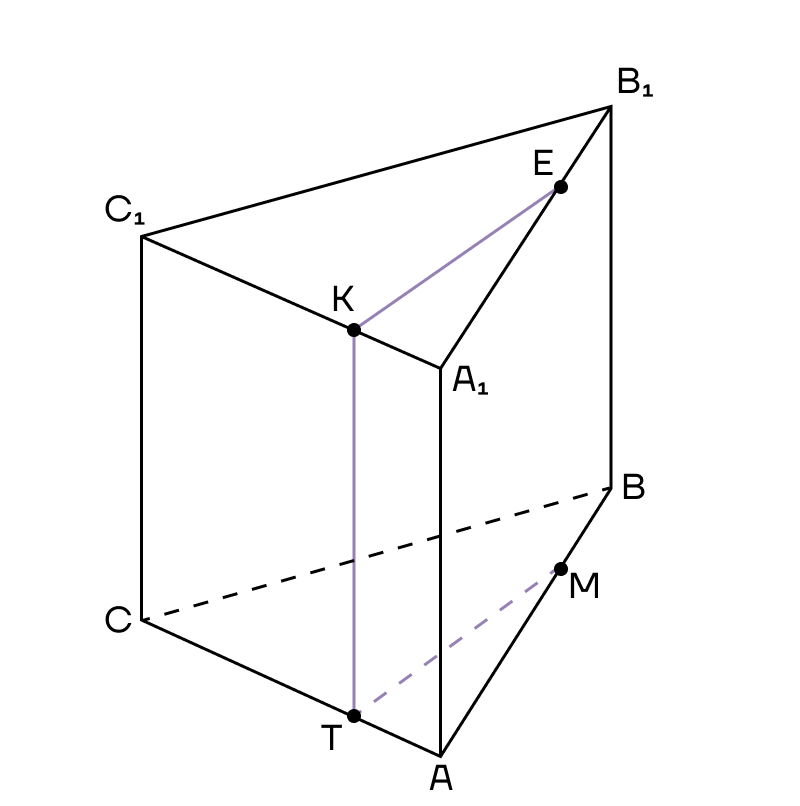
4. А теперь мы можем соединить Е и М, так как они лежат в одной плоскости. Четырехугольник КЕМТ — сечение призмы.
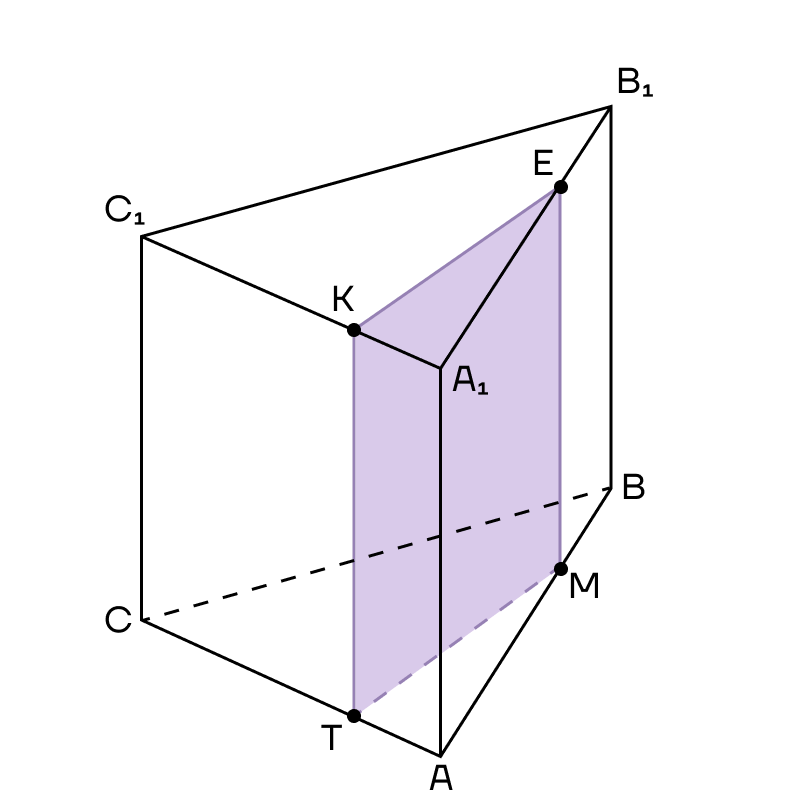
Осталось разобраться, в чем заключается комбинированный метод? Он включает в себя и метод следов, и метод внутреннего проектирования, то есть приемы из каждого метода могут применяться вместе в одной и той же задаче.
Все зависит от удобства решения и его быстроты: там, где невозможно применить метод внутреннего проектирования, можно применить метод следов. А там, где применять метод следов неудобно (или невозможно), можно применить метод внутреннего проектирования.
Примеры построения сечений
Рассмотрим несколько примеров построения сечений в различных фигурах.
Пример 1. В правильном тетраэдре провели апофему АТ, на середине которой отметили точку К. АЕ:ЕС = 1:5. Р — точка на ребре CD. Постройте сечение тетраэдра, проходящее через точки К, Е и Р.
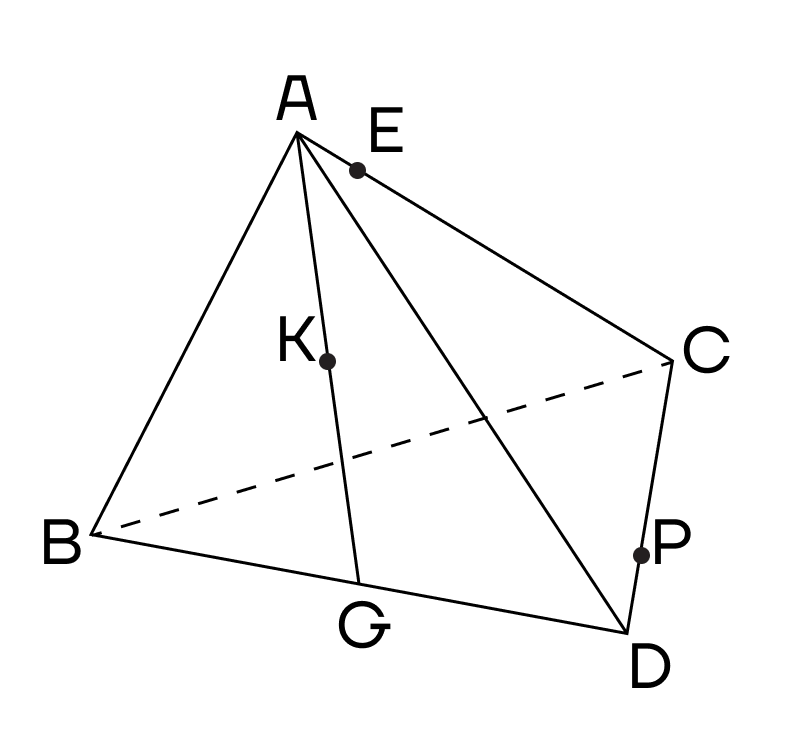
Решение. Подробнее про элементы пирамиды и тетраэдра можно прочесть в статье «Пирамида». Сейчас отметим, что апофема — высота боковой грани правильной пирамиды, проведенная к основанию.
1. Начнем решение с того, что соединим точки, лежащие в одной плоскости. Е и Р лежат в плоскости (ACD), значит их можно соединить.
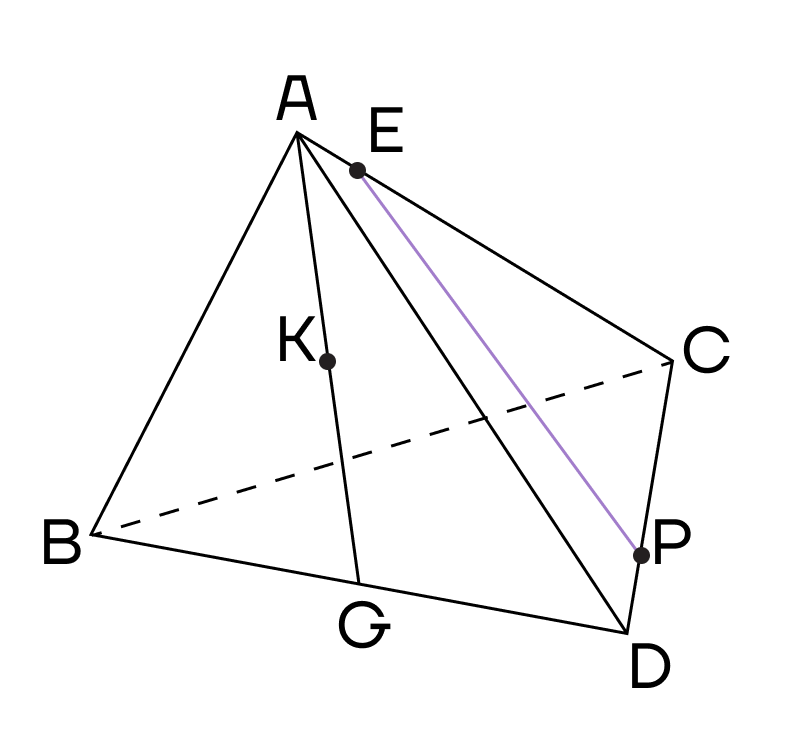
2. Рассмотрим плоскость (АСG). Проведем прямую CG. Точки К и Е лежат в одной плоскости, то есть их также можно соединить.
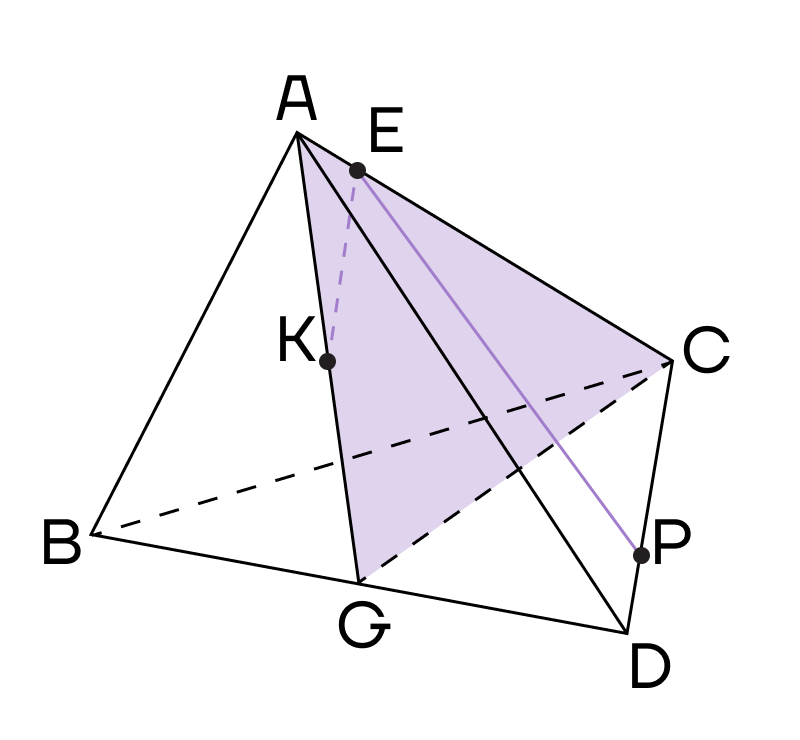
3. Воспользуемся методом следов и продлим прямые ЕК и CG до их пересечения в точке Т.
4. Теперь точки Т и Р будут лежать в одной плоскости основания, следовательно, их можно соединить. Пусть прямая ТР пересекает ребро BD в точке М.
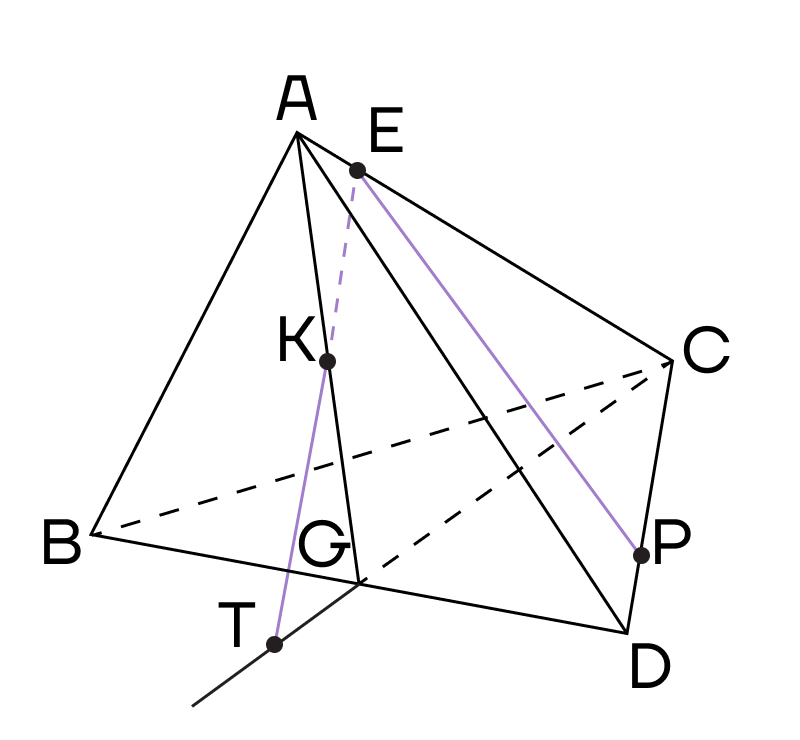
Тогда точки М и К лежат в одной плоскости (ABD) — их тоже можно соединить.
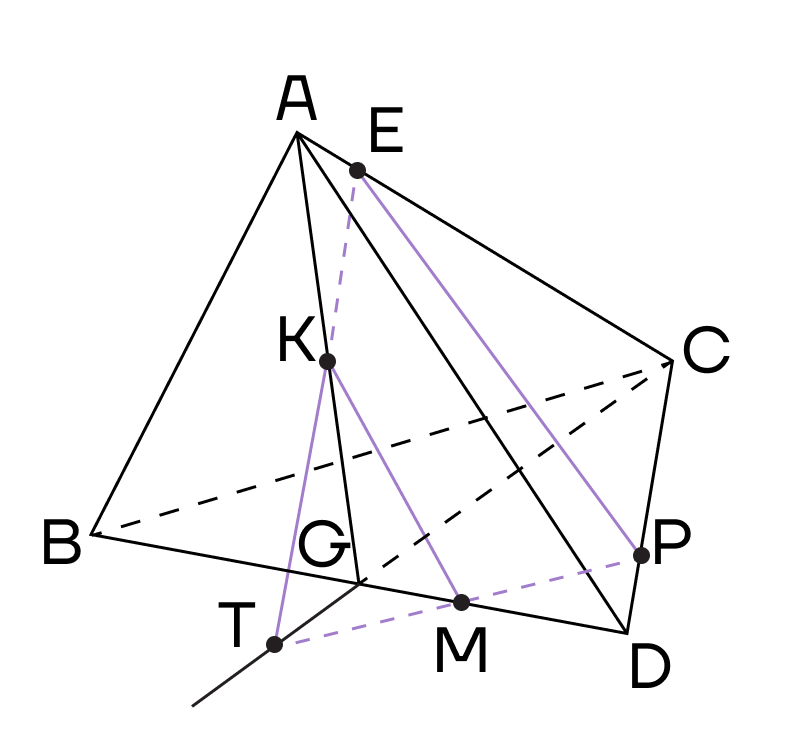
5. Продлим прямую МК до пересечения с ребром АВ в точке О. Точки О и Е лежат в одной плоскости (АВС), соединим их. Сечением тетраэдра будет четырехугольник ОЕРМ.
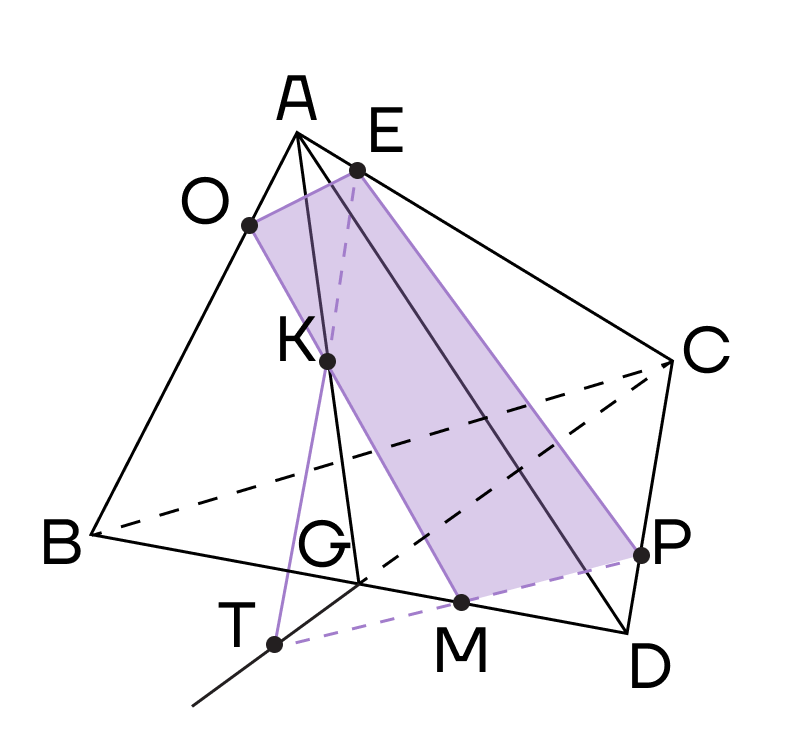
Пример 2. Дана треугольная призма. Постройте сечение призмы, проходящее через точки К, М, Т.
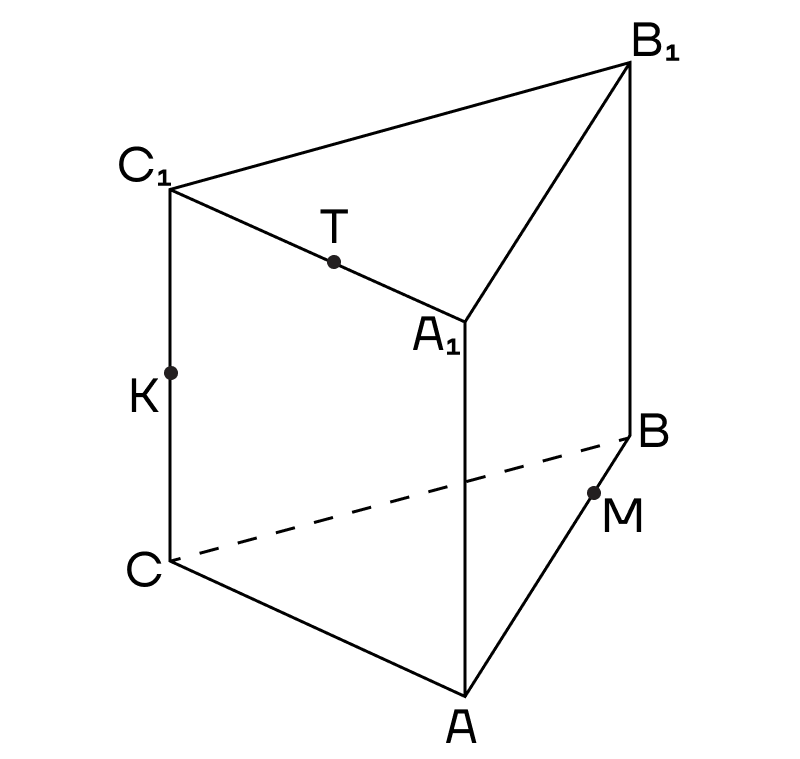
Решение. 1. Соединим точки, лежащие в одной плоскости. Это точки К и Т в плоскости (АСС1).
Воспользуемся методом следов и продолжим прямую ТК до пересечения с продолжением стороны АС в точке Р.
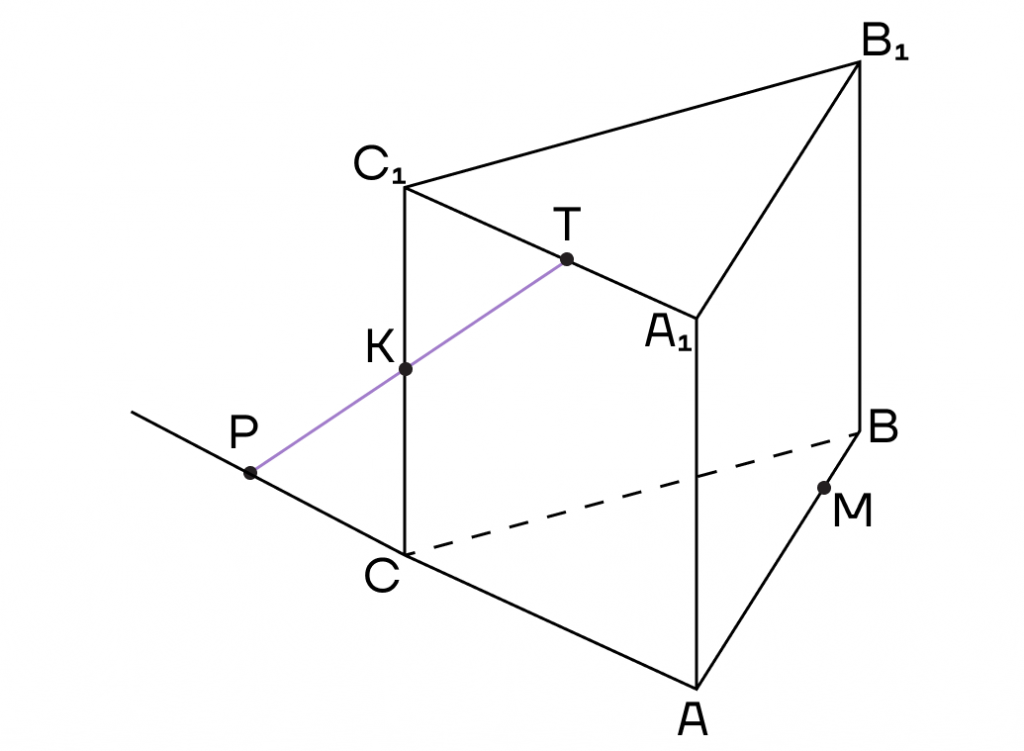
2. Точки Р и М лежат в одной плоскости (АВС), то есть их можно соединить. Пусть прямая РМ пересечет ребро ВС в точке Е.
Воспользуемся методом внутреннего проектирования и проведем из точки Т прямую, параллельную ЕМ. Пусть она пересечет ребро А1В1 в точке О.
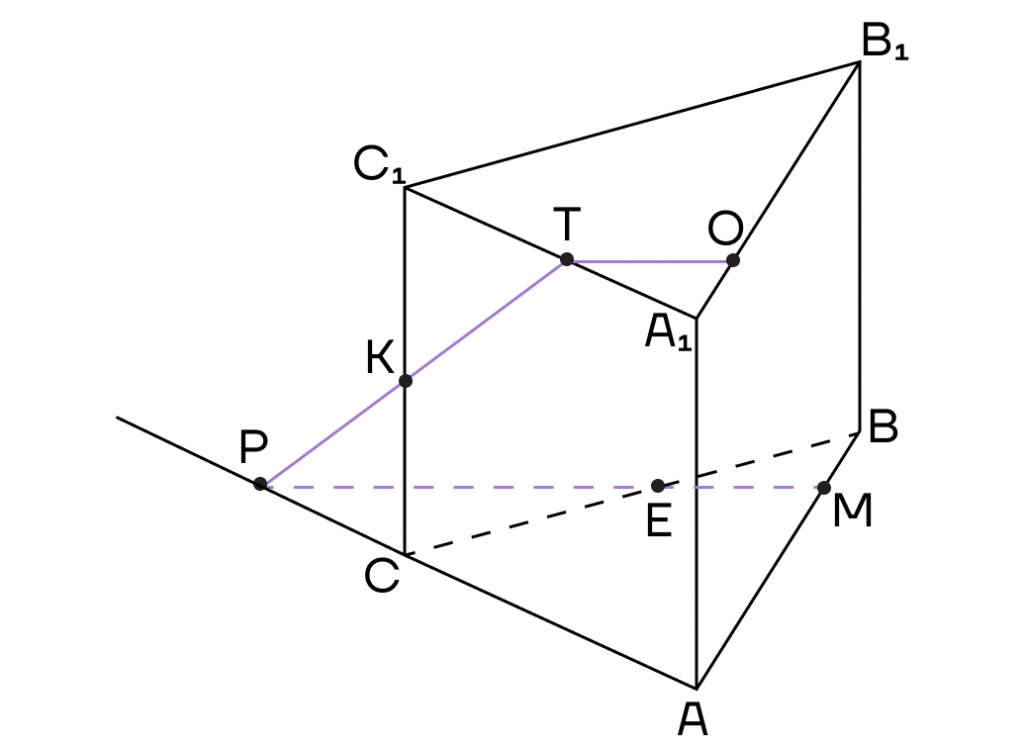
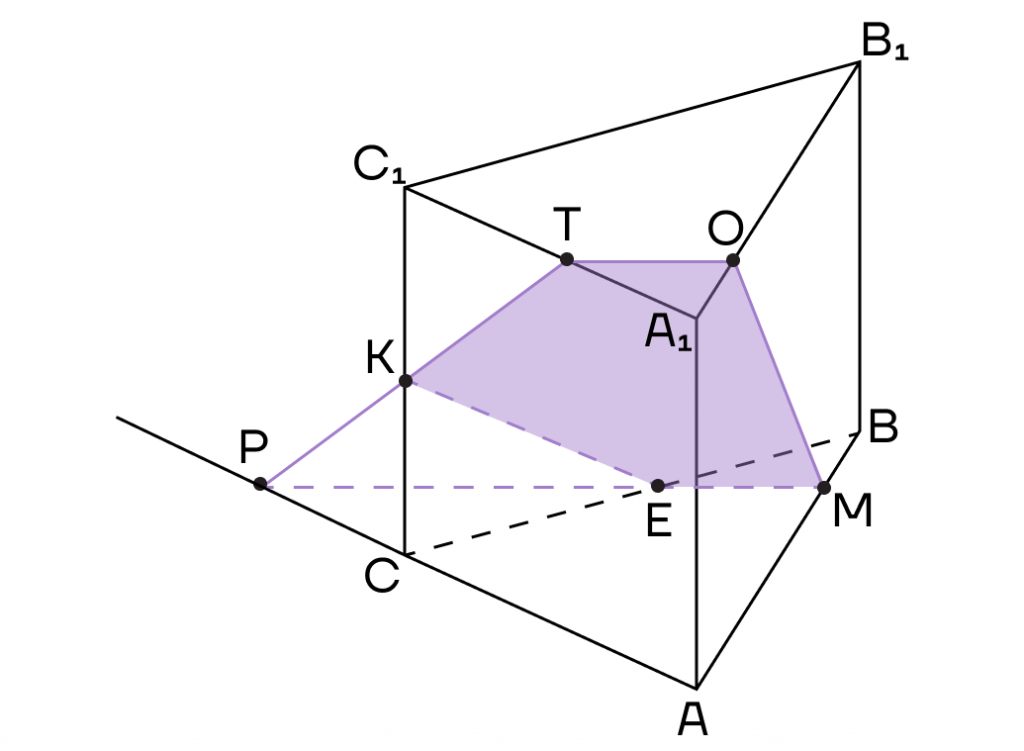
3. Осталось соединить точки, лежащие в одной плоскости. Это точки К и Е в плоскости (ВСС1) и точки О и М в плоскости (АВВ1).
Тогда КТОМЕ — сечение призмы.
Пример 3. Дан куб ABCDA1B1C1D1. М — середина ребра АА1. Постройте сечение куба, которое будет параллельно диагонали куба А1С и будет проходить через точки М и В.
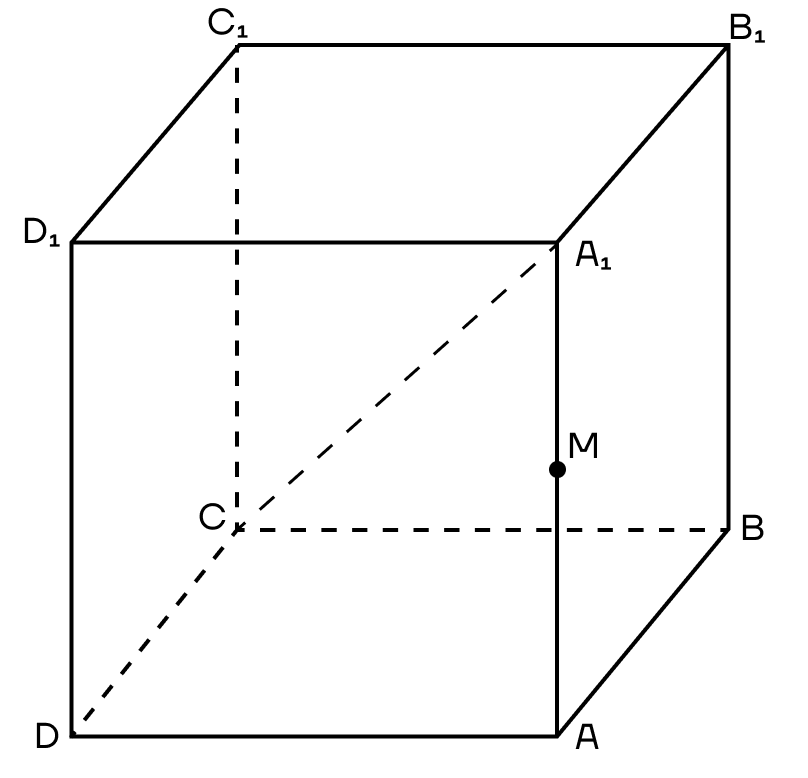
Решение. 1. Достроим прямую АС и рассмотрим плоскость (АА1С). Проведем в ней прямую, параллельную А1С из точки М. Пусть она пересечет АС в точке К.
2. Тогда МК — средняя линия треугольник АА1С, значит К — середина АС.
Подробнее про среднюю линию треугольника можно прочесть в статье «Треугольники».
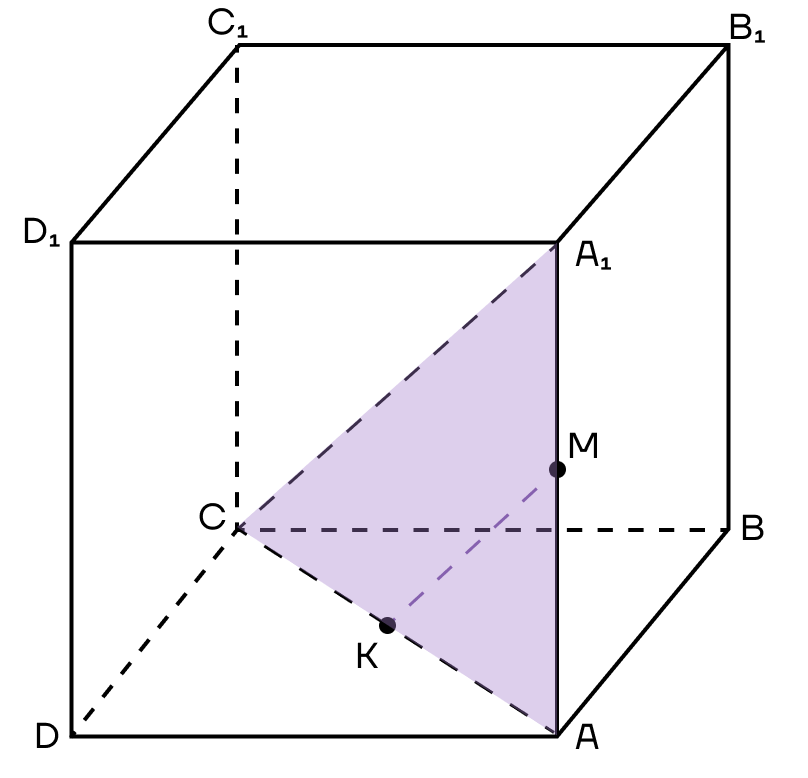
3. Точка К будет принадлежать сечению. Точки В и К лежат в плоскости (АВС) — их можно соединить.
4. В основании куба находится квадрат, его диагонали равны и точкой пересечения делятся пополам.
Подробнее про квадрат и его свойства можно прочитать в статье «Параллелограмм».
Поскольку К — середина диагонали АС, эта же точка будет серединой диагонали BD.
Следовательно, прямую ВК можно продлить до точки D.
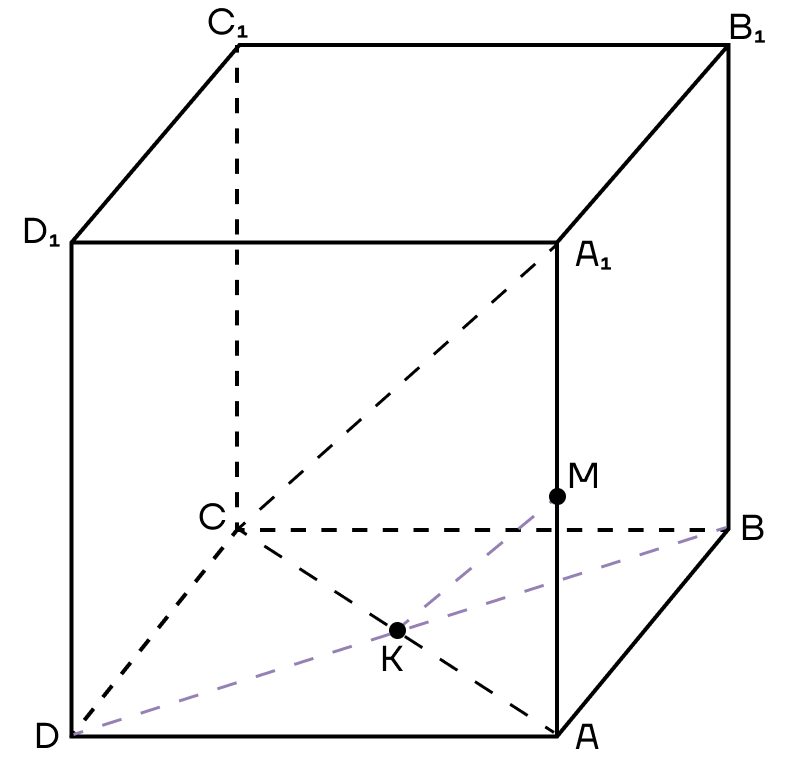
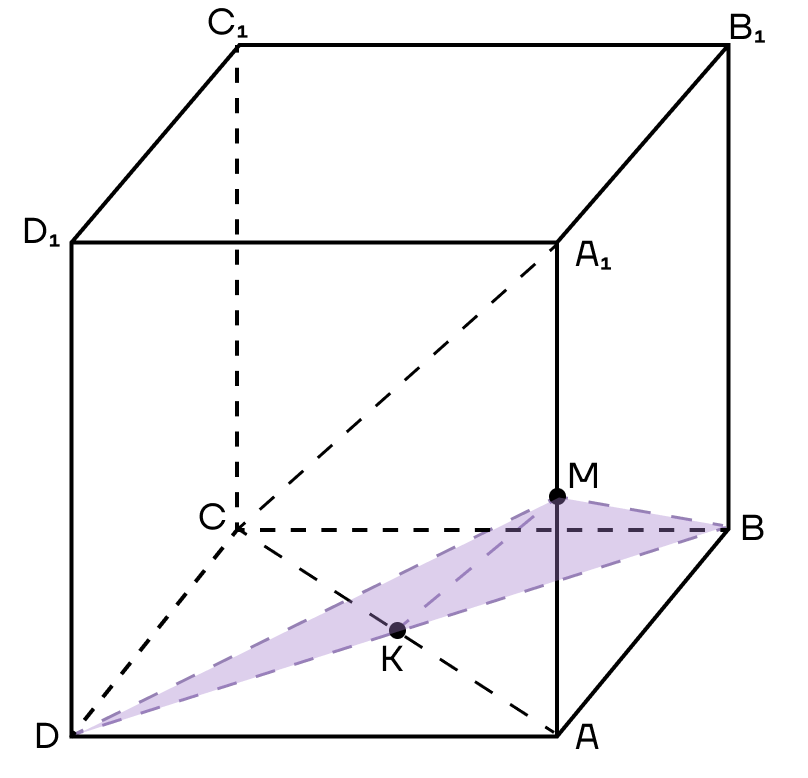
5. Осталось только соединить точки, которые лежат в одной плоскости. Это точки М и D в плоскости (ADD1) и точки М и В в плоскости (ABB1).
Тогда сечением будет треугольник DMB.
Мы рассмотрели сечения и основные способы их построения. В них нет ничего сложного и стоит помнить, что любое сечение можно представить в реальной жизни. Например, попробовать разрезать пластилиновые фигуры.
Фактчек
- Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью. При этом в многогранниках сечения представлены в виде многоугольников, вершины которых лежат на ребрах фигуры.
- Существует несколько методов построения сечения в многогранниках: метод следов, метод внутреннего проектирования и комбинированный метод.
- Метод следов заключается в том, что по следу сечения можно построить его полностью. След сечения — прямая, по которой секущая плоскость пересекает грань многогранника. В методе следов часто нужно продлевать линии и ребра до их пересечения.
- Метод внутреннего проектирования позволяет параллельно переносить сторону сечения в параллельных плоскостях. Это может быть удобно в случаях, когда метод следов невозможно или трудно применить.
- Комбинированный метод — метод, который сочетает в себе и метод следов, и метод внутреннего проектирования.
Проверь себя
Задание 1.
Какая форма сечения будет, если треугольную пирамиду разрезать параллельно основанию?
- Треугольник;
- Четырехугольник;
- Шестиугольник;
- Произвольный многоугольник с любым количеством углов.
Задание 2.
Где могут лежать вершины многоугольника, который образовывает сечение?
- Только в вершинах многогранника;
- На ребрах многогранника;
- Только на гранях многогранника;
- В любой точке на многограннике.
Задание 3.
Что такое след сечения?
- Продолжения сторон сечения;
- Вершины многоугольника, который образовывает сечение;
- Прямая, по которой секущая плоскость пересекает плоскость основания многогранника;
- Все вышеперечисленные варианты.
Задание 4.
Что можно сделать с точками, которые лежат на одной грани?
- Соединить;
- Ни в коем случае нельзя их соединять;
- Построить сечение, опираясь на две разные стороны, не соединяя стороны;
- Ни один из перечисленных вариантов.
Задание 5.
Как можно воспользоваться методом внутреннего проектирования?
- Произвольно переносить линии сечения в любых гранях;
- Произвольно переносить линии сечения в параллельных гранях;
- Перпендикулярно переносить линии сечения в перпендикулярных гранях;
- Параллельно переносить линии сечения в параллельных гранях.
Ответы: 1. — 1 2. — 2 3. — 3 4. — 1 5. — 4
���������� ������� ��������������.
������� ���������� ������� ��������������:
1) �������� ������ ����� �����, ������� � ����� ���������;
2) ���� ������ ����������� ��������� ������� � ������� �������������, ��� �����
�) ���� ����� ����������� ������ ������������� ��������� ������� � ������, ������������� ����� �� ������ (������� � ����� ���������);
�) ������������ ����� ��������� ������� ���������� �� ������������ ������.
������� ���������� �������:
������ 1.
���������� ������������� �������������� ABCDA1B1C1D1. �������� �������, ���������� ����� ����� M, N, L.
�������� ����� M � L, ������� � ��������� AA1D1D.
��������� ������ ML ( ������������� �������) � ������ A1D1, ��� ����� � ����� ��������� AA1D1D. ������� ����� X1.
����� X1 ����� �� ����� A1D1, � ������ � ��������� A1B1C1D1, �������� �� ������� N, ������� � ���� �� ���������.
X1 N ������������ � ������ A1B1 � ����� �.
�������� ����� K � M, ������� � ����� ��������� AA1B1B.
������ ������ ����������� ��������� ������� � ���������� DD1C1C:
��������� ������ ML (������������� �������) � ������ DD1, ��� ����� � ����� ��������� AA1D1D, ������� ����� X2;
��������� ������ KN (������������� �������) � ������ D1C1, ��� ����� � ����� ��������� A1B1C1D1, ������� ����� X3;
����� X2 � X3 ����� � ��������� DD1C1C. �������� ������ X2 X3 , ������� ��������� ����� C1C � ����� T, � ����� DC � ����� P. � �������� ����� L � P, ������� � ��������� ABCD.
MKNTPL – ������� �������.
������ 2.
���������� �� �� ����� ������ �� ���������� �������, �� ������������� ��������� ������������ ����������. ��� �������� ��� ���������� �������.

�������� ����� M � L, ������� � ��������� AA1D1D.

����� ����� N, �������� ������ NT ������������ ������ ML. ������ NT � ML ����� � ������������ ���������� �� �������� ���������������.

��������� ������ ML ( ������������� �������) � ������ A1D1, ��� ����� � ����� ��������� AA1D1D. ������� ����� X1.

����� X1 ����� �� ����� A1D1, � ������ � ��������� A1B1C1D1, �������� �� ������� N, ������� � ���� �� ���������.
X1 N ������������ � ������ A1B1 � ����� �.

�������� ����� K � M, ������� � ����� ��������� AA1B1B.

�������� ������ TP ����� ����� T, ����������� ������ KM ( ��� ����� � ������������ ����������).

�������� ����� P � L ( ��� ����� � ����� ���������).

MKNTPL – ������� �������.
Метод сечений многогранников в стереометрии
используется в задачах на построение. В его
основе лежит умение строить сечение
многогранника и определять вид сечения.
Данный материал характеризуется следующим
особенностями:
- Метод сечений применяется только для
многогранников, так как различные сложные
(наклонные) виды сечений тел вращения не входят в
программу средней школы. - В задачах используются в основном простейшие
многогранники. - Задачи представлены в основном без числовых
данных, чтобы создать возможность их
многовариантного использования.
Чтобы решить задачу построения сечения
многогранника ученик должен знать:
- что значит построить сечение многогранника
плоскостью; - как могут располагаться относительно друг
друга многогранник и плоскость; - как задается плоскость;
- когда задача на построение сечения
многогранника плоскостью считается решенной.
Поскольку плоскость определяется:
- тремя точками;
- прямой и точкой;
- двумя параллельными прямыми;
- двумя пересекающимися прямыми,
построение плоскости сечения проходит в
зависимости от задания этой плоскости. Поэтому
все способы построения сечений многогранников
можно разделить на методы.
Существует три основных метода построения
сечений многогранников:
- Метод следов.
- Метод вспомогательных сечений.
- Комбинированный метод.
Первые два метода являются разновидностями Аксиоматического
метода построения сечений.
Можно также выделить следующие методы
построения сечений многогранников:
- построение сечения многогранника плоскостью,
проходящей через заданную точку параллельно
заданной плоскости; - построение сечения, проходящего через заданную
прямую параллельно другой заданной прямой; - построение сечения, проходящего через заданную
точку параллельно двум заданным скрещивающимся
прямым; - построение сечения многогранника плоскостью,
проходящей через заданную прямую
перпендикулярно заданной плоскости; - построение сечения многогранника плоскостью,
проходящей через заданную точку перпендикулярно
заданной прямой.
В федеральный перечень учебников по геометрии
для 10-11 класов входят учебники авторов:
- Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др
(Геометрия, 10-11); - Погорелова А.В. (Геометрия, 7-11);
- Александрова А.Д., Вернера А.Л., Рыжик В.И.
(Геометрия, 10-11); - Смирновой И.М. (Геометрия, 10-11);
- Шарыгина И.Ф. (Геометрия, 10-11).
Рассмотрим подробнее учебники Л.С, Атанасяна и
Погорелова А.В.
В учебнике Л.С. Атанасяна на тему “Построение
сечений многогранников” выделено два часа. В 10
классе в теме “Параллельность прямых и
плоскостей” после изучения тетраэдра и
параллелепипеда отводится один час на изложение
параграфа “Задачи на построение сечений”.
Рассматриваются сечения тетраэдра и
параллелепипеда. И тема “Параллельность прямых
и плоскостей” завершается решением задач на
одном или двух часах (всего задач на построение
сечений в учебнике восемь).
В учебнике Погорелова А.В. на построение
сечений отводится около трех часов в главе
“Многогранники”: один – на изучение темы
“Изображение призмы и построение ее сечений”,
второй – на изучение темы “Построение пирамиды
и ее плоских сечений” и третий – на решение
задач. В списке задач, приведенных после темы,
задач на сечение насчитывается всего около
десяти.
Мы предлагаем систему уроков по теме
“Построение сечений многогранников” для
учебника Погорелова А.В.
Материал предлагается расположить в той
последовательности, в какой он может применяться
для обучения учащихся. Из изложения темы
“Многогранники” предлагается исключить
следующие параграфы: “Построение сечений
призмы” и “Построение сечений пирамиды” с тем,
чтобы систематизировать данный материал в конце
этой темы “Многогранники”. Классифицировать
его по тематике задач с примерным соблюдением
принципа “от простого к сложному” можно весьма
условно следующим образом:
- Определение сечения многогранников.
- Построение сечений призмы, параллелепипеда,
пирамиды методом следов. (Как правило в школьном
курсе стереометрии используются задачи на
построение сечений многогранников, решаемые
основными методами. Остальные методы, в связи с
их более высоким уровнем сложности, учитель
может оставить для рассмотрения на
факультативных занятиях или на самостоятельное
изучение. В задачах на построение основными
методами требуется построить плоскость сечения,
проходящую через три точки). - Нахождение площади сечений в многогранниках
(без использования теоремы о площади
ортогональной проекции многоугольника). - Нахождение площади сечений в многогранниках (с
применением теоремы о площади ортогональной
проекции многоугольника).
СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА
ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ
ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.(система уроков и факультативных
занятий по теме “Построение сечений
многогранников”)
УРОК 1.
Тема урока: “Построение сечений
многогранников”.
Цель урока: ознакомление с методами
построений сечений многогранников.
Этапы урока:
- Актуализация опорных знаний.
- Постановка задачи.
- Изучение нового материала:
А) Определение сечения.
Б) Методы построений сечений:
а) метод следов;
б) метод вспомогательных сечений;
в) комбинированный метод.
- Закрепление материала.
Примеры построений сечений методом следов.
- Подведение итогов урока.
Тест.
Ход урока.
- Актуализация опорных знаний.
- Постановка задачи.
- Изучение нового материала.
Вспомним:
– пересечение прямой с плоскостью;
– пересечение плоскостей;
– свойства параллельных плоскостей.
Вопросы к классу:
– Что значит построить сечение многогранника
плоскостью?
– Как могут располагаться относительно друг
друга многогранник и плоскость?
– Как задается плоскость?
– Когда задача на построение сечения
многогранника плоскостью считается решенной?
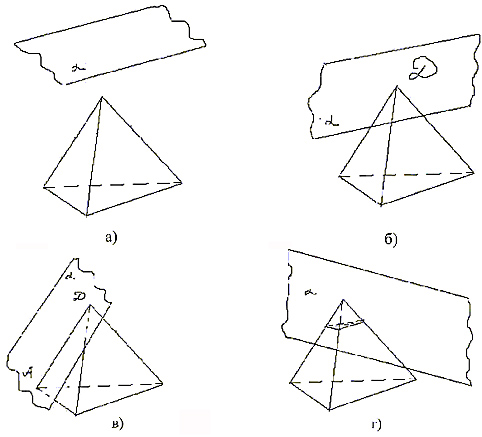
А) Итак, задача состоит в построении
пересечения двух фигур: многогранника и
плоскости ( рис.1). Это могут быть: пустая фигура
(а), точка (б), отрезок (в), многоугольник (г). Если
пересечение многогранника и плоскости есть
многоугольник, то этот многоугольник называется сечением
многогранника плоскостью.
Рис. 1
Будем рассматривать только случай, когда
плоскость пересекает многогранник по его
внутренности. При этом пересечением данной
плоскости с каждой гранью многогранника будет
некоторый отрезок. Таким образом, задача
считается решенной, если найдены все отрезки, по
которым плоскость пересекает грани
многогранника.
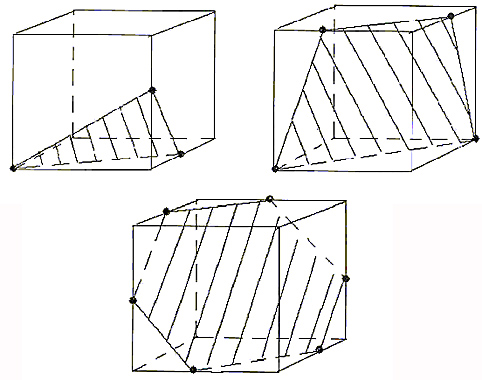
Исследуйте сечения куба (рис.2) и ответьте на
следующие вопросы:
Рис. 2
– какие многоугольники получаются в сечении
куба плоскостью? (Важно число сторон
многоугольника);
[ Предполагаемые ответы: треугольник,
четырехугольник, пятиугольник, шестиугольник.]
– может ли в сечении куба плоскостью получиться
семиугольник? А восьмиугольник и т.д.? Почему?
Давайте рассмотрим призму и ее возможные
сечения плоскостью ( на модели). Какие
многоугольники получаются?
Какой можно сделать вывод? Чему равно
наибольшее число сторон многоугольника,
полученного сечением многогранника с
плоскостью?
[ Наибольшее число сторон многоугольника,
полученного в сечении многогранника плоскостью,
равно числу граней многогранника.]
Б) а) Метод следов заключается в построении
следов секущей плоскости на плоскость каждой
грани многогранника. Построение сечения
многогранника методом следов обычно начинают с
построения так называемого основного следа
секущей плоскости, т.е. следа секущей плоскости
на плоскости основания многогранника.
б) Метод вспомогательных сечений
построения сечений многогранников является в
достаточной мере универсальным. В тех случаях,
когда нужный след (или следы) секущей плоскости
оказывается за пределами чертежа, этот метод
имеет даже определенные преимущества. Вместе с
тем следует иметь ввиду, что построения,
выполняемые при использовании этого метода,
зачастую получаются “скученными”. Тем не менее
в некоторых случаях метод вспомогательных
сечений оказывается наиболее рациональным.
Метод следов и метод вспомогательных сечений
являются разновидностями аксиоматического
метода построения сечений многогранников
плоскостью.
в) Суть комбинированного метода построения
сечений многогранников состоит в применении
теорем о параллельности прямых и плоскостей в
пространстве в сочетании с аксиоматическим
методом.
А теперь на примере решения задач рассмотрим метод
следов.
4. Закрепление материала.
Задача 1.
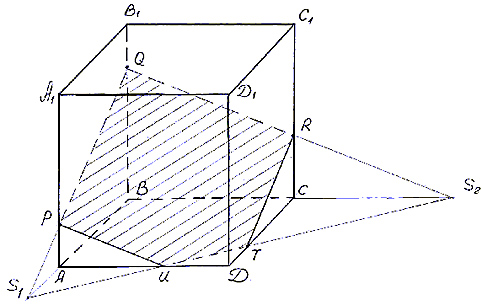
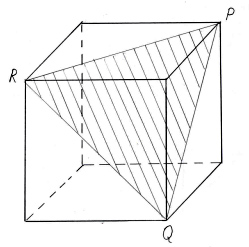
Построить сечение призмы ABCDA1B1C1D1
плоскостью, проходящей через точки P, Q, R (точки
указаны на чертеже (рис.3)).
Решение.
Рис. 3
- Построим след секущей плоскости на плоскость
нижнего основания призмы. Рассмотрим грань АА1В1В.
В этой грани лежат точки сечения P и Q. Проведем
прямую PQ. - Продолжим прямую PQ, которая принадлежит
сечению, до пересечения с прямой АВ. Получим
точку S1, принадлежащую следу. - Аналогично получаем точку S2 пересечением
прямых QR и BC. - Прямая S1S2 – след секущей плоскости
на плоскость нижнего основания призмы. - Прямая S1S2 пересекает сторону AD в
точке U, сторону CD в точке Т. Соединим точки P и U,
так как они лежат в одной плоскости грани АА1D1D.
Аналогично получаем TU и RT. - PQRTU – искомое сечение.
Задача 2.
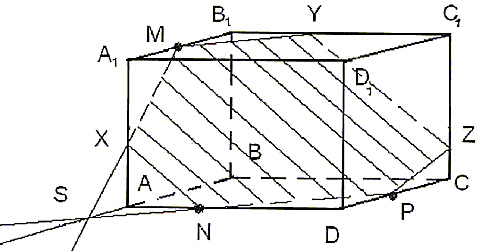
Построить сечение параллелепипеда ABCDA1B1C1D1
плоскостью, проходящей через точки M, N, P (точки
указаны на чертеже (рис.4)).
Решение.
Рис. 4
- Точки N и P лежат в плоскости сечения и в
плоскости нижнего основания параллелепипеда.
Построим прямую, проодящую через эти точки. Эта
прямая является следом секущей плоскости на
плоскость основания параллелепипеда. - Продолжим прямую, на которой лежит сторона AB
параллелепипеда. Прямые AB и NP пересекутся в
некоторой точке S. Эта точка принадлежит
плоскости сечения. - Так как точка M также принадлежит плоскости
сечения и пересекает прямую АА1 в некоторой
точке Х. - Точки X и N лежат в одной плоскости грани АА1D1D,
соединим их и получим прямую XN. - Так как плоскости граней параллелепипеда
параллельны, то через точку M можно провести
прямую в грани A1B1C1D1,
параллельную прямой NP. Эта прямая пересечет
сторону В1С1 в точке Y. - Аналогично проводим прямую YZ, параллельно
прямой XN. Соединяем Z с P и получаем искомое
сечение – MYZPNX.
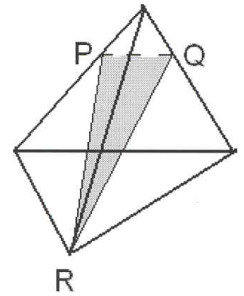
Задача 3 ( для самостоятельного
решения).
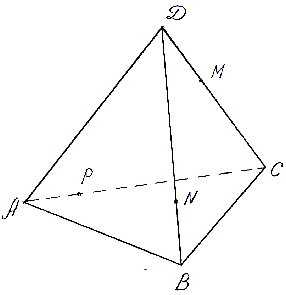
Построить сечение тетраэдра DACB плоскостью,
проходящей через точки M, N, P (точки указаны на
чертеже (рис.5)).
Рис. 5
5. Подведение итогов урока.
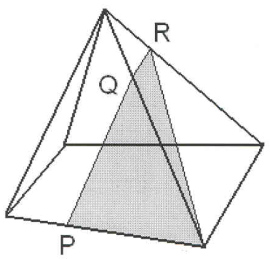
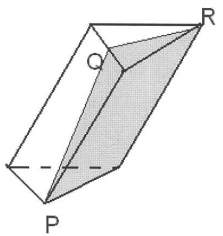
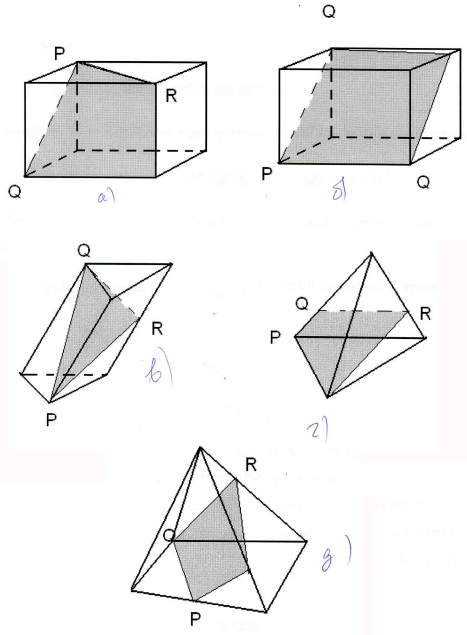
Ответьте на вопрос: являются ли закрашенные
фигуры сечениями изображенных многогранников
плоскостью PQR? И выполните правильное построение
(рис. 6).
Вариант 1.
а)
б)
в)
г)
д)
Вариант 2.
УРОК 2.
Тема урока: НАХОЖДЕНИЕ ПЛОЩАДИ СЕЧЕНИЯ.
Цель урока: познакомить со способами
нахождения площади сечения многогранника.
Этапы урока:
- Актуализация опорных знаний.
- Решение задач на нахождение площади сечения:
Вспомнить теорему о площади ортогональной
проекции многоугольника.
– без использования теоремы о площади
ортогональной проекции многоугольника;
– с использованием теоремы о площади
ортогональной проекции многоугольника.
3. Подведение итогов урока.
Ход урока.
- Актуализация опорных знаний.
- Решение задач.
Вспомним теорему о площади ортогональной
проекции многоугольника: площадь
ортогональной проекции многоугольника на
плоскость равна произведению его площади на
косинус угла между плоскостью многоугольника и
плоскостью проекции.
Задача 1.
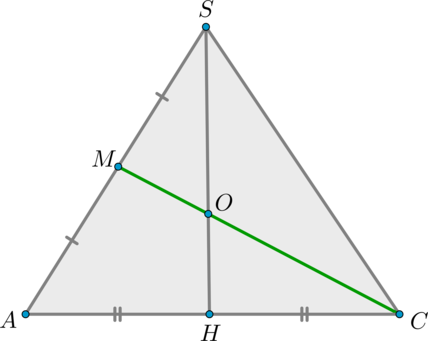
ABCD – правильная треугольная пирамида со
стороной основания AB равной а и высотой DH
равной h. Постройте сечение пирамиды
плоскостью, проходящей через точки D, C и М, где М –
середина стороны АВ, и найдите его площадь (рис.7).
Решение.
Сечением пирамиды является треугольник MCD.
Найдем его площадь.
- Так как основание пирамиды – равносторонний
треугольник и точка М – середина стороны, то СМ
является высотой и тогда, СМ =.
- Площадь треугольника можно найти:
S = 1/2 · DH · CM = 1/2 ·
=
Рис.7
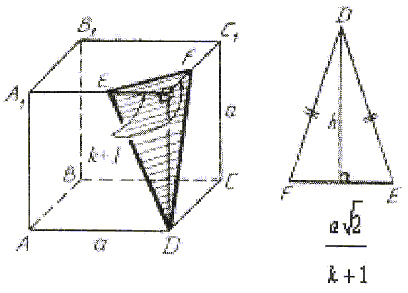
Задача 2.
Найти площадь сечения куба ABCDA1B1C1D1
с ребром а плоскостью, проходящей через
вершину D и точки Е и F на ребрах А1D1 и C1D1
соответственно, если A1E = k · D1E и C1F
= k · D1F.
Решение.
Построение сечения:
- Поскольку точки Е и F принадлежат плоскости
сечения и плоскости грани A1B1C1D1,
а две плоскости пересекаются по прямой, то прямая
EF будет являться следом секущей плоскости на
плоскость грани A1B1C1D1
(рис.8). - Аналогично получаются прямые ED и FD.
- EDF – искомое сечение.
Рис.8.
Задача 3 (для самостоятельного решения).
Построить сечение куба ABCDA1B1C1D1
со стороной а плоскостью, проходящей через
точки B, M и N, где Ь – середина ребра АА1, а N –
середина ребра СС1.
Решение.
Сечение строим методом следов.
Площадь сечения находим с помощью теоремы о
площади ортогональной проекции многоугольника.
Ответ: S = 1/2 · a2.
Четвертухина Наталия Константиновна
учитель математики МБОУ СОШ №50 г. Белгорода
Методы
построения сечений многогранников
В настоящее время многие школьники
испытывают трудности в изображении восприятия фигур в пространстве, в частности
в построении сечений, а построение сечений многогранников и других фигур широко
используется в строительном деле, архитектуре, машиностроение и во многих
других областях науки и техники. вместе с тем, задание 14 Единого
государственного экзамена представляет собой именно стереометрическую задачу.
Сечение
выпуклого многогранника – есть выпуклый многоугольник. Его вершины в общем
случае являются точками пересечения секущей плоскости с ребрами многогранника,
а стороны – отрезками, по которым секущая плоскость пересекает грани
многогранника.
Задачи на
сечения многогранника плоскостью обычно состоят в том, чтобы поострить
параллельную проекцию сечения, имея параллельную проекцию самого многогранника
и условия, которыми задается секущая плоскость, и вычислить площадь полученного
сечения или отношение, в котором секущая плоскость делит объем многогранника.
Решение каждой из двух частей такой задачи должно быть убедительно обосновано.
В зависимости
от взаимного положения многогранника и секущей плоскости сечение может быть
треугольником, четырехугольником и т.д., однако число сторон
многоугольника-сечения не может превышать числа всех граней данного
многогранника.
При
построении сечения многогранника плоскостью, независимо от применяемого при
этом метода, приходится решать две элементарные задачи:
1. Строить
точку пересечения прямой (ребра многогранника) секущей плоскостью.
2. Строить
линию пересечения двух плоскостей (секущей плоскости и плоскости грани).
|
Число граней многогранника. |
Многогранник. |
n – число |
|
|
Треугольная |
|
|
|
Четырехугольная |
|
|
|
Параллелепипед. |
|
1. Построение сечений многогранников на
основе системы аксиом стереометрии

многогранника плоскостью называется геометрическая фигура, представляющая собой множество всех точек пространства, принадлежащих одновременно данным многограннику и плоскости; плоскость при этом называется
секущей плоскостью.
Поверхность
многогранника состоит из ребер-отрезков и граней – плоских многоугольников. Так как прямая и плоскость пересекаются в точке, а две плоскости
– по прямой, то сечением многогранника плоскостью является плоский многоугольник; вершинами этого многоугольника служат
точки пересечения секущей плоскости с
ребрами многогранника, а сторонами – отрезки, по которым секущая плоскость
пересекает его грани. Это означает,
что для построения искомого сечения
данного многогранника плоскостью α
достаточно построить точки ее
пересечения с ребрами многогранника.
Затем последовательно соединить
отрезками эти точки, при этом выделить сплошными
линиями, видимые и штриховыми – невидимые
стороны полученного многоугольника – сечения (рис. 1-4).
Секущая плоскость α может быть
задана: тремя точками, не лежащими на одной
прямой; прямой и не принадлежащей
ей точкой; другими условиями,
определяющими ее положение относительно
данного Рис. 3
многогранника. Например, на рис. 1 построено
сечение четырехугольной пирамиды РАВСD плоскостью
α, заданной точками М, К и Н, принадлежащими ребрам соответственно РС, РD и РВ; на
рис. 2 секущая плоскость задана точками М, N и L, принадлежащими ребрам соответственно
АА1, В1С1 и АD куба АВСDА1B1C1D1; на рис. 3 секущая плоскость проходит через вершину А основания АВСD перпендикулярно
ребру РС правильной четырехугольной
пирамиды РАВСD, высота РО которой образует угол в 30° с боковым ребром;
на рис. 4 построено
сечение куба АВСВА1В1С1В1 плоскостью, проходящей через его центр М перпендикулярно диагонали А1С.
Рис. 4
2. Специальные методы построения сечений
2.1. Метод следов
Следом называют
прямую пересечения плоскости сечения и плоскости какой-либо грани
многогранника. Чтобы построить след, достаточно знать две его точки, т. е.
точки, лежащие одновременно в секущей плоскости и плоскости рассматриваемой
грани.
Основные правила
построения сечений методом следа:
1.
Если даны (или уже
построены) две точки плоскости сечения на одной грани многогранника, то след
сечения этой плоскости – прямая, проходящая через эти три точки.
2.
Если дана (или уже
построена) прямая пересечения плоскости сечения с основанием многогранника
(след на основании) и есть точка, принадлежащая определенной боковой грани, то
нужно определить точку пересечения данного следа с этой боковой гранью (точка
пересечения данного следа с общей прямой основания и данной боковой грани)
3.
Точку пересечения плоскости
сечения с основанием можно определить как точку пересечения какой-либо прямой в
плоскости сечения с ее проекцией на плоскость основания.
То есть, суть метода
заключается в построении вспомогательной прямой, являющейся изображением линии
пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее
всего строить изображение линии пересечения секущей плоскости с плоскостью
нижнего основания. Используя след, легко построить изображения точек секущей
плоскости, находящихся на боковых ребрах или гранях фигуры.
Для тех, кто знаком с
гомологией, удобно ее применять при нахождении образов точек нижнего основания
фигуры F – изображения фигуры. Последовательно соединяя образы этих точек,
получим изображение искомого сечения.
В дальнейшем будем
допускать вольность речи и говорить «строим сечение» вместо «строим изображение
сечения».
2.2. Метод внутреннего
проектирования в построении плоских сечений многогранников.
В некоторых учебных
пособиях метод построения сечений многогранников, который мы сейчас будем
рассматривать, называют методом внутреннего проектирования или методом
соответствий, или методом диагональных сечений. Мы примем первое название.
Задача
1. Постройте сечение пирамиды PABCDE плоскостью α = (МFR), если точки М, F и R являются
внутренними точками ребер соответственно РА, РС и РЕ (рис. 26, а).
Решение. Плоскость основания пирамиды обозначим β. Для построения
искомого сечения построим точки пересечения секущей плоскости α с ребрами
пирамиды.
Построим
точку пересечения секущей плоскости с ребром РD данной пирамиды.
Плоскости APD и CPE пересекают плоскость β по
прямым соответственно АD и СЕ, которые пересекаются в некоторой точке К (рис. 26, в). Прямая
РК=(АРD) ∩(СРЕ) пересекает прямую FR є α в некоторой точке К1:
К1 = РК ∩ FR (рис. 26, г), при этом К1
є α. Тогда: М є α, К1 є α => прямая МK є а. Поэтому точка Q = МК1 ∩ РD (рис. 26, д) есть точка пересечения ребра РD и
секущей плоскости: Q =α ∩ PD. Точка Q— вершина искомого сечения. Аналогично строим точку пересечения
плоскости α и ребра РВ. Плоскости ВРЕ и АРD пересекают плоскость β по прямым
соответственно ВЕ и АD, которые пересекаются в точке Н (рис. 26, е). Прямая РН = (ВРЕ) ∩
(АРD) пересекает прямую МQ в точке Н1 (рис.
26, ж). Тогда прямая RН1 пересекает
ребро РВ в точке N = α ∩ РВ — вершине сечения (рис. 26, з).
Таким
образом, последовательность «шагов» построения искомого сечения такова:
1. К = АD ∩ ЕС; 2. К1
= РК ∩ RF;
3. Q = МК1 ∩ РD; 4. H = BE ∩ АD;
5. Н1
= РН ∩ МQ; 6. N = RН1 ∩ РВ.
Пятиугольник MNFQR — искомое сечение (рис. 26, и).
Динамика
построения этого сечения пирамиды проиллюстрирована на рис. 26.
2.3. Комбинированный метод
построения сечений
Суть комбинированного метода построения сечений
многогранников состоит в применении теорем о параллельности прямых и плоскостей
в пространстве в сочетании с аксиоматическим методом.
Пример 1. На ребрах AB и AD пирамиды MABCD зададим
соответственно точки P и Q – середины этих ребер, а на ребре MC зададим точку
R. Построим сечение пирамиды плоскостью, проходящей через точки P, Q и R. 
Решение (рисунок 14):
1. Ясно, что основным следом плоскости PQR является
прямая PQ.
2. Найдем точку К, в которой плоскость МАС
пересекает прямую PQ. Точки К и R принадлежат и плоскости PQR, и плоскости MAC.
Поэтому, проведя прямую KR, мы получим линию пересечения этих плоскостей.
3. Найдем точку N=AC BD, проведем прямую MN и
найдем точку F=KR MN.
4. Точка F является общей точкой плоскостей PQR и
MDB, то есть эти плоскости пересекаются по прямой, проходящей через точку F.
Вместе с тем так как PQ – средняя линия треугольника ABD, то PQ параллена BD,
то есть прямая PQ параллельна и плоскости MDB. Тогда плоскость PQR, проходящая
через прямую PQ, пересекает плоскость MDB по прямой, параллельной прямой PQ, то
есть параллельной и прямой BD. Поэтому в плоскости MDB через точку F проведем
прямую, параллельную прямой BD.
5. Дальнейшие построения понятны из рисунка. В
итоге получаем многоугольник PQD’RB’ – искомое сечение.
2.3.1. Построение сечения, проходящего через заданную прямую
параллельную другой заданной прямой.
Пусть, например, требуется построить сечение
многогранника плоскостью @, проходящей через заданную прямую р параллельную
второй заданной прямой q. В общем случае решение этой задачи требует некоторых
предварительных построений, которые можно выполнять по следующему плану:
1). Через вторую прямую q и какую-нибудь точку W
первой прямой p проведем плоскость бетта (рис. 15 ).
2). В плоскости бетта через точку W проведем прямую
q’ параллельную q.
3). Пересекающимися прямыми p и q’. Определяется
плоскость @. На этом предварительные построения заканчиваются и можно
переходить к построению непосредственно сечения многогранника плоскостью @. В
некоторых случаях особенности конкретной задачи позволяет осуществить и болле
короткий план решения. Рассмотрим примеры.
2.3.2. Построение сечения, проходящего через заданную точку
параллельно двум заданным скрещивающимся прямым.
Пусть требуется построить сечение многогранника
плоскостью, проходящей через заданную точку К параллельно двум заданным
скрещивающимся прямым l и m. При решении задач этого вида можно применять
следующий план построения:
1.Выберем некоторую точку W. (Эта точка может лежать на одной из
заданных скрещивающихся прямых, может совпадать с точкой К.)
2.Через точку W проведем прямые l’ и m’. (Естественно, если точка W
лежит на одной из прямых, например на прямой l, то прямая l’ совпадает с прямой
l.)
3. Пересекающимися прямыми l’ и m’ определяется плоскость бетта –
плоскость вспомогательного сечения многогранника. Строим сечение многогранника
плоскостью бетта.
4. Построим сечения многогранника плоскостью альфа, проходящей через
точку K, параллельно плоскости бетта.