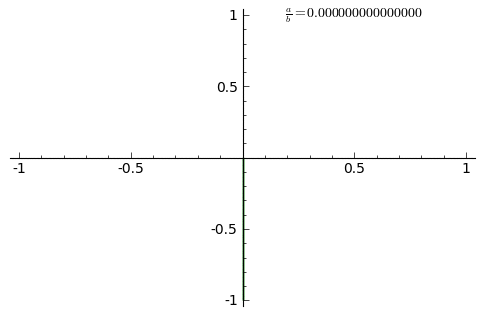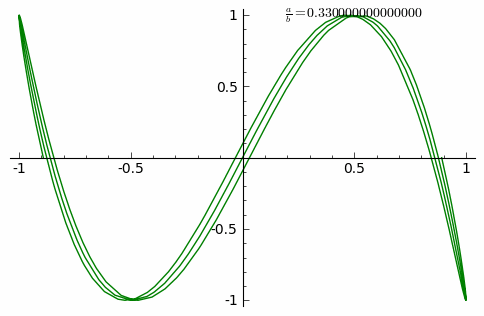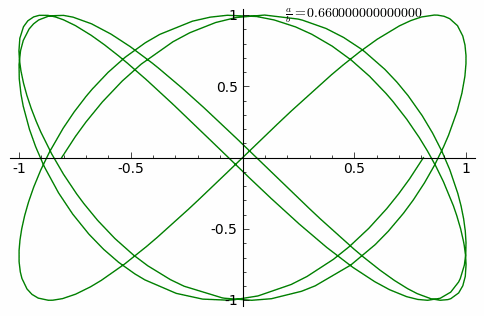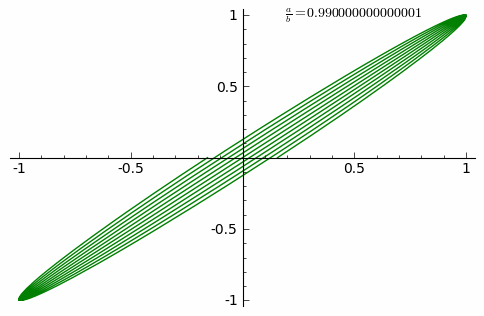Что такое фигуры Лиссажу?
Фигуры Лиссажу представляют из себя различные геометрически-красивые рисунки, которые вычерчиваются точкой, колеблющейся в двух взаимно-перпендикулярных направлениях на одной плоскости.

Чтобы было более понятно, давайте представим девочку на качели из покрышки:


И вот представьте, что сзади ее раскачивает папа, а сбоку — мама. То есть наша девочка будет одновременно летать вперед-назад, а также влево-вправо. Долго ли она продержится — это уже другой вопрос). Если в солнечный денек посмотреть на землю, то мы увидим, что тень девочки вырисовывает различную траекторию полета.
Почему бы нам не поиграться пучком электронов, отклоняя его одновременно и по вертикали и по горизонтали? Вспоминаем, как выглядит электронно-лучевая трубка осциллографа:

где
1 — это горизонтальные пластины
2 — вертикальные пластины
ну и остальные детали — это составляющие электронной пушки.
Подаем на вертикальные пластины один синусоидальный сигнал, а на горизонтальные — другой синусоидальный сигнал. В результате точка на осциллографе будет вырисовывать различные линии и кривые, в зависимости от частоты сигналов. Хотя, цифровой осциллограф и аналоговый почти не похожи по внутренней начинке, но принцип действия у них все равно схож.
Как получить фигуры Лиссажу
Итак, для того, чтобы вырисовывать фигуры Лиссажу, нам потребуются два генератора частоты.
Генератор №1
Генератор №2

и осциллограф с функцией XY-режима. В моем случае это цифровой осциллограф OWON

Думаю, почти во всех современных осциллографах есть режим XY, будь это аналоговый или цифровой осциллограф.
Режим XY-осциллографа
Как вы помните, при простом использовании осциллографа у нас по оси X было время, а по оси Y — напряжение. Поэтому, по умолчанию, мы на осциллографе смотрим изменение напряжения во времени. Но если с помощью нехитрой кнопки переключить в режим XY, то у нас по Y будет напряжение и по X…. тоже напряжение, но уже с другого генератора частоты. Если включить в таком режиме только один генератор, то мы увидим только одну прямую линию либо по вертикали, либо по горизонтали. Это аналогично тому, если бы нашу девочку раскачивал только папа или только мама. Наша девочка летела бы только по одной прямой траектории.

А что будет, если сбоку нашу девочку будет раскачивать мама, а сзади — папа? Тут уже траектория девочки будет хаотичной. Но во всяком хаосе рождается порядок. И первым его заметил французский математик Жюль Антуан Лиссажу.
Строим фигуры Лиссажу на осциллографе
Цепляем на один канал один генератор частоты, а на другой канал — другой генератор частоты:

На осциллографе мы должны увидеть два сигнала с разных генераторов частоты, благо у меня осциллограф двухканальный:

Теперь переводим осциллограф в режим XY. На моем осциллографе это делается с помощью кнопки Display

Ну а потом с помощью дисплейных клавиш выбираем режим XY

И получается примерно вот такая хаотическая картинка:

Ну еще бы, один генератор дергает точку по X, другой по Y и у каждого генератора разная частота.
А давайте возьмем один генератор и с него подадим сигнал на два канала сразу. Частота и фаза совпадают и на первом и втором канале, так как мы берем сигнал с одного и то же генератора. В результате у нас будет вот такая картинка:

Если взять 100 Герц на первом генераторе и на втором генераторе, то получим что-то типа этого:



В реальности же получается круг, который все время крутится и превращается то в эллипс, то в прямую, так как очень ровно подобрать частоту на первом и втором генераторе очень сложно. Хотя на практике можно подавать сигнал на один канал напрямую, а на другой — через фазовращатель.
Если увеличить частоту на одном из генераторов вдвое, то можно наблюдать уже другие фигуры:



Эта фигура тоже все время крутится на осциллографе.
Увеличиваем на одном генераторе частоту в кратное число раз, то есть было 100, потом 200, 300 и тд и получаем абсолютно новые 3D фигуры 😉
Различное отношение частот одного генератора к другому дает различные фигуры Лиссажу:

Вот такие фигуры вы будете видеть на экране своего осциллографа:

А вот такие фигуры Лиссажу получаются, если использовать пилообразный сигнал с обоих генераторов сразу при разных отношениях коэффициентов




А вот такие фигуры получаются, если на одном оставить синус, а на втором поставить пилу:


В основном фигуры Лиссажу в электронике можно использовать тогда, когда надо узнать частоту неизвестного генератора через образцовый генератор, частоту которого мы знаем, а также узнать сдвиг фаз между двумя одинаковыми сигналами. Ну и второе применение — это чисто визуальный кайф при вращении этих фигур на экранчике вашего осциллографа 😉
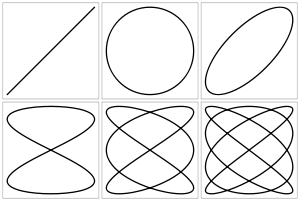
Фигу́ры Лиссажу́ — траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях.
Впервые изучены французским учёным Жюлем Антуаном Лиссажу.
Описание[править | править код]
Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или 

Если периоды обоих колебаний близки, то разность фаз линейно изменяется, вследствие чего наблюдаемый эллипс всё время деформируется. Это явление используется в электронике для сравнения частот и подстройки одной частоты под вторую — опорную частоту.
При многократно отличающихся по величине периодах колебаний фигуры Лиссажу представляют собой запутанную картину и не наблюдаются, например, на экране осциллографа, — в этом случае наблюдается светящийся прямоугольник.
Если отношение периодов представляет собой рациональное число, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в исходное положение, причём с совпадающим с исходным вектором скорости точки, в результате получаются замкнутые траектории. Если отношение периодов иррациональное число, то порождаются незамкнутые траектории.
Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.
Математическое выражение для кривой Лиссажу[править | править код]
Зависимость координат x и y от времени t описывается системой
где A, B — амплитуды колебаний, a, b — частоты, δ — сдвиг фаз.
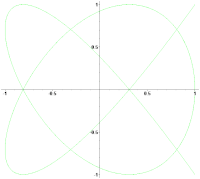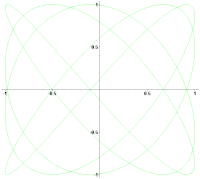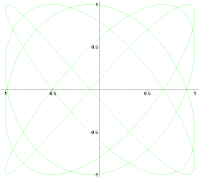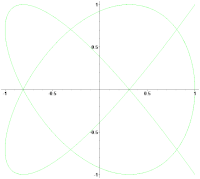
Вид кривой сильно зависит от соотношения a/b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности (A = B, δ = π/2 радиан) и отрезка прямой (δ = 0).
Ещё один пример фигуры Лиссажу — парабола (b/a = 2, δ = π/4). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии a/b — рациональное число.
Фигуры Лиссажу, где a = 1, b = N (N — натуральное число) и
являются полиномами Чебышёва первого рода степени N (см. их тригонометрическое определение).
Примеры[править | править код]
Анимация показывает изменение кривых при δ = 0 и постоянно возрастающем соотношении a/b от 0 до 1 с шагом 0,01:
Примеры фигур Лиссажу с δ = π/2, нечётным натуральным числом a, и также натуральным числом b, и |a − b| = 1:
-

a = 1, b = 2 (1:2)
-

a = 3, b = 2 (3:2)
-

a = 3, b = 4 (3:4)
-

a = 5, b = 4 (5:4)
-

a = 5, b = 6 (5:6)
-

a = 9, b = 8 (9:8)
Применение в технике — сравнение частот[править | править код]

Фигура Лиссажу на экране осциллографа
Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причём период цикла вращения является величиной, обратной разности частот, например, при периоде оборота 2 секунды разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счёт кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.
Вращение фигуры Лиссажу при незначительной расстройке частот
См. также[править | править код]
- Колебания
- Частота периодического процесса
- Маятник Фуко
- Конические сечения
- Связные звёзды
Литература[править | править код]
- Справочник по радиоэлектронным устройствам. В 2 томах / Под ред. Д. П. Линде. — М.: Энергия, 1978.
- Яворский Б. М., Детлаф А. А. Справочник по физике. — М.: Наука, 1981.
Ссылки[править | править код]
- Онлайн-построение фигур Лиссажу
- Circuits. Over Passive Circuits. Lissajous Figures
Допустим,
что материальная точка (тело) может
совершать колебания как вдоль оси x, так
и вдоль перпендикулярной оси Y. Если
возбудить оба колебания, материальная
точка будет двигаться по некоторой
криволинейной траектории, форма которой
зависит от разности фаз колебаний.
Выберем начало отсчета времени так,
чтобы начальная фаза одного колебания
была равна нулю. Тогда уравнения запишутся
следующим образом:
x=A·cos(ωt)
y=B·cos(ωt+α)
(22)
где
α – разность фаз складываемых колебаний,
A и B – амплитуды колебаний.
Выражения
(22) представляют собой заданное в
параметрической форме уравнение
траектории, по которой движется тело,
участвующее в обоих колебаниях. Чтобы
получить уравнение траектории в обычном
виде, нужно исключить из уравнений (22)
параметр . Из первого уравнения следует,
что:
cos(ωt)=x/A
(23)
следовательно,
sin(ωt)=±√(1-x2/A2)
(24)
Теперь
развернем косинус во втором уравнении
из (22) по формуле для косинуса суммы
(y/B=cos(ωt)·cosα-sin(ωt)·sinα) и подставим в него
вместо cos(ωt) и sin(ωt) их значения (23) и (24).
В результате получим:
y/B=(x/A)·cosα∓sinα√(1-x2/A2)
Перенесем
все члены без корня в левую часть
уравнения и возведем его в квадрат.
После несложных преобразований получим
уравнение эллипса, оси которого повернуты
относительно координатных осей:
(x2/A2)+(y2/B2)-(2·xy·cosα/AB)=sin2α
(25)
Ориентация
эллипса и величина полуосей зависят
довольно сложным образом от амплитуд
A и B и разности фаз α.
Рассмотрим
некоторые частные случаи:
1.
Разность фаз α=0.
В
этом случае уравнение (25) примет вид
[(x/A)-(y/B)]2=0,
откуда получается уравнение прямой:
y=Bx/A
(26).
Результирующее
движение является гармоническим с
частотой ω и амплитудой √(A2+B2)
(рис 8).

Рис.
8
2.
Разность фаз α=±π. В этом случае уравнение
(25) примет вид [(x/A)+(y/B)]2=0,
откуда получается, что результирующее
движение представляет собой гармоническое
колебание вдоль прямой (рис.9):
y=-Bx/A
(27)

Рис.
9
3.
Разность фаз α=±π/2.
Уравнение
(25) переходит в уравнение эллипса,
приведенного к координатным осям, причем
полуоси эллипса равны соответствующим
амплитудам колебаний (рис.10):
[(x/A)+(y/B)]2=1
(28)

Рис.
10
При
равенстве амплитуд A и B эллипс вырождается
в окружность. Случаи α=+π/2 и α=-π/2 отличаются
направлением движения по эллипсу или
по окружности.
Если
α=+π/2, уравнения (22) можно записать
следующим образом: x=A·cosωt; y=-B·sinωt.
В
момент t=0 тело находится в точке 1 (рис
10). В последующие моменты времени,
координата x уменьшается, а координата
y становится отрицательной. Следовательно,
движение совершается по часовой стрелке.
Если
α=-π/2, уравнения колебаний имеют вид:
x=A·cosωt; y=B·sinωt. Отсюда можно заключить,
что движение происходит против часовой
стрелки.
Из
сказанного следует, что равномерное
движение по окружности радиусом R с
угловой скоростью ω может быть представлено
как сумма двух взаимно перпендикулярных
колебаний:
x=R·cosωt
y=±R·sinωt
(29)
(знак
«+» в выражении для y соответствует
движению против часовой стрелки, знак
«-» – по часовой стрелке).
В
случае, когда частоты взаимно
перпендикулярных колебаний отличаются
на очень малую величину Δω, их можно
рассматривать как колебания одинаковой
частоты, но с медленно изменяющейся
разностью фаз. В самом деле, уравнения
колебаний можно представить следующим
образом:
x=A·cosωt
y=B·cos[ωt+(Δω+α)],
где
выражение (Δω+α) рассматривается как
разность фаз, медленно изменяющуюся со
временем по линейному закону.
Результирующее
движение в этом случае происходит по
медленно видоизменяющейся кривой,
которая будет последовательно принимать
форму, отвечающую всем значениям разности
фаз от -π до π.
Если
частоты взаимно перпендикулярных
колебаний неодинаковы, то траектория
результирующего движения имеет вид
довольно сложных кривых, называемых
фигурами Лиссажу.
На
рис.11 показана одна из простейших
траекторий, получающаяся при отношении
частот 1:2 и разности фаз π/2. Чем ближе к
единице рациональная дробь, выражающая
отношение частот колебаний, тем сложнее
оказывается фигура Лиссажу.

Рис.
11
Фигуры
Лиссажу позволяют найти частоту одного
из колебаний, если известна частота
другого. Это обусловлено тем, что
кратность частот легко находится с
помощью секущих, параллельных координатным
осям.
Фигу́ры
Лиссажу́ — замкнутые
траектории,
прочерчиваемые точкой, совершающей
одновременно два гармонических
колебания в
двух взаимно перпендикулярных
направлениях. Впервые изучены французским
учёным Жюлем
Антуаном Лиссажу.
Вид фигур зависит от соотношения
между периодами (частотами),
фазами иамплитудами обоих
колебаний. В простейшем случае равенства
обоих периодов фигуры представляют
собой эллипсы, которые при разности фаз
0 или ![]() вырождаются
вырождаются
в отрезки прямых, а при разности фаз ![]() и
и
равенстве амплитуд превращаются в
окружность. Если периоды обоих колебаний
неточно совпадают, то разность фаз всё
время меняется, вследствие чего эллипс
всё время деформируется. При существенно
различных периодах фигуры Лиссажу не
наблюдаются. Однако, если периоды
относятся как целые числа, то через
промежуток времени, равный наименьшему
кратному обоих периодов, движущаяся
точка снова возвращается в то же положение
— получаются фигуры Лиссажу более
сложной формы. Фигуры Лиссажу вписываются
в прямоугольник, центр которого совпадает
с началом координат,
а стороны параллельны осям координат
и расположены по обе стороны от них на
расстояниях, равных амплитудам колебаний.
Математическое
выражение для кривой Лиссажу
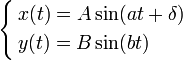
где A, B —
амплитуды колебаний, a, b —
частоты, δ —
сдвиг фаз
Вид
кривой сильно зависит от соотношения a/b.
Когда соотношение равно 1, фигура Лиссажу
имеет вид эллипса, при определённых
условиях она имеет
вид окружности (A = B, δ = π/2 радиан)
и отрезка прямой (δ =
0). Ещё один пример фигуры
Лиссажу — парабола (a/b =
2, δ =
π/2). При других соотношениях фигуры
Лиссажу представляют собой более сложные
фигуры, которые являются замкнутыми
при условии a/b — рациональное
число.
Фигуры
Лиссажу, где a = 1, b = N (N — натуральное
число)
и
![]()
являются полиномами
Чебышева первого
рода степени N.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Формирование изображения на экране осциллографа
Рассмотрим теперь взаимодействие узлов осциллографа при подаче на его вход исследуемого напряжения U . Пусть исследуемое переменное напряжение UY (например, напряжение осветительной сети с частотой 50 Гц) подается на вход Y к вертикально отклоняющим пластинам трубки. Оно может быть подведено к этим пластинам непосредственно или через усилитель вертикального отклонения луча. Усилителями пользуются в тех случаях, когда исследуемое напряжение мало и оно не обеспечивает необходимого отклонения луча (светящегося пятна) на экране трубки. При достаточной величине исследуемого напряжения его подводят непосредственно к отклоняющим пластинам. Если при этом к горизонтально отклоняющим пластинам (X – пластинам) напряжение не подведено, то световое пятно за один период колебания 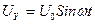 от центра экрана отклонится сначала вверх на величину, соответствующую амплитуде U0, а затем пятно начнет двигаться обратно, пройдя через центр экрана, дойдет до нижней точки и снова возвратится к центру. Поскольку частота колебаний рассматриваемого напряжения равна 50 Гц, то за одну секунду световое пятно совершит 50 полных движений и благодаря инерции светового восприятия изобразится на экране в виде сплошной вертикальной линии (рис. 36.2, а).
от центра экрана отклонится сначала вверх на величину, соответствующую амплитуде U0, а затем пятно начнет двигаться обратно, пройдя через центр экрана, дойдет до нижней точки и снова возвратится к центру. Поскольку частота колебаний рассматриваемого напряжения равна 50 Гц, то за одну секунду световое пятно совершит 50 полных движений и благодаря инерции светового восприятия изобразится на экране в виде сплошной вертикальной линии (рис. 36.2, а).
Длина этой линии в определенном масштабе, зависящем от чувствительности трубки, равна удвоенной амплитуде приложенного переменного напряжения. Очевидно, что аналогичная ситуация будет иметь место, если переменное напряжение подвести только к горизонтально отклоняющим пластинам X , при этом будет наблюдаться горизонтальная линия (рис. 36.2, б). Если одновременно к пластинам Yи X подвести два переменных напряжения одной и той же амплитуды, частоты и фазы, то перемещение луча будет вызвано одновременным воздействием двух сил, направленных в двух взаимно
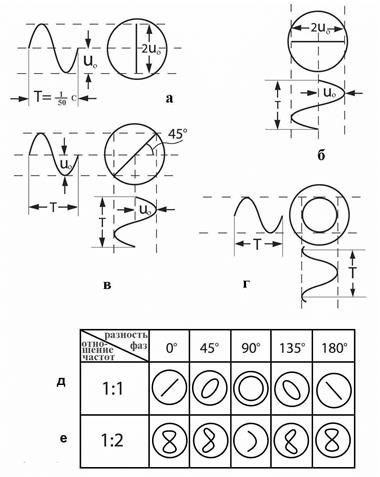 Рис. 36.2
Рис. 36.2
перпендикулярных направлениях. Таким образом, в каждый момент времени луч находится в точке экрана, соответствующей векторной сумме двух напряжений UX и UY . В итоге, как это видно из рис. 36.2, в, световое пятно будет двигаться по прямой линии под углом 45 0 к осям X и Y.Угол наклона зависит от соотношения амплитуд UX и UY . Если же при равных амплитудах и частотах изменять фазовый сдвиг φ между UX и UY , то на экране сформируется эллипс, вырождающийся в прямую линию при φ = 0, π, а при φ= π/2 – в окружность (рис. 36.2,г,д). При неравных но кратных между собой частотах напряжений UX и UY на экране луч описывает более сложные фигуры – так называемые фигуры Лиссажу. Например, при соотношении частот 1:2 и различных фазовых соотношения наблюдается ряд фигур, изображенных на рис. 36.2, е. Фигура Лиссажу неподвижна лишь при строго кратных соотношениях частот FX и FY , в противном случае фигура начинает совершать периодическое движение с частотой, равной разности частот /FX – FY/ = ΔF . Например, при ΔF =0,1 Гц, полный период движения фигуры составляет 10 с, что легко может быть определено визуально и даже измерено секундомером. Таким образом, с помощью фигур Лиссажу, имея в своем распоряжении источник образцовой (эталонной) частоты, можно с высокой степенью точности измерять неизвестные частоты и оценивать их стабильность.
Рассмотрим теперь, каким образом на экране осциллографа можно наблюдать саму форму кривой изменения исследуемого напряжения, т.е. получить на экране график зависимости исследуемой периодической функции от времени. При этом очевидно, что ось ординат получается непосредственно, если используемое напряжение UY приложить к вертикально отклоняющим пластинам Y.
Для обеспеченияже временного масштаба, т.е. развертки по оси X, необходимо отдельно сформировать такое напряжение, которое бы вызвало движение луча по экрану в горизонтальном направлении с постоянной скоростью. Такое движение может быть обеспечено линейно-растущим напряжением (рис. 36.3,а, участок ОА). При этом луч равномерно движется по экрану от его левого края (исходное напряжение в точке О меньше нулевого уровня, соответствующего положению луча в центре экрана) до правого (напряжение в точке А), после чего должен быть возвращен по возможности быстро в исходное положение, т.е. напряжение должно быть скачком уменьшено до исходного уровня U0 (участок АО ‘ , рис. 36.3, а). Участок ОА называется прямым ходом развертки, а скачкообразное уменьшение – участок АО ‘ – обратным ходом развертки, так как луч возвращается в исходное состояние. Будем полагать, что начало прямого хода развертки совпадает с нулевой точкой нашего исследуемого синусоидального напряжения (рис. 36.3, б).
Тогда при удачном выборе длительности прямого хода развертки к моменту окончания ее обратного хода луч может попасть точно в ту же точку 0, с которой началось его первое движение при прямом ходе развертки. В этом случае при периодическом повторении развертки луч проходит все время по своему следу, тем самым формируя на экране неподвижное изображение одного периода синусоиды (рис. 36.3, в). Правда, небольшой ее отрезок в конце (участок АО ‘ , рис. 36.3, в) попадает на обратный ход развертки, что несколько нарушает полную картину – на экране прочерчивается линия АО, соответствующая обратному ходу развертки. Однако в схеме осциллографа обычно предусмотрено устройство, вырабатывающее на время обратного хода отрицательное напряжение (импульсы отрицательной полярности на рис. 36.3, г), запирающие электронно-лучевую трубку, так что в эти моменты времени электронный луч отсутствует, и линия обратного хода не высвечивается.
Следовательно, период развертывающего напряжения (UР) должен быть выбран таким, чтобы за это время уложился целый период или несколько периодов N исследуемого напряжения UY , т.е. частота UY должна быть кратна частоте напряжения развертки. Если N не целое число, то каждому началу развертки соответствует другая фаза исследуемого напряжения и, следовательно, изображение перемещается в ту или другую сторону по экрану. Это перемещение будет тем медленнее, чем ближе N к целому числу. При N
Дата добавления: 2016-04-19 ; просмотров: 1632 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Фигуры Лиссажу
Что такое фигуры Лиссажу?
Фигуры Лиссажу представляют из себя различные геометрически-красивые рисунки, которые вычерчиваются точкой, колеблющейся в двух взаимно-перпендикулярных направлениях на одной плоскости.

Чтобы было более понятно, давайте представим девочку на качели из покрышки:

И вот представьте, что сзади ее раскачивает папа, а сбоку — мама. То есть наша девочка будет одновременно летать вперед-назад, а также влево-вправо. Долго ли она продержится — это уже другой вопрос). Если в солнечный денек посмотреть на землю, то мы увидим, что тень девочки вырисовывает различную траекторию полета.
Почему бы нам не поиграться пучком электронов, отклоняя его одновременно и по вертикали и по горизонтали? Вспоминаем, как выглядит электронно-лучевая трубка осциллографа:

1 — это горизонтальные пластины
2 — вертикальные пластины
ну и остальные детали — это составляющие электронной пушки.
Подаем на вертикальные пластины один синусоидальный сигнал, а на горизонтальные — другой синусоидальный сигнал. В результате точка на осциллографе будет вырисовывать различные линии и кривые, в зависимости от частоты сигналов. Хотя, цифровой осциллограф и аналоговый почти не похожи по внутренней начинке, но принцип действия у них все равно схож.
Как получить фигуры Лиссажу
Итак, для того, чтобы вырисовывать фигуры Лиссажу, нам потребуются два генератора частоты.

и осциллограф с функцией XY-режима. В моем случае это цифровой осциллограф OWON

Думаю, почти во всех современных осциллографах есть режим XY, будь это аналоговый или цифровой осциллограф.
Режим XY-осциллографа
Как вы помните, при простом использовании осциллографа у нас по оси X было время, а по оси Y — напряжение. Поэтому, по умолчанию, мы на осциллографе смотрим изменение напряжения во времени. Но если с помощью нехитрой кнопки переключить в режим XY, то у нас по Y будет напряжение и по X…. тоже напряжение, но уже с другого генератора частоты. Если включить в таком режиме только один генератор, то мы увидим только одну прямую линию либо по вертикали, либо по горизонтали. Это аналогично тому, если бы нашу девочку раскачивал только папа или только мама. Наша девочка летела бы только по одной прямой траектории.

А что будет, если сбоку нашу девочку будет раскачивать мама, а сзади — папа? Тут уже траектория девочки будет хаотичной. Но во всяком хаосе рождается порядок. И первым его заметил французский математик Жюль Антуан Лиссажу.
Строим фигуры Лиссажу на осциллографе
Цепляем на один канал один генератор частоты, а на другой канал — другой генератор частоты:

На осциллографе мы должны увидеть два сигнала с разных генераторов частоты, благо у меня осциллограф двухканальный:

Теперь переводим осциллограф в режим XY. На моем осциллографе это делается с помощью кнопки Display

Ну а потом с помощью дисплейных клавиш выбираем режим XY

И получается примерно вот такая хаотическая картинка:

Ну еще бы, один генератор дергает точку по X, другой по Y и у каждого генератора разная частота.
А давайте возьмем один генератор и с него подадим сигнал на два канала сразу. Частота и фаза совпадают и на первом и втором канале, так как мы берем сигнал с одного и то же генератора. В результате у нас будет вот такая картинка:

Если взять 100 Герц на первом генераторе и на втором генераторе, то получим что-то типа этого:



В реальности же получается круг, который все время крутится и превращается то в эллипс, то в прямую, так как очень ровно подобрать частоту на первом и втором генераторе очень сложно. Хотя на практике можно подавать сигнал на один канал напрямую, а на другой — через фазовращатель.
Если увеличить частоту на одном из генераторов вдвое, то можно наблюдать уже другие фигуры:



Эта фигура тоже все время крутится на осциллографе.
Увеличиваем на одном генераторе частоту в кратное число раз, то есть было 100, потом 200, 300 и тд и получаем абсолютно новые 3D фигуры 😉
Различное отношение частот одного генератора к другому дает различные фигуры Лиссажу:

Вот такие фигуры вы будете видеть на экране своего осциллографа:

А вот такие фигуры Лиссажу получаются, если использовать пилообразный сигнал с обоих генераторов сразу при разных отношениях коэффициентов




А вот такие фигуры получаются, если на одном оставить синус, а на втором поставить пилу:


В основном фигуры Лиссажу в электронике можно использовать тогда, когда надо узнать частоту неизвестного генератора через образцовый генератор, частоту которого мы знаем, а также узнать сдвиг фаз между двумя одинаковыми сигналами. Ну и второе применение — это чисто визуальный кайф при вращении этих фигур на экранчике вашего осциллографа 😉
Осциллографические развертки.
Напряжение, обеспечивающее перемещение электронного луча по горизонтали (оси времени), называется в осциллографах развертывающим напряжением, траектория, описываемая на экране ЭЛТ при отсутствии исследуемого напряжения, — разверткой, время, в течение которого описывается эта траектория, — длительностью развертки, а ее линейный размер по оси времени — длиной развертки.
Развертки, применяемые в современных аналоговых осциллографах, различаются по нескольким признакам:
• по форме развертывающего напряжения — пилообразные и синусоидальные;
- • по форме траектории на экране ЭЛТ (при одновременной подаче исследуемого и развертывающего напряжений) — линейные, круговые и спиральные;
- • по временным соотношениям — непрерывные, ждущие, ждуще- задержанные (лупа времени) и однократные.
Наиболее широко используется линейная развертка, создаваемая напряжением ?/х пилообразной формы и вырабатываемая генератором развертки. В зависимости от режима работы генератора развертки, как уже отмечалось ранее, линейная развертка может быть непрерывной или ждущей.
Непрерывная линейная развертка применяется для исследования гармонических процессов. Генератор развертки вырабатывает сигнал даже при отсутствии на его входе запускающего сигнала. К пластинам канала Y подводится исследуемое напряжение, а к пластинам канала X — напряжение, нарастающее (или убывающее) линейно, т.е. изменяющееся пропорционально времени. Рассмотрим основные параметры идеального и реального линейного развертывающего напряжения (рис. 2.13).
Рис. 2.13. Примеры линейно-нарастающего (а) и линейно-убывающего (б) идеального и реального развертывающего напряжения
Параметрами непрерывного реального развертывающего напряжения являются ?рх — время рабочего (прямого) хода луча, tox — время обратного хода луча, Тх — период повторения развертывающего напряжения.
Под действием только реального развертывающего напряжения электронный луч перемещается слева направо по экрану за время tpx
и быстро (так как ?ох « tpx) возвращается в исходное положение (справа налево). Развертывающее напряжение — периодическое, с периодом
поэтому перемещение луча на экране будет повторяться. Из-за инерционности ЭЛТ и человеческого глаза движение электронного луча незаметно, на экране будет видна светящаяся горизонтальная линия развертки.
При одновременной подаче исследуемого (на пластины канала У) и развертывающего (на пластины канала X) напряжения электронный луч будет перемещаться по экрану в соответствии с законом исследуемого сигнала. На рисунке 2.14 показано получение осциллограммы исследуемого сигнала при идеальной форме развертывающего напряжения и при Fx = Fy. Положения 0, 1, 2. осциллограммы на экране ЭЛТ в соответствующие моменты времени определяются мгновенными значениями исследуемого и развертывающего напряжения.
Рис. 2.14. Осциллограмма исследуемого сигнала при идеальной форме развертывающего напряжения
Если при Fy = Fx использовать реальное развертывающее напряжение, то осциллограмма на экране будет искажена. Обратный ход развертки tox Ф 0 приводит к получению неполного периода синусоиды, так как за время tox электронный луч возвращается в исходное положение не мгновенно. Для уменьшения искажений, вносимых tox, на время его действия, выключают электронный луч подачей запирающего импульса на вход канала Z.
При нарушении линейности развертывающего напряжения масштаб времени непостоянен, так как скорость изменения Ux (соответственно, и скорость движения электронного луча по горизонтали) все время уменьшается. В результате первый полупериод исследуемого сигнала будет непомерно растянут по сравнению с оригиналом, а последующие — сжаты, как показано на рис. 2.15.
Рис. 2.15. Осциллограмма исследуемого сигнала при реальной форме развертывающего напряжения
Для получения возможно меньших искажений осциллограммы развертывающее напряжение должно иметь высокую линейность с возможно меньшим временем tox.
Ждущая линейная развертка применяется для исследования импульсных сигналов. При этом генератор развертки запускается только с помощью сигнала запуска. На рисунке 2.16 приведено реальное ждущее линейное развертывающее напряжение, в котором к уже известным временным параметрам добавляется ?ож — время ожидания. Под действием ждущего напряжения электронный луч, проделав за время ?рх один прямой ход (слева направо) и за время ?ох — один обратный ход, остается некоторое время ?ож в состоянии ожидания (покоя). Затем процесс перемещения луча повторится. В результате на экране будет светящаяся горизонтальная линия развертки.
Рис. 2.16. Реальное ждущее линейное развертывающее напряжение
В осциллографах начало ждущей развертки несколько задержано относительно фронта исследуемого импульса UY. Поэтому для наблюдения короткого фронта исследуемый сигнал UY задерживают во времени в канале вертикального отклонения с помощью блока задержки (см. рис. 2.12).
Преимущества ждущей развертки по сравнению с непрерывной при исследовании импульсных сигналов рассмотрим на примере (рис. 2.17). Полученные осциллограммы показывают, что при использовании непрерывной линейной развертки размеры импульса по горизонтали будут занимать Уюо часть длины развертки, т.е. длительность импульса оказывается сжатой по оси времени настолько, что его вершина превращается в светящуюся точку, а сам импульс — в вертикальную линию. При таком масштабе невозможно наблюдать форму сигнала и измерить его временные параметры (длительность импульса — ?и, время установления переднего фронта — ?ф, время установления заднего среза — ?ср).
При использовании ждущей развертки того же периода следования и амплитуды, но с ?рх + ?ох = 2 мкс длительность исследуемого импульса становится сопоставимой с ?жр. В результате размеры исследуемого импульса займут по горизонтали половину всей длины линии развертки, т.е. произойдет увеличение длительности импульса примерно в 50 раз (без учета времени обратного хода).
Ждущая развертка должна отвечать некоторым требованиям:
Рис. 2.17. Осциллограммы исследуемого импульсного сигнала при использовании непрерывной (а) и ждущей (б) разверток
- • для получения минимальных искажений исследуемого сигнала развертка должна быть линейной (неэкспоненциальной), как и непрерывная пилообразная, с возможно меньшим обратным ходом;
- • для получения неподвижной осциллограммы при использовании ждущей и непрерывной линейной развертки необходимо применять синхронизацию.
- • для получения исследуемого сигнала в крупном масштабе по горизонтали необходимо выбрать положение органа управления, задающего масштаб, — переключателя «Длительность» («Время/дел.»). Например, необходимо исследовать и измерить импульсный сигнал прямоугольной формы длительностью ?и = 5 мкс осциллографом, у которого переключатель «Время/дел.» имеет положения 0,1 —0,2— 0,5—1—2—5—10—20—50 ps -0,1-0,2-0,5-1-2-5-10-20-50 ms. На рисунке 2.18 представлены осциллограммы импульсного сигнала с ?и = 5 мкс при разных положениях переключателя для четырех значений калиброванной развертки: 0,5—1—5 мкс—50 ps.
Анализ этих осциллограмм показывает, что из всех положений переключателя «Время/дел.» оптимальным является положение «1 ps», поскольку при этом положении хорошо видна форма сигнала и длительность импульса можно измерить с наименьшей погрешностью.
Синхронизация развертки — это принудительная «подгонка» частоты развертки к кратности частоты сигнала.
Рис. 2.18. Осциллограммы импульсного сигнала с ?и = 5 мкс при разных положениях переключателя
Наблюдать исследуемый сигнал на экране осциллографа и измерить его параметры можно только при неподвижной осциллограмме, что обеспечивается при условии равенства или кратности частот (периодов) развертывающего и исследуемого сигналов, т.е. при
где п — коэффициент частоты (периодов) сигнала: п = 1, 2,3.
Для выполнения этого условия и необходима синхронизация.
Внутренняя синхронизация осуществляется от внутреннего источника осциллографа. В качестве источника внешней синхронизации используется напряжение внешнего генератора. Синхронизация осуществляется короткими импульсами, вырабатываемыми блоком синхронизации, запускающими генератор развертки (см. рис. 2.12) и управляющими его работой. Эти импульсы можно синхронизировать не только с UY, но и со специальным внешним сигналом, поступающим на блок синхронизации при установке переключателя вида синхронизации в положение «Внеш.».
Например, в качестве исследуемого сигнала взята синусоида UY и рассмотрены три варианта соотношения периодов развертывающего напряжения Ux (рис. 2.19). Изображение синусоидального сигнала будет неподвижным при кратности п = 1, Fx = Fy (см. рис. 2.19, а). При отсутствии кратности оно скользит влево (см. рис. 2.19, б) либо вправо (см. рис. 2.19, в) — в зависимости от соотношения частот Fx и FY.
На практике при внутренней синхронизации неподвижность обеспечивается регулировкой «Стаб.», выведенной на лицевую панель прибора. Лучшие результаты по обеспечению постоянства кратности частоты сигнала дает синхронизация частоты генератора развертки частотой исследуемого напряжения или другой стабильной частотой, кратной частоте Fy.
Круговая развертка применяется при измерении частоты и фазовых сдвигов после подачи на пластины канала X синусоидального
Рис. 2.20. Схема формирования круговой синусоидальной развертки
Рис. 2.19. Графики, поясняющие движение изображения синусоидального сигнала: а — неподвижное; б — скользит в лево; в — скользит в право
напряжения. Круговая развертка формируется с помощью внешнего генератора синусоидального напряжения и вспомогательной фазосдвигающей RC-цепи (рис. 2.20) при отключенном внутреннем генераторе линейной развертки.
При прохождении синусоидального тока через последовательное соединение резистора и конденсатора падения напряжений на них оказываются сдвинутыми по фазе на 90°. При равенстве сопротивлений плеч RC-цепи
напряжения будут равные по амплитуде.
Рассмотрим пример подачи синусоиды на пластины канала Y и косинусоиды на пластины канала X. Синусоида и косинусоида имеют одинаковую частоту и сдвинуты по фазе на 90° (рис. 2.21).
Рис. 2.21. Осциллограммы круга при использовании синусоидальной круговой развертки
На рисунке 2.22 приведены осциллограммы для разных соотношений частот и фазовых сдвигов синусоидальных напряжений. Представленные осциллограммы получили название фигур Лиссажу по имени французского физика Жюля Антуана Лиссажу.
В основу осциллографических методов измерения частоты положен принцип сравнения частоты сигнала с известной высокостабильной частотой образцового развертывающего напряжения. Различают два метода: метод фигур Лиссажу и метод яркостной модуляции. Погрешность обоих методов измерения частоты зависит от стабильности частоты образцового генератора.
При измерении частоты методом фигур Лиссажу напряжение измеряемой (неизвестной) частоты Fx и образцовой частоты Fq при выключенной внутренней развертке подается на пластины каналов Y и X соответственно. Изменением образцовой частоты добиваются получения на экране неподвижной фигуры Лиссажу той или иной сложности.
Для определения Fx проводят горизонтальную и вертикальную касательные к фигуре и подсчитывают число касаний фигуры с горизонталью (пг = 2) и вертикалью (пв =1), как показано на рис. 2.23. Соотношение частот двух гармонических колебаний определяется как отношение количества точек касания с вертикалью к количеству точек касания с горизонталью. Для примера, приведенного на рисунке, при F0 = 50 Гц
Рис. 2.22. Фигуры Лиссажу при разных соотношениях частот и фазовых сдвигов
Метод фигур Лиссажу применяется для сравнительно малых соотношений частот Fx и Fq (не более 5—6): при большем соотношении частот усложняется подсчет количества точек касания. Точность этого метода измерения частоты оказывается высокой и определяется стабильностью частоты образцового генератора.
Рис. 2.23. Определение соотношения частот методом фигур Лиссажу
Для больших соотношений частот удобнее пользоваться методом яркостной модуляции (методом пунктирного круга) круговой развертки.
При измерении частоты методом яркостной модуляции источник напряжения с искомой частотой Fx используется для формирования на экране ЭЛТ осциллографа круговой развертки (с помощью RC-цепи), а напряжение генератора образцовой частоты подается на третий электрический вход осциллографа — модулятор (вход Z), показанный на рис. 2.24, а. Результирующее напряжение на модуляторе в этом случае будет изменяться с частотой F0, модулируя яркость изображения на экране с той же частотой. Если частоты Fx и F0 равны или кратны, то на экране появится неподвижное пунктирное изображение круга (рис. 2.24, б). При известных образцовой частоте F0 и количестве п подсвеченных дуг, можно записать
откуда
Рис. 2.24. Определение соотношения частот методом яркостной модуляции
Если поменять местами источники частот сигналов Fx и F0, то искомая частота определяется по формуле
Этот метод применим для соотношения частот 15—25. При большем соотношении безошибочный подсчет числа подсвеченных дуг по контуру круга затруднен.
Двухлучевые, двухканальные, скоростные, стробоскопические, запоминающие и цифровые осциллографы. Двухлучевые осциллографы позволяют одновременно наблюдать за двумя сигналами, характеризующими исследуемый объект, благодаря получению дополнительной информации. Эту задачу можно выполнить также и однолучевым осциллографом с внешним электронным коммутатором.
Основными узлами, отличающими двухлучевой осциллограф от однолучевого, является особая ЭЛТ, внутри которой помещены две отдельные электронно-оптические системы и две отдельные системы отклоняющих пластин, т.е. двухлучевая трубка представляет собой две однолучевые трубки, работающие на общий экран. Соответственно, в двухлучевом осциллографе имеются два канала вертикального отклонения и один общий генератор развертки. Калибратор амплитуды и длительности чаще всего также общие для двух лучей.
Для получения неподвижной осциллограммы (синхронизации) необходимо обеспечить кратность исследуемых сигналов:
Двухлучевой осциллограф отличается от однолучевого внешними признаками: он имеет два входа канала Y и по две регулировки «Яркость», «Фокус», «Астигматизм», «Перемещение по вертикали X».
Двухканальные осциллографы позволяют получить на экране изображение двух исследуемых сигналов с помощью электронного коммутатора, который периодически включает разные входы осциллографа. В таком осциллографе имеется также два одинаковых канала вертикального отклонения и однолучевая ЭЛТ. В зависимости от режима работы коммутатора реализуется один из режимов работы осциллографа: одноканальный (когда на экране виден один сигнал, подаваемый на один из входов — Y1 или Y2) или поочередный (когда на экране видны оба сигнала за счет переключения коммутатора во время каждого обратного хода развертки). По такому же принципу, как двухканальные осциллографы, строятся многоканальные осциллографы (с количеством каналов до восьми).
Двухканальный осциллограф отличается от двухлучевого таким внешним признаком, как наличие по одной регулировки: «Яркость», «Фокус», «Астигматизм».
Двухканальные осциллографы намного проще схематически и дешевле двухлучевых.
Скоростные осциллографы имеют ряд преимуществ по сравнению с универсальными, полоса пропускания которых — не более 50 МГц, при исследовании импульсных сигналов длительностью до сотых долей микросекунды. В электронике широко используе- ются импульсы наносекундного (10 -9 с) и даже пикосекундного (10 -12 с) диапазонов. Спектр частот таких сигналов простирается до десятков гигагерц и выше. Такие сигналы (сверхвысокочастотные) имеют малую амплитуду (порядка единиц-десятков милливольт) и при их исследовании возникают сложности, не позволяющие применять универсальные осциллографы для исследования СВЧ-сигналов. Эти сложности вызваны следующими факторами:
- • индуктивность подводящих проводов и паразитный резонанс. Частота резонанса должна быть намного больше высшей гармоники исследуемого сигнала;
- • влияние емкости пластин ЭЛТ на крутизну фронта исследуемого сигнала;
- • влияние конечного времени пролета электронов между пластинами ЭЛТ (примерно 1. 10 нс). Если за это время сигнал изменится, то отклонение электронного луча станет непредсказуемым;
- • необходимость для исследования СВЧ-сигналов очень широкой полосы пропускания по входу канала Y, которая приближенно может быть рассчитана по формуле
Тогда при длительности импульса ?и = 1 нс полоса пропускания будет 2Д/= 2 ГГц;
• необходимость для наблюдения СВЧ-сигналов и импульсов наносекундного диапазона высоких скоростей движения луча по экрану. Например, для получения изображений импульса длительностью 5 нс на экране трубки шириной / = 100 мм скорость движения луча должна быть до 20 000 км/с (U =
• нечеткость изображения сигнала на экране из-за огромной скорости вычерчивания осциллограммы лучом.
Перечисленные факторы должны быть учтены при разработке скоростных осциллографов, работающих в реальном масштабе времени. В таких осциллографах вместо ЭЛТ используют специальные приборы — лампы бегущей волны. При этом невозможно получить высокую чувствительность по каналу вертикального отклонения sY = 1 мм/В. Создание высокоскоростных разверток также затруднено, так как необходимо увеличивать напряжение развертки до нескольких сотен вольт.
Отечественные скоростные осциллографы имеют верхнюю граничную частоту не более 5. 7,5 ГГц, обладают низкой чувствительностью и потому непригодны для исследования СВЧ-сигналов с малыми амплитудами.
Стробоскопические осциллографы и приставки к универсальным осциллографам дают лучшие результаты: позволяют получить эквивалентную полосу частот до нескольких гигагерц при фактической полосе пропускания усилителя КВ О в несколько мегагерц и даже килогерц.
В стробоскопическом осциллографе искусственно уменьшается скорость развертки и полоса пропускания усилителя КВО. Такие осциллографы работают по принципу использования амплитудного временного анализа исследуемого напряжения с помощью узких импульсов — стробимпульсов.
Стробимпульсы позволяют получить представление о форме исследуемого сигнала не в виде непрерывной кривой, а в виде прерывистых дискретных значений сигнала — по одному на каждый период в соответствии с моментом действия стробимпульса.
Процесс преобразования масштаба времени осциллограммы в стробоскопическом осциллографе показан на рис. 2.25.
При поступлении исследуемого сигнала Uc (длительность tw период следования Тс) и узких стробимпульсов U2 (играющих роль переносчиков информации о сигнале) на стробоскопический смеситель преобразователя происходит амплитудно-импульсная модуляция, т.е. на выходе преобразователя амплитуда стробимпульса пропорциональна определенному мгновенному значению исследуемого сигнала.
При равенстве периодов входных напряжений преобразователя его выходные импульсы имеют постоянную амплитуду. Если же эти периоды отличаются друг от друга на постоянную величину A t (шаг считывания), то амплитуда выходных импульсов преобразователя изменяется. Период повторения стробимпульсов составляет Тст = Тс + At. Длительность шага считывания выбирают из условия A t = ?и / п (где п — целое число).
Рис. 2.25. Процесс преооразования масштаоа времени осциллограммы в стробоскопическом осциллографе: а — временные диаграммы; 6 — структурная схема преобразования
В результате преобразования первый стробимпульс U2 совпадает с началом первого (1) импульса Uc; второй стробимпульс сдвинут от начала второго (2) импульса Uc на А ?; третий стробимпульс сдвинут от начала третьего (3) импульса на 2Д t и т.д.
На выходе смесителя появляются короткие импульсы Щ, совпадающие по времени со стробимпульсами U2, но имеющие амплитуду, равную амплитуде исследуемых импульсов Uc в момент поступления стробимпульсов U2. Поэтому импульсы Нз называют стробимпульсами, промодулированными по амплитуде исследуемым сигналом ?/с. При этом огибающая этих импульсов по форме соответствует исследуемому сигналу и имеет укрупненный масштаб времени.
Степень укрупнения масштаба времени наблюдаемого импульса (временное преобразование) характеризуется коэффициентом kTp трансформации масштаба времени:
где п — количество стробимпульсов, считывающих импульсы Uc.
Поскольку
Современные стробоскопические осциллографы имеют kTp, выражаемый десятками тысяч, благодаря чему можно при обычных развертках исследовать импульсы наносекундного диапазона с частотами до нескольких гигагерц и с амплитудами от нескольких милливольт.
Запоминающие осциллографы позволяют запомнить сигнал на экране. В состав таких осциллографов входят блок памяти и специальная полутоновая запоминающая ЭЛТ — потенциалоскоп (рис. 2.26).
Рис. 2.26. Устройство потенциалоскопа
Перед люминесцентным экраном 1 расположена сетчатая мишень 2, представляющая собой мелкоструктурную сетку, покрытую слоем диэлектрика. Трубка имеет два прожектора. Записывающий прожектор 7 создает сфокусированный пучок электронов и сканирует поверхность мишени. Воспроизводящий прожектор 6 создает широкий расфокусированный пучок, непрерывно облучающий всю поверхность мишени. Внутри трубки помещена коллимирующая линза 5.
Потенциал мишени подобран таким образом, чтобы при отсутствии записанного изображения медленные электроны воспроизводящего пучка не могли через нее пройти. При наличии потенциального рельефа в этих точках мишени часть электронов проходит к экрану, вызывая его свечение. На экране появляется осциллограмма, повторяющая форму потенциального рельефа мишени. Запись стирается путем подачи на коллекторную сетку 3 (зафиксированную крепежным кольцом 4) отрицательного импульса, выравнивающего потенциал мишени.
Запоминающие осциллографы имеют следующие особенности:
- • способность хранить информацию в обесточенном состоянии длительное время (от нескольких минут до нескольких суток);
- • возможность индикации при высоких уровнях внешней освещенности, так как яркость изображения на экране сохраняется даже при попадании прямых солнечных лучей;
- • возможность исследования однократных и редко повторяющихся сигналов.
Аналоговые осциллографы имеют такие недостатки, как косвенность измерений параметров сигналов, относительно большая погрешность (10. 15%) и трудоемкость измерения.
Цифровые осциллографы позволяют наблюдать сигнал на экране и получать информацию о численном значении ряда параметров сигнала с меньшей погрешностью, чем с помощью аналоговых осциллографов. Достоинства цифровых осциллографов обеспечиваются тем, что параметры сигналов измеряются непосредственно на входе осциллографа, в то время как в аналоговом осциллографе параметры сигнала измеряются только после прохождения его через канал вертикального отклонения и с большой погрешностью.
Сопряжение цифровых осциллографов с микропроцессором позволяет наряду с традиционными параметрами сигналов (амплитудой, частотой, длительностью) определять среднеквадратичное значение напряжения сигнала и даже вычислять и отображать на экране ЭЛТ преобразование Фурье для любого сигнала.
В цифровых осциллографах обеспечивается полная цифровая обработка сигнала, поэтому в них чаще используются не ЭЛТ, а индикаторные панели, отображение результата измерения на которых осуществляется несколькими способами:
- • одновременным наблюдением изображения сигнала на экране и высвечиванием на индикаторной панели численных значений параметров;
- • определением значения параметра собственно оператором, который подводит к изображению сигнала на экране световые метки так, чтобы отметить измеряемый параметр по цифре на соответствующей регулировке;
- • применением специальных кинескопов (например матричных индикаторных панелей) и формированием изображения исследуемых сигналов и цифровой информации с помощью растра (растровый метод).
В цифровых осциллографах обеспечивается автоматическая установка оптимальных размеров изображения на экране.
Структурная схема осциллографа приведена на рис. 2.27. Параметры исследуемого сигнала определяются с помощью встроенных измерителей. По результатам измерений контроллер вычисляет требуемые коэффициенты отклонения по вертикали и горизонтали и через два интерфейса задает эти коэффициенты аппаратной части КВО и КГО, что обеспечивает неизменность размеров изображения по обоим направлениям и автоматическую синхронизацию сигнала.
Рис. 2.27. Структурная схема цифрового осциллографа
Кроме того, контроллер отслеживает положение органов управления на лицевой панели, и результаты опроса после кодирования вновь поступают в контроллер, который через интерфейс включает соответствующий режим автоматического измерения. Результаты измерения отображаются на отдельном световом табло (которое может быть встроено в экран ЭЛТ) одновременно с отображением амплитудного и временных параметров сигнала.
Методика измерения параметров сигналов осциллографом. Для получения возможно меньшей погрешности измерения осциллограф должен соответствовать основным метрологическим характеристикам.
К основным метрологическим характеристикам осциллографа относятся чувствительность (либо коэффициент отклонения), полоса пропускания, значение импеданса по входу канала Y, погрешность воспроизведения формы сигнала и измерения его параметров.
Чувствительность s выражается формулой
В техническом паспорте прибора приводится чувствительность по обоим каналам: по вертикальному каналу — sy и горизонтальному каналу – sx.
В современных осциллографах наиболее широкое применение нашел коэффициент отклонения, связанный с чувствительностью обратной зависимостью:
Полоса пропускания характеризует частотный диапазон сигналов, исследуемых и наблюдаемых на конкретном осциллографе. В этом частотном диапазоне сигнал измеряется с допустимой погрешностью. Амплитудно-частотная характеристика (АЧХ) прибора приведена на рис. 2.28, где /н и /в — нижняя и верхняя граничные частоты соответственно. Узкополосные осциллографы, как правило, обладают большей чувствительностью, чем широкополосные.
Рис. 2.28. Амплитудно-частотная характеристика осциллографа
Значение импеданса по входу канала Y — это активная RBX и реактивная (емкостная) Свх составляющие входного сопротивления осциллографа. Достоинством осциллографа является большее значение входного сопротивления, что влечет за собой малое собственное потребление мощности от источника исследуемого сигнала. Значение входной емкости прямо пропорционально связано с полосой пропускания осциллографа: чем меньше входная емкость прибора, тем шире частотный диапазон.
Погрешность воспроизведения формы сигнала (искажение) и измерения его параметров обусловлена кривизной экрана, трудностью точного отсчета линейных размеров по вертикали и горизонтали, неумением оператора настроить прибор. Такая погрешность может достигать 10. 15% и является главным недостатком аналоговых осциллографов.
Рассмотрим алгоритм подготовки осциллографа к работе:
• включить тумблер «Сеть». При этом должна загореться индикаторная лампочка;
[spoiler title=”источники:”]
http://www.ruselectronic.com/figury-lissazhu/
http://bstudy.net/729126/tehnika/ostsillograficheskie_razvertki
[/spoiler]
В одной из прошлых статей описывалось как определить разность фаз двух сигналов по фигуре Лиссажу. Но у фигур Лиссажу есть ещё одно интересное свойство и заключается оно в следующем: если известна частота одного из колебаний, то по виду фигуры Лиссажу можно определить частоту другого.
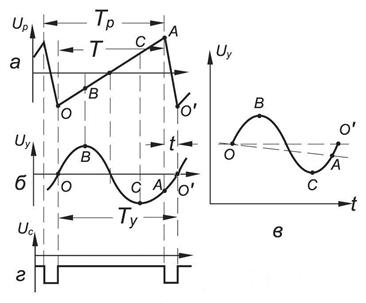
Для определения соотношения частот проведём горизонтальную и вертикальную прямые, пересекающие фигуру. При этом через точки пересечения линий самой фигуры эти прямые проходить не должны.
Тогда количество пересечений фигуры с горизонтальной прямой соответствует количеству изменений напряжения одного сигнала, а с вертикальной – количеству изменений напряжения другого сигнала. А из соотношения количества изменений сигналов можно найти соотношение частот колебаний.
А теперь тоже самое простыми словами, если синус с частотой 10KHz два раза пересекает горизонтальную прямую, а синус с неизвестной нам частотой пересекает четыре раза вертикальную прямую, то ясно что их частоты относятся как один к двум и частота неизвестного сигнала в два раза больше, то есть 20KHz. Кстати на осциллограмме выше частоты относятся как 6/4 или 3/2.
Почему мы один раз считаем пересечения с горизонтальной прямой, а второй с вертикальной?
Ответ на этот вопрос можно найти в определении фигуры Лиссажу:
Фигуры, получаемые при сложении взаимно перпендикулярных колебаний разных частот, называются фигурами Лиссажу.
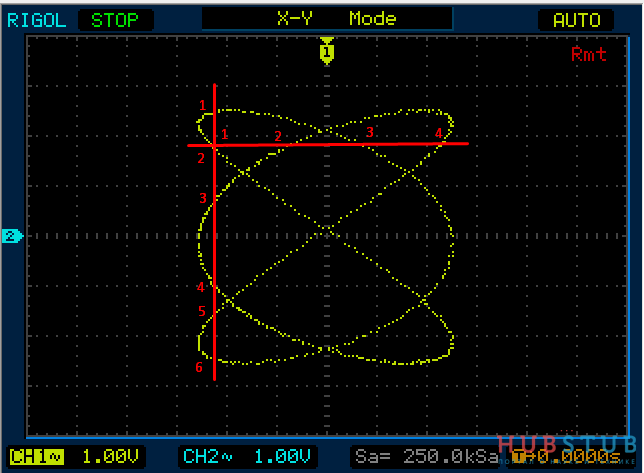
Давайте на подадим на оба входа осциллографа синус с частотой 1KHz и посмотрим как будут выглядеть фигура Лиссажу в зависимости от разности фаз между каналами.
Разность фаз равна 0 °.
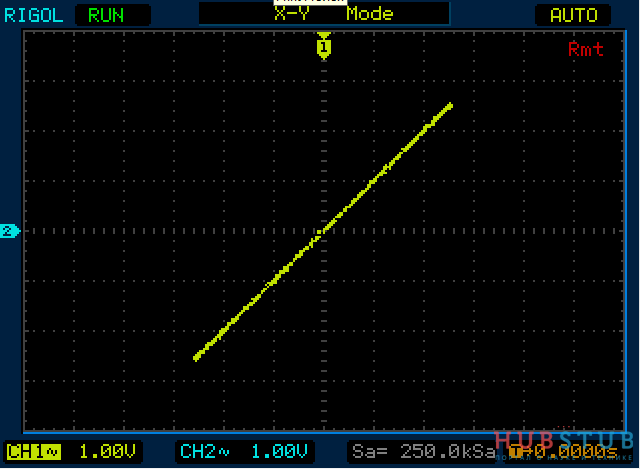
Разность фаз равна 45°.
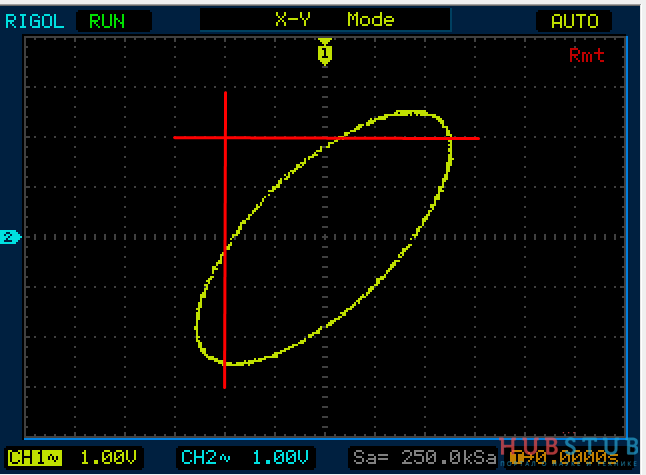
Разность фаз равна 90°.
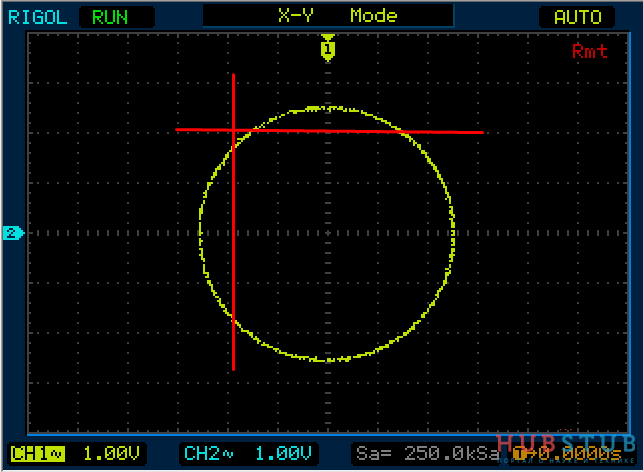
На осциллограммах видно, что количество пересечений с вертикальной и горизонтальной прямой одинаковое.
Теперь проделаем тоже самое но для частот 1KHz и 2KHz.
Разность фаз равна 0 °.
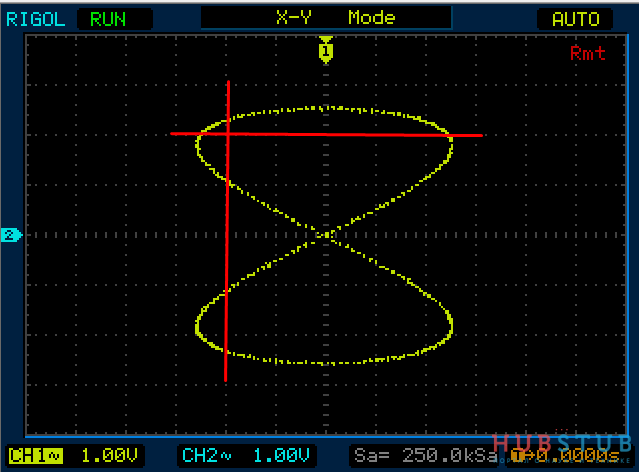
Разность фаз равна 45 °.
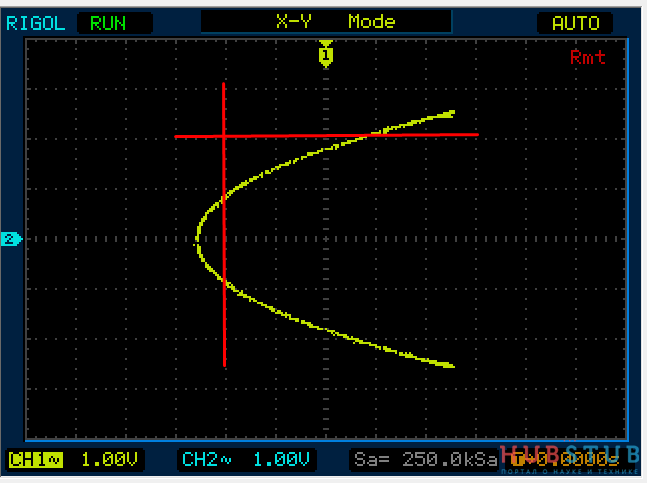
Разность фаз равна 90 °.
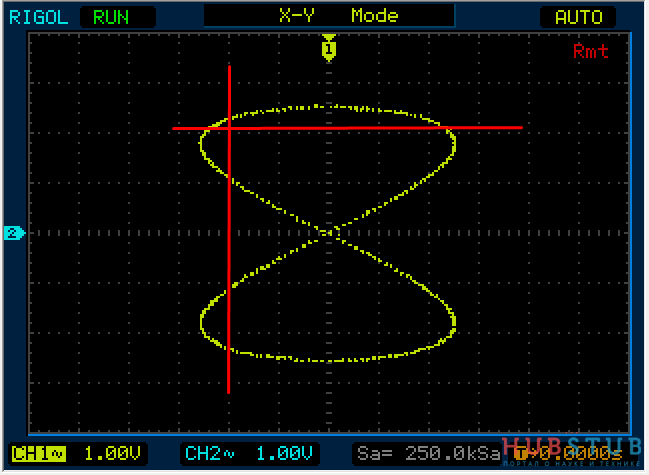
На осциллограммах видно, что количество пересечений с вертикальной прямой в два раза больше чем с горизонтальной.
Теперь на один вход подадим 1Khz, а на второй 3Khz и проделаем тоже самое.
Разность фаз равна 0 °.
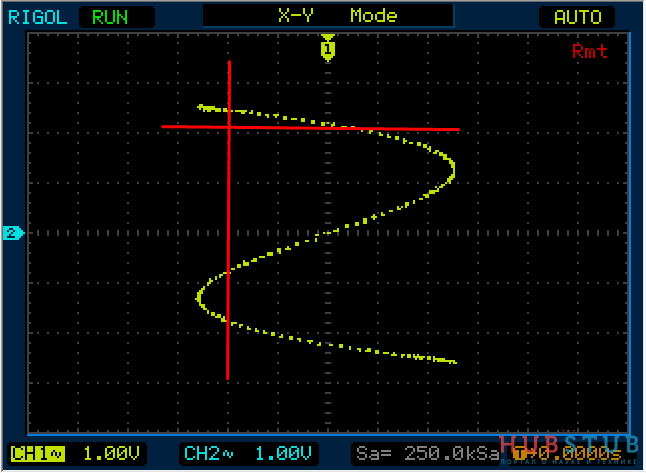
Разность фаз равна 45 °.
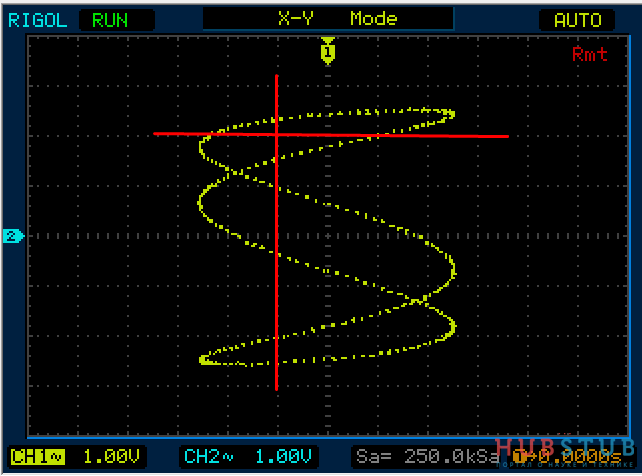
Разность фаз равна 90 °.
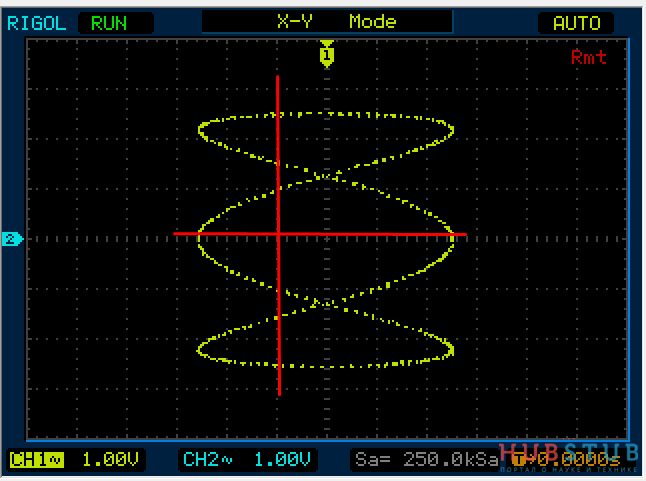
На осциллограммах видно, что количество пересечений с вертикальной прямой в три раза больше чем с горизонтальной.
Оказывается определить частоту неизвестного сигнала очень просто, если знать это замечательно свойство фигур Лиссажу.