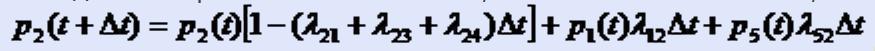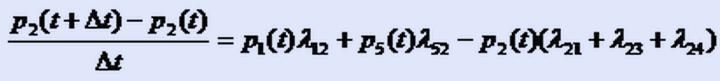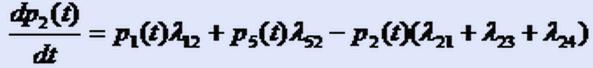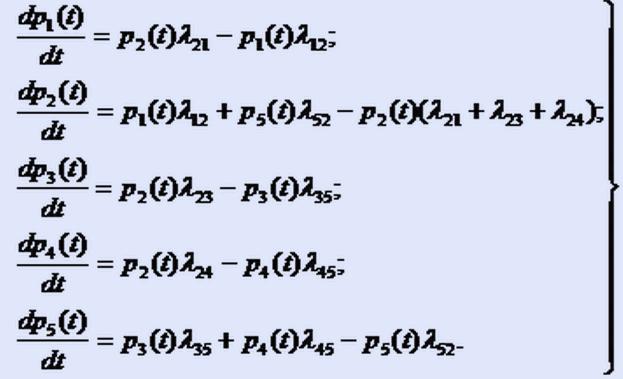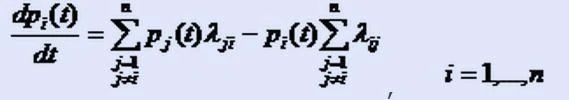Финальные вероятности
Для однородной
неразложимой цепи Маркова с конечным
числом состояний существует предел
,
j,
не зависящий от i,
который называется финальной вероятностью
j-го состояния, а их
совокупность – финальным
распределением.
Финальные вероятности
определяются из системы линейных
алгебраических уравнений
,
с учетом условия нормировки
.
Если ввести матричные
обозначения
,
,
,
то уравнения для нахождения финальных
вероятностей можно записать в виде
Если вероятности
состояний не зависят от t,
то есть Pj(t)Pj,
то Pj
называются стационарными
вероятностями, а их совокупность
стационарным
распределением.
Из прямой системы
уравнений для стационарных вероятностей
получим, что стационарное распределение
определяется системой уравнений
и условием нормировки
,
совпадающими с системой уравнений для
финальных вероятностей, следовательно,
стационарное и финальное распределения
совпадают.
Если для однородной
цепи Маркова для системы дифференциальных
уравнений в качестве начального
распределения qi(s)
выбрать финальное i,
то решение Pi(t)
этой системы совпадает с финальным
распределением, то есть для любых ts
выполняется равенство
.
В рассмотренном выше
примере 3.1 финальные вероятности можно
найти предельным переходом, устремив
t:
,
.
Время перехода из одного состояния в другое
Время перехода из
одного состояния в другое Tkj
при kj
для цепей Маркова с непрерывным временем
определяется следующими соотношениями:
для всех
. (3.5)
Если i=j,
то естественно Tjj=0,
поэтому рассматривается Tjj(t) –
длина интервала от текущего момента
времени t, до следующего
попадания в это состояния. Тогда
Tjj=MTjj(t)(t)=j
определяется из уравнения
. (3.6)
Пример 3.3.
Для
примера 3.1
найдите
среднее время перехода из одного
состояния в другое.
Решение: Для ij
получаем систему уравнений
откуда имеем
А для i=j
Статистический смысл финальных (стационарных) вероятностей
Уравнение (3.6) домножим
на j,
а уравнения системы (3.5) на i
для всех ij
и просуммируем полученные равенства,
запишем
.
Полученное равенство, в силу
,
перепишем в виде
.
Следовательно,
.
Здесь величина –1/qjj>0,
а величина Tjj
– среднее значение длины интервала от
текущего момента времени, когда цепь
Маркова находится в состоянии j
до момента следующего её попадания в
это состояние после выхода из него,
следовательно Tjj
равна сумме среднего значения остаточного
времени пребывания цепи Маркова в j-ом
состоянии и среднего значения Tj
– длины интервала от момента выхода
цепи Маркова из этого состояния до
момента возвращения в это состояние.
Время пребывания цепи Маркова в j-ом состоянии
Пусть величина j
– остаточное время пребывания цепи
Маркова в j-ом состоянии.
Обозначим её закон распределения
Bj(x)=Pjx,
тогда, используя марковское свойство
цепи, можно записать равенство
,
выполнив в котором несложные преобразования,
получим уравнение
,
определяющее вид функции Bj(x).
Из полученного
дифференциального уравнения следует,
что
,
следовательно, величина j
имеет экспоненциальное распределение
с параметром – qjj.
В силу свойства отсутствия последействия
экспоненциального распределения, полное
(не остаточное) время пребывания цепи
Маркова в j-ом состоянии
также имеет экспоненциальное распределение
с тем же параметром – qjj.
Среднее значение этого времени составляет
–1/qjj.
Таким образом, равенство
для финальных вероятностей можно
переписать в виде
,
следовательно, финальная (стационарная)
вероятность j
равна отношению среднего значения
времени пребывания цепи Маркова в j-ом
состоянии к сумме этого значения и
среднего значения Tj
– времени возвращения в это состояние,
то есть вероятность
j
имеет смысл доли времени проведённого
цепью в состоянии j.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнения Колмогорова. Предельные вероятности состояний
Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем на примере случайного процесса из задачи 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния Si в Sj происходят под воздействием простейших потоков событий с интенсивностями lij(i, j=0,1,2,3); так, переход системы из состояния S0 в S1 будет происходить под воздействием потока отказов первого узла,
а обратный переход из состояния S1 в S0 — под воздействием потока «окончаний ремонтов» первого узла и т.п.
Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система S имеет четыре возможных состояния: S0, S1, S2, S3.
Вероятностью i-го состояния называется вероятность pi(t) того, что в момент t система будет находиться в состоянии Si. Очевидно, что для любого момента t сумма вероятностей всех состояний равна единице:
. (8)
Рассмотрим систему в момент t и, задав малый промежуток Dt, найдем вероятность p0(t+Dt) того, что система в момент t+ Dt будет находиться в состоянии S0. Это достигается разными способами.
1. Система в момент t с вероятностью p0(t) находилась в состоянии S0, а за время Dt не вышла из него.
Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью (l01+l02), т.е. в соответствии с (15.7), с вероятностью, приближенно равной (l01+l02)Dt. А вероятность того, что система не выйдет из состояния S0, равна [1-(l01+l02)Dt]. Вероятность того, что система будет находиться в состоянии S0, по первому способу (т.е. того, что находилась в состоянии S0 и не выйдет из него за время Dt), равна по теореме умножения вероятностей:
p0(t)·[1-(λ01+λ02)*Δt].
2. Система в момент t с вероятностями р1(t) (или p2(t)) находилась в состоянии S1 или S2 и за время Dt перешла в состояние S0.
Потоком интенсивностью l10 (или l 20 — см. рис. 1) система перейдет в состояние S0 с вероятностью, приближенно равной l10Dt (или l20Dt). Вероятность того, что система будет находиться в состоянии S0 по этому способу, равна р1(t)×l10Dt (или р2(t)×l20Dt).
Применяя теорему сложения вероятностей, получим
p0(t+Δt)=p1·λ10·Δt+p2(t)·λ20·Δt+p0(t)[1-(λ01+λ02)·Δt],
откуда
Переходя к пределу при Dt→0 (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную p’0(t) (обозначим ее для простоты p’0):
p′0 = λ10·p1+λ20·p2+(λ10+λ20)·p0,
Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.
Рассуждая аналогично для других состояний системы S, можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:

Сформулируем правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).
В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).
Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном, случае вероятности состояний системы в начальный момент t = 0. Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии S0, т.е. при начальных условиях p0(0)=1, p1(0)=p2(0)=p3(0)=0.
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности системы pi(t) в предельном стационарном режиме, т.е. при t→∞, которые называются предельными (или финальными) вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.
Предельная вероятность состояния Si имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии. Например, если предельная вероятность состояния S0, т.е. p0=0,5, то это означает, что в среднем половину времени система находится в состоянии S0.
Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы S с графом состояний, изображенном на рис. 1, такая система уравнений имеет вид:

Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом, согласно которому слева в уравнениях стоит предельная вероятность данного состояния pi, умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
Задача 2. Найти предельные вероятности для системы S задачи 1, граф состояний которой приведен на рис. 1, при l01=1, l02=2, l10=2, l13=2, l20=3, l23=1, l31=3, l32=2.
Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или
3p0=2p1+3p2 (11)
4p1=p0+3p3
4p2=2p0+2p3
p0+p1+p2+p3=1
(Здесь мы вместо одного “лишнего” уравнения системы (10) записали нормировочное условие (8)).
Решив систему (11), получим p0=0,40, p1=0,20, p2=0,27, p3=0,13, т.е. в предельном, стационарном режиме система S в среднем 40% времени будет находиться в состоянии S0 (оба узла исправны), 20% — в состоянии S1 (первый узел ремонтируется, второй работает), 27% — в состоянии S2 (второй узел ремонтируется, первый работает) и 13% времени — в состоянии S3 (оба узла ремонтируются).
Задача 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы S в условиях задач 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность СМО имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).
Решение. Из задачи 2 следует, что в среднем первый узел исправно работает долю времени, равную p0+p3=0,40+0,27=0,67, а второй узел — p0+p1=0,40+0,20=0,60. В то же время первый узел находится в ремонте в среднем долю времени, равную p1+p3=0,20+0,13=0,33, а второй узел – p2+p3=0,27+0,13=0,40. Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен
Д=0,67 ×10+0,60×6-0,33 ×4-0,40×2=8,18 ден.ед.
Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока “окончаний ремонтов” каждого узла, т.е. теперь l10=4, l 20=6, l31 =6, l32=4 и система линейных алгебраических уравнений (10), описывающая стационарный режим системы вместе с нормировочным условием (8) примет вид:
3p0=4p1+6p2
6p1=p0+6p3
7p2=2p0+4p3
p0+p1+p2+p3=1
Решив систему, получим p0=0,60, p1=0,15, p2=0,20, p3=0,05.
Учитывая, что p0+p2=0,60+0,20=0,80, p0+p1=0,60+0,15=0,75, p1+p3=0,15+0,05=0,20,
p2+p3=0,20+0,05=0,25, а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден. ед., вычислим средний чистый доход в единицу времени:Д1=0,80 ×10+0,75×6-0,20 ×8-0,25×4=9,9 ден.ед.
Так как Д1 больше Д (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.
Пример. Техническое устройство может находиться в одном из трех состояний S0, S1, S2. Интенсивность потоков, переводящих устройство из состояния, заданы в таблице.
| Задача | Интенсивности потоков | |||||
| λ01 | λ02 | λ10 | λ12 | λ20 | λ21 | |
| 78 | 2 | 2 | 1 | 2 | 3 | 0 |
Необходимо построить размеченный граф состояний, записать систему уравнений Колмогорова, найти финальные вероятности и сделать анализ полученных решений.
Размеченный граф состояний имеет вид.
По графу запишем систему уравнений Колмогорова в общем виде:
p0(t) + p1(t) + p2(t) = 1
Вместо интенсивности потоков λij запишем их конкретные значения и получим искомую систему:
p0(t) + p1(t) + p2(t) = 1
Чтобы найти финальные вероятности состояний, в уравнениях Колмогорова отбросим первое уравнения, а по остальным составим систему алгебраических уравнений:
2p0-3p1 = 0
2p0+2p1-3p2=0
p0 + p1 + p2 = 1
Решим СЛАУ с помощью метода Гаусса.
Вывод: При достаточно большом времени работы техническое устройство с вероятностью p0 = 0.36 будет находиться в состоянии S0, с вероятностью p1 = 0.24 в состоянии S1 и с вероятностью p2 = 0.4 в состоянии S2.
Пример.
Техническое устройство может находиться в одном из трех состояний S0, S1, S2. Интенсивность потоков, которые переводят устройства из одного состояния во второе, известны λ01=2, λ10=4, λ21=2, λ12=3, λ20=4.
Необходимо построить размеченный граф состояний, записать систему уравнений Колмогорова, найти финальные вероятности и сделать анализ полученных решений.
Размеченный граф состояний имеет вид.
По графу запишем систему уравнений Колмогорова в общем виде:
Вместо интенсивности потоков λij запишем их конкретные значения и получим искомую систему:
Чтобы найти финальные вероятности состояний, в уравнениях Колмогорова отбросим первое уравнения, а по остальным составим систему алгебраических уравнений:
2p0-7p1+2p2=0
3p1-6p2=0
p0+p1+p2=1
Делим первое уравнение на 2, а второе на 3 и получим систему
p0-7p1+2p2=0
3p1-6p2=0
p0+p1+p2=1
Из третьего уравнения вычитаем первое
p0-3.5p1+p2=0
p1-2p2=0
4.5p1=1
Отсюда получим p1=0,22, p2=0,11 и p0=0,67.
Вывод: При достаточно большом времени работы техническое устройство с вероятностью p0 = 0,67 будет находиться в состоянии S0, с вероятностью p1 = 0,22 в состоянии S1 и с вероятностью p2 = 0,11 в состоянии S2.
Процесс гибели и размножения
В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения. Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.
Рис. 4
Рассмотрим упорядоченное множество состояний системы S0, S1, S2, …, Sk. Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния Sk возможны переходы только либо в состояние Sk-1, либо в состояние Sk+1. (При анализе численности популяций считают, что состояние Sk соответствует численности популяции, равной k, и переход системы из состояния Sk в состояние Sk+1 происходит при рождении одного члена популяции, а переход в состояние Sk-1, — при гибели одного члена популяции).
Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями lk, k+1 или lk+1, k.
По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния S0
λ01p0 = λ10p1 (12)
для состояния S1 – (l12+l10)p1=l01 p0+l21p2, которое с учетом (12) приводится к виду
λ12p1 = λ21p2 (13)
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:

к которой добавляется нормировочное условие
p0+p1+p2+…+pn=1 (15)
Решая систему (14), (15), можно получить

(17)
Легко заметить, что в формулах (17) для p1, p2, …, pn коэффициенты при p0 есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния Sk (k=1, 2, …, n), а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния Sk.
Задача 4.Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.
Рис. 5
Решение. По формуле (16) найдем
по (17) – т.е. в установившемся, стационарном режиме в среднем 70,6% времени система будет находиться в состоянии S0, 17,6% — в состоянии S1 и 11,8% — в состоянии S2.
|
|
Макеты страниц
Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, нам удобно будет представлять себе, что все переходы системы 
Если система S находится в каком-то состоянии 





Для наглядности очень удобно на графе состояний у каждой стрелки проставлять интенсивность того потока событий, который переводит систему по данной стрелке. Обозначим 

На рис. 17.1 дан граф состояний с проставленными у стрелок интенсивностями (мы будем называть такой граф размеченны 
Построим размеченный граф состояний для примера, данного в § 15 (техническое устройство из двух узлов). Напомним состояния системы:




Интенсивности потоков событий, переводящих систему из состояния в состояние, будем вычислять, предполагая, что среднее время ремонта узла не зависит от того, ремонтируется ли один узел или оба сразу.

Рис. 17.1.

Рис. 17.2.
Это будет именно так, если ремонтом каждого узла занят отдельный специалист. Найдем все интенсивности потоков событий, переводящих систему из состояния в состояние. Пусть система находится в состоянии 




Имея в своем распоряжении размеченный граф состояний системы, легко построить математическую модель данного процесса.
В самом деле, пусть рассматривается система S, имеющая 





Имея в своем распоряжении размеченный граф состояний, можно найти все вероятности состояний 

Рис. 17.3.
Покажем на конкретном примере, как эти уравнения составляются. Пусть система S имеет четыре состояния: 









Найдем вероятность первого варианта. Вероятность того, что в момент t система была в состоянии 







Значит, вероятность того, что за время 




Найдем вероятность второго варианта. Она равна вероятности того, что в момент t система будет в состоянии 



Складывая вероятности обоих вариантов (по правилу сложения вероятностей), получим:

Раскроем квадратные скобки, перенесем 


Устремим, как и полагается в подобных случаях, 



или, короче, отбрасывая аргумент t у функций 

Рассуждая аналогично для всех остальных состояний, напишем еще три дифференциальных уравнения. Присоединяя к ним уравнение (17.2), получим систему дифференциальных уравнений для вероятностей состояний:

Это — система четырех линейных дифференциальных уравнений с четырьмя неизвестными функциями 



Сформулируем теперь общее правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности какого-то 

Пользуясь этим правилом, запишем уравнения Колмогорова для системы S, размеченный граф состояний которой дан на рис. 17.2:

Чтобы решить уравнения Колмогорова и найти вероятности состояний, прежде всего надо задать начальные условия. Если мы точно знаем начальное состояние системы 



Как решать подобные уравнения? Вообще говоря, линейные дифференциальные уравнения с постоянными коэффициентами можно решать аналитически, но это удобно только когда число уравнений не превосходит двух (иногда — трех).
Если уравнений больше, обычно их решают численно — вручную или на ЭВМ.
Таким образом, уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени.
Поставим теперь вопрос: что будет происходить с вероятностями состояний при 



Предположим, что это условие выполнено и финальные вероятности существуют:

Финальные вероятности мы будем обозначать теми же буквами 

Как понимать эти финальные вероятности? При 





Как же вычислить финальные вероятности? Очень просто. Если вероятности 


Пользуясь этим правилом, напишем линейные алгебраические уравнения для финальных вероятностей состояний системы, граф состояний которой дан на рис. 17.2:

Эту систему четырех уравнений с четырьмя неизвестными 

и с его помощью решить систему. При этом одно (любое) из уравнений можно отбросить (оно вытекает как следствие из остальных).
Давайте зададимся численными значениями интенсивностей 
Уравнения примут вид:

Решая их, получим:

т. е. в предельном, стационарном режиме система S в среднем 40% времени будет проводить в состоянии 








Теперь оценим загрузку ремонтных органов (рабочих), занятых ремонтом узлов 1 и 2. Узел 1 ремонтируется долю времени, равную 

Здесь уже может возникнуть вопрос об оптимизации решения. Допустим, что мы можем уменьшить среднее время ремонта того или другого узла (может быть, и того, и другого), но это нам обойдется в какую-то сумму. Спрашивается, «стоит ли овчинка выделки»? Т. е. окупит ли увеличение дохода, связанное с ускорением ремонта, повышенные расходы на ремонт?
Предоставим читателю самостоятельно поставить и решить такую экономическую задачу. При этом ему придется решать систему четырех уравнений с четырьмя неизвестными, но это ничего (характер, как известно, укрепляется в бедствиях!).
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ПРЕДМЕТ И ЗАДАЧИ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ
- § 1. Что такое исследование операций и чем оно занимается
- § 2. Основные понятия и принципы исследования операций
- § 3. Математические модели операций
- ГЛАВА 2. РАЗНОВИДНОСТИ ЗАДАЧ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ И ПОДХОДОВ К ИХ РЕШЕНИЮ
- § 4. Прямые и обратные задачи исследования операций. Детерминированные задачи
- § 5. Проблема выбора решения в условиях неопределенности
- § 6. Многокритериальные задачи исследования операций. «Системный подход»
- ГЛАВА 3. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
- § 7. Задачи линейного программирования
- § 8. Основная задача линейного программирования
- § 9. Существование решения ОЗЛП и способы его нахождения
- § 10. Транспортная задача линейного программирования
- § 11. Задачи целочисленного программирования. Понятие о нелинейном программировании
- ГЛАВА 4. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- § 12. Метод динамического программирования
- § 13. Примеры решения задач динамического программирования
- 1. Прокладка наивыгоднейшего пути между двумя пунктами.
- 2. Задача о распределении ресурсов
- 3. Задача о загрузке машины.
- § 14. Задача динамического программирования в общем виде. Принцип оптимальности
- ГЛАВА 5. МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- § 15. Понятие о марковском процессе
- § 16. Потоки событий
- § 17. Уравнения Колмогорова для вероятностей состояний. Финальные вероятности состояний
- ГЛАВА 6. ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ
- § 18. Задачи теории массового обслуживания. Классификация систем массового обслуживания
- § 19. Схема гибели и размножения. Формула Литтла
- § 20. Простейшие системы массового обслуживания и их характеристики
- 2. Одноканальная СМО с неограниченной очередью.
- 3. n-канальная СМО с неограниченной очередью.
- 4. Одноканальная СМО с ограниченной очередью.
- 5. Замкнутая СМО с одним каналом и m источниками заявок.
- § 21. Более сложные задачи теории массового обслуживания
- ГЛАВА 7. СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ (МЕТОД МОНТЕ-КАРЛО)
- § 22. Идея, назначение и область применимости метода
- § 23. Единичный жребий и формы его организации
- § 24. Определение характеристик стационарного случайного процесса по одной реализации
- ГЛАВА 8. ИГРОВЫЕ МЕТОДЫ ОБОСНОВАНИЯ РЕШЕНИЙ
- § 25. Предмет и задачи теории игр
- § 26. Антагонистические матричные игры
- § 27. Методы решения конечных игр
- § 28. Задачи теории статистических решений
- ЛИТЕРАТУРА
Уравнение Колмогорова для вероятностей состояний[]
Уравнения Колмогорова – уравнения для переходной функции марковского случайного процесса.
Исчерпывающей количественной характеристикой Марковского процесса является совокупность вероятностей состояний, т.е. вероятностей pi(t) того, что в момент t процесс будет находиться в состоянии si(i =1…n).
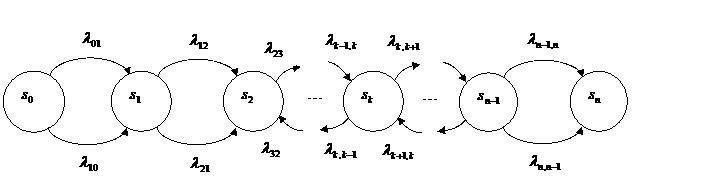
Граф состояний модели размножения и гибели
Рассмотрим, как определяются вероятности состояний по приведенному на рис. графу состояний, считая все потоки простейшими. В случайный момент времени t система может находиться в одном из состояний si с вероятностью pi(t). Придадим t малое приращение ∆t и найдем, например, p2(t+∆t) – вероятность того, что в момент t+∆t система будет в с состоянии s2. Это может произойти, во-первых, если система в момент была в состоянии s2 и за время t не вышла из него; во-вторых, если в момент t система была в состоянии s1 или s5 и за время ∆t перешла в состояние s2.
В первом случае надо вероятность p2(t) умножить на вероятность того, что за время ∆t система не перейдет в состояние s1, s3 или s4. Суммарный поток событий, выводящий систему из состояния s2, имеет интенсивность λ21+ λ23+ λ24. Значит, вероятность того, что за время ∆t система выйдет из состояния s2, равна (λ21+ λ23+ λ24)∆t. Отсюда вероятность первого варианта p2.1(t+∆t)= p2(t)[1-(λ21+ λ23+ λ24)∆t].
Найдем вероятность перехода в состояние s2. Если в момент t система находилась в состоянии s1 с вероятностью pi(t), то вероятность перехода в состояние s1 за время ∆t равна p2.2(t+∆t)= p1(t)λ12∆t.
Аналогично для состояния s5. p2.3(t+∆t)= p1(t)λ52∆t.
Складывая вероятности p2.1(t+∆t) + p2.2(t+∆t) + p2.2(t+∆t), получим.
Раскроем квадратные скобки, перенесем p2(t) в левую часть и разделим обе части на ∆t:
Если устремить ∆t к нулю, то слева получим производную функции p2(t):
Аналогичные уравнения можно вывести для всех остальных состояний. Получается система дифференциальных уравнений:
Эта система линейных дифференциальных уравнений дает возможность найти вероятности состояний, если задать начальные условия. В левой части каждого уравнения стоит производная вероятности i-го состояния, а в правой – сумма произведений вероятностей всех состояний, из которых ведут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность i-го состояния.
Представим уравнения Колмогорова в общем виде
Здесь учтено, что для состояний, не имеющих непосредственных переходов, можно считать .
http://www.life–prog.ru/view_modelirovanie.php?id =20
Финальные вероятности состояний[]
Если процесс, протекающий в системе, длится достаточно долго, то имеет смысл говорить о предельном поведении вероятностей Pi(t) при t -> infinity. В некоторых случаях существуют финальные (предельные) вероятности состояний:

не зависящие от того, в каком состоянии система находилась в начальный момент. Говорят, что в системе устанавливается предельный стационарный режим, при котором она переходит из состояния в состояние, но вероятности состояний Pi уже не меняются во времени. Система, для которой существуют финальные состояния, называется эргодической, а соответствующий случайный процесс – эргодическим.
Финальные вероятности системы могут быть получены путем решения системы линейных алгебраических уравнений, которые получаются из дифференциальных уравнений Колмогорова, если приравнять производные к нулю, а вероятностные функции состояний P0(t), P1(t),…, Pn(t) в правых частях уравнений Колмогорова заменить на неизвестные финальные вероятности P0, P1, P2,…Pn.
Таким образом, для системы с n+1 состояниями получается система n+1 линейных однородных алгебраических уравнений с n+1 неизвестными P0, P1, P2,…Pn, которые можно найти с точностью до постоянного множителя. Для нахождения их точных значений к уравнениям добавляют нормировочное условие P0 + P1 + … Pn = 1, пользуясь которым можно выразить любую из вероятностей через другие и отбросить одно из уравнений.
http://www.stat-mat.com/?p=567