У этого термина существуют и другие значения, см. Сила.
| Сила | |
|---|---|
 |
|
| Размерность | LMT−2 |
| Единицы измерения | |
| СИ | ньютон |
| СГС | дина |
| Примечания | |
| векторная величина |
| Классическая механика |
|---|
| История… |
|
Фундаментальные понятия
|
|
Формулировки
|
|
Разделы
|
|
Учёные
|
| См. также: Портал:Физика |
Си́ла — физическая векторная величина, являющаяся мерой воздействия на данное тело со стороны других тел или полей. Приложение силы обусловливает изменение скорости тела или появление деформаций и механических напряжений.
Деформация может возникать как в самом теле, так и в фиксирующих его объектах — например, пружинах.
Воздействие других тел на тело всегда осуществляется посредством полей, создаваемых телами и воспринимаемых рассматриваемым телом. Различные взаимодействия сводятся к четырём фундаментальным; согласно Стандартной модели физики элементарных частиц, эти фундаментальные взаимодействия (слабое, электромагнитное, сильное и, возможно, гравитационное) реализуются путём обмена калибровочными бозонами[1].
Для обозначения силы обычно используется символ F — от лат. fortis (сильный).
Общепринятое определение силы отсутствует, в современных учебниках физики сила рассматривается как причина ускорения[2]. Важнейший физический закон, в который входит сила, — второй закон Ньютона. Он гласит, что в инерциальных системах отсчёта ускорение материальной точки по направлению совпадает с равнодействующей силой, то есть суммой сил, приложенных к телу, а по модулю прямо пропорционально модулю равнодействующей и обратно пропорционально массе материальной точки.
Слово «сила» в русском языке является многозначным и нередко используется (само или в сочетаниях, в науке и обиходных ситуациях) в смыслах, отличных от физической трактовки термина.
Общая информация[править | править код]
Об определении силы[править | править код]
Для силы определяющей формулы 



Отсутствие теоретического (семантического) определения силы может быть восполнено изложением способа её измерения, в сочетании с описанием свойств обсуждаемой величины. В терминах логики этим формулируется так называемое операциональное определение[4].
Характеристики силы[править | править код]
Сила является векторной величиной. Она характеризуется модулем, направлением и точкой приложения. Также используют понятие линия действия силы, означающее проходящую через точку приложения силы прямую, вдоль которой направлена сила.
Зависимость силы от расстояния между телами может иметь различный вид, однако, как правило, при больших расстояниях сила стремится к нулю — поэтому отдалением рассматриваемого тела от других тел с хорошей точностью обеспечивается ситуация «отсутствия внешних сил»[5]. Исключения возможны в некоторых задачах космологии, касающихся тёмной энергии[6].
Кроме разделения по типу фундаментальных взаимодействий, существуют иные классификации сил, в том числе: внешние—внутренние (то есть действующие на материальные точки (тела) данной механической системы со стороны материальных точек (тел) не принадлежащих этой системе и силы взаимодействия между материальными точками (телами) данной системы[7]), потенциальные и нет (потенциально ли поле изучаемых сил), упругие—диссипативные, сосредоточенные—распределённые (приложены в одной или многих точках), постоянные или переменные во времени.
При переходе из одной инерциальной системы отсчёта в другую преобразование сил осуществляется так же, как и полей соответствующей природы (например, электромагнитных, если сила электромагнитная). В классической механике сила является инвариантом преобразований Галилея[8].
Системой сил называется совокупность сил, действующих на рассматриваемое тело или на точки механической системы. Две системы сил называют эквивалентными, если их действие по отдельности на одно и то же твердое тело или материальную точку одинаково при прочих равных условиях[7].
Уравновешенной системой сил (или системой сил, эквивалентной нулю) называется система сил, действие которой на твердое тело или материальную точку не приводит к изменению их кинематического состояния[7].
Размерность силы[править | править код]
Размерность силы в Международной системе величин (англ. International System of Quantities, ISQ), на которой базируется Международная система единиц (СИ), и в системе величин LMT, используемой в качестве основы для системы единиц СГС, — LMT−2. Единицей измерения в СИ является ньютон (русское обозначение: Н; международное: N), в системе СГС — дина (русское обозначение: дин, международное: dyn).
Примеры величин сил[править | править код]
Основной источник: [9]
| Пример | Сила (Н) |
|---|---|
| Сила притяжения между Солнцем и Землёй |  [10] [10]
|
| Сила притяжения между Землёй и Луной |  [10] [10]
|
| Сила тяги двигателей первой и второй ступеней ракеты-носителя «Союз» |  [11] [11]
|
| Сила тяги тепловоза 2ТЭ70 |  [12] [12]
|
| Сила притяжения между электроном и протоном в атоме водорода |  [10] [10]
|
| Сила звукового давления в ухе человека у порога слышимости |  [10] [10]
|
Равнодействующая системы сил[править | править код]
Если к незакреплённому телу приложено несколько сил, то каждая из них сообщает телу такое ускорение, какое она сообщила бы в отсутствие действия других сил. Это утверждение, основанное на опытных фактах, носит название принципа независимости действия сил (принципа суперпозиции). Поэтому при расчёте ускорения тела все действующие на него силы заменяют одной силой, называемой равнодействующей, а именно векторной суммой всех действующих сил. В частном случае равенства равнодействующей сил нулю ускорение тела также будет нулевым.
Измерение сил[править | править код]
Для измерения сил используются два метода: статический и динамический[13].
Исторический аспект понятия силы[править | править код]
В древнем мире[править | править код]
Человечество вначале стало воспринимать понятие силы через непосредственный опыт передвижения тяжёлых предметов. «Сила», «мощность», «работа» при этом были синонимами (как и в современном языке за пределами естествознания). Перенос личных ощущений на объекты природы привёл к антропоморфизму: все предметы, которые могут воздействовать на другие (реки, камни, деревья) должны быть живыми, в живых существах должна содержаться та же сила, которую человек чувствовал в себе.
С развитием человечества сила была обожествлена, причём как египетский, так и месопотамский боги силы символизировали не только жестокость и мощь, но и наведение порядка во вселенной[14]. Всемогущий Бог Библии также несёт в своих именах и эпитетах ассоциации с силой[15].
В античности[править | править код]
Когда греческие учёные стали задумываться о природе движения, понятие силы возникло как часть учения Гераклита о статике как балансе противоположностей[16]. Эмпедокл и Анаксагор пытались объяснить причину движения и пришли к понятиям, близким к понятию силы[16]. У Анаксагора «ум» движет внешней по отношению к нему материей[17]. У Эмпедокла движение вызывается борьбой двух начал, «любви» (филии) и «вражды» (фобии)[17], которые Платон рассматривал как притяжение и отталкивание[18]. При этом взаимодействие, по Платону, объяснялось в терминах четырёх элементов (огня, воды, земли и воздуха): близкие вещи притягиваются, земля к земле, вода к воде, огонь к огню[19]. В древнегреческой науке каждый элемент также имел своё место в природе, которое старался занять. Таким образом, сила тяжести, например, объяснялась двумя способами: притяжением подобных вещей и стремлением элементов занять своё место[20]. В отличие от Платона, Аристотель последовательно занимал вторую позицию, что отложило концепцию общей силы тяготения, которая бы объясняла движение земных и небесных тел, до времён Ньютона[20].
Для обозначения понятия силы Платон использовал термин «динамис» («возможность» движения). Термин употреблялся в расширенном смысле, близком к современному понятию мощности: химические реакции, тепло и свет все также представляли собой динамисы[21].
Аристотель рассматривал две разные силы: присущую самому телу («природу», физис) и силу, с которой одно тело тянет или толкает другое (при этом тела должны быть в контакте)[22]. Именно это понятие о силе и легло в основу аристотелевой механики, хотя дуализм и препятствовал количественному определению силы взаимодействия двух тел (так как вес был природной силой, не связанной с взаимодействием, и потому не мог использоваться в качестве стандарта)[23]. В случае природного движения (падения тяжёлого или подъёма лёгкого тела) Аристотель предложил формулу для скорости в виде отношения плотностей движущегося тела A и среды, сквозь которую происходит движение, B: v=A/B[24] (очевидная проблема для случая равных плотностей была отмечена уже в VI веке[25]).
Изучением сил в процессе конструирования простых механизмов занимался в III в. до н. э. Архимед[26]. Архимед рассматривал силы в статике и чисто геометрически, и потому его вклад в развитие понятия силы незначителен[27].
Вклад в развитие понятие силы внесли стоики. Согласно их учению, силы неразрывно связывали два тела через дальнодействующую «симпатию» или (у Посидония) через всеобщее напряжение, пронизывающее всё пространство. Стоики пришли к этим выводам путём наблюдения за приливами, где взаимодействие Луны, Солнца и воды в океане было трудно объяснить с позиции Аристотелева близкодействия (сам Аристотель считал, что Солнце, садясь в океан, вызывает ветры, приводящие к приливам)[28].
В доклассической механике[править | править код]
Бэкон и Оккам вернули в науку идею о дальнодействии.
Бэкон называл дальнодействующие силы species (обычно этот специфичный для Бэкона термин не переводится) и рассматривал их распространение в среде как цепочку близких взаимодействий. Такие силы, по Бэкону, имели вполне телесный характер, ближайшим эквивалентом в современной физике является волна[29].
Оккам первым отказался от аристотелевского описания взаимодействия как непосредственного контакта и декларировал возможность движителя воздействовать на движимое на расстоянии, приведя в качестве одного из примеров магниты[30].
Ревизии подвергалась и аристотелевская формула v=A/B. Уже в VI веке Иоанн Филопон рассматривал в качестве правой части разность A-B, что кроме проблемной ситуации с одинаковыми плотностями позволило также описать движение в вакууме[31]. В XIV веке Брадвардин предложил формулу v=log(A/B)[32].
У Кеплера[править | править код]
Взгляды Кеплера на силу претерпели быстрое изменение. Ещё в 1600 году Кеплер рассматривает силы как свойство, подобное душе, которое руководит движением небесных тел. Однако уже к 1605 году Кеплер пришёл к выводу, что притяжение — это не действие, а реакция, силы притяжения относятся к материальному миру и подлежат математическому изучению. В 1607 году Кеплер пришёл к выводу, что приливы вызываются воздействием силы притяжения Луны на океаны[33]. По мнению М. Дженнера, Кеплер пришёл к идее единой теории тяготения, охватывающей как падение тел, так и движение Луны, до Ньютона[34].
В классической механике[править | править код]
С зарождением классической механики Бекманом и Декартом был сформулирован закон сохранения количества движения. После осознания этого факта, который похоронил аристотелевскую связь силы и скорости, у исследователей оставалось два выхода: определить силу как причину изменения скорости или отбросить понятие силы как таковое. Сам Декарт вначале применял понятие силы, чтобы объяснить ускоренное падение тела на землю, но со временем в попытке геометризации физики пришёл к выводу, что понятие силы является искусственным, и в 1629 году описывал процесс свободного падения без упоминания «силы»[35]. С другой стороны, Галилей недвусмысленно рассматривал силу как причину увеличения скорости свободного падения[36].
У Ньютона[править | править код]
В трудах Ньютона понятие силы было тесно связано с тяготением, поскольку интерпретация кеплеровских результатов в области движения планет в то время занимала все умы[37]. Впервые понятие силы (лат. vis) встречается у Ньютона в «Началах» в двух контекстах: «присущей силы» (лат. vis insita), ньютоновской силы инерции и «приложенной силы» (лат. vis impressa), отвечающей за изменение движения тела. Ньютон также отдельно выделял центростремительную силу (к которой относил тяготение) с несколькими разновидностями: абсолютную силу (подобную современному полю тяготения), ускоряющую силу (эффект тяготения на единицу массы, современное ускорение) и движущую (произведение массы на ускорение)[38]. Ньютон не даёт общего определения силы. Как отмечает М. Дженнер, второй закон Ньютона не является определением силы у самого автора закона (который явно различал определения и законы), сила у Ньютона является пресуществующим понятием, интуитивно эквивалентным силе мускулов[39].
Современность[править | править код]
Конец XX века охарактеризовался спорами о том, необходимо ли в науке понятие силы и существуют ли силы в принципе — или это только термин, введённый для удобства[40].
Бигелоу с соавторами в 1988 году аргументировали, что силы по сути определяют причинно-следственные отношения и потому не могут быть отброшены[41]. М. Джеммер на это возразил, что в Стандартной модели и других физических теориях сила трактуется лишь как обмен моментом импульса, понятие силы потому сводится к более простому «взаимодействию» между частицами. Это взаимодействие описывается в терминах обмена дополнительными частицами (фотонами, глюонами, бозонами и, возможно, гравитонами)[40]. Джеммер приводит следующее упрощённое пояснение: два конькобежца скользят по льду плечо к плечу, у обоих в руках находится по мячу. Быстрый и одновременный обмен мячами приведёт к отталкивающему взаимодействию[42].
Стиннер отмечает, что эйнштейновский принцип эквивалентности сил гравитации и инерции по сути уничтожает понятие силы, в общей теории относительности внешние силы (F из уравнения F=ma) отсутствуют[43].
Ньютоновская механика[править | править код]
Ньютон задался целью описать движение объектов, используя понятия инерции и силы. Сделав это, он попутно установил, что всякое механическое движение подчиняется общим законам сохранения. В 1687 г. Ньютон опубликовал свой знаменитый труд «Математические начала натуральной философии», в котором изложил три основополагающих закона классической механики (законы Ньютона)[44][45].
Первый закон Ньютона[править | править код]
Первый закон Ньютона утверждает, что существуют системы отсчёта, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий[45]. Такие системы отсчёта называются инерциальными. Ньютон предположил, что каждый массивный (подразумевается: «обладающий массой», а не «громоздкий») объект имеет определённый запас инерции, характеризующий «естественное состояние» движения этого объекта. Эта идея отрицает взгляд Аристотеля, который рассматривал только покой «естественным состоянием» объекта. Первый закон Ньютона противоречит аристотелевской физике, одним из положений которой является утверждение о том, что тело может двигаться с постоянной скоростью лишь под действием силы. Тот факт, что в механике Ньютона в инерциальных системах отсчёта покой неотличим от равномерного прямолинейного движения, является обоснованием принципа относительности Галилея. Среди совокупности тел принципиально невозможно определить, какие из них находятся «в движении», а какие «покоятся». Говорить о движении можно лишь относительно конкретной системы отсчёта. Законы механики выполняются одинаково во всех инерциальных системах, другими словами, все они механически эквивалентны. Последнее следует из так называемых преобразований Галилея[46].
Второй закон Ньютона[править | править код]
Второй закон Ньютона имеет вид:
где 


Считается, что это «вторая самая известная формула в физике» («первой» значится формула эквивалентности массы и энергии), хотя сам Ньютон никогда явным образом не записывал свой второй закон в этом виде. Впервые данную форму закона можно встретить в трудах К. Маклорена и Л. Эйлера.
Третий закон Ньютона[править | править код]
Для любых двух тел (назовём их тело 1 и тело 2) третий закон Ньютона утверждает, что сила действия тела 1 на тело 2 сопровождается появлением равной по модулю, но противоположной по направлению силы, действующей на тело 1 со стороны тела 2[47]. Математически закон записывается так:
Этот закон означает, что силы всегда возникают парами «действие-противодействие»[45].
Фундаментальные взаимодействия[править | править код]
Все силы в природе основаны на четырёх типах фундаментальных взаимодействий. Максимальная скорость распространения всех видов взаимодействия равна скорости света в вакууме. Электромагнитные силы действуют между электрически заряженными телами, гравитационные — между массивными объектами. Сильное и слабое проявляются только на очень малых расстояниях, они ответственны за возникновение взаимодействия между субатомными частицами, включая нуклоны, из которых состоят атомные ядра.
Интенсивность сильного и слабого взаимодействия измеряется в единицах энергии (электрон-вольтах), а не единицах силы, и потому применение к ним термина «сила» объясняется существующей с античности традицией объяснять любые явления в окружаемом мире действием специфических для каждого явления «сил».
Понятие силы не может быть применено по отношению к явлениям субатомного мира. Это понятие из арсенала классической физики, ассоциирующейся (пусть даже только подсознательно) с ньютоновскими представлениями о силах, действующих на расстоянии. В субатомной физике таких сил уже нет: их заменяют взаимодействия между частицами, происходящие через посредство полей, то есть каких-то других частиц. Поэтому физики высоких энергий избегают употреблять слово сила, заменяя его словом взаимодействие[48].
Взаимодействие каждого типа обусловлено обменом соответствующими «переносчиками»: электромагнитное — виртуальными фотонами, слабое — векторными бозонами, сильное — глюонами (а на больших расстояниях — мезонами). В отношении гравитационного взаимодействия имеются теоретические предположения (например, в теории струн или М-теории), что с ним также может быть связан свой переносчик-бозон, называемый гравитоном, но его существование пока не доказано. Эксперименты по физике высоких энергий, проведённые в 70−80-х годах XX в., подтвердили идею о том, что слабое и электромагнитное взаимодействия являются проявлениями более глобального электрослабого взаимодействия[49]. В настоящее время делаются попытки объединения всех четырёх фундаментальных взаимодействий в одно (так называемая теория великого объединения).
Гравитация[править | править код]
Гравитация (сила тяготения) — универсальное взаимодействие между любыми видами материи. В рамках классической механики описывается законом всемирного тяготения, сформулированным Ньютоном в уже упомянутом труде «Математические начала натуральной философии». Ньютон получил величину ускорения, с которым Луна движется вокруг Земли, положив при расчёте, что сила тяготения убывает обратно пропорционально квадрату расстояния от тяготеющего тела. Кроме этого, им же было установлено, что ускорение, обусловленное притяжением одного тела другим, пропорционально произведению масс этих тел[50]. На основании этих двух выводов был сформулирован закон тяготения: любые материальные частицы притягиваются по направлению друг к другу с силой 



Здесь 
Более общей теорией гравитации является общая теория относительности Альберта Эйнштейна. В ней гравитация не характеризуется инвариантной силой, не зависящей от системы отсчёта. Вместо этого свободное движение тел в гравитационном поле, воспринимаемое наблюдателем как движение по искривлённым траекториям в трёхмерном пространстве-времени с переменной скоростью, рассматривается как движение по инерции по геодезической линии в искривлённом четырёхмерном пространстве-времени, в котором время в разных точках течёт по-разному. Причем эта линия в некотором смысле «наиболее прямая» — она такова, что пространственно-временной промежуток (собственное время) между двумя пространственно-временными положениями данного тела максимален. Искривление пространства зависит от массы тел, а также от всех видов энергии, присутствующих в системе[1].
Электромагнитное взаимодействие[править | править код]
- Электростатическое поле (поле неподвижных зарядов)
Развитие физики после Ньютона добавило к трём основным (длина, масса, время) величинам электрический заряд с размерностью «кулон» (C). Однако, исходя из требований практики, в качестве основной единицы измерения стали использовать не единицу заряда, а единицу силы электрического тока. Так, в системе СИ основной единицей является ампер, а единица заряда — кулон — производная от него.
Поскольку заряд как таковой не существует независимо от несущего его тела, электрическое взаимодействие тел проявляется в виде рассматриваемой в механике силы, служащей причиной ускорения. Применительно к электростатическому взаимодействию двух точечных зарядов с величинами 

где 


Сила направлена вдоль линии, соединяющей точечные заряды. Графически электростатическое поле принято изображать в виде картины силовых линий, представляющих собой воображаемые траектории, по которым перемещалась бы лишённая массы заряженная частица. Эти линии начинаются на одном и заканчиваются на другом заряде.
- Магнитостатическое поле (поле постоянных токов)
Существование магнитного поля признавалось ещё в средние века китайцами, использовавшими «любящий камень» — магнит в качестве прообраза магнитного компаса. Графически магнитное поле принято изображать в виде замкнутых силовых линий, густота которых (так же, как и в случае электростатического поля) определяет его интенсивность. Исторически наглядным способом визуализации магнитного поля были железные опилки, насыпаемые, например, на лист бумаги, положенный на магнит.
Эрстед установил, что текущий по проводнику ток вызывает отклонение магнитной стрелки.
Фарадей пришёл к выводу, что вокруг проводника с током создаётся магнитное поле.
Ампер высказал гипотезу, признанную в физике в качестве модели процесса возникновения магнитного поля, которая предполагает существование в материалах микроскопических замкнутых токов, обеспечивающих совместно эффект естественного или наведённого магнетизма.
Ещё, Ампером было установлено, что в находящейся в вакууме системе отсчёта, по отношению к которой заряд находится в движении, то есть ведёт себя как электрический ток, возникает магнитное поле, интенсивность которого определяется вектором магнитной индукции 
Тот же Ампер впервые измерил силу взаимодействия двух параллельных проводников с текущими по ним токами. Один из проводников создавал вокруг себя магнитное поле, второй реагировал на это поле сближением или удалением с поддающейся измерению силой, зная которую и величину силы тока можно было определить модуль вектора магнитной индукции.
Силовое взаимодействие между электрическими зарядами, не находящимися в движении относительно друг друга, описывается законом Кулона. Однако заряды, находящиеся в таком движении, порождают и магнитные поля, посредством которых созданные движением зарядов токи в общем случае приходят в состояние силового взаимодействия.
Принципиальным отличием силы, возникающей при относительном движении зарядов, от случая их стационарного размещения, является различие в геометрии этих сил. Для случая электростатики сила взаимодействия двух зарядов направлена по линии, их соединяющей. Поэтому геометрия задачи двумерна и рассмотрение ведётся в плоскости, проходящей через эту линию.
В случае токов сила, характеризующая магнитное поле, создаваемое током, расположена в плоскости, перпендикулярной току. Поэтому картина явления становится трёхмерной. Магнитное поле, создаваемое бесконечно малым по длине элементом первого тока, взаимодействуя с таким же элементом второго тока, в общем случае создаёт силу, действующую на него. При этом для обоих токов эта картина полностью симметрична в том смысле, что нумерация токов произвольна.
Закон взаимодействия токов используется для эталонирования постоянного электрического тока.
Сильное взаимодействие[править | править код]
Сильное взаимодействие — фундаментальное короткодействующее взаимодействие между адронами и кварками.
В атомном ядре сильное взаимодействие удерживает вместе положительно заряженные (испытывающие электростатическое отталкивание) протоны, происходит это посредством обмена пи-мезонами между нуклонами (протонами и нейтронами). Пи-мезоны живут очень мало, времени жизни им хватает лишь на то, чтобы обеспечить ядерные силы в радиусе ядра, потому ядерные силы называют короткодействующими. Увеличение количества нейтронов «разбавляет» ядро, уменьшая электростатические силы и увеличивая ядерные, но при большом количестве нейтронов они сами, будучи фермионами, начинают испытывать отталкивание вследствие принципа Паули. Также при слишком сильном сближении нуклонов начинается обмен W-бозонами, вызывающий отталкивание, благодаря этому атомные ядра не «схлопываются».
Внутри самих адронов сильное взаимодействие удерживает вместе кварки — составные части адронов. Квантами сильного поля являются глюоны. Каждый кварк имеет один из трёх «цветовых» зарядов, каждый глюон состоит из пары «цвет»-«антицвет». Глюоны связывают кварки в так называемый «конфайнмент», из-за которого на данный момент свободные кварки в эксперименте не наблюдались. При отдалении кварков друг от друга энергия глюонных связей возрастает, а не уменьшается как при ядерном взаимодействии. Затратив много энергии (столкнув адроны в ускорителе), можно разорвать кварк-глюонную связь, но при этом происходит выброс струи новых адронов. Впрочем, свободные кварки могут существовать в космосе: если какому-то кварку удалось избежать конфайнмента во время Большого взрыва, то вероятность аннигилировать с соответствующим антикварком или превратиться в бесцветный адрон для такого кварка исчезающе мала.
Слабое взаимодействие[править | править код]
Слабое взаимодействие — фундаментальное короткодействующее взаимодействие. Радиус действия 10−18 м. Симметрично относительно комбинации пространственной инверсии и зарядового сопряжения. В слабом взаимодействии участвуют все фундаментальные фермионы (лептоны и кварки). Это единственное взаимодействие, в котором участвуют нейтрино (не считая гравитации, пренебрежимо малой в лабораторных условиях), чем объясняется колоссальная проникающая способность этих частиц. Слабое взаимодействие позволяет лептонам, кваркам и их античастицам обмениваться энергией, массой, электрическим зарядом и квантовыми числами — то есть превращаться друг в друга. Одно из проявлений — бета-распад.
Производные виды сил[править | править код]
Всё многообразие проявляющих себя в природе сил в принципе может быть сведено к четырём фундаментальным, представленным в предыдущем разделе.
Например, трение — это проявление электромагнитных сил, действующих между атомами двух соприкасающихся поверхностей, и принципа запрета Паули[53], который не позволяет атомам проникать в область друг друга. Сила, возникающая при деформации пружины, описываемая законом Гука, также является результатом действия электромагнитных сил между частицами и принципа запрета Паули, заставляющих атомы кристаллической решётки вещества удерживаться около положения равновесия[1]. Сила тяжести — это результат действия фундаментального гравитационного притяжения на планете.
Однако на практике подобная детализация природы разных сил часто оказывается нецелесообразной или невозможной. Поэтому силы, «производные» по отношению к фундаментальным, обычно рассматриваются как самостоятельные характеристики взаимодействия тел и имеют свои наименования: «сила натяжения», «сила Ван-дер-Ваальса» и другие (см. список названий сил в физике).
Сила инерции[править | править код]
Сила инерции — сила, вводимая в неинерциальных системах отсчёта. Введение сил инерции производится для того, чтобы придать уравнениям движения тел в неинерциальных системах отсчёта ту же форму, какую имеет уравнение второго закона Ньютона в инерциальных системах. В ряде случаев такой подход позволяет сделать рассмотрение движения более удобным и наглядным, а решение соответствующих задач — более простым.
В частности, в системе отсчёта, связанной с равноускоренно движущимся телом, сила инерции направлена противоположно ускорению. Из полной силы инерции, представляющей собой сумму переносной и кориолисовой, могут быть для удобства выделены центробежная сила и сила Кориолиса.
Силы инерции принципиально отличаются от всех остальных сил тем, что никакому реальному взаимодействию тел они не соответствуют. При этом, ввиду равенства инерционной и гравитационной масс, согласно Принципу эквивалентности сил гравитации и инерции локально невозможно отличить, какая сила действует на данное тело — гравитационная или же сила инерции[источник не указан 3633 дня].
Применение термина «сила инерции» в элементарной физике не рекомендуется[источник не указан 952 дня], так как, по умолчанию, все уравнения движения в элементарной физике описывают движение относительно инерциальных систем отчёта и понятие «сила» всегда связано с воздействием какого-то внешнего объекта и не может существовать само по себе. Указание на диаграмме сил, действующих на тело, силы инерции оценивается в курсах элементарной физики как ошибка.
См. также[править | править код]
- Энергия
- Поле (физика)
- Вес
- Нерешённые проблемы современной физики
Примечания[править | править код]
- ↑ 1 2 3 Feynman, R. P., Leighton, R. B., Sands, M. Lectures on Physics, Vol 1 (неопр.). — Addison-Wesley, 1963. (англ.)
- ↑ Коэльо, 2010, с. 91.
- ↑ Коэльо, 2010.
- ↑ А. А. Ивин, А. Л. Никифоров, Словарь по логике (см. «определение операциональное»). — М.: Туманит, изд. центр ВЛАДОС (1997).
- ↑ И. Бутиков, А. С. Кондратьев. § 15. Инерция. Первый закон Ньютона // Физика для углублённого изучения 1. Механика. — С. 85, 87.
- ↑ Rupert W. Anderson. The Cosmic Compendium: The Big Bang & the Early Universe. — Lulu.com, 2015-03-28. — С. 86. — 244 с. — ISBN 9781329024182.
- ↑ 1 2 3 Тарасов В. Н., Бояркина И. В., Коваленко М. В., Федорченко Н. П., Фисенко Н. И. Теоретическая механика. — М., ТрансЛит, 2012. — C. 24-25
- ↑ В. И. Григорьев. Галилея принцип относительности. БСЭ, 3-е изд. (1969—1978). — «…силы… являются в классической механике инвариантами, т.е. величинами, не изменяющимися при переходе от одной системы отсчёта к другой». Дата обращения: 17 марта 2023.
- ↑ Кабардин О.Ф., Орлов В.А., Пономарёва А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 208
- ↑ 1 2 3 4 Кабардин О. Ф., Орлов В. А., Пономарёва А. В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — 3-е изд., перераб. — 208 c. — Тираж 143500 экз.
- ↑ Данные взяты из статьи Википедии Союз (ракета-носитель)
- ↑ Данные взяты из статьи Википедии ТЭП70
- ↑ Тарг С. М. Сила // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 494. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ Джеммер, 1999, с. 18—20.
- ↑ Джеммер, 1999, с. 21.
- ↑ 1 2 Джеммер, 1999, с. 25.
- ↑ 1 2 Джеммер, 1999, с. 26.
- ↑ Джеммер, 1999, с. 27.
- ↑ Джеммер, 1999, с. 31.
- ↑ 1 2 Джеммер, 1999, с. 32.
- ↑ Джеммер, 1999, с. 34—35.
- ↑ Джеммер, 1999, с. 36.
- ↑ Джеммер, 1999, с. 35—39.
- ↑ Джеммер, 1999, с. 39.
- ↑ Джеммер, 1999, с. 66.
- ↑ Heath,T.L. The Works of Archimedes (1897). Archive.org. Дата обращения: 14 октября 2007. Архивировано 23 августа 2011 года. (англ.)
- ↑ Джеммер, 1999, с. 41.
- ↑ Джеммер, 1999, с. 41—42.
- ↑ Джеммер, 1999, с. 60.
- ↑ Джеммер, 1999, с. 64.
- ↑ Стиннер, 1994, с. 79.
- ↑ Джеммер, 1999, с. 66—67.
- ↑ Джеммер, 1999, с. 81—83.
- ↑ Джеммер, 1999, с. 84.
- ↑ Джеммер, 1999, с. 103—104.
- ↑ Джеммер, 1999, с. 101.
- ↑ Джеммер, 1999, с. 116—117.
- ↑ Джеммер, 1999, с. 119—120.
- ↑ Джеммер, 1999, с. 124.
- ↑ 1 2 Джеммер, 1999, с. v.
- ↑ John Bigelow , Brian Ellis, and Robert Pargetter. Forces // Philosophy of Science 55, no. 4 (Dec., 1988): 614—630. doi:10.1086/289464 (англ.)
- ↑ Джеммер, 1999, с. v-vi.
- ↑ Стиннер, 1994, с. 83—84.
- ↑ University Physics, Sears, Young & Zemansky, pp. 18-38 (англ.)
- ↑ 1 2 3 Newton, I. The Principia Mathematical Principles of Natural Philosophy. — University of California Press, 1999. — ISBN 0-520-08817-4. (англ.)
- ↑ Мултановский В. В. Курс теоретической физики. Классическая механика. Основы специальной теории относительности. Релятивистская механика. — М.: Просвещение, 1988. — С. 80−81.
- ↑ Henderson, Tom Lesson 4: Newton’s Third Law of Motion (недоступная ссылка — история). The Physics Classroom (1996-2007). Дата обращения: 4 января 2008. Архивировано 23 августа 2011 года. (англ.)
- ↑ Капра, Фритьоф ДАО ФИЗИКИ. СПб.,”ОРИС”*”ЯНА-ПРИНТ”. 1994 г. 304 с. ISBN 5-88436-021-5
- ↑ Weinberg, S. Dreams of a Final Theory. — Vintage Books USA, 1994. — ISBN 0-679-74408-8. (англ.)
- ↑ University Physics, Sears, Young & Zemansky, pp. 59−82 (англ.)
- ↑ Sir Isaac Newton: The Universal Law of Gravitation. Astronomy 161 The Solar System. Дата обращения: 4 января 2008. Архивировано 23 августа 2011 года. (англ.)
- ↑ «Тяготение». Новиков И. Д. // Физическая энциклопедия. Гл. ред. Прохоров А. М. — М.: «Большая Российская энциклопедия», 1998. — Т. 5. — С. 188−193. — 760 с. — ISBN 5-85270-101-7.
- ↑ Nave, R Pauli Exclusion Principle. HyperPhysics***** Quantum Physics. Дата обращения: 2 января 2008. Архивировано 23 августа 2011 года. (англ.)
Литература[править | править код]
- Григорьев В. И., Мякишев Г. Я. — «Силы в природе»
- Ландау Л. Д., Лифшиц Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6.
- Guide to the Measurement of Force — prepared by The Institute of Measurement and Control, London (published 1998, re-issued 2013) — ISBN 0 904457 28 1
- Джеммер, Макс. Concepts of Force. — Mineola, NY: Dover Publications Inc., 1999. — ISBN 0-486-40689-X. (англ.)
- Stinner, Arthur. The story of force: from Aristotle to Einstein (англ.) // Physics education. — 1994. — Vol. 29, no. 2. — P. 77—85.
- Ricardo Lopes Coelho. On the Concept of Force: How Understanding its History can Improve Physics Teaching (англ.) // Sci & Educ. — 2010. — Vol. 19. — P. 91—113. — doi:10.1007/s11191-008-9183-1.
Содержание:
Сила:
При изучения природных явлений используют разные физические величины. Для того чтобы описать качественно и количественно взаимодействие тел, вводят физическую величину, которую называют силой.
Определение силы
Сила – это физическая величина, которая служит мерой взаимодействия тел и является причиной изменения скоростей тел или их частей.
Наблюдение. Если мы рассматриваем, например, взаимодействие руки с волейбольным мячом, то мы говорим: «Мяч действует с силой на руку или рука действует с силой на мяч».
Опыт. Подвесим на пружину яблоко (рис. 66).

Пружина удлинится. Если на неё подвесить два яблока, то она удлинится больше. Итак, два яблока действуют на пружину с большей силой, чем одно.
Результат действия одного тела на другое зависит от значения приложенной силы.
Чем плотнее закрыта дверь, тем с большей силой мы должны её толкать или тянуть на себя, чтобы отворить.
Для того чтобы легче открывать дверь, её ручку прикрепляют как можно дальше от петель. Попробуйте открыть дверь, толкая её в точке, размещённой вблизи петель. Вы убедитесь, что это сделать намного труднее, чем с помощью ручки. Результат действия одного тела на другое зависит от точки приложения силы.
Для достижения определённого результата действия, например, растяжения или сжатия пружины, закрытия или открытия двери, нужно прикладывать силы в разных направлениях.
Действие одного тела на другое зависит от направления действия силы.
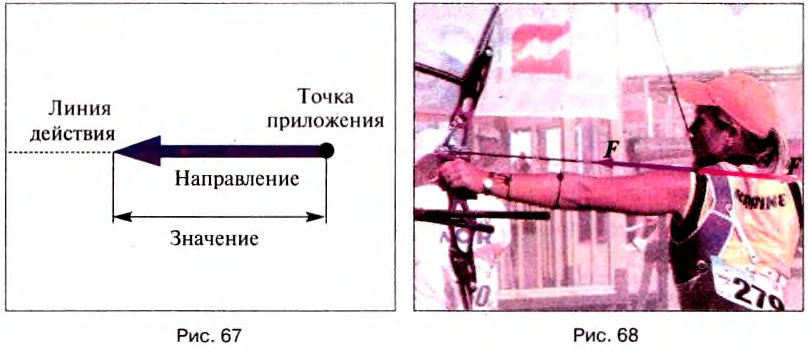
Графически силу изображают в виде отрезка прямой со стрелкой на конце (рис. 67).
Начало отрезка совмещают с точкой приложения силы. Длина отрезка в определённом масштабе равна значению силы. Стрелка показывает направление силы. Величины, характеризующиеся кроме числового значения еще и направлением в пространстве, называют векторными, или векторами (от латинского слова вектор — ведущий, несущий).
Почему тела изменяют свое состояние в пространстве
Любые изменения в природе происходят в результате взаимодействия между телами. Чтобы изменить положение вагона на рельсах, железнодорожники направляют к нему локомотив, который смещает вагон с места и приводит его в состояние движения (рис. 32). 
Парусник может длительное время стоять возле берега до тех пор, пока не подует попутный ветер и подействует на его паруса (рис. 33). Колеса игрушечного автомобиля могут вращаться с любой скоростью, но игрушка не изменит своего положения, если под игрушку не положить дощечку или линейку (рис.34). Форму или размер пружины можно изменить, лишь подвесив к ней груз или потянув рукой за один из его концов.
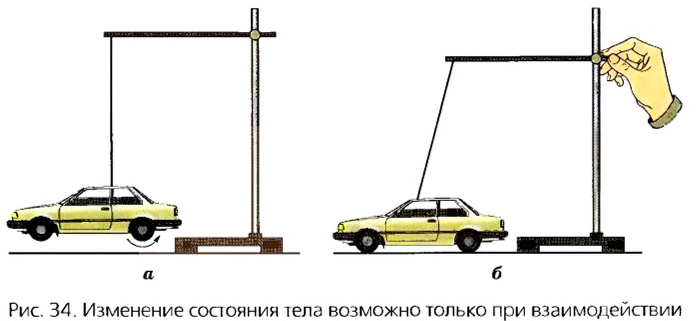
Все тела в природе так или иначе связаны между собой и действуют друг на друга или непосредственно, или через физические поля. Такое действие всегда является взаимным. Если тепловоз действует на вагон и изменяет его скорость, то скорость тепловоза при этом также изменяется благодаря обратному действию вагона. Солнце действует на все тела на Земле и на саму Землю, удерживая ее на орбите. Но и Земля притягивает Солнце и, в свою очередь, изменяет его траекторию. Таким образом, во всех случаях можно говорить только о взаимном действии тел – взаимодействии.
При взаимодействии могут изменяться скорости тел или их частей.
Однако, взаимодействуя с различными телами, данное тело будет изменять свою скорость по-разному. Так, парусник может приобрести скорость вследствие действия на него ветра. Но такой же результат можно получить, включив двигатель, который находится на паруснике. Парусник может сдвинуть с места и катер, действуя на него через трос. Чтобы каждый раз не называть все взаимодействующие тела, все эти действия объединяют одним понятием силы.
Что такое сила
Сила как физическое понятие может быть большей или меньшей, как и вызванные ею изменения в состоянии тела или его частей.
Сила – это физическое понятие, которое обобщает все взаимодействия, вследствие чего тело или его части изменяют свое состояние.
Действие тепловоза на вагон будет значительно интенсивнее, чем действие нескольких грузчиков. Под действием тепловоза вагон быстрее сдвинется с места и начнет двигаться с большей скоростью, чем тогда, когда вагон будут толкать грузчики, которые еле сдвинут его на небольшое расстояние или совсем его не сдвинут.
Сила как физическая величина количественно характеризует действие одного тела на другое.
Для того чтобы можно было производить математические расчеты, силу обозначают определенной буквой. Как правило, это латинская буква F.
Как и все другие физические величины, сила имеет единицы измерения. Современная наука пользуется единицей, которая называется ньютоном (Н). Единица получила такое название в честь английского ученого Исаака Ньютона, который внес значительную лепту в развитие физической и математической наук.
 Исаак Ньютон (1643-1727) – выдающийся английский ученый, основоположник классической физики. Научные труды касаются механики, оптики, астрономии и математики. Сформулировал основные законы классической механики, открыл закон всемирного тяготения, дисперсию света, развил корпускулярную теорию света, разработал дифференциальное и интегральное исчисление.
Исаак Ньютон (1643-1727) – выдающийся английский ученый, основоположник классической физики. Научные труды касаются механики, оптики, астрономии и математики. Сформулировал основные законы классической механики, открыл закон всемирного тяготения, дисперсию света, развил корпускулярную теорию света, разработал дифференциальное и интегральное исчисление.
Силы могут иметь различные значения. Так, на стакан с водой действует сила со стороны Земли, которая равна примерно 2 Н. А трактор, когда тянет плуг, действует на него с силой в несколько тысяч ньютонов.
Чем измеряют силу
Для измерения силы используют специальные приборы, называющиеся динамометрами (dina – сила; metro – меряю). Как правило, каждый такой прибор имеет измерительный элемент в виде пружины определенной формы (рис. 35).

Сила характеризуется направлением.
Указать числовое значение силы не всегда достаточно для определения результата ее действия. Важно знать точку ее приложения и направление действия.
Если высокий брусок, стоящий на столе, толкать в нижней части, то он будет скользить по поверхности стола. Если же к бруску приложить силу в верхней его части, то он просто перевернется (рис. 36).

Понятно, что направление падения бруска зависит от того, в каком направлении будем его толкать. Следовательно, сила имеет направление. От направления силы зависит изменение скорости тела, на которое эта сила действует.
Учитывая, что сила имеет направление и числовое значение, ее изображают в виде стрелки определенной длины и направления (вектора). Такая стрелка начинается в точке на теле, которая называется точкой приложения силы. На рисунке 37 изображена сила, значение которой равно 10 Н, направлена она слева направо и приложена в точке А.
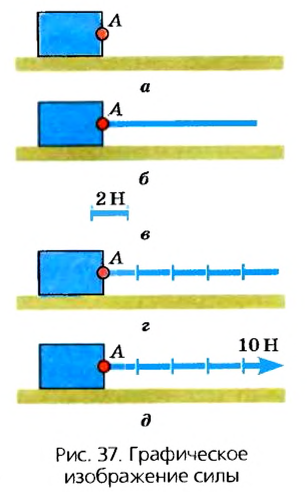
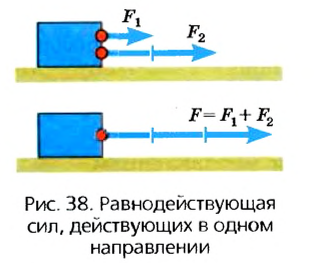
Пользуясь графическим методом, можно производить различные математические операции с силами. Так, если к одной точке на теле приложены силы 2 Н и 3 Н, которые действуют в одном направлении, то их можно заменить одной силой, которая будет приложена в той же точке и действовать в том же направлении, а ее значение будет равно сумме значений каждой из сил (рис. 38). Вектор этой силы будет иметь длину, равную сумме длин двух векторов.
Возможен и другой случай, когда силы, приложенные в одной точке тела, действуют в противоположных направлениях. Тогда их можно заменить одной силой, направленной в направлении большей силы, а ее значение будет равняться разности значений каждой силы (рис. 39). Длина вектора этой силы будет равна разности длин векторов приложенных сил.
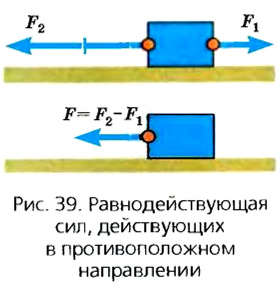
Сила, которой можно заменить действие нескольких сил, приложенных в определенной точке тела, называется равнодействующей.
Равнодействующая – это сила, действие которой равнозначно действию нескольких сил, приложенных к телу в определенной его точке.
Силу обозначают большой латинской буквой 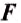 .
.
На рис. 68 спортсменка приготовилась стрелять из лука. В этом случае её рука действует на тетиву с силой направленной вправо, а тетива действует на руку с такой же по значению силой, направленной влево. Итак, значения сил одинаковы, но их направления противоположны.
- Заказать решение задач по физике
Сложение сил
Главная задача динамики – по действующей силе определить движение тела или по характеру движения тела установить, какая сила на него действует. Понятие о силе является основным в механике. И. Ньютон утверждал то, что мы называем силой, есть действие одного тела на другое, или их взаимодействие.
Действие одних тел на другие сообщает ускорение их движению. Полученное телом ускорение является внешним проявлением того, что оно взаимодействовало с другим телом. Когда мы говорим «сила», то подразумеваем, что на данное тело действуют другие тела.
Сила, являющаяся причиной изменения состояния движения тел или их деформации, характеризует взаимодействие тел, которое происходит при их непосредственном контакте (например столкновении) или через поля (рис. 2.2).
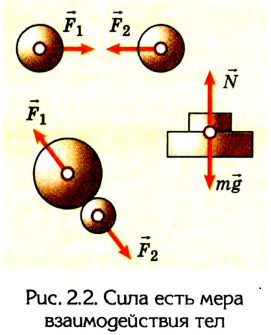
Сила – векторная величина, характеризующая действие, которое является причиной изменения состояния движения или покоя.
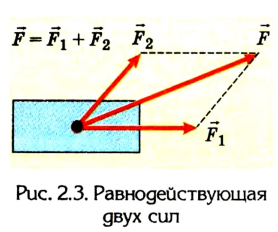
Действие на тело нескольких сил может быть заменено их равнодействующей (рис. 2.3), которую определяют геометрическим сложением этих сил как векторов:
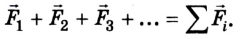
Не скорость тела, а ее изменение есть следствием действия силы (действия других тел).
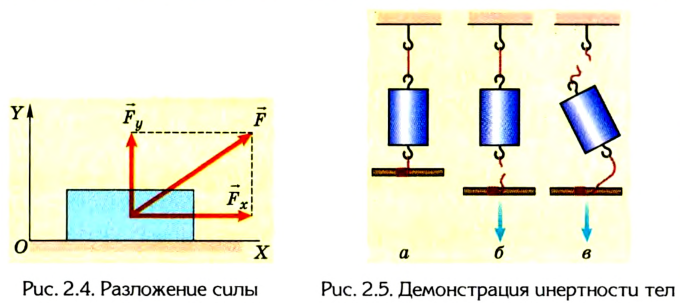
Помимо значения и направления сила характеризуется еще и точкой приложения, которую можно перемещать вдоль линии действия силы, если тело абсолютно твердое (не деформируется). Поскольку действия сил независимы, то сила может быть разложена на составляющие 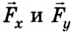 (рис. 2.4) как проекции на оси координат.
(рис. 2.4) как проекции на оси координат.
Для того чтобы выявить инертность тел и увидеть, как на нее влияет время их взаимодействия, проведем такой опыт. На тонкой нитке подвесим груз (рис. 2.5, а). Снизу к грузу прикрепим точно такую же нитку. Если резко дернуть за нижнюю нитку, то она оборвется, а груз останется висеть на верхней нитке (рис. 2.5, б). Если нижнюю нитку натягивать медленно, то оборвется верхняя нитка (рис. 2.5, в).
Когда мы резко дергаем за нижнюю нитку, взаимодействие руки и нитки кратковременно, груз не успевает изменить свою скорость – верхняя нитка не обрывается, т. к. груз имеет значительную инертность.
Если же за нижнюю нитку тянуть медленно (рука действует на груз продолжительное время), то груз набирает такую скорость, что его перемещение достаточно для разрыва и без того натянутой верхней нитки.
Как вы уже знаете, инертность тел определяется их массой, т. е. масса тела характеризует его инертность.
Во время тщательных исследований взаимодействия двух тел, например столкновения двух абсолютно упругих шаров, установлено, что отношение модулей ускорений взаимодействующих тел равно обратному отношению их масс: 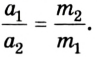
Следствием этого соотношения является один из методов измерения массы тел. Сначала выбирают тело, массу которого условно берут за единицу, – эталон массы. Между эталоном массы и телом, массу которого нужно измерить, можно поместить сжатую при помощи нитки пружину. Потом нитку поджечь и определить ускорение эталона 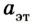 и исследуемого тела
и исследуемого тела 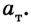 Из соотношения
Из соотношения 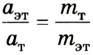 находим массу исследуемого тела:
находим массу исследуемого тела: 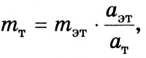
где 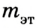 и
и 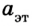 – масса и ускорение эталона (1 единица массы). Отсюда
– масса и ускорение эталона (1 единица массы). Отсюда 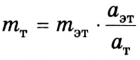 единиц массы.
единиц массы.
По международному соглашению за единицу массы принята масса эталона килограмма (рис. 2.6).

Килограмм (кг) – основная единица массы в Международной системе единиц (СИ). Килограмм равен массе международного прототипа килограмма – гире из платино-иридиевого сплава (90 % Pt, 10 % lr) в виде цилиндра диаметром и высотой 39 мм, хранящейся в Международном бюро мер и весов (г. Севр, предместье Парижа).
С достаточной точностью можно сказать, что массу 1 кг имеет 1  чистой воды
чистой воды 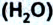 при 15 °C.
при 15 °C.
Для измерения массы тела часто используют способ сравнения масс тел с помощью весов. При этом учитывают способность тел взаимодействовать с Землей. Как подтверждают опыты, тела, имеющие одинаковую массу, одинаково притягиваются к Земле в данном месте.
Равнодействующая сила
При изучении физики в 7-м классе вы познакомились с понятием «сила», которое используется для описания взаимодействия тел.
Чтобы вспомнить основные характеристики силы, проведем опыт, например, с куском поролона, покоящимся на неподвижном столе, так как притяжение Земли уравновешено воздействием стола.
Используя пинцет, можно действовать на поролон в различных точках и видеть его поступательное, вращательное или более сложное движение в зависимости от направления, места и величины воздействия.
При этом легко наблюдать не только изменение скорости поролона, но и его деформацию (изменение формы и размеров) (рис. 34) в местах контакта поролона с пинцетом.

Рис. 34
Изменение скорости и деформация тел проявляются в любых опытах при самых разнообразных взаимодействиях, и поэтому принято следующее определение силы:
- сила — физическая векторная величина, являющаяся количественной мерой действия одного тела на другое, в результате которого изменяется скорость тела и происходит его деформация.
Опыт показывает, что результат воздействия силы определяется не только ее направлением и модулем, но и точкой приложения.
Единицей измерения силы в СИ является 1 ньютон (сокращенно 1 Н).
Вспомним исторически сложившиеся названия сил и их обозначения.
Силой тяжести 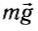 называется сила, с которой тело притягивается к Земле. Силой давления
называется сила, с которой тело притягивается к Земле. Силой давления 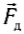 называется сила, с которой тело действует на опору или жидкость и газ действуют на стенки сосуда. Силой упругости
называется сила, с которой тело действует на опору или жидкость и газ действуют на стенки сосуда. Силой упругости 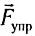 называется сила, возникающая при деформации тела. Силой реакции
называется сила, возникающая при деформации тела. Силой реакции 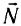 называется сила, действующая на тело со стороны опоры или подвеса. Силой сопротивления
называется сила, действующая на тело со стороны опоры или подвеса. Силой сопротивления 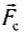 и силой трения
и силой трения 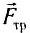 называются силы, препятствующие механическому движению тела.
называются силы, препятствующие механическому движению тела.
Силы могут действовать на поверхность тела (например, сила давления воздуха) (рис. 35) или быть приложены в некоторой условной точке (например, сила упругости нити в точке ее крепления к телу) (рис. 36).
Для упрощения математического описания механического движения тело рассматривается как материальная точка, если не указаны его размеры и форма. На рисунке тело чаще всего изображают прямоугольником.
Можно изображать силы, действующие на тело, приложенными в центре прямоугольника. Но обычно в центре прямоугольника изображают приложенной силу тяжести, а силу трения и силу реакции опоры рисуют приложенными в точке на нижней грани тела под его центром (рис. 37). Если на тело действуют другие тела, то необходимо учесть одновременно действие нескольких сил.
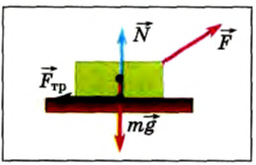
Рис. 37
При изучении физики в 7-м классе вы познакомились со сложением сил и научились складывать силы, действующие на тело вдоль одной прямой.
В этом случае действие, например, двух сил можно заменить одной силой. Модуль равнодействующей силы равен сумме или разности модулей двух слагаемых сил в зависимости от того, совпадают их направления (рис. 38, а, б) или противоположны (рис. 39. а, б). Направление равнодействующей двух сил совпадает с направлением большей силы.
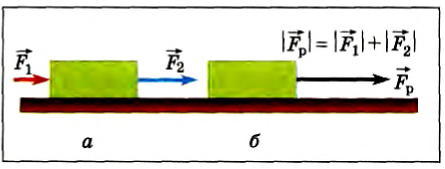
Рис. 38
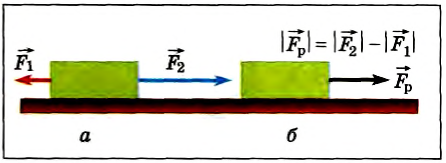
Рис. 39
А как складываются силы, если они направлены под некоторым углом друг к другу? Покажем на опыте, что они складываются также векторно. Подвесим груз массой 0,2 кг на динамометре, закрепленном на неподвижном штативе. Если груз покоится, то сила упругости пружины динамометра уравновешивает силу тяжести груза (рис. 40), а показания прибора равны: Fупр = mg = 2H (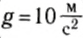 )
)
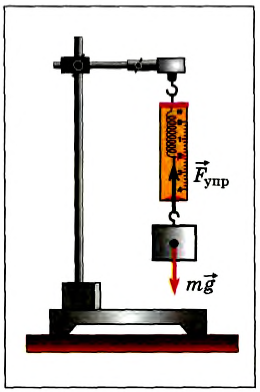
Рис. 40
Теперь подвесим этот же груз с помощью двух одинаковых динамометров (рис. 41, а), закрепленных на одной высоте. Меняя положения динамометров, а следовательно, угол между силами 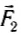 и
и 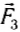 , действующими на груз со стороны динамометров, можно убедиться, что их показания зависят от этого угла и лишь при угле, равном нулю, в сумме равны 2 Н.
, действующими на груз со стороны динамометров, можно убедиться, что их показания зависят от этого угла и лишь при угле, равном нулю, в сумме равны 2 Н.
Следовательно, совместное действие сил 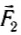 и
и 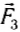 уравновешивает действие силы тяжести груза, но сумма модулей этих сил не равна 2 Н, т. е. силы нельзя складывать как скалярные величины.
уравновешивает действие силы тяжести груза, но сумма модулей этих сил не равна 2 Н, т. е. силы нельзя складывать как скалярные величины.
Когда угол между силами 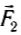 и
и 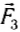 равен 120° (рис. 41,6), то сумма показаний динамометров — 4 Н, а сила тяжести груза все та же — 2 H. Но если найти в этом случае векторную сумму
равен 120° (рис. 41,6), то сумма показаний динамометров — 4 Н, а сила тяжести груза все та же — 2 H. Но если найти в этом случае векторную сумму 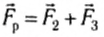 по правилу сложения векторов, то она по модулю равна Fp= 2 Н.
по правилу сложения векторов, то она по модулю равна Fp= 2 Н.
Следовательно, силы нужно складывать по правилам сложения векторов.
Модуль векторной суммы сил 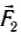 и
и 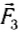 равен 2 H при любом значении угла между направлениями этих сил, а также и во всех случаях, когда модули сил не равны друг другу (рис. 41, в).
равен 2 H при любом значении угла между направлениями этих сил, а также и во всех случаях, когда модули сил не равны друг другу (рис. 41, в).
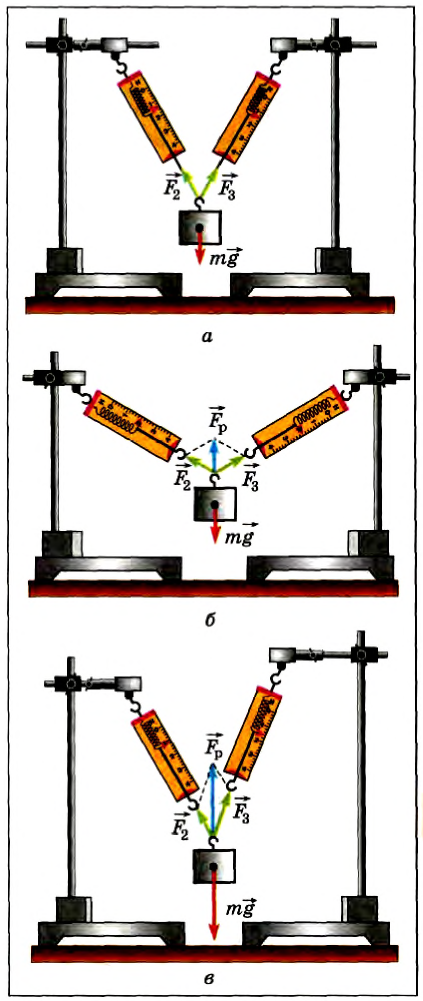
Рис. 41
Какие бы более сложные опыты не проводились (и при действии на тело нескольких сил), всегда результаты измерений показывают, что действие нескольких сил можно заменить их векторной суммой, т. е. силы складываются, как векторы, — геометрически.
Векторная сумма сил, действующих на тело, называется равнодействующей и определяется по формуле:
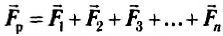
Если размерами тела нельзя пренебречь и силы приложены в разных его точках, то векторы сил можно перенести в одну точку, сохраняя модуль и направление, и векторно сложить (рис. 42).
Необходимо понимать, что равнодействующая сила заменяет действие нескольких сил только по отношению к движению тела в целом, но не заменяет действие каждой слагаемой силы в других отношениях.
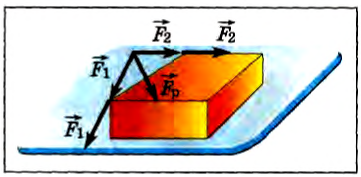
Рис. 42
Например, растянутая двумя руками пружина покоится (рис. 43), а значит, равнодействующая сил 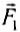 и
и 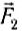 равна нулю, но каждая из этих сил деформирует соответственно подвес динамометра и пружину.
равна нулю, но каждая из этих сил деформирует соответственно подвес динамометра и пружину.
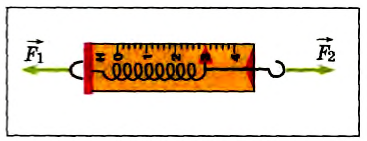
Рис. 43
Если тело движется с постоянной скоростью, то согласно первому закону Ньютона все воздействия на тело скомпенсированы, т. е. равнодействующая всех сил также должна быть равна нулю.
Главные выводы:
- Сила — физическая векторная величина, являющаяся количественной мерой действия одного тела на другое, в результате которого изменяется скорость тела и происходит его деформация.
- Сила характеризуется модулем, направлением, а также точкой приложения.
- Заменить действие нескольких сил можно равнодействующей силой, которая определяется как векторная сумма этих сил.
- При движении тела с постоянной скоростью (или в состоянии покоя) равнодействующая всех сил, действующих на него, равна нулю.
Что означает понятие “Сила” в физике
Вам хорошо известно слово «сила». Обычно смысл слова «сила» и образованных от него слов «силач», «сильный» и т. д. связан с возможностями человека, животного, механизма, с интенсивностью проявления природных явлений. Мы говорим «самый сильный человек», «сила воли», «сильные чувства», «сильный мороз», «сильный двигатель». А какое содержание вкладывают в слово «сила» физики?
Мы уже говорили о том, что причина изменения скорости движения тела — его взаимодействие с другими телами.
Чтобы теннисный мяч вернулся на сторону соперника, вы бьете по мячу ракеткой, но и мяч «бьет» по ракетке. Чтобы остановить велосипед, вы нажимаете на ручки тормоза и в то же время ощущаете, как они давят на ваши ладони. Обратите внимание: в любом случае результат зависит от того, насколько «сильным» будет взаимодействие: сильнее ударите по мячу — мяч наберет большую скорость (рис. 18.1); сильнее нажмете на тормоз — быстрее остановится велосипед. Мерой действия одного тела на другое служит физическая величина сила.
Сила — это физическая величина, которая является мерой действия одного тела на другое (мерой взаимодействия тел).
Силу обычно обозначают символом F. Единица силы в СИ — ньютон (названа в честь Исаака Ньютона): [F]=Н. 1 Н — это сила, которая, действуя на тело массой 1 кг в течение 1 с, изменяет скорость его движения на 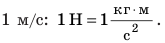 Чем больше сила и чем дольше она действует на тело, тем заметнее изменяется скорость движения тела (см. рис. 18.1). Чтобы тела разной массы за одинаковое время изменяли скорости своего движения одинаково, на них должны действовать разные силы (рис. 18.2).
Чем больше сила и чем дольше она действует на тело, тем заметнее изменяется скорость движения тела (см. рис. 18.1). Чтобы тела разной массы за одинаковое время изменяли скорости своего движения одинаково, на них должны действовать разные силы (рис. 18.2).


Графическое изображение сил
Сила, действуя на тело, может изменить скорость его движения как по значению, так и по направлению, поэтому сила определяется и значением, и направлением. Уже говорилось о том, что физические величины, имеющие значение и направление, называют векторными. Итак, сила — векторная величина. На рисунках вектор силы начинают в точке, к которой приложена сила (эту точку так и называют — точка приложения силы), и направляют в сторону действия силы. Длину стрелки иногда выбирают так, чтобы она в определенном масштабе соответствовала значению силы (рис. 18.3). Изменение скорости движения тела (по значению, по направлению) зависит от направления силы (см. таблицу на с. 123).
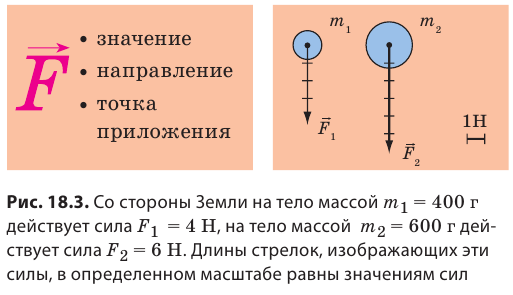
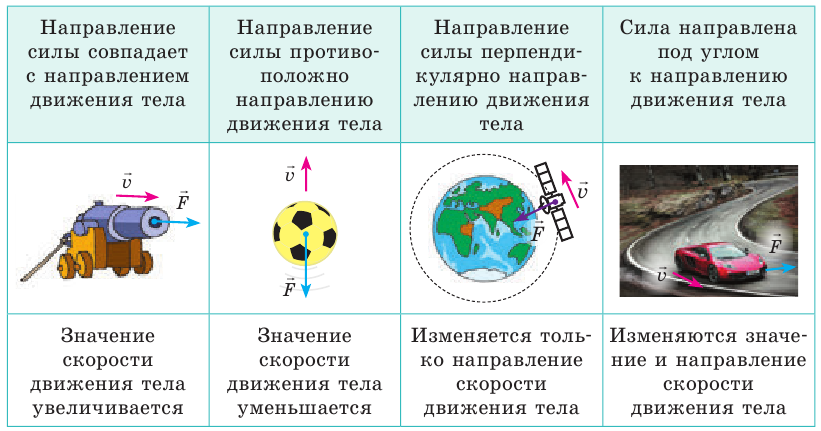
Сложение сил, действующие вдоль одной прямой
Обычно на тело действует не одна сила, а две, три или больше. Проведем опыт. Поставим на стол тележку и привяжем к ней две нити. Потянем за одну нить с силой 5 Н, а за другую — в том же направлении — с силой 3 Н (рис. 18.4). Тележка придет в движение, увеличивая свою скорость так, как если бы на нее действовала одна сила 8 Н. Силу 8 Н, которой в данном случае можно заменить две силы 5 и 3 Н, называют равнодействующей двух сил и обозначают символом R (или F). Силу, которая производит на тело такое же действие, как несколько одновременно действующих сил, называют равнодействующей этих сил. Если тележку одновременно тянуть за две нити в противоположные стороны (рис. 18.5), то силы не будут «помогать» друг другу разгонять тележку, а наоборот — будут «мешать». В этом случае тележка будет двигаться так, будто на нее действует одна сила 2 Н в направлении, в котором действует сила 5 Н, то есть равнодействующей сил 5 и 3 Н будет сила 2 Н.
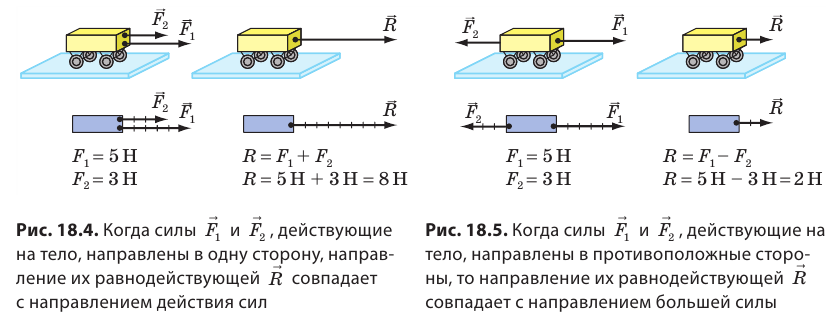
Как вы считаете, какой будет равнодействующая, если нити, привязанные к тележке с противоположных сторон, потянуть с силами, одинаковыми по значению, например 5 Н? Изменится ли в этом случае скорость движения тележки? 4 Выясняем, когда силы компенсируют друг друга Надеемся, вы правильно ответили на вопрос в п. 3 и самостоятельно пришли к выводу: если две силы равны по значению, противоположны по направлению и приложены к одному телу, то равнодействующая этих сил равна нулю. Силы уравновешивают (компенсируют) друг друга, поэтому причины для изменения скорости движения тела нет. Так, по горизонтальному прямолинейному отрезку шоссе автомобиль движется равномерно (рис. 18.6, а), если сила тяги его двигателя компенсирует силу сопротивления движению (сила сопротивления движению достаточно быстро остановит автомобиль, если двигатель не будет работать). Портфель в руке находится в состоянии покоя, если сила притяжения Земли, действующая на портфель, компенсируется силой, которую прикладывает к портфелю человек (рис. 18.6, б).
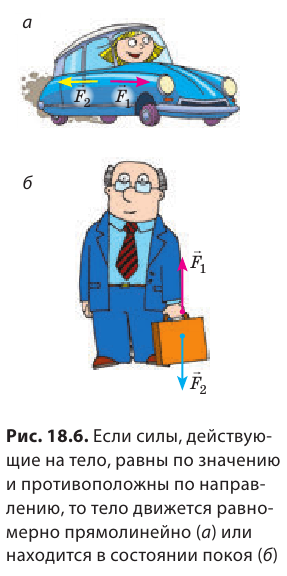
Итоги:
Сила F — физическая величина, являющаяся мерой действия одного тела на другое (мерой взаимодействия тел). Сила — причина изменения скорости движения тела. Единица силы в СИ — ньютон (Н). 1 Н равен силе, которая, действуя на тело массой 1 кг в течение 1 с, изменяет скорость его движения на 1 м/с.
Сила — векторная величина. Чтобы охарактеризовать силу, необходимо указать значение, направление и точку приложения силы. Если на тело действуют несколько сил, то их общее действие всегда можно заменить действием одной силы — равнодействующей. Равнодействующей сил, которые действуют на тело в одном направлении, является сила, значение которой равно сумме значений сил, а направление совпадает с направлением этих сил. Если две силы, действующие на тело, направлены в противоположные стороны, то направление равнодействующей совпадает с направлением большей силы, а для нахождения значения равнодействующей нужно из значения большей силы вычесть значение меньшей. Две силы компенсируют (уравновешивают) друг друга, если они равны по значению, противоположны по направлению и приложены к одному телу.
- Силы в механике
- Сила тяжести в физике
- Сила упругости в физике и закон Гука
- Деформация в физике
- Звук в физике и его характеристики
- Звуковые и ультразвуковые колебания
- Инерция в физике
- Масса тела в физике
I. Механика
Тестирование онлайн
Что надо знать о силе
Сила – векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как  , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом
, измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом 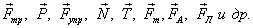
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле


Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.
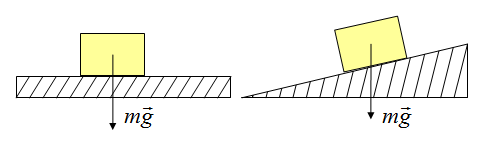
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:


Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
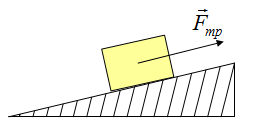
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы “говорит” реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, “сопротивляются”.
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой  , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как
, но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как 
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
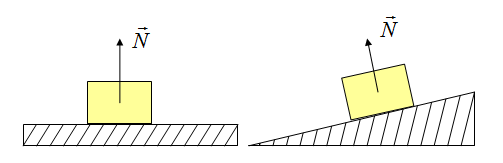
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину – уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации – сила упругости.
Закон Гука


Сила упругости направлена противоположно деформации.

Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле

При параллельном соединении жесткость

Жесткость образца. Модуль Юнга.


Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел здесь.
Вес тела
Вес тела – это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести – сила, которая возникает в результате взаимодействия с Землей. Вес – результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же – сила, которая приложена на опору (не на предмет)!
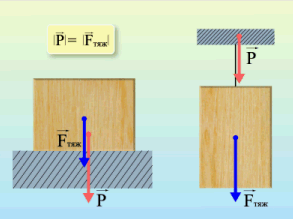
Формулы определения веса нет. Обозначается эта силы буквой  .
.
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.

Сила реакции опоры и вес – силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес – это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость – состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!

Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес – сила, измеряется в Ньютонах. Как верно ответить на вопрос: “Сколько ты весишь”? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка – отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
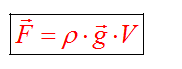

В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше – тонет.
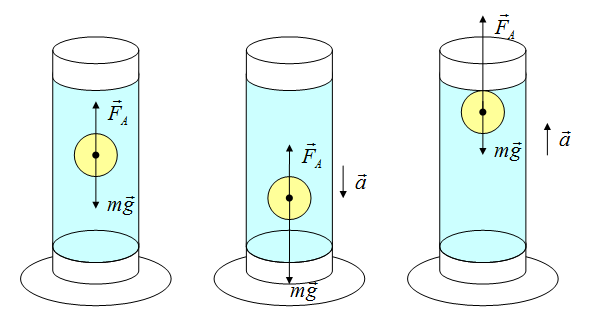
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку – в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
Силы трения*
Взаимосвязь силы тяжести, закона гравитации и ускорения свободного падения*
Содержание:
- Определение и формула силы
- Второй закон Ньютона
- Единицы измерения силы
- Примеры решения задач
Определение и формула силы
Определение
Силой называют векторную величину, которая характеризует взаимодействия тел. Ее модуль определяет «степень»
(интенсивность) воздействия. Направление силы совпадает с направлением ускорения, которое приобретает тело при взаимодействии с другими телами.
Силы способны изменять скорости тел и вызывать их деформации. Примером деформированного тела служит сжатая (растянутая) пружина.
Две силы считают равными по модулю и противоположными по направлению, если они приложены к одному телу, но ускорение такого тела равно нулю.
Второй закон Ньютона
Равнодействующая всех сил приложенных к телу (векторная сумма всех сил)
($bar{F}$) равна производной от импульса тела по времени:
$$bar{F}=sum_{i=1}^{n} bar{F}_{i}=frac{d bar{p}}{d t}(1)$$
где $bar{p}=m bar{v}$ – импульс тела, m–масса рассматриваемого тела,
$bar{v}$ – скорость. Надо отметить, что уравнение (1) строго применимо только относительно
материальной точки. Если рассматривается протяженное тело, то под скоростью понимают скорость движения центра масс тела.
Если масса материальной точки (m)не изменяется во времени, то формула, определяющая результирующую силу, приложенную к ней
(второй закон Ньютона) можно представить в виде:
$$bar{F}=m frac{d bar{v}}{d t}=m bar{a}(2)$$
где $bar{a}$ – ускорение, которое материальная точка приобретает в результате
воздействия на нее силы. Выражение (2) показывает то, что если
$bar{F}$=0, то тело (материальная точка) движется равномерно и прямолинейно или покоится.
Если сила, приложенная к телу, является постоянной (по модулю и направлению), то формулу для нее можно представить в виде:
$$F=frac{Delta p}{Delta t}=frac{mleft(v_{2}-v_{1}right)}{t_{2}-t_{1}}$$
Единицы измерения силы
Основной единицей измерения момента силы в системе СИ является: [F]=Н=(кг•м)/с2
В СГС: [F]=дин
1Н=105 дин
Примеры решения задач
Пример
Задание. Уравнения $x=alpha t^{3}, y=beta t$ ($alpha$ и
$beta$ – постоянные коэффициенты) задают движение материальной точки массы m=const.
Как изменяется по модулю сила, которая действует на точку?
Решение. В качестве основы для решения задачи используем второй закон Ньютона в виде:
$bar{F} = mbar{a} (1.1)$
Зная законы изменения координат точки в зависимости от времени определим уравнения изменения составляющих ускорения.
Для этого найдем производные по времени от соответствующих координат:
$$
begin{array}{c}
a_{x}=frac{d^{2} x}{d t^{2}}=6 alpha t(1.2) \
a_{y}=frac{d^{2} y}{d t^{2}}=0(1.3)
end{array}
$$
Так как модуль ускорения равен:
$$a=sqrt{a_{x}^{2}+a_{y}^{2}}(1.4)$$
то, учитывая выражения (1.2) и (1.3), получаем:
$a = 6 alpha t (1.5)$
Так как ay=0, то получаем, что сила, которая действует на нашу точку, направлена по оси X, так как направление ускорение
и силы совпадают, а мы получили:
$$bar{a}=6 alpha t cdot bar{i}(1.6)$$
где $bar{i}$ – единичный вектор, направленный по оси X.
Исходя из второго закона Ньютона, имеем:
$$F=m cdot 6 alpha t, bar{F}=m 6 alpha t cdot bar{i}$$
Ответ. Так как $F=m cdot 6 alpha t$, то с течением времени сила увеличивается по модулю.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Два параллелепипеда лежат на горизонтальной поверхности. Они соприкасаются. Данные тела могут
скользить по поверхности опоры без трения. Масса одного тела равна m1, второго – m2. Первое тело толкнули с силой F0.
Какова сила давления тел друг на друга (F)?
Решение. Сделаем рисунок.
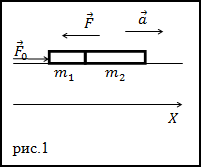
Рассмотрим, какие силы приложены к первому телув момент толчка, запишем для него второй закон Ньютона:
$$bar{F}_{0}+bar{F}+m_{1} bar{g}+bar{N}=m_{1} bar{a}(2.1)$$
где $m_{1} bar{g}$ – сила тяжести,
$bar{N}$ – реакция опоры,
$bar{a}$ – ускорение тела.
В проекции на ось Xуравнение (2.1) примет вид:
$$F_{0}-F=m_{1} a rightarrow F=F_{0}-m_{1} a(2.2)$$
Рассмотрим силы, приложенные к двум параллелепипедам как системе:
$$bar{F}_{0}+left(m_{1}+m_{2}right) bar{g}+overline{N^{prime}}=left(m_{1}+m_{2}right) bar{a}(2.3)$$
В проекции на ось X уравнение (2.3) примет вид:
$$F_{0}=left(m_{1}+m_{2}right) a(2.4)$$
Из уравнения (2.4) выразим ускорение:
$$a=frac{F_{0}}{m_{1}+m_{2}}$$
Подставим правую часть выражения (2.5) в (2.2) вместо ускорения:
$$F=F_{0}-m_{1} cdot frac{F_{0}}{m_{1}+m_{2}}$$
Ответ. $F=F_{0}-m_{1} cdot frac{F_{0}}{m_{1}+m_{2}}$
Читать дальше: Формула сопротивления.
Сила — это векторная физическая величина, имеющая направление и численное значение. Как же определить ее численное значение?
Что значит измерить какую-либо силу? Как вы уже знаете, для этого нам необходимо определить единицу измерения — некий эталон, принятый за единицу. За такую единицу можно принять любую силу. Например, силу тяжести, которая действует на какое-то определенное тело.
Также можно принять и силу упругости выбранной пружины, растянутой до некоторой длины. На данном уроке вы узнаете, какую силу приняли за единицу, получите формулу для определения силы тяжести и научитесь ею пользоваться для решения задач.
Единицы силы
Если изменяется скорость тела, то мы можем сказать, что на него действует сила. Итак, что принято за единицу силы?
За единицу силы принята сила, которая за время $1 space c$ изменяет скорость тела массой $1 space кг$ на $1 frac{м}{с}$.
Данная единица называется ньютоном ($1 space Н$). Она была названа в честь знаменитого английского физика, механика и астронома Исаака Ньютона (рисунок 1).
Часто используются и другие единицы — килоньютон ($кН$) и миллиньютон ($мН$).
$1 space кН = 1000 space Н$,
$1 space Н = 0,001 space кН$.
$1 space Н = 1000 space мН$,
$1 space мН = 0,001 space Н$.
Связь между силой тяжести и массой тела
Теперь мы знаем единицу измерения силы. Но как ее представить? С чем сравнить? Что это за сила в $1 space Н$?
Рассмотрим силу тяжести, равную $1 space Н$.
Доказано, что с такой силой притягивается к Земле тело массой приблизительно $frac{1}{10} space кг$. Если быть более точными, эта масса составляет $frac{1}{9.8} space кг$ (около $102 space г$). Но чему будет равна сила тяжести, действующая на тело другой массы?
Нам известно, что сила тяжести прямо пропорциональна массе рассматриваемого тела. Если мы возьмем два тела с разными массами, то во сколько раз отличаются друг от друга массы двух тел, во столько же раз будут отличаться силы тяжести, действующие на них.
Теперь используем новую информацию.
На тело массой $frac{1}{9.8} space кг$ действует сила тяжести в $1 space Н$.
Возьмем тело с массой в 2 раза большей — $frac{2}{9.8} space кг$. Тогда сила тяжести тоже будет в 2 раза больше — $2 space Н$.
Очевидно, что на тело с массой $frac{7}{9.8} space кг$ будет действовать сила тяжести, равная $7 space Н$, на тело с массой $frac{7.5}{9.8} space кг$ — $7.5 space Н$ и т.д.
А теперь возьмем тело с массой $frac{9.8}{9.8} space кг$. На него будет действовать сила тяжести, равная $9.8 space Н$. Посмотрите внимательнее на массу данного тела: $frac{9.8}{9.8} space кг = 1 space кг$.
На тело массой $1 space кг$ действует сила тяжести, равная $9.8 space Н$
Значение данной силы, действующей на тело массой $1 space кг$, можно записать как: $9.8 space frac{Н}{кг}$.
Формула для расчета силы тяжести. Ускорение свободного падения
Давайте снова используем свойство прямо пропорциональности массы и силы тяжести:
- если мы возьмем тело с массой $2 space кг$ (а это в 2 раза больше, чем масса $1 space кг$), то сила тяжести будет равна $19.6 space Н$ ($9.8 space Н cdot 2$)
- если мы возьмем тело с массой $3 space кг$ (а это в 3 раза больше, чем масса $1 space кг$), то сила тяжести будет равна $29.4 space Н$ ($9.8 space Н cdot 3$)
Так мы можем продолжать бесконечно, рассматривая тела различных масс. Таким образом,
Чтобы определить силу тяжести, действующую на тело любой массы, нужно $9.8 frac{Н}{кг}$ умножить на массу выбранного тела:
$F_{тяж} = 9.8 frac{Н}{кг} cdot m$.
Величину $9.8 frac{Н}{кг}$ обозначают буквой $g$ и называют ускорением свободного падения.
Так мы получили формулу для силы тяжести. Как рассчитать силу тяжести, действующую на тело любой массы?
$F_{тяж} = gm$
Если тело и опора неподвижны или движутся равномерно и прямолинейно, то мы получим формулу для веса тела.
По какой формуле можно определить вес тела?
$$P = F_{тяж} = gm$$
Примеры задач
Если для решения задачи не требуется особой точности, $g = 9.8 frac{Н}{кг}$ округляют до $g = 10 frac{Н}{кг}$. Если в тексте задачи нет информации о точности или используемой величине ускорения свободного падения, то используется $g = 9.8 frac{Н}{кг}$.
Задача №1
На столе лежит книга массой $700 space г$. Определите силу тяжести и вес книги. Покажите эти силы на рисунке, используя масштаб, где за $1 space Н$ равен $0.5 space си$. При расчетах используйте ускорение свободного падения равное $10 frac{Н}{кг}$.
Дано:
$m = 700 space г$
$g = 10 frac{Н}{кг}$
СИ:
$m = 0.7 space кг$
$F_{тяж} — ?$
$P — ?$
Показать решение и ответ
Скрыть
Решение:
Используем формулы: $F_{тяж} = gm$ и $P = gm$.
$F_{тяж} = P approx 10 frac{Н}{кг} cdot 0.7 space кг = 7 space Н$.
Сила тяжести и вес изображены на рисунке 2. Из условия задачи $1 space Н$ будет равен отрезку $0.5 space см$. Тогда сила в $7 space Н$ будет изображаться отрезком длиной $3.5 space см$. Сила тяжести у нас приложена к телу и направлена вертикально вниз (рисунок 2, а), а вес — к опоре и направлен перпендикулярно ей (в данном случае вертикально вниз — рисунок 2, б).
Ответ: $F_{тяж} = P = 7 space Н$.
Задача №2
Найдите вес воды объемом $4 space дм^3$. Вода находится в неподвижном сосуде.
Для решения этой задачи найдем табличное значение плотности воды — $1000 frac{кг}{м^3}$.
Переведем объем, выраженный в $дм^3$, в $м^3$:
$4 space дм^3 = 4 cdot 1 space дм cdot 1 space дм cdot 1 space дм = 4 cdot 0.1 space м cdot 0.1 space м cdot 0.1 space м = 4 cdot 0.001 space м^3 = 0.004 space м^3$.
Теперь можно записать условия задачи и решить ее.
Дано:
$V = 4 space дм^3$
$rho = 1000 frac{кг}{м^3}$
$g = 9.8 frac{Н}{кг}$
СИ:
$V = 0.004 space м^3$
$P — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для определения веса имеет вид:
$P = gm$.
Массу воды мы можем определить, зная ее плотность и объем:
$m = rho V$.
Подставим в формулу для определения веса:
$P = gm = g rho V$.
$P = 9.8 frac{Н}{кг} cdot 1000 frac{кг}{м^3} cdot 0.004 space м^3 = 39.2 space Н$.
Ответ: $P = 39.2 space Н$.
Задача №3
Люстра, подвешенная к потолку, действует на него с силой $63.7 space Н$. Найдите массу люстры.
Для того чтобы верно записать условия задачи, нужно понимать, как люстра действует на потолок. Люстра неподвижна, значит, речь идет о весе.
Дано:
$P = 63.7 space Н$
$g = 9.8 frac{Н}{кг}$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Итак, люстра действует на потолок своим весом. На люстру же действует сила тяжести, численно равная весу люстры.
Воспользуемся формулой:
$P = gm$.
Выразим массу:
$m = frac {P}{g}$.
$m = frac {63.7 space Н}{9.8 frac{Н}{кг}} = 6.5 space кг$.
Ответ: $m = 6.5 space кг$.
Больше задач на расчет силы тяжести, а также веса тела и силы упругости смотрите в отдельном уроке.
Упражнения
Упражнение №1
Определите силу тяжести, действующую на тело массой $3.5 space кг$; $400 space г$; $1.5 space т$; $60 space г$.
Дано:
$m_1 = 3.5 space кг$
$m_2 = 400 space г$
$m_3 = 1.5 space т$
$m_4 = 60 space г$
$g approx 10 frac{Н}{кг}$
СИ:
$m_2 = 0.4 space кг$
$m_3 = 1500 space кг$
$m_4 = 0.06 space кг$
$F_{тяж1} — ?$
$F_{тяж2} — ?$
$F_{тяж3} — ?$
$F_{тяж4} — ?$
Показать решение и ответ
Скрыть
Решение:
Для расчета силы тяжести будем использовать формулу: $F_{тяж} = gm$.
$F_{тяж1} = gm_1$,
$F_{тяж1} = 10 frac{Н}{кг} cdot 3.5 space кг = 35 space Н$.
$F_{тяж2} = gm_2$,
$F_{тяж2} = 10 frac{Н}{кг} cdot 0.4 space кг = 4 space Н$.
$F_{тяж3} = gm_3$,
$F_{тяж3} = 10 frac{Н}{кг} cdot 1500 space кг = 15000 space Н = 15 space кН$.
$F_{тяж4} = gm_4$,
$F_{тяж4} = 10 frac{Н}{кг} cdot 0.06 space кг = 0.6 space Н$.
Ответ: $F_{тяж1} = 35 space Н$, $F_{тяж2} = 4 space Н$, $F_{тяж3} = 15 space кН$, $F_{тяж4} = 0.6 space Н$.
Упражнение №2
Найдите вес тела, масса которого $5 space кг$, $300 space г$.
Дано:
$m_1 = 5 space кг$
$m_2 = 300 space г$
$g approx 10 frac{Н}{кг}$
$P_1 — ?$
$P_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Для расчета веса тел будем использовать формулу: $P = F_{тяж} = gm$.
$P_1 = gm_1$,
$P_1 = 10 frac{Н}{кг} cdot 5 space кг = 50 space Н$.
$P_2 = gm_2$,
$P_2 = 10 frac{Н}{кг} cdot 0.3 space кг = 3 space Н$.
Ответ: $P_1 = 50 space Н$, $P_2 = 3 space Н$.
Упражнение №3
Вес человека $700 space Н$. Определите его массу. Сделайте рисунок и покажите вес тела.
Дано:
$P = 700 space Н$
$g approx 10 frac{Н}{кг}$
$m — ?$
Показать решение и ответ
Скрыть
Решение:
Мы знаем, что вес тела будет равен силе тяжести, действующей на человека. Запишем формулу, связывающую эти величины, и рассчитаем массу тела человека.
$P = F_{тяж} = gm$,
$m = frac{P}{g}$,
$m = frac{700 space Н}{10 frac{Н}{кг}} = 70 space кг$.
На рисунке 3 изображен вес тела человека.
Масштаб: $200 space Н$ соответствует отрезку длиной $1 space см$. Так, вес изображен отрезком длиной $3.5 space см$.
В отличие от силы тяжести вес тела приложен к опоре, а не к центру тела. Так как человек стоит на полу, то вес приложен к точке между подошвами его обуви и полом.
Ответ: $m = 70 space кг$.
Упражнение №4
Выразите в ньютонах следующие силы: $240 space кН$, $25 space кН$, $5 space кН$, $0.2 space кН$.
Показать решение
Скрыть
Решение:
$F_1 = 240 space кН = 240 space 000 space Н$.
$F_2 = 25 space кН = 25 space 000 space Н$.
$F_3 = 5 space кН = 5000 space Н$.
$F_4 = 0.2 space кН = 200 space Н$.
Упражнение №5
На столе стоит телевизор массой $5 space кг$. Определите силу тяжести и вес телевизора. Изобразите эти силы на рисунке.
Дано:
$m = 5 space кг$
$g approx 10 frac{Н}{кг}$
$F_{тяж} — ?$
$P — ?$
Показать решение и ответ
Скрыть
Решение:
Телевизор неподвижен, поэтому вес тела и сила тяжести будут равны друг другу. Рассчитаем их:
$P = F_{тяж} = gm$,
$P = F_{тяж} = 10 frac{Н}{кг} cdot 5 space кг = 50 space Н$.
Для изображения сил выберем масштаб: $10 space Н$ соответствует отрезок длиной $1 space см$. На рисунке 4, а показана сила тяжести, действующая на телевизор. Она приложена к его центру. На рисунке 4, б показан вес, действующий на телевизор. Он приложен к опоре. Эти силы равны по модулю, поэтому при их изображении обратите внимание на то, чтобы отрезки были одинаковой длины (по $5 space см$ каждый).
Ответ: $P = F_{тяж} = 50 space Н$.




