Как найти фокус параболы через уравнение – Сайт, где вы сможете решить свои вопросы

Download Article

If you’ve ever cooked food with a parabolic oven in science class or seen the Death Star’s laser in Star Wars, you have an idea of what the focal point (or focus) of a parabola is. But how do you calculate the focus mathematically? We’ve provided the formulas and equations you need to find the focus of any parabola, and added several helpful sample problems that you might see on your next algebra exam!

Things You Should Know

1
Parabola: A parabola can be defined as the graph of a quadratic equation—that is, the curved line you’ll get if you plot the equation on graph paper. Or, if you want to be more technical, it’s a curved line in which all coordinate points $(x,y)$ along the line are equidistant from a specific focal point and a specific line called a directrix.^[1]
- In practical terms, it’s often easier to recognize parabolas in three dimensions. For example, think of large parabolic satellite dishes, or the clear plastic parabolic microphones you see on the sidelines of football games. Both of these direct waves (radio, sound, etc.) toward a single point—the focal point (or focus).
2

Vertex: The vertex is the “turning point” of a parabola—the point along the curve at which it changes direction. So, in a classic “U”-shaped parabola, the vertex is at the very bottom of the “U” shape. You need to know the $(x,y)$ coordinates of the vertex in order to find the coordinates of the focus.^[2]

Advertisement
3
Axis of symmetry: The axis of symmetry is a line that runs through the vertex point and divides the parabola exactly in half. The parabola is a mirror image of itself on either side of the axis of symmetry.^[3]
- For our needs, it’s also important that the vertex is always exactly halfway between the focus and the directrix along the axis of symmetry.
4
Directrix: The directrix is a straight line that crosses the axis of symmetry and is perpendicular to it. The directrix is always outside of the parabola but closest to the vertex. For example, in a classic “U” parabola, adding the directrix line makes it look like you underlined the “U.”^[4]
- The distance between the vertex and the directrix (at the axis of symmetry) is always exactly the same as that between the vertex and the focus.
5
Focus: The focus is a point along the axis of symmetry, inside the parabola, that is equal in distance from the vertex as is the directrix. So, if the directrix is 2 units away from the vertex, the focus is also 2 units away (and, as a result, 4 units away from the directrix).^[5]
- If you draw a straight line from the focus to any point along the curve of the parabola, and then draw a straight line from that point to intersect at a right angle with the directrix, you’ll find that both of those lines are always equal in length.

1

${displaystyle y=a(x-h^{2})+k}$ or ${displaystyle x=a(y-k)^{2}+h}$ . You’ll use one of these “vertex form of a parabola” equations based on the type of parabola you’re dealing with. A “regular” parabola that opens upward or downward (like a right-side up or upside-down “U”) needs to be converted into the form of the first equation, while a “sideways” parabola that opens to the side (like a forwards or backwards “C”) must be converted to the second.^[6]
2

${displaystyle (h,k+1/(4a))}$ or ${displaystyle (h+1/(4a),k)}$ . Once you have determined (or have been given) the coordinates of the parabola’s vertex, you’ll use one of these formulas to determine the coordinates of the focus. Here’s how to know which to use:^[7]

1

Put the equation into the vertex form of a parabola. Because the $x$ portion of the equation is squared, the correct vertex form is ${displaystyle y=a(x-h)^{2}+k}$ , meaning this is a “regular” parabola (it opens either up or down).
2
3

Solve for $a$ to find the focus coordinates.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Thanks for submitting a tip for review!

References

About This Article

Thanks to all authors for creating a page that has been read 3,279 times.

Did this article help you?

Источник

Парабола, её форма, фокус и директриса.

Начать изучение
Свойства параболы.

Начать изучение
Уравнение касательной к параболе.

Начать изучение

Парабола, её форма, фокус и директриса.

Определение.

Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^{2}=2pxlabel{ref15}
$$
при условии (p > 0).

Из уравнения eqref{ref15} вытекает, что для всех точек параболы (x geq 0). Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.

Форма параболы известна из курса средней школы, где она встречается в качестве графика функции (y=ax^{2}). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством (2p=a^{-1}).

Фокусом параболы называется точка (F) с координатами ((p/2, 0)) в канонической системе координат.

Директрисой параболы называется прямая с уравнением (x=-p/2) в канонической системе координат ((PQ) на рис. 8.11).

парабола

Рис. 8.11. Парабола.

Свойства параболы.

Утверждение.

Расстояние от точки (M(x, y)), лежащей на параболе, до фокуса равно
$$
r=x+frac{p}{2}.label{ref16}
$$

Доказательство.

Вычислим квадрат расстояния от точки (M(x, y)) до фокуса по координатам этих точек: (r^{2}=(x-p/2)^{2}+y^{2}) и подставим сюда (y^{2}) из канонического уравнения параболы. Мы получаем
$$
r^{2}=left(x-frac{p}{2}right)^{2}+2px=left(x+frac{p}{2}right)^{2}.nonumber
$$
Отсюда в силу (x geq 0) следует равенство eqref{ref16}.

Заметим, что расстояние от точки (M) до директрисы также равно
$$
d=x+frac{p}{2}.nonumber
$$

Следовательно, мы можем сделать следующий вывод.

Утверждение.

Для того чтобы точка (M) лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.

Доказательство.

Докажем достаточность. Пусть точка (M(x, y)) одинаково удалена от фокуса и от директрисы параболы:
$$
sqrt{left(x-frac{p}{2}right)^{2}+y^{2}}=x+frac{p}{2}.nonumber
$$

Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы eqref{ref15}. Это заканчивает доказательство.

Параболе приписывается эксцентриситет (varepsilon=1). В силу этого соглашения формула
$$
frac{r}{d}=varepsilonnonumber
$$
верна и для эллипса, и для гиперболы, и для параболы.

Уравнение касательной к параболе.

Выведем уравнение касательной к параболе в точке (M_{0}(x_{0}, y_{0})), лежащей на ней. Пусть (y_{0} neq 0). Через точку (M_{0}) проходит график функции (y=f(x)), целиком лежащий на параболе. (Это (y=sqrt{2px}) или же (y=-sqrt{2px}), смотря по знаку (y_{0}).) Для функции (f(x)) выполнено тождество ((f(x))^{2}=2px), дифференцируя которое имеем (2f(x)f'(x)=2p). Подставляя (x=x_{0}) и (f(x_{0})=y_{0}), находим (f'(x_{0})=p/y_{0}) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_{0}=frac{p}{y_{0}}(x-x_{0}).nonumber
$$
Упростим его. Для этого раскроем скобки и вспомним, что (y_{0}^{2}=2px_{0}). Теперь уравнение касательной принимает окончательный вид
$$
yy_{0}=p(x+x_{0}).label{ref17}
$$

Заметим, что для вершины параболы, которую мы исключили, положив (y_{0} neq 0), уравнение eqref{ref17} превращается в уравнение (x=0), то есть в уравнение касательной в вершине. Поэтому уравнение eqref{ref17} справедливо для любой точки на параболе.

Утверждение.

Касательная к параболе в точке (M_{0}) есть биссектриса угла, смежного с углом между отрезком, который соединяет (M_{0}) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).

Доказательство.

Рис. 8.12. Касательная к параболе.

Рассмотрим касательную в точке (M_{0}(x_{0}, y_{0})). Из уравнения eqref{ref17} получаем ее направляющий вектор (boldsymbol{v}(y_{0}, p)). Значит, ((boldsymbol{v}, boldsymbol{e}_{1})=y_{0}) и (cos varphi_{1}=y_{0}/boldsymbol{v}). Вектор (overrightarrow{FM_{0}}) имеет компоненты (x_{0}=p/2) и (y_{0}), а потому
$$
(overrightarrow{FM_{0}}, boldsymbol{v})=x_{0}y_{0}-frac{p}{2}y_{0}+py_{0}=y_{0}(x_{0}+frac{p}{2}).nonumber
$$
Но (|overrightarrow{FM_{0}}|=x_{0}+p/2). Следовательно, (cos varphi_{2}=y_{0}/|boldsymbol{v}|). Утверждение доказано.

Заметим, что (|FN|=|FM_{0}|) (см. рис. 8.12).

Источник

Координаты фокуса параболы: как найти, формула

Содержание:

Формулировка параболы в алгебре и геометрии
Что такое фокус параболы, определение
Как найти фокус параболы
- Уравнение расчета
- Чему равны координаты фокуса
Абсцисса фокуса параболы
Примеры расчета фокусного расстояния в задачах

Формулировка параболы в алгебре и геометрии

Определение

Парабола — совокупность точек на плоскости, расположенных на одинаковом удалении от фокуса F и директрисы d, в которую точка F не входит.

Парабола

Парабола является коническим сечением, или коникой. Это значит, что она возникает при пересечении плоскости с поверхностью кругового конуса. Плоскость сечения при этом параллельна одной из касательных плоскостей конуса.

Парабола в конусе

Точка пересечения параболы с ее осью называется вершиной. Она считается началом системы координат, канонической для данной кривой.

Что такое фокус параболы, определение

Определение

Расстояние от точки фокуса до любой точки параболы равняется расстоянию от этой точки к директрисе.

Если в фокус поместить источник света, все исходящие из него световые лучи после отражения от нее пойдут по прямым, параллельным оси симметрии. И наоборот, все световые лучи, идущие параллельно оси, после отражения от «стенок» кривой соберутся в одной точке. Это оптическое свойство широко применяется в конструкциях прожекторов, фар, фонарей, телескопов-рефлекторов.

Как найти фокус параболы

Уравнение расчета

Каноническое уравнение:

(y^2;=;2px)

Парабола на оси

Если расположить параболу слева от оси ординат, уравнение примет вид:

(y^2;=;-;2px)

Парабола отрицательное уравнение

Параметр p — расстояние от фокуса до директрисы, которая определяется уравнением:

(х;=;-frac p2)

Чтобы узнать расстояние r от любой точки параболы до фокуса, равное ее расстоянию до директрисы, нужно воспользоваться формулой:

(r;=;frac p2;+;x)

В полярной системе координат с центром в фокусе и направлением вдоль оси фокальный параметр можно найти по формуле:

(p;=;rho;times;(1;+;cosleft(varthetaright)))

Чему равны координаты фокуса

Фокус будет иметь координаты ((frac p2;;0)).

Абсцисса фокуса параболы

Также фокус и параметр p можно искать через так называемую фокальную хорду (Р_1Р_2).

Хорда параболы

Эта прямая, проходящая через фокус и параллельная директрисе, пересекает параболу в двух точках. Половина длины фокальной хорды будет равна параметру p, являясь абсолютной величиной ординаты любой из точек (Р_1, Р_2).

Абсцисса каждой из этих точек будет равна абсциссе фокуса (frac p2).

Для ординаты y каждой из точек (Р_1, Р_2):

(y^{2;}=;2p;times;frac p2;=;p^2).

Примеры расчета фокусного расстояния в задачах

Пример 1

Определить координаты фокуса параболы (y^{2;}=;4х).

Решение

Находим параметр p:

4 = 2p

p = 2

Координаты (1; 0).

Пример 2

Определить координаты фокуса параболы (y^{2;}=;6х).

Решение

Находим параметр p:

6 = 2p

p = 3

Координаты (1,5; 0).

Насколько полезной была для вас статья?

Рейтинг: 2.02 (Голосов: 47)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Парабола — это график функции описанный определённой формулой. Чтобы построить параболу нужно следовать формуле, определениям и уравнениям.

Парабола

Парабола – это множество точек плоскости, которые равноотделённые от заданной точки, что называется фокусом и заданной прямой под названием директриса.

Чтобы получить каноническое уравнение параболы, расположим директрису перпендикулярно оси , а фокус на оси так, чтобы начало координат помещался на одинаковом расстоянии от них (см. рис. 1). Обозначим через расстояние от фокуса к директрисе, тогда у фокуса будут координаты , .

Для произвольной точки параболы расстояний , а расстояние к директрисе . По определению из рис. 1 видим, что , а ${r} = sqrt{x - {pover{2}}^2} + y^2$ и поэтому:

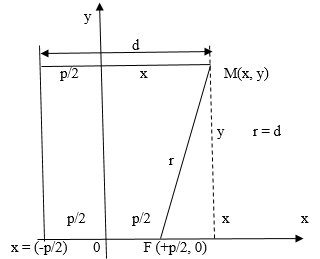
Парабола

Рис. 1

$sqrt{(x - {pover{2}})^2 + y^2} = x + {pover{2}}to{x}^2 - 2 * {pover2}}x + {p^2over{4}} + y^2 = x^2 + 2 * {pover{2}}x + {p^2over{4}}$

(1)

– каноническое уравнение параболы.

Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Что такое вершина параболы

Вершина параболы – это парабола, которая проходит через точки . Если точка $M_{1}(x , y)$ принадлежит параболе, то и $M_{2}(x , -y)$ тоже принадлежит параболе, так как из:

$y^2 = 2pxto{(-y)^2 = 2px}$ .

Значит, парабола симметрична относительно оси , её график достаточно построить в первой четверти, где из канонического уравнения параболы получается, что:

Чтобы найти вершину параболы, необходимо знать формулу: .

Давайте посмотрим, как данная формула действует, допустим дано уравнение:

Тогда:

, , . Чтобы найти величины , и , в квадратном уравнении коэффициент при , при , постоянная (коэффициент без переменной) = . Если взять тот же пример, , получается, что:

, , .

Форма и характеристики параболы

Исследуем за каноническим уравнением форму и расположение параболы:

1. В уравнении переменная входит в парной степени откуда получается, что парабола симметрична относительно оси . Ось – это ось, которая симметрична параболе.

2. Так как , тогда , откуда получается, что парабола расположена справа от оси .

3. При мы имеем , то есть парабола проходит через начало координат. Точка – это вершина параболы.

4. При увеличении значений переменной модуль тоже возрастает. Изобразим параболу на рисунке:

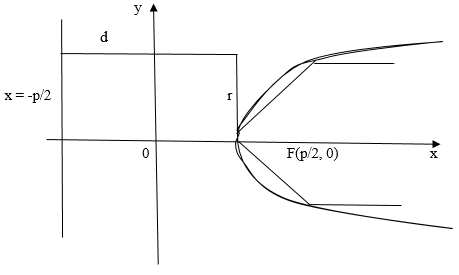
Возрастание параболы

Рис. 2

5. В полярной системе координат, у канонического уравнения параболы такой вид:

6. Уравнение , , , тоже описывают параболы:

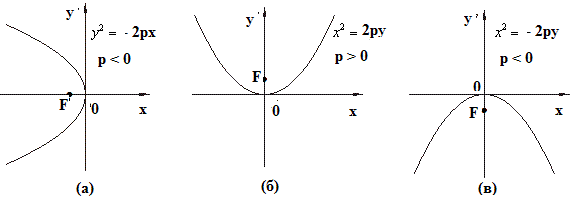
Парабола

Рис. 3

Оптическое свойство параболы

У параболы “оптическое” свойство, если: в фокусе параболы поместить источник света, тогда отбитые от параболы лучи будут параллельными оси . Это свойство учитывают при изготовлении прожекторов, зеркальных телескопов, теле- и радио антенн.

При положительном уравнении:

описывают параболу симметричную относительно с вершиной в точке , ветви которой направлены влево (рис. 3 (а)).

Аналогично изложенному, уравнение и описывают параболы с вершиной в точке симметрично относительно , ветви которой направлены соответственно вверх и вниз (см. рис. 3 (б) и (в)). Если например, уравнение решить относительно

$y = {1over{2p}}x^2$ и обозначить , тогда получим известное со школьного курса уравнение параболы . Теперь её фокусное расстояние .

Примеры решения

Задача

Найти координаты фокуса и составить уравнение директрисы параболы .

Решение

Сравнивая каноническое уравнение и данное , получим , , тогда. Так как уравнение директрисы , тогда в данном случае .

Ответ

координаты фокуса: , а уравнение директрисы параболы: .

Задача

Составить каноническое уравнение параболы:

а) с фокусом в точке ;

б) с фокусом в точке .

Решение

а). Так как фокус на положительной полуоси , тогда парабола симметрична относительно с вершиной в точке и , поэтому и согласно формуле (1) .

б). Фокус лежит на отрицательной полуоси с вершиной в точке , ветви направлены вниз, каноническое уравнение следует искать в виде . Фокусное расстояние параболы и уравнение запишется .

Ответ

а) каноническое уравнение параболы с фокусом в точке : ;

б) каноническое уравнение с фокусом в точке : .

Задача

Показать путём выделения полного квадрата, что уравнение – это уравнение параболы. Привести его к каноническому виду. Найти вершину, фокус, ось и директрису этой параболы.

Решение

Выделим относительно переменной полный квадрат

= $0to{4(x^2 - 3x)} + y + 6$ = $0to{4((x^2 - 2 * {3over{2}}x + {9over{4}}) - {9over{4}}) + y + 6$ = $0}to{4((x - {3over{2}}})^2 - 9 + y + 6$ = = $-4(x - {3over{2}})^2}to{(x - {3over{2}})^2}$ = .

Обозначим $y_{1} = y - 3$ , $x_{1} = x - {3over{2}}$ . Тогда в результате параллельного переноса координатных осей в новое начало, то есть в точку $O_{1}({3over{2}}, 3)$ , получим каноническое уравнение параболы ${x_{1}^2} = -{1over{4}}y_{1}$ .

Ветви этой параболы направлены вниз симметрично относительно оси $O_{1}Y_{1}$ , , – фокусное расстояние. В новой системе координат фокус находится в точке , уравнение директрисы в новой системе $y_{1} = {1over{16}}$ .

Повернёмся к старым координатам при помощи замены $y_{1} = y - 3$ , $x_{1} = x - {3over{2}}$ . Уравнение оси в новой системе $x_{1} = 0$ , а в старой – уравнение оси параболы.

Уравнение директрисы в новой системе координат $y_{1} = {1over{16}}$ , а в старой .

В новой системе $X_{1}O_{1}Y_{1}$ для фокуса $F(0, -{1over{16}}) x_{1} = 0$ , $y_{1} = -{1over{16}}$ , а в старой системе $x_{F} - {3over{2}} = 0to{x_{F}} = {3over{2}}$ , $y_{F} - 3 = -{1over{16}}to{y_{F} = -{1over{16}} + 3to{y_{F}} = {47over{16}}$ , то есть .

Ответ

Каноническое уравнение параболы – ${x_{1}^2} = -{1over{4}}y_{1}$ ;

вершина – ветви параболы направлены вниз;

$O_{1}Y_{1}$ , , $p_{2} = -{1over{16}}$ – фокусное расстояние, а фокус находится в точке ;

уравнение оси $x_{1} = 0$ ;

уравнение директрисы $y_{1} = {1over{16}}$ .

Источник

Парабола: формулы, примеры решения задач

Определение параболы. Параболой называется множество всех точек плоскости, таких, каждая из которых находится на одинаковом расстоянии от точки, называемой фокусом, и от прямой, называемой директрисой и не проходящей через фокус.

Каноническое уравнение параболы имеет вид:

где число p, называемое параметром параболы, есть расстояние от фокуса до директрисы.

На чертеже линия параболы – бордового цвета, директриса – ярко-красного цвета, расстояния от точки до фокуса и директрисы – оранжевого.

В математическом анализе принята другая запись уравнения параболы:

то есть ось параболы выбрана за ось координат. Можно заметить, что ax² – это квадратный трёхчлен ax² + bx + c , в котором b = 0 и c = 0 . График любого квадратного трёхчлена, то есть левой части квадратного уравнения, будет параболой.

Фокус параболы имеет координаты

Директриса параболы определяется уравнением .

Расстояние r от любой точки параболы до фокуса определяется формулой .

Для каждой из точек параболы расстояние до фокуса равно расстоянию до директрисы.

Пример 1. Определить координаты фокуса параболы

Решение. Число p расстояние от фокуса параболы до её директрисы. Начало координат в данном случае – в роли любой точки, расстояния от которой от фокуса до директрисы равны. Находим p:

Находим координаты фокуса параболы:

Пример 2. Составить уравнение директрисы параболы

Решение. Находим p:

Получаем уравнение директрисы параболы:

Пример 3. Составить уравнение параболы, если расстояние от фокуса до директрисы равно 2.

Решение. Параметр p – это и есть данное расстояние от фокуса до директрисы. Подставляем и получаем:

Траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Зона достижимости для пущенных камней вновь будет параболой. В данном случае речь идёт об огибающей кривой траекторий камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью.

Парабола обладает следующим оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения (фигур, получающихся при вращении параболы вокруг оси). Пучок параллельных лучей, двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.

Парабола

Парабола, её форма, фокус и директриса.

Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^<2>=2pxlabel
$$
при условии (p > 0).

Из уравнения eqref вытекает, что для всех точек параболы (x geq 0). Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.

Форма параболы известна из курса средней школы, где она встречается в качестве графика функции (y=ax^<2>). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством (2p=a^<-1>).

Фокусом параболы называется точка (F) с координатами ((p/2, 0)) в канонической системе координат.

Директрисой параболы называется прямая с уравнением (x=-p/2) в канонической системе координат ((PQ) на рис. 8.11).

Рис. 8.11. Парабола.

Свойства параболы.

Расстояние от точки (M(x, y)), лежащей на параболе, до фокуса равно
$$
r=x+frac

<2>.label
$$

Вычислим квадрат расстояния от точки (M(x, y)) до фокуса по координатам этих точек: (r^<2>=(x-p/2)^<2>+y^<2>) и подставим сюда (y^<2>) из канонического уравнения параболы. Мы получаем
$$
r^<2>=left(x-frac

<2>right)^<2>+2px=left(x+frac

<2>right)^<2>.nonumber
$$
Отсюда в силу (x geq 0) следует равенство eqref.

Заметим, что расстояние от точки (M) до директрисы также равно
$$
d=x+frac

<2>.nonumber
$$

Следовательно, мы можем сделать следующий вывод.

Докажем достаточность. Пусть точка (M(x, y)) одинаково удалена от фокуса и от директрисы параболы:
$$
sqrt<left(x-frac

<2>right)^<2>+y^<2>>=x+frac

<2>.nonumber
$$

Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы eqref. Это заканчивает доказательство.

Параболе приписывается эксцентриситет (varepsilon=1). В силу этого соглашения формула
$$
frac=varepsilonnonumber
$$
верна и для эллипса, и для гиперболы, и для параболы.

Уравнение касательной к параболе.

Выведем уравнение касательной к параболе в точке (M_<0>(x_<0>, y_<0>)), лежащей на ней. Пусть (y_ <0>neq 0). Через точку (M_<0>) проходит график функции (y=f(x)), целиком лежащий на параболе. (Это (y=sqrt<2px>) или же (y=-sqrt<2px>), смотря по знаку (y_<0>).) Для функции (f(x)) выполнено тождество ((f(x))^<2>=2px), дифференцируя которое имеем (2f(x)f'(x)=2p). Подставляя (x=x_<0>) и (f(x_<0>)=y_<0>), находим (f'(x_<0>)=p/y_<0>) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_<0>=frac

>(x-x_<0>).nonumber
$$
Упростим его. Для этого раскроем скобки и вспомним, что (y_<0>^<2>=2px_<0>). Теперь уравнение касательной принимает окончательный вид
$$
yy_<0>=p(x+x_<0>).label
$$

Заметим, что для вершины параболы, которую мы исключили, положив (y_ <0>neq 0), уравнение eqref превращается в уравнение (x=0), то есть в уравнение касательной в вершине. Поэтому уравнение eqref справедливо для любой точки на параболе.

Касательная к параболе в точке (M_<0>) есть биссектриса угла, смежного с углом между отрезком, который соединяет (M_<0>) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).

Рассмотрим касательную в точке (M_<0>(x_<0>, y_<0>)). Из уравнения eqref получаем ее направляющий вектор (boldsymbol(y_<0>, p)). Значит, ((boldsymbol, boldsymbol_<1>)=y_<0>) и (cos varphi_<1>=y_<0>/boldsymbol). Вектор (overrightarrow>) имеет компоненты (x_<0>=p/2) и (y_<0>), а потому
$$
(overrightarrow>, boldsymbol)=x_<0>y_<0>-frac

<2>y_<0>+py_<0>=y_<0>(x_<0>+frac

<2>).nonumber
$$
Но (|overrightarrow>|=x_<0>+p/2). Следовательно, (cos varphi_<2>=y_<0>/|boldsymbol|). Утверждение доказано.

Заметим, что (|FN|=|FM_<0>|) (см. рис. 8.12).

Парабола – определение и вычисление с примерами решения

Парабола:

Определение: Параболой называется геометрическое место точек равноудаленных от выделенной точки F, называемой фокусом параболы, и прямой (l), называемой директрисой.

Получим каноническое уравнение параболы. Выберем декартову систему координат так, чтобы фокус F лежал на оси абсцисс, а директриса проходила бы через точку, расположенную симметрично фокусу, перпендикулярно к оси абсцисс (Рис. 34). Пусть точка M(х; у) принадлежит параболе: Вычислим расстояния от точки M(х; у) до фокуса и директрисы

Рис. 34. Парабола, (уравнение директрисы.

Возведем обе части уравнения в квадрат

Раскрывая разность квадратов, стоящую в правой части уравнения, получим каноническое уравнение параболы: (а также аналогичные ему, см. Рис. 35а и Рис. 356).

Рис. 35а. Параболы и их уравнения.

Рис. 356. Параболы и их уравнения.

Найдем координаты точек пересечения параболы с координатными осями:

– точка пересечения параболы с осью абсцисс;
– точка пересечения параболы с осью ординат.

Определение: Точка О(0; 0) называется вершиной параболы.

Если точка М(х; у) принадлежит параболе, то ей принадлежат и точка следовательно, парабола симметрична относительно оси абсцисс.

Пример:

Дано уравнение параболы Определить координаты фокуса параболы и составить уравнение параболы.

Решение:

Так как из уравнения параболы следует, что следовательно, Таким образом, фокус этой параболы лежит в точке а уравнение директрисы имеет вид

Пример:

Составить каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат, а параметр р равен расстоянию от фокуса гиперболы до её асимптоты.

Решение:

Для определения координат фокусов гиперболы преобразуем её уравнение к каноническому виду.

Гипербола:

Следовательно, действительная полуось гиперболы а мнимая полуось – Гипербола вытянута вдоль оси абсцисс Ох. Определим расположение фокусов данной гиперболы Итак, Вычислим расстояние от фокуса до асимптоты которое равно параметру р:

Следовательно, каноническое уравнение параболы, фокус которой лежит на оси Ох слева от начала координат имеет вид:

Пример:

Составить каноническое уравнение параболы, фокус которой совпадает с одним из фокусов эллипса Написать уравнение директрисы.

Решение:

Для определения координат фокусов эллипса преобразуем его уравнение к каноническому виду. Эллипс:

Следовательно, большая полуось эллипса а малая полуось Так как , то эллипс вытянут вдоль оси абсцисс Ох. Определим расположение фокусов данного эллипса Итак, Так как фокус параболы совпадает с одним из фокусов или эллипса, то параметр р найдем из равенства уравнение параболы имеет вид Директриса определяется уравнением

Уравнение параболоида вращения

Пусть вертикальная парабола

расположенная в плоскости Охz, вращается вокруг своей оси (ось Oz). При вращении получается поверхность, носящая название параболоида вращения (рис. 207).

Для вывода уравнения поверхности рассмотрим произвольную точку параболоида вращения, и пусть эта точка получена в результате вращения точки N(X, 0, Z) данной параболы вокруг точки С(0, 0, Z).

Так как точки М и N расположены в одной и той же горизонтальной плоскости и CN = СМ как радиусы одной и той же окружности, то имеем

Подставляя формулы (2) в уравнение (1), получим уравнение параболоида вращения

Заметим, что форму параболоида вращения имеет поверхность ртути, находящейся в вертикальном цилиндрическом сосуде, быстро вращающемся вокруг своей оси. Это обстоятельство используют в технике для получения параболических зеркал.

Рекомендую подробно изучить предметы:

Геометрия
Аналитическая геометрия
Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

Многогранник
Решение задач на вычисление площадей
Тела вращения: цилиндр, конус, шар
Четырехугольник
Многогранники
Окружность
Эллипс
Гипербола

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

[spoiler title=”источники:”]

http://univerlib.com/analytic_geometry/second_order_lines_and_surfaces/parabola/

http://www.evkova.org/parabola

[/spoiler]

Источник

Things You Should Know

References

About This Article

Did this article help you?

Парабола, её форма, фокус и директриса.

Свойства параболы.

Уравнение касательной к параболе.

Координаты фокуса параболы: как найти, формула

Формулировка параболы в алгебре и геометрии

Что такое фокус параболы, определение

Как найти фокус параболы

Уравнение расчета

Чему равны координаты фокуса

Абсцисса фокуса параболы

Примеры расчета фокусного расстояния в задачах

Текст с ошибкой:

Поиск по содержимому

Парабола

Что такое вершина параболы

Форма и характеристики параболы

Оптическое свойство параболы

Примеры решения

Парабола: формулы, примеры решения задач

Парабола

Парабола, её форма, фокус и директриса.

Свойства параболы.

Уравнение касательной к параболе.

Парабола – определение и вычисление с примерами решения

Уравнение параболоида вращения

Вам также может понравиться

Как исправить код ошибки 409

Как найти нормальную девушку как у всех

Как найти мультик по гифке

Добавить комментарий Отменить ответ