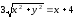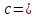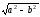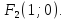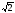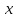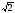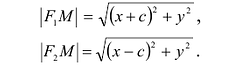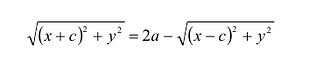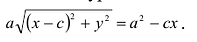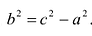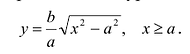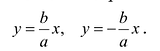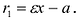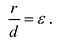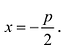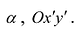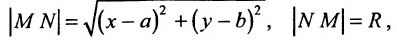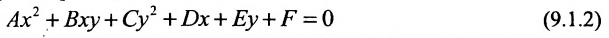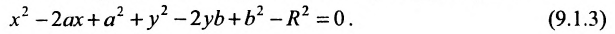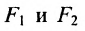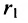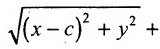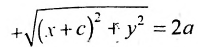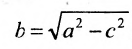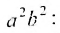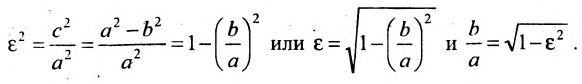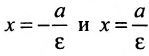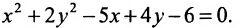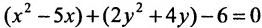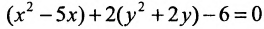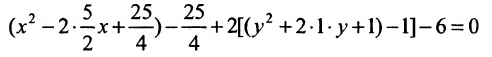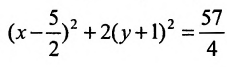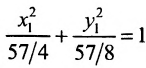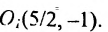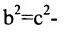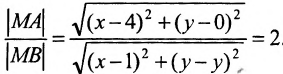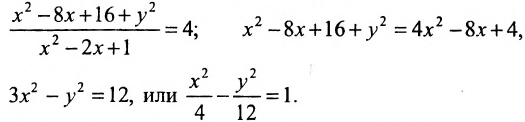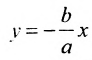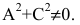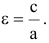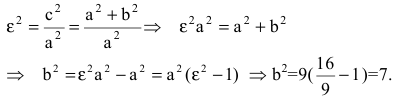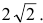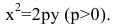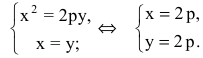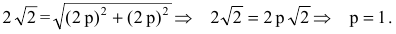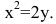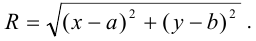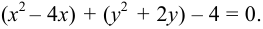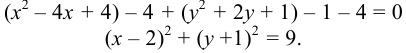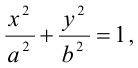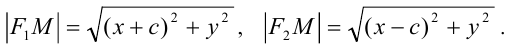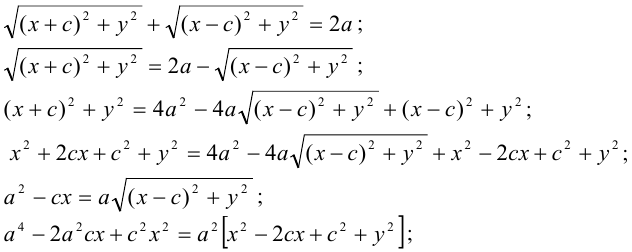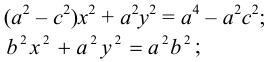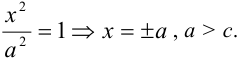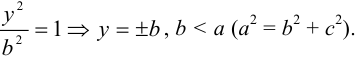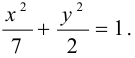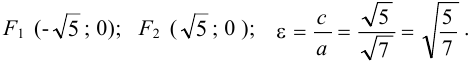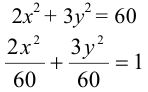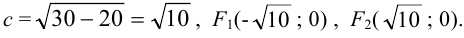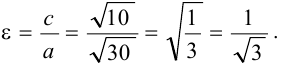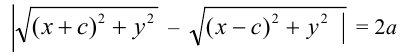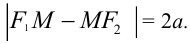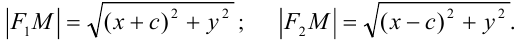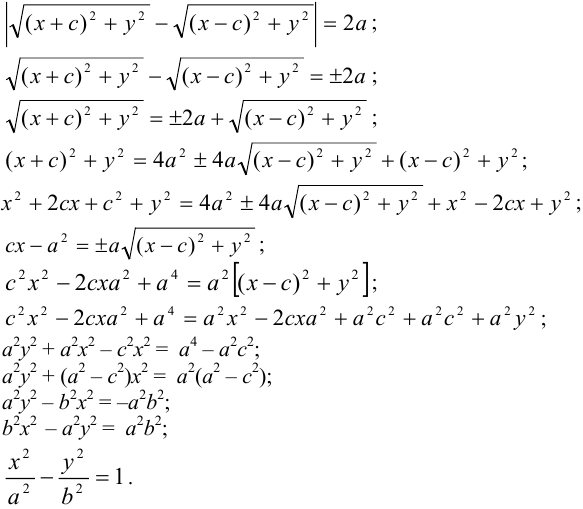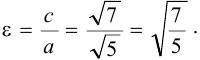Кривые второго порядка – определение и построение с примерами решения
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру – значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
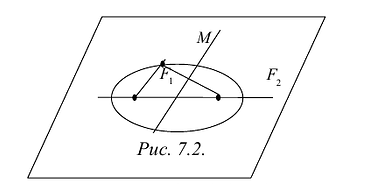
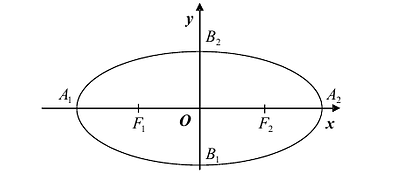
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
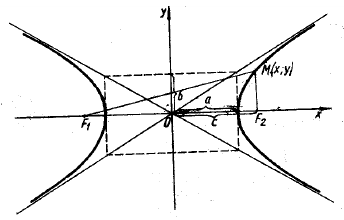
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 



Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

Пример:
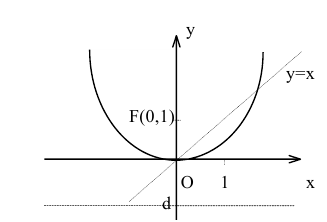
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию




Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
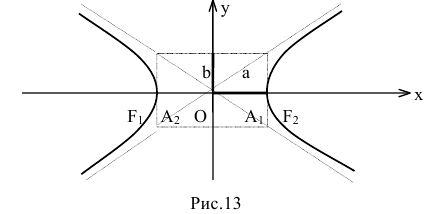
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b – соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат – его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

Пример:
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Кривые второго порядка
Кривая второго порядка – это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах – при вторых степенях одновременно не нули.
или можно встретить следующую форму записи:
К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
если Δ F1 и F2 – фокусы.
с – фокальное расстояние,
Каноническое уравнение эллипса с центром симметрии в начале координат:
2а – большая ось эллипса, 2b – малая ось эллипса.
а – большая полуось эллипса, b – малая полуось эллипса.
Если a = b, то имеем окружность с радиусов R = a = b:
Если центр эллипса находится не в начале координат, а в некоторой точке C(x0;y0), оси эллипса параллельны осям координат, то каноническое уравнение эллипса имеет вид:
Эксцентриситет – число, равное отношению фокального расстояния к большей полуоси:
Эксцентриситет характеризует отклонение эллипса от окружности, т.е. чем эксцентриситет больше, тем эллипс более сплющен, вытянут.
Гипербола – множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
с – фокальное расстояние,
Расстояние от центра гиперболы до одного из фокусов называется фокальным расстоянием.
Каноническое уравнение гиперболы с центром симметрии в начале координат:
x – действительная ось, y – мнимая ось.
а – действительная полуось, b – мнимая полуось.
Если центр гиперболы находится в некоторой точке C(x0;y0), оси симметрии параллельны осям координат, то каноническое уравнение имеет вид:
Эксцентриситет гиперболы – число, равное отношению фокусного расстояния к действительной полуоси.
Чем эксцентриситет меньше, тем гипербола более вытянута, сплюшена вдоль оси Ох.
Директриса гиперболы – прямые, параллельные мнимой оси гиперболы и отстоящая от нее на расстоянии a/Ε.
f1 – правая директриса, f2 – левая директриса.
Порядок построения гиперболы :
1. Строим прямоугольник со сторонами 2a и 2b.
2. Провести асимптоты гиперболы – диагонали построенного прямоугольника.
3. Строим гиперболу с вершинами в точках А 1 (-а;0), А 2 (а;0).
Парабола – множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F – фокус параболы, f – директриса параболы.
Кривые второго порядка. Эллипс: формулы и задачи
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:
,
где A, B, C, D, E, F – числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как и на рисунке ниже.
Каноническое уравнение эллипса имеет вид:
,
где a и b (a > b) – длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат – в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат – малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность – частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .
Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия – эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось – это a = 5 , меньшая полуось – это b = 4 . Получаем каноническое уравнение эллипса:
.
Точки и , обозначенные зелёным на большей оси, где
,
называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует “сплюснутость” эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
– если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
– если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат – каноническое уравнение эллипса:
.
Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:
.
Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:
.
Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет , а один из фокусов находится в точке (6; 0)
Продолжаем решать задачи на эллипс вместе
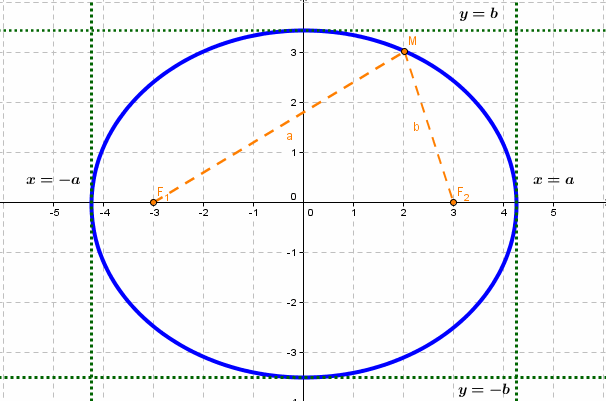
Если – произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и – расстояния до этой точки от фокусов , то формулы для расстояний – следующие:
.
Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями
,
называются директрисами эллипса (на чертеже – красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса
,
где и – расстояния этой точки до директрис и .
Пример 7. Дан эллипс . Составить уравнение его директрис.
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:
.
Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .
Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:
.
Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:
.
Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e – эксцентриситет и числа “эр” с подстрочными индексами 1 и 2 – искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.
,
так как из исходного уравнения эллипса .
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
[spoiler title=”источники:”]
http://matecos.ru/mat/matematika/krivye-vtorogo-poryadka.html
http://function-x.ru/curves_ellipse.html
[/spoiler]
В
аналитической геометрии на плоскости
подробно изучаются геометрические
свойства эллипса, гиперболы и параболы,
представляющих собой линии пересечения
кругового конуса с плоскостями, не
проходящими через его вершину. Эти линии
часто встречаются во многих задачах
естествознания и техники. Например,
движение материальной точки под
воздействием центрального поля силы
тяжести происходит по одной из этих
линий; в инженерном деле для конструирования
прожекторов, антенн и телескопов
пользуются важным оптическим свойством
параболы, заключающимся в том, что лучи
света, исходящие из определённой точки
(фокуса параболы), после отражения от
параболы образуют параллельный пучок.
Определение.
Кривой
второго порядка
называется геометрическое место точек
координатной плоскости, координаты
которых удовлетворяют алгебраическому
уравнению 2-й степени с двумя
неизвестными:
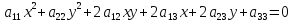
ОКРУЖНОСТЬ.
Определение.
Окружностью
называется геометрическое место точек
плоскости равноудаленных от одной
фиксированной точки плоскости, называемой
центром
окружности.
Определение.
Расстояние от любой точки окружности
до ее центра называется радиусом
окружности.
Теорема.
Окружность является кривой 2-го порядка
и ее уравнение имеет вид:
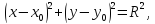
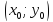
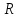
Определение.
Если центр окружности находится в начале
координат, то такая система координат
называется канонической
для окружности, а уравнение

окружности.
ЭЛЛИПС.
Определение.
Эллипсом
называется геометрическое место точек
плоскости, для которых сумма расстояний
до двух фиксированных точек плоскости,
называемых фокусами,
есть величина постоянная. Эту величину
принято обозначать через
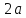
Определение.
Расстояние между фокусами эллипса
называется фокусным
расстоянием.
Фокусы эллипса принято обозначать
буквами
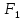
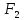
расстояние между ними – через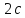
По определению эллипса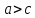
Определение.
Расстояния от точки
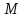
лежащей на эллипсе, до фокусов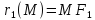
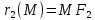
радиусами
точки
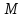
Замечание.
Из определения эллипса следует, что
точка
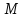
тогда, когда сумма её фокальных радиусов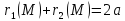
Определение.
Число
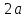
осью
эллипса, число
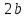
где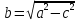
называетсямалой
осью
эллипса. Числа
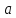
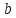
и малой
полуосями
эллипса.
Определение.
Отношение фокусного расстояния эллипса
к его большой оси называется эксцентриситетом
эллипса, и обозначается буквой
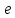
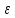
Определение.
Ось, на которой лежат фокусы эллипса,
называется фокальной
осью
эллипса.
В
канонической для эллипса системе
координат, оси координат являются
главными осями эллипса, а начало координат
является центром эллипса.
Определение.
Точки
эллипса, лежащие на его осях, называются
вершинами
эллипса.
Теорема.
(Каноническое уравнение эллипса.) Эллипс
является кривой 2-го порядка, и в
канонической для эллипса системе
координат его уравнение имеет вид: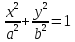
Теорема.
(Фокальные радиусы точки эллипса.) Пусть
в канонической для эллипса системе
координат точка
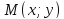
радиусы равны:
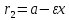
где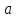
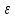
его эксцентриситет.
Определение.
В канонической для эллипса системе
координат прямые
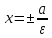
эллипса.
Теорема.
(Свойство директрис эллипса.) Пусть
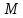
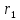
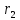
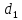
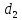
соответственно, расстояния от точки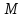
Тогда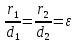
Теорема.
(Зеркальное свойство эллипса.) Луч света,
выпущенный из одного фокуса эллипса
после отражения от зеркала эллипса
проходит через второй его фокус.
Теорема.
В канонической для эллипса системе
координат уравнение касательной к
эллипсу в точке
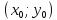
ГИПЕРБОЛА
Определение.
Гиперболой
называется геометрическое место точек
плоскости, модуль разности расстояний
которых до двух фиксированных точек
плоскости, называемых фокусами, есть
величина постоянная.
Фокусы
гиперболы принято обозначать буквами
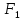

Расстояния от точки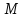
лежащей на гиперболе, до фокусов
обозначаются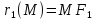
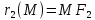
и называются еёфокальными
радиусами.
Замечание.
Из определения гиперболы следует, что
точка М является точкой гиперболы тогда
и только тогда, когда модуль разности
её фокальных радиусов
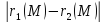
гиперболы. Эту константу принято
обозначать через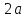
Определение.
Расстояние между фокусами гиперболы
называется фокусным
расстоянием.
Фокусное
расстояние для данной гиперболы есть
величина постоянная и ее принято
обозначать через


Замечание.
Так как сторона треугольника больше
модуля разности двух его других сторон,
то отсюда и из определения гиперболы
следует, что
Определение.
Число
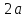
осью
гиперболы, число
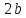
где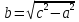
называетсямнимой
осью
гиперболы. Числа
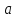
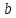
и мнимой полуосями
гиперболы.
Определение.
Отношение фокусного расстояния гиперболы
к её действительной оси называется
эксцентриситетом
гиперболы, и обозначается буквой
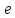
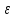
В
канонической для гиперболы системе
координат, оси координат являются
главными осями гиперболы, а начало
координат является центром гиперболы.
Теорема.
(Каноническое уравнение гиперболы.)
Гипербола является кривой 2-го порядка,
и в канонической для гиперболы системе
координат её уравнение имеет вид:

Определение.
Точки
гиперболы, лежащие на её действительной
оси, называются действительными
вершинами
гиперболы. Две точки плоскости
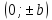
координат), лежащие на мнимой оси
гиперболы называютсямнимыми
вершинами
гиперболы.
Определение.
Две пары прямых, параллельных осям
гиперболы
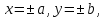
называетсяосновным
прямоугольником
гиперболы.
Гипербола
состоит из двух кривых, называемых её
ветвями,
которые в канонической системе
координат описываются уравнениями
Теорема.
Прямые
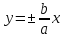
Теорема.
(Фокальные радиусы точек гиперболы.)
Пусть в канонической для гиперболы
системе координат точка
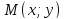
радиусы равны: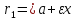
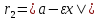
где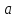
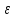
Определение.
В канонической для гиперболы системе
координат прямые
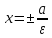
гиперболы.
Теорема.
(Свойство директрис гиперболы.) Пусть
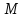
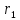
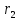
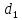
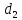
соответственно, расстояния от точки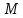
Тогда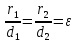
Теорема.
(Зеркальное свойство гиперболы.) Луч
света, выпущенный из одного фокуса
гиперболы после отражения от зеркала
гиперболы кажется наблюдателю идущим
из второго её фокуса.
Теорема.
В канонической для гиперболы системе
координат уравнение касательной к
гиперболе в точке
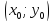
ПАРАБОЛА
Определение.
Параболой
называется геометрическое место точек
плоскости, расстояние от которых до
фиксированной прямой, называемой
директрисой,
равно расстоянию до фиксированной
точки, называемой фокусом.
Определение.
Расстояние от произвольной точки
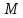
радиусом точки

Обозначения:
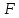
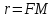
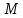
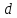
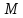
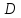
По
определению параболы, точка
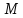
тогда, когда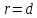
Определение.
Расстояние от фокуса параболы до ее
директрисы называется фокальным
параметром
параболы, и обозначается буквой
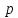
Замечание.
Из определений следует, что в канонической
для параболы системе координат фокус
имеет координаты
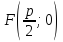
а директриса описывается уравнением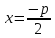
Теорема.
(Каноническое уравнение параболы.)
Парабола является кривой 2-го порядка,
и в канонической для неё системе координат
её уравнение имеет вид:
Теорема.
В канонической для параболы системе
координат, фокальный радиус точки
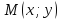
Теорема.
(Зеркальное свойство параболы.) Луч
света, выпущенный из фокуса параболы
после отражения от зеркала параболы
проходит параллельно её фокальной оси.
Теорема.
В канонической для параболы системе
координат уравнение касательной к
параболе в точке
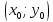
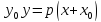
Определение.
Парабола
имеет одну ось симметрии, называемую
осью
параболы, с которой она пересекается в
единственной точке. Точка пересечения
параболы с осью называется ее вершиной.
Замечание.
Если координатная система выбрана так,
что ось абсцисс совмещена с осью параболы,
начало координат – с вершиной, но
парабола лежит в левой полуплоскости,
то ее уравнение будет иметь вид:
В
случае, когда начало координат находится
в вершине, а с осью совмещена ось ординат,
то парабола будет иметь уравнение:
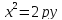
если она лежит в верхней полуплоскости,
и

если в нижней полуплоскости.
Полярная
система координат.
Определение.
Точка О называется полюсом,
а луч L
– полярной
осью.
Задание
какой-либо системы координат на плоскости
состоит в том, чтобы каждой точке
плоскости поставить в соответствие
пару действительных чисел, определяющих
положение этой точки на плоскости. В
случае полярной системы координат роль
этих чисел играют расстояние точки от
полюса и угол между полярной осью и
радиус– вектором этой точки. Этот угол
называется полярным
углом.
0
Можно
установить связь между полярной системой
координат и декартовой прямоугольной
системой, если поместить начало декартовой
прямоугольной системы в полюс, а полярную
ось направить вдоль положительного
направления оси
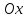
Тогда
координаты произвольной точки в двух
различных системах координат связываются
соотношениями:
x
= rcos;
y = rsin;
x2
+ y2
= r2.
Взаимосвязь
полярных и декартовых координат
определяется формулами:

В
полярной системе координат уравнения
эллипса, параболы или правой ветви
гиперболы имеют вид:
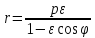
причем, данное уравнение задает эллипс,
если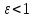
параболу, если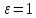
гиперболу, если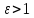
Левая ветвь гиперболы задается уравнением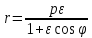
Инварианты
кривых второго порядка.
Определение.
Инвариантами
уравнения линии второго порядка
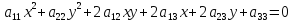
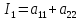
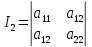
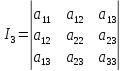
Определение.
Если инвариант
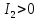
то линия называется линией эллиптического
типа, если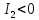
то – гиперболического типа, если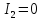
то – параболического типа.
Таблица
для определения типа кривой второго
порядка.
|
|
|
|||||
|
|
|
|
|
|||
|
|
|
|
|
|
парабола |
пара |
|
эллипс |
точка |
|
гипербола |
пара |
Решение
типовых задач.
Задача
№1.
Составить
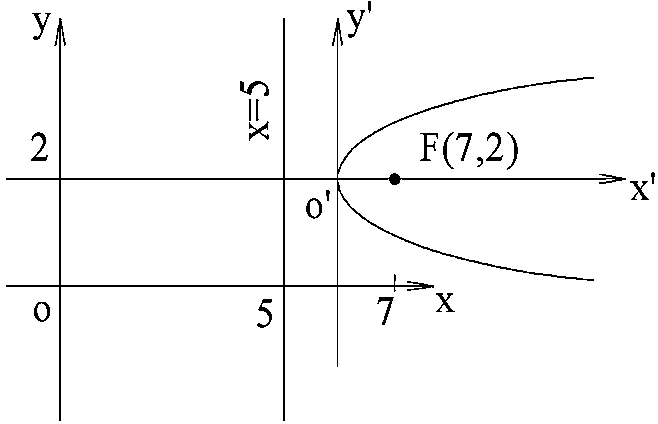
уравнение параболы, если даны её фокус
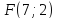
Решение:
I
способ
Пусть
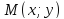
(по определению параболы) расстояние
от точки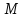
равно её расстоянию
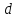
Возведём
в квадрат обе части, получим искомое
уравнение:
II
способ
Сделаем
чертёж:
|
Очевидно, Вершина |
|
Совершим
параллельный перенос системы
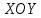
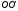
В
полученной системе координат
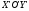
вид:
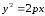
где
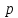
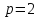
Тогда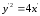
Из формул параллельного переноса
следует: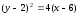
Поэтому уравнение параболы примет вид: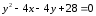
Ответ:
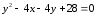
Задача
№2.
Найти
фокус и директрису параболы

Решение:
выразим из уравнения:
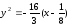
Сделаем
преобразование системы координат
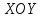
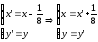
Тогда
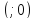
это преобразование есть параллельный
перенос.
Уравнение
параболы в системе
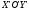
вид:
|
|
Очевидно, |
Перейдём
к исходной системе координат: уравнение
директрисы:
Фокус
F
имеет координаты:
Ответ:

Задача
№3.
Точка
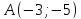
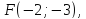
уравнением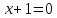
Составить уравнение этой гиперболы.
Решение:
Пусть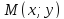
теореме об отношении расстояний
(отношение расстоянияr
от любой точки гиперболы до фокуса к
расстоянию d
от этой точки до соответствующей
директрисы есть величина постоянная,
равная эксцентриситету гиперболы):
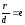
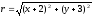
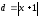
найдём, применив теорему для данной
точки
тогда
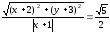
Сделав
соответствующие преобразования, получим
уравнение: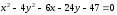
Ответ:
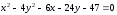
Задача
№4.
Точка
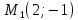
на эллипсе, фокус которого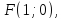
уравнением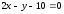
Составить уравнение этого эллипса.
Решение:
Решение
этой задачи аналогично предыдущей
задачи.
Пусть
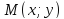
об отношении расстояний имеем: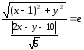
e
найдём по этой же теореме, используя
точку
Тогда
уравнение эллипса примет вид:
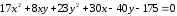
Ответ:
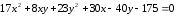
Задача
№5.
Из
фокуса параболы
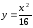
через центр эллипса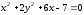
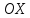
и найти длину перпендикуляра.
Решение:
Найдём
координаты центра эллипса, для этого
преобразуем его уравнение:
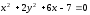
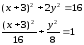
Итак,
координаты
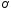
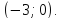
проходит через точку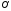
угловой коэффициент прямой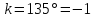
поэтому уравнение прямой примет вид: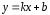
т.е.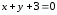
Найдём
фокус параболы
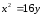
т.е.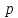
Искомая
длина перпендикуляра – это расстояние
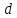
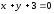
поэтому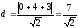
Ответ:
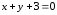
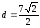
Задача
№6.
Даны
вершина параболы
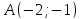

Составить уравнение этой параболы.
Решение:
Найдём
фокус параболы, для этого опустим из
вершины
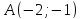
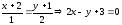
Эта прямая является осью симметрии
параболы.
Найдём
точку
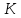
пересечение оси симметрии параболы с
её директрисой: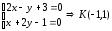
Фокус
параболы – это конец отрезка
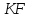
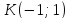
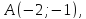
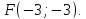
найдём её уравнение.
Ответ:
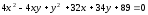
Задача
№7.
Определить,
при каких значениях
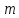
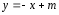
1)
пересекает эллипс
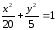
2)
касается его;
3)
проходит вне этого эллипса.
Решение:
Решая
систему
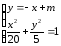
получим уравнение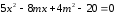
-
Чтобы
прямая пересекала эллипс, нужно чтобы
полученное квадратное уравнение
относительно x
имело два решения, для этого дискриминант
D>0.
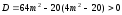
Откуда
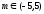
-
Чтобы
прямая касалась эллипса, нужно чтобы
,
т.е. -
Нет
пересечений, если
т.е.
Ответ:1)
при
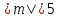
2)
при
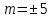
3)
при
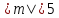
Задача
№8.
Провести
касательные к эллипсу
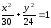
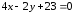
Решение:
Если
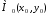
точка касания, то уравнение касательной
к эллипсу имеет вид: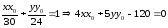
Угловой
коэффициент
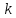
этой касательной равен: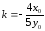
Но
касательная параллельна прямой
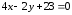
поэтому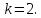
решим систему: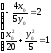
Оттуда
точка
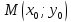
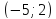
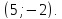

будем иметь уравнения касательных: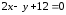
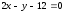
Расстояние
между касательными – это расстояние
от точки
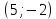
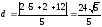
Ответ: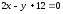
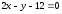
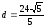
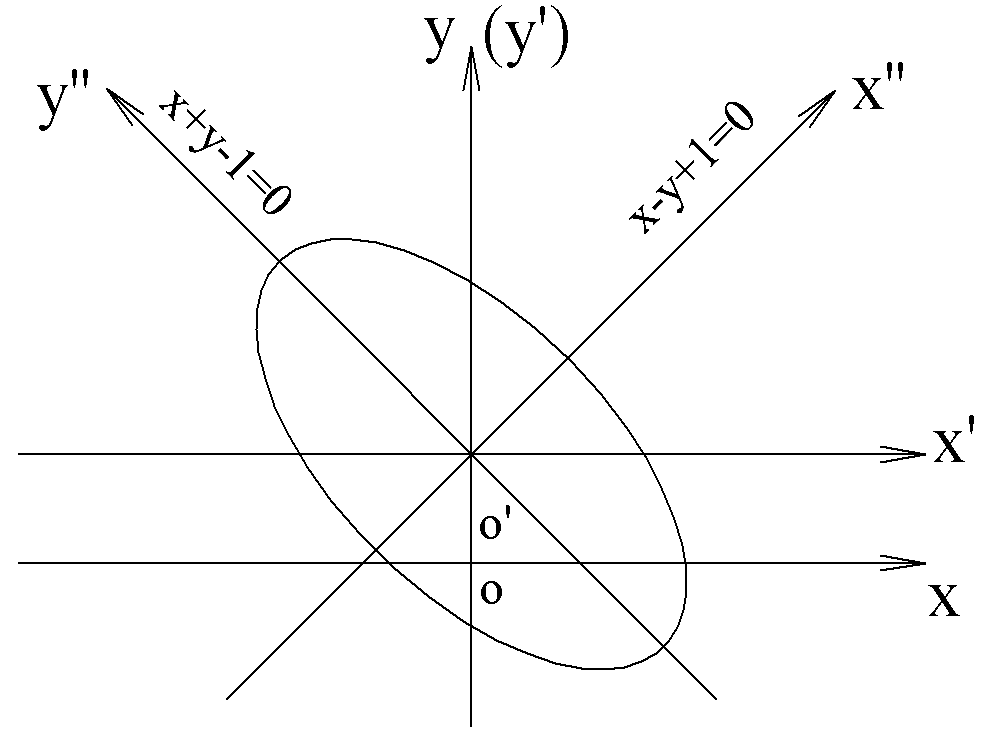
Задача
№9.
Написать
уравнение эллипса, для которого прямые
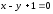
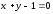
соответственно большая и малая оси, и
длины полуосей которого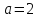
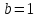
Решение:
Найдём
центр
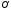
|
Обозначим Через В |
|
Повернём
систему
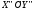
с системой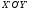
Формулы поворота:
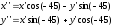
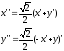
А
уравнение эллипса примет вид:
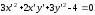
Сделаем
второе преобразование: параллельно
перенесём систему
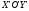
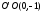
Формулы
параллельного переноса:

Уравнение
эллипса в системе
примет
вид:
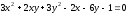
Ответ: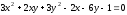
Задача
№10.
Не
приводя преобразование координат,
установить, какой геометрический образ
определяет уравнение, и найти величины
его полуосей:
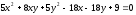
Решение:
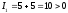
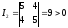
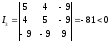
Итак,
уравнение определяет эллипс. Составим
характеристическое уравнение:
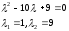
Тогда
преобразованное уравнение примет вид:
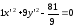
Откуда
каноническое уравнение примет вид:
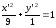
Ответ:
эллипс,
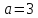
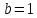
Задача
№11.
Не
приводя преобразования координат,
установить тип кривой и найти величины
её полуосей:
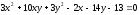
Решение:
Уравнение
определяет гиперболу. Т.к.
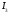
то действительной осью является ось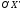
Составим характеристическое уравнение:
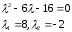
Каноническое
уравнение гиперболы:
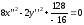
т.е.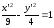
Ответ:
гипербола,
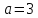
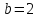
Задача
№12.
Не
приводя преобразования координат,
установить тип кривой и найти величины
её полуосей: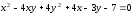
Решение:
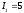
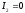
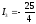
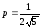
Каноническое уравнение: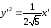
Ось
параболы определяется уравнением:
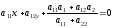
В
разбираемом случае имеем:
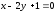
Вершину параболы находим как точку
пересечения линии с её осью из системы
уравнений:
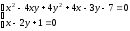
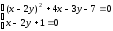
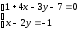
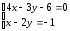
Вершина
параболы
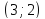
Единичный направляющий вектор оси
параболы в сторону вогнутости при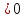
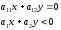
В
рассматриваемом случае имеем:
Имеем:
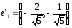

Ответ:
парабола,
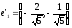
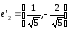
Задача
№13.
Не
приводя преобразования координат,
установить тип кривой и найти величины
её полуосей: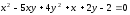
Решение:
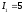
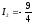
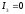
находиться как центр линий:
Точка
пересечения
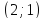
Направляющие векторы прямых находятся
как векторы асимптотических направлений:
Направляющие
векторы прямых:
Уравнения
прямых:
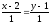
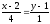
Ответ:
пересекающиеся прямые:
Задача
№14.
Не
приводя преобразования координат,
установить тип кривой и найти величины
её полуосей:
Решение:
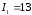
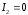
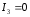
пара прямых (действительных, мнимых или
совпадающих).
Чтобы
решить, какие это прямые, достаточно
найти точки пересечения данной линии
с осью
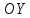
Имеем:
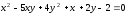
= 0, или
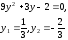
действительные параллельные прямые.
Направляющие векторы прямых имеют
асимптотические направления и находятся
из уравнения: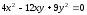
Направляющие
векторы прямых
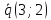
Их угловой коэффициент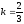
Уравнения прямых: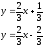
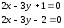
Ответ:
параллельные прямые:
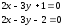
Задача
№15.
Установить,
какие линии определяются следующими
уравнениями:
1)
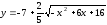
2)
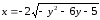
Решение:
1)
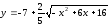
ОДЗ:
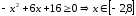
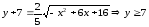
После
преобразований уравнение эллипса
принимает вид:
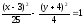
Итак,
координаты центра эллипса
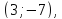
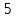
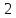
Учитывая, что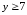
можно сказать, что искомой линией
является половина эллипса, расположенная
над прямой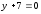
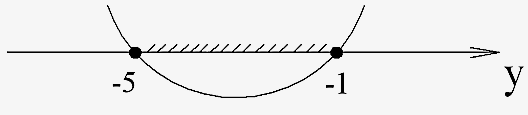
2)
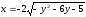
|
ОДЗ: |
|
|
|
|
Т.к. Итак, Центр
Ответ:
в |
Задача
№16.
Определить,
какие линии определяются следующими
уравнениями:
Изобразить
линии на чертеже.
Решение:
1)
ОДЗ:
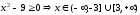
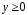
Ответ:
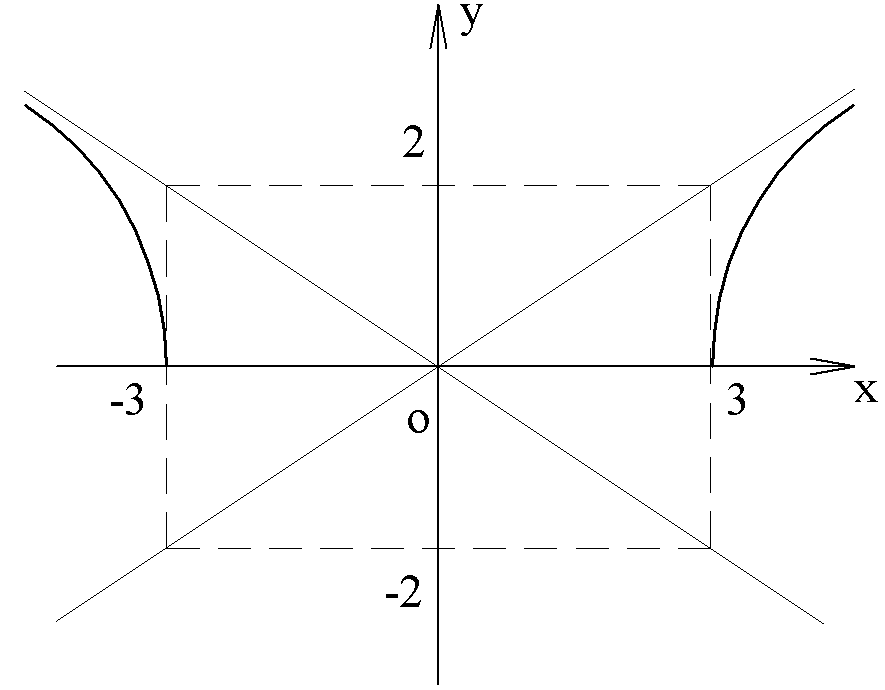
часть гиперболы
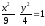
расположенная в верхней полуплоскости.
|
Ответ: |
|
|
|
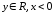
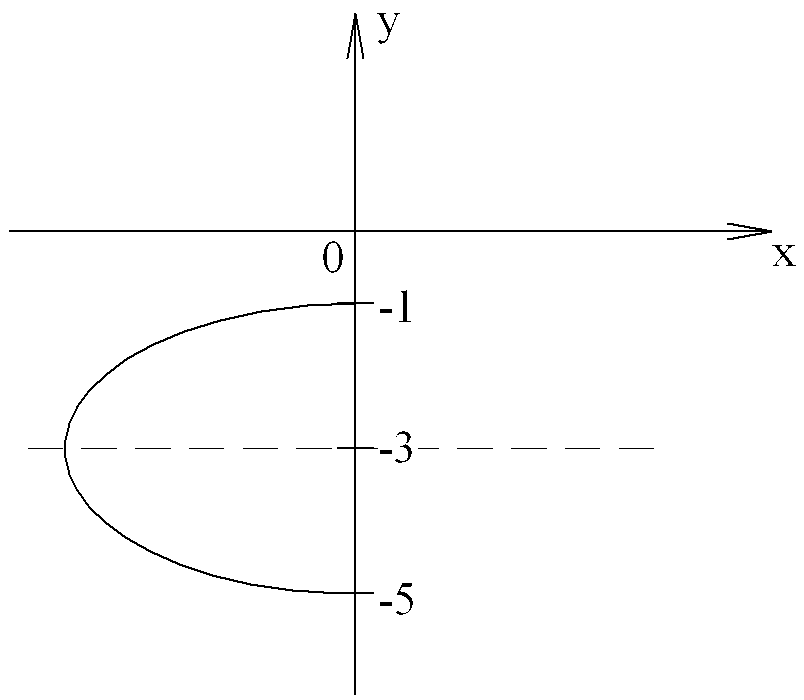
Ответ:
Ветвь гиперболы
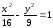
расположенная
в
левой полуплоскости.
Задача
№17.
Уравнение
кривой в полярной системе координат
имеет вид:
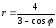
Найти уравнение кривой в декартовой
прямоугольной системе координат,
определит тип кривой, найти фокусы и
эксцентриситет. Схематично построить
кривую.
Решение.
Воспользуемся
связью декартовой прямоугольной и
полярной системы координат:
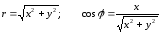
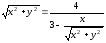
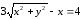
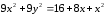
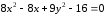
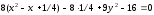
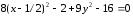
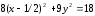
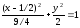
Получили
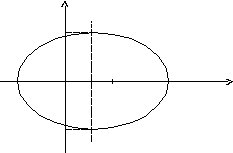
каноническое уравнение эллипса. Из
уравнения видно, что центр эллипса
сдвинут вдоль оси
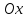
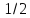
равна
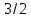
меньшая полуось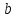
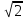
половина расстояния между фокусами
равно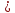
Эксцентриситет равен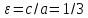
Фокусы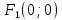
y
F1
F2
-1 0
½ 1 2
–
Образовательным
результатом после изучения данной темы
является сформированность компонент,
заявленных во введении, совокупности
компетенций (знать, уметь, владеть) на
двух уровнях: пороговый и продвинутый.
Пороговый уровень соответствует оценке
«удовлетворительно», продвинутый
уровень соответствует оценкам «хорошо»
или «отлично» в зависимости от результатов
защиты кейс-заданий.
Для
самостоятельной диагностики данных
компонент вам предлагаются следующие
задания.
Содержание:
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру – значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде
- Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
- если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.
Это определение в более компактной записи выглядит следующим образом. Уравнение 

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения 
Возможны два вида задач:
- дано уравнение
и надо построить фигуру Ф, уравнением которой является
;
- дана фигура Ф и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
- Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
- Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 

Точки 
Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины 2а закрепить в точках 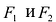
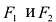
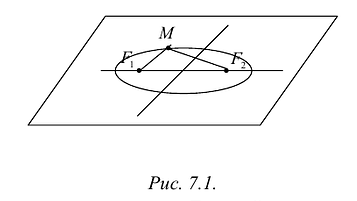
Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось Ох походила через фокусы 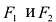
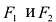
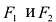
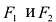
Пусть М(х,у) – произвольная точка эллипса, тогда:
Подставляя сюда значения 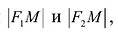
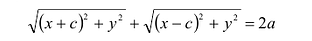
Уравнение (1) и есть уравнение эллипса. Преобразуя, упростим
его:
Возведя обе части уравнения в квадрат и приведя подобные члены, получим:
Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем 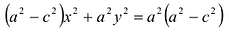
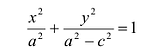
Положительную величину 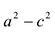
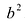
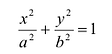
Оно называется каноническим уравнение эллипса.
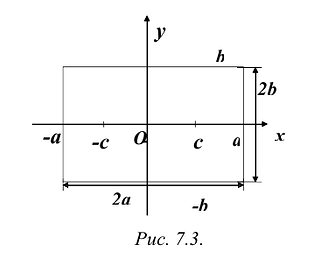
Координаты точек эллипса ограничены неравенствами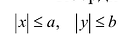
Заметим, что в уравнение (7.3) входят лишь четные степени х и у. Поэтому, если точка M(х,у) принадлежит эллипсу, то и точки 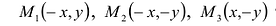
Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения (7.3) имеем:
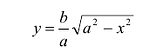
При возрастании x от 0 до а, у монотонно убывает от а до 0. График функции изображен на Рис. 7.4.
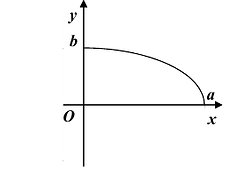
Достроив остальные четверти эллипса по симметрии, получим весь эллипс (Рис. 7.5).
Рис. 7.5. Оси симметрии эллипса (оси Ох и Оу) называются просто его осями, а центр симметрии – точка О – центром эллипса. Точки 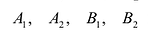
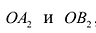
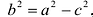
Если а =Ь, то уравнение (7.3) можно переписать в виде:

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку 

Число 


Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами 







Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 

Точки 

Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение: 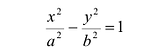
Уравнение (7.6) называется каноническим уравнением гиперболы.
Из уравнения (7.6) видно, что 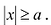
Так как в уравнение входят только четные степени x и у, то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (7.6) для первой четверти, имеем:
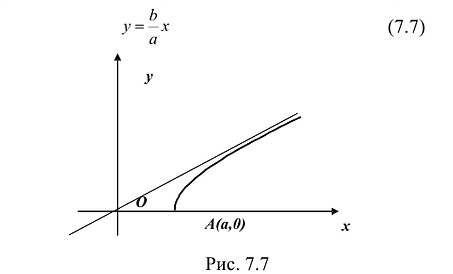
График этой функции от точки A(а,0) уходит неограниченно вправо и вверх (Рис. 7.7), и как угодно близко подходит к прямой:
Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты
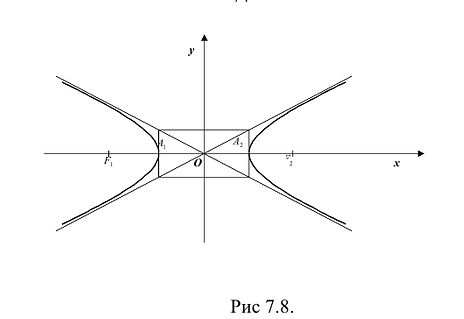
Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны 2а и 2Ь параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 7.8).
Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки 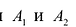
Эксцентриситетом гиперболы называется число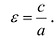
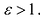
Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами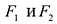
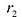
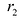
Для правой – ветви 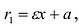
Для левой – ветви
Прямые 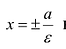
Парабола
Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки F (фокуса) и данной прямой 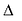
Для вывода канонического уравнения параболы ось Ох проводят через фокус F перпендикулярно директрисе 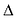
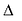
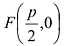
В выбранной системе координат уравнение параболы имеет вид:
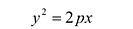
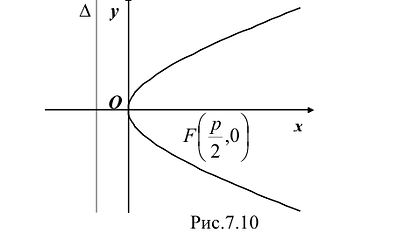
Это уравнение называется каноническим уравнением параболы. Из уравнения (7.8) видно, что л: может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси Оу. Так как уравнение (7.8) содержит у только в четной степени, то парабола симметрична относительно оси Ох и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти 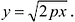
При неограниченном возрастании x неограниченно растет и у. Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии. Сделаем рисунок параболы (Рис. 7.10).
Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется вершиной параболы.
Исследование на плоскости уравнения второй степени
Рассмотрим уравнение:
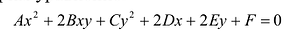
где среди коэффициентов А, В, С есть отличные от нуля, т.е. (7.9) – уравнение второй степени относительно х и у.
Возьмем на плоскости две прямоугольные системы координат: Оху, которую будем называть старой, и новую, полученную из Оху поворотом ее вокруг начала координат на угол
Старые координаты х, у выражаются через новые координаты 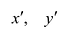
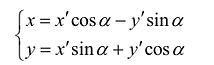
Подставив выражения для х и у в уравнение (8), получим: 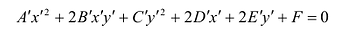
Это уравнение в системе координат 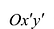
Если в уравнении (7.9) 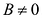
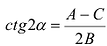
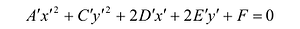
Преобразуя это уравнение и применяя параллельный перенос координатных осей, придем к уравнению:
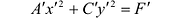
В зависимости от знаков коэффициентов уравнения (7.13) рассмотрим следующие случаи:
Рассматривая далее методично все случаи, придем к выводу: уравнение вида (7.9) задает одну из следующих фигур: эллипс, гиперболу, параболу, пару пересекающихся прямых, пару параллельных прямых, прямую, точку или пустое множество.
Кривые второго порядка в высшей математике
Выяснение взаимосвязей между различными показателями экономического характера часто приводит к форме этих связей в виде гиперболы и параболы. В этой лекции приведём краткие сведения обо всех кривых второго порядка.
Окружность
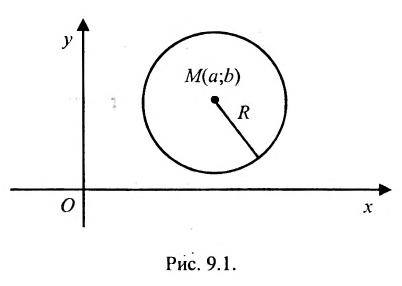
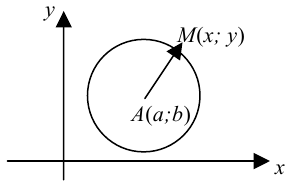
Определение 9.1. Окружностью называется геометрическое место точек, равноудаленных от данной точки – центра окружности.
Если точка 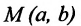
или
Найдём условия, при которых общее уравнение второй степени с двумя переменными
определяет окружность. Раскрыв скобки в (9.1.1), получим
Сравнивая (9.1.2) и (9.1.3), находим условия А = С, В = О,
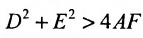
Эллипс
Определение 9.2. Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами.
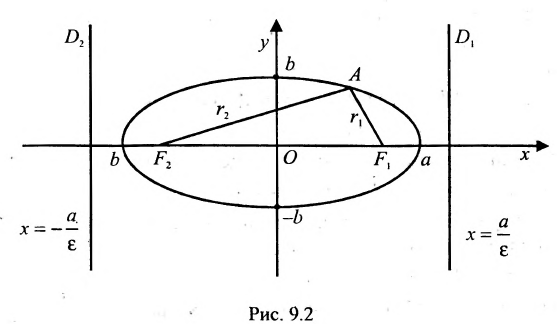
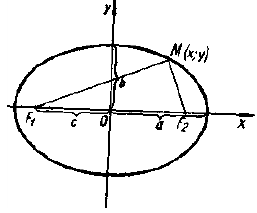
Пусть на плоскости хОу (рис. 9.2) дан эллипс с фокусами 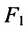
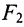
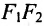
Если точка А – произвольная точка эллипса с координатами (х, у), то
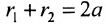
где 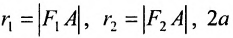
расположены симметрично относительно начала координат, то они имеют координаты (с,0) и (-с,0) соответственно. Воспользовавшись формулой для вычисления расстояния между двумя точками, находим 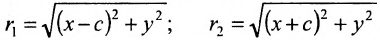
и 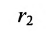
Обе части этого уравнения возведем в квад-Упростив и обозначив
получим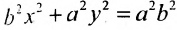
Уравнение (9.2.2) называется каноническим уравнением эллипса, где а – большая полуось, b – малая полуось.
Это уравнение второго порядка, следовательно, эллипс есть линия второго порядка. Для определения формы эллипса служит его эксцентриситет 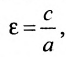
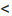
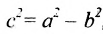
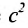
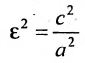
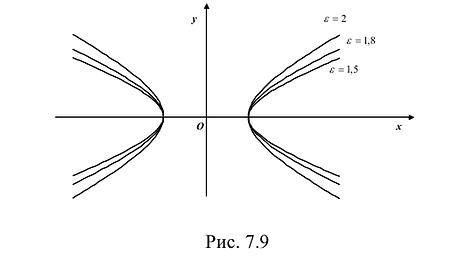
Следовательно, эксцентриситет определяется отношение осей эллипса; а отношение осей определяется эксцентриситетом. Чем ближе эксцентриситет к единице, тем меньше 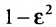
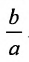
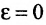
Две прямые, перпендикулярные к большей оси эллипса и расположенные симметрично относительно центра на расстоянии 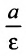
Пример:
Исследовать, какая линия определяется уравнением
Решение:
Сгруппируем члены, содержащие одну и туже переменную, получим
Из второй скобки вынесем коэффициент при 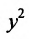
В каждой из скобок выделим полный квадрат
или
Произведём замену: 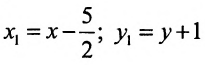
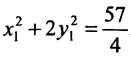
Разделив обе части этого уравнения на 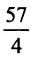
Заданное уравнение определяет эллипс с полуосями 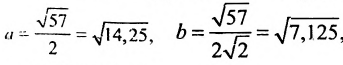
Выбираем на плоскости произвольным образом прямоугольную систему координат хОу. С помощью параллельного переноса переносим оси координат в новое начало в точку 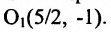
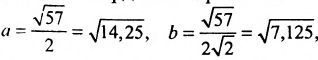
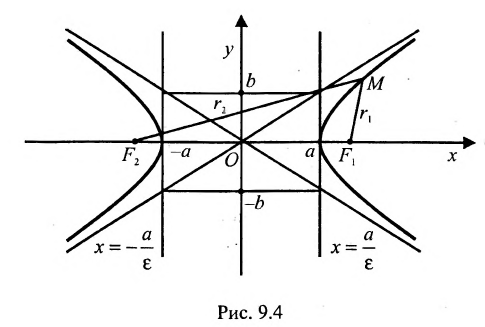
Гипербола
Определение 9.3.1. Гиперболой называется геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, меньшая, чем расстояние между фокусами и отличная от нуля (указанная разность берется по абсолютному значению).
Пусть М- произвольная точка гиперболы с фокусами 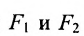
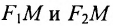
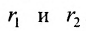
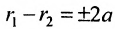
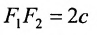
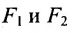
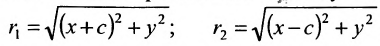
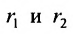
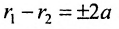
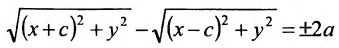
Возведя в квадрат обе части этого уравнения и обозначая 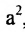
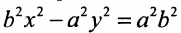
Уравнение (9.3.1)- это каноническое уравнение гиперболы, линии второго порядка.
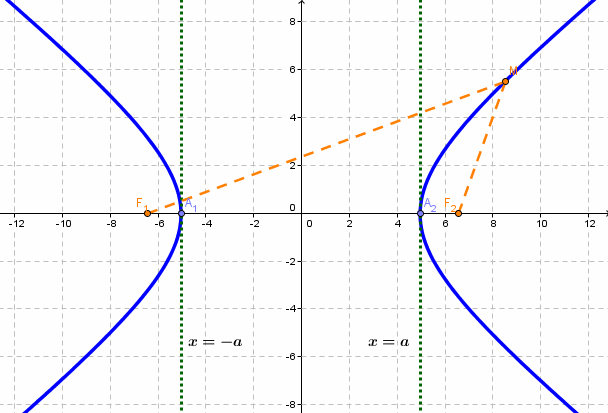
Прямоугольник со сторонами 2а и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником. Его диагонали совпадают с асимптотами гиперболы 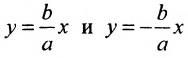
Уравнение вида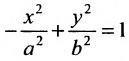
Форму гиперболы характеризует её эксцентриситет 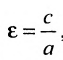
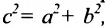
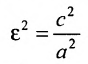
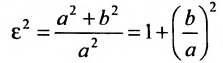
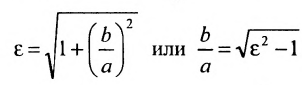
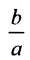
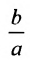
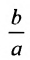
Прямые, заданные уравнениями 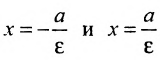
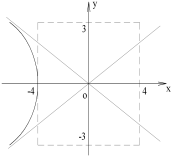
Пример:
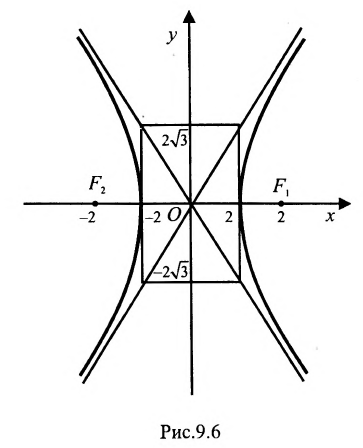
Составить уравнение геометрического места точек, отношение расстояний которых от данной точки А(4, 0) и от данной прямой х=1 равно 2.
Решение:
В системе координат хОу построим точку А(4, 0) и прямую х = 1. Пусть М(х, у) – произвольная точка искомого геометрического места точек. Опустим перпендикуляр MB на данную прямую х = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то её абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно, B(1, у) (рис. 9.6).По условию задачи 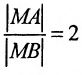
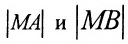
Возводя в квадрат левую и правую части равенства и последовательно преобразовывая, находим уравнение:
Полученное уравнение определяет гиперболу, у которой действительная полуось -а = 2, а мнимая 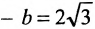
Определим фокусы гиперболы. Для гиперболы выполняется равенство 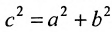
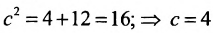
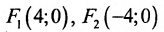
А(4, 0) является правым фокусом гиперболы.
Эксцентриситет полученной гиперболы равен
Подставив значения а и b в уравнения асимптот 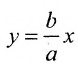
у =—получим уравнения асимптот гиперболы: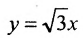
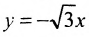
Для построения гиперболы строим основной прямоугольник с полуосями 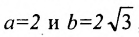
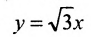
- Заказать решение задач по высшей математике
Парабола
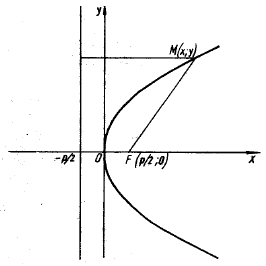
Определение 9.4.1. Параболой называется геометрическое место точек, для каждой из которых, расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой,(директриса не проходит через фокус).
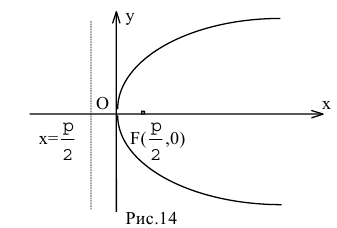
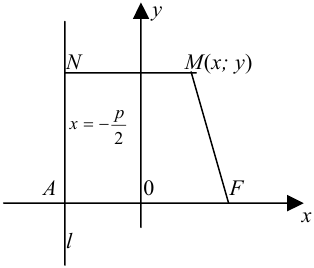
Обозначим фокус параболы – F, расстояние от фокуса до директрисы – р(р > 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А – произвольная точка плоскости с координатами (х, у) и пусть 

Тогда 




Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения 
Легко показать, что уравнение 

и сделаем параллельный перенос по формулам
В новых координатах преобразуемое уравнение примет вид: 

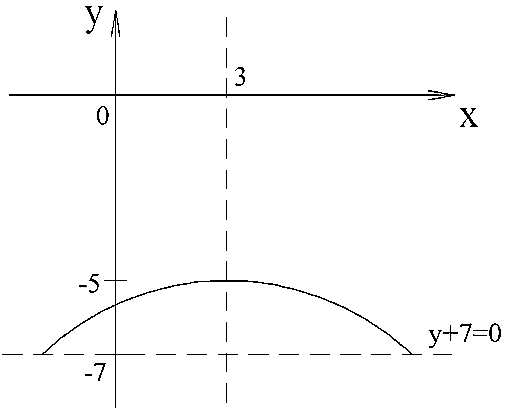
Пример:
Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию



Кривые второго порядка на плоскости
Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:
где коэффициенты А, В и С не равны одновременно нулю
Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.
Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.
Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС<0.
Кривая второго порядка принадлежит параболическому типу, если коэффициент В равен нулю: В=0 и только один из коэффициентов А и С не равен нулю: АС=0 и
Рассмотрим канонические (простейшие) уравнения эллипса, гиперболы и параболы.
Эллипсом называется множество всех точек плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.
Геометрическое свойство точек эллипса выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину, о которой идет речь в определении эллипса, обозначим через 2а: 2а>2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

Число а называют большей полуосью эллипса, число 
шей полуосью эллипса, 2а и 2b – соответственно большей и меньшей осями эллипса. Точки 

Координатные оси являются осями симметрии эллипса, а начало координат – его центром симметрии. Центр симметрии эллипса называется центром эллипса.
Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.
В случае а=b каноническое уравнение эллипса принимает вид 
Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.
Так, в случае а>b эксцентриситет эллипса выражается формулой:
Эксцентриситет изменяется от нуля до единицы 

Пример:
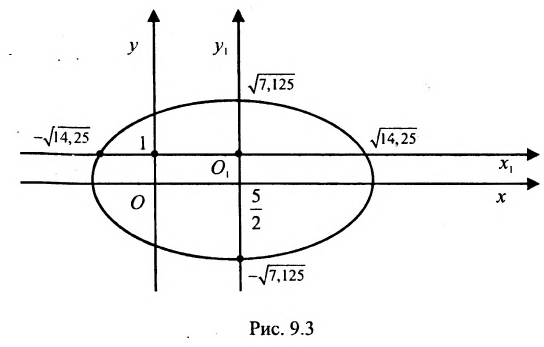
Показать, что уравнение
является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.
Решение:
Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:


Найдем эксцентриситет эллипса:
Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке 

В новой системе координат координаты 
Переходя к старым координатам, получим:
Построим график эллипса.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а<2с. Точка М(х,у) принадлежит гиперболе тогда и только тогда, когда ее координаты удовлетворяют уравнению
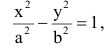
Число а называют действительной полуосью гиперболы, число
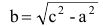
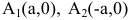
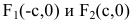
Координатные оси являются осями симметрии гиперболы, а начало координат – ее центром симметрии. Центр симметрии гиперболы называется центром гиперболы.
Точки гиперболы по мере удаления от начала координат неограниченно (асимптотически) приближаются к прямым у=±kх (где 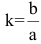
Эксцентриситетом гиперболы называется отношение фокусного расстояния к длине действительной оси:
Эксцентриситет гиперболы изменяется от единицы до бесконечности 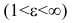
Замечание. Каноническое уравнение 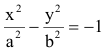
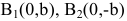
Пример:
Составить каноническое уравнение гиперболы с центром в начале координат, если ее действительная полуось равна трем, а эксцентриситет -четырем третьим.
Решение:
Каноническое уравнение гиперболы имеет вид
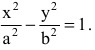
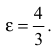
Следовательно, уравнение искомой гиперболы:
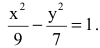
Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом параболы, и от данной прямой, называемой директрисой и не проходящей через фокус.
Расстояние между фокусом и директрисой обозначим р. Для того чтобы точка М(х,у) принадлежала параболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнению 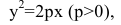
Точка O(0,0) называется вершиной параболы, число р – параметром параболы, 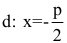
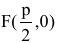
Если поменять ролями оси Ох и Оу, то каноническое уравнение параболы примет вид 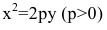
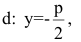
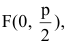
Замечание. Канонические уравнения параболы можно рассматривать и в случае, когда ветви направлены влево или вниз:
Пример:
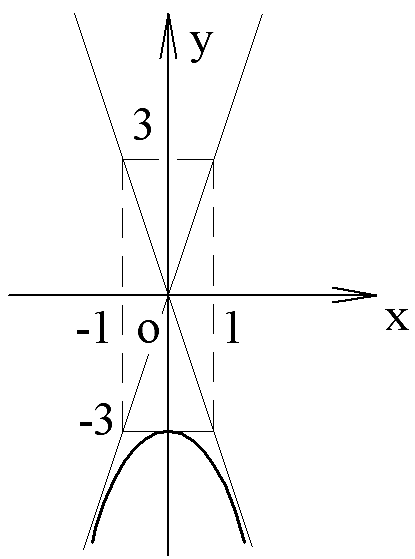
Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе первого координатного угла отрезок длиной
Решение:
Каноническое уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и ветвями, направленными вверх, имеет вид:
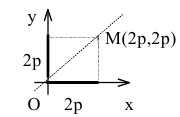
Уравнение биссектрисы первого координатного угла у=х. Найдем точки пересечения параболы с биссектрисой. Для этого решим систему уравнений
Следовательно, точка М(2р,2р) будет принадлежать параболе. С другой стороны, парабола отсекает на биссектрисе отрезок длиной 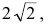
По теореме Пифагора
Тогда искомое уравнение параболы
Уравнение директрисы параболы: у=-1, координаты ее фокуса F(0,1).
Задача решена.
- Евклидово пространство
- Матрица – виды, операции и действия с примерами
- Линейный оператор – свойства и определение
- Многочлен – виды, определение с примерами
- Числовые множества
- Вектор – определение и основные понятия
- Прямая – понятие, виды и её свойства
- Плоскость – определение, виды и правила
Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов 
Таким образом кривая второго порядка является частным случаем алгебраической кривой.
История[править | править код]
Впервые кривые второго порядка изучались Менехмом, учеником Евдокса[1][2]. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы образованного ими угла, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур (см. ниже).
Однако эти научные знания нашли применение лишь в XVII веке, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, при достижении второй космической скорости — по параболе, а при скорости, большей второй космической, — по гиперболе.
Инварианты[править | править код]
Вид кривой зависит от четырёх инвариантов:
- инварианты относительно поворота и сдвига системы координат:
- инвариант относительно поворота системы координат (полуинвариант):[источник не указан 3579 дней]
Иногда встречающееся выражение «инвариант кривой» является неточным. Если умножить уравнение на ненулевое число k, то получится уравнение, задающее ту же самую кривую. При этом значения инвариантов изменятся. 
Классификация кривых второго порядка относительно значений инвариантов[править | править код]
| Кривая | Уравнение | Инварианты | |||
|---|---|---|---|---|---|
| Эллипс | 
|

|

|

|
|
| Точка (пара мнимых пересекающихся прямых) | 
|

|
|||
| Мнимый эллипс | 
|

|
|||
| Гипербола | 
|

|

|
||
| Пара пересекающихся прямых | 
|

|
|||
| Парабола | 
|

|

|
||
| Пара параллельных прямых | 
|

|

|
||
| Прямая | 
|

|
|||
| Пара мнимых параллельных прямых | 
|

|
Невырожденные кривые[править | править код]
Кривая второго порядка называется невырожденной, если 
Вырожденные кривые[править | править код]
Кривая второго порядка называется вырожденной, если 
Характеристическая квадратичная форма и характеристическое уравнение[править | править код]
Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой
Так, например, невырожденная кривая 

или
Корни этого уравнения являются собственными значениями вещественной симметричной матрицы
и, как следствие этого, всегда вещественны[3].
Диаметры и центр кривой второго порядка[править | править код]
Диаметром кривой второго порядка называется геометрическое место середин параллельных хорд этой кривой. Полученный таким образом диаметр называется сопряжённым этим хордам или их направлению. Диаметр, сопряжённый хордам, образующим угол 

Если выполняется условие 

Координаты центра 

Решая эту систему относительно 


Если кривая центральная, то перенос начала координат в её центр приводит уравнение к виду

где 
Главные оси и вершины кривой второго порядка[править | править код]
Главной осью кривой второго порядка называется её диаметр, перпендикулярный к сопряжённым с ним хордам. Этот диаметр является осью симметрии кривой. Каждая центральная кривая 

Направляющие косинусы нормалей к главным осям удовлетворяют уравнениям

где 

Из всех видов кривых второго порядка только окружность имеет неопределённые главные направления.
Уравнения[править | править код]
Общее уравнение в матричном виде[править | править код]
Общее уравнение кривой можно записать в матричном виде
или
Канонический вид[править | править код]
Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу выше). Параметры канонических уравнений весьма просто выражаются через инварианты 

Замечание. При переходе к канонической форме уравнения может понадобиться умножить уравнение на число, не равное нулю. Поэтому численные значения инвариантов канонического уравнения могут отличаться от значений инвариантов для исходного уравнения. Неизменными остаются знаки величин 

Для центральной кривой в каноническом виде её центр 
Через эксцентриситет[править | править код]
Каноническое уравнение любой невырожденной кривой второго порядка при помощи подходящего преобразования начала координат может быть приведено к виду

В этом случае кривая проходит через начало новой системы координат, а ось Ox является осью симметрии кривой. Данное уравнение выражает тот факт, что невырожденная кривая второго порядка является геометрическим местом точек, отношение расстояний которых 




Уравнение директрисы кривой выражается уравнением 


Если кривая второго порядка центральная (эллипс или гипербола), то прямая

является осью симметрии и, следовательно, кривая имеет два фокуса и две директрисы.
Параметр 
Полярные координаты[править | править код]
Если взять в качестве полюса полярной системы координат 



Кривая, заданная своими пятью точками[править | править код]
Кривая второго порядка вполне определяется пятью своими точками, если никакие четыре из них не лежат на одной прямой. Уравнение кривой, проходящей через точки 





Кривая, заданная пятью точками вырождается в том и только в том случае, когда три из заданных точек лежат на одной прямой.
Касательные и нормали[править | править код]
Уравнение касательной к кривой второго порядка 


Уравнение нормали к кривой второго порядка в точке 

Полюсы и поляры[править | править код]
Уравнение
помимо касательной определяет прямую, называемую полярой точки 

Теоремы о полюсах и полярах:[источник не указан 3579 дней]
- Если прямая, проведённая через полюс
пересекает поляру в точке
а кривую второго порядка — в точках
и
то точки
и
гармонически разделяют отрезок
то есть выполняется условие
- Если точка лежит на некоторой прямой, то её поляра проходит через полюс этой прямой. Если прямая проходит через некоторую точку, то её полюс лежит на поляре этой точки.
- Диаметр кривой второго порядка есть поляра бесконечно удалённой точки, через которую проходят сопряжённые ему хорды, а центр кривой есть полюс бесконечно удалённой прямой.
- Фокус кривой есть центр пучка, обладающего тем свойством, что полюс любой его прямой принадлежит перпендикулярной к ней прямой этого пучка. Директриса есть поляра фокуса.
Из этих утверждений, в частности, следует, что:
- если через точку можно провести две касательные к кривой, то поляра этой точки проходит через точки касания;
- касательные к кривой в концах диаметра параллельны сопряжённым ему хордам;
- точка пересечения касательных к кривой в концах любой её хорды, проходящей через фокус, лежит на директрисе;
- каждая хорда, проходящая через фокус, перпендикулярна к прямой, проведённой через её фокус и точку пересечения касательных в концах хорды.
Теоремы, связанные с кривыми второго порядка[править | править код]
- Теорема Паскаля: точки пересечения противоположных сторон шестиугольника, вписанного в кривую второго порядка, лежат на одной прямой.
- Теорема Брианшона: диагонали, проходящие через противоположные вершины шестиугольника, описанного около кривой второго порядка, пересекаются в одной точке.
См. также[править | править код]
- Коническое сечение
- Квадрика
- Поверхности второго порядка
- Кривая третьего порядка
- Плоская кривая четвёртой степени
Ссылки[править | править код]
- Общее уравнение кривой второго порядка Архивная копия от 30 января 2020 на Wayback Machine
- Кривые второго порядка
- Кривые второго порядка: гипербола, парабола
Литература[править | править код]
- Александров А.Д., Нецветаев Н.Ю. Глава II (Кривые второго порядка) // Геометрия. — М.: Наука, 1990. — С. 32—57.
- Акопян А.В., Заславский А.А. Геометрические свойства кривых второго порядка. — М.: МНЦМО, 2007.
- Прасолов В.В., Тихомиров В.М. Геометрия. — М.: МНЦМО, 2007.
- Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 64—69.
Примечания[править | править код]
- ↑ Розенфельд Б. А. Аполлоний Пергский Архивная копия от 12 ноября 2015 на Wayback Machine. — М.: МЦНМО, 2004. — С. 32.
- ↑ Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. Menaechmus (англ.) — биография в архиве MacTutor.
- ↑ Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 64.
Кривые линии второго порядка
Общее уравнение кривых второго порядка имеет вид: 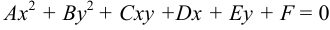
где 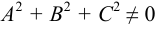
К кривым линиям второго порядка относятся: окружность, эллипс, гипербола и парабола.
Окружность
Окружностью называется множество точек плоскости, равноудаленных от одной и той же точки — центра окружности.
Утверждение. Окружность является кривой второго порядка и ее каноническое уравнение имеет вид:
где 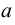
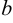
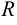
Доказательство. Рассмотрим окружность с заданными параметрами в системе координат на плоскости. Возьмем произвольную точку этой окружности 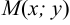
По формуле расстояния между двумя точками имеем:
Возведем обе части уравнения в квадрат и получим
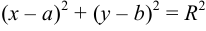
Задача №24.
Показать, что уравнение 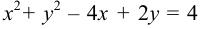
Решение:
Заданное уравнение приведем к виду 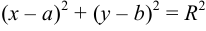
Сгруппируем члены, содержащие только 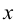
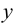
Допишем теперь до квадрата разности и суммы:
Кривая является окружностью с центром 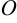
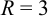
Эллипс
Эллипсом называется множество точек плоскости, сумма расстояний каждой из которых от двух данных точек, называемых фокусами, есть величина постоянная равная 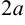
Утверждение. Эллипс является кривой второго порядка, и каноническое уравнение эллипса имеет вид:
где 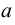
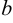
Доказательство. Пусть 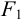
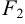
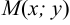
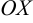
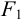
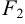
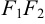
Предположим, что расстояние между фокусами равно 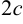
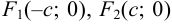
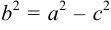
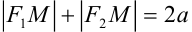
Получаем:
или
Если 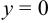
Если 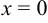
Число 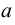
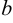
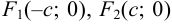
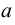
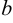
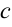
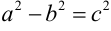
Эксцентриситетом эллипса называется отношение 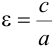
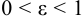
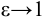
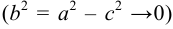
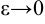
Если 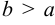
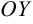
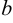
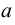
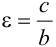
Задача №25.
Найти координаты фокусов эллипса и его эксцентриситет, если известно уравнение эллипса:
Решение:
Уравнение имеет канонический вид и 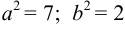
Найдем 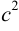
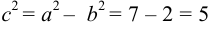
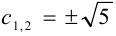
Задача №26.
Показать, что уравнение 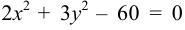
Решение:
Приведем уравнение к каноническому виду:
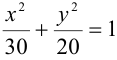
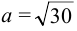
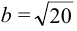
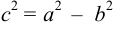
Эксцентриситет
Гипербола
Гиперболой называется множество точек плоскости, абсолютное значение разности расстояний которых от двух точек, называемых фокусами, есть величина постоянная.
или
Утверждение. Гипербола является кривой второго порядка, и ее каноническое уравнение имеет вид: 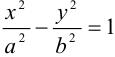
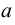
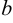
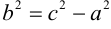
Доказательство. Пусть 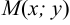
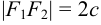
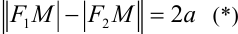
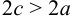
Положим 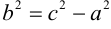
Если 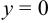
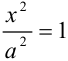
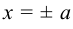
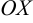
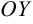
Эксцентриситетом гиперболы называют отношение 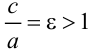
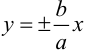
Задача №27.
Составить каноническое уравнение гиперболы, если 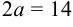
Решение:
Так как 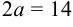
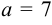
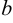
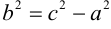
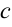
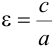
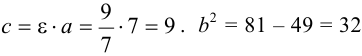
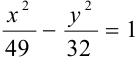
Задача №28.
Показать, что уравнение 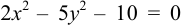
Решение:
Приведем уравнение к каноническому виду:
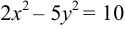
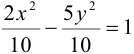
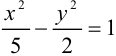
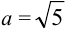
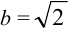
Найдем координаты фокуса. 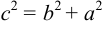
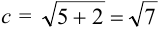
Значит 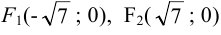
Эксцентриситет
Асимптоты имеют следующие уравнения:
Парабола
Параболой называется множество точек плоскости, каждая из которой одинаково удалена от данной точки 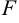
Утверждение. Парабола является кривой второго порядка и ее каноническое уравнение имеет вид: 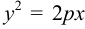
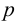
Доказательство. Построим систему координат так, чтобы ось 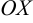
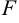
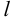
Предположим расстояние 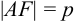
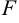
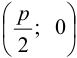
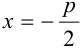
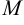
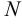
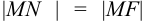
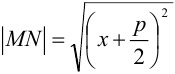
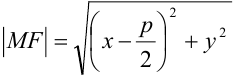
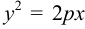
Если 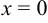
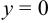
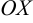
Если 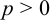
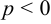
Задача №29.
Найти координаты фокуса и уравнение директрисы следующей параболы 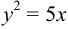
Решение:
Запишем уравнение следующим образом:
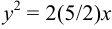
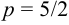
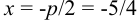
Координаты фокуса: 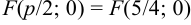
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:




















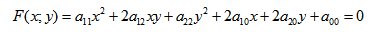
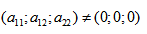
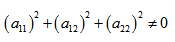
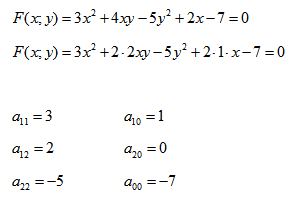
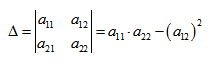
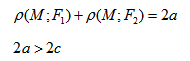


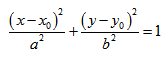
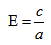
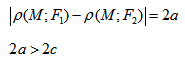

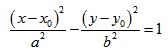
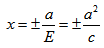
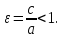
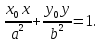
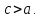
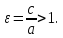
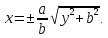

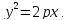
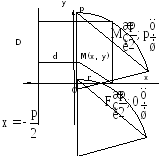
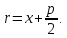
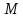
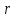
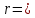
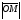
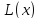
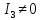
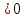
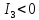
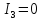
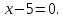
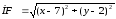
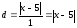
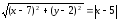
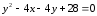
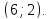
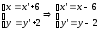
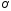
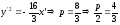
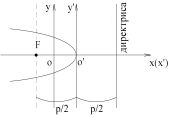
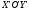 уравнение директрисы имеет вид:
уравнение директрисы имеет вид: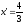 .
.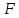 имеет координаты
имеет координаты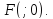
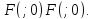
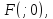
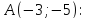
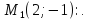
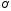
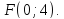
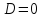 ,
,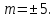
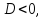 т.е.
т.е.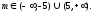
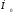
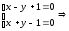
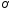
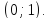
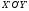 систему координат, началом которой
систему координат, началом которой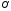
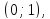 а
а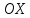 и
и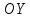 .
.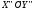 обозначим систему координат с началом
обозначим систему координат с началом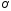
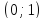 и осями координат, совпадающими с
и осями координат, совпадающими с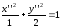

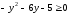
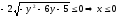
 ,
, .
. ,
,
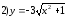
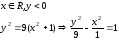
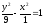 ,
,