Как найти фокус сферического зеркала

Для уже введённого нами сферического зеркала существует два условно разных типа задач:

• задачи на построение в сферическом зеркале
• задачи на формулу для сферического зеркала

Первый тип задач основан на фактическом построении хода лучей от источника и поиска пересечения отражённых от зеркала лучей. Рассмотрим ряд изображений, полученных от точечного источника, который будем помещать на различных расстояниях от зеркала. Напомним, для сферического зеркала существует 3 просчитанных траектории хода луча (рис. 1).

1. синий. Луч, проходящий через фокус, отражаясь от зеркала, проходит параллельно главной оптической оси (свойство фокуса),
2. зелёный. Луч, падающий на главный оптический центр сферического зеркала, отражается под тем же углом (законы отражения),
3. красный. Луч, идущий параллельно главной оптической оси, после отражения проходит через фокус (свойство фокуса).

И помним о том, что точка пересечения двух любых отражённых лучей является изображением предмета ().

Введём обозначения: пусть  — фокусное расстояние (расстояние от оптического центра зеркала до фокуса),  — расстояние от предмета до зеркала,  — расстояние от изображения до зеркала. Проанализируем ход лучей при различных положениях источника:

• (источник находится очень далеко от сферического зеркала). В этом случае, мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 2). Пустим два луча параллельно главной оптической оси.

Т.к. все лучи, идущие параллельно главной оптической оси, после отражения проходят через фокус, то точка фокуса и является точкой пересечения отражённый лучей, тогда она же и есть изображение источника (точечное, действительное).

• (источник находится за двойным фокусным расстоянием) (рис. 3).

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через фокус (отражается параллельно главной оптической оси). Для визуализации изображения введём описание предмета через стрелку. Точка пересечения отразившихся лучей — изображение (уменьшенное, действительное, перевёрнутое). Положение — между фокусом и двойным фокусом.

• (источник находится ровно в двойном фокусе) (рис. 4).

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через фокус (отражается параллельно главной оптической оси). Точка пересечения отразившихся лучей — изображение (того же размера, действительное, перевёрнутое). Положение — ровно в двойном фокусе.

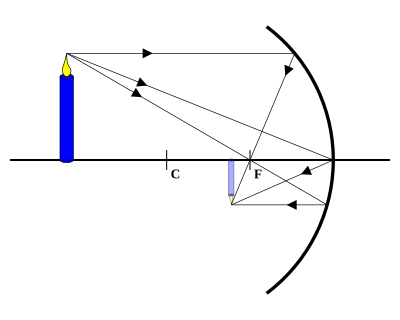
• (источник между фокусом и двойным фокусом) (рис. 5).

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через фокус (отражается параллельно главной оптической оси). Точка пересечения отразившихся лучей — изображение (увеличенное, действительное, перевёрнутое). Положение — за двойным фокусом.

• (источник находится ровно в фокусе сферического зеркала) (рис. 6).

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и падающего в главный оптический центр зеркала (отражается под углом падения). В этом случае, оба отражённых луча оказались параллельными друг другу, т.е. точка пересечения отражённых лучей отсутствует. Это говорит о том, что изображения нет.

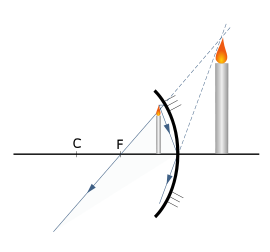
• (источник находится между фокусом и главным оптическим центром) (рис. 7).

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и падающего в главный оптический центр зеркала (отражается под углом падения). Однако отражённые лучи расходятся, т.е. сами отражённые лучи не пересекутся, зато могут пересечься продолжения лучей. Точка пересечения продолжений отразившихся лучей — изображение (увеличенное, мнимое, прямое). Положение — за зеркалом.

Таким образом, часть фраз, присутствующих в задаче и характеризующих изображение (его величину, мнимость/действительность, расположение и т.д.), может намекать на конкретный рисунок и облегчать построение и решение самой задачи. Достаточно часто численные данные в таких задачах берутся из рисунков, на которых расстояния заданы в виде пропорций (рисунок по клеточкам).

Второй тип задач — задачи с числовыми значениями расстояний  ,  — и . Для сферического зеркала выводится соотношение:

(1)

Такого типа задачи решаются геометрически и самой формулой (1).

Вывод: задачи со сферическими зеркалами, в целом, разделяются на два огромных класса: задачи на построение (логика вышеописанных рисунков) и задачи на формулу для сферического зеркала, которые можно определить по наличию численных значений для параметров, входящих в уравнение (1).

2017-11-29 23:05

Найдем положение фокуса

 сферического зеркала, т. е. точки, в которой пересекутся после отражения в подобном зеркале лучи, параллельные его главной оси. Как мы знаем, для получения параллельного пучка лучей источник нужно удалить весьма далеко, т. е. положить в формуле (91.6)

. В этом случае

 есть фокусное расстояние зеркала. Для величины фокусного расстояния, пользуясь формулой (91.6), находим

. (92.1)

Соединяя формулы (91.6) и (92.1), получим формулу зеркала в виде

, (92.2)

т.е. в виде, аналогичном формуле (89.6) тонкой линзы.

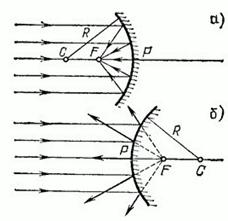
Рис. 206. Фокусы сферических зеркал: а) вогнутое зеркало; б) выпуклое зеркало. (Лучи показаны падающими на значительную часть сферических зеркал. Их следует представлять себе пересекающими зеркало на малой высоте от оси, т.е. захватывающими малую часть зеркала.)

В случае вогнутого зеркала фокус расположен на середине расстояния между полюсом и центром слева от полюса (рис. 206, а); в случае выпуклого зеркала фокус расположен на расстоянии

 справа от полюса, т.е. является мнимым (рис. 206, б).

Пользуясь тем, что источник и его изображение находятся в сопряженных между собой точках, мы можем сразу сделать вывод, что если точечный источник света находится в фокусе зеркала, то его изображение находится в бесконечности, т. е. из зеркала выходит параллельный пучок лучей. Это условие служит основой для получения при помощи вогнутых зеркал параллельных световых пучков, точнее, пучков, близких к параллельным. О применении этого условия к устройству прожекторов мы уже говорили в гл. VIII.

Заметим, что при рассмотрении свойств сферического зеркала, как и в случае линзы, мы предполагали, во-первых, что используется очень узкий пучок лучей, прилегающих к оси зеркала, и, во-вторых, что применяется точечный источник света. Оба эти требования, конечно, вполне строго выполнены быть не могут. Вопрос о том, насколько существенны отступления от этих требований, в каждой конкретной задаче должен решаться особо.

Главный фокус сферического зеркала.

Пусть точка

находится очень далеко от точки

,
так что

.

Тогда из формулы сферического зеркала
запишем:

.

Изображения (точка

)
будет находиться в точке, расстояние
до которой от зеркала равно

.

Эту точку называют главным фокусом
зеркала и обозначают буквой

.

Расстояние главного фокуса от зеркала

называется фокусным расстоянием
сферического зеркала и обозначается
также

.

Формулу сферического зеркала можно
теперь записать в виде

.

Лучи, падающие на зеркало из точки

,
находящейся бесконечно далеко от зеркала
можно считать параллельными. Поэтому
ход лучей имеют вид.

Пусть пучок параллельных лучей падает
на сферическое вогнутое зеркало
параллельно побочной оптической оси.
Отраженные лучи сойдутся в некоторой
точке

,
принадлежащей плоскости проходящей
через фокус зеркала перпендикулярно
главной оптической оси. Эта плоскость
называется фокальный плоскостью зеркала.

Из обратимости световых лучей следует,
что если поместить точечный источник
света в главный фокус

или в любую точку

фокальной плоскости, то после отражения
от сферической поверхности получится
параллельный пучок световых лучей.

Мнимое изображение, мнимый фокус в сферическом зеркале.

Поместим точечный источник

между центром сферического зеркала и
точкой

.
После отражения от зеркала пересекаются
в одной точке не отраженные лучи, которые
будут расходиться, а их продолжения
точка пересечения продолжений лучей
дает мнимое изображение источника

.

Если направить пучок параллельных
лучей параллельно главной оптической
оси на выпуклое сферическое зеркало,
то отраженные лучи будут расходящимися.

Их продолжения пересекаются в одной
точке, находящейся за зеркалом. Она
называется главным фокусом выпуклого
зеркала.

Вследствие того, что в фокусе пересекаются
не сами отраженные лучи, а их продолжения,
то это означает, что главный фокус
выпуклого зеркала является мнимым.

При этом по-прежнему

.

Анализ формулы сферического зеркала.

В общем случае формулу сферического
зеркала можно записать в виде

,

Где знак

соответствует действительному изображению
и действительному главному фокусу
(вогнутое сферическое зеркало)

Знак

соответствует мнимому изображению и
мнимому главному фокусу (выпуклое
сферическое зеркало)

Например, пусть изображение – мнимое,
а фокус – действительный. Тогда

.

Если в задаче неизвестен характер
изображения или свойства фокуса, то
перед соответствующей величиной следует
ставить знак

.

Точка, в которой сходятся продолжения
падающих на зеркало сходящихся лучей,
называется мнимым источником. Для
мнимого источника перед

следует также писать знак

.

Оптической силой сферического зеркала
называется величина, обратная фокусному
расстоянию

,

.

Для вогнутого зеркала оптическая сила
считается положительной, для выпуклого
отрицательной.

Построение изображений в сферическом зеркале.

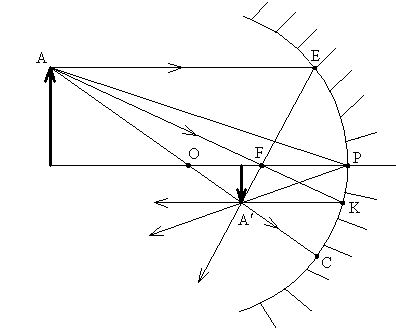
Для построения изображения какой-либо
точки предмета удобнее всего использовать
следующие лучи:

1. Луч, проходящий через оптический центр
   зеркала. Отраженный луч идет по той же
   прямой. Это лучи
   

   на рисунке.

2. Луч, проходящий через фокус зеркала.
   Отраженный луч параллелен главной
   оптической оси. На рисунке это луч
   
   .

3. Луч, падающий на зеркало в его полюсе.
   Отраженный луч симметричен с падающим
   относительно главной оптической оси.
   Это луч
   
   .

4. Луч, параллельный главной оптической
   оси. Отраженный луч проходит через
   фокус зеркала. Это лучи
   

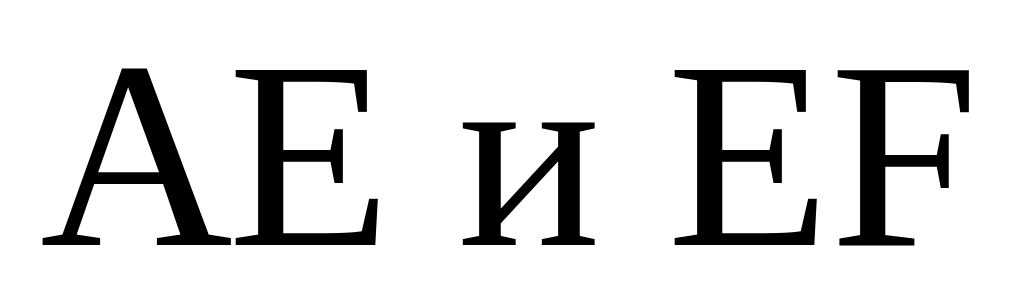
   на рисунке.

Все отраженные лучи проходят через
точку

,
которая является действительным
изображением точки

.

Для построения

достаточно взять любые два из перечисленных
лучей.

Изображение предмета может быть
действительным и мнимым. Если изображение
перевернуть, то оно в общем случае не
совпадает с размерами предмета.

Обозначим

– линейный размер предмета

– линейный размер изображения

Линейным увеличением называется
отношение линейного размера изображения
к линейному размеру предмета.

.

Из подобных треугольников

:

,

.

Если предмет не лежит целиком в плоскости,
перпендикулярной главной оптической
оси, то различные его части увеличиваются
по-разному. Происходит искажение при
рассматривании предмета в сферическом
зеркале.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Сферическое зеркало — зеркало, отражающая поверхность которого имеет вид сегмента сферы.

Описание[править | править код]

Сферическое зеркало может быть выпуклым или вогнутым — в зависимости от того, какая сторона сегмента сферы — выпуклая или вогнутая — является отражающей. Центр соответствующей сферическому зеркалу сферы называется его центром или оптическим центром, середина сегмента — полюсом зеркала, прямая, проходящая через центр и полюс — главной оптической осью зеркала. Другие прямые, проходящие через центр зеркала и точку, отличную от полюса, называются его побочными оптическими осями.

Параксиальные лучи, параллельные главной оптической оси выпуклого сферического зеркала, так же как и продолжения параксиальных лучей, параллельных главной оптической оси вогнутого сферического зеркала, пересекаются в одной точке, называемой его фокусом. Он расположен посередине между центром и полюсом зеркала, то есть расстояние (f) его до зеркала равно половине радиуса (R):

У сферического зеркала, как вообще у любого зеркала, отсутствует хроматическая аберрация, но выражена сферическая аберрация. Сферическая аберрация выражена потому, что в отличие от параболического зеркала (то есть сегмента параболоида вращения), сферическое зеркало может собирать в одной точке лишь параксиальные лучи, то есть те из лучей, параллельных главной оптической оси, которые близки к этой оси. Сферическая аберрация в одном из примеров применения сферического вогнутого зеркала, зеркально-линзовом телескопе системы Дмитрия Максутова, устраняется компенсированием специально подобранной линзой — мениском.

Известным примером выпуклого сферического зеркала является ёлочный шар.

Построение изображения в сферическом зеркале[править | править код]

Проще всего построить изображение отрезка, перпендикулярного главной оптической оси зеркала и настолько небольшого по высоте, что луч, исходящий из его верхней точки и параллельный главной оптической оси зеркала — параксиальный. Его изображение будет также перпендикулярным главной оптической оси зеркала, расстояние его от зеркала при известном расстоянии от зеркала до предмета и фокусного расстояния зеркала можно вычислить по формуле зеркала. Высота изображения (y’) будет равна произведению высоты предмета (y) на отношение расстояния от изображения до зеркала (v) к расстоянию от зеркала до предмета (u):

Для вогнутого сферического зеркала[править | править код]

Если сферическое зеркало вогнутое, возможны различные случаи расположения изображения относительно зеркала при различных расстояниях до предмета. Буквой C обозначен центр зеркала, а буквой F — его фокус. При u>f формула зеркала имеет вид:

а при u<f:

Для построения взято три луча (хотя достаточно и двух):

• луч, параллельный главной оптической оси после отражения от зеркала пройдёт через его фокус;
• луч, проходящий через фокус после отражения пойдёт параллельно главной оптической оси;
• луч, падающий на полюс зеркала после отражения пойдёт под углом, равным углу падения (по закону отражения света).

Если предмет приближён к зеркалу и находится на расстоянии, превышающем расстояние от зеркала до его центра, то изображение его будет действительным, перевёрнутым и уменьшенным и расположится на отрезке между центром и фокусом.

Если предмет помещён в центре зеркала, то его изображение также будет расположено в центре зеркала. Изображение получается действительным, перевёрнутым и равным по величине предмету.

Если предмет помещён между центром и фокусом, то изображение будет расположено дальше от зеркала, чем его центр и будет действительным, перевёрнутым и увеличенным.

Если предмет ближе фокуса к зеркалу, то изображение — мнимое, прямое, увеличенное, по другую сторону зеркала от предмета.

Для выпуклого сферического зеркала[править | править код]

Построение изображения в выпуклом сферическом зеркале проще, чем в вогнутом: здесь при любом расстоянии предмета до зеркала его изображение будет расположено за зеркалом. На рисунке ниже буквой F обозначен фокус выпуклого зеркала, буквой V — полюс, y (в формуле u) — высота предмета, y’ (в формуле v) — высота изображения. Формула зеркала в этом случае имеет вид:

Для построения взято два луча:

• луч от верхней точки предмета, параллельный главной оптической оси, отразится от зеркала, и продолжение этого отражённого луча пройдёт через фокус и через верхнюю точку изображения;
• луч от верхней точки предмета, продолжение которого проходит через фокус, после отражения пойдёт параллельно главной оптической оси, а продолжение этого отражённого луча также пройдёт через верхнюю точку изображения.

Таким образом, верхней точкой изображения будет точка пересечения продолжения первого отражённого луча и продолжения второго отражённого луча.

См. также[править | править код]

• Линза

Литература[править | править код]

• Ландсберг Г.С. Элементарный учебник физики. — 13-е изд. — М.: Физматлит, 2003. — Т. 3. Колебания и волны. Оптика. Атомная и ядерная физика. — С. 249—266. — 656 с. — ISBN 5922103512.

Сферические зеркала находят широкое применение в различных приборах и устройствах. Для их использования необходимо уметь рассчитывать их характеристики (положения изображений, их увеличения). Как же это можно сделать?

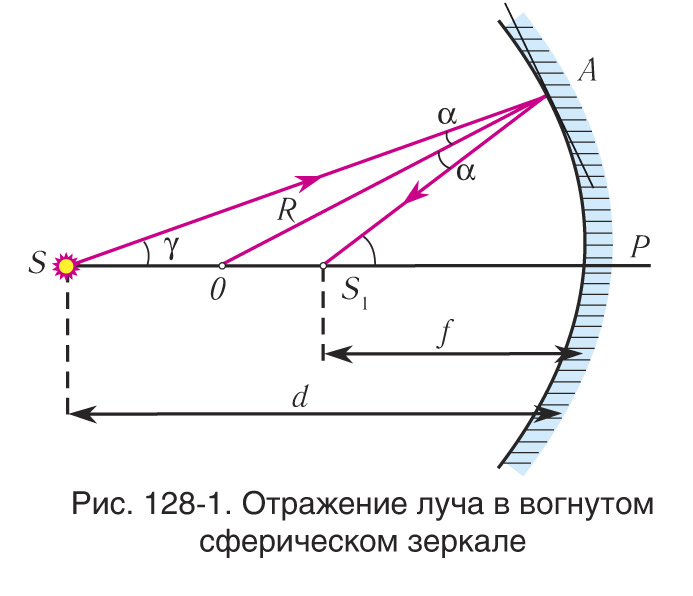
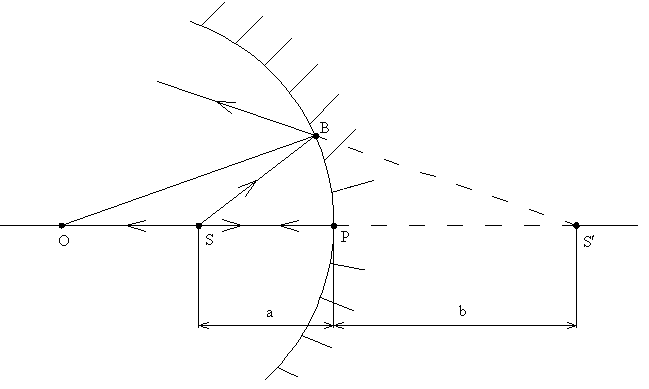
Получим формулу вогнутого сферического зеркала. Пусть точечный источник света S расположен на главной оптической оси за центром зеркала (рис. 128-1).

Расстояние SP от источника до зеркала обозначим SP = d . Луч SA после отражения пересечет ось в  точке  S₁. Расстояние от зеркала до точки S1 обозначим S₁P = f.

В ΔSAS₁ линия AO является биссектрисой SAS₁ и делит противоположную сторону на отрезки, пропорциональные двум другим сторонам треугольника:

Для луча  SA, близкого к оптической оси

Кроме того, SO = d – R и OS₁ = R – f. 

Подставляя  эти значения в пропорцию, получим

.

Это равенство приводится к виду (сделайте это сами):

Полученная формула называется формулой сферического зеркала.

Обратите внимание, что данная формула получилась при использовании приближенных равенств (1), т.е. она верна при падании на линзу параксиальных лучей.

Проанализируем полученную формулу. Если источник удалить от зеркала бесконечно далеко, то лучи, падающие на зеркало, будут идти параллельно оптической оси. Слагаемое  станет равным нулю. Расстояние f будет равно некоторому значению F, и формула зеркала примет вид:

.

Откуда находим 

Таким образом, лучи, параллельные главной оптической оси зеркала, отразившись от него, пересекаются в точке F, лежащей на главной оси и расположенной от полюса зеркала на расстоянии, равном половине его радиуса (см. рис. 114).

Это точка называется главным фокусом зеркала. Величина D, обратная фокусному расстоянию сферического зеркала, называется его оптической силой:

.

Единицей измерения оптической силы в СИ является диоптрия: 1 дптр = 1м^-1.

Исходя из принципа обратимости лучей, можно сделать вывод, что лучи света от источника, помещенного в главный фокус зеркала, отразившись от него, пойдут параллельно главной оптической оси (см. рис. 147).

Расстояния d и R для любого луча, выходящего из точки S и падающего на зеркало, остаются неизменными. Поэтому луч после отражения будет пересекать ось в точке S₁ . Таким образом, лучи, выходящие из какой-либо точки S на главной оси, расположенной за центром линзы, пересекаются после отражения от зеркала в одной и той же точке S₁, также расположенной на этой оси. Эта точка S₁ называется действительным изображением точки S .

Для действительных предмета, изображения и фокуса расстояния d, f и F считаются положительными, а для мнимых d, f и F  — отрицательными.

Фокус выпуклого зеркала всегда мнимый, вогнутого — действительный.

Отметим, что при падении на зеркало расходящегося пучка, предмет будет действительным. При падении на зеркало сходящегося пучка, предмет будет мнимым.

Вогнутые зеркала используются для получения параллельных пучков света в различных отражателях или рефлекторах для освещения удаленных предметов (фары, прожекторы). Для этого следует поместить источник света в главном фокусе (рис. 128-2) вогнутого зеркала.

Полученное свойство фокусировки параллельного пучка лучей является приближенным и справедливым лишь для узкого пучка, т. е. лучей не слишком отстоящих от оптической оси. Для широких пучков имеет место сферическая аберрация, т.е. далекие от оптической оси лучи пересекают ее не в фокусе (см. рис. 128-2). Изображение при этом искажается — становится нерезким. Подобные искажения называются аберрациями оптических систем.

Сферическая аберрация — явление, при котором лучи, далеко отстоящие от главной оптической оси,  соберутся не в форме зеркала, а в точке, расположенной на меньшем расстоянии от него. В результате точечный объект будет изображаться пятном. Для получения точечного осевого изображения зеркало должно быть параболическим (см. рис. 128-2, 128-3).

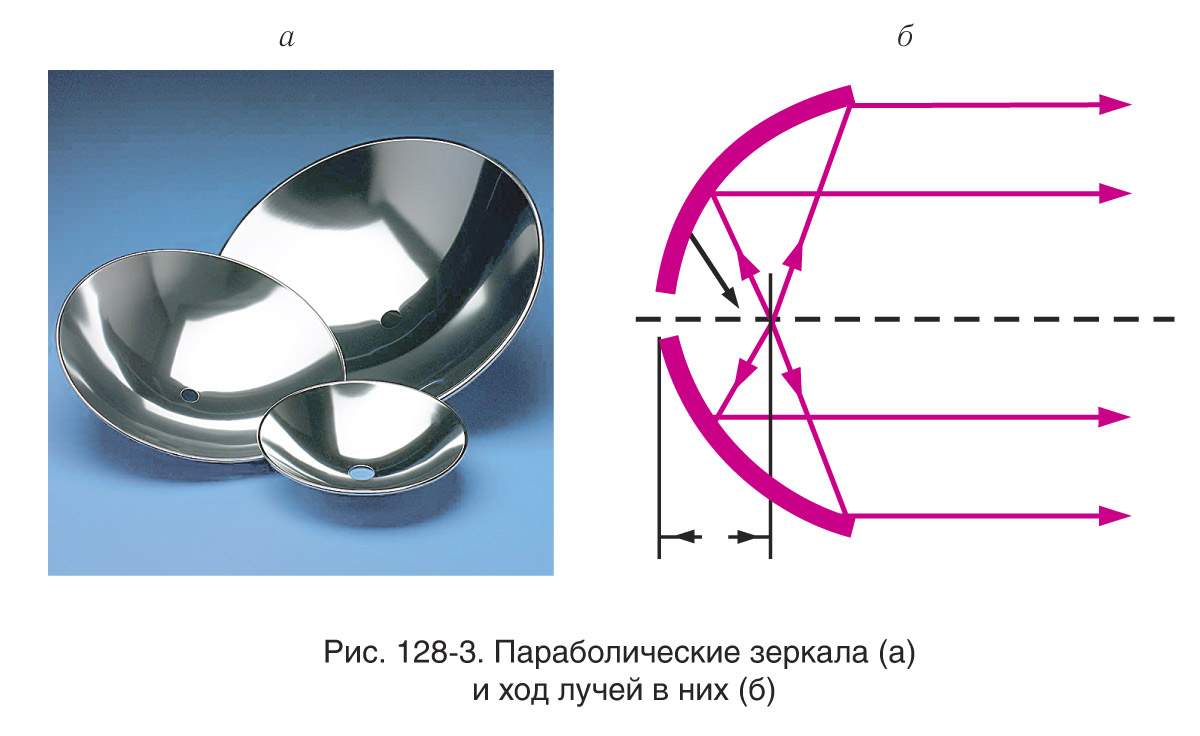
Такие зеркала используются во всех крупнейших телескопах. Но даже в них параллельные пучки, идущие под небольшими углами к оптической оси, после отражения не пересекаются в одной точке и дают сильно искаженные внеосевые изображения. Поэтому пригодное для работы поле зрения оказывается очень небольшим порядка нескольких десятков угловых минут.