Как найти фокус системы двух линз

Система двух линз

Допустим, что предмет А находится в фокусе первой линзы. Луч, вышедший из первой линзы, будет параллельным оптической оси и, следовательно, пройдет через фокус второй линзы. Рассматривая эту систему как одну линзу, можно написать

. Так как 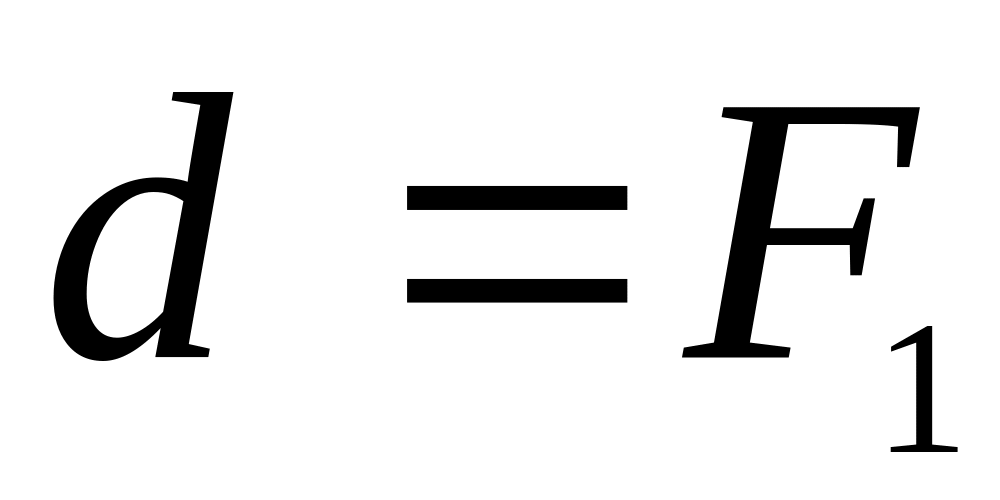, , 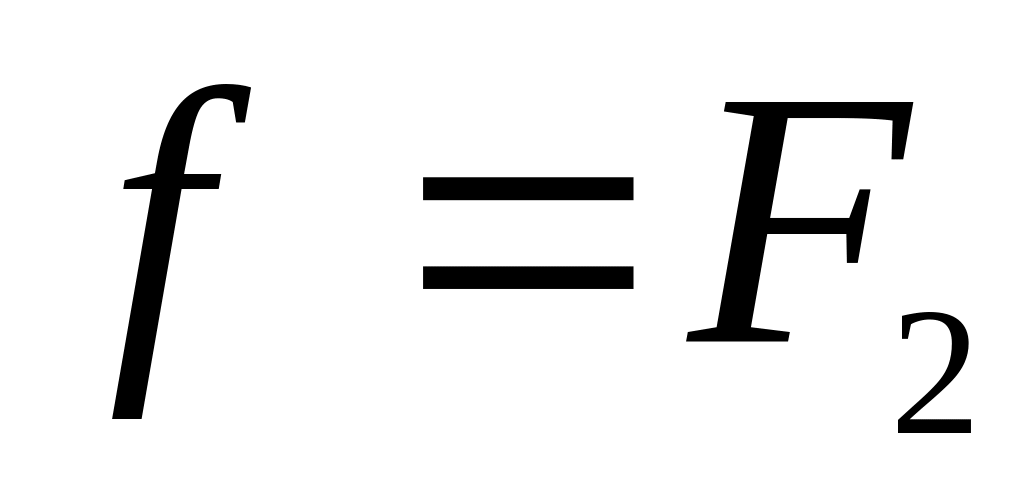то .

Этот результат верен и для более сложной системы тонких линз. Оптическая сила системы линз будет равна сумме оптических сил составных частей

.

В случаях двух отдельных линз с фокусными расстояниями F₁ и F₂, расположенными вдоль одной и той же оси на расстоянии (а) друг от друга:

.

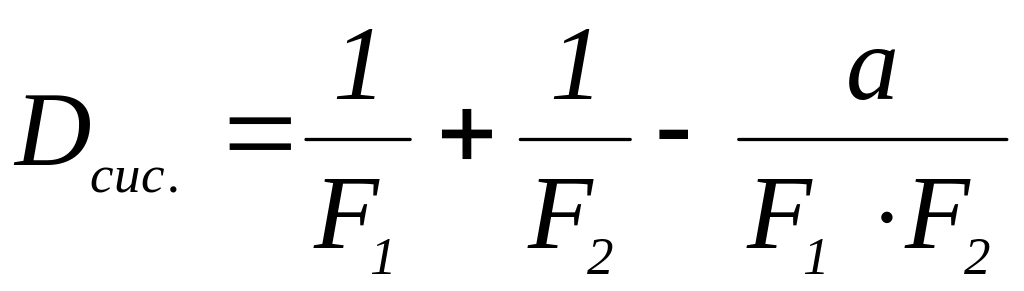Яркость изображения, получаемого с помощью линзы, зависит от значений ее диаметра и оптической силы. Величину называют относительным отверстием, а — светосилой линзы, где 2r – диаметр линзы.

Светосила обуславливает яркость изображения, образуемого любой оптической системой, и зависит от плотности световой энергии, проходящей через линзу и дающей изображение предмета.

Линза обеспечивает геометрически правильное и резкое изображение только при условии параксиальности (лучи идут под малыми углами к главной оптической оси) световых лучей и отсутствии дисперсии. При несоблюдении этих условий в изображении, которое дает линза, наблюдаются определенные недостатки и искажения. Основными из них являются: сферическая аберрация, кривизна поля и дисторсия, хроматическая аберрация, астигматизм наклонных пучков.

1. Сферическая аберрация. Это явление заключается в том, что лучи, удаленные от главной оптической оси, сильнее преломляются линзой, чем лучи, близкие к оси (параксиальные). Вследствие этого имеет место отклонение от гомоцентричности. На рисунке (4) показан пучок параллельных главной оптической оси лучей, которые, после преломления, практически не собираются в одной точке и дают расплывчатое изображение (пятно).

Сферическая аберрация

2. Хроматическая аберрация. Проходя через линзу, белые лучи разлагаются на спектральные цвета так же, как при прохождении через призму. Как следствие дисперсии, изображение белого источника света оказывается на экране окрашенным в спектральные цвета.

3. Астигматизм. Изображение прямого источника света, от которого падают на линзу сильно наклоненные к главной оптической оси лучи, получается не в одной плоскости в виде двух искривленных линий. Астигматизм имеет место в результате неодинакового преломления лучей, проходящих через линзу в различных меридианных плоскостях. Применяя соответствующим образом подобранные комбинации линз с недостатками, имеющими противоположный характер, можно добиться устранения их, что и делают на практике.

В данной работе предлагается определить фокусное расстояние тонких собирающих и рассеивающих линз.

Фокусное расстояние собирающей линзы можно определить, используя уравнение (3) и (7), если измерить соответствующие величины.

Фокусное расстояние рассеивающей линзы можно определить следующими способами:

1. Зная фокусное расстояние собирающей линзы, составляют систему 2-х плотно сдвинутых линз (собирающей и рассеивающей), дающую действительное изображение. Определив опытным путем, фокусное расстояние полученной системы, вычисляют фокусное расстояние рассеивающей линзы из формулы:

; откуда ;

2. Если на пути лучей, исходящих из точки А (рис. 5), поставить собирающую линзу, то лучи, преломляясь в ней, дадут изображение (точка Д). При помещении рассеивающей линзы за собирающей, в результате рассеивания, действительное изображение переместится в положение С. Пользуясь принципом обратимости лучей (обратимы в данном случае точки С и А), можно положить, что точка С – есть предмет для рассеивающей линзы. Тогда ее изображение будет лежать в точке Д. Следовательно, расстояние от рассеивающей линзы до точки С будет d, а от рассеивающей линзы до точки Д – f.

И змеряя эти расстояния и учитывая, что f – отрицательно, по формуле (3) рассчитывают фокусное расстояние рассеивающей линзы.

_{Определение фокусного расстояния рассеивающей линзы}

Источник

Комбинации линз

Узнайте, как определить фокусное расстояние объединенных линз. Читайте правила расчета фокусного расстояния линзы, объективы ахромат, выпуклая и вогнутая линзы.

Составная линза отображает несколько простых линз с общей осью.

Задача обучения

Основные пункты

Термины

• Ахроматический дублет – две простые линзы, объединенные так, чтобы хроматическая аберрация одной частично компенсировала вторую.
• Афокальная система – не создает сходимости или расходимости пучка, то есть обладает бесконечной эффективной фокусной дистанцией.
• Аберрация – сходимость к различным точкам световых лучей.

Комбинации линз

Обычная линза представлена одним оптическим элементом, а вот составная – несколькими простыми с общей осью. Применение ряда элементов дает возможность исправлять оптические аберрации, вроде хроматической, созданной показателями преломления в стекле.

Наиболее простой вариант – пребывание линз в соприкосновении. Если они тонкие, то объединенная фокусная дистанция:

Если эти линзы отстранены на некую дистанцию:

Заднее фокусное расстояние (ЗФР)

Дистанцию от второй линзы к фокусу комбинированных именуют задней фокальной:

Если дистанция разделения приравнивается к нулю, то объединенная фокусная и ЗФР бесконечны. Это пара линз, преобразующих параллельный узел в другой параллельный узел. Подобную систему именуют афокальной, потому что она не дает чистого схождения или расхождения. Здесь линзы формируют наиболее простую разновидность оптического телескопа. Увеличение высчитывается по формуле:

У всех преломляющихся телескопов присутствует единый принцип. Объединение объектива и другого типа окуляра используют, чтобы собрать свет, чье количество превосходит показатель, доступный человеческим глазам

Телескоп с двумя выпуклыми линзами создает отрицательное увеличение (инвертированное изображение), а выпуклая и вогнутая линзы – положительное (вертикальное).

Ахроматы

Это линза, созданная для ограничения эффектов хроматической и сферической аберрации. Они корректируются, чтобы свести две длины волны (чаще всего красную и синюю/фиолетовую) в фокус одной плоскости.

Наиболее известный тип – ахроматический объектив. Представлен двумя отдельными стеклянными линзами с разным количеством дисперсии. Обычно один элемент выступает вогнутым (кремень), а второй выпуклый (кровель-стекло). Элементы устанавливаются рядом и скрепляются, чтобы хроматическая аберрация одной уменьшала вторую.

В кровельной линзе положительная мощность не совсем равна отрицательной у кремневой. Вместе они создают слабую положительную линзу, сводящую две длины волны в один фокус.

(а) – Хроматическая аберрация создается из-за зависимости показателя преломления линзы от длины волны. Мощность увеличивается сильнее для фиолетового (V), чем для красного (R). (b) – Ахроматический дублет может частично корректировать хроматические аберрации, но требует линзы из разных материалов и камеры

Источник

ГЛАВНОЕ ФОКУСНОЕ РАССТОЯНИЕ – расстояние от (задней) главной точки до (заднего) главного фокуса фотографического объектива. Главное фокусное расстояние является важнейшей характеристикой фотографического объектива и гравируется на его оправе вместе с другими данными. Чем больше главное фокусное расстояние, тем крупнее при прочих равных условиях изображение. Каждый объектив имеет два главных фокусных расстояния: переднее, отсчитваемое от передней главной точки до переднего главного фокуса и изображаемое на схемах слева от объектива, и заднее, отсчитываемое от задней главной точки до заднего главного фокуса и расположенное справа от объектива. Оба эти расстояния постоянны и равны между собой и отсчитываются в противоположные стороны. В объективах с переменным фокусным расстоянием главное фокусное расстояние изменяется увеличением или уменьшением расстояния между отдельными линзами объектива. Вместе с тем изменяется и масштаб изображения. Величина главного фокусного расстояния отдельной линзы определяется радиусами кривизны и показателем преломления стекла, из которого линза изготовлена: где r 1 и r 2 – радиусы кривизны соответственно первой и второй поверхности линзы. Главное фокусное расстояние системы линз зависит как от главных фокусных расстояний линз, составляющих систему, так и от их взаимного расстояния. Для системы из двух линз главное фокусное расстояние определяется формулой: где f – главное фокусное расстояние системы; f 1 – главное фокусное расстояние первой линзы; f 2 – главное фокусное расстояние второй линзы; Δ – оптический интервал, т. е. расстояние от задней главной точки первой линзы до передней главной точки задней линзы.

22. Объективы с переменным фокусным расстоянием. Устройство объективов с переменным фокусным расстоянием

По
способу построения оптической схемы
объектива выделяют два основных типа:

• Трансфокатор представляет
  собой оптическую систему,
  состоящую из афокальной панкратической
  насадки с переменным угловым увеличением
  и объектива с постоянным фокусным
  расстоянием. Исправление аберраций
  производится для обеих частей
  трансфокатора по отдельности. В такой
  системе трансфокатором могут называть
  только афокальную насадку.

• Вариообъектив представляет
  собой оптическую систему, рассчитанную
  как единое целое с точки зрения аберраций.
  По сравнению с трансфокатором позволяет
  достичь лучшего исправления многих
  аберраций при меньшем числе линз и
  компонентов, а также добиться большей
  геометрической светосилы во всём
  диапазоне фокусных расстояний. По схеме
  вариообъектива построен фотографический
  объектив «Рубин-1»,
  киносъёмочные объективы «Вариогоир».

В
широком применении находятся объективы
обоих типов, и оба термина часто
применяются к ним как синонимы.

Трансфока́тор (Ва́риообъекти́в или
«зум»
от англ. zoom) — объектив с
переменным фокусным
расстоянием.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Явление преломления света на сферической поверхности раздела двух оптических сред позволяет получать изображения светящихся предметов. Эта возможность осуществляется с помощью линзы — прозрачного тела, ограниченного двумя сферическими поверхностями. Линза является основным оптическим элементом в таких приборах, как фотоаппарат, проекционный фонарь, микроскоп, телескоп и т. д.

На рисунке 1 показан разрез преломляющей сферической поверхности, разделяющей две оптические среды с различными показателями преломления. Очевидно, качественное изображение любого предмета возможно только в том случае, когда пучок лучей, исходящих из любой точки предмета (например, из точки (P)), после преломления соберется снова в точку. Вообще говоря, сферическая граница раздела двух сред не обеспечивает этого условия. Так, луч (NB) после преломления пересечет ось (PQ), строго говоря, в другой точке, нежели луч (MA). Однако при некоторых условиях пучок лучей, испущенных точкой, может собраться практически в точку. Это будет в том случае, когда высота (h), на которой все лучи этого пучка пересекают преломляющую поверхность, мала по сравнению с радиусом кривизны (OC) преломляющей поверхности. Другими словами, когда мал угол (alpha). Лучи, удовлетворяющие этому условию, называются параксиальными. Для удаленных источников требование малости угла (alpha) эквивалентно требованию малости угла (u). Но малость угла (u) не является достаточным условием параксиальности. Действительно, луч, параллельный оси (PQ) ((u = 0)), но достаточно удаленный от нее ((h) велико), не будет параксиальным.

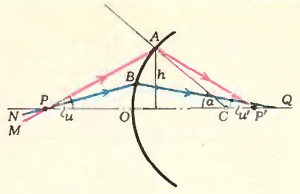
Таким образом, в зависимости от того, сколь хорошо выполняется условие параксиальности, в окрестности точки (P) будет более или менее большой кружок размытия. Однако на практике нет необходимости делать его меньше некоторой, вполне определенной, величины. Например, если кружок размытия станет меньше элемента сетчатки глаза (зерна фотоэмульсии на фотопленке, неровностей матового стекла и т. п.), он будет восприниматься нами как точка. Его дальнейшее уменьшение в нашем зрительном ощущении ничего не изменит.

Всюду в дальнейшем мы будем иметь дело только с параксиальными лучами (можно, в принципе, придумать такие преломляющие поверхности, для которых условие параксиальности лучей не является обязательным. Однако наиболее просты в изготовлении именно сферические поверхности). Кроме того, ограничимся рассмотрением только тонких линз, то есть таких линз, фокусные расстояния которых существенно больше их толщины.

Если тонкая линза изготовлена из материала с показателем преломления (n), слева от линзы находится среда показателем преломления (n_1), а справа — с показателем преломления (n_2), то имеют место соотношения:

(frac{{{n_2}}}{{{F_2}}} = frac{{n – {n_1}}}{{{R_1}}} + frac{{n – {n_2}}}{{{R_2}}}),    (1)

(frac{{{n_1}}}{{{F_1}}} = frac{{n – {n_1}}}{{{R_1}}} + frac{{n – {n_2}}}{{{R_2}}}),    (2)

Здесь (F_1) и (F_2) — переднее и заднее фокусные расстояния линзы, (R_1) и (R_2) — радиусы кривизны, соответственно, передней и задней поверхностей линзы. Эти соотношения можно получить (проделайте это самостоятельно!), рассматривая ход лучей, идущих от бесконечно удаленного источника, находящегося в первом случае слева от линзы, а втором случае — справа. В частности, когда с обеих сторон от линзы находится воздух ((n_1 = n_2 = 1)),

(frac{1}{{{F_1}}} = frac{1}{{{F_2}}} = left( {n – 1} right)left( {frac{1}{{{R_1}}} + frac{1}{{{R_2}}}} right)).    (3)

Принято считать, что если поверхность своей выпуклой стороной обращена к среде с меньшим показателем преломления, то ее радиус кривизны (R) положителен ((R > 0)), в противном случае (R < 0). Линзы, у которых фокусное расстояние положительно ((F > 0)), называются положительными или собирающими, если же (F < 0) — отрицательными или рассеивающими. Величина (D = frac{1}{F}) называется оптической силой линзы; она измеряется в диоптриях.

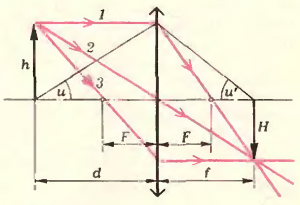
При построении изображений, полученных с помощью тонких линз, используют три основных (или базисных) луча, показанных на рисунке 2. С помощью этого рисунка нетрудно получить формулу тонкой линзы:

(frac{1}{d} + frac{1}{f} = frac{1}{F}),

а также выражения для её линейного (поперечного) увеличения:

(Gamma = frac{H}{h} = frac{f}{d} = frac{{f – F}}{F} = frac{F}{{d – F}})

и для углового увеличения:

(gamma = frac{{tg,u’}}{{tg,u}} = frac{{h/f}}{{h/d}} = frac{d}{f} = frac{1}{Gamma }).

Рассмотрим теперь несколько конкретных задач.

Задача 1

На поверхности воды (n_в = 1,3) лежит двояковыпуклая тонкая стеклянная линза (n_{ст} = 1,5) с радиусами кривизны (R_1 = R_2 = 10) см. Определите переднее и заднее фокусные расстояния линзы. Чему равно фокусное расстояние этой линзы в воздухе?

Это относительно простая задача. Непосредственное применение формул (1) и (2), где (n_1 = 1), (n_2 = n_в = 1,3) и (n = n_{ст} = 1,5), дает

({F_1} approx 14) см и ({F_2} approx 18,5) см.

Для фокусного расстояния линзы в воздухе формула (3) приводит к результату (F = 10) см.

Задача 2

На рисунке 3 дан ход луча (ABC) через тонкую положительную линзу. Построить ход произвольного луча (DE) после преломления в линзе.

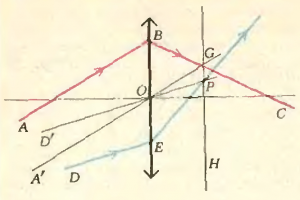
Проведем (A’O), параллельный лучу (AB) и проходящий через оптический центр линзы. Он не преломится. Точка (O) пересечения этого луча с лучом (BC) лежит в фокальной плоскости (H). Луч (D’O), параллельный (DE), пересечет фокальную плоскость в точке (P). Через эту же точку пройдет, преломившись, и луч (DE).

3адача 3

Какие очки вы пропишите близорукому человеку, который может читать текст, расположенный не далее 20 см?

Очки ни в коей мере не исправляют дефектов человеческого глаза. Их роль сводится к тому, чтобы отобразить объекты окружающего мира на такое расстояние, с которого глаз четко различает предметы. В нашем случае для того чтобы близорукий человек мог видеть удаленные предметы, например, звезду, очки должны создавать изображение звезды не далее 20 см от глаза, а глаз будет рассматривать уже это изображение. Предположим, что линза очков вплотную придвинута к глазу (небольшой зазор между линзой и глазом несущественно исказит приведенные ниже расчеты), и запишем формулу линзы:

(frac{1}{d} – frac{1}{f} = frac{1}{F}),

Здесь (d) —расстояние до звезды, а (f) — максимальное расстояние от изображения звезды до глаза. Член (frac{1}{f}) берется со знаком минус, поскольку изображение мнимое. Так как (d) очень велико, можно смело положить (frac{1}{d} = 0). По условию задачи (f = 20) см. Отсюда

(F = – 20) см, (D = – 5) дптр.

Таким образом, близорукому человеку следует прописать очки с рассеивающими линзами оптической силы -5 дптр.

Задача 4

С помощью линзы с фокусным расстоянием (F) на экране получают уменьшенное и увеличенное изображения предмета, находящегося на расстоянии (L) от экрана. Найти отношение размеров изображений.

Пусть высота предмета равна (h). Тогда изображение имеет высоту (H = Gamma h), и отношение размеров изображений есть

(frac{{{H_1}}}{{{H_2}}} = frac{{{Gamma _1}h}}{{{Gamma _2}h}} = frac{{{f_1}/{d_1}}}{{{f_2}/{d_2}}}).

Теперь нам нужно найти (d_1), (d_2), (f_1) и (f_2). По формуле линзы (frac{1}{d} + frac{1}{f} = frac{1}{F}), а из условия задачи (d + f = L). Исключив (d), получим квадратное уравнение

[{f^2} – fL + FL = 0,]

откуда

[{f_{1,2}} = frac{L}{2} pm sqrt {frac{{{L^2}}}{4} – FL} .]

Кроме того, из свойства обратимости лучей (d_1 = f_2) и (d_2 = f_1). Таким образом,

[frac{{{H_1}}}{{{H_2}}} = frac{{f_1^2}}{{f_2^2}} = {left( {frac{{L/2 + sqrt {{L^2}/4 – FL} }}{{L/2 – sqrt {{L^2}/4 – FL} }}} right)^2}.]

Задача 5

С помощью положительной линзы получают изображения двух точечных источников (A) и (B). Один из них расположен на оптической оси на двойном фокусном расстоянии от линзы, другой смещен от оси так, что прямая, соединяющая источники, образует с оптической осью угол (varphi = 30^circ) (рис. 4) Под каким углом (psi ) к оси следит расположить плоский экран, чтобы одновременно получить на нем четкие изображения обоих источников?

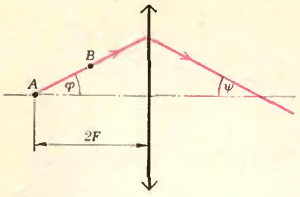
Очевидно, экран нужно расположить по лучу (AB) (проведенному от источника (A) через точку (B)) после его преломления в линзе. Используем формулу для углового увеличения:

(gamma = frac{1}{Gamma } = frac{d}{f} = frac{F}{f-F}).

Здесь (f) — расстояние от изображения источника (A) до линзы, a (F) — фокусное расстояние линзы. Поскольку (A) находится на двойном фокусном расстоянии от линзы, (f = 2F). Следовательно,

(gamma = frac{F}{{2F – F}} = 1,) и (psi = varphi = 30^circ ).

Задача 6

Сложный объектив состоит из двух тонких линз: положительной с фокусным расстоянием (F_1 = 20) см и отрицательной с фокусным расстоянием (F_2 = -10) см. Линзы расположены на расстоянии (l = 15) см друг от друга. С помощью объектива получают на экране изображение Солнца. Какое фокусное расстояние (f) должна иметь тонкая линза, чтобы изображение Солнца, полученное с ее помощью, имело такой же размер?

Здесь мы уже имеем дело с системой линз.

Найдем размер изображения Солнца, создаваемого сложным объективом, рассматривая ход лучей последовательно в обеих линзах. Изображение, создаваемое первой линзой, находится, очевидно, в ее фокальной плоскости. Размер этого изображения ({H_1} = {F_1}tgalpha ), где (alpha) — угловой диаметр Солнца, видимый с Земли (рис.5). Увеличение, даваемое второй линзой, равно (frac{{{H_2}}}{{{H_1}}} = frac{{{f_2}}}{{{d_2}}}). По формуле линзы имеем

[ – frac{1}{{{d_2}}} + frac{1}{{{f_2}}} = frac{1}{{{F_2}}},]

где (d_2 = F_1 – l) (изображение Солнца в первой линзе является мнимым источником для второй). Отсюда

[{f_2} = frac{{{F_2}left( {{F_1} – l} right)}}{{{F_1} + {F_2} – l}}.]

Таким образом, размер изображения, создаваемого всем объективом,

[{H_2} = frac{{{F_1}{F_2}tgalpha }}{{{F_1} + {F_2} – l}}.]

Одиночная линза с фокусным расстоянием (F) дает изображение, имеющее размер ({H_2} = F;tgalpha ). Сопоставляя два последних выражения, получим

[F = frac{{{F_1}{F_2}}}{{{F_1} + {F_2} – l}} = frac{{20left( { – 10} right)}}{{20 + left( { – 10} right) – 15}} = 40;см]

Только что разобранная задача является частным случаем более общей, практически важной задачи: дана система двух (или более) тонких линз с общей оптической осью; необходимо найти одну тонкую линзу, действие которой эквивалентно действию данной системы. Эта задача будет полностью решена, если мы найдем фокусное расстояние эквивалентной линзы и ее местоположение (или, что то же самое, положение ее фокуса). Попробуйте вывести соответствующие формулы самостоятельно. Для ориентировки приведем окончательные результаты: фокусное расстояние искомой эквивалентной линзы равно

[F = frac{{{F_1}{F_2}}}{Delta },]

а ее фокус находится от второй линзы на расстоянии (f_2), равном

[{f_2} = frac{{{F_2}left( {Delta – {F_2}} right)}}{Delta }.]

Здесь (F_1) и (F_2) — фокусные расстояния первой и второй линз соответственно, а (Delta) — расстояние между задним фокусом первой линзы и передним фокусом второй (его называют оптическим интервалом). Принято считать (Delta > 0), если передний фокус второй линзы лежит левее заднего фокуса первой линзы, и (Delta < 0) в противном случае.

В заключение предлагаем несколько задач для самостоятельного решения.

Упражнения

1. На рисунке 6 дан ход луча (ABC) через тонкую отрицательную линзу. Определить построением фокусное расстояние линзы.

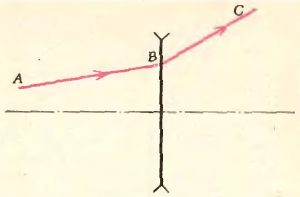
1. Какие очки вы пропишите дальнозоркому человеку, который резко видит предметы, расположенные не ближе 50 см?
2. Положительная линза дает действительное изображение с увеличением в 2 раза. Определить фокусное расстояние линзы, если расстояние между линзой и изображением 24 см.
3. Предмет в виде отрезка длиной (l) расположен вдоль оптической оси тонкой положительной линзы с фокусным расстоянием (F). Середина отрезка находится на расстоянии (d) от линзы. Линза дает действительное изображение всех точек предмета. Определить продольное увеличение предмета.
4. Положительная линза с фокусным расстоянием (F) и отрицательная с фокусным расстоянием (-F) расположены на расстоянии (a) друг от друга так, что их оптические оси совпадают. На расстоянии (a) перед положительной линзой находится источник света. Изображение этого источника, даваемое системой линз, располагается на таком же расстоянии (a) за отрицательной линзой. Определить это расстояние.
5. Оптическая система состоит на двух линз: собирающей с фокусным расстоянием (F_1 = 30) см и рассеивающей с фокусным расстоянием (F_2 = – 30) см. Оптические оси линз совпадают. Параллельный пучок лучей падает на первую линзу и, пройдя через систему, собирается в некоторой точке, лежащей на оптической оси. На сколько сместится эта точка, если линзы поменять местами?
6. В проекционном аппарате используется сложный объектив, состоящий из двух собирающих линз с фокусными расстояниями (F_1 = 20) см и (F_2 = 15) см. Линзы расположены на расстоянии (a=5) см друг от друга. Определить, с каким увеличением будет проецироваться диапозитив на экран, находящийся на расстоянии (b=10) м от объектива проектора. К диапозитиву обращена линза с фокусным расстоянием (F_2).

Источник: Журнал “Квант”, №4 1977 г. Автор: Е. Кузнецов.

Цель работы: с помощью экспериментальной установки
исследовать, как изменяется фокусное расстояние двух линз, сложенных вместе.

Для выполнения работы нам предлагается оборудование из
комплекта № 4 в составе: собирающие линзы № 1 и № 2, экран и линейка (или
оптическая скамья с миллиметровой шкалой).

Прежде чем начать выполнять работу давайте с вами вспомним,
что линзами называют прозрачные тела, ограниченные криволинейными (чаще
всего сферическими) или криволинейной и плоской поверхностями.

Прямая, проходящая через центры сферических поверхностей,
называется главной оптической осью линзы.

Если на линзу падает пучок света, лучи которого параллельны
главной оптической оси, то после преломления в линзе: они пересекаются
(собираются) в одной точке, лежащей на главной оптической оси в собирающей
линзе, или пересекаются их продолжения в рассеивающей линзе.

Напомним, что точка, в которой пересекаются преломлённые
линзой лучи, падающие параллельно главной оптической оси, или их продолжения,
называется главным фокусом линзы. Обозначается он большой латинской
буквой «Эф» (F).

А расстояние от оптического центра линзы до её главного
фокуса, называется фокусным расстоянием. Его тоже принято обозначать
латинской буквой «Эф» (F),
а единицей его измерения в СИ является метр:

[F] = [м].

Кроме того, различные линзы по-разному преломляют лучи света.
Так вот, для количественной оценки преломляющей способности линзы вводят
величину, называемую оптической силой линзы, которая обратно
пропорциональна фокусному расстоянию:

Также опыт показывает, что общая оптическая сила двух или более тонких линз, сложенных
вместе, равна алгебраической сумме оптических сил этих линз:

D = D₁ + D₂ + 
+ D_n.

И если расписать оптические силы линз, то получится, что
фокусное расстояние системы линз окажется меньше наименьшего фокусного
расстояния:

Вот это мы с вами сегодня и проверим. Итак, первое, что нам с
вами необходимо сделать — это нарисовать рисунок нашей экспериментальной
установки. Для этого мы в бланке ответов изобразим две тонкие собирающие линзы
так, чтобы их оптические центры на одной прямой, то есть чтобы их главные
оптические оси совпадали. Также укажем положение главного фокуса системы линз,
в котором и будут собираться преломлённые линзой лучи света, параллельные
главной оптической оси.

В качестве источника света нам предлагают использовать свет
от удалённого окна, так как в этом случае лучи, идущие к линзе от каждой его
точки, можно считать параллельными друг другу. То есть изображение предмета
получается в фокальной плоскости. И чем дальше от линзы находится предмет, тем
точнее будет измерение фокусного расстояния.

Теперь запишем формулы, которыми будем пользоваться при
выполнении данной работы. Во-первых, это формула оптической сила линзы:

Далее мы запишем, что общая
оптическая сила двух тонких линз, сложенных вместе, равна
алгебраической сумме оптических сил этих линз:

D = D₁ + D₂.

Используя предыдущую формулу, распишем оптические силы линз
так, как это показано на экране:

И выразим отсюда фокусное расстояние системы линз:

Теперь составим небольшую таблицу. В первой колонке мы будем
записывать фокусное расстояние первой линзы. Во-второй — линзы № 2. А в третьей
и четвёртой колонке мы с вами запишем фокусные расстояние системы двух линз.

Теперь приступим непосредственно к работе. Итак, для начала
на оптической скамье установим линзу № 1 и экран так, чтобы последний находился
на нулевой отметке миллиметровой шкалы.

Развернём всю нашу установку так, чтобы свет от дальнего окна
примерно попадал на линзу.

Теперь, медленно перемещая линзу вдоль оптической скамьи,
попытаемся на экране получить чёткое изображение окна. Как только окно попадёт
в фокус — зафиксируем положение линзы и определим расстояние, на котором
находится линза от экрана (именно линза, а не подставка, на которой она
располагается). В нашем случае фокусное расстояние оказалось равным 100 мм.
Заносим это значение в нашу таблицу с учётом погрешности измерения:

Убираем линзу номер один. А вместо неё на скамье
устанавливаем вторую линзу. Опять медленно перемещая линзу вдоль оптической
скамьи, стараемся получить на экране чёткое изображение окна.

Когда окно попадает в фокус мы вновь фиксируем положение
линзы и определяем расстояние от экрана до линзы. Заносим и это значение в нашу
таблицу с учётом погрешности измерения:

Возвращаем на скамью первую линзу, поставив её так, чтобы она
оказалась первой от окна. Совмещаем линзы. И находим их фокусное расстояние тем
же способом, что и в предыдущих двух случаях.

Если нашли окно в фокусе, то измеряем расстояние от экрана до
системы линз и заносим значение фокусного расстояния в таблицу:

Теперь мы с вами должны поменять местами линзы один и два и
повторить наши измерения

Найденное фокусное расстояние также заносим в таблицу с
учётом погрешности измерения:

Глядя на результаты наших экспериментов, мы с вами можем
сделать следующий вывод: фокусное расстояние системы двух разных линз, в
пределах погрешности измерения, не зависит от порядка расположения линз и
оказалось меньше наименьшего из фокусных расстояний двух линз.

Для введённых нами линз существует два условно разных типа задач:

• задачи на построение в собирающей и рассеивающей линзах
• задачи на формулу для тонкой линзы

Первый тип задач основан на фактическом построении хода лучей от источника и поиска пересечения преломлённых в линзах лучей. Рассмотрим ряд изображений, полученных от точечного источника, который будем помещать на различных расстояниях от линз. Для собирающей и рассеивающей линзу существуют рассмотренные (не нами) траектории распространения луча (рис. 1) от источника .

Для собирающей линзы (рис. 1.1) лучи:

1. синий. Луч, идущий вдоль главной оптической оси, после преломления проходит через передний фокус.
2. зелёный. Луч, проходящий через оптический центр линзы, не испытывает преломления (не отклоняется от первоначального направления).
3. красный. Луч, идущий через передний фокус, после преломления распространяется параллельно главной оптической оси.

Пересечение любых из этих двух лучей (чаще всего выбирают лучи 1 и 2) дают изображение ().

Для рассеивающей линзы (рис. 1.2) лучи:

1. синий. Луч, идущий параллельно главной оптической оси, преломляется так, что продолжения луча проходит через задний фокус.
2. зелёный. Луч, проходящий через оптический центр линзы, не испытывает преломления (не отклоняется от первоначального направления).

Пересечение продолжений рассмотренных лучей даёт изображение ().

Аналогично сферическому зеркалу, получим набор изображений от предмета, расположенного на различных расстояниях от зеркала. Введём те же обозначения: пусть  — расстояние от предмета до линзы,  — расстояние от изображения до линзы,  — фокусное расстояние (расстояние от фокуса до линзы).

Для собирающей линзы:

• (источник находится очень далеко от линзы). В этом случае мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 2). Пустим два луча параллельно главной оптической оси линзы.

Т.к. все лучи, идущие параллельно главной оптической оси линзы, после преломления в линзе проходят через фокус, то точка фокуса и является точкой пересечения преломлённых лучей, тогда она же и есть изображение источника (точечное, действительное).

• (источник находится за двойным фокусным расстоянием) (рис. 3).

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Для визуализации изображения введём описание предмета через стрелку. Точка пересечения преломившихся лучей — изображение (уменьшенное, действительное, перевёрнутое). Положение — между фокусом и двойным фокусом.

• (источник находится ровно в двойном фокусе) (рис. 4).

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Точка пересечения преломившихся лучей — изображение (того же размера, действительное, перевёрнутое). Положение — ровно в двойном фокусе.

• (источник между фокусом и двойным фокусом) (рис. 5)

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется).  Точка пересечения преломившихся лучей — изображение (увеличенное, действительное, перевёрнутое). Положение — за двойным фокусом.

• (источник находится ровно в фокусе собирающей линзы) (рис. 6)

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). В этом случае, оба преломлённых луча оказались параллельными друг другу, т.е. точка пересечения отражённых лучей отсутствует. Это говорит о том, что изображения нет.

• (источник находится между фокусом и главным оптическим центром) (рис. 7)

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Однако преломлённые лучи расходятся, т.е. сами преломлённые лучи не пересекутся, зато могут пересечься продолжения этих лучей. Точка пересечения продолжений преломлённых лучей — изображение (увеличенное, мнимое, прямое). Положение — по ту же сторону, что и предмет.

Для рассеивающей линзы построение изображений предметов практически не зависит от положения предмета, так что ограничимся произвольным положением самого предмета и характеристикой изображения.

• (источник находится очень далеко от линзы). В этом случае, мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 8). Пустим два луча параллельно главной оптической оси линзы.

Т.к. все лучи, идущие параллельно главной оптической оси линзы, после преломления в линзе должны проходить через фокус (свойство фокуса), однако после преломления в рассеивающей линзе лучи должны расходится. Тогда в фокусе сходятся продолжения преломившихся лучей. Тогда точка фокуса и является точкой пересечения продолжений преломлённых лучей, т.е. она же и есть изображение источника (точечное, мнимое).

• любое другое положение источника (рис. 9).

Воспользуемся ходом луча, идущего параллельно главной оптической оси (продолжение отражённого луча проходит через передний фокус) и идущего через главный оптический центр линзы (не преломляется). Тогда изображением будет пересечение продолжений преломлённых лучей.

Второй тип задач связан с формулой тонкой линзы. Такие задачи основываются на числовых данных параметров, характеризующих положение источника, изображения или фокуса линзы. Рассмотрим произвольную систему (рис. 10). Пусть положение источника (), изображения () и фокуса системы () задано.

Тогда взаимосвязь между параметрами положения элементов можно описать формулой:

(1)

Важно: для использования формулы (1) необходимо помнить правило расстановки знаков. Если линза собирающая, то , если рассеивающая, то . В случае действительных предметов и изображений: , , а в случае мнимых предметов и изображений:  и .

И последним параметром, характеризующим линзы или систему линз, является оптическая сила линзы (). Её нахождение довольно простое:

(2)

Размерность оптической силы линзы: м=дптр (диоптрии). Оптическая сила собирающей линзы положительна, рассеивающей — отрицательна.

Вывод: задачи с линзами, в целом, разделены на два класса. Задачи на построение основываются на рисунках 2-9. Достаточно проанализировать ход лучей и найти изображение (рис.1). Численные значения в дано указывают на задачи на формулу тонкой линзы (1).