Тонкие линзы. Построение изображений.
-
Собирающая линза: действительное изображение точки.
-
Собирающая линза: действительное изображение предмета.
-
Собирающая линза: мнимое изображение точки.
-
Собирающая линза: мнимое изображение предмета.
-
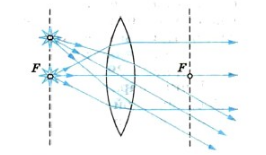
Собирающая линза: предмет в фокальной плоскости.
-
Рассеивающая линза: мнимое изображение точки.
-
Рассеивающая линза: мнимое изображение предмета.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: построение изображений в линзах, формула тонкой линзы.
Правила хода лучей в тонких линзах, сформулированные в предыдущей теме, приводят нас к важнейшему утверждению.
Теорема об изображении. Если перед линзой находится светящаяся точка , то после преломления в линзе все лучи (или их продолжения) пересекаются в одной точке
.
| Напомним ещё раз, что это касается не вообще всех лучей, а только параксиальных, то есть образующих малые углы с главной оптической осью. В предыдущей теме мы договорились, что рассматриваем только параксиальные лучи. Лишь для них работают наши правила хода лучей сквозь тонкие линзы. |
Точка называется изображением точки
.
Если в точке пересекаются сами преломлённые лучи, то изображение называется действительным. Оно может быть получено на экране, так как в точке
концентрируется энергия световых лучей.
Если же в точке пересекаются не сами преломлённые лучи, а их продолжения (так бывает, когда преломлённые лучи расходятся после линзы), то изображение называется мнимым. Его нельзя получить на экране, поскольку в точке
не сосредоточено никакой энергии. Мнимое изображение, напомним, возникает благодаря особенности нашего мозга – достраивать расходящиеся лучи до их мнимого пересечения и видеть в этом пересечении светящуюся точку.Мнимое изображение существует лишь в нашем сознании.
Теорема об изображении служит основой построения изображений в тонких линзах. Мы докажем эту теорему как для собирающей, так и для рассеивающей линзы.
к оглавлению ▴
Собирающая линза: действительное изображение точки.
Сперва рассмотрим собирающую линзу. Пусть – расстояние от точки
до линзы,
– фокусное расстояние линзы. Имеются два принципиально разных случая:
и
(а также промежуточный случай
). Мы разберём эти случаи поочерёдно; в каждом из них мы
обсудим свойства изображений точечного источника и протяжённого объекта.
Первый случай: . Точечный источник света
расположен дальше от линзы, чем левая фокальная плоскость (рис. 1).
 |
| Рис. 1. Случай a>f: действительное изображение точки S |
Луч , идущий через оптический центр, не преломляется. Мы возьмём произвольный луч
, построим точку
, в которой преломлённый луч пересекается с лучом
, а затем покажем, что положение точки
не зависит от выбора луча
(иными словами, точка
является одной и той же для всевозможных лучей
). Тем самым окажется, что все лучи, исходящие из точки
, после преломления в линзе пересекаются в точке
и теорема об изображении будет доказана для рассматриваемого случая
.
Точку мы найдём, построив дальнейший ход луча
. Делать это мы умеем: параллельно лучу
проводим побочную оптическую ось
до пересечения с фокальной плоскостью в побочном фокусе
, после чего проводим преломлённый луч
до пересечения с лучом
в точке
.
Теперь будем искать расстояние от точки
до линзы. Мы покажем, что это расстояние выражается только через
и
, т. е. определяется лишь положением источника и свойствами линзы, и не зависит тем самым от конкретного луча
.
Опустим перпендикуляры и
на главную оптическую ось. Проведём также
параллельно главной оптической оси, т. е. перпендикулярно линзе. Получим три пары подобных треугольников:
, (1)
, (2)
. (3)
В результате имеем следующую цепочку равенств (номер формулы над знаком равенства указывает, из какой пары подобных треугольников данное равенство получено).
(4)
Но , так что соотношение (4) переписывается в виде:
. (5)
Отсюда находим искомое расстояние от точки до линзы:
. (6)
Как видим, оно и в самом деле не зависит от выбора луча . Следовательно, любой луч
после преломления в линзе пройдёт через построенную нами точку
, и эта точка будет действительным изображением источника
Теорема об изображении в данном случае доказана.
Практическая важность теоремы об изображении состоит вот в чём. Коль скоро все лучи источника пересекаются после линзы в одной точке – его изображении
– то для построения изображения достаточно взять два наиболее удобных луча. Какие именно?
Если источник не лежит на главной оптической оси, то в качестве удобных лучей годятся следующие:
– луч, идущий через оптический центр линзы – он не преломляется;
– луч, параллельный главной оптической оси – после преломления он идёт через фокус.
Построение изображения с помощью этих лучей показано на рис. 2.
 |
| Рис. 2. Построение изображения точки S, не лежащей на главной оптической оси |
Если же точка лежит на главной оптической оси, то удобный луч остаётся лишь один – идущий вдоль главной оптической оси. В качестве второго луча приходится брать “неудобный” (рис. 3).
 |
| Рис. 3. Построение изображения точки S, лежащей на главной оптической оси |
Посмотрим ещё раз на выражение ( 5). Его можно записать в несколько ином виде, более симпатичном и запоминающемся. Перенесём сначала единицу влево:
Теперь разделим обе части этого равенства на a:
(7)
Соотношение (7) называется формулой тонкой линзы (или просто формулой линзы). Пока что формула линзы получена для случая собирающей линзы и для . В дальнейшем мы выведем модификации этой формулы для остальных случаев.
Теперь вернёмся к соотношению (6). Его важность не исчерпывается тем, что оно доказывает теорему об изображении. Мы видим также, что не зависит от расстояния
(рис. 1, 2) между источником
и главной оптической осью!
Это означает, что какую бы точку отрезка
мы ни взяли, её изображение будет находиться на одном и том же расстоянии
от линзы. Оно будет лежать на отрезке
– а именно, на пересечении отрезка
с лучом
, который пойдёт сквозь линзу без преломления. В частности, изображением точки
будет точка
.
Тем самым мы установили важный факт: изображением отрезка лужит отрезок
. Отныне исходный отрезок, изображение которого нас интересует, мы называем предметом и обозначаем на рисунках красной стрелочкой. Направление стрелки нам понадобится для того, чтобы следить – прямым или перевёрнутым получается изображение.
к оглавлению ▴
Перейдём к рассмотрению изображений предметов. Напомним, что пока мы находимся в рамках случая . Здесь можно выделить три характерных ситуации.
1. . Изображение предмета является действительным, перевёрнутым, увеличенным (рис. 4; двойной фокус обозначен
). Из формулы линзы следует, что в этом случае будет
(почему?).
Такая ситуация реализуется, например, в диапроекторах и киноаппаратах – эти оптические приборы дают на экране увеличенное изображение того, что находится на плёнке. Если вам доводилось показывать слайды, то вы знаете, что слайд нужно вставлять в проектор перевёрнутым – чтобы изображение на экране выглядело правильно, а не получилось вверх ногами.
Отношение размера изображения к размеру предмета называется линейным увеличением линзы и обозначается Г – (это заглавная греческая “гамма”):
.
Из подобия треугольников и
получим:
. (8)
Формула (8) применяется во многих задачах, где фигурирует линейное увеличение линзы.
2. . В этом случае из формулы (6) находим, что и
. Линейное увеличение линзы согласно (8) равно единице, т. е. размер изображения равен размеру предмета (рис. 5).
 |
| Рис. 5.a=2f: размер изображения равен размеру предмета |
3. . В этом случае из формулы линзы следует, что
(почему?). Линейное увеличение линзы будет меньше единицы – изображение действительное, перевёрнутое, уменьшенное (рис. 6).
 |
| Рис. 6.a>2f: изображение действительное, перевёрнутое, уменьшенное |
Данная ситуация является обычной для многих оптических приборов: фотоаппаратов, биноклей, телескопов – словом, тех, в которых получают изображения удалённых объектов. По мере удаления предмета от линзы его изображение уменьшается в размерах и приближается к фокальной плоскости.
Рассмотрение первого случая нами полностью закончено. Переходим ко второму случаю. Он уже не будет столь объёмным.
к оглавлению ▴
Собирающая линза: мнимое изображение точки.
Второй случай: . Точечный источник света
расположен между линзой и фокальной плоскостью (рис. 7).
 |
| Рис. 7. Случай a < f: мнимое изображение точки |
Наряду с лучом , идущим без преломления, мы снова рассматриваем произвольный луч
. Однако теперь на выходе из линзы получаются два расходящихся луча
и
. Наш глаз продолжит эти лучи до пересечения в точке
.
Теорема об изображении утверждает, что точка будет одной и той же для всех лучей
, исходящих из точки
. Мы опять докажем это с помощью трёх пар подобных треугольников:
Снова обозначая через расстояние от
до линзы, имеем соответствующую цепочку равенств (вы уже без труда в ней разберётесь):
. (9)
Отсюда
. (10)
Величина не зависит от луча
, что и доказывает теорему об изображении для нашего случая
. Итак,
– мнимое изображение источника
. Если точка
не лежит на главной оптической оси, то для построения изображения
удобнее всего брать луч, идущий через оптический центр, и луч, параллельный главной оптической оси (рис. 8).
 |
| Рис. 8. Построение изображения точки S, не лежащей на главной оптической оси |
Ну а если точка лежит на главной оптической оси, то деваться некуда – придётся довольствоваться лучом, падающим на линзу наклонно (рис. 9).
 |
| Рис. 9. Построение изображения точки S, лежащей на главной оптической оси |
Соотношение (9) приводит нас к варианту формулы линзы для рассматриваемого случая . Сначала переписываем это соотношение в виде:
,
а затем делим обе части полученного равенства на a:
. (11)
Сравнивая (7) и (11), мы видим небольшую разницу: перед слагаемым стоит знак плюс, если изображение действительное, и знак минус, если изображение мнимое.
Величина , вычисляемая по формуле (10), не зависит также от расстояния
между точкой
и главной оптической осью. Как и выше (вспомните рассуждение с точкой
), это означает, что изображением отрезка
на рис. 9 будет отрезок
.
к оглавлению ▴
Учитывая это, мы легко строим изображение предмета, находящегося между линзой и фокальной плоскостью (рис. 10). Оно получается мнимым, прямым и увеличенным.
Такое изображение вы наблюдаете, когда разглядываете мелкий предмет в увеличительное стекло – лупу. Случай полностью разобран. Как видите, он качественно отличается от нашего первого случая
. Это не удивительно – ведь между ними лежит промежуточный “катастрофический” случай
.
к оглавлению ▴
Собирающая линза: предмет в фокальной плоскости.
Промежуточный случай:. Источник света
расположен в фокальной плоскости линзы (рис. 11).
Как мы помним из предыдущего раздела, лучи параллельного пучка после преломления в собирающей линзе пересекутся в фокальной плоскости – а именно, в главном фокусе, если пучок падает перпендикулярно линзе, и в побочном фокусе при наклонном падении пучка. Воспользовавшись обратимостью хода лучей, мы заключаем, что все лучи источника , расположенного в фокальной плоскости, после выхода из линзы пойдут параллельно друг другу.
 |
| Рис. 11. a=f: изображение отсутствует |
Где же изображение точки ? Изображения нет. Впрочем, никто не запрещает нам считать, что параллельные лучи пересекаются в бесконечно удалённой точке. Тогда теорема об изображении сохраняет свою силу и в данном случае – изображение
находится на бесконечности.
Соответственно, если предмет целиком расположен в фокальной плоскости, изображение этого предмета будет находиться на бесконечности (или, что то же самое, будет отсутствовать).
Итак, мы полностью рассмотрели построение изображений в собирающей линзе.
к оглавлению ▴
Рассеивающая линза: мнимое изображение точки.
К счастью, здесь нет такого разнообразия ситуаций, как для собирающей линзы. Характер изображения не зависит от того, на каком расстоянии предмет находится от рассеивающей линзы, так что случай тут будет один-единственный.
Снова берём луч и произвольный луч
(рис. 12). На выходе из линзы имеем два расходящихся луча
и
, которые наш глаз достраивает до пересечения в точке
.
 |
| Рис. 12. Мнимое изображение точки S в рассеивающей линзе |
Нам снова предстоит доказать теорему об изображении – о том, что точка будет одной и той же для всех лучей
. Действуем с помощью всё тех же трёх пар подобных треугольников:
.
Имеем:
(12)
Отсюда
. (13)
Величина b не зависит от луча span
, поэтому продолжения всех преломлённых лучей span
пересекутся в точке
– мнимом изображении точки
. Теорема об изображении тем самым полностью доказана.
Вспомним, что для собирающей линзы мы получили аналогичные формулы (6) и (10). В случае их знаменатель обращался в нуль (изображение уходило на бесконечность), и поэтому данный случай разграничивал принципиально разные ситуации
и
.
А вот у формулы (13) знаменатель не обращается в нуль ни при каком a. Стало быть, для рассеивающей линзы не существует качественно разных ситуаций расположения источника – случай тут, как мы и сказали выше, имеется только один.
Если точка не лежит на главной оптической оси, то для построения её изображения удобны два луча: один идёт через оптический центр, другой – параллельно главной оптической оси (рис. 13).
 |
| Рис. 13. Построение изображения точки S, не лежащей на главной оптической оси |
Если же точка лежит на главной оптической оси, то второй луч приходится брать произвольным (рис. 14).
 |
| Рис. 14. Построение изображения точки S, лежащей на главной оптической оси |
Соотношение (13) даёт нам ещё один вариант формулы линзы. Сначала перепишем:
,
а потом разделим обе части полученного равенства на a:
(14)
Так выглядит формула линзы для рассеивающей линзы.
Три формулы линзы (7), (11) и (14) можно записать единообразно:
если соблюдать следующую договорённость о знаках:
– для мнимого изображения величина считается отрицательной;
– для рассеивающей линзы величина считается отрицательной.
Это очень удобно и охватывает все рассмотренные случаи.
к оглавлению ▴
Величина , вычисляемая по формуле (13), опять-таки не зависит от расстояния
между точкой
и главной оптической осью. Это снова даёт нам возможность построить изображение предмета
, которое на сей раз получается мнимым, прямым и уменьшенным (рис. 15).
 |
| Рис. 15. Изображение мнимое, прямое, уменьшенное |
Разберем задачи ЕГЭ по теме: Тонкие линзы. Построение изображений.
1. Тонкая собирающая линза с фокусным расстоянием F находится между двумя точечными источниками света на расстоянии d=15 см от одного из них. Источники расположены на главной оптической оси на расстоянии L=22,5 см друг от друга. Найдите фокусное расстояние линзы, если их изображения получились в одной точке. Ответ выразите в сантиметрах.
Дано:
= 15 см = 0,15 м
= 22,5 см=0,225 м
Найти:
Фокусное расстояние F – ?
Решение:
Тонкая собирающая линза дает различные виды изображений: увеличенные (уменьшенные), прямые (обратные), действительные (мнимые). Характеристика изображения зависит от расстояния от предмета до линзы, т.е. от соотношения d и F.
Так как в задаче говорится о получении изображений в одной точке, то один из точечных источников должен находиться за фокусом линзы – он дает действительное изображение. Второй точечный источник должен находиться перед фокусом – он дает мнимое изображение.
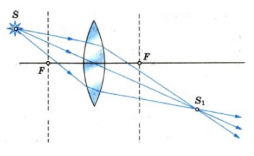
На рис. 1 представлено получение изображения для точечного источника света , находящегося на расстоянии больше фокусного,
– изображение точечного источника света
.
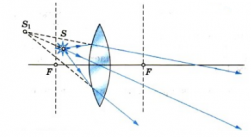
На рис. 2 представлено получение изображения для точечного источника света , находящегося на расстоянии меньше фокусного,
– изображение точечного источника света
.
После создания модели, поясняющей условие этой задачи, можно переходить к её решению. Для этого надо применить формулу тонкой линзы для двух случаев. С учетом правила знаков , так как изображение в первом случае действительное, во втором – мнимое.
Сложим эти два уравнения и учтем, что Так как изображения в двух случаях получались в одной точке, то
Определим, что (м).
(м)
(см).
Ответ: 10
2. Какая из точек (1, 2, 3 или 4) является изображением точки S, созданным тонкой собирающей линзой с фокусным расстоянием F (см. рисунок)?
Решение:
Для получения изображения точечного источника S необходимо осуществить построение двух любых лучей, исходящих от этого источника. Самым «удобным» лучом является луч, проходящий через оптический центр линзы. Такие лучи, после прохождения через линзу, не меняют своего направления. На рисунке таким лучом является луч 1-1ʹ.
Второй и третий лучи от точечного источника S попадают на линзу произвольно. Дальнейший ход таких лучей определяется следующим алгоритмом:
- необходимо построить побочные оптические оси, параллельные падающим лучам (на рисунке они проведены пунктирной линией);
- провести фокальную плоскость и найти точки пересечения этой плоскости с побочными оптическими осями;
- продолжить ход световых лучей после прохождения через линзу (на рисунке это лучи 2ʹ и 3ʹ).
Поэтому изображением точечного источника S (точки S) будет являться точка 2.
При решении этой задачи мы рассмотрели ход трех лучей сквозь линзу, для получения ответа достаточно взять любую комбинацию лучей (1-1ʹ и 2 – 2ʹ) или (1-1ʹ и 3 – 3ʹ ).
Ответ: 2
3. Спираль лампочки расположена вблизи главной оптической оси тонкой рассеивающей линзы на расстоянии а от неё перпендикулярно этой оси, причем , где F – модуль фокусного расстояния линзы. Затем рассеивающую линзу заменили на собирающую с фокусным расстоянием F. Установите соответствие между видом линзы, использованной в опыте, и свойствами даваемого ею изображения.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| Виды линз | Свойства изображения |
| А) линза рассеивающая | 1) мнимое, прямое, уменьшенное |
| Б) линза собирающая | 2) мнимое, перевёрнутое, увеличенное |
| 3) действительное, перевёрнутое, увеличенное | |
| 4) действительное, прямое, увеличенное |
Решение
Решение подобных задач опирается на умение строить изображения протяженных (имеющих размеры) предметов при прохождении лучей через линзу.
Рис.1
На рис.1 выполнено построение изображения предмета АВ в тонкой собирающей линзе. Для этого применялись следующие лучи:
1-1ʹ – луч, проходящий через оптический центр, не преломляется;
2 – 2ʹ – луч, падающий на линзу параллельно главной оптической оси, после преломления идет через фокус, расположенный за линзой .
Полученное изображение АʹВʹ имеет следующие характеристики:
увеличенное (размер изображения превышает размер предмета),
перевернутое (направления стрелок АВ и АʹВʹ противоположны),
действительное (предмет и его изображения находятся по разные стороны от линзы).
Рис.2
На рис.2 выполнено построение изображения предмета АВ в тонкой рассеивающей линзе. Для этого применялись следующие лучи:
1-1ʹ – луч, проходящий через оптический центр, не преломляется;
2 – 2ʹ – луч, падающий на линзу параллельно главной оптической оси, после преломления идет через фокус, расположенный перед линзой .
Полученное изображение АʹВʹ имеет следующие характеристики:
уменьшенное (размер изображения меньше размера предмета),
прямое (направления стрелок АВ и АʹВʹ совпадают),
мнимое (предмет и его изображения находятся с одной стороны от линзы).
Полученные изображения и их характеристики приводят к следующему ответу:
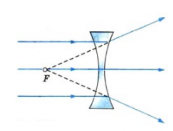
4. На рисунке показан ход лучей от точечного источника света S через тонкую линзу. Какова оптическая сила этой линзы? (Ответ дать в диоптриях.)
Решение:
На рисунке представлен ход световых лучей от точечного источника света S. Луч, проходящий через оптический центр, не меняет своего направления. Второй луч, идущий параллельно главной оптической оси, после преломления идет через фокус. Это позволяет определить фокусное расстояние линзы. Согласно рисунку, оно равно двум клеткам. С учётом указанного масштаба, длина одной клетки равна 4 см. Таким образом, фокусное расстояние этой линзы F=8 см = 0,08 м.
Так как оптическая сила линзы (дптр).
Ответ: 12,5
Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Тонкие линзы. Построение изображений.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Фокусное расстояние линзы — расстояние от оптического центра линзы до ее главного фокуса
Данная формула справедлива только для тонкой линзы. Линза называется тонкой, если ее толщина много меньше, чем радиусы кривизны R1 и R2 обеих поверхностей
Следует знать, что знаки величин u, v, f выбираются исходя из конкретной ситуации. Например для действительного изображения от действительного предмета в собирающей линзе — все эти величины будут положительными. Если возьмем мнимое изображение, то расстояние до него (v) принимается отрицательным, а если предмет будет мнимый, то расстояние до него (u) будет отрицательным, если линза рассеивающая — фокусное расстояние (f) отрицательно.
Если же хотите посчитать фокусное расстояние для любой линзы, то вам потребуется:
Линза называется положительной (собирающей), если ее фокусное расстояние положительно (F>0), и отрицательной (рассеивающей), если ее фокусное расстояние меньше нуля (F<0). Существует несколько вариантов линз:
Линзы симметричны, то есть они имеют одинаковое фокусное расстояние независимо от направления света — слева или справа, что, однако, не относится к другим характеристикам, например, аберрациям, величина которых зависит от того, какой стороной линза повёрнута к свету.
В Формуле мы использовали :
— Фокусное расстояние линзы
— Расстояние от предмета, до линзы
— Расстояние от линзы, до изображения
— Относительный показатель преломления
— Радиус кривизны передней части линзы
— Радиус кривизны задней части линзы
Фокусное расстояние отрицательной
линзы определяется с помощью вспомогательной
положительной линзы.
Способ 1.
Если на пути лучей, выходящих из источника
S и сходящихся в точке
S1 после
преломления в собирающей линзе 1 (рис.3)
поместить рассеивающую линзу 2 так,
чтобы расстояние a1
было меньше ее фокусного расстояния,
то изображение источника S
удалится от линзы 1. Предположим, что
оно переместится в точку S2.
Для линзы 2 точка S1
является предметом, а S2
– изображением.
Тогда, согласно (1) можно найти положение
заднего фокуса рассеивающей линзы:
(3)
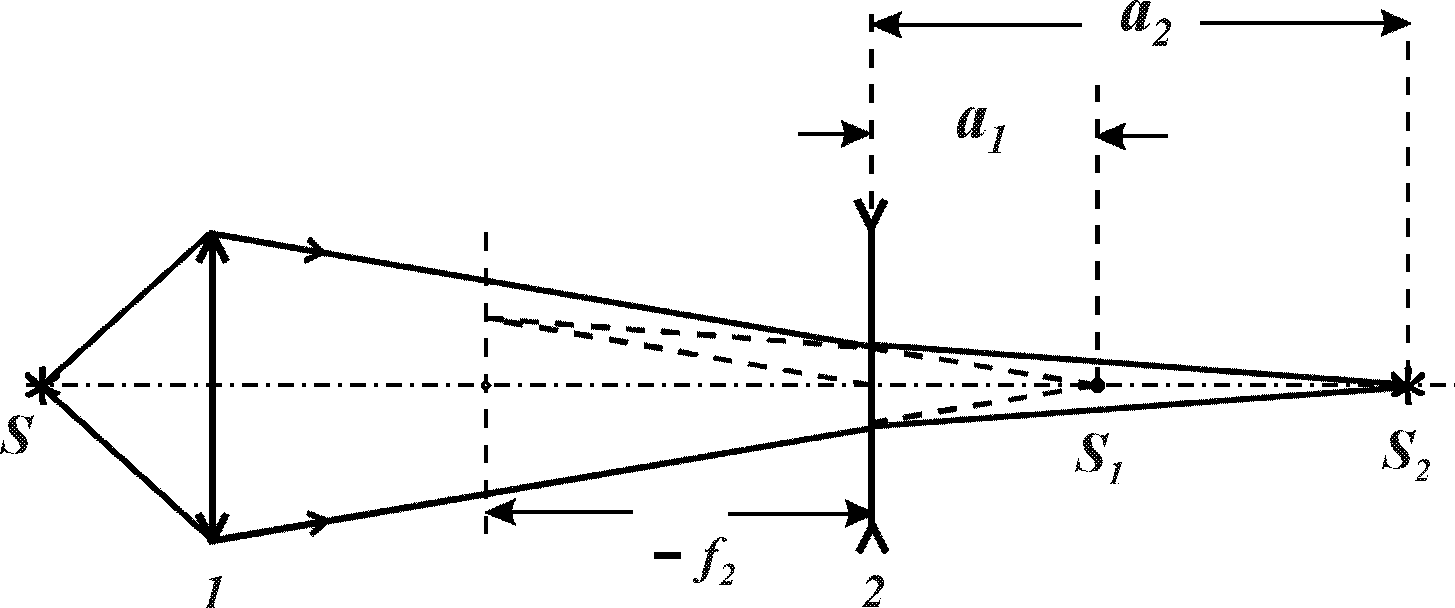
Рис.3. К определению
фокусного расстояния тонкой рассеивающей
линзы способом 1.
Порядок
выполнения задания:
-
На оптической скамье поместить
осветитель, собирающую линзу и экран.
Перемещая экран, получить на нем
отчетливое изображение креста. Отметить
это положение экрана (точка S1). -
На оптическую скамью между найденным
положением точки S1
и собирающей линзой 1 поместить вблизи
экрана исследуемую рассеивающую линзу
2. -
Перемещая экран, вновь найти отчетливое
изображение креста (точка S2). -
Определив расстояния a1
и a2 (рис.3), по
формуле (3) вычислить фокусное расстояние
f рассеивающей
линзы.
Способ 2.
Создадим с помощью собирающей линзы 1
и точечного источника света S
сходящийся пучок света (рис.4). На его
пути установим рассеивающую линзу 2.
Изображение источника, даваемое
собирающей линзой S1,
можно рассматривать как мнимый источник
для рассеивающей линзы 2.
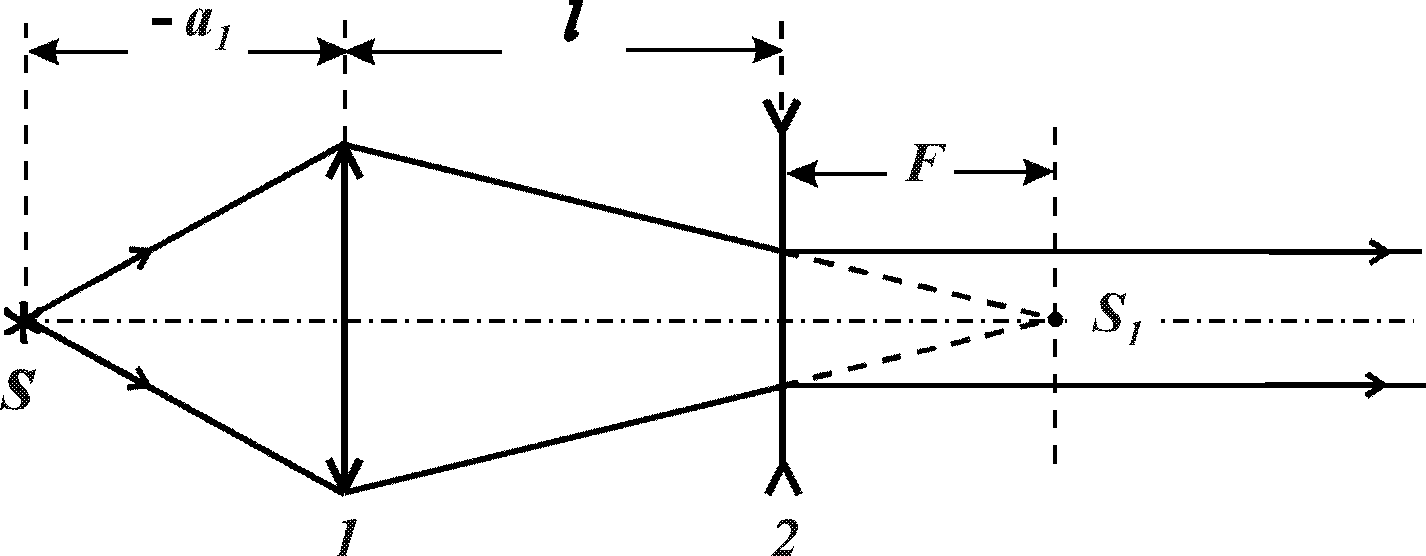
Рис.4. К определению
фокусного расстояния тонкой рассеивающей
линзы способом 2.
Если положение мнимого источника
совпадет с фокусом рассеивающей линзы,
то из нее выйдет параллельный пучок
света (рис.4). На этом основан второй
способ определения фокусного расстояния
рассеивающей линзы.
Согласно формуле (1) для собирающей линзы
1 с учетом обозначений рис.4 можно
записать:
,
где l и F
длины соответствующих отрезков. Отсюда:
(4).
Порядок
выполнения задания:
-
Найти, как и в предыдущем способе,
положение изображения, даваемого
собирающей линзой 1 (точку S1). -
Убрать экран с оптической скамьи и
поместить исследуемую рассеивающую
линзу между найденным положением точки
S1 и собирающей
линзой 1. -
Поместить за рассеивающей линзой
оптическую трубу, установленную на
бесконечность. -
Перемещением рассеивающей линзы 2
добиться четкого изображения креста
в поле зрения трубы. -
Зная положения линз и фокусное расстояние
собирающей линзы f2
(данные взять из упражнения 1), по формуле
(4) определить модуль фокусного расстояние
F рассеивающей линзы
и записать фокусные расстояния
рассеивающей линзы f1
и f2.
Контрольные
вопросы.
-
Центрированная оптическая система
(ЦОС). -
Кардинальные элементы ЦОС. Построение
изображений в ЦОС. -
Матричный способ описания ЦОС.
-
Толстая линза. Тонкая линза. Оптическая
сила линзы. -
Методы определения фокусных расстояний
собирающих и рассеивающих линз. -
Сформулируйте цель работы, опишите
экспериментальную часть и обсудите
результаты.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
физика! ! срочно! помогите.
Знаток
(373),
закрыт
10 лет назад
Станислав Греблюрве
Просветленный
(27346)
10 лет назад
Задача. Дано: d = 20 см = 0,2 м; f = 40 см = 0,4м; Определить F – ? D – ? N – ?Решение: Фокусное расстояние определяем по формуле линзы: 1/F = 1/d + 1/f; или, преобразовав, F = df/(d + f); При подстановке значений величин в формулу необходимо учесть, что расстояние до мнимого изображения берется со знаком «минус»
( – ). F = 0,2*(-0,4)/(0,2 – 0,4) = 0,4 (м) ; Оптическая сила D = 1/F D = 1/0,4 = 2,5 (дптр) . 2,5 диоптрии. Увеличение линзы равно Г = f/d; Г = 0,4/0,2 = 2; Примечание: я не брался бы за эту задачу, если бы не видел неправильного ответа. Поблагодарите пользователя за желание помочь, но, запишите решение, предложенное мною. Успеха вам и «питерки»!
Источник: геометрическая оптика
Александр Потанин
Мастер
(2248)
10 лет назад
фокусное расстояние линзы определим из формулы тонкой линзы: 1/F = 1/f + 1/d. Запишем эту формулу в удобном нам виде: F = (f*d)/(f+d). Подставляя данные, получаем F= 13,3см.
оптическая сила линзы определяется по формуле D=1/F или D=1/f + 1/d. При подстановке получаем результат 7,5дптр.
Увеличение линзы Г = f/d = 2
Мы уже познакомились с явлением преломления света на границе двух плоских сред. Но на практике особый интерес представляет явление преломления света на сферических поверхностях линз.
Определение
Линза — прозрачное тело, ограниченное сферическими поверхностями.
Какими бывают линзы?
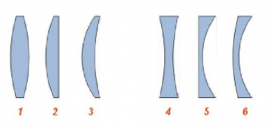
По форме различают следующие виды линз:
- Выпуклые — линзы, которые посередине толще, чем у краев.
- Вогнутые — линзы, которые посередине тоньше, чем у краев.
Выпуклые линзы тоже имеют разновидности:
- Двояковыпуклая — линза, ограниченная с обеих сторон выпуклыми сферическими поверхностями (СП). Такая линза изображена ниже на рисунке 1.
- Плосковыпуклая — линза, ограниченная выпуклой СП с одной стороны и плоской поверхностью с другой (рис. 2)
- Вогнуто-выпуклая — линза, ограниченной с одной стороны вогнутой СП, а с другой — выпуклой СП (рис. 3).
Разновидности вогнутых линз:
- Двояковогнутая — линза, ограниченная с обеих сторон вогнутыми СП (рис. 4).
- Плосковогнутая — линза, ограниченная вогнутой СП с одной стороны и плоской поверхностью с другой (рис. 5)
- Выпукло-вогнутая — линза, ограниченной с одной стороны выпуклой СП, а с другой — вогнутой СП (рис. 6).
Тонкая линза
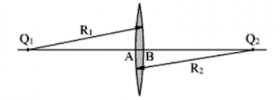
Мы будем говорить о линзах, у которых толщина l = AB намного меньше радиусов сферических поверхностей этой линзы R1 и R2. Такие линзы называют тонкими.
Определение
Тонкая линза — линза, толщина которой пренебрежимо мала по сравнению с радиусами сферических поверхностей, которыми она ограничена.
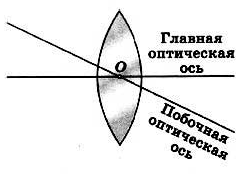
Главная оптическая ось тонкой — прямая, проходящая через центры сферических поверхностей линзы (на рисунке она соответствует прямой O1O2).
Оптический центр линзы – точка, расположенная в центре линзы на ее главной оптической оси (на рисунке ей соответствует точка О). При прохождении через оптический центр линзы лучи света не преломляются.
Побочная оптическая ось — любая другая прямая, проходящая через оптический центр линзы.
Изображение в линзе
Подобно плоскому зеркалу, линза создает изображения источников света. Это значит, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в точку (изображение) независимо от того, какую часть линзы прошли лучи.
Определение
Оптическое изображение — картина, получаемая в результате действия оптической системы на лучи, испускаемые объектом, и воспроизводящая контуры и детали объекта.
Практическое использование изображений часто связано с изменением масштаба изображений предметов и их проектированием на поверхность (киноэкран, фотоплёнку, фотокатод и т. д.). Основой зрительного восприятия предмета является его изображение, спроектированное на сетчатку глаза.
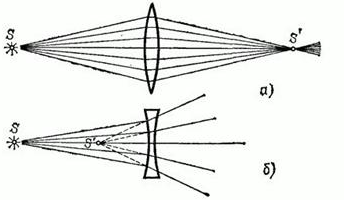
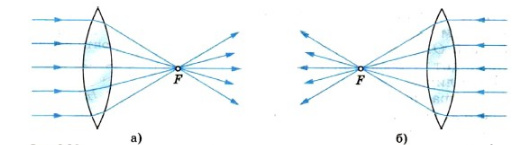
Изображения разделяют на действительные и мнимые. Действительные изображения создаются сходящимися пучками лучей в точках их пересечения (см. рисунок а). Поместив в плоскости пересечения лучей экран или фотоплёнку, можно наблюдать на них действительное изображение.
Если лучи, выходящие из оптической системы, расходятся, но если их мысленно продолжить в противоположную сторону, они пересекутся в одной точке (см. рисунок б). Эту точку называют мнимым изображением точки-объекта. Она не соответствует пересечению реальных лучей, поэтому мнимое изображение невозможно получить на экране или зафиксировать на фотоплёнке. Однако мнимое изображение способно играть роль объекта по отношению к другой оптической системе (например, глазу или собирающей линзе), которая преобразует его в действительное.
Собирающая линза
Обычно линзы изготавливают из стекла. Все выпуклые линзы являются собирающими, поскольку они собирают лучи в одной точке. Любую из таких линз условно можно принять за совокупность стеклянных призм. В воздухе каждая призма отклоняет лучи к основанию. Все лучи, идущие через линзу, отклоняются в сторону ее главной оптической оси.
Если на линзу падают световые лучи, параллельные главной оптической оси, то при прохождении через нее они собираются на одной точке, лежащей на оптической оси. Ее называют главным фокусом линзы. У выпуклой линзы их два — второй главный фокус находится с противоположной стороны линзы. В нем будут собираться лучи, которые будут падать с обратной стороны линзы.
Главный фокус линзы обозначают буквой F.
Определение
Фокусное расстояние — расстояние от главного фокуса линзы до их оптического центра. Оно обозначается такой же букой F и измеряется в метрах (м).
В однородных средах главные фокусы собирающих линз находятся на одинаковом расстоянии от оптического центра.
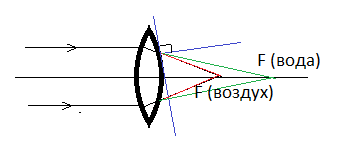
Пример №1. Что произойдет с фокусным расстоянием линзы, если ее поместить в воду?
Вода — оптически более плотная среда, поэтому преломленные лучи будут располагаться ближе к перпендикуляру, восстановленному к разделу двух сред. Следовательно, фокусное расстояние увеличится. На рисунке лучам, выходящим из линзы в воздухе, соответствуют красные линии. Лучам, выходящим из линзы в воде — зеленые. Видно, что зеленые линии больше приближены к перпендикуляру, восстановленному к разделу двух сред, что соответствует закону преломления света.
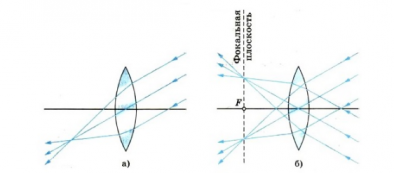
Направим три узких параллельных пучка лучей от осветителя под углом к главной оптической оси собирающей линзы. Мы увидим, что пересечение лучей произойдет не в главном фокусе, а в другой точке (рисунок а). Но точки пересечения независимо от углов, образуемых этими пучками с главной оптической осью, будут располагаются в плоскости, перпендикулярной главной оптической оси линзы и проходящей через главный фокус (рисунок б). Эту плоскость называют фокальной плоскостью.
Поместив светящуюся точку в фокусе линзы (или в любой точке ее фокальной плоскости), получим после преломления параллельные лучи.
Если сместить источник дальше от фокуса линзы, лучи за линзой становятся сходящимися и дают действительное изображение.
Когда же источник света находится ближе фокуса, преломленные лучи расходятся и изображение получается мнимым.
Рассеивающая линза
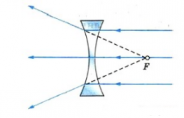
Вогнутые линзы обычно являются рассеивающими (лучи, выходя из них, не собираются, а рассеиваются). Это бывает если, поместить вогнутую линзу в оптически менее плотную среду по сравнению с материалом, из которого изготовлена линза. Так, стеклянная линза в воздухе является рассеивающей.
Если направить на вогнутую линзы световые лучи, являющиеся параллельными главной оптической оси, то образуется расходящийся пучок лучей. Если провести их продолжения, то они пересекутся в главном фокусе линзы. В этом случае фокус (и изображение в нем) является мнимым. Этот фокус располагается на фокусном расстоянии, равном F.
Другой мнимый фокус находится по другую сторону линзы на таком же расстоянии при условии, что среда по обе стороны линзы одинаковая.
Оптическая сила линзы
Оптическая сила линзы — величина, характеризующая преломляющую способность симметричных относительно оси линз и центрированных оптических систем, состоящих из таких линз.
Обозначается оптическая сила линзы буквой D. Единица измерения — диоптрий (дптр). Оптической силой в 1 дптр обладает линза с фокусным расстоянием 1 м.
Оптическая сила линзы равна величине, обратной ее фокусному расстоянию:
D=±1|F|
D > 0, если линза собирающая, D < 0, если линза рассеивающая. Чем ближе к линзе ее фокусы, тем сильнее линза преломляет лучи, собирая или рассеивая их, и тем больше оптическая сила линзы.
Пример №2. Найти фокусное расстояние линзы, если ее оптическая сила равна –5 дптр.
Так как оптическая силы линзы отрицательная, речь идет о рассеивающей линзе. Следовательно, будем использовать формулу:
D=−1|F|
Отсюда:
|F|=−1D=−1−5=0,2 (м)
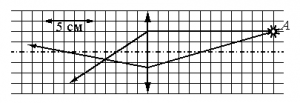
Задание EF18041
Ответ:
а) 14 дптр
б) 20 дптр
в) 17 дптр
г) 33 дптр
Алгоритм решения
1.Записать формулу для нахождения оптической силы линзы.
3.Найти точку на главной оптической оси точку главного фокуса линзы.
4.Вычислить фокусное расстояние и перевести его в СИ.
5.Вычислить оптическую силу линзы.
Решение
Оптическая сила линзы определяется формулой:
D=1F
На рисунке видно, что 5 клеток = 5 см. Следовательно, 1 клетка = 1 см. После прохождения сквозь линзу лучи света, параллельные главной оптической оси, фокусируются в главном фокусе, который лежит на этой оси. Значит, фокус находится в точке пересечения этой оси и луча. От него до линзы 3 клетки. Следовательно, фокусное расстояние равно 3 см, или 0,03 м.
Отсюда:
D=10,03≈33 (дптр)
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17706
Стеклянную линзу (показатель преломления стекла nстекла = 1,54), показанную на рисунке, перенесли из воздуха (nвоздуха = 1) в воду (nводы = 1,33). Как изменились при этом фокусное расстояние и оптическая сила линзы?
Ответ:
а) Фокусное расстояние уменьшилось, оптическая сила увеличилась.
б) Фокусное расстояние увеличилось, оптическая сила уменьшилась.
в) Фокусное расстояние и оптическая сила увеличились.
г) Фокусное расстояние и оптическая сила уменьшились.
Алгоритм решения
1.Установить характер преломления лучей линзой при ее перемещении из воздуха в воду.
2.Выяснить, как от этого зависят фокусное расстояние и оптическая сила линзы.
Решение
Чтобы узнать, что произойдет с лучами света при прохождении их сквозь линзу, погруженную воду, найдем относительные показатели преломления:
nвоздух−стекло=nстеклоnвоздух=1,541=1,54
nвода−стекло=nстеклоnвода=1,541,33≈1,16
Видно, что относительный показатель преломления уменьшился. Значит, преломленный линзой луч будет менее отклоняться от нормали, проведенной в точке падения на линзу. Следовательно, чтобы достигнуть главной оптической оси, ему придется пройти большее расстояние. Это говорит о том, что фокусное расстояние линзы увеличится.
Оптическая сила линзы — величина, обратная ее фокусному расстоянию. Если оно увеличится, то оптическая сила уменьшится.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18076
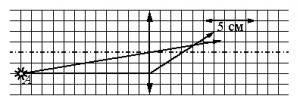
Какова приблизительно оптическая сила этой линзы?
Ответ:
а) –33,3 дптр
б) 7,7 дптр
в) 25,0 дптр
г) 33,3 дптр
Алгоритм решения
1.Записать формулу для нахождения оптической силы линзы.
2.Рассчитать длину 1 клетки.
3.Найти точку на главной оптической оси точку главного фокуса линзы.
4.Вычислить фокусное расстояние и перевести его в СИ.
5.Вычислить оптическую силу линзы.
Решение
Оптическая сила линзы находится по формуле:
D=1F
На рисунке видно, что 5 соответствуют 5 см. Следовательно, 1 клетка равна 1 см. После прохождения сквозь линзу лучи света, параллельные главной оптической оси, фокусируются в фокусе, который лежит на этой оси. Из рисунка видно, фокус находится в точке пересечения этой оси и луча, параллельного ей. Эту точку и линзу разделяют 3 клетки. Следовательно, фокусное расстояние равно 3 см, или 0,03 м.
Отсюда:
D=10,03≈33,3 (дптр)
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.3k