Random converter
- Калькуляторы
- Микроскопия
Калькулятор фокусного расстояния объектива микроскопа
Калькулятор определяет фокусное расстояние объектива микроскопа по заданному увеличению и длине тубуса (для микроскопов с заданной длиной тубуса) или стандартному фокусному расстоянию (для микроскопов с коррекцией на бесконечность). Калькулятор может определять любое из трех значений, если известны два другие значения. Для расчета введите два известных значения и нажмите кнопку Рассчитать.
Пример 1: Рассчитать фокусное расстояние объектива микроскопа 10×, рассчитанного на длину тубуса 160 мм.
Пример 2: Рассчитать фокусное расстояние скорректированного на бесконечность объектива 40×, если стандартное фокусное расстояние объектива тубуса равно 160 mm.
Увеличение объектива
Mobj ×
Длина тубуса или стандартное фокусное расстояние тубусной системы
Ltube
Фокусное расстояние объектива
Fobj
Поделиться ссылкой на этот калькулятор, включая входные параметры
Определения и формулы
Оптические системы объективов микроскопов бывают двух типов: с конечной длиной тубуса и скорректированные на бесконечность. В системах с конечной длиной тубуса (или «биологических») изображение объекта, имеющее форму круга, формируется объективом микроскопа в плоскости промежуточного действительного изображения, находящейся непосредственно под окуляром. Для формирования этого изображения не нужны никакие дополнительные линзы или объективы. Однако в таких системах иногда всё же имеется дополнительная линза, устанавливаемая между объективом и камерой. Она предназначена для коррекции размера изображения, чтобы он совпадал с размером матрицы камеры. Это может быть, например, рассеивающая линза, если изображение не помещается на матрице камеры. Подробнее о фото- и видеосъемке через микроскоп
Гравировка на объективе показывает тип его оптической системы. Если там написано, например, 160/0,17, это означает, что объектив предназначен для использования в микроскопе с конечной длиной тубуса. Если же там имеется символ бесконечности (∞), это означает, что объектив рассчитан для использования в микроскопе с коррекцией на бесконечность. Длина тубуса представляет собой расстояние между фокальными точками объектива и окуляров. Чаще всего встречаются микроскопы с длиной тубуса 160 мм. Некоторые изготовители микроскопов используют другие значения длины тубуса.
В большинстве современных микроскопов используются оптика, скорректированная на бесконечную длину тубуса, в которой объектив формирует изображение рассматриваемого под микроскопом объекта в бесконечности в виде параллельных лучей. Для того, чтобы это изображение можно было увидеть в фокусе в плоскости промежуточного изображения, между объективом и плоскостью промежуточного изображения таких микроскопов устанавливается дополнительная оптическая система. Эта оптическая система обычно называется корректирующим объективом тубуса или тубусной оптической системой.
Скорректированные на бесконечность микроскопы позволяют устанавливать в тубусе между объективом и окулярами дополнительные оптические компоненты и при этом не требуется коррекция фокуса и не вносятся дополнительные искажения. В микроскопах, скорректированных на бесконечность, понятие «длина тубуса» отсутствует и вместо него используется понятие стандартного фокусного расстояния тубусной системы, которое у различных изготовителей варьируется от 160 до 200 мм. Leica и Nikon используют 200 мм, Olympus — 180 мм.
В маркировке современных объективов для микроскопов указывается длина тубуса или символ бесконечности и увеличение. Там никогда не указывают фокусное расстояние, так как это избыточная информация, поскольку фокусное расстояние можно легко рассчитать по формуле:
где Fobj — фокусное расстояние объектива, Ltube — длина тубуса для системы с конечной длиной тубуса или стандартное фокусное расстояние (фокусное расстояние объектива тубуса) для системы с коррекцией на бесконечность, и Mobj — увеличение объектива. Эта формула и используется в данном калькуляторе.
Микроскопия для детей
Многие считают, что малыши четырех–пяти лет не могут нормально пользоваться микроскопом, потому у них еще слабо развито внимание и другие способности, необходимые для данного вида деятельности. Однако, если их родители занимаются с детьми и всё делают вместе, тогда введение в микроскопию могло бы быть неплохим введением в науку в целом.
Рассматривая под микроскопом обычные предметы вроде монет, волос, сахара или соли, ребенок видит их совсем иначе, чем привык. Например, он может узнать, что, казалось бы, гладкая поверхность пластмассовой игрушки на самом деле покрыта сетью царапин. Представьте себе что будет чувствовать ребенок, если показать ему как выглядит и движется накрытая покровным стеклом смешанная с каплей воды капля крови из его собственной коленки, которую он только что поцарапал!
Понятно, что трудно удержать внимание малыша, если задание для него слишком сложное или если оно не требует постоянного внимания. Поэтому если вы хотите, чтобы малышу понравилась микроскопия, попробуйте сделать так, чтобы у них была причина сконцентрировать внимание. Играйте с ними, сделайте так, чтобы им нужно было всё делать своими руками — и успех обязательно придет!
Если малышу интересно, он может заниматься одним и тем же делом 25 и даже 30 минут. Я помню, как доверил четырехлетнему сыну накачать полностью спущенное колесо от машины ручным насосом. Думал, не справится. Как бы не так! Он долго пыхтел над ним, но накачал до требуемого давления. Совместные эксперименты с вашим сыном или внучкой сближают детей и их родителей или бабушек и дедушек и помогают им лучше узнать друг друга. А с микроскопом, вполне возможно, что и взрослые узнают что-то новое вместе со своим малышом!
Делай как я! Не забывайте, что прежде, чем начать учить своего малыша, вы должны сами как следует научиться пользоваться микроскопом (если не умеете). Вы — модель для своего чада и, соответственно, вы должны показывать пример того, что и как нужно делать правильно. Покажите ему как правильно пользоваться микроскопом и вполне вероятно, что ваш малыш будет делать так же, как и вы.
Как выбрать микроскоп для домашнего обучения
Детский набор «Микроскоп» или нормальный биологический микроскоп? Какой микроскоп купить малышу? Я бы не рекомендовал покупать дешевый детский микроскоп или детский набор «Микроскоп», такой как показан на рисунке. Оптика этих микроскопов очень плохая, механика тоже никудышняя, всё в них трясется и шатается. Поле зрения очень мало. Такой микроскоп не может дать нормальную картинку. Освещение образца в них обычно делается с помощью зеркала или маломощного светодиода. Я считаю, что подобные комплекты для детей практически бесполезны и могут только оттолкнуть их от изучения предмета. Это просто достаточно дорогие игрушки. В них может быть неплохой скальпель или пробирки, но микроскоп там никудышний. Лучше стоит купить микроскоп подороже, а не выбрасывать деньги на ветер, покупая ненужную игрушку.
Детский набор «Микроскоп» — не рекомендуется
Например, я купил за 160 долларов, в том числе и для занятий с четырехлетней внучкой, показанный на иллюстрациях биологический микроскоп, который доукомплектовал двумя мощными малогабаритными светодиодными источниками света для просмотра образцов не только в проходящем, но и в отраженном свете. Такой микроскоп позволяет рассматривать, например, жуков. Двойное освещение обязательно нужно иметь при занятиях с малышами, так как оно позволяет рассматривать непрозрачные предметы.
Биологический, цифровой или карманный микроскоп? Карманный микроскоп со светодиодным освещением, работающий от батарейки, можно купить менее, чем за пять долларов, и подарить его ребенку как игрушку, с которой он может заниматься самостоятельно. В такой микроскоп можно рассматривать любые непрозрачные объекты и их не нужно устанавливать на предметные стекла. Малые размеры и батарейное питание позволяет использовать такой микроскоп где угодно. Подробнее о цифровых и обычных микроскопах и их сравнение
Недорогой цифровой микроскоп может кому-то показаться неплохим выбором. Однако нужно помнить, что лучшие цифровые микроскопы — биологические, снабженные камерой. К тому же, для съемки через окуляр можно использовать мобильный телефон, в котором имеется очень неплохая камера (подробнее о камерах в микроскопии). Изображения с телефона можно переписать и на компьютер. Поэтому, как мне кажется, лучше всего для занятий с малышами приобрести недорогой (не дороже 200 долларов) биологический микроскоп с широкопольными окулярами и четырьмя ахроматическими объективами (4×, 10×, 40×, and 100×). Ваш малыш сможет пользоваться иммерсионным объективом 100× когда подрастет, а это случится очень скоро! У таких объективов должна быть стандартная (как правило RMS) резьба, позволяющая устанавливать в микроскоп и другие стандартные объективы. Микроскоп также должен иметь ручки грубой и точной фокусировки.
Цифровой микроскоп Supereyes B011 с 5-мегапиксельной камерой и объективом L1000 (слева) и недорогой (15 долларов) безымянный USB 2-мегапиксельный микроскоп с подставкой (справа)
Если вам интересно как не стоит покупать микроскоп, вот статья, в которой я делюсь печальным опытом покупки микроскопа, который я все же довел до ума.
Стереомикроскоп или обычный биологический микроскоп? Стереомикроскопы обычно используются для научных исследований в биологии, при изготовлении ювелирных изделий, при изготовлении и ремонте электронных изделий и исследовании отказов оборудования, в микрохирургии, при изготовлении часов а также во многих других областях. Они предназначены для наблюдения объектов с небольшим увеличением (до 1/10 увеличения биологических микроскопов) и обычно используют свет, отраженный от поверхности наблюдаемых объектов. В таких микроскопах имеется два оптических канала, один или два объектива и два окуляра, которые обеспечивают получение объемного изображения наблюдаемого объекта. Как мне кажется, для использования в образовательных целях обычный биологический микроскоп более удобен, особенно если установить на нем две мощные (5–8 Вт) светодиодные лампы для получения возможности просматривать образцы в отраженном свете. Такой микроскоп показан на нескольких иллюстрациях в этой статье.
Биологический бинокулярный микроскоп за 160 долларов (10 000 руб.) с механическим предметным столом и дополнительным самодельным освещением для просмотра образцов с отраженном свете: 1 — окуляр, 2 — головка, 3 — объективы, 4 — верхнее освещение, 5 — механический предметный стол, 6 — ручки регулировки фокусировки, 7 — выключатель нижнего осветителя, 8 — выключатели верхних светодиодных ламп, 9 — ручки регулировки положения образца на предметном столе
Освещение с помощью светодиодов, галогенных ламп или ламп накаливания? В последние годы в микроскопии нормой становится светодиодное освещение, так как светодиоды имеют много преимуществ по сравнению с традиционно используемыми в микроскопии лампами накаливания, галогенными и ксеноново-ртутными лампами. Поэтому, конечно, нужно выбирать только светодиодное освещение.
Монокулярный или бинокулярный? Для детей лучше подойдет монокулярный микроскоп. Однако не стоит забывать, что малыши быстро растут и десятилетнему ребенку (а также вам!) значительно удобнее пользоваться бинокулярным микроскопом. Поэтому лучше сразу начать с бинокулярного микроскопа хорошего качества, оборудованного механическим предметным столиком и комбинированным освещением для просмотра объектов как в проходящем, так и в отраженном свете. Стоит потратить немного больше денег и купить микроскоп хорошего качества, который ваш ребенок сможет использовать не только до школы, но и в старших классах, а затем при получении высшего образования.
С механическим или неподвижным предметным столом? Предметный стол с регулировкой положения исследуемого препарата позволяет перемещать его по двум осям. Это особенно важно, если образец рассматривают при большом увеличении, так как в этом случае точно подвинуть руками препарат к нужному месту практически невозможно. Механический предметный стол существенно упрощает пользование микроскопом. Поэтому да, ваш новый микроскоп должен быть оборудован предметным столом с регулировкой положения образца по двум осям.
Объяснение ребенку устройства микроскопа
Изготовление препаратов из картона от упаковочной коробки
Попробуйте объяснить ребенку, что микроскоп похож на обычную лупу, только он сложнее и содержит несколько дополнительных элементов, облегчающих его использование, а также обеспечивающих большее увеличение, по сравнению с лупой. Назовите ребенку только основные части микроскопа: окуляр, головка, объективы, верхнее освещение для просмотра объектов в отраженном свете, предметный стол, выключатели освещения и ручки регулировки положения образца на предметном столе. Если вы объясняете устройство микроскопа нескольким детям, стоит попросить их повторить названия. Однако, если вы объясняете только своему ребенку, которого вы хорошо знаете, вы определенно увидите понимает он или нет, не задавая лишних вопросов. Полное описание основных частей микроскопа приведено в этой статье.
Изготовление препаратов с детьми
Когда ваш новенький бинокулярный биологический микроскоп с механическим предметным столом прибыл, приготовьте для занятий несколько чашек Петри с различными объектами. Можно начать с сахара, соли, муки и песка. Чтобы просматривать эти объекты на предметном столе, нужно изготовить препараты. Конечно, можно использовать препараты, изготовленные в лаборатории. Набор из 100 препаратов в деревянной коробке можно приобрести на eBay или Ali всего за 40 долларов (2500 руб.) Однако для малышей, конечно, будет лучше, если они изготовят препараты самостоятельно из подручных материалов с вашей помощью.
Приклеивание липкой ленты к импровизированному «покровному стеклу»
Разметьте несколько прямоугольников размером 25 × 75 мм на куске тонкого картона от упаковочной коробки и попросите малыша вырезать их детскими ножницами. Это будут наши «предметные стекла». Потом помогите ему пробить отверстие диаметром 5–6 мм. Попросите ребенка оторвать кусочек прозрачной липкой ленты и приклеить к обратной стороне каждого прямоугольника. Покажите малышу как прижать картонные «предметные стекла» к веществам в чашках Петри, поднять их и аккуратно стряхнуть лишнее вещество. Всё, первые препараты готовы для просмотра под микроскопом! Предложите малышу включить освещение, помогите ему настроить резкость и объясните как пользоваться ручками грубой и точной фокусировки. Объясните, что всегда нужно начинать с меньшего увеличения, а потом переходить к большему.
А теперь объясните малышу, что микроскоп — не игрушка, а точный и довольно дорогой оптический прибор. Объясните, что микроскоп требует аккуратного обращения и покажите как безопасно пользоваться им и препаратами.
На что посмотреть в микроскоп
- Лук
- Вода из лужи
- Монеты
- Бумажные деньги
- Мазок со щеки
- Различные волокна
- Сахар
- Соль
- Мука
- Песок
- Перья
- Кровь
- Зубной камень
- Цветочная пыльца
- Лезвие ножа
- Муравьи
- Дрозофилы
- Сосновые иглы
- Снежинки (зимой на улице на холодном покровном стекле)
- Печать
Страницы: [1] 2 След.» Все Вниз
A A A A

Тема: Как измерить фокусное растояние окуляра ? (Прочитано 8603 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Привет,
Есть окуляр от микроскопа у него плавня регулировка от 10х до 15х. Как вычислить или померить его фокусное растояние?
Спасибо.
Записан
Для этого достаточно поделить 250 на увеличение окуляра и получится его фокус. В вашем случае F= 25 – 16.666мм.
Записан
А что есть 250 ? откуда эта цифра ?
Записан
Цифра 250 это расстояние наилучшего видения для глаза, выраженное в милиметрах соответственно фокус тоже будет в мм.
Записан
В мире констант и Постоянных есть, безусловно, свои особенности. В данном случае 250 мм – это принято расстояние для наилучшего рассматривания предметов ( допустим мелких).
Увеличение окуляра ( и микроскопа ) – это как бы насколько мы ближе чем 250 мм рассматриваем предмет. Микроскопы Левенгука – лучшее подтверждение.
Записан
Astel-150.
Извините не знал что Вы уже ответили.
Записан
Записан
Ничего страшного, ваш ответ более полный.
Записан
Есть ещё одни окуляр, если его можно назвать окуляром, я его вытащил из видеокамеры, похоже там в системе 2 линзы, эта штука стояла как раз пред ПЗС. Если ей проэцировать изображение лампочьки то резкость наводится примерно на 20 мм – это и есть фокусное растояние сиитемы ?
Записан
to UL8GBX:
Окуляры в этих видеокамерах наверняка изготовлены из пластмассовых линз.
Записан
Это была не дешовая и страая SVHS камера Panasonic, из стекла и дикое подозрение с просветлением, на отсвет красновато-фиолетовые блики.
Записан
Ну, не знаю.
У меня на работе где-то лежит видеокамера, кажется тоже Panasonic, образца 97 года. Стоила тогда – жуть! Всё таки лучше использовать окуляры от микроскопа, неплохие окуляры от биноклей Российского производства. Ну а про астрономические окуляры я и говорить не буду.
Записан
AlAn
1. Если известна кратность окуляра, то расстояние наилучшего зрения (250мм) нужно разделить на кратность.
2. Самый простой способ, если у Вас есть объектив с известным фокусным расстоянием, и диаметром, то можно днем навести прибор на небо и померить диаметр выходного зрачка, увеличение равно отношению диаметра объектива к диаметру выходного зрачка. Затем разделите фокусное расстояние объектива на увеличение, и Вы получите фокусное расстояние окуляра. (Диаметр выходного зрачка при больших увеличениях невелик, и лучше измерять его лупой, имеющей шкалу, обычно точность такой шкалы 0,1мм).
3.Можно так же поставить окуляр на оптическую скамью, и померить фокусное расстояние напрямую. Если необходимо описание методов, через пару дней наберу текст и перешлю файл в Ваш адрес.
Записан
AlAn
Есть ещё одни окуляр, если его можно назвать окуляром, я его вытащил из видеокамеры, похоже там в системе 2 линзы, эта штука стояла как раз пред ПЗС. Если ей проэцировать изображение лампочьки то резкость наводится примерно на 20 мм – это и есть фокусное растояние сиитемы ?
Это справедливо только для тонких линз. Окуляр – это система линз, и его фокус не равен расстоянию до резкого изображения
Записан
Да очень интересны методы и думаю не только мне.
Спасибо.
Записан
AlAn
Хорошо, помещу в форуме.
Записан
AlAn
Кстатьи, UL8GBX! Раз у Вас переменное фокусное расстояние, то есть смысл опредилить его для разных положений механизма изменения фокусного расстояния, и построить график зависимости F от Х, или нанести соответствующие метки на механизм.
Записан
Померил методом 2. Взял прозрачьную линейку и положил ее на бумагу, направил на небо и поймал самое резкое пятно. Что то метод не очень как ни странно есть несколько растоний когда пятно резкое.
Интересно бы описание “оптической скамьи” я как понимаю ей можно будет мерить и фокусное растояние объективов.
Спасибо.
Записан
Выходной зрачок это изображение апертурной диафрагмы, построенное оптическими элементами, установленными после этой диафрагмы. Так как в телескопической системе, с помощью которой Вы пытались вторым способом определить фокусное расстояние окуляра, имеется единственная апертурная диафрагма, то и выходной зрачок будет одним единственным. Все остальные изображения не выходные зрачки, а изображения различных световых диаметров различных линз, входящих в оптическую систему. Рассуждая теоретически этих изображений может быть столько же, сколько границ раздела воздух-стекло (удвоенное количество компонентов) имеется в применяемом объективе. Чтобы выходной зрачок ни с чем не спутать поместите перед первой линзой объектива (максимально близко к ней) какой-нибудь предмет, например, небольшой кусочек бумаги. Тогда изображение круга с резким изображением этого кусочка и будет выходным зрачком.
А на оптическую скамью, человеку, не имеющему к ней доступа, рассчитывать не приходится. Помимо «рельса» необходимы еще коллиматор с набором мир или каких-нибудь иных баз, и измерительный микроскоп (или на худой конец измерительная лупа).
« Последнее редактирование: 14 Ноя 2004 [21:58:16] от Митрофанов Павел »
Записан
Всем успехов и во всем.
С уважением.
AlAn
Определение фокусного расстояния положительной тонкой линзы
Способ 1.
Фокусное расстояние можно определить исходя из формулы
1/a1+1/a2=1/f
где:
а1 – расстояние от источника до главной плоскости линзы,
а2 – расстояние от главной плоскости до изображения,
f – фокусное расстояние f=a1*f2/(a1+a2).
S – источник света,
S’ – изображение.
Метод годится для тонких линз, но можно применять и для объективов, только расстояния нужно измерять примерно от середины толщины линзы, естественно вносится ошибка.
На экране получают изображение источника и измеряют расстояния a1 и a2. Метод требует положения метки на центре толщины линзы. Если проведена серия опытов, то можно 1/f определить из графика с осями 1/a1 и 1/a2.
Способ 2.
В этом опыте положение указателя не сказывается на результате измерений. Пусть расстояние между экраном и предметом больше 4f. При этом найдутся два положения линзы дающих резкое изображение предмета. Из соображений симметрии ясно a1=a2’ и a2=a1’. Обозначим расстояние между экраном и предметом L, а между положениями линз l.
Фокусное расстояние можно вычислить по формуле
f=(L^2-l^2)/(4L)
Источник и экран закрепляются на направляющих, как можно точнее измеряется расстояние между ними, затем находят первое положение системы, при котором на экране видно резкое изображение источника, отмечают первую точку (допустим от левого края оправы), затем передвигают линзу до получения второго резкого изображения источника, снова отмечают точку, и измеряют расстояние, на которое передвинута система. Можно вычислять фокусное расстояние.
Мне по случаю досталось два прибора для наблюдения спутников, труба тяжеленная, толщина стенки около сантиметра, чугун, известно только увеличение всей системы, а объектив и окуляр? Диаметр объектива 120мм классный ахромат.
В качестве оптической скамьи я использовал обыкновенную гардину длиной три метра, на которой перемещал объектив, в результате получил f=560мм. Сейчас мы с nickas_ом делаем телескопы с коротким фокусом в качестве кометоискателей, а так как внутри была система изменения увеличения, мы взяли от нее отрицательный ахромат, и думаем попробовать получить эквивалентный фокус около 1400мм. Правда, Astel-150, считает, что могут вылезти аберрации, но как говорил вождь всех народов – попытка не пытка.
Трубу кстати взяли пластмассовую для канализации диаметром 160мм. Вес без окулярной части около 4кг.
P.S. Не могу найти тетрадь, в которую выписывал эти методы, есть еще несколько, в том числе и для рассеивающих линз.
Записан
- Печать
Страницы: [1] 2 След.» Все Вверх
- Астрофорум – астрономический портал »
- Практическая астрономия »
- Телескопостроение, оптика (Модераторы: Ivan7enych, dont_panic) »
- Как измерить фокусное растояние окуляра ?
Объектив микроскопа. Увеличение, разрешение изображения, метки и резьбы на объективе
Объектив микроскопа является ключевым компонентом для достижения высокой производительности микроскопа. Это часть, которая расположена рядом с наблюдаемым объектом, обычно на довольно небольшом расстоянии в несколько миллиметров.
Полезные статьи:
Объективы для фотоаппарата, виды, параметры
Телескопы, виды, принцип работы
Все статьи
Обычно объектив микроскопа создает промежуточное изображение, которое затем дополнительно увеличивается с помощью окуляра (окулярной линзы). Особенно в случаях с большим увеличением, большая часть увеличения обеспечивается объективом.
Большинство объективов основаны на преломляющей оптике, содержащей несколько линз. Например, простой с низким содержанием может содержать менисковую линзу и ахромат. С высоким разрешением обычно содержит более сложную комбинацию различных типов линз полусферического, менискового, ахроматического дублета и триплета.
Существуют также отражающие объективы, содержащие изогнутые зеркала и без линз. Они естественно ахроматичны и могут быть выгодны для работы в областях с экстремальными длинами волн. Кроме того, они могут демонстрировать меньшие потери оптической мощности.
Увеличение объектива микроскопа
Микроскопы часто содержат несколько объективов на поворотном носике, например, сканирующий объектив с увеличением всего в 4 раза, промежуточный (маленький объектив) с 10-кратным увеличением и большой объектив с высоким разрешением с 40-кратным или 100-кратным увеличением. Например, окуляр может увеличивать изображение в 5 или 10 раз.
Обратите внимание, что само по себе большое увеличение бесполезно, если оно только увеличивает изображения без повышения уровня детализации. Также часто используются кольца с цветовой кодировкой, указывающие различные значения увеличения, например, черный для 1 ×, желтый для 4 ×, зеленый для 10 × и т.д.
Полезное и пустое увеличение
В принципе, можно добиться произвольного усиления изображения, например, с помощью каскадных увеличительных оптических приборов. Однако увеличение полезно только до некоторой степени. Например, рассмотрим использование микроскопа:
- Увеличение микроскопа считается полезным (или годным к употреблению) до тех пор, пока оно позволяет видеть больше деталей объектов. В ситуации, когда достигнутое разрешение все еще ограничено разрешением наблюдающего глаза, большее увеличение все еще было бы полезно.
- Однако после этого увеличение становится “пустым”: хотя полученные изображения становятся больше, они не разрешают больше деталей, потому что разрешение ограничено, например, дифракцией или несовершенством оптического прибора.
Та же ситуация возникает при просмотре цифровых изображений на экране. Как только изображение отображается в размере, при котором каждый пиксель изображения соответствует хотя бы одному пикселю экрана, отображается вся доступная информация об изображении. Дальнейшее увеличение увеличения может быть полезно только в том случае, если у наблюдателя возникают трудности с разрешением пикселей экрана.
Фокусное расстояние
Фокусное расстояние объектива микроскопа обычно составляет от 2 мм до 40 мм. Однако этот параметр часто считается менее важным, поскольку увеличения и числовой апертуры достаточно для количественной оценки основных характеристик микроскопа.
Числовая апертура
Чем больше увеличение, тем выше также требуемая числовая апертура. Это фактор, который в конечном итоге ограничивает достижимое разрешение изображения. Существуют разные способы расчета разрешения изображения и немного разные обстоятельства, но они приводят к аналогичным значениям разрешения, которые примерно равны λ / (2 NA), где λ – оптическая длина волны (примерно от 400 до 700 нм), а NA – числовая апертура. Например, NA, равный 1, обеспечивает разрешение изображения примерно 250 нм для зеленого света. Для небольшого увеличения может быть вполне достаточно NA 0,1.
Наибольшие числовые апертуры достигаются при использовании сухих объективов, работающих с воздухом между объективом и объектом, составляют приблизительно 0,95. Значительно более высокие значения, например, 1,5 или даже выше, могут быть достигнуты с иммерсионными объективами, где зазор между объектом и объективом заполнен жидкостью – водой или некоторым количеством иммерсионного масла с более высоким показателем преломления, часто несколько выше 1.5. Оптимизированные иммерсионные масла обладают не только высоким показателем преломления, но также подходящей вязкостью и низкой склонностью к образованию пятен на поверхностях. Их можно оставлять на объективе в течение длительного времени, не повреждая его.
Обратите внимание, что погружение в масло может работать неправильно, например, при наблюдении за биологическим образцом в водном растворе, и масло находится только между защитным стеклом и объективом. Возможно, для таких случаев придется использовать специальные объективы для погружения в воду. Для оптимального освещения также может потребоваться погружение в масло с этой стороны.
Коррекция изображения объективов микроскопа
Для объективов с высокой числовой апертурой, высокое качество изображения может быть достигнуто только при значительных усилиях по исправлению различных видов оптических аберраций, таких как сферическая, астигматизм, кома, кривизна поля, искажение изображения и хроматические аберрации. Например, плоскоапохроматические объективы, имеющие особо сложную конструкцию, обеспечивают оптимальную коррекцию плоского поля в сочетании с хорошими ахроматическими свойствами.
Хроматические аберрации в основном являются результатом зависимости фокусного расстояния от длины волны. Они приводят к искажению цветного изображения. Для обычной микроскопии они могут быть весьма актуальны, в отличие от других типов оптической микроскопии, например, некоторых типов лазерной микроскопии. Наилучшее подавление хроматических аберраций достигается при использовании апохроматических объективов.
При больших увеличениях влияние покровного стекла с точки зрения хроматических и сферических аберраций может быть весьма важным. Поэтому объективы для использования в таких областях, как биология, где часто требуются покровные накладки, разработаны с интегрированной коррекцией покровных накладок. Коррекция часто выполняется для стандартной толщины скольжения 170 мкм. Отклонение всего в 10 мкм уже может быть довольно проблематичным для объектива с высоким NA, например, 0,95. Некоторые объективы позволяют регулировать скорректированную толщину покровного слоя.
Обратите внимание, что некоторые конструкции микроскопов рассчитаны на коррекцию некоторых остаточных аберраций объектива с помощью окулярной линзы.
К сожалению, идеальных решений не существует; поэтому приходится идти на определенные компромиссы, которые приводят к различным оптимизированным решениям для разных применений. Например, оптимальные свойства плоского поля наиболее важны для измерительных микроскопов; тогда можно допускать несколько большие хроматические аберрации.
Объективы микроскопа с конечной и бесконечной коррекцией
Для старых микроскопов обычно требуются объективы с конечной коррекцией. Здесь предполагается, что объект расположен немного ниже передней фокальной плоскости объектива, а промежуточное изображение получается на конечном расстоянии, например, 160 мм от объектива. Такой объектив предназначен для минимальных искажений изображения в данной конфигурации.
Объективы с конечной коррекцией всегда рассчитаны на определенную длину трубки, например, в соответствии со стандартом DIN или JIS (которые отличаются длиной трубки на 10 мм). Использование объектива неправильного стандарта может значительно ухудшить качество получаемого изображения.
Современные микроскопы в основном требуют объективов с поправкой на бесконечность, когда промежуточное изображение только объектива находится на бесконечном расстоянии. Здесь требуется дополнительная линза в микроскопе для формирования промежуточного изображения на диафрагме окуляра.
Основные характеристики объективов микроскопа
Диапазон длин волн
Оптические микроскопы обычно работают на основе изображения с помощью видимого света, то есть в области длин волн от 400 нм до 700 нм. Поэтому большинство объективов микроскопа оптимизированы для этого диапазона длин волн, с наибольшим акцентом на область от 480 нм до 640 нм. Однако существуют объективы с расширенным диапазоном, например, от 400 до 950 нм, и другие, которые работают дальше в инфракрасном диапазоне. Например, это требуется для лазерных микроскопов, где требуется передача инфракрасных лазерных лучей.
Обратите внимание, что важно не только иметь хорошую пропускаемость во всем диапазоне длин волн, но и ахроматические характеристики. В обычных световых микроскопах это необходимо, чтобы избежать искажений цветного изображения. В конфокальных многофотонных флуоресцентных микроскопах важно иметь те же положения фокуса для инфракрасного лазерного излучения, что и для флуоресцентного света.
Метки на объективах микроскопа
Ключевые параметры часто легко найти на этикетках с лазерной гравировкой на внешней стороне объектива. Некоторые примеры:
- Метка “50 × / 0,8” указывает на 50-кратное увеличение и числовую апертуру 0,8, вероятно, для сухого объектива.
- “100 × / 1,30 oil” означает 100-кратное увеличение и числовую апертуру 1,30, достигаемую с помощью иммерсионного масла.
- “∞ / 0.17” указывает на объектив с поправкой на бесконечность и компенсацией сферических аберраций при толщине покровного стекла 0.17 мм, в то время как “160/0. 17” указывает на объектив с конечной поправкой для микроскопов с длиной трубки 160 мм и такой же толщиной покровного стекла.
- “WD 0,21” указывает на рабочее расстояние 0,21 мм.
- “DIC” обозначает конструкцию для получения изображений с дифференциальным индексом контрастности.
- “plan fluor” обозначает объектив, апохроматический в плане, т. е. с коррекцией плоского поля и свойствами апохромата.
- “DIN” указывает, что объектив изготовлен в соответствии со стандартом DIN (Deutsche Industrie Norm) для микроскопов в отношении длины трубки, в то время как “JIS” указывает на японский стандарт с несколько более длинной трубкой.
Резьбы на объективах микроскопа
В большинстве случаев объектив микроскопа крепится к окуляру микроскопа с помощью резьбы. К сожалению, разные производители используют разные размеры резьбы для разных типов приболров. В некоторых случаях для установки объектива на микроскоп с другой резьбой можно использовать специальные адаптеры.
Для освещения в темном поле предварительно больше, обеспечивая дополнительное пространство для света подсветки; поэтому они обычно используются с более крупными нитями.
Другие свойства объективов микроскопа
Рабочее расстояние
Другим практически важным фактором является рабочее расстояние между объективом и объектом. Для объективов с высоким NA обычно требуются небольшие рабочие расстояния, но их также можно в некоторой степени оптимизировать в качестве цели проектирования (возможно, несколько снижая NA или коррекцию).
Для объективов с погружением в масло относительно небольшое рабочее расстояние действительно хорошо, поскольку в противном случае потребовалось бы больше иммерсионной жидкости, и ее было бы сложнее удерживать на месте.
Некоторые микроскопы допускают подачу светового излучения через объектив на образец. Затем важно, чтобы в объективе не было значительного рассеяния света.
Конструкция объективов микроскопа
Хотя объектив микроскопа иногда называют объективной линзой, обычно он содержит несколько линз. Чем выше числовая апертура и чем выше требуемое качество изображения, тем более сложные конструкции необходимы. В объективах микроскопа высокого класса также могут использоваться асферические линзы.
Разработка высококачественного объектива микроскопа является довольно сложной задачей, для которой требуются значительные знания в области оптики и мощное программное обеспечение для проектирования оптики. Такие конструкции предполагают сложные компромиссы, которые должны быть надлежащим образом обработаны в соответствии с важностью различных аспектов для конкретного применения.
Фокусировка луча и соединение волокон с объективами микроскопа
Объективы микроскопа иногда используются для приложений вне микроскопии. Например, они могут использоваться для точной фокусировки лазерных лучей с размерами пятна в несколько микрометров или даже ниже 1 мкм. Если входной луч является коллимированным лучом, лучше всего подойдет объектив с поправкой на бесконечность.
Объектив должен иметь числовую апертуру, которая хорошо соответствует расходимости луча, связанной с требуемым размером пятна. Радиус входного луча также должен быть выбран соответствующим образом, т.е, рассчитанный исходя из требуемого размера пятна и фокусного расстояния. Сложность может заключаться в определении фокусного расстояния, поскольку объективный объектив часто указывает только увеличение, а преобразование в фокусное расстояние зависит от конструкции микроскопа.
Другое приложение запускает свет в одномодовое волокно или коллимирует свет из такого волокна. Опять же, объектив должен иметь соответствующую числовую апертуру порядка, чем у волокна. Для таких применений хроматические аберрации часто не являются проблемой, поэтому не требуется использовать хроматическую коррекцию объектива. Кроме того, широкое поле зрения не требуется.
С другой стороны, объектив микроскопа для видимого света может не обладать идеальными свойствами, например, для пропускания ближнего инфракрасного света в волокно, и его мощность ограничена (но обычно не указывается). Поэтому объектив микроскопа может быть не идеальным решением для такого применения. Однако, возможно, придется использовать его, например, если нет других объективов для достижения требуемого малого размера пятна.
Микроскоп это оптический прибор для получения (мнимого изображения) его возможность к увеличению ограничивается дифракционными явлениями так они ограничивают полезное увеличение этого микроскопа. Бывают микроскопы: простейшие, медицинские, электронные, измерительные и некоторые другие. Служит средством анализа исследуемой поверхности и как самостоятельная единица не может служить средством измерения, но к примеру связь микроскопа с (вычислительными машинами) используется как средство измерения.
Что такое микроскоп
Оптическая система строения микроскопа состоит из двух линз: объектива и окуляра. Схематизируя явление, можно сказать, что объектив дает промежуточное действительное увеличенное изображение предмета, которое рассматривается в окуляр как в лупу. Окуляр образует еще более увеличенное мнимое изображение, которое воспринимается глазом.
Рассмотрим несколько подробнее вопрос о восприятии глазом изображения, образуемого окуляром. В простейшем виде окуляр представляет собой собирающую линзу, которую помещают перед глазом так, чтобы ее задний главный фокус находился вблизи оптического центра глаза, а рассматриваемый предмет был расположен несколько ближе переднего главного фокуса.
Лучи, исходящие из точек предмета, преломляются в линзе и выходят из нее слегка расходящимся пучком. Вступая в глаз, лучи преломляются в его средах и пересекаются на сетчатой оболочке, образуя действительное изображение предмета, значительно увеличенное по сравнению с тем, которое получилось бы при наблюдении предмета невооруженным глазом.
Окуляр микроскопа образует мнимое изображение, величину которого нельзя непосредственно измерить. Для того чтобы судить о достигаемом при этом увеличении, вводят понятие об угловом увеличении оптического прибора. Угловое увеличение kуг численно равняется отношению угла зрения βпр на предмет, когда он рассматривается с помощью оптического прибора, к углу зрения βгл на этот же предмет при наблюдении его невооруженным глазом:
kуг = βпр/βгл
Угловое увеличение показывает, во сколько раз величина изображения предмета на сетчатке глаза в первом случае больше, чем во втором.
Ход лучей через окуляр микроскопа

По условиям хода луча эта точка должна быть действительным изображением точки Б предмета. Второй луч из точки Б пройдет через оптический центр О линзы и преломится в оптических средах глаза так, чтобы пересечься с первым лучом в той же точке Б» Точку Б»» глаз относит к точке Б’ мнимого изображения точки Б.
Угол зрения глаза, вооруженного окуляром, есть угол β’. Из ∆O’Оb, принимая во внимание, что Ob = А Б = d, тангенс угла р’ равен отношению величины d предмета к фокусному расстоянию f линзы:
tgβ’ = d/f.
При наблюдении невооруженным глазом предмет располагается на расстоянии наилучшего зрения s. В этом случае тангенс угла зрения β (рис. 2) определится как отношение величины предмета к расстоянию наилучшего зрения:
tgβ =d/s.
Тогда угловое увеличение окуляра (по малости углы зрения можно заменить их тангенсами):
k ок = β’/β = tgβ’/tgβ = d/f : d/s = s/f
Увеличение окуляра

Увеличение, достигаемое с помощью окуляра, можно определить в следующем опыте (рис. 3). На оптической скамье С, несколько ближе переднего главного фокуса линзы Л, служащей окуляром, помещается достаточно освещенный предмет П, например черная стрелка на белой линейке (или на матовом стекле, освещенном с обратной стороны). Глаз Г располагается вдоль главной оси линзы Л на расстоянии, примерно равном фокусному расстоянию линзы.
Несколько сбоку на оптической скамье на расстоянии s = 25 см от глаза помещают вертикально масштабную линейку М с делениями и нанесенной на нее такой же величины d стрелкой. Затем наблюдают совместно линейку и изображение, которое дает окуляр. Отмечают на линейке отрезок d’, который глазу представляется равным по величине наблюдаемому изображению. Этот отрезок определяется углом зрения, под которым глаз видит мнимое изображение стрелки.
В то же время самой стрелке, нанесенной на линейке, соответствует угол зрения на нее невооруженным глазом. Нетрудно заключить, что отношение величин отрезка d’ и стрелки d будет численно равно угловому увеличению kок окуляра:
kок = β’/β ≈ tgβ’/tgβ = d‘/d.
Увеличение микроскопа
Предмет А Б помещается несколько дальше переднего главного фокуса объектива. При этом плоскость промежуточного изображения А ‘Б’ находится за двойным фокусным расстоянием объектива. Окуляр Ok располагается так, чтобы эта плоскость была несколько ближе к линзе, чем передний главный фокус окуляра.
Ход лучей через окуляр и глаз может быть построен упрощенно в соответствии с рис, 2, при этом промежуточное изображение А’ Б‘ рассматривается как предмет, расположенный перед окуляром. Таким путем находятся точки Б»’ изображения на сетчатке и Б» — мнимого изображения. Если при этом желательно показать также и действительный ход лучей, образовавших точку Б’ промежуточного изображения, то из точки Б» проводятся линии Б»а и Б»b к точкам а и b пересечения продолжения лучей с главной плоскостью окуляра. Дальше лучи строятся как продолжение этих линий до пересечения с главной плоскостью глаза, а затем непосредственно к точке Б»’.
Покажем это построение по правилам. Через оптический центр О’ окуляра проводятся побочные оси, параллельные этим лучам до пересечения в точках си d с фокальной плоскостью MN окуляра, в данном случае совпадающей с главной плоскостью глаза.
Рассматриваемые лучи проходят через эти точки как через фокусы. Дальнейший ход этих лучей определится аналогично путем построения параллельных им побочных осей через оптический центр О глаза до пересечения с фокальной плоскостью Фгл глаза и т. д.
Угловое увеличение микроскопа kм численно равняется произведению линейного увеличения объектива kоб и углового увеличения окуляра kок: kм = kоб • kок.
Линейное увеличение линзы, как указывалось, k = b/a. Применяя эту формулу к объективу микроскопа, можно считать расстояние а от предмета до объектива равным фокусному расстоянию объектива: а = f1. Расстояние от объектива до изображения равняется сумме фокусного расстояния объектива f1 и так называемой оптической длины тубуса L0 (расстояние между задним главным фокусом объектива и передним главным фокусом окуляра):
b = f1 + L0
или, пренебрегая фокусным расстоянием объектива по сравнению с оптической длиной тубуса (последняя обычно в десятки раз больше): b ≈ L0. Тогда увеличение объектива:
kок = (f1 + L0)/f1 ≈ L0/f1
Увеличение окуляра:
kок = s/f2 , где f2 — фокусное расстояние окуляра. Следовательно, увеличение микроскопа:
kм = kоб • kок = (L0s)/f1f2
Увеличение микроскопа равняется отношению произведения оптической длины тубуса на расстояние наилучшего зрения к произведению фокусных расстояний объектива и окуляра.
Увеличение объектива и окуляра называется их собственным увеличением и указывается на оправе линз.
Свойства микроскопа
Свойства простейшего микроскопа с небольшим увеличением можно изучить на модели, подобной модели (рис. 3), которая дополнена второй линзой — объективом. Перед объективом на соответствующем расстоянии располагается наблюдаемый предмет.
Пользуясь масштабной линейкой М, расположенной сбоку на расстоянии 25 см, и сравнивая величину отрезка d’, соответствующего углу зрения β’ на мнимое изображение, образуемое микроскопом, с величиной d самой стрелки, можно, аналогично предыдущему случаю, определить увеличение микроскопа kм = d’/d . (на рисунке обозначено: П — предмет, О — осветитель, Об — объектив, Ок — окуляр, М — масштабная линейка).
Разрешающая способность микроскопа

При прохождении света через мельчайшие детали предмета происходит дифракция, в результате которой при определенных условиях изображение этих деталей может терять резкость контуров, может иметь место нарушение подобия изображения предмету и, наконец, изображение может вообще не получиться. Поэтому, например, в оптическом микроскопе нельзя увидеть фильтрующиеся вирусы, отдельные белковые молекулы и т. п.
Свойства оптической системы давать изображение достаточно мелких объектов без нарушения подобия их предмету называют разрешающей способностью системы. Разрешающая способность характеризуется пределом разрешения или наименьшим расстоянием между двумя светящимися (или освещенными) точками, изображение которых в данной оптической системе наблюдается раздельно. Чем меньше предел разрешения z, тем выше разрешающая способность оптического прибора. Применяя это к микроскопированию биологических объектов, можно считать, что предел разрешения обусловливает наименьшую величину тек структурных деталей которые могут различаться в препарате.
Теория разрешения микроскопа
Теория разрешающей способности микроскопа разработана Э. Аббе, а затем советскими физиками Л. И. Мандельштамом и Д. С. Рождественским. Выводами этой теории и пользуются на практике. Для лучшего понимания этих выводов и особенно для выяснения значения апертурного угла объектива для разрешающей способности микроскопа, рассмотрим этот вопрос предварительно в более упрощенной форме.
Рассмотрим образование с помощью объектива изображения светящегося отверстия S достаточно малого диаметра d, на которое падает пучок параллельных монохроматических лучей (рис. 4). Проходя через отверстие, свет испытывает дифракцию и лучи его отклоняются в стороны. Объектив собирает отклонившиеся лучи и в сопряженной плоскости образует изображение отверстия.
При этом можно рассмотреть два случая. Первый, когда апертурный угол объектива ϴ больше угла α дифракции лучей, тогда все дифрагировавшие лучи собираются объективом и принимают участие в образовании изображения (рис. 4, а). В этом случае оно будет геометрически во всем подобно предмету. Второй случай, когда апертурный угол ϴ объектива меньше угла а дифракции лучей, тогда не все исходящие из отверстия лучи собираются объективом и принимают участие в образовании изображения (рис. 4, б). В этом случае можно ожидать, что изображение не будет полностью геометрически подобно предмету. Степень нарушения подобия будет зависеть от того, какая часть дифрагировавших лучей не примет участия в образовании изображения.
Для того чтобы все отклонившиеся лучи были собраны объективом, необходимо чтобы его апертурный угол ϴ был не меньше угла а дифракции или в пределе был ему равен:
ϴ = α.
Угол а отклонения лучей при дифракции тем больше, чем больше длина волны λ и чем меньше диаметр d отверстия. Допустим для наших упрощенных рассуждений, что между величинами α и λ существует прямая и между α и d обратная пропорциональность, т. е. α ≈ λ/d.
Заменяя на основании вышесказанного угол дифракции α апертурным углом ϴ, получим ϴ ≈ λ/d, откуда d ≈ λ/ϴ. Таким образом, диаметр d отверстия, при котором обеспечивается подобие между изображением и предметом, может быть тем меньше, чем короче длина волны λ и чем больше апертурный угол ϴ объектива.
Посмотрим, какой вид примут эти соотношения в случае наклонного падения лучей на отверстие. Угол наклона лучей сделаем равным апертурному углу. Будем считать достаточным условием для сохранения подобия между изображением и предметом попадания в объектив всех дифрагировавших лучей хотя бы по одну сторону от первоначального направления. При этом, как видно из рисунка, необходимо, чтобы апертурный угол ϴ был не меньше половины угла α дифракции:
ϴ = α/2;
Тогда аналогично предыдущему можно получить соотношение d ≈ λ/2ϴ.
Следовательно, в данном случае условия разрешения улучшаются.
Перенося наши рассуждения на условия микроскопирования, можно считать, что диаметр d отверстия соответствует наименьшей величине структурных деталей препарата, т. е. принять его за предел разрешения микроскопа d = z. Тогда можно сказать, что предел разрешения будет тем меньше, чем короче длина волны λ света и чем больше апертурный угол в объектива, с помощью которого образуется изображение. При прямом падении лучей z ≈ λ/ϴ и при наклонном (под углом равным ϴ) падении лучей
z ≈ λ/2ϴ
В теории Аббе микроскопируемый предмет уподобляется дифракционной решетке и рассматриваются условия образования ее изображения с помощью объектива. Пусть решетка освещена пучком перпендикулярно падающих на нее параллельных лучей монохроматического света. Лучи, претерпевшие дифракцию на щелях решетки Р, собираются объективом Л в его фокальной плоскости, образуя систему дифракционных максимумов (0,1 и 1′, 2 и 2′ , 3 и 3‘ и т. д.).
За фокальной плоскостью лучи, идущие от максимумов различного порядка, опять расходятся, интерферируют между собой и, падая на экран Э, расположенный в сопряженной плоскости, дают изображение решетки. Если в этом участвуют лучи от всех максимумов, изображение решетки будет достаточно резким.
Если задержать лучи от максимумов высших порядков, то изображение решетки потеряет в резкости, но может быть еще приемлемым, если в нем различаются отдельные щели, т. е. выполняется условие их разрешения. Согласно теории Аббе для этого необходимо, чтобы в образовании изображения решетки участвовали лучи не меньше, чем от нулевого максимума и максимума первого порядка, хотя бы с одной стороны. Если задержать лучи от всех максимумов, кроме нулевого, то изображения не получится, так как на экран будут падать прямые, не пересекающиеся между собой лучи, которые создадут только равномерную освещенность экрана.
Пример разрешения микроскопа
Указанные явления можно показать на опыте. Спроектируем при помощи объектива Л на экран Э изображение сетки С из тонких вертикальных проволок (сетка в данном случае служит дифракционной решеткой), осветив ее с помощью конденсора К сходящимся пучком света ( при наклонном падении лучей, которое дает сходящийся пучок, дифракцию света можно наблюдать на более грубых объектах).
Поместим в фокальной плоскости объектива параллельно вертикальным проволокам сетки щелевую диафрагму Д и будем постепенно суживать ее щель. При этом диафрагма будет ограничивать количество дифракционных максимумов, лучи от которых участвуют в изображении вертикальных проволок сетки (горизонтальных проволок, оставленных для контроля по сторонам сетки, это касаться не будет).
Вначале изображение сетки только теряет в яркости. При достаточном сужении щели изображение теряет резкость, но проволоки в нем еще разрешены, при еще большем сужении щели изображение проволок бледнеет, расплывается и, наконец, исчезает.
Такие же результаты можно получить, если вместо задержания лучей от боковых максимумов с помощью диафрагмы ограничить доступ в линзу лучей, образующих эти максимумы, путем сужения апертурного угла объектива.
Для разрешения щелей в изображении дифракционной решетки па теории Аббе необходимо, чтобы в образовании ее изображения участвовали лучи от максимумов нулевого и первого порядка. Для этого направления лучей, образующих эти максимумы, должны лежать в пределах апертурного угла объектива. Другими словами, апертурный угол объектива ϴ должен быть больше или в пределе, равен углу а4 отклонения лучей, образующих максимум 1-го порядка:
ϴ = α4.
Предел разрешения в этом случае может быть приравнен периоду решетки: z = d.
Тогда, используя формулу дифракционной решетки d = —— и подставляя в нее указанные величины, получим
z = λ/sinϴ
Предел разрешения численно равен отношению длины волны света к синусу апертурного угла объектива.
Это — в случае перпендикулярного падения света на предмет, что имеет место только в простейших микроскопах. В более совершенных микроскопах предмет освещается сходящимся пучком лучей, образуемым с помощью конденсора К. При этом вследствие концентрации света на небольшом участке предмета значительно повышается яркость изображения, а в связи с наклонным падением лучей улучшаются условия разрешения.
Угол падения лучей на плоскость предмета в этом случае обусловлен выходным углом φ конденсора . Однако лучи света от конденсора входят в объектив только в пределах апертурного угла ϴ объектива. Поэтому угол ϴ надо считать наибольшим углом наклона лучей к плоскости предмета.
При падении лучей на дифракционную решетку под углом φ направление на максимум первого порядка обусловлено выражением:
d (sin α’1 + sin φ) = φ.
Используя эту формулу в теории Аббе, надо заменить угол дифракции α’1 на апертурный угол ϴ, принять во внимание, что угол падения лучей φ также равен апертурному углу ϴ и приравнять период решетки d пределу разрешения z. В результате получим:
z = d = λ/sin ϴ.
Предел разрешения объектива при наклонном освещении предмета численно равен отношению длины волны света к удвоенному синусу апертурного угла объектива.
Иммерсия объектива

Иммерсия заключается в том, что между предметом и объективом помещается капля жидкости, показатель преломления которой близок к показателю преломления стекла. Например, глицерина (п = 1,45), кедрового масла (п = 1,51) или монобромнафталина (п = 1,66). Ход световых лучей сравнительно в простом (сухом) и в иммерсионном объективах показан на рис. 5, на котором обозначено: П — препарат, С — покровное стекло, И — иммерсионная среда, О — фронтальная линза объектива и К — конденсор. При наличии между покровным стеклом и объективом воздуха лучи, падающие на препарат под углом, большим предельного р, испытывают на границе стекла и воздуха полное внутреннее отражение (рис. 5, а); отражение лучей происходит также и от наружной поверхности объектива.
В иммерсионном объективе свет от предмета до объектива проходит по оптически однородной среде и не испытывает отражения (рис. 5, б). Это значительно повышает яркость изображения, что имеет существенное значение для микроскопа с большим увеличением. Например, для микроскопа с увеличением в 400 раз площадь изображения по сравнению с площадью предмета увеличивается в 160 000 раз, во столько же раз уменьшается его яркость по сравнению с яркостью предмета.
Для иммерсионного объектива, при котором между предметом и первой линзой находится не воздух, а среда с показателем преломления п, длина волны λn света, падающего на объектив:
λn = λ/n ,
где λ—длина волны света в воздухе. Подставляя эти данные в формулу для предела разрешения, получим:
z = λn/2sin θ = λ/2nsinθ
т.е. предел разрешения иммерсионного объектива при наклонном освещении предмета численно равен отношению длины волны света к удвоенному произведению показателя преломления иммерсионной среды на синус апертурного угла объектива.
Величина А = sin θ для сухого или Ап = n sin θ для иммерсионного объектива называется числовой апертурой и для сухого объектива обозначается на его оправе вместе с увеличением. Учитывая это, можно сказать, что предел разрешения микроскопа равняется длине волны света, при котором производится наблюдение, деленной на числовую апертуру при перпендикулярном падении света на предмет z = λ/A, или деленной на удвоенную числовую апертуру при наклонном освещении z = λ/2A
Числовая апертура объектива характеризует предел разрешения всего микроскопа, так как последующие линзы в силу устройства прибора имеют большие апертуры. Она позволяет сравнивать между собой разрешающую способность различных микроскопов. Последняя тем выше, чем больше апертура. Апертурный угол может иметь величину до 70°, тогда для сухого объектива числовая апертура А = sin θ = sin 70° = 0,94. Для иммерсионного объектива при п= 1,5 числовая апертура Ап =пА = 1,5•0,94 = 1,4.
Тогда при освещении предмета белым светом, считая X = 0,555 мк (длина волны, к которой глаз наиболее чувствителен), предел разрешения для сухого микроскопа при прямом освещении z ≈ 0,5 мк, при наклонном освещении z ≈ 0,3 мк и для иммерсионного объектива z ≈ 0,2 мк.
Дальнейшее повышение разрешающей способности оптического микроскопа может быть достигнуто только путем уменьшения длины волны света, с помощью которого производится исследование, например, путем применения ультрафиолетового излучения и фотографирования наблюдаемых объектов. Для этого имеются специальные микроскопы с кварцевой оптикой.
Статья на тему Микроскоп
Добавил:
Вуз:
Предмет:
Файл:
random books / Цуканова., Карпова – Геометрическая оптика. Учебное пособие по курсу ”Прикладная оптика” (2002).pdf
Скачиваний:
35
Добавлен:
07.03.2020
Размер:
3.41 Mб
Скачать
Цель работы: Приобретение практических навыков габаритного и аберрационного расчетов наблюдательной части микроскопа.
1.Задание для работы
1.1.Исходя из заданных характеристик визуальной части микроскопа необходимо выполнить габаритный расчет, который включает в себя определение фокусных расстояний микроскопа, объектива, окуляра, а также (если потребуется) тубусной линзы, расстояний между главными плоскостями компонентов, числовой апертуры объектива, размеров и положения апертурной диафрагмы и выходного зрачка, определение размера полевой диафрагмы, линейного поля микроскопа, разрешающей способности и глубины резко изображаемого пространства.
1.2.По полученным данным подобрать объектив, окуляр, тубусную линзу из каталогов или из библиотеки оптических систем программы “ОПАЛ”.
1.3.Составить оптическую систему визуальной части микроскопа и определите расстояния между компонентами.
1.4.Выполнить построение хода апертурного, главного и двух наклонных лучей.
1.5.Определить аберрации наблюдательной части микроскопа.
2.Краткая теория
Микроскоп предназначен для наблюдения и измерения мельчайших предметов или их деталей, неразличимых невооруженным глазом.
Микроскопы различных предназначений состоят из следующих оптических частей:
•осветительной системы,
•визуальной, фотографической или проекционной.
Все объекты исследования под микроскопом можно разбить на две группы:
•прозрачные,
•непрозрачные.
Микроскопы для проходящего света применяются при работе с прозрачными объектами, а микроскопы для отраженного света – с непрозрачными объектами.
97

Осветительная система должна создать интенсивное и равномерное освещение всего поля микроскопа. Она состоит из (рисунок 7.1.):
1.источника света;
2.коллектора (осветительной линзы);
3.расположенной около коллектора ирисовой диафрагмы, служащей полевой диафрагмой;
4.конденсора.
Рисунок 7.1. Ход лучей в осветительной части микроскопа в проходящем свете.
В передней фокальной плоскости конденсора находится вторая ирисовая диафрагма, служащая апертурной. Осветительная система микроскопа рассчитывается обычно по методу Келера. Коллектор изображает источник света в апертурную диафрагму. Конденсор проецирует полевую диафрагму в плоскость предмета. Выходящие из конденсора параллельные пучки лучей равномерно освещают предмет. Структура источника не воспроизводится на плоскости освещаемого предмета. Эта система позволяет, также, при помощи ирисовых диафрагм раздельно регулировать величину освещаемого поля и величину апертуры. Осветительная система по Келера создает у освещаемого предмета телецентрический ход главного луча, что очень важно для измерительных микроскопов. Телецентрический ход лучей у
98
предмета устраняет ошибку измерений, возникающую благодаря неточности наводки на резкость.
Числовые апертуры, а также размеры источника света и линейного поля объектива долны согласоваться друг с другом и удовлетворять условию:
|
y0 |
Aкол = yоб Аоб = yоб А‘кон , |
(7.1) |
|
где 2 y0 – размер светящегося тела нити, мм; |
||
|
2 yоб |
– размер освещаемого объекта, мм; |
Акол = n sin σAкол – числовая апертура коллектора в пространстве предметов; Аоб = n sin σAоб – числовая апертура объектива в пространстве предметов;
|
А‘кон = n‘ sin σ‘Aкон |
– числовая апертура конденсора в пространстве |
изображений.
Исходными данными для расчета осветительной части являются: Аоб , 2 yоб . Конденсор выбирается из каталога. Числовая апертура конденсора в пространстве изображений А‘кон должна быть меньше апертуры объектива в пространстве предметов Аоб .
Формулы для определения увеличения конденсора:
|
βкон |
= − |
2 yоб |
= − |
fкон |
= − |
z |
′ |
= − ′ |
= − |
Акон |
. |
(7.2) |
|
′ |
||||||||||||
|
кон |
Акон |
|||||||||||
|
DПД |
zкон |
fкон |
Акон |
Аоб |
Расстояние от главной задней плоскости коллектора до апертурной диафрагмы выбирается в пределах а‘кол = −zкон = 200 ÷300мм.
Определение диаметра апертурной диафрагмы:
|
DАД |
= −2zкон Aкон = −2 fкон Aоб = 2 y0′. |
(7.3) |
||||||
|
Фокусное расстояние конденсора, в среднем, составляет |
f ‘кон =10мм и |
|||||||
|
изменяется от 7 до 20 мм. |
||||||||
|
Вычисление числовой апертуры коллектора: |
||||||||
|
А |
= |
yоб Aоб |
. |
(7.4) |
||||
|
кол |
y0 |
|||||||
|
Определение линейного увеличения коллектора: |
||||||||
|
βкол |
= − |
DАД |
. |
(7.5) |
||||
|
2 y0 |
||||||||
|
Определение фокусного расстояния коллектора: |
||||||||
|
′ |
′ |
|||||||
|
= 1 −βкол . |
(7.6) |
|||||||
|
fкол |
||||||||
|
aкол |
99

Определение расстояния от переднего фокуса коллектора до светящегося тела лампы накала:
|
z |
= |
f |
′ |
||||
|
кол |
кол |
. |
(7.7) |
||||
|
β |
|||||||
|
кол |
|||||||
|
Вычисление диаметра полевой диафрагмы коллектора: |
|||||||
|
DПД |
= − |
2 yоб |
. |
(7.8) |
|||
|
βкон |
|||||||
|
Определение положения объекта относительно заднего фокуса |
|||||||
|
конденсора: |
|||||||
|
′ |
′ |
(7.9) |
|||||
|
zкон |
= −βкон fкон . |
Рассмотрим формирование изображения визуальной системой микроскопа, состоящей из объектива и окуляра (рисунок 7.2).
Предмет расположен перед передним фокусом объектива (вблизи него),
впередней фокальной плоскости микроскопа. Увеличенное, действительное, перевернутое изображение предмета строится объективом в передней фокальной плоскости окуляра (глаз работает без аккомодации). Там же устанавливается полевая диафрагма (в отсчетном микроскопе – это измерительная шкала). Вследствие телецентрического хода главного луча в пространстве предметов, входной зрачок микроскопа находится в бесконечности. Объектив микроскопа создает изображение входного зрачка
всвоей задней фокальной плоскости. Здесь и помещается апертурная диафрагма микроскопа. В этом же месте возникает изображение апертурной диафрагмы осветительной системы и источника света.
Расстояние между задним фокусом объектива и передним фокусом окуляра ∆0 называется оптической длиной тубуса микроскопа.
Из рисунка 7.2 видно, что фокусное расстояние микроскопа f ‘ì –
величина отрицательная. Следовательно, визуальная часть микроскопа в отличие от лупы представляет собой отрицательную оптическую систему.
Основными характеристиками микроскопа являются: видимое увеличение Г , линейное поле 2 yоб , числовая апертура Aоб . К остальным
характеристикам относятся: линейный предел разрешения δ, диаметр выходного зрачка D‘ , глубина резко изображаемого пространства T .
Под видимым увеличением микроскопа понимают отношение тангенса угла, под которым видно изображение предмета через микроскоп, к тангенсу угла, под которым наблюдается предмет невооруженным глазом с расстояния наилучшего видения:
100

|
= |
tgω‘ |
. |
(7.10) |
||
|
Г |
|||||
|
tgω |
Рисунок 7.2. Ход лучей в наблюдательной системе микроскопа, состоящей из объектива и окуляра
Основные формулы для расчета
1. Видимое увеличение микроскопа:
|
= |
250 = − |
∆0 |
250 =βоб |
= |
500 Aоб |
, |
|||||||||||||||||
|
Г |
Гок |
||||||||||||||||||||||
|
fм′ |
fоб′ fок′ |
D′ |
|||||||||||||||||||||
|
где βоб – линейное увеличение объектива; |
|||||||||||||||||||||||
|
fоб′ |
– фокусное расстояние объектива; |
||||||||||||||||||||||
|
fок′ |
– фокусное расстояние окуляра; |
||||||||||||||||||||||
|
= 250 – видимое увеличение окуляра. |
|||||||||||||||||||||||
|
Гок |
|||||||||||||||||||||||
|
fок′ |
|||||||||||||||||||||||
|
2. |
Линейное увеличение объектива: |
||||||||||||||||||||||
|
βоб = − |
DПД |
= |
A |
n sin σА |
= − |
∆ |
′ = |
a′ |
. |
||||||||||||||
|
′ = |
′ |
об |
об |
||||||||||||||||||||
|
об |
0 |
||||||||||||||||||||||
|
2 yоб |
Aоб |
n sin σ‘А |
fоб |
aоб |
|||||||||||||||||||
|
об |
101
3. Определение фокусного расстояния микроскопа f ‘ì , положения заднего фокуса микроскопа относительно заднего фокуса окуляра z‘F ‘ и положения переднего фокуса микроскопа относительно переднего фокуса
|
объектива zF . |
|||||||||||||||||||||||
|
f |
′ |
′ |
′ |
||||||||||||||||||||
|
fм′ = − |
об |
fок |
, |
(7.13) |
|||||||||||||||||||
|
∆0 |
|||||||||||||||||||||||
|
z′F ‘= |
fок′2 |
, |
(7.14) |
||||||||||||||||||||
|
∆ |
0 |
||||||||||||||||||||||
|
zF |
= |
fоб |
fок′ |
, |
(7.15) |
||||||||||||||||||
|
∆0 |
|||||||||||||||||||||||
|
где |
fîá |
– |
переднее фокусное расстояние объектива, в |
иммерсионных |
|||||||||||||||||||
|
микроскопах |
f ‘об ≠ − fоб . |
||||||||||||||||||||||
|
4. Определение размера апертурной диафрагмы микроскопа: |
|||||||||||||||||||||||
|
DАД |
= 2∆0 tgσ‘A |
2 f ‘об Aоб , |
(7.16) |
||||||||||||||||||||
|
об |
|||||||||||||||||||||||
|
где σ‘ A |
– апертурный угол объектива в пространстве изображения, причем: |
||||||||||||||||||||||
|
îá |
|||||||||||||||||||||||
|
tgσ‘A |
= |
D‘ |
. |
(7.17) |
|||||||||||||||||||
|
об |
2 f ‘ок |
||||||||||||||||||||||
|
5. |
Определение положения выходного зрачка микроскопа относительно |
||||||||||||||||||||||
|
заднего фокуса окуляра: |
|||||||||||||||||||||||
|
z‘ |
p‘ |
= |
f ‘ок2 |
. |
(7.18) |
||||||||||||||||||
|
∆ |
0 |
||||||||||||||||||||||
|
6. Определение линейного увеличения окуляра в зрачках: |
|||||||||||||||||||||||
|
βP |
= − |
D‘ |
= − |
f ‘ок |
. |
(7.19) |
|||||||||||||||||
|
ок |
DАД |
∆0 |
|||||||||||||||||||||
|
7. Определение числовой апертуры объектива в пространстве |
|||||||||||||||||||||||
|
изображений: |
|||||||||||||||||||||||
|
A‘об |
= n‘sin(arctg |
D‘ |
) , |
(7.20) |
|||||||||||||||||||
|
2 f ‘ок |
|||||||||||||||||||||||
|
или: |
|||||||||||||||||||||||
|
A‘об |
= n‘sin(arctg |
D‘АД |
) . |
(7.21) |
|||||||||||||||||||
|
2∆0 |
8. Определение диаметра полевой диафрагмы микроскопа:
102
|
DПД = 2 y‘об = 2 yоб βоб = 2 f ‘ок tgω‘, |
(7.22) |
где 2ω‘ – угловое поле микроскопа в пространстве изображений.
9. Определение разрешающей способности микроскопа в линейной
|
мере: |
||||||||||||||
|
δ = |
λ |
, |
(7.23) |
|||||||||||
|
2A |
||||||||||||||
|
об |
||||||||||||||
|
где λ – длина волны света в мм. |
||||||||||||||
|
10.Определение глубины резко изображаемого пространства: |
||||||||||||||
|
Т = Т |
+Т |
= |
250 |
+ |
λ |
, |
(7.24) |
|||||||
|
а |
в |
2А2 |
||||||||||||
|
Γ2 |
об |
|||||||||||||
|
м |
где Та – аккомодационная глубина; Тв – волновая глубина.
Если изображение проецируется на экране или в плоскости полевой диафрагмы располагается сетка, то Та = 0 ,тогда:
|
Т =Т |
= |
λ |
. |
(7.25) |
||
|
в |
2 А2 |
|||||
|
об |
Из условия полного использования глазом разрешающей способности микроскопа, полагая разрешающую способность глаза Ψ‘гл = 2′÷4′ ,получаем
следующее соотношение для полезного увеличения микроскопа:
|
500Aоб ≤ Γм ≤1000Аоб . |
(7.26) |
Применение микроскопов с увеличением, больше полезного, не выявляет новых подробностей предмета, но при этом требуется более точная фокусировка, т.к. глубина резко изображаемого пространства уменьшается.
|
Подставляя в последнее выражение |
Γ = |
500А |
, получим, что диаметр |
|
|
м |
D‘ |
|||
|
выходного зрачка лежит в приделах: |
||||
|
0,5мм≤ D‘p ≤1мм. |
(7.27) |
Отсюда следует, что диаметр выходного зрачка микроскопа меньше диаметра зрачка глаза.
Величина ∆0 изменяется от 160мм до 200мм в зависимости от фокусного
расстояния объектива. Для того, чтобы выдержать эти значения, положение объективов при их установке на прибор фиксируется нижним срезом тубуса микроскопа.
103

Рисунок 7.3. Схема тубуса упрощенного микроскопа.
Оправа окуляра опирается на верхний срез тубуса (рисунок 7.3). Расстояние от нижнего до верхнего среза тубуса называется механической длиной тубуса, которая стандартизована. Она равна 160мм для микроскопов, работающих в проходящем свете, и 190мм для микроскопов, работающих в отраженном свете. Остальные стандартные величины показаны на рисунке 7.3.
В комплект микроскопа входят наборы объективов и окуляров, позволяющие получать различные значения видимого увеличения микроскопа. На оправе объектива гравируется его линейное увеличение и числовая апертура, а на оправе окуляра – видимое увеличение. Тубус микроскопа (рисунок 7.3), в нижнюю часть которого ввертывается объектив, а в верхнюю – окуляр, имеет согласованные посадные размеры с оправами объективов и окуляров.
Увеличения объективов для проходящего и фокусные расстояния для отраженного света, для тубуса бесконечность, изменяются в геометрической прогрессии со знаменателем 1.6. Это соответствует ряду Ra5 (ГОСТ 663669). Номинальные значения видимых увеличений окуляров рекомендуется выбирать из ряда Ra10 и они соответствуют кратности: 4; 6.3; 10; 12.5; 16; 20; 25.
Известно также третья длина тубуса – бесконечность, встречающаяся в микроскопах, работающих в отраженном свете. В этом случае из объектива выходит параллельный пучок лучей, т.к. предмет расположен в передней
104
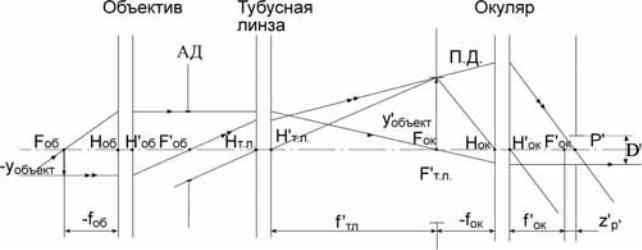
фокальной плоскости объектива (рисунок 7.4). Изображение расположено в задней фокальной плоскости тубусной линзы.
Тубусные линзы представляют собой двухлинзовый склеенный ахроматический объектив и имеют f ‘т. л. =250; 190; 125мм.
Рисунок 7.4. Ход лучей в наблюдательной части микроскопа, содержащей объектив с тубусом бесконечность.
Основные формулы для расчета
1. Линейное увеличение объективной части микроскопа, состоящей из объектива и тубусной линзы:
|
βоб+т. л. = − |
f ‘ |
т. л. |
= − |
DПД |
. |
(7.28) |
|||||||||||
|
f ‘об |
2 yоб |
||||||||||||||||
|
2. |
Видимое увеличение микроскопа: |
||||||||||||||||
|
= − |
f ‘т. л. |
. |
(7.29) |
||||||||||||||
|
Γ =β |
об+т. л. |
Γ |
Γ |
||||||||||||||
|
ок |
f ‘об |
ок |
|||||||||||||||
3. Тубусная линза совместно с окуляром представляют собой телескопическую систему, видимое увеличение которой:
|
f |
‘ |
DАД |
|||||||||||
|
Γт. л+окуляр = − |
т. л. |
= |
. |
(7.30) |
|||||||||
|
D‘ |
|||||||||||||
|
f ‘ок |
|||||||||||||
|
4. Удаление выходного зрачка от заднего фокуса окуляра: |
|||||||||||||
|
z‘p‘ = |
z |
p |
f ‘2 |
, |
(7.31) |
||||||||
|
ок |
|||||||||||||
|
f ‘т2 |
|||||||||||||
|
. л. |
|||||||||||||
|
где zp |
– |
расстояние от переднего фокуса тубусной линзы до апертурной |
диафрагмы.
105

Расстояние от апертурной диафрагмы до тубусной линзы колеблется от
0.05до 0.75 фокусного расстояния линзы.
3.Указания по выполнению работы
3.1.По заданным исходным данным и приведенным выше формулам рассчитать видимое увеличение микроскопа Γ, числовую апертуру объектива Aоб ,разрешающую способность δ, диаметр выходного зрачка.
3.2.По апертуре Aоб выбирается микрообъектив. Если микрообъектив имеет конечную длину тубуса, то в каталоге указаны βоб , линейное поле
объектива в пространстве предметов 2 yоб , линейное поле микроскопа в пространстве изображений 2 y‘об = DПД , расстояние от первой поверхности
объектива до плоскости предметов, расстояние от последней поверхности объектива до изображения.
В отчете представить конструктивные параметры объектива, параксиальные характеристики: f ‘об , S‘F ‘ , SF , S‘H ‘ , SH и чертеж объектива с
указанием отрезков S‘ и S .
3.3. Далее необходимо рассчитать диаметр апертурной диафрагмы DАД ;
оптическую длину тубуса; видимое увеличение окуляра, его фокусное расстояние; увеличение окуляра в зрачках; удаление выходного зрачка.
3.4. По фокусному расстоянию окуляра f ‘ок и размеру полевой диафрагмы DÏÄ выбрать из каталога окуляр визуальной части микроскопа.
В микроскопии применяются следующие типы окуляров: Гюйгенса, Кельнера, Аббе (ортоскопические), симметричные, широкоугольные, компенсационные.
Окуляры Гюйгенса и Кельнера применяются в микроскопах совместно с объективами ахроматами. Угловые поля 2ω‘ и удаления выходных зрачков
|
S‘p‘ |
этих окуляров соответственно |
2ω‘=30o и 2ω‘= 40o ÷50o , S‘p‘ |
f ‘ок |
и |
||||||
|
3 |
||||||||||
|
f ‘ок |
||||||||||
|
S‘p‘ |
= |
. |
||||||||
|
2 |
||||||||||
|
Симметричные |
окуляры |
применяются |
в |
основном |
для |
|||||
|
микрофотографирования |
и реже для визуального |
наблюдения, для них |
||||||||
|
2ω‘ = 40o , S‘p‘ 0,75 f ‘ок . |
Окуляры |
Аббе (ортоскопические) применяются |
совместно с объективами ахроматами средних апертур при больших увеличениях. Угловые поля этих окуляров 2ω‘ = 40o иS‘p‘ 0,75 f ‘ок . Для
компенсации хроматизма увеличения объективов апохроматов с плоским
106
полем применяются компенсационные окуляры. Фокусное расстояние окуляра не пересчитывается. Поэтому при несоответствии рассчитанного фокусного расстояния с фокусным расстоянием из каталога, необходимо уточнить видимое увеличение микроскопа по формуле:
|
= βоб |
Γок , |
(7.32) |
|||||
|
Γ |
|||||||
|
где Γок |
= |
250 |
. |
(7.33) |
|||
|
f ‘ок |
из каталога |
||||||
В отчете представить чертеж окуляра с указанием отрезков S‘F ‘ и SF ,
положения и размера полевой диафрагмы, конструктивные и параксиальные характеристики окуляра.
3.5. При расчете визуальной части микроскопа с тубусной линзой по апертуре Aоб выбирают микрообъектив с тубусом бесконечность. Для
такого объектива известны фокусное расстояние f ‘об , линейное поле в пространстве предметов 2 yоб , расстояние от первой поверхности до
плоскости предметов.
Тубусная линза выбирается из каталога двухлинзовых объективов по относительному отверстию, угловому полю, фокусному расстоянию. Относительное отверстие ее не превышает, как правило, 1:10. Угловое поле определяется по формуле:
|
tgω |
= |
DПД |
= |
y‘ |
об |
. |
(7.34) |
|
т. л. |
2 f ‘т. л. |
f ‘т. л. |
|||||
Входным зрачком для тубусной линзы является апертурная диафрагма визуальной части микроскопа. Расстояние от апертурной диафрагмы до тубусной линзы колеблется от 0.05 до 0.75 фокусного расстояния линзы.
3.6. В микроскопах средних и больших увеличений, содержащих сложные объективы, апертурной диафрагмой служит оправа одной из последних линз объектива или специальная диафрагма, устанавливаемая между последней линзой и задним фокусом объектива. В микроскопах малых увеличений с простыми объективами, а также в визирных микроскопах, применяемых в геодезических и контрольно-измерительных приборах, апертурной диафрагмой является оправа объектива. В отсчетных микроскопах апертурная диафрагма устанавливается в задней фокальной плоскости объектива, что обеспечивает телецентрический ход главных лучей в пространстве предметов. Это ослабляет влияние параллакса на точность измерений.
107

3.7.Далее необходимо определить все расстояния между компонентами
ипредставить оптическую схему визуальной части упрощенного микроскопа. На этом чертеже необходимо указать также основные
характеристики: Γ – видимое увеличение, 2 yоб – линейное поле микроскопа в постранстве предметов, Aоб – числовая апертура, S‘p‘ – удаление выходного
зрачка от последней поверхности окуляра.
3.8. По программе «Опал» определяются аберрации объектива и окуляра в обратном ходе, и в отчете приводятся таблицы и графики аберраций.
4. Задания для работы
|
Фокусное |
|||||||
|
Числовая |
Разрешающая |
Видимое |
расстояние |
||||
|
№ варианта |
способность, |
тубусной |
|||||
|
апертура, Aоб |
|||||||
|
увеличение, Γ |
|||||||
|
линзы, |
|||||||
|
δ (мм) |
|||||||
|
f ‘т. л. (мм) |
|||||||
|
1 |
0,1 |
– |
– |
– |
|||
|
2 |
0,2 |
– |
– |
– |
|||
|
3 |
0,3 |
– |
– |
– |
|||
|
4 |
0,4 |
– |
– |
– |
|||
|
5 |
0,5 |
– |
– |
– |
|||
|
6 |
0,6 |
– |
– |
– |
|||
|
7 |
0,7 |
– |
– |
– |
|||
|
8 |
0,8 |
– |
– |
– |
|||
|
9 |
0,9 |
– |
– |
– |
|||
|
10 |
1,0 |
– |
– |
– |
|||
|
11 |
1,1 |
– |
– |
– |
|||
|
12 |
1,2 |
– |
– |
– |
|||
|
13 |
0,1 |
– |
-50 X |
– |
|||
|
14 |
0,2 |
– |
-100 X |
– |
|||
|
15 |
0,3 |
– |
-150 X |
– |
|||
|
16 |
0,4 |
– |
-200 X |
– |
|||
|
17 |
0,5 |
– |
-250 X |
– |
|||
|
18 |
0,6 |
– |
-300 X |
– |
|||
|
19 |
0,7 |
– |
-350 X |
– |
|||
|
20 |
– |
– |
-400 X |
– |
|||
|
21 |
– |
– |
-450 X |
– |
108
|
22 |
– |
– |
-500 X |
– |
|
23 |
– |
0,0025 |
||
|
24 |
– |
0,0018 |
||
|
25 |
– |
0,0014 |
||
|
26 |
– |
0,0011 |
||
|
27 |
– |
0,0009 |
||
|
28 |
– |
0,00078 |
||
|
29 |
– |
0,00068 |
||
|
30 |
– |
0,00061 |
||
|
31 |
– |
0,00055 |
||
|
32 |
– |
0,0005 |
||
|
33 |
– |
0,00045 |
||
|
34 |
– |
– |
-200 X |
250 |
|
35 |
– |
– |
-220 X |
250 |
|
36 |
– |
– |
-250 X |
190 |
|
37 |
– |
– |
-270 X |
190 |
|
38 |
– |
– |
-300 X |
190 |
|
39 |
– |
– |
-350 X |
190 |
109
Соседние файлы в папке random books
- #
- #
- #
- #
- #
- #
- #
- #
- #












