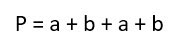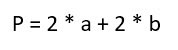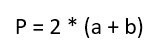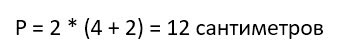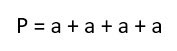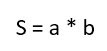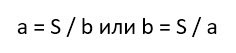Периметр прямоугольника
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое периметр прямоугольника и по каким формулам его можно посчитать.
Тема в общем-то простая, каждый из нас изучал ее еще в начальных классах. Тем не менее с возрастом кто-то мог что-нибудь и подзабыть.
Но для начала предлагаем освежить теоретическую базу и вспомнить, что такое прямоугольник.
Что такое прямоугольник и что такое периметр
Прямоугольник – это геометрическая фигура, которая представляет собой четырехугольник, а конкретно параллелограмм (фигура, у которой противоположные стороны равны и параллельны). Но параллелограмм не обычный, а с особенностями. У него все стороны пересекаются друг с другом под прямым углом.
Выглядит прямоугольник соответственно:
А частным случаем прямоугольника является квадрат:
У такого прямоугольника стороны не только пересекаются под прямым углом, но и равны между собой.
Как и многие термины в математике, жир слово пришло к нам из Древней Греции. Дословно оно означает «περιμετρέο» — «окружность» или «измерять вокруг». Таким образом,
Периметр – это совокупная длина границ любой геометрической фигуры. Этим словом обозначают как сами границы, так и их математическое значение.
С этим словом мы часто встречаемся в повседневной жизни. Например, когда нужно поставить забор на дачном участке, то его устанавливают по периметру участка. И мы понимаем, что речь идет о границах.
Также, солдаты или полицейские часто стоят в оцеплении «по периметру» какой-то территории. А кулинары часто украшают торт фруктами или кремовыми цветами также «по периметру».
Как найти периметр прямоугольника
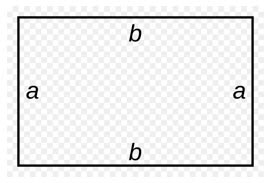
Возьмем для примера такой прямоугольник:
Исходя из общего определения, чтобы посчитать периметр прямоугольника, надо просто сложить все его стороны.
Периметр в математике обозначается латинской буквой «Р». И соответственно формула выглядит так:
С учетом равенства сторон, формулы можно существенно упростить:
или
Предположим, что у нас длина прямоугольника равна 4 сантиметрам, а ширина 2. Тогда периметр этой геометрической фигуры составит:
И тут появляется важное замечание. Периметр измеряется в тех же величинах, что и длины сторон прямоугольника. Это могут быть миллиметры, сантиметры, метры, километры и так далее.
В случае с квадратом, который, напомним, является частным случаем прямоугольника, посчитать периметр еще проще. Благодаря тому, что у него все стороны равны (назовем их условно «а»), формула выглядит так:
или
Опять же приведем конкретный пример. Если возьмем квадрат со стороной 4 сантиметра, то его периметр составит P = 4 * 4 = 16 сантиметров.
Другие формулы для расчета периметра прямоугольника
Иногда школьникам предлагают такую задачу – нужно вычислить периметр прямоугольника, зная его площадь и длину одной стороны.
Тут надо знать, как вычисляется сама площадь. Для этого надо просто перемножить длины двух сторон:
Соответственно, мы можем определить длину недостающей нам стороны. Для этого надо просто разделить площадь на другую сторону:
Таким образом, мы у нас будут значения обеих сторон прямоугольника. А уже после периметр вычисляется по стандартной формуле.
Бывают и более сложные задачи по нахождению периметра прямоугольники, например, как в приведенном ниже видео:
Вместо заключения
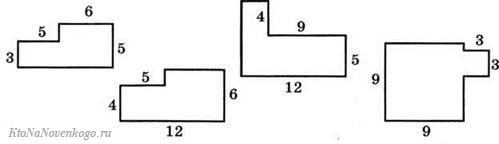
Зная длины сторон, можно вычислять и периметры более сложных прямоугольных фигур. Вот таких:
Страшно выглядят они только на первый взгляд. А на деле, надо просто провести недостающую линию и разделить каждую из фигур на два прямоугольника. Далее вычисляем их по отдельности и складываем друг с другом. Как результат – общий периметр фигуры.
Вот и все, что мы хотели сегодня рассказать.
Download Article
Download Article
The perimeter of a rectangle is the sum total length of all of its sides.[1]
A rectangle is defined as a quadrilateral, or a geometric shape with four sides. In a rectangle, both sets of opposite sides are congruent, meaning that they are the same length.[2]
While not all rectangles are squares, all squares can be considered rectangles, and a compound shape may be composed of rectangles.[3]
-
1
Write down the basic formula for finding the perimeter of a rectangle. This formula will help guide you as you calculate the perimeter of your own rectangle. The basic formula is: P = 2 * (l + w).[4]
- Perimeter is always the total distance around the outside edge of any shape, whether it is simple or compound.
- In this equation, P stands for “perimeter,” l refers to the length of the rectangle, and w refers to the width of the rectangle.
- Length always has a greater value than width.
- Because opposite sides of a rectangle are equal, both lengths will be the same and both widths will be the same. This is why you write the equation as a multiplication of the sum of the length and width by 2.
- You can also write the equation as P = l + l + w + w to make this very clear.
-
2
Find the length and the width of your rectangle. For a basic math problem at school, the length and width of the rectangle will be provided in the problem. These are usually next to the figure of the rectangle.[5]
- If you are calculating the perimeter of a rectangle in real life, use a ruler, yardstick, or tape measure to find the length and width of the area that you are trying to measure. If you’re measuring outdoors, measure all sides to see if the opposites are truly congruent.
- For example, l = 14 centimeter (5.5 in), w = 8 centimeter (3.1 in).
Advertisement
-
3
Add the length and width.[6]
After you identify your length and width, you want to plug them into the “l” and “w” slots in the perimeter equation.- When you are working out your perimeter equations, note that according to the order of operations, mathematical expressions contained inside brackets or parentheses are solved before those outside of the parentheses.[7]
So, you’ll begin solving your equation by adding the length and width. - For example, P = 2 * (l + w) = 2 * (14 + 8) = 2 * (22).
- When you are working out your perimeter equations, note that according to the order of operations, mathematical expressions contained inside brackets or parentheses are solved before those outside of the parentheses.[7]
-
4
Multiply the sum of the length and width by two. When you’re looking the formula for the perimeter of a rectangle, the “(l + w)” is multiplied by two. Once you’ve completed this multiplication, you have the perimeter of your rectangle.[8]
- This multiplication takes into account the other two sides of your rectangle. When you added together the width and length, you only added together two sides of the shape.
- Since the other two sides of the rectangle are equal to the two already added together, you can simply multiply this measurement by two in order to find the total sum of all four sides.
- For example, P = 2 * (l + w) = 2 * (14 + 8) = 2 * (22) = 44 centimeter (17.3 in).
-
5
Add l + l + w + w. Instead of adding two sides of your rectangle and multiplying by two, you can simply add all four sides together directly to find the perimeter of your rectangle.[9]
- If you struggle with the concept of perimeter, this is a great place to start.
- For example, P = l + l + w + w = 14 + 14 + 8 + 8 = 44 centimeter (17.3 in).
Advertisement
-
1
Write down the formula for area and the formula for the perimeter of a rectangle. Even though you already know the area of the rectangle in this problem, you will still need to use the area formula to find missing information.
- The area of a rectangle is a measurement of the two-dimensional space within the rectangle, or the number of square units within the rectangle.
- The formula used to find the area of a rectangle is A = l * w.
- The formula used to find the perimeter of a rectangle is P = 2 * (l + w)
- In the above formulas, A stands for “area,” P stands for “perimeter,” l refers to the length of the rectangle, and w refers to the width of the rectangle.
-
2
Divide the total area by the side measurement you know. This will allow you to find the measurement of the missing side of your rectangle, whether it is the length or the width. Finding this missing piece of information will then allow you to calculate perimeter.
- Because you multiply the length and width together to find the area, dividing the area by the width will give you the length. Likewise, dividing the area by the length will give you the width.
- For example, A = 112 centimeter (44.1 in) squared, l = 14 centimeter (5.5 in)
- A = l * w
- 112 = 14 * w
- 112/14 = w
- 8 = w
-
3
Add the length and width. Now that you have measurements for both the length and width, you can plug them into the formula for rectangular perimeter.[10]
- In this problem, you add length and width together first because this part of the equation occurs in parentheses.
- According to the order of operations, you always do the part of the equation in parentheses first.
-
4
Multiply the sum of the length and width by two. Once you’ve added the length and width of your rectangle together, you can find its perimeter by multiplying by two. This takes into account the additional two sides of your rectangle.[11]
- You are able to find the perimeter of the rectangle by adding length and width and multiplying by two because the opposite sides of a rectangle are equal in length.
- Both lengths of the rectangle are the same, and both widths are the same.
- For example, P = 2 * (14 + 8) = 2 * (22) = 44 centimeter (17.3 in).
Advertisement
-
1
Write down the basic formula for perimeter.[12]
Perimeter is the sum total of all outer sides of any given shape, including irregular and compound shapes.- A standard rectangle has four sides. The two sides composing the length are equal to each other, and the two sides composing the width are equal to each other. Therefore, the perimeter is the sum of those four sides.
- A compound rectangle has at least six sides. Think of a capital “L” or “T” shape. The top “branch” can be separated into one rectangle and the bottom “bar” can be separated into another. The perimeter of this shape, however, does not rely on breaking up the compound rectangle into two separate rectangles. Instead, the perimeter is simply: P = s1 + s2 + s3 + s4 + s5 + s6.
- Each “s” represents a different side of your compound rectangle.
-
2
Find the measurement of each side. In a standard educational math problem, the measurement of all sides should be provided.[13]
- This example uses the abbreviations L, W, l1, l2, w1, and w2. The uppercase L and W stand for the full lengths and widths of the shape. The lowercase ls and ws stand for the smaller lengths and widths.
- As such, the formula P = s1 + s2 + s3 + s4 + s5 + s6 equals P = L + W + l1 + l2 + w1 + w2.
- Variables, like “w” or “l” are simply placeholders for unknown numeric values.[14]
- Example: L = 14 centimeter (5.5 in), W = 10 centimeter (3.9 in), l1 = 5 centimeter (2.0 in), l2 = 9 centimeter (3.5 in), w1 = 4 centimeter (1.6 in), w2 = 6 centimeter (2.4 in)
- Note that l1 and l2 will equal L. Similarly, w1 and w2 will equal W.
-
3
Add all the sides together. By plugging the numeric values of the sides into your equations, you’ll be able to find the perimeter of your compound shape.[15]
- P = L + W + l1 + l2 + w1 + w2 = 14 + 10 + 5 + 9 + 4 + 6 = 48 centimeter (18.9 in)
Advertisement
-
1
Organize the information you do have. You can still find the perimeter of a compound rectangle as long as you have at least one full length or full width and at least three of the minor width or length measurements.
- For an “L”-shaped compound rectangle, use the formula P = L + W + l1 + l2 + w1 + w2
- In this formula, P stands for “perimeter.” The uppercase L and W stand for the full lengths and widths of the entire compound shape. The lowercase ls and ws stand for the smaller lengths and widths in the compound shape.
- Example: L = 14 centimeter (5.5 in), l1 = 5 centimeter (2.0 in), w1 = 4 centimeter (1.6 in), w2 = 6 centimeter (2.4 in); missing: W, l2
-
2
Use the measurements you have to find the missing side measurements. In this example, the full length, L, will be equal to the sum of l1 and l2. Likewise, the full width, W, will be equal to the sum of w1 and w2. Using this knowledge, add and subtract the measurements you do have to find the two missing measurements.
- Example: L = l1 + l2; W = w1 + w2
- L = l1 + l2
- 14 = 5 + l2
- 14 – 5 = l2
- 9 = l2
- W = w1 + w2
- W = 4 + 6
- W = 10
- Example: L = l1 + l2; W = w1 + w2
-
3
Add your sides together. Once you have subtracted to find your missing measurements, you can add all of your sides together to find the perimeter of the compound rectangle. Now, you’ll use the original perimeter formula.[16]
- P = L + W + l1 + l2 + w1 + w2 = 14 + 10 + 5 + 9 + 4 + 6 = 48 centimeter (18.9 in)
Advertisement
Calculator, Practice Problems, and Answers
Add New Question
-
Question
How can I find the side of a rectangle if perimeter is given?
You can’t. With any given perimeter, an infinite number of length-width combinations would be possible.
-
Question
How do I find the perimeter with difficult shapes?
It can help to break difficult shapes up into simpler shapes. Use area formulas for these simpler shapes to help you find all the side lengths of the complex shape.
-
Question
Can I figure out the perimeter of an odd shape if I know its area?
No, the “oddness” of the shape makes it impossible to know the perimeter without more information.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
Thanks for submitting a tip for review!
Things You’ll Need
- Pencil
- Paper
- Calculator (optional)
- Ruler, yardstick, or tape measure (if calculating for a real space)
References
About This Article
Article SummaryX
To find the perimeter of a rectangle, use the formula P = 2 × (l + w). First, find the length and width of the rectangle, and place them in the “l” and “w” variables in the equation. Then, add these measurements together. For example, for a rectangle with a length of 14 cm and a width of 8 cm, you would add them to get 22 cm. Multiply the sum of the numbers by 2 to get the perimeter, which in this case would be 44 cm. Be sure to label your answer with the proper units! If you need to find the perimeter of a rectangle if you only know the area and the length of one side, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 284,846 times.
Did this article help you?
Прямоугольник — это геометрическая фигура, четырехугольник, параллелограмм, у которого все углы прямые, то есть равны 90 градусов.
Чтобы найти периметр прямоугольника, нужно сложить длины всех его сторон.
Онлайн-калькулятор периметр прямоугольника
Формула периметра прямоугольника
P=a+b+a+b=2⋅a+2⋅b=2⋅(a+b)P=a+b+a+b=2cdot a+2cdot b=2cdot (a+b)
a,ba, b — длины двух смежных сторон прямоугольника.
Свойства прямоугольника
Перечислим некоторые свойства прямоугольника:
- Все углы прямоугольника прямые.
- Противоположные стороны прямоугольника равны и параллельны.
- Диагонали прямоугольника равны и точкой пересечения делятся пополам.
Разберем задачу на нахождение периметра прямоугольника.
В прямоугольнике длина a составляет 18 см, а ширина b — 12 см. Чему равен периметр прямоугольника?
Решение
a=18a=18
b=12b=12
Воспользуемся формулой нахождения периметра прямоугольника и подставим вместо aa и bb их численные значения:
P=2⋅(a+b)=2⋅(18+12)=2⋅30=60P=2cdot (a+b)=2cdot (18+12)=2cdot 30=60 см.
Ответ: 60 см.
Ищете, где заказать заказать контрольную работу недорого онлайн? Обратитесь к профильным экспертам на Студворк!
Тест по теме «Периметр прямоугольника»
По какой формуле высчитывают периметр прямоугольника?
Анонимный вопрос
2 ноября 2018 · 156,0 K
Мне интересны множество тем: от психологии до космоса…) · 2 нояб 2018
Периметр фигуры – это сумма длин ее сторон. Для простотого прямоугольника подойдет формула:
P=2*(a+b), a и b -длины прилегающих сторон прямоугольника.
Для правильного прямоугольника (квадрат), у которого все стороны равны, формулу можно упростить до:
P=4*a, где a – длина стороны квадрата.
90,0 K
Спасибо, Выручили! А то формулу подзабыла.
Комментировать ответ…Комментировать…
Не перестаю узнавать новое. Люблю путешествия и все с этим связанное. Много лет работаю в… · 2 нояб 2018
Периметр прямоугольника равен сумме длин его сторон. А так как у прямоугольника противоположные стороны равны, то периметр можно найти по формуле:
P=2(a+b), где a и b – стороны прямоугольника.
17,5 K
Комментировать ответ…Комментировать…
Начнем с того, что периметр прямоугольника можно посчитать по разным формулам.
Самая известная формула периметра прямоугольника: P = a * b, где P – периметр, a и b – длины двух смежных сторон прямоугольника.
Смотри на картинку ниже.
Кроме того, зная площадь прямоугольника и длину одной из сторон прямоугольника, можно также найти периметр. Это менее известная формула… Читать далее
1,5 K
Комментировать ответ…Комментировать…
Периметр высчитывают сложением(как нас раньше учили),а площадь умножением; Р=а+а+а+а: а площадь S=4*а. Вот и все вроде бы как это и есть правильная формула
11,3 K
А как найти формулу периметра прямоугольного параллелепипеда???
Комментировать ответ…Комментировать…
Периметр прямоугольника
Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.
Периметр прямоугольника — это сумма длин всех его ребер.
Основные свойства прямоугольника:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- противоположные стороны фигуры равны и параллельны друг другу;
- сумма всех углов равна 360 градусов;
- диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
- диагонали делят фигуру на два одинаковых прямоугольных треугольника;
- по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
- стороны рассматриваемого четырехугольника также являются его высотами;
- точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
- диагональ этого четырехугольника — это диаметр описанной окружности;
- вокруг него всегда можно описать окружность.
Варианты нахождения периметра прямоугольника
По сторонам
Если нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:
(P=2(a+b))
где (a) и (b) — это две соседние стороны фигуры.
По любой стороне и площади
Зная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.
Так как площадь прямоугольника — это произведение двух его смежных сторон ((S=atimes b)), чтобы найти неизвестную сторону, нужно поделить площадь на известную величину: (b=frac Sa).
Получается, что формула для расчета (P) рассматриваемой фигуры будет выглядеть следующим образом:
(P=2(frac Sa+a))
По любой стороне и диагонали
В случае, если мы знаем длину одного из ребер и диагональ данного четырехугольника, мы можем найти вторую сторону с помощью теоремы Пифагора.
(b=sqrt{d^2-a^2})
где (d) — диагональ прямоугольника, а (b) — неизвестная сторона.
Чтобы рассчитать сумму длин всех сторон, нужно воспользоваться формулой:
(P=2(a+sqrt{d^2-a^2}))
По любой стороне и радиусу описанной окружности
Когда нам известна одна из сторон и радиус описанной окружности вокруг прямоугольника, мы можем узнать его неизвестное ребро. Из свойств прямоугольника помним, что точка пересечения диагоналей фигуры — это центр описанной окружности. Это значит, что 1/2 диагонали — это радиус этой окружности. Таким образом, по теореме Пифагора мы можем узнать неизвестную сторону прямоугольника:
(b=sqrt{4R^2-a^2})
где (R) — радиус описанной окружности.
Тогда формула для расчета P будет выглядеть так:
(P=2(a+sqrt{4R^2-a^2}))
Примеры решения задач
Задача 1
Известно, что стороны прямоугольника равны 5 см и 7 см. Найти его периметр.
Решение:
Применяем самую первую формулу для расчета:
(P=2(a+b))
Получается:
(P=2(5+7)=24) см
Ответ: 24 см.
Задача 2
Мы знаем, что площадь четырехугольника с прямыми углами составляет 24 (см^2), одна из его сторон равна 6 см. Вычислить Р фигуры.
Решение:
Берем формулу (P=2(frac Sa+a)) и подставляем известные значения:
(P=2(frac{24}6+6)=2times10=20) см
Ответ: 20 см.
Задача 3
Дан прямоугольник со стороной 3 см и диагональю 5 см. Нужно высчитать P данной фигуры.
Решение:
Вспоминаем формулу для расчета (P=2(a+sqrt{d^2-a^2})) и вставляем известные величины:
(P=2;(3+sqrt{5^2-3^2})=2(3+sqrt{25-9})=2times7=14) см
Ответ: 14 см.
Задача 4
Вокруг прямоугольника с ребром 3 см описали окружность с радиусом 5 см. Определить P заданной фигуры.
Решение:
В этом случае для расчета суммы длин всех сторон применяем формулу (P=2(a+sqrt{4R^2-a^2})). Используем известные значения и получаем:
(P=2;(3+sqrt{4times5^2-3^2})=2(3+sqrt{100-9})=2(3+sqrt{91})=6+2sqrt{91}) см.
Ответ: (6+2sqrt{91}) см.