Инфоурок
›
Алгебра
›Конспекты›Алгоритм определения формулы линейной функции по графику
Алгоритм определения формулы линейной функции по графику
Скачать материал
без ожидания
Скачать материал
без ожидания
- Сейчас обучается 1153 человека из 83 регионов
- Сейчас обучается 97 человек из 36 регионов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 256 881 материал в базе
-
Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
Тема
16. Линейная функция и её график
Больше материалов по этой теме
Другие материалы
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика написания учебной и научно-исследовательской работы в школе (доклад, реферат, эссе, статья) в процессе реализации метапредметных задач ФГОС ОО»
-
Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС юридических направлений подготовки»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация маркетинга в туризме»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс повышения квалификации «Мировая экономика и международные экономические отношения»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Скачать материал (медленно)
Настоящий материал опубликован пользователем Хидиятова Залифа Даутовна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 6 месяцев
- Подписчики: 0
- Всего просмотров: 102026
-
Всего материалов:
37
(Задание подобного вида есть в ВПР по математике за 7 класс)
Семён Муратов
1 декабря 2019 · 297,0 K
Наставник по математике.
Помогаю воронежским школьникам разобраться в математике и… · 16 мая 2021
b равна точке, в которой график пересекает ось у
к находим следующим способом:
-
выбираем 2 точки на прямой, располагающиеся в узлах координатной решетки.
-
считаем от нижней точки до верхней количество клеток вбок и вверх.
-
к=количество клеток вверх делить на количество клеток вбок
-
при подсчете клеток вбок, учитываем направление движения: вправо плюс, влево минус
9,7 K
Комментировать ответ…Комментировать…
младший научный сотрудник ФТИ им. Иоффе · 2 дек 2019 ·
нужно взять на графике две любые точки (на практике удобно брать те, которые с удобными целыми координатами). Например, пусть по графику видно, что при x = x1, y = y1, при x = x2, y = y2. Две точки (x1,y1) и (x2,y2) подставляются в формулу линейной функции и получается система уравнений относительно k и b. y1 = k*x1 + b, y2 = k*x2 + b. сначалы вычитаем одно из другого и… Читать далее
119,7 K
Линейная функция описывает любую прямую формулой y=k(x+a) +b, где: а- сдвиг по оси х, b-сдвиг по оси у…. Читать дальше
Комментировать ответ…Комментировать…
Студент. Делаю необычные исследования · 9 мар 2021
Можно использовать способ перемещение. По сути график линейной функции это график прямой пропорциональности (проходящий через начало координат) только смещенное, это смещение и есть b. Если мы перенесем график к началу координат то м сможем найти все данные как у функции прямой пропорциональности, с помощью уравнения
7,2 K
Комментировать ответ…Комментировать…
Достаточно замерить угол n наклона прямой к оси Х (при чем угол будет положительным если прямая находится от оси Х протв движения часовой стрелки и отрицательным если наоборот) Найдем коэффициент
k=tgn ; коэффициент b будет равен ординате точки пересечения прямой с ординатой (осью “Y”)
Подставляем эти значения в уравнение y=kx+b и получаем ур=е данной прямой.
13,8 K
Комментировать ответ…Комментировать…
построить график линейной функции:
a)
y=13x+1,x∈−6;3
; b)
y=13x+1,x∈−6;3
.
Составим таблицу значений функции:
| (x) | (-6) | (3) |
| (y) | (-1) | (2) |
Построим на координатной плоскости (xOy) точки ((-6;-1)) и ((3;2)) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции
y=13x+1,x∈−6;3
.
Точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены тёмными кружочками.
b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
Поэтому точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены светлыми кружочками.
По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
В случае
a)
y=13x+1,x∈−6;3
, имеем:
yнаиб
(= 2) и
yнаим
(= -1);
b)
y=13x+1,x∈−6;3
, концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.
В этой статье мы рассмотрим линейную функцию, график линейной функции и его свойства. И, как обычно, решим несколько задач на эту тему.
Линейной функцией называется функция вида 
В уравнении функции число 
, которое мы умножаем на 
называется коэффициентом наклона.
Например, в уравнении функции 
;
в уравнении функции 
;
в уравнении функции 
;
в уравнении функции 
.
Графиком линейной функции является прямая линия.
1. Чтобы построить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.
Например, чтобы построить график функции 
, удобно взять 
и 
, тогда ординаты эти точек будут равны 
и 
.
Получим точки А(0;2) и В(3;3). Соединим их и получим график функции :
2. В уравнении функции коэффициент 
отвечает за наклон графика функции:
Коэффициент 
отвечает за сдвиг графика вдоль оси 
:
На рисунке ниже изображены графики функций 
; 
; 
Заметим, что во всех этих функциях коэффициент больше нуля, и все графики функций наклонены вправо. Причем, чем больше значение , тем круче идет прямая.
Во всех функциях 
– и мы видим, что все графики пересекают ось OY в точке (0;3)
Теперь рассмотрим графики функций ; 
; 
На этот раз во всех функциях коэффициент меньше нуля, и все графики функций наклонены влево.
Заметим, что чем больше |k|, тем круче идет прямая. Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)
Рассмотрим графики функций ; 
; 
Теперь во всех уравнениях функций коэффициенты равны. И мы получили три параллельные прямые.
Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
График функции (b=3) пересекает ось OY в точке (0;3)
График функции (b=0) пересекает ось OY в точке (0;0) – начале координат.
График функции (b=-2) пересекает ось OY в точке (0;-2)
Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции .
Если k<0 и b>0, то график функции имеет вид:
Если k>0 и b>0, то график функции имеет вид:
Если k>0 и b<0, то график функции имеет вид:
Если k<0 и b<0, то график функции имеет вид:
Если k=0 , то функция превращается в функцию 
и ее график имеет вид:
Ординаты всех точек графика функции равны
Если b=0, то график функции 
проходит через начало координат:
Это график прямой пропорциональности.
3. Отдельно отмечу график уравнения 
. График этого уравнения представляет собой прямую линию, параллельую оси все точки которой имеют абсциссу .
Например, график уравнения 
выглядит так:
Внимание! Уравнение не является функцией, так как различным значениям функции соответствует одно и то же значение аргумента, что не соответствует определению функции.
4. Условие параллельности двух прямых:
График функции 
параллелен графику функции 
, если 
5. Условие перпендикулярности двух прямых:
График функции перпендикулярен графику функции , если 
или 
6. Точки пересечения графика функции с осями координат.
С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда 
. То есть точка пересечения с осью OX имеет координаты (
;0):
Рассмотрим решение задач.
1. Постройте график функции , если известно, что он проходит через точку А(-3;2) и параллелен прямой y=-4x.
В уравнении функции два неизвестных параметра: k и b. Поэтому в тексте задачи должны быть два условия, характеризующих график функции.
а) Из того, что график функции параллелен прямой y=-4x, следует, что k=-4. То есть уравнение функции имеет вид 
б) Нам осталось найти b. Известно, что график функции проходит через точку А(-3;2). Если точка принадлежит графику функции, то при подстановке ее координат в уравнение функции, мы получим верное равенство:
отсюда b=-10
Таким образом, нам надо построить график функции 
Точка А(-3;2) нам известна, возьмем точку B(0;-10)
Поставим эти точки в координатной плоскости и соединим их прямой:
2. Написать уравнение прямой, проходящей через точки A(1;1); B(2;4).
Если прямая проходит через точки с заданными координатами, следовательно, координаты точек удовлетворяют уравнению прямой . То есть если мы координаты точек подставим в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим 
. Подставим значение k в первое уравнение системы, и получим b=-2.
Итак, уравнение прямой 
.
3. Постройте график уравнения 
Чтобы найти, при каких значениях неизвестного произведение нескольких множителей равно нулю, нужно каждый множитель приравнять к нулю и учесть ОДЗ каждого множителя.
Это уравнение не имеет ограничений на ОДЗ. Разложим на множители вторую скобку и приравняем каждый множитель к нулю. Получим совокупность уравнений:
Построим графики всех уравнений совокупности в одной коорднатной плоскости. Это и есть график уравнения :
4. Постройте график функции , если он перпендикулярен прямой 
и проходит через точку М(-1;2)
Мы не будем строить график, только найдем уравнение прямой.
а) Так как график функции , если он перпендикулярен прямой , следовательно 
, отсюда 
. То есть уравнение функции имеет вид 
б) Мы знаем, что график функции проходит через точку М(-1;2). Подставим ее координаты в уравнение функции. Получим:
, отсюда 
.
Следовательно, наша функция имеет вид: 
.
5. Постройте график функции 
Упростим выражение, стоящее в правой части уравнения функции.
Важно! Прежде чем упрощать выражение, найдем его ОДЗ.
Знаменатель дроби не может быть равен нулю, поэтому 
, 
.
Тогда наша функция принимает вид:
То есть нам надо построить график функции 
и выколоть на нем две точки: с абсциссами x=1 и x=-1:
И.В. Фельдман, репетитор по математике.
Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.
Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.
Число k называется угловым коэффициентом прямой.
Свойства линейной функции
- Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
- Областью значений также является множество всех действительных чисел.
- Функция не имеет ни наибольших, ни наименьших значений.
- При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
- При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
- При k=0 прямая параллельна оси х.
- Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.
Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.
Пример №1
Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:
Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).
Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:
у=2х – 1=2×0 – 1= –1;
у=2х – 1=2×3 – 1= 5.
Вписываем в таблицу значения у:
Теперь строим систему координат, отмечаем в ней точки с координатами А(0; –1) и В(3;5), проводим через эти две точки прямую.
Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.
Пример №2.
Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).
Пример №3
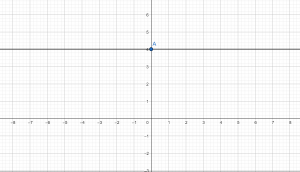
Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.
Задание OM1106o
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ:
КОЭФФИЦИЕНТЫ:
1) k>0, b<0 2) k>0, b>0 3) k<0, b<0
ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>900) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.
У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<900). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.
В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.
Ответ: 213
pазбирался: Даниил Романович | обсудить разбор
Задание OM1103o
Установите соответствие между функциями и их графиками.
Функции:
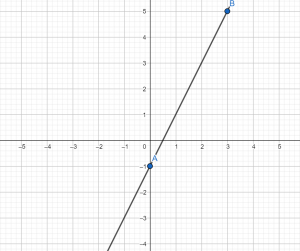
A) y = 3x
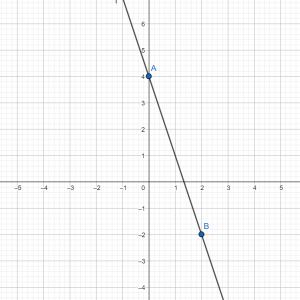
Б) y = -3x
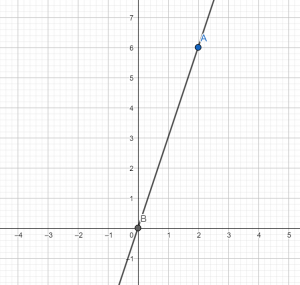
В) y = (1/3)x
Графики:
Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:
y = kx + b
График данной функции зависит от k и b.
- если k < 0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
- коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если b > 0, то выше ноля в точке y = b
- если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1
Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.
Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 6.1k
