Как найти формулу по таблице истинности

Как найти формулу по таблице истинности

0

0

0

0

0

0

1

0

0

1

0

0

0

1

1

1

1

0

0

0

1

0

1

1

1

1

0

1

1

1

1

1

Выбираем строки, где
и
выписываем конъюнкции всех переменных,
при чем, если переменная в этом наборе
равна 1, то записываем ее саму, а если
переменная = 0, то ее отрицание.

Для данного примера

коньюнкция этих дизъюнкций и будет
искомой формулой:

Определение:Конъюнкция
называетсяэлементарной, если
все переменные, входящие в нее, различны.
Количество букв, входящих в элементарную
конъюнкцию или элементарную дизъюнкцию,
называетсярангом.

Число 1 считается элементарной конъюнкцией
ранга 0. Переменная считается элементарной
конъюнкцией или элементарной дизъюнкцией
ранга 1. Число 0 считается элементарной
дизъюнкцией ранга 0. Любую конъюнкцию
переменных, не являющуюся тождественно
ложной, можно привести к виду элементарной,
а любую дизъюнкцию букв, не являющуюся
тождественно истинной, также можно
привести к виду элементарной. Для этого
надо применить свойства коммутативности,
идемпотентности и ассоциативности
конъюнкции и дизъюнкции.

Строго доказано, что любую формулу
булевой алгебры можно выразить с помощью
операций , &,.
Интуитивно этот факт очевиден, вспомним
алгоритм составления формулы по таблице
истинности. При этом мы используем
только эти операции. Такая форма записи
называетсядизъюнктивной нормальной
формой(ДНФ). Это своеобразный механизм
нормализации формул алгебры логики.

Определение:ДНФ– это
дизъюнкция различных элементарных
конъюнкций (т.е. каждая конъюнкция
состоит из элементарных высказываний
или их отрицаний).

Аналогично определяется КНФ – коньюктивная
нормальная форма.

Определение:Если в ДНФ все
элементарные конъюнкции имеют один и
тот же ранг, равный числу переменных,
от которых зависит ДНФ, то она называетсясовершенной (СДНФ).

Теорема. Для любой функции, не
являющейся тождественно ложной,
существует и притом единственная СДНФ.

Следствие. Любую булеву функцию,
не являющуюся тождественно ложной можно
представить в виде суперпозиции&,,,
причем отрицание относится только к
переменным.

Определение:Система логических
операций называется функционально
полной, если с помощью этих операций и
констант этой системы можно представить
любую функцию булевой алгебры.

Системы {&,,};
{,};
{&,},{/}
– являются функционально полными

{&,}
– функционально неполная.

Мы примем эти факты без доказательства,
и решая задачи, будем стараться любую
формулу представить с помощью {&,,}.
Позже мы более подробно обсудим вопрос
функциональной полноты и неполноты
системы операций.

Тема 1.7. Методы упрощения логических выражений. Методы решения логических задач.

Рассмотрим пример решения логической
задачи.

Пример:

После обсуждения состава участников
экспедиции решено, что должны выполняться
два условия.

  1. Если поедет Арбузов, то должны ехать
    Брюквин или Вишневский

  2. Если поедут Арбузов и Вишневский то
    поедет Брюквин

Составить логическую формулу принятия
решения в символической форме, упростить
полученную формулу и сформулировать
по ней новое условие формирования
экспедиции.

Введём переменные и соответствующие
им элементарные высказывания.

– поедет Арбузов

– поедет Брюквин

– поедет Вишневский

Тогда выработанные условия формирования
экспедиции будут выглядеть следующим
образом:

Составим общую формулу и упростим
выражение

т.е. если поедет Арбузов, то поедет
Брюквин.

Пример:

Если завтра будет хорошая погода, то мы
пойдем на пляж или поедем в лес. Составим
формулу нашего поведения на завтра.

–
хорошая погода

– мы пойдем на пляж

– мы поедем в лес

Теперь построим отрицание этой фразы

т.о. получим высказывание “Завтра
будет хорошая погода, и мы не пойдем в
лес и на пляж.

Желающие могут построить таблицу
истинности и проверить это утверждение.

Пример:

По подозрению в совершенном преступлении,
задержаны Браун, Джон и Смит. Один из
них уважаемый в городе старик, второй
чиновник, а третий известный мошенник.
В ходе следствия старик говорил правду,
мошенник лгал, а третий задержанный в
одном случае говорил правду, а в другом
лгал.

Вот что они говорили:

Браун: Я совершил это. Джон не виноват.
(Б&Д)

Джон: Браун не виноват. Преступник Смит.
(Б&С)

Смит: Я не виноват. Виноват Браун (С&Б)

Опишем эти высказывания формально:

– преступление совершил Браун

– преступление совершил Джон

– преступление совершил Смит

Тогда их слова описываются следующими
выражениями:

Браун:

Джон:

Смит:

Т.к. по условиям задачи две из этих &ложны и одна истинна, то

Составим таблицу истинности

NN

1

0

0

0

0

0

0

0

2

0

0

1

0

1

0

1

3

0

1

0

0

0

0

0

4

0

1

1

0

1

0

1

5

1

0

0

1

0

1

1

6

1

0

1

1

0

0

1

7

1

1

0

0

0

1

1

8

1

1

1

0

0

0

0

  1. Исключим из рассмотрения те наборы, на
    которых
    (по условию задачи одна из&- истинна, следовательно,)
    1, 3, 8

  2. Исключим случай 5, т.к. в нем две &истинны, что противоречит условию
    задачи.

  3. В случаях 4, 6, 7 у нас в начальном наборе
    две 1 , т.е. 2 преступника, а по условию
    задачи он один.

Остается только случай 2 , т.е. преступник
Смит, и оба его высказывания ложны.

следовательно–
ложно и–
истинно

=
1 – Джон уважаемый старик

Остается, что Браун чиновник, и поскольку
– ложно , то– истинно.

Пользуясь законами и тождествами булевой
алгебры можно упрощать логические
выражения.

Пример:

Упражнение:

(X&Y&Z)(X&Y&Z)X&Y

Соседние файлы в папке Коспект лекций

  • #

    16.03.2016266 б10desktop.ini

  • #

    16.03.201611.67 Кб10Folder.htt

  • #
  • #
  • #
  • #
  • #
  • #
Источник

Продолжим рассмотрение раздела «Логика высказываний». Ознакомиться с основными понятиями этого раздела можно по ссылкам:

https://zen.yandex.ru/media/id/603a418d1684900aa2499416/logika-vyskazyvanii-postroenie-tablic-istinnosti-6239460b8d70de4bf0b7ac3f

В этой лекции будет представлен перечень различных законов логики высказываний, а также рассмотрена методика получения формул логики высказываний по заданной таблице истинности.

В результате изучения этой лекции предполагается, что обучающийся ознакомится законами, позволяющими производить эквивалентные преобразования, например, приводящие к сокращению записи формулы.

Краткая характеристика лекции
Краткая характеристика лекции

Законы логики высказываний.

В предыдущей лекции (https://zen.yandex.ru/media/id/603a418d1684900aa2499416/logika-vyskazyvanii-postroenie-tablic-istinnosti-6239460b8d70de4bf0b7ac3f ) было сформулировано понятие «Таблица истинности» и представлены таблицы истинности рассмотренных ранее логических операций.

В этой лекции будут представлены часто использующиеся законы логики высказываний, а также рассмотрены некоторые специальные формулы логики высказываний.

В таблице ниже представлены Законы, которые содержат базовые логические операции: логическое отрицание, логическую конъюнкцию и логическую дизъюнкцию. Пусть P, Q, R – произвольные высказывания логики высказываний, тогда справедливы следующие законы: законы коммутативности (они же называются переместительными законами), законы ассоциативности (они же называются сочетательными законами), и законы дистрибутивности (также они называются распределительными законами).

Законы коммутативности, ассоциативности и дистрибутивности логики высказываний
Законы коммутативности, ассоциативности и дистрибутивности логики высказываний

Законы коммутативности и ассоциативности также выполняются и в случае рассмотрения логических операций: эквивалентность, «исключающее или», Штрих Шеффера и Стрелка Пирса.

Относительно коммутативности можно вспомнить стихотворение Бориса Заходера «Вопросительная песенка», текст стихотворения приведён на рис. ниже.

Законы коммутативности
Законы коммутативности

На рисунке ниже в таблице представлены Законы, которые также содержат базовые логические операции: логическое отрицание, логическую конъюнкцию и логическую дизъюнкцию. Пусть P, Q, R – произвольные высказывания логики высказываний, тогда справедливы следующие законы: законы идемпотентности, законы поглощения, закон двойного отрицания и законы расщепления.

Вторая часть основных законов логики высказываний
Вторая часть основных законов логики высказываний

На рисунке ниже (в теореме 2) показаны законы, которые позволяют выражать одни логические операции через другие, особенно важными являются законы, которые выражают импликацию, эквивалентность и логическую операцию «исключающее или» через базовые операции: логическое отрицание, логическую конъюнкцию и логическую дизъюнкцию.

Пусть P, Q и R – произвольные высказывания логики высказываний, тогда справедливы следующие законы. Перечень законов будет представлен на рисунке ниже. Обратите внимание на указанные законы де Моргана, они часто применяются для приведения сложных формул логики высказываний к упрощённому виду.

Законы логики высказываний, выражающие одни операции через другие
Законы логики высказываний, выражающие одни операции через другие

В перечне ниже представлены законы, выражающие одни логические операции через другие, а именно через Штрих Шеффера в левой части таблицы, и Стрелку Пирса – в правой части таблицы.

Законы логики высказываний, выражающие логические операции через Штрих Шеффера (стрелку Пирса)
Законы логики высказываний, выражающие логические операции через Штрих Шеффера (стрелку Пирса)

Прежде, чем перейти к следующей группе законов логики высказываний сформулируем пару определений.

Понятия тавтологии и противоречия
Понятия тавтологии и противоречия

Для того чтобы построить противоречие из тавтологии, необходимо взять отрицание тавтологии.

Ниже представлены некоторые примеры формул логики высказываний, являющихся тавтологиями.

Примеры тавтологий
Примеры тавтологий

Сформулируем в виде теоремы законы логики высказываний, использующие понятия тавтологии и противоречия.

Итак, для любого высказывания P справедливо, что конъюнкция высказывания P с тавтологией даёт в результате само высказывание P.

Конъюнкция высказывания Pс противоречием даёт в результате противоречие.

Также выполняется, что для любого высказывания P дизъюнкция высказывания P с тавтологией даёт в результате тавтологию, а дизъюнкция высказывания P с противоречием даёт в результате само высказывание P.

Также ниже показаны закон противоречия, заключающийся в том, что конъюнкция высказывания P и его отрицания даёт в результате противоречие, а также записан закон исключенного третьего, согласно которому дизъюнкция высказывания P и его отрицания даёт в результате тавтологию. Итак, на формальном языке эти законы записываются как показано на картинке далее.

Законы логики высказываний с тавтологией и противоречием
Законы логики высказываний с тавтологией и противоречием

Составление формулы по заданной таблице истинности.

Рассмотрим важную тему, связанную с построением формул логики высказываний по заданной таблице истинности.

Сформулируем сначала несколько определений.

Дизъюнктивная нормальная форма
Дизъюнктивная нормальная форма
Конъюнктивная нормальная форма
Конъюнктивная нормальная форма

Итак, рассмотрим первый способ составления формулы по заданной таблице истинности. В результате использования этого способа получается формула в виде дизъюнктивной нормальной формы, т.е. представляет собой дизъюнкцию элементарных конъюнкций.

Составление формулы в виде ДНФ
Составление формулы в виде ДНФ

Рассмотрим второй способ составления формулы по заданной таблице истинности.

В результате использования этого способа получается формула в виде конъюнктивной нормальной формы, т.е. представляет собой конъюнкцию элементарных дизъюнкций.

Составление формулы в виде КНФ
Составление формулы в виде КНФ

Перед рассмотрением практического примера отметим ещё пару определений.

Совершенные нормальные формы
Совершенные нормальные формы

Для примера рассмотрим таблицу истинности, как показано на картинке ниже.

Пример составления формулы в виде СДНФ и СКНФ по заданной таблице истинности
Пример составления формулы в виде СДНФ и СКНФ по заданной таблице истинности

Сначала выберем строки, где значения F(x, y, z) = 1, это строки с номерами 2, 3 и 6.

Следовательно, совершенная дизъюнктивная нормальная форма будет состоять из 3 слагаемых, при этом в каждом слагаемом будет три переменных x, y, z (2, 3 и 4 столбцы). Можно сразу сделать заготовки формул, как показано внизу картинки.

Аналогичную заготовку делаем для совершенной конъюнктивной нормальной формы, она будет состоять из 5 слагаемых, потому что значений в заданной таблице истинности, равных нулю, ровно 5.

Далее навешиваем отрицания: в СДНФ по правилу: если переменная в соответствующей строке имеет ложное значение, то в соответствующем слагаемом она записывается с отрицанием, в СКНФ наоборот.

Получается соответствующий результат (показан ниже).

Пример составления формулы в виде СДНФ и СКНФ по заданной таблице истинности (с навешенными отрицаниями)
Пример составления формулы в виде СДНФ и СКНФ по заданной таблице истинности (с навешенными отрицаниями)

Таким образом, по любой таблице истинности можно записать формулу с виде СДНФ или СКНФ, после этого, воспользовавшись законами логики высказываний, произвести эквивалентными преобразования для сокращения формулы.

В качестве Упражнений предлагаются следующие варианты.

Упражнение 1.

В комментариях запишите закон логики высказываний, который не упомянут в лекции, естественно, хотелось бы, чтобы законы не повторялись. Обратите внимание, что для выполнения этого Упражнения перспективно рассмотреть законы, относящиеся не к базовым логическим операциям.

Упражнение 2.

Предлагается взять дату написания комментария, число и месяц, сложить два значения, результат перевести в двоичную систему счисления, далее перед получившимся числом в двоичной системе счисления заполнить нулями до восьмизначного числа, затем для этого восьмизначного числа необходимо записать СДНФ и СКНФ.

Например, для 30 марта СДНФ будет состоять из 2 слагаемых, поскольку имеется две единицы в таблице истинности, а СКНФ– соответственно из шести (см. рис. ниже).

Пример выполнения упражнения 2
Пример выполнения упражнения 2

Упражнение 3.

Запишите в комментарий под видео СДНФ и СКНФ для следующих формул (по вариантам).

Варианты для составления СДНФ и СКНФ
Варианты для составления СДНФ и СКНФ
Источник

Для любой логической формулы можно построить бесконечное количество равносильных ей формул. Для этого потребуется произвести некоторое количество тождественных преобразований. Одной из главных задач в алгебре логики является нахождение канонических форм формул. Проще говоря таких, которые построены по одному канону (правилу).

Форма представления какой-либо логической функции будет считаться нормальной, если она выражена через конъюнкцию, дизъюнкцию, а также отрицание переменных. Среди всех нормальных форм можно выделить совершенно нормальные. Это тот случай, когда функция может быть записана только одним единственным способом.

Классы СКНФ и СДНФ

В при решении задач в алгебре логики особая роль отводится классам конъюнктивных и дизъюнктивных совершенно нормальных форм. Они основаны на стандартных понятиях элементарной конъюнкции и дизъюнкции.

Определение 1 — 2

Элементарной конъюнкцией принято называть формулу в том случае, когда она представляет собой конъюнкцию любого количества переменных, которые берутся без отрицания либо с отрицанием. При этом одночленной элементарной конъюнкцией считается только одна единственная переменная либо ее отрицание.

Элементарной дизъюнкцией называют формулу при условии, что она будет являться дизъюнкцией некоторого любого количества переменных и отрицаний, при этом она может быть и одночленной.

СКНФ

Форма любой логической формулы нормального типа не может содержать знаки эквивалентности, импликации, а также отрицания неэлементарных формул. Она может существовать только в двух видах:

  • КНФ – конъюнктивная нормальная форма, представляющая собой конъюнкцию нескольких дизъюнкций. К примеру, [(A vee bar{B} vee C) wedge(A vee C)];
  • ДНФ – дизъюнктивная нормальная форма, которая является дизъюнкцией нескольких конъюнкций. К примеру, [(A wedge bar{B} wedge C) vee(A wedge C)].

Определение 3

Совершенной конъюнктивной нормальной формой (СКНФ) называют КНФ, удовлетворяющую нескольким условиям:

  1. В ней не содержится двух и более элементарных дизъюнкций;
  2. Во всех дизъюнкциях отсутствуют одинаковые переменные;
  3. Каждая ДНФ содержит в себе все переменные из входящих в нее КНФ.

Любую булеву формулу, не являющуюся тождественной истиной, можно представить в виде СКНФ.

Правила построения СКНФ

В алгебре логики для любого набора переменных, при котором конечное значение функции становится нулевым, можно записать сумму. При этом переменные, имеющие числовые значение больше единицы, должны браться с отрицательным знаком.

Построение должно осуществляться по следующему алгоритму:

  1. В таблице нужно отметить такие наборы переменных, при которых [f=1].
  2. Для каждого выбранного набора переменных записываем КНФ, при этом если значение какой-либо из них равно 1, то она включается в неизменном виде, иначе – ее отрицание.
  3. На последнем этапе все полученные конъюнкции следует связать операциями дизъюнкции.

СНДФ

Определение 4

Совершенной дизъюнктивной нормальной формой (СНДФ) называют удовлетворяющую нескольким условиям ДНФ. Всего должно выполняться три условия:

  1. В ДНФ не должно содержаться двух и более одинаковых СКНФ.
  2. Ни в одной из конъюнкций не должно содержаться одинаковых переменных.
  3. В каждой элементарной КНФ должны содержаться все переменные, входящих в нее ДНФ, при этом их порядок должен полностью совпадать.

Любую булеву формулу в алгебре логики, не являющуюся тождественно ложной, можно представить в виде СНДФ, но только в одном единственном виде.

Правила построения СДНФ

Если существует определённый набор переменных, при котором значение функции равно единице, то можно записать произведения, учитывая, что переменные, значение которых больше нуля, нужно брать с отрицанием.

Алгоритм построения будет следующим:

  1. В таблице отмечаются все те наборы переменных, при которых [f=0]
  2. Для каждого отмеченного набора всех переменных записывается ДНФ, при этом если значение какой-либо из них равно нулю, то включается сама переменная, в любом другом случае ее нужно инвертировать.
  3. В конце все полученные дизъюнкции связываются друг с другом операциями конъюнкции.

Нет времени решать самому?

Наши эксперты помогут!

Примеры нахождения СКНФ и СДНФ

Рассмотрим несколько примеров нахождения СКНФ и СДНФ с помощью данных таблицы истинности.

Примеры 1 — 2

Необходимо по таблице истинности записать логическую функцию.

Примеры нахождения СКНФ и СДНФ 1

Решение. Для того чтобы выполнить задачу будем использовать правило построения СДНФ.

Примеры нахождения СКНФ и СДНФ 2

Получим СДНФ, которая имеет следующий вид:

[Fleft(x_{1}, x_{2}, x_{3}right)=left(overline{x_{1}} wedge overline{x_{2}} wedge overline{x_{3}}right) veeleft(overline{x_{1}} wedge overline{x_{2}} wedge x_{3}right) veeleft(x_{1} wedge overline{x_{2}} wedge overline{x_{3}}right) veeleft(x_{1} wedgeright.left.overline{x_{2}} wedge x_{3}right) veeleft(x_{1} wedge x_{2} wedge x_{3}right)]
Далее будем действовать согласно правилу построения СКНФ:

Примеры нахождения СКНФ и СДНФ 3

В результате получим:

[Fleft(x_{1}, x_{2}, x_{3}right)=left(x_{1} wedge overline{x_{2}} wedge x_{3}right) wedgeleft(x_{1} wedge overline{x_{2}} wedge overline{x_{3}}right) wedgeleft(overline{x_{1}} wedge overline{x_{2}} wedge x_{3}right)]

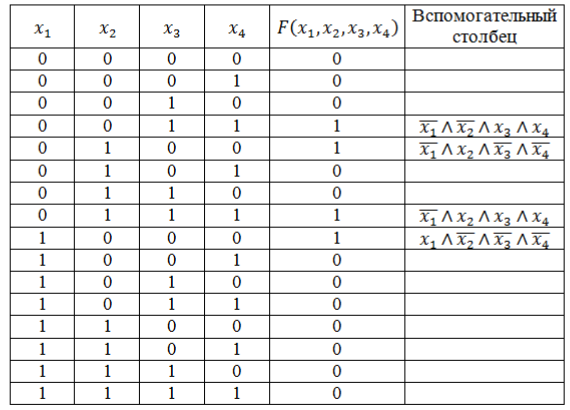
Требуется представить функцию, которая задана в таблице в виде СДНФ и СКНФ.

Примеры нахождения СКНФ и СДНФ 4

Решение: Для начала запишем в СНДФ заданную логическую функцию. Чтобы было проще, добавим еще один вспомогательный столбец. Руководствуемся правилом составления СДНФ и учитываем, что требуется ввести знак отрицания, если значение переменной будет нулевым. Это нужно для того, чтобы они не превратили в нули основной функции значение конъюнкции.

Примеры нахождения СКНФ и СДНФ 5

Значения, которые получились во вспомогательном столбце соединяем знаком дизъюнкции, в результате чего получаем искомую логическую функцию, которая примет следующий вид:

[Fleft(x_{1}, x_{2}, x_{3}, x_{4}right)=(bar{x} wedge bar{y} wedge z wedge f) veeleft(overline{x_{1}} wedge overline{x_{2}} wedge overline{x_{3}} wedge overline{x_{4}}right) veeleft(overline{x_{1}} wedge x_{2} wedge x_{3} wedgeright.left.x_{4}right) veeleft(x_{1} wedge overline{x_{2}} wedge overline{x_{3}} wedge overline{x_{4}}right)]

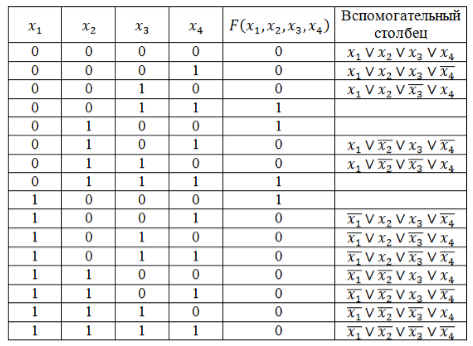
После этого потребуется записать логическую функцию в СКНФ. Для этого используем правило ее составления и вводим знаки отрицания для тех переменных, значение которых равно 1. Если пренебречь инвертированием единичных значений, то они могут превратить ДНФ в единицы основных функций.

Примеры нахождения СКНФ и СДНФ 6

Все полученные нами значения во вспомогательном столбце соединяем знаком конъюнкции и в итоге получаем логическую функцию в следующем виде.
[Fleft(x_{1}, x_{2}, x_{3}, x_{4}right)=left(x_{1} vee x_{2} vee x_{3} vee x_{4}right) wedgeleft(x_{1} vee x_{2} vee x_{3} vee overline{x_{4}}right) wedgeleft(x_{1} vee x_{2} veeright.\left.overline{x_{3}} vee x_{4}right) wedgeleft(x_{1} vee overline{x_{2}} vee x_{3} vee overline{x_{4}}right) wedgeleft(x_{1} vee overline{x_{2}} vee overline{x_{3}} vee x_{4}right) wedgeleft(overline{x_{1}} vee x_{2} vee x_{3} veeright.\left.overline{x_{4}}right) wedgeleft(overline{x_{1}} vee x_{2} vee overline{x_{3}} vee x_{4}right) wedgeleft(overline{x_{1}} vee x_{2} vee overline{x_{3}} vee overline{x_{4}}right) wedgeleft(overline{x_{1}} vee overline{x_{2}} vee x_{3} vee x_{4}right) wedge\left(overline{x_{1}} vee overline{x_{2}} vee x_{3} vee overline{x_{4}}right) wedgeleft(overline{x_{1}} vee overline{x_{2}} vee overline{x_{3}} vee x_{4}right) wedgeleft(overline{x_{1}} wedge overline{x_{2}} wedge overline{x_{3}} wedge overline{x_{4}}right)]
После рассмотрения примеров построения СДНФ и СКНФ с использованием таблицы истинности, стал понятен принцип построения логических функций.

Источник
Автор статьи

Диана Загировна Филиппенкова

Эксперт по предмету «Информатика»

Задать вопрос автору статьи

Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.

Нормальная форма существует в двух видах:

  1. конъюнктивная нормальная форма (КНФ) — конъюнкция нескольких дизъюнкций, например, $left(Avee overline{B}vee Cright)wedge left(Avee Cright)$;

  2. дизъюнктивная нормальная форма (ДНФ) — дизъюнкция нескольких конъюнкций, например, $left(Awedge overline{B}wedge Cright)vee left(Bwedge Cright)$.

СКНФ

Совершенная конъюнктивная нормальная форма (СКНФ) — это КНФ, удовлетворяющая трем условиям:

  • не содержит одинаковых элементарных дизъюнкций;

  • ни одна из дизъюнкций не содержит одинаковых переменных;

  • каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.

Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.

Правила построения СКНФ по таблице истинности

Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.

СДНФ

Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, удовлетворяющая трем условиям:

  • не содержит одинаковых элементарных конъюнкций;

  • ни одна из конъюнкций не содержит одинаковых переменных;

  • каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.

Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.

Правила построения СДНФ по таблице истинности

Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.

Примеры нахождения СКНФ и СДНФ

Пример 1

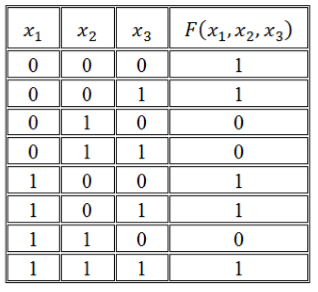
Записать логическую функцию по ее таблице истинности:

Рисунок 1.

Решение:

Воспользуемся правилом построения СДНФ:

Рисунок 2.

Получим СДНФ:

[Fleft(x_1, x_2, x_3right)=left(overline{x_1}wedge overline{x_2}wedge overline{x_3}right)vee left(overline{x_1}wedge overline{x_2}wedge x_3right)vee left(x_1wedge overline{x_2}wedge overline{x_3}right)vee left(x_1wedge overline{x_2}wedge x_3right)vee left(x_1wedge x_2wedge x_3right)]

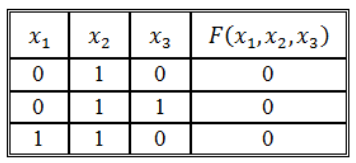
Воспользуемся правилом построения СКНФ:

Рисунок 3.

Получим СКНФ:

[Fleft(x_1, x_2, x_3right)=left(x_1vee overline{x_2}vee x_3right)wedge left(x_1vee overline{x_2}vee overline{x_3}right)wedge left(overline{x_1}vee overline{x_2}vee x_3right)]

«Построение СКНФ и СДНФ по таблице истинности» 👇

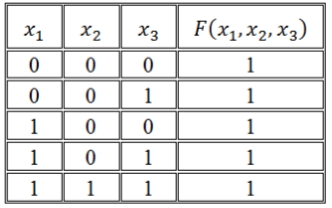
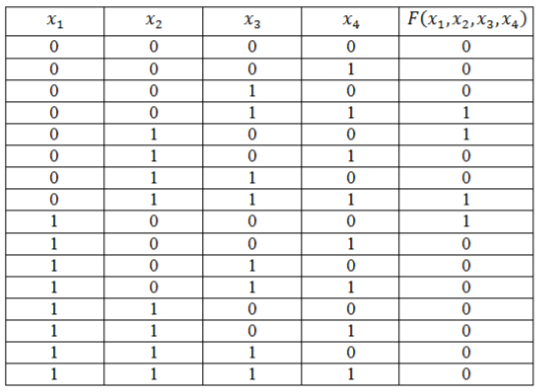
Пример 2

Функция задана таблицей истинности:

Рисунок 4.

Представить эту функцию в виде СДНФ и СКНФ.

Решение:

  1. Запишем логическую функцию в СДНФ. Для удобства решения добавим к таблице вспомогательный столбец.

    Используя правило составления СДНФ не забываем вводить знак отрицания для переменных со значением 0. Инвертировать нулевые значения переменных обязательно, т.к. иначе они превратят значения конъюнкций в нули основной функции.

    Рисунок 5.

    Полученные во вспомогательном столбце конъюнкции соединим знаком дизъюнкции и получим искомую логическую функцию в виде СДНФ:

    [Fleft(x_1,x_2,x_3,x_4right)=left(overline{x}wedge overline{y}wedge zwedge fright)vee left(overline{x_1}wedge x_2wedge overline{x_3}wedge overline{x_4}right)vee left(overline{x_1}wedge x_2wedge x_3wedge x_4right)vee left(x_1wedge overline{x_2}wedge overline{x_3}wedge overline{x_4}right).]

  2. Запишем логическую функцию в СКНФ.

    Используя правило составления СКНФ не забываем вводить знак отрицания для переменных со значением 1. Инвертировать единичные значения переменных обязательно, т.к. иначе они превратят значения дизъюнкций в единицы основной функции.

    Рисунок 6.

    Полученные во вспомогательном столбце дизъюнкции соединим знаком конъюнкции и получим искомую логическую функцию в виде СКНФ:

    [Fleft(x_1,x_2,x_3,x_4right)=left(x_1vee x_2vee x_3vee x_4right)wedge left(x_1vee x_2vee x_3vee overline{x_4}right)wedge left(x_1vee x_2vee overline{x_3}vee x_4right)wedge left(x_1vee overline{x_2}vee x_3vee overline{x_4}right)wedge left(x_1vee overline{x_2}vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee x_2vee x_3vee overline{x_4}right)wedge left(overline{x_1}vee x_2vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee x_2vee overline{x_3}vee overline{x_4}right)wedge left(overline{x_1}vee overline{x_2}vee x_3vee x_4right)wedge left(overline{x_1}vee overline{x_2}vee x_3vee overline{x_4}right)wedge left(overline{x_1}vee overline{x_2}vee overline{x_3}vee x_4right)wedge left(overline{x_1}vee overline{x_2}vee overline{x_3}vee overline{x_4}right).]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Логические выражения и таблица истинности

Примеры задач с решениями по этой теме Пройти тестирование по теме Контрольная по теме

 Таблица истинности — таблица, показывающая,  какие значения принимает составное высказывание при  всех сочетаниях (наборах)  значений  входящих в него простых высказываний.

Логическое выражение — составные высказывания в виде формулы.

Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».

Алгоритм построения  таблицы  истинности:

1.    подсчитать количество переменных n в логическом выражении;

2.   определить число строк в таблице по формуле m=2n, где n — количество переменных;

3.   подсчитать количество логических операций в формуле;

4.   установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5.   определить количество столбцов: число переменных + число операций;

6.   выписать наборы входных переменных;

7.   провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.

Заполнение таблицы:

1.      разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;

2.      разделить колонку  значений  второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;

3.      продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.

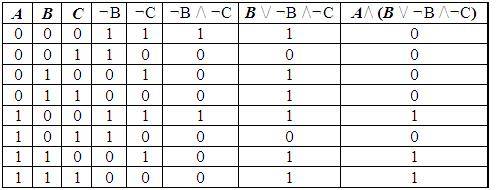
Пример 1. Для формулы  A/ (B / ¬B /¬C) постройте  таблицу истинности.

 Количество логических переменных 3, следовательно, количество строк — 23 = 8.

Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.

 Логические выражения и таблица истинности

Пример 2. Определите истинность  логического выражения  F(А, В) = (А/ В)/(¬А/¬В) .

1. В выражении две переменные А и В (n=2).

2.  mстрок=2n, m=22=4 строки.

3. В формуле 5 логических операций.

4. Расставляем порядок действий

1) А/ В;  2) ¬А;  3) ¬В;  4) ¬А/¬В;  5) (А/ В)/(¬А/¬В).

5. Кстолбцов=n+5=2+5=7 столбцов.

А

В

А/ В

¬А

¬В

¬А/¬В

F

0

0

0

1

1

1

0

0

1

1

1

0

1

1

1

0

1

0

1

1

1

1

1

1

0

0

0

0

 Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.

Пример 3. Построёте таблицу истинности для логического выражения

F = (A/ B) / ¬С

  1. В данной функции три логические переменные – А, В, С
  2. количество строк таблицы = 23 =8
  3. В формуле 3 логические операции.
  4. Расставляем порядок действий

1) А/ В;  2) ¬С; 3) (AVB) / ¬С  .

  1. количество столбцов таблицы = 3 + 3 = 6

А

В

С

A/B

¬С

(A/B) / ¬С

0

0

0

0

1

0

0

0

1

0

0

0

0

1

0

1

1

1

0

1

1

1

0

0

1

0

0

1

1

1

1

0

1

1

0

0

1

1

0

1

1

1

1

1

1

1

0

0

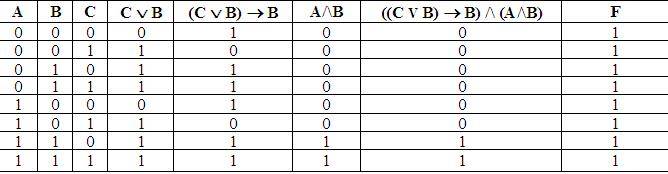
Пример 4.  Определите истинность формулы: F = ((С /В) =>  В) / (А / В) => В.

Построим таблицу истинности этой формулы.

 Логические выражения и таблица истинности

Ответ: формула является тождественно истинной.

Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.

Дан фрагмент таблицы истинности выражения F:

X

Y

Z

F

0

0

0

1

0

0

1

0

0

1

0

1

Какое выражение соответствует F?

 1) ¬X/¬Y/Z                      2) ¬X/¬Y/Z                  3) X/Y/¬Z              4) X/Y/Z

 Решение (вариант 1, через таблицы истинности):

Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:

X

Y

Z

F

¬X

¬Y

¬Z

¬X/¬Y/Z

¬X/¬Y/Z

X/Y/¬Z

X/Y/Z

0

0

0

1

1

1

1

0

1

1

0

0

0

1

0

1

1

0

1

1

0

1

0

1

0

1

1

0

1

0

1

1

1

 Очевидно, что значения заданной функции F совпадают со значениями выражения X/Y/¬Z. Следовательно, правильный ответ – 3.

Ответ: 3

 Решение (Вариант 2):

Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y  и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.

 Рассмотрим данный конкретный пример:

1)      первое заданное выражение  ¬X/¬Y/Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;

2)      второе заданное выражение ¬X/¬Y/Z = 1 при X=0, Y=0, Z=1, что не соответствует  второй строке таблицы;

3)      третье выражение   X/Y/¬Z    соответствует F при всех предложенных комбинациях X,Y и Z;

4)      четвертое выражение X/Y/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.

Ответ: 3

Источник

Добавить комментарий