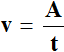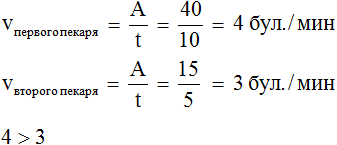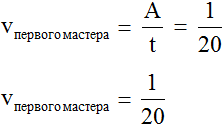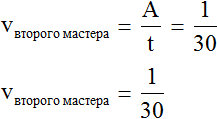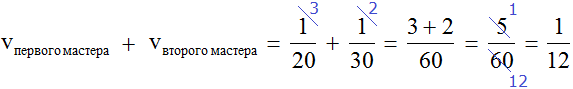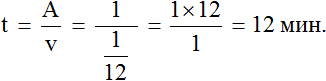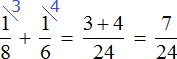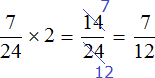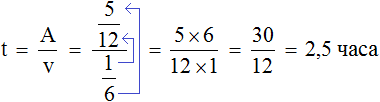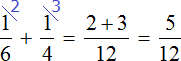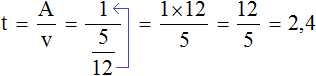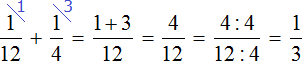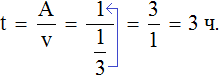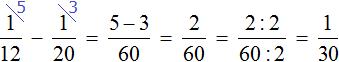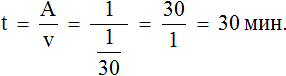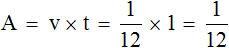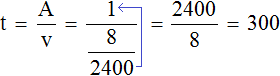Ничего сложного в задачах на формулу работы нет.
V – производительность труда – работа, которую выполнили за единицу времени.
t – время
А – работа.
Чтобы найти производительность, надо работу разделить на время:
V = A : t
Чтобы найти работу, надо производительность умножить на время.
A= V * t
Чтобы найти время, надо работу разделить на производительность.
t = A : V
Задачи для тренировки:
- Одна девочка рисует за неделю 25 рисунков, другая – 35 рисунков. Сколько всего рисунков нарисуют девочки за 2 дня?
- Производительность самого большого станка 5шт/час. За какое время на этом станке выточат 100 деталей?
- За 81 минут бабушка связала 9 шнурков. Сколько времени тратила бабушка на 1 шнурок.
- Дашин принтер за 10 секунд напечатал 500 листов. Какова производительность принтера?
- Я съедаю за 1 минуту 2 семечка. Сколько семечек я съем за 37 минут?
- Коля напечатал на компьютере 320 знаков за 8 минут. С какой скоростью печатает Коля?
- В первый день Наташа слепила из пластилина 12 шариков за 6 минут, а на следующий день за это же время 18 шариков. В какой день производительность Наташи была выше и насколько?
- Бригада Саши изготовляет 276 деталей за 6 часов, а бригада Поли – 336 деталей за 8 часов. У какой бригады производительность труда выше и на сколько?
- Производительность труда у бабушки 3 шарфика в месяц. Сколько шарфиков свяжет бабушка за год?
- Команда девочек за 3 часа собрала 33 кг яблок, а команда мальчиков за 5 часов собрала 55 кг яблок. У какой команды производительность труда выше и на сколько?
- Катя вышивает 3 цветочка за час. Сколько цветочков вышьет Катя за 3 часа?
- Люда прочитала книгу за 6 дней. Сколько страниц читывала Люда каждый день, если в книге 360 страниц? А Людина мама напечатала 240 страниц доклада за такое же количество дней. Сколько страниц в день печатала мама?
- Папа сделал 49 деревянных кубиков за 7 дней. Какова его производительность труда?
- За 100 дней сколько столяр сделает лавочек, если его производительность 2 лавочки в день?
- Тетя шьет 5 мягких игрушек за 25 дней. Какова ее производительность труда?
- Повар состряпал 45 пирожков за 3 часа. Какова его производительность?
Файл для распечатки.
Как решать задачи с работой по математике
Как утверждают многие источники, решение задач развивает логическое и интеллектуальное мышление. Задачи «на работу» являются одними из самых интересных. Для того, чтобы научиться решать такие задачи, необходимо уметь представлять процесс работы, о которой в них говорится.
Инструкция
Задачи «на работу» имеют свои особенности. Для их решения необходимо знать определения и формулы. Запомните следующее:
А=Р*t – формула работы;
P=A/t – формула производительности;
t=A/P – формула времени, где А – работа, Р- производительность труда, t- время.
Если в условии задачи не указана работа, то её принимайте за 1.
На примерах разберем, как решаются такие задачи.
Условие. Два рабочих, работая одновременно, вскопали огород за 6 ч. Первый рабочий мог бы выполнить ту же работу за 10 ч. За сколько часов второй рабочий может вскопать огород?
Решение: Примем всю работу за 1. Тогда, в соответствии с формулой производительности – P=A/t , 1/10 часть работы делает первый рабочий за 1час. 6/10 он делает за 6 часов. Следовательно, второй рабочий за 6 часов делает 4/10 работы ( 1 – 6/10). Мы определили, что производительность второго рабочего равна 4/10. Время совместной работы, по условию задачи, составляет 6 часов. За Х примем то, что надо найти, т.е. работу второго рабочего. Зная, что t=6, P=4/10, составим и решим уравнение:
0,4х=6,
х=6/0,4,
х=15.
Ответ: Второй рабочий может вскопать огород за 15 часов.
Разберем еще один пример: Для наполнения контейнера водой имеются три трубы. Первой трубе для наполнения контейнера необходимо времени в три раза меньше, чем второй, и на 2 ч больше, чем третьей. Три трубы, работая одновременно, наполнили бы контейнер за 3ч, но по условиям эксплуатации одновременно могут работать только две трубы. Определите минимальную стоимость наполнения контейнера, если стоимость 1ч работы одной из труб равно 230 рублей.
Решение: Эту задачу удобно решать с помощью таблицы.
1). Возьмем всю работу за 1. За Х возьмем время, необходимое третьей трубе. По условию первой трубе надо на 2 часа больше, чем третьей. Тогда первой трубе понадобиться (Х+2) часа. А третьей трубе надо в 3 раза больше времени, чем первой, т.е. 3(Х+2). Опираясь на формулу производительности, получим: 1/(Х+2) – производительность первой трубы, 1/3(Х+2) – второй трубы, 1Х – третьей трубы. Занесем все данные в таблицу.
Работа Время,час производительность
1 труба А=1 t=(Х+2) P=1/Х+2
2 труба А=1 t=3(Х+2) P=1/3(Х+2)
3 труба А=1 t=Х P=1/Х
Вместе А=1 t=3 P=1/3
Зная, что совместная производительность равна 1/3, составим и решим уравнение:
1/(Х+2)+1/3(Х+2)+1/Х=1/3
1/(Х+2)+1/3(Х+3)+1/Х-1/3=0
3Х+Х+3Х+6-Х2-2Х=0
5Х+6-Х2=0
Х2-5Х-6=0
При решении квадратного уравнения находим корень. Получается,
Х=6(часов) – время, которое понадобиться третьей трубе для наполнения контейнера.
Из этого следует, что время, которое надо первой трубе равно (6+2)=8 (часов), а второй = 24(часа).
2). Из полученных данных делаем вывод, что минимальное время – это время работы 1 и3 труб ,т.е. 14ч.
3). Определим минимальную стоимость наполнения контейнера двумя трубами.
230*14=3220(руб.)
Ответ: 3220 руб.
Есть задачи наиболее сложнее, где необходимо вводить несколько переменных.
Условие: Специалист и стажер, работая вместе, сделали определенную работу за 12 дней. Если бы сначала специалист выполнил один половину всей работы, а потом вторую половину закончил один стажер, то на все было бы потрачено 25 дней.
а) Найдите время, которое мог бы потратить специалист на завершение всей работы, при условии, что он будет работать один и быстрее стажера.
б) Как поделить работникам полученные за совместное выполнение работы 15000 рублей?
1).Пусть всю работу специалист может выполнить за X дней, а стажер за Y дней.
Получим, что за 1 день специалист выполняет за 1/X работы, а стажер за 1/Yработы.
2). Зная, что работая вместе, на всю работу у них ушло 12 дней, получим:
(1/X+1/Y)=1/12 – ‘это первое уравнение.
По условию, работая по очереди, в одиночку, было затрачено 25 дней, получим:
X/2+Y/2=25
X+Y=50
Y=50-X – это второе уравнение.
3) Подставим второе уравнение в первое, получим: (50 – х +х) / (х(х-50)) = 1/12
X2-50X + 600 = 0,х1= 20,х2=30 (тогда Y=20) не удовлетворяет условию.
Ответ: X=20,Y=30.
Деньги нужно делить обратно пропорционально затраченному на выполнение работы времени. Т.к. специалист работал быстрее и, как следствие, может сделать больше. Поделить деньги надо в отношении 3:2. Специалисту 15000/5*3 = 9000 руб.
Стажеру 15000/5*2 = 6000 руб.
Полезные советы: Если вы не поняли условие задачи, не надо приступать к ее решению. Сначала внимательно прочитайте задачу, выделите все, что известно, и что надо найти. Если это возможно, нарисуйте рисунок – схему. Так же можно воспользоваться таблицами. Использование таблиц и схем может облегчить понимание и решение задачи.
Обратите внимание
Общая производительность равна сумме производительностей.
Источники:
- Задачи и решения.
- как найти работу математика
Продолжаем изучать элементарные задачи по математике. Сегодня мы рассмотрим очень интересную физическую величину — производительность.
Что такое сила?
Сила — это физическое явление, способное изменять форму материальных тел, вызывать их движение, менять направление и скорость движения этих тел или приводить тело в состояние покоя.
Примеры сил:
- ребята слепили снеговика, а хулиганы его разрушили. Получается, что хулиганы приложили к снеговику свою силу, тем самым вызвали изменение формы снеговика;
- на дворе стояла тележка. Прохожий случайно задел её и тележка сдвинулась с места. Получается, что прохожий применил силу к тележке и вызвал её движение;
- далее тот же прохожий остановил тележку, чтобы она далеко не уехала. Получается, что прохожий применил силу, тем самым привел тележку в состояние покоя.
Сила является физической величиной — мерой воздействия на тело других тел. Сила обозначается заглавной латинской буквой F.
Что такое работа?
Работа — это количественная мера действия силы на тело. Работа зависит от количества силы, приложенной на тело и от направления этой силы, а также от перемещения данного тела.
Например, если мы попробуем сдвинуть шкаф с места и он сдвинется, то можно сказать, что мы совершили работу, поскольку сила, которую мы приложили, привела к тому, что шкаф совершил перемещение на некоторое расстояние.
Если же мы, к примеру, попробуем толкнуть стену, то стена с места не сдвинется, а значит и работа не будет совершена, поскольку сила была приложена, но эта сила не вызвала никакого перемещения стены.
Работа обозначается заглавной латинской буквой A.
Производительность
Производительностью называют работу, выполненную за единицу времени. Под единицей подразумевается 1 час, 1 минута или 1 секунда. Производительность обозначается латинской буквой v
Рассмотрим следующий пример. Два пекаря пекли булочки. Первый пекарь испёк 40 булочек за 10 минут, а второй 15 булочек за 5 минут. Как узнать, кто из пекарей работал быстрее, первый или второй?
Работал быстрее тот, кто за одну минуту выпекает больше булочек. Говорят, что у него производительность больше. Для нахождения производительности предусмотрено следующее правило:
Чтобы найти производительность, надо выполненную работу разделить на время работы.
Также, можно воспользоваться формулой:
где v — производительность, A — выполненная работа, t — время работы.
Вернемся к нашей задаче. Зная правило или формулу нахождения производительности, можно определить сколько булочек приходится на одну минуту.
Найдём производительность первого пекаря. Разделим работу, которую он выполнил, на время которое он на нее затратил. Выполненная работа это количество испеченных им булочек, то есть 40, а время — 10 минут
40 : 10 = 4 булочки в минуту
Аналогично найдём производительность второго пекаря. Разделим 15 на 5
15 : 5 = 3 булочки в минуту
4 > 3
Первый пекарь в минуту выпекает больше булочек чем второй, значит его производительность выше. Отсюда делаем вывод, что работает он быстрее второго пекаря.
Также можно воспользоваться формулой нахождения производительности. В этом случае решение принимает следующий вид:
Под буквой v можно делать метки, указывающие для кого/чего мы находим производительность.
Задача 2. Тому нужно за 2 дня прочитать книгу, в которой 100 страниц. В первый день он читал 4 часа со скоростью 12 страниц в час. С какой скоростью ему надо читать оставшуюся часть книги, если у него есть на это 4 часа?
Узнаем сколько страниц Том прочитал в первый день. Он читал 12 страниц в час. Чтению в первый день он посвятил 4 часа, поэтому для нахождения количества прочитанных страниц в первый день, нужно 12 умножить на 4
12 × 4 = 48 страниц прочитано в первый день
Узнаем сколько страниц осталось прочесть. Вычтем из общего количества страниц (100) количество прочитанных страниц (48)
100 − 48 = 52 страницы осталось прочесть
Осталось прочесть 52 страницы. Теперь найдем такую производительность, при которой Том сможет прочесть 52 страницы за 4 часа. Раскидаем 52 страницы на 4 часа поровну
52 : 4 = 13 страниц в час
Ответ: чтобы прочитать оставшуюся часть книги за 4 часа, Том должен читать ее со скоростью 13 страниц в час.
Замечание. В некоторых источниках слово «производительность» может быть заменено на слова «скорость», «эффективность», «продуктивность», «плодотворность».
Задача 3. Один насос работал 4 часа, выкачивая 158 вёдер воды в час, а другой — 3 часа, выкачивая 169 вёдер воды в час. Определить какой из насосов выкачал больше вёдер.
Решение
Определим сколько всего вёдер выкачал каждый насос по отдельности. Для этого умножим их производительность на время их работы:
158 в/ч × 4 = 632 вёдер выкачал первый насос
169 в/ч × 3 = 507 вёдер выкачал второй насос
632 > 507
Ответ: первый насос выкачала больше вёдер, чем второй.
Задача 4. За 2 часа насос выкачал 80 литров воды. Определить сколько литров он выкачает за 5 часов.
Решение
Сначала нужно определить сколько литров воды насос выкачивает за час. Для этого 80 литров разделим на 2 часа — получим 40 литров
80 : 2 = 40 литров в час
За один час насос выкачивает 40 литров воды. За 5 часов выкачает в пять раз больше
40 × 5 = 200 литров
Ответ: за 5 часов насос выкачает 200 литров воды.
Если известны производительность и время работы, то можно найти выполненную работу. Выполненная работа равна производительности умноженной на время работы:
A = v × t
Например, если производительность пекаря составляет 50 булочек в час, и он проработал 4 часа, то можно найти всю выполненную работу за эти четыре часа. Для этого производительность (50 бул/ч) нужно умножить на время его работы (4ч)
50 × 4 = 200 булочек
Если известны работа и производительность, то можно найти время работы. Время работы равно отношению выполненной работы к производительности:
Например, если в неделю бригада отстраивает 2 этажа, то можно узнать сколько недель потребуется для отстройки 8 этажей. Чтобы определить время отстройки восьми этажей, нужно выполненную работу (8 этажей) разделить на производительность (2 эт./нед):
8 : 2 = 4 нед.
Либо с помощью формулы, приведенной выше:
Если в неделю строится 2 этажа, то 8 этажей будет отстроено за четыре недели. В данном случае вся работа была равна восьми. Производительность была равна двум, поскольку по определению производительность есть работа, выполненная за единицу времени – в нашем случае два этажа за неделю.
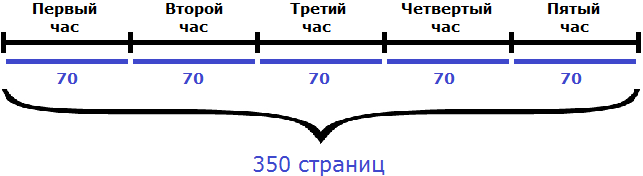
Задача 6. Принтер работает с производительностью 70 стр./ч. Сколько страниц он напечатает за 5 часов?
Решение
Если в час принтер печатает 70 страниц, то за 5 часов он напечатает в 5 раз больше:
70 × 5 = 350 страниц
Также, решение можно записать с помощью формулы нахождения работы. В данном случае, количество напечатанных страниц являются выполненной работой:
A = v × t = 70 × 5 = 350 страниц
A = 350 страниц
Задача 7. Принтер напечатал 350 страниц за 5 часов. С какой производительностью он работал?
Решение
Если в течении пяти часов принтер напечатал 350 страниц, то в течении часа он печатал 
. То есть работал с производительностью 70 страниц в час:
350 : 5 = 70 стр./ч.
Либо с помощью формулы нахождения производительности:
Задача 8. Принтер работал с производительностью 70 страниц в час и напечатал 350 страниц. Определить время работы принтера.
Решение
Выражение «работал с производительностью 70 страниц в час» означает, что в каждом часе принтер печатал по 70 страниц. И это продолжалось до тех пор, пока он не напечатал 350 страниц. Очевидно, что разделив 350 страниц по 70, мы определим время работы принтера, то есть узнаем сколько часов он работал
350 : 70 = 5 ч.
Либо с помощью формулы нахождения времени:
Задача 9. Машинистка в первый день напечатала 48 страниц рукописи, а во второй день — на 12 страниц больше, чем в первый. На всю работу в эти 2 дня она затратила 9 часов. Сколько часов работала она в каждый из этих дней, если производительность её не менялась ?
Решение
Определим сколько страниц напечатала машинистка во второй день. В условии сказано, что напечатала она на 12 страниц больше, чем в первый:
48 + 12 = 60 страниц во второй день.
Определим сколько страниц машинистка напечатала за два дня:
48 + 60 = 108 страниц за два дня.
На эту работу машинистка затратила 9 часов. Также сказано, что производительность её не менялась. Если мы разделим выполненную работу (108) на время выполнения (9), то определим производительность машинистки:
108 : 9 = 12 страниц в час.
Теперь мы можем определить сколько часов работала машинистка в каждый из двух дней. Для этого поочередно разделим выполненные работы в каждом из двух дней на производительность:
48 : 12 = 4 часа работала машинистка в первый день
60 : 12 = 5 часов работала машинистка во второй день.
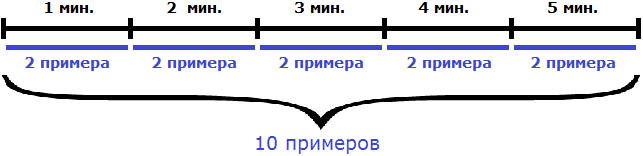
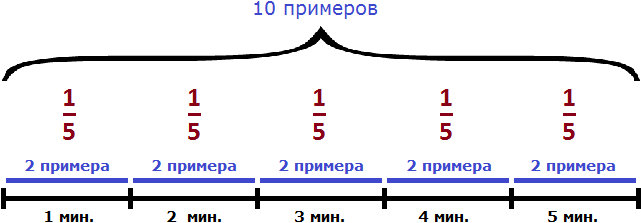
Задача 10. Джон решил 10 примеров за 5 минут. С какой производительностью он решал эти примеры?
10 примеров это выполненная Джоном работа. 5 минут — время работы. Разделим выполненную работу на время работы и определим производительность Джона:
10 : 5 = 2 примера в минуту.
Производительность Джона равна двум примерам в минуту.
Задача 11. Джон решил несколько примеров за 5 минут. С какой производительностью он решил эти примеры?
Это та же самая задача, что и предыдущая, но в ней работа не выражена каким-либо числом. Сказано лишь то, что Джон выполнил эту работу за 5 минут. Поэтому, конкретную производительность в такой задаче узнать нельзя. Но можно воспользоваться дробями. Обозначим выполненную работу через единицу. Тогда производительность работы Джона будет выражаться дробью – частью примеров, решенных за единицу времени. Если вы изучили задачи на дроби, то должны понимать о чем идёт речь.
Итак, обозначим выполненную работу через единицу:
A = 1
Мы знаем, что для нахождения производительности, выполненную работу нужно разделить на время. Время работы у нас равно пяти минутам. Поэтому, единицу делим на пять минут:
Дробь выражает часть работы, выполненную Джоном за единицу времени. Если мы вернемся к предыдущей задаче, где выполненная работа была равна десяти примерам и найдем одну пятую от этой работы, то получим 2
Выражать выполненную работу через единицу часто приходится при решении задач на совместную работу.
Задачи на совместную работу
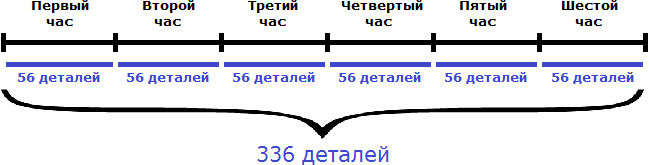
Задача 1. Первый мастер за 2 часа изготавливает 64 детали, а второй за 3 часа – 72 детали. За сколько часов они изготовят 336 деталей?
В данной задаче речь идет о совместной работе. Необходимо определить производительность обоих мастеров и найти время за которое они изготовят 336 деталей.
Для начала определим производительность первого мастера:
64 : 2 = 32 дет./час
Определим производительность второго мастера:
72 : 3 = 24 дет./час
Определим совместную производительность мастеров. Для этого сложим количество деталей, которые они изготавливают по отдельности за единицу времени. То есть сложим их производительности:
32 дет./час + 24 дет./час = 56 дет./час
Вместе за один час мастера изготавливают 56 деталей. Чтобы узнать за сколько часов они изготовят 336 деталей, нужно определить сколько раз 336 содержит по 56
336 : 56 = 6 часов
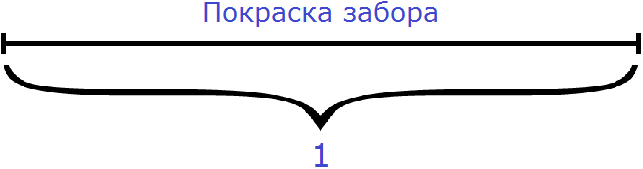
Задача 2. Первый мастер может покрасить забор за 20 минут, а второй мастер – за 30 минут. За сколько минут, работая вместе, они могут покрасить забор?
Решение
В данной задаче, в отличие от предыдущей, работа не выражена каким-либо числом. Сказано лишь то, что эту работу первый мастер может выполнить за 20 минут, а второй за 30 минут.
В такой ситуации можно воспользоваться дробями. Мы можем обозначить всю работу (покраску забора) через единицу.
Итак, обозначим работу (покраску забора) через единицу:
A = 1
Производительность первого мастера будет выражáться дробью 
. То есть за одну минуту он покрасит одну двадцатую часть забора. Единица это вся работа, а двадцать минут это время работы. Запишем производительность первого мастера с помощью формулы нахождения производительности:
А производительность второго мастера будет выражáться дробью 
. То есть за одну минуту он покрасит одну тридцатую часть забора:
Определим общую производительность мастеров. Для этого сложим дроби, выражающие производительность первого и второго мастеров:
это дробь, выражающая общую производительность обоих мастеров. То есть за одну минуту мастера вместе покрасят часть забора.
Определим время за которое мастера покрасят забор вместе. Для этого воспользуемся формулой нахождения времени: разделим выполненную работу на общую производительность мастеров. Выполненная работа у нас выражена единицей, а производительность — дробью
Ответ: работая вместе, мастера покрасят забор за 12 минут.
Задача 3. Первый рабочий может выполнить заказ за 8 часов, а второй за 6 часов. Два часа они работали вместе, а заканчивал работу один второй рабочий. Сколько времени потребовалось для выполнения этого заказа?
Решение
Обозначим всю работу через единицу
A = 1
Тогда первый рабочий за один час может выполнить 
часть работы, а второй рабочий 
часть работы. А вместе за один час они могут выполнить 
часть работы
Рабочие работали вместе два часа, поэтому умножим часть работы, выполняемую ими за один час на 2:
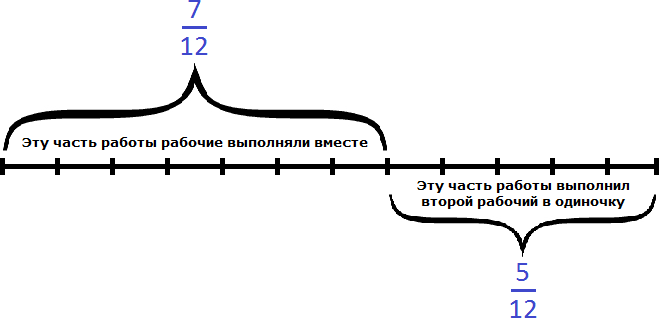
Остальную часть работы, а именно 
работы заканчивал один второй рабочий:
Второй рабочий за один час мог выполнить часть работы. Чтобы определить время за которое он завершил оставшуюся часть работы, воспользуемся формулой нахождения времени.
Переменная A теперь равна , переменная v —
Теперь определим общее время заказа. Первые два часа рабочие работали вместе, остальную часть работы второй рабочий выполнил за два с половиной часа, отсюда имеем 4,5 ч.
2 + 2,5 = 4,5 ч.
Ответ: для выполнения заказа потребовалось 4,5 ч.
Задача 4. Одна труба наполняет бассейн за 6 ч, а другая – за 4 ч. За
сколько часов наполняют бассейн обе трубы, работая вместе?
Решение
Обозначим работу (наполнение бассейна) через единицу
A = 1
Тогда первая труба за один час выполнит часть работы, а вторая труба — 
часть работы. Работая вместе за один час они выполнят 
часть работы:
Определим время за которое обе трубы наполняют бассейн, работая вместе:
2,4 это два целых часа и четыре десятых часа
2,4 = 2 ч + 0,4 ч
А четыре десятых часа это 24 минуты
60 мин. × 0,4 = 24 мин.
Ответ: работая вместе обе трубы наполнят бассейн за 2 ч 24 мин.
Задачи для самостоятельного решения
Задача 1. Первая бригада может выполнить некоторое задание за 12 часов, вторая – за 4 часа. За сколько часов они выполнят задание, если будут работать вместе?
Решение
Обозначим работу через единицу:
A = 1
Тогда первая бригада за один час выполнит часть работы, а вторая за один час часть работы. Их общая производительность равна сумме дробей и :
Определим время за которое обе бригады выполнят задание, работая вместе:
Ответ: обе бригады выполнят задание за 3 часа.
Задача 2. Лошадь съедает копну сена за 1 сутки, корова может съесть такую же копну за 3 суток, а овца за 6 суток. За какое время съедят эту копну лошадь, корова и овца вместе.
Решение
Работа в данном случае это съедание копны сена. Обозначим её через единицу:
A = 1
Тогда производительность лошади будет выражáться единицей, производительность коровы — дробью 
, производительность овцы — дробью . Их совместная производительность равна следующей сумме:
Определим время, за которое лошадь, корова и овца съедят 1 копну сена:
Ответ: лошадь, корова и овца съедят 1 копну сена за 
суток или 16 часов.
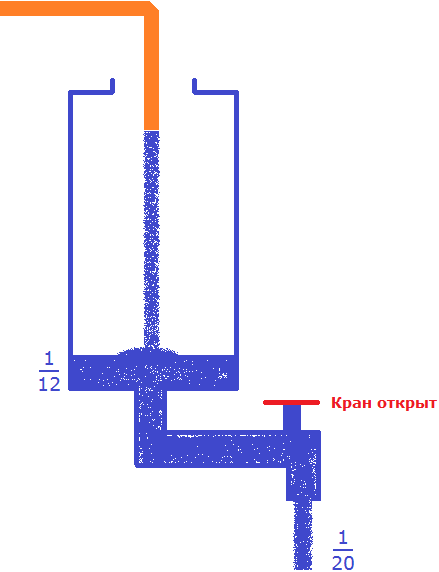
Задача 3. Сосуд наполняется шлангом за 12 мин, а полный сосуд опорожняется при открытии крана за 20 мин. За какое время наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг?
Решение
Работа в данном случае это наполнение сосуда. Обозначим эту работу через единицу:
A = 1
В условии сказано, что сосуд наполняется шлангом за 12 минут. Значит в минуту будет наполняться часть сосуда. При этом сказано, что одновременно открыт кран сосуда и из него вытекает вода, которой наполняется сосуд. Вода, которая вытекает равна части сосуда, поскольку в условии сказано, что полный сосуд опорожняется за 20 минут.
В сосуд поступает воды больше, чем вытекает. Дробь больше, чем .
Несмотря на то, что часть поступающей в сосуд воды будет вытекать, с каждой минутой сосуд будет пополняться на определенную часть. Узнаем, что эта за часть. Для этого из поступающей части вычтем ту часть, которая вытекает:
Каждую минуту сосуд будет наполняться на .
Определим время за которое наполнится пустой сосуд, если одновременно открыть кран и вливать в него воду через шланг:
Ответ: если одновременно открыть кран и вливать в пустой сосуд воду через шланг, то он наполнится за 30 минут.
Задача 4. Через первую трубу бассейн можно заполнить за 20 ч, через вторую за 30 ч. Какая часть бассейна заполнится через обе трубы за 1 ч?
Решение
Работа в данном случае это заполнение бассейна. Обозначим эту работу через единицу:
A = 1
Производительность заполнения бассейна через первую трубу будет выражáться дробью , через вторую трубу — дробью . Совместная производительность будет выражáться дробью
Производительность по определению есть работа, выполненная за единицу времени. Значит дробь является ответом к задаче, поскольку нас интересовало какая часть бассейна заполнится через обе трубы за 1 час. Это можно проверить, воспользовавшись формулой нахождения работы. Переменная v у нас имеет значение , а переменная t равна единице (одному часу). Формула нахождения работы позволит нам определить какая часть работы будет выполнена за 1 час:
Ответ: за один час заполнится часть бассейна.
Задача 5. На прокладку траншеи требуется затратить 10 ч. Экскаватор проработал 8 ч, после чего ему осталось пройти 50 м. Найти общую длину траншеи.
Решение
В задаче подразумевается, что экскаватор работал с одинаковой производительностью на протяжении всей работы. На работу требовалось затратить 10 ч. Проработано было 8 ч. Значит осталось еще 2 часа. На 2 часа приходятся оставшиеся 50 метров траншеи. Если разделить 50 метров на 2, то можно определить сколько метров экскаватор прокладывает за один час:
50 : 2 = 25 м./ч
В час экскаватор прокладывал 25 метров. Работал он 10 часов. Умножим 25 на 10, мы определим общую длину траншеи:
25 × 10 = 250 м
Ответ: общая длина траншеи составляет 250 м.
Задача 6. Ванна заполняется холодной водой за 6 мин 40 с, горячей – за 8 мин. Кроме того, если из полной ванны вынуть пробку, вода вытечет за 13 мин 20 с. Сколько времени понадобится, чтобы наполнить ванну полностью, при условии, что открыты оба крана, но ванна не заткнута пробкой?.
Решение
Для удобства переведем время данное в задаче в секунды
6 мин 40 с = 400 с
8 мин = 480 с
13 мин 20 с = 800 с
Обозначим заполнение ванны через единицу:
A = 1
Производительность первого крана будет выражáться дробью 
, производительность второго крана — дробью 
. Совместная производительность обоих кранов равна сумме дробей и
Одновременно с открытыми двумя кранами, вынута пробка из ванны. Поэтому часть поступающей в ванну воды сразу выходит через слив. Эта часть будет выражáться дробью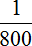 
.
С каждой секундой ванна будет пополняться на определенную часть воды. Узнаем какая это часть. Для этого из поступающей части воды вычтем ту часть, которая вытекает через слив.
Определим сколько времени понадобится, чтобы наполнить ванну:
Ванна наполнится за 300 секунд. Поскольку задача завершена, секунды можно обратно перевести в минуты. Триста секунд это пять минут:
300 : 60 = 5 мин
Ответ: ванна заполнится за 5 мин.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
2-й способ решения — без таблицы
Как обойтись без составления таблицы?
Сразу составить уравнение.
Для этого определим, какая величина нам не нужна в уравнении, чтобы затем приравнять.
Производительность? Ее и надо найти. Работа? Она нам дана по условию, поэтому глупо от нее избавляться. Остается время: оно нам и неизвестно, и не нужно.
Слева от знака равно будем писать формулу времени для первого рабочего, а справа – для второго.
Напомню, что первый работал на ( displaystyle 2) часа дольше, поэтому к времени второго надо будет прибавить ( displaystyle 2):
( displaystyle frac{112}{x}=frac{112}{x+1}+2)
То же самое уравнение, что и в первом способе, только без таблицы и системы уравнений.
А теперь вспомним, что я говорил в сааамом начале: задачи на работу и на движение – это то же самое. Спорное заявление, да? Ну, давай проверим, есть ли аналогия.
Во-первых, сравним формулы:
| Движение | Работа |
| ( displaystyle v=frac{S}{t}) | ( displaystyle P=frac{A}{t}) |
| Скорость движения | Скорость выполнения работы, т.е. производительность |
| Пройденный путь | Выполненная работа |
| Потраченное на движение время | Потраченное на работу время |
Теперь рассмотрим задачу:
Пример №1
Расстояние ( displaystyle 112) км первый велосипедист проезжает на ( displaystyle 2) часа дольше, чем второй.
Сколько км в час проезжает первый велосипедист, если известно, что второй за час проезжает на один километр больше, чем первый?
Ничего не напоминает? Да я же просто заменил слова: «Заказ» на «расстояние», «деталь» на «километр», «рабочий» на «велосипедист», «выполняет» на «проезжает». Суть осталась той же. Даже решение будет точно таким же (разберу здесь только II способ – без таблицы).
Пусть скорость первого ( displaystyle x), тогда второго ( displaystyle x+1). Сколько времени едет первый? ( displaystyle frac{112}{x}). Сколько времени едет второй? ( displaystyle frac{112}{x+1}). На сколько время первого больше, чем второго? На ( displaystyle 2) часа:
( displaystyle frac{112}{x}=frac{112}{x+1}+2).
То же самое уравнение! Вот и получается, что работа и движение – одно и то же.
Как решать задачи на совместную работу
Задачи на совместную работу отличаются от обычных, представленных выше, тем, что в них работа выполняется одновременно (совместно) несколькими рабочими (трубами и т.д.).
Пример №2
Первая труба заполняет бассейн за ( displaystyle 6) часов, а вторая – за ( displaystyle 4).
За какое время они заполнят бассейн, работая вместе?
Решение
Во-первых, давай придумаем аналогию с движением.
Придумал?
Бассейн – это путь. Допустим, из ( displaystyle A) в ( displaystyle B). Итак, первый автомобиль проезжает путь ( displaystyle AB) за ( displaystyle 6) часов, второй – за ( displaystyle 4).
А теперь как сформулировать вопрос? За какое время они проедут весь путь, двигаясь вместе? Бред.
Если двигаться параллельно, то каждый проходит весь путь самостоятельно. А в какой ситуации нам важно, какой путь автомобили проходят в сумме? Все гениальное просто: если они движутся навстречу друг другу!
Тогда что нас просят найти? Время, через которое они встретятся.
Поразмысли немного над этой аналогией. Все понял? Тогда идем дальше.
Какова «скорость» (а по-настоящему, производительность) первого? Путь (работа) деленный на время: ( displaystyle {{P}_{1}}=frac{A}{{{t}_{1}}}=frac{A}{6}). А второго? ( displaystyle {{P}_{2}}=frac{A}{{{t}_{2}}}=frac{A}{4}).
С какой производительностью работают две трубы вместе (не забывай, это задачи на совместную работу)? Берем количество литров, которое налила в бассейн первая труба за один час, прибавляем количество литров, которое налила в бассейн вторая труба за один час, – именно столько наливают в бассейн обе трубы за один час. То есть производительности складываются:
( displaystyle P={{P}_{1}}+{{P}_{2}})
То же самое, что и относительная скорость: с какой скоростью второй автомобиль приближается к первому? Со скоростью, равной сумме скоростей: ( displaystyle v={{v}_{1}}+{{v}_{2}}).
Итак,
( displaystyle P={{P}_{1}}+{{P}_{2}}=frac{A}{6}+frac{A}{4}=frac{5A}{12}).
Тогда время, за которое с такой производительностью будет выполнена работа ( A):
( displaystyle t=frac{A}{P}=frac{A}{frac{5A}{12}}=frac{12}{5}=2,4) (ч)
Итак, правило:
При совместной работе производительности складываются
А теперь давай рассмотрим самый сложный пример, научившись решать который, ты сможешь с легкостью справится с любой задачей на ЕГЭ.
Пример 8
На изготовление ( displaystyle 600) деталей первый рабочий тратит на ( displaystyle 10) часов меньше, чем второй рабочий на изготовление ( displaystyle 500) таких же деталей. За какое время, работая совместно, они изготовят партию в ( displaystyle 1000) деталей, если известно, что за час первый рабочий делает на ( displaystyle 5) деталей больше?
Решение:
Давай определимся, что нам нужно найти? Нам нужно найти время, за которое рабочие изготовят ( displaystyle 1000) деталей, то есть: ( displaystyle frac{1000}{{{P}_{1}}+{{P}_{2}}}).
Значит, нужно найти ( displaystyle {{P}_{1}}) и ( displaystyle {{P}_{2}}).
Первый рабочий за час делает на ( displaystyle 5) деталей больше. Обозначим производительность первого рабочего за х, тогда производительность второго – ( displaystyle x-5).
( displaystyle 600) деталей первый рабочий делает за ( displaystyle {{t}_{1}}) часов, а ( displaystyle 500) таких же деталей второй рабочий делает за ( displaystyle {{t}_{2}}={{t}_{1}}+10) часов.
То есть: ( displaystyle {{t}_{1}}=frac{600}{x}, a {{t}_{2}}={{t}_{1}}+10=frac{500}{x-5}).
Приравняв ( displaystyle {{t}_{1}}), получаем уравнение:
Оборудование: учебник Л.Г. Петерсон Математика. 3 класс. Часть 3, демонстрационные материалы, раздаточные материалы с задачами трех уровней, карточки с формулами, компьютерная презентация, мультимедийный проектор, экран, компьютер.
- Основные цели урока:
- Сформировать представление о величине «производительность», выявить зависимость между величинами: объемом выполненной работы (А), производительностью (V) и временем (t), сформировать способность к построению формулы работы А=v×t.
- Формировать умение находить по формуле работы v и t и использовать формулу работы для решения задач.
- Тренировать способность детей к решению задач на все изученные виды зависимости между величинами.
- Закрепить алгоритм умножения многозначного числа на трехзначное.
- Развивать самостоятельность, умения преодолевать трудности в учении, используя проблемные ситуации, разноуровневые задания, самостоятельные упражнения.
- Развивать мыслительные операции, внимание, речь, коммуникативные способности, прививать интерес к математике.
Ход урока
I. ЭМОЦИОНАЛЬНЫЙ НАСТРОЙ НА ПРЕДСТОЯЩУЮ ДЕЯТЕЛЬНОСТЬ
Долгожданный дан звонок
Начинается урок.
Постарайтесь все понять,
Учитесь тайны открывать,
Ответы полные давать,
Ни минуты не терять!
Чтоб за работу получать
Только лишь отметку «пять».
II. АКТУАЛИЗАЦИЯ ЗНАНИЙ УЧАЩИХСЯ
1. Устный счет
– Вот песочные часы, песок высыпается в нижнюю часть за 1 минуту.
– Сколько заданий вы выполните за 1 минуту. (1 ученик выполняет у доски)
- У 640-560х0=
- М 240:60х100=
- Ф 3х(180-90)-70=
- А (940-720)х4=
- Л 1000:5х4=
- Р 400:50х40=
- О (320-80)х1=
Самопроверка. Самооценивание.
Критерии выставления оценок:
- «5» – без ошибок
- «4» – 1 ошибка
- «3» – 3-4 ошибки
- «2» – 5 и более ошибок
– Что интересного заметили в ответах? (Все числа трехзначные, круглые, кратные 2,4,5,8,10).
– Расположите ответы в порядке возрастания.
| Ф | О | Р | М | У | Л | А |
| 200 | 240 | 320 | 400 | 630 | 800 | 880 |
– Что мы называем формулой? (Формулой мы называем равенство, которое помогает нам установить зависимость между величинами).
2. Повторение известных формул.
– Какие формулы вы знаете?
Учитель переворачивает на доске таблички.
– А все ли таблички открыты? (Нет).
– Что это значит? (Сегодня урок открытия новых знаний, нам предстоит открыть новые формулы)
– Будем сами открывать новые знания. Желаю вам успешной работы.
Работа в группах
Восстановите формулы. На табличке с формулами закрыта стикером величина.
1 группа
|
2 группа
|
3 группа
|
4 группа
|
Ученики крепят под названиями таблички с восстановленными формулами.
Проверка. (Чтобы найти …, надо …)
– По какому правилу можно получить 2 последние формулы? (По правилу нахождения неизвестного множителя).
– Для чего вам нужны формулы? (Для решения задач).
– Как вы думаете, какое теперь задание я вам предложу? (Решение задач).
3. Решение задач
На листочках даны задачи трех уровней каждому ученику.
– Прочитать задания, выбрать уровень сложности, записать только решение.
1 уровень
|
2 уровень
|
3 уровень
|
Самопроверка.
Сравните свое решение с правильным (слайд 1).
1 уровень
|
2 уровень
|
3 уровень
|
– Если вы решали задания 1 уровня, и все решили без ошибок, запишите себе три балла. Задания 2 уровня соответствуют 4 баллам. 5 баллов ставит себе тот, кто решил задания 3 уровня и не допустил ни одной ошибки.
– Что общего в задачах, которые вы решали? (Задачи на движение).
– Какой формулой вы воспользовались, когда решали задачи? (Формулой пути).
– Как найти путь? (S=v×t)
– Как из этой формулы можно получить ещё две? (Находим неизвестный множитель: V= s÷t; t=s÷t).
III. ПОСТАНОВКА ПРОБЛЕМЫ
– А сейчас я вам предложу «вкусную задачу». Мама одной ученицы приготовила для вас эту задачу. Видеоролик включается (слайд 2): «На масленицу я вам напекла гору вкусных блинов. Я их выпекала в несколько приемов. В начале, я выпекала 3 блина в минуту. Сколько блинов приготовила я, работая 20 минут».
– Подберите формулу к задаче.
– Чем эта задача отличается от тех, которые мы решали. (Задачи были с известными величинами: стороны и площадь; время, скорость и путь; стоимость, количество и цена. А в этой задаче не все величины знакомы, знаем только время).
– Почему возникли затруднения? (Новые величины, нет формул).
IV. ОТКРЫТИЕ ДЕТЬМИ НОВОГО ЗНАНИЯ
Как же назвать эту формулу?
– Что нужно найти в задаче? (Сколько всего блинов испекла мама, т.е. её работу).
Эта формула называется «ФОРМУЛА РАБОТЫ».
– О каких величинах ещё идет речь? (Выпекала 3 блина в минуту, т.е. скорость работы).
– Скорость работы называют «ПРОИЗВОДИТЕЛЬНОСТЬЮ». Обозначим эту величину буквой «V».
– Что еще известно в задаче? (Время работы).
– О какой величине идет речь? (О времени).
– Какой буквой обозначается эта величина? («t»).
– Запишите в таблицу величины.
– Что нужно узнать в задаче? (Количество всех блинов, т.е. какую работу выполнила мама)
– Как найти количество блинов, которые испекла мама за 20 минут, если известно, что за 1 минуту мама выпекает 3 блина. (Надо 3 блина умножить на 20 минут: 3×20=60 блинов испекла мама).
– Записать в тетрадь решение.
– Какую величину находим? (Работу).
– Как находили? (Производительность работы умножили на время).
– Запишите формулу зависимости этих величин.
– Все ли формулы открыты? (Нет).
– Чтобы их открыть, нужно отдохнуть.
Физпауза
– Выведите две другие формулы.
– По какому правилу можно получить? (По правилу нахождения неизвестного множителя)
– Какую величину будете находить? (Время)
– Чтобы найти время нужно работу разделить на производительность труда.
– Запишите эту формулу в тетради и на доске.
– Какая величина еще неизвестна? (Производительность труда)
– А что такое производительность труда? (Это работа, выполненная за единицу времени).
– Как найти производительность?
– Все ли формулы открыты? (Да)
– Как можно проверить правильность ваших выводов? (Можно посмотреть в учебнике). Работа с учебником (с.43).
– Сравните выведенные вами формулы.
– Прочтите формулировки.
– Как найти работу?
– Время работы?
– Как называется работа, выполненная за единицу времени? (Производительность труда).
– А теперь мы вернемся к практической работе, которую выполняли в начале урока. Сколько заданий вы выполнили за одну минуту? Это наша производительность.
– Одинаковым ли было количество заданий у каждого из вас? (Нет, одни выполнили больше заданий, другие – меньше).
– Что можно сказать о производительности труда наших учеников? (Она разная. Это зависело от того, кто сразу начал работу, кто отвлекался, кто хорошо знает таблицу умножения,..).
А если бы вы решали 10 минут, сколько всего таких заданий вы бы выполнили? Какие задачи теперь сможете решать (Задачи на работу).
V. ПЕРВИЧНОЕ ЗАКРЕПЛЕНИЕ ВО ВНЕШНЕЙ РЕЧИ
– Откройте учебник на стр. 44, №1.
– Какое задание надо выполнить? (Объяснить смысл предложений)
а) Вася каждый час съедает 3 мороженых. А сколько мороженых Вася съест за 2 часа? (3×2=6 мороженых)
– Какую величину находили? (Работу).
б) Оля за одну минуту лепит 2 штуки пельменей. Дополните условие и поставьте вопрос к задаче.
№2. Какое задание будете выполнять? (Решать задачу).
– Прочтите задачу.
– Анализ задачи. Один из учащихся анализирует условие задачи.
– Какие величины известны? Что надо найти?
– Как ответить на вопрос задачи?
| t ч | 2 | 4 | 6 | 7 | 9 | t |
| А дет |
- V= 8 дет/ч
- A= V×t
– Найдите работу, выполненную мастером за 6 часов, 7 часов. (Учащиеся работают в парах)
– Найдите работу за 9 часов и за время t самостоятельно.
Заполненная таблица вывешивается на доску.
| t ч | 2 | 4 | 6 | 7 | 9 | t |
| А дет | 16 | 32 | 48 | 56 | 72 | 8×t |
- V= 8 дет/ч
- A= 8×t
VI. САМОСТОЯТЕЛЬНАЯ РАБОТА С САМОПРОВЕРКОЙ ПО ЭТАЛОНУ
По данным таблицы составьте задачи и решите их.
1 вариант – с.44, №4а; 2 вариант – с.44, № 4б.
Проверьте по эталону (слайд 3)?
– Какой формулой пользовались? Как решали? Правильность оцените с помощью знаков «+» или «-». У кого все верно? Молодцы!
VII. ВКЛЮЧЕНИЕ В СИСТЕМУ ЗНАНИЙ И ПОВТОРЕНИЕ
Где сможем применить полученное знание? (При решении задач)
№5, стр. 44. Двое учащихся работают на закрытой части доски, остальные – в тетрадях. Фронтально проводится проверка правильности выполнения задания.
– Чем пользовались? (Алгоритм решения задач, формулой работы, алгоритмом умножения многозначных чисел).
– Кто допустил ошибки? Проанализируйте их. Запишите ответ задачи. Можно ли по этой записи определить число автомобилей, которые выпускает завод:
- за 5 дней (1040 м)
- за 6 дней (1248 м)
- за 60 дней (12480 м)
- за 300 дней (62400 м).
– Можно ли, не вычисляя, сказать, на сколько второе произведение больше первого? (208×365 < 208×366 на 208).
VII. РЕФЛЕКСИЯ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ НА УРОКЕ
– Какие цели ставили на уроке? (Установить, какие величины описывают процесс выполнения работы, ввести обозначения этих величин и установить взаимосвязь между ними, т.е. построить формулу работы).
– Что явилось итогом работы? (Формулы).
– Достигли вы этой цели? Докажите.
– Заполните эталон. (слайд 4)
Формула…….(работы)
…(Производительность) – это работа, выполненная за единицу времени.
– Если затрудняетесь, где можно найти ответ? (В учебнике).
– Вы сами сделали открытие и ряд изученных формул пополнился.
Проанализируйте свою работу. (Внимательно слушал, смотрел, сделал открытие, все получилось – доволен собой/ не доволен).
Оцените свою работу на полях тетради – нарисуйте лицо человечка.
– Благодарю вас за активную работу на уроке.
Урок я хочу закончить пословицей о труде.
Всегда помните: «Всякое умение трудом дается».
VIII. ДОМАШНЕЕ ЗАДАНИЕ
Презентация (слайд 5).
- На слайде представлены данные о ежегодном выпуске автомобилей на российских заводах. Почему заводы выпускают разное количество машин? От чего это зависит? (От опыта работы, возраста, модернизации, от производительности труда, оборудования). Придумайте задачи на нахождение производительности, времени, работы, используя данные из таблицы.
- Найти пословицы и поговорки о работе.
- Решить №6, стр. 45.
