Как найти формулу зависимости функции

Как найти формулу зависимости функции

Как найти k и b по графику линейной функции?

В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции , т.е. найти (k) и (b) по графику. Примеры таких заданий (решения будут внизу статьи):

В статье я расскажу про два простых способа найти (k) и (b), если известен график линейной функции.

Способ 1

Первый способ основывается на трех фактах:

Линейная функция пересекает ось (y) в точке (b).
Примеры:

Но не советую определять так (b), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.

Если функция возрастает, то знак коэффициента (k) плюс, если убывает – минус, а если постоянна, то (k=0).

Чтоб конкретнее определить (k) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить (k) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.

(b=3) – это сразу видно. Функция идет вниз, значит (k 0). (k=+frac=frac<4><4>=1,b=1). (f(x)=x+1).

Теперь перейдем к функции (g(x)). Найдем координаты точек (D) и (E): (D(-2;4)), (E(-4;1)). Можно составить систему:

Вычтем второе уравнение из первого, чтоб убрать (b):

(g(x)=1,5x+7). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем (f(x)) и (g(x)).

Картинку в хорошем качестве, можно скачать нажав на кнопку “скачать статью”.

График линейной функции, его свойства и формулы

О чем эта статья:

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:

Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Графический способ — наглядно. Его мы и разберем в этой статье.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х – 2. Значит:

если х = 0, то у = -2;

если х = 2, то у = -1;

если х = 4, то у = 0 и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.

Функция Коэффициент k Коэффициент b
y = 2x + 8 k = 2 b = 8
y = −x + 3 k = −1 b = 3
y = 1/8x − 1 k = 1/8 b = −1
y = 0,2x k = 0,2 b = 0

Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.

Свойства линейной функции

Область определения функции — множество всех действительных чисел.

Множеством значений функции является множество всех действительных чисел.

График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.

Функция не имеет ни наибольшего, ни наименьшего значений.

Четность и нечетность линейной функции зависят от значений коэффициентов k и b:

b ≠ 0, k = 0, значит, y = b — четная;

b = 0, k ≠ 0, значит, y = kx — нечетная;

b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;

b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.

Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.

График функции пересекает оси координат:

ось абсцисс ОХ — в точке (−b/k; 0);

ось ординат OY — в точке (0; b).

x = −b/k — является нулем функции.

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;

если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;

если b 0, то график функции y = kx + b выглядит так:

0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png” style=”height: 600px;”>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png” style=”height: 600px;”>

Если k > 0 и b

В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.

Условие перпендикулярности двух прямых:

График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.

Координаты точки пересечения с осью OY: (0; b).

С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.

Координаты точки пересечения с осью OX: (−b/k; 0).

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:

Таким образом, нам надо построить график функции y = -4x – 10

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.

Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k = 3.

Подставим значение k в первое уравнение системы, и получим b = -2.

Ответ: уравнение прямой y = 3x – 2.

Построение графика зависимости в Microsoft Excel

Одной из типичных математических задач является построение графика зависимости. В нем отображается зависимость функции от изменения аргумента. На бумаге выполнить данную процедуру не всегда просто. Но инструменты Excel, если в должной мере овладеть ими, позволяют выполнить данную задачу точно и относительно быстро. Давайте выясним, как это можно сделать, используя различные исходные данные.

Процедура создания графика

Зависимость функции от аргумента является типичной алгебраической зависимостью. Чаще всего аргумент и значение функции принято отображать символами: соответственно «x» и «y». Нередко нужно произвести графическое отображение зависимости аргумента и функции, которые записаны в таблицу, или представлены в составе формулы. Давайте разберем конкретные примеры построения подобного графика (диаграммы) при различных заданных условиях.

Способ 1: создание графика зависимости на основе данных таблицы

Прежде всего, разберем, как создать график зависимости на основе данных, предварительно внесенных в табличный массив. Используем таблицу зависимости пройденного пути (y) от времени (x).

    Выделяем таблицу и переходим во вкладку «Вставка». Кликаем по кнопке «График», которая имеет локализацию в группе «Диаграммы» на ленте. Открывается выбор различных типов графиков. Для наших целей выбираем самый простой. Он располагается первым в перечне. Клацаем по нему.

Программа производит построение диаграммы. Но, как видим, на области построения отображается две линии, в то время, как нам нужна только одна: отображающая зависимость пути от времени. Поэтому выделяем кликом левой кнопки мыши синюю линию («Время»), так как она не соответствует поставленной задаче, и щелкаем по клавише Delete.

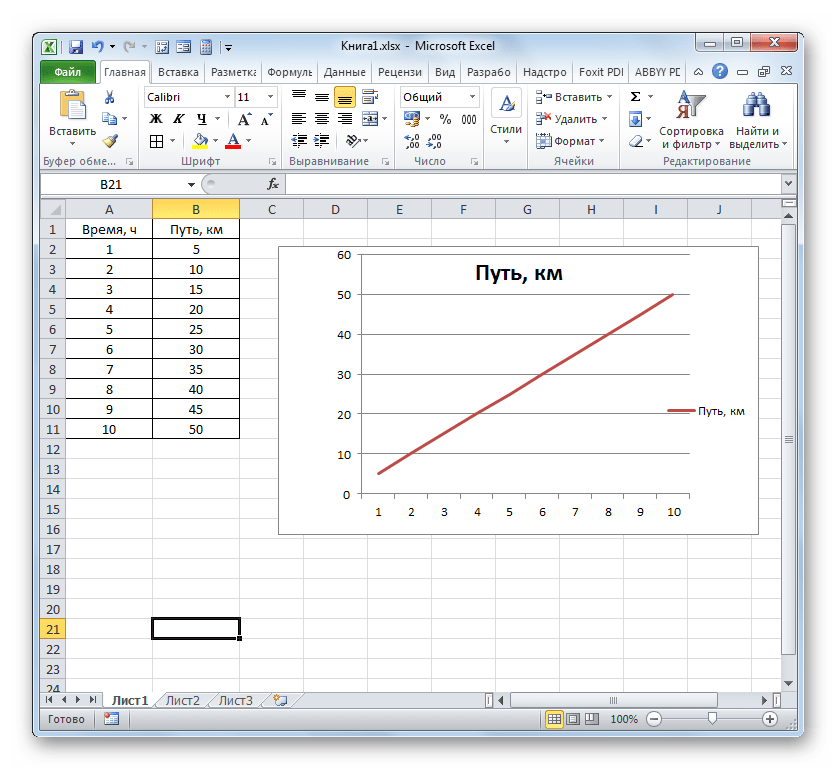
Собственно на этом построение простейшего графика зависимости можно считать завершенным. При желании также можно отредактировать наименования диаграммы, её осей, удалить легенду и произвести некоторые другие изменения. Об этом подробнее рассказывается в отдельном уроке.

Способ 2: создание графика зависимости с несколькими линиями

Более сложный вариант построения графика зависимости представляет собой случай, когда одному аргументу соответствуют сразу две функции. В этом случае потребуется построить две линии. Для примера возьмем таблицу, в которой по годам расписана общая выручка предприятия и его чистая прибыль.

  1. Выделяем всю таблицу вместе с шапкой.

Как и в предыдущем случае, жмем на кнопку «График» в разделе диаграмм. Опять выбираем самый первый вариант, представленный в открывшемся списке.

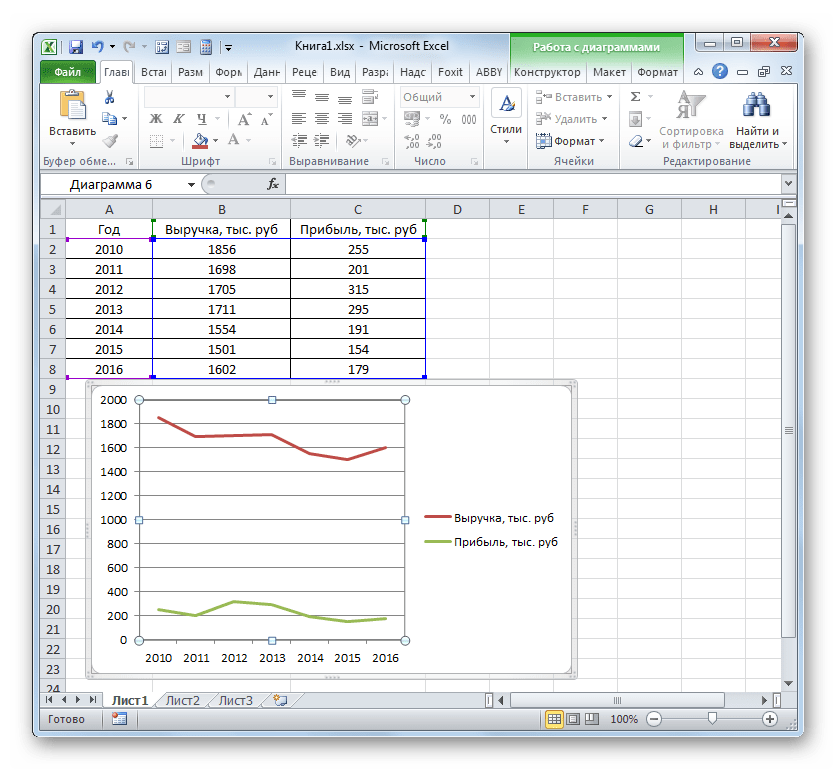
Программа производит графическое построение согласно полученным данным. Но, как видим, в данном случае у нас имеется не только лишняя третья линия, но ещё и обозначения на горизонтальной оси координат не соответствуют тем, которые требуются, а именно порядку годов.

Сразу удалим лишнюю линию. Ею является единственная прямая на данной диаграмме — «Год». Как и в предыдущем способе, выделяем линию кликом по ней мышкой и жмем на кнопку Delete.

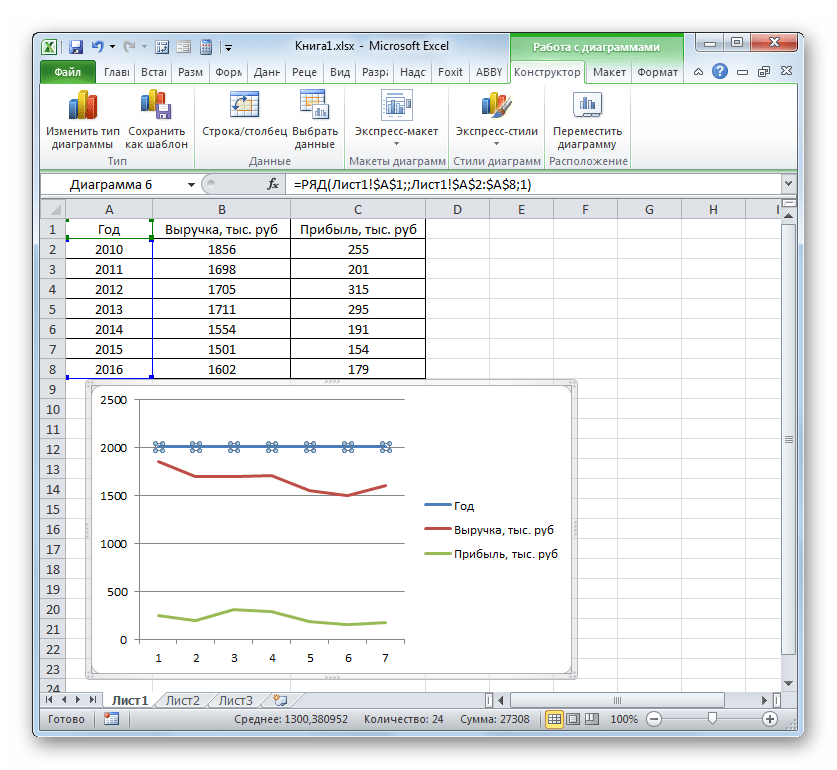
Линия удалена и вместе с ней, как вы можете заметить, преобразовались значения на вертикальной панели координат. Они стали более точными. Но проблема с неправильным отображением горизонтальной оси координат все-таки остается. Для решения данной проблемы кликаем по области построения правой кнопкой мыши. В меню следует остановить выбор на позиции «Выбрать данные…».

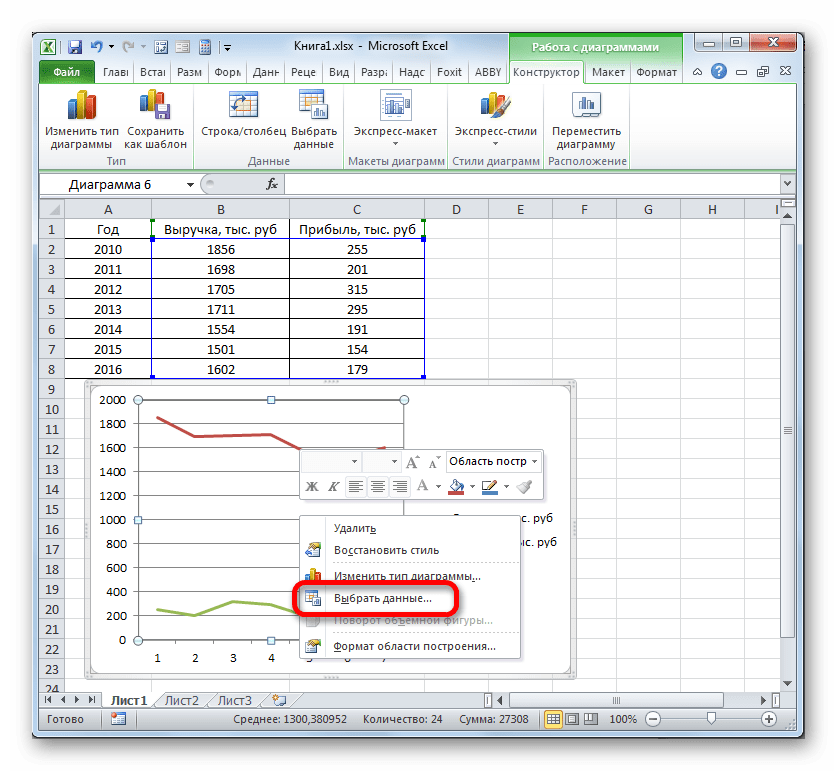
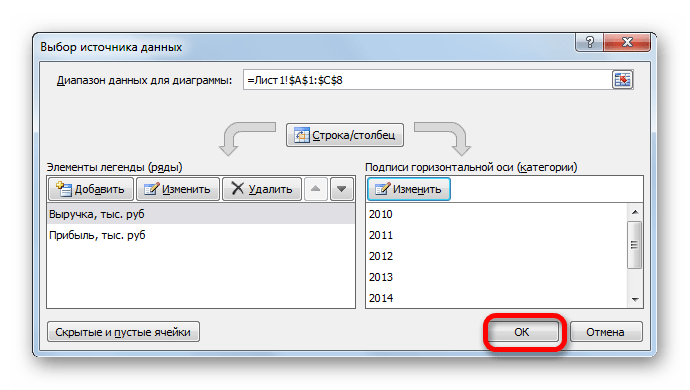
Открывается окошко выбора источника. В блоке «Подписи горизонтальной оси» кликаем по кнопке «Изменить».

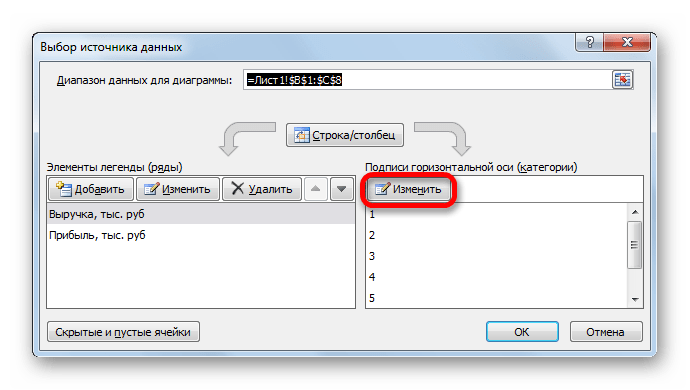
Открывается окошко ещё меньше предыдущего. В нём нужно указать координаты в таблице тех значений, которые должны отображаться на оси. С этой целью устанавливаем курсор в единственное поле данного окна. Затем зажимаем левую кнопку мыши и выделяем всё содержимое столбца «Год», кроме его наименования. Адрес тотчас отразится в поле, жмем «OK».

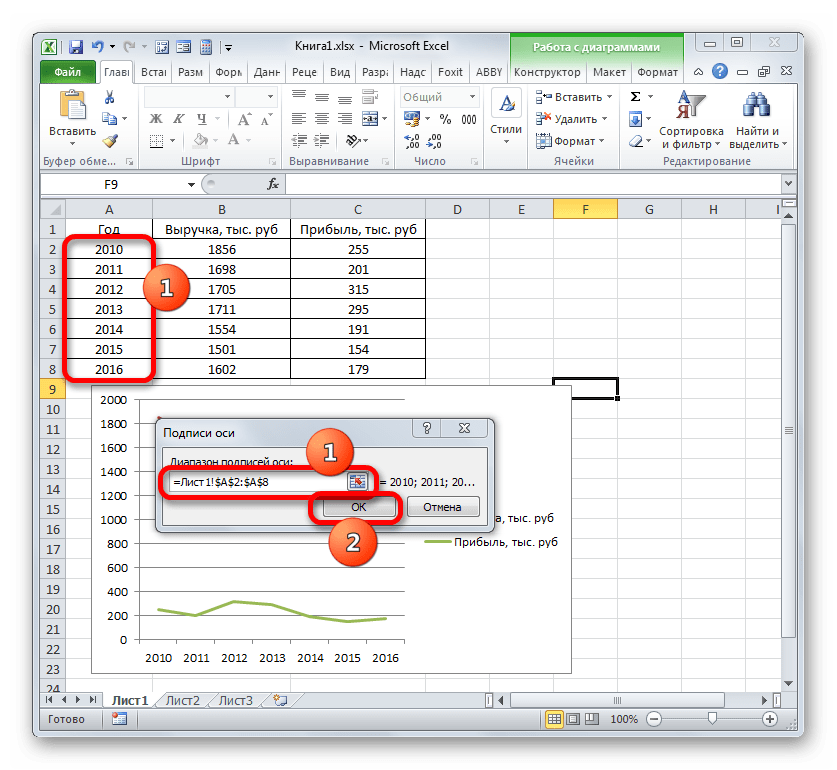
Вернувшись в окно выбора источника данных, тоже щелкаем «OK».

  • После этого оба графика, размещенные на листе, отображаются корректно.

    • Способ 3: построение графика при использовании различных единиц измерения

    В предыдущем способе мы рассмотрели построение диаграммы с несколькими линиями на одной плоскости, но при этом все функции имели одинаковые единицы измерения (тыс. руб.). Что же делать, если нужно создать графики зависимости на основе одной таблицы, у которых единицы измерения функции отличаются? В Экселе существует выход и из этого положения.

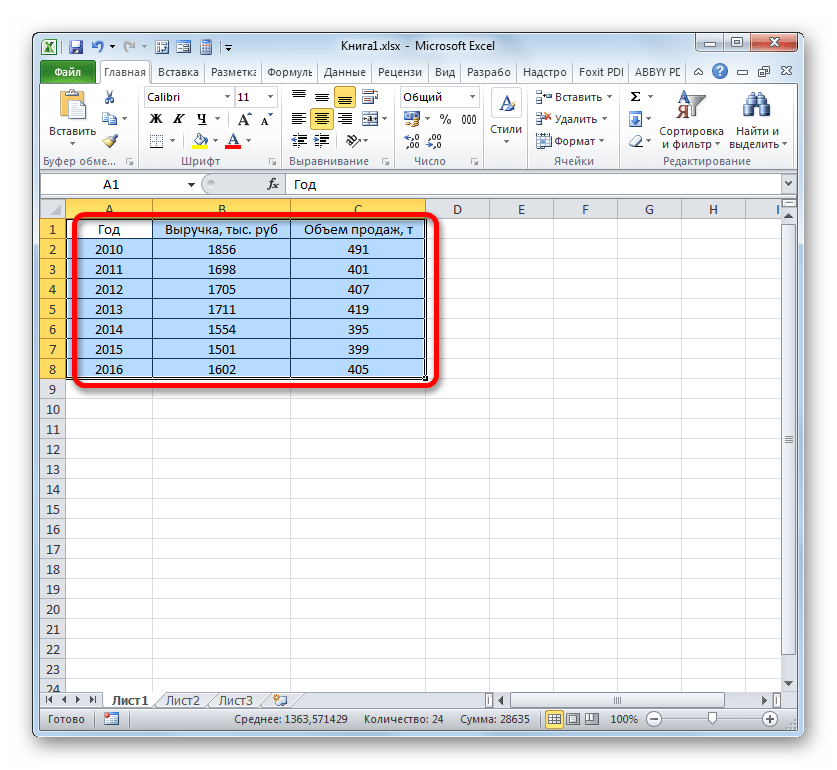
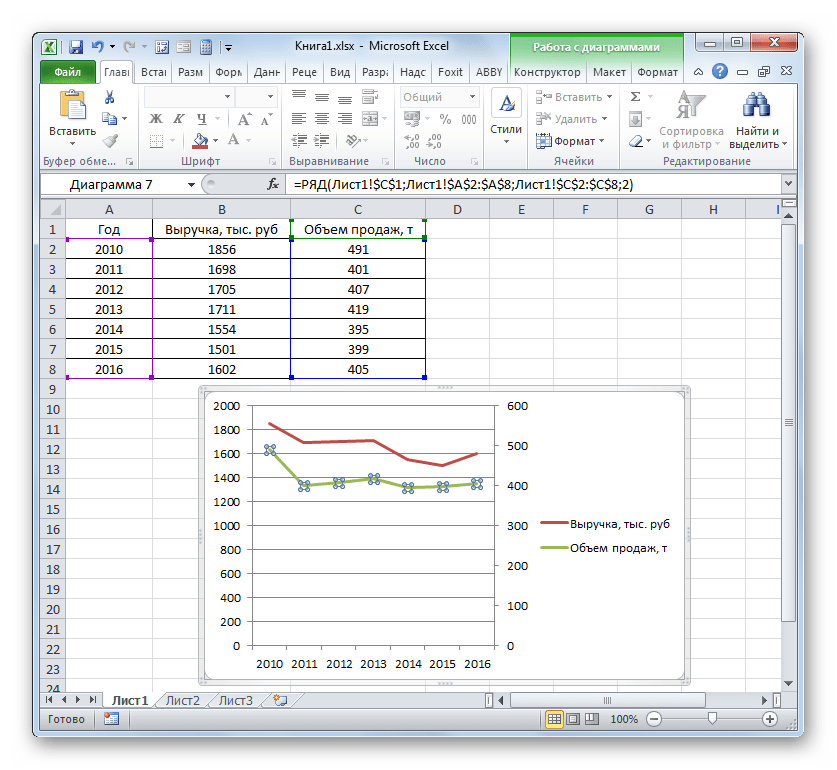
    Имеем таблицу, в которой представлены данные по объему продаж определенного товара в тоннах и по выручке от его реализации в тысячах рублей.

      Как и в предыдущих случаях выделяем все данные табличного массива вместе с шапкой.

    Клацаем по кнопке «График». Снова выбираем первый вариант построения из перечня.

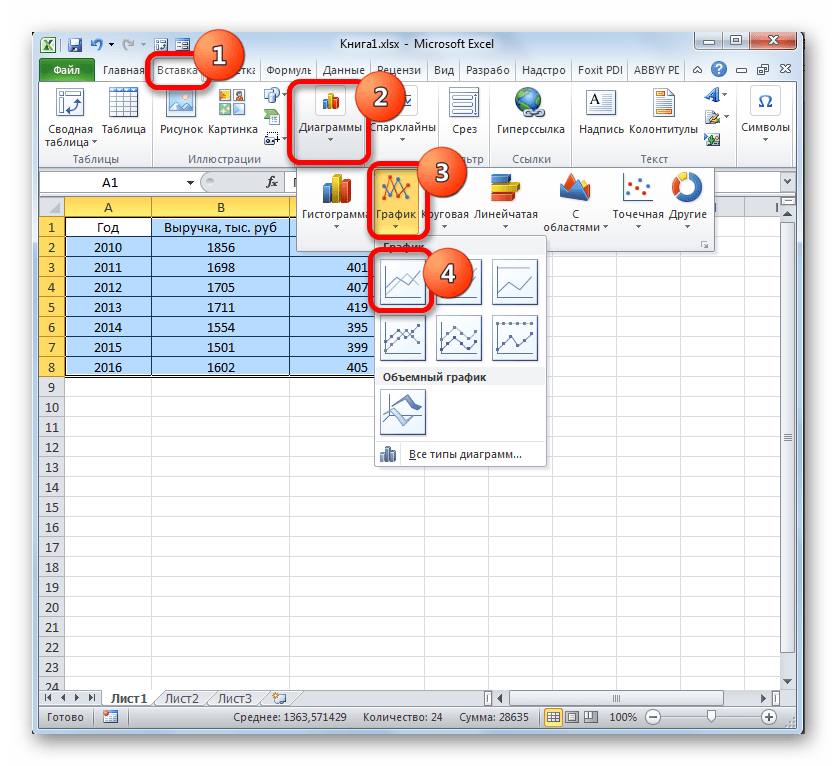
    Набор графических элементов сформирован на области построения. Тем же способом, который был описан в предыдущих вариантах, убираем лишнюю линию «Год».

    Как и в предыдущем способе, нам следует на горизонтальной панели координат отобразить года. Кликаем по области построения и в списке действий выбираем вариант «Выбрать данные…».

    В новом окне совершаем щелчок по кнопке «Изменить» в блоке «Подписи» горизонтальной оси.

    В следующем окне, производя те же действия, которые были подробно описаны в предыдущем способе, вносим координаты столбца «Год» в область «Диапазон подписей оси». Щелкаем по «OK».

    При возврате в предыдущее окно также выполняем щелчок по кнопке «OK».

    В нашем случае для обозначения выручки оставим ту вертикальную ось, которая уже имеется, а для линии «Объём продаж» создадим вспомогательную. Клацаем по данной линии правой кнопкой мышки и выбираем из перечня вариант «Формат ряда данных…».

    Запускается окно формата ряда данных. Нам нужно переместиться в раздел «Параметры ряда», если оно было открыто в другом разделе. В правой части окна расположен блок «Построить ряд». Требуется установить переключатель в позицию «По вспомогательной оси». Клацаем по наименованию «Закрыть».

  • После этого вспомогательная вертикальная ось будет построена, а линия «Объём продаж» переориентируется на её координаты. Таким образом, работа над поставленной задачей успешно окончена.

    • Способ 4: создание графика зависимости на основе алгебраической функции

    Теперь давайте рассмотрим вариант построения графика зависимости, который будет задан алгебраической функцией.

    У нас имеется следующая функция: y=3x^2+2x-15. На её основе следует построить график зависимости значений y от x.

      Прежде, чем приступить к построению диаграммы, нам нужно будет составить таблицу на основе указанной функции. Значения аргумента (x) в нашей таблице будут указаны в диапазоне от -15 до +30 с шагом 3. Чтобы ускорить процедуру введения данных, прибегнем к использованию инструмента автозаполнения «Прогрессия».

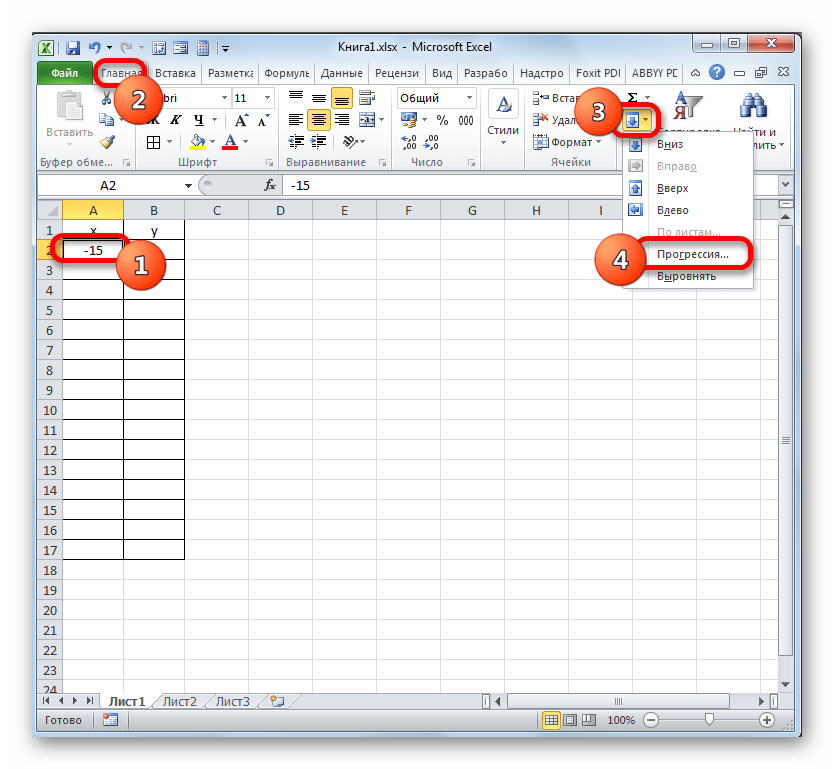
    Указываем в первой ячейке столбца «X» значение «-15» и выделяем её. Во вкладке «Главная» клацаем по кнопке «Заполнить», размещенной в блоке «Редактирование». В списке выбираем вариант «Прогрессия…».

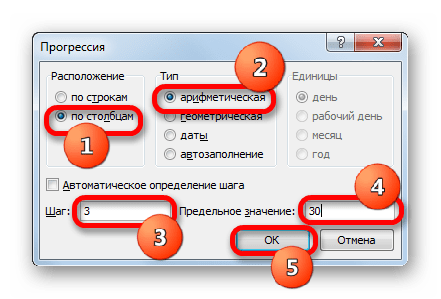
    Выполняется активация окна «Прогрессия». В блоке «Расположение» отмечаем наименование «По столбцам», так как нам необходимо заполнить именно столбец. В группе «Тип» оставляем значение «Арифметическая», которое установлено по умолчанию. В области «Шаг» следует установить значение «3». В области «Предельное значение» ставим цифру «30». Выполняем щелчок по «OK».

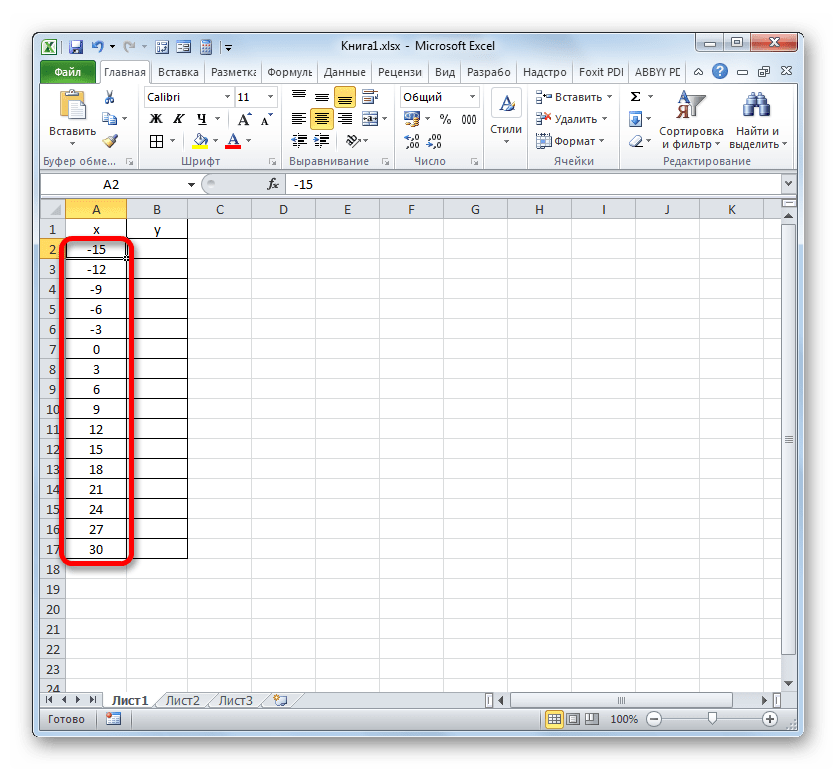
    После выполнения данного алгоритма действий весь столбец «X» будет заполнен значениями в соответствии с заданной схемой.

    Теперь нам нужно задать значения Y, которые бы соответствовали определенным значениям X. Итак, напомним, что мы имеем формулу y=3x^2+2x-15. Нужно её преобразовать в формулу Excel, в которой значения X будут заменены ссылками на ячейки таблицы, содержащие соответствующие аргументы.

    Выделяем первую ячейку в столбце «Y». Учитывая, что в нашем случае адрес первого аргумента X представлен координатами A2, то вместо представленной выше формулы получаем такое выражение:

    Записываем это выражение в первую ячейку столбца «Y». Для получения результата расчета щелкаем по клавише Enter.

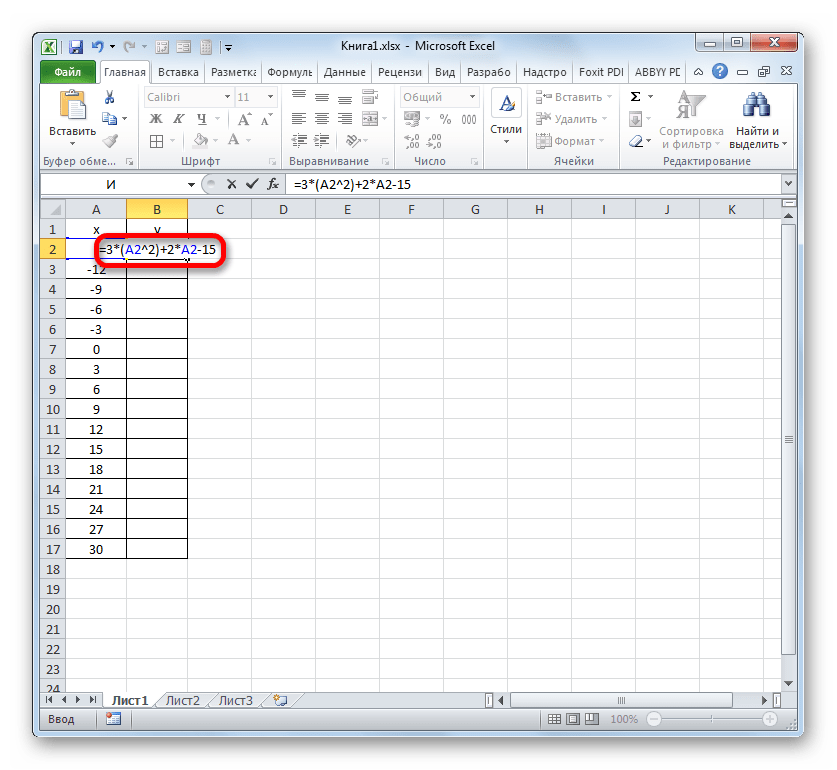
    Результат функции для первого аргумента формулы рассчитан. Но нам нужно рассчитать её значения и для других аргументов таблицы. Вводить формулу для каждого значения Y очень долгое и утомительное занятие. Намного быстрее и проще её скопировать. Эту задачу можно решить с помощью маркера заполнения и благодаря такому свойству ссылок в Excel, как их относительность. При копировании формулы на другие диапазоны Y значения X в формуле будут автоматически изменяться относительно своих первичных координат.

    Наводим курсор на нижний правый край элемента, в который ранее была записана формула. При этом с курсором должно произойти преображение. Он станет черным крестиком, который носит наименование маркера заполнения. Зажимаем левую кнопку мыши и тащим этот маркер до нижних границ таблицы в столбце «Y».

    Вышеуказанное действие привело к тому, что столбец «Y» был полностью заполнен результатами расчета формулы y=3x^2+2x-15.

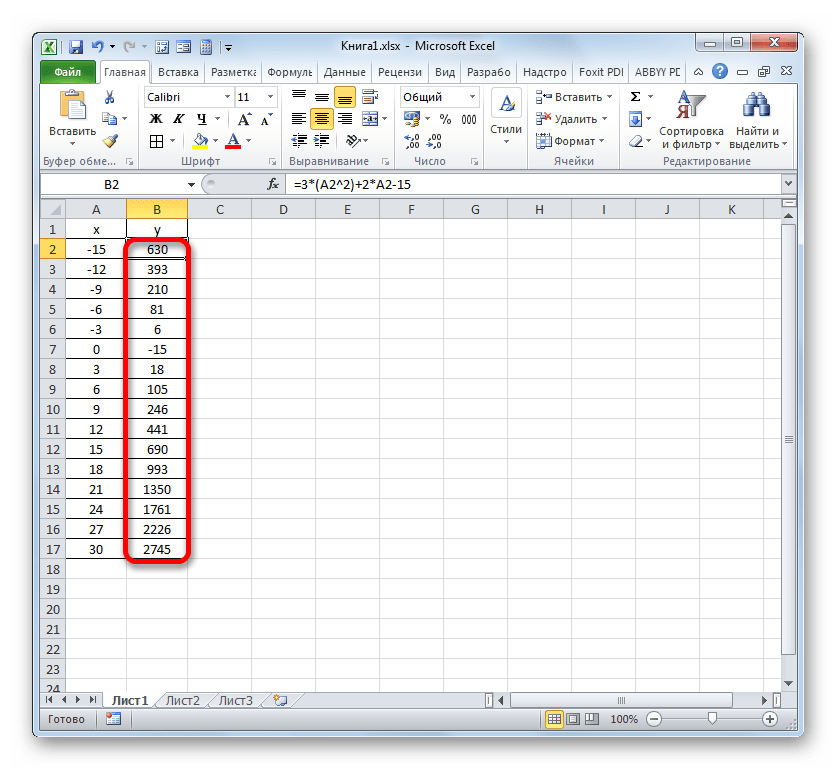
    Теперь настало время для построения непосредственно самой диаграммы. Выделяем все табличные данные. Снова во вкладке «Вставка» жмем на кнопку «График» группы «Диаграммы». В этом случае давайте из перечня вариантов выберем «График с маркерами».

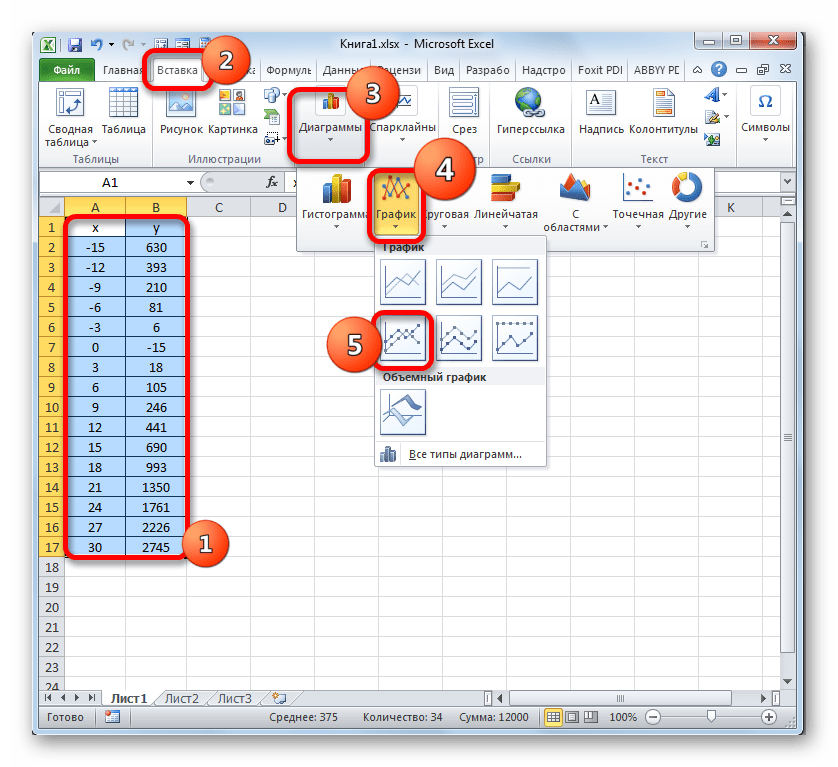
    Диаграмма с маркерами отобразится на области построения. Но, как и в предшествующих случаях, нам потребуется произвести некоторые изменения для того, чтобы она приобрела корректный вид.

    Прежде всего, удалим линию «X», которая разместилась горизонтально на отметке 0 координат. Выделяем данный объект и жмем на кнопку Delete.

    Легенда нам тоже не нужна, так как мы имеем только одну линию («Y»). Поэтому выделяем легенду и снова жмем по клавише Delete.

    Теперь нам нужно значения в горизонтальной панели координат заменить на те, которые соответствуют столбцу «X» в таблице.

    Кликом правой кнопки мыши выделяем линию диаграммы. В меню перемещаемся по значению «Выбрать данные…».

    В активировавшемся окне выбора источника клацаем по уже хорошо знакомой нам кнопке «Изменить», располагающейся в блоке «Подписи горизонтальной оси».

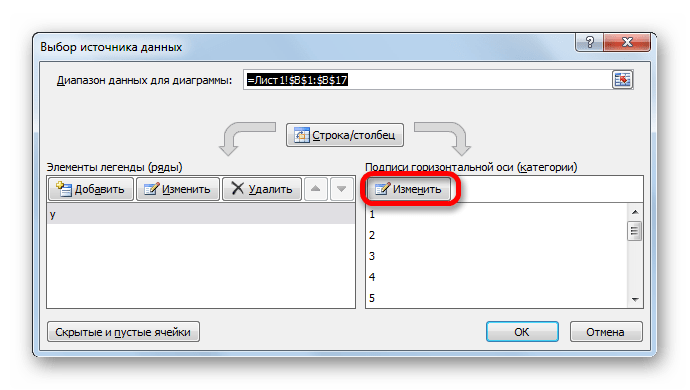
    Запускается окошко «Подписи оси». В области «Диапазон подписей оси» указываем координаты массива с данными столбца «X». Ставим курсор в полость поля, а затем, произведя необходимый зажим левой кнопки мыши, выделяем все значения соответствующего столбца таблицы, исключая лишь его наименование. Как только координаты отобразятся в поле, клацаем по наименованию «OK».

    Вернувшись к окну выбора источника данных, клацаем по кнопке «OK» в нём, как до этого сделали в предыдущем окне.

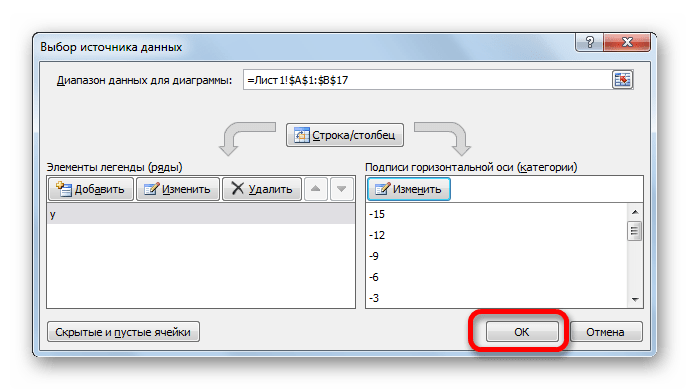
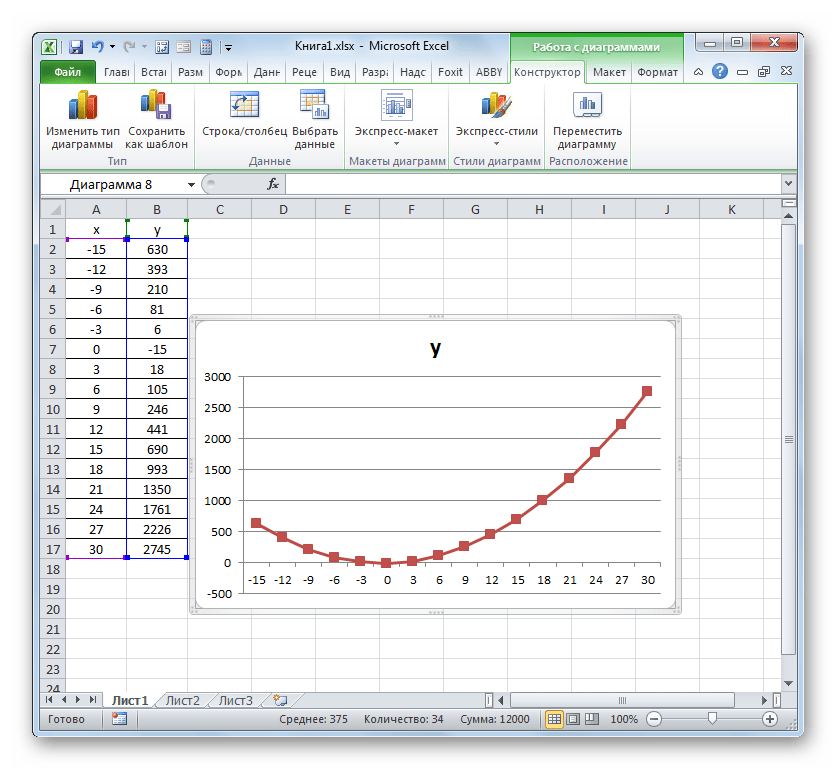
  • После этого программа произведет редактирование ранее построенной диаграммы согласно тем изменениям, которые были произведены в настройках. График зависимости на основе алгебраической функции можно считать окончательно готовым.

    • Как видим, с помощью программы Excel процедура построения графика зависимости значительно упрощается в сравнении с созданием его на бумаге. Результат построения можно использовать как для обучающих работ, так и непосредственно в практических целей. Конкретный вариант построения зависит от того, на основе чего строится диаграмма: табличные значения или функция. Во втором случае перед построением диаграммы придется ещё создавать таблицу с аргументами и значениями функций. Кроме того, график может быть построен, как на основе одной функции, так и нескольких.

    Помимо этой статьи, на сайте еще 12686 инструкций.
    Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

    Отблагодарите автора, поделитесь статьей в социальных сетях.

    [spoiler title=”источники:”]

    http://skysmart.ru/articles/mathematic/grafik-linejnoj-funkcii

    http://lumpics.ru/how-build-relationship-chart-in-excel/

    [/spoiler]

    Источник

    Содержание

    1. Что такое прямая зависимость
    2. Содержание статьи
    3. Прямая зависимость
    4. Примеры прямой зависимости
    5. Что такое Функция?
    6. Понятие функции
    7. Функция. Аргумент. Прямая и обратная зависимость
    8. Содержание
    9. Аргумент и функция
    10. Примеры аргумента и функции
    11. Запись функции
    12. Прямая и обратная пропорциональность
    13. Основные определения
    14. Прямо пропорциональные величины
    15. Обратно пропорциональные величины
    16. Свойства функции обратной пропорциональности:
    17. Потренируемся
    18. Функции

    Что такое прямая зависимость

    Содержание статьи

    1 540d27479b6dc540d27479b71a

    Прямая зависимость

    Как и многие другие виды зависимостей, прямая зависимость в математике может быть выражена формулой, отражающей характер взаимосвязи между ее компонентами. Так, формула, соответствующая прямой зависимости, обыкновенно имеет вид y = kx. В указанном соотношении y представляет собой функцию, то есть зависимую переменную, определяемую значениями других компонентов, входящих в состав формулы. x в данном случае выполняет роль аргумента, то есть независимой переменной, значение которой определяет значение зависимой переменной, то есть функции.

    При этом обе этих переменных, как зависимая, так и независимая, имеют свойство изменять свое значение. При этом третий компонент формулы, коэффициент k, представляет собой определенное число, которое в данной формуле является постоянным и не изменяется. Таким образом, формула прямой зависимости может, например, иметь вид y = 5x. При этом стандартный вид формулы, отражающей прямую зависимость, предполагает, что в качестве коэффициента используются положительные числа, а ноль и отрицательные числа не могут выступать в качестве таких коэффициентов.

    Примеры прямой зависимости

    Таким образом, содержательно наличие прямой зависимости между двумя переменными означает, что увеличение независимой переменной обязательно вызовет увеличение зависимой переменной, причем размер этого увеличения будет определяться коэффициентом k. Так, в приведенном выше примере увеличение x на единицу приведет к увеличению y на 5, поскольку коэффициент k = 5.

    Источник

    Что такое Функция?

    5fd391250ab9d005138771

    7 класс, 11 класс, ЕГЭ/ОГЭ

    Статья находится на проверке у методистов Skysmart.
    Если вы заметили ошибку, сообщите об этом в онлайн-чат
    (в правом нижнем углу экрана).

    Понятие функции

    Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

    1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

    Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

    Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

    2. Функция — это определенное действие над переменной.

    Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

    В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

    5fd3915cab3d6391169475

    В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

    3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

    Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

    Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

    Например, для функции вида

    5fd391bcaca36035546399

    область определения выглядит так:

    И записать это можно так: D (y): х ≠ 0.

    Область значений — множество у, то есть это значения, которые может принимать функция.

    Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

    Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

    В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

    Источник

    Функция. Аргумент. Прямая и обратная зависимость

    Содержание

    Вокруг нас происходит множество событий или процессов, которые можно измерить. При этом величина одних зависит от величины каких-либо других.

    Так, например, от того, сколько мы испишем страниц в тетради, зависит количество оставшихся в стержне чернил. Чем больше кружек наполнено компотом, тем меньше его останется в кастрюле. Чем больше мама оставит денег на обеды, тем больше можно на них купить мороженого. А чем сильнее велосипедист крутит педали, тем больше километров он проедет. Придумайте свои примеры?

    В наших описанных выше примерах первые два имеют обратную зависимость, то есть при увеличении одной величины (количество страниц и кружек в наших случаях), уменьшается вторая (количество чернил и компота в кастрюле).

    kompot i kruzhkiОбратная зависимость

    Примеры с велосипедистом и мороженым имеют прямую зависимость, то есть при увеличении одной величины (скорость движения педалями и количество оставленных мамой денег) увеличивается и другая (пройденное расстояние и количество мороженого).

    dengi i morozhПрямая пропорциональность

    Зависимость, которая показывает как одна величина связана с другой величиной, как раз и называется функцией.

    Аргумент и функция

    Зависимые и независимые переменные могут обозначаться и любыми другими буквами (латинскими или греческими).

    Примеры аргумента и функции

    Запись функции

    Слово «функция» произошло от латинского слова functio – исполнение, осуществление. Это одно из главных понятий в математике, показывающее зависимость одних переменных величин от других. Понятие «величина» в данном случае может включать в себя совершенно любое число.

    Переменные могут принимать как положительные, так и отрицательные значения.

    Источник

    Прямая и обратная пропорциональность

    5fda160b276a1165996409

    Статья находится на проверке у методистов Skysmart.
    Если вы заметили ошибку, сообщите об этом в онлайн-чат
    (в правом нижнем углу экрана).

    Основные определения

    Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.

    Зависимости также можно классифицировать по формам: функциональная и статистическая.

    Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.

    В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.

    Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.

    Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.

    Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.

    Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.

    Есть две разновидности пропорциональностей:

    Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

    Прямо пропорциональные величины

    Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

    Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

    5fda170d737da576965683

    Свойство прямо пропорциональной зависимости:

    Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

    Примеры прямо пропорциональной зависимости:

    Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.

    Формула прямой пропорциональности

    y = kx,

    где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.

    Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

    Формула коэффициента прямой пропорциональности:

    Графиком прямо пропорциональной зависимости величин является прямая линия.

    Например, при k = 2 график выглядит так:

    5fda170dc4c33746851936

    Пример 1.

    В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.

    Пример 2.

    Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?

    Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.

    Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.

    Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:

    Ответ: 20 человек напишут 420 постов за 12 дней.

    Обратно пропорциональные величины

    Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.

    Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».

    5fda170de467a064865999

    Свойство обратной пропорциональности величин:

    Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

    Примеры обратно пропорциональной зависимости:

    Формула обратной пропорциональности

    где y и x — это переменные величины,

    k — постоянная величина, которую называют коэффициентом обратной пропорциональности.

    Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

    Формула коэффициента обратной пропорциональности:

    Графиком обратно пропорциональной зависимости величин является гипербола.

    5fda170e07e4f620108494

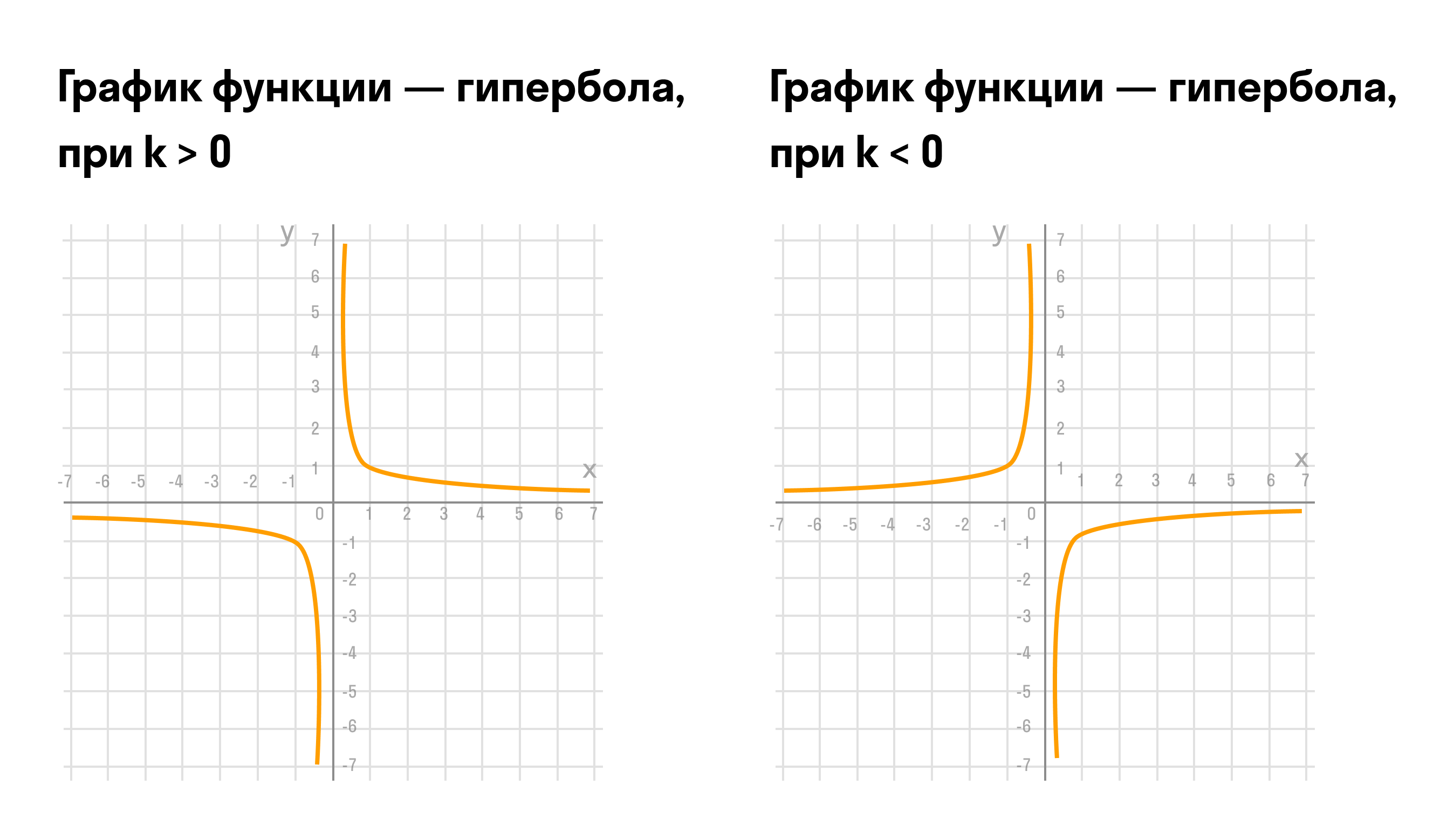
    Свойства функции обратной пропорциональности:

    Потренируемся

    Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

    Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

    Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

    Соотношения равны, но перевернуты относительно друг друга.

    Источник

    Функции

    Если две переменные величины находятся между собой в такой зависимости, что каждому значению одной переменной соответствует строго определённое значение другой, то первая величина называется аргументом, а вторая его функцией.

    Функция — это зависимая переменная величина. Аргумент — это независимая переменная. Зависимость функции от аргумента называется функциональной зависимостью.

    Если нужно указать на тот факт, что y функция от x, не акцентируя внимания на то, в какой именно зависимости находится функция от аргумента, то пишут просто:

    Иногда, чтобы показать, что y зависит от x, пишут просто:

    Обратите внимание, что вместо y и x могут использоваться любые другие буквы.

    Значение y, соответствующее заданному значению x, называют значением функции. Все значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют множество значений функции. Для функции f приняты следующие обозначения:

    D(f) — область определения функции
    (множество значений аргумента).

    E(f) — множество значений функции.

    Пример. Возьмём формулу нахождения расстояния по скорости и времени:

    где S — это расстояние, v — скорость, а t — время. Если взять скорость, равную 50 км/ч, то каждому неотрицательному значению t будет соответствовать строго определённое значение S:

    t (ч) 1 1,5 2 2,5 3
    S (км) 50 75 100 125 150

    Источник

    Источник

    Подбор уравнения к графику.

    Часто возникает ситуация когда нужно получить некую эмпирическую зависимость выраженную неким уравнением или формулой F=f(x) тогда как исходные данные представляют собой дискретные величины. Иными словами нужно получить формулу зависимости экспериментальных данных с целью дальнейшего прогноза или получения точного значения в промежуточном диапазоне, где нет возможности установить параметры экспериментально. Для этого необходимо подобрать эмпирическую зависимость к экспериментальным данным по уже имеющимся зрительно похожим графическим зависимостям к имеющимся установленным экспериментально графику.

    Однако часто зависимость бывает достаточна сложна для того что бы было возможно подобрать уравнение без применения специального программного обеспечения.. В данной статье я расскажу как пользоваться программой Eureqa Formulize. Рассмотрим все на примере. Исходные данные: вводим в таком порядке:

    текст при наведении

    Вот тут просматриваем зависимость:

    текст при наведении

    Здесь выбираем какие функции можно использовать. Тая я выбрал постоянную величину, умножение, сложение, вычитание, синус и косинус.

    текст при наведении

    Жмем старт (RUN) и смотрим сходимость функции:

    текст при наведении

    А в этом окошке просматриваем возможные варианты уравнения. Можем также их отсортировать по «точности» нажав на “Fit”:

    текст при наведении

    Ждем. И когда надоест ждать или увидите ту функцию которая скорее всего вас устраивает зрительно (простота формулы) и графически (визуальное совпадение) останавливаем процесс. Я выбрал вот эту функцию:

    текст при наведении

    А это её проверка в Microsoft Excel:

    текст при наведении

    текст при наведении

    Таким образом, мы получили примерную зависимость волшебных звездочек от просмотров:

    текст при наведении

    Примечание.

    Точки были построены экспериментально по общедоступной информации в сети интернет. Параметры К и Z (S) обновляются в разный момент времени из-за чего возможны некоторые отклонения.

    Думаю особый интерес вызывает значения N в диапазоне Z = (0;6):

    текст при наведении

    Источник

    Ôункциональные зависимости между величинами могут задаваться различными способами: с помощью формул, графиков, таблиц, словесных описаний. Совершенствованию умений пользоваться этими способами, получать из них необходимую информацию посвящен данный параграф.

    1. Понятие функции, способы ее задання

    Характерной особенностью функциональной зави-

    симости является то, что для каждого допустимого значения одной из переменных она однозначно определяет значения второй переменной. Так, для каждого значе-

    ния t по формуле s = 3t – 1 можно найти лишь одно значение s. Напомним сначала то, что изучалось о функциональных зависимостях ранее.

    Пусть заданы две переменные х и у, принимающие числовые значения, и D — множество значений переменной х.

    Зависимость между переменными х и у, которая для каждого значения х из D определяет единственное значение у, называется функциональной зависимостью или функцией у от х с областью определения D.

    Переменную х в таких зависимостях называют независимой переменной или аргументом, переменную у — зависимой переменной. Функции обычно обозначают латинскими (иногда греческими) буквами — f, g, F, ϕ и т. п.

    Функция — от латинского function — действие, выполнение.

    Функциональные зависимости

    47

    Область определения функции f часто обозначают D(f). Значение переменной у, которое соответствует х, называют значением функции f в точке х и обозначают f(х). Запись «у = f(х)» означает, что задана функция f. Функциональную зависимость переменной у от х иногда записывают так: у = у(х).

    Множество значений, которые принимает зависимая переменная у, если х пробегает область определения функции f, называют

    множеством значений этой функции и обозначают Е(f).

    !Фраза «задать функцию у от х» означает сформулировать правило, с помощью которого для каждого допустимого значения переменной х можно найти соответствующее ему значение переменной у.

    Существуютразличныеспособызаданняфункции.Вматематике функциональная зависимость чаще всего задается формулами.

    Какизвестно,линейнаяфункциязадаетсяформулой:y = kx +b, где k и b — некоторые числа, х — аргумент. Например, функции

    у=2х–3(здесь k = 2, b = – 3), у = –0,5х + 2 (здесь k = – 0,5, b = 2), у = 4х (здесь k = 4, b = 0), у = 5 (здесь k = 0, b = 5) являются линейными.

    Квадратичная функция задается формулой: y = ax2 + bx + c,

    где a, b, c – некоторые числа, а ≠ 0, х — аргумент. Например, функции у = х2, у = 3х2 + 1, у = 2х2 + х – 4 являются квадратичными. (Укажите для каждой из этих функций, чему равняются коэффициенты a, b, c.)

    Обратная пропорциональность задается формулой y = kx ,

    где k ≠ 0 — некоторое число, х — аргумент.

    Такой способ задания функции называется аналитическим. Заметим, что не всякая зависимость между переменными является функциональной. Например, зависимость между переменными у и х, заданная уравнением х2 + у2 = 1, не является функциональной, так как, например, значению х = 0 соответствуют два

    значения у: у1 = –1, у2 = 1.

    !Если функция задана формулой, то при отсутствии дополнительных замечаний или условий считают, что ее областью определения является множество всех значений независимой переменной, при которых эта формула имеет смысл. Её иногда называют естественной областью определения функции.

    48

    Функции, их свойства и графики

    Так, линейная функция y = kx + b, квадратичная функция y = ax2 + + bx + c определены при всех значениях х, то есть D(y) = (–∞; +∞).

    Обратная пропорциональность y = kx определена при всех зна-

    чениях х, кроме х = 0, то есть D(y) = (– ∞; 0) (0; + ∞). Естественной областью определения функции у = x является промежуток [0; + ∞), поскольку извлечение квадратного корня возможно толь-

    ко из неотрицательных чисел.

    3

    1)область определения функции; x2 −1 . Найти:

    2)значение функции в точке х = –2;

    3)значения аргумента, при которых функция принимает значение 1.

    1) Функция определена при всех значениях х, для которых знаменатель дроби не равен нулю, то есть при всех х, кроме х = ±1.

    Следовательно, D(y) = (−∞;−1) (−1;1) (1;+∞).

    2) Значение функции в точке х = – 2 равно:

    y(−2) =

    3

    =

    (−2)2 −1

    =43−1 =1 .

    3)Чтобы найти значения аргумента, при которых функция

    принимает значение 1,

    решим уравнение 1 =

    3

    . Получим:

    x2

    −1

    х2 – 1 = 3, х2 = 4, х1 = – 2,

    х2 = 2. Следовательно, в этих точках фун-

    кция принимает значение 1.

    Ответ. 1) (−∞;−1) (−1;1) (1;+∞); 2) 1; 3) – 2; 2.

    При решении многих прикладных задач область определения функции устанавливают, исходя из физического или геометрического смысла задачи. Например, если рассматривать зависимость площади квадрата от длины его стороны х, то областью оп-

    ределения этой функции будет интервал (0; + ∞), так как длина

    стороны квадрата может выражаться только положительным числом. В таком случае иногда пишут: y = x2 , х > 0.

    ! Обратите внимание на то, что функции y = x2 и y = x2 ,

    х > 0 различны. У них не только не совпадают области

    Функциональные зависимости

    49

    определения, они также обладают различными свойс-

    твами, в чем убедимся впоследствии.

    В математике и ее приложениях очень распространен графи-

    ческий способ задания функции. Существует много самопи-

    шущих приборов, которые вычерчивают кривые, устанавливая

    тем самым зависимость между исследуемыми величинами. Так,

    сейсмограф вычерчивает график колебания земной коры. По это-

    му графику можно, например, изучать силу и характер толчков

    при землетрясении.

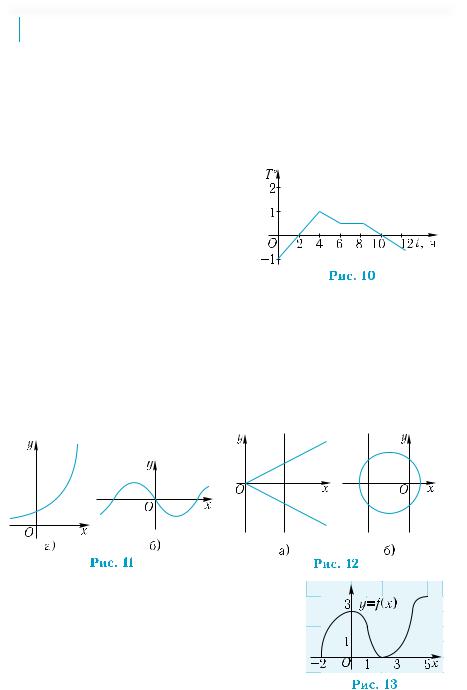
    С помощью линии, изображен-

    ной на рис. 10, можно для каждого

    момента времени 0 ≤ t ≤ 12 указать

    единственное значение

    температу-

    ры среды Т, то есть эта линия задает

    функциональнуюзависимостьмежду

    переменными t и Т.

    Не всякая линия на координатной плоскости задаёт некоторую

    функцию. Чтобы некоторая линия определяла функциональную

    зависимость у от х, необходимо и достаточно, чтобы каждая пря-

    мая, параллельная оси у, и ось у пересекали эту линию не более

    чем в одной точке. Так, линии на рис. 11 определяют функцио-

    нальные зависимости у

    от х. Линии, изображённые на рис. 12,

    не задают функции у от

    х, так как можно указать вертикальные

    прямые, пересекающие линию в двух точках.

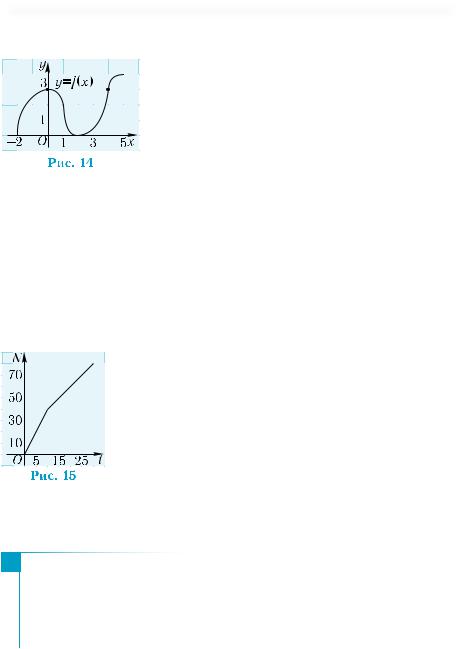
    Пример 2. Функция y = f(x) задана гра-

    фически (рис. 13). Указать:

    1) её область определения;

    2) её множество значений;

    3) значение функции при х = 5;

    50

    Функции, их свойства и графики

    4) значение аргумента х, при котором функция принимает значе-

    ние 3.

    1) Областью определения функции яв-

    ляется отрезок [–2; 5].

    2) Множеством значений функции явля-

    ется отрезок [0; 4].

    3) f(5) = 4.

    4) Проведем прямую у = 3 и найдем ее

    точки пересечения с графиком функции

    у = f(x) (рис. 14). Это точки с координатами

    (0; 3) и (4; 3). Следовательно, значение 3 функция принимает при

    х = 0 и при х

    = 4.

    Ответ. 1) [–2; 5]; 2) [0; 4]; 3) 4; 4) 0; 4.

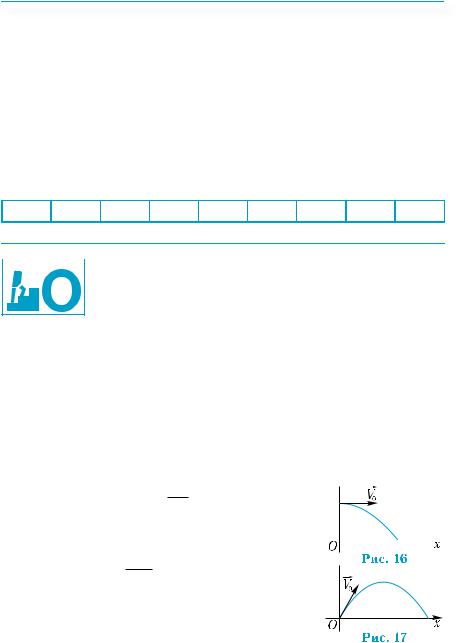
    Пример 3.

    На рис. 15 изображена зависимость N(t) количест-

    ва деталей, изготовленных рабочим, от времени t (в днях).

    1) Сколько деталей изготовил рабочий за первые 10 дней?

    2) За какие 10 дней — первые или последние — рабочий изгото-

    вил больше деталей?

    3) За сколько дней рабочий изготовил 50 деталей?

    1) Найдем значение функции N(t) при t = 10.

    Обратите внимание на масштаб по оси t и оси N.

    Имеем: N(10) = 40, то есть за первые 10 дней из-

    готовлено 40 деталей.

    2) За последние десять дней изготовлено

    N(30) – N(20) = 80 – 60 = 20 деталей, то есть мень-

    ше, чем за первые 10 дней.

    3) Необходимо найти значение аргумента, при

    которомфункцияпринимаетзначение50. Прове-

    дем прямую N = 50 до пересечения с графиком функции N = N(t).

    Получим, что 50 деталей рабочий изготовил за 15 дней.

    Ответ. 1) 40; 2) за первые; 3) 15.

    !В рассмотренном примере функция N(t) определена для натуральных значений аргумента. Её графиком являетсяконечнаясовокупностьточек.Длянаглядностионисоединены отрезками. Такой приём построения изображения зависимостей будем использовать и в дальнейшем, если он не приводит к недоразумениям.

    Кроме аналитического и графического способов задания функций, применяется также табличный способ. В физике и технике час-

    Функциональные зависимости

    51

    то зависимости между переменными фиксируются на шкалах измерительных приборов. В таких случаях функцию задают в виде таблицы, в первой строке которой содержатся значения независимой переменной x1, x2, x3, …, во второй — соответствующие им значения функции. Наиболее распространёнными являются таблицы с постояннымиразностямиx2 –x1,x3 –x2,…,причемзначениеразности называется шагом таблицы. Для таких таблиц независимая переменная принимает значения x0, x0 + h, x0 + 2h, …, где h — шаг таблицы.Так,приведеннаянижетаблицапоказываетдинамикуизменения объема пассажирских перевозок (в млн. людей) в нашей стране по железным дорогам, начиная с 2000 года.

    2000 2001 2002 2003 2004 2005 2006 2007 2008

    1,16 1,29 1,77 2,37 3,23 3,81 4,35 4,87 6,17

    Функциональные зависимости широко исполь-

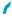
    зуются на практике. Много процессов и явлений описываются линейной функцией. Например, при равномерном движении пройденный путь прямо пропорционален времени движения; давление газа р при постоянном объеме прямо пропорционально его температуре T: p = cT (законШарля);напряжениеUвэлектрическойцеписпостоянным сопротивлением R прямо пропорционально силе тока I : U = RI (закон Ома). Зависимость силы F, действующей на пружину, от

    величины ее растяжения х имеет вид F = – kx (закон Гука). Немало физических зависимостей моделируются с помощью

    квадратичной функции. Например, закон движения тела вдоль координатнойпрямой поддействиемпостояннойсилы можно предста-

    вить в виде: x = x0 +v0t + at22 , зависимость кине-

    тической энергии тела W, масса которого равняется m, от скорости движения v выражает-

    ся формулой: W = mv22 . Тела, брошенные гори-

    зонтально или под углом к горизонту, будут двигаться под действием силы тяжести по

    параболическим траекториям (рис. 16, 17). Обратно пропорциональными являются:

    — зависимость времени, необходимого на преодоление данного пути, от скорости;

    52

    Функции, их свойства и графики

    —зависимость между сторонами прямоугольника при заданной площади;

    —зависимость между давлением газа и его объемом при постоянной температуре.

    Пример 4. При свободном падении тела с достаточно большой высоты с начальной скоростью v0 = 10 м/с зависимость пройденного

    пути от времени t ≥ 0 выражается формулой: s = v0t + gt22 , де s — путь, м; t — время, с; g ≈ 10 м/с2 — ускорение свободного падения.

    1)Какой путь пройдет тело за первые 2 с?

    2)За какое время тело пройдет 15 м?

    1) Чтобы ответить на первый вопрос, нужно вычислить значение функции s при t = 2: s(2) ≈10 2+ 10222 = 40 (м).

    2)Чтобы ответить на второй вопрос, нужно решить квадратное

    уравнение: 10t + 5t2 =15 . Оно имеет два корня: –3 и 1, но условию задачи удовлетворяет только значение t = 1. Следовательно, тело преодолеет 15 м примерно за 1 с.

    Ответ. 1) ≈40 м; 2) ≈1 с.

    Пример 5. Некоторая масса газа при температуре 20°С имела объем 107 см3, а при 40°С объем равнялся 114 см3.

    1) Опираясь на закон Гей-Люссака, найти функциональную зависимость объема газа от температуры.

    2) Каким будет объем газа при 0°С?

    1) По закону Гей-Люссака, объем газа V линейно зависит от температуры t: V = a + bt, где a и b — некоторые числа. Найдем эти числа, используя условие задачи. Так как V(20) = 107, V(40) = 114, то имеем систему уравнений относительно a и b:

    107 = a + 20b, Отсюда: b = 0,35, a = 100. Итак, V = 100 + 0,35t.114 = a + 40b.

    2) V(0) = 100 + 0,35 0 = 100 (см3). Ответ. 1) V = 100 + 0,35t; 2) 100 см3.

    9 Контрольные вопросы

    1°. Какие из следующих зависимостей являются функциональными:

    а) каждому двузначному числу ставится в соответствие сумма его цифр;

    Функциональные зависимости

    53

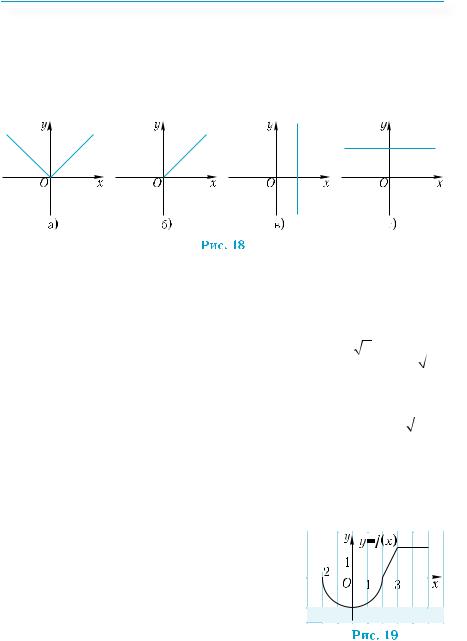
    б) каждому числу, не равному нулю, ставится в соответствие обратное к нему число; в) каждому числу ставится в соответствие целое число, меньшее его?

    2°. Какая из линий, изображенных на рис. 18, а)–г), не задаёт функциональную зависимость у от х?

    3.

    x

    в точке х = – 1; х = 0?

    2x −1

    4.

    В скольких точках функция у = х2 – 2х принимает значение 0;

    –1; –2?

    1 ; 2)

    1

    5.

    Длякакойизследующихфункций:1) y =

    y =

    x;3) y =

    ;

    x

    x

    4) y = x2 областью определения служит промежуток (0; + ∞)?

    1 − x

    2

    2

    ; 4) y = (

    2

    6.

    Даны функции: 1) y =

    2

    ; 2)

    y = x ;3) y = (1 − x)

    x ) .

    а) Какая из них является линейной; квадратичной; обратной

    пропорциональностью?

    б) В каких точках квадратичная функция принимает значе-

    ние 1?

    в) Какая из функций не обращается в 0?

    7.

    Для графически заданной

    функции

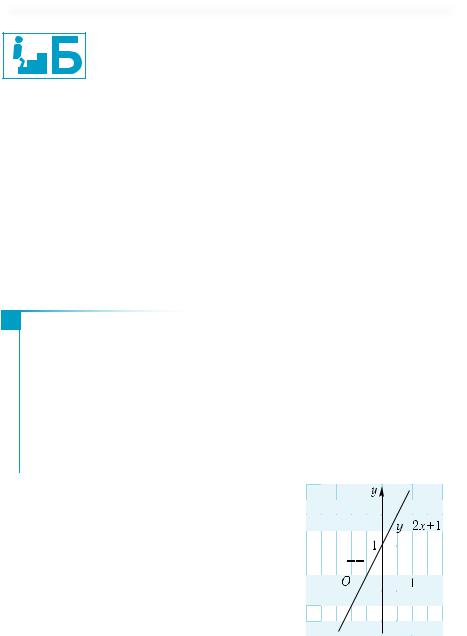
    y = f(x) (рис. 19) найдите:

    а) область определения;

    б) множество значений;

    в) значения функции в точке х

    = 0; х = 4;

    г) нули функции, то есть точки, в которых функция обращается в 0.

    54

    Функции, их свойства и графики

    2. График функции

    Графической способ задания функции более на- гляден по сравнению с аналитическим. По графи- ку легко охарактеризовать исследуемую величину. Например, по графику, изображенному на рис. 10, можно сказать, что температура в течение 12 часов изменялась от –1° до +1°. По графику видно также, когда температура повышалась, когда понижалась, а когда оставалась неизменной. Поэтому часто аналитическое задание функции сопровождают графиком. В данном пункте рассматриваются графики уже известных вам функций и некоторые способы построения графиков.

    График функции y = f(x) — это множество точек координатной плоскости с координатами (х; f(x)), где х — произвольное число из области определения функции.

    Для построения графика функции y = f(x) на плоскости вводят прямоугольную систему координат и строят точки с координата-

    ми (x; f(x)).

    !Абсолютноточнопостроитьграфикфункцииневозможно, так как невозможно точно изобразить даже одну точку (х0; f(х0)) на координатной плоскости, а тем более если их бесконечное множество. Поэтому под построением графика функции понимают построение линии, отображающей основные особенности «идеального» графика. Такую линию называют эскизом графика. Следовательно, построить график функции — значит построить эскиз графика, то есть отобразить графически все основные свойства функции.

    Графиком линейной функции y = kx + b является, как вам уже известно, прямая линия. Для ее построения достаточно найти две точки графика и через них провести прямую. Например, для построения графи- ка функции у = 2х + 1 возьмем точки пересе- чения прямой с осями координат, то есть

    1

    и проведем через

    точки А(0; 1) и

    B

    −

    2

    ; 0

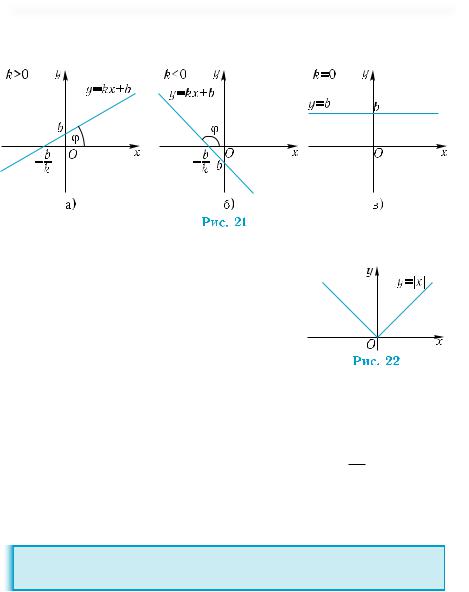
    них прямую (рис. 20). Число k равно тангенсу угла ϕ наклона прямой y = kx + b к оси

    х и называется ее угловым коэффициентом. На рис. 21, а), б)

    Функциональные зависимости

    55

    изображены графики линейных функций в зависимости от знака k. Если k = 0, то имеем постоянную функцию y = b, график которой изображен на рис. 21, в).

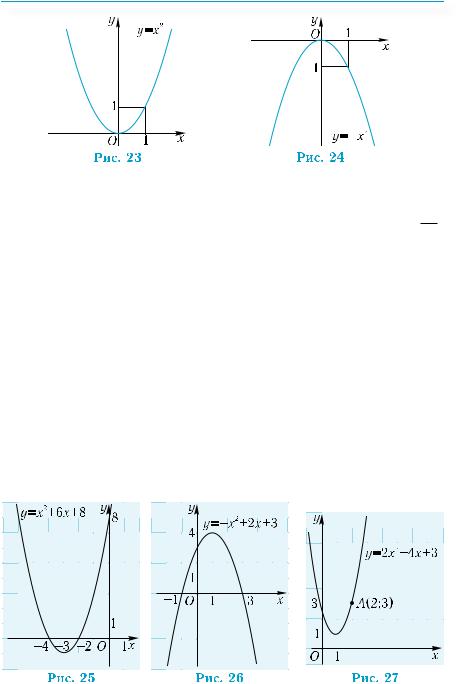
    Пример 6. Построить график функции y = |x|.

    Так как

    x

    x,eсли x ≥ 0,

    то для неот-

    =

    −x,eсли x < 0,

    рицательных значений х график функции

    y = |x| совпадает с графиком функции у = х, а

    для отрицательных — с графиком функции

    у = –х (рис. 22).

    Графиком квадратичной функции у = ах2 + bх + с является парабола. Ее расположение на координатной плоскости зависит от коэффициентов a, b, c. Направление ее ветвей определяется знаком числа а: при а > 0 они направлены вверх, при а < 0 — вниз.

    Вершина ее находится в точке с абсциссой x0 = − 2ba . Парабола

    может не иметь общих точек с осью х, а может иметь с ней одну или две общие точки. Это зависит от количества корней квадратного уравнения ах2 + bх + с = 0.

    Парабола — по гречески παραβολη (parabole) от παραβολλειν (parabollein) — прикладываю, сравниваю.

    Параболу обычно строят по ее характерным точкам: вершине и точкам пересечения с осями координат. Графики функций у = х2 и у = –х2 изображены на рис. 23, 24.

    Рассмотрим на конкретных примерах построение графиков квадратичных функций.

    56

    Функции, их свойства и графики

    Пример 7. Построить график функции:

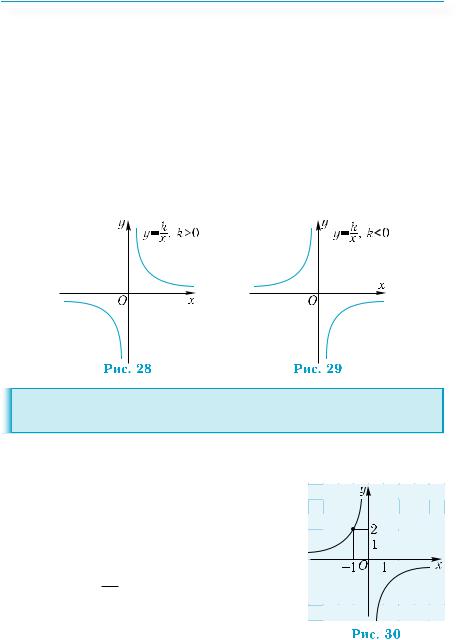
    1) у = х2 + 6х + 8; 2) у = – х2 + 2х + 3; 3) у = 2х2 – 4х + 3.

    1) Найдем абсциссу вершины параболы по формуле x0 = −2ba : x0 = −62 = −3.

    Ордината вершины находится вычислением значения квадратичной функции при х0 = – 3: у0 = у(– 3) = 9 – 18 + 8 = – 1. Итак, координаты вершины — (–3; –1). Найдем точки пересечения графика с осью абсцисс. Для этого решим уравнение: х2 + 6х + 8 = 0. Получим: х1 = –4; х2 = –2. Найдем точку пересечения графика с осью у. Для этого вычислим значение функции у = х2 + 6х + 8 при х = 0: у(0) = 8. График пересекает ось у в точке с координатами (0; 8). Ветви параболы направлены вверх, так как коэффициент при х2 положителен. На основании полученных результатов построим график (рис. 25).

    2) Вершина параболы находится в точке с координатами (1; 4). Точки пересечения параболы с осью абсцисс имеют координаты (–1; 0) и (3; 0). График функции пересекает ось у в точке с коорди-

    Функциональные зависимости

    57

    натами (0; 3). Ветви параболы направлены вниз. График изображен на рис. 26.

    3) Вершина параболы находится в точке с координатами (1; 1). Парабола не пересекает ось х, поскольку уравнение 2х2 – 4х + 3 = 0 не имеет корней. Парабола пересекает ось у в точке с координатами (0; 3). Для уточнения положения графика вычислим значение функции в точке х = 2: у(2) = 3, то есть парабола проходит через точку А(2; 3). График изображен на рис. 27.

    Графиком обратной пропорциональности y = kx является гипербола, расположение которой зависит от знака k (рис. 28, 29).

    Гипербола (по гречески νπερβολη) — избыток, преуве-

    личение.

    Пример 8.

    На рис. 30 изображен график обратной пропорци-

    ональности. Задать эту зависимость формулой.

    Обратная пропорциональность задает-

    ся формулой y = k . Необходимо найти чис-

    x

    ло k. График функции проходит через точку

    с координатами (–1; 2), то есть имеет место

    равенство: 2 =

    k . Отсюда k = – 2.

    −1

    Ответ. y = − 2 .

    x

    Существуют различные способы построе-

    ния графиков функций. Один из них — построение по несколь-

    ким точкам.

    58

    Функции, их свойства и графики

    !Произвольной выбор точек и построение графика по этим точкам может привести к существенным ошибкам.

    Например, чтобы построить график функции некоторую таблицу ее значений.

    х –4 –3 –2 –1 1 2

    у

    −

    1

    −

    1

    −

    1

    –1

    1

    1

    4

    3

    2

    2

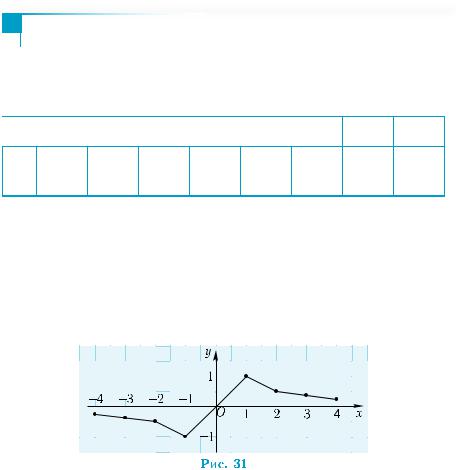
    Теперь изобразим соответствующие точки на координатной плоскости и, соединив их, получим кривую, изображенную на

    рис. 31. Однако она совсем не похожа на график функции y = 1x .

    Вы его хорошо знаете — это гипербола (см. рис. 28). Какие мы допустили ошибки? Дело в том, что график функции нужно строить не по произвольно взятым точкам, а по характерным для данной функции точкам.

    Проще всего построить график линейной функции. Для этого достаточно найти две точки, принадлежащие графику, и через них провести прямую. Характерными точками для квадратичной функции являются вершина параболы и точки пересечения параболы с осями координат. А для обратной пропорциональности характерной является точка х = 0, в которой ее график «разрывается».

    В дальнейшем вы познакомитесь с общими методами нахождения характерных точек.

    Другой способ построения графиков функций основан на гео-

    метрических преобразованиях. Так, зная график функции

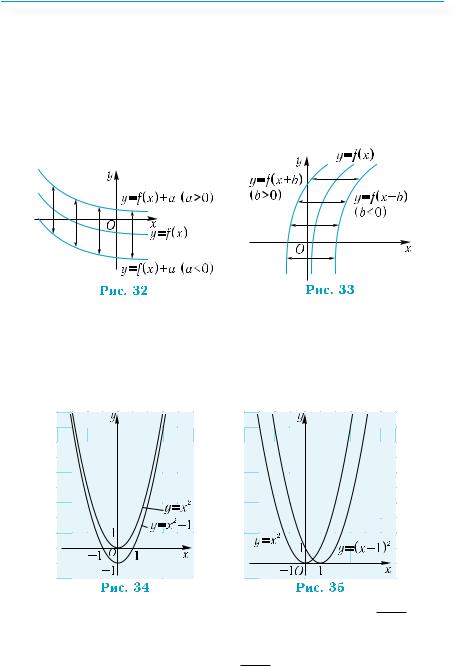
    у=f(х),можнопостроитьграфикифункций у=f(х)+аиу= f(х+b), где а и b — некоторые числа, по следующим правилам.

    Функциональные зависимости

    59

    График функции у = f (х) + а можно получить из графика функции у = f (х) параллельным переносом его вдоль оси у на |а| единиц: в направлении оси у, если а > 0 и в

    противоположном направлении, если а < 0 (рис. 32). График функции у = f(х + b) можно получить из графика функции у = f (х) параллельным переносом его вдоль оси х на |b| единиц: в направлении оси х, если b < 0 и в

    противоположном направлении, если b > 0 (рис. 33).

    Например,графикфункцииу= х2 –1можнополучитьпараллель- нымпереносомграфикафункцииу= х2 наоднуединицувнаправлении, противоположном направлению оси у, так как х2 – 1 = х2 + (–1) (рис. 34). График функции у = (х – 1)2 можно получить из графика функции у = х2 параллельным переносом последнего на одну единицу в направлении оси х, так как (х – 1)2 = (х + (–1))2 (рис. 35).

    Пример 9.

    Сколько корней имеет уравнение x2 = −

    1

    ?

    x + 2

    Уравнение имеет столько корней, сколько общих точек име-

    ют графики функций у = х2 и y = −

    1

    . Построим графики этих

    x + 2

    функций в одной системе координат.

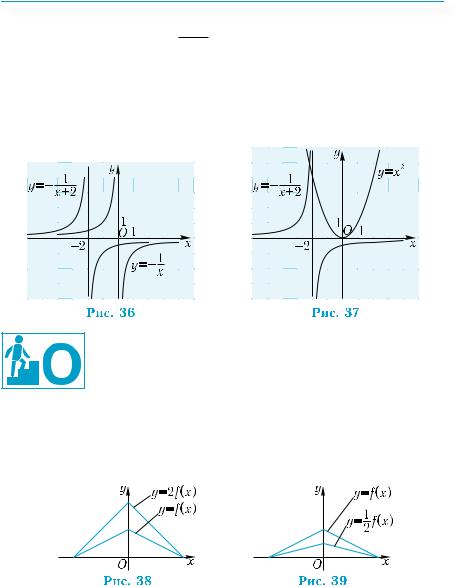
    60

    Функции, их свойства и графики

    График функции y = − x 1+ 2 можно получить из графика фун-

    кции y = − 1x параллельным переносом последнего вдоль оси х на

    2 единицы влево (рис. 36). Тогда из рис. 37 видно, что уравнение имеет один корень.

    Ответ. Один корень.

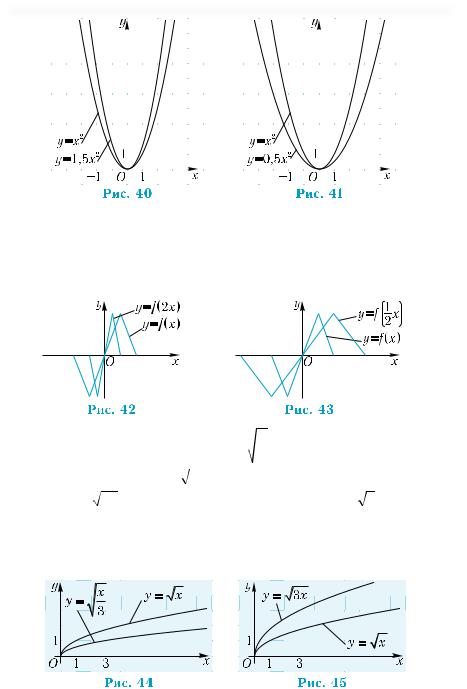
    Теперь напомним, как зная график функции у = f(х) можнопостроитьграфикифункцийу=kf(х)иу=f(ωх),

    где k и ω — некоторые положительные числа.

    График функции у = kf(x) (k > 0) можно получить из графика функции y = f(x) растяжением его в k раз от

    оси х при k > 1 (рис. 38) и сжатием в 1 раз к оси х при k

    0<k<1(рис.39).

    Пример 10. Построить графики функций у = 1,5 х2, у = 0,5х2.

    График функции у = 1,5 х2 получим из графика функции

    у= x2 растяжением от оси х в 1,5 раза (рис. 40). График функции

    у= 0,5х2 получим из графика у = x2 сжатием его к оси х в 2 раза

    (рис. 41).

    Функциональные зависимости

    61

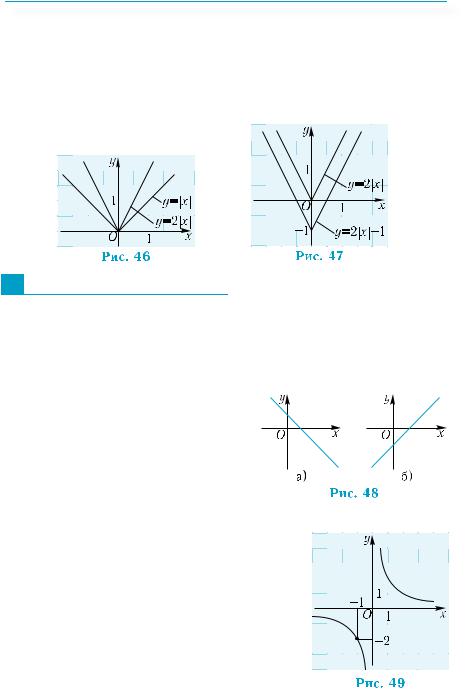
    График функции y = f(ωx) (ω > 0) можно получить из графика функции у = f (х) сжатием его к оси у в ω раз

    при ω > 1 (рис. 42) и растяжением его в 1 раз от оси у

    ω

    при 0 < ω < 1 (рис. 43).

    Например, график функции y =

    x

    можно построить, растя-

    3

    нув график функции у = x от оси у в 3 раза (рис. 44). График функции y = 3x получим из графика функции у = x , сжав его

    к оси у в 3 раза (рис. 45).

    При построении графика функции иногда приходится выполнять несколько геометрических преобразований.

    62

    Функции, их свойства и графики

    Пример

    11. Построить график функции у = 2|х| – 1.

    Построение выполняется в два этапа, исходя из графика функции у = |х|:

    1) график функции у = |х| растягивается от оси х вдвое (рис. 46); 2) полученный график параллельно переносится на одну еди-

    ницу в отрицательном направлении оси у (рис. 47).

    9

    Контрольные вопросы

    1°.

    Проходит ли график функции у= 5х + 2 через точку:

    а) А(0; 5);

    б) В(0; 2);

    в) С(–1; –2);

    г) D(–1; –3)?

    2°.

    В каких точках прямая у = 1 – 4х пересекает оси координат?

    3°.

    Укажите несколько точек, через которые проходит график ли-

    нейной функции у = –2.

    и b,

    4°.

    Какие знаки имеют числа k

    если график линейной функции

    у = kх + b

    изображен на рис. 48?

    5°.

    У каких из следующих парабол

    ветви направлены вверх:

    а) у = 1 –

    х + 2х2;

    б) у = 5х – 3х2 – 1;

    в) у = 1 –

    х2?

    6°.

    Чему равна абсцисса вершины параболы:

    а) у = 1 – 3х + 2х2;

    б) у = – 5х2 + х

    – 2;

    в) у = (х + 5)(х

    – 1)?

    7°.

    Найдите обратную пропорциональность,

    график которой изображен на рис. 49.

    8°.

    Сколько точек пересечения имеют гра-

    фики функций:

    Функциональные зависимости

    63

    2

    2

    2

    9°.

    а) у =

    x , у

    = х;

    б) у = x

    , у = –х;

    в) у = – x , у = х2?

    На сколько единиц и в каком направлении следует параллель-

    но перенести гиперболу y = 1

    , чтобы получить гиперболу:

    1

    x

    б) y = 1

    а) y =

    ;

    + 4?

    x + 4

    x

    10°.На сколько единиц и в каком направлении следует парал-

    лельно перенести параболу

    у = х2, чтобы ее вершина оказа-

    лась в точке с координатами: а) (–2; 0);

    б) (0; 2)?

    11°.Какой формулой может быть за-

    дана функция, график которой

    изображен на рис. 50, если он по-

    лучен с помощью геометрических

    преобразований из графика фун-

    кции y =

    x ?

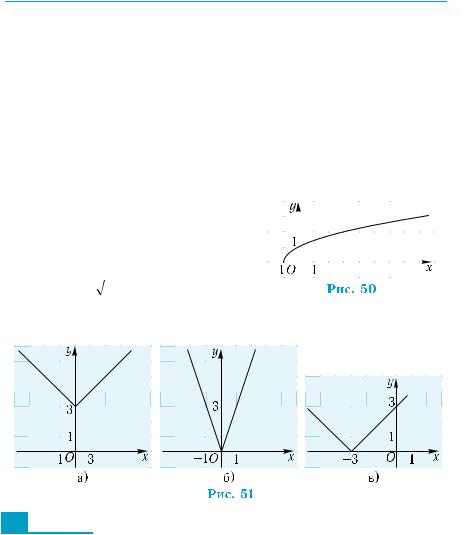
    12.Для каждой из функций y = |x + 3|, y = |x| + 3, y = 3|x| подберите соответствующий график на рис.51, а) – в).

    Задачи

    46.

    Дана функция f(x) = x2 − 2x −3. Найдите:

    1°) f(−2), f(3),

    1

    ;

    f

    2

    3) корни уравнения f(x) = f(0).

    2°) нули функции;

    2x +1

    47°.Дана функция y =

    . Найдите значения аргумента, при

    x +1

    которых функция принимает значения: 1) – 2; 2) 2; 3) 3.

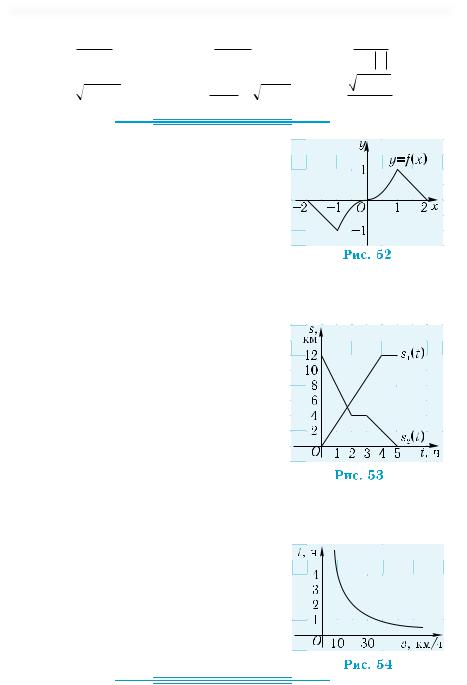
    64

    Функции, их свойства и графики

    48. Найдите область определения функции:

    1°)

    y =

    5x +1;

    2°)

    y =

    5x +1 ;

    3°)

    y =

    1

    ;

    x2 + 4

    x2 −4

    2− x

    4°)

    y =

    3−2x ;

    5)

    y =

    x

    +

    2− x ; 6)

    y =

    1 − x2 .

    x +3

    x

    49. Функция у = f(х) задана графически

    (рис. 52).

    1°) Какова её область определения?

    2°) Каково множество значений фун-

    кции?

    3°) Сколько нулей имеет функция?

    4°) Укажите все значения

    х, при ко-

    торых функция принимает положи-

    тельные (отрицательные) значения?

    5) Чему равно наибольшее (наименьшее) значение функции?

    6) Сколько корней имеет уравнение f(x) = 0,5?

    50. На рис. 53 изображены графики дви-

    жений двух пешеходов навстречу друг

    другу по шоссе, соединяющему пункты

    А и Б; s1(t) и s2(t) — расстояния от А, со-

    ответственно, до первого и второго пе-

    шеходов в момент времени t.

    1°)Каковорасстояниемеждупунктами?

    2°) Сколько километров прошел пер-

    вый пешеход за первые два часа?

    3) Какой из пешеходов к моменту

    встречи преодолел большее расстоя-

    ние?

    4) Какой из пешеходов пришел в пункт назначения первым?

    51. На рис. 54 приведен график зависи-

    мости

    времени

    t, необходимого на

    путь из пункта А в пункт Б, от скоро-

    сти движения v. С какой скоростью

    нужно двигаться, чтобы добраться из

    А в Б менее чем за 2 часа?

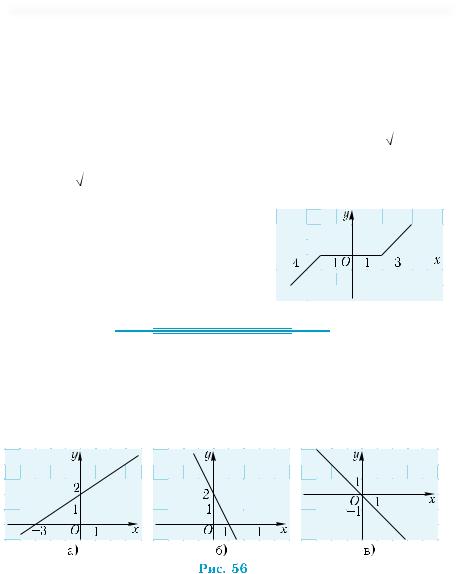
    Функциональные зависимости

    65

    52°.Постройте график функции:

    1) y =

    x −3

    ;

    2)

    y = −3;

    3) y = −

    2

    ;

    4) y = x2 −5x + 4;

    x

    2

    5) y = −3x2 −2x +1;

    6) y = x2 −4x + 4;

    7) y = (x + 2)(x −4).

    53.Постройте график функции с помощью геометрических преобразований:

    1°)

    y = (x −0,5)

    2

    2°)

    2

    −0,5;

    3) y =

    x2

    4°)

    x + 2;

    ;

    y = x

    ;

    y =

    2

    5°)

    y = x −2;

    6°)

    1

    7°) y

    1

    8)

    x 2

    y =

    ;

    =

    +3;

    y =

    .

    x −3

    x

    2

    54.На рис. 55 изображен график функции y = f(x). Постройте график фун-

    кции: 1°) y = f(x – 1); 2°) y = f(x) – 1;

    3)y = f(2x);

    4)y = 2f(x).

    55.Найдите линейную функцию, если:

    1°) ее график проходит через точки А(1; –1) и В(2; –1);

    2)ее график составляет угол 135° с осью х и проходит через точку А(0; 2).

    Задайте с помощью формулы функции, графики которых изображены на рис. 56, а)–в).

    57.Напряжение в электрической цепи равномерно растет, то есть линейно зависит от времени. В начале опыта напряжение равнялось 10 В, а в конце опыта, длившегося 5 с, напряжение увеличилось в 1,5 раза.

    1)Выразите зависимость напряжения от времени и постройте график этой функции.

    2)Каким было напряжение через 3 с после начала опыта?

    66

    Функции, их свойства и графики

    58°.Найдите обратную пропорциональность, если известно, что ее график проходит через точку А(–1; 3). Постройте ее график.

    59. По закону Бойля–Мариотта, давление р и объем газа V связаны формулой p = Vc , где с — некоторое число, постоянное для дан-

    ной массы и температуры газа. Постройте график этой зависимости, если при давлении р = 10 Па объем газа равен 0,5 л.

    60.

    Какие из следующих пар точек симметричны относительно

    оси у, а какие — относительно начала координат:

    1)

    А(0; 1),

    В(1; 0);

    2)

    А(0; 1),

    В(0; –1);

    3)

    А(1; 2),

    В(–1; 2);

    4)

    А(1; 2),

    В(–1; –2)?

    Упражнения для повторения

    61.

    Укажите функции, графики которых симметричны относи-

    тельно оси у, а которых — относительно начала координат:

    1) у = х;

    2) у = – х + 1; 3) у =

    1

    62.

    х2; 4) у = х3;

    5) y = x .

    Докажите, что большему значению аргумента соответствует

    большее значение функции: 1) у = 2х+ 1; 2) y =

    x.

    63. Чему равно расстояние между точками координатной прямой: 1) А(х) и В(2); 2) А(а) и В(–3); 3) А(а) и B(b); 4) A(a) и B(–b)?

    Итог

    Основные понятия

    Определение

    Геометрическая интерпре-

    тация, примеры

    Зависимость

    между перемен-

    Например, высота от самолета

    ными х и у, которая для каж-

    до поверхности земли является

    дого значения х из D опреде-

    функцией времени его пребы-

    ляет единственное значение у,

    вания в полете.

    называется

    функциональной

    зависимостью у от х с областью

    определения D.

    График функции у = f(х) — это

    График линейной функции —

    множество

    точек координат-

    прямая.

    квадратичной функ-

    ной плоскости с координатами

    График

    (х; f(х)), где

    х — произвольное

    ции — парабола.

    число из области определения

    График

    обратной пропорцио-

    функции.

    нальности –— гипербола.
    Источник

    Рассмотрим:

    (7)

    Пусть функции (7) определены и дифференцируемы в некоторой области .

    Опр.: Некоторая функция называется зависимой в области От остальных функций из совокупности (7), если ее можно представить в виде

    , (8)

    Где дифференцируемая функция своих аргументов.

    Если никакая из функций системы (7) не может быть выражена через остальные функции, то функции данной системы, выраженные формулой (8), по функции (7) называются независимой.

    Примеры:

    1)

    открытый круг радиуса .

    – зависима

    2)

    Докажем, что – независимы от противного.

    Предположим

    то

    Рассмотрим изменение переменных по оси , т. е. .

    (противоречие)

    (по прямым)

    – независимые, что и требовалось доказать.

    , (1)

    Где Определены и дифференцируемы в некоторой области .

    Теорема 1

    Пусть функции (1) дифференцируемы в некоторой окрестности точки (n<m). Пусть якобиан указанных функций по какой либо выборке переменных не равен 0.

    Тогда функции (1) являются независимыми в окрестности .

    Из m имеющихся переменных для участия в вычисления якобиана выбираются n. Если хотя бы один из указанных якобианов не равен 0, то функции независимы.

    Следствие

    Если функции (1) являются зависимыми, то все якобианы вида: равны нулю. В знаменателе якобиана рассматриваются всевозможные выборки переменных.

    Док-во теоремы 1:

    Допустим, что .

    Проведем доказательство методом от противного, т. е. допустим, что одна из функций системы (1) является зависимой от остальных функций:

    Где функция F дифференцируема в окрестности .

    Вычислим частичную производную , по некоторой переменной .

    ,

    где .

    Подчеркнуты представители якобиана.

    В идеале надо расписать по всем индексам.

    Рассмотрим последнее равенство в точке . При этом множители при подчеркнутых слагаемых превращаются в коэффициенты. Поэтому получаем, что k-я строка якобиана является зависимой от остальных строк. Следовательно, якобиан равен 0, что противоречит начальному предположению.

    ч. т. д.

    < Предыдущая   Следующая >
    Источник

    Добавить комментарий