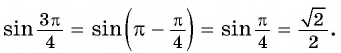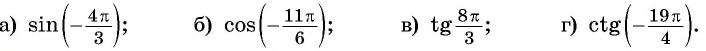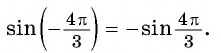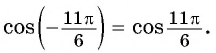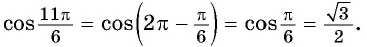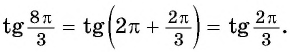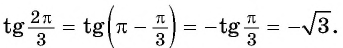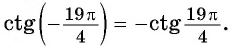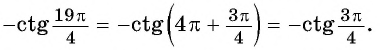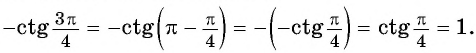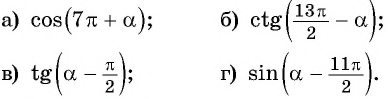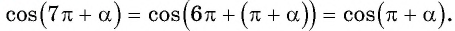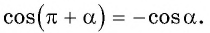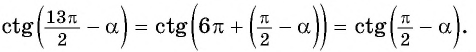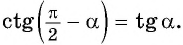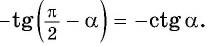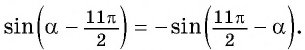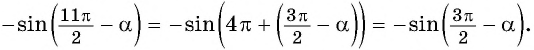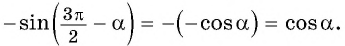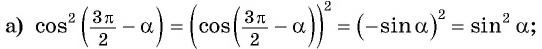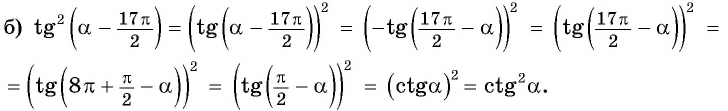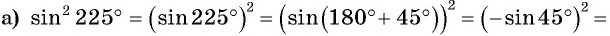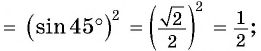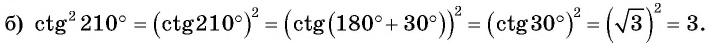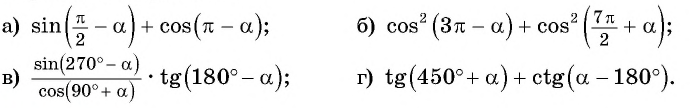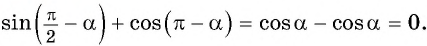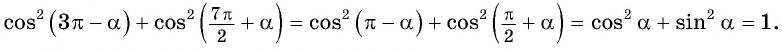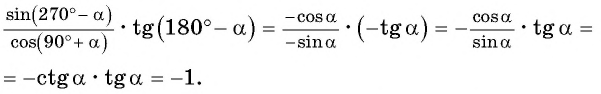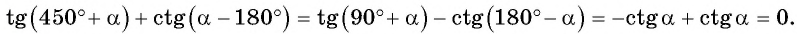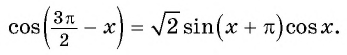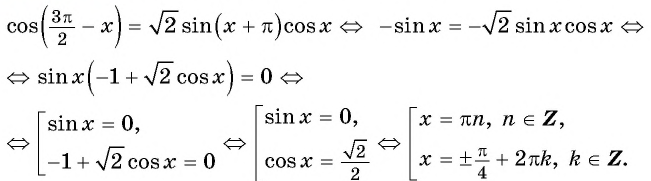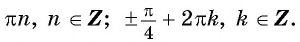Формулы приведения разработаны для углов, представленных в одном из следующих видов: (frac{pi}{2}+a), (frac{pi}{2}-a), (π+a), (π-a), (frac{3pi}{2}+a), (frac{3pi}{2}-a), (2π+a) и (2π-a). Аналогично их можно использовать для углов представленных в градусах: (90^°+a), (90^°-a), (180^°+a), (180^°-a), (270^°+a), (270^°-a), (180^°+a), (180^°-a). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
Как быстро получить любую формулу приведения
Для начала обратите внимание, что все формулы имеют похожий вид:

Здесь нужно пояснить термин «кофункция» – это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.
Функция: Кофункция:
(sin) (a) (→) (cos) (a)
(cos) (a) (→) (sin) (a)
(tg) (a) (→) (ctg) (a)
(ctg) (a) (→) (tg) (a)
Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс
или котангенс, он либо останется синусом, либо превратиться в косинус. А котангенс никогда не станет синусом или косинусом, он либо останется котангенсом, либо станет тангенсом. И так далее.
Едем дальше. Так как исходная функция и ее аргумент нам обычно даны, то весь вывод нужной формулы сводится к двум вопросам:
– как определить знак перед конечной функцией (плюс или минус)?
– как определить меняется ли функция на кофункцию или нет?
Как определить знак перед конечной функцией (плюс или минус)?
Какой знак был у исходной функции в исходной четверти, такой знак и нужно ставить перед конечной функцией.
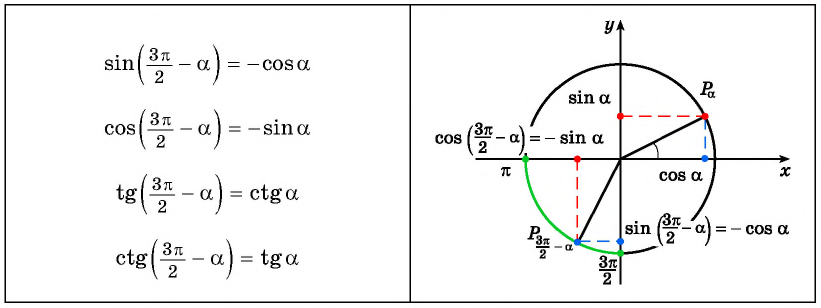
Например, выводим формулу приведения для (cos(frac{3pi}{2}-a) =….) С исходной функцией понятно – косинус, а исходная четверть?
Для того, чтобы ответить на этот вопрос, представим, что (a) – угол от (0) до (frac{pi}{2}), т.е. лежит в пределах (0°…90^°) (хотя это может быть не так, но для определения знака данная условность необходима). В какой четверти тригонометрической окружности при таком условии будет находиться точка, обозначающая угол (frac{3pi}{2}-a)?
Чтобы ответить на вопрос, надо от точки, обозначающей (frac{3pi}{2}), повернуть в отрицательную сторону на угол (a).

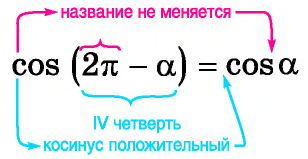
В какой четверти мы окажемся? В третьей. А какой же знак имеет косинус в третьей четверти? Минус. Поэтому перед итоговой функцией будет стоят минус: (cos(frac{3pi}{2}-a)=-…)
Менять ли функцию на кофункцию или оставить прежней?
Здесь правило еще проще:
– если «точка привязки» (frac{pi}{2}) ((90^°)) или (frac{3pi}{2}) ((270^°))– функция меняется на кофункцию;
– если «точка привязки» (π) ((180^°)) или (2π) ((360^°)) – функция остается той же.
То есть, при аргументах исходной функции (frac{pi}{2}+a), (frac{pi}{2}-a), (frac{3pi}{2}+a) или (frac{pi}{2}-a), мы должны поменять функцию, а при аргументах (π+a), (π-a), (2π+a) или (2π-a) – нет. Для того, чтоб это легче запомнить, вы можете воспользоваться мнемоническим правилом, которое в школе называют «лошадиным правилом»:
Точки, обозначающие (frac{pi}{2}) ((90^°)) и (frac{3pi}{2}) ((270^°)), расположены вертикально, и если вы переводите взгляд с одной на другую и назад, вы киваете головой, как бы говоря «да».

Точки же, обозначающие (π) ((180^°)) и (2π) ((360^°)), расположены горизонтально, и если вы переводите взгляд между ними, вы мотаете головой, как бы говоря «нет».

Эти «да» и «нет» – и есть ответ на вопрос: «меняется ли функция?».
Таким образом, согласно правилу, в нашем примере выше (cos(frac{3π}{2}-a)=…) косинус будет меняться на синус. В конечном итоге получаем, (cos(frac{3π}{2}-a)=-sin) (a). Это и есть верная формула приведения.
Примеры с формулами приведения:
Зачем нужны формулы привидения? Ну, например, они позволяют упрощать выражения или находить значения некоторых тригонометрических выражений без использования калькулятора.
Пример. (Задание из ЕГЭ) Найдите значение выражения (frac{18 cos {{41}^°} }{sin {{49}^°}})
Решение:
|
(frac{18 cos {{41}^°} }{sin{{49}^°}}=) |
Углы ({41}^°) и ({49}^°) нестандартные, поэтому «в лоб» без калькулятора вычислить непросто. Однако использовав формулы привидения, мы легко найдем правильный ответ. |
|
|
(=frac{18 cos {41^° }}{sin {({90}^°-{41}^°)}}=) |
Теперь применим к синусу формулу приведения:
(sin{(90^°-41^°)}=cos 41^° ) |
|
|
(=frac{18 cos {41^° }}{cos {{41}^°}}=) |
В числителе и знаменателе получились одинаковые косинусы. Сокращаем их. |
|
|
(= 18) |
Записываем ответ |
Ответ: (18)
Пример. Найдите значение выражения (frac{3 sin{(pi-a)}-cos(frac{pi}{2}+a) }{cos {(frac{3pi}{2}-a)}})
Решение:
|
(frac{3 sin{(pi-a)}-cos(frac{pi}{2}+a) }{cos {(frac{3pi}{2}-a)}}=) |
Рассмотрим первое слагаемое числителя: (sin(π-a)). Воспользуемся формулами приведения, выведя ее самостоятельно:
Таким образом, (sin(π-a)=sina) |
|
|
(=frac{3 sin{a}-cos(frac{pi}{2}+a) }{cos {(frac{3pi}{2}-a)}}=) |
Второе слагаемое числителя: (cos{(frac{π}{2} + a)}):
Таким образом, (cos{(frac{π}{2} + a)}=-sina) |
|
|
(=frac{3 sin{a}-(-sin{a}) }{cos {(frac{3pi}{2}-a)}}=) |
Теперь знаменатель: (cos(frac{3π}{2} – a)). Его мы разобрали выше, он равен минус синусу. (cos(frac{3π}{2} – a)=-sin{a}) |
|
|
(=frac{3 sin{a}-(-sin{a}) }{-sin {a}}=) |
Раскрываем скобки и приводим подобные слагаемые. |
|
|
(=frac{3 sin{a}+sin{a}}{-sin {a}}=frac{4sin{a}}{-sin{a}}) |
Сократив на (sin{a}), получаем ответ. |
|
|
(=frac{4 }{-1}=)(-4) |
Ответ: (-4)
Пример. Вычислить чему равен (ctg(-a-frac{7π}{2})), если (tg) (a=2)
Решение:
|
(ctg(-a-frac{7π}{2}) =) |
Здесь сразу формулу приведения применять нельзя, так как аргумент нестандартный. Что не так? Прежде всего, (a) стоит первой, хотя должна быть после «точки привязки». Поменяем местами слагаемые аргумента, сохраняя знаки. |
|
|
(= ctg(-frac{7π}{2}-a) =) |
Уже лучше, но все еще есть проблемы – «точка привязки» с минусом, а такого аргумента у нас нет. Избавимся от минуса, вынеся его за скобку внутри аргумента.
|
|
|
(= ctg(-(frac{7π}{2}+a)) =) |
Теперь вспомним о том, что котангенс – функция нечетная, то есть |
|
|
(= – ctg(frac{7π}{2}+a) =) |
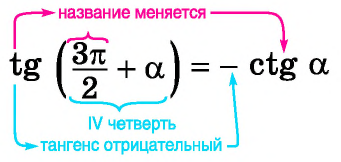
Несмотря на то, что точка привязки (frac{7π}{2}) мы все равно можем использовать формулы приведения, потому что (frac{7π}{2}) лежит на пересечении одной из осей и числовой окружности (смотри пояснение ниже). ((frac{7π}{2}+a)) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» – вертикальная, то есть функцию меняем. Окончательно имеем (ctg(frac{7π}{2}+a)=-tg a) . |
|
|
(= – (- tg) (a) = tg) (a = 2) |
Готов ответ. |
Ответ: (2)
Еще раз проговорим этот важный момент: с точки зрения формулы приведения (frac{7π}{2}) – это тоже самое, что и (frac{3π}{2}). Почему? Потому что (frac{7π}{2}=frac{3π+4π}{2}=frac{3π}{2}+frac{4π}{2}=frac{3π}{2}+2π). Иными словами, они отличаются ровно на один оборот (2π). А на значения тригонометрических функций количество оборотов никак не влияет:
(cos) (t=cos (t+2π)=cos (t+4π)=cos (t+6π)= …=cos (t-2π)=cos (t-4π)=cos (t-6π)…)
(sin) (t=sin (t+2π)=sin (t+4π)=sin (t+6π)= …=sin (t-2π)=sin (t-4π)=sin (t-6π)…)
Аналогично с тангенсом и котангенсом (только у них «оборот» равен (π)).
(tg) (t=tg(t+π)=tg(t+2π)=tg(t+3π)= …=tg(t-π)=tg(t-2π)=tg(t-3π)…)
(ctg) (t=ctg(t+π)=ctg(t+2π)=ctg(t+3π)= …=ctg(t-π)=ctg(t-2π)=ctg(t-3π)…)
Таким образом, (-ctg(frac{7π}{2}+a)=- ctg(frac{3π}{2}+2π+a)=- ctg(frac{3π}{2}+a)).
То есть, для определения знака и необходимости смены функции важно лишь местоположение «точки привязки», а не её значение, поэтому так расписывать не обязательно (но можно если вы хотите впечатлить своими знаниями учительницу).
Ответы на часто задаваемые вопросы
Вопрос: Есть ли формулы приведения с аргументами ((frac{π}{3}-a)),((frac{π}{4}+a)),((frac{7π}{6}+a)) или тому подобное?
Ответ: К сожалению, нет. В таких ситуациях выгодно использовать формулы разности и суммы аргументов. Например, (cos(frac{π}{3}-a)=cosfrac{π}{3} cosa+sinfrac{π}{3} sina=frac{1}{2}cosa+frac{sqrt{3}}{2} sina).
Смотрите также Как доказать тригонометрическое тождество?
$$ctg(pi-alpha)=-ctg(alpha);$$
Давайте вместо угла (alpha) возьмем какой-нибудь реальный угол. Суть от этого не изменится. Чтобы усложнить задачу, я не буду рисовать рисунок. Нарисуйте окружность сами и по пунктам сделайте пример.
Пример 7
$$cos(3pi+frac{pi}{6})=?;$$
- Угол ((3pi+frac{pi}{6})) лежит в третьей четверти. Действительно, (3pi=2pi+pi) можно представить как полный круг плюс еще половина;
- В третьей четверти косинус отрицательный. Знак минус;
- (3pi) лежит на горизонтальной оси в точке (C). Значит косинус не меняется на синус;
$$cos(3pi+frac{pi}{6})=-cos(frac{pi}{6})=-frac{sqrt{3}}{2};$$
До этого мы рассматривали примеры, когда угол (alpha) был острым. А что, если он больше (90^o)?
В этом случае нам придется сделать из него острый угол. Рассмотрим пример:
Пример 8
$$tg(frac{pi}{2}-frac{5pi}{6})=?;$$
Угол (frac{5pi}{6}) – тупой угол. Для того, чтобы воспользоваться формулой приведения, можно представить:
$$frac{5pi}{6}=pi-frac{pi}{6};$$
Подставим в исходный пример
$$tg(frac{pi}{2}-frac{5pi}{6})=tg(frac{pi}{2}-pi+frac{pi}{6})=tg(frac{pi}{6}-frac{pi}{2});$$
Угол (frac{pi}{6}) острый и теперь можно воспользоваться правилом лошади.
- ((frac{pi}{6}-frac{pi}{2})) лежит в четвертой четверти. Отмечаем (frac{pi}{6}) и по часовой стрелке вычитаем из него (frac{pi}{2});
- В четвертой четверти тангенс отрицательный;
- (frac{pi}{2}) лежит на вертикальной оси, тангенс меняется на котангенс;
$$tg(frac{pi}{2}-frac{5pi}{6})=tg(frac{pi}{6}-frac{pi}{2})=-ctg(frac{pi}{6})=-sqrt{3};$$
У любопытного читателя может возникнуть вопрос: а почему данный алгоритм называется правилом лошади? При чем тут, казалось бы, лошадь?
Лошадь, действительно, не при чем. Но дело в том, что когда вы определяете в третьем пункте, меняется ли наша тригонометрическая функция на противоположную или нет, то в случае, если дополнительный угол к (alpha) лежит на вертикальной оси, мы как бы смотрим вверх-вниз, киваем головой, как лошадь, говоря себе: «Да, меняем». Или если угол лежит на горизонтальной оси, то мы киваем влево вправо вдоль горизонтальной оси, как бы говоря: «Нет, не меняем». Такое вот странное название у правила.
Данная статья посвящена подробному изучению тригонометрических формул приведения. Дан полный список формул приведения, показаны примеры их использования, приведено доказательство верности формул. Также в статье дано мнемоническое правило, которое позволяет выводить формулы приведения, не запоминая каждую формулу.
Формулы приведения. Список
Фомулы приведения позволяют приводить основные тригонометрические функции углов произвольной величины к функциям углов, лежащих в интервале от 0 до 90 градусов (от 0 до π2 радиан). Оперировать углами от 0 до 90 градусов гораздо удобнее, чем работать со сколь угодно большими значениями, поэтому формулы приведения широко применяются при решении задач тригонометрии.
Прежде, чем мы запишем сами формулы, уточним несколько важных для понимания моментов.
- Аргументами тригонометрических функций в формулах приведения являются угды вида ±α+2π·z, π2±α+2π·z, 3π2±α+2π·z. Здесь z – любое целое число, а α – произвольный угол поворота.
- Не обязательно учить все формулы приведения, количество которых довольно внушительно. Существует мнемоническое правило, которо позволяет легко вывести нужную формулу. Речь о мнемоническом правиле пойдет позже.
Теперь перейдем непосредственно к формулам приведения.
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов. запишем все формулы в виде таблицы.
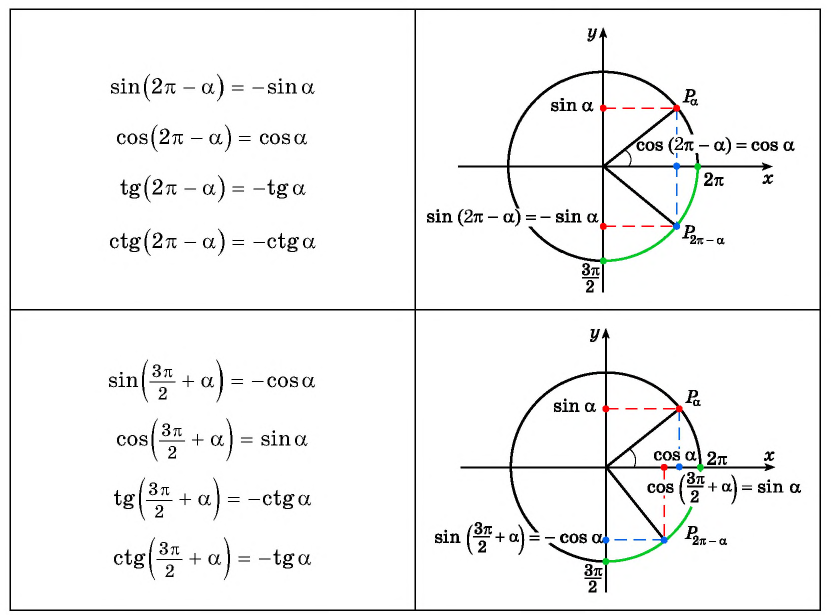
sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα
В данном случае формулы записаны с радианами. Однако можно записать их и с использованием градусов. Достаточно только перевести радианы в градусы, заменив π на 180 градусов.
Примеры использования формул приведения
Покажем, как пользоваться формулами приведения и как указанные формулы применяются при решении практических примеров.
Угол под знаком тригонометрической функции можно представить не одним, а множеством способов. Например, аргумент тригонометрической функции может быть представлен в видах ±α+2πz, π2±α+2πz, π±α+2πz, 3π2±α+2πz. Продемонстрируем это.
Возьмем угол α=16π3. Это угол можно записать так:
α=16π3=π+π3+2π·2α=16π3=-2π3+2π·3α=16π3=3π2-π6+2π
В зависимости от представления угла используется соответствующая формула приведения.
Возьмем тот же угол α=16π3 и вычислим его тангенс
α=16π3, tg α=?
Представим угол α=16π3 в виде α=π+π3+2π·2
Этому представлению угла будет соответствовать формула приведения
tg(π+α+2πz)=tg α
Получим
tg 16π3=tgπ+π3+2π·2=tgπ3
Воспользовавшись таблицей, укажем значение тангенса
tgπ3=3
Теперь используем другое представление угла α=16π3.
α=16π3, tg α=?α=-2π3+2π·3tg16π3=tg-2π3+2π·3=-tg2π3=-(-3)=3
Наконец, для третьего представления угла запишем
α=16π3=3π2-π6+2πtg3π2-α+2πz=ctg αtg α=tg (3π2-π6+2π)=ctgπ6=3
Теперь приведем пример на использование формул приведения посложнее
Представим sin 197° через синус и косинус острого угла.
Для того, чтобы можно было применять формулы приведения, нужно представить угол α=197° в одном из видов
±α+360°·z, 90°±α+360°·z, 180°±α+360°·z, 270°±α+360°·z. Согласно условию задачи, угол должен быть острым. Соответственно, у нас есть два способа для его представления:
197°=180°+17°197°=270°-73°
Получаем
sin197°=sin(180°+17°)sin197°=sin(270°-73°)
Теперь посмотрим на формулы приведения для синусов и выберем соответствующие
sin(π+α+2πz)=-sinαsin(3π2-α+2πz)=-cosαsin 197°=sin(180°+17°+360°·z)=-sin17°sin 197°=sin(270°-73°+360°·z)=-cos73°
Мнемоническое правило
Формул приведения много, и, к счастью, нет необходимости заучивать их наизусть. Существуют закономерности, по которым можно выводить формулы приведения для разных углов и тригонометрических функций. Эти закономерности называются мнемоническим правилом. Мнемоника – искусство запоминания. Мнемоническое правило состоит из трех частей, или содержит три этапа.
1. Аргумент исходной функции представляется в одном из видов
±α+2πzπ2±α+2πzπ±α+2πz3π2±α+2πz
Угол α должен лежать в пределах от 0 до 90 градусов.
2. Определяется знак исходной тригонометрической функции. Такой же знак будет иметь функция, записываемая в правой части формулы.
3. Для углов ±α+2πz и π±α+2πz название исходной функции остается неизменным, а для углов π2±α+2πz и 3π2±α+2πz соответственно меняется на “кофункцию”. Синус – на косинус. Тангенс – на котангенс.
Чтобы пользоваться мнемоническим праилом для формул приведения нужно уметь определять знаки тригонометрических функций по четвертям единичной окружности. Разберем примеры применения мнемонического правила.
Запишем формулы приведения для cosπ2-α+2πz и tgπ-α+2πz. α – улог первой четверти.
1. Так как по условию α – улог первой четверти, мы пропускаем первый пункт правила.
2. Определим знаки функций cosπ2-α+2πz и tgπ-α+2πz. Угол π2-α+2πz также является углом первой четверти, а угол π-α+2πz находится во второй четверти. В первой четверти функция косинуса положительна, а тангенс во второй четверти имеет знак минус. Запишем, как будут выглядеть искомые формулы на этом этапе.
cosπ2-α+2πz=+tgπ-α+2πz=-
3. Согласно третьему пункту для угла π2-α+2π название функции изменяется на конфуцию, а для угла π-α+2πz остается прежним. Запишем:
cosπ2-α+2πz=+sin αtgπ-α+2πz=-tg α
А теперь заглянем в формулы, приведенные выше, и убедимся в том, что мнемоническое правило работает.
Рассмотрим пример с конкретным углом α=777°. Приведем синус альфа к тригонометрической функции острого угла.
1. Представим углол α=777° в необходимом виде
777°=57°+360°·2777°=90°-33°+360°·2
2. Исходный угол – угол первой четверти. Значит, синус угла имеет положительный знак. В итоге имеем:
3. sin 777°=sin(57°+360°·2)=sin 57°sin 777°=sin(90°-33°+360°·2)=cos 33°
Теперь рассмотрим пример, который показывает, как важно правильно определить знак тригонометрической функции и правильно представить угол при использовании мнемонического правила. Повторим еще раз.
Угол α должен быть острым!
Вычислим тангенс угла 5π3. Из таблицы значений основных тригонометрических функций можно сразу взять значение tg 5π3=-3, но мы применим мнемоническое правило.
tg 5π3=?
Представим угол α=5π3 в необходимом виде и воспользуемся правилом
tg 5π3=tg3π2+π6=-ctgπ6=-3tg 5π3=tg2π-π3=-tgπ3=-3
Если же представить угол альфа в виде 5π3=π+2π3, то результат применениея мнемонического правила будет неверным.
tg 5π3=tgπ+2π3=-tg2π3=-(-3)=3
Неверный результат обусловлен тем, что угол 2π3 не явдяется острым.
Формулы приведения. Доказательство
Доказательство формул приведения основывается на свойствах периодичности и симметричности тригонометрических функций, а также на свойстве сдвига на углы π2 и 3π2. Доказательство справедливости всех формул приведения иожно проводить без учета слагаемого 2πz, так как оно обозначает изменение угла на целое число полных оборотов и как раз отражает свойство периодичности.
Первые 16 формул следуют напрямую из свойств основных тригонометрических функций: синуса, косинуса, тангенса и котанганса.
Приведем доказательство формул приведения для синусов и косинусов
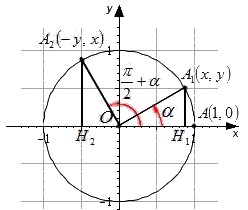
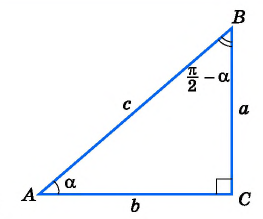
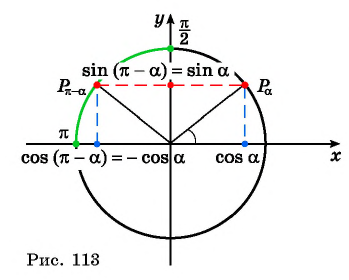
sinπ2+α=cos α и cosπ2+α=-sin α
Посмотрим на единичную окружность, начальная точка которой после повоторота на угол α перешла в точку A1x, y, а после поворота на угол π2+α – в точку A2. Из обеих точек проведем перпендикуляры к оси абсцисс.
Два прямоугольных треугольника OA1H1 и OA2H2 равны по гипотенузе и прилежащим к ней углам. Из расположения точек на окружности и равенства треугольников можно сделать вывод о том, что точка A2 имеет координаты A2-y, x. Используя определения синуса и косинуса, запишем:
sin α=y, cosα=x, sinπ2+α=x, cosπ2+α=y
Отсюда
sinπ2+α=cos α, cosπ2+α=-sinα
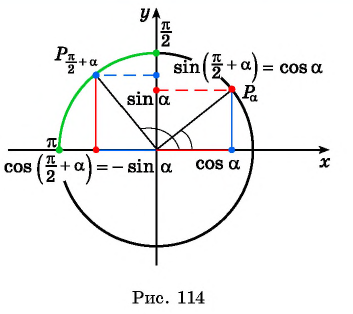
С учетом основных тождеств тригонометрии и только что доказанного, можно записать
tgπ2+α=sinπ2+αcosπ2+α=cos α-sin α=-ctg αctgπ2+α=cosπ2+αsinπ2+α=-sin αcosα=-tg α
Для доказательства формул приведения с аргументом π2-α его необходимо представить в виде π2+(-α). Например:
cosπ2-α=cosπ2+(-α)=-sin(-α)=sinα
В доказательстве используются свойства тригонометрических функций с аргументами, противоположными по знаку.
Все остальные формулы приведения можно доказать на базе записанных выше.
При изучении геометрии вы установили, что
если
Свойство периодичности тригонометрических функций позволяет свести вычисление значений синуса, косинуса, тангенса и котангенса произвольного угла к вычислению значений этих функций при значениях аргумента, принадлежащих промежутку 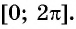
На практике принято сводить значения тригонометрических функций произвольного угла к вычислению значений этих функций для угла, принадлежащего промежутку 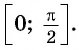
Это можно делать с помощью формул приведения.
Рассмотрим промежуток 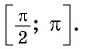
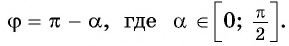
Например,
Поскольку ординаты точек 
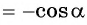
Тогда для 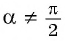
А для 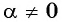
Вместе с тем любое число 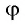
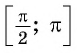
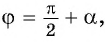
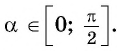
Так как ордината точки 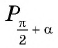
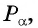
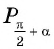
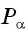
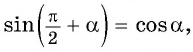
Для 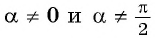
Так как любое число 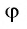
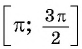
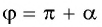
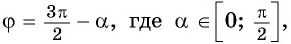
Поскольку любое число 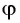
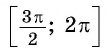
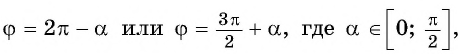
Проанализировав полученные формулы, можно заметить закономерности, позволяющие сформулировать правило, с помощью которого можно применять формулы приведения, не заучивая их:
В правой части формулы приведения ставится тот знак, который имеет в соответствующей четверти исходная функция, если считать, что угол 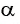
Если в формуле приведения аргумент имеет вид:
-
то название функции не меняется;
-
то название функции меняется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
Например, применим полученное правило для выражения
- Если считать, что угол
— острый, то —
— угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».
- Поскольку аргумент имеет вид
то название функции «косинус» нужно поменять на «синус». Таким образом, получим:
Пример:
Приведите выражение к тригонометрической функции числа 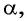
Решение:
Применим правило:
а) 1. Так как 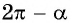
2. Поскольку аргумент имеет вид 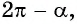
б) 1. Так как 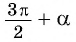
2.Поскольку аргумент имеет вид 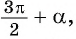
в) 1. Так как 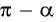
2. Поскольку аргумент имеет вид 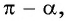
Пример:
Используйте формулы приведения и найдите значение выражения:
Решение:
Первый способ:
- Так как
угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».
- Поскольку аргумент имеет вид
то название функции «синус» не меняется. Значит,
Второй способ:
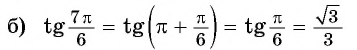
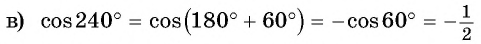
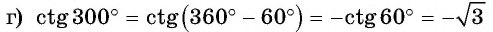
- Заказать решение задач по высшей математике
Пример:
Вычислите, используя формулы приведения:
Решение:
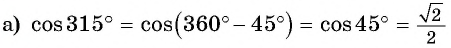
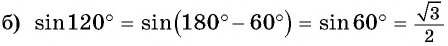

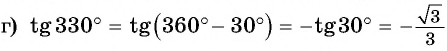
Пример:
Найдите значение выражения:
Решение:
а) Так как синус — нечетная функция, то
Применим формулы приведения:
б) Воспользуемся свойством четности косинуса и получим:
По формулам приведения:
в) Воспользуемся свойством периодичности тангенса и получим:
Применим формулы приведения:
г) Поскольку котангенс — нечетная функция, то
Используем свойство периодичности котангенса и получим:
Пример:
По формулам приведения:
Приведите к тригонометрической функции угла
Решение:
а) Используем свойство периодичности косинуса и получим:
По формулам приведения:
б) Воспользуемся свойством периодичности котангенса:
Применим формулы приведения:
в) Так как тангенс — нечетная функция, то 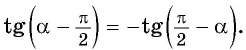
г) Поскольку синус — нечетная функция, то
Воспользуемся свойством периодичности синуса и получим:
По формулам приведения:
Пример:
Приведите к тригонометрической функции угла 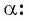
Решение:
Пример:
Вычислите:
Решение:
Пример:
Упростите выражение:
Решение:
а) Применим формулы приведения:
б)Воспользуемся периодичностью косинуса и формулами приведения и получим:
в)Применим формулы приведения:
г) Используем периодичность тангенса, нечетность котангенса и формулы приведения:
Пример:
Решите уравнение:
Решение:
Применим формулы приведения и получим:
Ответ:
- Синус, косинус, тангенс суммы и разности
- Формулы двойного аргумента
- Формулы преобразования суммы и разности синусов (косинусов) в произведение
- Корень n-й степени из числа и его свойства
- Функции y=tg x и y=ctg x – их свойства, графики
- Арксинус, арккосинус, арктангенс и арккотангенс числа
- Тригонометрические уравнения
- Тригонометрические неравенства
Определение. Формулами приведения называют формулы, которые позволяют перейти от тригонометрических функций вида к функциям аргумента
. С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до
радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.
Формулы приведения:
Для использования формул приведения существует два правила.
1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то название функции остается без изменений.
Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет
2. Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».
На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.
Пример:
Вычислить
Воспользуемся формулами приведения:
Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен “+”. Значит у приведенной функции тоже будет знак «+». Это мы применили второе правило.
Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.
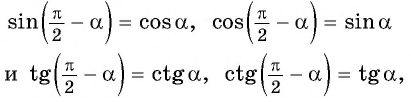
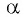
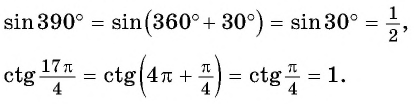
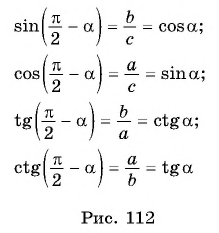
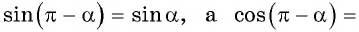
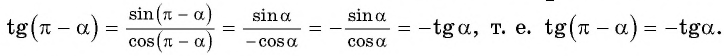
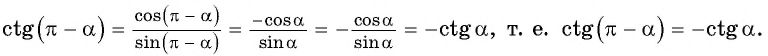
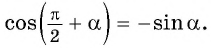
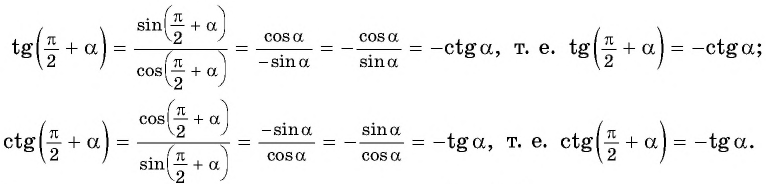
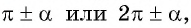 то название функции не меняется;
то название функции не меняется;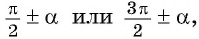 то название функции меняется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).
то название функции меняется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс).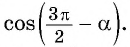
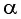 — острый, то —
— острый, то — 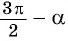 — угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».
— угол третьей четверти. В третьей четверти косинус (исходная функция) отрицательный, значит, в правой части равенства нужно поставить знак «минус».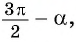 то название функции «косинус» нужно поменять на «синус». Таким образом, получим:
то название функции «косинус» нужно поменять на «синус». Таким образом, получим: 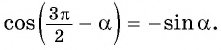
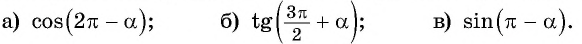
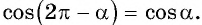
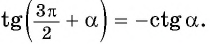
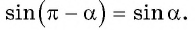

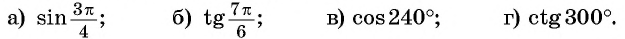
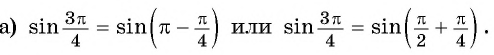
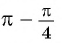 угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».
угол второй четверти, в которой синус положительный, то в правой части равенства не нужно ставить знак «минус».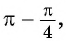 то название функции «синус» не меняется. Значит,
то название функции «синус» не меняется. Значит,